03/12/2010
Kurt Gödel und die mathematische Logik, Volume 5 Par Werner DePauli-Schimanovich
07:00 Publié dans Kurt Gödel und die mathematische Logik | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Théorie des nombres, Volume 1 Par Adrien Marie Legendre
06:56 Publié dans Théorie des nombres, Théorie des nombres, Volume 1 Par Adrien Marie Leg | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Nombres premiers et décomposition en produit de facteurs premiers
Théorie des nombres -- Nombres premiers Source : http://www.bibmath.net/dico/index.php3?action=affiche&...
Théorie des nombres -- Factorisation
Un nombre entier p positif supérieur strict à 1 est dit premier s'il n'admet que 2 diviseurs positifs : 1 et p (remarquons que 1 n'est pas premier). Dans le cas contraire, cet entier est dit composé.
Ex : 7 est premier. 24 est composé : 2 divise 24.
Ex : 24=23×3.
06:53 Publié dans Nombres premiers et décomposition en produit | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Nombres p-adiques
Théorie des nombres
Algèbre -- Anneaux
Algèbre -- Corps
Analyse -- Topologie -- Vocabulaire général
|.|p est une norme sur Q, avec des propriétés très différentes de la valeur absolue. Par exemple,
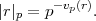


| Définition : Le corps des nombres p-adiques, noté Qp, est le complété de Q pour la norme p-adique. |
Source : http://www.bibmath.net/dico/index.php3?action=affiche&...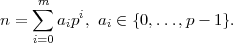 La suite (ai) est définie par
La suite (ai) est définie par
Les nombres p-adiques sont ceux qui s'écrivent modulo p.
modulo p.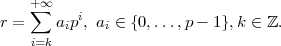 Cette série est convergente pour la distance p-adique. L'écriture précédente s'appelle décomposition de Hensel de r. Finalement, l'ensemble des entiers p-adiques, noté Zp, est l'ensemble des r de Qp s'écrivant
Cette série est convergente pour la distance p-adique. L'écriture précédente s'appelle décomposition de Hensel de r. Finalement, l'ensemble des entiers p-adiques, noté Zp, est l'ensemble des r de Qp s'écrivant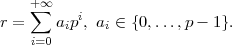 C'est un sous-anneau de Qp.
C'est un sous-anneau de Qp. Les nombres p-adiques ont été introduits par Hensel en 1897. Son idée était de pouvoir utiliser la théorie des séries entières en arithmétique. Depuis, toute une branche des mathématiques, l'analyse p-adique, s'est développée sur ses idées.
Les nombres p-adiques ont été introduits par Hensel en 1897. Son idée était de pouvoir utiliser la théorie des séries entières en arithmétique. Depuis, toute une branche des mathématiques, l'analyse p-adique, s'est développée sur ses idées.
06:51 Publié dans Nombres p-adiques | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Adhérence (mathématiques)
En topologie, l'adhérence d'une partie d'un espace topologique est le plus petit ensemble fermé contenant cette partie. On retrouve cette notion particulièrement dans la convergence de suites dans les espaces métriques avec la notion de valeur d'adhérence.Adhérence (mathématiques)
![]() Pour les articles homonymes, voir Adhérence.
Pour les articles homonymes, voir Adhérence.
Sommaire[masquer] |
En topologie, l'adhérence d'une partie X d'un espace topologique E est le plus petit ensemble fermé de E qui contienne X. L'existence d'un tel fermé est claire : il existe au moins un fermé contenant X, à savoir l'espace E lui-même ; d'autre part, l'intersection de tous les fermés contenant X est un fermé contenant X, et est le plus petit ayant cette propriété. L'adhérence de X est aussi appelée fermeture de X et se note souvent On dit d'un point x de E qu'il est adhérent à X lorsque tout voisinage de x rencontre X. L'adhérence de X est égale à l'ensemble des points qui lui sont adhérents. En effet : Intuitivement, l'adhérence d'une partie X contient tous les points de l'espace qui sont dans X ou qui sont trop près de X pour que l'on puisse y « bricoler » localement sans toucher à X. Dans un espace métrique (la topologie est issue d'une distance sur l'espace considéré), l'adhérence d'un ensemble X de E est l'ensemble contenant toutes les limites de suitesconvergentes dans E et formées des éléments de X. Caractère archimédien de L'adhérence d'un intervalle de Assez souvent on parle de On dit qu'une partie X d'un espace topologique E est dense lorsque son adhérence est l'espace E tout entier. Une telle partie se caractérise donc par le fait que tout ouvert non vide en contient un point. Ainsi, le caractère archimédien de Un point x de X est dense si {x} est dense. On l'appelle parfois aussi point générique. Intuitivement, les parties denses d'un espace sont donc des parties qui sont très grosses : on ne peut pas les éviter. Dans un espace métrique, on définit des boules ouvertes et des boules fermées, et la tentation est grande d'utiliser Néanmoins, c'est faux en général ; voyons l'exemple le plus simple : soit un ensemble E, avec au moins deux éléments. On définit une métrique dessus ainsi : la distance entre deux points distincts est 1. La boule ouverte de rayon 1 centrée en un point est donc ce point. La boule fermée de rayon 1 centrée en un point est donc l'espace entier. L'adhérence de la boule ouverte de rayon 1 centrée en un point est le point. Si dans le cadre d'espaces vectoriels sur Considérons l'ensemble Dans ce cas, l'adhérence de {0} est l'espace NB : en géométrie algébrique, ce genre de situation est très courant, car l'espace de base, le spectre d'anneau, vérifie souvent ce genre de propriétés ; en fait, cet exemple esthoméomorphe à Définitions [modifier]
 .
.Caractérisations [modifier]
Ensemble des points adhérents [modifier]
 , car celui-ci serait alors un voisinage de x ne rencontrant pas X ; donc il appartient à
, car celui-ci serait alors un voisinage de x ne rencontrant pas X ; donc il appartient à 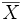 .
.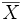 . Puisque x est dans U, x n'est pas dans
. Puisque x est dans U, x n'est pas dans 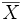 .
.Espaces métriques et suites [modifier]
Exemples [modifier]
 : l'ensemble des réels
: l'ensemble des réels  est l'adhérence de l'ensemble des rationnels
est l'adhérence de l'ensemble des rationnels  . En effet, tout ouvert contenant un irrationnel contient un rationnel. Tout irrationnel est donc dans l'adhérence de
. En effet, tout ouvert contenant un irrationnel contient un rationnel. Tout irrationnel est donc dans l'adhérence de  .
. , c'est l'intervalle fermé de mêmes bornes : l'adhérence de
, c'est l'intervalle fermé de mêmes bornes : l'adhérence de ![]-infty,a[](http://upload.wikimedia.org/math/1/c/5/1c5b9412c130c8defab790b16ed84156.png) est l'intervalle
est l'intervalle ![]-infty,a]](http://upload.wikimedia.org/math/8/0/8/808c7c08c83f0fc314006726dbc75c22.png) .
.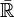 comme adhérence de
comme adhérence de  , mais cette notion veut simplement dire qu'on étend la notion de convergence aux valeurs infinies : ainsi la suite des entiers converge dans
, mais cette notion veut simplement dire qu'on étend la notion de convergence aux valeurs infinies : ainsi la suite des entiers converge dans 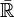 vers
vers  . Cela permet de donner un sens différent à la notion de divergence : ce qui diverge n'admet pas de limite, fût elle infinie. C'est le concept de droite réelle achevée.
. Cela permet de donner un sens différent à la notion de divergence : ce qui diverge n'admet pas de limite, fût elle infinie. C'est le concept de droite réelle achevée.Densité [modifier]
 fait que
fait que 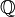 est dense dans
est dense dans  .
.Pièges [modifier]
Boules ouvertes et boules fermées [modifier]
 dans ce cadre. Il est vrai que dans un certain nombre de cas, cela marche bien, notamment les
dans ce cadre. Il est vrai que dans un certain nombre de cas, cela marche bien, notamment les  avec la distance usuelle, et plus généralement pour la distance
avec la distance usuelle, et plus généralement pour la distance 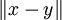 dans un espace vectoriel normé...
dans un espace vectoriel normé... ou
ou  normés de dimension finie, les propriétés de l'adhérence restent assez intuitives, il faut aussi se méfier des caractéristiques des espaces de dimension infinie.
normés de dimension finie, les propriétés de l'adhérence restent assez intuitives, il faut aussi se méfier des caractéristiques des espaces de dimension infinie.Un point c'est petit [modifier]
 des entiers naturels. On y définit une topologie (via des fermés) de la façon suivante :
des entiers naturels. On y définit une topologie (via des fermés) de la façon suivante :
 tout entier, ce qui signifie qu'on ne peut pas mettre le point 0 de côté pour travailler au voisinage d'un autre point. C'est un point dense/générique.
tout entier, ce qui signifie qu'on ne peut pas mettre le point 0 de côté pour travailler au voisinage d'un autre point. C'est un point dense/générique. par simple substitution des nombres premiers aux entiers non nuls.
par simple substitution des nombres premiers aux entiers non nuls.Voir aussi [modifier]
06:49 Publié dans Adhérence (mathématiques) | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
02/12/2010
Glossaire de topologie
Ceci est un glossaire de quelques termes utilisés en topologie. Ce glossaire est divisé en deux parties. La première traite des concepts généraux, et la seconde liste différents types d'espaces topologiques. Dans ce glossaire, tous les espaces sont supposés topologiques.Glossaire de topologie
Sommaire[masquer] |
Accessible : voir l'axiome de séparation T1. Adhérence Base ou base d'ouverts Base de voisinages : voir Système fondamental de voisinages. Boule Cauchy : voir Suite de Cauchy. Compact : voir les axiomes de recouvrement. Complet Complètement de Hausdorff : voir l'axiome de séparation T2½. Complètement normal : voir l'axiome de séparation T5. Complètement régulier : voir l'axiome de séparation T3½. Composante connexe Connexe, connexe par arcs : voir les notions de connexité. Continu Contractile : voir les notions de connexité. Convergent Dense Dérivé Discontinu Discret Distance Engendrée : voir Topologie engendrée. Espace de Fréchet Espace de Hausdorff : voir l'axiome de séparation T2. Espace de Kolmogorov : voir l'axiome de séparation T0. Espace de Tychonoff : voir l'axiome de séparation T3½. Espace métrique Espace polonais Espace topologique Faiblement normal : voir les axiomes de séparation. Fermé Fermeture : voir Adhérence. Filtre : Un filtre sur un ensemble E est un ensemble non vide de parties non vides de E qui est stable par sur-parties et intersections finies. Dans un espace topologique, les voisinages d'un point forment un filtre. Fin Fonctionnellement séparés Fréchet : voir l'axiome de séparation T1, ou le type d'espace vectoriel topologique dit de Fréchet. Frontière Fσ : Une partie d'un espace topologique est un Fσ si c'est une réunion dénombrables de fermés. Gδ : Une partie d'un espace topologique est un Gδ si c'est une intersection dénombrables d'ouverts. Grossière : voir Topologie grossière. Hausdorff : : voir l'axiome de séparation T2 ou Séparé. Homéomorphisme Homogène Homotopie Induite : voir Topologie induite. Intérieur Isolé : voir Point isolé. Kolmogorov : voir l'axiome de séparation T0 ou Espace de Kolmogorov. Limite Lindelöf : voir l'axiome de recouvrement Espace de Lindelöf. Localement : voir Propriété locale. Maigre Métrique : voir Espace métrique. Métrisable Moins fine : voir Topologie moins fine. Normal : voir les axiomes de séparation. Ouvert Paracompact : voir les axiomes de recouvrement. Parfait Parfaitement normal : voir les axiomes de séparation. Partition de l'unité Plus fine : voir Topologie plus fine. Point d'accumulation Point isolé Polonais : voir Espace polonais. Prébase Produit : voir Topologie produit. Quasi-compact : voir les axiomes de recouvrement. Quotient Raffinement Rare Recouvrement Relativement compact Régulier : voir l'axiome de séparation T3. Séparable Séparant Séparé : voir l'axiome de séparation T2. Simplement connexe : voir les notions de connexité. Sous-recouvrement Système fondamental de voisinages Suite de Cauchy T0, T1, T2, T2½, T3, T3½, T4, T5 : voir les axiomes de séparation. Topologie Topologie discrète Topologie engendrée Topologie grossière Topologie induite Topologie moins fine Topologie plus fine Topologie produit C'est la topologie la moins fine rendant continues toutes les projections Topologie quotient Topologique : voir Espace topologique. Totalement discontinu : voir les notions de connexité. Tychonoff : voir l'axiome de séparation T3½ ou Complètement régulier. Uniformisable : dont la topologie est induite par une structure d'espace uniforme ; voir l'axiome de séparation T3½ ou Complètement régulier. Valeur d'adhérence Voisinage Les espaces topologiques peuvent être qualifiés de différentes manières en termes de séparation, de recouvrements ou de connexité. Certains des termes employés ici peuvent avoir été définis autrement dans la littérature ancienne (voir l'histoire des axiomes de séparation). T0 ou de Kolmogorov : dans lequel pour tout couple de points distincts, il existe un voisinage de l'un qui ne contient pas l'autre. T1 ou accessible ou de Fréchet : dont tous les singletons sont fermés. T2 ou de Hausdorff ou séparé : dans lequel deux points distincts admettent toujours des voisinages disjoints. T2½ ou complètement de Hausdorff : dans lequel deux points distincts admettent toujours des voisinage fermés disjoints. Régulier : séparé et dont tout point admet une base de voisinages fermés. Complètement régulier ou de Tychonoff : séparé et uniformisable, ou encore : sous-espace d'un compact. Faiblement normal : complètement régulier et dans lequel deux ouverts disjoints quelconques ont deux voisinages fermés disjoints dont l'un est à base dénombrable. Normal : séparé et dans lequel deux fermés disjoints quelconques possèdent toujours des voisinages disjoints. Le lemme d'Urysohn garantit alors que ces deux fermés sontfonctionnellement séparés. Complètement normal : dont tout sous-espace est normal. Parfaitement normal : séparé et dont tout fermé est le lieu d'annulation d'une fonction continue réelle. Les axiomes de recouvrement traitent de l'existence de raffinements ou de sous-recouvrements particuliers pour un recouvrement quelconque de l'espace considéré. Paracompact : espace séparé dont tout recouvrement ouvert admet un raffinement localement fini. Lindelöf : dont tout recouvrement ouvert admet un sous-recouvrement dénombrable. Quasi-compact : dont tout recouvrement ouvert admet un sous-recouvrement fini. Compact : quasi-compact et séparé. σ-compact ou sigma-compact : recouvert par une famille dénombrable de parties compactes. Localement compact : séparé, et dont chaque point admet un système fondamental de voisinages compacts. Séquentiellement compact : dans lequel toute suite admet au moins une valeur d'adhérence. Les hypothèses de connexité décrivent la cohésion de l'espace ou de certains voisinages, ou l'existence de déformations (homotopies) entre certaines applications continues vers l'espace considéré. Connexe : qui n'est pas l'union disjointe de deux ouverts non vides. Localement connexe : dont chaque point admet un système fondamental de voisinages connexes. Totalement discontinu : dont les seules parties connexes sont les singletons. Connexe par arcs : dont tout couple de points (x,y) est relié par un chemin (ou arc), c'est-à-dire une application continue Localement connexe par arcs : dont chaque point admet un système fondamental de voisinages connexes par arcs. Simplement connexe : connexe par arcs et dans lequel toute application continue Contractile : pour lequel l'application identité de X est homotope à une application constante.Généralités [modifier]
A [modifier]
B [modifier]
C [modifier]
D [modifier]
 satisfaisant les propriétés suivantes :
satisfaisant les propriétés suivantes :
 .
.E [modifier]
F [modifier]
L'ensemble vide et l'espace sont donc des fermés. L'union de deux fermés est un fermé et l'intersection d'une famille quelconque de fermés est un fermé.G [modifier]
H [modifier]
 est une application continue
est une application continue ![H : Xtimes [0,1] to Y](http://upload.wikimedia.org/math/e/9/0/e90fbf798237734541171ebfcd412898.png) telle que
telle que  . Les applications f et g sont alors dites homotopes.
. Les applications f et g sont alors dites homotopes.I [modifier]
K [modifier]
L [modifier]
M [modifier]
N [modifier]
O [modifier]
P [modifier]
Q [modifier]
R [modifier]
 est un recouvrement dont chaque élément est inclus dans un élément de
est un recouvrement dont chaque élément est inclus dans un élément de  .
.S [modifier]
 de voisinages de ce point tel que tout autre voisinage de ce point contient un élément de
de voisinages de ce point tel que tout autre voisinage de ce point contient un élément de  .
.T [modifier]
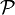 de parties d'un ensemble est celle dont les ouverts sont les réunions quelconques d'intersections finies d'éléments de
de parties d'un ensemble est celle dont les ouverts sont les réunions quelconques d'intersections finies d'éléments de 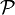 . L'ensemble
. L'ensemble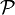 constitue une prébase de la topologie engendrée.
constitue une prébase de la topologie engendrée.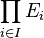 est la topologie engendrée par les
est la topologie engendrée par les  où un nombre fini d'éléments Ui sont des ouverts des espaces topologiques correspondants et les autres sont les espaces Ei correspondants.
où un nombre fini d'éléments Ui sont des ouverts des espaces topologiques correspondants et les autres sont les espaces Ei correspondants.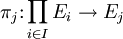 .
. une relation d'équivalence sur E, la topologie quotient sur l'ensemble quotient
une relation d'équivalence sur E, la topologie quotient sur l'ensemble quotient  est l'ensemble des parties de
est l'ensemble des parties de  dont lespréimages sont des ouverts de E. C'est la topologie la plus fine rendant continue la projection canonique, qui à tout élément de E associe sa classe d'équivalence..
dont lespréimages sont des ouverts de E. C'est la topologie la plus fine rendant continue la projection canonique, qui à tout élément de E associe sa classe d'équivalence..U [modifier]
V [modifier]
Propriétés d'espaces topologiques [modifier]
Axiomes de séparation [modifier]
Axiomes de recouvrement [modifier]
Connexité [modifier]
![p:[0,1]to X](http://upload.wikimedia.org/math/c/2/9/c2908a2ef3893f387f5f8042ee82d2b9.png) telle que p(0) = x et p(1) = y.
telle que p(0) = x et p(1) = y. est homotope à une application constante.
est homotope à une application constante.
21:39 Publié dans Glossaire, Glossaire de topologie | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Transformation géométrique
Catégorie:Transformation géométrique
Articles dans la catégorie « Transformation géométrique »
| Outils : Arborescence de la catégorie (graphique) Recherches : Recherche interne • avec CatScan (requêtes simples) |
Cette catégorie contient les 45 pages suivantes.
21:38 Publié dans Transformation géométrique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Transformation géométrique
On appelle transformation géométrique, toute bijection d'une partie d'un ensemble géométrique dans lui-même. On peut tenter une ou des classifications de ces transformations. D'abord selon la dimension de l'ensemble géométrique ; on distinguera donc principalement les transformations planes et les transformations dans l'espace. On peut aussi classer les transformations d'après leurs éléments conservés : Chacune de ces classes contient la précédente.Transformation géométrique
![]() Pour les articles homonymes, voir Transformation.
Pour les articles homonymes, voir Transformation.
| image de départ | isométrie | similitude |
 |
 |
 |
| transformation affine | transformation homographique | inversions |
Et enfin, englobant les précédentes :
 |
 |
 |
 |
| transformation conforme | transformation équivalente | difféomorphisme | homéomorphisme |
On crée alors des groupes et des sous-groupes de transformations. L'étude de la géométrie est en grande partie l'étude de ces transformations. Il existe aussi des transformations qui ne sont pas définies dans le plan ou l'espace tout entier. Parmi celles-ci on peut citer les inversions, les homologies qui sont des transformations homographiquesClassification non exhaustive des transformations selon leur degré de complexité [modifier]
21:37 Publié dans Transformation géométrique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Transformation géométrique
Catégorie:Transformation géométrique
Articles dans la catégorie « Transformation géométrique »
| Outils : Arborescence de la catégorie (graphique) Recherches : Recherche interne • avec CatScan (requêtes simples) |
Cette catégorie contient les 45 pages suivantes.
21:37 Publié dans Transformation géométrique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Transformation géométrique
Catégorie:Transformation géométrique
Articles dans la catégorie « Transformation géométrique »
| Outils : Arborescence de la catégorie (graphique) Recherches : Recherche interne • avec CatScan (requêtes simples) |
Cette catégorie contient les 45 pages suivantes.
21:35 Publié dans Transformation géométrique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Groupe diédral
En mathématiques, le groupe diédral noté Dn, pour Groupe diédral
 , ou parfois D2n, est un groupe d'ordre 2n qui s'interprète notamment comme le groupe des isométries du plan conservant un polygone régulier à n côtés. Le groupe est constitué de n éléments correspondant aux rotationset n autres correspondant aux réflexions. Le groupe D1 est le groupe cyclique d'ordre 2, noté C2 ; le groupe D2 est le groupe de Klein à quatre éléments. Parmi les groupes diédraux Dn, ce sont les deux seuls à être abéliens.
, ou parfois D2n, est un groupe d'ordre 2n qui s'interprète notamment comme le groupe des isométries du plan conservant un polygone régulier à n côtés. Le groupe est constitué de n éléments correspondant aux rotationset n autres correspondant aux réflexions. Le groupe D1 est le groupe cyclique d'ordre 2, noté C2 ; le groupe D2 est le groupe de Klein à quatre éléments. Parmi les groupes diédraux Dn, ce sont les deux seuls à être abéliens.
Sommaire[masquer] |
Le groupe Dn peut être défini par la suite exacte scindée suivante : où Cn est un groupe cyclique d'ordre n, C2 est cyclique d'ordre 2, la section étant donnée par l'action d'un relevé σ du générateur de C2, sur un générateur τ du groupe cyclique d'ordre n : Ce groupe est donc produit semi-direct de Cn par C2 suivant le morphisme ψ, où l'unité de C2 agit sur Cn comme l'application identique et l'autre élément de C2 agit sur Cn par inversion. Explicitement: Une présentation est alors : Plus explicitement les générateurs sont des σ, τ et les relations qu'ils vérifient sont de la forme : On peut ainsi dresser une liste complète des éléments du groupe : Une présentation alternative, où μ = τσ dans le système de générateurs de la présentation précédente, est : Plus explicitement les générateurs sont des σ, μ et les relations qu'ils vérifient sont de la forme : On voit ainsi que le groupe diédral admet un système de deux générateurs distincts tous deux d'ordre 2. Les groupes diédraux sont les seuls groupes finis possédant cette propriété1. Le groupe diédral d'ordre 2n peut aussi être vu comme le groupe d'automorphisme du graphe constitué seulement d'un cycle avec n sommets (si n ≥ 3). On peut définir de la façon suivante une représentation du groupe diédral Dn : avec On reconnaît que la matrice φ(τ) est une matrice de rotation d'angle Les graphes de cycles de groupes diédraux sont constitués d'un cycle à n éléments et de cycles à 2 éléments. Le sommet sombre dans les graphes de cycle ci-dessous de divers groupes diédraux représente l'élément identité, et les autres sommets sont les autres éléments du groupe. Un cycle est constitué des puissances successives de l'un ou l'autre élément connecté à l'élément identité. Présentation et définitions équivalentes [modifier]
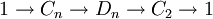
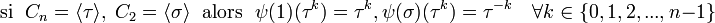 .
.
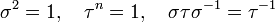 .
.

 .
.Interprétation géométrique [modifier]
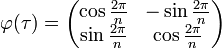 et
et  . Cette représentation est en fait à valeurs dans le groupe
. Cette représentation est en fait à valeurs dans le groupe 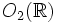 .
. , et la matrice φ(σ) une matrice de réflexion. Ces transformations laissent effectivement invariant le polygone régulier centré en l'origine à n côtés.
, et la matrice φ(σ) une matrice de réflexion. Ces transformations laissent effectivement invariant le polygone régulier centré en l'origine à n côtés.Graphe de cycle [modifier]
| D2 | D3 | D4 | D5 | D6 | D7 |
|---|
Le sous-ensemble des rotations Certaines propriétés des groupes diédraux Dn avec n ≥ 3 dépendent de la parité de n. Elles peuvent souvent facilement être déduites de la représentation géométrique de ce groupe. où D2n est l'ensemble de départ Dn*C2 celui d'arrivée, h et ε étant définis modulo 2, et k modulo n. Les générateurs des groupes diédraux sont choisis comme dans la première partie de l'article. Si n est impair, le groupe Dn admet 2 représentations irréductibles complexes de degré 1 : En revanche, si n est pair, il existe 4 représentations irréductibles de degré 1 : Les autres représentations irréductibles sont toutes de degré 2 ; elles sont en nombre où ω désigne une racine primitive ne de l'unité, et h parcourt les entiers compris entre 1 et n-1. On peut vérifier que deux telles représentations sont isomorphes seulement pour h1 et h2vérifiant h1+h2=n. On obtient alors le nombre annoncé de représentations irréductibles de degré 2 non isomorphes, et donc toutes les représentations irréductible du groupe diédral, par la formule liant le nombre de représentations irréductibles à l'ordre du groupe. En plus des groupes diédraux finis, on trouve le groupe diédral infini D∞. Tout groupe diédral est généré par une rotation r et une réflexion. Si la rotation est un multiple rationnel d’une rotation totale, alors il existe un entier n tel que rn soit l’identité, et on est en présence d’un groupe diédral fini d’ordre 2n. Mais si la rotation n’est pas un multiple rationnel d’une rotation totale, alors il n’existe pas de tel n et le groupe résultant a un nombre infinid’éléments ; on le note D∞. Il admet pour présentation et est isomorphe au produit semi-direct de Z par C2, ainsi qu’au produit libre C2 * C2. Il s’agit de l’automorphisme de groupes du graphe constitué d’un chemin infini vers les deux extrémités. De façon équivalente, il s’agit du groupe des isométries de Z. Pour tout groupe abélien H, le groupe diédral généralisé de H, noté Dih(H), est le produit semi-direct de H par C2, l'action de C2 sur H étant l'inversion, i.e. où φ(0) est l'application identité et φ(1) l'inversion des éléments. On obtient ainsi, si H et C2 sont tous deux notés additivement : pour tous h1, h2 dans H et t2 dans C2. (Si C2 est noté multiplicativement, ces deux formules se résument en (h1, t1) * (h2, t2) = (h1 + t1h2, t1t2) .) Le sous-groupe de Dih(H) constitué des éléments de la forme (h, 0) est un sous-groupe normal d'indice 2, isomorphe à H. Quant aux éléments de la forme (h, 1), chacun est son propre inverse. Les classes de conjugaison sont Ainsi, pour tout sous-groupe M de H, les éléments correspondants (m,0) forment aussi un sous-groupe normal de Dih(H) isomorphe à M, et l'on a : Exemples : Dih(H) est abélien si et seulement si le produit semi-direct est direct, c'est-à-dire si et seulement si chaque élément de H est son propre inverse, i.e. H est un 2-groupe abélien élémentaire : Dih(C2k) = C2k+1.Propriétés [modifier]
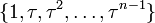 est un sous-groupe normal.
est un sous-groupe normal.

Représentations [modifier]

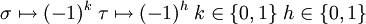
 si n est impair, respectivement
si n est impair, respectivement  si n est pair. On peut les définir comme suit :
si n est pair. On peut les définir comme suit :
Groupe diédral infini [modifier]


Groupe diédral généralisé [modifier]
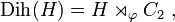
Bibliographie [modifier]
Notes et références [modifier]
21:33 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Groupe de Weyl
En mathématiques, et en particulier dans la théorie des algèbres de Lie, le groupe de Weyl d'un système de racines Le système de racines de Le groupe de Weyl d'un groupe de Lie semi-simple, d'une algèbre de Lie semi-simple, d'un groupe algébrique linéaire semi-simple, etc. est le groupe de Weyl du système de racines de ce groupe ou de cette algèbre. Enlever les hyperplans définis par les racines de La base du système de racine qui respecte le choix de Les groupes de Weyl sont des exemples des groupes de Coxeter. Ceci signifie qu'ils ont une sorte particulière de présentation dans laquelle chaque générateur Si G est un groupe algébrique linéaire semisimple sur un corps algébriquement clos (plus généralement un groupe déployé), et T est un tore maximal, le normalisateur N de T contient Tcomme sous-groupe d'indice fini et le groupe de Weyl W de G est isomorphe à N/T. Si B est un sous-groupe de Borel de G, i.e. un sous-groupe connexe résoluble maximal choisi pour contenir T, alors nous obtenons une décomposition de Bruhat ce qui provoque la décomposition de la variété de drapeaux G/B en cellules de Schubert (voir Grassmannienne).Groupe de Weyl
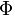 est le sous-groupe du groupe d'isométries du système de racines engendré par les réflexions orthogonales par rapport aux hyperplans orthogonaux aux racines.
est le sous-groupe du groupe d'isométries du système de racines engendré par les réflexions orthogonales par rapport aux hyperplans orthogonaux aux racines.Exemple [modifier]
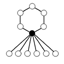
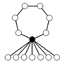
 est constitué des sommets d'un hexagone régulier centré à l'origine. Le groupe complet des symétries de ce système de racines est par conséquent legroupe diédral d'ordre 12. Le groupe de Weyl est engendré par les réflexions à travers les droites bissectant les paires de côtés opposés de l'hexagone ; c'est le groupe diédral d'ordre 6.
est constitué des sommets d'un hexagone régulier centré à l'origine. Le groupe complet des symétries de ce système de racines est par conséquent legroupe diédral d'ordre 12. Le groupe de Weyl est engendré par les réflexions à travers les droites bissectant les paires de côtés opposés de l'hexagone ; c'est le groupe diédral d'ordre 6.Les chambres de Weyl [modifier]
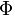 découpe l'espace euclidien en un nombre fini de régions ouvertes, appelées les chambres de Weyl. Celles-ci sont permutées par l'action sur le groupe de Weyl, et un théorème établit que cette action est simplement transitive. En particulier, le nombre de chambres de Weyl est égal à l'ordre du groupe de Weyl. Tout vecteur v différent de zéro divise l'espace euclidien en deux demi-espaces bordant l'hyperplan
découpe l'espace euclidien en un nombre fini de régions ouvertes, appelées les chambres de Weyl. Celles-ci sont permutées par l'action sur le groupe de Weyl, et un théorème établit que cette action est simplement transitive. En particulier, le nombre de chambres de Weyl est égal à l'ordre du groupe de Weyl. Tout vecteur v différent de zéro divise l'espace euclidien en deux demi-espaces bordant l'hyperplan  orthogonal à v, nommés
orthogonal à v, nommés  et
et 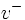 . Si v appartient à une certaine chambre de Weyl, aucune racine ne se trouve dans
. Si v appartient à une certaine chambre de Weyl, aucune racine ne se trouve dans  , donc chaque racine se trouve dans
, donc chaque racine se trouve dans  ou
ou 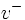 , et si
, et si 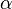 se trouve dans l'un d'eux, alors
se trouve dans l'un d'eux, alors  se trouve dans l'autre. Ainsi,
se trouve dans l'autre. Ainsi,  constitué d'exactement la moitié des racines de
constitué d'exactement la moitié des racines de 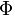 . Bien sûr,
. Bien sûr, 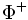 dépend de v, mais il ne change pas si v reste dans la même chambre de Weyl.
dépend de v, mais il ne change pas si v reste dans la même chambre de Weyl.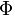 est l'ensemble des racines simples dans
est l'ensemble des racines simples dans 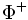 , i.e., les racines qui ne peuvent pas être écrites comme une somme de deux racines dans
, i.e., les racines qui ne peuvent pas être écrites comme une somme de deux racines dans 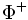 . Ainsi, les chambres de Weyl, l'ensemble
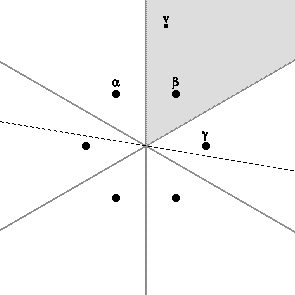
. Ainsi, les chambres de Weyl, l'ensemble 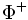 et la base en déterminent un autre, et le groupe de Weyl agit simplement transitivement dans chaque cas. L'illustration suivante montre les six chambres de Weyl d'un système de racines
et la base en déterminent un autre, et le groupe de Weyl agit simplement transitivement dans chaque cas. L'illustration suivante montre les six chambres de Weyl d'un système de racines  , un choix de v, l'hyperplan
, un choix de v, l'hyperplan  (indiqué par une droite en pointillé) et les racines positives
(indiqué par une droite en pointillé) et les racines positives 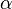 ,
,  , et
, et 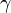 . La base dans ce cas est (
. La base dans ce cas est (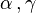 }.
}.Les groupes de Coxeter [modifier]
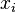 est d'ordre deux, et les relations autres que
est d'ordre deux, et les relations autres que  sont de la forme
sont de la forme  . Les générateurs sont les réflexions données par les racines simples et
. Les générateurs sont les réflexions données par les racines simples et 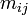 est 2, 3, 4 ou 6 dépendant si les racines i et jfont un angle de 90, 120, 135 ou 150 degrés, i.e., si dans le Diagramme de Dynkin, elles ne sont pas connectées, connectées avec une arête simple, connectées par une double arête ou connectées par une triple arête. La longueur d'un élément du groupe de Weyl est la longueur du mot le plus court représentant cet élément en termes de ces générateurs standards.
est 2, 3, 4 ou 6 dépendant si les racines i et jfont un angle de 90, 120, 135 ou 150 degrés, i.e., si dans le Diagramme de Dynkin, elles ne sont pas connectées, connectées avec une arête simple, connectées par une double arête ou connectées par une triple arête. La longueur d'un élément du groupe de Weyl est la longueur du mot le plus court représentant cet élément en termes de ces générateurs standards.
21:32 Publié dans Groupe de Weyl | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Forme de Killing
Dans la théorie des algèbres de Lie, la forme de Killing est une forme bilinéaire symétrique naturellement associée à toute algèbre de Lie. Elle reflète un certain nombre de propriétés des algèbres de Lie (semi-simplicité, résolubilité…). Soit g une K-algèbre de Lie, où K désigne un corps (commutatif). La représentation adjointe définit pour tout vecteur x de g un endomorphisme K-linéaire ad(x) du K-espace vectoriel g : Si g est de dimension finie, il existe une forme bilinéaire symétrique B définie par : où Tr désigne l'opérateur trace. Cette forme est appelée forme de Killing de g. La forme de Killing est l'unique forme bilinéaire symétrique sur g, invariante sous l'action des automorphismes de la K-algèbre de Lie g et vérifiant l'identité remarquable : Curieusement, la forme de Killing a été définie par Henri Cartan, tandis que la matrice de Cartan a été définie par Wilhelm Killing (en).Forme de Killing
Définition [modifier]

![Bleft([x,y],zright)=Bleft(x,[y,z]right)](http://upload.wikimedia.org/math/5/3/5/5358cbdd3d95b2f7f83b373ba0cd8c6f.png) .
.Voir aussi [modifier]
21:31 Publié dans Forme de Killing | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Algèbre enveloppante
Algèbre enveloppante
|
|
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
En mathématiques, on peut construire l'algèbre enveloppante U(L) d'une algèbre de Lie L. Il s'agit une algèbre associative unitaire qui permet de rendre compte de la plupart des propriétés de L. Si A est une algèbre associative sur un corps K, on peut facilement la munir d'une structure d'algèbre de Lie, en posant [x,y]=xy-yx. On note l'algèbre de Lie ainsi obtenue AL. La construction d'une algèbre enveloppante répond au problème réciproque : à partir d'une algèbre de Lie, on construit une algèbre associative dont le commutateur correspond au crochet dont on était parti. Soit L une algèbre de Lie sur un corps K. Soit T(L) l'algèbre tensorielle de L. On construit U(L) à partir de T(L) en imposant les relations Plus formellement, on note I l'idéal bilatère engendré par les On peut caractériser l'algèbre enveloppante de L par la propriété universelle suivante : U(L) est l'unique algèbre assocative telle que pour toute K-algèbre associative A et tout morphisme d'algèbre de Lie Construction [modifier]
![xotimes y-yotimes x=[x,y]](http://upload.wikimedia.org/math/b/d/2/bd2240aecf197b2db0010dfee8f15c66.png) .
.![xotimes y-yotimes x-[x,y]](http://upload.wikimedia.org/math/e/4/8/e4819d4c89717203131bdeddfc38bd8a.png) . U(L) est alors le quotient de T(L) par l'idéal I. L'injection canonique de L dans T(L) fournit alors un morphisme
. U(L) est alors le quotient de T(L) par l'idéal I. L'injection canonique de L dans T(L) fournit alors un morphisme  .
.Propriété universelle [modifier]
 , il existe un unique morphisme d'algèbre associative
, il existe un unique morphisme d'algèbre associative 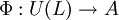 tel que
tel que 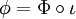 .
.Autres propriétés [modifier]
21:30 Publié dans Algèbre enveloppante | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Crochet de Lie
Crochet de Lie
|
|
Cet article ne cite pas suffisamment ses sources (août 2007).
Si vous connaissez le thème traité, merci d'indiquer les passages à sourcer avec {{Référence souhaitée}} ou, mieux, incluez les références utiles en les liant aux notes de bas de page. (Modifier l'article)
|
Le crochet de Lie est une loi de composition interne [,] sur un espace vectoriel V, qui lui confère une structure d'algèbre de Lie. Le commutateur [u,v]=uv-vu de deux endomorphismesen constitue un des exemples les plus simples. Le nom de crochet de Lie, ou simplement crochet, est souvent employé pour le crochet de Lie de deux champs de vecteurs sur une variété différentielle.
Sommaire[masquer] |
Soit un espace vectoriel V sur un corps Un crochet de Lie vérifie : L'antisymétrie implique [x,x] = 0 pour tout corps pour lequel Si on combine la bilinéarité avec l'antisymétrie [λx + x',y] = − [y,λx + x'] on peut ne vérifier la linéarité que sur une seule composante:[λx + x',y] = λ[x,y] + [x',y]. Muni d'un crochet de Lie, un espace vectoriel devient une algèbre de Lie. Soit V une variété différentielle et X et Y deux champs de vecteurs sur V. On note X . f la dérivée de la fonction f dans la direction du champ X. Le crochet de Lie de X et Y est l'unique champ de vecteur, noté [X,Y], tel que, pour toute fonction f indéfiniment dérivable, On montre en effet qu'un champ de vecteurs Z peut être caractérisé par la façon dont il dérive les applications. On vérifie en outre que l'application [,] définit bien un crochet de Lie sur les champs de vecteurs. Voir pour les démonstrations l'article dérivée de Lie. Lorsque deux champs de vecteurs ont un crochet nul, on dit qu'ils commutent.Définition générale [modifier]
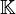 . Un crochet de Lie est une loi de composition interne sur V (c'est-à-dire que le crochet de Lie de deux vecteurs est encore un vecteur :
. Un crochet de Lie est une loi de composition interne sur V (c'est-à-dire que le crochet de Lie de deux vecteurs est encore un vecteur : ![forall x,yin V,quad [x,y]in V](http://upload.wikimedia.org/math/c/9/0/c90e2410e31abf79d4f6e106317124d8.png) ), vérifiant les propriétés suivantes :
), vérifiant les propriétés suivantes :
![forall x,x',yin V,lambda,muinmathbb K, [lambda x+mu x', y]=lambda[x,y]+mu [x',y],](http://upload.wikimedia.org/math/c/0/1/c01d118d897c2d3f49c20c718d51ae12.png)
![forall x,y,y'in V,lambda,muinmathbb K,[x,lambda y+mu y']=lambda[x,y]+mu [x,y']](http://upload.wikimedia.org/math/4/f/e/4fe65ba8376181cbed9147b7c0c055c0.png) .
.![forall xin V,quad [x,x]=0](http://upload.wikimedia.org/math/d/8/8/d88816febe6581ab9bb2e732129847f6.png)
![forall x,y,zin V, [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0](http://upload.wikimedia.org/math/c/6/c/c6c225e906d1dc76d5e14589e036be94.png) .
.
![forall x,yin V, [x,y]=-[y,x]](http://upload.wikimedia.org/math/e/e/e/eeeffe9a658fc19122b5102dad29c923.png) .
.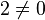 (corps de caractéristique différente de deux).
(corps de caractéristique différente de deux).Crochet de Lie de deux champs de vecteurs [modifier]
![[X,Y]cdot f = Xcdot (Ycdot f) -Y cdot (Xcdot f)](http://upload.wikimedia.org/math/8/7/2/87246955c4529cfe2065604eaff72625.png)
Bibliographie [modifier]
Voir aussi [modifier]
21:30 Publié dans Crochet de Lie | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Classification de Bianchi
La classification de Bianchi est une classification des algèbres de Lie réelles de dimension 3, donnée par Luigi Bianchi.Classification de Bianchi
Classification de Bianchi [modifier]
| Type | Description | Exemple | Groupe de Lie | Matrice |
|---|---|---|---|---|
| Type I | Abélienne | R³, muni d'un crochet nul | R³ comme groupe additif | M = 0 |
| Type II | Nilpotente et unimodulaire | H³, l'algèbre de Heisenberg | Le Groupe de Heisenberg de dimension 3 | M nilpotente non nulle |
| Type III | Résoluble et pas unimodulaire | Rx... | RxG : Produit direct du groupe additif R et du groupe G des matrices triangulaires supérieures de déterminant 1 | M a une unique valeur propre nulle |
| Type IV | Résoluble et pas unimodulaire | M est une matrice non semi-simple possédant une unique valeur propre, qui est non nulle. | ||
| Type V | Résoluble et non unimodulaire | M est une matrice semi-simple possédant une unique valeur propre. | ||
| Type VI | Résoluble et non unimodulaire | M a deux valeurs propres réelles distinctes non nulles et de somme non nulle. | ||
| Type VI0 | Résoluble et unimodulaire | so(1,1) | SO(1,1) | M possède deux valeurs propres réelles distinctes de somme nulle. |
| Type VII | Résoluble et unimodulaire | M a des valeurs propres non réelles et non imaginaires pures. | ||
| Type VII0 | Résoluble et unimodulaire | Groupe des isométries directes du plan euclidien | M ne possède que des valeurs propres imaginaires pures non nulles. | |
| Type VIII | Semisimple et unimodulaire | sl2(R) | SL2(R) | Irréalisable |
| Type IX | Semisimple et unimodulaire | o3(R) ou su2(C) | SO3(R) ou SU2(C) | Irréalisable |
En cosmologie, cette classification est utilisée pour les espace-temps homogènes de dimension 3+1. L'univers de Friedmann-Lemaître-Robertson-Walker est isotrope, ce qui est un cas particulier du type I, V et IX décrit ci-dessus. Le cas général correspond à univers homogène, mais dont l'expansion est anisotrope, c'est-à-dire dont le taux d'expansion est différent suivant trois directions orthogonales . Le type IX de la classification de Bianchi (la Métrique de Kasner est un cas particulier) révèle une dynamique particulièrement complexe de l'expansion. Celle-ci se faisant par la succession d'époques de type expansion anisotrope (avec deux directions en expansion, une en contraction) qui sont séparées par des périodes où les taux d'expansion dans les trois directions changent de façon brutale et relativement chaotique.Intérêt pour la cosmologie [modifier]
Références [modifier]
21:29 Publié dans Classification de Bianchi | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Bialgèbre de Lie
Bialgèbre de Lie
|
|
Cet article est une ébauche concernant les mathématiques.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
En mathématiques, une bialgèbre de Lie est une algèbre de Lie munie d'une application (appelée coproduit ou cocommutateur) telle que l'application duale δ * soit un crochet de Lie, et telle que δ soit un cocycle : Remarque importante : Une bialgèbre de Lie n'est pas a proprement parler une bialgèbre. En effet, on exige en général d'une bialgèbre que son algèbre sous-jacente soit unitaire etassociative.
![delta([X,Y]) = left( operatorname{ad}_X otimes 1 + 1 otimes operatorname{ad}_X right) delta(Y) - left( operatorname{ad}_Y otimes 1 + 1 otimes operatorname{ad}_Y right) delta(X)](http://upload.wikimedia.org/math/1/0/2/10207876644736180447ff35d551f701.png)
21:27 Publié dans Bialgèbre de Lie | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Algèbre de Lie
En mathématiques, une algèbre de Lie, nommée en l'honneur du mathématicien Sophus Lie, est un espace vectoriel qui est muni d'un crochet de Lie, c'est-à-dire d'une loi de composition interne bilinéaire, antisymétrique et qui vérifie l'identité de Jacobi. Une algèbre de Lie est un cas particulier d'algèbre sur un corps.Algèbre de Lie
Sommaire[masquer] |
Soit Une algèbre de Lie sur Le produit [x,y] est appelé crochet de Lie (ou simplement crochet) de x et y. Puisque le crochet est une fonction bilinéaire alternée de x,y, on a aussi l'identité [x,y] = − [y,x] pour tousx,y dans Une sous-algèbre de Lie de Remarque : contrairement aux algèbres tensorielles (et aux algèbres de Clifford, dont les algèbres extérieures), les algèbres de Lie ne sont pas unitaires, ni associatives. Un morphisme d'algèbre de Lie Un idéal de Si Une représentation d'une algèbre de Lie Le morphisme Les algèbres de Lie sont naturellement associées aux groupes de Lie. Si G est un groupe de Lie et 1 son élément neutre, alors l'espace tangent en 1 à G est une algèbre de Lie ; la construction exacte de cette algèbre est détaillée dans la section correspondante de l'article Groupe de Lie. La même construction est valable pour les groupes algébriques. On note en général en petites lettres gothiques l'algèbre de Lie associée à un groupe de Lie, ou à un groupe algébrique. Ainsi, comme on l'a déjà vu, Si φ est un morphisme de groupes entre deux groupes de Lie G et H, et si l'on suppose φ différentiable, alors sa différentielle en l'identité sera un morphisme entre les algèbres de Lie La classification des algèbres de Lie est utilisée de façon cruciale pour l'étude des groupes de Lie, des groupes algébriques et de leurs représentations. Si Une algèbre de Lie est dite nilpotente lorsque toute suite de commutateurs Plus précisément, définissons Ci par S'il existe un i tel que Ci=0, on dit que L'algèbre Le théorème d'Engel affirme que toute sous-algèbre nilpotente de Définissons par récurrence Di par S'il existe un i tel que Di=0, on dit que Un exemple d'algèbre de Lie résoluble est donné par l'algèbre Le théorème de Lie montre que, si On dit qu'une algèbre de Lie Lorsque On peut montrer que, sous les mêmes hypothèses, toute algèbre de Lie semi-simple est en fait une somme directe d'algèbres de Lie simples. Les algèbres de Lie simples de dimension finie sur le corps L'algèbre de Lie Les algèbres de Lie semi-simples de dimension finie sur le corps EI, EII, EIII, EIV (de type E6) EV, EVI, EVII (de type E7) EVIII, EIX (de type E8) FI, FII (de type F4) et GI (de type G2) suivant la notation d'Helgason1) Il n'y a pas de classification générale des algèbres de Lie de dimension infinie mais plusieurs classes de telles algèbres ont été étudiées. Il existe différentes sortes de généralisations des algèbres de Lie, on citera les superalgèbres de Lie, les groupes quantiques, les algèbres de Leibniz, les algèbres pré-Lie.Définitions, exemples et premières propriétés [modifier]
Définition [modifier]
 un corps.
un corps. est un espace vectoriel
est un espace vectoriel  sur
sur  muni d'une application bilinéaire
muni d'une application bilinéaire ![(x,y) mapsto [x,y]](http://upload.wikimedia.org/math/7/5/e/75e87350f83275e11f126171780fd7ca.png) de
de 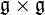 dans
dans  qui vérifie les propriétés suivantes:
qui vérifie les propriétés suivantes:
![forall x in mathfrak{g}, [x,x]=0](http://upload.wikimedia.org/math/f/3/2/f3223a3fe063412bb2f5033ba34850f5.png) ;
;![forall x,y,z in mathfrak{g}, [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0](http://upload.wikimedia.org/math/6/7/d/67d115952cf9c1c691b6053868febb0d.png)
 . L'identité (2) ci-dessus est appelée l'identité de Jacobi.
. L'identité (2) ci-dessus est appelée l'identité de Jacobi. est un sous-espace vectoriel de
est un sous-espace vectoriel de  stable pour le crochet de Lie. Toute sous-algèbre de Lie de
stable pour le crochet de Lie. Toute sous-algèbre de Lie de  est munie de manière évidente d'une structure d'algèbre de Lie sur
est munie de manière évidente d'une structure d'algèbre de Lie sur  .
.Quelques exemples classiques d'algèbres de Lie [modifier]
![forall x,y in E, [x,y]=0](http://upload.wikimedia.org/math/4/7/b/47b2e0b6393e77c2e6376834f8c87276.png) . Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne.
. Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne.![forall x,y in A, [x,y]=x*y-y*x](http://upload.wikimedia.org/math/5/9/7/59711ef28af13f749a361b567295a858.png) (c'est lecommutateur des deux éléments x et y). Il est facile de vérifier que l'on définit ainsi sur A une structure d'algèbre de Lie.
(c'est lecommutateur des deux éléments x et y). Il est facile de vérifier que l'on définit ainsi sur A une structure d'algèbre de Lie. est contenue dans une algèbre associative, appelée algèbre enveloppante, dans laquelle le crochet de Lie coïncide avec le crochet définit ci-dessus. L'algèbre enveloppante est beaucoup plus grande que l'algèbre de départ.
est contenue dans une algèbre associative, appelée algèbre enveloppante, dans laquelle le crochet de Lie coïncide avec le crochet définit ci-dessus. L'algèbre enveloppante est beaucoup plus grande que l'algèbre de départ. , l'espace des matrices
, l'espace des matrices 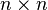 à coefficients dans
à coefficients dans  . C'est une algèbre associative pour le produit matriciel usuel. On peut donc également lui donner une structure d'algèbre de Lie, avec le crochet [A,B] = AB − BA. On note
. C'est une algèbre associative pour le produit matriciel usuel. On peut donc également lui donner une structure d'algèbre de Lie, avec le crochet [A,B] = AB − BA. On note  cette algèbre, lorsque l'on considère sa structure d'algèbre de Lie.
cette algèbre, lorsque l'on considère sa structure d'algèbre de Lie. stable par le crochet est une algèbre de Lie. Ainsi, on peut vérifier que l'ensemble des matrices de trace nulle est une algèbre de Lie, que l'on note
stable par le crochet est une algèbre de Lie. Ainsi, on peut vérifier que l'ensemble des matrices de trace nulle est une algèbre de Lie, que l'on note  .
. .
. avec le produit vectoriel comme crochet de Lie est une algèbre de Lie.
avec le produit vectoriel comme crochet de Lie est une algèbre de Lie.Morphismes et idéaux [modifier]
 est une application linéaire φ qui respecte le crochet de Lie, c'est-à-dire telle que
est une application linéaire φ qui respecte le crochet de Lie, c'est-à-dire telle que![forall a,b in mathfrak{g}, phi([a,b])=[phi(a),phi(b)]](http://upload.wikimedia.org/math/7/9/f/79fe9d02198bb8da7ba2c3fe5df52add.png) .
. est un sous-espace vectoriel
est un sous-espace vectoriel  tel que
tel que ![forall ginmathfrak{g}, forall hin mathfrak{h}, [g,h]inmathfrak{h}](http://upload.wikimedia.org/math/9/f/e/9fe5cc6e32f7a61a988f42d549cb43b3.png) . C'est en particulier une sous-algèbre de Lie. Si une algèbre de Lie n'admet pas d'idéal non trivial, elle est dite simple.
. C'est en particulier une sous-algèbre de Lie. Si une algèbre de Lie n'admet pas d'idéal non trivial, elle est dite simple. est un idéal de
est un idéal de  , on peut former le quotient de
, on peut former le quotient de  par
par  : c'est l'espace vectoriel quotient
: c'est l'espace vectoriel quotient 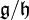 , muni du crochet défini par
, muni du crochet défini par ![[g+mathfrak{h},g'+mathfrak{h}] = [g,g']](http://upload.wikimedia.org/math/8/2/d/82d29f5c4eb7af6feb2661af74a7bd29.png) . La projection
. La projection 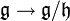 est alors un morphisme d'algèbres de Lie.
est alors un morphisme d'algèbres de Lie. est un morphisme
est un morphisme 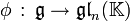 . Autrement dit, c'est une application linéaire telle que φ([g,h]) = φ(g)φ(h) − φ(h)φ(g).
. Autrement dit, c'est une application linéaire telle que φ([g,h]) = φ(g)φ(h) − φ(h)φ(g). défini par ad(g)(h) = [g,h] définit une représentation de
défini par ad(g)(h) = [g,h] définit une représentation de  , appelée représentation adjointe. L'identité de Jacobi exprime précisément le fait que ad respecte le crochet. Le noyau de cette représentation est le centre
, appelée représentation adjointe. L'identité de Jacobi exprime précisément le fait que ad respecte le crochet. Le noyau de cette représentation est le centre ![Z(mathfrak{g})={ginmathfrak{g}forall hinmathfrak{g} [g,h]=0}](http://upload.wikimedia.org/math/a/f/e/afe7160b530a847134d5f4291027ee9c.png) de l'algèbre de Lie
de l'algèbre de Lie 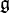 .
.Relation avec les groupes de Lie et les groupes algébriques [modifier]
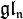 désigne l'ensemble des matrices carrées de taille n et
désigne l'ensemble des matrices carrées de taille n et 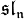 désigne l'ensemble des matrices carrées de taille n de trace nulle. De la même façon,
désigne l'ensemble des matrices carrées de taille n de trace nulle. De la même façon,  désigne l'ensemble des matrices carrées A de taille n antisymétriques, etc. Dans tous ces exemples, le crochet de Lie n'est rien d'autre que le commutateur : [A,B]=AB-BA.
désigne l'ensemble des matrices carrées A de taille n antisymétriques, etc. Dans tous ces exemples, le crochet de Lie n'est rien d'autre que le commutateur : [A,B]=AB-BA. et
et  de G et H. En particulier, à une représentation de G différentiable, on associe une représentation de
de G et H. En particulier, à une représentation de G différentiable, on associe une représentation de  .
.Classification [modifier]
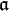 et
et 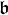 sont deux sous-algèbres de Lie d'une algèbre de Lie
sont deux sous-algèbres de Lie d'une algèbre de Lie  , notons
, notons ![[mathfrak{a},mathfrak{b}]](http://upload.wikimedia.org/math/c/5/2/c528d5c197e3f72db0a9bbc760333ee4.png) le sous-espace vectoriel engendré par les éléments de la forme [a,b] pour
le sous-espace vectoriel engendré par les éléments de la forme [a,b] pour  et
et 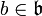 .
.Algèbres de Lie nilpotentes [modifier]
![[[[g_1,g_2],g_3],dots,g_n]](http://upload.wikimedia.org/math/4/8/a/48ab7757f1f2f8ed370a0f9d8acecd13.png) finit par être nulle, lorsque n devient suffisamment grand.
finit par être nulle, lorsque n devient suffisamment grand. et
et ![C_{i+1}=[C_i,mathfrak{g}]](http://upload.wikimedia.org/math/3/b/2/3b21f80fad4a73cdcc2c55569abfd0d0.png) .
. est nilpotente. Cette notion est à mettre en parallèle avec celle de groupe nilpotent. Il est facile de voir que toute algèbre de Lie abélienne est nilpotente.
est nilpotente. Cette notion est à mettre en parallèle avec celle de groupe nilpotent. Il est facile de voir que toute algèbre de Lie abélienne est nilpotente. des matrices triangulaires strictes, c'est-à-dire de la forme
des matrices triangulaires strictes, c'est-à-dire de la forme  fournit un exemple d'algèbre de Lie nilpotente.
fournit un exemple d'algèbre de Lie nilpotente. est en fait simultanément trigonalisable et donc conjuguée à une sous-algèbre de
est en fait simultanément trigonalisable et donc conjuguée à une sous-algèbre de  .
.Algèbres de Lie résolubles [modifier]
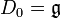 et Di + 1 = [Di,Di]
et Di + 1 = [Di,Di] est résoluble. Comme dans le cas des algèbres nilpotentes, cette notion correspond à celle de groupe résoluble. Il est facile de voir que toute algèbre de Lie nilpotente est résoluble.
est résoluble. Comme dans le cas des algèbres nilpotentes, cette notion correspond à celle de groupe résoluble. Il est facile de voir que toute algèbre de Lie nilpotente est résoluble.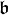 des matrices triangulaires supérieures dans
des matrices triangulaires supérieures dans  .
.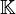 est algébriquement clos et de caractéristique nulle, alors toute sous-algèbre de Lie résoluble de
est algébriquement clos et de caractéristique nulle, alors toute sous-algèbre de Lie résoluble de  est conjuguée à une sous-algèbre de
est conjuguée à une sous-algèbre de 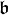
Algèbres de Lie semi-simples et réductives [modifier]
 est semi-simple lorsqu'elle ne contient pas d'idéal résoluble non trivial.
est semi-simple lorsqu'elle ne contient pas d'idéal résoluble non trivial.  est dite réductive lorsque sa représentation adjointe est semi-simple.
est dite réductive lorsque sa représentation adjointe est semi-simple.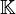 est de caractéristique nulle, et que
est de caractéristique nulle, et que  est de dimension finie, la semi-simplicité de
est de dimension finie, la semi-simplicité de  est équivalente à la non-dégénerescence de la forme de Killing K(x,y) définie par K(x,y) = tr(ad(x)ad(y)), où tr désigne la trace. Par ailleurs,
est équivalente à la non-dégénerescence de la forme de Killing K(x,y) définie par K(x,y) = tr(ad(x)ad(y)), où tr désigne la trace. Par ailleurs,  est réductive si et seulement si
est réductive si et seulement si ![[mathfrak{g},mathfrak{g}]](http://upload.wikimedia.org/math/3/f/1/3f1683bcf0fa96e29329efca70a1d284.png) est semi-simple.
est semi-simple. des nombres complexes sont classifiées par les diagrammes de Dynkin. Il y a donc 4 familles d'algèbres de Lie simples (ou 3 si on considère Bn et Dn comme une même famille) et 5 algèbres de Lie exceptionnelles, correspondant chacune à un diagramme de Dynkin différent.
des nombres complexes sont classifiées par les diagrammes de Dynkin. Il y a donc 4 familles d'algèbres de Lie simples (ou 3 si on considère Bn et Dn comme une même famille) et 5 algèbres de Lie exceptionnelles, correspondant chacune à un diagramme de Dynkin différent.
 correspond l'algèbre de Lie
correspond l'algèbre de Lie 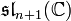 .
.
 correspond l'algèbre de Lie
correspond l'algèbre de Lie 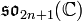 .
.
 correspond l'algèbre de Lie
correspond l'algèbre de Lie  .
.
 correspond l'algèbre de Lie
correspond l'algèbre de Lie  .
.
 est, elle, réductive et son algèbre de Lie dérivée est
est, elle, réductive et son algèbre de Lie dérivée est 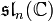 .
. des nombres réels sont classifiées par les involutions d'algèbres de Lie complexe ou, de façon équivalente, par lesinvolutions de systèmes de racines. Ceci correspond à la notion d'algèbre de Lie symétrique. Comme classe d'algèbre de Lie simple réelle, on peut citer:
des nombres réels sont classifiées par les involutions d'algèbres de Lie complexe ou, de façon équivalente, par lesinvolutions de systèmes de racines. Ceci correspond à la notion d'algèbre de Lie symétrique. Comme classe d'algèbre de Lie simple réelle, on peut citer:
Dimension infinie [modifier]
Généralisation [modifier]
Références [modifier]
Voir aussi [modifier]
21:26 Publié dans Algèbre de Lie | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
ABSTRACT ALGEBRA ON LINE
ABSTRACT ALGEBRA ON LINE
This site contains many of the definitions and theorems from the area of mathematics generally called abstract algebra. It is intended for undergraduate students taking an abstract algebra class at the junior/senior level, as well as for students taking their first graduate algebra course. It is based on the books Abstract Algebra, by John A. Beachy and William D. Blair, and Abstract Algebra II, by John A. Beachy.
The site is organized by chapter. The page containing the Table of Contents also contains an index of definitions and theorems, which can be searched for detailed references on subject area pages. Topics from the first volume are marked by the symbol ![]() and those from the second volume by the symbol
and those from the second volume by the symbol ![]() . To make use of this site as a reference, please continue on to the Table of Contents.
. To make use of this site as a reference, please continue on to the Table of Contents.
- TABLE OF CONTENTS (No frames)
-
TABLE OF CONTENTS (Frames version)
Interested students may also wish to refer to a closely related site that includes solved problems: the
- OnLine Study Guide for Abstract Algebra.
REFERENCES
Abstract Algebra, Second Edition, by John A. Beachy and William D. Blair
ISBN 0-88133-866-4, © 1996, 427 pages
Waveland Press, P.O. Box 400, Prospect Heights, Illinois, 60070, Tel. 847 / 634-0081
Abstract Algebra II
This set of lecture notes was expanded into the following text.
Introductory Lectures on Rings and Modules, by John A. Beachy
ISBN 0-521-64407-0, © 1999, 238 pages
Cambridge University Press, London Mathematical Society Student Texts #47
In addition to the Table of Contents, this page contains an index of definitions and theorems, so it can be searched for detailed references on subject area pages. Topics from the first volume are marked by the symbol
Click here for the version with frames.
The site is maintained by John Beachy as a service to students.
email: beachy@math.niu.edu | John Beachy's homepage | About this document
TABLE OF CONTENTS
 Integers
Integers
 Functions
Functions
 Groups
Groups
 Polynomials
Polynomials
 Rings
Rings Fields
Fields
 Structure of Groups
Structure of Groups Galois Theory
Galois Theory
 Unique Factorization
Unique Factorization
 Modules
Modules Structure of Noncommutative Rings
Structure of Noncommutative Rings
 Ideal Theory of Commutative Rings
Ideal Theory of Commutative Rings
INDEX
Index of Definitions
- abelian group
- action, of a group
- algebraic element
- algebraic extension
- algebraic numbers
- alternating group
- annihilator, of a module
- Artinian module
- Artinian ring
- ascending central series
- associated prime ideal
- automorphism, of a group
- automorphism, of a ring
- bicommutator, of a module
- bilinear function
- bimodule
- center of a group
- centralizer, of an element
- characteristic, of a ring
- codomain, of a function
- commutative ring
- commutator
- completely reducible module
- composite number
- composition, of functions
- composition series, for a group
- composition series, for a module
- congruence class of integers
- congruence, modulo n
- congruence, of polynomials
- conjugate, of a group element
- constructible number
- coset
- cycle of length k
- cyclic group
- cyclic module
- cyclic subgroup
- cyclotomic polynomial
- Dedekind domain
- degree of a polynomial
- degree of an algebraic element
- degree of an extension field
- derived subgroup
- dense subring
- dihedral group
- disjoint cycles
- division ring
- divisor, of a polynomial
- divisor, of an integer
- divisor, of zero
- direct product, of groups
- direct product, of modules
- direct sum, of modules
- direct sum, of rings
- domain, of a function
- equivalence class
- equivalence classes defined by a function
- equivalence relation
- essential submodule
- Euclidean domain
- Euler's phi-function
- even permutation
- extension field
- factor, of a polynomial
- factor, of an integer
- factor group
- factor ring
- faithful module
- field
- finite extension field
- finite group
- finitely generated module
- fixed subfield
- formal derivative
- fractional ideal
- free module
- Frobenius automorphism
- function
- Galois field
- Galois group of a polynomial
- general linear group
- generator, of a cyclic group
- greatest common divisor, of integers
- greatest common divisor, of polynomials
- greatest common divisor, in a principal ideal domain
- group
- group algebra
- group ring
- holomorph (of the integers mod n)
- homomorphism, of groups
- homomorphism, of modules
- homomorphism, of rings
- ideal
- idempotent element, of a ring
- image, of a function
- index of a subgroup
- injective module
- inner automorphism, of a group
- integer
- integral closure
- integral domain
- integral extension
- integrally closed domain
- invariant subfield
- inverse function
- invertible element, in a ring
- irreducible element, in a ring
- irreducible polynomial
- isomorphism, of groups
- isomorphism, of rings
- Jacobson radical, of a module
- kernel, of a group homomorphism
- kernel, of a ring homomorphism
- Krull dimension
- leading coefficient
- least common multiple, of integers
- left ideal
- Legendre symbol
- linear action
- localization at a prime ideal
- maximal ideal
- maximal submodule
- minimal polynomial
- minimal submodule
- module
- Moebius function
- monic polynomial
- multiple, of an integer
- multiplicity, of a root
- nil ideal
- nil radical
- nilpotent element, of a ring
- nilpotent ideal
- Noetherian module
- Noetherian ring
- normal extension
- normal subgroup
- normalizer, of a subgroup
- one-to-one function
- onto function
- odd permutation
- orbit
- order of a group
- order of a permutation
- p-group
- partition of a set
- perfect extension
- permutation
- permutation group
- primary ideal
- primitive polynomial
- principal left ideal
- product, of polynomials
- projective module
- polynomial
- prime ideal, of a commutative ring
- prime ideal, of a noncommutative ring
- prime module
- prime number
- prime ring
- primitive ideal
- primitive ring
- principal ideal
- principal ideal domain
- quadratic residue
- quaternions
- radical, for modules
- radical, of an ideal
- radical extension
- regular element
- relatively prime integers
- right ideal
- ring
- ring of differential operators
- root of a polynomial
- root of unity
- semidirect product
- semiprime ideal
- semiprime ring
- semiprimitive ring
- semisimple Artinian ring
- simple extension
- semisimple module
- separable polynomial
- separable extension
- simple group
- simple ring
- simple extension
- simple module
- skew field
- small submodule
- socle of a module
- solvable by radicals
- split homomorphism
- splitting field
- stabilizer
- subfield
- subgroup
- subring
- Sylow subgroup
- symmetric group
- tensor product
- torsion module
- torsionfree module
- transcendental element
- transposition
- unique factorization domain
- unit, of a ring
- von Neumann regular ring
- well-ordering principle
- zero divisor
Index of Theorems
- An algebraic extension of an algebraic extension is algebraic(6.2.10)
- Artin-Wedderburn theorem(11.3.2)
- Artin's lemma(8.3.4)
- Baer's criterion for injectivity(10.5.9)
- Burnside's theorem(7.2.8)
- Cauchy's theorem(7.2.10)
- Cayley's theorem(3.6.2)
- Characteristic of an integral domain(5.2.10)
- Characterization of completely reducible modules(10.2.9)
- Characterization of completely reducible rings(10.5.6)
- Characterization of constructible numbers(6.3.6)
- Characterization of Dedekind domains(12.1.6)
- Characterization of equations solvable by radicals(8.4.6)
- Characterization of finite fields(6.5.2)
- Characterization of finite normal separable extensions(8.3.6)
- Characterization of free modules(10.2.3)
- Characterization of integral elements(12.2.2)
- Characterization of internal direct products(7.1.3)
- Characterization of invertible functions(2.1.8)
- Characterization of the Jacobson radical(11.2.10)
- Characterization of linear actions(7.9.5)
- Characterization of nilpotent groups(7.8.4)
- Characterization of Noetherian modules(10.3.3)
- Characterization of normal subgroups(3.8.7)
- Characterization of projective modules(10.2.11)
- Characterization of semisimple Artinian rings(11.3.4)
- Characterization of prime ideals(11.1.3)
- Characterization of semidirect products(7.9.6)
- Characterization of semiprime ideals(11.1.7)
- Characterization of semisimple modules(10.5.3)
- Characterization of subgroups(3.2.2)
- Characterization of subrings(5.1.3)
- Chinese remainder theorem, for integers(1.3.6)
- Chinese remainder theorem, for rings(5.7.9)
- Class equation(7.2.6)
- Class equation (generalized)(7.3.6)
- Classification of cyclic groups(3.5.2)
- Classification of groups of order less than sixteen
- Classification of groups of order pq(7.4.6)
- Cohen's theorem(12.4.1)
- Computation of Euler's phi-function(1.4.8)
- Construction of extension fields(4.4.8)
- Correspondence between roots and linear factors(4.1.11)
- Dedekind's theorem on reduction modulo p
- Properties of Dedekind domains(12.1.4)
- Degree of a tower of finite extensions(6.2.4)
- DeMoivre's theorem(A.5.2)
- The direct product of nilpotent groups is nilpotent(7.8.2)
- Disjoint cycles commute(2.3.4)
- Division algorithm for integers(1.1.3)
- Division algorithm for polynomials(4.2.1)
- Eisenstein's irreducibility criterion(4.3.6)
- Endomorphisms of indecomposable modules(10.4.6)
- Existence of finite fields(6.5.7)
- Existence of greatest common divisors (for integers)(1.1.6)
- Existence of greatest common divisors (for polynomials)(4.2.4)
- Existence of greatest common divisors, in a principal ideal domain(9.1.6)
- Existence of irreducible polynomials(6.5.12)
- Existence of maximal submodules(10.1.8)
- Existence of quotient fields(5.4.4)
- Existence of splitting fields(6.4.2)
- Existence of tensor products(10.6.3)
- Euclidean algorithm for integers
- Euclidean algorithm for polynomials(Example 4.2.3)
- Euclid's lemma characterizing primes(1.2.5)
- Euclid's theorem on the infinitude of primes(1.2.7)
- Euler's theorem(1.4.11)
- Euler's theorem(Example 3.2.12)
- Euler's criterion(6.7.2)
- Every Euclidean domain is a principal ideal domain(9.1.2)
- Every field of characteristic zero is perfect(8.2.6)
- Every finite extension is algebraic(6.2.9)
- Every finite separable extension is a simple extension(8.2.8)
- Every finite field is perfect(8.2.7)
- Every PID is a UFD(9.1.12)
- Finite integral domains are fields(5.1.8)
- Every finite p-group is solvable(7.6.3)
- Finitely generated torsion modules over a PID(10.3.9)
- Finitely generated torsionfree modules over a PID(10.7.5)
- First isomorphism theorem(7.1.1)
- Fitting's lemma for modules(10.4.5)
- Frattini's argument(7.8.5)
- Fundamental theorem of algebra(8.3.10)
- Fundamental theorem of arithmetic(1.2.6)
- Fundamental theorem of finitely generated modules over a PID(10.7.5)
- Fundamental theorem of Galois theory(8.3.8)
- Fundamental theorem of finite abelian groups(7.5.4)
- Fundamental homomorphism theorem for groups(3.8.8)
- Fundamental homomorphism theorem for rings(5.2.6)
- F[x] is a principal ideal domain(4.2.2)
- On Galois groups(8.4.3, 8.4.4)
- Galois groups of cyclotomic polynomials(8.5.4)
- Galois groups over finite fields(8.1.7)
- Galois groups and permutations of roots(8.1.4)
- Gauss's lemma(4.3.4)
- When the group of units modulo n is cyclic(7.5.11)
- Hilbert basis theorem(10.3.7)
- Hilbert's nullstellensatz(12.4.9)
- Hopkin's theorem(11.3.5)
- Ideals in the localization of an integral domain(5.8.11)
- Impossibility of trisecting an angle(6.3.9)
- Incomparability, lying-over, and going up(12.2.9)
- Insolvability of the quintic(8.4.8)
- Irreducibility of cyclotomic polynomials(8.5.3)
- Irreducible ideals are primary(12.3.6)
- Irreducible polynomials over R(A.5.7)
- Jacobson density theorem(11.3.7)
- Jordan-Holder theorem for groups(7.6.10)
- Jordan-Holder theorem for modules(10.4.2)
- Kronecker's theorem(4.4.8)
- Krull's theorem(12.4.6)
- Krull-Schmidt theorem(10.4.9)
- Lagrange's theorem(3.2.10)
- Lasker-Noether decomposition theorem(12.3.10)
- Maschke's theorem(10.5.8)
- Maximal subgroups in nilpotent groups(7.8.5)
- Moebius inversion formula(6.6.6)
- The multiplicative group of a finite field is cyclic(6.5.10)
- Nakayama's lemma(11.2.8)
- The nil radical is nilpotent (in Noetherian rings)(12.4.3)
- Number of irreducible polynomials over a finite field(6.6.9)
- Number of roots of a polynomial(4.1.12)
- Order of a permutation(2.3.8)
- Order of the Galois group of a polynomial(8.1.6)
- Partial fractions(Example 4204)
- Every p-group is abelian(7.2.9)
- Every permutation is a product of disjoint cycles(2.3.5)
- The polynomial ring over a UFD is a UFD(9.2.6)
- The ring of power series is Noetherian(12.4.2)
- Prime and maximal ideals(5.3.9)
- Prime ideals in a principal ideal domain(5.3.10)
- Generalized principal ideal theorem(12.4.7)
- Quadratic reciprocity law(6.7.3)
- Rational roots(4.3.1)
- Remainder theorem(4.1.9)
- Schur's lemma(10.1.11)
- Second isomorphism theorem(7.1.2)
- Simplicity of PSL(2,F)(7.7.9)
- Simplicity of the alternating group(7.7.4)
- The smallest nonabelian simple group(7.10.7)
- On solvable groups(7.6.7, 7.6.8)
- Splitting fields are unique(6.4.5)
- Structure of simple extensions(6.1.6)
- Subgroups of cyclic groups(3.5.1)
- Sylow's theorems(7.4.1, 7.4.4)
- When the symmetric group is solvable(7.7.2)
- Unique factorization of integers(1.2.6)
- Unique factorization of polynomials(4.2.9)
- Wedderburn's theorem(8.5.6)
- Source : http://www.math.niu.edu/~beachy/aaol/contents.html#index
07:32 Publié dans ABSTRACT ALGEBRA ON LINE | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
GALOIS THEORY
GALOIS THEORY
Excerpted from Beachy/Blair, Abstract Algebra, 2nd Ed., © 1996Chapter 8
- 8.1 The Galois group of a polynomial
- 8.2 Multiplicity of roots
- 8.3 The fundamental theorem of Galois theory
- 8.4 Solvability by radicals
- 8.5 Cyclotomic polynomials
- 8.6 Computing Galois groups
Forward | Back | Table of Contents | About this document
The Galois group of a polynomial
To study solvability by radicals of a polynomial equation f(x) = 0, we let K be the field generated by the coefficients of f(x), and let F be a splitting field for f(x) over K. Galois considered permutations of the roots that leave the coefficient field fixed. The modern approach is to consider the automorphisms determined by these permutations. We note that any automorphism of a field F must leave its prime subfield fixed.8.1.1. Proposition. Let F be an extension field of K. The set of all automorphisms  : F -> F such that
: F -> F such that  (a) = a for all a in K is a group under composition of functions.
(a) = a for all a in K is a group under composition of functions.
8.1.2. Definition. Let F be an extension field of K. The set
{ 
 Aut(F) |
Aut(F) |  (a) = a for all a
(a) = a for all a  K }
K }
8.1.3. Definition. Let K be a field, let f(x)  K[x], and let F be a splitting field for f(x) over K. Then Gal(F/K) is called the Galois group of f(x) over K, or the Galois group of the equation f(x) = 0 over K.
K[x], and let F be a splitting field for f(x) over K. Then Gal(F/K) is called the Galois group of f(x) over K, or the Galois group of the equation f(x) = 0 over K.
8.1.4. Proposition. Let F be an extension field of K, and let f(x)  K[x]. Then any element of Gal(F/K) defines a permutation of the roots of f(x) that lie in F.
K[x]. Then any element of Gal(F/K) defines a permutation of the roots of f(x) that lie in F.
8.1.5. Lemma. Let f(x)  K[x] be a polynomial with no repeated roots and let F be a splitting field for f(x) over K. If
K[x] be a polynomial with no repeated roots and let F be a splitting field for f(x) over K. If  : K -> L is a field isomorphism that maps f(x) to g(x)
: K -> L is a field isomorphism that maps f(x) to g(x)  L[x] and E is a splitting field for g(x) over L, then there exist exactly [F:K] isomorphisms
L[x] and E is a splitting field for g(x) over L, then there exist exactly [F:K] isomorphisms  : F -> E such that
: F -> E such that  (a) =
(a) =  (a) for all a in K.
(a) for all a in K.
8.1.6. Theorem. Let K be a field, let f(x)  K[x], and let F be a splitting field for f(x) over K. If f(x) has no repeated roots, then |Gal(F/K)| = [F:K].
K[x], and let F be a splitting field for f(x) over K. If f(x) has no repeated roots, then |Gal(F/K)| = [F:K].
8.1.7. Corollary. Let K be a finite field and let F be an extension of K with [F:K] = m. Then Gal(F/K) is a cyclic group of order m.
Multiplicity of roots
8.2.1. Definition. Let f(x) be a polynomial in K[x], and let F be a splitting field for f(x) over K. If f(x) has the factorizationf(x) = (x - r1)m1 (x - r2)m2 · · · (x - rt)mt
over F, then we say that the root ri has multiplicity mi.If mi=1, then ri is called a simple root.
8.2.2. Definition. Let f(x)  K[x], with f(x) =
K[x], with f(x) = 
 ak xk. The formal derivative f'(x) of f(x) is defined by the formula
ak xk. The formal derivative f'(x) of f(x) is defined by the formula
f'(x) = 
 k ak xk-1,
k ak xk-1,
8.2.3. Proposition. The polynomial f(x) in K[x] has no multiple roots if and only if gcd(f(x),f'(x)) = 1.
8.2.4. Proposition. Let f(x) be an irreducible polynomial over the field K. Then f(x) has no multiple roots unless chr(K) = p  0 and f(x) has the form
0 and f(x) has the form
f(x) = a0 + a1 xp + a2 x2p + · · · + an xnp.
8.2.5. Definition. A polynomial f(x) over the field K is called separable if its irreducible factors have only simple roots.An algebraic extension field F of K is called separable over K if the minimal polynomial of each element of F is separable.
The field F is called perfect if every polynomial over F is separable.
8.2.6. Theorem. Any field of characteristic zero is perfect. A field of characteristic p>0 is perfect if and only if each of its elements has a pth root.
8.2.7. Corollary. Any finite field is perfect.
8.2.8. Theorem. Let F be a finite extension of the field K. If F is separable over K, then it is a simple extension of K.
The fundamental theorem of Galois theory
8.3.1. Proposition. Let F be a field, and let G be a subgroup of Aut(F). Then{ a  F |
F |  (a) = a for all
(a) = a for all 
 G }
G }
8.3.2. Definition. Let F be a field, and let G be a subgroup of Aut (F). Then
{ a  F |
F |  (a) = a for all
(a) = a for all 
 G }
G }
8.3.3. Proposition. If F is the splitting field over K of a separable polynomial and G = Gal(F/K), then FG = K.
8.3.4. Lemma. [Artin] Let G be a finite group of automorphisms of the field F, and let K = FG. Then
[F:K]  | G |.
| G |.
8.3.6. Theorem. The following conditions are equivalent for an extension field F of K:
- (1) F is the splitting field over K of a separable polynomial;
- (2) K = FG for some finite group G of automorphisms of F;
- (3) F is a finite, normal, separable extension of K.
Example. 8.3.1. The Galois group of GF(pn) over GF(p) is cyclic of order n, generated by the automorphism  defined by
defined by  (x) = xp, for all x in GF(pn). This automorphism is usually known as theFrobenius automorphism of GF(pn).
(x) = xp, for all x in GF(pn). This automorphism is usually known as theFrobenius automorphism of GF(pn).
8.3.8. Theorem. [Fundamental Theorem of Galois Theory] Let F be the splitting field of a separable polynomial over the field K, and let G = Gal(F/K).
- (a) There is a one-to-one order-reversing correspondence between subgroups of G and subfields of F that contain K:
- (i) If H is a subgroup of G, then the corresponding subfield is FH, and
H = Gal(F/FH).
-
(ii) If E is a subfield of F that contains K, then the corresponding subgroup of G is H = Gal(F/E), and
E = FH.
- (i) If H is a subgroup of G, then the corresponding subfield is FH, and
- (b) For any subgroup H of G, we have
[F:FH] = | H | and [FH:K] = [G:H].
- (c) Under the above correspondence, the subgroup H is normal if and only if the subfield E = FH is a normal extension of K. In this case,
Gal(E/K)
 Gal(F/K) / Gal(F/E).
Gal(F/K) / Gal(F/E).
 (E)
(E)  E for all
E for all in Gal(F/K). In the context of the fundamental theorem, we say that two intermediate subfields E1 and E2 are conjugate if there exists
in Gal(F/K). In the context of the fundamental theorem, we say that two intermediate subfields E1 and E2 are conjugate if there exists 
 Gal(F/K) such that
Gal(F/K) such that  ( E1 ) = E2. We now show that the subfields conjugate to an intermediate subfield E correspond to the subgroups conjugate to Gal(F/E). Thus E is a normal extension if and only if it is conjugate only to itself.
( E1 ) = E2. We now show that the subfields conjugate to an intermediate subfield E correspond to the subgroups conjugate to Gal(F/E). Thus E is a normal extension if and only if it is conjugate only to itself.
8.3.9. Proposition. Let F be the splitting field of a separable polynomial over the field K, and let E be a subfield such that K  E
E  F, with H = Gal(F/E). If
F, with H = Gal(F/E). If 
 Gal(F/K), then
Gal(F/K), then
Gal(F/ (E)) =
(E)) =  H
H  -1.
-1.
Solvability by radicals
In most results in this section we will assume that the fields have characteristic zero, in order to guarantee that no irreducible polynomial has multiple roots. When we say that a polynomial equation is solvable by radicals, we mean that the solutions can be obtained from the coefficients in a finite sequence of steps, each of which may involve addition, subtraction, multiplication, division, or taking nth roots. Only the extraction of an nth root leads to a larger field, and so our formal definition is phrased in terms of subfields and adjunction of roots of xn-a for suitable elements a.8.4.1. Definition. An extension field F of K is called a radical extension of K if there exist elements u1, u2, ... , um in F such that
- (i) F = K (u1, u2, ... , um), and
-
(ii) u1n1
 K and uini
K and uini  K ( u1, ... , ui-1 ) for i = 2, ... , m and n1, n2, ... , nm
K ( u1, ... , ui-1 ) for i = 2, ... , m and n1, n2, ... , nm  Z.
Z.
 K[x], the polynomial equation f(x) = 0 is said to be solvable by radicals if there exists a radical extension F of K that contains all roots of f(x).
K[x], the polynomial equation f(x) = 0 is said to be solvable by radicals if there exists a radical extension F of K that contains all roots of f(x).
8.4.2. Proposition. Let F be the splitting field of xn - 1 over a field K of characteristic zero. Then Gal(F/K) is an abelian group.
8.4.3. Theorem. Let K be a field of characteristic zero that contains all nth roots of unity, let a  K, and let F be the splitting field of xn-a over K. Then Gal(F/K) is a cyclic group whose order is a divisor of n.
K, and let F be the splitting field of xn-a over K. Then Gal(F/K) is a cyclic group whose order is a divisor of n.
8.4.4. Theorem. Let p be a prime number, let K be a field that contains all pth roots of unity, and let F be an extension of K. If [F:K] = |Gal(F/K)| = p, then F = K(u) for some u  F such that up
F such that up  K.
K.
8.4.5. Lemma. Let K be a field of characteristic zero, and let E be a radical extension of K. Then there exists an extension F of E that is a normal radical extension of K.
8.4.6. Theorem. Let f(x) be a polynomial over a field K of characteristic zero. The equation f(x) = 0 is solvable by radicals if and only if the Galois group of f(x) over K is solvable.
Theorem 7.7.2 shows that Sn is not solvable for n  5, and so to give an example of a polynomial equation of degree n that is not solvable by radicals, we only need to find a polynomial of degree n whose Galois group over Q is Sn.
5, and so to give an example of a polynomial equation of degree n that is not solvable by radicals, we only need to find a polynomial of degree n whose Galois group over Q is Sn.
8.4.7. Lemma. Any subgroup of S5 that contains both a transposition and a cycle of length 5 must be equal to S5 itself.
8.4.8. Theorem. There exists a polynomial of degree 5 with rational coefficients that is not solvable by radicals.
Cyclotomic polynomials
8.5.1. Definition. Let n be a positive integer, and let be the complex number
be the complex number  = cos
= cos  + i sin
+ i sin  , where
, where  = 2
= 2  / n. The polynomial
/ n. The polynomial
 n (x) =
n (x) =  k (x -
k (x -  k),
k),
8.5.2. Proposition. Let n be a positive integer, and let  n(x) be the nth cyclotomic polynomial. The following conditions hold:
n(x) be the nth cyclotomic polynomial. The following conditions hold:
- (a) deg (
 n (x)) =
n (x)) =  (n);
(n); -
(b) xn - 1 =
 d | n
d | n  d (x);
d (x); -
(c)
 n (x) is monic, with integer coefficients.
n (x) is monic, with integer coefficients.
 n(x) is irreducible over Q, for every positive integer n.
n(x) is irreducible over Q, for every positive integer n.
8.5.4. Theorem. For every positive integer n, the Galois group of the nth cyclotomic polynomial  n(x) over Q is isomorphic to Zn×.
n(x) over Q is isomorphic to Zn×.
Example. 8.5.2. A regular n-gon is constructible if and only if  (n) is a power of 2. If p is an odd prime, and
(n) is a power of 2. If p is an odd prime, and  (p) is a power of 2, then p must have the form p = 2k + 1, where k is a power of 2. Such primes are called Fermat primes. The only known examples are 3, 5, 17, 257, and 65537. This implies, for example, that a regular 17-gon is constructible.
(p) is a power of 2, then p must have the form p = 2k + 1, where k is a power of 2. Such primes are called Fermat primes. The only known examples are 3, 5, 17, 257, and 65537. This implies, for example, that a regular 17-gon is constructible.
A set that satisfies all the axioms of a field except for commutativity of multiplication is called a division ring or skew field.
8.5.6. Theorem. [Wedderburn] Any finite division ring is a field.
Computing Galois groups
8.6.1. Definition. Let G be a group acting on a set S. We say that G acts transitively on S if for each pair of elements x,y in S there exist an element g in G such that y = gx.If G is a subgroup of the symmetric group Sn, then G is called a transitive group if it acts transitively on the set { 1, 2, ... , n }.
8.6.2. Proposition. Let f(x) be a separable polynomial over the field K, with roots r1 , ... , rn in its splitting field F. Then f(x) is irreducible over K if and only if Gal(F/K) acts transitively on the roots of f(x).
8.6.3. Lemma. Let p be a prime number, and let G be a transitive subgroup of Sp. Then any nontrivial normal subgroup of G is also transitive.
8.6.4. Lemma. Let p be a prime number, and let G be a solvable, transitive subgroup of Sp. Then G contains a cycle of length p.
8.6.5. Proposition. Let p be a prime number, and let G be a solvable, transitive subgroup of Sp. Then G is a subgroup of the normalizer in Sp of a cyclic subgroup of order p.
Let f(x) be a polynomial of degree n over the field K, and assume that f(x) has roots r1, r2, ... , rn in its splitting field F. The element  of F defined by
of F defined by
 =
=  (ri - rj)2,
(ri - rj)2,
 i < j
i < j  n, is called the discriminant of f(x).
n, is called the discriminant of f(x).
It can be shown that the discriminant of any polynomial f(x) can be expressed as a polynomial in the coefficients of f(x), with integer coefficients. This requires use of elementary symmetric functions, and lies beyond the scope of what we have chosen to cover in the book.
We have the following properties of the discriminant:
- (i)

 0 if and only if f(x) has distinct roots;
0 if and only if f(x) has distinct roots; -
(ii)

 K;
K; -
(iii) If

 0, then a permutation
0, then a permutation 
 Sn is even if and only if it leaves unchanged the sign of
Sn is even if and only if it leaves unchanged the sign of
 (ri-rj) .
(ri-rj) .
 , and let F be its splitting field over K. Then every permutation in Gal(F/K) is even if and only if
, and let F be its splitting field over K. Then every permutation in Gal(F/K) is even if and only if  is the square of some element in K.
is the square of some element in K.
We now restrict our attention to polynomials with rational coefficients. The next lemma shows that in computing Galois groups it is enough to consider polynomials with integer coefficients. Then a powerful technique is to reduce the integer coefficients modulo a prime and consider the Galois group of the reduced equation over the field GF(p).
8.6.7. Lemma. Let f(x) = xn + an-1 xn-1 + · · · + a1 x + a0  Q[x], and assume that
Q[x], and assume that
ai = bi / d for d, b0, b1, ... , bn-1  Z.
Z.
Then dn f(x/d) is monic with integer coefficients, and has the same splitting field over Q as f(x).
If p is a prime number, we have the natural mapping  : Z[x] -> Zp[x] which reduces each coefficient modulo p. We will use the notation
: Z[x] -> Zp[x] which reduces each coefficient modulo p. We will use the notation  ( f(x) ) = fp(x).
( f(x) ) = fp(x).
Theorem [Dedekind]. Let f(x) be a monic polynomial of degree n, with integer coefficients and Galois group G over Q, and let p be a prime such that fp(x) has distinct roots. If fp(x) factors in Zp[x] as a product of irreducible factors of degrees n1, n2, ... , nk, then G contains a permutation with the cycle decomposition
(1,2, ... ,n1) (n1+1, n1+2, ... , n1+n2) · · · (n-nk+1, ... ,n),
relative to a suitable ordering of the roots.
07:30 Publié dans GALOIS THEORY | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook