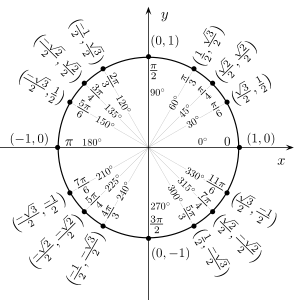
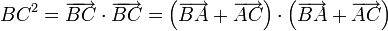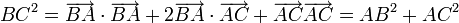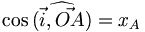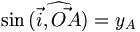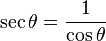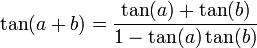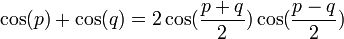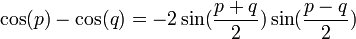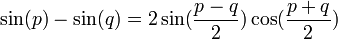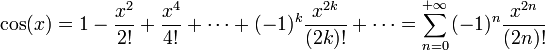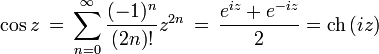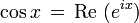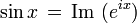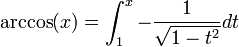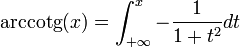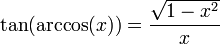02/12/2010
Un cours de DEA sur la théorie de Galois
07:26 Publié dans Un cours de DEA sur la théorie de Galois | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Théorie de Galois
En mathématiques et plus précisément en algèbre, la théorie de Galois est l'étude des extensions de corps commutatifs, par le biais d'une correspondance avec des groupes de transformations sur ces extensions, les groupes de Galois. Cette méthode féconde, qui constitue l'exemple historique, a essaimé dans bien d'autres branches des mathématiques, avec par exemple la théorie de Galois différentielle, ou la théorie de Galois des revêtements. Cette théorie est née de l'étude par Évariste Galois des équations algébriques. L'analyse de permutations des racines permet d'expliciter une condition nécessaire et suffisante de résolubilité par radicaux. Ce résultat est connu sous le nom de théorème d'Abel-Ruffini. Les applications sont très variées. Elles s'étendent de la résolution de vieilles conjectures comme la détermination des polygonesconstructibles à la règle et au compas démontrée par le théorème de Gauss-Wantzel à la géométrie algébrique à travers, par exemple, lethéorème des zéros de Hilbert.Théorie de Galois
Sommaire[masquer] |
La théorie de Galois voit ses origines dans l'étude des équations algébriques. Elle se ramène à l'analyse des équations polynomiales. Une approche par des changements de variables et des substitutions a permis à des mathématiciens comme Al-Khwarizmi1 (783 850), Tartaglia (1499 1557), Cardano2 (1501 1576) ou Ferrari (1522 1565) de résoudre tous les cas jusqu'au degré quatre. Cette approche ne permet pas d'aller plus loin et deux siècles seront nécessaires pour apporter de nouvelles idées. Gauss (1777 1855) utilise les polynômes cyclotomiques3 pour apporter une contribution à un problème ouvert depuis l'antiquité: celui de la construction à la règle et au compas de polygones réguliers. Il construit en particulier l'heptadécagone, polygone régulier à 17 côtés. Son approche, typiquement galoisienne bien avant la découverte de la théorie, lui vaut le surnom de prince des mathématiciens. Son travail est complété par Wantzel4 (1814 1848), qui donne une condition nécessaire et suffisante de constructibilité des polygones réguliers et démontre l'impossibilité de la trisection de l'angle et de la duplication du cube. Dans le cas général, l'équation quintique n'admet pas de solution par radicaux. C'est la raison pour laquelle une démarche à l'aide de substitutions et changements de variables devient stérile. Lagrange5 (1736 1813) et Vandermonde6(1735 1796) utilisent la notion de permutation à la fin du xviiie siècle et pressentent l'importance de cet outil dans le cadre de l'équation polynomiale. Ruffini7 (1765 1822) est le premier à prévoir l'impossibilité de la solution générale et que la compréhension du phénomène réside dans l'étude des permutations des racines. Sa démonstration reste néanmoins peu rigoureuse et partielle. Le mathématicien norvégien Abel (1802 1829) publie une démonstration8 en 1824 qui finit par convaincre la communauté scientifique. Elle ne propose pas à l'époque de condition nécessaire et suffisante de résolubilité. En étudiant le problème de l'équation algébrique, Galois (1811 1832) met en évidence les premiers éléments de la théorie qui porte maintenant son nom. Ses écrits sont perdus ou tombent dans l'oubli. Un mémoire9 est finalement retrouvé par Liouville (1809 1882) qui le présente à l'Académie des sciences en 1843. Les travaux de Galois accèdent alors in extremis à la postérité. Galois, pour la première fois dans l'histoire des mathématiques, met en évidence une structure abstraite qu'il appelle groupe. À la différence de ses prédécesseurs, il n'étudie pas une incarnation particulière comme les permutations de Lagrange ou les groupes cycliques de Gauss, mais une structure générale définie par un ensemble et une loi. Cette démarche, particulièrement novatrice, est à l'origine de l'algèbre moderne. Liouville en parle dans les termes suivants : « Cette méthode, vraiment digne de l'attention des géomètres, suffirait seule pour assurer à notre compatriote un rang dans le petit nombre des savants qui ont mérité le titre d'inventeur. »10 L'apport majeur de Galois, c'est-à-dire l'utilisation d'une structure algébrique comme outil fondamental, est rapidement compris par la communauté mathématique. Cauchy (1789 1855)publie vingt-cinq articles sur les groupes dont un sur son célèbre théorème11. Cayley (1821 1895) donne la première définition abstraite d'un groupe12. Enfin, Jordan (1838 1922) diffuse largement les idées de Galois. Son livre13 de 1870 présente les travaux de Galois comme une théorie générale sur des groupes, dont le théorème sur la résolution des équations n'est qu'une application. En France, la théorie de Galois est identifiée à celle des groupes à cette époque. D'autres structures sont mises en évidence, particulièrement en Allemagne. Indépendamment des travaux de Galois, Kummer (1810 1893) étudie14 des anneaux et découvre l'ancêtre de la notion d'idéal. Kronecker (1823 1891) et Dedekind (1831 1916) développent les prémisses de la théorie des anneaux et des corps15. Kronecker établit le pont entre les écoles française et allemande. Il donne la définition moderne de groupe de Galois à partir d'automorphismes de corps. À la fin du xixe siècle, Weber (1842 1913) réalise une synthèse16 des différents travaux. La théorie de Galois est alors pour la première fois identifiée avec celle des corps commutatifs. Un nouvel axe d'analyse enrichit la théorie de Galois. En 1872, Klein (1849 1925) se fixe comme objectif de classifier les différentes géométries de l'époque. Il dégage, dans son célèbre programme d'Erlangen, le principe général qu'une géométrie est définie par un espace et un groupe opérant sur cet espace, appelé groupe des isométries. Un pont est ainsi établi entre la théorie des groupes et la géométrie. Ces premiers groupes correspondent à des groupes de Lie et n'appartiennent pas directement à ceux de la théorie de Galois. En 1877 Klein remarque17 que le groupe des isométries laissant invariant l'icosaèdre est isomorphe au groupe de Galois d'une équation quintique. La théorie de Galois s'étend à la géométrie algébrique. Les groupes de Galois prennent alors la forme de revêtements aussi appelés revêtement de Galois. David Hilbert (18621943) étudie les corps de nombres quadratiques et apporte une contribution majeure à la théorie en démontrant18 son célèbre théorème des zéros. Ce théorème possède aussi une interprétation géométrique sur les variétés algébriques. La théorie est maintenant enrichie d'une nouvelle branche: la théorie de Galois géométrique. Elle s'avère particulièrement féconde. Les travaux de Hilbert ouvrent d'autres branches de la théorie de Galois. Le théorème des zéros permet l'étude des premiers groupes de Galois d'ordre infini. Son théorème d'irréductibilité ouvre la problématique inverse. Elle s'énonce de la manière suivante : si G est un groupe alors est-il le groupe de Galois d'une extension? Enfin les travaux de Picard (1856 1941) et Vessiot (1865 1952) ouvrent une autre voie pour l'étude des groupes de Galois d'ordre infini, la théorie de Galois différentielle. Les travaux de Hilbert ont ouvert l'étude des cas où le groupe de Galois est d'ordre infini et commutatif. Ce vaste sujet prend le nom de théorie des corps de classes. Elle est maintenant achevée et est souvent considérée comme un des plus beaux succès des mathématiques du siècle. La formalisation définitive19 de la théorie de Galois est donnée par Artin. L'adjonction de l'algèbre linéaire permet une exposition plus claire et concise. La théorie utilise maintenant toutes les grandes structures de l'algèbre, les groupes, les anneaux, les corps et les espaces vectoriels. Elle dispose maintenant de ramifications importantes en géométrie algébrique. Elle est la base d'une quantité majeure des grandes réalisations mathématiques du xxe siècle. L'alliance de la géométrie et de l'algèbre est presque systématiquement utilisée. On peut citer par exemple les travaux des mathématiciens Jean-Pierre Serre (Médaille Fields 1954) et Grothendieck (Médaille Fields 1966) avec une refonte de la géométrie algébrique, Faltings(Médaille Fields 1986) pour ses travaux sur les modules de Galois démontrant le théorème de Mordell ou Laurent Lafforgue (Médaille Fields 2002) sur le Programme de Langlands, une généralisation de la théorie des corps de classes. Le petit théorème de Fermat nous indique que si a est un entier et p un nombre premier alors: Il est possible de démontrer ce théorème en remarquant que Fp le quotient de l'ensemble des nombres entiers par son idéal engendré par p est un corps, car p est un nombre premier. (Fp*, .) est un groupe fini de cardinal p -1. Le théorème de Lagrange assure que tout élément de ce groupe à la puissance p -1 est égal à l'unité, ce qui démontre le théorème. Conclusion : Ce cas est particulièrement aisé car la structure du corps est simple. Il illustre néanmoins le fait qu'une structure de corps est un outil utile en théorie algébrique des nombres. D'autres théorèmes d'arithmétique modulaire comme la loi de réciprocité quadratique demandent une compréhension beaucoup plus profonde de la structure des corps. C'est la raison pour laquelle la démonstration ne put être trouvée malgré leurs efforts par Euler (1707 1783) ou Lagrange et qu'il fallut attendre Gauss et ses polynômes cyclotomiques pour conclure. Soit L l'ensemble des éléments de la forme a + b.√2 où a et b sont des rationnels. Montrons que L est un corps : L est clairement stable pour l'addition et le passage à l'opposé, et est donc un groupe additif. Il est stable pour la multiplication et le passage à l'inverse des éléments non nuls, en effet: Ces deux dernières propositions montrent que L est un sous-corps des nombres réels. L est aussi un espace vectoriel de dimensiondeux sur les nombres rationnels, car il possède pour base 1 et √2. Un tel corps s'appelle une extension quadratique. Montrons que L ne contient pas la racine cubique de deux : Soit l un élément de L, alors de l 2 est une combinaison linéaire à coefficients rationnels de 1 et √2 car ces deux éléments forment une base et l 2 est un élément de L. il existe donc deux rationnels α etβ tel que l'égalité suivante est vraie: Et pour tout élément l de L il existe un polynôme de degré inférieur ou égal à deux ayant pour racine l. Or, le plus petit degré du polynôme non nul à coefficients rationnels qui annule la racine cubique de deux est trois, et la proposition est démontrée. Conclusion : Wantzel a démontré que les nombres constructibles à la règle et au compas sont soit dans une extension quadratique, soit dans une extension quadratique dont les coefficients sont pris dans une extension quadratique et ainsi de suite. On parle alors de tour d'extension quadratique. Il est possible de démontrer par un raisonnement analogue à celui présenté ici que la racine cubique de deux n'est pas élément d'une tour d'extension quadratique. Voilà pourquoi la duplication du cube est impossible. Le choix judicieux de corps particuliers est la clé de la résolution de cette antique conjecture. Considérons un exemple d'équation du troisième degré : Détermination d'un élément du groupe de Galois : Le polynôme P[X] est un polynôme irréductible à coefficients rationnels. La théorie de Galois nous indique qu'il existe un corps L qui est une extension des rationnels contenant toutes les racines deP[X]. Cette extension est de dimension six. De plus, il existe un sous-corps K de L tel que L est de dimension trois sur K et j la première racine cubique de l'unité est élément de K. Le groupe de Galois de L sur K est l'ensemble des automorphismes de corps de L laissant invariant tout élément de K. La théorie de Galois nous indique que ce groupe a trois éléments, soit g un élément du groupe différent de l'identité. Diagonalisation de g : Le théorème de Lagrange nous assure que g3 est égal à l'identité. Si l est un élément non nul de L, alors l, g(l) et g2(l) forment une base de L sur K. Considérant g comme opérateur linéaire, son polynôme caractéristique est X3 - 1 et ses valeurs propres sont 1, j et j2. Il existe une base (u, v, w) de L sur K constituée de vecteurs propres, car le nombre de valeurs propres est égal à la dimension de L sur K. On a donc g(u)=j·u, g(v)=j2·v et g(w)=w. De plus, 1 + j + j2 = 0. Détermination de l'image des racines par g : Soit x1, une racine de P[X]. L'image d'une racine par g est une racine, en effet: On en déduit que x1, g(x1) et g2(x1) sont les trois racines de P. On peut repésenter x1 comme somme de vecteurs propres de g:x1 = u + v + w (léger abus de notation: w sera en l'occurrence 0, ne formant plus une base comme ci-dessus). Les trois égalités suivantes sont alors vérifiées: Calcul des valeurs des racines : Il suffit d'utiliser les relations entre coefficients et racines pour montrer que : On en déduit que u 3 et v 3 vérifient l'équation X2 + X + 1 = 0. Ce qui permet de conclure que x1 est égal à 2 cos(2π/9), 2 cos(8π/9) ou 2 cos(14π/9). Conclusion : Le groupe de Galois, permet la résolution de l'équation cubique par une diagonalisation d'un endomorphisme. La méthode est généralisable si et seulement si le groupe de Galois possède de bonnes propriétés, en fait s'il est résoluble. Ces exemples ont un point commun, ce sont les propriétés des structures algébriques qui permettent de trouver les solutions. Pour le premier exemple, la propriété démontrée par Lagrange sur les groupes (et donc les groupes multiplicatifs des corps) finis permet de conclure. Dans le deuxième exemple, ce sont les propriétés associées sur la dimension d'un l'espace vectoriel qui sont utilisées. Dans le troisième cas, sont utilisés les propriétés des corps et de leurs extensions, des groupes avec le théorème de Lagrange et celle des espaces vectoriels avec les propriétés de réduction d'endomorphisme dans le cas où le polynôme minimal est scindé. La théorie de Galois offre une richesse dans les structures algébriques permettant de résoudre nombre de cas très différents et dans des domaines éloignés. La théorie algébrique des nombres est l'étude des nombres racines d'un polynôme à coefficients entiers, appelés nombres algébriques. La théorie de Galois est ici essentielle car elle offre la structure la plus adéquate d'analyse, à savoir l'extension finie la plus petite contenant les nombres étudiés. Un sous-ensemble joue un rôle particulier : celui des entiers algébriques, ils correspondent à la généralisation des entiers dans l'extension. L'étude de cet ensemble ajoute à la théorie de Galois de nombreuses propriétés issues de la théorie des anneaux. Les entiers algébriques jouent un rôle important pour la résolution d'équations d'arithmétique modulaire ou diophantiennes. On peut citer comme application de la théorie de Galois à ce domaine, le théorème de Gauss-Wantzel qui détermine tous les polygones réguliers constructibles à la règle et au compas. La Théorie de Kummer s'applique aux équations diophantiennes et permet de valider le grand théorème de Fermat pour presque tous les entiers inférieurs à cent. Enfin, dans le cadre de l'arithmétique modulaire, la loi de réciprocité d'Artin généralise la loi de réciprocité quadratique de Gauss et résout le neuvième problème de Hilbert. La cryptographie est la discipline qui s'attache à protéger un message. Le cadre théorique maintenant le plus utilisé consiste à définir unalgorithme qui, associé à une clef permet de créer un nouveau message dit cryptogramme signifiant qu'il est chiffré. Le message chiffré est simple à déchiffrer, c'est-à-dire simple à transformer en message d'origine avec une clef et difficile sans celle-ci pour la personne qui s'efforce alors de le décrypter. Dans une partie des théories modernes de cryptographie, les lettres du message sont choisies dans un corps fini. Le cadre est donc celui de la théorie de Galois. Il est naturel que les outils associés soient ceux de la théorie. L'arithmétique modulaire (cf par exemple l'algorithme RSA) est très largement employée. Si les techniques simples reposent sur des résultats élémentaires comme le théorème de Bézout, le théorème des restes chinoisou l'exponentiation modulaire, les développements actuels utilisent des outils plus subtils comme les courbes elliptiques (cf une clé privée inviolable ?). La problématique de la théorie des équations algébriques est celle qui donna naissance à la théorie de Galois. Elle complète le théorème d'Abel-Ruffini en proposant une condition nécessaire et suffisante pour l'existence d'une expression par radicaux des racines d'un polynôme. Elle permet néanmoins d'aller plus loin. Le théorème de Kronecker-Weber explicite précisément la structure des extensions rationnelles associées aux polynômes ayant des racines s'exprimant par radicaux. Il devient alors possible de résoudre explicitement toutes les équations de cette nature. Elle possède pour champs d'application tous les corps, offrant un outil puissant à l'arithmétique modulaire. Beaucoup de lois de réciprocité, de même nature que celle démontrée par Gauss dans le cas quadratique sont ainsi démontrables grâce à la théorie de Galois. Abel puis Hermite (1822 1902) ont travaillé sur une autre approche : les fonctions elliptiques. Elles permettent, par exemple, d'exprimer les racines de toute équation polynomiale. La théorie géométrique de Galois intégre cette notion à travers les courbes elliptiques. Le grand théorème de Fermat a été démontré à l'aide de méthodes de cette nature. Il existe une théorie de Galois un peu particulière traitant des équations différentielles polynomiales. Cette théorie prend le nom de théorie de Galois différentielle. Elle étudie une famille particulière de corps appelée extension différentielle. Ces corps possèdent des groupes de Galois. La résolution d'une équation algébrique correspond aussi à l'analyse du groupe associé et permet la résolution d'une équation différentielle. Le corps commutatif est l'objet de la théorie de Galois. C'est donc naturellement la structure centrale de la théorie. La technique la plus importante de construction correspond à l'extension, c'est-à-dire à un corps qui contient le corps d'origine. À partir d'un corps de base, souvent le plus petit, celui engendré par l'unité, qui est un corps cyclique (construit à partir d'un groupe cyclique d'ordre un nombre premier) ou celui des rationnels une nouvelle structure est créée. Cette méthode permet la création d'une zoologie décrivant les différentes propriétés de la structure. Un corps peut ainsi être par exemple algébrique, simple, parfait, quadratique,séparable, cyclotomique ou algébriquement clos. Il existe des théorèmes importants, comme celui de l'élément primitif ou celui de Wedderburn qui assurent que tout corps fini est commutatif. Une extension possède une structure d'espace vectoriel sur son corps de base. Cette structure est importante à deux titres: Elle permet de classifier l'étude des différents corps, ceux de dimension finie dit encore extension finie et les autres. De même qu'en algèbre linaire, le premier cas est infiniment plus simple que l'autre. Elle est ensuite un outil qui permet la démonstration de nombreuses propriétés en adjoignant à la théorie les théorèmes d'algèbres linéaires. On peut citer par exemple le théorème de Gauss-Wantzel dont la démonstration se trouve dans le paragraphe applications des tours d'extension quadratique ou le théorème d'Abel-Ruffini qui utilise une diagonalisationd'endomorphisme. Le cas de dimension infinie est largement plus complexe, il est partiellement traité dans la théorie des corps de classe. Un outil important de la théorie est le polynôme formel. Et la structure d'anneau est celle de l'ensemble des polynômes. Il est utilisé par exemple pour construire des extensions. Une extension est ainsi souvent le quotient de l'anneau des polynômes par un idéal engendré par un polynôme irréductible. Un polynôme joue un rôle particulier dans la théorie: le polynôme minimal qui est le polynôme unitaire de plus petit degré qui possède pour racine un élément donné. Ainsi, une extension est algébrique si tous les éléments possèdent un polynôme minimal, quadratique si le polynôme minimal de tout élément est de degré inférieur ou égal à deux, séparable si aucun polynôme minimal n'a de racine multiple, cyclotomique si l'extension est engendrée par une racine d'un polynôme cyclotomique. Un corps est parfait si toute extension est séparable. La théorie algébrique des nombres utilise aussi souvent des sous-ensembles d'une extension ne disposant que d'une structure d'anneau, comme par exemple les entiers algébriques. Cette structure est l'apport majeur du mathématicien portant le nom de la théorie. Le groupe de Galois est le groupe des automorphismes d'une extension laissant invariant le corps de base. Sous certaines conditions relativement générales, le corps est entièrement caractérisé par son groupe de Galois. Une extension satisfaisant ces conditions est dite galoisienne. En particulier, si la structure d'espace vectoriel est de dimension finie, alors le groupe d'une extension abélienne a pour ordre la dimension du groupe. Comme il est largement plus simple d'étudier un groupe fini qu'une structure de corps, l'analyse du groupe est une puissante méthode pour comprendre le corps. Le groupe de Galois est à l'origine de nombreux théorèmes. On peut citer le théorème fondamental de la théorie, le théorème d'Abel-Ruffini ou celui de Kronecker-Weber. Le terme de classique est largement utilisé, même s'il ne possède pas de définition précise. On le trouve par exemple, sur la page de présentation d'un membre de l'Académie des sciences : Jean-Pierre Ramis. Il est aussi utilisé largement par Daniel Bertrand professeur à l'université de Paris VI. Il désigne en général la théorie recouvrant les extensions algébriques finies et séparables. la théorie traite essentiellement des extensions normales et donc galoisiennes. Les résultats principaux sont le théorème de l'élément primitif et le théorème fondamental de la théorie de Galois. Ce cadre permet par exemple la démonstration du théorème d'Abel-Ruffini de Gauss-Wantzel ou de Kronecker-Weber, il est utilisé dans la classification des corps finis. L'étendue de cette théorie couvre l'état de la science à l'époque de Weber c'est-à-dire la fin du xixe siècle, même si maintenant elle est très généralement présenté avec le formalisme d'Artin. Cela correspond un peu au cas de la dimension finie pour l'algèbre linéaire. La théorie de Galois classique traite le cas des extensions algébriques finies. Toutefois, elle ne s'avère pas assez puissante pour traiter aussi celui des extensions algébriques infinies. Pour cela une étude algébrique ne s'avère pas suffisante, il faut y ajouter l'utilisation de propriétés topologiques. Une extension algébrique est dite galoisienne si elle est séparable et normale. Son groupe de Galois peut alors être défini comme dans le cas classique, mais on y ajoute une topologie qui en fait un groupe topologique compact. Dans le cas d'une extension finie, cette topologie est discrète, de sorte que la seule information contenue dans le groupe de Galois est de nature algébrique. Dans ce cadre, il existe un analogue au théorème fondamental de la théorie de Galois, qui donne une correspondance entre les sous-groupes fermés du groupe de Galois et les extensions intermédiaires de corps. Il est en général difficile de déterminer le groupe de Galois d'une extension donnée, mais la question réciproque est tout aussi intéressante: soit un groupe donné, y a-t-il une extension sur un corps donné qui possède ce groupe comme groupe de Galois? Si oui la ou les préciser. C'est à cette question que la théorie inverse cherche à répondre. Dans le cas des groupes finis, un premier résultat montre que si n est un entier strictement positif alors il existe une extension du corps des rationnels ayant pour groupe de Galois legroupe symétrique d'ordre n. Par exemple, le corps de décomposition du polynôme rationnel Xn - X - 1 admet pour groupe de Galois le groupe symétrique d'ordre n. Le théorème de Cayley et le théorème fondamental de la théorie de Galois permet d'en déduire que, pour tout groupe fini G, il existe une extension d'un corps de nombres (c'est-à-dire une extension finiedes nombres rationnels) ayant G pour groupe de Galois. De façon plus précise la théorie inverse cherche à répondre à trois questions : Malgré d'importants progrès durant les trente dernières années du xxe siècle, en 2006 les trois questions restent très largement ouvertes. Certaines fonctions obtenues par addition, multiplication, division et composition de fonctions élémentaires (polynômes, exponentielle et logarithme par exemple) n'admettent aucuneprimitive qui puisse s'obtenir de la même manière. C'est le cas par exemple de la fonction gaussienne d'expression x ↦ exp(−x2/2). Ce fait est généralisé par la théorie de Galois différentielle, qui permet de déterminer, dans un ensemble des fonctions élémentaires, celles qui admettent une primitive élémentaire. Cette théorie étudie des corps particuliers appelés corps différentiels. Ce sont les corps K munis d'une dérivation δ, c'est-à-dire d'une application vérifiant la propriété suivante : Cette branche traite d'une famille de corps, il est donc naturel de la considérer comme un cas particulier de la théorie de Galois. Cependant l'analogie va plus loin et à bien des égards, cette théorie ressemble à la théorie classique. La différence principale est que, dans ce contexte, le groupe de Galois n'est plus un groupe fini mais en général un groupe algébrique.Histoire [modifier]
Genèse [modifier]
Gauss et les polynômes cyclotomiques [modifier]
Théorème d'Abel-Ruffini [modifier]
Évariste Galois [modifier]
Structures algébriques [modifier]
Théories de Galois [modifier]
Apports du XXe siècle [modifier]
Exemples [modifier]
Petit théorème de Fermat [modifier]

Duplication du cube [modifier]
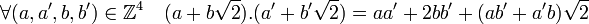


Équation cubique [modifier]
![P[X]=0 quad avec quad P[X]=X^3-3X+1;](http://upload.wikimedia.org/math/f/f/8/ff8d27380fe47a3187dffab0b36de1a4.png)
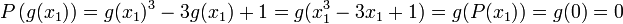
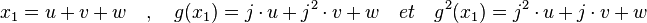
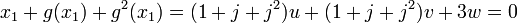 , donc
, donc 
 , donc
, donc 
 , donc
, donc 
Synthèse [modifier]
Applications [modifier]
Théorie algébrique des nombres [modifier]
Cryptographie [modifier]
Théorie des équations algébriques [modifier]
Géométrie algébrique [modifier]
Les structures utilisées [modifier]
Corps commutatifs [modifier]
Espace vectoriel [modifier]
Anneau [modifier]
Groupe [modifier]
Topologie [modifier]
Théories de Galois [modifier]
Théorie classique [modifier]
Théorie de Galois infinie [modifier]
Théorie géométrique [modifier]
Théorie inverse [modifier]
Théorie différentielle [modifier]

Théorie des corps de classes [modifier]
Notes et références [modifier]
Voir aussi [modifier]
Bibliographie [modifier]
Liens externes [modifier]
07:25 Publié dans Théorie de Galois | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Corps (mathématiques)
En mathématiques, et plus précisément en algèbre, un corps est une structure algébrique. De manière informelle, un corps est un ensemble dans lequel il est possible d'effectuer des additions, des soustractions, des multiplications et des divisions. Des exemples élémentaires de corps sont le corps des nombres rationnels (noté La théorie des corps est appelée, par certains, théorie de Galois[réf. nécessaire] ; cependant, la théorie de Galois désigne en général une méthode d'étude qui s'applique en particulier aux corps commutatifs et aux extensions de corps, qui forment l'exemple historique, mais s'étend aussi à bien d'autres domaines, par exemple l'étude des équations différentielles (théorie de Galois différentielle), ou des revêtements. Autrement dit, la théorie de Galois est une branche de la théorie des corps.Corps (mathématiques)
![]() Pour les articles homonymes, voir Corps.
Pour les articles homonymes, voir Corps. ), le corps des nombres réels (noté
), le corps des nombres réels (noté  ), le corps des nombres complexes (noté
), le corps des nombres complexes (noté  ) et le corps
) et le corps  des congruences modulo p où p est un nombre premier. L'exemple le plus simple de corps non commutatif (parfois appelés anneau à division, suivant l'anglais) est celui des quaternions.
des congruences modulo p où p est un nombre premier. L'exemple le plus simple de corps non commutatif (parfois appelés anneau à division, suivant l'anglais) est celui des quaternions.
Sommaire[masquer] |
Jusqu'au xixe siècle, les ensembles de nombres ont paru tellement naturels que l'on ne s'est jamais préoccupé de leur donner un nom, ni même de définir avec précision leur structure1. Cependant, avec la naissance de l'étude des nombres algébriques, il est apparu d'autres ensembles de nombres que les rationnels, les réels et les complexes. Il est devenu nécessaire de préciser la structure de corps, puis la notion d'entiers sur ce corps et enfin la notion d'anneau. C'est à l'école allemande que l'on doit le développement de ces notions. C'est Richard Dedekind qui définit pour la première fois la structure de corps (Körper en allemand)2 et c'est la raison pour laquelle un corps quelconque est souvent nommé K ou Un corps est un ensemble K muni de deux lois internes notées en général + et × vérifiant les axiomes suivants : On parle alors du corps Les premiers corps étudiés étant des ensembles de nombres (rationnels, réels, complexes, algébriques), la multiplication y était commutative. C'est la raison pour laquelle, initialement, dans la définition d'un corps, la multiplication devait être commutative. Actuellement, la tendance est plutôt de ne pas exiger la commutativité de la multiplication3 ou du moins de préciser la nature des corps étudiés4 ; on appelle alors corps commutatif un corps dont la multiplication est commutative. Les corps non commutatifs sont parfois appelés corps gauches ou anneaux à division. Cette terminologie est inspirée de l'anglais où un corps commutatif est appelé field (champ) et un corps non nécessairement commutatif division ring(anneau à division). Exemples de corps : Un sous-corps d'un corps K est une partie non vide L de K, stable par S'il existe un entier naturel n non nul tel que Par exemple le corps Ce sont les corps dont le nombre d'éléments est fini. L'étude des corps finis est tardive dans l'étude des corps. On démontre qu'un corps fini est toujours commutatif, de cardinal égal à la puissance d'un nombre premier. Il est en fait possible de dresser la liste de tous les corps finis (à isomorphisme près). Le plus petit corps fini est celui des booléens, dont voici les tables d'addition et de multiplication :Fragments d'histoire [modifier]
 . En 1910, Ernst Steinitz fonde la théorie axiomatique des corps. La structure de corps s'insère dans une hiérarchie comprenant le monoïde, le groupe, l'anneau, et donne lieu à la définition de l'espace vectoriel, et de l'algèbre.
. En 1910, Ernst Steinitz fonde la théorie axiomatique des corps. La structure de corps s'insère dans une hiérarchie comprenant le monoïde, le groupe, l'anneau, et donne lieu à la définition de l'espace vectoriel, et de l'algèbre.Définition et exemple [modifier]

 .
.
 est un corps commutatif ;
est un corps commutatif ; est un corps commutatif ;
est un corps commutatif ;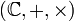 est un corps commutatif ;
est un corps commutatif ; est un corps non commutatif ;
est un corps non commutatif ; , où p est un nombre premier, est un corps commutatif.
, où p est un nombre premier, est un corps commutatif. et
et 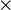 , telle que L munie des lois induites soit un corps.
, telle que L munie des lois induites soit un corps.Caractéristique [modifier]
 (avec n termes) est nul, on appelle caractéristique du corps le plus petit entier positif non nul vérifiant cette propriété. S'il n'existe pas d'entier non nul vérifiant cette propriété, on dit que le corps est de caractéristique nulle (parfois aussi grande que l'on veut).
(avec n termes) est nul, on appelle caractéristique du corps le plus petit entier positif non nul vérifiant cette propriété. S'il n'existe pas d'entier non nul vérifiant cette propriété, on dit que le corps est de caractéristique nulle (parfois aussi grande que l'on veut). est de caractéristique nulle alors que le corps
est de caractéristique nulle alors que le corps  est de caractéristique p. On démontre qu'un corps possède toujours pour caractéristique soit 0 soit un nombre premier.
est de caractéristique p. On démontre qu'un corps possède toujours pour caractéristique soit 0 soit un nombre premier.Corps finis [modifier]
| + | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
| x | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
Les corps finis les plus connus sont les corps de congruences modulo un nombre premier comme dans le cas ci-dessus, mais il en existe une infinité d’autres, comme par exemple ceux-ci, respectivement à quatre et neuf éléments, dont nous donnons ci-dessous les « tables de Pythagore », successivement pour la première loi de composition dite « addition », puis pour la deuxième dite « multiplication ». Nous désignons dans chaque cas comme a l’élément neutre de la première loi de composition, b celui de la deuxième. Quatre éléments :
| + | a | b | c | d |
| a | a | b | c | d |
| b | b | a | d | c |
| c | c | d | a | b |
| d | d | c | b | a |
| x | a | b | c | d |
| a | a | a | a | a |
| b | a | b | c | d |
| c | a | c | d | b |
| d | a | d | b | c |
Neuf éléments :
| + | a | b | c | d | e | f | g | h | i |
| a | a | b | c | d | e | f | g | h | i |
| b | b | c | a | e | f | d | h | i | g |
| c | c | a | b | f | d | e | i | g | h |
| d | d | e | f | g | h | i | a | b | c |
| e | e | f | d | h | i | g | b | c | a |
| f | f | d | e | i | g | h | c | a | b |
| g | g | h | i | a | b | c | d | e | f |
| h | h | i | g | b | c | a | e | f | d |
| i | i | g | h | c | a | b | f | d | e |
| x | a | b | c | d | e | f | g | h | i |
| a | a | a | a | a | a | a | a | a | a |
| b | a | b | c | d | e | f | g | h | i |
| c | a | c | b | g | i | h | d | f | e |
| d | a | d | g | c | f | i | b | e | h |
| e | a | e | i | f | g | b | h | c | d |
| f | a | f | h | i | b | d | e | g | c |
| g | a | g | d | b | h | e | c | i | f |
| h | a | h | f | e | c | g | i | d | b |
| i | a | i | e | h | d | c | f | b | g |
L'ensemble Plus généralement, un anneau unitaire est un ensemble A muni de deux lois + et ×, et vérifiant les axiomes suivants : Si l'anneau A est intègre, c’est-à-dire si ou encore, l'anneau est presque un corps car il ne lui manque plus que l'inversibilité pour la multiplication. Exemple : Un anneau intègre (unitaire) est un corps si et seulement si {0} et A (les idéaux triviaux) sont les seuls idéaux. Un anneau intègre (unitaire) A est un corps si et seulement si tout A-module est libre. Partant du corps L'étude des polynômes à coefficient dans un corps commutatif et la recherche de leurs racines a développé considérablement la notion de corps. Si f est un polynôme de degré n sur un corps commutatif K, l'équation f(x) = 0 est une équation algébrique dans K. Si, de plus, f est un polynôme irréductible, l'équation est dite irréductible. Lorsque n ≥ 2, trouver les solutions d'une telle équation demande de se placer dans un corps plus grand que K, une extension de corps. Par exemple, l'équation x2 − 2 = 0 est irréductible dans Un corps de rupture d'un polynôme est, par exemple, un corps minimal contenant K et une racine de f. Le corps de décomposition de f est le plus petit corps contenant K ainsi que toutes les racines de f. L'étude des corps de décomposition d'un polynôme et du groupe de permutations de ses racines forme la branche des mathématiques que l'on appelle la théorie de Galois. On retrouve la théorie des corps dans l'étude de certaines fonctions comme les fonctions rationnelles ou les fonctions elliptiques.Corps et anneau [modifier]
 n'est pas un corps car la plupart des éléments de
n'est pas un corps car la plupart des éléments de 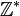 ne sont pas inversibles : par exemple, il n'existe pas d'entier relatif n tel que 2n = 1 donc 2 n'est pas inversible.
ne sont pas inversibles : par exemple, il n'existe pas d'entier relatif n tel que 2n = 1 donc 2 n'est pas inversible.
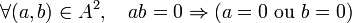 ,
,
 est le corps des fractions de
est le corps des fractions de 
Corps et espace vectoriel [modifier]
 , il est naturel de s'intéresser à
, il est naturel de s'intéresser à  , ensemble des n-uplet de réels. On est amené à le munir d'une addition et d'une multiplication par un réel. La structure ainsi définie (une addition interne munissant l'ensemble d'une structure de groupe et une multiplication externe possédant des propriétés de distributivité et d'associativité) est appelée espace vectoriel sur
, ensemble des n-uplet de réels. On est amené à le munir d'une addition et d'une multiplication par un réel. La structure ainsi définie (une addition interne munissant l'ensemble d'une structure de groupe et une multiplication externe possédant des propriétés de distributivité et d'associativité) est appelée espace vectoriel sur  . Il est alors naturel de définir ce que pourrait être un espace vectoriel sur un corps K quelconque.
. Il est alors naturel de définir ce que pourrait être un espace vectoriel sur un corps K quelconque.Corps et équation algébrique [modifier]
 mais possède des racines dans
mais possède des racines dans  ou mieux dans
ou mieux dans ![mathbb Q[sqrt 2]](http://upload.wikimedia.org/math/d/b/5/db51c502f6ea3908be57943d0ba5af9a.png) . L'équation x2 + 1 = 0 ne possède pas de solution dans
. L'équation x2 + 1 = 0 ne possède pas de solution dans  mais en possède dans
mais en possède dans  ou mieux dans
ou mieux dans ![mathbb Q[i]](http://upload.wikimedia.org/math/2/8/3/2830a273d48073b03c768cce92401ea7.png) .
.Propriétés [modifier]
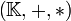 un corps commutatif. Alors tout polynôme de degré n admet au plus n zéros (ou racines) dans
un corps commutatif. Alors tout polynôme de degré n admet au plus n zéros (ou racines) dans  .
.
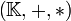 un corps commutatif. Alors tout sous-groupe fini de
un corps commutatif. Alors tout sous-groupe fini de  est un groupe cyclique.
est un groupe cyclique.Autres champs d'étude [modifier]
Structures additionnelles [modifier]
Voir aussi [modifier]
Notes et références [modifier]
Liens internes [modifier]
Sources [modifier]
07:24 Publié dans Corps (mathématiques) | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
01/12/2010
Analogues de la factorielle
Analogues de la factorielle
En mathématiques, de nombreuses fonctions analogues à la fonction factorielle ont été définies ; cette page recense les variantes les plus fréquemment rencontrées.
Sommaire[masquer] |
Primorielle [modifier]
La fonction primorielle est similaire à la fonction factorielle, mais ne prend en compte que le produit des nombres premiers.
Multifactorielles [modifier]
Afin d'alléger l'écriture, une notation courante est d'utiliser plusieurs points d'exclamation pour noter une fonction multifactorielle, le produit d'un facteur sur deux (n!!), sur trois (n!!!) ou plus.
n!!, la double factorielle de n, est définie de façon récurrente par :
Par exemple :
Certaines identités découlent de la définition :
Il faut faire attention de ne pas interpréter n!! comme la factorielle de n!, qui serait écrite (n!)! et est un nombre largement plus grand. Certains mathématiciens ont suggéré la notation alternative n!2 pour la double factorielle et d'une façon similaire n!n pour les autres multifactorielles, mais cet usage ne s'est pas répandu.
La double factorielle est la variante la plus commune, mais il est possible de définir de façon similaire la triple factorielle, etc. De façon générale, la ke factorielle, notée n!(k), est définie de façon récurrente par :
Hyperfactorielle [modifier]
L'hyperfactorielle de n, notée H(n), est définie par :
Pour n = 1, 2, 3, 4,... les valeurs de H(n) sont 1, 4, 108, 27 648,... (suite A002109 de l’OEIS).
La fonction hyperfactorielle est similaire à la fonction factorielle, mais produit de plus grands nombres. Sa croissance est en revanche comparable.
Superfactorielle [modifier]
Neil Sloane et Simon Plouffe ont défini la superfactorielle en 1995 comme le produit des n premières factorielles :
Par exemple, la superfactorielle de 4 est :
La suite des superfactorielles débute (depuis n = 0) par :
L'idée fut étendue en 2000 par Henry Bottomley à la superduperfactorielle, produit des n premières superfactorielles, débutant (depuis n = 0) par :
puis, par récurrence, à n'importe quelle factorielle de niveau supérieur, où la factorielle de niveau m de n est le produit des n premières factorielles de niveau m-1, c’est-à-dire, en notant f(n,m) la factorielle de n de niveau m :
où f(n,0) = n pour n > 0 et f(0,m) = 1.
Superfactorielle (définition alternative) [modifier]
Clifford Pickover, dans son livre Keys to Infinity (1995), définit la superfactorielle de n, notée n$ ($ étant un signe factoriel ! portant un S superposé), comme :
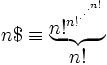 ,
,
ou, en utilisant la notation de Knuth :
 .
.
Les premiers éléments de la suite des superfactorielles sont :
Sous-factorielle [modifier]
La fonction sous-factorielle, notée !n, sert à calculer le nombre de permutations possible de n objets distincts de manière à ce qu'aucun objet ne se trouve à sa place.
Par exemple, il existe !n façon de glisser n lettres dans n enveloppes affranchies et adressées de manière à ce qu'aucune des lettres ne soit dans la bonne enveloppe.
Il existe différentes façons de calculer la sous-factorielle
Où Γ est la fonction gamma incomplète et e la base du logarithme népérien.
Où [x] désigne l'entier le plus proche de x
Les premières valeurs de cette fonction sont :
- !1 = 0
- !2 = 1
- !3 = 2
- !4 = 9
- !5 = 44
- !6 = 265
- !7 = 1854
- !8 = 14833
- !9 = 133496
- !10 = 1334961
- !11 = 14684570
- !12 = 176214841
- !13 = 2290792932
22:42 Publié dans Analogues de la factorielle | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Mathématiques discrètes
Mathématiques discrètes
|
|
Cet article est une ébauche concernant les mathématiques.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
Les mathématiques discrètes, parfois appelées mathématiques finies, sont l'étude des structures mathématiques fondamentalement discrètes, dans le sens où la notion de continuité n'est pas exigée ou supportée. La plupart des objets étudiés en mathématiques discrètes, si ce n'est pas la totalité, sont des ensembles dénombrables comme celui des entiers.
Les mathématiques discrètes sont devenues populaires ces dernières décennies du fait de leurs applications dans l'informatique. Les notations et les concepts des mathématiques discrètes sont utilisés pour exprimer ou étudier des problèmes et des objets en algorithmique et en programmation.
Les mathématiques discrètes incluent habituellement une partie de :
- la théorie des nombres ;
- la combinatoire ;
- la théorie des graphes ;
- la théorie de l'information ;
- la théorie des langages ;
- la théorie de la calculabilité et de la complexité.
22:40 Publié dans Mathématiques discrètes | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
22/11/2010
Andrew Wiles
Source : http://fr.wikipedia.org/wiki/Andrew_Wiles
Andrew Wiles
Sir Andrew John Wiles (né le 11 avril 1953 à Cambridge, Angleterre) est un mathématicien britannique, professeur à l'université de Princeton, aux États-Unis. Il est surtout connu pour sa démonstration du dernier théorème de Fermat en 1994, résolvant ainsi l'un des problèmes les plus connus de l'histoire des mathématiques.
Sommaire[masquer] |
Biographie [modifier]
Il entre à Clare College en 1974 pour y préparer un Ph.D. en mathématiques sur les lois de réciprocité et la conjecture de Birch et Swinnerton-Dyer, qu'il obtient en 1979. Il devient professeur à l'Université de Princeton au New Jersey en 1982.
En ce qui concerne la démonstration du dernier théorème de Fermat, l'odyssée de Wiles commence en 1985 quand Ken Ribet, partant d'une idée de Gerhard Frey, démontre que ce théorème résulterait de la conjecture de Shimura-Taniyama-Weil qui affirme que toute courbe elliptiqueest paramétrable par une forme modulaire. Bien que moins familière que le théorème de Fermat, elle est la plus significative, car elle touche au cœur de la théorie des nombres.
Cependant, personne n'a la moindre piste de travail pour la démontrer. Travaillant dans le plus grand secret pendant huit ans, et faisant part de ses idées et progrès à Nicholas Katz, un collègue de Princeton, Wiles démontre la conjecture de Shimura-Taniyama-Weil et, par conséquent, le théorème de Fermat. Comme toute démonstration de cette ampleur, elle est un tour de force riche en nouvelles idées.
Pour dévoiler sa démonstration, Wiles s'y prend de manière quasi théâtrale. Il annonce trois conférences (les 21, 22 et 23 juin 1993) sans en donner l'objet, ce qu'il ne fait que lors de la dernière en précisant que le grand théorème de Fermat est un corollaire de ses principaux résultats. Il agit ainsi pour s'assurer que la paternité de sa démonstration ne lui soit pas disputée après coup.
Dans les mois qui suivent, le manuscrit de sa démonstration circule auprès d'un petit nombre de mathématiciens. Plusieurs critiques sont émises contre la démonstration que Wiles a présentée en 1993, presque toutes de l'ordre du détail et résolues rapidement, sauf une, qui met en évidence une lacune. Avec l'aide de Richard Taylor, Wiles réussit à contourner le problème soulevé, en octobre 1994. Son travail met ainsi fin à une recherche qui a duré plus de 300 ans.
Il est aussi l'auteur d'autres travaux importants en théorie des nombres. Avec John Coates (qui fut son directeur de thèse), il a obtenu plusieurs résultats sur la conjecture de Birch et Swinnerton-Dyer et a collaboré avec Barry Mazur sur les extensions cyclotomiques.
Il est fait Chevalier commandeur de l'Ordre de l'Empire britannique (KBE) en 20001.
Bibliographie [modifier]
- Simon Singh, Le Dernier Théorème de Fermat, Hachette Littératures collection Pluriel Sciences
Notes et références [modifier]
- London Gazette : n° 55710, p. 34 [archive], 31-12-1999
Lien externe [modifier]
- (en) Biographie
- (en) Le texte de la preuve du dernier théorème de Fermat (pdf de 10 Mo)
08:45 Publié dans Andrew Wiles | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Diophante d'Alexandrie
Source : http://fr.wikipedia.org/wiki/Diophante
Diophante d'Alexandrie
Diophante d'Alexandrie (env. 200/214 - env. 284/298) était un mathématicien grec. Surtout connu pour son étude des équations diophantiennes, il est surnommé le « père de l'algèbre ».
Sommaire[masquer] |
Biographie [modifier]
Peu de choses sont connues de sa vie. Il vécut à Alexandrie et mourut à 84 ans. Diophante était probablement un babylonien hellène. Son œuvre est en partie perdue.
Il est connu pour son étude des équations à variables rationnelles ( ) et les équations diophantiennes furent nommées en son honneur. Son nom donne l'adjectif diophantien, souvent utilisé en théorie des nombres pour décrire un problème qui s'y rapporte.
) et les équations diophantiennes furent nommées en son honneur. Son nom donne l'adjectif diophantien, souvent utilisé en théorie des nombres pour décrire un problème qui s'y rapporte.
Son ouvrage le plus important est son Arithmétique, qui influença les mathématiciens arabes et plus tard ceux de la Renaissance.
Diophante a aussi écrit un traité sur les nombres polygonaux, le plus ancien de cette science ; il ne nous en reste que 10 livres sur 131. Six d'entre eux ont été publiés en latin et annotés par Claude-Gaspard Bachet en 1621, en latin et grec et annotés par Pierre de Fermat à Toulouse en1670 (après sa mort), et ont été traduits en français par Simon Stevin et Albert Girard en 1625 (après la mort de Stevin).
Diophante s'intéresse notamment aux problèmes suivants :
- résolution d'équations quadratiques (du type ax2=bx+c).
- détermination de valeurs faisant de 2 expressions linéaires des carrés (ex: trouver x tel que 10x+9 et 5x+4 sont tous deux des carrés).
- décomposition d'un nombre en somme de 2 carrés. Il semble que Diophante sache d'expérience que les entiers de la forme 4n+3 ne s'écrivent pas comme la somme de 2 carrés.
- partage d'un carré en 2 carrés : il explique notamment comment partager 16 en somme de 2 carrés : (16/5)2+(12/5)2. C'est en marge de ce problème que Fermat inscrit sur son exemplaire des Arithmetica sa fameuse note, selon laquelle il est impossible de partager un cube en 2 cubes, un bicarré en 2 bicarrés, et plus généralement une puissance quelconque sauf le carré, en 2 puissance de même exposant. Il faudra attendre 1995 pour avoir une démonstration de ce résultat par Andrew Wiles.
Son épitaphe [modifier]
Mais il est également connu pour son épitaphe : problème, attribué à Métrodore (vers 500), permettant de trouver l'âge de Diophante d'Alexandrie à sa mort. Ce problème partage la vie de Diophante en parties inégales représentées par des fractions et permet de calculer la durée de sa vie, soit 84 ans. Voici le problème en abrégé : L'enfance de Diophante occupa un sixième de toute sa vie. Le douzième fut pris par son adolescence. Après une nouvelle période équivalente au septième de sa vie, il se maria. Cinq ans plus tard, il eut un fils. La vie de ce fils fut exactement une demie de celle de son père. Diophante mourut quatre ans après la mort de son fils.
Une version de ce problème a été composée en alexandrins par H. Eutrope :
Passant, sous ce tombeau repose Diophante.
Ces quelques vers tracés par une main savante
Vont te faire connaître à quel âge il est mort.
Des jours assez nombreux que lui compta le sort,
Le sixième marqua le temps de son enfance ;
Le douzième fut pris par son adolescence.
Des sept parts de sa vie, une encore s'écoula,
Puis s'étant marié, sa femme lui donna
Cinq ans après un fils qui, du destin sévère
Reçut de jours hélas ! deux fois moins que son père.
De quatre ans, dans les pleurs, celui-ci survécut.
Dis, si tu sais compter, à quel âge il mourut.
La réponse revient à résoudre l'équation suivante : x/6 + x/12 + x/7 + 5 + x/2 + 4 = x. On trouve x = 84 ans, âge auquel Diophante mourut.
Annexes [modifier]
Bibliographie [modifier]
Voir aussi la bibliographie des Irem (France).
- Arithmétique (vers 250). Tome 3 ; éd. et tr. Roshdi Rashed. Paris : les Belles Lettres, 1984. (Collection des Universités de France). ccvi-264p. ISBN 2-251-00375-4.
- Arithmétique. Tome 4 ; éd. et tr. Roshdi Rashed. Paris : les Belles Lettres, 1984. (Collection des Universités de France). cxxxiv-322p. ISBN 2-251-00376-2.
- Cet article comprend des extraits du Dictionnaire Bouillet. Il est possible de supprimer cette indication, si le texte reflète le savoir actuel sur ce thème, si les sources sont citées, s'il satisfait aux exigences linguistiques actuelles et s'il ne contient pas de propos qui vont à l'encontre des règles de neutralité de Wikipédia.
Notes et références [modifier]
Liens externes [modifier]
- (en) J. J. O'Connor et E. F. Robertson, Diophantus
- Épitaphe de diophante
08:44 Publié dans Diophante d'Alexandrie | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
21/11/2010
Théorie des corps de classes
Source : http://fr.wikipedia.org/wiki/Th%C3%A9orie_des_corps_de_cl...
Théorie des corps de classes
|
|
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
En mathématiques, la théorie des corps de classes est une branche majeure de la théorie algébrique des nombres qui a pour objet la classification des extensions abéliennes, c'est-à-dire galoisiennes et de groupe de Galois commutatif, d'un corps donné. Plus précisément, il s'agit de décrire et de construire ces extensions en termes de propriétés arithmétiques du corps de base lui-même.
La plupart des résultats centraux ont été démontrés dans la période s'étendant entre 1900 et 1950. La théorie a été nommée ainsi en rapport avec les idées, conjectures et résultats de ses débuts, tel que le corps de classes de Hilbert, et s'organisa vers 1930.
De nos jours, le terme est généralement utilisé comme synonyme de l'étude de toutes les extensions abéliennes des corps de nombres algébriques (et plus généralement des corps globaux), mais aussi des corps de nombres p-adiques (et plus généralement des corps locaux).
Une autre ligne importante est la recherche de générateurs explicites pour les corps de classes de corps de nombres algébriques, c'est-à-dire de générateurs donnés par les valeurs defonctions transcendantes. C'est le Kronecker Jugendtraum (rêve de jeunesse de Kronecker). Il n'est encore réalisé que pour de rares cas, notamment celui du corps des rationnels (théorème de Kronecker-Weber, où les générateurs sont des racines de l'unité, c'est-à-dire des valeurs de la fonction exponentielle), et des corps quadratiques imaginaires (cas des corps à multiplication complexe, où les générateurs sont des valeurs de fonctions elliptiques).
Sommaire[masquer] |
Formulation en langage contemporain [modifier]
En langage moderne, il existe une extension abélienne maximale A de K, qui sera de degré infini sur K; et associée à A, un groupe de Galois G qui sera un groupe profini, donc ungroupe topologique compact, et aussi abélien. Nous nous intéressons à la description de G en termes de K.
Le résultat fondamental de la théorie des corps de classes établit que le groupe G est naturellement isomorphe à la complétion profinie du groupe des classes d'idèles (en) de K. Par exemple, lorsque K est le corps des nombres rationnels, le groupe de Galois G est (naturellement isomorphe à) un produit infini du groupe des unités des entiers p-adique pris sur tous les nombres premiers p, et l'extension abélienne maximale correspondante des rationnels est le corps engendré par toutes les racines de l'unité. Ceci était connu comme le théorème de Kronecker-Weber, originellement énoncé par Kronecker.
Pour une description du cas général, voir l'article détaillé : formation de classes.
En pratique, le programme prend la forme suivante. Étant donné un corps K et fixée une clôture séparable Ksep de K, on cherche à associer à toute extension finie abélienne L de Kincluse dans Ksep un groupe topologique C(L) et un homomorphisme continu de groupes NL/K de C(L) dans C(K) de manière que :
- L'application qui à L associe NL/K(C(L)) est une bijection entre extensions finies abéliennes de K incluse dans Ksep et sous-groupes ouverts d'indice fini de C(K).
- Pour chaque extension finie abélienne L/K incluse dans Ksep, on a un isomorphisme de groupes rL/K de Gal(L/K) dans C(K)/NL/K(C(L)), appelé application de réciprocité.
La théorie du corps de classes a été décrite pour une famille variée de corps, parmi lesquels les corps de nombres algébriques et les corps de nombres p-adiques.
L'exemple le plus simple est celui des corps finis. Si K est un corps fini de cardinal q, on pose 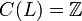 et NL/K est égal à la multiplication par le degré [L/K] de L/K, pour toute extension finie L de K incluse dans Ksep. On a un homomorphisme de groupes de
et NL/K est égal à la multiplication par le degré [L/K] de L/K, pour toute extension finie L de K incluse dans Ksep. On a un homomorphisme de groupes de  dans Gal(Ksep/K) injectif et d'image dense, qui envoie 1 sur le Frobenius de K, c'est-à-dire sur l'automorphisme
dans Gal(Ksep/K) injectif et d'image dense, qui envoie 1 sur le Frobenius de K, c'est-à-dire sur l'automorphisme  . Si σ est un élément de Gal(L/K), il existe un unique n dans
. Si σ est un élément de Gal(L/K), il existe un unique n dans ![Z/[L:K]Z,](http://upload.wikimedia.org/math/f/1/b/f1b6e1618137683fe022a247fc9d95dc.png) tel que φKn prolonge σ. L'application de réciprocité est définie par
tel que φKn prolonge σ. L'application de réciprocité est définie par  .
.
Théorie du corps de classes local [modifier]
Il s'agit de la partie de la théorie concernant les corps locaux. Dans ce qui suit, on se restreint aux corps locaux dont le corps résiduel est fini.
Si K est un corps local de corps résiduel fini, il existe un homomorphisme de groupes topologiques, injectif et d'image dense, du groupe multiplicatif de K sur le groupe de Galois de l'extension abélienne maximale de K. Cet homomorphisme, appelé le symbole d'Artin (en), est défini de la façon suivante : à chaque élément premier de K est associé un automorphisme qui, restreint à toute sous-extension abélienne non ramifiée, est l'automorphisme de Frobenius de cette extension, et le symbole d'Artin se factorise à travers les groupes de normes associées aux sous-extensions finies. Il y a alors une correspondance de Galois des sous-extensions de l'extension abélienne maximale de K avec les sous-groupes (fermés pour la topologie de Krull) du groupe de Galois de cette extension, et donc, via le symbole d'Artin, avec les sous-groupes du groupe multiplicatif de K.
Le cas particulier le plus frappant est celui du groupe des unités : il est associé à l'extension non ramifiée maximale de K.
Corps de classes global [modifier]
Pour K un corps de nombres, la correspondance du corps de classes s'énonce comme la collection des correspondances locales en toutes les places non archimédiennes de K, à l'aide des idèles (en).
Historique [modifier]
La généralisation prit place dans un projet historique à long terme impliquant les formes quadratiques, les lois de réciprocité (en), les travaux de Kummer et de Kronecker/Hensel sur les idéaux et ses achèvements, la théorie de la cyclotomie, les extensions de Kummer, les conjectures de Hilbert et les démonstrations par de nombreux mathématiciens (Takagi, Hasse,Artin, Furtwängler (en) et d'autres). Le théorème d'existence de Takagi crucial était connu en 1920 et tous les autres résultats principaux vers 1930. La propriété de principalisation est une des dernières conjectures classiques à avoir été démontrée.
Dans les années 1930 et ultérieurement, l'usage des extensions infinies et de la théorie de Krull sur leurs groupes de Galois a été considérée comme de plus en plus utile. Elle se mélange avec la dualité de Pontryagin pour donner une formulation plus claire mais plus abstraite du résultat central, la loi de réciprocité d'Artin (en). Elle est aussi basée sur la théorie d'Iwasawa.
Après que les résultats furent reformulés en termes de cohomologie galoisienne, avec la notion de formation de classes, ce domaine subit une relative stagnation. Le programme de Langlands lui donna une impulsion nouvelle, dans sa forme de « théorie non abélienne des corps de classes (en) » , bien que cette description puisse être à présent considérée comme restrictive si elle est confinée à la question de savoir comment les idéaux premiers se décomposent dans les extensions galoisiennes générales.
Références [modifier]
- (en) Georges Gras, Class Field Theory : From Theory to Practice [détail des éditions]
- (en) Jürgen Neukirch, Algebraic number theory [détail des éditions]
- (en) Jürgen Neukirch, Alexander Schmidt, Kay Wingberg Cohomology of number fields [détail des éditions]
- Jean-Pierre Serre, Corps locaux [détail des éditions]
Liens externes [modifier]
- (en) Page de J. S. Milne, professeur émérite à l'Université du Michigan
- Un texte sur cette théorie sur le blog de Maurice Mischler, de l'université de Lausanne
21:42 Publié dans Théorie des corps de classes | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Conjecture de Dubner
Source : http://fr.wikipedia.org/wiki/Conjecture_de_Dubner
Conjecture de Dubner
Selon Harvey Dubner :
- Si un p-jumeau est un nombre premier ayant un jumeau, alors tout nombre pair supérieur à 4208 est la somme de deux p-jumeaux.1
Cette conjecture a été vérifiée par logiciel pour tous les nombres pairs jusqu'à 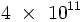
Si cette conjecture était démontrée, cela prouverait à la fois la conjecture de Goldbach (tout nombre pair est la somme de deux nombres premiers) et la conjecture des nombres premiers jumeaux (il existe une infinité de nombres premiers jumeaux).
Sommaire[masquer] |
Généralisation [modifier]
L'intérêt de la conjecture de Dubner par rapport à la conjecture de Goldbach, c'est qu'elle est plus exigeante, dans la mesure où les nombres premiers jumeaux sont plus rares que les nombres premiers.
Si on considère comme miraculeuse la conjecture de Goldbach, la conjecture de Dubner l'est encore plus.
En généralisant encore, voici quatre nouvelles conjectures dérivées, encore plus exigeantes :
Nommons min-jumeau le plus petit d'une paire de nombres premiers jumeaux, et max-jumeau le plus grand d'une paire de nombres premiers jumeaux.
- Tout nombre pair (assez grand) est la somme de deux min-jumeaux.
- Tout nombre pair (assez grand) est la somme de deux max-jumeaux.
- Tout nombre pair (assez grand) est la somme d'un min-jumeau et d'un max-jumeau, avec min-jumeau>max-jumeau.
- Tout nombre pair (assez grand) est la somme d'un min-jumeau et d'un max-jumeau, avec min-jumeau<max-jumeau.
Sources [modifier]
- Harvey Dubner, "Twin Prime Conjectures", Journal of Recreational Mathematics, Vol.30(3), 1999-2000
- Jean-Paul Delahaye, "Nombres premiers inévitables et pyramidaux", Pour la science n°296, juin 2002, pages 98 à 102
Articles connexes [modifier]
Liens externes [modifier]
Notes [modifier]
- Les deux nombres ne sont pas jumeaux entre eux, mais chacun dispose d'un jumeau.
21:41 Publié dans Conjecture de Dubner | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Nombres premiers jumeaux
Source : http://fr.wikipedia.org/wiki/Conjecture_des_nombres_premi...
Nombres premiers jumeaux
En mathématiques, deux nombres premiers jumeaux sont deux nombres premiers qui ne diffèrent que de 2. Hormis pour la paire (2, 3), cette distance de 2 est la plus petite distance possible entre deux nombres premiers. Les plus petits nombres premiers jumeaux sont 3 et 5, 5 et 7, 11 et 13.
Au 15 janvier 2007, les plus grands nombres premiers jumeaux connus sont 2003663613 × 2195000±1, qui possèdent 58 711 chiffres en écriture décimale et furent découverts par Éric Vautier dans le cadre des projets de calcul distribué Twin Prime Search et PrimeGrid1.
La conjecture des nombres premiers jumeaux stipule qu'il existe une infinité de nombres premiers jumeaux ; les observations numériques et des raisonnements heuristiquesjustifient la conjecture, mais aucune démonstration n'en a encore été faite.
Sommaire[masquer] |
Définition [modifier]
Soit (p,q) un couple de nombres entiers tel que p et q soient tous les deux des nombres premiers et p < q. On dit que (p,q) forme un couple de nombres premiers jumeaux si q = p + 2.
Liste des premiers nombres premiers jumeaux [modifier]
L'ensemble des nombres premiers jumeaux jusqu'à 1000 :
| (3, 5) | (5, 7) | (11, 13) | (17, 19) | (29, 31) |
| (41, 43) | (59, 61) | (71, 73) | (101, 103) | (107, 109) |
| (137, 139) | (149, 151) | (179, 181) | (191, 193) | (197, 199) |
| (227, 229) | (239, 241) | (269, 271) | (281, 283) | (311, 313) |
| (347, 349) | (419 , 421) | (431 , 433) | (461 , 463) | (521 , 523) |
| (569 , 571) | (599 , 601) | (617 , 619) | (641 , 643) | (659 , 661) |
| (809 , 811) | (821 , 823) | (827 , 829) | (857 , 859) | (881 , 883) |
Quelques propriétés [modifier]
- Le couple (2,3) est le seul couple de nombres premiers consécutifs.
- En omettant le couple (2,3), 2 est la plus petite distance possible entre deux nombres premiers ; deux nombres premiers jumeaux sont ainsi deux nombres impairs consécutifs.
- Tout couple de nombres premiers jumeaux (à l'exception du couple (3,5)) est de la forme (6n − 1,6n + 1) pour un certain entier n. En effet, toute série de trois nombres entiers naturels consécutifs comporte au moins un multiple de 2 (éventuellement deux) et un seul multiple de 3 ; ces deux multiples sont confondus entre les deux nombres premiers jumeaux.
- Il est possible de démontrer que, pour tout entier
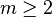 , le couple (m,m + 2) est constitué de nombres premiers jumeaux si et seulement si
, le couple (m,m + 2) est constitué de nombres premiers jumeaux si et seulement si ![4[(m-1)! + 1] + m equiv 0 mod m(m+2)](http://upload.wikimedia.org/math/9/a/f/9af894ecf844d14a19355b74d51b74fb.png) . Cette caractérisation modulaire et factorielle des nombres premiers jumeaux a été découverte par P. A. Clement en19492.
. Cette caractérisation modulaire et factorielle des nombres premiers jumeaux a été découverte par P. A. Clement en19492. - La série des inverses de nombres premiers jumeaux est convergente vers la constante de Brun, au contraire de la série des inverses de nombres premiers. Cette propriété fut démontrée par Viggo Brun en 19193.
Record [modifier]
Le 15 janvier 2007, deux projets de calcul distribué, Twin Prime Search et PrimeGrid, ont découvert le plus grand couple de nombres premiers jumeaux actuellement connu (c’est-à-dire en janvier 2007). Le découvreur est le français Éric Vautier1.
Le couple record est 2003663613 × 2195000±1 ; les deux nombres possèdent 58 711 chiffres en écriture décimale.
Conjecture des nombres premiers jumeaux [modifier]
La conjecture des nombres premiers jumeaux affirme qu'il existe une infinité de nombres premiers jumeaux:
Il existe une infinité de nombres premiers p tels que p + 2 soit aussi premier.
Bien que la plupart des chercheurs en théorie des nombres pensent que cette conjecture est vraie, elle n'a jamais été démontrée. Ils se basent sur des observations numériques et des raisonnements heuristiques utilisant la distribution probabiliste des nombres premiers.
En 1849, Alphonse de Polignac émit une conjecture plus générale : la conjecture de De Polignac dont le cas n = 2 correspond à la conjecture des nombres premiers jumeaux.
Il existe également une version plus forte de cette conjecture : la conjecture de Hardy-Littlewood, qui fournit une loi de distribution des nombres premiers jumeaux et qui s'inspire duthéorème des nombres premiers.
La conjecture des nombres premiers jumeaux est un cas particulier de la conjecture de Schinzel.
Résultats partiels [modifier]
En 1940, Paul Erdős démontra l'existence d'une constante c < 1 et d'une infinité de nombres premiers p tels que :
- p' − p < cln(p) où p' désigne le nombre premier suivant immédiatement p.
Ce résultat fut plusieurs fois amélioré ; en 1986, Maier montra qu'une constante c < 0,25 pouvait être atteinte.
En 2003, Goldston et Yildirim ont démontré que, pour tout c > 0, il existe une infinité de nombres premiers p tels que p' - p < c ln(p).
En 1966, J.R. Chen a démontré l'existence d'une infinité de nombres premiers p tels que p + 2 soit le produit d'au plus deux facteurs premiers (un tel nombre, produit d'au plus deux facteurs premiers, est dit 2-presque-premier).
Son approche fut celle de la théorie du crible, qu'il utilisa pour traiter de façon similaire la conjecture des nombres premiers jumeaux et la conjecture de Goldbach.
La conjecture de Hardy-Littlewood [modifier]
Il existe aussi une généralisation de la conjecture des nombres premiers jumeaux, connue sous le nom de conjecture de Hardy - Littlewood, en rapport avec la distribution des premiers jumeaux, par analogie avec le théorème des nombres premiers. Soit π2(x) le nombre de nombres premiers p ≤ x tels que p + 2 soit aussi premier.
On note C2 le nombre obtenu de la façon suivante :
(ici le produit s'étend à l'ensemble des nombres premiers p ≥ 3). C2 est appelé constante des nombres premiers jumeaux4
Alors la conjecture de Hardy-Littlewood s'énonce de la façon suivante :
(ce qui signifie que le quotient des deux expressions tend vers 1 quand x tend vers l'infini).
Comme le second membre à une limite infinie quand x tend vers l'infini, cette conjecture démontrerait que le nombre de nombres premiers jumeaux est bien infini.
Cette conjecture peut être justifiée (mais pas démontrée) en supposant que 1/ln(t) est la fonction de densité de la distribution des nombres premiers, une hypothèse suggérée par le théorème des nombres premiers. Cette conjecture est un cas particulier d'une conjecture plus générale appelée conjecture des n-uplets premiers de Hardy-Littlewood5 utilisée dans les recherches sur la conjecture de Goldbach.
Notes et références [modifier]
- (en) [pdf] Twin Prime Search, Communiqué officiel de la découverte du 15 janvier 2007 [archive]
- (en) P.A. Clement, Congruences for sets of primes, American Mathematical Monthly n° 56 (1949), pp. 23-25
- Viggo Brun, La série 1/5 + 1/7 + 1/11 + 1/13 + 1/17 + 1/19 + 1/29 + 1/31 + 1/41 + 1/43 + 1/59 + 1/61 + ... où les dénominateurs sont "nombres premiers jumeaux" est convergente ou finie, Bulletin des Sciences Mathématiques n°43 (1919), pp. 100-104 et 124-128
- Cette constante est parfois appelée constante de Shah-Wilson et son double nommée constante des nombres premiers jumeaux d'après Weisstein, Eric W. "Twin Primes Constant." From MathWorld--A Wolfram Web Resource [archive]
- d'après Weisstein, Eric W. "Twin Prime Conjecture." From MathWorld--A Wolfram Web Resource. [archive]
Voir aussi [modifier]
Articles connexes [modifier]
- Conjecture de Dubner
- Constante de Brun
- Nombre premier
- Nombre premier de Chen
- Nombres premiers cousins
- Nombres premiers sexy
Liens externes [modifier]
- (en) Twin Primes (Chris Caldwell)
- (en) Introduction to Twin Primes and Brun's Constant (Xavier Gourdon, Pascal Sebah)
- (en) Site de Primegrid. Projet de calcul réparti utilisant BOINC afin de rechercher des nombres premiers jumeaux
- Liste des 10001 premières paires de nombres premiers jumeaux (p,p+2), présentées par leur moyenne p+1
21:40 Publié dans NOMBRES PREMIERS, Nombres premiers jumeaux | Lien permanent | Commentaires (1) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Théorème des quatre carrés de Lagrange
Source : http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_des_quatr...
Théorème des quatre carrés de Lagrange
Le théorème des quatre carrés de Lagrange, est également connu sous le nom de conjecture de Bachet ; il a été énoncé pour la première fois par Claude-Gaspard Bachet de Méziriac en 1621, dans les notes accompagnant sa traduction en latin du Diophante. C'est un cas particulier du Problème de Waring. Démontré en 1770 par le mathématicien françaisJoseph Louis Lagrange, il correspond à une équation diophantienne qui se résout avec les techniques de l'arithmétique modulaire. Il s'énonce de la façon suivante :
Plus formellement, pour tout entier positif n, il existe des entiers positifs a, b, c, d tels que :
Le mathématicien français Adrien-Marie Legendre améliora le théorème en 1798 en affirmant qu'un entier positif peut être exprimé comme la somme d'au plus trois carrés si et seulement s'il n'est pas de la forme
 .
.
Sa démonstration était incomplète, laissant une brèche qui fut comblée plus tard par le mathématicien allemand Carl Friedrich Gauss.
Le théorème des quatre carrés de Lagrange est un cas particulier du théorème du nombre polygonal de Fermat (en) et du problème de Waring.
La démonstration du théorème repose (en partie) sur l'identité des quatre carrés d'Euler :
Sommaire[masquer] |
Démonstration basée sur les quaternions d'Hurwitz [modifier]
Nous allons travailler sur l'ensemble des quaternions d'Hurwitz, également appelés entiers d'Hurwitz, qui sont des quaternions particuliers.
Quelques propriétés [modifier]
Les entiers d’Hurwitz [modifier]
Les entiers d’Hurwitz sont les nombres de la forme : a.(1 + i + j + k) / 2 + b.i + c.j + d.k avec  . Avec h = (1 + i + j + k) / 2, on peut écrire l’ensemble des entiers d’Hurwitz sous la forme
. Avec h = (1 + i + j + k) / 2, on peut écrire l’ensemble des entiers d’Hurwitz sous la forme ![mathbb{Z} [h,i,j,k]](http://upload.wikimedia.org/math/8/4/0/840ef30ae2eae5cbde635ada3b76039c.png)
On a alors la somme et le produit des deux entiers d’Hurwitz est un entier d’Hurwitz (les entiers d'Hurwitz forment un sous anneau de l'anneau formé par l'ensemble des quaternions, l'addition et la multiplication usuelles).
On rappelle que la norme d’un quaternion (et donc d’un entier d’Hurwitz) de la forme α = a + b.i + c.j + d.k est 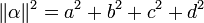
Il existe donc 24 nombres unités : 8 formés par 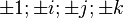 et 16 formés par
et 16 formés par 
Identité des quatre carrés d’Euler [modifier]
On démontre que si deux nombres s’écrivent sous forme de somme de quatre carrés, alors leur produit s’écrit aussi sous forme de somme de quatre carrés. On peut le démontrer, soit à partir de l’identité des quatre carrés d’Euler, soit en écrivant que la norme d’un produit est le produit des normes.
Division [modifier]
Les entiers d’Hurwitz obéissent à la propriété de la division selon laquelle, de la même manière qu’avec la division euclidienne :
Si a et b sont des entiers d’Hurwitz, b non nul, il existe un quotient q et un reste r tel que :
a=b.q+r avec 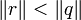 , q et r étant des entiers d’Hurwitz.
, q et r étant des entiers d’Hurwitz.
Les quaternions d'Hurwitz forment donc un anneau euclidien à gauche et à droite.
Par exemple :
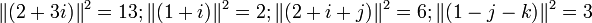
Comme 2 + 3i = (1 + i).(2 + i + j) + (1 − j − k),
2+3i divisé par 1+i admet comme couple (quotient,reste) le couple (2+i+j,1-j-k) Ce couple n’est pas unique puisque cette division admet aussi le couple (2+i+k,1+j-k)
On dira que a divise b (ou que a admet comme diviseur b) s’il existe q tel que a = b.q. q est alors unique.
Entier d’Hurwitz premier [modifier]
Un entier d’Hurwitz p est premier s’il n’admet comme diviseur que les nombre unités et p fois les nombres unités.
Or, si a divise b,  divise
divise  . Donc si
. Donc si  est premier, il ne peut exister d’entier divisant x ayant une norme différente de 1 ou de
est premier, il ne peut exister d’entier divisant x ayant une norme différente de 1 ou de  , donc x est un nombre d’Hurwitz premier.
, donc x est un nombre d’Hurwitz premier.
1+i est, par exemple, un entier d’Hurwitz premier, car  est premier.
est premier.
Algorithme d’Euclide [modifier]
On peut définir un algorithme d’Euclide dans ![mathbb{Z} [h,i,j,k]](http://upload.wikimedia.org/math/8/4/0/840ef30ae2eae5cbde635ada3b76039c.png) , de la même manière que dans
, de la même manière que dans  .
.
On peut ainsi trouver un plus grand diviseur commun à a et b (noté pgcd(a ,b)), c'est-à-dire celui ayant la plus grande norme. En toute rigueur, étant donné la non commutativité de cet ensemble, on doit définir un plus grand diviseur commun à droite, et un plus grand diviseur commun à gauche.
De même que dans  , on peut alors trouver u et v tels que pgcd(a,b)=a.u+b.v, avec u et v des entiers d’Hurwitz.
, on peut alors trouver u et v tels que pgcd(a,b)=a.u+b.v, avec u et v des entiers d’Hurwitz.
Propriété de la division d’un produit par un entier réel d’Hurwitz premier [modifier]
Si p est un entier réel d’Hurwitz premier (c'est-à-dire un nombre premier appartenant à  ) , et qui divise a.b, où a et b sont des entiers d’Hurwitz, alors p divise a ou p divise b.
) , et qui divise a.b, où a et b sont des entiers d’Hurwitz, alors p divise a ou p divise b.
Preuve
Supposons que p premier divise a.b mais ne divise pas a. Alors, un pgcd de a et p est 1, et il existe u et v tels que au+pv=1.
Alors en multipliant par b de chaque coté, on obtient bau+bpv=b. p divise ab donc bau, et p divise p donc bpv (comme p appartient à  , p commute avec les quaternions) .
, p commute avec les quaternions) .
Donc p divise b.
Théorème et lemme préliminaires [modifier]
Tout d’abord, remarquons que 0, 1 et 2 peuvent s’écrire sous forme de somme de 4 carrés (0 = 02 + 02 + 02 + 02;1 = 12 + 02 + 02 + 02 et 2 = 12 + 12 + 02 + 02).
Théorème [modifier]
Tout entier premier de  qui n’est pas un entier d’Hurwitz premier peut s’écrire sous forme de somme de quatre carrés.
qui n’est pas un entier d’Hurwitz premier peut s’écrire sous forme de somme de quatre carrés.
Preuve
Soit p remplissant les conditions précédentes. On peut donc écrire p sous la forme p = (a + bi + cj + dk)γ , avec  et
et 
On a alors le conjugué de p (égal à p puisque p appartient à  ) :
) : 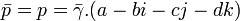
Alors 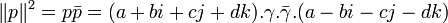
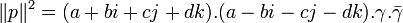 car
car 
Donc  avec (a2 + b2 + c2 + d2) et
avec (a2 + b2 + c2 + d2) et 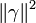 strictement supérieure à 1 et strictement inférieure à p.
strictement supérieure à 1 et strictement inférieure à p.
Étant donné que p est premier, la seule décomposition de p2 est donc p.p. On en déduit que (a2 + b2 + c2 + d2) = p.
Si a, b, c et d sont des entiers, p s’écrit comme somme de quatre carrés.
Si ce sont des demis-entiers, on peut alors trouver w tel que :
 et a + bi + cj + dk = w + a1 + b1i + c1j + d1k avec a1,b1,c1 et d1 des entiers pairs. On remarque que
et a + bi + cj + dk = w + a1 + b1i + c1j + d1k avec a1,b1,c1 et d1 des entiers pairs. On remarque que 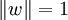
On a alors :
p = (a + bi + cj + dk)(a − bi − cj − dk)


Or comme a1,b1,c1 et d1 sont des entiers pairs, 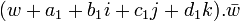 ne donnera que des entiers et sera donc de la forme A+Bi+Cj+Dk, avec A, B, C et D des entiers. De même pour son conjugué, d’où : p = (A + Bi + Cj + Dk)(A − Bi − Cj − Dk) = A2 + B2 + C2 + D2
ne donnera que des entiers et sera donc de la forme A+Bi+Cj+Dk, avec A, B, C et D des entiers. De même pour son conjugué, d’où : p = (A + Bi + Cj + Dk)(A − Bi − Cj − Dk) = A2 + B2 + C2 + D2
Donc p s’écrit comme somme de quatre carrés.
Lemme [modifier]
Soit p un entier premier impair, alors il existe l et m tels que p divise 1 + l2 + m2 (p, l et m appartenant à  )
)
Preuve
Soit p premier impair. Les différentes classes de congruence modulo p sont 0, 1, -1, ..., (p-1)/2, -(p-1)/2. Il y en a donc p.
 est équivalent à ( a
est équivalent à ( a  b ou a
b ou a  –b ) (modulo p). Les différents carrés modulo p sont donc 02,12,...,((p − 1) / 2)2. Il y en a donc 1 + (p − 1) / 2 = (p + 1) / 2.
–b ) (modulo p). Les différents carrés modulo p sont donc 02,12,...,((p − 1) / 2)2. Il y en a donc 1 + (p − 1) / 2 = (p + 1) / 2.
De même pour − 1 − m2, il y a (p + 1) / 2 éléments qui sont de cette forme, différents, modulo p. Supposons que ces deux ensembles soient disjoints. Alors il y aurait (p + 1) / 2 + (p + 1) / 2 = p + 1 éléments dans  , ce qui est faux puisqu’il y en a p. Donc au moins un élément est simultanément de la forme l2 et de la forme − 1 − m2 modulo p, donc il existe l et m tel que
, ce qui est faux puisqu’il y en a p. Donc au moins un élément est simultanément de la forme l2 et de la forme − 1 − m2 modulo p, donc il existe l et m tel que  modulo p c'est-à-dire
modulo p c'est-à-dire 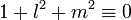 modulo p.
modulo p.
Il existe donc l et m tel que p divise 1 + l2 + m2.
Théorème des quatre carrés [modifier]
Tout entier de  peut s’écrire sous forme de somme de quatre carrés.
peut s’écrire sous forme de somme de quatre carrés.
Preuve
Soit p un entier impair premier. Il existe donc d’après le lemme précédant l et m entier tel que p divise 1 + l2 + m2. Donc p divise 1 + l2 + m2 = (1 + li + mj)(1 − li − mj).
Supposons que p soit un entier d’Hurwitz premier. Alors d’après un théorème précédant, p divise 1 + li + mj ou p divise 1 − li − mj. Or, ni  ni
ni  ne sont des entiers d’Hurwitz. Donc p n’est pas un entier d’Hurwitz premier.
ne sont des entiers d’Hurwitz. Donc p n’est pas un entier d’Hurwitz premier.
D’après le théorème précédant, p peut donc s’écrire sous forme de somme de quatre carrés.
Donc, si p est un entier impair premier, p peut donc s’écrire sous forme de somme de quatre carrés.
Si p=0, p=1 ou p=2, nous avons déjà vu que p peut s’écrire sous forme de somme de quatre carrés.
Si p est un entier, non premier, strictement supérieur à 2, alors p peut s’écrire sous forme de produit de nombre premiers. Ces nombres premiers peuvent s’écrire sous forme de carrés, et leur produits aussi, d’après la remarque sur l’identité des quatre carrés d’Euler. Donc p peut s’écrire sous forme de somme de quatre carrés.
Finalement, tout élément de  peut s’écrire sous forme de somme de quatre carrés.
peut s’écrire sous forme de somme de quatre carrés.
Fonctions arithmétiques [modifier]
Les fonctions arithmétiques permettent d'obtenir des résultats plus généraux. Si on pose r4(n) comme étant le nombre de façon de décomposer n sous forme d'une somme de 4 carrés, on obtient le résultat suivant:
 , pour | x | < 1.
, pour | x | < 1.
Moyennant l'utilisation des séries de Lambert, on en déduit le théorème suivant, dit théorème de Jacobi :
Par exemple, 1 n'est divisible que par lui-même, qui n'est pas congru à 0 modulo 4. Donc r4(1) = 8
3 des 8 formes sont :
1 = 12 + 02 + 02 + 02
1 = 02 + 12 + 02 + 02
1 = ( − 1)2 + 02 + 02 + 02
Articles connexes [modifier]
21:37 Publié dans Théorème des quatre carrés de Lagrange | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Problème de Waring
Source : http://fr.wikipedia.org/wiki/Probl%C3%A8me_de_Waring
Problème de Waring
En théorie des nombres, le problème de Waring, proposé en 1770 par Edward Waring, demande si, pour tout entier naturel k, il existe un entier naturel s tel que tout entier soit la somme d'au plus s puissances ke d'entiers. La réponse affirmative fut apportée par David Hilbert en 1909. Ce sujet est parfois décrit comme le théorème de Hilbert-Waring.
Pour chaque k, nous notons le plus petit s par g(k). Nous avons g(1) = 1. Quelques calculs montrent que 7 requiert 4 carrés, 23 requiert 9 cubes, et 79 requiert 19 puissances quatrièmes. Waring conjectura que ces valeurs étaient les meilleures possibles.
Le théorème des quatre carrés de Lagrange de 1770 affirme que chaque nombre naturel est la somme d'au plus quatre carrés ; puisque trois carrés ne sont pas suffisants, ce théorème établit g(2) = 4. Ce théorème fut conjecturé par Fermat en 1640 et sa première mention date de 1621.
Au fil des années, divers résultats sur les valeurs de g furent établis, en utilisant des techniques de démonstration de plus en plus sophistiquées et complexes. Par exemple, Liouvillemontra que g(4) vaut au plus 53. Hardy et Littlewood démontrèrent que tous les nombres suffisamment grands sont la somme d'au plus 19 puissances quatrièmes.
L'égalité g(3) = 9 fut établie entre 1909 et 1912 par Wieferich et A. J. Kempner, l'égalité g(4) = 19 en 1986 par R. Balasubramanian, F. Dress et J.-M. Deshouillers, l'égalité g(5) = 37 en 1964 par Chen Jingrun et l'égalité g(6) = 73 en 1940 par Pillai.
Toutes les autres valeurs de g sont connues aujourd'hui, grâce au travail de Dickson, Pillai, Rubugunday et Niven. Leur énoncé contient deux cas et il est conjecturé que le second cas ne peut jamais se produire ; dans le premier cas, la formule se lit
- g(k) = E((3/2)k) + 2k - 2 pour k ≥ 6.
Sommaire[masquer] |
Les majorations provisoires [modifier]
Avant que soient trouvées les valeurs exactes de g(n), des majorations avaient été déterminées. En voici quelques unes, pour n de 3 à 8.
Majoration de g(3) [modifier]
- 17 (Maillet, 1895)
- 13 (A. Fleck, 1906)
- 9 (Wieferich, 1909), valeur exacte.
Majoration de g(4) [modifier]
- 53 (J. Liouville, 1859)
- 47 (S. Réalis, 1878)
- 45 (É. Lucas, 1878)
- 41 (É. Lucas, 1878)
- 39 (A. Fleck, 1906)
- 38 (E. Landau, 1907)
- 37 (A. Wieferich, 1909)
- 35 (L. E. Dickson, 1933)
- 22 (H.E. Thomas, 1973)
- 21 (R. Balasubramanian, 1979)
- 20 (R. Balasubramanian, 1985)
- 19 (R. Balasubramanian, F. Dress, J.-M. Deshouillers, 1986), valeur exacte
Majoration de g(5) [modifier]
- 192 (A. Fleck, 1906)
- 59 (A. Wieferich, 1909)
- 58 (Baer, 1913)
- 54 (L.E. Dickson, 1933)
- 37 (Chen Jingrun, 1965), valeur exacte.
Majoration de g(6) [modifier]
- 970, (A.J. Kempner, 1912)
- 478 (Baer, 1913)
- 183 (James, 1934)
- 73 (K.C.S. Pillai, 1940), valeur exacte.
Majoration de g(7) [modifier]
- 3806 (A. Wieferich, 1909)
- 322 (James, 1934)
- 143, valeur exacte.
Majoration de g(8) [modifier]
- 36 119 (A. Hurwitz, 1908)
- 31 353 (A.J. Kempner, 1912)
- 595 (James, 1934)
- 279, valeur exacte.
Bibliographie [modifier]
- W. J. Ellison: Waring's problem. American Mathematical Monthly, volume 78 (1971), pp. 10-76. (Exposé, contenant une formule précise pour g(k) et une version simplifiée de la preuve d'Hilbert)
- Hans Rademacher et Otto Toeplitz, The Enjoyment of Mathematics (1933) (ISBN 0-691-02351-4). (Contient une preuve du théorème de Lagrange, accessible aux étudiants)
21:36 Publié dans Problème de Waring | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Médaille Fields
Source : http://fr.wikipedia.org/wiki/M%C3%A9daille_Fields
Médaille Fields
| Médaille Fields | |
 |
|
| Nom original | Fields Medal |
|---|---|
| Description | Prix récompensant une contribution majeure en mathématiques |
| Organisateur | Union mathématique internationale |
| Date de création | 1936 |
| Actuel récipiendaire | |
| Site officiel | http://www.mathunion.org/ |
La médaille Fields est la plus prestigieuse récompense pour la reconnaissance de travaux en mathématiques, souvent comparée par les médias au prix Nobel1, à tort car elle en diffère sur certains aspects essentiels (distinction de travaux exceptionnels, limite d'âge, récompense financière modeste), ce qui fait du prix Abel un meilleur équivalent du prix Nobel (récompense plutôt d'une œuvre dans son ensemble)2. Son but est d'apporter un soutien aux mathématiciens jeunes qui ont déjà apporté des contributions majeures. Elle est attribuée tous les quatre ans au cours du congrès international des mathématiciens à, au plus, quatre mathématiciens devant avoir moins de 40 ans au 1er janvier de l'année en cours. Les lauréats se voient attribuer chacun une médaille et un prix de 15 000 dollars canadiens (soit un peu plus de 10 000 euros)3.
John Charles Fields (1863-1932) proposa la création de cette médaille en 1923 lors d'une réunion internationale à Toronto. À sa mort, en 1932, il lègue ses biens à la science afin de financer la médaille. À l'origine, seules deux médailles étaient décernées tous les quatre ans. La Seconde Guerre mondiale a interrompu l'attribution de cette distinction jusqu'en 1950. La décision de passer à quatre lauréats au plus date de 1966.
Sommaire[masquer] |
Liste des lauréats [modifier]
- 1936 : Lars Ahlfors (
 Finlande), Jesse Douglas (
Finlande), Jesse Douglas ( États-Unis)
États-Unis) - 1950 : Laurent Schwartz (
 France), Atle Selberg (
France), Atle Selberg ( Norvège)
Norvège) - 1954 : Jean-Pierre Serre (
 ), Kunihiko Kodaira (
), Kunihiko Kodaira ( Japon)
Japon) - 1958 : René Thom (
 ), Klaus Roth (
), Klaus Roth ( Royaume-Uni)
Royaume-Uni) - 1962 : Lars Hormander (
 Suède), John Milnor (
Suède), John Milnor ( )
) - 1966 : Michael Atiyah (
 ), Paul Cohen (
), Paul Cohen ( ), Alexandre Grothendieck (
), Alexandre Grothendieck ( ), Stephen Smale (
), Stephen Smale ( )
) - 1970 : Alan Baker (
 ), Heisuke Hironaka (
), Heisuke Hironaka ( ), Sergueï Novikov (
), Sergueï Novikov ( Union soviétique), John Griggs Thompson (
Union soviétique), John Griggs Thompson ( )
) - 1974 : Enrico Bombieri (
 Italie), David Mumford (
Italie), David Mumford ( )
) - 1978 : Pierre Deligne (
 Belgique), Charles Fefferman (
Belgique), Charles Fefferman ( ), Gregori Margulis (
), Gregori Margulis ( ), Daniel Quillen (
), Daniel Quillen ( )
) - 1982 : Alain Connes (
 ), William Thurston (
), William Thurston ( ), Shing-Tung Yau (
), Shing-Tung Yau ( )
) - 1986 : Simon Donaldson (
 ), Gerd Faltings (
), Gerd Faltings ( Allemagne), Michael Freedman (
Allemagne), Michael Freedman ( )
) - 1990 : Vladimir Drinfeld (
 4), Vaughan Frederick Randal Jones (
4), Vaughan Frederick Randal Jones ( Nouvelle-Zélande), Shigefumi Mori (
Nouvelle-Zélande), Shigefumi Mori ( ), Edward Witten (
), Edward Witten ( )
) - 1994 : Jean-Christophe Yoccoz (
 ), Pierre-Louis Lions (
), Pierre-Louis Lions ( ), Efim Zelmanov (
), Efim Zelmanov ( Russie), Jean Bourgain (
Russie), Jean Bourgain ( )
) - 1998 : Richard Ewen Borcherds (
 Afrique du Sud), William Timothy Gowers (
Afrique du Sud), William Timothy Gowers ( ), Maxim Kontsevich (
), Maxim Kontsevich ( ), Curtis McMullen (
), Curtis McMullen ( )
) - 2002 : Laurent Lafforgue (
 ), Vladimir Voevodsky (
), Vladimir Voevodsky ( )
) - 2006 : Wendelin Werner (
 ), Andreï Okounkov (
), Andreï Okounkov ( ), Grigori Perelman [médaille déclinée] (
), Grigori Perelman [médaille déclinée] ( ), Terence Tao (
), Terence Tao ( Australie)
Australie) - 2010 : Cédric Villani (
 ), Ngô Bảo Châu (
), Ngô Bảo Châu ( Viêt Nam,
Viêt Nam, ), Elon Lindenstrauss (
), Elon Lindenstrauss ( Israël), Stanislav Smirnov (
Israël), Stanislav Smirnov ( )
)
Circonstances inhabituelles [modifier]
En 1966, Alexandre Grothendieck a boycotté la cérémonie devant lui remettre une médaille Fields, tenue à Moscou, pour protester contre les actions militaires soviétiques mises en place en Europe de l’Est5.
En 1970, Sergueï Novikov, en raison des restrictions mises en place à son encontre par le gouvernement soviétique, fut incapable de voyager pour se rendre au congrès à Nice pour recevoir sa médaille.
En 1978, Gregori Margulis, en raison des restrictions mises en place à son encontre par le gouvernement soviétique, fut incapable de voyager pour se rendre au congrès à Helsinki pour recevoir sa médaille. La récompense fut reçue en son nom par Jacques Tits, qui dit à cette occasion : « Je ne peux pas ne pas exprimer ma profonde déception — sans doute partagée par beaucoup de monde ici — due à l'absence de Margulis à cette cérémonie. En raison du sens symbolique de cette ville d'Helsinki, j'ai vraiment eu l'espoir grandissant que j'aurais au moins la chance de rencontrer un mathématicien que j'ai seulement connu à travers son travail et pour qui j'ai le plus grand respect et la plus grande admiration6. »
En 1982, le congrès aurait dû se tenir à Varsovie mais fut reprogrammé l'année suivante, en raison de l'instabilité politique du pays. Les récompenses furent annoncées à la neuvième Assemblée Générale de l'IMU plus tôt dans l'année et remises lors du congrès de Varsovie en 1983.
En 1998, au CIM, Andrew Wiles fut présenté par le président du comité de la médaille Fields, Yuri Manin (en), avec la première plaque d'argent de l'IMU en reconnaissance de sa démonstration du dernier théorème de Fermat. Don Zagier fit référence à la plaque comme une « médaille Fields de poids ». Pour expliquer cette récompense, il est fréquemment mis en avant le fait que Wiles avait dépassé l'âge limite de la médaille Fields (40 ans7). Pourtant, bien que Wiles ait déjà légèrement dépassé l'âge limite en 1994, il avait alors été pressenti favori pour gagner la médaille ; ce ne fut finalement pas envisageable car un trou dans la démonstration fut trouvé à l'été 1993, qui ne fut comblé par Wiles qu'en 19958,9.
En 2003, un autre équivalent du Prix Nobel pour les mathématiques a été créé en Norvège, le prix Abel. Le premier prix a été attribué au Français Jean-Pierre Serre, déjà plus jeune lauréat de la médaille Fields en 1954.
En 2006, Grigori Perelman, lauréat pour sa démonstration de la conjecture de Poincaré, refusa la médaille Fields10 et n'assista pas au congrès11.
Un même problème, savoir si une variété homotopiquement équivalente à une sphère de dimension n est ou non une sphère de dimension n (voir Conjecture de Poincaré), a vu l'attribution de trois médailles Fields, la première en 1966 à Stephen Smale, la deuxième en 1986 à Michael Freedman, la troisième vingt ans plus tard à Grigori Perelman.
Classement par pays [modifier]
| États-Unis | 13 | |
| France | 11 | |
| URSS (3) / Russie (6) | 9 | |
| Royaume-Uni | 5 | |
| Japon | 3 | |
| Belgique | 2 | |
| Afrique du Sud | 1 | |
| Finlande | 1 | |
| Israël | 1 | |
| Italie | 1 | |
| Norvège | 1 | |
| Nouvelle-Zélande | 1 | |
| Suède | 1 | |
| Allemagne | 1 | |
| Australie | 1 | |
| Vietnam | 1 |
Classement par institutions [modifier]
À leur nomination, les médaillés Fields travaillaient dans les institutions suivantes12 :
La médaille [modifier]
La médaille a été dessinée par le sculpteur canadien R. Tait McKenzie (en)13.
Sur l'avers, un portrait de profil d'Archimède et une citation en latin du poète Manilius http://fr.wikipedia.org/wiki/Marcus_Manilius, Astronomica, IV, v. 392 http://www.filosofico.net/manilioastronomica.htm : « Transire suum pectus mundoque potiri » (mot à mot : « traverser ton propre coeur (= franchir tes limites) et te rendre maître de l'univers (par la connaissance »).
Sur le revers, l'inscription latine :
- CONGREGATI
- EX TOTO ORBE
- MATHEMATICI
- OB SCRIPTA INSIGNIA
- TRIBUERE
Traduction : « Les mathématiciens s'étant rassemblés du monde entier ont remis cette récompense en raison de remarquables écrits. »
Dans l'arrière-plan, une représentation de la tombe d'Archimède, avec la gravure de son théorème « De la sphère et du cylindre » (une sphère et un cylindre circonscrit de mêmes hauteur et diamètre, travail duquel il était le plus fier) derrière un rameau.
La tranche porte le nom du lauréat.
Dans les arts [modifier]
- Dans le film Un conte de Noël, le personnage joué par Hippolyte Girardot est médaillé Fields. Il est amusant de noter que c'est Cédric Villani, qui depuis a obtenu lui-même la médaille Fields en 2010, qui a couvert de formules le tableau sur lequel est censé écrire Hippolyte Girardot.
- Dans le film Will Hunting, le personnage fictif Gerald Lambeau aurait reçu la médaille Fields pour des travaux en combinatoire.
- Dans le film Un homme d'exception, John Forbes Nash se plaint de ne pas avoir reçu la médaille Fields.
- Dans la série télévisée Eureka, Nathan Stark dit avoir reçu la médaille Fields.
- Dans la série télévisée Numb3rs, le mathématicien fictif Charlie Eppes explique à Megan Reeves l'inexistence d'un prix Nobel des mathématiques.
Notes et références [modifier]
- Alfred Nobel ne s'est jamais expliqué des motifs justifiant l'absence des mathématiques parmi les disciplines récompensées par un Prix Nobel.
- Mathématiques : quelle pérennité pour le prestige français ? [archive] Intervention de Michel Brouédans l'émission de Science publique du 1er septembre 2010 (8 min 10 dans le podcast)
- (en) Eric W. Weisstein, Fields Medal [archive], MathWorld. (page consultée le 24 août 2010)
- Vladimir Drinfeld est parfois considéré comme ukrainien mais l'indépendance ukrainienne fut proclamée le 24 août 1991.
- (en) Allyn Jackson, « As If Summoned from the Void: The Life of Alexandre Grothendieck », dansNotices of the American Mathematical Society, vol. 51, no 10, novembre 2004, p. 1196-1212[ [pdf]texte intégral [archive] (page consultée le 24 août 2010) ], p. 1198
- (en) John J. O'Connor et Edmund F. Robertson, « Gregori Margulis [archive] », MacTutor History of Mathematics archive, Université de St Andrews.(page consultée le 24 août 2010)
- (en) Andrew John Wiles [archive], Encyclopædia Britannica (page consultée le 24 août 2010)
- (en) Andrew J. Wiles awarded the "IMU silver plaque" [archive], Medieninformation Nr. 183, 18 août 1998, Université technique de Berlin (page consultée le 24 août 2010)
- (en) Allyn Jackson, « Borcherds, Gowers, Kontsevich, and McMullen Receive Fields Medals », dans Notices of the American Mathematical Society, vol. 45, no 10, novembre 1998, p. 1358-1360[ [pdf]texte intégral [archive] (page consultée le 24 août 2010) ], p. 1360
- (en) « Maths genius turns down top prize », dans BBC News, 22 août 2006 [ texte intégral [archive](page consultée le 24 août 2010) ]
- (en) Justin Mullins, « Prestigious Fields Medals for mathematics awarded », dans New Scientist, 31 août 2006 [ texte intégral [archive] (page consultée le 24 août 2010) ]
- http://www.infoplease.com/ipa/A0192505.html#axzz0xhlSGy2N [archive]
- (en) The Fields Medal [archive] (site officiel)
Voir aussi [modifier]
Lien externe [modifier]
- (en) Site officiel
21:34 Publié dans Médaille Fields | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Recherche mathématique
Source : http://fr.wikipedia.org/wiki/Recherche_math%C3%A9matique
Recherche mathématique
La recherche mathématique est une branche de la recherche scientifique.
Sommaire[masquer] |
Domaines de recherche [modifier]
Centres internationaux de recherche [modifier]
- African Institute for Mathematical Sciences
- Clay Mathematics Institute
- The Geometry center
- Institut des hautes études scientifiques
- Institute for advanced research
- Isaac Newton Institute
- Max Planck institute for Mathematics in the Sciences
- Reasearch Institute for Mathematical Sciences
- Santa Fe Institute
Revues, publications [modifier]
Récompenses en mathématiques [modifier]
21:33 Publié dans Recherche mathématique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Mathématicien
Source : http://fr.wikipedia.org/wiki/Math%C3%A9maticien
Mathématicien
|
|
Cet article ne cite pas suffisamment ses sources (avril 2010).
Si vous connaissez le thème traité, merci d'indiquer les passages à sourcer avec {{Référence souhaitée}} ou, mieux, incluez les références utiles en les liant aux notes de bas de page. (Modifier l'article)
|
|
|
Cet article est une ébauche concernant l'épistémologie.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
Un mathématicien est au sens restreint un chercheur en mathématiques, par extension toute personne faisant des mathématiques la base de son activité principale. Ce terme recouvre une large palette de compétences et de pratiques très différentes, avec néanmoins en commun un vocabulaire et un formalisme spécifiques, ainsi qu'une exigence de rigueur propre à cette discipline.
Le terme générique mathématicien peut se décliner pour des domaines plus restreints, comme algébriste, analyste, arithméticien, géomètre,probabiliste, statisticien, logicien etc.
Un mathématicien est véritablement reconnu s'il est admis qu'il a contribué significativement au développement de la science mathématique.
Les personnes mettant en oeuvre les résultats mathématiques pour les profits d'une autre discipline ou activité ne sont pas pour autant considérées comme mathématiciens.
Sommaire[masquer] |
Sur le sens du mot mathématicien [modifier]
On trouve essentiellement deux usages différents de ce mot : le mathématicien peut désigner une personne travaillant activement dans la recherche mathématique1, ce qui donne la plupart du temps lieu, de nos jours, à des publications dans des revues à comité de lecture. Ainsi sont classés Henri Poincaré ou Andrew Wiles, par exemple. D'un autre côté, le mathématicien peut désigner une personne versée dans les mathématiques2, ou qui a travaillé dans un domaine connexe (enseignement des mathématiques ne donnant pas lieu à de la recherche, épistémologie, pédagogie, ou même par des oeuvres de vulgarisation scientifique). Ainsi peuvent être classés Denis Guedj ou Stella Baruk.
Activités essentielles d'un mathématicien [modifier]
Il n'y a pas de définition précise ou de restriction a priori de l'activité d'un mathématicien3, en dehors de l'objectif d'un apport à sa discipline.
Le travail principal d'un mathématicien peut ainsi prendre pour objectif la résolution des problèmes ouverts et la vérification des conjectures. Dans ce contexte, le terme problème est à distinguer des exercices que posent les professeurs aux élèves, et dont les solutions sont déjà connues. Les problèmes peuvent se poser lors de modélisations en physique, en économie, en informatique, etc. ou lors de tentatives de généralisations de découvertes antérieures.
Ces travaux peuvent nécessiter un élargissement ou un approfondissement des résultats déjà acquis dans un domaine des mathématiques, mais également consister en la recherche de liens entre des domaines différents.
La découverte et la caractérisation d'un domaine d'étude nouveau peuvent également être un résultat de l'activité d'un mathématicien.
Les mathématiciens s'imposent une rigueur méthodologique qui peut faire paraître singulière leur discipline. Le formalisme et l'exposition rigoureuse des travaux, y compris des étapes intermédiaires, sont des points estimés nécessaires à l'acceptation des résultats obtenus. Le travail de vérification, ou de réfutation le cas échéant, des résultats présentés par d'autres mathématiciens fait également partie de l'activité d'un mathématicien. Pour certains exposés particulièrement complexes ou difficiles, ces vérifications peuvent nécessiter la contribution de plusieurs mathématiciens travaillant de manière concertée.
Emplois dans le monde contemporain [modifier]
Les mathématiciens se spécialisent souvent dans différentes branches des mathématiques. On distingue parfois les mathématiques pures des mathématiques appliquées. Cette distinction n'est cependant ni formalisée, ni de compréhension commune à l'ensemble des mathématiciens.
L'usage grandissant des mathématiques dans de nombreuses disciplines et techniques offre aux mathématiciens des opportunités d'emploi diverses. Ils sont parfois employés par des entreprises privées ou étatiques, ou comme professeurs dans un cadre universitaire, souvent en complément de leurs travaux de recherche. En tant que spécialistes de leur discipline, ou d'une partie des mathématiques, certains mathématiciens sont intégrés dans des équipes multidisciplinaires travaillant sur un sujet plus vaste (physique, informatique, modélisations, ...).
Distinctions et prix [modifier]
Il n'existe pas de prix Nobel pour les mathématiciens. La médaille Fields est cependant considérée par beaucoup comme une distinction de même valeur et à ce titre parfois appelée prix Nobel des mathématiques. Notons cependant que ce prix est réservé aux mathématiciens de moins de 40 ans4.
Parmi les autres distinctions prestigieuses figurent notamment :
- le prix Abel
- le prix Nevanlinna
- le prix Wolf
- le prix Fermat
- le prix Loève
- le prix Clay (parfois nommé prix du millénaire)
- le prix Crafoord
- le prix Carl-Friedrich-Gauss pour les mathématiques appliquées
- le prix Pólya et la médaille De Morgan, décernés par la London Mathematical Society
Titres particuliers [modifier]
- Le Prince des mathématiciens : surnom donné à Carl Friedrich Gauss eu égard à l'ampleur de sa contribution aux mathématiques.
Données démographiques [modifier]
Un annuaire mondial de mathématiciens, publié par l'Union mathématique internationale, est accessible sur le site de l'Union.
A cet usage, l'Union Mathématique Internationale a précisé la définition du mathématicien retenue :
On appelle mathématicien actif toute personne qui a publié dans les 4 dernières années au moins 2 articles référencés dans les 3 grandes bases de données bibliographiques, à savoir ZentraleBlatt fürtabon Mathematik, Mathematical Reviews et Referatnyi Zhurnal.
Restrictive, mais opératoire, cette définition permet un dénombrement des mathématiciens en activité.
En France, une autre définition considère comme mathématicien toute personne employée au titre des mathématiques par l'université ou un organisme de recherche; en ce sens, il existe entre 3 500 et 4 000 mathématiciens en France, dont la très grande majorité (environ 3 200) sont à l'université, la plupart étant également actifs au sens de la définition précédente.
Selon Alain Connes, David Hilbert et Henri Poincaré sont les derniers mathématiciens à avoir une maîtrise complète de la recherche de leur époque5. Selon leurs dires, il y aurait entre 15 000 et 20 000 mathématiciens.
Bien que la majorité des mathématiciens reconnus soient des hommes, la profession s'est féminisée, en particulier depuis la Seconde Guerre mondiale. Cette féminisation, moins forte en mathématiques pures qu'en mathématiques appliquées, marque cependant le pas depuis plusieurs années, en particulier en haut de l'échelle : parmi les 75 mathématiciens admis à l'Institut universitaire de France depuis sa fondation, on ne compte aucune femme.
Notes et références [modifier]
- Qu'est-ce qu'un mathématicien ? [archive] Entretien avec André Lichnerowicz
- Mathématicien [archive] sur le site du TLFI
- Un mathématicien est une machine à transformer le café en théorèmes. Paul Erdös
- Voir à ce sujet les péripéties concernant Andrew Wiles dans le paragraphe Circonstances inhabituelles de l'article sur la médaille Fields.
- Alain Connes, triangles de pensée, Éditions Odile Jacob, p.127.
Bibliographie [modifier]
- Didier Nordon, Les obstinations d'un mathématicien. Regards sur la science pour la science, Belin, 2003.
- Pierre Lecomte , Le mathématicien et ses esclaves, Éditions de l'Université de Liège, 2009.
- Paul Lévy, Quelques aspects de la pensée d'un mathématicien. Librairie scientifique et technique, A. Blanchard, 1970.
- Eric Temple Bell, Les grands mathématiciens, texte traduit par Ami Gandillon, Payot, 1961.
- Encyclopédie méthodique: dictionnaire des jeux mathématiques, contenant l'analyse, les recherches, les calculs, les probabilités les tables numériques, publiés par plusieurs célèbres mathématiciens, relativement aux jeux de hasard et de combinaisons, et suite du Dictionnaire des jeux, Chez H. Agasse, 1798
- Histoire des mathématiques, dans laquelle on rend compte de leurs progrès depuis leur origine jusqu'à nos jours; où l'on expose le tableau & le développement des principales découvertes, les contestations qu'elles ont fait naître & les principaux traits de la vie des mathématiciens les plus..., Jean-Étienne Montucla, Bibliothèque interuniversitaire (Nancy), Chez Ch. Ant. Jombert, 1758.
Voir aussi [modifier]
Articles connexes [modifier]
21:32 Publié dans Liste des mathématiciens arabes, Mathématiciens | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
SPECIAL MATHS BREVET 2010
SPECIAL MATHS BREVET 2010 SUJET METROPOLE 2009 DU 1ER JUILLET Source : http://www.intellego.fr/doc/22390




21:30 Publié dans SPECIAL MATHS BREVET 2010 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Introduction aux mathématiques élémentaires
Introduction aux mathématiques élémentaires
| Chapitre 1 : | Proportionnalité |
|---|---|
| Chapitre 2 : | Calcul littéral |
| Chapitre 3 : | Initiation à la statistique |
| Chapitre 4 : | Initiation à l'arithmétique |
| Chapitre 5 : | Priorités, distributivité |
| Chapitre 6 : | Fraction |
| Chapitre 7 : | Mesure en géométrie |
| Chapitre 8 : | Nombre entier relatif |
| Chapitre 9 : | Puissances |
| Chapitre 10 : | Triangles et parallèles |
| Chapitre 11 : | Triangle rectangle |
| Chapitre 12 : | Vecteur |
On entend par mathématiques élémentaires les bases des mathématiques de l'enseignement secondaires. Elles restent très concrètes, tant par leurs objets (les nombres et les figures du plan et de l'espace) que par leur méthode (peu axiomatisée, privilégiant les exemples et les applications). Nous avons regroupé ici par thèmes les domaines usuels des mathématiques élémentaires. Les objectifs de cette leçon sont : Cette leçon est de niveau 6. Les prérequis conseillés sont : Ces contributeurs sont prêts à vous aider concernant ce cours :Objectifs
![]() Vous pouvez discuter ou modifier ces objectifs en modifiant cette section.
Vous pouvez discuter ou modifier ces objectifs en modifiant cette section.Niveau et prérequis conseillés
![]() Vous pouvez discuter cette évaluation ou indiquer des prérequis manquants en modifiant cette section.
Vous pouvez discuter cette évaluation ou indiquer des prérequis manquants en modifiant cette section.Référents
![]() Vous pouvez vous proposer comme référent en modifiant cette section.
Vous pouvez vous proposer comme référent en modifiant cette section.
10:15 Publié dans Introduction aux mathématiques élémentaires | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Calcul numérique - Nombres Premiers
Source : http://www.vivelesmaths.com/
Calcul numérique - Nombres Premiers
L'ensemble des nombres considérés est N



10:10 Publié dans Calcul numérique - Nombres Premiers | Lien permanent | Commentaires (1) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Triangle rectangle
Source : http://fr.wikipedia.org/wiki/Triangle_rectangle
Triangle rectangle
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Logique |
| Arithmétique |
| Probabilités |
| Statistiques |
Un triangle rectangle est un triangle dont l'un des angles est droit. On nomme alors hypoténuse le côté opposé à l'angle droit. De plus, on appellecathète chaque côté adjacent à l'angle droit.
Sommaire[masquer] |
Intérêt [modifier]
La connaissance des triangles rectangles et de leurs relations métriques permettent de travailler sur de nombreux problèmes. Par exemple :
- on peut décomposer tout triangle en deux triangles rectangles ;
- dans un repère orthonormé
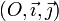 , si un point M se projette selon H sur l'axe
, si un point M se projette selon H sur l'axe 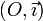 et selon I sur l'axe
et selon I sur l'axe 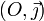 , alors OHM et OMI sont des triangles rectangles ;
, alors OHM et OMI sont des triangles rectangles ; - d'un point de vue vectoriel, un vecteur
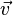 se décompose selon
se décompose selon
les vecteurs forment un triangle rectangle ;
forment un triangle rectangle ; - de manière générale, la trigonométrie concerne les relations dans le triangle rectangle.
Principales propriétés [modifier]
Aire [modifier]
Comme pour tout triangle, pour calculer l'aire d'un triangle rectangle, on multiplie base et hauteur correspondantes, et on divise le tout par deux. Si ABC est rectangle en A, chacun des côtés AB et AC peut être considéré comme une hauteur, la base étant alors l'autre côté de l'angle droit (AC et AB respectivement). L'aire "S" du triangle est donc égale à S = (AB * AC) / 2.
Par exemple, on a un triangle rectangle en A avec AB = 4cm, AC = 3cm, et l'hypoténuse BC = 5 cm. On a S = (4 * 3) / 2 = 6, donc l'aire du triangle rectangle est de 6cm².
Remarque : On pourrait bien sûr utiliser aussi le troisième côté, l'hypoténuse BC, comme base, et trouver le même résultat, mais la hauteur associée à BC devrait être calculée, elle n'est pas directement un côté.
Théorème de Pythagore [modifier]
Le Théorème de Pythagore précise que :
si un triangle ABC est rectangle en A, alors le carré de l'hypoténuse est égal à la somme des carrés des côtés adjacents, soit : BC2 = AC2 + AB2 Réciproquement, tout triangle ABC vérifiant l'égalité précédente est un triangle rectangle en A.
Ce théorème est une conséquence de la définition de la distance entre deux points à partir du carré scalaire de leur vecteur. En effet
puisque 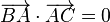 car les vecteurs
car les vecteurs  et
et 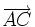 sont orthogonaux.
sont orthogonaux.
Voir l'article Théorème de Pythagore pour d'autres démonstrations.
Théorème de la médiane [modifier]
Pour un triangle rectangle, le théorème de la médiane s'énonce ainsi
si M est le milieu de l'hypoténuse, alors AM=½BC. On peut également dire que le point A est situé sur le cercle de diamètre [BC]. Réciproquement, si A est un point quelconque du cercle de diamètre [BC] alors le triangle ABC est rectangle en A
Il existe plusieurs démonstrations de ce théorème. Le sens direct peut se montrer de manière purement géométrique : par définition M est le milieu de [BC]. Le triangle rectangle ABC est un demi-rectangle ABCD. Un rectangle est un parallélogramme, donc ses diagonales se coupent en leur milieu, donc M, milieu de [BC], est aussi celui de [AD]. Les diagonales d'un rectangle sont de longueur égales, donc AD = BC et AM = AD / 2 = BC / 2 .
On peut aussi faire appel aux vecteurs :
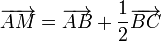 et
et  , d'où :
, d'où :  ,
,
Ces deux derniers vecteurs sont orthogonaux, donc : AM² = (AB² + AC²)/4
D'autre part, en appliquant le théorème de Pythagore au triangle ABC, on obtient : BC² = AB² + AC². Et finalement : AM = BC / 2
On peut également appliquer le théorème de l'angle au centre, qui permet en outre de démontrer la réciproque. Considérons le cercle circonscrit au triangle ABC et notons O son centre. D'après le théorème de l'angle au centre l'angle BOC est le double de l'angle BAC. Donc
Ainsi les points B, O et C sont alignés. Comme de plus BO=OC on voit que O est le milieu de [BC] donc O=M.
Réciproquement, si on sait que A est un point du cercle de diamètre [BC]. D'après le théorème de l'angle au centre, l'angle BAC est la moitié de l'angle BOC, donc il vaut π/2. Ainsi le triangle BAC est rectangle en A.
Ce théorème se généralise dans un triangle quelconque. Voir à ce propos l'article théorème de la médiane.
Centre de gravité [modifier]
Avec les notations précédentes (ABC rectangle en A et M le milieu de [BC]) : le centre de gravité G vérifie
(voir Triangle > Médianes et centre de gravité), et M se projette aux milieux de [AB] et de [AC] (ABM et ACM sont des triangles isocèles). Le point G se projette donc au tiers de [AB] et de [AC] :
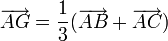 .
.
Autres propriétés [modifier]
Pour tout nombre entier n supérieur ou égal à 3, on peut toujours trouver un triangle rectangle dont la longueur d'un côté de l'angle droit est n et la longueur des deux autres côtés sont des nombres entiers. En effet :
- Si n est un nombre pair, n = 2k
Il suffit de prendre la longueur de l'autre côté de l'angle droit égal à k2 - 1. Le théorème de Pythagore nous donne alors une hypoténuse de longueur égale à k2+1. - Si n est un nombre impair, n = 2k + 1
Il suffit de prendre la longueur de l'autre côté de l'angle droit égal à 2k2 + 2k. Le théorème de Pythagore nous donne alors une hypoténuse de longueur égale à 2k2 + 2k + 1.
Voir aussi [modifier]
Articles connexes [modifier]
10:08 Publié dans Triangle rectangle | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Fonction trigonométrique
Source : http://fr.wikipedia.org/wiki/Cosinus
Fonction trigonométrique
En mathématiques, les fonctions trigonométriques sont des fonctions d'angle importantes pour étudier les triangles, lescercles et modéliser des phénomènes périodiques. Les fonctions trigonométriques ne sont rien d'autre que des longueurs relatives à la mesure d'un angle sur le cercle unité, mais elles sont utilisées dans de nombreuses autres applications. Elles sont parfois définies comme rapports de deux longueurs des côtés d'un triangle rectangle contenant l'angle, ou, plus généralement, comme somme d'une série entière.
Chacune de ces trois approches sera présentée ci-dessous. Il y a six fonctions trigonométriques de base :
- sinus (sin) ;
- cosinus (cos) ;
- tangente (tan), notée aussi tang ou tg ;
- cotangente (cotan), notée aussi cotg ou cot ;
- sécante (sec), notée aussi séc ;
- cosécante (cosec), notée aussi coséc ou csc.
Le sinus, le cosinus et la tangente sont de loin les plus utilisées. Plusieurs relations entre ces fonctions sont énumérées à la page des identités trigonométriques.
Sommaire[masquer] |
Lignes trigonométriques [modifier]
Un triangle quelconque rectiligne (ou sphérique) possède six parties dont trois côtés et trois angles. Toutes ces parties ne sont pas utiles à la construction du triangle, par exemple les seules données de la longueur de deux de ses côtés et de l'angle entre ces côtés permet de compléter le triangle. Mais connaissant seulement les trois angles, il est impossible de retrouver le triangle, puisqu'il existe une infinité de triangles ayant les trois mêmes angles (triangles semblables). En fait il suffit de connaître trois de ces parties dont un côté pour construire un triangle.
Le problème de la détermination avec exactitude des parties manquantes du triangle fut étudié en particulier en Europe à partir du Moyen Âge. Les méthodes géométriques ne donnant, à l'exception des cas simples, que des constructions approximatives et insuffisantes à cause de l'imperfection des instruments utilisés, les recherches s'orientèrent plutôt vers des méthodes numériques afin d'obtenir des constructions avec un degré de précision voulu.
Et l'un des objectifs de la trigonométrie fut donc de donner des méthodes pour calculer toutes les parties d'un triangle, c'est-à-dire pour résoudre un triangle. Pendant longtemps les géomètres cherchèrent en vain des relations entre les angles et les côtés des triangles. Une de leurs plus grandes idées fut de se servir des arcs plutôt que des angles pour effectuer leurs mesures.
Un arc est un arc de cercle décrit de l'un des sommets du triangle comme centre et compris entre les côtés se rapportant au sommet. Ces considérations menèrent tout naturellement les géomètres à remplacer les arcs par les segments de droites dont ils dépendent.
Ces segments s'appellent les lignes trigonométriques. Il s'agit en fait d'un autre vocable pour désigner les fonctions trigonométriques (sin x, cos x, tan x, ...) appelées aussi fonctions circulaires. Des relations entre les côtés et certaines lignes liées aux arcs s'établissent de manière à ce que les lignes puissent être déterminées à partir de certains arcs et réciproquement. Une convention fondamentale oblige alors à ne considérer que les lignes trigonométriques rapportées à des cercles de rayon 1. Ces lignes trigonométriques définissent les fonctions trigonométriques modernes.
Les fonctions trigonométriques mathématiques sont celles qui s'appliquent à des mesures d'angles données en radians. Mais il est encore d'usage de garder les mêmes noms de fonctions pour les autres unités de mesures comme les degrés ou les grades.
Définitions dans un triangle rectangle [modifier]
Pour définir les fonctions trigonométriques en un angle Â, considérons un triangle rectangle arbitraire qui contient l'angle Â.
Nous emploierons les noms suivants pour désigner les côtés du triangle rectangle :
- l’hypoténuse est le côté opposé à l'angle droit, une jambe de l'angle  et le côté le plus long du triangle,
- le côté opposé est le côté opposé à l'angle Â, qui nous intéresse,
- le côté adjacent est le côté qui est une jambe de l'angle Â, qui n'est pas l'hypoténuse.
On notera:
- o : la longueur du côté opposé
- a : la longueur du côté adjacent
- h : la longueur de l'hypoténuse
1) Le sinus d'un angle est le rapport de la longueur du côté opposé par la longueur de l'hypoténuse :
- sin(Â) = longueur du côté opposé / longueur de l'hypoténuse = o/h.
Notez que ce rapport ne dépend pas du triangle rectangle particulier choisi, aussi longtemps qu'il contient l'angle Â, puisque tous ces triangles rectangles sont semblables.
2) Le cosinus d'un angle est le rapport de la longueur du côté adjacent par la longueur de l'hypoténuse :
- cos(Â) = longueur de côté adjacent / longueur de l'hypoténuse = a/h.
3) La tangente d'un angle est le rapport de la longueur du côté opposé à la longueur du côté adjacent :
- tan(Â) = longueur du côté opposé / longueur du côté adjacent = o/a.
- Cosinus = Adjacent/Hypoténuse ;
- Sinus = Opposé/Hypoténuse ;
- Tangente = Opposé/Adjacent.
Les trois fonctions restantes sont définies en utilisant les trois fonctions ci-dessus.
4) La cosécante de  notée cosec(Â) est l'inverse du sinus de Â, 1/sin(Â), c'est-à-dire le rapport de la longueur de l'hypoténuse par la longueur du côté opposé :
- cosec(Â)=longueur de l'hypoténuse / longueur du côté opposé = h/o.
5) La sécante de  notée sec(Â) est l'inverse du cosinus de Â, 1/cos(Â), c'est-à-dire le rapport de la longueur de l'hypoténuse par la longueur du côté adjacent:
- sec(Â)=longueur de l'hypoténuse / longueur du côté adjacent = h/a.
6) La cotangente de  notée cotg(Â) est l'inverse de la tangente de Â, 1/tan(Â), c'est-à-dire le rapport de la longueur du côté adjacent par la longueur du côté opposé:
- cotg(Â)= longueur du côté adjacent / longueur du côté opposé = a/o.
Il existe un moyen mnémotechnique pour apprendre facilement les formules du sinus, du cosinus et de la tangente : SOHCAHTOA ou plus simple CAHSOHTOA qui, dit plus rapidement donne: "casse-toi"
- SOH (Sin= Opposé/Hypotènuse)
- CAH (Cos= Adjacent/Hypotènuse)
- TOA (Tan= Opposé/Adjacent)
- Sinopphyp(sin=opp/hyp)
- Cosadjhyp(cos=adj/hyp)
- Tanoppadj(tan=opp/adj)
Valeurs remarquables [modifier]
Il existe des tables de valeurs des fonctions trigonométriques, mais ces valeurs peuvent également être calculées par une calculatrice. Pour quelques angles simples, les valeurs peuvent être calculées à la main, comme dans les exemples suivants :
Supposons que l'on ait un triangle rectangle dans lequel les deux angles sont égaux et valant donc 45 degrés (π/4 radians). Puisque les longueurs a et b sont égales, nous pouvons choisir a = b = 1.
Maintenant, on peut déterminer le sinus, le cosinus et la tangente d'un angle de 45 degrés. En utilisant le théorème de Pythagore,  . Ceci est illustré dans la figure de droite.
. Ceci est illustré dans la figure de droite.
Par conséquent,
 ,
,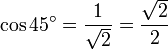 ,
,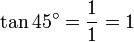
Pour déterminer les valeurs des fonctions trigonométriques pour des angles de 60 degrés (π/3 radians) et de 30 degrés (π/6 radians), nous commençons par considérer un triangle équilatéral de longueur latérale 1. Tous ses angles sont de 60 degrés. En le divisant en deux, nous obtenons un triangle rectangle dont un angle est de 30 degrés. On obtient :
 ,
, ,
,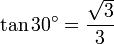
et
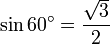 ,
,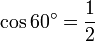 ,
,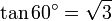 .
.
On peut se souvenir de ces valeurs en construisant la table suivante : en mettant dans l'ordre 0, π/6 (30°), π/4 (45°), π/3 (60°) et π/2 (90°), le sinus prend les valeurs 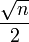 , et pour le cosinus, on prend l'ordre inverse.
, et pour le cosinus, on prend l'ordre inverse.
| Angle | 0 | π/6 30° | π/4 45° | π/3 60° | π/2 90° |
|---|---|---|---|---|---|
| sin |  0 |
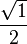 1/2 |
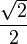 |
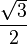 |
 1 |
| cos |  1 |
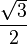 |
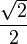 |
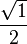 1/2 |
 0 |
| tan | 0 | 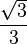 |
1 | 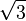 |
ind. |
- Autres valeurs remarquables :
Zéros [modifier]
 .
.
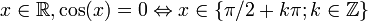 .
.
Définitions à partir du cercle unité [modifier]
Les six fonctions trigonométriques peuvent également être définies à partir du cercle unité. La définition géométrique ne fournit presque pas de moyens pour le calcul pratique; en effet elle se fonde sur des triangles rectangles pour la plupart des angles. Le cercle trigonométrique, en revanche, permet la définition des fonctions trigonométriques pour tous les réels positifs ou négatifs, pas seulement pour des angles de mesure en radians comprise entre  .
.
Dans un plan muni d'un repère orthonormé  , le cercle trigonométrique est le cercle de centre O et de rayon 1. Si l'on considère un point A(xA, yA) sur le cercle, alors on a :
, le cercle trigonométrique est le cercle de centre O et de rayon 1. Si l'on considère un point A(xA, yA) sur le cercle, alors on a :
Sur le cercle ci-contre, nous avons représenté certains angles communs, et nous avons indiqué leurs mesures en radians figurant dans l'intervalle [ − 2π,2π], soit deux mesures par angle et même trois pour l'angle nul.
Notez que nous mesurons les angles positifs dans le sens trigonométrique, contraire à celui des aiguilles d'une horloge, et les angles négatifs dans le sens horaire. Une demi-droite qui fait un angle θ avec la demi-droite positive 0x de l'axe des abscisses coupe le cercle en un point de coordonnées (cosθ,sinθ). Géométriquement, cela provient du fait que l'hypoténuse du triangle rectangle ayant pour sommets les points de coordonnées (0, 0), (cos θ, 0) et (cos θ, sin θ) est égale au rayon du cercle donc à 1. On a donc  et
et 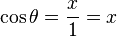 . Le cercle unité peut être considéré comme une façon de regarder un nombre infini de triangles obtenus en changeant les longueurs des côtés opposés et adjacents mais en gardant la longueur de leur hypoténuse égale à 1.
. Le cercle unité peut être considéré comme une façon de regarder un nombre infini de triangles obtenus en changeant les longueurs des côtés opposés et adjacents mais en gardant la longueur de leur hypoténuse égale à 1.
Bien que seulement le sinus et le cosinus aient été définis directement par le cercle unité, les autres fonctions trigonométriques peuvent être définies par:
Le cercle unité a pour équation :
Cela donne immédiatement la relation
Relations entre sinus et cosinus [modifier]
- NB : Les valeurs d'angles sont en radians.
Pour définir les angles strictement plus grands que 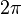 ou strictement négatifs, il suffit d'effectuer des rotations autour du cercle. De cette façon, le sinus et le cosinus deviennent desfonctions périodiques de période
ou strictement négatifs, il suffit d'effectuer des rotations autour du cercle. De cette façon, le sinus et le cosinus deviennent desfonctions périodiques de période 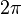 :
:
- pour tout angle
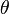 et tout entier k :
et tout entier k : 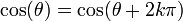
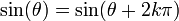
Ceci exprime le caractère périodique de ces fonctions. Grâce au cercle, et avec des considérations géométriques simples, on peut voir que
car 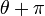 et
et 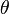 sont diamétralement opposés sur le cercle.
sont diamétralement opposés sur le cercle.
car 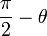 est le point symétrique de
est le point symétrique de 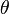 par rapport à la bissectrice de
par rapport à la bissectrice de 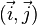 .
.
car 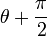 se déduit de
se déduit de 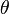 par rotation d'un quart de tour.
par rotation d'un quart de tour.
car 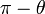 est le symétrique de
est le symétrique de 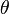 par rapport à
par rapport à  .
.
car  est le symétrique de
est le symétrique de 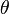 par rapport à
par rapport à  .
.
Ces formules font partie des identités trigonométriques.
Relations trigonométriques [modifier]
Représentations graphiques [modifier]
Voici les représentations graphiques des fonctions sinus, cosinus et tangente:
Parité des fonctions [modifier]
sinus est une fonction impaire :  on a
on a 
cosinus est une fonction paire :  on a
on a 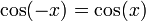
tangente est une fonction impaire : 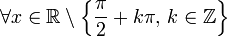 on a
on a 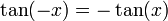
Limites et dérivées [modifier]
On a  ,
, 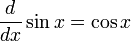 ,
,  et
et 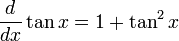 .
.
On trouvera d'autres relations sur la page consacrée aux identités trigonométriques.
Définitions à partir des séries entières [modifier]
Ici, et généralement en analyse, il est de la plus grande importance que tous les angles soient mesurés en radians. On peut alors définir
Ces définitions sont équivalentes à celles données ci-dessus ; on peut le justifier avec la théorie des séries de Taylor, et avec le fait que la dérivée du sinus est le cosinus et que celle du cosinus est l'opposé du sinus.
Ces définitions sont souvent utilisées comme point de départ des traités rigoureux d'analyse et de la définition du nombre π puisque la théorie des séries est bien connue. La dérivabilitéet la continuité sont alors faciles à établir, de même que les formules d'Euler en analyse complexe reliant les fonctions trigonométriques à la fonction exponentielle, ainsi que l'identité d'Euler. Les définitions utilisant les séries ont l'avantage supplémentaire de permettre de prolonger les fonctions sinus et cosinus en des fonctions analytiques dans tout le plan complexe.
Il n'est pas possible d'obtenir des séries aussi simples pour les autres fonctions trigonométriques, mais on a, par exemple
où Bn est le n-ème nombre de Bernoulli. Ces expressions se traduisent sous forme de fractions continues, elles ont permis à Lambert de démontrer l'irrationalité du nombre π (cf l'articleFraction continue).
Relations avec la fonction exponentielle et les nombres complexes [modifier]
On peut montrer à partir de la définition des séries que les fonctions sinus et cosinus sont respectivement la partie imaginaire et la partie réelle de la fonction exponentielle quand son argument est imaginaire pur :
Cette relation a été trouvée par Euler.
où i2 = −1.
Voir à ce sujet l'article Trigonométrie complexe
Fonctions réciproques [modifier]
Les fonctions trigonométriques ne sont pas bijectives. En les restreignant à certains intervalles, les fonctions trigonométriques réalisent des bijections. Les applications réciproques (arcsin, arccos, arctan, arccosec, arcsec et arccotg) sont habituellement définies par :
- pour tous réels x et y tels que
- -1 ≤ x ≤ 1, -π/2 ≤ y ≤ π/2
- y = arcsin(x) si et seulement si x = sin(y)
- pour tous réels x et y tels que
- -1 ≤ x ≤ 1, 0 ≤ y ≤ π,
- y = arccos(x) si et seulement si x = cos(y)
- pour x réel quelconque et y tel que
- -π/2 < y < π/2,
- y = arctan(x) si et seulement si x = tan(y)
- pour tous réels x et y tels que
- (x ≤ -1 ou x ≥ 1), (-π/2 ≤ y ≤ π/2 et y ≠ 0),
- y = arccosec(x) si et seulement si x = cosec(y)
- pour tous réels x et y tels que
- (x ≤ -1 ou x ≥ 1), (0 ≤ y ≤ π et y ≠ π/2),
- y = arcsec(x) si et seulement si x = sec(y)
- pour tous réels x et y tels que
- x ? 0, (0 < y < π et y? π/2),
- y = arccotg(x) si et seulement si x = cotg(y)
Ces fonctions peuvent s'écrire sous forme d'intégrales indéfinies :
Égalités pratiques :
Propriétés et applications [modifier]
Les fonctions trigonométriques, comme leur nom le suggère, ont une importance cruciale en trigonométrie, mais interviennent aussi dans l'étude des fonctions périodiques.
En trigonométrie [modifier]
En trigonométrie, elles fournissent des relations intéressantes entre les longueurs des côtés et les angles d'un triangle quelconque.
Considérons un triangle quelconque :
- la loi des sinus s'écrit:
Cette relation peut être démontrée en divisant le triangle en deux triangles rectangles et en utilisant la définition ci-dessus du sinus.
Le nombre commun  apparaissant dans le théorème est l'inverse du diamètre du cercle circonscrit au triangle (cercle passant par les trois points A, B et C). La loi des sinus est utile pour calculer des longueurs inconnues des côtés dans un triangle quelconque si deux angles et un côté sont connus. C'est une situation courante survenant dans latriangulation, une technique pour déterminer des distances inconnues en mesurant deux angles et une distance.
apparaissant dans le théorème est l'inverse du diamètre du cercle circonscrit au triangle (cercle passant par les trois points A, B et C). La loi des sinus est utile pour calculer des longueurs inconnues des côtés dans un triangle quelconque si deux angles et un côté sont connus. C'est une situation courante survenant dans latriangulation, une technique pour déterminer des distances inconnues en mesurant deux angles et une distance.
- la loi des cosinus ou théorème d'Al-Kashi est une généralisation du théorème de Pythagore
À nouveau, ce théorème peut être démontré en divisant le triangle en deux triangles rectangles. La loi des cosinus est utile pour déterminer les données inconnues d'un triangle si deux des côtés et un angle sont connus. Remarquons que l'angle connu doit être contenu dans les deux côtés dont nous connaissons la longueur.
- Il y a également la loi des tangentes :
L'utilisation des fonctions trigonométriques ne se limite pas seulement à l'étude des triangles. Les fonctions trigonométriques sont des fonctions périodiques dont les représentations graphiques correspondent à des modèles caractéristiques d'ondes, utilisés pour modéliser des phénomènes oscillatoires tels que le bruit ou les ondes de la lumière. Chaque signal peut être écrit comme une somme (en général infinie) de fonctions de sinus et de cosinus de différentes fréquences; ce sont les séries de Fourier.
Pour avoir un formulaire de relations entre les fonctions trigonométriques, consultez les identités trigonométriques.
En analyse harmonique [modifier]
Les fonctions sinus et cosinus apparaissent aussi dans la description d'un mouvement harmonique simple, un concept important en physique. Dans ce contexte les fonctions sinus et cosinus sont utilisées pour décrire les projections sur un espace à une dimension d'un mouvement circulaire uniforme, le mouvement d'une masse au bout d'un ressort, ou une approximation des oscillations de faible écart angulaire d'un pendule.
Les fonctions trigonométriques sont aussi importantes dans d'autres domaines que celui de l'étude des triangles. Elles sont périodiques et leurs représentations graphiques sont des sinusoïdes et peuvent servir à modéliser des phénomènes périodiques comme le son, les ondes de lumière. Tout signal, vérifiant certaines propriétés, peut être décrit par une somme (généralement infinie) de fonctions sinus et cosinus de différentes fréquences ; c'est l'idée de base de l'analyse de Fourier, dans laquelle les séries trigonométriques sont utilisées pour résoudre de nombreux problèmes aux valeurs limites dans des équations aux dérivées partielles. Par exemple un signal carré, peut être décrit par une série de Fourier :
Histoire [modifier]
Les traces les plus anciennes d'utilisation de sinus seraient apparues dans le Sulba Sutras écrit en indien ancien dans la période du viiie siècle av. J.-C. au vie siècle av. J.-C.
Les fonctions trigonométriques furent plus tard étudiées par Hipparque de Nicée (185-125 av. J.-C.), Âryabhata (476-550), Varahamihira, Brahmagupta, Muhammad ibn Mūsā al-Khuwārizmī, Abu l-Wafa, Omar Khayyam, Bhāskara II, Nasir ad-Din at-Tusi, Regiomontanus (1464), Al-Kachi (quatorzième siècle), Ulugh Beg (quatorzième siècle), Madhava (1400),Rheticus et son disciple Valentin Otho.
L'ouvrage Introductio in analysin infinitorum (1748) de Leonhard Euler fut en grande partie à l'origine des considérations analytiques des fonctions trigonométriques en Europe en les définissant à partir de développements en séries, et présenta les formules d'Euler.
Références [modifier]
Bibliographie [modifier]
- Guilmin, Adrien Cours élémentaire de trigonométrie rectiligne Gallica
- Lefébure de Fourcy et Louis-Étienne Eléments de trigonométrie Gallica
- Maor, Eli, Trigonometric Delights, Princeton Univ. Press. (1998). Reprint edition (25 février, 2002): ISBN 0-691-09541-8. (en)
- Needham, Tristan, Preface" to Visual Complex Analysis. Oxford University Press, (1999). ISBN 0-19-853446-9. (en)
- O'Connor, J.J., and E.F. Robertson, Trigonometric functions, Archive de l'histoire des mathématiques de MacTutor. (1996). (en)
- O'Connor, J.J., and E.F. Robertson, Madhava of Sangamagramma, Archive de l'histoire des mathématiques de MacTutor. (2000). (en)
- Pearce, Ian G., Madhava of Sangamagramma, Archive de l'histoire des mathématiques de MacTutor. (2002). (en)
- Weisstein, Eric W., Tangente de MathWorld, consulté le 21 janvier 2006.
Voir aussi [modifier]
Liens internes [modifier]
- Trigonométrie
- Algorithme de calcul CORDIC
- Comment construire des tables trigonométriques
- Similarité cosinus
- Sinus cardinal
- Trigonométrie complexe
- Trigonométrie hyperbolique
Liens externes [modifier]
- Étymologie du mot « sinus » sur le site « Principia » d'histoire et philosophie des sciences
- GonioLab: Visualisée des Cercle trigonométrique, fonctions de trigonométriques et hyperboliques (Java Web Start)
- Isométries de la sinusoïde et morphisme : note pour lycéens (étudiants du secondaire), sur le site personnel de X. Hubaut, professeur à l'Université libre de Bruxelles
10:07 Publié dans Fonction trigonométrique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
















































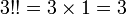
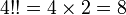
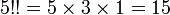
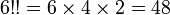
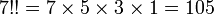


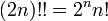
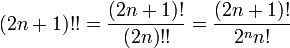

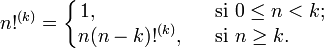
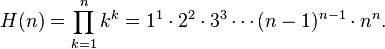





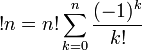
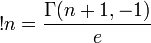
![!n = left [ frac {n!}{e} right ]](http://upload.wikimedia.org/math/b/c/6/bc6b78cafc03ee3a79b30031c1d705a4.png)

 avec
avec  et
et  suite
suite 







![forall n in mathbb{N}^*, r_4(n) = 8 sum_{d|n, d notequiv 0[4]}{d}](http://upload.wikimedia.org/math/f/2/d/f2de8fa897b940dd87bfb7457bc12e72.png)