01/12/2010
Analogues de la factorielle
Analogues de la factorielle
En mathématiques, de nombreuses fonctions analogues à la fonction factorielle ont été définies ; cette page recense les variantes les plus fréquemment rencontrées.
Sommaire[masquer] |
Primorielle [modifier]
La fonction primorielle est similaire à la fonction factorielle, mais ne prend en compte que le produit des nombres premiers.
Multifactorielles [modifier]
Afin d'alléger l'écriture, une notation courante est d'utiliser plusieurs points d'exclamation pour noter une fonction multifactorielle, le produit d'un facteur sur deux (n!!), sur trois (n!!!) ou plus.
n!!, la double factorielle de n, est définie de façon récurrente par :
Par exemple :
Certaines identités découlent de la définition :
Il faut faire attention de ne pas interpréter n!! comme la factorielle de n!, qui serait écrite (n!)! et est un nombre largement plus grand. Certains mathématiciens ont suggéré la notation alternative n!2 pour la double factorielle et d'une façon similaire n!n pour les autres multifactorielles, mais cet usage ne s'est pas répandu.
La double factorielle est la variante la plus commune, mais il est possible de définir de façon similaire la triple factorielle, etc. De façon générale, la ke factorielle, notée n!(k), est définie de façon récurrente par :
Hyperfactorielle [modifier]
L'hyperfactorielle de n, notée H(n), est définie par :
Pour n = 1, 2, 3, 4,... les valeurs de H(n) sont 1, 4, 108, 27 648,... (suite A002109 de l’OEIS).
La fonction hyperfactorielle est similaire à la fonction factorielle, mais produit de plus grands nombres. Sa croissance est en revanche comparable.
Superfactorielle [modifier]
Neil Sloane et Simon Plouffe ont défini la superfactorielle en 1995 comme le produit des n premières factorielles :
Par exemple, la superfactorielle de 4 est :
La suite des superfactorielles débute (depuis n = 0) par :
L'idée fut étendue en 2000 par Henry Bottomley à la superduperfactorielle, produit des n premières superfactorielles, débutant (depuis n = 0) par :
puis, par récurrence, à n'importe quelle factorielle de niveau supérieur, où la factorielle de niveau m de n est le produit des n premières factorielles de niveau m-1, c’est-à-dire, en notant f(n,m) la factorielle de n de niveau m :
où f(n,0) = n pour n > 0 et f(0,m) = 1.
Superfactorielle (définition alternative) [modifier]
Clifford Pickover, dans son livre Keys to Infinity (1995), définit la superfactorielle de n, notée n$ ($ étant un signe factoriel ! portant un S superposé), comme :
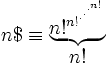 ,
,
ou, en utilisant la notation de Knuth :
 .
.
Les premiers éléments de la suite des superfactorielles sont :
Sous-factorielle [modifier]
La fonction sous-factorielle, notée !n, sert à calculer le nombre de permutations possible de n objets distincts de manière à ce qu'aucun objet ne se trouve à sa place.
Par exemple, il existe !n façon de glisser n lettres dans n enveloppes affranchies et adressées de manière à ce qu'aucune des lettres ne soit dans la bonne enveloppe.
Il existe différentes façons de calculer la sous-factorielle
Où Γ est la fonction gamma incomplète et e la base du logarithme népérien.
Où [x] désigne l'entier le plus proche de x
Les premières valeurs de cette fonction sont :
- !1 = 0
- !2 = 1
- !3 = 2
- !4 = 9
- !5 = 44
- !6 = 265
- !7 = 1854
- !8 = 14833
- !9 = 133496
- !10 = 1334961
- !11 = 14684570
- !12 = 176214841
- !13 = 2290792932
22:42 Publié dans Analogues de la factorielle | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook









































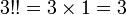
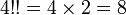
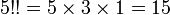
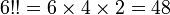
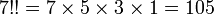


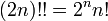
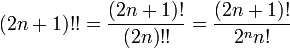

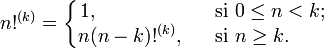
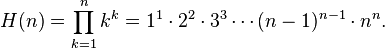




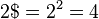

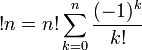
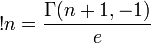
![!n = left [ frac {n!}{e} right ]](http://upload.wikimedia.org/math/b/c/6/bc6b78cafc03ee3a79b30031c1d705a4.png)

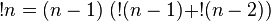
 avec
avec  et
et  suite
suite
Les commentaires sont fermés.