20/11/2010
The Octonions
The Octonions
John C. Baez
Department of Mathematics
University of California
Riverside CA 92521
John C. Baez
Department of Mathematics
University of California
Riverside CA 92521
May 16, 2001
Published in Bull. Amer. Math. Soc. 39 (2002), 145-205.
Errata in Bull. Amer. Math. Soc. 42 (2005), 213.
Also available in Postscript and PDF formats.
Abstract:
The octonions are the largest of the four normed division algebras. While somewhat neglected due to their nonassociativity, they stand at the crossroads of many interesting fields of mathematics. Here we describe them and their relation to Clifford algebras and spinors, Bott periodicity, projective and Lorentzian geometry, Jordan algebras, and the exceptional Lie groups. We also touch upon their applications in quantum logic, special relativity and supersymmetry.
Table of Contents:
- Introduction
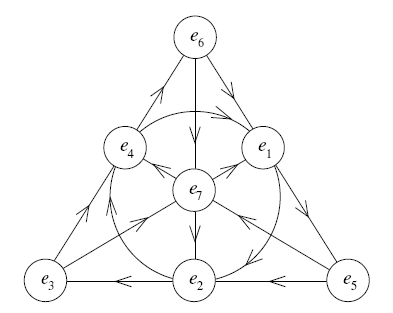
- Constructing the Octonions
- Octonionic Projective Geometry
- Projective Lines
- OP1 and Bott Periodicity
- OP1 and Lorentzian Geometry
- OP2 and the Exceptional Jordan Algebra
- Exceptional Lie Algebras
- Conclusions
- Bibliography
- Octonions Online
links to other websites containing material about the octonions. - Brougham Bridge
pictures of the bridge where Hamilton carved his definition of the quaternions. - On Quaternions and Octonions: Their Geometry, Arithmetic and Symmetry
my review of John Conway and Derek Smith's book.

- Division algebras and supersymmetry
A paper with John Huerta.
12:22 Publié dans The Octonions | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook