21/11/2010
Complexes - Forme algébrique, équations, interprétation géométrique
Complexes - Forme algébrique, équations, interprétation géométrique
z = a + ib
![]()

(voir: second degré)

10:05 Publié dans Complexes - Forme algébrique, équations | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Produit scalaire
Source : http://fr.wikipedia.org/wiki/Produit_scalaire
Produit scalaire
En géométrie vectorielle, le produit scalaire est une opération algébrique s'ajoutant aux lois s'appliquant aux vecteurs. À deux vecteurs elle associe leur produit, qui est un nombre (ouscalaire). Elle permet d'exploiter les notions de la géométrie euclidienne traditionnelle : longueurs, angles, orthogonalité en dimension deux et trois, mais aussi de les étendre à des espaces vectoriels réels de toute dimension, et aux espaces vectoriels complexes.
Comme il existe deux grandes manières de définir les vecteurs, soit par une approche purement algébrique (cf espace vectoriel), soit par une approche géométrique à l'aide des bipoints(ou couple ordonné de points, cf Vecteur), il existe de même deux manières de présenter le produit scalaire : une manière algébrique, (objet de l'article Espace préhilbertien) et une manière géométrique, à l'aide de bipoints.
L'objectif de cet article est de présenter le produit scalaire de manière géométrique dans un espace euclidien traditionnel et de montrer comment cette notion peut s'étendre à tout espace vectoriel.
Sommaire[masquer] |
Aperçu des applications du produit scalaire [modifier]
Le produit scalaire possède de multiples applications. En physique, il est, par exemple, utilisé pour modéliser le travail d'une force. En géométrie analytique il permet de déterminer le caractère perpendiculaire de deux droites ou d'une droite et d'un plan. Ce domaine est le sujet de cet article. Dans le cas de la dimension finie quelconque, il dispose de nombreuses applications algébriques : il permet de classifier les quadriques, offre des outils pour la réduction d'endomorphismes ou encore est à la base de multiples techniques statistiques comme la méthode des moindres carrés ou l'analyse en composantes principales. En géométrie, il confère à l'espace vectoriel une structure d'espace métrique disposant de nombreuses propriétés comme la complétude. Ces applications sont traitées dans les articles Espace euclidien et Espace hermitien. Le produit scalaire est aussi utilisé dans des espaces de dimension infinie, il permet alors de résoudre des équations aux dérivées partielles. La théorie devient plus subtile et de nombreux résultats, vrais en dimension finie, prennent une autre forme. Cet aspect du produit scalaire est traité dans les articles Espace préhilbertien et Espace de Hilbert.
Enfin, l'article géométrie euclidienne propose une synthèse de l'histoire, des implications et applications du produit scalaire en dimension finie.
Fragments d'histoire [modifier]
Élément important de calcul en géométrie euclidienne, le produit scalaire apparaît cependant assez tard dans l'histoire des mathématiques. On en trouve trace chez Hamilton en 1843 lorsqu'il crée le corps des quaternions. Peano le définit ensuite associé à un calcul d'aire ou de déterminant. Roberto Marcolongo et Cesare Burali-Forti le définissent seulement à l'aide du cosinus d'un angle et lui donnent le nom de produit intérieur ou produit scalaire. C'est sous cette forme qu'il apparaît par la suite. Sa qualité de forme bilinéaire symétrique sera ensuite exploitée en algèbre linéaire et, de propriété, deviendra définition.
La notation du produit scalaire à l'aide d'un point ou d'une croix provient de Josiah Willard Gibbs, dans les années 1880.
Pourtant, selon le site Earliest known uses of some of the mathematical words, l'expression produit scalaire apparait pour la première fois dans une publication scientifique dans un livre de William Kingdon Clifford daté de 1878. Cette paternité est néanmoins remise en cause par M. J Crowe pour qui Clifford est une transition entre l'algèbre des quaternions décrite par Hamilton et la formalisation des espaces vectoriels.
Définitions et premières propriétés [modifier]
Dans cette section, on considèrera un espace traditionnel tel qu'il est défini par Euclide : plan ou espace formé de points dans lequel les notions de distance et d'angle sont connues. On sait aussi calculer le cosinus de tout angle géométrique. Sont également utilisables le théorème de Pythagore, celui d'Al-Kashi et le théorème de Thalès. La construction géométrique des vecteurs dans un tel espace est détaillée dans l'article Vecteur.
Soient deux vecteurs représentés par des bipoints de mêmes origines (O, A) et (O, B). De tels représentants existent quel que soit le choix des vecteurs. Dans le reste de l'article, la longueur du bipoint (O, A) est notée OA ou parfois |OA|, c'est donc un nombre réel positif.
- Définition :
- Etant donnés des points O, A et B, on considère les vecteurs représentés par les bipoints OA et OB.
- Lorsque ces vecteurs sont non nuls le produit scalaire est le nombre réel OA·OB·cos(θ) où θ représente l'angle orienté AOB.
- Si l'un des vecteurs est nul alors le produit scalaire est nul.
- Dans tous les cas, on note ce produit scalaire :

Dans le cas où aucun des vecteurs n'est nul, cette définition prend la forme suivante :
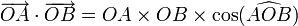
Ici cos désigne la fonction mathématique cosinus et  représente l'angle géométrique de sommet O dessiné par les points A, O et B.
représente l'angle géométrique de sommet O dessiné par les points A, O et B.
Dans le cas où les deux vecteurs sont égaux, la notation suivante est utilisée :

La valeur du produit scalaire correspond alors à l'aire d'un carré de côté OA.
- Définition :
- La norme euclidienne d'un vecteur représenté par un bipoint AB est la distance qui sépare A de B. En général, elle est notée
 .
. - Elle est égale à la racine carrée du produit scalaire du vecteur avec lui-même.
![left| overrightarrow {AB} right| = sqrt[]{overrightarrow {AB}cdotoverrightarrow {AB}}](http://upload.wikimedia.org/math/f/8/6/f86ba421646aa922511015ee1522f466.png)
Une inégalité évidente est vérifiée par le produit scalaire ainsi défini :
- Inégalité de Cauchy-Schwarz
- Soient O, A et B trois points du plan, la valeur absolue du produit scalaire des deux vecteurs d'extrémités O, A et O, B est toujours inférieure ou égale au produit des normes des deux vecteurs. Cette majoration s'écrit :

L'égalité a lieu si et seulement si les trois points sont alignés. Cette majoration provient du fait que la fonction cosinus prend ses valeurs dans l'intervalle d'extrémité 1 et -1. Pour que l'égalité ait lieu, il faut et il suffit que le cosinus ait pour valeur soit 1 soit -1, c'est-à-dire que l'angle soit nul ou plat. Ce qui signifie bien que les trois points sont alignés. Une fois encore, cette inégalité est l'objet de l'article Inégalité de Cauchy-Schwarz, l'article suppose encore une formalisation algébrique différente de celle choisie ici.
Propriétés géométriques [modifier]
Projeté [modifier]
La définition précédente suppose connue la définition de la fonction cosinus. Il est possible d'éviter de faire appel à cette fonction.
Soit A, B et C trois points distincts, la trigonométrie du triangle rectangle permet de calculer le produit scalaire grâce à une projection orthogonale. En effet, si H est le projeté orthogonal de C sur la droite (AB), le produit scalaire est alors en valeur absolue égal au produit des distances AH et AB. Si Ase trouve entre H et B, le produit scalaire est négatif et positif sinon. On remarque que si H est confondu avec A, alors le produit scalaire est nul.
|
|
|
Le produit scalaire est parfois utilisé sous cette forme pour déterminer le travail d'une force lors d'un déplacement : Le travail de la force F selon le trajet u est le produit scalaire des deux vecteurs. Dans la seconde illustration, ce travail est égal à - AB × AH.
Théorème d'Al-Kashi [modifier]
Il existe une manière plus générale d'exprimer le théorème de Pythagore. Elle traite le cas d'un triangle quelconque. Avec les notations de la figure de droite, ce résultat, nommé théorème d'Al-Kashi s'exprime de la manière suivante :
 ou encore
ou encore 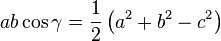
La démonstration se trouve dans l'article détaillé. Ce résultat s'exprime en termes de produit scalaire :
- Théorème d'Al-Kashi
- Soient A, B et C trois points quelconques, alors la formule suivante est toujours vérifiée :

Le caractère plus général de cette formulation permet d'expliciter et de démontrer simplement les propriétés algébriques du produit scalaire. Le théorème de la médiane est un cas particulier explicité dans l'article à ce sujet.
Produit scalaire comme une aire [modifier]
L'expression par le produit scalaire du théorème d'Al-Kashi suggère une formulation du produit scalaire en termes d'aire. Le produit scalaire, en utilisant les notations du paragraphe sur le projeté, correspond à l'aire du rectangle de base AH et de hauteur AB.
Considérons le produit scalaire dans un plan orienté, de x vers y dans la figure de droite. Le produit scalaire des vecteurs x et y est égal à l'aire orientée du parallélogramme construit grâce aux vecteurs y et xr. Le vecteur xr est l'image du vecteur x par une rotation d'angle droit direct. Cette approche est celle de Peano. Pour ce faire, il utilise un outil appelé déterminant, et utilise la formulation suivante du produit scalaire, par construction géométrique, équivalente à celle de l'article :

Sur le dessin, les parallélogrammes ont été déformés en rectangle de même aire par la propriété de cisaillement. L'aire verte correspond à un produit scalaire positif et l'aire rose à un produit scalaire négatif.
Cette forme géométrique possède un avantage certain, elle permet d'établir les propriétés algébriques du produit scalaire. Ces propriétés sont utiles, à la fois pour établir une expression analytique utile à la résolution de nombreux problèmes et pour établir une nouvelle formulation à la fois plus générale et plus opérationnelle.
Orthogonalité, colinéarité et angle [modifier]
De telles définitions du produit scalaire donnent des outils intéressants pour vérifier une orthogonalité, une colinéarité ou déterminer un angle géométrique.
Orthogonalité : les vecteurs  et
et  sont orthogonaux si l'un ou l'autre des vecteurs est nul ou si l'angle géométrique AOB est droit. En termes de produit scalaire, cela se traduit par une seule condition
sont orthogonaux si l'un ou l'autre des vecteurs est nul ou si l'angle géométrique AOB est droit. En termes de produit scalaire, cela se traduit par une seule condition  et
et  sont orthogonaux si et seulement si
sont orthogonaux si et seulement si 
Colinéarité : les vecteurs  et
et  sont colinéaires si et seulement si les points O, A et B sont sur une même droite. En termes de produit scalaire, cela se traduit par
sont colinéaires si et seulement si les points O, A et B sont sur une même droite. En termes de produit scalaire, cela se traduit par  et
et  sont colinéaires si et seulement si
sont colinéaires si et seulement si 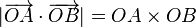
Angle géométrique : Si  et
et  sont deux vecteurs non nuls, l'angle géométrique AOB est déterminé par l'égalité
sont deux vecteurs non nuls, l'angle géométrique AOB est déterminé par l'égalité 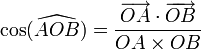
Propriétés algébriques [modifier]
Pour une raison de simplicité, d'autres notations sont utilisées. Les vecteurs ne sont plus notés comme des bipoints, comme par exemple  mais simplement avec une lettre :
mais simplement avec une lettre :  . Le produit scalaire est alors toujours noté par un point :
. Le produit scalaire est alors toujours noté par un point : 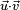 . Il arrive aussi que les vecteurs soient notés sans flèches, pour éviter la confusion entre le produit d'un scalaire par un vecteur et le produit scalaire entre deux vecteurs, le produit scalaire est alors noté (u, v) ou encore
. Il arrive aussi que les vecteurs soient notés sans flèches, pour éviter la confusion entre le produit d'un scalaire par un vecteur et le produit scalaire entre deux vecteurs, le produit scalaire est alors noté (u, v) ou encore 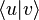 . Une convention, pas toujours suivie consiste à choisir des lettres grecques pour les scalaires, permettant ainsi d'éviter des confusions. Dans la suite de l'article, la convention suivie est celle du vecteur surmonté d'une flèche et du produit scalaire noté par un point.
. Une convention, pas toujours suivie consiste à choisir des lettres grecques pour les scalaires, permettant ainsi d'éviter des confusions. Dans la suite de l'article, la convention suivie est celle du vecteur surmonté d'une flèche et du produit scalaire noté par un point.
Le terme de produit scalaire suggère l'existence d'une opération qui, à deux vecteurs, associe un scalaire. Dans un espace vectoriel, les scalaires sont les coefficients par lesquels on a le droit de multiplier les vecteurs. Dans une approche élémentaire, ces scalaires sont des réels. Le fait d'appeler cette opération un produit suggère l'existence de propriétés que l'on attend généralement d'un produit (commutativité, distributivité par rapport à l'addition...).
Symétrie [modifier]
La symétrie est une propriété qui s'applique aux fonctions de deux variables prises dans un même ensemble. Soit un ensemble E et une fonction f définie dans E×E. Elle est dite symétrique si et seulement si :

Le cadre de cette définition est celui du produit scalaire, qui à deux vecteurs associe un nombre.
Comme la longueur du segment [B, C] est celle du segment [C, B], le théorème d'Al-Kashi établit la symétrie du produit scalaire :
- Symétrie du produit scalaire
- Le produit scalaire défini sur un espace vectoriel E est symétrique, c'est-à-dire que la proposition suivante est toujours vérifiée :

Bilinéarité [modifier]
Le produit scalaire dans un espace vectoriel E est compatible à droite avec l'addition. Cette propriété signifie que le produit scalaire d'un vecteur par une somme de deux vecteurs est égal à la somme des deux produits scalaires :

La figure de gauche illustre cette compatibilité. Elle est la conséquence du fait que la translation laisse invariante l'aire d'une surface. Une applicationde cette nature, laissant invariant les angles, les longueurs et par voie de conséquence les surfaces est appelée isométrie. Le rectangle vert a pour surface le produit scalaire de 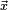 avec
avec 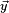 , le rectangle bleu a pour surface le produit scalaire de
, le rectangle bleu a pour surface le produit scalaire de 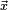 avec
avec  . La somme des deux surfaces est bien égale à la surface du rectangle orange qui est le produit scalaire de
. La somme des deux surfaces est bien égale à la surface du rectangle orange qui est le produit scalaire de 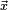 avec
avec  . En effet, la translation laisse invariante la surface. L'égalité recherchée est bien vérifiée.
. En effet, la translation laisse invariante la surface. L'égalité recherchée est bien vérifiée.
La symétrie du produit scalaire ainsi que la compatibilité à droite démontre la compatibilité à gauche de l'addition :

Il est de même possible de parler de compatibilité à droite pour le produit par un scalaire. Cette propriété prend la forme suivante :

Le point désigne ici à la fois la multiplication par un scalaire et le produit scalaire. L'usage des flèches ainsi que des lettres grecques pour désigner des nombres permet d'éviter l'ambigüité.
Cette compatibilité est une conséquence du théorème de Thalès. La figure de droite illustre cette propriété. Le rectangle violet possède une hauteur égale à celle du triangle vert, et sa base est égale à OD. Les deux triangles OAB et OCD sont semblables il est donc possible d' appliquer le théorème de Thalès, il démontre que comme OC = λ⋅OA, alors OD = λ⋅OB. Sa surface est donc bien multipliée par λ.
Comme précédemment, la symétrie possède pour conséquence la compatibilité à gauche :
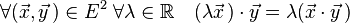
Ainsi, l'application, pour un 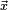 qui au vecteur
qui au vecteur 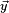 associe le nombre
associe le nombre  vérifie la propriété suivante :
vérifie la propriété suivante :

On dit alors que l'application produit scalaire est linéaire à droite, elle est de même linéaire à gauche. Une telle application est dite bilinéaire. L'application a pour valeurs des nombres, on parle alors de forme.
- Bilinéarité : le produit scalaire est une forme bilinéaire.
Caractère défini positif [modifier]
Le produit scalaire d'un vecteur avec lui-même est égal à l'aire d'un carré de côté la longueur d'un de ses représentants. En conséquence, le produit scalaire d'un vecteur avec lui-même est toujours positif. Cette valeur est nulle si et seulement si le vecteur est nul car seul le vecteur nul possède un représentant de longueur nulle. On en déduit la définition et la proposition suivantes :
- Une forme à deux variables est dite définie positive si et seulement si pour tout vecteur non nul x, l'image de (x,x) est strictement positive.
- Le produit scalaire est une forme définie positive.
Bilan : produit scalaire réel [modifier]
Un produit scalaire est une forme bilinéaire symétrique définie positive sur un espace vectoriel sur les nombres réels.
Les propriétés algébriques vues dans le cas de la dimension 2 ou 3 sont suffisantes pour définir un produit scalaire dans un espace vectoriel réel quelconque.
Soit  un espace vectoriel réel.
un espace vectoriel réel.
On dit qu'une application φ :
est un produit scalaire si elle est :
-
- bilinéaire : φ est linéaire relativement à chaque argument (l'autre étant fixé).
- symétrique :
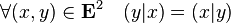
- positive :

- définie :

Il est naturel de se poser la question réciproque : Est-il possible de définir une géométrie à l'aide d'un espace vectoriel et d'un produit scalaire ? La longueur est alors donnée par la norme, et l'angle θ entre deux vecteurs 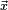 et
et  par la formule :
par la formule :

Une telle géométrie vérifie les inégalités triangulaires et de Cauchy-Schwarz, le théorème de Thalès, de Pythagore, ses isométries sont les rotations et les symétries.
Espace euclidien [modifier]
Un espace euclidien est un espace vectoriel sur  , de dimension finie et muni d'un produit scalaire.
, de dimension finie et muni d'un produit scalaire.
Un tel espace possède de nombreuses propriétés à la fois algébriques et géométriques. Le produit scalaire met en évidence des applications linéaires particulières aux propriétés multiples. Elles permettent, entre autres, de définir de nombreuses structures additionnelles, souvent elles aussi euclidiennes. Elle offre un cadre géométrique qui permet de généraliser bon nombre de résultats vrais sur les nombres réels. Il devient ainsi possible d'appliquer des résultats de l'analyse réelle à la géométrie différentielle.
Expression analytique [modifier]
Base orthonormale [modifier]
Dans un espace vectoriel de dimension deux ou trois, les propriétés algébriques permettent l'expression du produit scalaire à l'aide d'un système de coordonnées. Elle est plus simple si la base est choisie orthonormale, c'est-à-dire si ses vecteurs sont tous de norme égale à un et s'ils sont tous orthogonaux deux à deux. Par exemple en dimension trois, si la base orthonormale est notée ( ,
,  ,
,  ), si les deux vecteurs
), si les deux vecteurs 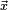 et
et 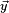 ont pour coordonnées respectives : (x1, x2, x3) et (y1, y2, y3), on obtient alors la formule :
ont pour coordonnées respectives : (x1, x2, x3) et (y1, y2, y3), on obtient alors la formule :

Elle s'obtient à partir du développement des deux vecteurs dans la base :
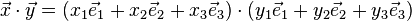
Avec les propriété de bilinéarité et de symétrie, on montre que :
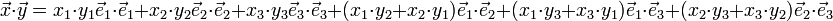
Or  est égal à un car la base est normée et si i est différent de j alors
est égal à un car la base est normée et si i est différent de j alors  est nul car la base est orthogonale.
est nul car la base est orthogonale.
Écriture matricielle [modifier]
Il existe une manière simple d'exprimer le produit scalaire, à l'aide de matrices. Les deux vecteurs 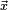 et
et 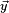 du paragraphe précédent prennent alors la forme suivante :
du paragraphe précédent prennent alors la forme suivante :

Les matrices X et Y représentent les deux vecteurs. À l'aide de l'opération transposée et de la multiplication des matrices, on obtient l'égalité :
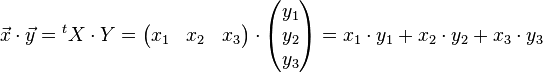
Base quelconque [modifier]
Si la base ( ,
, 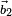 ,
,  ) est choisie quelconque, l'expression du produit scalaire est plus complexe. Notons (φ1, φ2, φ3) et (ψ1, ψ2, ψ3) les coordonnées des vecteurs
) est choisie quelconque, l'expression du produit scalaire est plus complexe. Notons (φ1, φ2, φ3) et (ψ1, ψ2, ψ3) les coordonnées des vecteurs 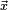 et
et 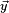 dans cette nouvelle base. On a alors l'égalité :
dans cette nouvelle base. On a alors l'égalité :


La matrice M est appelée la matrice de Gram du produit scalaire dans la base ( ,
, 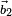 ,
,  ). Elle possède de nombreuses propriétés, elle est symétrique suivant une diagonale, elle est donc diagonalisable, ses valeurs propres sont toutes strictement positives. Une telle matrice est dite matrice définie positive.
). Elle possède de nombreuses propriétés, elle est symétrique suivant une diagonale, elle est donc diagonalisable, ses valeurs propres sont toutes strictement positives. Une telle matrice est dite matrice définie positive.
On montre que la donnée d'une matrice définie positive et d'une base dans un espace vectoriel réel de dimension n permettent de définir un produit scalaire de manière unique.
Généralisation aux espaces vectoriels complexes [modifier]
Produit scalaire hermitien [modifier]
Pour adapter la définition du produit scalaire réel aux espaces vectoriels complexes, nous avons besoin de la notion de « semi-linéarité » :
Une application f d'un espace vectoriel complexe  dans
dans  est dite semi-linéaire si elle vérifie :
est dite semi-linéaire si elle vérifie :
Soit donc maintenant  un espace vectoriel complexe.
un espace vectoriel complexe.
On dit qu'une application φ :
est un produit scalaire hermitien à gauche (ou simplement un produit scalaire) si elle est :
-
- sesquilinéaire à gauche : c'est-à-dire
-
- linéaire relativement au second argument (le premier étant fixé)
- semi-linéaire relativement au premier argument (le second étant fixé)
- symétrique hermitienne :
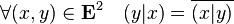
- positive :

- définie :

Remarque : la convention de linéarité à droite, semi-linéarité à gauche n'est pas universelle, certains auteurs utilisent la convention inverse. Dans un espace vectoriel complexe, muni d'un tel produit scalaire, sont encore vérifiés le théorème de Pythagore, l'inégalité de Cauchy-Schwarz et l'inégalité triangulaire.
Espace préhilbertien [modifier]
Un espace préhilbertien est un espace vectoriel réel ou complexe, généralement de dimension infinie, que l'on a muni d'un produit scalaire. La définition du produit scalaire quitte alors le champ de la géométrie traditionnelle.
Exemples [modifier]
- Dans l'espace
 , on définit le produit scalaire canonique :
, on définit le produit scalaire canonique :  .
.
- Dans l'espace
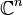 , on définit le produit scalaire canonique :
, on définit le produit scalaire canonique :  .
.
- Soit
 le
le  -espace vectoriel des fonctions continues de l'intervalle
-espace vectoriel des fonctions continues de l'intervalle ![[a,, b]](http://upload.wikimedia.org/math/d/2/5/d2524b9940ce1c636bfb26ae09a941d2.png) dans
dans  .
.
- L'application
 est un produit scalaire sur E.
est un produit scalaire sur E.
- Soit
![E=C([a,, b],mathbb{C})](http://upload.wikimedia.org/math/6/a/1/6a1ecef636c975ee4b38c1f179f891a9.png) le
le  -espace vectoriel des fonctions continues de l'intervalle
-espace vectoriel des fonctions continues de l'intervalle ![[a,, b]](http://upload.wikimedia.org/math/d/2/5/d2524b9940ce1c636bfb26ae09a941d2.png) dans
dans  ,
,
- L'application :
 est un produit scalaire sur
est un produit scalaire sur  .
. - Remarque : Si , au lieu de travailler sur des fonctions continues, on travaille sur des fonctions continues par morceaux, la forme bilinéaire construite est bien positive mais n'est pas définie : (f|f) = 0 implique que f est nulle sauf sur un nombre fini de points.
Espace hermitien [modifier]
Un espace hermitien est un espace vectoriel défini sur les nombres complexes, de dimension finie et disposant d'un produit hermitien, correspondant à une généralisation du cas réel. Le terme de produit scalaire est aussi utilisé dans ce contexte. Les résultats et propriétés des espaces euclidiens se traduisent souvent simplement dans cet espace.
Espace de Hilbert [modifier]
Un espace de Hilbert peut être réel ou complexe. Il correspond exactement aux deux cas précédents, à la différence que la dimension n'est pas nécessairement finie. Si la théorie et les démonstrations sont différentes de la situation en dimension finie, certains résultats se généralisent. Une hypothèse topologique est néanmoins souvent nécessaire, celle de lacomplétude de l'espace métrique associé. Pour cette raison, un espace de Hilbert est par définition complet.
Cet espace est utilisé pour résoudre des problèmes d'analyse fonctionnelle, particulièrement des équations aux dérivées partielles.
Voir aussi [modifier]
Articles connexes [modifier]
- Orthogonalité
- Projection orthogonale
- Espace de Hilbert
- Espace quadratique
- Groupe orthogonal
- Mesures secondaires
Sources [modifier]
- Rudolf Bkouche, D'où vient le produit scalaire ?, site de l'ENS
10:04 Publié dans Produit scalaire | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Polynômes - Equations de degré 3
Polynômes - Equations de degré 3
(x - a)(ax² + bx + c = 0)
![]()

On pourra revoir les chapitres Signe de ax + b et Signe de ax² + bx + c

| Source : | http://www.vivelesmaths.com/ |
|
10:00 Publié dans Polynômes - Equations de degré 3 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Endomorphisme nilpotent
Source : http://fr.wikipedia.org/wiki/Endomorphisme_nilpotent
Endomorphisme nilpotent
Un endomorphisme nilpotent est un morphisme d'un objet mathématique sur lui-même, qui, composé par lui-même un nombre suffisant de fois, donne le morphisme nul. C’est donc (lorsque les endomorphismes de cet objet forment un anneau) un élément nilpotentde cet anneau.
En algèbre linéaire, on considère les endomorphismes nilpotents d’un espace vectoriel. Un exemple est donné dans l'illustration. Ils interviennent dans la réduction des endomorphismes, c’est-à-dire la représentation d'un endomorphisme quelconque sous une forme la plus simple possible. Cette réduction sert par exemple pour la résolution d'équations différentielles linéaires.
On retrouve également le concept de nilpotence dans l'étude des groupe de Lie, avec l'analyse des algèbres de Lie nilpotentes.
Les endomorphismes nilpotents d'un espace vectoriel sont l'objet principal de cet article. Lorsque de plus cet espace est de dimension finie, chacun de ses endomorphismes est représenté par une matrice (dans une base de l'espace vectoriel concerné). L'endomorphisme est alors nilpotent si et seulement s'il a une matrice nilpotente, ce qui, par le calcul, permet une approche plus concrète du concept (toutes les propriétés générales des endomorphismes nilpotents ont leur pendant dans le contexte plus particulier des matrices nilpotentes), et offre d'importantes applications pratiques.
Sommaire[masquer] |
Définition [modifier]
Soit E un espace vectoriel sur un corps K et u un endomorphisme de E. L'endomorphisme u est dit nilpotent si et seulement s'il existe un entier n>0 tel que un = 0. Le plus petit entier naturel n vérifiant cette propriété est alors appelé indice (de nilpotence) de l'endomorphisme u.
Soit x un vecteur de E, on appelle indice de x (pour l'endomorphisme nilpotent u) le plus petit entier naturel p tel que up(x) = 0.
Un sous-espace cyclique de E (pour l'endomorphisme nilpotent u) est un sous-espace vectoriel de E engendré par une famille de la forme (x, u(x), u2(x), ..., up-1(x)), où x est un vecteur d'indice p.
Intérêt du concept [modifier]
Nilpotence et réduction [modifier]
Un enjeu important en mathématique est celui de la réduction, c’est-à-dire de la décomposition d'un concept en sous-concepts plus simples et qui décrivent l'intégralité du concept initial. Dans le cadre des applications linéaires la réduction est traitée dans l'article Réduction d'endomorphisme. En dimension finie, les endomorphismes nilpotents jouent un rôle important dans le cas ou 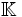 est un corps algébriquement clos. Un corps est dit algébriquement clos si et seulement si tous les polynômes sont scindés, autrement dit si tous les polynômes s'écrivent comme produit de polynômes du premier degré. C'est par exemple le cas pour les nombres complexes. Sous cette hypothèse, la théorie de la réduction d'endomorphisme montre que le cas général se résume à la somme d'un endomorphisme diagonalisable et d'un nilpotent. Ce résultat est connu sous le nom de Décomposition de Dunford.
est un corps algébriquement clos. Un corps est dit algébriquement clos si et seulement si tous les polynômes sont scindés, autrement dit si tous les polynômes s'écrivent comme produit de polynômes du premier degré. C'est par exemple le cas pour les nombres complexes. Sous cette hypothèse, la théorie de la réduction d'endomorphisme montre que le cas général se résume à la somme d'un endomorphisme diagonalisable et d'un nilpotent. Ce résultat est connu sous le nom de Décomposition de Dunford.
Si le corps n'est pas algébriquement clos, alors il est toujours possible d'étendre l'espace vectoriel sur un corps algébriquement clos. Cette technique est largement utilisée. Pour lesréels, la physique n'utilise pratiquement que cette approche.
Applications [modifier]
Puisqu'il est possible d'étendre à la clôture algébrique, la réduction des endomorphismes dans ce contexte joue un rôle essentiel en mathématique. Les endomorphismes nilpotents sont donc nécessaires à divers branches des mathématiques. En algèbre linéaire, ils interviennent naturellement dans la réduction de Jordan qui correspond à un cas important de réduction des endomorphismes. Les techniques utilisées sont celles des polynômes d'endomorphismes. Les conséquences se retrouvent sur la résolution de systèmes d'équations linéaires, dans la résolution d'équations différentielles linéaires où ils apparaissent comme des cas limites. En mathématiques appliquées, ils sont importants pour la recherche d'algorithmes, on utilise alors essentiellement les matrices nilpotentes où des représentations simples sont alors nécessaires.
Propriétés [modifier]
L'exemple illustre l'essentiel des propriétés des endomorphismes nilpotents. On y trouve des propriétés sur l'indice des endomorphismes et des vecteurs, des conditions nécessaires et suffisantes grâce aux polynômes. Des réductions avec une décomposition en espaces propres et l'existence d'une base réduite. Il existe aussi des propriétés calculatoires des matrices nilpotentes traitées dans l'article Matrice nilpotente.
Nilpotence et indice [modifier]
L'indice d'un endomorphisme nilpotent possède deux grandes propriétés :
-
- L'indice d'un endomorphisme nilpotent est inférieur ou égal à la dimension de l'espace (pour la démonstration penser à utiliser la suite (kerfn)).
- Il existe un vecteur dont l'indice est celui de l'endomorphisme.
Nilpotence et polynômes en dimension finie [modifier]
Les polynômes fournissent non seulement des conditions nécessaires et suffisantes pour la nilpotence, mais renseignent de plus sur l'indice.
-
- Un endomorphisme est nilpotent si et seulement si son polynôme caractéristique est égal à ( − X)n ou n est la dimension de l'espace.
- Un endomorphisme est nilpotent si et seulement si son polynôme minimal est égal à Xp ou p est l'indice de l'endomorphisme.
- Le polynôme minimal d'un vecteur x est égal à
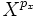 ou px est l'indice du vecteur x.
ou px est l'indice du vecteur x.
Nilpotence et réduction en dimension finie [modifier]
Le principe de réduction consiste à trouver une décomposition en somme directe de sous-espaces stables de l'espace vectoriel. Il en existe une pour les endomorphismes nilpotents. Et elle est compatible avec la réduction de Jordan. Cette approche est générale à l'analyse des endomorphismes. Dans le cas des endomorphismes nilpotents, elle est intimement liée à la notion de base réduite. Tout endomorphisme nilpotent u d'un espace vectoriel E non réduit au vecteur nul vérifie les propriétés suivantes :
-
- Si
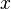 est un vecteur d'indice p alors la famille
est un vecteur d'indice p alors la famille 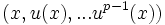 est libre. C'est donc une base du sous-espace cyclique qu'elle engendre.
est libre. C'est donc une base du sous-espace cyclique qu'elle engendre. - Pour tout sous-espace stable F de E (en particulier pour tout sous-espace cyclique), l'endomorphisme de F obtenu par restriction de u est, lui aussi, nilpotent (donc vérifie toutes les propriétés de cette liste, dès que F n'est pas réduit au vecteur nul).
- u possède une unique valeur propre : 0 (en particulier, son noyau n'est pas réduit au vecteur nul).
- E est somme directe de sous-espaces cycliques non réduits au vecteur nul.
- Une telle décomposition est "maximale", au sens où toute autre décomposition de E en somme directe de sous-espaces stables non réduits au vecteur nul est constituée d'au plus autant de sous-espaces.
- Si
Applications en mathématiques [modifier]
Matrice nilpotente [modifier]
Les résultats théoriques obtenus à l'aide de l'analyse des endomorphismes nilpotents ont des conséquences importantes sur les matrices nilpotentes. Ces résultats sont traités dans l'article Matrice nilpotente.
Réduction des endomorphismes [modifier]
Dans le cas où le corps est algébriquement clos et en dimension finie, les endomorphismes nilpotents jouent un rôle particulier dans la problématique de la réduction des endomorphismes. Le cas général, celui où toutes les racines du polynôme minimal sont simples, correspond aux endomorphismes diagonalisables. Ce cas génère un ensemble d'endomorphismes partout dense. En revanche, en cas de racine multiple, alors il existe une composante nilpotente.
Cette décomposition joue un rôle important dans les calculs que l'on observe dans l'univers des matrices. Elle permet par exemple de prouver que toute matrice est trigonalisable et offre une forme particulièrement simple en bloc de Jordan.
De nombreux algorithmes relèvent directement de cette décomposition. Elle permet d'accélérer massivement la résolution d'un système d'équations linéaires.
Équation différentielle linéaire [modifier]
La réduction de Jordan joue un rôle particulier pour les équations différentielles linéaires. Par exemple, dans le cas où les coefficients sont constants, alors le calcul de l'exponentielle d'une matrice dans le cas général est largement plus simple dans le cas d'une représentation matricielle réduite par la méthode de Jordan. Il est alors important de pouvoir calculer l'exponentielle d'une matrice nilpotente. Ce cas est exposé dans l'article Matrice nilpotente.
Groupes de Lie [modifier]
Dans l'étude des groupes de Lie, on s'intéresse parfois à ce que l'on appelle groupes de Lie nilpotents. Comme pour tout groupe de Lie, leur structure est décrite par leur fibré tangent, qui est muni d'une structure d'algèbre de Lie. Les représentations de ces algèbres dans les endomorphismes s'obtiennent à partir d'endomorphismes nilpotents.
Sources [modifier]
Liens internes [modifier]
principaux articles utilisés pour les démonstrations
Principaux articles utilisant la notion d'endomorphisme nilpotent
09:58 Publié dans Endomorphisme nilpotent | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Réduction d'endomorphisme
Source : http://fr.wikipedia.org/wiki/R%C3%A9duction_des_endomorph...
Réduction d'endomorphisme
En mathématiques, et plus particulièrement en algèbre linéaire, la réduction d'endomorphisme est une technique mathématique qui a pour objectif d'exprimer des matrices et desendomorphismes sous une forme plus simple, notamment pour faciliter les calculs. Cela consiste essentiellement à trouver une base de l'espace vectoriel qui permet d'exprimer plus simplement l'endomorphisme dans cette nouvelle base, et à décomposer l'espace en sous-espace vectoriels stables par l'endomorphisme.
Motivation [modifier]
Le concept de réduction [modifier]
La technique de réduction en algèbre est fréquente, elle consiste à réduire un concept, en sous-concepts les plus simples possible et permettant de reconstruire le cas général. Dans le cas des endomorphismes (c’est-à-dire des applications linéaires d'un espace vectoriel dans lui-même) la technique consiste à décomposer l'espace vectoriel en espaces plus petits. Cette réduction doit posséder six propriétés :
- L'endomorphisme définit par restriction un nouvel endomorphisme sur chacun des sous-espaces (c'est-à-dire chacun est un sous-espace vectoriel stable), ainsi la petite structure est une entité intrinsèque avec sa propre cohérence.
- Les différents sous-espaces sont en somme directe, c'est à dire indépendants les uns des autres. En conséquence, l'intersection de deux de ces sous-espaces est toujours réduite au vecteur nul.
- Les différents sous-espaces engendrent l'espace entier (ils sont supplémentaires), ce qui offre l'exhaustivité de l'analyse.
- La réduction décrit l'intégralité de la structure originelle.
- Elle est maximale, c'est-à-dire qu'il n'existe pas de décomposition en éléments plus petits et donc plus simple.
- Elle est aussi simple que possible, c'est-à-dire que pour chacune des sous-structures il n'existe pas de représentation plus élémentaire.
Toutefois, elle n'est pas unique.
Endomorphisme et vecteur propre [modifier]
La structure d'espace vectoriel sur lequel s'applique l'endomorphisme possède des propriétés différentes selon les cas. Dans l'hypothèse où la dimension est finie, alors la structure ducorps détermine l'essentiel des propriétés de réduction. Une approche très générale, pour établir la relation entre la structure du corps et la réduction des endomorphismes consiste à analyser la structure de l'anneau des polynômes associée au corps. Cette approche est analysée dans l'article polynôme d'endomorphisme. Le cas le plus simple est celui où le corps est dit algébriquement clos, c'est-à-dire que tout polynôme admet au moins une racine. C'est le cas des nombres complexes. Alors la réduction est particulièrement efficace. La notion de valeur propre devient le bon outil dans ce contexte. Lorsqu'il existe une base de vecteurs propres, on parle de diagonalisation. Tout endomorphisme n'est pas diagonalisable, en revanche sur un espace vectoriel réel ou complexe de dimension finie, les endomorphismes diagonalisables sont denses topologiquement.
Réduction de Jordan [modifier]
Il y a 2 obstacles qui empêchent que tout endomorphisme soit diagonalisable. Le premier est constitué des endomorphismes nilpotents ; il a été analysé par le mathématicien Camille Jordan. On montre que tout endomorphisme en dimension finie sur un corps algébriquement clos se décompose en sous-espaces caractéristiques où l'endomorphisme est la somme d'une homothétie et d'un endomorphisme nilpotent.
Le deuxième obstacle apparaît lorsque l'espace vectoriel n'est pas sur un corps algébriquement clos, comme les nombres réels par exemple. Dans ce cas les polynômes caractéristique et minimal peuvent avoir des facteurs premiers de degré supérieur ou égal à 2. Pour ces facteurs de plus haut degré, le concept de valeur propre doit être généralisé en celui de chaîne de Jordan. On dit qu'un polynôme P de degré d est une chaîne de Jordan d'un endomorphisme u si
- il existe un vecteur x non nul tel que P(u)(x)=0 ;
- la famille
 est libre.
est libre.
L'intérêt de cette notion est que la famille (x,...,ud-1(x)) engendre un sous-espace vectoriel stable par u, sur lequel la matrice de u est la matrice compagnon de Jordan de P.
Quand le degré d vaut 1, on retrouve la définition de valeur propre usuelle. On peut montrer que tout facteur premier du polynôme minimal d'un endomorphisme est une chaîne de Jordan de cet endomorphisme. Par conséquent tout endomorphisme admet une base où sa matrice a une diagonale formée de blocs matrices compagnons et de moitié inférieure gauche nulle (c'est donc une matrice presque triangulaire supérieure).
Endomorphisme et distance [modifier]
Il existe un cas particulier d'espace vectoriel : ceux qui sont munis d'une distance compatible avec la structure vectorielle. Un cas important est celui où la distance est euclidienne (ou hermitienne dans le cas complexe). L'ajout de cette structure offre une nouvelle voie d'accès à la problématique de la réduction d'endomorphisme. S'il est compatible avec la distance, c'est-à-dire s'il est normal, alors une nouvelle approche est possible. Dans ce contexte, l'exception nilpotente est absente. La réduction est plus simple et les techniques algorithmiques associées plus rapides.
Analyse fonctionnelle et opérateur linéaire [modifier]
Ce cas guide Hilbert dans une nouvelle direction. La généralisation de l'approche aux opérateurs différentiels. Ces opérateurs comme le laplacien ou le d'alembertien sont la clé d'importants problèmes en physique. Ils peuvent se représenter comme une équation linéaire, mais dans un espace de dimension infinie. Si l'approche générale de Jordan est vouée à l'échec car les polynômes ne s'appliquent pas dans ce contexte, en revanche ces opérateurs présentent les bonnes propriétés de compatibilité vis-à-vis d'une distance qu'il est possible de définir sur l'espace. Hilbert, propose une approche novatrice, consistant à étudier les propriétés géométriques de ces espaces de dimension infinie, au lieu de se limiter à une analyse d'un point particulier : la fonction solution de l'équation. Cette approche ouvre une nouvelle branche des mathématiques devenue essentielle au siècle dernier: l'analyse fonctionnelle. La physique moderne, aussi bien sous sa forme quantique que sous sa forme relativiste, utilise largement cette vision des choses.
Histoire [modifier]
Cas général de la dimension finie [modifier]
Dans toute cette section, E désigne un espace vectoriel sur un corps K, et sa dimension, supposée finie, est notée n.
Réduction et sous-espaces propres [modifier]
Il existe un premier candidat naturel pour une réduction, elle correspond à une décomposition en sous-espaces propres. Une présentation complète du concept est proposé dans l'article détaillé.
Un vecteur propre est un vecteur non nul dont l'image par u est colinéaire au vecteur d'origine. Le rapport de colinéarité est appelé valeur propre. L'ensemble des vecteurs propres pour une valeur propre donnée associée au vecteur nul forme un sous-espace vectoriel appelé sous-espace propre.
Une décomposition en sous-espaces propres représente donc un grand nombre des propriétés recherchées pour une réduction.
- Les espaces propres sont stables par l'endomorphisme.
- L'intersection de deux sous-espaces propres est réduite au vecteur nul.
- La restriction de l'endomorphisme à un sous-espace propre est une homothétie, c'est-à-dire une application qui à un vecteur x associe le vecteur λ.x.
Les propriétés recherchées dans la réduction sont presque rassemblées.
Diagonalisation [modifier]
Il suffirait en effet d'une propriété supplémentaire pour permettre une réduction à l'aide de cette approche : que la somme directe des sous-espaces propres soit l'espace vectoriel entier. Cela équivaut à l'existence d'une base B de vecteurs propres. Les deux propriétés manquantes sont alors réunies, car la réduction est composée de sous-espaces de dimension 1, ceux qui sont engendrés par les vecteurs de la base. Cette décomposition est maximale car il n'existe pas de décomposition en somme directe de sous-espaces non réduits au vecteur nul qui contiennent plus de sous-espaces que la dimension de l'espace.
Le fait que B soit une base garantit que la décomposition engendre bien l'espace entier.
En termes plus formels, les trois propositions suivantes sont équivalentes. Elles fournissent la définition d'un premier cas de réduction pour u.
-
- u est diagonalisable.
- Il existe une base de vecteurs propres.
- La somme des dimensions des sous-espaces propres est égale à la dimension de l'espace entier.
- La somme des sous-espaces propres est l'espace entier.
- Toute représentation matricielle de u est diagonalisable.
Une démonstration se trouve dans l'article Diagonalisation, sauf pour la dernière équivalence qui est traitée dans Matrice diagonale.
Diagonalisation et polynôme caractéristique [modifier]
Il existe d'autres propriétés importantes associées à cette définition. Elles proviennent essentiellement d'une approche polynomiale sur l'endomorphisme. Le polynôme caractéristique deu est, en dimension finie, un outil puissant d'analyse des endomorphismes. Il est défini comme le déterminant suivant : det(u -λ.I ). Comme le déterminant s'annule si et seulement si le noyau de l'application linéaire associée n'est pas réduit au vecteur nul, le polynôme possède comme racines les valeurs propres de l'endomorphisme. Trois propriétés relient diagonalisabilité et polynôme caractéristique.
-
- Si le polynôme caractéristique de u possède n racines distinctes alors u est diagonalisable.
C'est une condition suffisante, mais non nécessaire. Considérons le cas d'une homothétie dans le cas où n est strictement supérieur à 1. Le polynôme caractéristique ne possède qu'une racine multiple. Pourtant l'endomorphisme est clairement diagonalisable car toute base est constituée de vecteurs propres uniquement. Il existe de plus la condition nécessaire suivante :
-
- Si u est diagonalisable, alors son polynôme caractéristique est scindé.
Dire que le polynôme caractéristique P(X) est scindé signifie qu'il peut s'écrire comme produit de puissances de polynômes de degré 1 :
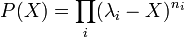
Pour l'obtention d'une condition nécessaire et suffisante à partir du polynôme caractéristique, une définition supplémentaire est nécessaire.
-
- la multiplicité algébrique d'une valeur propre est son ordre de multiplicité en tant que racine du polynôme caractéristique.
La multiplicité algébrique d'une valeur propre λ est donc l'exposant du polynôme (X-λ) dans le polynôme caractéristique. Cette définition permet de formuler une condition nécessaire et suffisante de diagonalisabilité.
-
- u est diagonalisable si et seulement si tout sous-espace propre possède une dimension égale à la multiplicité algébrique de la valeur propre associée.
Endomorphisme diagonalisable et polynôme minimal [modifier]
Si l'approche par le polynôme caractéristique offre des premiers résultats, elle n'est néanmoins pas intégralement satisfaisante. En effet, le calcul du polynôme est souvent lourd, et la recherche de la dimension des sous-espaces propres n'est pas simple.
Le concept de polynôme d'endomorphisme propose un autre candidat, souvent plus pertinent pour l'analyse des applications linéaires en dimension finie. C'est le polynôme minimal. À l'instar du polynôme caractéristique, ses racines sont aussi les valeurs propres. Sa spécificité s'exprime dans la condition nécessaire et suffisante suivante :
-
- u est diagonalisable si et seulement si son polynôme minimal est scindé sur K et à racines simples.
Cas où le polynôme minimal est scindé [modifier]
Réduction et endomorphisme nilpotent [modifier]
Même dans le cas où le polynôme minimal est scindé, il existe au moins un cas où la diagonalisation est impossible, celui des endomorphismes nilpotents. L'unique valeur propre est 0, donc l'unique sous-espace propre est son noyau. En conséquence le seul endomorphisme nilpotent diagonalisable est l'endomorphisme nul.
Les endomorphismes nilpotents disposent néanmoins d'une réduction traitée et démontrée dans l'article Endomorphisme nilpotent dans le paragraphe nilpotence et réduction en dimension finie. Un sous-espace cyclique de E (pour l'endomorphisme nilpotent u) est un sous-espace vectoriel engendré par une famille de la forme (x, u(x), u2(x), ...).
-
- Si u est nilpotent alors E est somme directe de sous-espaces cycliques pour u.
Nous y trouvons bien toutes les caractéristiques d'une réduction, une décomposition en somme directe de sous-espaces stables qui engendre l'espace entier. Dans l'article détaillé on montre de plus que cette décomposition est maximale.
Décomposition de Dunford [modifier]
Si le cas des endomorphismes nilpotents apparaît dans un premier temps comme une exception au cas diagonalisable, la théorie des polynômes d'endomorphismes nous montre que cette exception est unique. Plus précisément, la proposition suivante, connue sous le nom de décomposition de Dunford est vraie :
-
- Si le polynôme minimal de u est scindé alors u est la somme d'un endomorphisme diagonalisable et d'un endomorphisme nilpotent qui commutent entre eux.
Dans le contexte du théorème, le polynôme minimal 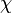 s'écrit sous la forme suivante :
s'écrit sous la forme suivante :

Les noyaux  sont appelés les sous-espaces de E caractéristiques de u.
sont appelés les sous-espaces de E caractéristiques de u.
Les quatre propriétés suivantes résument l'essentiel des propriétés associées à la décomposition de Dunford :
-
- Les λi sont les valeurs propres de u.
- L'espace E est somme directe des sous-espaces caractéristiques.
- Les sous-espaces caractéristiques sont stables par u. La restriction de u à
 est la somme d'une homothétie de rapport
est la somme d'une homothétie de rapport  et d'un endomorphisme nilpotent d'ordre
et d'un endomorphisme nilpotent d'ordre 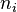 .
. - Les projecteurs sur les sous-espaces caractéristiques s'expriment sous forme de polynômes d'endomorphisme de u.
L'hypothèse que le polynôme minimal soit scindé représente une contrainte souvent faible. Le fait que les nombres complexes forment un corps algébriquement clos garantit déjà la généralité de la condition. Pour le cas des nombres réels, il est toujours possible d'étendre l'espace vectoriel aux corps des complexes pour la recherche des solutions, puis dans un deuxième temps de ne choisir que des solutions réelles. Pour les applications, cette démarche est souvent utilisée par les physiciens.
Réduction de Jordan [modifier]
La décomposition de Dunford n'est néanmoins pas une réduction. En effet, cette décomposition n'est pas maximale. Un sous-espace caractéristique se décompose encore.
Sur un sous-espace caractéristique Ei, la restriction de l'endomorphisme s'exprime comme la somme d'une homothétie et d'un endomorphisme nilpotent. En réduisant cet endomorphisme nilpotent comme indiqué précédemment, on décompose Ei en sous-espaces (stables par l'homothétie). La réduction des endomorphismes nilpotents fournit ainsi une décomposition maximale en sous-espaces stables à l'aide de la définition des espaces de Jordan.
-
- Un sous-espace de Jordan pour u est un sous-espace vectoriel de E possédant une base (e1, e2, ... , ep) telle que :
![exists lambdain K ;forall i in [1,p-1]; u(e_i)=lambda e_i + e_{i+1}quad et quad u(e_p)=lambda e_p](http://upload.wikimedia.org/math/d/2/5/d2598a5b960dfe353326272a37107de2.png)
Cette définition nous permet alors de décrire une réduction de Jordan pour u :
-
- Si le polynôme minimal de u est scindé alors E est somme directe de sous-espaces de Jordan, et il n'existe aucune décomposition de E en somme directe de sous-espaces, stables par u et non réduits au vecteur nul, comportant plus de composantes qu'une décomposition de Jordan.
Cas du corps des réels [modifier]
Comme pour un corps quelconque, on peut complexifier ou utiliser la décomposition de Frobenius.
Cas d'un corps quelconque [modifier]
La décomposition de Frobenius est la plus adaptée lorsqu'on ne veut pas travailler sur un corps algébriquement clos.
Une autre approche possible consiste à plonger le corps K dans sa clôture algébrique  puis le cas-espace E dans le produit tensoriel
puis le cas-espace E dans le produit tensoriel  . Un endomorphisme de E se prolonge alors de façon unique à
. Un endomorphisme de E se prolonge alors de façon unique à 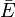 . Le point de vue matriciel est alors avantageux puisqu'on conserve la même matrice pour l'endomorphisme initial ou son prolongement, elle est simplement considérée comme matrice de
. Le point de vue matriciel est alors avantageux puisqu'on conserve la même matrice pour l'endomorphisme initial ou son prolongement, elle est simplement considérée comme matrice de 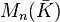 .
.
Utilisation de la réduction en dimension finie [modifier]
La diagonalisation est souvent la meilleure approche pour les problèmes concrets. Les matrices diagonalisables étant dense dans l'ensemble des matrices à coefficients complexes, l'imprécision des données initiales fait qu'une matrice correspondant à un problème réel est toujours diagonalisable.
En statistique, la diagonalisation permet de faire une analyse en composante principale.
La réduction des matrices (diagonalisation ou réduction de Jordan) permette un calcul des puissances de cette matrice ainsi que de son exponentielle. Par ailleurs, le calcul de exp(tA)est particulièrement utile pour résoudre les systèmes différentiels linéaires à coefficients constants.
Réduction et forme bilinéaire en dimension finie [modifier]
Les matrices symétriques réelles (qui représentent des formes bilinéaires symétriques réelles) sont diagonalisables en base orthonormée.
Réduction et analyse fonctionnelle [modifier]
09:57 Publié dans Réduction d'endomorphisme | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Lemme des noyaux
Source : http://fr.wikipedia.org/wiki/Lemme_des_noyaux
Lemme des noyaux
En algèbre linéaire, le lemme des noyaux est un résultat sur la réduction des endomorphismes. Dans un espace vectoriel E sur un corps K, si un opérateur u de E est annulé par un polynôme P(X) à coefficients dans K, alors ce lemme prévoit une décomposition de E comme somme directe de sous-espaces vectoriels stables par u. Ces derniers se définissent comme noyaux de polynômes en u, les projecteurs associés étant eux-mêmes des polynômes en u.
La démonstration traduit l'identité de Bezout portant sur les polynômes à des sous-espaces vectoriels. Résultat fondamental, le lemme des noyaux conduit à la décomposition de Dunford puis à la décomposition de Jordan. Plus modestement, le lemme des noyaux montre qu'un opérateur u est diagonalisable s'il est annulé par un polynôme à racines simples.
Sommaire[masquer] |
Enoncé [modifier]
Lemme des noyaux — Soit E un espace vectoriel sur un corps K et soit f un endomorphisme de E. Si ![P_1,ldots,P_n in K[X]](http://upload.wikimedia.org/math/1/9/2/192527f1c86d44ab5e67ee58757eb75c.png) (avec
(avec  ) sont premiers entre eux deux à deux, alors les sous-espaces vectoriels Vi = ker(Pi(f)) (où
) sont premiers entre eux deux à deux, alors les sous-espaces vectoriels Vi = ker(Pi(f)) (où 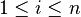 ) sont en somme directe et
) sont en somme directe et
De plus, la projection sur Vi parallèlement à  est Qi(f) pour un polynôme Qi.
est Qi(f) pour un polynôme Qi.
Démonstration [modifier]
Réduction au cas n = 2 [modifier]
On montre d'abord par récurrence sur n que si le lemme est vrai pour n = 2, il est vrai pour tout n. Il n'y a rien à montrer pour le cas n = 1 (la projection mentionnée est l'identité, qui estQ(f) avec Q le polynôme constant 1). Si n > 2 on pose  alors
alors  et Q est premier avec Pn (car d'après le théorème de Bachet-Bézoutchacun des facteurs Pi de Q est inversible modulo Pn, et leur produit Q l'est donc aussi). Alors le cas n = 2 dit que
et Q est premier avec Pn (car d'après le théorème de Bachet-Bézoutchacun des facteurs Pi de Q est inversible modulo Pn, et leur produit Q l'est donc aussi). Alors le cas n = 2 dit que 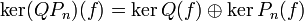 , avec les projections correspondantes données par des polynômes en l'endomorphisme f; l'hypothèse de récurrence permet de décomposer
, avec les projections correspondantes données par des polynômes en l'endomorphisme f; l'hypothèse de récurrence permet de décomposer 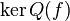 commer somme directe des
commer somme directe des 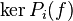 pour
pour 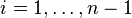 , et les projections de
, et les projections de 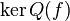 sur ces facteurs se composent avec celle sur
sur ces facteurs se composent avec celle sur 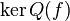 pour donner des projections requises
pour donner des projections requises  .
.
Le cas n = 2 [modifier]
On voit sans problème que l'espace V = ker(P1P2)(f) contient les espaces 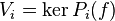 pour i = 1,2, et donc aussi leur somme; il s'agit de montrer que la somme V1 + V2 est directe et égale à V tout entier (avec des projections polynômes en
pour i = 1,2, et donc aussi leur somme; il s'agit de montrer que la somme V1 + V2 est directe et égale à V tout entier (avec des projections polynômes en  ). D'après le théorème de Bachet-Bézout, il existe
). D'après le théorème de Bachet-Bézout, il existe ![Q_1,Q_2 in K[X]](http://upload.wikimedia.org/math/2/1/3/213ec71c5566f54610e89067d66f8792.png) tel que P1Q1 + P2Q2 = 1, et par conséquent (P1Q1 + P2Q2)(f) = idE (l'application identité de E). Notons
tel que P1Q1 + P2Q2 = 1, et par conséquent (P1Q1 + P2Q2)(f) = idE (l'application identité de E). Notons
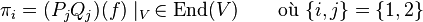 ,
,
donc  et
et  .
.
Pour voir que la somme V1 + V2 est directe, on considère  . On a
. On a  , et la somme est directe.
, et la somme est directe.
Pour voir que V1 + V2 = V on considère 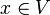 . On a
. On a 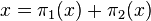 avec
avec  car
car
 ,
,
et on a 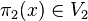 pour des raisons similaires. On conclut que
pour des raisons similaires. On conclut que  et donc V = V1 + V2.
et donc V = V1 + V2.
Finalement, les projections de  sur les facteurs sont
sur les facteurs sont  et
et 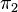 : on a déjà vu que l'image de
: on a déjà vu que l'image de 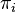 est contenue dans Vi, et qu'il s'annule sur l'autre facteur, donc il reste à voir que
est contenue dans Vi, et qu'il s'annule sur l'autre facteur, donc il reste à voir que 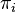 est l'identité sur Vi. Pour
est l'identité sur Vi. Pour  on a
on a  , donc c'est vérifié.
, donc c'est vérifié.
Applications [modifier]
Le lemme des noyaux sert pour la réduction des endomorphismes. Par exemple :
Réduction à une forme diagonale par blocs — Soit E un espace vectoriel de dimension finie sur un corps K et soit f un endomorphisme de E. Soit ![Pin K[X]](http://upload.wikimedia.org/math/4/f/a/4facb36da11821b818abd66b424a6a76.png) unpolynôme annulateur de f (par exemple son polynôme minimal, ou son polynôme caractéristique d'après le théorème de Cayley-Hamilton) et
unpolynôme annulateur de f (par exemple son polynôme minimal, ou son polynôme caractéristique d'après le théorème de Cayley-Hamilton) et  la factorisation de Pavec les polynômes Pi irréductibles et distincts. Alors il existe une base
la factorisation de Pavec les polynômes Pi irréductibles et distincts. Alors il existe une base  de E et des matrices
de E et des matrices  telles que
telles que
où  (en fait la partie de
(en fait la partie de  correspondant au bloc Ai est une base de
correspondant au bloc Ai est une base de 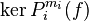 ), et
), et 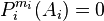 .
.
09:56 Publié dans Lemme des noyaux | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Théorème d'Abel (analyse)
Source : http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_d'Abel_(a...
Théorème d'Abel (analyse)
Le théorème d'Abel, ou théorème de convergence radiale d'Abel, est un outil central de l'étude des séries entières.
Théorème — Soit  une série entière (à coefficients complexes) de rayon de convergence égal à R.
une série entière (à coefficients complexes) de rayon de convergence égal à R.
Si 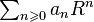 converge, alors :
converge, alors :
 .
.Remarque : dans le cas où la série  est absolument convergente, le résultat est trivial, il n'y a donc pas lieu d'invoquer ce théorème.
est absolument convergente, le résultat est trivial, il n'y a donc pas lieu d'invoquer ce théorème.
En effet, sous cette condition,  converge normalement donc uniformément sur [0, R] ; on retrouve immédiatement :
converge normalement donc uniformément sur [0, R] ; on retrouve immédiatement :

 . Encore par le critère de convergence des séries alternées, on peut affirmer que
. Encore par le critère de convergence des séries alternées, on peut affirmer que  converge, d'où :
converge, d'où :
09:54 Publié dans Théorème d'Abel (analyse) | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Sommation par parties
Source : http://fr.wikipedia.org/wiki/Lemme_d'Abel
Sommation par parties
La sommation par parties est l'équivalent pour les séries de l'intégration par parties. On l'appelle également transformation d'Abel ou sommation d'Abel ou lemme d'Abel.
Sommaire[masquer] |
Énoncé [modifier]
Soient deux suites  et
et 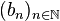 . Si l'on pose
. Si l'on pose
alors
Cette opération, qui transforme l'expression de la série à étudier, est utile pour prouver certains critères de convergence de SN.
Similitude avec l'intégration par parties [modifier]
La formule de l'intégration s'écrit : ![int_a^b f(x) g'(x),dx = left[ f(x) g(x) right]_{a}^{b} - int_a^b f'(x) g(x),dx](http://upload.wikimedia.org/math/0/c/c/0cc4450e2b913b0d32c34fac3ec1aea3.png)
Si on laisse de côté les conditions aux limites, on s'aperçoit que l'intégration par parties consiste à intégrer une des deux fonctions présentes dans l'intégrale initiale (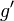 devient
devient  ) et à dériver l'autre (
) et à dériver l'autre ( devient
devient  ).
).
La sommation par parties consiste en une opération analogue dans le domaine discret, puisque l'une des deux séries est sommée ( devient
devient  ) et l'autre est différenciée (
) et l'autre est différenciée ( devient
devient ).
).
On peut considérer la formule sommatoire d'Abel comme une généralisation de ces deux formules.
Applications [modifier]
On se place par la suite dans le cas où  , car sinon on sait que
, car sinon on sait que 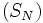 est grossièrement divergente.
est grossièrement divergente.
Si 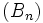 est bornée par un réel M et que
est bornée par un réel M et que  est une série absolument convergente, alors la série
est une série absolument convergente, alors la série 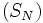 est convergente.
est convergente.

La somme de la série vérifie par ailleurs l'inégalité : 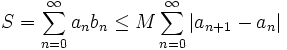
Exemples [modifier]
 et
et 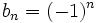
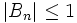 et
et 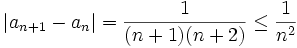
On sait que la série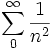 converge (voir fonction zêta de Riemann), donc les conditions exposées ci-dessus sont toutes réunies.
converge (voir fonction zêta de Riemann), donc les conditions exposées ci-dessus sont toutes réunies. converge.
converge.
NB: Cet exemple peut également être prouvé grâce au critère de convergence des séries alternées. et
et 
(Nous ne définissons ici la somme qu'à partir du rang n=1 au lieu de n=0, mais cela n'affecte en rien l'existence de la limite de la série.)
Comme précédemment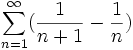 converge absolument, et
converge absolument, et  est bornée d'après l'expression du noyau de Dirichlet.
est bornée d'après l'expression du noyau de Dirichlet.
Par conséquent converge.
converge.- La sommation par parties sert dans la preuve du théorème d'Abel.
Voir aussi [modifier]
09:52 Publié dans Sommation par parties | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
20/11/2010
Lambda-calcul
Source : http://fr.wikipedia.org/wiki/Lambda-calcul
Lambda-calcul
« La notion de λ-définissabilité fut la première de ce qui est accepté maintenant comme l'équivalent exact des descriptions mathématiques pour lesquelles des algorithmes existent. »
— Stephen Kleene, in « Origins of Recursive Function Theory », IEEE Annals of the History of Computing, 1981, vol. 3, n°1, p. 52
Le lambda-calcul (ou λ-calcul) est un système formel inventé par Alonzo Church dans les années 1930, qui fonde les concepts de fonction et d'application. Il a été le premier formalisme utilisé pour définir et caractériser les fonctions récursives et donc il a une grande importance dans la théorie de la calculabilité, à l'égal des machines de Turing et du modèle de Herbrand-Gödel. Il a depuis été appliqué comme langage de programmation théorique et comme métalangage pour la démonstration formelle assistée par ordinateur. Le lambda-calcul peut être ou non typé.
Le lambda-calcul est apparenté à la logique combinatoire de Haskell Curry.
Syntaxe [modifier]
Le lambda calcul définit des entités syntaxiques que l'on appelle des lambda-termes (ou parfois aussi des lambda expressions) et qui se rangent en trois catégories :
- les variables : x, y... sont des lambda-termes ;
- les applications : u v est un lambda-terme si u et v sont des lambda-termes ;
- les abstractions : λ x.v est un lambda-terme si x est une variable et v un lambda-terme.
L’application peut être vue ainsi : si u est une fonction et si v est son argument, alors u v est le résultat de l'application à v de la fonction u.
L’abstraction λ x.v peut être interprétée comme la formalisation de la fonction qui, à x, associe v, où v contient en général des occurrences de x.
Ainsi, la fonction1 f qui prend en paramètre le lambda-terme x et lui ajoute 2 (c'est-à-dire en notation mathématique courante la fonction f: x ↦ x+2) sera dénotée en lambda-calcul par l'expression λ x.x+2. L'application de cette fonction au nombre 3 s'écrit (λ x.x+2)3 et s'« évalue » (ou se normalise) en l'expression 3+2.
Notations, conventions et concepts [modifier]
Parenthésage [modifier]
Pour délimiter les applications, on utilise des parenthèses, mais une utilisation trop abondante de parenthèses peut conduire à des expressions illisibles, donc pour raccourcir et clarifier les expressions, on supprime des parenthèses ; ainsi x1 x2 ... xn est équivalent à ((x1 x2) ... xn).
Il y a en fait deux conventions :
- Association à gauche, l'expression ((M0 M1) (M2M3)) s'écrit M0 M1 (M2M3). Quand une application s'applique à une autre application, on ne met de parenthèse que sur l'application de droite. Formellement, la grammaire du lambda calcul parenthésé est alors
- Λ ::= Var | λ var Λ | Λ (Λ)
- Parenthésage du terme de tête, l'expression ((M0 M1) (M2M3)) s'écrit (M0) M1 (M2) M3. Un terme entre parenthèses est le premier d'une suite d'applications. Ainsi les arguments d'un terme sont facilement identifiables. Formellement, la grammaire du lambda-calcul parenthésé est alors
- Λ ::= Var | λ var Λ | ΛΛ |Λ (Λ)
Curryfication [modifier]
Un lambda-terme ne prend qu'un seul argument, mais Shönfinkel et Curry ont introduit la curryfication et montré qu'on peut ainsi contourner cette restriction de la façon suivante : la fonction qui au couple (x, y) associe u est considérée comme une fonction qui, à x, associe une fonction qui, à y, associe u. Elle est donc notée : λx.(λy.u). Cela s'écrit aussi λx.λy.u ouλxλy.u ou tout simplement λxy.u. Par exemple, la fonction qui, au couple (x, y) associe x+y sera notée λx.λy.x+y ou plus simplement λxy.x+y.
Variables libres et variables liées [modifier]
Dans les expressions mathématiques en général et dans le lambda calcul en particulier, il y a deux catégories de variables : les variables libres et les variables liées (ou muettes). En lambda-calcul, une variable est liée2 par un λ. Une variable liée a une portée3 et cette portée est locale ; de plus, on peut renommer une variable liée sans changer la signification globale de l'expression entière où elle figure. Une variable qui n'est pas liée est dite libre.
Variables liées en mathématiques [modifier]
Par exemple dans  , x est libre, mais y est liée (par le dy). Ceci est la même expression que
, x est libre, mais y est liée (par le dy). Ceci est la même expression que  car y était un nom local, tout comme l'est z. Par contre
car y était un nom local, tout comme l'est z. Par contre  ne correspond pas à la même expression car le z est libre.
ne correspond pas à la même expression car le z est libre.
Tout comme l'intégrale lie la variable d'intégration, le λ lie la variable qui le suit.
Exemples: Dans λx.xy, la variable x est lié et la variable y libre. On peut récrire ce terme en λt.ty.
λxyzt.z(xt)ab(zsy) est équivalent à λwjit. i(wt)ab(isj)
Définition formelle des variables libres en lambda-calcul [modifier]
On définit l'ensemble VL(t) des variables libres d'un terme t par récurrence :
- si x est une variable alors VL(x) = {x}
- si u et v sont des lambda-termes alors VL(u v) = VL(u) ∪ VL(v)
- si x est une variable et u un lambda-terme alors VL(λx.u) = VL(u) {x}
Si un lambda-terme n'a pas de variables libres, on dit qu'il est clos (ou fermé) on dit aussi que ce lambda-terme est un combinateur (d'après le concept apparenté de logique combinatoire).
Substitution et α-conversion [modifier]
L'outil le plus important pour le lambda-calcul est la substitution qui permet de remplacer, dans un terme, une variable par un terme. Ce mécanisme est à la base de la réduction qui est le mécanisme fondamental de l'évaluation des expressions donc du « calcul » des lambda-termes.
La substitution dans un lambda terme t d'une variable x par un terme u est notée t[x := u]. Il faut prendre quelques précautions pour définir correctement la substitution afin d'éviter le phénomène de capture de variable qui pourrait, si l'on n'y prend pas garde, rendre liée une variable qui était libre avant que la substitution n'ait lieu. Par exemple, si u contient la variable libre y et si x apparaît dans t comme occurrence d'un sous terme de la forme λy.v, le phénomène de capture pourrait apparaître. L'opération t[x := u] s'appelle la substitution dans t de xpar u et se définit par récurrence sur t :
- si t est une variable alors t[x := u]=u si x=t et t sinon
- si t = v w alors t[x := u] = v[x := u] w[x := u]
- si t = λy.v alors t[x := u] = λy.(v[x := u]) si x≠y et t sinon
Remarque : dans le dernier cas on fera attention à ce que y ne soit pas une variable libre de u. En effet, elle serait alors « capturée » par le lambda externe. Si c'est le cas on renommey et toutes ses occurrences dans v par une variable z qui n'apparaît ni dans t ni dans u.
L'α-conversion identifie λy.v et λz.v[y := z]. Deux lambda-termes qui ne diffèrent que par un renommage (sans capture) de leurs variables liées sont dits α-convertibles. L'α-conversion est une relation d'équivalence entre lambda-termes.
Exemples :
- (λx.xy)[y := a] = λx.xa
- (λx.xy)[y := x] = λz.zx (et non λ x.xx, qui est totalement différent, cf remarque ci-dessus)
Remarque : l'α-conversion doit être définie avec précaution avant la substitution. Ainsi dans le terme λx.λy.xyλz.z, on ne pourra pas renommer brutalement x en y (on obtiendraitλy.λy.yyλz.z) par contre on peut renommer x en z.
Définie ainsi la substitution est un mécanisme externe au lambda-calcul, on dit aussi qu'il fait partie de la méta-théorie. A noter que certains travaux visent à introduire la substitution comme un mécanisme interne au lambda-calcul, conduisant à ce qu'on appelle les calculs de substitutions explicites.
Réductions [modifier]
Une manière de voir les termes du lambda-calcul consiste à les concevoir comme des arbres ayant des nœuds binaires (les applications), des nœuds unaires (les λ-abstractions) et des feuilles (les variables). Les réductions4 ont pour but de modifier les termes, ou les arbres si on les voit ainsi ; par exemple, la réduction de (λx.xx)(λy.y) donne (λy.y)(λy.y).
On appelle rédex un terme de la forme (λx.u) v . On définit la bêta-contraction (ou β-contraction) de (λx.u) v comme u[x := v]; on dit qu'un terme C[u] se réduit5 en C[u'] si u est un redex qui se β-contracte en u', on écrit alors C[u]→C[u'], la relation → est appelée réduction.
Exemple de réduction :
(λx.xy)a donne (xy)[x := a] = ay .
On note →* la fermeture réflexive transitive6 de la relation → de réduction et =β sa fermeture réflexive symétrique et transitive (appelée bêta-conversion ou bêta-équivalence).
La β-conversion permet de faire une "marche arrière" à partir d'un terme. Cela permet, par exemple, de retrouver le terme avant une β-réduction. Passer de x à (λy.y)x .
On peut écrire M =β M' si ∃ N1, ..., Np tels que M = N1, M'=Np et Ni→ Ni+1 ou Ni+1→ Ni .
Cela signifie que dans une conversion on peut appliquer des réductions ou des relations inverses des réductions (appelées expansions).
On définit également une autre opération, appelée êta-réduction (ou son inverse la êta-expansion), définie ainsi : λx.ux →η u, lorsque x n'apparait pas libre dans u. En effet, ux s'interprète comme l'image de x par la fonction u. Ainsi, λx.ux s'interprète alors comme la fonction qui, à x, associe l'image de x par u, donc comme la fonction u elle-même.
Enfin, si on s'est donné des primitives, on peut fixer leur comportement calculatoire au moyen des règles de delta-réduction. Par exemple, si on s'est donné les entiers et + comme termes supplémentaires, les tables d'addition serviront de delta-règles. Comme les primitives sont par définition complètement étrangères au lambda-calcul, leurs règles de calcul peuvent a priori adopter n'importe quelle forme. Toutefois, si on veut étendre les propriétés mentionnées ci-dessous au cas d'un calcul avec des primitives, on est amené à faire quelques hypothèses sur les règles ajoutées.
La normalisation : notion de calcul [modifier]
Le calcul associé à un lambda-terme est la suite de réductions qu'il engendre. Le terme est la description du calcul et la forme normale du terme7 (si elle existe) en est le résultat.
Un lambda-terme t est dit en forme normale si aucune bêta-contraction ne peut lui être appliquée, c'est-à-dire si t ne contient aucun rédex. Ou encore, s'il n'existe aucun lambda-terme utel que t → u.
Exemple: λx.y(λz.z(yz)) .
On dit qu'un lambda-terme t est normalisable s'il existe un terme u tel que t =β u. Un tel u est appelé la forme normale de t.
On dit qu'un lambda-terme t est fortement normalisable si toutes les réductions à partir de t sont finies.
Exemples:
-
- Posons Δ ≡ λx.xx . L'exemple par excellence de lambda-terme non fortement normalisable est obtenu en appliquant ce terme à lui même, autrement dit:
- Ω = (λx.xx)(λx.xx) = ΔΔ
Le lambda terme Ω n'est pas fortement normalisable car sa réduction boucle indéfiniment sur elle-même. - (λx.xx)(λx.xx) → (λx.xx)(λx.xx).
- (λx.x)((λy.y)z) est un lambda-terme fortement normalisable.
- (λx.y)(ΔΔ) est normalisable et sa forme normale est y, mais il n'est pas fortement normalisable.
- (λx.xxx)(λx.xxx) → (λx.xxx)(λx.xxx)(λx.xxx) → (λx.xxx)(λx.xxx)(λx.xxx)(λx.xxx) → ... crée des termes de plus en plus grand.
Si un terme est fortement normalisable, alors il est normalisable.
Théorème de Church-Rosser : soient t et u deux termes tels que t =β u. Il existe un terme v tel que t →* v et u →* v.
Théorème du losange (ou de confluence) : soient t, u1 et u2 des lambda-termes tels que t →* u1 et t →* u2. Alors il existe un lambda-terme v tel que u1 →* v et u2 →* v.
Grâce au Théorème de Church-Rosser on peut facilement montrer l'unicité de la forme normale ainsi que la cohérence du lambda-calcul (c’est-à-dire qu'il existe au moins deux termes distincts non bêta-convertibles).
Différents lambda-calculs [modifier]
Sur la syntaxe et la réduction du lambda-calcul on peut adapter différents calculs en restreignant plus ou moins la classe des termes. On peut ainsi distinguer deux grandes classes de lambda-calculs : le lambda-calcul non typé et les lambda-calculs typés. Les types sont des annotations des termes qui ont pour but de ne garder que les termes qui sont normalisables, éventuellement en adoptant une stratégie de réduction. On espère8 ainsi avoir un lambda-calcul qui satisfait les propriétés de Church-Rosser et de normalisation.
La correspondance de Curry-Howard relie un lambda calcul typé à une système de déduction naturelle. Elle énonce qu'un type correspond à une proposition et un terme correspond à une preuve, et réciproquement.
Le lambda-calcul non typé [modifier]
Des codages simulent les objets usuels de l'informatique dont les entiers naturels, les fonctions récursives et les machines de Turing. Réciproquement le lambda-calcul peut être simulé par une machine de Turing. Grâce à la thèse de Church on en déduit que le lambda-calcul est un modèle universel de calcul.
Les booléens [modifier]
Dans la partie Syntaxe, nous avons vu qu'il est pratique de définir des primitives. C'est ce que nous allons faire ici.
- vrai = λab.a
- faux = λab.b
Ceci n'est que la définition d'un codage, et l'on pourrait en définir d'autres.
Nous remarquons que :
- vrai x y →* x
et que :
- faux x y →* y
Nous pouvons alors définir un lambda-terme représentant l'alternative: if-then-else. C'est une fonction à trois arguments, un booléen b et deux lambda termes u et v, qui retourne le premier si le booléen est vrai et le second sinon.
- ifthenelse = λbuv.(b u v)
Notre fonction est bien vérifiée:
- ifthenelse vrai x y = (λbuv.(b u v)) vrai x y
- ifthenelse vrai x y → (λuv.(vrai u v)) x y
- ifthenelse vrai x y →* (vrai x y)
- ifthenelse vrai x y →* ( (λxy.x) x y)
- ifthenelse vrai x y →* x
On verra de la même manière que
- ifthenelse faux x y →* y
À partir de là nous avons aussi un lambda-terme pour les opérations booléennes classiques :
- non = λb.ifthenelse b faux vrai
- et = λab.ifthenelse a b faux (ou bien λab.ifthenelse a b a)
- ou = λab.ifthenelse a vrai b (ou bien λab.ifthenelse a a b)
Les entiers [modifier]
Le codage des entiers qui suit s'appelle les entiers de Church du nom de leur concepteur. On pose :
- 0 = λfx.x
- 1 = λfx.f x
- 2 = λfx.f (f x)
- 3 = λfx.f (f (f x))
et d'une manière générale :
- n = λfx.f (f (...(f x)...)) = λfx.f nx avec f itérée n fois.
Ainsi, l'entier n est vu comme la fonctionnelle, qui au couple ≺f, x≻, associe f n(x).
Quelques fonctions [modifier]
Il y a deux manières de coder la fonction successeur, soit en ajoutant un f en tête, soit en queue. Au départ nous avons n = λfx.f n x et nous voulons λfx.f n+1 x. Il faut pouvoir rajouter unf soit au début des f « sous » les lambdas soit à la fin.
- Si nous choisissons de le mettre en tête, il faut pouvoir entrer « sous » les lambdas. Pour cela, si n est notre entier, on forme d'abord n f x, ce qui donne f n x. En mettant un f en tête, on obtient : f (n f x) → f(f n x) = f n+1 x. Il suffit alors de compléter l'entête pour reconstruire un entier de Church : λfx.f (n f x) = λfx.f n+1 x (nous aurions bien sûr pu prendre d'autres noms de variables que f et x à l'étape précédente et donc nous aurions gardé ces noms ici). Enfin pour avoir la « fonction » successeur il faut bien entendu prendre un entier en paramètre, donc rajouter un lambda. Nous obtenons λnfx.f(n f x). Le lecteur pourra vérifier que (λnfx.f(n f x)) 3 = 4, avec 3 = λfx.f(f(f x))) et 4 = λfx.f(f(f(f x)))).
- Si par contre nous voulions mettre le f en queue, il suffit d'appliquer n f x non pas à x, mais à f x, à savoir n f (f x), ce qui se réduit à fn (f x) = fn+1 x. On n'a plus qu'à refaire l'emballage comme dans le cas précédent et on obtient λnfx.n f (f x). La même vérification pourra être faite.
Les autres fonctions sont construites avec le même principe. Par exemple l'addition en « concaténant » les deux lambda-termes : λnpfx.n f (p f x).
Pour coder la multiplication, on utilise le f pour « propager » une fonction sur tout le terme : λnpf.n (p f)
L'exponentielle n'est pas triviale contrairement à ce que son écriture laisse penser, et lors de la réduction on est obligé de renommer les variables : λnp.p n
Le prédécesseur et la soustraction ne sont pas simples non plus. On en reparlera plus loin.
On peut définir le test à 0 ainsi : if0thenelse = λnab.n (λx.b) a, ou bien en utilisant les booléens λn.n (λx.faux) vrai.
Les itérateurs [modifier]
Définissons d'abord une fonction d'itération sur les entiers : itère = λnuv.n u v
v est le cas de base et u une fonction. Si n est nul, on calcule v, sinon on calcule u n(v).
Par exemple l'addition qui provient des équations suivantes
- add(0, p) = p
- add(n+1, p) = (n+p) + 1
peut être définie comme suit. Le cas de base v est le nombre p, et la fonction u est la fonction successeur. Le lambda-terme correspondant au calcul de la somme est donc :
- add = λnp.itère n successeur p
On remarquera que add n p →* n successeur p.
Les couples [modifier]
On peut coder des couples par c = λz.z a b où a est le premier élément et b le deuxième. On notera ce couple (a, b). Pour accéder aux deux parties on utilise π1 = λc.c (λab.a) et π2 = λc.c (λab.b). On reconnaîtra les booléens vrai et faux dans ces expressions et on laissera le soin au lecteur de réduire π1(λz.z a b) en a.
Les listes [modifier]
On peut remarquer qu'un entier est une liste dont on ne regarde pas les éléments, en ne considérant donc que la longueur. En rajoutant une information correspondant aux éléments, on peut construire les listes d'une manière analogue aux entiers : [a1 ; ... ; an] = λgy. g a1 (... (g an y)...). Ainsi :
- [] = λgy.y
- [a1] = λgy.g a1 y
- [a1 ; a2] = λgy.g a1 (g a2 y)
Les itérateurs sur les listes [modifier]
De la même manière qu'on a introduit une itération sur les entiers on introduit une itération sur les listes. la fonction liste_it se définit par λlxm.l x m comme pour les entiers. Le concept est à peu près le même mais il y a des petites nuances. Nous allons voir par un exemple.
exemple : La longueur d'une liste est définie par
- longueur ([]) = 0
- longueur (x :: l) = 1 + longueur l
x :: l est la liste de tête x et de queue l (notation ML). La fonction longueur appliquée sur une liste l se code par :
- λl.liste_it l (λym.add (λfx.f x) m) (λfx.x)
ou tout simplement
- λl.l (λym.add 1 m) 0
Les arbres binaires [modifier]
Le principe de construction des entiers, des couples et des listes se généralise aux arbres binaires :
- constructeur de feuille : feuille = λngy.y n
- constructeur de nœud : nœud = λbcgy.g (b g y) (c g y) (avec b et c des arbres binaires)
- itérateur : arbre_it = λaxm.a x m
Un arbre est soit une feuille, soit un nœud. Dans ce modèle, aucune information n'est stockée au niveau des nœuds, les données (ou clés) sont conservées au niveau des feuilles uniquement. On peut alors définir la fonction qui calcule le nombre de feuilles d'un arbre : nb_feuilles = λa.arbre_it a (λbc.add b c) (λn.1), ou plus simplement: nb_feuilles = λa.a add (λn.1)
Le prédécesseur [modifier]
Pour définir le prédécesseur sur les entiers de Church, il faut utiliser les couples. L'idée est de reconstruire le prédécesseur par itération : pred = λn.π1 (itère n (λc.(π2 c, successeur (π2c))) (0,0)). Puisque le prédécesseur sur les entiers naturels n'est pas défini en 0, afin de définir une fonction totale, on a ici adopté la convention qu'il vaut 0.
On vérifie par exemple que pred 3 →* π1 (itère 3 (λc.(π2 c, successeur (π2 c))) (0,0)) →* π1 (2,3) →* 2.
On en déduit que la soustraction est définissable par : sub = λnp.itère p pred n avec la convention que si p est plus grand que n, alors sub n p vaut 0.
La récursion [modifier]
En combinant prédécesseur et itérateur, on obtient un récurseur. Celui-ci se distingue de l'itérateur par le fait que la fonction qui est passée en argument a accès au prédécesseur.
rec = λnfx.π1 (n (λc.(f (π2 c) (π1 c), successeur (π2 c))) (x, 0))
Combinateur de point fixe [modifier]
Un combinateur de point fixe permet de construire pour chaque F, une solution à l'équation X = F X . Ceci est pratique pour programmer des fonctions qui ne s'expriment pas simplement par itération, telle que le pgcd, et c'est surtout nécessaire pour programmer des fonctions partielles.
Le combinateur de point de fixe le plus simple, dû à Curry, est : Y = λf.(λx.f(x x))(λx.f(x x))
On vérifie que  quel que soit g. Grâce au combinateur de point fixe, on peut par exemple définir une fonction qui prend en argument une fonction et teste si cette fonction argument renvoie vrai pour au moins un entier: teste_annulation = λg.Y (λfn.ou (g n) (f (successeur n))) 0.
quel que soit g. Grâce au combinateur de point fixe, on peut par exemple définir une fonction qui prend en argument une fonction et teste si cette fonction argument renvoie vrai pour au moins un entier: teste_annulation = λg.Y (λfn.ou (g n) (f (successeur n))) 0.
Par exemple, si on définit la suite alternée des booléens vrai et faux : alterne = λn.itère n non faux, alors, on vérifie que : teste_annulation alterne →* ou (alterne 0) (Y (λfn.ou (alterne n) (f successeur n)) (successeur 0)) →* ou (alterne 1) (Y (λfn.ou (alterne n) (f successeur n)) (successeur 1)) →* vrai.
On peut aussi définir le pgcd : pgcd = Y (λfnp.if0thenelse (sub p n) (if0thenelse (sub n p) p (f p (sub n p))) (f n (sub p n))).
Connexion avec les fonctions partielles récursives [modifier]
Le récurseur et le point fixe sont des ingrédients clés permettant de montrer que toute fonction partielle récursive est définissable en λ-calcul lorsque les entiers sont interprétés par les entiers de Church. Réciproquement, les λ-termes peuvent être codés par des entiers et la réduction des λ-termes est définissable comme une fonction (partielle) récursive. Le λ-calcul est donc un modèle de la calculabilité.
Le lambda-calcul simplement typé [modifier]
On annote les termes par des expressions que l'on appelle des types ; pour cela on fournit un moyen de donner un type à un terme, si ce moyen réussit on dit que le terme est bien typé. Outre le fait que cela donne une indication sur ce que « fait » la fonction, par exemple, elle transforme les objets d'un certain type en des objets d'un autre type, cela permet de garantir la normalisation forte, c'est-à-dire que pour tous les termes, toutes les réductions aboutissent à une forme normale (qui est unique pour chaque terme de départ). Autrement dit, tous les calculs menés dans ce contexte terminent. Les types simples sont construits comme les types des fonctions, de fonctions de fonctions, des fonctions de fonctions de fonctions vers les fonctions etc. Quoiqu'il puisse paraitre, le pouvoir expressif de ce calcul est très limité (ainsi, l'exponentielle ne peut y être définie, ni même la fonction 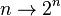 ).
).
Plus formellement, les types simples sont construits de la manière suivante:
- un type de base ι (si on a des primitives, on peut aussi se donner plusieurs types de bases, comme les entiers, les booléens, les caractères, etc. mais cela n'a pas d'incidence au niveau de la théorie).
- si τ1 et τ2 sont des types,
 est un type.
est un type.
Intuitivement, le second cas représente le type des fonctions acceptant un élément de type τ1 et renvoyant un élément de type τ2.
Un contexte Γ est un ensemble de paires de la forme (x,τ) où x est une variable et τ un type. Un jugement de typage est un triplet 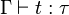 (on dit alors que t est bien typé dans Γ), défini récursivement par:
(on dit alors que t est bien typé dans Γ), défini récursivement par:
- si
 , alors
, alors  .
. - si
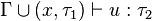 , alors
, alors  .
. - si
 et
et  , alors
, alors 
Si on a ajouté des constantes au lambda calcul, il faut leur donner un type (via Γ).
Les lambda-calculs typés d'ordres supérieurs [modifier]
Le lambda-calcul simplement typé est trop restrictif pour exprimer toutes les fonctions calculables dont on a besoin en mathématiques et donc dans un programme informatique. Un moyen de dépasser l'expressivité du lambda-calcul simplement typé consiste à autoriser des variables de type et à quantifier sur elles, comme cela est fait dans le système F ou lecalcul des constructions. Le Système T de Gödel qui fusionne la récursion primitive et le lambda-calcul simplement typé offre aussi, au prix d'un enrichissement, un système plus expressif. Dans ce système, on peut coder, grâce à l'ordre supérieur, de nouveaux algorithmes comme la fonction d'Ackermann qui est non primitive récursive.
Notes [modifier]
- Cette explication semble introduire des constantes entières et des opérations, comme + et *, mais il n'en est rien, car ces concepts peuvent être décrits par des lambda termes spécifiques dont ils ne sont que des abréviations.
- En mathématiques, les variables sont liées par ∀ ou par ∃ ou par ∫ ... dx.
- La portée est la partie de l'expression où la variable a la même signification.
- Attention « réduction » ne veut pas dire que la taille diminue !
- C[ ] est appelé un contexte.
- De nombreux auteurs notent cette relation ↠.
- Le terme issu de la réduction à partir duquel on ne peut plus réduire.
- Espoir fondé en général, mais encore faut-il le démontrer !
Bibliographie [modifier]
- (en) Henk Barendregt, The Lambda-Calculus, volume 103, Elsevier Science Publishing Company, Amsterdam, 1984.
- Marcel Crabbé, Le calcul lambda, Cahiers du centre de logique, numéro 6, 1986.
- Jean-Louis Krivine, Lambda-Calcul, types et modèles, Masson 1991, traduction anglaise accessible sur le site de l'auteur [1].
- (en) Steven Fortune, Daniel Leivant, Michael O'Donnell, « The Expressiveness of Simple and Second-Order Type Structures » dans Journal of the ACM vol. 30 (1983), p. 151-185.
- (en) Jean-Yves Girard, Paul Taylor, Yves Lafont, Proofs and Types, Cambridge University Press, New York, 1989 (ISBN 0-521-37181-3).
- Hervé Poirier, « La Vraie Nature de l'intelligence », dans Science et Vie no 1013 (février 2002), p. 38-57.
- Francis Renaud, Sémantique du temps et lambda-calcul, Presses universitaires de France, 1996 (ISBN 2-13-047709 7)
18:23 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Alexandre-Théophile Vandermonde
Source : http://fr.wikipedia.org/wiki/Alexandre-Th%C3%A9ophile_Van...
Alexandre-Théophile Vandermonde
|
|
Cet article est une ébauche concernant un mathématicien.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
Alexandre-Théophile Vandermonde (parfois appelé Alexis-Théophile), né à Paris le 28 février 1735 et mort à Paris le 1er janvier 1796, est un mathématicien français. Il fut aussiéconomiste, musicien et chimiste, travaillant notamment avec Étienne Bézout et Antoine Lavoisier. Son nom est maintenant surtout associé à un déterminant.
Il commence à faire des mathématiques en 1770. Son Mémoire sur la résolution des équations (1771), qui préfigure la théorie de Galois, porte sur les fonctions symétriques et la solution des polynômes cyclotomiques. Dans les Remarques sur des problèmes de situation (1771), il étudie le problème du cavalier. Son Mémoire sur des irrationnelles de différens ordres avec une application au cercle (1772) porte sur la combinatoire, et son Mémoire sur l'élimination (1772) sur les fondations de la théorie des déterminants. Ces communications, présentées à l'Académie des sciences, constituent toute son œuvre mathématique. Le déterminant de Vandermonde n'y apparaît pas explicitement.
En 1771, il devient membre de l'Académie des sciences. En janvier 1792, il devient membre de la Société patriotique du Luxembourg, créée par Jean-Nicolas Pache, avec Gaspard Monge, Jean Henri Hassenfratz et Jean-Baptiste Marie Meusnier de La Place.
A partir de 1794, Vandermonde sera membre du Conservatoire national des arts et métiers, examinateur au concours d'entrée de l'École polytechnique, professeur à l'École normale supérieure.
Vandermonde a donné son nom à la société secrète des élèves du Conservatoire national des arts et métiers fondée sur le modèle de celle de Yale University.
Article connexe [modifier]
Liens externes [modifier]
- (en) John J. O'Connor et Edmund F. Robertson, « Alexandre-Théophile Vandermonde », MacTutor History of Mathematics archive, Université de St Andrews.
- Ouvrage de Vandermonde numérisé par le SICD des Universités de Strasbourg
18:16 Publié dans Alexandre-Théophile Vandermonde | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Théorie des graphes
Source : http://fr.wikipedia.org/wiki/Th%C3%A9orie_des_graphes
Théorie des graphes
| Pour la notion mathématique utilisée en Théorie des ensembles, voir Graphe d'une fonction. |
La théorie des graphes est une théorie informatique et mathématique. Les algorithmes élaborés pour résoudre des problèmes concernant les objets de cette théorie ont de nombreuses applications dans tous les domaines liés à la notion de réseau (réseau social, réseau informatique, Télécom…) et dans bien d'autres domaines (e.g. génétique) tant le concept de graphe, à peu près équivalent à celui de relation binaire (à ne pas confondre donc avec graphe d'une fonction), est général. De grands théorèmes difficiles, comme le Théorème des quatre couleurs et le Théorème des graphes parfaits, ont contribué à asseoir cette matière auprès des mathématiciens, et les questions qu'elle laisse ouvertes, comme la Conjecture d'Hadwiger, en font une branche vivace des Mathématiques discrètes.
Sommaire[masquer] |
Définition de graphe et vocabulaire [modifier]
Intuitivement, un graphe est un ensemble de points, dont certaines paires sont directement reliées par un lien. Ces liens peuvent être orientés, c'est-à-dire qu'un lien entre deux points uet v relie soit u vers v, soit v vers u : dans ce cas, le graphe est dit orienté. Sinon, les liens sont symétriques, et le graphe est non-orienté.
Dans la littérature récente de la théorie des graphes, les points sont appelés les sommets (en référence aux polyèdres) ou les nœuds (en références à la loi des nœuds). Les liens sont appelés arêtes dans les graphes non-orienté et arcs dans un graphe orienté.
L'ensemble des sommets est le plus souvent noté V, tandis que E désigne l'ensemble des arêtes. Dans le cas général, un graphe peut avoir des arêtes multiples, c'est-à-dire que plusieurs arêtes différentes relient la même paire de points. De plus, un lien peut être une boucle, c'est-à-dire ne relier qu'un point à lui-même. Un graphe est simple si il n'a ni liens multiples ni boucles, il peut alors être défini simplement par un couple G = (V,E), où E est un ensemble de paires d'éléments de V. Dans le cas d'un graphe simple orienté, E est un ensemble de couples d'éléments de V. Notons qu'un graphe sans arête multiple peut être représenté par une relation binaire, qui est symétrique si le graphe est non-orienté.
Pour définir un graphe général, il faut une fonction d'incidence γ qui associe à chaque arête une paire de sommets (ou un couple en cas orienté). Ainsi, un graphe est un triplet G = (V,E,γ) avec  . Toutefois l'usage veut que l'on note simplement G = (V,E), sachant que ce n'est parfaitement rigoureux que pour les graphes simples.
. Toutefois l'usage veut que l'on note simplement G = (V,E), sachant que ce n'est parfaitement rigoureux que pour les graphes simples.
Origines [modifier]
Un article du mathématicien suisse Leonhard Euler, présenté à l'Académie de Saint Pétersbourg en 1735 puis publié en 1741, traitait du problème des sept ponts de KönigsbergA 1, ainsi que schématisé ci-dessous. Le problème consistait à trouver une promenade à partir d'un point donné qui fasse revenir à ce point en passant une fois et une seule par chacun des sept ponts de la ville de Königsberg. Un chemin passant par toute arête exactement une fois fut nommé chemin eulérien, ou circuit eulérien s'il finit là où il a commencé. Par extension, un graphe admettant un circuit eulérien est dit graphe eulérien, ce qui constitue donc le premier cas de propriété d'un graphe. Euler avait formulé1 qu'un graphe n'est eulérien que si chaque sommet a un nombre pair d'arêtes. L'usage est de s'y référer comme théorème d'Euler, bien que la preuve n'y ait été apportée que 130 ans plus tard par le mathématicien allemand Carl HierholzerA 2. Un problème similaire consiste à passer par chaque sommet exactement une fois, et fut d'abord résolu avec le cas particulier d'un cavalier devant visiter chaque case d'un échiquier par le théoricien d'échec arabe Al-Adli dans son ouvrage Kitab ash-shatranj paru vers 840 et perdu depuisA 3. Ce problème du cavalier fut étudié plus en détails au xviiie sièclepar les mathématiciens français Alexandre-Théophile VandermondeA 4, Pierre de Rémond de Montfort et Abraham de Moivre; le mathématicien britannique Thomas Kirkman étudia le problème plus général du parcours où on ne peut passer par un sommet qu'une fois, mais un tel parcours prit finalement le nom de chemin hamiltonien d'après le mathématicien irlandaisWilliam Rowan Hamilton, et bien que ce dernier n'en ait étudié qu'un cas particulierA 5. On accorde donc à Euler l'origine de la théorie des graphes parce qu'il fut le premier à proposer un traitement mathématique de la question, suivi par Vandermonde.
Au milieu du XIXe siècle, le mathématicien britannique Arthur Cayley s'intéressa aux arbres, qui sont un type particulier de graphe n'ayant pas de cycle, i.e. dans lequel il est impossible de revenir à un point de départ sans faire le chemin inverse. En particulier, il étudia le nombre d'arbres à n sommetsA 6 et montra qu'il en existe 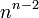 . Ceci constitua « une des plus belles formules en combinatoire énumérative »A 7, domaine consistant à compter le nombre d'éléments dans un ensemble fini, et ouvrit aussi la voie à l'énumération de graphes ayant certaines propriétés. Ce champ de recherche fut véritablement initié par le mathématicien hongrois George PólyaA 8, qui publia un théorème d'énumération en 1937A 9, et le mathématicien hollandais Nicolaas Govert de Bruijn. Les travaux de Cayley, tout comme ceux de Polya, présentaient des applications à la chimie et le mathématicien anglais James Joseph Sylvester, co-auteur de Cayley, introduisit en 1878 le terme de "graphe" basé sur la chimie :
. Ceci constitua « une des plus belles formules en combinatoire énumérative »A 7, domaine consistant à compter le nombre d'éléments dans un ensemble fini, et ouvrit aussi la voie à l'énumération de graphes ayant certaines propriétés. Ce champ de recherche fut véritablement initié par le mathématicien hongrois George PólyaA 8, qui publia un théorème d'énumération en 1937A 9, et le mathématicien hollandais Nicolaas Govert de Bruijn. Les travaux de Cayley, tout comme ceux de Polya, présentaient des applications à la chimie et le mathématicien anglais James Joseph Sylvester, co-auteur de Cayley, introduisit en 1878 le terme de "graphe" basé sur la chimie :
« Il peut ne pas être entièrement sans intérêt pour les lecteurs de Nature d'être au courant d'une analogie qui m'a récemment fortement impressionné entre des branches de la connaissance humaine apparemment aussi dissemblables que la chimie et l'algèbre moderne. […] Chaque invariant et covariant devient donc exprimable par un graphe précisément identique à un diagramme Kékuléan ou chemicograph.A 10 »
Un des problèmes les plus connus de théorie des graphes vient de la coloration de graphe, où le but est de déterminer combien de couleurs différentes suffisent pour colorer entièrement un graphe de telle façon qu'aucun sommet n'ait la même couleur que ses voisins. En 1852, le mathématicien sud-africain Francis Guthrie énonça le problème des quatre couleurs par une discussion à son frère, qui demandera à son professeur Auguste De Morgan si toute carte peut être coloriée avec quatre couleurs de façon à ce que des pays voisins aient des couleurs différentes. De Morgan envoya d'abord une lettre au mathématicien irlandais William Rowan Hamilton, qui n'était pas intéressé, puis le mathématicien anglais Alfred Kempe publia une preuve erronéeA 11 dans l’American Journal of Mathematics, qui venait d'être fondé par Sylvester. L'étude de ce problème entraîna de nombreux développements en théorie des graphes, par Peter Guthrie Tait, Percy John Heawood,Frank Ramsey et Hugo Hadwiger.
Les problèmes de factorisation de graphe émergèrent ainsi à la fin du XIXe siècle en s'intéressant aux sous-graphes couvrants, c'est-à-dire aux graphes contenants tous les sommets mais seulement une partie des arêtes. Un sous-graphe couvrant est appelé un k-facteur si chacun de ses sommets a k arêtes et les premiers théorèmes furent donnés par Julius PetersenA 12; par exemple, il montra qu'un graphe peut être séparé en 2-facteurs si et seulement si tous les sommets ont un nombre pair d'arêtes (mais il fallut attendre 50 ans pour que Bäbler traite le cas impairA 13). Les travaux de Ramsey sur la coloration, et en particulier les résultats du mathématicien hongrois Pal Turan, permirent le développement de la théorie des graphes extrémaux s'intéressant aux graphes atteignant le maximum d'une quantité particulière (par exemple le nombre d'arêtes) avec des contraintes donnéesA 14, telles que l'absence de certains sous-graphes.
Dans la seconde moitié du xxe siècle, le mathématicien français Claude Berge contribue au développement de la théorie des graphes par ses contributions sur les graphes parfaitsA 15 et l'introduction du terme d’hypergraphe (suite à la remarque de Jean-Marie Pla l'ayant utilisé dans un séminaire) avec un monographeA 16 sur le sujet. Son ouvrage d'introduction à la théorie des graphesA 17 proposa également une alternative originale, consistant plus en une promenade personnelle qu'une description complète. Il marquera également la recherche française en ce domaine, par la création conjointe avec Marcel-Paul Schützenberger d'un séminaire hebdomadaire à l'Institut Henri Poincaré, des réunions le lundi à la Maison des Sciences de l'Homme, et la direction de l'équipe Combinatoire de Paris.
Flots dans les réseaux [modifier]
Les Allemands Franz Ernst Neumann et Jacobi, respectivement physicien et mathématicien, fondèrent en 1834 une série de séminaires. Le physicien allemand Gustav Kirchhoff était un des étudiants participant au séminaire entre 1843 et 1846, et il étendit le travail de Georg Ohmpour établir en 1845 les Lois de Kirchhoff exprimant la conservation de l'énergie et de la charge dans un circuit électrique. En particulier, sa loi des nœuds stipule que la somme des intensités des courants entrant dans un nœud est égale à celle qui en sort. Un circuit électrique peut se voir comme un graphe, dans lequel les sommets sont les nœuds du circuit, et les arêtes correspondent aux connexions physiques entre ces nœuds. Pour modéliser les courants traversant le circuit, on considère que chaque arête peut-être traversée par un flot. Ceci offre de nombreuses analogies, par exemple à l'écoulement d'un liquide comme l'eau à travers un réseau de canauxB 1, ou la circulation dans un réseau routier. Comme stipulé par la loi des nœuds, le flot à un sommet est conservé, ou identique à l'entrée comme à la sortie; par exemple, l'eau qui entre dans un canal ne disparaît pas et le canal n'en fabrique pas, donc il y a autant d'eau en sortie qu'en entrée. De plus, une arête a une limite de capacité, tout comme un canal peut transporter une certaine quantité maximale d'eau. Si l'on ajoute que le flot démarre à un certain sommet (la source) et qu'il se termine à un autre (le puits), on obtient alors les principes fondamentaux de l'étude des flots dans un graphe.
Si on considère que la source est un champ pétrolifère et que le puits est la raffinerie où on l'écoule, alors on souhaite régler les vannes de façon à avoir le meilleur débit possible de la source vers le puits. En d'autres mots, on cherche à avoir une utilisation aussi efficace que possible de la capacité de chacune des arêtes, ce qui est le problème de flot maximum. Supposons que l'on « coupe » le graphe en deux parties, telle que la source est dans l'une et le puits est dans l'autre. Chaque flot doit passer entre les deux parties, et est donc limité par la capacité maximale qu'une partie peut envoyer à l'autre. Trouver la coupe avec la plus petite capacité indique donc l'endroit où le réseau est le plus limité, ce qui revient à établir le flot maximal qui peut le traverserB 2. Ce théorème est appelé flot-max/coupe-min et fut établi en 1956.
L’étude des flots réseaux se généralise de plusieurs façons. La recherche d'un maximum, ici dans le cas du flot, est un problème d'optimisation, qui est la branche des mathématiques consistant à optimiser (i.e. trouver un minimum ou maximum) une fonction sous certaines contraintes. Un flot réseau est soumis à trois contraintesB 3 : la limite de capacité sur chaque arête, la création d'un flot non nul entre la source et le puits (i.e. la source crée un flot), et l'égalité du flot en entrée/sortie pour tout sommet autre que la source et les puits (i.e.ils ne consomment ni ne génèrent une partie du flot). Ces contraintes étant linéaires, le problème d'un flot réseau fait partie de laprogrammation linéaire. Il est également possible de rajouter d'autres variables au problème pour prendre en compte davantage de situations : on peut ainsi avoir plusieurs sources et puits, une capacité minimale sur chaque arête, un coût lorsqu'on utilise une arête, ou une amplification du flot passant par une arête.
Introduction de probabilités [modifier]
Jusqu'au milieu du XXe siècle, l'algorithme construisant un graphe n'avait rien d'aléatoire : tant que les paramètres fournis à l'algorithme ne changeaient pas, alors le graphe qu'il construisait était toujours le même. Une certaine dose d'aléatoire fut alors introduite, et les algorithmes devinrent ainsi probabilistes. Le mathématicien d'origine russe Anatol Rapoport eut d'abord cette idée en 1957C 1 mais elle fut proposée indépendamment deux ans après, de façon plus formelle, par les mathématiciens hongrois Paul Erdős et Alfréd RényiC 2. Ceux-ci se demandèrent à quoi ressemble un graphe « typique » avec n sommets et m arêtes. Ils souhaitaient ainsi savoir quelles propriétés pouvaient être trouvées avec n sommets, et m arêtes créées au hasard. Une quantité fixe m n'étant pas pratique pour répondre à cette questionC 3, il fut décidé que chaque arête existerait avec une probabilité p. Ceci fut le début de la théorie des graphes aléatoires, où l'on considère un nombre de sommets n assez grand, et l'on s'intéresse à la probabilité p suffisante pour que le graphe ait une certaine propriété.
Erdős et Rényi découvrirent que le graphe n'évoluait pas de façon linéaire mais qu'il y avait au contraire une probabilité critique p après laquelle il changeait de façon radicale. Ce comportement est bien connu en physique : si l'on observe un verre d'eau que l'on met dans un congélateur, il ne se change pas progressivement en glace mais plutôt brutalement lorsque la température passe en dessous de 0°C. L'eau avait deux phases (liquide et glace) et passe de l'une à l'autre par un phénomène nommé transition de phase, la transition étant rapide autour d'un point critique qui est dans ce cas la température de 0°C. Pour nombre de propriétés observées, les graphes aléatoires fonctionnent de la même manièreC 4 : il existe une probabilité critique  en dessous de laquelle ils se trouvent dans une phase sous-critique, et au-dessus de laquelle ils passent en phase sur-critique. Dans le cas d'un graphe aléatoire, la probabilité que l'on observe la propriété nous intéressant est faible en phase sous-critique mais devient très forte (i.e. quasi-certitude) en phase sur-critique; le tracé de la probabilité d'avoir la propriété en fonction de p a donc une allure bien particulière, simplifiée dans le schéma à droite.
en dessous de laquelle ils se trouvent dans une phase sous-critique, et au-dessus de laquelle ils passent en phase sur-critique. Dans le cas d'un graphe aléatoire, la probabilité que l'on observe la propriété nous intéressant est faible en phase sous-critique mais devient très forte (i.e. quasi-certitude) en phase sur-critique; le tracé de la probabilité d'avoir la propriété en fonction de p a donc une allure bien particulière, simplifiée dans le schéma à droite.
Au-delà du vocabulaire commun des phases, la théorie des graphes aléatoires se retrouve enphysique statistique sous la forme de la théorie de la percolationC 5. Cette dernière visait à l'origine à étudier l'écoulement d'un fluide à travers un matériau poreux. Par exemple, si l'on immerge une pierre ponce dans un seau rempli d'eauC 6, on s'intéresse à la façon dont l'eau va s'écouler dans la pierre. Pour modéliser ce problème, on se concentre sur les paramètres importants : l'âge ou la couleur de la pierre n'importe pas, tandis que les ouvertures ou 'canaux' dans lesquels peut circuler l'eau sont primordiaux. L'abstraction la plus simple est de voir une pierre comme une grille, où chaque canal existe avec une probabilité p. On retrouve ainsi le modèle du graphe aléatoire, mais avec une contrainte spatiale : un arc ne peut exister entre deux sommets que s'ils sont voisins dans la grille. Cependant, cette contrainte peut-être levée pour établir une équivalence entre la théorie des graphes et celle de la percolation. Tout d'abord, un graphe de n sommets peut être représenté par une grille avec n dimensions; puisqu'on s'intéresse au cas où n est assez grand, c'est-à-dire  , ceci établit une équivalence avec la percolation en dimension infinie. De plus, il existe une dimension critique
, ceci établit une équivalence avec la percolation en dimension infinie. De plus, il existe une dimension critique 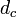 telle que le résultat ne dépend plus de la dimension dès que celle-ci atteint
telle que le résultat ne dépend plus de la dimension dès que celle-ci atteint 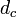 ; on pense que cette dimension critique est 6, mais elle n'a pu être prouvéeC 7 que pour 19.
; on pense que cette dimension critique est 6, mais elle n'a pu être prouvéeC 7 que pour 19.
De nombreux modèles ont été proposés depuis le début des années 2000 pour retrouver des phénomènes observés dans des graphes tels que celui représentant les connexions entre des acteurs de Hollywood (obtenu par IMDb) ou des parties du Web. En 1999, Albert-Laszlo Barabasi et Réka Albert expliquèrent qu'un de ces phénomènes « est une conséquence de deux mécanismes : le réseau grandit continuellement avec l'ajout de nouveaux sommets, et les nouveaux sommets s'attachent avec certaines préférences à d'autres qui sont déjà bien en place »C 8. Une certaine confusion s'installa autour de leur modèle : s'il permet effectivement d'obtenir le phénomène souhaité, il n'est pas le seul modèle arrivant à ce résultat et on ne peut donc pas conclure en voyant le phénomène qu'il résulte d'un processus d'attachement préférentiel. Les phénomènes de petit monde et de libre d'échelle, pour lesquels de très nombreux modèles ont été proposés, peuvent être réalisés simplement par des graphes aléatoiresC 9 : la technique de Michael Molley et Bruce ReedC 10 permet d'obtenir l'effet de libre d'échelle, tandis que celle de Li, Leonard et Loguinov conduit au petit-mondeC 11.
Représentations et invariants [modifier]
Étiquetage et morphismes [modifier]
Formellement un graphe est étiqueté : chaque sommet ou arête appartient à un ensemble, donc porte une étiquette. Typiquement, les graphes sont étiquetés par des nombres entiers, mais une étiquette peut en fait appartenir à n'importe quel ensemble : ensemble de couleurs, ensemble de mots, ensemble des réels. Les exemples ci-contre montrent des graphes étiquetés par des entiers et par des lettres. L'étiquetage d'un graphe peut-être conçu de façon à donner des informations utiles pour des problèmes comme le routage : partant d'un sommet u, on veut arriver à un sommet v, c'est-à-dire que l'on souhaite acheminer une information de u à v. Selon la façon dont les sommets sont étiquetés, les étiquettes que portent uet v peuvent nous permettre de trouver facilement un chemin. Par exemple, dans le graphe de Kautz où la distance maximale entre deux sommets est D, imaginons que l'on soit à un sommet étiqueté (x1,x2,...,xD) et que l'on souhaite aller à (y1,y2,...,yD) : il suffit de décaler l'étiquette en introduisant la destinationD 1, ce qui donne le chemin 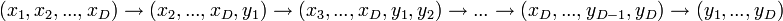 . Ce chemin se lit de la façon suivante : si on se trouve au sommet étiqueté (x1,x2,...,xD) alors on va vers le voisin portant l'étiquette (x2,...,xD,y1), et ainsi de suite.
. Ce chemin se lit de la façon suivante : si on se trouve au sommet étiqueté (x1,x2,...,xD) alors on va vers le voisin portant l'étiquette (x2,...,xD,y1), et ainsi de suite.
On se retrouve cependant face à un problème : si on regarde plus haut l'illustration de la liste des arbres à 2, 3 et 4 sommets, beaucoup d'entre eux ont exactement la même structuremais un étiquetage différent (donné ici par des couleurs). Pour étudier uniquement la structure, il faut donc un outil permettant d'ignorer l'étiquetage, c'est-à-dire de donner une équivalence structurelle. Pour cela, on introduit la notion de morphisme. Un morphisme de graphesD 2, ou homomorphisme de graphe, est une application entre deux graphes qui respecte la structure des graphes. Autrement dit l'image du graphe G dans H doit respecter les relations d'adjacences présentes dans G. Plus précisément, si G et H sont deux graphes, une application  est un morphisme de graphe si f = (fV,fE) où
est un morphisme de graphe si f = (fV,fE) où  transforme les sommets de G en ceux de H, et
transforme les sommets de G en ceux de H, et  les arêtes de G en celles de H en respectant la contrainte suivante : s'il existe une arête
les arêtes de G en celles de H en respectant la contrainte suivante : s'il existe une arête  entre deux sommets de G alors il doit y avoir une arête
entre deux sommets de G alors il doit y avoir une arête  entre les deux sommets correspondants de H. On dit de l'homomorphisme f qu'il est une injection (respectivement surjection) si ses deux fonctions fV et fE sont injectives (respectivement surjectives); si elles sont à la fois injectives et surjectives, c'est-à-dire bijectives, alors f est un isomorphisme. Si deux graphes sont isomorphes, alors ils ont la même structure : peu importe la façon dont ils sont dessinés ou étiquetés, il est possible de déplacer les sommets ou de changer les étiquettes pour que l'un soit la copie conforme de l'autre, ainsi qu'illustré ci-dessous. On désigne alors par graphe non étiqueté la classe d'équivalence d'un graphe pour la relation d'isomorphisme. Deux graphes isomorphes seront alors considérés comme égaux si on les considère en tant que graphes non étiquetés.
entre les deux sommets correspondants de H. On dit de l'homomorphisme f qu'il est une injection (respectivement surjection) si ses deux fonctions fV et fE sont injectives (respectivement surjectives); si elles sont à la fois injectives et surjectives, c'est-à-dire bijectives, alors f est un isomorphisme. Si deux graphes sont isomorphes, alors ils ont la même structure : peu importe la façon dont ils sont dessinés ou étiquetés, il est possible de déplacer les sommets ou de changer les étiquettes pour que l'un soit la copie conforme de l'autre, ainsi qu'illustré ci-dessous. On désigne alors par graphe non étiqueté la classe d'équivalence d'un graphe pour la relation d'isomorphisme. Deux graphes isomorphes seront alors considérés comme égaux si on les considère en tant que graphes non étiquetés.
| Graphe G | Graphe H | Isomorphisme entre G et H |
|---|---|---|
 |
 |
ƒ(a) = 1
ƒ(b) = 6 ƒ(c) = 8 ƒ(d) = 3 ƒ(g) = 5 ƒ(h) = 2 ƒ(i) = 4 ƒ(j) = 7 |
Le mot graphe peut désigner, selon les contextes, un graphe étiqueté ou non étiqueté. Quand on parle du graphe du web, les étiquettes sont des URL et ont un sens. Le mot est utilisé pour désigner un graphe étiqueté. À l'opposé le graphe de Petersen est toujours considéré à isomorphisme près, donc non étiqueté, seules ses propriétés structurelles étant intéressantes.
Graphes et algèbre linéaire [modifier]
Tout graphe G = (V,E) peut être représenté par une matrice. Les relations entre arêtes et sommets, appelées les relations d'incidence, sont toutes représentées par la matrice d'incidence du graphe. Les relations d'adjacences (si deux sommets sont reliés par une arête ils sont adjacents) sont représentés par sa matrice d'adjacence. Elle est définie par
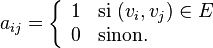
| Graphe | Représentation par une matrice d'adjacence | Représentation par une matrice laplacienne (non normalisée) |
|---|---|---|
 |
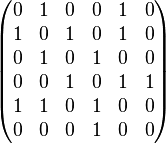 |
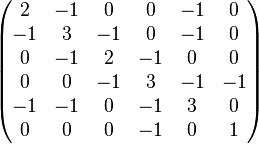 |
De nombreuses informations d'un graphe peuvent-être représentées par une matrice. Par exemple, la matrice des degrés D est une matrice diagonale où les éléments Dii correspondent au nombre de connexions du sommet i, c'est-à-dire à son degré. En utilisant cette matrice et la précédente, on peut également définir la matrice laplacienne L = D − A; on obtient sa forme normalisée L' par L' = D − 1 / 2LD − 1 / 2 = I − D − 1 / 2AD − 1 / 2, où I dénote la matrice identité, ou on peut aussi l'obtenir directement par chacun de ses éléments :

Ces représentations dépendent de la façon dont les sommets du graphe sont étiquetés. Imaginons que l'on garde la même structure que dans l'exemple ci-dessus et que l'on inverse les étiquettes 1 et 6 : on inverse alors les colonnes 1 et 6 de la matrice d'adjacence. Il existe en revanche des quantités qui ne dépendent pas de la façon dont on étiquette les sommets, tels que le degré minimal/maximal/moyen du graphe. Ces quantités sont des invariants du graphe : elles ne changent pas selon la numérotation. Tandis qu'une matrice d'adjacence ou laplacienne varie, son spectre, c'est-à-dire l'ensemble de ses valeurs propres  , est un invariant. L'étude du rapport entre les spectres et les propriétés d'un graphe est le sujet de la théorie spectrale des graphesD 3; parmi les rapports intéressants, le spectre donne des renseignements sur le nombre chromatique, le nombre de composantes connexes et les cycles du graphe.
, est un invariant. L'étude du rapport entre les spectres et les propriétés d'un graphe est le sujet de la théorie spectrale des graphesD 3; parmi les rapports intéressants, le spectre donne des renseignements sur le nombre chromatique, le nombre de composantes connexes et les cycles du graphe.
Décompositions arborescentes et en branches [modifier]
Les graphes permettant de représenter de nombreuses situations, il existe de nombreux algorithmes (i.e. programmes) les utilisant. Lacomplexité d'un algorithme consiste essentiellement à savoir, pour un problème donné, combien de temps est nécessaire pour le résoudre et quel est l'espace machine que cela va utiliser. Certaines représentations de graphes permettent d'obtenir de meilleures performances, c'est-à-dire que le problème est résolu plus rapidement ou en occupant moins d'espace. Dans certains cas, un problème NP-complet (classe la plus ardue) sur une représentation d'un graphe peut être résolu en temps polynomial (classe simple) avec une autre représentation; l'idée n'est pas qu'il suffit de regarder le graphe différemment pour résoudre le problème plus vite, mais que l'on « paye » pour le transformer et que l'on « économise » alors pour résoudre le problème. Une telle transformation est la décomposition arborescente proposée par les mathématiciensRobertson et Seymour dans leur série Graph Minors D 4. Intuitivement, une décomposition arborescente représente le graphe d'origine G par un arbre, où chaque sommet correspond à un sous-ensemble des sommets de G, avec quelques contraintes. Formellement, pour un graphe donné G = (V,E), sa décomposition arborescente est (f,T) où T est un arbre et f une fonction associant à chaque sommet  un ensemble de sommets
un ensemble de sommets 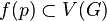 . Trois contraintes doivent être satisfaites :
. Trois contraintes doivent être satisfaites :
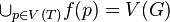 . La décomposition n'oublie aucun sommet du graphe d'origine.
. La décomposition n'oublie aucun sommet du graphe d'origine. tel que
tel que 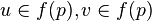 .
.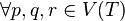 si q est sur le chemin de p à r alors
si q est sur le chemin de p à r alors  . Si l'on prend l'intersection des sommets abstraits par deux nœuds de l'arbre, alors cette intersection doit être contenue dans un sommet intermédiaire. Sur l'exemple ci-contre, l'intersection de {A,B,C} et {C,D,E} est {C} qui est bien contenue dans le sommet intermédiaire {C,B,E}.
. Si l'on prend l'intersection des sommets abstraits par deux nœuds de l'arbre, alors cette intersection doit être contenue dans un sommet intermédiaire. Sur l'exemple ci-contre, l'intersection de {A,B,C} et {C,D,E} est {C} qui est bien contenue dans le sommet intermédiaire {C,B,E}.
La largeur arborescente tw(G) d'une décomposition (f,T) d'un graphe G est 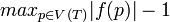 , c'est-à-dire la taille du plus grand ensemble représenté par un sommet moins 1; on peut la voir comme l'abstraction maximale : pour un sommet de l'arbre, jusqu'à combien de sommets du graphe représente-t-on ? Construire la décomposition arborescente d'un graphe quelconque avec la plus petite largeur arborescente est un problème NP-durD 5. Cependant, cela peut-être fait rapidement pour certains graphesD 6, ou approximéeD 7 pour d'autres tels les graphes planaires (i.e. pouvant être dessinés sans croiser deux arêtes).
, c'est-à-dire la taille du plus grand ensemble représenté par un sommet moins 1; on peut la voir comme l'abstraction maximale : pour un sommet de l'arbre, jusqu'à combien de sommets du graphe représente-t-on ? Construire la décomposition arborescente d'un graphe quelconque avec la plus petite largeur arborescente est un problème NP-durD 5. Cependant, cela peut-être fait rapidement pour certains graphesD 6, ou approximéeD 7 pour d'autres tels les graphes planaires (i.e. pouvant être dessinés sans croiser deux arêtes).
Robertson et Seymour développèrent également le concept de décomposition en branches. Pour la comprendre, il faut introduire davantage de vocabulaire sur un arbre. Dans les graphes, un arbre est dessiné "à l'envers" : on démarre de la racine en haut, et on descend jusqu'à atteindre les feuilles en bas; tout sommet n'étant pas une feuille est appelé un 'nœud interne'. La décomposition en branches résulte en un arbre dans lequel tout nœud interne a exactement trois voisins (comme sur l'exemple ci-contre), et où chaque feuille représente une arête du graphe d'origine. La profondeur minimale de la décomposition d'un graphe G est notée bw(G), et on a la relation 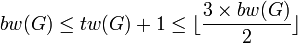 . De même que pour la décomposition arborescente, il est NP-dur de construire une décomposition en branches avec bw(G) minimal pour un graphe quelconque; dans ce cas, cette construction est réalisable pour un graphe planaireD 8.
. De même que pour la décomposition arborescente, il est NP-dur de construire une décomposition en branches avec bw(G) minimal pour un graphe quelconque; dans ce cas, cette construction est réalisable pour un graphe planaireD 8.
Ces représentations sont utilisées sur des problèmes NP-complets par des techniques de programmation dynamique, qui prennent généralement un temps exponentiel en bw(G) ou tw(G). Un tel problème est par exemple l'ensemble dominant : on veut savoir s'il y a un sous-ensemble D de sommets de taille au plus k tel qu'un sommet n'étant pas dans D y soit relié par une arête. Si le graphe est planaire, cette technique permet de résoudre le problèmeD 9 en temps 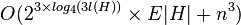 .
.
Aspect algorithmique [modifier]
Structures de données [modifier]
La façon dont le graphe est représenté en tant que objet mathématique a été exposée dans la section précédente. Dans l'aspect algorithmique de la théorie des graphes, on cherche à concevoir un processus efficace pour traiter un problème faisant intervenir un graphe. Les principaux critères d'efficacités d'un processus sont le temps nécessaire avant d'obtenir la réponse, et l'espace que le processus consomme dans son travail. La façon dont on représente le graphe influence la performance en temps et en espace : par exemple, si l'on veut connaître l'existence d'une arête entre deux sommets, la matrice d'adjacence permettra d'obtenir un résultat immédiatement, ce que l'on appelle en θ(1). En revanche, une opération de base telle que trouver le voisin d'un sommet est en O(n) sur une matrice d'adjacence : dans le pire des cas, il faudra scanner la totalité de la colonne pour s'apercevoir qu'il n'y a pas de voisin. Une autre structure de données est la liste d'adjacences, consistant en un tableau dont l'entrée i donne la liste des voisins du sommet i : sur une telle structure, trouver un voisin se fait en θ(1) tandis que l'existence d'une arête est en O(n). Ainsi, au niveau du temps, le choix de la structure dépend des opérations de base que l'on souhaite optimiser.
| Représentation par liste d'adjacence du graphe ci-contre: | ||
| 0 | adjacent à | 0,1,2,3 |
| 1 | adjacent à | 0 |
| 2 | adjacent à | 0,3,4 |
| 3 | adjacent à | 0,2 |
| 4 | adjacent à | 2 |
De même, l'espace qu'une structure consomme dépend du type de graphe considéré : un raccourci abusif consiste à dire qu'une liste d'adjacences consomme moins d'espace qu'une matrice car celle-ci sera creuse, mais cela prend par exemple plus d'espace pour stocker un graphe aléatoire avec les listes qu'avec une matrice; dans le cas général, une matrice utilise un espace θ(n2) et les listes utilisent 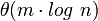 donc si le graphe est dense alors m peut-être suffisamment grand pour qu'une matrice consomme moins d'espace, et si le graphe est peu dense alors les listes consommeront moins d'espace. Des modifications simples d'une structure de données peuvent permettre d'avoir un gain appréciable : par exemple, dans une représentation partiellement complémentée d'une liste, un bit spécial indique si la liste est celle des voisins présents ou manquants; cette technique permet d'avoir des algorithmes linéaires sur le complément d'un graphe E 1.
donc si le graphe est dense alors m peut-être suffisamment grand pour qu'une matrice consomme moins d'espace, et si le graphe est peu dense alors les listes consommeront moins d'espace. Des modifications simples d'une structure de données peuvent permettre d'avoir un gain appréciable : par exemple, dans une représentation partiellement complémentée d'une liste, un bit spécial indique si la liste est celle des voisins présents ou manquants; cette technique permet d'avoir des algorithmes linéaires sur le complément d'un graphe E 1.
Tandis que ces structures sont locales, il existe aussi des structures de données distribuées. Le principe de ces structures est de concevoir un schéma d'étiquetage tel que, pour deux sommets x et y, on puisse répondre à une question comme « quelle est la distance entre x et y » uniquement en utilisant les étiquettes de ces nœuds; une telle utilisation des étiquettes a été vue en section 4.1 avec le graphe de Kautz où l'on peut déduire le chemin entre deux sommets uniquement grâce à leur étiquette, et la longueur de ce chemin nous donne la distance. Un étiquetage est efficace s'il permet de répondre à une question donnée uniquement en utilisant deux étiquettes, tout en minimisant le nombre maximum de bits d'une étiquetteE 2. Outre la distance, une question type peut-être de tester l'adjacence, c'est-à-dire de savoir si deux sommets sont voisins; notons que cela se ramène également au cas particulier d'une distance 1. Le premier exemple d'étiquetage efficace pour tester l'adjacence fut proposé dans le cas des arbres, et chaque étiquette est constituée de deux parties de  bits : la première partie identifie le sommet, et un nombre allant jusqu'à n nécessite
bits : la première partie identifie le sommet, et un nombre allant jusqu'à n nécessite  bits pour être codé, tandis que la seconde partie identifie le parent de ce sommet; pour tester l'adjacence, on utilise le fait que deux sommets sont voisins dans un arbre si et seulement si l'un est le parent de l'autreE 3.
bits pour être codé, tandis que la seconde partie identifie le parent de ce sommet; pour tester l'adjacence, on utilise le fait que deux sommets sont voisins dans un arbre si et seulement si l'un est le parent de l'autreE 3.
Sous-graphes utiles : séparateurs, spanners et arbres de Steiner [modifier]
L'efficacité d'un schéma d'étiquetage est lié à la taille des séparateurs du graphe.
Définition — un séparateur S est un sous-ensemble de sommet qui « sépare » les sommets du graphe en deux composants A1 et A2 tel que 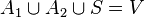 et il n'y a pas d'arêtes entre des sommets de A1 et A2.
et il n'y a pas d'arêtes entre des sommets de A1 et A2.
Si un graphe a des séparateurs de taille r(n), alors on peut par exemple concevoir des étiquettes de 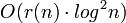 bits pour la distance; ceci permet directement d'en déduire l'étiquetage pour des graphes dont on connaît la taille des séparateurs, tels un graphe planaire où le séparateur est de taille
bits pour la distance; ceci permet directement d'en déduire l'étiquetage pour des graphes dont on connaît la taille des séparateurs, tels un graphe planaire où le séparateur est de taille  E 4. Enfin, il ne faut pas considérer que la taille de l'étiquetage mais également le temps nécessaire, étant donnés deux étiquettes, pour effectuer le décodage répondant à la question (i.e. quelle est la distance ? sont-ils voisins ?).
E 4. Enfin, il ne faut pas considérer que la taille de l'étiquetage mais également le temps nécessaire, étant donnés deux étiquettes, pour effectuer le décodage répondant à la question (i.e. quelle est la distance ? sont-ils voisins ?).
Réduction de données [modifier]
De nombreux problèmes sur les graphes sont NP-complets, c'est-à-dire durs à résoudre. Cependant, cette dureté est inégale : certaines parties du problème peuvent être particulièrement dures, et en constituent ainsi le cœur, tandis que d'autres sont assez faciles à gérer. Ainsi, avant d'exécuter un algorithme sur un problème qui peut-être dur, il est préférable de passer du temps à réduire ce problème pour ne plus avoir à considérer que son cœur.
Notions connexes [modifier]
- Un graphe est également un espace topologique de dimension 1 dont la généralisation est un complexe simplicial.
Notes [modifier]
- Au regard des mathématiques modernes, la formulation d'Euler est une conjecture puisque le résultat est énoncé sans preuve. Cependant, les mathématiques en son temps ne présentaient pas la même rigueur : tandis que conjecturer un résultat signifie maintenant que l'on renonce à le démontrer, pour Euler l'absence d'une preuve peut signifier que celle-ci n'était pas considérée utile.
Références [modifier]
|
|
18:12 Publié dans Théorie des graphes | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Intégrale de chemin
Source : http://fr.wikipedia.org/wiki/Int%C3%A9grale_de_chemin
Intégrale de chemin
Une intégrale de chemin (« path integral » en anglais) est une intégrale fonctionnelle, c'est-à-dire que l'intégrant est une fonctionnelle et que la somme est prise sur des fonctions, et non sur des nombres réels (ou complexes) comme pour les intégrales ordinaires. On a donc ici affaire à une intégrale en dimension infinie. Ainsi, on distinguera soigneusement l'intégrale de chemin (intégrale fonctionnelle) d'une intégrale ordinaire calculée sur un chemin de l'espace physique, que les mathématiciens appellent intégrale curviligne 1.
C'est Richard Feynman qui a introduit les intégrales de chemin en physique dans sa thèse, soutenue en mai 1942, portant sur la formulation de la mécanique quantique basée sur lelagrangien 2. En raison de la Seconde Guerre mondiale, ces résultats ne seront publiés qu'en 1948 3. Cet outil mathématique s'est rapidement imposé en physique théorique avec sa généralisation à la théorie quantique des champs, permettant notamment une quantification des théories de jauge non-abéliennes plus simple que la procédure de quantification canonique.
Par ailleurs, le mathématicien Mark Kac a ensuite développé un concept similaire pour la description théorique du mouvement brownien, s'inspirant de résultats obtenus par Norbert Wiener dans les années 1920. On parle dans ce cas de la formule de Feynman-Kac, qui est une intégrale pour la mesure de Wiener.4
Sommaire[masquer] |
Genèse du concept d'intégrale de chemin [modifier]
Alors qu'il est étudiant de 3e cycle sous la direction de Wheeler à l'université de Princeton, le jeune Feynman cherche une méthode de quantification basée sur le lagrangien pour pouvoir décrire un système ne possédant pas nécessairement d'hamiltonien. Sa motivation première est de quantifier la nouvelle formulation de l'électrodynamique classique basée sur l'action à distance qu'il vient juste de développer avec Wheeler5.
Au printemps de 1941, il rencontre Herbert Jehle, alors visiteur à Princeton, qui lui indique lors d'une soirée à la Nassau Tavern l'existence d'un article de Dirac qui discute précisément la quantification à partir du lagrangien 6. Jehle précise à Feynman que cette formulation permet une approche relativiste covariante bien plus aisée que celle basée sur le hamiltonien. Le lendemain, les deux physiciens se rendent à la bibliothèque pour étudier l'article de Dirac. Ils y lisent notamment la phrase suivante : pour deux instants  et
et 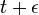 voisins, l'amplitude de transition élémentaire :
voisins, l'amplitude de transition élémentaire :
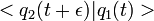 est analogue à est analogue à ![exp ( i S[q]/hbar ),](http://upload.wikimedia.org/math/f/0/f/f0f0ac1206095833ebdf16daf0b0873c.png) |
Dans cette formule, la grandeur ![S[q(t)],](http://upload.wikimedia.org/math/0/e/9/0e9fd62e69c48d17f5295b0c4d75f7a8.png) est l'action classique :
est l'action classique :
![S[q_2(t + epsilon) ,q_1(t)] = int_{t}^{t + epsilon} L(q,dot{q}) dt = L left( q_1, frac{q_2-q_1}{epsilon} right) epsilon,](http://upload.wikimedia.org/math/f/f/e/ffe056acc92b67324e8f86305088fa1b.png) |
Afin de comprendre ce que Dirac veux dire par analogue, Feynman étudie le cas d'une particule non relativiste de masse  pour laquelle le lagrangien s'écrit :
pour laquelle le lagrangien s'écrit :
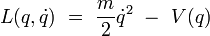 |
On sait que :
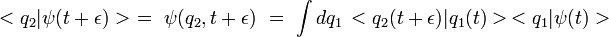 |
Feynman suppose alors une relation de proportionnalité :
![psi(q_2,t + epsilon) = A int dq_1 , exp , left( , i , frac{S[q(t)]}{hbar} , right) psi(q_1,t)](http://upload.wikimedia.org/math/7/0/f/70f482eccc0090e48a8ac8cb398a1cc1.png) |
où  est une constante inconnue. En présence de Jehle, Feynman démontre que cette équation implique que
est une constante inconnue. En présence de Jehle, Feynman démontre que cette équation implique que 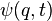 obéit à l'équation de Schrödinger :
obéit à l'équation de Schrödinger :
![left[ , - frac{hbar^2}{2m} frac{partial^2 ~~}{partial q^2} + V(q) , right] psi(q,t) = i , hbar frac{partial ~~}{partial t}psi(q,t)](http://upload.wikimedia.org/math/9/4/b/94bb8fbd11b93cd266a0f0eb81ceefd8.png) |
à la condition que la constante inconnue A soit égale à :
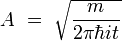 |
À l'automne 1946, lors du bicentenaire de l'université de Princeton, Feynman rencontra Dirac et le bref échange suivant eut lieu:
- - Feynman : « Saviez-vous que ces deux grandeurs étaient proportionnelles ? »
- - Dirac : « Elles le sont ? »
- - Feynman : « Oui. »
- - Dirac : « Oh ! C'est intéressant. »
Cette réponse laconique mettra un point final à la discussion ... Pour plus de détails historiques, on lira avec profit l'article de Schweber 7.
Rappels sur le propagateur de l'équation de Schrödinger [modifier]
Pour simplifier les notations, on se restreint ci-dessous au cas d'une seule dimension d'espace. Les résultats s'étendent sans difficulté à un nombre quelconque de dimensions.
Définition [modifier]
Considérons une particule de masse  non relativiste, décrite en mécanique quantique par une fonction d'onde. Supposons que l'on se donne la condition initiale
non relativiste, décrite en mécanique quantique par une fonction d'onde. Supposons que l'on se donne la condition initiale 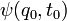 à un instant initial
à un instant initial 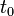 fixé. Alors, la fonction d'onde à un instant ultérieur
fixé. Alors, la fonction d'onde à un instant ultérieur  , solution de l'équation de Schrödinger, est donnée par l'équation intégrale :
, solution de l'équation de Schrödinger, est donnée par l'équation intégrale :
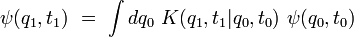 |
où  est le propagateur de la particule :
est le propagateur de la particule :
 |
 est l'opérateur hamiltonien de la particule.
est l'opérateur hamiltonien de la particule.
Équation de Chapman-Kolmogorov [modifier]
Rappelons que, si  , le propagateur obéit à l'équation de Chapman-Kolmogorov :
, le propagateur obéit à l'équation de Chapman-Kolmogorov :
 |
Cette relation va nous permettre de trouver l'expression du propagateur en termes d'une intégrale de chemin.
Expression du propagateur en termes d'intégrale de chemin [modifier]
Cherchons l'expression du propagateur  entre l'instant initial
entre l'instant initial 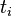 et l'instant final
et l'instant final  .
.
Application de l'équation de Chapman-Kolmogorov [modifier]
On découpe l'intervalle de temps 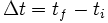 en
en 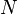 intervalles de temps élémentaires de durée
intervalles de temps élémentaires de durée  en introduisant les
en introduisant les  instants :
instants :
 |
avec 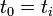 et
et  . Il y a donc
. Il y a donc  instants intermédiaires
instants intermédiaires  entre l'instant initial
entre l'instant initial 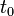 et l'instant final
et l'instant final  . Pour que les intervalles de temps aient une durée
. Pour que les intervalles de temps aient une durée  élémentaire, la limite
élémentaire, la limite 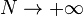 est sous-entendue.
est sous-entendue.
L'application de l'équation de Chapman-Kolmogorov une première fois permet d'écrire :
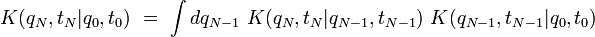 |
puis, en l'appliquant une deuxième fois :
 |
et ainsi de suite. On obtient au final après  applications aux
applications aux  temps intermédiaires8 :
temps intermédiaires8 :
![K(q_N,t_N|q_0,t_0) = int left[ , prod_{k=1}^{N-1} dq_k , right] K(q_N,t_N|q_{N-1},t_{N-1}) times dots times K(q_{k+1},t_{k+1}|q_{k},t_{k}) times dots times K(q_{1},t_{1}|q_0,t_0)](http://upload.wikimedia.org/math/d/5/2/d525ac09f5944c10cacd8c1969dc1628.png) |
On est ainsi amené à considérer le propagateur élémentaire :
 |
Propagateur élémentaire : formule de Feynman-Dirac [modifier]
Pour une particule de masse  non relativiste à une dimension dans un potentiel, dont l'opérateur Hamiltonien s'écrit :
non relativiste à une dimension dans un potentiel, dont l'opérateur Hamiltonien s'écrit :
 |
et le propagateur élémentaire s'écrit :
![K(q_{k+1},t_{k+1}|q_{k},t_{k}) = < q_{k+1} |e^{-i , [ , hat{H}_0 + V(hat{q}) , ] , epsilon /hbar} | q_k >](http://upload.wikimedia.org/math/7/9/9/79913cbea2dd47ca49c3d2bf6a19afd6.png) |
On utilise la formule de Trotter-Kato :
![e^{t(hat{A} + hat{B})} = lim_{n to infty} left[ e^{hat{A}t/n} times e^{hat{B}t/n} right]^n](http://upload.wikimedia.org/math/6/a/7/6a7af09d6c118d00474c31ca24a8276d.png) |
Cette formule n'est pas triviale, car les opérateurs  et
et 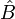 ne commutent en général pas ! On obtient ici :
ne commutent en général pas ! On obtient ici :
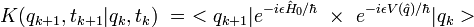 |
On peut sortir l'exponentielle contenant le potentiel qui ne dépend que de la position :
 |
L'élément de matrice restant est le propagateur de la particule libre, donc on peut finalement écrire l'expression :
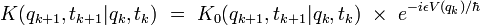 |
Or l'expression du propagateur libre est connue exactement :
 |
On remarque que l'argument de l'exponentielle peut se réécrire en termes d'une expression discrètisée de la vitesse :
 |
comme :
 |
On en déduit que le propagateur élémentaire s'écrit :
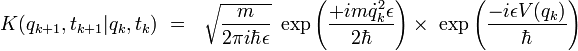 |
Les arguments des deux exponentielles étant maintenant des nombres complexes, on peut écrire sans difficultés :
 |
soit encore :
![K(q_{k+1},t_{k+1}|q_{k},t_{k}) = sqrt{frac{m}{2 pi i hbar epsilon}} exp left[ + frac{i}{hbar} left( frac{m}{2} dot{q}_k^2 - V(q_k) right) epsilon right]](http://upload.wikimedia.org/math/d/2/e/d2e6c64d9a6b0993d7984a6756c4d2a8.png) |
Le terme entre parenthèse représente le Lagrangien de la particule :
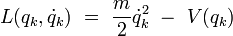 |
d'où la formule de Feynman-Dirac pour le propagateur élémentaire :
![K(q_{k+1},t_{k+1}|q_{k},t_{k}) = sqrt{frac{m}{2 pi i hbar epsilon}} exp left[ + frac{i}{hbar} L(q_k,dot{q}_k) epsilon right]](http://upload.wikimedia.org/math/4/d/a/4dac735213dbe66e97e99cd56ce05dee.png) |
Intégrale de chemin [modifier]
On injecte l'expression de Feynman-Dirac dans la formule générale :
![K(q_N,t_N|q_0,t_0) = int left[ , prod_{k=1}^{N-1} dq_k , right] K(q_N,t_N|q_{N-1},t_{N-1}) times dots times K(q_{k+1},t_{k+1}|q_{k},t_{k}) times dots times K(q_{1},t_{1}|q_0,t_0)](http://upload.wikimedia.org/math/d/5/2/d525ac09f5944c10cacd8c1969dc1628.png) |
Il vient :
![K(q_N,t_N|q_0,t_0) = left( , frac{m}{2 pi i hbar epsilon} , right)^{N/2} int left[ , prod_{k=1}^{N-1} dq_k , right] exp left[ + frac{i}{hbar} L(q_{N-1},dot{q}_{N-1}) epsilon right] times dots times exp left[ + frac{i}{hbar} L(q_k,dot{q}_k) epsilon right] times dots times exp left[ + frac{i}{hbar} L(q_0,dot{q}_0) epsilon right]](http://upload.wikimedia.org/math/1/9/5/1958e35f000c6df83210aedf460d91a7.png) |
L'argument des exponentielles étant des nombres complexes, on peut écrire :
![K(q_N,t_N|q_0,t_0) = left( , frac{m}{2 pi i hbar epsilon} , right)^{N/2} int left[ , prod_{k=1}^{N-1} dq_k , right] exp left[ + frac{i}{hbar} left[ , L(q_{N-1},dot{q}_{N-1}) + dots + L(q_k,dot{q}_k) + dots + L(q_0,dot{q}_0) , right] epsilon right]](http://upload.wikimedia.org/math/6/3/a/63a8e31f7a4b036d75d0d1387c09b498.png) |
On reconnait dans l'argument de l'exponentielle une discrétisation de l'action classique :
![lim_{Ntoinfty} sum_{k=1}^{N-1} L(q_k,dot{q}_k) epsilon = int_{t_0}^{t_N} L(q(t),dot{q}(t)) dt = S left[ , q(t) , right]](http://upload.wikimedia.org/math/f/9/5/f9528674af5aeaf41cbd5441eb7d1203.png) |
On en déduit avec Feynman l'expression du propagateur comme intégrale fonctionnelle sur tous les chemins continus :
![K(q_N,t_N|q_0,t_0) = int mathcal{D}q(t) textrm{e}^{ + frac{i , S left[ , q(t) , right]}{hbar}}](http://upload.wikimedia.org/math/1/1/d/11de894d712ef0667ca37000ce0e709c.png) |
avec la mesure formelle9 :
![mathcal{D}q(t) = lim_{Ntoinfty} left( , frac{m}{2 pi i hbar epsilon} , right)^{N/2} left[ , prod_{k=1}^{N-1} dq_k , right]](http://upload.wikimedia.org/math/4/6/7/4673b2ac26a7fc1248cb2842e76d3746.png) |
Interprétation [modifier]
La formule de Feynman :
![K(q_f,t_f|q_i,t_i) = int mathcal{D}q(t) textrm{e}^{ + frac{i , S left[ , q(t) , right]}{hbar}}](http://upload.wikimedia.org/math/c/4/4/c44fe6f004a074e716d66ac3cf21b97c.png) |
admet l'interprétation suivante : pour calculer l'amplitude de transition du point initial  à l'instant
à l'instant 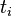 vers le point final
vers le point final  à l'instant tf, il faut considèrer tous les chemins continus10
à l'instant tf, il faut considèrer tous les chemins continus10  vérifiants les conditions aux limites :
vérifiants les conditions aux limites : 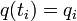 et
et  . Chaque chemin se voit attribuer un « poids » complexe de module unité :
. Chaque chemin se voit attribuer un « poids » complexe de module unité : ![exp ( i S[q(t)]/hbar ),](http://upload.wikimedia.org/math/d/d/1/dd1e01dee08cad29a0c1208abd9811ed.png) , où
, où ![S[q(t)],](http://upload.wikimedia.org/math/0/e/9/0e9fd62e69c48d17f5295b0c4d75f7a8.png) est l'action classique calculée sur ce chemin. On « somme » alors cette infinité non dénombrable de poids complexes, et on obtient in fine l'amplitude de transition désirée.
est l'action classique calculée sur ce chemin. On « somme » alors cette infinité non dénombrable de poids complexes, et on obtient in fine l'amplitude de transition désirée.
Cette interprétation est l'œuvre de Feynman seul, Dirac n'ayant pas franchi le pas. Elle est implicite dans sa thèse de 1942, et explicite dans la publication de 1948.
Limite semi-classique [modifier]
Dans la limite où l'action du système est beaucoup plus grande que  , on peut utiliser un développement du type semi classique, où y est une petite perturbation de la trajectoire classique xc: x = xc + y
, on peut utiliser un développement du type semi classique, où y est une petite perturbation de la trajectoire classique xc: x = xc + y
Considérons un Lagrangien standard:
![mathcal{L}[x,dot{x}]= frac{mdot{x}^{2}}{2}- V(x)](http://upload.wikimedia.org/math/a/a/b/aabc30b9b9f82daf69db73f1f376c7c4.png)
On écrit alors l'action sous la forme suivante, en se limitant au deuxième ordre:
![S[x] approx S[x_{c}]+ int_{t_{i}}^{t_{f}}dt underbrace{frac{delta S}{delta x(t)}|_{x_{c}}}_{=0} y(t) + frac{1}{2} int_{t_{i}}^{t_{f}}dt_{1} dt_{2} frac{delta^{2} S}{delta x(t_{1})delta x(t_{2}) }|_{x_{c}}y(t_{1})y(t_{2})Longrightarrow](http://upload.wikimedia.org/math/a/2/a/a2af42c15acf496b8eb59cbf9e0fcc11.png)
![S[x]approx S[x_{c}]+ frac{1}{2} int_{t_{i}}^{t_{f}}dt (m dot{y}^{2} - V''(x_{c}) y^{2})](http://upload.wikimedia.org/math/3/1/6/31659c3c8a96ea1bff7209fd7974bdb8.png)
on peut donc approximer le propagateur:
![K(x_{f},t_{f};x_{i},t_{i}) approx e^{i S[x_{c}]/ hbar} int mathcal{D}[y] e^{i int_{t_{i}}^{t_{f}}dt (m dot{y}^{2} - V''(x_{c}) y^{2})/2hbar}](http://upload.wikimedia.org/math/3/4/a/34a01a003d70ba5737366c55bdc21769.png)
une intégration par partie de l'exposant ramène à une forme Gaussienne:
![K(x_{f},t_{f};x_{i},t_{i})approx e^{i S[x_{c}]/ hbar} int mathcal{D}[y] e^{i int_{t_{i}}^{t_{f}}dt (y[-m frac{d^{2}}{dt^{2}} - V''(x_{c}] y)/2hbar}](http://upload.wikimedia.org/math/2/9/2/2922ad0fcf82f997d7c301df4ff54768.png)
Définissons l'opérateur 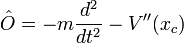
les règles de calcul des intégrales Gaussiennes fournissent:
![K(x_{f},t_{f};x_{i},t_{i}) approx cste cdot sqrt{frac{1}{Det (hat{O})}}cdot e^{i S[x_{c}]/ hbar}](http://upload.wikimedia.org/math/6/7/0/670ad65fe69c000b2c03ba8e2ee198cf.png)
Considérons maintenant la fonction Ψ(t) définie comme suit:
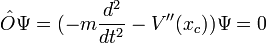
avec les conditions de bords:
Ψ(ti) = 0
Ψ'(ti) = 1
On peut alors montrer que:
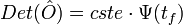
ce qui nous donne pour l'approximation du propagateur:
![K(x_{f},t_{f};x_{i},t_{i}) approx sqrt{frac{A}{Psi(t_{f})}}cdot e^{i S[x_{c}]/ hbar}](http://upload.wikimedia.org/math/c/f/2/cf282603976ee6a16a78d82e308ab3ce.png)
on détermine la constante A à partir du propagateur de la particule libre:
![K_{fp}(x_{f},t_{f};x_{i},t_{i})=sqrt{frac{m}{2pi i hbar (t_{f}-t_{i})}} e^{i S[x_{c}]/ hbar}](http://upload.wikimedia.org/math/5/8/a/58aedadc4a116db583b15d5e1960c58f.png)
dans le cas de la particule libre, la fonction Ψ qui satisfait les conditions exposées plus haut est Ψ(t) = t − ti, ce qui nous donne immédiatement une expression pour A. On obtient finalement l'approximation dite semi-classique du propagateur:
![K(x_{f},t_{f};x_{i},t_{i}) approx sqrt{frac{m}{2 pi i hbar Psi(t_{f})}}cdot e^{i S[x_{c}]/ hbar}](http://upload.wikimedia.org/math/a/4/0/a400c660a68b8b9d59da52c147c417f3.png)
cette approximation est puissante, et peut même donner parfois un résultat exact, comme par exemple dans le cas où le potentiel est celui d'un oscillateur harmonique de fréquence ω. Dans ce cas, la fonction Ψ doit satisfaire, en plus des conditions de bord:

et on obtient l'expression exacte du propagateur de l'oscillateur harmonique, par l'approximation semi-classique:
![K_{ho}(x_{f},t_{f};x_{i},t_{i}) = sqrt{frac{m omega}{2 pi i hbar sin omega(t_{f}-t_{i})}}cdot e^{i S[x_{c}]/ hbar}](http://upload.wikimedia.org/math/2/a/b/2ab2a18072011a587efc8f885ee46092.png)
avec l'action classique de l'oscillateur harmonique:
![S_{cl}[x]= int_{t_{i}}^{t_{f}} dt mathcal{L}[x,dot{x}] = frac{momega}{2}left[(x_{f}^{2}+x_{i}^{2})cotomega (t_{f}-t_{i})-frac{2x_{i}x_{f}}{sinomega (t_{f}-t_{i})}right]](http://upload.wikimedia.org/math/0/8/f/08fa3dfef8fd286276232bc536be0a08.png)
à noter une autre formulation équivalente de l'approximation semi-classique, dite de Van Vleck-Pauli-Morette, qui découle directement de la précédente:

Bibliographie [modifier]
Textes historiques [modifier]
- Richard P. Feynman ; The principle of least action in quantum mechanics, thèse de l'université de Princeton. Cette thèse vient d'être publiée par Laurie M. Brown (cf. ci-dessous).
- Richard P. Feynman ; Space-time approach to non-relativistic quantum mechanics, Review of Modern Physics 20 (1948) 267. Cet article est reproduit dans : Julian Schwinger (ed) ;Selected papers on quantum electrodynamics, Dover Publications, Inc. (1958) (ISBN 0-486-60444-6).
- PAM Dirac ; The lagrangian in quantum mechanics, Physikalische Zeitschrift der Sowjetunion 3(1) (1932) 64. Cet article est reproduit dans : Julian Schwinger (ed) ; Selected papers on quantum electrodynamics, Dover Publications, Inc. (1958) (ISBN 0-486-60444-6).
- Laurie M. Brown (Editor) ; Feynman's thesis: a new approach to quantum theory, World Scientific (2005),(ISBN 981-256-380-6). Contient la thèse originale de Feynman, ainsi que les deux articles précédents.
Ouvrages de références [modifier]
- Jean Zinn-Justin ; Intégrale de chemin en mécanique quantique : Introduction, Collection savoirs actuels, E.D.P. Sciences/C.N.R.S. Editions (2003), (ISBN 2-86883-660-7). Excellente introduction au sujet, ce livre est le fruit de nombreuses années d'enseignement au Magistère Interuniversiataire de Physique de l'E.N.S.
- Claude Cohen-Tannoudji ; Compléments de mécanique quantique, (1966). Cours donné en 1966 par le prix Nobel 1997 (Collège de France, Paris). Aborde la formulation Lagrangienne de la mécanique quantique, et l'utilisation des fonctions de Green. Notes de cours rédigées en 1966 par Serge Haroche (Collège de France, Paris).
- Richard P. Feynman and André R. Hibbs, Quantum Mechanics and Path Integrals, New York: McGraw-Hill (1965), (ISBN 0-07-020650-3).
- Larry S. Schulman ; Techniques & Applications of Path Integration, Jonh Wiley & Sons (New York-1981), ISBN . Réédité par Dover Publications, Inc. (2005), (ISBN 0-486-44528-3). Une autre référence, un peu plus moderne que la précédente.
- Christian Grosche & Frank Steiner; Handbook of Feynman Path Integrals, Springer Tracts in Modern Physics 145, Springer-Verlag (1998), (ISBN 3-540-57135-3).
- Philippe A. Martin ; L'intégrale fonctionnelle ; Presses Polytechniques Universitaires Romandes (1996), (ISBN 2-88074-331-1).
- Lundqvist & co ; Path Summation ; World scientific (1988), (ISBN 9971-5-0597-5).
- Martin Veltman ; Diagrammatica, CambridgeLNP
- Lewis H. Ryder ; Quantum Field Theory (Cambridge University Press, 1985), (ISBN 0-521-33859-X).
- R.J. Rivers ; Path Integrals Methods in Quantum Field Theory, Cambridge University Press (1987), (ISBN 0-521-25979-7).
- Hagen Kleinert, Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 4th edition, World Scientific (Singapore, 2004), (ISBN 981-238-107-4). (Disponible aussi en ligne au format pdf).
- Christian Grosche ; An introduction into the Feynman path integral, cours donné au Quantenfeldtheorie und deren Anwendung in der Elementarteilchen- und Festkörperphysik, Universität Leipzig, 16-26 November 1992. Texte complet disponible sur l'ArXiv : hep-th/9302097.
- Sanjeev Seahra ; Path Integrals in Quantum Field Theory, notes du cours Quantum Field Theory donné en 2000 par Eric Poisson à l'University of Waterloo (Canada). Texte complet disponible au format pdf.
- Richard MacKenzie ; Path integral methods and applications, cours donné aux Rencontres du Vietnam: VIth Vietnam School of Physics, Vung Tau, Vietnam, 27 December 1999 - 8 January 2000. Texte complet disponible sur l'ArXiv : quant-ph/0004090.
- Gert Roepstorff ; Path Integral Approach to Quantum Physics, Springer-Verlag (1994), (ISBN 3-540-55213-8).
Approche mathématiquement rigoureuse [modifier]
- S. Albeverio & R. Hoegh-Krohn. ; Mathematical Theory of Feynman Path Integral, Lecture Notes in Mathematics 523, Springer-Verlag (1976), ISBN .
- James Glimm et Arthur Jaffe Quantum Physics: a Functional Integral Point of View, New York: Springer-Verlag (1981), (ISBN 0-387-90562-6).
- Gerald W. Johnson and Michel L. Lapidus ; The Feynman Integral and Feynman's Operational Calculus, Oxford Mathematical Monographs, Oxford University Press (2002), (ISBN 0-19-851572-3).
- Etingof, Pavel ; Geometry and Quantum Field Theory, M.I.T. OpenCourseWare (2002). Ce cours en ligne, conçu pour les mathématiciens, est une introduction rigoureuse à la théorie quantique des champs via les intégrales fonctionnelles.
- Cécile DeWitt-Morette ; Feynman's path integral - Definition without limiting procedure, Communication in Mathematical Physics 28(1) (1972) pp. 47–67. Texte complet disponible sur : Euclide Project.
- Pierre Cartier & Cécile DeWitt-Morette ; A new perspective on functional integration, Journal of Mathematical Physics 36 (1995) pp. 2137-2340. Texte complet disponible sur l'ArXiv :funct-an/9602005.
- Pierre Cartier ; L'intégrale de chemin de Feynman : d'une vue intuitive à un cadre rigoureux, dans : Leçons de mathématiques d'aujourd'hui, Collection Le sel et le fer, Cassini (2000) pp.27-59 (ISBN 2-84225-007-9).
- Alain Connes & Dirk Kreimer : Communication in Mathematical Physics 210 (2000)1. 249-273
- Alain Connes & Marcolli : Communication in Mathematical Physics 216 (2001),1, 215-241
- Alain Connes ; page personnelle, articles 137, 148, 155, 157, 158, 162, 165, 167.
Notes et références [modifier]
- Les physiciens qualifient l'intégrale curviligne d'un champ de vecteur de circulation (par exemple, le travail d'une force.)
- Richard P. Feynman ; The principle of least action in quantum mechanics, thèse de l'université de Princeton. Cette thèse vient d'être publiée dans Laurie M. Brown (Editor) ; Feynman's thesis: a new approach to quantum theory, World Scientific (2005),(ISBN 981-256-380-6).
- Richard P. Feynman ; Space-time approach to non-relativistic quantum mechanics, Review of Modern Physics 20 (1948) 267. Cet article est reproduit dans : Julian Schwinger (ed) ; Selected papers on quantum electrodynamics, Dover Publications, Inc. (1958) (ISBN 0-486-60444-6), ainsi que dans : Laurie M. Brown (Editor) ; Feynman's thesis: a new approach to quantum theory, World Scientific (2005),(ISBN 981-256-380-6).
- Il existe clairement un lien formel entre les deux types d'intégrales de chemins - Feynman et Wiener -, car alors que l'équation de Schrödinger d'une particule massive non relativiste libre s'écrit :
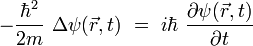 où ψ est la fonction d'onde quantique, l'équation de la diffusion dans l'espace pour la densité de probabilité P s'écrit :
où ψ est la fonction d'onde quantique, l'équation de la diffusion dans l'espace pour la densité de probabilité P s'écrit :  On voit clairement qu'il suffit de poser :
On voit clairement qu'il suffit de poser :  pour le coefficient de diffusion, et : t = iτ pour le temps pour transformer l'équation de Schrödinger en équation de la diffusion. Or, il se trouve que l'intégrale de chemin de Wiener - pour l'équation de la diffusion - est plus facile à définir mathématiquement rigoureusement que celle de Feynman - pour l'équation de Schrödinger. Certains auteurs ont donc proposé de définir l'intégrale de Feynman à partir de la mesure de Wiener en faisant un prolongement analytique pour les temps imaginaires.
pour le coefficient de diffusion, et : t = iτ pour le temps pour transformer l'équation de Schrödinger en équation de la diffusion. Or, il se trouve que l'intégrale de chemin de Wiener - pour l'équation de la diffusion - est plus facile à définir mathématiquement rigoureusement que celle de Feynman - pour l'équation de Schrödinger. Certains auteurs ont donc proposé de définir l'intégrale de Feynman à partir de la mesure de Wiener en faisant un prolongement analytique pour les temps imaginaires. - Cette théorie ne sera publiée qu'en 1945 : John Archibald Wheeler & Richard P. Feynman ; Review of Modern Physics 17 (1945) 157.
- PAM Dirac ; The lagrangian in quantum mechanics, Physikalische Zeitschrift der Sowjetunion 3(1) (1932) 64. Cet article est reproduit dans : Julian Schwinger (ed) ; Selected papers on quantum electrodynamics, Dover Publications, Inc. (1958) (ISBN 0-486-60444-6), ainsi que dans : Laurie M. Brown (Editor) ; Feynman's thesis: a new approach to quantum theory, World Scientific (2005),(ISBN 981-256-380-6).
- Silvian S. Schweber ; Feynman's visualization of space-time processes, Review of Modern Physics 58(2) (1986) 449-508.
- Cette équation avait été écrite par Dirac dans son article de 1933.
- Un gros problème dans cette définition est que cette "mesure formelle" n'est pas une vraie mesure au sens rigoureux du mathématicien. Pour une définition rigoureuse de l'intégrale de Feynman, consulter les traités - souvent très techniques - de la bibliographie.
- L'analogie avec le mouvement Brownien montre que les chemins qui contribuent de façon significative à l'intégrale de Feynman sont continus, mais non différentiables. Plus précisément, ce sont des chemins Lipchitziens d'exposants 1/2.
18:09 Publié dans Intégrale de chemin | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Mouvement brownien
Source : http://fr.wikipedia.org/wiki/Mouvement_brownien
Mouvement brownien
Le mouvement brownien, ou processus de Wiener est une description mathématique du mouvement aléatoire d'une « grosse » particule immergée dans un fluide et qui n'est soumise à aucune autre interaction que des chocs avec les « petites » molécules du fluide environnant. Il en résulte un mouvement très irrégulier de la grosse particule, qui a été décrit pour la première fois en 1827 par le botaniste Robert Brown en observant des mouvements de particules à l'intérieur de grains de pollen de Clarkia pulchella (une espèce de fleur sauvage nord-américaine), puis de diverses autres plantes1.
La description physique la plus élémentaire du phénomène est la suivante :
- entre deux chocs, la grosse particule se déplace en ligne droite avec une vitesse constante ;
- la grosse particule est accélérée lorsqu'elle rencontre une molécule de fluide ou une paroi.
Ce mouvement permet de décrire avec succès le comportement thermodynamique des gaz (théorie cinétique des gaz), ainsi que le phénomène de diffusion. Il est aussi très utilisé dans des modèles de mathématiques financières.
Sommaire[masquer] |
Aspects historiques [modifier]
Brown aperçut dans le fluide situé à l’intérieur des grains de pollen (le mouvement brownien n'a pas été observé sur les grains de pollen eux-mêmes comme souvent mentionné), de très petites particules agitées de mouvements apparemment chaotiques. Ceux-ci ne pouvaient s’expliquer par des écoulements, ni par aucun autre phénomène physique connu. Dans un premier temps, Brown les attribua donc à une activité vitale. L'explication correcte du phénomène viendra plus tard.
Brown n'est pas exactement le premier à avoir fait cette observation. Il signale lui-même que plusieurs auteurs avaient suggéré l’existence d’un tel mouvement (en lien avec les théoriesvitalistes de l'époque). Parmi ceux-ci, certains l’avaient effectivement décrit. On peut mentionner en particulier l’abbé John Turberville Needham (1713-1781), célèbre à son époque pour sa grande maîtrise du microscope.
La réalité des observations de Brown a été discutée tout au long du XXe siècle. Compte tenu de la médiocre qualité de l'optique dont il disposait, certains ont contesté qu'il ait pu voir véritablement le mouvement brownien, qui intéresse des particules de quelques micromètres au plus. Les expériences ont été refaites par l’Anglais Brian Ford au début des années 1990, avec le matériel employé par Brown et dans les conditions les plus semblables possibles 2. Le mouvement a bien été observé dans ces conditions, ce qui valide les observations de Brown.
Rudiments mathématiques [modifier]
Notion de processus stochastique [modifier]
La difficulté de modélisation du mouvement brownien réside dans le fait que ce mouvement est aléatoire et que statistiquement, le déplacement est nul : il n'y a pas de mouvement d'ensemble, contrairement à un vent ou un courant. Plus précisément :
- à un instant donné, la somme vectorielle des vitesses de toutes les particules s'annule (il n'y a pas de mouvement d'ensemble) ;
- si l'on suit une particule donnée au cours du temps, le barycentre de sa trajectoire est son point de départ, elle « virevolte » autour du même point.
Il est difficile dans ces conditions de caractériser le mouvement. La solution fut trouvée par Louis Bachelier, et présentée dans sa thèse soutenue le 29 mars 1900. Il démontra que ce qui caractérise le mouvement, ce n'est pas la moyenne arithmétique des positions <X> mais la moyenne quadratique  : si x(t) est la distance de la particule à sa position de départ à l'instant t, alors :
: si x(t) est la distance de la particule à sa position de départ à l'instant t, alors :

On démontre que le déplacement quadratique moyen est proportionnel au temps3 :
 |
où d est la dimension du mouvement (linéaire, plan, spatial), D le coefficient de diffusion, et t le temps écoulé.
Définition mathématique [modifier]
On peut définir de façon formelle un mouvement brownien: c'est un processus stochastique  dont les accroissements disjoints sont indépendants et tels que Bt + s − Bt suit une loi normale de moyenne nulle et de variance s.
dont les accroissements disjoints sont indépendants et tels que Bt + s − Bt suit une loi normale de moyenne nulle et de variance s.
Cette définition permet de démontrer des propriétés du mouvement brownien, comme par exemple sa continuité (presque sure), le fait que presque surement, la trajectoire n'est différentiable nulle part, et de nombreuses autres propriétés.
On pourrait également définir le mouvement brownien par rapport à sa variation quadratique moyenne. Cette définition, classiquement appelée théorème de Levy, donne la caractérisation suivante: un processus stochastique à trajectoires continues dont la variation quadratique est t est un mouvement brownien. Ceci se traduit mathématiquement par le fait que pour une filtration donnée,  et
et 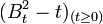 sont des martingales.
sont des martingales.
Formule d'Einstein [modifier]
La formule précédente permet de calculer le coefficient de diffusion d'un couple particule-fluide. En connaissant les caractéristiques de la particule diffusante ou du fluide, on peut en déduire les caractéristiques de l'autre. En connaissant les caractéristiques des deux, on peut évaluer le nombre d'Avogadro à l'aide de la formule d'Einstein (1905) :
où 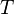 est la température,
est la température, 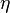 la viscosité du fluide,
la viscosité du fluide,  le rayon de la particule,
le rayon de la particule,  la constante des gaz parfaits et
la constante des gaz parfaits et 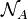 le nombre d'Avogadro : le physicien Jean Perrin évalua ce dernier nombre en 1908 grâce à cette formule.
le nombre d'Avogadro : le physicien Jean Perrin évalua ce dernier nombre en 1908 grâce à cette formule.
Considérations énergétiques [modifier]
La quantité d'énergie mise en œuvre par le mouvement brownien est négligeable à l'échelle macroscopique. On ne peut pas en tirer de l'énergie pour réaliser un mouvement perpétuel de seconde espèce, et violer ainsi le deuxième principe de la thermodynamique.
Toutefois, il a été démontré que certains processus biologiques à l'échelle cellulaire peuvent orienter le mouvement brownien afin d'en soutirer de l'énergie 4.Cette transformation ne contrevient pas au deuxième principe de la thermodynamique tant et aussi longtemps qu'un échange de rayonnement peut maintenir la température du milieu donc la vitesse moyenne des particules. Il faut aussi considérer que la dissipation de ce mouvement brownien sous forme d'énergie utilisable engendre une croissance de l'entropie globale du système (ou de l'univers).
Quelques modélisations dans un espace euclidien [modifier]
Équation de Langevin (1908) [modifier]
Dans l'approche de Langevin5, la grosse particule brownienne de masse m animée à l'instant t d'une vitesse v(t) est soumise à deux forces :
- une force de frottement fluide du type
 , où k est une constante positive ;
, où k est une constante positive ; - un bruit blanc gaussien η(t)
Bruit blanc gaussien :
Un bruit blanc gaussien η(t) est un processus stochastique de moyenne nulle :
et totalement décorrélé dans le temps ; sa fonction de corrélation à deux points vaut en effet :
Dans cette formule, Γ est une constante positive, et δ(t) est la distribution de Dirac.
Dans ces deux formules, la moyenne est prise sur toutes les réalisations possibles du bruit blanc gaussien. On peut formaliser ceci en introduisant une intégrale fonctionnelle, encore appelée intégrale de chemin d'après Feynman, définie pour la mesure gaussienne dite « mesure de Wiener »6. Ainsi, on écrit :
où
est la dérivée de η par rapport au temps t.
Le principe fondamental de la dynamique de Newton conduit à l'équation stochastique de Langevin :
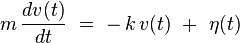 |
Processus d’Ornstein-Uhlenbeck [modifier]
Le processus d'Ornstein-Uhlenbeck est un processus stochastique décrivant (entre autres) la vitesse d'une particule dans un fluide, en dimension 1.
On le définit comme étant la solution Xt de l'équation différentielle stochastique suivante :  , où Bt est un mouvement brownien standard, et avec X0 une variable aléatoire donnée. Le terme dBt traduit les nombreux chocs aléatoires subis par la particule, alors que le terme − Xtdt représente la force de frottement subie par la particule.
, où Bt est un mouvement brownien standard, et avec X0 une variable aléatoire donnée. Le terme dBt traduit les nombreux chocs aléatoires subis par la particule, alors que le terme − Xtdt représente la force de frottement subie par la particule.
La formule d'Itô appliquée au processus etXt nous donne :  , soit, sous forme intégrale :
, soit, sous forme intégrale : 
Par exemple, si X0 vaut presque sûrement x, la loi de Xt est une loi gaussienne de moyenne xe − t et de variance 1 − e − 2t, ce qui converge en loi quand t tend vers l'infini vers la loi gaussienne centrée réduite.
Marches aléatoires [modifier]
On peut aussi utiliser un modèle de marche aléatoire (ou au hasard), où le mouvement se fait par sauts discrets entre positions définies (on a alors des mouvements en ligne droite entre deux positions), comme par exemple dans le cas de la diffusion dans les solides. Si les xi sont les positions successives d'une particule, alors on a après n sauts :
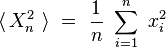 |
Marche aléatoire à une dimension d'espace (Exemple) [modifier]
Considérons la marche aléatoire d'une particule sur l'axe Ox. On suppose que cette particule effectue des sauts de longueur a entre deux positions contigües situées sur le réseau : 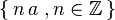 de maille a sur l'axe, chaque saut ayant une durée τ.
de maille a sur l'axe, chaque saut ayant une durée τ.
Il faut encore se donner un nombre p tel que : 0 < p < 1. L'interprétation physique de ce paramètre est la suivante :
- p représente la probabilité que la particule fasse un saut vers la droite à chaque instant ;
- q = 1 - p représente la probabilité que la particule fasse un saut vers la gauche à chaque instant.
Le cas du mouvement brownien correspond à faire l'hypothèse d'isotropie spatiale. Toutes les directions de l'espace physique étant a priori équivalentes, on pose l'équiprobabilité :
 |
La figure ci-dessous montre un exemple typique de résultat : on trace les positions successives x(k) de la particule aux instants k, partant de la condition initiale x(0)=0.
Probabilités de transition conditionnelle [modifier]
On définit la probabilité de transition conditionnelle :
 |
comme étant la probabilité de trouver la particule au site ma à l'instant sτ sachant qu'elle était au site na à l'instant initial 0.
L'hypothèse d'isotropie conduit à écrire la loi d'évolution de cette probabilité de transition conditionnelle :
![P(n|m,s+1) = frac{1}{2} left[ P(n|m+1,s) + P(n|m-1,s) right]](http://upload.wikimedia.org/math/c/1/9/c1962a0570f739a072a91d95db7a7203.png) |
On en déduit la relation suivante :
![P(n|m,s+1) , - , P(n|m,s) = frac{1}{2} left[ P(n|m+1,s) , + , P(n|m-1,s) , - , 2 P(n|m,s) right]](http://upload.wikimedia.org/math/2/d/4/2d4ab377d3fe32f133a429a78461d030.png) |
Convergence vers le mouvement brownien. Équation de Fokker-Planck [modifier]
Prenons la limite continue de l'équation précédente lorsque les paramètres :
On verra à la fin du calcul que la combinaison a2 / 2τ doit en fait rester constante dans cette limite continue.
Il vient, en réintroduisant le paramètre adéquat pour faire un développement limité :
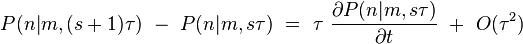 |
D'autre part, on peut écrire :
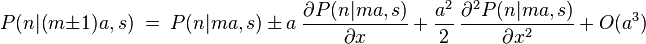 |
de telle sorte que le crochet se réduise à :
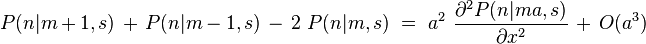 |
On en déduit l'équation de Fokker-Planck :
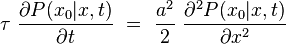 |
qu'on peut réécrire :
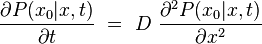 |
en introduisant le coefficient de diffusion :
 |
Solution de l'équation de Fokker-Planck [modifier]
En plus de l'équation de Fokker-Planck, la densité de probabilité de transition conditionnelle P(x0 | x,t) doit vérifier les deux conditions supplémentaires suivantes :
- la normalisation des probabilités totales :
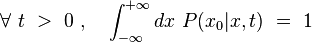 |
- la condition initiale :
 |
où δ(x) est la distribution de Dirac.
La densité de probabilité de transition conditionnelle P(x0 | x,t) est donc essentiellement une fonction de Green de l'équation de Fokker-Planck. On peut démontrer qu'elle s'écrit explicitement :
![P(x_0|x,t) = frac{1}{sqrt{4 pi D t}} exp , left[ - frac{(x-x_0)^2}{4 D t} right]](http://upload.wikimedia.org/math/4/e/f/4ef9103fd364124fb442ece5704cbc62.png) |
Moments de la distribution :
Posons x0 = 0 pour simplifier. La densité de probabilité de transition conditionnelle P0(x,t) = P(0 | x,t) permet le calcul des divers moments :
La fonction P0 étant paire, tous les moments d'ordre impair sont nuls. On peut facilement calculer tous les moments d'ordre pair en posant :
et en écrivant que :
On obtient explicitement :
On retrouve notamment pour le moment d'ordre deux :
Mouvement brownien sur une variété riemannienne [modifier]
On appelle mouvement brownien sur une variété riemannienne V le processus stochastique continu markovien dont le semigroupe de transition à un paramètre est engendré par 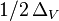 , où ΔV est l'opérateur de Laplace-Beltrami sur la variété V.
, où ΔV est l'opérateur de Laplace-Beltrami sur la variété V.
Annexes [modifier]
Bibliographie [modifier]
- Aspects historiques
- Jean Perrin, Mouvement brownien et réalité moléculaire, Annales de Chimie et de Physique 19 (8e série), (1909), 5-104. Possibilité de consulter et de télécharger le texte complet au format pdf depuis le site Gallica de la BNF.
- Jean Perrin, Les atomes, (1913) Éditions Félix Alcan, Paris, [détail des éditions]
- Albert Einstein, Investigations on the Theory of the Brownian Movement, Dover Publications, Inc. (1985), ISBN 0-486-60304-0. Réédition des articles originaux d'Einstein sur la théorie du mouvement brownien.
- Mouvement brownien dans l'espace euclidien
- Bertrand Duplantier ; Le mouvement brownien, Séminaire Poincaré : Einstein, 1905-2005 (Paris, 8 avril 2005). Texte complet disponible ici.
- Bernard Derrida et Eric Brunet, Le mouvement brownien et le théorème de fluctuation-dissipation, dans : Michèle Leduc & Michel Le Bellac (éditeurs) ; Einstein aujourd'hui, EDP Sciences (Janvier 2005), ISBN 2-86883-768-9.
- Jean-François Le Gall, Intégration, Probabilités et Processus Aléatoires, cours du Magistère de mathématiques de l'ENS (2005). Le dernier chapitre (14) est une introduction au mouvement brownien. Format pdf.
- Jean-François Le Gall, Mouvement brownien et calcul stochastique, cours de DEA donné à l'université Paris 6 (1996 et 1997). Format pdf.
- Jean-François Le Gall, Mouvement brownien, processus de branchement et superprocessus, cours de DEA donné à l'université Paris 6 (1994). Format pdf.
- Paul Lévy, Processus stochastiques et mouvement brownien, Gauthier-Villars (2e édition - 1965). Réédité par Jacques Gabay (1992), ISBN 2-87647-091-8.
- Mark Kac, Random Walk and the Theory of Brownian Motion, American Mathematical Monthly 54(7) (1947), 369-391. Texte au format pdf.
- Mark Kac, Integration in Function Space and some of Its Applications, Lezioni Fermiane, Accademia Nazionale dei Lincei, Scuola Normale Superiore, Pisa, Italy (1980). Texte au format pdf.
- Edward Nelson, Dynamical Theories of Brownian Motion, Princeton University Press (1967). Texte au format pdf.
- Patrick Roger, Probabilités, statistique et processus stochastiques, Pearson Education France (2004).
- Mouvement brownien sur une variété riemannienne
- Elton P. Hsu ; Stochastic Analysis on Manifolds, American Mathematical Society (janvier 2002), ISBN 0-8218-0802-8.
- Elton P. Hsu ; A Brief Introduction to Brownian Motion on a Riemannian Manifold, (2003). Cours donné à Kyoto, disponible au format pdf.
- Mark A. Pinsky ; Isotropic transport process on a Riemannian manifold, Transaction of the American Mathematical Society 218 (1976), 353-360.
- Mark A. Pinsky ; Can You Feel the Shape of a Manifold with Brownian Motion ?, Expositiones Mathematicae 2 (1984), 263-271.
- Nicolas Th. Varopoulos ; Brownian motion and random walks on manifolds, Annales de l'Institut Fourier 34(2) (1984), 243-269. Texte disponible au format pdf.
- Alexander Grigor'yan ; Analytic and geometric background of recurrence and non-explosion of the Brownian motion on Riemannian manifolds, Bulletin of the American Mathematical Society 36(2) (1999), 135-249. Texte en ligne.
Notes et références [modifier]
- Robert Brown ; A brief account of microscopical observations made in the months of June, July and August, 1827, on the particles contained in the pollen of plants; and on the general existence of active molecules in organic and inorganic bodies., Philosophical Magazine 4 (1828), 161-173. Fac-similé disponible au format pdf [archive].
- Brian J. Ford ; Brownian movement in Clarkia pollen: a reprise of the first observations, The Microscope, 40 (4): 235-241, 1992 Reproduction en ligne de l'article [archive]
- Pour un mouvement rectiligne régulier, c'est le déplacement x(t) qui serait proportionnel au temps.
- (PESKIN C. S. (1); ODELL G. M.;OSTER G. F.;Biophysical journal (Biophys. j.)ISSN 0006-3495, CODEN BIOJAU; 1993, vol. 65, no1, pp. 316-324 (42 ref.);Cellular motions and thermal fluctuations : the Brownian ratchet) [archive]
- Paul Langevin, « Sur la théorie du mouvement brownien », Comptes-rendus de l'Académie des Sciences 146 (1908), 530-532. Lire en ligne sur Gallica [archive]
- Cf. e.g. : Mark Kac ; Integration in Function Space and some of Its Applications, Lezioni Fermiane, Accademia Nazionale dei Lincei, Scuola Normale Superiore, Pisa, Italy (1980). Texte au formatpdf [archive].
Voir aussi [modifier]
Liens internes [modifier]
Liens externes [modifier]
18:06 Publié dans Mouvement brownien | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Mathématiques financières
Source : http://fr.wikipedia.org/wiki/Math%C3%A9matiques_financi%C...
Mathématiques financières
Les mathématiques financières sont une branche des mathématiques appliquées ayant pour but la modélisation, la quantification et la compréhension des phénomènes régissant lesmarchés financiers. Elles utilisent principalement des outils issus de l'actualisation, de la théorie des probabilités, du calcul stochastique, des statistiques et du calcul différentiel.
L'actualisation et l'utilisation des probabilités remontent à plusieurs siècles. Toutefois, il est considéré que la théorie moderne des marchés financiers remonte au MEDAF et à l'étude du problème d'évaluation des options dans les années 1950-1970.
Sommaire[masquer] |
Nature aléatoire des marchés [modifier]
L'observation empirique du cours des actifs financiers montre que ceux-ci ne sont pas déterminés de façon certaine par leur histoire. En effet, les nombreuses opérations d'achat ou de vente ne sont pas prévisibles, font souvent intervenir des éléments n'appartenant pas à l'historique et modifient le cours de l'actif. Celui-ci est donc souvent représenté par un processus chaotique. Benoit Mandelbrot a établi par des considérations statistiques qu'un modèle aléatoire ordinaire, par exemple gaussien, ne pouvait convenir. L'aléa reste cependant souvent modélisé par un mouvement brownien1, bien que des modèles plus élaborés (par exemple, le modèle de Bates) tiennent compte de la non-continuité des cours (présence de sauts dus à des chocs boursiers), ou de la non-symétrie des mouvements à la baisse et à la hausse.
Hypothèse de non arbitrage [modifier]
L'une des hypothèses fondamentales des modèles usuels est qu'il n'existe aucune stratégie financière permettant, pour un coût initial nul, d'acquérir une richesse certaine dans une date future. Cette hypothèse est appelée absence d'opportunités d'arbitrage. Elle est justifiée théoriquement par l'unicité des prix caractérisant un marché en concurrence pure et parfaite. Pratiquement, il existe des arbitrages qui disparaissent très rapidement du fait de l'existence d'arbitragistes, acteurs sur les marchés dont le rôle est de détecter ce type d'opportunités et d'en profiter. Ceux-ci créent alors une force qui tend à faire évoluer le prix de l'actif vers son prix de non-arbitrage.
Hypothèse de complétude des marchés [modifier]
Une autre hypothèse, beaucoup plus remise en question, est que tout flux à venir peut être répliqué exactement, et quel que soit l'état du monde, par un portefeuille d'autres actifs bien choisis. Les modèles ne comprenant pas les hypothèses de non arbitrage et de complétude des marchés sont dits modèles de marchés imparfaits.
Probabilité risque-neutre [modifier]
Une des conséquences des hypothèses de non arbitrage et de complétude des marchés est l'existence et l'unicité à équivalence près d'une mesure de probabilité dite probabilité martingale ou « probabilité risque-neutre » telle que le processus des prix actualisés des actifs ayant une source de risque commune est une martingale sous cette probabilité. Cette probabilité peut s'interpréter comme celle qui régirait le processus de prix des sous-jacents de ces actifs si l'espérance du taux de rendement de ceux-ci était le taux d'intérêt sans risque (d'où le terme risque-neutre: aucune prime n'est attribuée à la prise de risque).
Un processus stochastique est une martingale par rapport à un ensemble d'information si son espérance en date t conditionnelle à l'information disponible en date s < t est égale à la valeur du processus en date s, c'est-à-dire qu'un processus A(u) est une martingale si l'espérance conditionnelle de A(t) par rapport a la filtration F(s) est A(s) (i.e : ![mathbb{E}left[A_t|mathcal{F}_sright]=A_s](http://upload.wikimedia.org/math/f/2/3/f23b63c07f72e3fc4b9be0147672843f.png) ).
).
Le problème d'évaluation des produits dérivés [modifier]
L'évaluation (on dit aussi pricing ou, à tort, « valorisation » qui signifie « augmenter la valeur ») des produits dérivés se ramène souvent au calcul du prix aujourd'hui d'un actif dont on ne connaît le prix qu'à une date future. Il se ramène donc au calcul d'une espérance conditionelle. Le modèle Black-Scholes est un exemple de solution analytique au problème d'évaluation des options d'achat (call) ou de vente (put) d'un actif sous jacent. Dans le cas d'un call, le problème s'écrit :
 ,
,
où St est le cours de l'actif, K est le prix d'exercice (ou Strike), r(s) est le taux d'intérêt instantané sans risque à la date s, t est la date « d'aujourd'hui », T est la maturité de l'option, c’est-à-dire la date à laquelle la décision d'exercice peut être prise.
La formule de Black et Scholes est un exemple de solution analytique à ce problème, sous des hypothèses restrictives sur la dynamique du sous-jacent. Voir aussi option.
Une obligation convertible peut s'évaluer comme un lot comprenant une option d'achat et une obligation classique.
Taux d'intérêt et dérivés de taux d'intérêt [modifier]
Les modèles simples supposent que le taux d'intérêt, c'est-à-dire le loyer de l'argent est constant. Cette hypothèse est centrale, car sous l'hypothèse d'absence d'opportunités d'arbitrage, un portefeuille non risqué rapporte ce taux d'intérêt. Or cette approximation n'est évidemment plus admissible dès que le cours de l'actif est essentiellement lié au niveau du taux d'intérêt (par exemple, le cours des obligations à taux variable, des swaptions...) ne peuvent être expliqués par un modèle à taux d'intérêt fixe.
On modélisera donc le taux d'intérêt par un processus aléatoire, auquel on demandera:
- d'être au mieux compatible avec l'ensemble des courbes des taux observables
- d'avoir des propriétés réalistes, comme de ne pas autoriser des taux négatifs, de rendre compte de l'effet de retour à la moyenne (mean reversion), ...
Les travaux de Vasicek ont permis d'exhiber un processus, dérivé du processus d'Ornstein-Uhlenbeck, cohérent, dont le loyer de l'argent ne dépend que du taux instantané (overnight) mais autorisant des taux négatifs. Des modèles plus élaborés (processus CIR, ...), faisant partie de la famille dite des modèles affines de taux court, ont permis de remédier à cette lacune, mais ne satisfont pas vraiment les spécialistes du fait de la difficulté d'interprétation financière des paramètres de diffusion et de leur incapacité à épouser exactement la courbe des taux zéro-coupon spot. Heath, Jarrow et Morton ont proposé une famille de modèles cohérents, dont la dynamique ne dépend que d'une fonction facilement interprétable (la volatilité du taux forward), et capables de rendre compte de n'importe quelle courbe de taux donnée. Des modèles dits de marché (BGM ou Libor Forward) connaissent un certain succès dans l'explication du prix des caps et des floors.
Toutefois, à la différence du marché des dérivés d'options où le modèle de Black et Scholes, plus ou moins arrangé pour le débarrasser de ses imperfections (volatilité constante, taux d'intérêt constant, ...) occupe une place prépondérante, aucun modèle de taux ne fait l'unanimité des spécialistes. Les taux d'intérêts sont en effet soumis à des pressions exogènes très importantes, qui rendent caduques très rapidement toutes les calibrations possibles. À l'heure actuelle, les publications et les recherches à ce sujet sont abondantes.
Dérivés de crédit [modifier]
Les dérivés de crédit sont des produits dérivés dont les flux dépendent d'événements de crédits intervenant sur un sous-jacent. Ces produits servent à prévenir la dégradation de la qualité de signature d'une contrepartie, c'est-à-dire son aptitude à assumer ses obligations de paiement ("CDS"'ou Credit default swap, "CLN" ou "Credit linked Notes"). Ils peuvent servir également à améliorer la qualité de signature d'une partie d'un panier d'actifs ("CDOs" ou "Collateralized debt obligations" ).
Dérivés climatiques [modifier]
Les dérivés climatiques sont des produits financiers dont les flux dépendent d'un événement totalement indépendant de la structure des marchés financiers, lié à un événement climatique. Par exemple, un produit peut assurer à son détenteur une rente dans le cas où la température relevée en un lieu fixé par contrat dépasse ou reste en dessous d'une température de référence considérée comme normale. Ces produits — récents — ont pour vocation de permettre à des entreprises touristiques ou agricoles de se prémunir contre des aléas climatiques. Ils s'apparentent donc à des produits d'assurance, négociés directement sur les marchés financiers.
Notes et références [modifier]
Voir aussi [modifier]
Articles connexes [modifier]
Liens externes [modifier]
- (fr) Cours d'introduction aux mathématiques financières : Calculs Stochastiques pour la finance
Bibliographie [modifier]
- Pierre Bonneau, Mathématiques financières, Coll. Economie, Paris, Dunod, 1980.
- Jean-Marcel Dalbarade, Mathématiques des marchés financiers, Ed. Eska, 2005, ISBN 2-7472-0846-X.
- Benoît Mandelbrot & Richard Hudson, Une approche fractale des marchés, éditions Odile Jacob, 2005
17:33 Publié dans Mathématiques financières | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Nombre superréel
Source : http://fr.wikipedia.org/wiki/Nombre_superr%C3%A9el
Nombre superréel
En mathématiques, les nombres superréels comprennent une catégorie plus inclusive que les nombres hyperréels.
Supposons que X soit un espace de Tychonoff, aussi appelé un espace 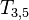 , et C(X) une algèbre des fonctions continues à valeurs réelles sur X. Supposons que P soit un idéal premierdans C(X). Alors, l'anneau quotient A = C(X)/P est par définition un domaine intégral qui est une algèbre réelle et qui peut être vue comme totalement ordonnée. Le corps quotient F de A est un corps superréel si F contient strictement les nombres réels
, et C(X) une algèbre des fonctions continues à valeurs réelles sur X. Supposons que P soit un idéal premierdans C(X). Alors, l'anneau quotient A = C(X)/P est par définition un domaine intégral qui est une algèbre réelle et qui peut être vue comme totalement ordonnée. Le corps quotient F de A est un corps superréel si F contient strictement les nombres réels  , c’est-à-dire que F n'est pas isomorphe à l'ordre de
, c’est-à-dire que F n'est pas isomorphe à l'ordre de  , bien qu'ils peuvent être isomorphes en tant que corps.
, bien qu'ils peuvent être isomorphes en tant que corps.
Si l'idéal premier P est un idéal maximal, alors F est un corps de nombres hyperréels.
La terminologie est due à Dales et Woodin.
Références [modifier]
- H. Garth Dales and W. Hugh Woodin : Super-Real Fields, Clarendon Press, 1996.
- L. Gillman and M. Jerison : Rings of Continuous Functions, Van Nostrand, 1960.
17:31 Publié dans Nombre superréel | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Paul Erdõs' papers
1929:
1932:
1934:
1935:
1936:
1937:
1938:
1939:
1940:
1941:
1942:
1943:
1944:
1945:
1946:
1947:
1948:
1949:
1950:
1951:
1952:
1953:
1954:
1955:
1956:
1957:
1958:
1959:
1960:
*** Remark: Prof. Schinzel has pointed out that this paper contained some error and that was rectified by Kevin Ford. The corrected version will also be posted soon. (It can be found in Schinzel' ``Selecta'')
1961:
1962:
1963:
1964:
1965:
1966:
1967:
1968:
1969:
1970:
1971:
1972:
1973:
1974:
1975:
1976:
1977:
1978:
1979:
1980:
1981:
1982:
1983:
1984:
1985:
1986:
1987:
1988:
1989:
1990:
14:05 Publié dans Paul Erdõs' papers | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Frank Nelson Cole Prize in Number Theory
This prize (and the Frank Nelson Cole Prize in Algebra ) was founded in honor of Professor Frank Nelson Cole on the occasion of his retirement as Secretary of the American Mathematical Society after twenty-five years of service and as Editor-in-Chief of the Bulletin for twenty-one years. The original fund was donated by Professor Cole from moneys presented to him on his retirement, and was augmented by contributions from members of the Society. The fund was later doubled by his son, Charles A. Cole. The prize is for a notable paper in number theory published during the preceding six years. To be eligible, the author should be a member of the American Mathematical Society or the paper should have been published in a recognized North American journal. Currently, the US$5,000 prize is awarded every three years. Next award: January 2011. Sixteenth award, 2008: To Manjul Bhargava for his revolutionary work on higher composition laws. Fifteenth award, 2005 : To Peter Sarnak for his fundamental contributions to number theory and in particular his book Random Matrices, Frobenius Eigenvalues and Monodromy, written jointly with his Princeton colleague Nicholas Katz. Fourteenth award, 2002 : To Henryk Iwaniec for his fundamental contributions to analytic number theory, and to Richard Taylor for several outstanding advances in algebraic number theory. Thirteenth, 1997 : To Andrew J. Wiles for his work on the Shimura-Taniyama conjecture and Fermat's Last Theorem, published in Modular elliptic curves and Fermat's Last Theorem, Ann. of Math. 141 (1995), 443-551. Twelfth award, 1992: To Karl Rubin for his work in the area of elliptic curves and Iwasawa Theory with particular reference to his papers Tate-Shafarevich groups and L-functions of elliptic curves with complex multiplicationand The "main conjectures" of Iwasawa theory for imaginary quadratic fields and to Paul Vojta for his work on Diophantine problems with particular reference to his paper Siegel's theorem in the compact case. Eleventh award, 1987: To Dorian M. Goldfeld for his paper, Gauss's class number problem for imaginary quadratic fields, Bulletin of the American Mathematical Society, volume 13, (1985), pp. 23-37; and to Benedict H. Gross and Don B. Zagier for their paper, Heegner points and derivatives of L-Series, Inventiones Mathematicae, volume 84 (1986), pp. 225-320. Tenth award, 1982: To Robert P. Langlands for pioneering work on automorphic forms, Eisenstein series and product formulas, particularly for his paper Base change for GL(2), Annals of Mathematics Studies, volume 96, Princeton University Press, 1980; and to Barry Mazur for outstanding work on elliptic curves and Abelian varieties, especially on rational points of finite order, and his paper Modular curves and the Eisenstein ideal, Publications Mathematiques de l'Institut des Hautes Etudes Scientifiques, volume 47 (1977), pp. 33-186. Ninth award, 1977: To Goro Shimura for his two papers, Class fields over real quadratic fields and Heche operators, Annals of Mathematics, Series 2, volume 95 (1972), pp. 130-190; and On modular forms of half integral weight, Annals of Mathematics, Series 2, volume 97 (1973), pp. 440-481. Eighth award, 1972: To Wolfgang M. Schmidt for the following papers: On simultaneous approximation of two algebraic numbers by rationals, Acta Mathematica (Uppsala), volume 119 (1967), pp. 27-50; T-numbers do exist, Symposia Mathematica, volume IV, Academic Press, 1970, pp. 1-26; Simultaneous approximation to algebraic numbers by rationals, Acta Mathematica (Uppsala), volume 125 (1970), pp. 189-201; On Mahler's T-numbers, Proceedings of Symposia in Pure Mathematics, volume 20, American Mathematical Society, 1971, pp. 275-286. Seventh award, 1967: To James B. Ax and Simon B. Kochen for a series of three joint papers, Diophantine problems over local fields. I, II, III, American Journal of Mathematics, volume 87 (1965), pp. 605-630, 631-648, and Annals of Mathematics, Series 2, volume 83 (1966), pp. 437-456. Sixth award, 1962: To Kenkichi Iwasawa for his paper, Gamma extensions of number fields, Bulletin of the American Mathematical Society, volume 65 (1959), pp. 183-226; and to Bernard M. Dwork for his paper, On the rationality of the zeta function of an algebraic variety, American Journal of Mathematics, volume 82 (1960), pp. 631-648. Fifth award, 1956: To John T. Tate for his paper, The higher dimensional cohomology groups of class field theory, Annals of Mathematics, Series 2, volume 56 (1952), pp. 294-297. Fourth award, 1951: To Paul Erdös for his many papers in the theory of numbers, and in particular for his paper,On a new method in elementary number theory which leads to an elementary proof of the prime number theorem, Proceedings of the National Academy of Sciences, volume 35 (1949), pp. 374-385. Third award, 1946: To H. B. Mann for his paper, A proof of the fundamental theorem on the density of sums of sets of positive integers, Annals of Mathematics, Series 2, volume 43 (1942), pp. 523-527. Second award, 1941: To Claude Chevalley for his paper, La théorie du corps de classes, Annals of Mathematics, Series 2, volume 41 (1940), pp. 394-418. First award, 1931: To H. S. Vandiver for his several papers on Fermat's last theorem published in the Transactions of the American Mathematical Society and in the Annals of Mathematics during the preceding five years, with special reference to a paper entitled On Fermat's last theorem, Transactions of the American Mathematical Society, volume 31 (1929), pp. 613-642. Source : http://www.ams.org/profession/prizes-awards/ams-prizes/co...Frank Nelson Cole Prize in Number Theory
14:02 Publié dans Frank Nelson Cole Prize in Number Theory | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Prix Frank Nelson Cole
Le prix Frank Nelson Cole, ou plus simplement prix Cole, fait partie des récompenses décernées par l'American Mathematical Society (AMS). Le prix Cole est en réalité double : un des prix couronne une contribution remarquable en algèbre, tandis qu'un second prix distingue une contribution remarquable en théorie des nombres. Le prix est ainsi nommé en l'honneur du mathématicien américain Frank Nelson Cole (1861–1926), par ailleurs membre de l'AMS pendant plus de vingt-cinq ans. Bien que l'éligibilité au prix ne soit pas strictement fondée sur la nationalité, il est toutefois nécessaire que les futurs lauréats soient membres de l'AMS et publient leurs travaux de recherche mathématiques dans les plus importantes revues scientifiques américaines. Le premier prix Cole en algèbre a été remis en 1928 à Leonard Eugene Dickson pour son livre Algebren und ihre Zahlentheorie (Orell Füssli, Zürich et Leipzig, 1927), tandis que le premier prix relatif à des recherches sur la théorie des nombres a été remis en 1931 à Harry Vandiver pour un article traitant du dernier théorème de Fermat.Prix Frank Nelson Cole
Lauréats de la catégorie « algèbre » [modifier]
Lauréats de la catégorie « théorie des nombres » [modifier]
Liens externes [modifier]
14:01 Publié dans Prix Frank Nelson Cole | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
The Erdös Number Project
|
|
The Erdös Number Project |
| This is the website for the Erdös Number Project, which studies research collaboration among mathematicians. This site is maintained by Jerry Grossman at Oakland University, with the collaboration of Patrick Ion (ion@ams.org) at Mathematical Reviews and Rodrigo De Castro(rdcastro@matematicas.unal.edu.co) at the Universidad Nacional de Colombia, Bogota. Please address all comments, additions, and corrections to Jerry at grossman@oakland.edu. Erdös numbers have been a part of the folklore of mathematiciansthroughout the world for many years. For an introduction to our project, a description of what Erdös numbers are, what they can be used for, who cares, and so on, choose the “What’s It All About?” link below. To find out who Paul Erdös is, look at this biography at the MacTutor History of Mathematics Archive, or choose the “Information about Paul Erdös” link below. Some useful information can also be found in this Wikipedia article, which may or may not be totally accurate. |
WHAT’S INSIDE: SPECIAL NOTES: We have finished updating the lists of Erdös coauthors. There are about 1100 new people with Erdös number 2, compared to three years ago.
NOTES: The data shown on this site are based primarily on all items appearing in MatchSciNet through mid-2010. The next update will probably occur around 2015. If you have any additions or corrections to our lists, PLEASE send them. New coauthorships that appear in MathSciNet will be included at the next update, but if you know of other new coauthors, please contact Jerry Grossman.
If you are an Erdös coauthor, I would really appreciate your sending me a complete list of your coauthors (with full names).
One thing we’d really like to do is give more accurate information on some of the old coauthors’ status — whether they are still alive. Look at the list of coauthors arranged by date of first paper with Erdös to see, in chronological order, those we don’t know about (if there is no asterisk, then we assume the person is still alive, except as noted in the addenda file). If anyone has any information that one or more of these are deceased (or, as Paul Erdös would say, “has left”), please let us know. (We know some are alive; please report only those that have passed on, and report only Erdös coauthors, since there is no way we could extend this convention to those with Erdös number 2.)
You are visitor number since we started keeping track on July 3, 1996, using
 .
.
URL = http://www.oakland.edu/enp
This page was last updated on October 20, 2010 (but subpages may have been updated more recently).
However, the lists of coauthors and the various other statistics on this site are updated about once every three years. The current version was posted on October 20, 2010 and includes all information listed in MathSciNet through mid-2010. The next update will probably occur around 2015.Source : http://www.oakland.edu/enp/
14:00 Publié dans The Erdös Number Project | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Paul Erdős
Paul Erdős (Erdős Pál /ˈɛrdøːʃ paːl/ en hongrois), né le 26 mars 1913 à Budapest (Hongrie) et décédé le 20 septembre 1996 à Varsovie(Pologne), est un mathématicien hongrois célèbre pour son excentricité, le nombre de ses publications scientifiques (environ 1500) et de ses collaborateurs. Son œuvre prolifique a donné naissance au concept de nombre d'Erdős représentant le degré de séparation entre le mathématicien hongrois, la centaine de collaborateurs directs, coauteurs d'articles, de nombre 1, indirects, de nombre 2, etc.Paul Erdős
Sommaire[masquer] |
La vie de Paul Erdős a été tout entière consacrée à ses travaux de recherche. Vivant dans un grand dénuement (il n’avait pas de femme, pas d’emploi, pas même une maison pour l’attacher quelque part ; il vivait avec une vieille valise et un sac plastique orange de supermarché ; la seule possession qui comptait pour lui était son petit calepin1), il est un chercheur très prolifique, toutes disciplines confondues, avec plus de 1 500 articles de recherche publiés. En particulier, nombre de ces articles visait à étudier ses domaines de prédilection (théorie des graphes,théorie des nombres, combinatoire) sous des angles différents, et à améliorer sans cesse l'élégance des démonstrations. Parmi ses contributions, le développement de la théorie de Ramsey et de l'application de la méthode probabiliste en particulier se distinguent. Âgé d'un an lorsque survient la Première Guerre mondiale, Erdős voit son père capturé par l'armée russe. Sa mère, redoutant de ne pouvoir veiller sur ses enfants hors du foyer, préfère dès lors engager un précepteur. Toutefois, elle-même étant professeur de mathématiques, elle lui transmet le goût de cette discipline, ce qui amènera le jeune Erdős à s'intéresser très tôt à des problèmes mathématiques. Ayant obtenu sa thèse de mathématiques en Hongrie en 1934, il est contraint par ses origines juives à s'exiler dans un premier temps à l'université de Manchester puis aux États-Unis. Il travaille à l'université de Princeton, puis est ensuite invité par Ulam à l'université James Madison. C'est à cette époque qu'il parvient, avec le mathématicien Atle Selberg, à établir une preuve élégante du théorème des nombres premiers. Mais Selberg publie seul le document, et obtient la médaille Fields l'année suivante2. Installé à l'université Purdue en Indiana, Erdős est invité à rejoindre le programme de développement de la bombe atomique américaine en 1943, mais sa candeur le fait échouer lors des entretiens. Ce n'est qu'en 1948 qu'il peut retourner en Hongrie pour retrouver sa famille revenue de déportation. Quelques années plus tard, en 1950, le maccarthysme bat son plein aux États-Unis et il est accusé de communisme. En conséquence, il n'est plus autorisé à circuler aux États-Unis. Il est fait membre étranger de la Royal Society en 1989. Installé durant les années 1960 en Israël, Erdős ne peut à nouveau fouler le sol américain qu'en 1963. Il entreprend dès lors une carrière de chercheur et professeur itinérant, et finit par décéder dans sa chambre d'hôtel à l'âge de 83 ans. Paul Hoffman, Paul Erdös : 1913-1996 : l'homme qui n'aimait que les nombres, Éditions Belin, 2000 (ISBN 2-7011-2539-1)Biographie [modifier]
Anecdotes [modifier]
Notes et références [modifier]
Voir aussi [modifier]
Bibliographie [modifier]
Articles connexes [modifier]
Liens externes [modifier]
13:59 Publié dans Paul Erdős | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook








































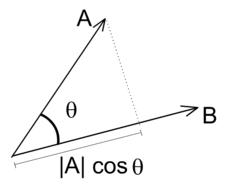
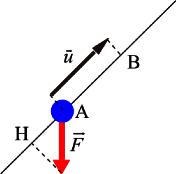
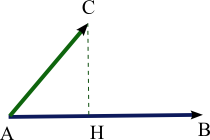

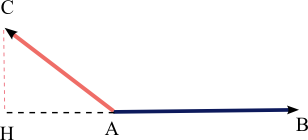
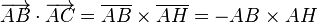






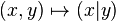





![bigoplus_{i=1}^n ker left[ P_i(f) right] = ker left[ left( prod_{i=1}^n P_i right)(f) right].](http://upload.wikimedia.org/math/b/a/4/ba40b11861f53424230392d973cac669.png)


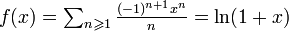 . Comme
. Comme  converge (d'après le
converge (d'après le 














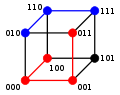

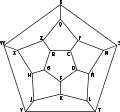







![langle , eta(t_1) eta(t_2) , rangle = int left[ , mathcal{D}eta(t) , right] eta(t_1) eta(t_2) textrm{e}^{ - frac{1}{2 Gamma} int_{t_1}^{t_2}dot{eta}^2(tau) d tau}](http://upload.wikimedia.org/math/e/8/5/e85cc21a084d55d7c5a30ab23c0b6313.png)
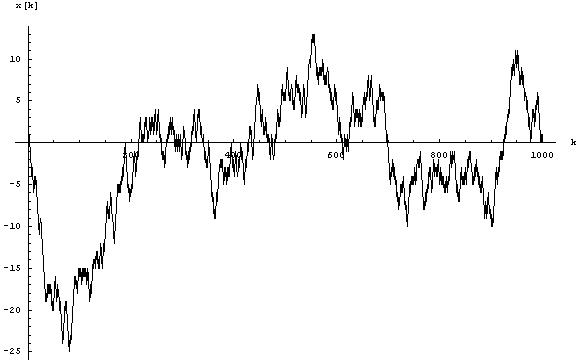

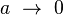
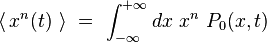

![langle , x^n(t) rangle = sqrt{frac{alpha}{pi}} int_{-infty}^{+infty} dx x^{2n} mathrm{e}^{- alpha x^2} = (-1)^n sqrt{frac{alpha}{pi}} frac{d^n~}{d alpha^n} left[ , int_{-infty}^{+infty} dx mathrm{e}^{- alpha x^2} , right]](http://upload.wikimedia.org/math/0/5/9/05965e5ff539bd952bf459b51919f95e.png)
![langle , x^n(t) rangle = (-1)^n sqrt{frac{alpha}{pi}} frac{d^n~}{d alpha^n} left[ , sqrt{frac{pi}{alpha}} , right] = (-1)^n sqrt{alpha} frac{d^n~}{d alpha^n} left[ , frac{1}{sqrt{alpha}} , right]](http://upload.wikimedia.org/math/c/7/e/c7e7f082a6be250398c5c942fac6c510.png)
![langle , x^2(t) rangle = - , sqrt{alpha} , frac{d~}{d alpha} , left[ , frac{1}{sqrt{alpha}} , right] = (- , sqrt{alpha}) , times , left( - , frac{1}{2alpha^{3/2}} right) = frac{1}{2 alpha} = 2 D t](http://upload.wikimedia.org/math/5/f/7/5f78ede57ea50823f63bdba87b681b37.png)

