21/11/2010
Lemme des noyaux
Source : http://fr.wikipedia.org/wiki/Lemme_des_noyaux
Lemme des noyaux
En algèbre linéaire, le lemme des noyaux est un résultat sur la réduction des endomorphismes. Dans un espace vectoriel E sur un corps K, si un opérateur u de E est annulé par un polynôme P(X) à coefficients dans K, alors ce lemme prévoit une décomposition de E comme somme directe de sous-espaces vectoriels stables par u. Ces derniers se définissent comme noyaux de polynômes en u, les projecteurs associés étant eux-mêmes des polynômes en u.
La démonstration traduit l'identité de Bezout portant sur les polynômes à des sous-espaces vectoriels. Résultat fondamental, le lemme des noyaux conduit à la décomposition de Dunford puis à la décomposition de Jordan. Plus modestement, le lemme des noyaux montre qu'un opérateur u est diagonalisable s'il est annulé par un polynôme à racines simples.
Sommaire[masquer] |
Enoncé [modifier]
Lemme des noyaux — Soit E un espace vectoriel sur un corps K et soit f un endomorphisme de E. Si ![P_1,ldots,P_n in K[X]](http://upload.wikimedia.org/math/1/9/2/192527f1c86d44ab5e67ee58757eb75c.png) (avec
(avec  ) sont premiers entre eux deux à deux, alors les sous-espaces vectoriels Vi = ker(Pi(f)) (où
) sont premiers entre eux deux à deux, alors les sous-espaces vectoriels Vi = ker(Pi(f)) (où 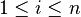 ) sont en somme directe et
) sont en somme directe et
De plus, la projection sur Vi parallèlement à  est Qi(f) pour un polynôme Qi.
est Qi(f) pour un polynôme Qi.
Démonstration [modifier]
Réduction au cas n = 2 [modifier]
On montre d'abord par récurrence sur n que si le lemme est vrai pour n = 2, il est vrai pour tout n. Il n'y a rien à montrer pour le cas n = 1 (la projection mentionnée est l'identité, qui estQ(f) avec Q le polynôme constant 1). Si n > 2 on pose  alors
alors  et Q est premier avec Pn (car d'après le théorème de Bachet-Bézoutchacun des facteurs Pi de Q est inversible modulo Pn, et leur produit Q l'est donc aussi). Alors le cas n = 2 dit que
et Q est premier avec Pn (car d'après le théorème de Bachet-Bézoutchacun des facteurs Pi de Q est inversible modulo Pn, et leur produit Q l'est donc aussi). Alors le cas n = 2 dit que 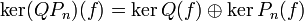 , avec les projections correspondantes données par des polynômes en l'endomorphisme f; l'hypothèse de récurrence permet de décomposer
, avec les projections correspondantes données par des polynômes en l'endomorphisme f; l'hypothèse de récurrence permet de décomposer 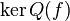 commer somme directe des
commer somme directe des 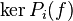 pour
pour 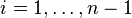 , et les projections de
, et les projections de 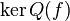 sur ces facteurs se composent avec celle sur
sur ces facteurs se composent avec celle sur 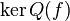 pour donner des projections requises
pour donner des projections requises  .
.
Le cas n = 2 [modifier]
On voit sans problème que l'espace V = ker(P1P2)(f) contient les espaces 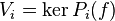 pour i = 1,2, et donc aussi leur somme; il s'agit de montrer que la somme V1 + V2 est directe et égale à V tout entier (avec des projections polynômes en
pour i = 1,2, et donc aussi leur somme; il s'agit de montrer que la somme V1 + V2 est directe et égale à V tout entier (avec des projections polynômes en  ). D'après le théorème de Bachet-Bézout, il existe
). D'après le théorème de Bachet-Bézout, il existe ![Q_1,Q_2 in K[X]](http://upload.wikimedia.org/math/2/1/3/213ec71c5566f54610e89067d66f8792.png) tel que P1Q1 + P2Q2 = 1, et par conséquent (P1Q1 + P2Q2)(f) = idE (l'application identité de E). Notons
tel que P1Q1 + P2Q2 = 1, et par conséquent (P1Q1 + P2Q2)(f) = idE (l'application identité de E). Notons
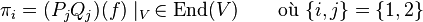 ,
,
donc  et
et  .
.
Pour voir que la somme V1 + V2 est directe, on considère  . On a
. On a  , et la somme est directe.
, et la somme est directe.
Pour voir que V1 + V2 = V on considère 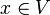 . On a
. On a 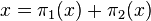 avec
avec  car
car
 ,
,
et on a 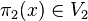 pour des raisons similaires. On conclut que
pour des raisons similaires. On conclut que  et donc V = V1 + V2.
et donc V = V1 + V2.
Finalement, les projections de  sur les facteurs sont
sur les facteurs sont  et
et 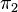 : on a déjà vu que l'image de
: on a déjà vu que l'image de 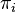 est contenue dans Vi, et qu'il s'annule sur l'autre facteur, donc il reste à voir que
est contenue dans Vi, et qu'il s'annule sur l'autre facteur, donc il reste à voir que 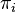 est l'identité sur Vi. Pour
est l'identité sur Vi. Pour  on a
on a  , donc c'est vérifié.
, donc c'est vérifié.
Applications [modifier]
Le lemme des noyaux sert pour la réduction des endomorphismes. Par exemple :
Réduction à une forme diagonale par blocs — Soit E un espace vectoriel de dimension finie sur un corps K et soit f un endomorphisme de E. Soit ![Pin K[X]](http://upload.wikimedia.org/math/4/f/a/4facb36da11821b818abd66b424a6a76.png) unpolynôme annulateur de f (par exemple son polynôme minimal, ou son polynôme caractéristique d'après le théorème de Cayley-Hamilton) et
unpolynôme annulateur de f (par exemple son polynôme minimal, ou son polynôme caractéristique d'après le théorème de Cayley-Hamilton) et  la factorisation de Pavec les polynômes Pi irréductibles et distincts. Alors il existe une base
la factorisation de Pavec les polynômes Pi irréductibles et distincts. Alors il existe une base  de E et des matrices
de E et des matrices  telles que
telles que
où  (en fait la partie de
(en fait la partie de  correspondant au bloc Ai est une base de
correspondant au bloc Ai est une base de 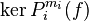 ), et
), et 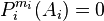 .
.
09:56 Publié dans Lemme des noyaux | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook








































![bigoplus_{i=1}^n ker left[ P_i(f) right] = ker left[ left( prod_{i=1}^n P_i right)(f) right].](http://upload.wikimedia.org/math/b/a/4/ba40b11861f53424230392d973cac669.png)


Les commentaires sont fermés.