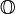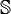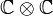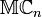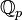11/12/2010
L'indicatrice de Carmichael
Définition Soit Lemme [Théorème de Carmichael] On a Pour cela, écrivons PPCM La deuxième affirmation est claire. LemmeL'indicatrice de Carmichael
![]() un entier
un entier ![]() . On définit
. On définit ![]() comme le maximum des ordres
comme le maximum des ordres![]() des éléments du groupe
des éléments du groupe ![]() . On appelle indicatrice de Carmichaell'expression
. On appelle indicatrice de Carmichaell'expression ![]() .
.![]() est premier, on a
est premier, on a ![]() car le groupe
car le groupe ![]() est cyclique d'ordre
est cyclique d'ordre ![]() .
.![]() pour tout entier
pour tout entier ![]() premier à
premier à ![]() . Réciproquement, si
. Réciproquement, si ![]() vérifie
vérifie ![]() pour tout entier
pour tout entier ![]() premier à
premier à ![]() , alors
, alors ![]() est multiple de
est multiple de ![]() .
.
Démonstration. Soit ![]() un élément d'ordre
un élément d'ordre ![]() et
et ![]() un élément d'ordre
un élément d'ordre ![]() . Nous allons montrer que
. Nous allons montrer que ![]() contient un élément dont l'ordre est PPCM
contient un élément dont l'ordre est PPCM ![]() . Il s'ensuivra que
. Il s'ensuivra que ![]() PPCM
PPCM ![]() et donc que
et donc que ![]() divise
divise ![]() .
.![]() , où
, où ![]() divise
divise ![]() ,
, ![]() divise
divise ![]() et
et ![]() ,
, ![]() sont premiers entre eux. Alors
sont premiers entre eux. Alors ![]() est d'ordre
est d'ordre ![]() ,
, ![]() est d'ordre
est d'ordre ![]() et donc leur produit est d'ordre
et donc leur produit est d'ordre ![]() PPCM
PPCM ![]() d'après le lemme
d'après le lemme ![[*]](http://www.les-mathematiques.net/images/crossref.png)
![]() .
.![]()
![]() ,
, ![]() et
et ![]() pour tout
pour tout ![]() .
.![]() est un nombre premier impair
est un nombre premier impair![]() , on a
, on a ![]() .
.![]() où
où ![]() et
et ![]() sont premiers entre eux, on a
sont premiers entre eux, on a ![]() PPCM
PPCM ![]() .
.![]() PPCM
PPCM ![]()
![]() divise
divise ![]() , nous avons
, nous avons
![]()
![]() premier à 561 (comme dans le petit théorème de Fermat). Un nombre
premier à 561 (comme dans le petit théorème de Fermat). Un nombre ![]() tel que
tel que ![]() pour tout entier
pour tout entier ![]() premier à
premier à ![]() s'appelle un nombre de Carmichael. Voici le tableau des premiers
s'appelle un nombre de Carmichael. Voici le tableau des premiers ![]() nombres de Carmichael non premiers.
nombres de Carmichael non premiers.
| décomposition | |||
Démonstration. Les parties a) et b) résultent du théorème ![[*]](http://www.les-mathematiques.net/images/crossref.png)
![]() . Pour c), nous avons l'isomorphisme de groupes
. Pour c), nous avons l'isomorphisme de groupes![]()
![]() est clairement égal au PPCM des ordres des deux composantes. Ceci implique que l'ordre maximal d'un couple sera le PPCM des ordres maximaux atteints dans chaque composante.
est clairement égal au PPCM des ordres des deux composantes. Ceci implique que l'ordre maximal d'un couple sera le PPCM des ordres maximaux atteints dans chaque composante. ![]()
![]()
![]()
![]()
![]()
suivant: Résidus quadratiques monter: bad précédent: Structure du groupe des Table des matièresBernhard_Keller
Source : http://www.les-mathematiques.net/b/a/d/node21.php3
11:55 Publié dans L'indicatrice de Carmichael | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Interprétation géométrique
D'après les théorèmes cités ci-dessus, deux cas seulement sont possibles Interprétation géométrique
Nous considérons le plan ![]() et nous appelons points entiers les points
et nous appelons points entiers les points ![]() à coordonnées entières
à coordonnées entières ![]() . Soient
. Soient ![]() tels que
tels que![]() . Notons
. Notons ![]() la droite dans
la droite dans ![]() formée des points
formée des points ![]() tels que
tels que ![]() . Alors l'ensemble des solutions
. Alors l'ensemble des solutions ![]() de l'équation de Bézout
de l'équation de Bézout ![]() s'identifie à l'ensemble des points entiers de la droite
s'identifie à l'ensemble des points entiers de la droite ![]() .
.![includegraphics[width=12.0cm height=8.0cm]{droites.eps}](http://www.les-mathematiques.net/b/a/d/img629.png)
Dans le deuxième cas, l'ensemble des points entiers est obtenu en rajoutant un multiple entier d'un vecteur ![]() ne contient aucun point entier
ne contient aucun point entier![]() contient une infinité de points entiers.
contient une infinité de points entiers.![]() à un point entier
à un point entier ![]() fixé de la droite. Le vecteur
fixé de la droite. Le vecteur ![]() peut être identifié avec un point entier de distance minimale à l'origine sur la droite
peut être identifié avec un point entier de distance minimale à l'origine sur la droite ![]() . Notons que cette droite contient exactement deux tels points (à savoir
. Notons que cette droite contient exactement deux tels points (à savoir ![]() et
et ![]() ).
).
Bernhard_Keller
Source : http://www.les-mathematiques.net/b/a/d/node9.php3
11:54 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Éléments d'analyse
Les Éléments d'analyse sont une série de 9 volumes écrits par le mathématicien français Jean Dieudonné. À l'origine, seul le premier volume, Foundations of Modern Analysis, publié en 1960, était prévu. J. Dieudonné l'écrit suite à une série de cours dispensés à l'université du Michigan. Dans ce premier volume, l'auteur souhaite présenter les connaissances minimales en analyse que doit acquérir un étudiant en mathématiques ou en physique. Plus tard, ce premier tome sera traduit en français sous le titre Fondements de l'Analyse moderne. Dieudonné y ajoutera 8 volumes supplémentaires écrits directement en français.Éléments d'analyse
Tome I1 I - Éléments de la théorie des ensembles. II - Nombres réels. III - Espaces métriques. IV - Propriétés particulières à la droite réelle. V - Espaces normés. VII - Espaces de fonctions continues. VIII - Calcul différentiel. Appendice au Chapitre IX. - Application des fonctions analytiques à la topologie plane. X - Théorèmes d'existence. Annexe - Éléments d'algèbre linéaire. BIBLIOGRAPHIE Tome II2 XII - Compléments de topologie et d'algèbre topologique. XIII - Intégration. XIV - Intégration dans les groupes localement compacts. XV - Algèbres normées et théorie spectrale. Tome III3 XVI -Variétés différentielles. I. Distributions et opérateurs différentiels. Annexe -Compléments d'algèbre (suite). Tome IV4 XVIII - Calcul différentiel sur une variété différentielle. XIX - Groupe de Lie et algèbres de Lie. XXI -Groupes de Lie compacts et groupes de Lie semi-simples.5 XXII - Analyse harmonique.6 XXIII - Équations fonctionnelles linéaires.7 Première partie - Opérateurs pseudo-différentiels XXIII - Équations fonctionnelles linéaires.8 Deuxième partie - Problèmes aux limites XXIV - Topologie algébrique et topologie différentielle élémentaire9 Plan de l'ouvrage [modifier]
Tome I : Fondements de l'Analyse moderne [modifier]
VI - Espaces de Hilbert.
IX - Fonctions analytiques.
XI - Théorie spectrale élémentaire.
INDEXTome II [modifier]
Tome III [modifier]
XVII - Calcul différentiel sur une variété différentielle.
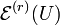 (U ouvert dans
(U ouvert dans  ).
).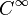 (resp. Cr) de fibrés vectoriels.
(resp. Cr) de fibrés vectoriels. .
.
BIBLIOGRAPHIE
INDEXTome IV [modifier]
II.Théorie globale élémentaire des équations différentielles du premier et du second ordre.
Théorie locale élémentaire des systèmes différentiels.
XX - Connexions principales et géométrie riemannienne.
Annexe -Compléments d'algèbre (suite).
BIBLIOGRAPHIE
INDEXTome V : Groupes de Lie compacts et groupes de Lie semi-simples [modifier]
Annexe -Compléments d'algèbre (suite).
BIBLIOGRAPHIE
INDEXTome VI : Analyse harmonique [modifier]
 ).
).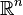 .
.Tome VII : Équations fonctionnelles linéaires, Première partie : Opérateurs pseudo-différentiels [modifier]
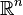 .
.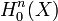 .
.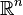 .
.
BIBLIOGRAPHIE
INDEXTome VIII : Équations fonctionnelles linéaires, Deuxième partie : problèmes aux limites [modifier]
 .
.
BIBLIOGRAPHIE
INDEXTome IX : Topologie algébrique et topologie différentielle élémentaire [modifier]
BIBLIOGRAPHIE
INDEXRéférences [modifier]
11:52 Publié dans Éléments d'analyse | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Jean Dieudonné
Jean Alexandre Eugène Dieudonné est un mathématicien français né le 1er juillet 1906 à Lille et mort le 29 novembre 1992 à Paris.Jean Dieudonné
Sommaire[masquer] |
Jean Dieudonné est né à Lille en 1906. En 1915, sa famille fuit l'occupation de Lille par l'Allemagne durant la Première Guerre mondiale et s'installe à Paris en 1916. Sa famille l'envoie en Angleterre en 1919 pour une année scolaire. Il obtient le premier prix au concours général de mathématiques en 1923. En 1924, il intègre l'École normale supérieure à l'âge de 18 ans. Il est reçu cacique à l'agrégation en 1927. Il obtient une bourse de l'Université de Princeton, puis une de la fondation Rockefeller. Il soutient sa thèse intitulée Recherche sur quelques problèmes relatifs aux polynômes et aux fonctions bornées en 1931. En décembre 1934, il participe à la fondation du groupe Bourbaki, dont il sera un des moteurs pendant de nombreuses années. Il fut maître de conférences à Nancy en 1937, puis à Clermont-Ferrand durant l'occupation, où était repliée l'université de Strasbourg, avant de partir pour le continent américain. Il fut d'abord professeur à l'université de São Paulo au Brésil de 1946 à 1948, puis aux États-Unis en 1952 à l'université du Michigan, pour revenir en France en 1959 à l'IHES. Il finira sa carrière à l'université de Nice où il obtient un poste en 1964. Il sera également le doyen de cette université. Le 24 juin 1968 il est élu membre non résidant de l'Académie des sciences. Avec Laurent Schwartz, il supervisa les premières recherches d'Alexandre Grothendieck à l'université de Nancy, posant de nouvelles bases à la géométrie algébrique. Recevant le grand prix de l'Académie des sciences en 1944, il en deviendra membre en 1968. Outre ses publications au sein de Bourbaki, on lui doit notamment : L'Euro-Institut d'Actuariat (EURIA) à Brest porte aujourd'hui son nom ainsi que le Laboratoire de Mathématiques (Unité Mixte de Recherche CNRS - UMR 6621) de l'Université de Nice Sophia-Antipolis.Biographie [modifier]
Travaux [modifier]
Publications [modifier]
Remarque [modifier]
Voir aussi [modifier]
11:51 Publié dans Jean Dieudonné | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Abrégé d'histoire des mathématiques
L'Abrégé d'histoire des mathématiques a été écrit par un groupe de mathématiciens sous la direction de Jean Dieudonné et est publié aux éditions Hermann. Ce livre a la vocation de donner un aperçu de l'évolution des concepts mathématiques sur la période 1700-1900. Les auteurs reconnaissent que l'histoire mathématique à partir de 1900 est très riche mais ils estimaient ne pas avoir assez de recul pour en parler. Une caractéristique de cet écrit réside dans le fait qu'il a été écrit par des mathématiciens et non par des historiens ; les auteurs apportent leur regard technique sur la rigueur des premières preuves, indiquent les erreurs importantes commises par les mathématiciens de cette période.Abrégé d'histoire des mathématiques
Cette partie a été écrite par Jean Dieudonné. Cette partie a été écrite par Jean Dieudonné. Cette partie a été écrite par Jean Dieudonné et Jean Guérindon. Cette partie a été écrite par Jean Dieudonné et Jean Guérindon. Cette partie a été écrite par Jean-Luc Verley. Cette partie a été écrite par William et Fern Ellison. Cette partie est l'œuvre de Pierre Dugac (de). Ceci est dû à Christian Houzel. Ce chapitre a été rédigé par Jean Dieudonné. Ce chapitre est dû à Paulette Libermann (de). L'auteur de cette partie est Guy Hirsch. Cela est l'œuvre de Marcel Guillaume. Jean Dieudonné (dir.), Abrégé d'histoire des mathématiques 1700-1900 [détail des éditions] Introduction [modifier]
L'analyse mathématique au xviiie siècle [modifier]
L'algèbre et la géométrie jusqu'en 1840 [modifier]
L'algèbre et la géométrie depuis 1840 [modifier]
Les fonctions analytiques [modifier]
Théorie des nombres [modifier]
Fondements de l'analyse [modifier]
Fonctions elliptiques et intégrales abéliennes [modifier]
L'analyse fonctionnelle [modifier]
Géométrie différentielle [modifier]
Topologie [modifier]
Axiomatique et logique [modifier]
Référence [modifier]
11:50 Publié dans Abrégé d'histoire des mathématiques | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Anneau (mathématiques)
En algèbre générale, un anneau est une structure algébrique sur laquelle deux opérations satisfont certaines des propriétés de l'addition et la multiplication des nombres.Anneau (mathématiques)
![]() Pour les articles homonymes, voir Anneau.
Pour les articles homonymes, voir Anneau.
Sommaire[masquer] |
L'étude des corps et des anneaux trouve son origine dans l'école allemande du XIXe siècle. Elle est développée par les mathématiciens Kummer, Dedekind, Kronecker et Hilbert. Elle naît de l'étude des équations algébriques, des nombres algébriques et de la recherche d'une démonstration du grand théorème de Fermat. Elle conduira à un développement important de l'algèbre générale et de la géométrie algébrique. Dans le Xe Supplément de sa seconde édition des Leçons sur la théorie des nombres de Dirichlet, en 1871, Dedekind considère, à côté de la notion de corps (Körper), l'anneau des entiers d'un corps de nombres algébriques ; il introduira un peu plus tard d'autres anneaux qu'il appelle ordres (Ordnung). Mais c'est David Hilbert qui emploie le terme d'anneau (Ring) pour définir ce qui est toujours à l'époque un anneau commutatif unitaire, dans son Rapport sur les nombres (Zahlbericht) de 1897 pour la Deutsche Mathematiker-Vereinigung1. Un anneau est un triplet (A, +, ∙) tel que : Depuis les années 1960, Nicolas Bourbaki2 et de nombreux auteurs3 imposent dans leur définition à un anneau d'être unifère (on dit aussi unitaire), c'est-à-dire que la loi associative . admet un élément neutre noté 1 ou 1A qui vérifie : Un morphisme d'anneaux est une application entre deux anneaux A et B, compatible avec les lois de ces anneaux, c'est-à-dire qui vérifie : Si on suppose dans la définition que les anneaux sont unitaires, l'application f doit transformer l'unité de l'anneau unitaire A en l'unité de B. Si f est une bijection, on dit que f est un isomorphisme d'anneaux. On dit que deux anneaux A et B sont isomorphes si il existe un isomorphisme de A sur B. Soit n un entier naturel supérieur à 1, x un élément de l'anneau A, on note xn pour désigner l’élément de A défini par récurrence à partir de : On a : Pour tout entier naturel non nul n, xn résulte de n-1 associations de la seconde loi de composition interne associative ·, en utilisant n valeurs successives toutes égales à x (l’ordre de ces compositions est sans importance car elles sont associatives) Si l'anneau A est unitaire, on pose habituellement x0 = 1A. Si xy=yx, on dit que x et y sont permutables et alors Précisons tout de suite que cette multiplication ne fait pas partie de la structure de l'anneau, mais elle apparaît de façon naturelle pour tout anneau. Il s'agit tout simplement de la multiplication par un entier appliquée au groupe additif de l'anneau. L'élément na est défini par De plus, cette loi externe est compatible avec la multiplication de l'anneau : Cela confère alors à l'anneau une structure de Cette structure additionnelle est très utilisée pour les différentes théories de cohomologie. Voir Formule du binôme de Newton. Cette formule est applicable à tout couple d'éléments permutables. Elle se généralise à toute famille finie d'éléments permutables deux à deux : Formule du multinôme. L'ensemble à un seul élément {0} muni des opérations 0+0=0 et 0.0=0 est un anneau, appelé anneau nul. La notion de pseudo-anneau de carré nul est plus intéressante : on dit qu'un pseudo-anneau A est de carré nul7 si le produit de deux éléments de A est toujours nul. Si le pseudo-anneau est unitaire, il est alors réduit à 0 car pour tout élément x de A, on a : x=1.x=0. Tout groupe abélien (A, +) peut être muni d'une structure de pseudo-anneau nul en posant x.y=0. L'anneau opposé Aop d'un anneau A possède le même groupe additif sous-jacent que A et sa multiplication est effectuée dans l'ordre opposé : si l'on note Il est clair que si A est commutatif, A = Aop. L'ensemble des éléments réguliers et des diviseurs de zéro forment une partition de A {0} Un anneau de Boole, noté Quelques propriétés des anneaux de Boole : Exemple : l'ensemble des parties Les notions d'anneau de Boole et d'algèbre de Boole sont intimement liées (voir l'article Algèbre de Boole (structure)). Une partie B d'un anneau A est un sous-anneau de (A, +, .) si : Un anneau intégralement clos est un anneau commutatif unitaire intègre égal à sa fermeture intégrale dans son corps des fractions. Cependant, la structure de sous-anneau (excepté le cas d'un anneau dans son corps des fractions) est moins riche en résultats que celle d'idéal ou de module sur un anneau. Plus intéressante que la structure de sous-anneau, la structure d'idéal s'apparente à celle de sous-groupe distingué dans un groupe. Un idéal I (à droite ou à gauche) est un sous-groupe additif de A vérifiant Un idéal à droite et à gauche est appelé idéal bilatère. Un idéal bilatère permet de créer un anneau quotient : le groupe quotient commutatif A/I peut être muni d'une multiplication associative et distributive par rapport à l'addtion, et donc d'une structure d'anneau. Selon les propriétés des idéaux d'un anneau A, on distingue des familles d'anneaux particuliers: Une dérivation d'un anneau A à valeurs dans un A-module M est une application additive de A dans M Cette notion est en particulier vérifiée par la dérivée d'une fonction (de variable réelle, par exemple); elle en est une généralisation utilisée en géométrie algébrique et en calcul différentielsur les variétés (par exemple pour définir le crochet de Lie). Toute application de dérivation vérifie la formule de Leibniz. La théorie des anneaux étant une branche très riche de l'algèbre, il est difficile de se repérer dans la jungle des anneaux particuliers. Le schéma ci-dessous donne une illustration partielle de leur hiérarchie - une flèche fait passer du général au particulier. On peut remarquer que l'anneau qui se détache de cette hiérarchie est l'anneau euclidien : c'est celui qui va posséder le plus de propriétés. S. Mac Lane & G. Birkhoff ; Algèbre [détail des éditions]Aspect historique [modifier]
Définitions [modifier]
 B, de transformer l'unité de A en l'unité de B. Cette définition (les anneaux sont supposés unitaires) est récente et n'était pas adoptée à l'origine.
B, de transformer l'unité de A en l'unité de B. Cette définition (les anneaux sont supposés unitaires) est récente et n'était pas adoptée à l'origine.Opérations sur les éléments d'un anneau [modifier]
Puissances dans un anneau [modifier]
 .
.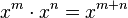 .
. .
.Eléments permutables dans un anneau et anneaux commutatifs [modifier]
 .
.
Multiplication par un entier relatif [modifier]
 avec n termes a
avec n termes a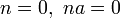


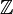 -algèbre associative. En particulier, si l'anneau est unitaire, on peut multiplier son unité par tout entier, et cela définit une application de Zdans A . Il est clair, d'après sa définition, que cette application est le seul morphisme d'anneaux unitaires de Z vers A. On peut alors définir la caractéristique de l'anneau comme l'entier naturel n qui engendre le noyau de ce morphisme. En effet, le noyau de ce morphisme est un idéal de Z et s'écrit alors nZ.
-algèbre associative. En particulier, si l'anneau est unitaire, on peut multiplier son unité par tout entier, et cela définit une application de Zdans A . Il est clair, d'après sa définition, que cette application est le seul morphisme d'anneaux unitaires de Z vers A. On peut alors définir la caractéristique de l'anneau comme l'entier naturel n qui engendre le noyau de ce morphisme. En effet, le noyau de ce morphisme est un idéal de Z et s'écrit alors nZ.Formule du binôme [modifier]
Exemples [modifier]
 muni de l'addition (la loi +) et de la multiplication (la loi ∙) est un anneau commutatif unitaire.
muni de l'addition (la loi +) et de la multiplication (la loi ∙) est un anneau commutatif unitaire.
 .
.
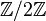 pour les lois + et * est un anneau à deux éléments. 0 correspond aux nombres pairs et 1 aux nombres impairs. On retrouve alors les résultats suivants :
pour les lois + et * est un anneau à deux éléments. 0 correspond aux nombres pairs et 1 aux nombres impairs. On retrouve alors les résultats suivants :
 , l'ensemble des nombres réels,
, l'ensemble des nombres réels,  , l'ensemble des nombres complexes,
, l'ensemble des nombres complexes,  , munis de l'addition et de la multiplication usuelles sont des anneaux (unitaires) commutatifs.
, munis de l'addition et de la multiplication usuelles sont des anneaux (unitaires) commutatifs. , munis de l'addition et de la multiplication usuelles est un anneau (unitaire) commutatif qui n'est pas un corps.
, munis de l'addition et de la multiplication usuelles est un anneau (unitaire) commutatif qui n'est pas un corps.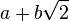 , où a et b sont des entiers relatifs, muni de l'addition et de la multiplication usuelles est un anneau commutatif, mais pas un corps.
, où a et b sont des entiers relatifs, muni de l'addition et de la multiplication usuelles est un anneau commutatif, mais pas un corps.
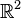 .
.
Anneau nul [modifier]
Anneau opposé [modifier]
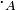 et
et 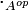 les multiplications respectives de A et Aop, on a
les multiplications respectives de A et Aop, on a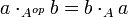
Éléments remarquables d'un anneau [modifier]
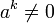 . Si un anneau est sans élément nilpotent, on dit qu'il est réduit.
. Si un anneau est sans élément nilpotent, on dit qu'il est réduit.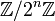 où n≥2.
où n≥2.
Divisibilité dans un anneau commutatif [modifier]
Anneaux remarquables [modifier]
Anneaux de Boole [modifier]
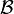 , est un anneau unitaire dans lequel tout élément est idempotent pour la multiplication i.e.
, est un anneau unitaire dans lequel tout élément est idempotent pour la multiplication i.e. 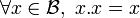
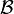 est de caractéristique 2, i.e.
est de caractéristique 2, i.e. 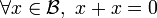
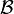 est un anneau commutatif.
est un anneau commutatif.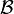 n'est pas intègre, sauf s'il est réduit à un ou à deux éléments.
n'est pas intègre, sauf s'il est réduit à un ou à deux éléments.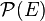 d'un ensemble
d'un ensemble  muni de la différence symétrique considérée comme addition i.e.
muni de la différence symétrique considérée comme addition i.e.  et de l'intersection considérée comme multiplication i.e.
et de l'intersection considérée comme multiplication i.e.  est un anneau de Boole. Tout anneau de Boole fini est de cette forme8.
est un anneau de Boole. Tout anneau de Boole fini est de cette forme8.Anneaux intègres, réduits, factoriels et euclidiens [modifier]
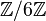 est un anneau réduit mais non intègre car 2 et 3 sont des diviseurs de zéro dans cet anneau.
est un anneau réduit mais non intègre car 2 et 3 sont des diviseurs de zéro dans cet anneau.
![mathbb Z[i]](http://upload.wikimedia.org/math/e/2/a/e2abb021e74e2b38379dfefd04b2b086.png) est un anneau euclidien dans lequel le couple (q,r) n'est pas unique
est un anneau euclidien dans lequel le couple (q,r) n'est pas unique des entiers relatifs est un anneau euclidien pour v = valeur absolue
des entiers relatifs est un anneau euclidien pour v = valeur absolue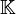 est un corps commutatif, l'anneau
est un corps commutatif, l'anneau ![mathbb K[X]](http://upload.wikimedia.org/math/1/1/c/11cf18672fa8c102e5d2ec8bdfe203c8.png) est un anneau euclidien pour v = degré du polynôme.
est un anneau euclidien pour v = degré du polynôme.Sous-anneaux [modifier]
 .
.Exemples [modifier]
Dans le cas unitaire [modifier]
 est un anneau unitaire dont l'élément neutre pour la multiplication
est un anneau unitaire dont l'élément neutre pour la multiplication  est différent de la matrice identité
est différent de la matrice identité  Ce n'est donc pas un sous-anneau deM2, ni de l'anneau des matrices diagonales.
Ce n'est donc pas un sous-anneau deM2, ni de l'anneau des matrices diagonales.Dans le cas non-unitaire [modifier]
 est un anneau unitaire, et l'ensemble B des couples (0 ; n) ayant la première composante nulle est un sous anneau qui a la particularité d'être unitaire mais de ne pas avoir la même unité que l'anneau
est un anneau unitaire, et l'ensemble B des couples (0 ; n) ayant la première composante nulle est un sous anneau qui a la particularité d'être unitaire mais de ne pas avoir la même unité que l'anneau 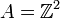 . Ce dernier a 1A = (1;1) comme unité et le sous anneau a pour unité 1B = (0;1).
. Ce dernier a 1A = (1;1) comme unité et le sous anneau a pour unité 1B = (0;1).Construction de sous-anneaux [modifier]
Idéaux d'un anneau [modifier]
Exemples [modifier]
Anneaux quotients [modifier]
Anneaux commutatifs définis par une propriété de leurs idéaux [modifier]
Modules sur un anneau [modifier]
Dérivation [modifier]
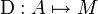 vérifiant l'identité de Leibniz :
vérifiant l'identité de Leibniz :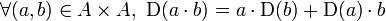
Classification des anneaux remarquables [modifier]
Sources [modifier]
Références [modifier]
Nathan Jacobson Basic Algebra,
Michael Artin Algebra,
Frank Anderson et Kent Fuller Rings and categories of modules,
Matsumara et Reid Commutative Ring Theory
11:49 Publié dans Anneau (mathématiques) | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Nombre surréel et pseudo-réel
En mathématiques, les nombres surréels sont les éléments d'un corps1 qui inclut tous les nombres réels, ainsi que tous les ordinaux transfinis et leurs inverses, respectivement plus grands et plus petits que n'importe quel nombre réel positif. Les nombres surréels ont été introduits par John Conway et popularisés par Donald Knuth en 1974 dans son livre Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness (Les nombres surréels : comment deux ex-étudiants se mirent aux mathématiques pures et trouvèrent le bonheur total)2. Les nombres pseudo-réels, également introduits par Knuth, sont une sur-classe des nombres surréels, construit avec des conditions plus faibles que ces derniers.Nombre surréel et pseudo-réel
Sommaire[masquer] |
La construction des nombres surréels est similaire à la construction des nombres réels via les coupures de Dedekind, mais utilise le concept de récurrence transfinie. Elle repose sur la construction de nouveaux nombres représentés grâce à deux ensembles de nombres déjà construits, L et R (pour left et right, gauche et droite), éventuellement vides. Le nouveau nombre ainsi construit, noté Soient L et R deux ensembles de nombres surréels tels que : Alors, Étant donné un nombre surréel Pour éviter l'inflation d'accolades, on abrégera On constate qu'il s'agit d'une définition récurrente ; ce point sera explicité plus tard. Pour que la définition ci-dessus ait un sens, il est nécessaire de définir une relation binaire (notée ≤) sur les nombres surréels. Soient deux nombres surréels Là encore, cette définition est récurrente. Cette relation ne définit qu'un pré-ordre car elle n'est pas antisymétrique (on peut avoir Il s'agit d'une relation d'équivalence et l'ordre induit par Il est possible de montrer que ces opérations sont bien définies sur les nombres surréels. On peut les généraliser sans ambiguïté aux classes d'équivalence définie plus haut par : Finalement, on peut montrer que ces opérations sur les classes d'équivalence définissent un corps ordonné, avec la mention qu'elles ne forment pas un ensemble, mais une classe propre. Il est possible de montrer qu'il s'agit du plus grand corps ordonné, c'est-à-dire que tout corps ordonné peut y être plongé ; en particulier, ce corps est réel clos. À partir de maintenant, on ne fera plus la distinction entre un nombre surréel et sa classe d'équivalence et on appellera directement cette dernière nombre surréel. On l'a vu, les deux définitions précédentes utilisent le principe de récurrence. Il est possible d'utiliser la récurrence ordinaire, mais il est plus intéressant de prendre en compte larécurrence transfinie. Il est également nécessaire de créer un nombre surréel afin d'initier la récurrence ; Désignons par Nn, pour un ordinal n, l'ensemble des nombres surréels créés à l'étape n de la récurrence, en prenant Les nombres surréels créés en un nombre fini d'étapes (par un raisonnement de récurrence ordinaire, donc) sont assimilés aux rationnels dyadiques (c'est-à-dire les nombres p / 2n où p et n sont entiers). On définit de proche en proche : Mais aussi de nouveaux objets qui ne sont pas des ordinaux, comme On peut montrer que On obtient les nombres pseudo-réels (pseudo-real numbers selon la terminologie de Knuth) au lieu des nombres surréels si on enlève la condition qu'aucun élément de l'ensemble de droite ne peut être inférieur où égal à un élément quelconque de l'ensemble de gauche. Les nombres surréels forment un sous-ensemble des nombres pseudo-réels. Ces nombres pseudo-réels peuvent s'interpréter comme les valeurs de certains jeux. Ils sont à la base de la théorie des jeux combinatoires initiée par John Conway.Nombres surréels [modifier]
Présentation [modifier]
 , sera plus grand que tout nombre de L et plus petit que tout nombre de R, selon un ordre qui sera défini plus loin. Pour que cela soit possible, on impose une restriction sur L et R : il faut que chaque nombre de L soit plus petit que chaque nombre de R.
, sera plus grand que tout nombre de L et plus petit que tout nombre de R, selon un ordre qui sera défini plus loin. Pour que cela soit possible, on impose une restriction sur L et R : il faut que chaque nombre de L soit plus petit que chaque nombre de R.Définition [modifier]
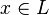 et tout
et tout  ,
, 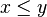
 est un nombre surréel.
est un nombre surréel. , on appelle XL et XR l'ensemble de gauche et l'ensemble de droite de X, respectivement.
, on appelle XL et XR l'ensemble de gauche et l'ensemble de droite de X, respectivement. en
en  ,
, 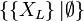 en
en  et
et 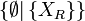 en
en 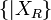 .
.Ordre [modifier]
 et
et  .
.  si et seulement si pour tout
si et seulement si pour tout 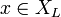 , on ne rencontre jamais
, on ne rencontre jamais  et si pour tout
et si pour tout  , on n'a jamais
, on n'a jamais  .
. et
et 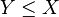 sans que X = Y, c'est le cas par exemple avec
sans que X = Y, c'est le cas par exemple avec 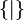 et
et 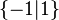 ). Pour contourner ce problème, on définit une nouvelle relation sur les nombres surréels :
). Pour contourner ce problème, on définit une nouvelle relation sur les nombres surréels : .
. sur les classes d'équivalences est un ordre total, une classe d'équivalence pouvant alors être considérée comme un nombre unique.
sur les classes d'équivalences est un ordre total, une classe d'équivalence pouvant alors être considérée comme un nombre unique.Opérations [modifier]

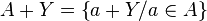 et
et 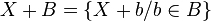 .
.
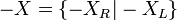
 .
.
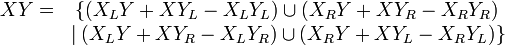
 .
.
Construction [modifier]
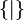 peut être défini grâce à l'ensemble vide et répond à cette fonction.
peut être défini grâce à l'ensemble vide et répond à cette fonction. . On appelle date de naissance d'un nombre surréel Xle plus petit ordinal n tel que
. On appelle date de naissance d'un nombre surréel Xle plus petit ordinal n tel que 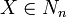 .
.Exemples [modifier]

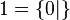 et
et 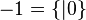
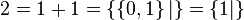 et
et 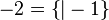
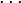
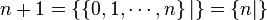 .
.

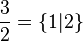

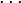
 qui est plus grand que n'importe quel nombre entier
qui est plus grand que n'importe quel nombre entier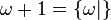
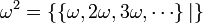

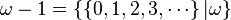


 qui est strictement positif mais inférieur à tout
qui est strictement positif mais inférieur à tout  , pour n entier positif.
, pour n entier positif.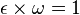 .
.Nombres pseudo-réels [modifier]
Voir aussi [modifier]
Liens externes [modifier]
Bibliographie [modifier]
Notes et références [modifier]
11:45 Publié dans Nombre surréel et pseudo-réel | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
08/12/2010
Les métamorphoses du calcul , Une étonnante histoire de mathématiques
19:29 Publié dans Les métamorphoses du calcul, Livres | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Dans la jungle des nombres premiers
19:27 Publié dans Dans la jungle des nombres premiers | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Histoire des nombres
19:25 Publié dans Histoire des nombres, Livres | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
La beauté des mathématiques
19:24 Publié dans La beauté des mathématiques | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Nicolas Bourbaki : histoire d'un génie des mathématiques qui n'a jamais existé
19:22 Publié dans Livres, Nicolas Bourbaki : histoire d'un génie des mathéma | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Hasard et complexité en mathématiques : la quête d'oméga
19:20 Publié dans Hasard et complexité en mathématiques : la quête d, Livres | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Mathématiques et physique
Mathématiques et physiqueBernard Diu
19:18 Publié dans Livres, Mathématiques et physique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Les systèmes complexes , Mathématiques et biologie
19:17 Publié dans Les systèmes complexes , Mathématiques et biologie, Livres | Lien permanent | Commentaires (1) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Les énigmes mathématiques du 3ème millénaire
19:15 Publié dans Les énigmes mathématiques du 3ème millénaire, Livres | Lien permanent | Commentaires (1) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Les inattendus mathématiques , Art, casse-tête, paradoxes
19:13 Publié dans Les inattendus mathématiques , Art, casse-tête, pa, Livres | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Jacques-Louis Lions , Un mathématicien d'exception
19:12 Publié dans Jacques-Louis Lions , Un mathématicien d'exception, Livres | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Un mathématicien aux prises avec le siècle
19:10 Publié dans Livres, Un mathématicien aux prises avec le siècle | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Evariste Galois, mathématicien humaniste et révolutionnaire
19:08 Publié dans Evariste Galois, mathématicien humaniste et révolu | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook