Aspect historique [modifier]
L'étude des corps et des anneaux trouve son origine dans l'école allemande du XIXe siècle. Elle est développée par les mathématiciens Kummer, Dedekind, Kronecker et Hilbert. Elle naît de l'étude des équations algébriques, des nombres algébriques et de la recherche d'une démonstration du grand théorème de Fermat. Elle conduira à un développement important de l'algèbre générale et de la géométrie algébrique.
Dans le Xe Supplément de sa seconde édition des Leçons sur la théorie des nombres de Dirichlet, en 1871, Dedekind considère, à côté de la notion de corps (Körper), l'anneau des entiers d'un corps de nombres algébriques ; il introduira un peu plus tard d'autres anneaux qu'il appelle ordres (Ordnung). Mais c'est David Hilbert qui emploie le terme d'anneau (Ring) pour définir ce qui est toujours à l'époque un anneau commutatif unitaire, dans son Rapport sur les nombres (Zahlbericht) de 1897 pour la Deutsche Mathematiker-Vereinigung1.
Un anneau est un triplet (A, +, ∙) tel que :
Depuis les années 1960, Nicolas Bourbaki2 et de nombreux auteurs3 imposent dans leur définition à un anneau d'être unifère (on dit aussi unitaire), c'est-à-dire que la loi associative . admet un élément neutre noté 1 ou 1A qui vérifie :
- 1.x = x.1 = x
- Anneau unitaire : un anneau est dit unitaire si la loi ∙ dispose d'un élément neutre, noté 1.
- En terminologie universitaire française4 et en terminologie anglaise5 les anneaux sont souvent considérés par défaut comme unitaires. Dans le cas contraire, si la loi ∙ ne dispose pas d'élément neutre, on dit que A est un pseudo-anneau ou une algèbre associative. Cependant, comme les auteurs pour qui un anneau n'est pas nécessairement unitaire restent nombreux, il convient d'une part de toujours s'assurer de la définition concrètement utilisée, et il n'est pas inutile d'ajouter l'adjectif "unitaire" même si ce seraitredondant. Si A est un pseudo-anneau non unitaire, on peut construire un anneau unitaire A' qui contient A comme sous-anneau non unitaire6.
- Les auteurs qui supposent les anneaux unitaires imposent aux sous-anneaux de contenir l'unité de l'anneau et aux morphismes d'anneaux : A
 B, de transformer l'unité de A en l'unité de B. Cette définition (les anneaux sont supposés unitaires) est récente et n'était pas adoptée à l'origine.
B, de transformer l'unité de A en l'unité de B. Cette définition (les anneaux sont supposés unitaires) est récente et n'était pas adoptée à l'origine.
Un morphisme d'anneaux est une application entre deux anneaux A et B, compatible avec les lois de ces anneaux, c'est-à-dire qui vérifie :
- f(a+b)=f(a)+f(b)
- f(a.b)=f(a).f(b)
Si on suppose dans la définition que les anneaux sont unitaires, l'application f doit transformer l'unité de l'anneau unitaire A en l'unité de B.
- f(1A) = 1B
Si f est une bijection, on dit que f est un isomorphisme d'anneaux.
On dit que deux anneaux A et B sont isomorphes si il existe un isomorphisme de A sur B.
Opérations sur les éléments d'un anneau [modifier]
Puissances dans un anneau [modifier]
Soit n un entier naturel supérieur à 1, x un élément de l'anneau A, on note xn pour désigner l’élément de A défini par récurrence à partir de :
- x1 = x et
 .
.
On a :
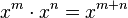 .
.
Pour tout entier naturel non nul n, xn résulte de n-1 associations de la seconde loi de composition interne associative ·, en utilisant n valeurs successives toutes égales à x (l’ordre de ces compositions est sans importance car elles sont associatives)
 .
.
Si l'anneau A est unitaire, on pose habituellement x0 = 1A.
Eléments permutables dans un anneau et anneaux commutatifs [modifier]
Si xy=yx, on dit que x et y sont permutables et alors  .
.
- Anneau commutatif : un anneau est commutatif si sa seconde loi est aussi commutative, c'est-à-dire si tous ses éléments sont permutables.
- Voir article détaillé : Anneau commutatif
- Convention : Le terme « anneau » est souvent employé pour désigner un anneau commutatif unitaire. Il faut donc prêter garde au contexte dans lequel ce terme est employé.
Multiplication par un entier relatif [modifier]
Précisons tout de suite que cette multiplication ne fait pas partie de la structure de l'anneau, mais elle apparaît de façon naturelle pour tout anneau. Il s'agit tout simplement de la multiplication par un entier appliquée au groupe additif de l'anneau. L'élément na est défini par
De plus, cette loi externe est compatible avec la multiplication de l'anneau :

Cela confère alors à l'anneau une structure de 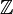 -algèbre associative. En particulier, si l'anneau est unitaire, on peut multiplier son unité par tout entier, et cela définit une application de Zdans A . Il est clair, d'après sa définition, que cette application est le seul morphisme d'anneaux unitaires de Z vers A. On peut alors définir la caractéristique de l'anneau comme l'entier naturel n qui engendre le noyau de ce morphisme. En effet, le noyau de ce morphisme est un idéal de Z et s'écrit alors nZ.
-algèbre associative. En particulier, si l'anneau est unitaire, on peut multiplier son unité par tout entier, et cela définit une application de Zdans A . Il est clair, d'après sa définition, que cette application est le seul morphisme d'anneaux unitaires de Z vers A. On peut alors définir la caractéristique de l'anneau comme l'entier naturel n qui engendre le noyau de ce morphisme. En effet, le noyau de ce morphisme est un idéal de Z et s'écrit alors nZ.
Cette structure additionnelle est très utilisée pour les différentes théories de cohomologie.
Formule du binôme [modifier]
Voir Formule du binôme de Newton.
Cette formule est applicable à tout couple d'éléments permutables.
Elle se généralise à toute famille finie d'éléments permutables deux à deux : Formule du multinôme.
- L'ensemble des entiers relatifs,
 muni de l'addition (la loi +) et de la multiplication (la loi ∙) est un anneau commutatif unitaire.
muni de l'addition (la loi +) et de la multiplication (la loi ∙) est un anneau commutatif unitaire.
- L'ensemble des entiers congruents modulo un nombre entier donné p est un anneau commutatif unitaire pour la loi provenant la congruence ; il est noté
 .
.
- Ainsi
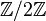 pour les lois + et * est un anneau à deux éléments. 0 correspond aux nombres pairs et 1 aux nombres impairs. On retrouve alors les résultats suivants :
pour les lois + et * est un anneau à deux éléments. 0 correspond aux nombres pairs et 1 aux nombres impairs. On retrouve alors les résultats suivants :
- Un pair plus un pair est pair (0+0=0).
- Un impair plus un pair est impair (0+1=1+0=1).
- Un impair plus un impair est pair (1+1=0).
- Un pair fois un entier quelconque est pair (0*x=0).
- Un impair fois un impair est impair (1*1=1).
- Un corps est un cas particulier d'anneau (unitaire) pour lequel tous les éléments non nuls sont inversibles pour la loi (.).
- En particulier, l'ensemble des nombres rationnels,
 , l'ensemble des nombres réels,
, l'ensemble des nombres réels,  , l'ensemble des nombres complexes,
, l'ensemble des nombres complexes,  , munis de l'addition et de la multiplication usuelles sont des anneaux (unitaires) commutatifs.
, munis de l'addition et de la multiplication usuelles sont des anneaux (unitaires) commutatifs.
- L'ensemble des nombres décimaux,
 , munis de l'addition et de la multiplication usuelles est un anneau (unitaire) commutatif qui n'est pas un corps.
, munis de l'addition et de la multiplication usuelles est un anneau (unitaire) commutatif qui n'est pas un corps.
- L'ensemble des réels s'écrivant
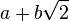 , où a et b sont des entiers relatifs, muni de l'addition et de la multiplication usuelles est un anneau commutatif, mais pas un corps.
, où a et b sont des entiers relatifs, muni de l'addition et de la multiplication usuelles est un anneau commutatif, mais pas un corps.
- Les endomorphismes d'un espace vectoriel (applications linéaires de l'espace vers lui-même) forment un anneau, avec l'addition de fonction pour la loi +, et la composition pour la loi ∙. L'identité est un élément neutre pour ∙, donc c'est un anneau unitaire. Il n'est pas commutatif en général. C'est une grande source de contre-exemples à des affirmations fausses sur les anneaux.
- Plus généralement les endomorphismes d'un groupe abélien forment un anneau.
- L'ensemble des matrices 2 × 2, à coefficients réels, muni de l'addition et de la multiplication est aussi un anneau non commutatif unitaire, isomorphe à l'anneau des endomorphismes de l'espace vectoriel
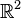 .
.
- L'ensemble des polynômes à coefficients dans un anneau commutatif est aussi un anneau commutatif.
- L'ensemble des applications d'un ensemble X à valeurs dans un anneau, muni des lois héritées de l'anneau (c'est-à-dire (f+g)(x)=f(x)+g(x) et (f*g)(x)=f(x)*g(x)) forme un anneau notéAX.
L'ensemble à un seul élément {0} muni des opérations 0+0=0 et 0.0=0 est un anneau, appelé anneau nul.
La notion de pseudo-anneau de carré nul est plus intéressante : on dit qu'un pseudo-anneau A est de carré nul7 si le produit de deux éléments de A est toujours nul. Si le pseudo-anneau est unitaire, il est alors réduit à 0 car pour tout élément x de A, on a : x=1.x=0. Tout groupe abélien (A, +) peut être muni d'une structure de pseudo-anneau nul en posant x.y=0.
L'anneau opposé Aop d'un anneau A possède le même groupe additif sous-jacent que A et sa multiplication est effectuée dans l'ordre opposé : si l'on note 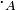 et
et 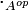 les multiplications respectives de A et Aop, on a
les multiplications respectives de A et Aop, on a
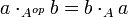
Il est clair que si A est commutatif, A = Aop.
Éléments remarquables d'un anneau [modifier]
- Élément inversible : un élément a ∈ A d'un anneau unitaire est dit inversible lorsqu'il existe un élément b de l'anneau tels que
- a∙b = b∙a = 1. On appelle parfois les éléments inversibles les éléments unités (ou simplement unités). On note l'ensemble des inversibles : A*.
- Voir article détaillé : Élément inversible
- Les éléments inversibles de Z sont -1 et 1
- Élément régulier : un élément a ∈ A est dit régulier à droite (resp. à gauche) si et seulement si le seul élément x de A tel que x∙a = 0 (resp. a∙x=0) est x = 0; on note l'ensemble des réguliers : A×
- Un élément inversible est nécessairement régulier mais la réciproque est fausse.
- Diviseur de zéro : un élément non nul a ∈ A est un diviseur de 0 à droite (resp. à gauche) s'il existe un élément b de A non nul et tel que b∙a = 0 (resp. a∙b = 0). Si un anneau commutatif est sans diviseur de 0, on dit qu'il est intègre.
L'ensemble des éléments réguliers et des diviseurs de zéro forment une partition de A {0}
- Voir article détaillé : Diviseur de zéro
- Élément nilpotent : un élément a ∈ A est dit nilpotent d'ordre n s'il existe un entier n non nul tel que an=0 et que pour tout k appartenant à {0;n-1}
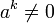 . Si un anneau est sans élément nilpotent, on dit qu'il est réduit.
. Si un anneau est sans élément nilpotent, on dit qu'il est réduit.
- Un élément nilpotent non nul est un diviseur de zéro.
- 2 est nilpotent dans tous les anneaux
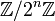 où n≥2.
où n≥2. - Si a est nilpotent (et l'anneau est unitaire), (1-a) est inversible
- Élément central : un élément qui commute (pour la multiplication) avec tout autre élément de A.
- Élément idempotent ou projecteur : un élément a ∈ A est appelé projecteur ou idempotent lorsque a∙a = a2 = a.
- Toute projection sur un sous-espace vectoriel est un projecteur dans l'anneau des endomorphismes décrit ci-dessus.
- Diviseur : si a ∈ A est non nul, et d ∈ A. On dit que d est un diviseur de a à droite (resp. à gauche) si et seulement s'il existe b ∈ A tel que a = b∙d (resp. a = d∙b). Si l'anneau est commutatif, on parle simplement de diviseur.
Divisibilité dans un anneau commutatif [modifier]
- Éléments associés : dans un anneau commutatif unitaire, deux éléments a et b sont associés si il existe un élément inversible u tel que a = u∙b, ce qui équivaut, si l'anneau est intègre, à : a divise b et b divise a.
- Élément irréductible : Dans un anneau commutatif unitaire, un élément a ∈ A non inversible est irréductible si et seulement si ses seuls diviseurs dans A sont les éléments inversibles u ou les éléments s'écrivant a∙u (éléments associés à u).
- Élément premier : Dans un anneau commutatif unitaire, un élément p ∈ A est dit premier si, pour tous éléments a et b de A, si p divise a∙b et si p ne divise pas a alors p divise b
- Dans un anneau commutatif unitaire intègre, un élément premier est irréductible, mais la réciproque n'est pas toujours vraie.
- Élément extrémal : Dans un anneau commutatif unitaire, un élément non inversible p ∈ A est dit extrémal si tout élément a de A, non divisible par p, est étranger avec p, c'est-à-dire que il existe deux éléments de A : u et v, tels que au+pv=1. En termes d'idéaux (voir plus loin), cela signifie que l'idéal des multiples de p : (p) est un idéal maximal de A (ce qui équivaut à l'importante propriété : "A / (p) est un corps".)
- Dans un anneau commutatif unitaire intègre, un élément maximal est premier, mais la réciproque n'est pas toujours vraie.
- Éléments premiers entre eux : dans un anneau commutatif unitaire intègre, deux éléments a et b sont premiers entre eux si et seulement si, pour tout d de A, si d divise a et ddivise b alors d est un élément inversible.
Anneaux remarquables [modifier]
Anneaux de Boole [modifier]
Un anneau de Boole, noté 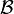 , est un anneau unitaire dans lequel tout élément est idempotent pour la multiplication i.e.
, est un anneau unitaire dans lequel tout élément est idempotent pour la multiplication i.e. 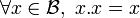
Quelques propriétés des anneaux de Boole :
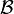 est de caractéristique 2, i.e.
est de caractéristique 2, i.e. 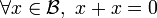
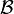 est un anneau commutatif.
est un anneau commutatif.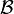 n'est pas intègre, sauf s'il est réduit à un ou à deux éléments.
n'est pas intègre, sauf s'il est réduit à un ou à deux éléments.
Exemple : l'ensemble des parties 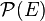 d'un ensemble
d'un ensemble  muni de la différence symétrique considérée comme addition i.e.
muni de la différence symétrique considérée comme addition i.e.  et de l'intersection considérée comme multiplication i.e.
et de l'intersection considérée comme multiplication i.e.  est un anneau de Boole. Tout anneau de Boole fini est de cette forme8.
est un anneau de Boole. Tout anneau de Boole fini est de cette forme8.
Les notions d'anneau de Boole et d'algèbre de Boole sont intimement liées (voir l'article Algèbre de Boole (structure)).
Anneaux intègres, réduits, factoriels et euclidiens [modifier]
- Anneau intègre : anneau dans lequel tout élément non nul est régulier i.e. qu'aucun élément n'est un diviseur de zéro. Par définition, tout anneau intègre est unitaire et/ou commutatif.
- Anneau réduit : un anneau est dit réduit si et seulement si son élément nul est le seul élément nilpotent.
- Exemple :
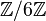 est un anneau réduit mais non intègre car 2 et 3 sont des diviseurs de zéro dans cet anneau.
est un anneau réduit mais non intègre car 2 et 3 sont des diviseurs de zéro dans cet anneau.
- Corps : un corps est un anneau unitaire dont tous les éléments non nuls sont inversibles.
- Tout anneau intègre fini est nécessairement un corps.
-
- Corps des fractions d'un anneau intègre
- Un anneau commutatif unitaire intègre (ou domaine d'intégrité) est presque un corps mais certains éléments ne sont pas toujours inversibles. On démontre que l'on peut plonger tout anneau commutatif intègre dans un corps appelé corps des fractions de A.
- Remarque : il n'est pas nécessaire que l'anneau soit unitaire, car l'élément neutre apparaît de toute façon dans la construction du corps des fractions.
- Anneau factoriel : anneau commutatif unitaire intègre dans lequel tous les éléments se décomposent de manière unique (aux inversibles près) en produit d'éléments irréductibles.
- plus exactement pour tout a de A, il existe n éléments irréductibles p1, p2, ..., pn tels que a = p1p2...pn. Cette décomposition est unique à l'ordre des pi près et au produit par des éléments inversibles près.
- Anneau euclidien : anneau commutatif unitaire intègre dans lequel on peut définir une division euclidienne.
- Plus précisément, il existe une application v (appelé stathme euclidien) de A{0} dans N telle que pour tout a et b de A, b non nul, il existe un couple (q, r) de A2 tel que a = bq + r avec r nul ou v(r) < v(b)
![mathbb Z[i]](http://upload.wikimedia.org/math/e/2/a/e2abb021e74e2b38379dfefd04b2b086.png) est un anneau euclidien dans lequel le couple (q,r) n'est pas unique
est un anneau euclidien dans lequel le couple (q,r) n'est pas unique- L'anneau
 des entiers relatifs est un anneau euclidien pour v = valeur absolue
des entiers relatifs est un anneau euclidien pour v = valeur absolue - Si
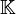 est un corps commutatif, l'anneau
est un corps commutatif, l'anneau ![mathbb K[X]](http://upload.wikimedia.org/math/1/1/c/11cf18672fa8c102e5d2ec8bdfe203c8.png) est un anneau euclidien pour v = degré du polynôme.
est un anneau euclidien pour v = degré du polynôme.
Une partie B d'un anneau A est un sous-anneau de (A, +, .) si :
- (B, +) est un sous-groupe de (A,+)
- B est stable pour la loi .
- S'il est requis que les anneaux soient unitaires (cela dépendant de la définition utilisée), alors le sous anneau doit lui être aussi unitaire et son 1 doit provenir du 1 de l'anneau initial (1A = 1B), ce qui équivaut à
 .
.
- Un sous-anneau B est un anneau pour les opérations + et . restreintes à B.
Dans le cas unitaire [modifier]
- Dans l'anneau commutatif (unitaire) Z, 2 Z est un idéal, qui n'a pas d'élément unité, ce n'est donc pas un anneau et encore moins un sous-anneau de Z.
- Dans l'ensemble des matrices carrées M2 (à coefficients dans R par exemple), anneau non-commutatif unitaire, l'ensemble des matrices de la forme :
 est un anneau unitaire dont l'élément neutre pour la multiplication
est un anneau unitaire dont l'élément neutre pour la multiplication  est différent de la matrice identité
est différent de la matrice identité  Ce n'est donc pas un sous-anneau deM2, ni de l'anneau des matrices diagonales.
Ce n'est donc pas un sous-anneau deM2, ni de l'anneau des matrices diagonales.
Dans le cas non-unitaire [modifier]
- 2 Z est cette fois-ci un (pseudo-)anneau et c'est bien un sous anneau de Z.
 est un anneau unitaire, et l'ensemble B des couples (0 ; n) ayant la première composante nulle est un sous anneau qui a la particularité d'être unitaire mais de ne pas avoir la même unité que l'anneau
est un anneau unitaire, et l'ensemble B des couples (0 ; n) ayant la première composante nulle est un sous anneau qui a la particularité d'être unitaire mais de ne pas avoir la même unité que l'anneau 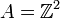 . Ce dernier a 1A = (1;1) comme unité et le sous anneau a pour unité 1B = (0;1).
. Ce dernier a 1A = (1;1) comme unité et le sous anneau a pour unité 1B = (0;1).
Construction de sous-anneaux [modifier]
- Éléments entiers sur un sous-anneau B : dans un anneau commutatif unitaire intègre A contenant un sous-anneau B, un élément x ∈ A est entier sur B si et seulement si x est solution d'une équation P(x) = 0 où P est un polynôme unitaire à coefficient dans B.
- L'anneau Z des entiers relatifs est un sous-anneau de l'anneau Q des rationnels. Les seuls éléments de Q entiers sur Z sont les entiers relatifs.
- L'anneau Z des entiers relatifs est un sous-anneau de l'anneau Q[i] des complexes s'écrivant a + ib, a et b étant des rationnels . Les éléments de Q[i] entiers sur Z sont les complexes s'écrivant a + ib, a et b étant des entiers relatifs.
- Fermeture intégrale d'un sous-anneau B : dans un anneau commutatif unitaire intègre A contenant un sous-anneau B, la fermeture intégrale de B dans A est l'ensemble des éléments de A entiers sur B. C'est un sous-anneau de A contenant B comme sous-anneau.
Un anneau intégralement clos est un anneau commutatif unitaire intègre égal à sa fermeture intégrale dans son corps des fractions.
- L'anneau des entiers relatifs est intégralement clos.
- Plus généralement : un anneau factoriel est intégralement clos.
- Le centre Z(A) d'un anneau A est par définition Z(A)={x∈A / ∀y∈A, x.y=y.x}, c’est-à-dire l'ensemble des éléments qui commutent avec tous les autres pour la loi ".". C'est un sous-anneau.
- L'intersection de deux sous-anneaux d'un même anneau, est un sous-anneau.
- L'image d'un anneau par un homomorphisme d'anneau est un sous-anneau de l'anneau d'arrivée. (Si les anneaux sont unitaires, on impose aux morphismes de transformer unité en unité.)
Cependant, la structure de sous-anneau (excepté le cas d'un anneau dans son corps des fractions) est moins riche en résultats que celle d'idéal ou de module sur un anneau.
Idéaux d'un anneau [modifier]
Article détaillé :
Idéal.
Plus intéressante que la structure de sous-anneau, la structure d'idéal s'apparente à celle de sous-groupe distingué dans un groupe.
Un idéal I (à droite ou à gauche) est un sous-groupe additif de A vérifiant
- pour tout x de I et tout a de A, ax ∈ I pour un idéal à droite
- pour tout x de I et tout a de A, xa ∈ I pour un idéal à gauche
Un idéal à droite et à gauche est appelé idéal bilatère.
- {0} est un idéal bilatère de tout anneau, l'idéal nul.
- A est un idéal bilatère de A.
- Si a a un élément de l'anneau A, l'ensemble des multiples à droite de a (les éléments de la forme ax) est un idéal à droite de A. Il est noté (a).
- L'intersection de deux idéaux (resp. à gauche, resp. à droite) de A est un idéal de A (resp. à gauche, resp. à droite).
Anneaux quotients [modifier]
Un idéal bilatère permet de créer un anneau quotient : le groupe quotient commutatif A/I peut être muni d'une multiplication associative et distributive par rapport à l'addtion, et donc d'une structure d'anneau.
Anneaux commutatifs définis par une propriété de leurs idéaux [modifier]
Selon les propriétés des idéaux d'un anneau A, on distingue des familles d'anneaux particuliers:
- Anneau principal : anneau commutatif unitaire intègre dont tous les idéaux sont principaux.
- Voir article détaillé : Anneau principal
- Un anneau euclidien est principal
- Un anneau principal est factoriel
- Anneau noethérien : anneau commutatif unitaire dont les idéaux sont engendrés par un nombre fini d'éléments
- Voir article détaillé : Anneau noethérien
- Anneau artinien : anneau commutatif unitaire dont toute suite d'idéaux décroissante (pour l'inclusion) est stationnaire.
- Voir article détaillé : Anneau artinien
- Anneau local : anneau commutatif unitaire dans lequel il n'existe qu'un seul idéal maximal.
- Anneau de Bézout : Anneau commutatif unitaire intègre dans lequel tout idéal de type fini est principal
- Anneau de Dedekind : Anneau noethérien intégralement clos dans lequel tout idéal premier non nul est maximal.
- Voir article détaillé : Anneau de Dedekind
Modules sur un anneau [modifier]
Une dérivation d'un anneau A à valeurs dans un A-module M est une application additive de A dans M 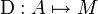 vérifiant l'identité de Leibniz :
vérifiant l'identité de Leibniz :
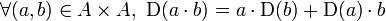
Cette notion est en particulier vérifiée par la dérivée d'une fonction (de variable réelle, par exemple); elle en est une généralisation utilisée en géométrie algébrique et en calcul différentielsur les variétés (par exemple pour définir le crochet de Lie). Toute application de dérivation vérifie la formule de Leibniz.
Classification des anneaux remarquables [modifier]
La théorie des anneaux étant une branche très riche de l'algèbre, il est difficile de se repérer dans la jungle des anneaux particuliers. Le schéma ci-dessous donne une illustration partielle de leur hiérarchie - une flèche fait passer du général au particulier.
On peut remarquer que l'anneau qui se détache de cette hiérarchie est l'anneau euclidien : c'est celui qui va posséder le plus de propriétés.

- ↑ Jean Dieudonné (dir.), Abrégé d'histoire des mathématiques 1700-1900 [détail des éditions] , vol. 1, p. 111-112, 201-203, et D. Hilbert, Die Theorie der algebraischen Zahlkörper, Jahresbericht der DMV 4, (1897), p. 175-546, §31.
- ↑ N. Bourbaki, Algèbre, chapitre 1
- ↑ Serge Lang Algebra,
Nathan Jacobson Basic Algebra,
Michael Artin Algebra,
Frank Anderson et Kent Fuller Rings and categories of modules,
Matsumara et Reid Commutative Ring Theory
- ↑ Bourbaki, Algèbre, chapitre 1 ; Ramis, Deschamp, Odoux, Cours de mathématiques spéciales
- ↑ voir wikipedia anglophone : en:Ring(mathematics)
- ↑ N. Bourbaki, Algèbre, chapitre 2 (ed. de 1970), Appendice
- ↑ N. Bourbaki, Algèbre, chapitre I, page 97
- ↑ Pour une étude plus approfondie, cf Des anneaux de Boole [archive] par Giordano Favi (2005) Journal de l'IMA.
S. Mac Lane & G. Birkhoff ; Algèbre [détail des éditions]
![]() Pour les articles homonymes, voir Anneau.
Pour les articles homonymes, voir Anneau. B, de transformer l'unité de A en l'unité de B. Cette définition (les anneaux sont supposés unitaires) est récente et n'était pas adoptée à l'origine.
B, de transformer l'unité de A en l'unité de B. Cette définition (les anneaux sont supposés unitaires) est récente et n'était pas adoptée à l'origine. .
.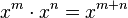 .
. .
. .
. avec n termes a
avec n termes a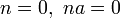


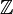 -algèbre associative. En particulier, si l'anneau est unitaire, on peut multiplier son unité par tout entier, et cela définit une application de Zdans A . Il est clair, d'après sa définition, que cette application est le seul morphisme d'anneaux unitaires de Z vers A. On peut alors définir la caractéristique de l'anneau comme l'entier naturel n qui engendre le noyau de ce morphisme. En effet, le noyau de ce morphisme est un idéal de Z et s'écrit alors nZ.
-algèbre associative. En particulier, si l'anneau est unitaire, on peut multiplier son unité par tout entier, et cela définit une application de Zdans A . Il est clair, d'après sa définition, que cette application est le seul morphisme d'anneaux unitaires de Z vers A. On peut alors définir la caractéristique de l'anneau comme l'entier naturel n qui engendre le noyau de ce morphisme. En effet, le noyau de ce morphisme est un idéal de Z et s'écrit alors nZ. muni de l'addition (la loi +) et de la multiplication (la loi ∙) est un anneau commutatif unitaire.
muni de l'addition (la loi +) et de la multiplication (la loi ∙) est un anneau commutatif unitaire. .
.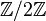 pour les lois + et * est un anneau à deux éléments. 0 correspond aux nombres pairs et 1 aux nombres impairs. On retrouve alors les résultats suivants :
pour les lois + et * est un anneau à deux éléments. 0 correspond aux nombres pairs et 1 aux nombres impairs. On retrouve alors les résultats suivants :
 , l'ensemble des nombres réels,
, l'ensemble des nombres réels,  , l'ensemble des nombres complexes,
, l'ensemble des nombres complexes,  , munis de l'addition et de la multiplication usuelles sont des anneaux (unitaires) commutatifs.
, munis de l'addition et de la multiplication usuelles sont des anneaux (unitaires) commutatifs. , munis de l'addition et de la multiplication usuelles est un anneau (unitaire) commutatif qui n'est pas un corps.
, munis de l'addition et de la multiplication usuelles est un anneau (unitaire) commutatif qui n'est pas un corps.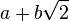 , où a et b sont des entiers relatifs, muni de l'addition et de la multiplication usuelles est un anneau commutatif, mais pas un corps.
, où a et b sont des entiers relatifs, muni de l'addition et de la multiplication usuelles est un anneau commutatif, mais pas un corps.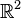 .
.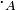 et
et 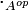 les multiplications respectives de A et Aop, on a
les multiplications respectives de A et Aop, on a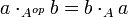
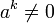 . Si un anneau est sans élément nilpotent, on dit qu'il est réduit.
. Si un anneau est sans élément nilpotent, on dit qu'il est réduit.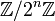 où n≥2.
où n≥2.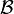 , est un anneau unitaire dans lequel tout élément est idempotent pour la multiplication i.e.
, est un anneau unitaire dans lequel tout élément est idempotent pour la multiplication i.e. 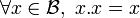
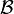 est de caractéristique 2, i.e.
est de caractéristique 2, i.e. 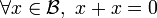
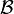 est un anneau commutatif.
est un anneau commutatif.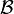 n'est pas intègre, sauf s'il est réduit à un ou à deux éléments.
n'est pas intègre, sauf s'il est réduit à un ou à deux éléments.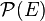 d'un ensemble
d'un ensemble  muni de la différence symétrique considérée comme addition i.e.
muni de la différence symétrique considérée comme addition i.e.  et de l'intersection considérée comme multiplication i.e.
et de l'intersection considérée comme multiplication i.e.  est un anneau de Boole. Tout anneau de Boole fini est de cette forme8.
est un anneau de Boole. Tout anneau de Boole fini est de cette forme8.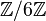 est un anneau réduit mais non intègre car 2 et 3 sont des diviseurs de zéro dans cet anneau.
est un anneau réduit mais non intègre car 2 et 3 sont des diviseurs de zéro dans cet anneau.![mathbb Z[i]](http://upload.wikimedia.org/math/e/2/a/e2abb021e74e2b38379dfefd04b2b086.png) est un anneau euclidien dans lequel le couple (q,r) n'est pas unique
est un anneau euclidien dans lequel le couple (q,r) n'est pas unique des entiers relatifs est un anneau euclidien pour v = valeur absolue
des entiers relatifs est un anneau euclidien pour v = valeur absolue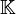 est un corps commutatif, l'anneau
est un corps commutatif, l'anneau ![mathbb K[X]](http://upload.wikimedia.org/math/1/1/c/11cf18672fa8c102e5d2ec8bdfe203c8.png) est un anneau euclidien pour v = degré du polynôme.
est un anneau euclidien pour v = degré du polynôme. .
. est un anneau unitaire dont l'élément neutre pour la multiplication
est un anneau unitaire dont l'élément neutre pour la multiplication  est différent de la matrice identité
est différent de la matrice identité  Ce n'est donc pas un sous-anneau deM2, ni de l'anneau des matrices diagonales.
Ce n'est donc pas un sous-anneau deM2, ni de l'anneau des matrices diagonales. est un anneau unitaire, et l'ensemble B des couples (0 ; n) ayant la première composante nulle est un sous anneau qui a la particularité d'être unitaire mais de ne pas avoir la même unité que l'anneau
est un anneau unitaire, et l'ensemble B des couples (0 ; n) ayant la première composante nulle est un sous anneau qui a la particularité d'être unitaire mais de ne pas avoir la même unité que l'anneau 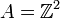 . Ce dernier a 1A = (1;1) comme unité et le sous anneau a pour unité 1B = (0;1).
. Ce dernier a 1A = (1;1) comme unité et le sous anneau a pour unité 1B = (0;1).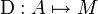 vérifiant l'identité de Leibniz :
vérifiant l'identité de Leibniz :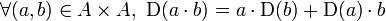
 |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook









































Les commentaires sont fermés.