20/11/2010
Variables indépendantes et identiquement distribuées
En statistique, des variables indépendantes et identiquement distribuées (iid) sont des variables aléatoires qui ont toutes la même loi de probabilité et sont mutuellement indépendantes. En inférence statistique ou en apprentissage automatique, il est très courant de supposer que le tirage des échantillons d'apprentissage sont i.i.d. C'est une condition souvent nécessaire à l'application des théorèmes les plus courants. En particulier le théorème de la limite centrale dans sa forme classique stipule que la somme de variables aléatoires tendent vers unedistribution normale quand ces variable sont i.i.d. Un exemple de tirage aléatoire i.i.d est celui du pile ou face. Chaque lancer de pièce suit la même loi de Bernoulli de paramètre p et est indépendant de ceux qui l'ont précédé ou vont lui succéder. Si p = 0.5 (pile et face ont la même chance d'apparition), et que nous avons obtenu 10 fois face lors des 10 tirages précédents, les chances d'obtenir pile et face lors du prochain tirage sont néanmoins égales. Dans l'exemple précédent, le tirage ne serait plus i.i.d : Variables indépendantes et identiquement distribuées
Exemples [modifier]
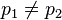 ) car dans ce cas les tirages ne suivent pas la même loi. Il restent néanmoins indépendants.
) car dans ce cas les tirages ne suivent pas la même loi. Il restent néanmoins indépendants.
09:25 Publié dans Variables indépendantes et identiquement distribué | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
19/11/2010
Théorie des probabilités
La théorie des probabilités est l'étude mathématique des phénomènes caractérisés par le hasard et l'incertitude. Les objets centraux de la théorie des probabilités sont les variables aléatoires, les processus stochastiques, et lesévénements: ils traduisent de manière abstraite des événements non déterministes ou des quantités mesurées qui peuvent parfois évoluer dans le temps d'une manière apparemment aléatoire. En tant que fondement mathématique desstatistiques, la théorie des probabilités est essentielle à la plupart des activités humaines qui nécessitent une analyse quantitative d'un grand nombre de mesures. Les méthodes de la théorie des probabilités s'appliquent également à la description de systèmes complexes dont on ne connait qu'en partie l'état, comme en mécanique statistique. Une grande découverte de la physique du vingtième siècle fut la nature probabiliste de phénomènes physiques à une échelle microscopique, décrite par la mécanique quantique.Théorie des probabilités
Sommaire[masquer] |
La théorie mathématique des probabilités trouve ses origines dans l'analyse de jeux de hasard par Gerolamo Cardano au seizième siècle, et par Pierre de Fermat et Blaise Pascal au dix-septième siècle. Bien qu'un simple pile ou face ou un lancer de dés soit un événement aléatoire, en les répétant de nombreuses fois on obtient une série de résultats qui va posséder certaines propriétés statistiques, que l'on peut étudier et prévoir. Deux résultats mathématiques fondamentaux à ce propos sont la loi des grands nombres et le théorème de la limite centrale. Initialement, la théorie des probabilités considérait surtout les événements discrets, et ses méthodes étaient principalement combinatoires. Mais des considérations analytiques ont forcé l'introduction de variables aléatoires continues dans la théorie. Cette idée prend tout son essor dans la théorie moderne des probabilités, dont les fondations ont été posées parAndreï Nikolaevich Kolmogorov. Kolmogorov combina la notion d'univers, introduite par Richard von Mises et la théorie de la mesure pour présenter son système d'axiomes pour la théorie des probabilités en 1933. Très vite, son approche devint la base incontestée des probabilités modernes. La théorie discrète des probabilités s'occupe d'événements dans le cadre d'un univers fini ou dénombrable. Exemples: lancer de dés, expériences avec des paquets de cartes, et marche aléatoire. Définition classique: Initialement, la probabilité d'un événement était définie comme le nombre de cas favorables pour l'événement, divisé par le nombre total d'issues possibles à l'expérience aléatoire. Par exemple, si l'événement est obtenir un nombre pair en lançant le dé, sa probabilité est donnée par Définition moderne : La définition moderne commence par un ensemble appelé univers, qui correspond à l'ensemble des issues possibles à l'expérience dans la définition classique. Il est noté On définit ensuite un événement comme un ensemble d'issues, c'est-à-dire un sous-ensemble de Ω. La probabilité d'un évènement E est alors définie de manière naturelle par : Ainsi, la probabilité de l'univers est 1, et la probabilité de l'événement impossible (l'ensemble vide) est 0. Pour revenir à l'exemple du lancer de dés, on peut modéliser cette expérience en se donnant un univers Ω = {1;2;3;4;5;6} correspondant aux valeurs possibles du dé, et une fonction fqui à chaque La théorie des probabilités continue s'occupe des événements qui se produisent dans un univers continu (par exemple la droite réelle). Définition classique: La définition classique est mise en échec lorsqu'elle est confrontée au cas continu (cf. paradoxe de Bertrand). Définition moderne Si l'univers est la droite réelle La fonction de répartition doit satisfaire les propriétés suivantes : Si Pour un ensemble Si la densité de probabilité existe, on peut alors la réécrire : Tandis que la densité de probabilité n'existe que pour les variables aléatoires continues, la fonction de répartition existe pour toute variable aléatoire (y compris les variables discrètes) à valeurs dans Ces concepts peuvent être généralisés dans les cas multidimensionnel sur La probabilité d'un événement donné A, Historique [modifier]
Théorie des probabilités discrète [modifier]
 , puisque trois faces sur six ont un nombre pair.
, puisque trois faces sur six ont un nombre pair.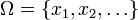 . Ensuite, on a besoin d'une fonction f définie sur Ω, qui va associer à chaque élément de Ω sa probabilité, satisfaisant donc les propriétés suivantes :
. Ensuite, on a besoin d'une fonction f définie sur Ω, qui va associer à chaque élément de Ω sa probabilité, satisfaisant donc les propriétés suivantes :
![f(x)in[0,1]mbox{ pour tout }xin Omega](http://upload.wikimedia.org/math/0/e/7/0e77ec055bf042c11b977174cb518c4d.png)
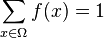

 associe
associe  .
.Théorie des probabilités continue [modifier]
 , alors on admet l'existence d'une fonction appelée fonction de répartition
, alors on admet l'existence d'une fonction appelée fonction de répartition 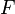 , qui donne
, qui donne  pour une variable aléatoire X. Autrement dit, F(x) retourne la probabilité que X soit inférieur ou égal à x.
pour une variable aléatoire X. Autrement dit, F(x) retourne la probabilité que X soit inférieur ou égal à x.
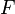 est une fonction croissante et continue à droite.
est une fonction croissante et continue à droite.
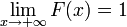
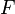 est dérivable, alors on dit que la variable aléatoire X a une densité de probabilité
est dérivable, alors on dit que la variable aléatoire X a une densité de probabilité 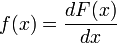 .
.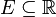 , la probabilité que la variable aléatoire X soit dans
, la probabilité que la variable aléatoire X soit dans 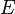 est définie comme :
est définie comme :
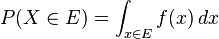
 .
. et d'autres univers continus.
et d'autres univers continus.Principes fondamentaux [modifier]
 , est représentée par un nombre compris entre 0 et 1. L'événement impossible a une probabilité de 0 et l'événement certain a une probabilité de 1. Il faut savoir que la réciproque n'est pas vraie. Un événement qui a une probabilité 0 peut très bien se produire dans le cas où un nombre infini d'événements différents peut se produire. Ceci est détaillé dans l'article Ensemble négligeable.
, est représentée par un nombre compris entre 0 et 1. L'événement impossible a une probabilité de 0 et l'événement certain a une probabilité de 1. Il faut savoir que la réciproque n'est pas vraie. Un événement qui a une probabilité 0 peut très bien se produire dans le cas où un nombre infini d'événements différents peut se produire. Ceci est détaillé dans l'article Ensemble négligeable.
| Évènement | Probabilité |
|---|---|
| probabilité de A | ![mathbb{P}(A)in[0,1],](http://upload.wikimedia.org/math/e/8/0/e80064214aea988389b07fc8d173b9cd.png) |
| probabilité de ne pas avoir A |  |
| probabilité d'avoir A ou B |  |
| probabilité conditionnelle de A, sachant B |
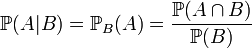 |
| probabilité d'avoir A et B | 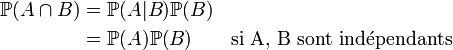 |
Certaines distributions peuvent être un mélange de distributions discrètes et continues, et donc n'avoir ni densité de probabilité ni fonction de masse. La distribution de Cantor constitue un tel exemple. L'approche moderne des probabilités résout ces problèmes par l'utilisation de la théorie de la mesure pour définir un espace probabilisé et aboutir aux axiomes des probabilités développés par Kolmogorov Un espace probabilisé comporte trois parties: Dans cette optique, pour des événements deux à deux disjoints (c'est-à-dire, d'intersection deux à deux vide) A1, A2, A3…, la probabilité de leur union apparaît comme la somme de leurs probabilités, ou, avec les notations mathématiques, C'est le troisième et dernier axiome des probabilités. Par exemple, et toujours pour un dé à 6 faces, la probabilité de tirer un 1 ou un 2 En plus de permettre une meilleure compréhension et une unification des théories discrètes et continues des probabilités, l'approche de la théorie de la mesure nous permet aussi de parler de probabilités en dehors de Certaines variables aléatoires sont fréquemment rencontrées en théorie des probabilités car on les retrouve dans de nombreux processus naturels ; leur loi a donc une importance particulière. Les lois discrètes les plus fréquentes sont la loi uniforme discrète, la loi de Bernoulli, ainsi que les lois binomiale, de Poisson et géométrique. Les lois uniforme continue,normale, exponentielle et gamma sont parmi les plus importantes lois continues. En théorie des probabilités, il y a plusieurs notions de convergence pour les variables aléatoires. En voici une liste: Un processus stochastique est un processus aléatoire qui dépend du temps. Un processus stochastique est donc une fonction de deux variables : le temps et la réalisation ω d'une certaine expérience aléatoire. Quelques exemples d'utilisation des processus stochastiques incluent le mouvement brownien, les fluctuations du marché boursier, ou la reconnaissance vocale. En temps discret, ces processus sont aussi connus sous le nom de Séries temporelles et servent entre autres en économétrie. Parmi les processus stochastiques, les chaînes de Markov constituent l'exemple le plus simple et sans doute celui qui a le plus d'applications pratiques. Une chaîne de Markov est un processus stochastique possédant la propriété markovienne. Dans un tel processus, la prédiction du futur à partir du présent ne nécessite pas la connaissance du passé. Il suffit alors de connaître l'état de la chaîne à un instant t pour savoir comme elle évoluera au temps t+1, il n'est pas nécessaire de connaître tout le passé entre 0 et t pour prévoir l'évolution de la chaîne. Une chaîne en temps discret est une séquence X1, X2, X3, ... de variables aléatoires. La valeur Xn étant l'état du processus au moment n. Si la distribution de probabilité conditionnellede Xn+1 sur les états passés est une fonction de Xn seulement, alors de façon mathématique: où x est un état quelconque du processus, Cette propriété de Markov s'oppose à la notion d'hystérésis où l'état actuel dépend de l'histoire et non seulement de l'état actuel. Ces chaînes de Markov ou des modèles de Markov cachés interviennent dans l'étude de la marche aléatoire et ont de nombreux champs d'application: filtre anti-spam, mouvement brownien, hypothèse ergodique, théorie de l'information,reconnaissance des formes, algorithme de Viterbi utilisé en téléphonie mobile, etc... Citons entre autres comme cas particuliers de chaînes de Markov la marche aléatoire qui sert en particulier à l'étude de la diffusion ou du jeu de pile ou face. Une marche aléatoire est une chaîne de Markov où la probabilité de transition ne dépend que de x-y. Autrement dit une chaîne de Markov où l'on a: P(Xn + 1 = x | Xn = y) = f(x − y). Un jeu de pile ou face où l'on jouerait 1 à chaque lancer est un exemple de marche aléatoire. Si on a y après n lancers,P(Xn + 1 = x | Xn = y) = 1 / 2 si (x-y)=+1 ou -1 et 0 sinon. (on a une chance sur deux de gagner 1 et une chance sur deux de perdre 1) Les équations différentielles stochastiques sont une forme d'équation différentielle incluant un terme de bruit blanc. Ces équations différentielles stochastiques remplacent les équations différentielles ordinaires lorsque l'aléatoire entre en jeu. Au premier ordre par exemple: Pour faire une analogie avec la physique, μ(X(t)) est la vitesse moyenne au point X(t) et σ est lié au coefficient de diffusion (voir à ce propos l'exemple donné dans lemme d'Itô). Lelemme d'Itô et l'intégrale d'Itô permettent alors de passer de ces équations stochastiques à des équations aux dérivées partielles classiques ou à des équations intégrales. Par exemple en utilisant le lemme d'Itô on obtient pour la probabilité de se trouver à l'instant t au point x: Ce lemme est particulièrement important car il permet de faire le lien entre l'étude d'équations stochastiques et les équations aux dérivées partielles qui relèvent de l'analyse. Ce lemme permet entre autres d'obtenir les équation de Fokker-Planck en physique et de traiter le mouvement brownien par des équations aux dérivées partielles classiques ou de modéliser les cours de la bourse en Mathématiques financières. 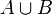 est la réunion de A et B.
est la réunion de A et B.  est l'intersection de A et de B.
est l'intersection de A et de B. 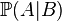 est appelé la probabilité conditionnelle de A sachant B. C'est la probabilité d'avoir A quand on sait que l'on a B. Par exemple, pour un dé à 6 faces la probabilité d'avoir un 2 (A) quand on sait que le résultat est pair (B) est égal à
est appelé la probabilité conditionnelle de A sachant B. C'est la probabilité d'avoir A quand on sait que l'on a B. Par exemple, pour un dé à 6 faces la probabilité d'avoir un 2 (A) quand on sait que le résultat est pair (B) est égal à  car la probabilité d'avoir à la fois un 2 et un nombre pair est égal à 1/6 et la probabilité d'avoir un nombre pair est égal à 1/2. Ici on remarque que
car la probabilité d'avoir à la fois un 2 et un nombre pair est égal à 1/6 et la probabilité d'avoir un nombre pair est égal à 1/2. Ici on remarque que  car on a toujours un nombre pair quand on a 2.
car on a toujours un nombre pair quand on a 2.La théorie des probabilités aujourd'hui [modifier]
 : C'est une tribu sur les événements Ω. Cet ensemble contient tous les résultats possibles de l'événement au sens large. Par exemple pour un dé à 6 faces il contient la possibilité d'avoir un 1 ou un 2: {1, 2}, la possibilité de ne rien sortir comme résultat: l'ensemble vide
: C'est une tribu sur les événements Ω. Cet ensemble contient tous les résultats possibles de l'événement au sens large. Par exemple pour un dé à 6 faces il contient la possibilité d'avoir un 1 ou un 2: {1, 2}, la possibilité de ne rien sortir comme résultat: l'ensemble vide 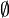 , la possibilité de sortir n'importe quel face du dé {1, 2, 3, 4, 5, 6}. En général en probabilité on se contente de prendre la tribu borélienne. À titre d'exemple la tribu borélienne pour le résultat d'un dé à 4 faces est donné (celle pour le dé à 6 faces est encore plus grande mais suit le même principe):
, la possibilité de sortir n'importe quel face du dé {1, 2, 3, 4, 5, 6}. En général en probabilité on se contente de prendre la tribu borélienne. À titre d'exemple la tribu borélienne pour le résultat d'un dé à 4 faces est donné (celle pour le dé à 6 faces est encore plus grande mais suit le même principe):
 : Cette mesure ou probabilité est la probabilité de réaliser l'un des éléments de
: Cette mesure ou probabilité est la probabilité de réaliser l'un des éléments de  . Cette probabilité est comprise entre 0 et 1 pour tous les éléments de
. Cette probabilité est comprise entre 0 et 1 pour tous les éléments de  , c'est lepremier axiome des probabilités. Par exemple pour un dé a 6 faces: la probabilité d'avoir {1} est 1/6, la probabilité de Ω={1, 2, 3, 4, 5, 6}, tirer n'importe laquelle des 6 faces, est 1 (ceci est aussi toujours le cas, c'est le deuxième axiome des probabilités), la probabilité de l'ensemble vide ø est 0. Ceci est toujours le cas, c'est également une conséquence des axiomes des probabilités.
, c'est lepremier axiome des probabilités. Par exemple pour un dé a 6 faces: la probabilité d'avoir {1} est 1/6, la probabilité de Ω={1, 2, 3, 4, 5, 6}, tirer n'importe laquelle des 6 faces, est 1 (ceci est aussi toujours le cas, c'est le deuxième axiome des probabilités), la probabilité de l'ensemble vide ø est 0. Ceci est toujours le cas, c'est également une conséquence des axiomes des probabilités.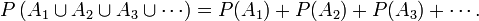
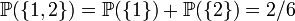
 , notamment dans la théorie des processus stochastiques. Par exemple pour l'étude du mouvement brownien, la probabilité est définie sur un espace de fonctions.
, notamment dans la théorie des processus stochastiques. Par exemple pour l'étude du mouvement brownien, la probabilité est définie sur un espace de fonctions.Lois de probabilité [modifier]
Convergence de variables aléatoires [modifier]
 converge en loi vers la variable aléatoire
converge en loi vers la variable aléatoire  si et seulement si la suite des mesures images
si et seulement si la suite des mesures images  converge étroitement vers la mesure image μX. En particulier dans le cas réel, il faut et il suffit que les fonctions de répartition convergent simplement vers la fonction de répartition de X en tout point de continuité de cette dernière.
converge étroitement vers la mesure image μX. En particulier dans le cas réel, il faut et il suffit que les fonctions de répartition convergent simplement vers la fonction de répartition de X en tout point de continuité de cette dernière. converge en probabilité vers
converge en probabilité vers  ssi
ssi  ,
,  . Cette convergence implique la convergence en loi.
. Cette convergence implique la convergence en loi. converge presque sûrement vers
converge presque sûrement vers  ssi
ssi  . Elle implique la convergence en probabilité, donc la convergence en loi.
. Elle implique la convergence en probabilité, donc la convergence en loi. :
:  converge dans
converge dans  vers
vers  ssi
ssi 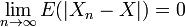 . Elle implique aussi la convergence en probabilité.
. Elle implique aussi la convergence en probabilité.Le calcul stochastique [modifier]
Chaîne de Markov [modifier]

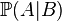 est la probabilité d'avoir A quand on sait que l'on a B par exemple ici la probabilité d'avoir une certaine valeur pour Xn + 1 quand on connaît la valeur de Xn. L'identité ci-dessus est la propriété de Markov pour le cas particulier d'une chaîne en temps discret. La probabilité P(Xn + 1 = x | Xn = y) est appelée la probabilité de transition de x à y ; c'est la probabilité d'aller de x à y au temps n et a une importance particulière pour l'étude de ces chaînes. Nous considérons ici uniquement des chaînes de Markov en temps discret mais il faut savoir qu'il existe une généralisation en temps continu.
est la probabilité d'avoir A quand on sait que l'on a B par exemple ici la probabilité d'avoir une certaine valeur pour Xn + 1 quand on connaît la valeur de Xn. L'identité ci-dessus est la propriété de Markov pour le cas particulier d'une chaîne en temps discret. La probabilité P(Xn + 1 = x | Xn = y) est appelée la probabilité de transition de x à y ; c'est la probabilité d'aller de x à y au temps n et a une importance particulière pour l'étude de ces chaînes. Nous considérons ici uniquement des chaînes de Markov en temps discret mais il faut savoir qu'il existe une généralisation en temps continu.Équations différentielles stochastiques [modifier]


Voir aussi [modifier]
Articles connexes [modifier]
Liens externes [modifier]
22:52 Publié dans Théorie des probabilités | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
JOURNAL OF NONCOMMUTATIVE GEOMETRY
The Journal of Noncommutative Geometry covers the noncommutative world in all its aspects. It is devoted to publication of research articles which represent major advances in the area of noncommutative geometry and its applications to other fields of mathematics and theoretical physics. Topics covered include in particular: DOI: 10.4171/JNCG Source : http://www.ems-ph.org/journals/journal.php?jrn=jncgJOURNAL OF NONCOMMUTATIVE GEOMETRY
The Journal of Noncommutative Geometry is covered in:
Mathematical Reviews (MR), Current Mathematical Publications (CMP), MathSciNet, Zentralblatt für Mathematik, Zentralblatt MATH Database, Science Citation Index Expanded (SCIE), CompuMath Citation Index (CMCI), Current Contents/Physical, Chemical & Earth Sciences (CC/PC&ES), ISI Alerting Services, Journal Citation Reports/Science Edition, Web of Science.
22:46 Publié dans JOURNAL OF NONCOMMUTATIVE GEOMETRY | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Documents d'Alain Connes
Documents
Ouvrages
Derniers articles publiés
Anciens articles récemment mis à disposition
Liste exhaustive des articles à disposition
Articles de synthèse
Cours au Collège de France
Autres conférences
Documents divers
22:44 Publié dans Documents d'Alain Connes | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Szolem Mandelbrojt Collège de France
Professeurs disparus |
22:43 Publié dans Szolem Mandelbrojt, Szolem Mandelbrojt Collège de France | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Szolem Mandelbrojt
Szolem Mandelbrojt, né à Varsovie le 20 janvier 1899 et mort à Paris le 23 septembre 1983 est un mathématicien français d'origine polonaise. Il est membre fondateur du groupeBourbaki. Il est titulaire de la chaire de mathématique et mécanique au Collège de France de 1938 à 1972. Il est élu membre de l'Académie des sciences en 1972. Szolem Mandelbrojt est l'oncle de Benoît Mandelbrot. Dernier né d’une famille nombreuse, ses frères et sœurs, notamment Calel, de quinze ans son aîné, jouent un rôle important dans son éducation. Sa sœur Fanny ainsi que Calel accompagné de sa femme Bertha et de ses deux fils Benoît, futur inventeur des fractales, et Léon le rejoindront en France peu avant la guerre. À Varsovie il s’initie aux mathématiques par la lecture de René Baire, Émile Borel, Georg Cantor et surtout Jacques Hadamard, puis il passe l’année scolaire 1919 à Kharkov où il est l’auditeur unique des cours de Serge Bernstein. Arrivé en France en 1920, il partage un deux pièces avec Georges Politzer, fréquente les philosophes Jean Wahl, Norbert Guterman, les poètes Pierre Morhange, Max Jacob, mais avant tout il suit les cours de Picard, de Lebesgue, et surtout les séminaires et leçons au Collège de France de Jacques Hadamard. Il se lance alors seul dans la théorie du prolongement analytique des séries de Taylor et soutient, encouragé par Paul Montel, sa thèse en 1923. Il est naturalisé Français en 1926. Il succède au Collège de France à Jacques Hadamard en 1938, après avoir été chargé de cours à l’Université de Lille puis professeur à l’Université de Clermont-Ferrand. Membre fondateur du groupe Bourbaki, il s’en écarte pendant la guerre pour continuer à se consacrer à l’analyse mathématique (voir « souvenirs à bâtons rompus… »). Mobilisé en septembre 1939, il décline le classement en « affectation spéciale », qui lui est proposé en tant que professeur au Collège de France, et sert dans une unité combattante. Immédiatement après l’armistice du 22 juin 1940, il est invité à enseigner au Rice Institute à Houston. Il obtient de Vichy un visa de sortie grâce à son service dans une unité combattante et il se rend à Houston avec sa femme Gladys et leur fils Jacques. Après avoir offert ses services dès 1942 aux Forces françaises libres, il est révoqué du Collège de France en 1942. En 1944-45, il est membre de la mission scientifique française auprès des Forces Françaises Libres à Londres créée par Louis Rapkine. Réintégré à la Libération, il reprend son enseignement au Collège de France en 1945. Officier de la Légion d’Honneur, il a obtenu de nombreux prix et distinctions. Il a formé de nombreux mathématiciens, notamment à Clermont-Ferrand le polonais Gorny, puis à Paris les Français Jean-Pierre Kahane, Paul Malliavin, les Israéliens Shmuel Agmon etYitzhak Katznelson, l’Indien U.N.Singh Anecdote : en 1947 Szolem Mandelbrojt organise un congrès d'analyse harmonique à Nancy, et invite Norbert Wiener C'est à la suite de ce congrès qu'est apparu le néologismeCybernétique On pourra avoir une introduction à son œuvre mathématique qui comprend environ 200 articles et plusieurs livres, dans Szolem Mandelbrojt, SELECTA, Gauthier-Villars, 1981. Il a exposé ses idées générales et ses sentiments sur les mathématiques et la création mathématique dans une conférence au Collège Philosophique « Pourquoi je fais des mathématiques » Revue de métaphysique et de morale, 57, no 4, pages 422-429 (octobre-décembre 1952). On pourra également consulter pour sa biographie, ses idées et une description, entre autres, de la vie mathématique d’avant guerre… « Souvenirs à bâtons rompus de Szolem Mandelbrojt recueillis en 1970 et préparés par Benoît Mandelbrot », Cahier du séminaire d’histoire des mathématiques, 6 (1985), pages 1-40. Szolem Mandelbrojt
Biographie [modifier]
Liens externes [modifier]
22:42 Publié dans Szolem Mandelbrojt | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Numdam
NUMDAM Source : http://www.numdam.org/numdam-bin/feuilleter?j=SB
Séminaire Bourbaki |
|||||||||||||||||||||||||||||||||||||||||||||
| 1948-2002
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||
22:40 Publié dans Numdam | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Association des collaborateurs de Nicolas Bourbaki
 |
L'Association des Collaborateurs de Nicolas Bourbaki a été créée en 1935.
Un séminaire de Physique, le Séminaire Poincaré, a été créé en 2001 sur le modèle du Séminaire BourbakiSource : http://www.bourbaki.ens.fr/ |
22:37 Publié dans Association des collaborateurs de Nicolas Bourbaki | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Nicolas Bourbaki
Nicolas Bourbaki est un mathématicien imaginaire, sous le nom duquel un groupe de mathématiciens francophones, formé en 1935 à Besse-et-Saint-Anastaise (Besse-en-Chandesse à l'époque) en Auvergne sous l'impulsion d'André Weil, a commencé à écrire et éditer des textes mathématiques à la fin des années 1930. L'objectif premier était la rédaction d'un traité d'analyse. Le groupe s'est constitué en association, l'Association des amis de Nicolas Bourbaki, le 30 août 1952. Sa composition a évolué avec un renouvellement constant de générations. Sous le nom Nicolas Bourbaki fut publiée une présentation cohérente des mathématiques, appuyée sur la notion de structure, dans une série d'ouvrages sous le titre Éléments de mathématique. Cette œuvre est à ce jour inachevée. Elle a eu une influence sur l'enseignement des mathématiques et sur l'évolution des mathématiques du xxe siècle. Toutefois, elle connaît de nombreuses critiques : incompatibilité[réf. nécessaire] entre le formalisme retenu et la théorie des catégories, style trop rigoureux[réf. nécessaire], manque d'exemples, incompréhension des étudiants, etc. L'activité du groupe cependant a dépassé la rédaction d'ouvrages, par exemple avec l'organisation des séminaires Bourbaki.Nicolas Bourbaki
![]() Pour les articles homonymes, voir Bourbaki.
Pour les articles homonymes, voir Bourbaki.
Sommaire[masquer] |
Le nom de famille Bourbaki était le nom emprunté par Raoul Husson en 1923 lors d'un canular, alors qu'il était élève en troisième année de l'École normale supérieure. Il s'était donné l'apparence d'un mathématicien barbu du nom du professeur Holmgren pour donner une fausse conférence, volontairement incompréhensible et avec des raisonnements subtilement faux1. L'objectif aurait été la démonstration d'un prétendu « théorème de Bourbaki ». Cette histoire amusa tellement le groupe, que le nom « Bourbaki » fut choisi. Le choix de ce nom par Husson connaît trois explications possibles : Le nom Bourbaki a été arrêté en juillet 1935 lors du congrès fondateur de Besse-en-Chandesse. Extrait d'une lettre2 de Jean Dieudonné à la rédaction du Cahiers du séminaire d'histoire des mathématiques : Le prénom Nicolas a été choisi par Éveline de Possel4 à la fin de 19355, afin que puisse être communiquée une fausse note biographique à l'académie des sciences. Toutefois, la mention N. Bourbaki, dans les premiers écrits publiés sous ce nom, ne renvoie pas à l'initiale de Nicolas. N était écrit tant que le nom du professeur était inconnu6. Depuis les débuts, les Éléments de mathématique sont publiés sous le nom de N. Bourbaki. Le seul ouvrage publié sous le nom de Nicolas Bourbaki se trouve être les Éléments d'histoire des mathématiques. On remarquera que si le mathématicien N. Bourbaki parle de « mathématique », l'historien Nicolas Bourbaki parle des mathématiques. En 1935, dans une lettre à Élie Cartan, Weil introduit N. Bourbaki comme un professeur de Poldévie, pays imaginaire d'Europe centrale. D'après Maurice Mashaal, ce risque pris fut une nécessité pour pouvoir publier des travaux sous ce pseudonyme. Une prétendue nation poldève avait déjà été évoquée en 1929 par le journaliste d'Action française Alain Mellet pour mystifier les députés républicains de gauche7. Le nom Poldévie est resté. Il est notamment mentionné comme le lieu de travail de Nicolas Bourbaki dans la Notice sur la vie et l'œuvre de Nicolas Bourbaki. Le groupe Bourbaki s'est constitué dans un contexte où une génération de mathématiciens potentiels avait été décimée par la Première Guerre mondiale. Les jeunes normaliens qui constituèrent le groupe se trouvaient donc sans prédécesseurs immédiats au sein de l'Université, sauf Gaston Julia, et avaient pour interlocuteurs des chercheurs du xixe siècle (Élie Cartan, Henri Lebesgue, Jacques Hadamard8, Picard, Goursat). La critique de Bourbaki portait sur : À l'origine, au début de leurs prises de fonction à l'université de Strasbourg, Henri Cartan et André Weil se retrouvent à devoir enseigner l'intégration et le calcul différentiel. Ils sont alors peu satisfaits des traités disponibles, en particulier du Traité d'analyse d'Édouard Goursatqu'ils utilisent pour leur cours. Leur vient alors l'idée de réunir des amis, également anciens camarades de l'École normale supérieure de la rue d'Ulm (sauf Szolem Mandelbrojt), avec la volonté de rédiger un tel traité les satisfaisant. Le groupe d'amis, les membres fondateurs de ce qui deviendra Bourbaki, est à cette époque composé d'André Weil9 et Jean Delsarte (promotion 1922), d'Henri Cartan, Jean Coulomb et René de Possel (promotion 1923), Jean Dieudonné et Charles Ehresmann (promotion 1924), Claude Chevalley (promotion 1926) et Szolem Mandelbrojt. Parmi les règles qui organisent ce groupe secret de mathématiciens, il est décidé qu'à l'âge de 50 ans, tout membre de Bourbaki devra céder sa place aux jeunes générations. Pour l'anecdote, André Weil, à l'occasion de la fête d'anniversaire des 50 ans de Dieudonné, fit lire au groupe Bourbaki une lettre où il annonçait son retrait du groupe, car il avait lui-même dépassé l'âge limite. Cet éclat (chose à laquelle on peut s'attendre de la part de Weil) eut son effet mais les cinquantenaires traînèrent un peu les pieds pour partir. La première réunion de travail a lieu dans un café du quartier latin10 en décembre 1934. En juillet de l'année suivante, le groupe se retrouve pour la première fois à Besse-en-Chandesse. Ils pensent alors que trois ans seront suffisants pour mener l'entreprise à son terme. En fait, le premier chapitre nécessitera quatre ans de travail et, très rapidement, c'est un traité sur la mathématique qui devient le projet du groupe : les Éléments de mathématique, œuvre collective publiée sous le pseudonyme de N. Bourbaki. L'ampleur de la tâche fait qu'elle se poursuit encore... Le premier volume des Éléments de mathématique à être publié, en 1939, fut le Fascicule de résultats de la Théorie des ensembles. La publication des volumes suivants ne respecta pas l'ordre du traité (Théorie des ensembles, Algèbre, Topologie générale, ...). Même si Nicolas Bourbaki n'est pas mort aujourd'hui, on considère que l'influence de Bourbaki a été la plus importante dans les années 1960-70. À cette époque, son importance était telle que les choix réalisés par Bourbaki ont influencé toute la recherche française en mathématiques, et peut-être même l'enseignement à travers la réforme Lichnerowicz[réf. nécessaire]. Nicolas Bourbaki totalise 5 médailles Fields (la plus importante récompense en mathématiques) à travers Laurent Schwartz (1950), Jean-Pierre Serre (1954), Alexandre Grothendieck(1966), Alain Connes (1982) et Jean-Christophe Yoccoz (1994). Dans la lignée dadaïste de sa naissance, le faire-part de décès suivant fut publié pour annoncer la « mort » de Nicolas Bourbaki : ont la douleur de vous faire part du décès de M. Nicolas Bourbaki, leur père, frère, fils, petit-fils arrière-petit-fils et petit-cousin respectivement pieusement décédé le11 novembre 1968, jour anniversaire de la victoire, en son domicile de Nancago. La crémation aura lieu le samedi 23 novembre 1968 à 15 heures au cimetière des fonctions aléatoires, métro Markov et Gödel. Selon les vœux du défunt, une messe sera célébrée en l'église Notre-Dame des problèmes universels, par son éminence le Cardinal Aleph 1 en présence des représentants de toutes les classes d'équivalence et des corps algébriquement clos constitués. Une minute de silence sera observée par les élèves des Écoles normales supérieures et des classes de Chern. Ce que les mathématiques doivent à Bourbaki est essentiellement : On est redevable à Bourbaki d'un travail de clarification des concepts, de précision dans la formulation, d'une recherche — parfois aride — de structure, de classification systématique et exhaustive des mathématiques. En littérature, l'Oulipo copie indéniablement la « méthode » Bourbaki de travail collectif et de mise en évidence systémique des structures profondes de la création littéraire. À noter qu'un membre important de l'Oulipo, Jacques Roubaud est un mathématicien qui a été très marqué par Bourbaki. C'est par exemple lui qui a écrit l'avis de décès de Bourbaki, sous forme de canular. Le structuralisme lacanien ou celui de Lévi-Strauss en ethnologie, à la même époque, dénote d'une quête de structures fondamentales dont on peut débattre s'il s'agit de l'influence de Bourbaki ou d'un certain « air du temps »15. Le philosophe des sciences Jules Vuillemin fut influencé par Bourbaki (La philosophie de l'algèbre). Il est inutile d'imaginer un groupe qui ait influencé les autres groupes. André Weil (1906) est sensiblement de la même génération qu'André Breton (1896), Jacques Lacan (1900), ouClaude Lévi-Strauss (1908). Tous ces groupes avaient atteint leur apogée en 1964. Une rencontre s'est opérée géographiquement au mois de janvier 1964 lorsque le directeur de l'École normale, Robert Flacelière a mis à la disposition de Jacques Lacan une salle dans les locaux de son école. (Séminaire Livre XI, Les Quatre concepts fondamentaux de la psychanalyse). D'un côté Jacques Lacan souhaitait la venue des mathématiciens pour formuler les structures algébriques et topologiques qu'il considérait à l'œuvre dans la psychanalyse ; de l'autre lesmathématiciens voyaient là, peut-être avec un certain amusement, une application concrète des mathématiques fondamentales. C'est sensiblement à cette époque que le groupe Bourbaki fit paraître la Théorie des ensembles dont Lacan fit un très grand usage. Ce qui distinguerait le groupe des mathématiciens des autres groupes, ce serait son côté fermé et réservé aux mathématiciens de haut niveau de l'École normale supérieure, alors que le structuralisme prétendrait intéresser tous les praticiens des sciences humaines : littérature, politique, psychanalyse, ethnologie, linguistique. Il y a bien sûr un point commun, qui est le retour aux sources, la recherche des fondements et la rupture épistémologique. Mais les deux groupes sont néanmoins restés sur leur quant-à-soi.Explications sur la biographie imaginaire [modifier]
Bourbaki [modifier]
Prénom [modifier]
Poldévie [modifier]
Histoire de Bourbaki [modifier]
Origines [modifier]
L'âge d'or de Bourbaki [modifier]
La mort de Bourbaki [modifier]
On se réunira devant le bar « aux produits directs », carrefour des résolutions projectives, anciennement place Koszul.Héritage et influence [modifier]
En mathématique [modifier]
 pour désigner le produit tensoriel et l'introduction du terme « algèbre multilinéaire » ;
pour désigner le produit tensoriel et l'introduction du terme « algèbre multilinéaire » ;Dans d'autres disciplines [modifier]
Mathématiciens ayant appartenu à Bourbaki [modifier]
Membres fondateurs [modifier]
Membres non-fondateurs [modifier]
Les noms des membres actuels de Bourbaki sont tenus secrets.Membres actuels [modifier]
Références [modifier]
Notes [modifier]
Bibliographie [modifier]
Liens [modifier]
Liens internes [modifier]
Liens externes [modifier]
22:35 Publié dans Nicolas Bourbaki | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Augustin-Louis Cauchy - Œuvres complètes, série 1, tome 1
 |
Augustin-Louis Cauchy - Œuvres complètes, série 1, tome 1 |
Mémoires présentés par divers savants à l'Académie royale des sciences de l'Institut de France et imprimés par son ordre. Sciences mathématiques et physiques. Tome I, imprimé par autorisation du Roi à l'Imprimerie royale; 1827
Table des matières | Texte intégral PDF (Gallica)
22:33 Publié dans Augustin-Louis Cauchy - Œuvres complètes, série 1, | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Augustin Louis Cauchy
Augustin Louis Cauchy
![]() Pour les articles homonymes, voir Cauchy.
Pour les articles homonymes, voir Cauchy.
| Augustin Louis Cauchy | |
|---|---|
 Cauchy vers 1840. Lithographie de Zéphirin Belliard d'après une peinture de Jean Roller. |
|
| Naissance | 21 août 1789 Paris (France) |
| Décès | 23 mai 1857 (à 67 ans) Sceaux (Hauts-de-Seine) (France) |
| Nationalité | |
| Champs | Mathématicien |
| Institution | École polytechnique |
| Diplômé | École polytechnique, École nationale des ponts et chaussées |
| Célèbre pour | Séries (critère de Cauchy), analyse complexe, Algèbre (théorème de Cauchy) |
| Distinctions | Académie des sciences Son nom est sur la Liste des soixante-douze noms de savants inscrits sur la tour Eiffel |
| modifier |
|
Augustin Louis, baron Cauchy, né à Paris le 21 août 1789 et mort à Sceaux (Hauts-de-Seine) le 23 mai 1857, est unmathématicien français, membre de l’Académie des sciences et professeur à l’École polytechnique. Catholique fervent, il est le fondateur de nombreuses œuvres charitables, dont l’Œuvre des Écoles d’Orient. Royaliste légitimiste, il s’exila volontairement lors de l'avènement de Louis-Philippe, après les Trois Glorieuses. Sa position politique et religieuse lui valut nombre d’oppositions. Il fut l'un des mathématiciens les plus prolifiques, quoique devancé par Leonhard Euler, avec près de 800 parutions et sept ouvrages ; sa recherche couvre l’ensemble des domaines mathématiques de l’époque. On lui doit notamment en analyse l’introduction des fonctions holomorphes et des critères de convergence des séries et des séries entières. Ses travaux sur lespermutations furent précurseurs de la théorie des groupes. En optique, on lui doit des travaux sur la propagation des ondes électromagnétiques. Son œuvre a fortement influencé le développement des mathématiques au xixe siècle. La négligence dont fit preuve Cauchy envers les travaux d'Évariste Galois et de Niels Abel, perdant leurs manuscrits, a cependant entaché son prestige.
Sommaire[masquer] |
Né le 21 août 1789 à Paris, Augustin Louis Cauchy est le fils aîné de Louis François Cauchy(1760-1848) et de Marie-Madeleine Desestre (1767- 1839)1. Son père fut premier commis du Lieutenant général de police de Paris Louis Thiroux de Crosne en 1789 ; suite à l’exécution de ce dernier en avril 1794, Louis François se retira à Arcueil pour fuir la dénonciation et la Terreur. Sa famille subit néanmoins la loi du maximum et connut la famine. Il retourna occuper des postes administratifs divers en juillet2 et fut nommé secrétaire général du Sénat conservateur le1er janvier 1800. Il obtint un appartement de fonction au palais du Luxembourg sous l'Empire. Il fut proche du ministre de l’Intérieur et mathématicien Pierre-Simon de Laplace (1749-1827) et du sénateur et mathématicien Joseph-Louis Lagrange (1736-1813). Augustin Louis reçoit une première éducation chrétienne de son père ; il apprend le latin, la littérature et la science. Il fréquente ensuite l’École centrale du Panthéon et se voit décerner en1803 et en 1804 divers prix dans les épreuves littéraires du Concours général3. Il fréquente le lycée Napoléon et a notamment pour professeur Jacques Binet. À 16 ans, en 1805, il est reçu deuxième au concours l'École polytechnique, pour lequel il est interrogé par Jean-Baptiste Biot. Des amis de la famille, Berthollet, Lagrange, et Laplace, l'ont soutenu durant ses études secondaires. Il est reçu premier au corps prestigieux de l'École nationale des ponts et chaussées en 1807. Devenu aspirant ingénieur, il est appelé à participer à la construction du canal de l'Ourcq puis du pont de Saint-Cloud. L’ingénierie apparaissait alors comme le domaine naturel d’application des mathématiques. Le 18 janvier 1810, il est nommé pour s’occuper du chantier du port de Cherbourg, qui devait devenir une position militaire stratégique du Premier Empire. Cauchy quitte ce poste en mars. Pendant son séjour à Cherbourg, il commence ses premiers travaux en mathématiques durant son temps libre, indépendamment des institutions académiques. Après qu’un premier écrit est égaré par Gaspard de Prony(1755-1839)4, il publie, encouragé par Lagrange, ses deux premiers mémoires, portant sur les polyèdres, en février 1811 et en janvier 1812. Il donne aussi des heures officieuses d’enseignement pour préparer des étudiants aux examens d’entrée, et se passionne pour l’histoire naturelle5. Durant une grave maladie (dont les causes peuvent être attribuées à un surmenage6 ou aux séquelles de la famine qu’il connut durant son enfance), il retourne en automne 1812 à Paris, et prend quelques mois de congés. Après qu'un poste de professeur-adjoint lui est refusé, il est appelé par son ancien professeur Pierre-Simon Girard à participer de nouveau en mars 1813 au chantier de l'Ourcq. À cette époque, sous l’influence de Lagrange et de Laplace, il exprime le souhait d’abandonner ses travaux d’ingénieur pour se consacrer aux mathématiques7. Deux demandes auprès de l'Académie des sciences, appelée alors l'Institut, furent appuyées par Laplace et Siméon Denis Poisson(1741-1840), en mai 1813 et en novembre 1814 après la mort de Lagrange et de Lévêque, mais furent toutes deux rejetées8. Cauchy reçoit temporairement un poste à la Société philomathique en décembre 1814. En 1816, il remporte le prix des mathématiques pour des travaux sur la propagation des ondes. Membre de la La Congrégation depuis ses études à Polytechnique9, Cauchy peut bénéficier de l'importance que prend ce mouvement dès le début de la Seconde Restauration. Il devient professeur assistant à l’École polytechnique en novembre 1815, puis professeur d'analyse et de mécanique en décembre. Suite à une ordonnance du 21 mars 1816 rétablissant les Académies, il intègre l'académie des sciences sous nomination royale, parallèlement au renvoi d'importants mathématiciens connus pour leurs positions républicaines et libérales, Lazare Carnot(1753-1823) et Gaspard Monge (1746-1818)10. Cauchy est durement accusé par ses pairs : « Il accepta sans hésiter, non par intérêt, jamais il ne fut sensible à un motif pareil, mais par conviction11. » En 1818, il épouse Aloïse de Bure12, avec laquelle il aura deux filles, Alicia (1819) et Mathilde (1823). Il donne chaque année à l'École polytechnique un cours d'analyse jusqu'en 1830. Ses collègues, François Arago (1786-1853) et Alexis Thérèse Petit 1791-1820) contestent l'insuffisance supposée de ses cours d'analyse, tandis certains élèves en critiquent la surcharge horaire13. Invité à les rédiger, il publie divers traités durant cette période : une première partie des notes de cours sous le titre Analyse algébrique en 1821 ; puis les notes complètes sous le titre Leçons sur le calcul différentiel en 1829, sans tenir compte des exigences de ses collègues et du ministère. À l'issue des Trois glorieuses (juillet 1830), son cléricalisme revendiqué et sa position antilibérale le contraignent à l'exil. En effet, royaliste dévoué à Charles X, il refuse de prêter serment au nouveau roi Louis-Philippe comme l'exige la loi du 30 août 1830. En conséquence, il perd son poste à l’École polytechnique en novembre. À cause de son attachement à la dynastie des Bourbons et par réaction au soutien des étudiants de l’École polytechnique à la Révolution, Cauchy s'exile volontairement à Fribourg en Suisse en septembre 1830, sa femme et ses enfants restant à Paris14. Il tente vainement d'y fonder une Académie où les savants émigrés pourraient enseigner15. Sur invitation du roi de Piémont, Charles-Albert, il occupe la chaire nouvellement créée de physique sublime à l'université de Turin en janvier 1832. Il effectue un voyage à Rome et est reçu par le pape Grégoire XVI. Après l’enlèvement de son frère cadet Amédée Cauchy à 26 ans, Augustin fait deux voyages consécutifs à Paris. Refusant de rentrer en France malgré les demandes réitérées de sa famille, il accepte l’invitation du roi en exil Charles X de devenir le précepteur du duc de Bordeaux Henri d'Artois(1820-1883). Il est choisi pour ses connaissances scientifiques et son attachement à la religion. Il s’installe en 1833 à Prague, bientôt rejoint par sa femme en 1834. Devenu membre de l’Académie de Prague, il séjourne en 1835 à Toeplitz, puis en 1836 à Budweitz, Kirchberg, et Gloritz. En remerciement pour son dévouement, Charles X le crée baron en 1839. Il regagne Paris fin 1838, souhaitant rester politiquement neutre, et reprend sa place à l'Académie. Toutefois, il ne récupère pas son poste d’enseignant à l’École polytechnique. Alors qu'il avait peu publié durant son séjour en Allemagne, il publie près d’un article par semaine de 1839 à février 1848, excepté en 1844. En novembre 1839, il est élu pour succéder àGaspard de Prony au Bureau des longitudes. Mais, parce qu'il refuse de prêter serment, sa nomination est officiellement rejetée par le gouvernement en 1843. Il rend l’affaire publique en décembre. La même année, il est candidat à la chaire de mathématiques du Collège de France, laissée vacante après la mort de Lacroix (1765-1843), qu'il se voit refuser au profit ducomte Libri. L’insurrection en février 1848 conduit à la suppression temporaire du serment politique. Après la fuite du comte Libri pour poursuites judiciaires pour vols et vente illégale de livres, Cauchy postule à nouveau à la chaire de mathématiques du Collège de France, mais se retire au profit de Joseph Liouville (1809-1882), finalement élu en janvier 1851. En 1849, Cauchy devient, à la suite d'Urbain Le Verrier (1811-1877), titulaire de la chaire d'astronomie mathématique à la Faculté des sciences de Paris. Victor Puiseux, un de ses amis et élèves, lui succèdera à sa mort. Il prend aussi une chaire à la Sorbonne. Cauchy refuse de prêter serment à Napoléon III (1808-1873), en 1852. Il n'en est cependant pas moins maintenu dans ses fonctions, grâce à l'intervention d’Hippolyte Fortoul (1811-1856)16. En 1857, Cauchy est impliqué dans des querelles à propos de la mécanique. Le 23 mai vers 4 h du matin heure locale, il meurt d'un rhume dans la maison familiale de sa femme à Sceaux. Il est enterré au cimetière de Sceaux17. Son dernier vœu fut que son œuvre fasse l'objet d'une publication intégrale18. Catholique convaincu, proche des Jésuites, Augustin Cauchy s’engagea dans une confrérie, la Congrégation, lors de ses études. Il fut critiqué dès son séjour à Cherbourg pour son usage de prier matin et soir : « On dit que ma dévotion me fera tourner la tête19. » De retour à Paris, il utilisa à plusieurs reprises sa position à l’Académie pour promouvoir sa pensée. Il défendait notamment ouvertement le créationnisme. En1824, il condamna les recherches en neurologie de Franz Joseph Gall (1758-1828). Sa prise de position, considérée comme non scientifique, fut fortement condamnée dans la presse écrite par Stendhal (1783-1842) dans deux articles successifs. Il éprouvait une antipathie pour les idées libérales issues du xviiie siècle et s’engagea pour la liberté d’enseignement en défendant les écolesjésuites dès son retour en France en 1838. Supprimées en 1772 et rétablies sous la Restauration, elles furent remises en cause sous la Monarchie de Juillet. Engagé aux côtés de Xavier de Ravignan, prêtre de Notre-Dame, Cauchy fit appel à l’Institut : « Catholique, je ne peux rester indifférent aux intérêts de la religion ; géomètre, je ne peux rester indifférent aux intérêts de la Science. […] Vous ne considérez pas comme des ennemis de la civilisation, ceux-là même qui ont éclairé et civilisé tant de peuples divers20. » Pierre-Antoine Berryer (1790-1868),Charles de Montalembert (1810-1870) et de Vatisménil le soutinrent dans sa démarche. Il est probable que les raisons pour lesquelles il ne put entrer au Collège de France en 1843 soient son engagement aux côtés des jésuites et la forte opposition du comte Libri21. Seuls certains établissements des jésuites furent finalement fermés en 1845. L’affaire prit fin en 1848 : la Deuxième République assura l’indépendance de l’enseignement. Cauchy fonda diverses œuvres catholiques : Cauchy est un monarchiste antilibéral. Il utilisa sa position à l'Académie pour promouvoir la pensée royaliste22, et s’exila volontairement en 1830 pour s’opposer au nouveau régime. Il considérait la dynastie des Bourbons comme « les soutiens de la religion et de la civilisation chrétienne, les défenseurs des idées et des principes auxquels il avait voué de bonne heure son âme et son cœur23. » Son engagement politique lui valut de fortes oppositions au sein de l'Institut, puis de l'Académie, venant notamment de Poinsot ou d'Arago. Cependant, Arago apporta son soutien en1839 à Cauchy pour sa candidature au Bureau des longitudes24. Il connut aussi des oppositions avec les ministères, par son refus réitéré de prêter un serment de fidélité à chaque nouveau régime. Le génie de Cauchy fut reconnu dès son plus jeune âge. Dès 1801, Lagrange eut ce commentaire : « Vous voyez ce petit homme, eh bien ! Il nous remplacera tous tant que nous sommes de géomètres25. » La prédominance de Cauchy en sciences s’explique par la multitude de ses domaines d’études : ses travaux « embrassent à peu près toutes les branches des sciences mathématiques, depuis la théorie des nombres et la géométrie pure jusqu’à l’astronomie et l’optique26. » Bien que ses talents de mathématicien aient été applaudis, les faveurs dont il bénéficia durant la Seconde Restauration ne furent pas appréciées. Critiquant ouvertement Laplace et Poisson, il connut rapidement des conflits avec ses anciens appuis à qui il devait ses premières publications. Ses rapports avec Poisson se dégradèrent avec le temps et une rivalité entre eux s’installa. Ses votes à l’Académie étaient considérés comme orientés. Malgré l’influence de Cauchy sur les nouvelles générations, ses dernières années furent obscurcies par une querelle de priorité en mécanique, où il refusa de reconnaître son erreur. En tant que membre de l’Académie, Cauchy devait lire et corriger les articles envoyés. Il commit une négligence envers les travaux de Niels Henrik Abel (1802-1829) et d'Évariste Galois(1811-1832). Son avis sur le mémoire d'Abel tarda et le rapport fourni en juin 1829 fut finalement défavorable ; les recherches de Galois lui avaient été soumises en mai et n'eurent aucune réponse. Une telle attitude lui a été violemment reprochée. Dans sa biographie, Valson donne une explication : « On doit l’excuser de n’avoir pas toujours eu le temps de s’occuper des publications d’autrui, quand il n’a pas trouvé dans le cours de sa propre vie le loisir nécessaire pour relier et classer ses travaux personnels27. » L’ensemble des travaux de Cauchy furent publiés de 1882 à 1974 chez Gauthier-Villars, dans les Œuvres complètes en 27 tomes qui rassemblent environ 800 articles couvrant l’analyse, l’algèbre, la mécanique et les probabilités28. Lors de la préparation de ses cours et conférences, Cauchy réfléchit sur les fondements de l’analyse et introduisit des définitions rigoureuses de notions seulement intuitivement utilisées avant lui29. Une partie importante de ses travaux concerne l’introduction des fonctions holomorphes et les séries convergentes30. Avant les travaux de Cauchy en analyse, les séries et séries de fonctions étaient couramment utilisées dans les calculs, sans le développement d'un formalisme précis et cela conduisait à des erreurs fréquentes, car les mathématiciens ne se posaient pas de question sur l'éventuelle divergence des séries utilisées, comme l'a remarqué Cauchy. Dans son Cours d’Analyse, il définit rigoureusement la convergence des séries et étudie en particulier les séries à termes positifs : les sommes partielles convergent si et seulement si elles sont bornées. Il donne des résultats de comparaison de séries. Il déduit de la convergence des séries trigonométriques un critère de convergence qui porte aujourd’hui son nom, le critère de Cauchy : si la limite supérieure de la suite | an | 1 / n est strictement inférieure à 1, la série de terme général an converge. Intéressé par les séries entières (appelées alors séries de puissances), il met en évidence l'existence d'un rayon de convergence (qu’il appelle cercle de convergence), et en donne une méthode de calcul, conséquence de son critère de convergence. Il démontre que sous certaines hypothèses, le produit des sommes de deux séries convergentes peut s’obtenir comme la somme d’une série, appelée par la suite produit de Cauchy. Il en donne une version pour les séries entières. Une fonction régulière était à tort considérée comme la somme de sa série de Maclaurin : autrement dit, on pensait à tort qu'une fonction indéfiniment dérivable était déterminée par la suite de ses dérivées successives en un point. En 1822, Cauchy relève deux problèmes : d’une part, le rayon de convergence de cette série entière peut être nul, et d’autre part, sur l’intersection des domaines de définition, la fonction et la somme de sa série de Maclaurin ne sont pas nécessairement égales. Cependant des solutions d’équations différentielles linéaires avaient été exprimées sous forme de séries entières sans aucune justification. Après avoir exhibé des exemples de fonctions plates, Cauchy s’intéresse de près audéveloppement de Taylor, et évalue le reste sous forme de la détermination principale. Il donne ainsi des conditions suffisantes pour obtenir des réponses positives aux questions soulevées. Toujours dans son Cours d’Analyse, il énonce et démontre le théorème des valeurs intermédiaires31, démonstration déjà finalisée par Bolzano en 1817 à partir du critère de Cauchy pour la convergence des suites32. Chez Cauchy, la notion première est celle de quantité variable. C'est à partir de cette notion que sont définies les notions de limite et d'infiniment petit. Ensuite Cauchy définit la continuité à l'aide des infiniment petits : d'un accroissement infiniment petit de x résulte un accroissement infiniment petit de y. Il précise les notions de limite ; et formalise en termes de limites la continuité et la dérivabilité. Il est arrêté dans ses travaux par une nuance qu'il ne perçoit pas : la différence entre convergence simple et convergence uniforme33. Pourtant, la convergence simple (convergence d'une suite de fonctions en chaque point d'évaluation) n'est pas une condition suffisante pour préserver la continuité par passage à la limite. Il est le premier à donner une définition sérieuse de l’intégration. Il définit l’intégrale d’une fonction d’une variable réelle sur un intervalle comme une limite d’une suite de sommes de Riemann prises sur une suite croissante de subdivisions de l’intervalle considéré. Sa définition permet d'obtenir une théorie de l’intégration pour les fonctions continues. Dans son Analyse algébrique, il définit les logarithmes et les exponentielles comme uniques fonctions continues vérifiant respectivement les équations fonctionnelles f(x + y) = f(x)f(y)et f(xy) = f(x) + f(y). Bien qu'il se soit efforcé de donner des bases rigoureuses à l'analyse, il ne s'est pas interrogé sur l’existence du corps des nombres réels, établie plus tard parGeorg Cantor. Dans son cours de Polytechnique, Leçon de calcul différentiel et intégral, il apporte clarté et rigueur aux résolutions des équations différentielles linéaire d'ordre un 34 et s'intéressa aux équations au dérivées partielles (théorème de Cauchy-Lipschitz). On doit à Cauchy l'introduction des fondements de l'analyse complexe. Sous l’influence de Laplace, il présente dans le mémoire Sur les intégrales définies (1814) la première écriture des équations de Cauchy-Riemann comme condition d'analyticité pour une fonction d'une variable complexe. Dans cet article, il s’intéresse à l’intégration d’une fonction analytique d’une variable complexe sur le contour d’un rectangle, donne la définition de résidu, et fournit un premier calcul de résidu. Dans Sur les intégrales définies prises entre des limites imaginaires(1825), il donne la première définition d'intégrale curviligne, démontre l'invariance par homotopie (formulée en termes d'analyse), et énonce précisément le théorème des résidus pour les fonctions analytiques comme outil pour le calcul d'intégrales. En 1831, Cauchy propose une expression du nombre de racines complexes d’un polynôme dans une région du plan complexe. Si F et P sont des polynômes, il démontre : où l'intégrale est prise sur le contour du domaine U, et où la somme porte sur les racines de P appartenant au domaine U. Durant son séjour à Turin, il déduit de la formule de Cauchy précédemment énoncée une expression des coefficients de la série de Taylor d'une fonction analytique d'une variable complexe comme intégrales. Il en déduit les inégalités dites de Cauchy et des résultats sur la convergence des fonctions analytiques d’une variable complexe. Ses travaux seront publiés en 1838 et poursuivis par Laurent, qui fournit comme généralisation des séries entières les séries de Laurent. Vers 1845, Cauchy s'inspire des travaux des mathématiciens allemands sur les nombres imaginaires, et en particulier l'écriture trigonométrique. Il repousse dans un premier temps cet aspect géométrique pour ensuite l'utiliser dans ses propres travaux. Il définit la notion de dérivée d'une fonction d'une variable complexe ; il établit ensuite l'équivalence entre dérivabilité et analyticité, fondant ainsi la définition des fonctions holomorphes. Tous ses résultats précédents sur le sujet concernent les fonctions holomorphes ; la formule de Cauchy devint un outil central dans l’étude des fonctions holomorphes, et il étudie alors à nouveau les équations de Cauchy-Riemann. Lagrange avait démontré que la résolution d’une équation algébrique générale de degré n passe par l’introduction d’une équation intermédiaire : sa résolvante dont le degré est le nombre de fonctions à n variables obtenues par permutation des variables dans l’expression d’une fonction polynomiale. Ce nombre est un diviseur de n! : ce résultat est aujourd’hui vu comme une conséquence de l’actuel théorème de Lagrange. En 1813, Cauchy améliore cette estimation et démontre que ce nombre est supérieur au plus petit diviseur premier de n. Son résultat fut généralisé ensuite en l’actuel théorème de Cauchy. Il fut le premier à réaliser une étude des permutations comme des objets (appelés alors substitutions). Il introduit les écritures encore utilisées aujourd’hui pour noter les permutations ; il définit le produit, l’ordre, et établit l’existence et l’unicité de la décomposition des permutations en produit de cycles (substitutions circulaires) à supports disjoints. Les travaux de Cauchy et de Lagrange sur le sujet sont considérés comme précurseurs de la théorie des groupes. Cependant, Cauchy ne connaissait pas la théorie des groupes et donna sans le savoir une première étude du groupe symétrique. En algèbre linéaire, il écrivit un traité sur le déterminant35 contenant l'essentiel des propriétés de cette application. Il étudia la diagonalisation des endomorphismes symétriques réels et qu'il démontra en dimension deux et trois36 et dans le cas où le polynôme caractéristique ne possède aucune racine multiple37. Enfin, il formalisa la notion de polynôme caractéristique38. En 1811, il s’intéresse dans son premier mémoire à l’égalité de polyèdres convexes dont les faces sont égales. Il propose une démonstration du théorème de Descartes-Euler, concernant les nombres de sommets, de faces et d'arêtes d'un polyèdre convexe. Sa preuve consiste à projeter le polyèdre en un graphe planaire suivant ce qui est aujourd’hui appelé une projection stéréographique. Cependant, Cauchy commit une erreur, en ne faisant pas d’hypothèse claire sur les polyèdres étudiés. Dans son second mémoire en 1812, il donna des formules pour calculer les angles diédraux. En mécanique, Cauchy proposa pour décrire la matière d’opposer à la continuité de la matière un système de points matériels dont les mouvements sont continus. Selon Cauchy, les forces entre ces particules doivent devenir négligeables sur les distances estimables. Cauchy énonça des lois sur les variations de tension, de condensation et de dilatation. Il fit une étude sur l’élasticité des corps. S’intéressant à la variation des molécules d’éther, Cauchy établit les équations de propagation de la lumière en 1829. Il établit les modes depolarisation des ondes planes, mises en évidence par des travaux antérieurs de Fresnel. S’intéressant aux conditions limites au niveau d’une interface, Cauchy démontra les lois de la réflexion et de la réfraction de la lumière. Il retrouva les résultats de Brewster sur la variation de l’angle de polarisation lors d’une réflexion ou d’une réfraction. Enfin, il démontra l’existence d’ondes évanescentes, vérifiée expérimentalement par Jasmin. Sous l’influence de Coriolis, Cauchy étudia la dispersion de la lumière. Ses travaux sur les ombres rejetèrent une des objections à la théorie ondulatoire de la lumière. Il mit en évidence le phénomène de diffraction. En astronomie, sa recherche sur les séries lui permit de réviser la théorie des perturbations mise en place par Lagrange, Laplace, et Poisson pour étudier la stabilité du système solaire. Cauchy s’intéressa de plus près aux calculs astronomiques à partir de son élection au Bureau des Longitudes en 1839. En 1842, il proposa des méthodes de calculs de primitives d’expressions rationnelles en cosinus et sinus ; ces méthodes furent motivées par le développement de la fonction perturbative. En 1845, le mémoire de Le Verrier sur la planète Pallasest vérifié en quelques heures par Cauchy. Les travaux de Cauchy sur le principe du minimax permirent de développer la théorie de la décision statistique. En 1853, il étudia, via leurs fonctions caractéristiques, une famille de distributions paires répondant à un problème variationnel39, parmi lesquelles figurent la loi normale et la loi de Cauchy, découverte par Poisson. Faisant usage des fonctions caractéristiques, il publia une démonstration du théorème central limite. Biographie [modifier]
Sous le Premier Empire [modifier]
Exil [modifier]
Retour en France [modifier]
Position [modifier]
Engagement religieux [modifier]
Engagement politique [modifier]
Position scientifique [modifier]
Travaux [modifier]
Analyse [modifier]
Analyse complexe [modifier]
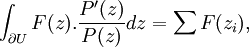
Algèbre [modifier]
Géométrie [modifier]
Mécanique et optique [modifier]
Probabilités [modifier]
Principales publications [modifier]
Hommages [modifier]
Notes et références [modifier]
Bibliographie [modifier]
Liens internes [modifier]
![]()
Liens externes [modifier]
|
Wikimedia Commons propose des documents multimédia libres sur Cauchy. |
22:31 Publié dans Augustin Louis Cauchy | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Espaces préhilbertiens complexes
Définition Une application d'un Une application semi-linéaire est un semi-isomorphisme si et seulement si elle est semi-linéaire et bijective. Une forme semi-linéaire est une application semi-linéaire d'un Etant donnés Une forme sesquilinéaire sur Une forme sesquilinéaire hermitienne Etant donné un produit scalaire hermitien On appelle espace préhilbertien complexe un Remarquons que le fait que pour une forme sesquilinéaire hermitienne Une forme sesquilinéaire est donc semi-linéaire par rapport à la première variable et linéaire par rapport à la seconde. Exemples: Sur Les inégalités de Schwartz Démonstration: Evidente, en utilisant Théorème [Inégalité de Cauchy-Schwartz] Dans un espace préhilbertien complexe Démonstration: Soit Corollaire [Inégalité de Minkowski] Dans un espace préhilbertien complexe Démonstration: Par le lemme Proposition Dans le cas euclidien Espaces préhilbertiens complexes
![]() -espace vectoriel
-espace vectoriel ![]() dans un
dans un ![]() -espace vectoriel
-espace vectoriel ![]() est dite semi-linéaire si
est dite semi-linéaire si ![]()
![]()
![]()
![]()
![]() -espace vectoriel dans
-espace vectoriel dans ![]() .
.![]() et
et ![]() des
des ![]() -espace vectoriel une application
-espace vectoriel une application ![]() de
de ![]() est dite forme sesquilinéaire sur
est dite forme sesquilinéaire sur ![]() si
si ![]()
![]() l'application
l'application ![]() est une forme linéaire sur
est une forme linéaire sur ![]()
![]()
![]() l'application
l'application ![]() est une forme semi-linéaire sur
est une forme semi-linéaire sur ![]()
![]() est dite hermitienne lorsque en outre
est dite hermitienne lorsque en outre ![]() .
.![]() sur
sur ![]() est dite produit scalaire hermitien sur
est dite produit scalaire hermitien sur ![]() si
si ![]() . On note généralement alors
. On note généralement alors![]()
![]() , on définit une norme hermitienne; il s'agit de l'application
, on définit une norme hermitienne; il s'agit de l'application ![]() . On verra plus loin qu'il s'agit d'une norme.
. On verra plus loin qu'il s'agit d'une norme.![]() -espace vectoriel muni d'un produit scalaire hermitien. Un sous-espace vectoriel
-espace vectoriel muni d'un produit scalaire hermitien. Un sous-espace vectoriel ![]() d'un espace préhilbertien complexe
d'un espace préhilbertien complexe ![]() muni d'un produit scalaire hermitien, muni de la restriction du produit scalaire hermitien à
muni d'un produit scalaire hermitien, muni de la restriction du produit scalaire hermitien à ![]() , est appelée sous-espace préhilbertien de
, est appelée sous-espace préhilbertien de ![]() (c'est un espace préhilbertien).
(c'est un espace préhilbertien).![]() On n'a à aucun moment imposé que la dimension soit finie.
On n'a à aucun moment imposé que la dimension soit finie. ![]() La notation
La notation ![]() peut être remplacée par
peut être remplacée par ![]() ,
, ![]() ,
, ![]() , ou même
, ou même ![]() .
. ![]() on ait
on ait ![]() découle du fait que
découle du fait que ![]() est hermitienne; il suffit de vérifier que
est hermitienne; il suffit de vérifier que![]() .
.![]() Une forme linéaire n'est pas nécéssairement une forme semi-linéaire
Une forme linéaire n'est pas nécéssairement une forme semi-linéaire![]() Une forme semi-linéaire n'est pas nécéssairement une forme linéaire
Une forme semi-linéaire n'est pas nécéssairement une forme linéaire![]() le produit scalaire hermitien canonique est défini par
le produit scalaire hermitien canonique est défini par ![]() .
. ![]() et de Minkowski
et de Minkowski![]() montrées dans la partie
montrées dans la partie![[*]](http://www.les-mathematiques.net/images/crossref.png) sont valables ici aussi; mais la démonstration, basée sur la bilinéarité et utilisant les formes quadratiques, n'est plus valable.
sont valables ici aussi; mais la démonstration, basée sur la bilinéarité et utilisant les formes quadratiques, n'est plus valable. ![]()
![]() la partie réelle de
la partie réelle de ![]() .
.
![]() .
.![]()
![]()
![]()
![]()
![]() .
.
![]() l'argument de
l'argument de ![]() , alors pour tout
, alors pour tout ![]() réel, au vu du lemme
réel, au vu du lemme ![[*]](http://www.les-mathematiques.net/images/crossref.png) :
:![]()
![]() est négatif ou nul, ce qui donne l'inégalité annoncée. Le cas d'égalité est le cas où le discriminant est nul.
est négatif ou nul, ce qui donne l'inégalité annoncée. Le cas d'égalité est le cas où le discriminant est nul.![]()
![]()
![]()
![]()
![]() ou
ou ![]() avec
avec ![]() .
.
![[*]](http://www.les-mathematiques.net/images/crossref.png) , on a
, on a![]()
![]()
![]()
![]()
![]()
![]() , retrouver le produit scalaire à partir de la norme était facile; dans le cas hermitien
, retrouver le produit scalaire à partir de la norme était facile; dans le cas hermitien![]() c'est un peu plus compliqué:
c'est un peu plus compliqué:![]()

![]() La dernière ligne est un bon moyen mnémotechnique, mais il faut bien penser que l'on a un signe moins dans le coefficient de l'exponentiel en dehors de
La dernière ligne est un bon moyen mnémotechnique, mais il faut bien penser que l'on a un signe moins dans le coefficient de l'exponentiel en dehors de ![]() et un signe plus à l'intérieur.
et un signe plus à l'intérieur.
![]()
![]()
![]()
![]()
suivant: Espaces préhilbertiens monter: Espaces préhilbertiens et espaces précédent: Espaces préhilbertiens réels IndexC_Antonini,J_F_Quint,P_Borgnat,J_Bérard,E_Lebeau,E_Souche,A_Chateau,O_Teytaud
Source : http://www.les-mathematiques.net/b/c/i/node3.php3
22:29 Publié dans Espaces préhilbertiens complexes | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Inégalité de Cauchy-Schwarz
En mathématiques, l'inégalité de Cauchy-Schwarz, aussi appelée inégalité de Schwarz1, ou encore inégalité de Cauchy-Bunyakovski-Schwarz2, se rencontre dans de nombreux domaines tels que l'algèbre linéaire, l'analyse avec les séries et en intégration. Cette inégalité s'applique dans le cas d'un espace vectoriel sur le corps des nombres réels ou complexes muni d'un produit scalaire. Dans le cas complexe, le produit scalaire désigne une forme hermitienne définie positive. Son contexte général est donc celui d'un espace préhilbertien. Cette inégalité possède de nombreuses applications, comme le fait d'établir l'inégalité triangulaire montrant que la racine carrée de la forme quadratique associée au produit scalaire est une norme, ou encore que le produit scalaire est continu. Elle fournit des justifications ou des éclairages dans des théories où le contexte préhilbertien n'est pas central. Elle doit son nom à Hermann Amandus Schwarz3 et à Augustin Louis Cauchy4.Inégalité de Cauchy-Schwarz
Sommaire[masquer] |
Le théorème s'énonce couramment de la façon suivante : Théorème 1 — Soit De plus, les deux membres sont égaux si et seulement si x et y sont linéairement dépendants. Les démonstrations présentées ici sont valables aussi bien dans le cadre d'un espace préhilbertien complexe que réel, sauf bien sûr la dernière. Lorsque y=0, l'énoncé est clairement vrai, par conséquent on supposera y non nul. En outre, pour la première démonstration, qui est la plus connue, on suppose que le nombre Posons, pour tout réel t, Par construction, cette expression polynomiale du second degré est positive ou nulle pour tout réel t. On en déduit que son discriminant est négatif ou nul : d'où l'inégalité annoncée. Une variante plus directe est de poser et d'utiliser que (Ce t0 n'est autre que la valeur en laquelle P atteint son minimum, mais cette propriété n'est pas utilisée.) Si (x,y) est lié alors x=λy pour un certain scalaire λ et l'on en déduit immédiatement : Réciproquement, si |<x,y>|=||x|| ||y|| alors le discriminant ci-dessus est nul donc P admet une racine réelle (double) t, et pour ce t on a donc x=-ty, si bien que (x,y) est lié. Ou plus directement (avec le t0 de la variante ci-dessus) : l'hypothèse équivaut à P(t0)=0 donc à x=-t0y. Une variante6 utilise l'identité du théorème de Pythagore. Un calcul direct permet de voir que les vecteurs et donc qui donne l'inégalité souhaitée. Cette démonstration consiste en fait6 à calculer la norme du projeté orthogonal du vecteur x sur la droite vectorielle engendrée par y. L'égalité correspond donc au cas où x et y sont linéairement dépendants. Dans l'espace euclidien (Pour n=3, une preuve et une interprétation géométrique figurent dans identité de Lagrange dans R3). Cette identité se démontre de la façon suivante. L'inégalité de Cauchy-Schwarz a des applications importantes. Elle permet notamment de montrer que l'application Elle permet également de définir l'angle non orienté entre deux vecteurs non nuls d'un espace préhilbertien réel, par la formule : Dans le cas de l'espace euclidien Dans le cas des fonctions à valeurs complexes de carré intégrable7, elle s'écrit Cette inégalité est un cas particulier des inégalités de Hölder. L'inégalité seule est vraie dans le contexte un peu plus général d'un semi-produit scalaire (i.e. sans supposer que la forme quadratique associée est définie), en notant encore || || la semi-norme associée : Théorème 210 — Soit Pour démontrer ce théorème 2, il suffit10 d'ajouter à la preuve algébrique de l'inégalité du théorème 1 un petit argument dans le cas où ||y||=0. Cette inégalité fournit le corollaire suivant. Corollaire10 — Pour qu'une forme bilinéaire symétrique positive (resp. une forme hermitienne positive) soit définie, (il faut et) il suffit qu'elle soit non dégénérée. Le corollaire se démontre de la façon suivante. Pour prouver le sens non immédiat de l'équivalence, supposons que la forme Espace euclidien • Espace hermitien • Forme bilinéaire • Forme quadratique • Forme sesquilinéaire • Orthogonalité • Base orthonormale • Projection orthogonale • Inégalité de Cauchy-Schwarz • Inégalité de Minkowski • Matrice positive • Matrice définie positive • Décomposition QR • Déterminant de Gram •Espace de Hilbert • Base de Hilbert • Théorème spectral • Théorème de Stampacchia • Théorème de Riesz • Théorème de Lax-Milgram • Théorème de représentation de RieszÉnoncé [modifier]
 un espace préhilbertien réel ou complexe. Alors, pour tous vecteurs x et y de E,
un espace préhilbertien réel ou complexe. Alors, pour tous vecteurs x et y de E,
Démonstrations [modifier]
 est réel. On obtient la généralisation du cas étudié par multiplication du vecteur x(ou y) par un nombre complexe convenable de module égal à 1. Ceci étant
est réel. On obtient la généralisation du cas étudié par multiplication du vecteur x(ou y) par un nombre complexe convenable de module égal à 1. Ceci étant  devient réel sans changer de module;
devient réel sans changer de module;  et
et  ne varient pas non plus5.
ne varient pas non plus5.Inégalité [modifier]

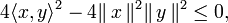
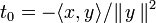
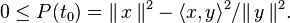
Cas d'égalité [modifier]


Variante géométrique [modifier]
 et
et  sont orthogonaux. Alors, par le théorème de Pythagore on a :
sont orthogonaux. Alors, par le théorème de Pythagore on a :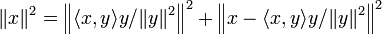 ,
,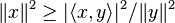
Le cas particulier Rn [modifier]
 muni du produit scalaire usuel
muni du produit scalaire usuel 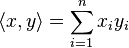 , où
, où 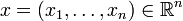 et
et  , une alternative aux démonstrations générales ci-dessus est de déduire l'inégalité (et le cas d'égalité) d'une identité très similaire à celle de la variante géométrique, l'identité de Lagrange, qui s'écrit :
, une alternative aux démonstrations générales ci-dessus est de déduire l'inégalité (et le cas d'égalité) d'une identité très similaire à celle de la variante géométrique, l'identité de Lagrange, qui s'écrit :

Conséquences et applications [modifier]
Conséquences [modifier]
 est une norme car elle vérifie l'inégalité triangulaire. Une conséquence est que le produit scalaire est une fonction continue pour la topologie induite par cette norme.
est une norme car elle vérifie l'inégalité triangulaire. Une conséquence est que le produit scalaire est une fonction continue pour la topologie induite par cette norme.
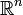 muni du produit scalaire canonique, l'inégalité de Cauchy-Schwarz s'écrit :
muni du produit scalaire canonique, l'inégalité de Cauchy-Schwarz s'écrit :
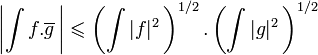 .
.Autres applications [modifier]
On la retrouve aussi dans le théorème de Lax-Milgram.
En théorie des probabilités toujours, dans l'espace des variables aléatoires admettant un moment d'ordre 2, l'inégalité de Cauchy-Schwarz fournit l'inégalité  , qui compare l'espérance du produit de deux variables aléatoires au produit des espérances de leurs carrés8. Elle permet d'établir que le coefficient de corrélation de deux variables aléatoires est un réel compris entre -1 et 19.
, qui compare l'espérance du produit de deux variables aléatoires au produit des espérances de leurs carrés8. Elle permet d'établir que le coefficient de corrélation de deux variables aléatoires est un réel compris entre -1 et 19.
Généralisation [modifier]
 un espace vectoriel réel (resp. complexe) muni d'une forme bilinéaire symétrique positive (resp. d'une forme hermitienne positive). Alors, pour tous vecteurs x et y de E,
un espace vectoriel réel (resp. complexe) muni d'une forme bilinéaire symétrique positive (resp. d'une forme hermitienne positive). Alors, pour tous vecteurs x et y de E,
 est positive et non dégénérée, et montrons qu'elle est définie. Soit x un vecteur dont la semi-norme est nulle. Le théorème 2 montre que pour tout vecteur y on a
est positive et non dégénérée, et montrons qu'elle est définie. Soit x un vecteur dont la semi-norme est nulle. Le théorème 2 montre que pour tout vecteur y on a 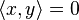 , donc, par non dégénérescence, x = 0.
, donc, par non dégénérescence, x = 0.Références [modifier]
Notes et références [modifier]
 , selon qu'on applique le théorème 1 énoncé en début d'article ou le théorème 2 du paragraphe Généralisation.
, selon qu'on applique le théorème 1 énoncé en début d'article ou le théorème 2 du paragraphe Généralisation.Liens externes [modifier]
Bibliographie [modifier]
22:28 Publié dans Inégalité de Cauchy-Schwarz | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Lemme de Schwarz
Lemme de Schwarz
|
|
Cet article est une ébauche concernant les mathématiques.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
Le lemme de Schwarz est un lemme d'analyse complexe. Lemme — Soit f une fonction holomorphe dans le disque ouvert D de centre 0 et de rayon 1, et telle que : Alors on a : Si, de plus, il existe un élément non nul z0 de D vérifiant | f(z0) | = | z0 | , ou bien si | f'(0) | = 1, alors il existe un nombre complexe a de module 1 tel que f(z) = az pour tout z appartenant à D. Le lemme de Schwarz est utilisé notamment pour déterminer les automorphismes du disque D dans lui-même.


 pour tout z appartenant à D et
pour tout z appartenant à D et  .
.
22:27 Publié dans Lemme de Schwarz | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Théorème de Schwarz
Théorème de Schwarz
|
|
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
Le théorème de Schwarz, également appelé théorème de Clairaut, peut s'énoncer ainsi : Théorème de Schwarz — Soit f, une fonction numérique de n variables, définie sur un ensemble ouvert U de ℝn. Si les dérivées partielles existent à l'ordre p et sontcontinues en un point x de U, alors le résultat d'une dérivation à l'ordre p ne dépend pas de l'ordre dans lequel se fait la dérivation par rapport aux p variables considérées. Dans le cas particulier des fonctions de deux variables x et y, on obtient : Le résultat ci-dessus peut tomber en défaut lorsque les hypothèses ne sont pas vérifiées. Considérons la fonction : Les dérivées sont : et Les dérivées partielles croisées d'ordre 2 en (0,0) sont Considérons la forme différentielle exacte suivante, où f est une fonction de classe C2 : Nous savons alors que : En appliquant le théorème de Schwarz nous en déduisons immédiatement la relation : (par dérivation et inversion de l'ordre de dérivation...)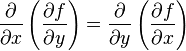
Un contre-exemple [modifier]

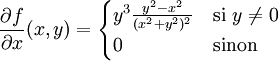
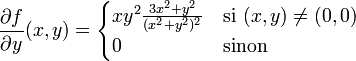
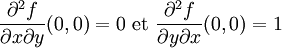
Application du théorème de Schwarz aux formes différentielles exactes [modifier]

 et
et 
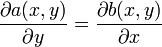
22:26 Publié dans Théorème de Schwarz | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Hermann Amandus Schwarz
Hermann Amandus Schwarz
|
|
Cet article est une ébauche concernant un mathématicien.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
Hermann Amandus Schwarz, né le 25 janvier 1843 à Hermsdorf, en Silésie (aujourd'hui la ville de Jerzmanowa, en Pologne) et mort le 30 novembre 1921 à Berlin est un mathématicien allemand. Ses travaux sont marqués par une forte interaction entre l'analyse et la géométrie. Il a travaillé à Halle, Göttingen puis à Berlin, sur des sujets allant de la théorie des fonctions à la géométrie différentielle en passant par lecalcul des variations.Voir aussi [modifier]
22:25 Publié dans Hermann Amandus Schwarz | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Théorème isopérimétrique
En géométrie, un théorème isopérimétrique traite d'une question concernant les compacts d'un espace métrique muni d'une mesure. Un exemple simple est donné par les compacts d'un plan euclidien. Les compacts concernés sont ceux de mesures finies ayant une frontière aussi de mesure finie. Dans l'exemple choisi, les compacts concernés sont ceux dont la frontière est une courbe rectifiable, c'est-à-dire essentiellement non fractale. Les mesures du compact et de sa frontière sont naturellement différentes, dans l'exemple choisi, la mesure du compact est celle d'une surface, celle de la frontière, une longueur. Un théorème isopérimétrique caractérise les compacts ayant la mesure la plus grande possible pour une mesure de leur frontière fixée. Dans le plan euclidien en utilisant la mesure de Lebesgue, un théorème isopérimétrique indique qu'un tel compact est un disque. En dimension 3, toujours avec une géométrie euclidienne, une autre version du théorème indique que c'est une sphère. D'une manière plus générale, dans un espace euclidien de dimension n, muni de la mesure de Lebesgue, l'optimum est obtenu par une sphère, ce qui donne l'inégalité isopérimétrique suivante, si K est un compact et B la boule unité : Un autre exemple de résultat est obtenu si le choix de la mesure est celui du nombre de points d'un réseau inclus dans le solide K, et si les compacts choisis sont des polytopesconvexes à sommets entiers. En dimension 2 si le réseau est Z2, on trouve le théorème de Pick, indiquant que la mesure du polytope P (c'est-à-dire le nombre de points de Z2 qu'il contient) est égale à sa surface plus la moitié des points que contient sa surface plus un. Un théorème isopérimétrique est souvent difficile à établir. Même un cas simple, comme celui du plan euclidien muni de la mesure de Lebesgue, est relativement technique à démontrer. Une des méthodes partielles de preuve, connue depuis la démonstration de Hurwitz en 1901 est d'utiliser un résultat d'analyse, issu de la théorie des séries de Fourier, connu sous le nom d'inégalité de Wirtinger. Le résultat reste partiel car il ne traite que des surfaces dont la frontière est une courbe de classe C1. Les théorèmes isopérimétriques sont actuellement l'objet d'une intense recherche en mathématiques, en particulier en analyse fonctionnelle et en théorie des probabilité, suite à leurs liens étroits avec les phénomènes de concentration de la mesure. Une approche plus élémentaire est proposée dans l'article Isopérimétrie.Théorème isopérimétrique
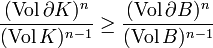
Sommaire[masquer] |
La connaissance de théorème isopérimétrique est ancienne, près de 3 000 ans1. Le résultat essentiel de l'époque est l'œuvre de Zénodore iie siècle av. J.-C. qui démontre un résultat que l'on exprimerait maintenant de la manière suivante : S'il existe un polygone à n côtés de surface maximale à périmètre donné, alors il est régulier2. Cette partie de l'histoire est traitée dans l'article Isopérimétrie. Les études des théorème isopérimétriques datant de l'antiquité se fonde exclusivement sur la géométrie du triangle. Ces méthodes, assez élémentaires, ne permettent pas d'aller beaucoup plus loin. Par exemple, démontrer l'existence d'une solution est hors de portée. Il faut attendre près de 2 000 ans pour que l'étude de cette question soit enrichie à l'aide d'apports théoriques de nature différente. Jacques Bernoulli (1654-1705) étudie la question pour répondre à des questions de mécanique statique et plus précisément s'intéresse à la forme que doit posséder une poutre pour offrir le maximum de résistance possible, la résolution d'une telle question débouche sur un théorème isopérimétrique, le demi-cercle est parfois la forme offrant la meilleure résistance. Si Bernoulli ne parvient pas à finaliser un résultat, il utilise de nouveaux outils issus du calcul différentiel. Le mariage de la géométrie et de l'analyse est promis à un grand avenir, même si un théorème isopérimétrique n'est pas encore accessible. Le xixe siècle est celui des progrès majeurs. La première avancée est le fruit du travail de Jakob Steiner (1796-1863). Il montre que, si une solution existe, elle est nécessairement unique et c'est le disque. Pour cela, il développe un outil, maintenant appelé symétrisation de Steiner3 et encore utilisé pour établir des théorèmes d'isopérimétrie. Son idée majeure consiste à remarquer que, si l'on coupe une solution à l'aide d'une droite en deux parties de surfaces égales, il est possible de construire une nouvelle surface optimale à l'aide de la duplication d'une des deux parties. Sa démonstration est présentée dans l'article Isopérimétrie. Pour l'obtention d'une preuve complète, au moins en dimension 2, une difficulté majeure n'est toujours pas franchie, celle de la preuve de l'existence d'une solution. Les premiers éléments de réponse proviennent de la démarche initiée par Bernoulli. Une hypothèse supplémentaire, un peu étrange, est supposée : la frontière de la surface est lisse. L'étrangeté provient du fait qu'une ondulation sur la surface a tendance à plus augmenter le périmètre que l'aire. Plus la courbe frontière est irrégulière, plus elle est loin de l'optimale, mais plus la démonstration devient difficile4. Karl Weierstrass (1815-1897) formalise le calcul des variations et établit les bases de l'analyse fonctionnelle. Cette approche consiste à étudier non pas une courbe spécifique, mais un ensemble de courbes qui varient, par exemple à l'aide d'un paramètre. En faisant varier ces courbes, on montre que le cercle est l'optimum recherché5. Au moins pour la dimension 2, une fois l'existence d'un optimum établi pour les surfaces à la frontière régulière, il n'est plus trop difficile de montrer le théorème général, on sait en effet approximer une courbe fermée continue par une autre continûment dérivable. La généralisation aux dimensions supérieures est naturelle. Dans un premier temps, on suppose l'existence d'une solution au théorème et on montre que cette solution est nécessairement une sphère de dimension n. Le raisonnement est très physique, c'est celui qui détermine la forme d'une bulle de savon. L'équilibre de la bulle est le fruit de deux forces qui s'annulent : la pression due à l'aire enfermée dans la bulle et la tension superficielle de la surface. Un rapide calcul de variation montre que la courbure moyenne de la sphère est nécessairement constante. En 1900, on sait que le seul compact strictement convexe de courbure moyenne constante est une sphère6. Une fois encore, la démonstration de l'existence d'une solution s'avère la partie délicate. Une première démonstration en dimension 3 est l'œuvre H. A. Schwarz en 18907.8 Si la démarche fondée sur le calcul variationnel débouche, la généralisation à des dimensions supérieures n'est pas aisée. Une autre approche, issue de la théorie algébrique des nombres est finalement plus prometteuse. Hermann Minkowski (1864-1909) développe une approche géométrique qui l'amène à étudier le nombre de points à coordonnées entières que contiennent certains convexes, problème proche de l'isopérimétrie. La fonction qui associe à un convexe compact de Rn, le cardinal de son intersection avec le réseau Zn est une mesure. Le théorème de Minkowski, qui procède de cette logique, permet d'élucider de manière élégante la structure du groupe des classes d'idéaux. Une nouvelle structure géométrique est étudiée ; au lieu de considérer une géométrie euclidienne de dimension n, Minkowski étudie un ensemble dont les points sont des compacts convexes. Cet ensemble est muni d'uneaddition. Felix Hausdorff (1868-1942) trouve une distance naturelle pour un espace un peu plus vaste, celui des compacts. La topologie associée à cette distance est bien adaptée. Les fonctions volumes et surfaces, qui associent à un convexe compact sa mesure et la mesure de sa frontières sont continues. Il en est de même pour la somme de Minkwoski. Enfin, l'espace est complet ainsi que le sous-ensemble des convexes. Enfin les polytopes forment un ensemble dense. En dimension 2, l'étude de la somme de Minkwoski et de la sphère de rayon t et de centre le vecteur nul avec un convexe compact donne l'expression polynomiale a + pt + πt2, où adésigne l'aire du convexe et p son périmètre. Démontrer le théorème isopérimétrique en dimension 2 revient à montrer que p2 est plus grand que 4πa, ce qui revient à dire que l'expression polynomiale précédente admet des racines réelles, ce que fait Minkowski9. T. Bonnesen va plus loin, en 1921 il démontre que si r est le rayon d'un cercle inscrit et R le rayon d'un cercle circonscrit, on dispose de la majoration suivante10 : Autrement dit, l'égalité ne peut avoir lieu que si le convexe est un disque. Cette démarche peut être généralisée aux dimensions supérieures. A. Aleksandrov et W. Fenchel utilisent cette démarche pour établir le théorème isopérimétrique général, pour les géométries euclidiennes et la mesure de Lebesgue11 en 1937.12 Dans tout le paragraphe, S désigne une surface fermée convexe d'un plan euclidien dont l'aire, noté a, est finie et strictement positive ; le périmètre l'est aussi et est noté p. Dans le plan euclidien, le théorème isopérimétrique prend la forme suivante : Ce théorème est souvent exprimé sous une forme équivalente, dite inégalité isopérimétrique : Aucune hypothèse n'est nécessaire sur la nature de la surface. Cependant, si elle n'est pas suffisamment régulière, le périmètre n'est pas fini, l'inégalité ne possède alors aucun intérêt. En dimension 2, on dispose d'une propriété qui simplifie grandement les choses : Intuitivement, ce théorème est relativement évident. L'enveloppe convexe de S possède une aire strictement plus grande et un périmètre strictement plus petit que S, si l'ensemble n'est pas convexe. Pour cette raison, il est pertinent de ne s'intéresser qu'aux surfaces convexes. Comme l'aire et le périmètre, s'ils existent, d'un convexe est le même que celui de son adhérence, se limiter aux convexes fermés ne réduit en rien la généralité des solutions trouvées. Enfin, comme toute surface de périmètre fini est bornée, si elle est fermée, elle est nécessairement compacte (cf. l'article Topologie d'un espace vectoriel de dimension finie). L'article Isopérimétrie établit encore deux résultats à l'aide de la géométrie du triangle : La partie plus difficile à établir est l'existence de telles surfaces. Une première manière de simplifier la question est du supposer que la frontière est suffisamment régulière. En 1904, Hurwitz propose une démonstration particulièrement élégante13, qui se fonde sur l'inégalité de Wirtinger : Le prix à payer contre l'élégance et la simplicité est le caractère partiel de la solution. L'existence d'une solution optimale est bien démontrée, mais uniquement si la frontière est lisse. Or la frontière peut être quelconque. Évidemment, si elle n'est pas finie, la formule est vraie mais possède peu d'intérêt.14 Les démonstrations historiques ont toutes un chainon manquant. Elles montrent qu'une surface, polygonale ou quelconque, qui ne possède pas la bonne propriété : être régulier ou être un disque, n'est pas un optimum. En revanche, elle ne montre pas qu'un tel optimum existe. Une fois l'existence d'un tel optimum démontrée, on sait alors qu'il est unique et l'on connait sa géométrie. Mais la démonstration de cette existence est l'élément qui bloque les démonstrations pendant de si nombreux siècles. Elle demande une compréhension d'un aspect alors mal maitrisé de la géométrie : la topologie. Les preuves actuelles procèdent d'une démarche encore inconnue à l'époque de Steiner. La géométrie étudiée n'est plus le plan euclidien, support de la surface étudiée, mais un univers où chaque point est une surface. Elle est illustrée sur la figure de gauche dans le cas particulier des triangles. La fonction considérée est celle qui, à un triangle de périmètre 3, associe son aire. Le triangle est représenté par deux paramètres,c la longueur d'une arête et φ l'angle entre deux arêtes dont celle de longueur c. Si l'angle est de mesure nulle ou égale à π, l'aire est nulle, il en est de même si c est égal à 0 ou à 3/2. La représentation graphique montre que le maximum est bien atteint. Dans ce cas particulier, le sommet est le triangle décrit par le couple (1, π/3). Dans le cas des polygones à n sommets, où n est un entier supérieur à 2, la configuration est relativement simple. On identifie un polygone à un vecteur de R2n. L'ensemble des polygones devient une partie d'un espace vectoriel euclidien, cette fois-ci, de dimension 2n. La topologie d'un espace euclidien dispose d'une propriété adéquate. Un théorème assure que les ensembles fermés et bornés sont des compacts. La fonction, qui à un polygone associe son aire est continue. Un des charmes des compacts est que toute fonction continue, définie sur un compact et à valeur dans R atteint ses bornes. La configuration est analogue à celle de la figure de gauche. Ce qui permet d'établir le chainon manquant : Pour le cas général, une démarche analogue à la précédente ne permet pas de conclure. En se limitant aux convexes compacts, la zone qui nous intéresse est bien un fermé borné, mais la dimension de l'espace est ici infinie. Or si la dimension n'est pas finie, le théorème de Riesz montre qu'un fermé borné comme la boule unité n'est jamais compact. De plus, la fonction périmètre n'est plus continue, on peut approcher de plus en plus précisément un disque de rayon 1 par des carrés de plus en plus petits, l'approximation garde un périmètre égal à 8 sans s'approcher de la valeur 2π, même si elle devient excellente. En revanche, il est possible d'approcher précisément la frontière d'un convexe compact par un polygone de périmètre plus petit et de surface presque égale à celle du convexe. Cette propriété, et le fait d'avoir établi le théorème isopérimétrique pour les polygones, permet aisément de montrer qu'aucune surface de périmètre p ne peut posséder une aire supérieure à celle d'un disque de même périmètre. Le disque est ainsi un des optimums recherchés, et les travaux de Steiner montrent que cet optimum est unique. On pourrait croire que les deux démonstrations précédentes closent le débat du problème isopérimétrique du plan euclidien E. Il n'en est rien. La démarche d'Hurwitz n'apporte aucune information si la frontière n'est pas suffisamment lisse. Celle présentée au dernier paragraphe se généralise mal aux dimensions supérieures. A partir de la dimension 3, il ne faut plus espérer trouver des polyèdres convexes réguliers, encore appelés solides de Platon approchant avec la précision voulue la sphère. Il n'existe que 5 solides de ce type. Hausdorff et Minkowski développent une autre approche, fondée sur une géométrie un peu différente. Ici, le terme de géométrie désigne l'étude d'un ensemble muni d'une distance et d'une opération algébrique compatible. L'espace considéré est celui des compacts non vides, la distance celle deHausdorff et l'opération est la somme de Minkowski, dont la compatibilité avec la distance se traduit par la continuité de l'opération. La somme de Minkowski P + Q correspond à l'ensemble des sommes dont le premier membre est élément de P et le second de Q : Si S désigne un convexe compact non vide et t.B la boule fermée de centre le vecteur nul et de rayon t, l'aire de la somme S + t.B prend la forme suivante, connue sous le nom de formule de Steiner-Minkowski :15 Ici, a désigne l'aire de S et p son périmètre. Cette somme est illustrée sur la figure de gauche dans le cas d'un hexagone. La somme correspond à l'ensemble des points du plan à une distance inférieure ou égale à t de S. Appliquer à l'hexagone jaune de la figure de gauche, on peut décomposer cette somme en trois régions. La première correspond à la figure initiale Sen jaune, la deuxième aux points situés sur un rectangle de côté une arête du polygone et de largeur t, correspondant aux 6 rectangles bleus. L'aire des surfaces bleues est égale à p.t. Enfin, à chaque sommet est associée une portion de disque de rayon t, en vert sur la figure. L'union de ces portions de disque forme un disque complet, d'où le dernier terme de la formule. La démonstration dans le cas non polygonal est donnée dans l'article détaillé. La surface s'exprime comme un polynôme de degré 2, son discriminant est égal à p2 - 4π.a. On reconnait là le terme de l'inégalité isopérimétrique. Démontrer le théorème revient à dire que le discriminant n'est jamais négatif, ou encore que le polynôme admet au moins une racine. Ce résultat s'obtient directement comme une conséquence de l'inégalité de Brunn-Minkowski. A y regarder de près, le paragraphe précédent propose bien une méthode généralisable pour montrer l'inégalité isopérimétrique, mais elle n'indique pas comment traiter le cas de l'égalité. Plus précisément, la démonstration n'indique pas que seul le cercle est la solution, partie difficile de la démonstration qui a bloqué tant de monde depuis l'Antiquité. Il existe bien une preuve, donnée dans l'article isopérimétrie et fondée sur une symétrisation de Steiner. Elle est mal commode à généraliser en dimension quelconque. Bonnesen trouve une expression simple, en fonction d'un cercle inscrit et d'un circonscrit. Le cercle est dit inscrit dans un compact S s'il est inclus dans S et si son rayon r est maximal. Un cercle est dit circonscrit dans S s'il contient S et si son rayon R est minimal. L'inégalité de Bonnesen s'exprime de la manière suivante, si a est l'aire du compact et p son périmètre16 : Ce résultat signifie que le discriminant du polynôme du second degré, qui à t associe l'aire de la surface S + t.B admet deux racines distinctes si un cercle inscrit possède un rayon strictement plus petit qu'un cercle circonscrit. Autrement dit, pour le l'égalité isopérimétrique ait lieu, il est nécessaire que les deux rayons soient égaux, ce qui ne peut arriver que pour le cercle. Un autre résultat, un peu plus fort indique que les deux valeurs -R et -r se situent entre les deux racines, comme illustré sur la figure de droite. De la même manière, on en déduit la nécessité de l'égalité entre R et r pour atteindre l'optimal. Une bulle de savon est une réponse naturelle au théorème isopérimétrique en dimension 3. La tension superficielle de la bulle possède une énergie potentielle minimale si sa surface l'est. L'équilibre statique est obtenu quand la surface est minimale pour enserrer la quantité d'air enfermée dans la membrane de savon. La sphère est l'unique surface réalisant cet optimum, d'où la forme de la bulle. En dimension trois, on dispose du théorème suivant : De manière plus générale, si μ désigne la mesure de Lebesgue dans un espace euclidien de dimension n, μn-1 la mesure équivalente pour les sous-variétés de dimension n - 1 et si Kest un compact mesurable de frontière aussi mesurable, alors : Ici, B désigne la boule unité. Un rapide calcul permet de déduire de cette majoration les inégalités isopérimétriques pour n égal à 2 ou 3. Certaines démonstrations, établies en dimension 2, se généralisent aisément aux dimensions quelconques. C'est, par exemple, le cas pour la formule de Leibniz donnant l'expression d'un déterminant. Un résultat faisant appel à la topologie est très souvent beaucoup plus complexe à établir. Un exemple célèbre est celui de la conjecture de Poincaré. Si le résultat équivalent en dimension 2 est relativement simple, en dimension 3 il s'avère redoutable à démontrer. Sans atteindre des extrêmes aussi techniques, démontrer le théorème isopérimétrique pour un espace euclidien de dimension quelconque est plus ardu qu'en dimension 2. Une première difficulté, déjà citée, provient du fait qu'il n'existe pas de suite infinie de polygones réguliers convexes à partir de la dimension 3. Cependant, un contournement est aisément imaginable. La géométrie des convexes diffère. A partir de la dimension 3, une enveloppe convexe d'un compact n'est pas nécessairement de frontière de mesure plus petite que la mesure de la frontière du compact. Un contre exemple est donné en dimension 3 par une variété analogue à la chambre à air d'un vélo. Son enveloppe convexe contient deux disques supplémentaires, dont l'aire peut être supérieure à celle de la moitié de la surface de la variété qui n'est pas à la frontière de l'enveloppe convexe. Enfin, le sens à donner au mot mesure de la frontière n'est pas aussi simple à partir de la dimension 3, que dans le plan. Dans le plan, définir la longueur d'une courbe est aisé avec l'approche de Jordan, on considère la borne supérieure de l'ensemble des lignes polygonales sont les sommets sont ordonnés et situés sur la courbe (cf l'article Longueur d'un arc). A partir de la dimension 3, cette démarche n'est plus possible, il existe des suites de polyèdres dont les points sont tous sur la surface d'une portion de cylindre située entre deux plans parallèles dont la suite des surfaces diverge. Un exemple est donné sur la figure de droite. La notion de forme volume permet bien de définir une mesure n - 1 dimensionnelle pour la frontière du compact, elle suppose cependant que la frontière est suffisamment lisse, c'est-à-dire qu'elle définisse une variété de dimension n - 1 de classe C2. Pour obtenir une définition générale de la mesure de la frontière du compact étudié dans un espace euclidien E de dimension n, Minkowski définit la notion de contenu k dimensionnel, ici k désigne un entier plus petit que n. Soit D un compact fermé de E, son contenu k dimensionnel Mn-k(D) est le suivant19 : Ici, Bp désigne la boule unité d'un espace euclidien de dimension p. En toute rigueur, on devrait parler de contenu k dimensionnel inférieur. La figure de droite illustre le concept pour la frontière d'un compact. La partie supérieure de la fraction définissant le contenu correspond au volume d'un tube de section un disque de rayon t si la figure est en dimension 3. Si la frontière est une variété de classe C2, le volume du tube est égal à sa longueur que multiple la surface du disque de rayon t, si t n'est pas trop grand. Le rapport définissant le contenu est toujours égal à la longueur de la variété20 Dans le cas plus général d'une variété compacte de dimension k et de classe C2, le volume du tube s'exprime comme un polynôme de degré n - kdont le terme de plus petit degré est égal à la mesure de la variété. La mesure est alors définie à l'aide de la forme volume canonique. Ce résultat se conçoit bien intuitivement, l'intersection du tube en un point de la variété par l'espace affine orthogonal à la variété en ce point est une boule de dimension n - k et de rayon t. En première approximation, le volume du tube est le produit de la mesure de cette boule par celle de la variété. Le choix du contenu de Minkowski pour mesurer la frontière du compact considéré est pertinent. On peut s'en rendre compte par l'étude de l'égalité isopérimétrique dans le cas d'une boule r.B de rayon r d'un espace euclidien E de dimension n. Sa mesure est égale à21 : Si la surface est désignée par la lettre S, on a : La deuxième égalité indique que le tube engendré par la surface Sn-1 est composé des points de la boule de rayon r + t qui ne sont pas éléments de la boule r - t. Ce volume se calcule aisément : On en déduit : Ce qui est bien l'égalité isopérimétrique. L'inégalité de Brunn-Minkowski permet aisément de démontrer l'inégalité isopérimétrique, dans le cas d'un compact non vide K. Appliquée à K et à t.B, on obtient : Autrement dit : Il suffit de remarquer que le terme de gauche admet pour limite inférieure le contenu n - 1 dimensionnel de la frontière de K. Ce résultat est connu sous le nom de formule de Steiner-Minkowski. On obtient : Ce qui correspond bien à l'inégalité isopérimétrique. Aucune hypothèse n'a été faite sur la nature du compact K.22 La démonstration est à la fois simple et rapide, mais il manque l'unicité de la solution. Des hypothèses supplémentaires permettent une démonstration plus simple de cette unicité. Le cas général ne peut s'exprimer aisément ; pour s'en rendre compte, il suffit de considérer une boule dans laquelle on plante une aiguille infiniment fine. Il existe deux cas où le théorème isopérimétrique s'exprime aisément. Dans le cas des convexes compacts, ou dans le cas des variétés à bord de classe C2, l'unicité de l'optimum se démontre à l'aide de l'inégalité d'Alexandrov-Fenchel.Fragments d'histoire [modifier]
Prémisses [modifier]
Calcul variationnel [modifier]
Géométrie des convexes [modifier]
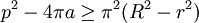
Plan euclidien [modifier]

Démonstrations géométriques élémentaires [modifier]
Calcul des variations [modifier]
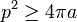
Polygone et Steiner [modifier]
Somme de Minkowski [modifier]

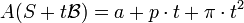
Inégalité de Bonnesen [modifier]
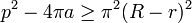
Dimension supérieure [modifier]
Enoncé [modifier]
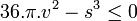
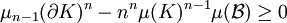
Difficultés [modifier]
Variété différentielle [modifier]
Contenu de Minkowski [modifier]

Egalité isopérimétrique pour la boule [modifier]




Inégalité de Brunn-Minkowski [modifier]
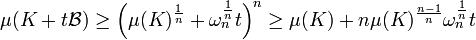
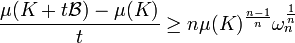
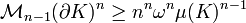
Inégalité d'Alexandrov-Fenchel [modifier]
Voir aussi [modifier]
Notes [modifier]
Références [modifier]
22:24 Publié dans Théorème isopérimétrique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Extrema liés - Multiplicateurs de Lagrange
Analyse -- Fonctions de plusieurs variables
| Théorème : Soient f, g1,..., gp des fonctions de classe C1 sur un ouvert U de Rn, à valeurs dans R et X l'ensemble défini par :X={x de U; g1(x)=...=gp(x)=0}.Si la restriction de f à X admet un extrémum local en a, et si les différentielles dg1(a),...,dgp(a) sont des formes linéaires indépendantes, alors il existe des réels c1,...,cp tels que :df(a)=c1dg1(a)+...+cpdgp(a)Ces réels c1,...,cp sont appelés multiplicateurs de Lagrange. |
Ce théorème a une interprétation géométrique naturelle. Prenons un arc  tracé sur X avec
tracé sur X avec  . La fonction (d'une variable réelle)
. La fonction (d'une variable réelle)  admet un extrémum local en 0, d'où l'on tire :
admet un extrémum local en 0, d'où l'on tire : Maintenant,
Maintenant,  est un vecteur tangent à X en a, et en fait tous les vecteurs tangents à X en a s'obtiennent de cette façon. Ainsi, df(a)(v)=0 pour tout vecteur v tangent à X en a. Mais l'ensemble de ces vecteurs tangents est l'intersection des noyaux de dgi(a) et l'inclusion
est un vecteur tangent à X en a, et en fait tous les vecteurs tangents à X en a s'obtiennent de cette façon. Ainsi, df(a)(v)=0 pour tout vecteur v tangent à X en a. Mais l'ensemble de ces vecteurs tangents est l'intersection des noyaux de dgi(a) et l'inclusion entraine la relation du théorème par un résultat élémentaire d'algèbre linéaire.
entraine la relation du théorème par un résultat élémentaire d'algèbre linéaire.
Exemple
Cherchons le maximum de la fonction sur l'ensemble défini par
sur l'ensemble défini par En un point où le maximum est atteint, on a forcément xi>0 et on peut appliquer le théorème précédent avec g(x)=(x1+...+xn)/n-1. On obtient
En un point où le maximum est atteint, on a forcément xi>0 et on peut appliquer le théorème précédent avec g(x)=(x1+...+xn)/n-1. On obtient Mais
Mais et
et ce qui entraîne
ce qui entraîne En particulier, on obtient que tous les ai sont égaux et qu'il sont tous égaux à 1. Ainsi, sur X, on a f(x)<=1. Par homogénéité, on obtient l'inégalité des moyennes arithmétiques et géométriques
En particulier, on obtient que tous les ai sont égaux et qu'il sont tous égaux à 1. Ainsi, sur X, on a f(x)<=1. Par homogénéité, on obtient l'inégalité des moyennes arithmétiques et géométriques
22:21 Publié dans Extrema liés - Multiplicateurs de Lagrange | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
La méthode du Lagrangien
3.4 La méthode du Lagrangien
La méthode que nous étudions dans cette séance est, en fait, une généralisation de la règle du multiplicateur de Lagrange pour résoudre des problèmes d’optimisation avec des contraintes d’égalité. Nous examinerons le cas d'une seule contrainte à deux variables .
Définition Soit le problème : s.c. .
On appelle Lagrangien associé à ce problème la fonction :
.
Le Lagrangien permet d’introduire la contrainte dans la fonction objectif avec une certaine pénalité . On se retrouve ainsi à maximiser une fonction à trois variables sans contrainte.
Si, maintenant, on cherche les points stationnaires du Lagrangien , cela veut dire que nous cherchons tel que .
Nous déduisons alors le système suivant comportant trois équations:
Dans les deux premières équations, on reconnaît les conditions d’optimum du premier ordre : , alors que la troisième est équivalente à la contrainte de départ imposée par le modèle : , au point (point admissible).
La méthode du Lagrangien transforme donc un problème d'optimisation d'un modèle avec contraintes d'égalité à celui de recherche des points stationnaires d’une fonction sans contrainte. De plus, puisque pour tout point optimal , la valeur du Lagrangien est la même que celle de l'objectif en ce point :
Exemple Résoudre par la méthode du Lagrangien :
s.c. .
On forme d'abord le Lagrangien : . On optimise ensuite , une fonction à trois variables pour laquelle on cherche les points stationnaires tel que :
Þ .
Þ .
.
Avec et dans la troisième équation, on a : ,
d'où Þ .
Reportant à son tour la valeur de dans les deux premières expressions, on retrouve :
et .
Donc est le seul point stationnaire du Lagrangien, et par conséquent, est le seul point extrémal du problème original avec contrainte (trouvé sans avoir à énoncer les conditions d’optimum du premier ordre!).
Remarque sur la nature du point extrémal Il faut faire attention car il n’est pas certain que soit un maximum (sous contraintes) pour l'objectif. Pour les contraintes d'égalité, le seul cas facile à résoudre au complet est celui impliquant des contraintes affines parce qu'elles définissent automatiquement un domaine convexe. On peut alors vérifier la convexité/concavité de la fonction objectif. En pratique, on choisit généralement de construire des modèles mathématiques que l'on est capable de résoudre !
- Dans l'exemple précédent, la contrainte est affine et on peut donc vérifier que l'objectif est strictement concave (le Hessien est toujours défini négatif). L'optimum sous contrainte trouvé est bel et bien un maximum absolu.
Dans les autres cas, il faut avoir recours à des outils mathématiques plus complexes, par exemple, les conditions du second ordre qui utilisent la notion de Hessien bordé (voir Breton et Haurie, p. 185-193).
3.5 Interprétation de
Considérons le problème d'optimisation suivant, où le côté droit de la contrainte d'égalité est exprimé par la quantité b : .
Le Lagrangien associé à ce problème est donné par . À l'optimalité, nous avons déjà mentionné que . Ainsi,
Le coefficient de b est . Ainsi, ce multiplicateur de Lagrange représente l'effet sur la valeur optimale de la fonction objectif si l'on modifie d'une unité la valeur de b. Il faut bien s'entendre que c'est un calcul approximatif.
|
donne une approximation de la variation de lorsqu’on augmente d'une unité le côté droit b de la contrainte . |
Ainsi, si f est une fonction de profit (en $) et b représente la main-d’œuvre en nombre d’employés, alors signifie que le profit augmenterait (approximativement) de 200$ si on augmentait la main-d’œuvre d'un employé additionnel. À noter que si l'on diminue le nombre d'employés, l'effet est en sens inverse !
Mentionnons finalement que dans le cas d'un modèle d'optimisation comportant plusieurs contraintes, un tel multiplicateur est associé spécifiquement à chacune d'entre elles.
Exemple s.c. .
Pour ce problème, on a trouvé : . Si on augmente b de une unité (donc ), alors la valeur optimale de devrait diminuer de 2 unités (environ). Résoudre ce problème en utilisant EXCEL et montrer que la nouvelle solution est donnée par :
et … une diminution de 2,04.
- Vérifier que la valeur du multiplicateur est maintenant .
Exercice Une entreprise fabrique deux modèles de vélos de montagne: le modèle X est plus abordable et se vend 500$ l'unité, tandis que le modèle Y se vend 1000$ l'unité. Les coûts totaux de fabrication (en $) sont exprimés par la fonction suivante: où x est le nombre de vélos du modèle X et y est le nombre de vélos du modèle Y, produits mensuellement. On suppose que chaque vélo produit peut être vendu sur le marché.
a) Donner , la fonction des profits totaux mensuels. ¨ Cette fonction est-elle convexe, concave ou sans forme particulière?
b) La capacité de production de l'entreprise est de 150 vélos par mois. En supposant que l'entreprise désire utiliser à pleine capacité son usine, trouver la répartition de la production mensuelle permettant de maximiser les profits. ¨ Prouvez qu'il s'agit bien d'un maximum absolu. ¨ Donnez la valeur du profit mensuel.
c) Le patron de l'entreprise s'interroge sur la pertinence de vouloir produire à pleine capacité. Il se demande si la solution qu'il obtiendrait sans cette contrainte serait plus intéressante. Aidez-le à répondre à cette question en trouvant la solution qui maximise les profits sans cette contrainte. ¨ Prouvez qu'il s'agit bien d'un maximum absolu. ¨ La solution obtenue est-elle réalisable pour l'entreprise? ¨ Donnez la valeur du profit mensuel.
d) Déterminez le signe du multiplicateur de Lagrange du problème résolu en b). ¨ Interpréter ce signe en vous appuyant sur les résultats obtenus en b) et c).
Solution
a)
.
; det(H(x, y))>0 et -10<0, "(x, y); p(x, y) est strict. concave.
b) Par substitution : y = 150 – x.
.
; x = 55 (Þ y = 95).
, "x Þ p(x) est une fonction strictement concave.
Þ x= 55 est un maximum absolu de p(x) .
Þ (x, y) = (55, 95) est un maximum absolu de p(x, y) avec p(55, 95) = 65 312,50$.
Ce problème peut aussi se résoudre par la méthode du Lagrangien.
c)
Par a), ce point stationnaire est un maximum absolu car la fonction est concave.
La solution n'est pas réalisable pour l'entreprise, dépassant la capacité de 150.
Le profit p(80, 120) = 70 000$.
d) On a vu que toute augmentation de capacité est rentable. Le multiplicateur est donc de signe positif. Par calcul, on trouve
Exercice Résoudre le problème précédent à l'aide d’EXCEL.
Problèmes résolus
Problème 1 Résoudre le problème suivant par la méthode du lagrangien:
.
Réponse
Le Lagrangien est . Les conditions du premier ordre sont :
On a (1) = (2)
.
On remplace dans (3):
- Si
Þ
- Si
Þ
Problème 2 Une grande brasserie veut allouer un budget de 500 000$ à la publicité au cours des six prochains mois. Les annonces publicitaires seront présentées dans deux médias : la télévision et les journaux. Les profits générés par cette campagne sont estimés par la fonction suivante :
s.c. x + y = 500
où x = montant investi dans la publicité dans les journaux (en milliers de $) et
y = montant investi dans la publicité à la télévision (en milliers de $).
En considérant que le budget est totalement dépensé, déterminer l'allocation aux deux médias qui permette de maximiser les profits de la brasserie en utilisant la méthode du Lagrangien. Quel est le profit maximum obtenu ? Vérifier que le point stationnaire est un maximum absolu. Interpréter le multiplicateur de Lagrange.
Réponse
Le Lagrangien est:
Les conditions du premier ordre sont :
En remplaçant y = 250 + x dans L'l, on obtient :
, et .
Le domaine est convexe car la contrainte est affine. Il suffit alors de vérifier que P(x,y) est concave pour que (125,375) soit un maximum absolu :
est strictement concave.
Le point (125,375) est donc un maximum absolu du problème d’optimisation sous contrainte.
L’interprétation économique que l’on peut donner à = 250 est que si les dépenses en publicité augmentent de 1000$, les profits augmenteront de 250$. Ce n’est donc pas rentable, même si le signe du multiplicateur de Lagrange est positif, car les unités relatives à la contrainte sont en milliers de $, ce qui amènerait une perte de 750$ dans l'éventualité où une augmentation d'une unité sur la contrainte de publicité se produisait.
Problème 3 Au ministère de l'agriculture, on a établi la fonction de profit suivante pour les fermes cultivant des germes de soja et des pistaches :
où P(x, y) sont les profits annuels en $, x représente le nombre d'acres plantés en germes de soja, et y donne le nombre d'acres plantés en pistaches. Un fermier possède une terre de 500 acres. Comment devrait-il allouer ses terres à ces deux cultures pour obtenir un profit maximal ? Utiliser la méthode du Lagrangien. Montrer qu'il s'agit d'un maximum absolu et donner le montant du profit obtenu. Interpréter le multiplicateur de Lagrange. En vous basant sur cette interprétation, suggéreriez-vous au fermier d’augmenter la surface totale consacrée à ces deux cultures ou, au contraire, de la diminuer ?
Réponse
Le Lagrangien est: et les conditions du premier ordre sont :
En remplaçant y* = 100 dans L'l:, on a = 600 - 2x* - 2y* = - 400.
Le point (400,100) est un maximum absolu du problème d’optimisation sous contrainte car on maximise une fonction concave sous un domaine convexe (contrainte affine).
L’interprétation économique que l’on peut donner à = -400 signifie qu’en ne cultivant pas tous les champs (c.-à-d. ses 500 acres de champs), le fermier augmenterait ses profits, à cause du signe négatif de . En effet, lorsque le fermier satisfait la contrainte, ses profits ne sont que de 60 000$, alors qu'ils sont de 110 000$ lorsque l'on ne tient pas compte de la contrainte (il cultive alors 300 acres de champs).
Source : © École des Hautes Études Commerciales, Montréal, Québec, 1999.
22:20 Publié dans La méthode du Lagrangien | Lien permanent | Commentaires (1) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Multiplicateur de Lagrange
Le multiplicateur de Lagrange est une méthode permettant de trouver les points stationnaires (maximum, minimum...) d'une fonction dérivable d'une ou plusieurs variables, sous contraintes. On cherche à trouver l'extremum, un minimum ou un maximum, d'une fonction φ de n variables à valeurs dans les nombres réels, ou encore d'un espace euclidien de dimension n, parmi les points respectant une contrainte, de type ψ(x) = 0 où ψ est une fonction du même ensemble de départ que φ. La fonction ψ est à valeurs dans un espace euclidien de dimension m. Elle peut encore être vue comme m fonctions à valeurs réelles, décrivant m contraintes. Si l'espace euclidien est de dimension 2 et si la fonction ψ est à valeurs dans R, correspondant à une contrainte mono-dimensionnelle, la situation s'illustre par une figure analogue à celle de droite. La question revient à rechercher le point situé le plus haut, c'est-à-dire le maximum de φ, dans l'ensemble des points rouges, c'est-à-dire ceux qui vérifient la contrainte. Le théorème clé se conçoit aisément dans l'exemple de dimension 2. Le point recherché est celui où la courbe rouge ne monte ni ne descend. En termes plus techniques, cela correspond à un point où la différentielle de ψ possède un noyau orthogonal augradient de φ en ce point. Le multiplicateur de Lagrange est une méthode offrant une condition nécessaire. Les fonctions φ et ψ sont différentiables et leurs différentielles continues, on parle de fonction de classe C1. On considère λ un vecteur pris dans l'ensemble d'arrivée de ψ et la fonction L définie par : L'opérateur représenté par un point est le produit scalaire. Si x0 est une solution recherchée, il existe un vecteur λ0 tel que la fonction L admet une différentielle nulle au point (x0, λ0). Les coordonnées du vecteur λ0 sont appelées multiplicateurs de Lagrange. Cette technique permet de passer d'une question d'optimisation sous contrainte à une optimisation sans contrainte, celle de la fonction L. La méthode se généralise aux espaces fonctionnels. Un exemple est donnée par la question de la chaînette, qui revient à rechercher la position que prend au repos, une chaînette attachée à ses deux extrémités. L'optimisation correspond à la position offrant un potentiel minimal, la contrainte est donnée par la position des extrémités et la longueur de la chaînette, supposée fixe. Cette méthode permet de trouver des plus courts chemins sous contrainte, ou encore des géodésiques. Le principe de Fermat ou celui de moindre action permet de résoudre de nombreuses questions à l'aide de cette méthode. Hugh Everett généralise la méthode aux fonctions non-dérivables, souvent choisies convexes. Pour une résolution effective, il devient nécessaire de disposer d'un algorithme déterminant l'optimum (ou les optima) d'une fonction. Dans le cas non dérivable, on utilise souvent une heuristique adéquate.Multiplicateur de Lagrange
![]() Pour les articles homonymes, voir Théorème de Lagrange.
Pour les articles homonymes, voir Théorème de Lagrange.
Sommaire[masquer] |
Soit v0 un nombre strictement positif, l'objectif est de trouver la portion de cylindre de rayon r et de hauteur h de surface minimale et de volume v0. Pour cela on définit deux fonctions, v et s qui à (r, h) associent respectivement le volume et la surface de la portion de cylindre. On dispose des égalités : La figure de droite représente la fonction s, qui à r et h associe la surface. La ligne bleue correspond aux points de volume égal à 1, l'objectif est de trouver le point bleu, de plus petite surface pour un volume égal à 1. On définit une fonction c et L de la manière suivante : La méthode de Lagrange consiste à rechercher un point tel que la différentielle de L soit nulle. Sur un tel point, la dérivée partielle en λ est nulle, ce qui signifie que la fonction c est nulle, ou encore que la contrainte est respectée. Si l'on identifie s avec son approximation linéaire tangente, son comportement sur la contrainte, aussi identifiée à son approximation linéaire tangente est aussi nécessairement nulle. Ce comportement est illustré par la droite en vert sur la figure. Le long de cette droite, la fonction c est nulle, à l'ordre 1, la fonctions l'est alors nécessairement. Il suffit, en conséquence, de calculer la différentielle de L, et plus précisément ses trois dérivées partielles, pour l'exemple choisi : On trouve les valeurs suivantes : L'exemple précédent possède l'avantage d'une représentation graphique simple, guidant l'intuition. En revanche, il est trop simple pour que la méthode du multiplicateur de Lagrange soit la meilleure dans ce cas. En effet, on peut aussi calculer la valeur de h pour que l'aire de la frontière soit égale à v0, on trouve : Il devient possible d'exprimer le volume du cylindre d'aire égale à v0 en fonction de r et le calcul revient à trouver le minimum d'une fonction de R dans R. Pour se convaincre de la pertinence de la méthode, on peut rechercher le triangle d'aire maximale et de périmètre p, choisi strictement positif. Si (x, y, z) est le triplet des longueurs des côtés du triangle, son aire A est égale à : Il est plus simple de maximiser la fonction φ qui associe le quart du carré de A, la contrainte est donnée par la fonction ψ qui associe au triangle la différence du périmètre et de p : Un triangle n'est défini, pour un couple (x, y, z), que si les trois coordonnées sont positives et si la somme de deux coordonnées est supérieure à la troisième. Soit D cet ensemble de points, sur la frontière de D, la fonction φ est nulle. On cherche un point de l'intérieur de D tel que φ soit maximal dans l'ensemble des points d'image par ψ nulle. Comme l'intersection de l'image réciproque de 0 par ψ et de D est un compact, il existe au moins un maximum. On définit comme dans l'exemple précédent la fonction L par : Si (a, b, c) est un triangle de périmètre p et d'aire maximale, il existe une valeur λ0 telle que la différentielle de L au point (a, b, c, λ0) soit nulle. Un calcul de dérivée partielle montre que ce quadruplet est solution du système d'équations : On en déduit que a, b et c sont tous racines de l'équation : Si les trois valeurs sont distinctes, elles correspondent aux trois racines de l'équation (1), leur somme est égale au coefficient de degré 2, c'est-à-dire à 0. Un tel point ne peut être dans l'intérieur de D car il est soit égal au triplet nul, soit contient une coordonnée strictement négative. On en conclut qu'au moins deux coordonnées sont égales, par exemple b et c. On peut alors ajouter une cinquième équation aux quatre que fournissent le calcul des dérivées partielles : y = z. En remplaçant z par y dans la première et deuxième équation, on obtient : On trouve trois cas : x = 0 correspond à un point de la frontière de D et c'est un minimum de φ, x = y correspond au triangle équilatéral et x = -2.y est un cas impossible car a est nécessairement strictement positif. L'unique solution est le triangle équilatéral de côté p/3 car a = b = c et la somme des trois longueurs est égale à p. Remarque : L'objectif est ici d'illustrer la méthode du multiplicateur de Lagrange, on a trouvé le maximum d'une fonction φ dans l'intérieur de D, sous la contrainte définie par ψ. Si l'objectif est uniquement de résoudre le problème isopérimétrique pour le triangle, une solution plus simple est donnée dans l'article sur l'isopérimétrie. Soit E et F deux espaces vectoriels réels de dimensions respectives n et m avec n plus grand que m. Soit φ une fonction de E dans Si (e1, ..., en) est une base de E, chaque point x de E s'exprime comme une combinaison linéaire des éléments de la base : Cette remarque permet de voir les fonctions φ et ψ de deux manières. Elles peuvent être vues comme des fonctions d'une unique variable x de E, ce qui rend l'écriture plus concise et favorise une compréhension plus simple, mais plus abstraite des mécanismes en jeu. Les applications peuvent aussi être vues comme fonctions de n variables x1, ..., xn, ce qui présente une rédaction plus lourde mais plus aisée pour les calculs effectifs. L'espace F est de dimension m, si (f1, ..., fm) est une base de F, la fonction ψ peut aussi être vue comme mfonctions de n variables : L'ensemble G peut être vu comme une unique contrainte exprimée par une fonction à valeurs dans F ou encore comme m contraintes exprimées par les égalités ψj(x) = 0, à valeurs dansR. Les fonctions φ et ψ sont de classe C1, ce qui signifie qu'elles sont différentiables, autrement dit elles admettent chacune une application linéaire tangente en chaque point. Le terme C1 signifie aussi que les applications qui, à un point associent les différentielles, soit de φ soit de ψ sont continues. L'optimum recherché vérifie une propriété analogue à celle du théorème de Rolle. Un corollaire de ce théorème, illustré à gauche, indique que l'optimum, un maximum ou un minimum, s'il se situe dans l'intervalle ouvert ]a, b[, possède une tangente horizontale, ce qui signifie encore que sa différentielle est nulle. C'est un résultat de cette nature qui est recherché. On peut le visualiser sur la figure de droite, si n et m sont respectivement égaux à 2 et à 1. On représente φ (noté f sur la figure de droite) en bleu par ses courbes de niveau, comme les géographes. Les flèches représentent le gradient de la fonction φ. La différentielle de φ est une application linéaire de E dans R, c'est-à-dire une forme duale. Il est d'usage de considérer E comme un espace euclidien, de choisir la base de E orthonormale et d'identifier la différentielle avec le vecteur de E qui représente la forme duale. Dans ce cas, l'approximation linéaire tangente s'écrit : La lettre o désigne un petit o selon la notation de Landau et le point entre le gradient de φ et h symbolise le produit scalaire. Le vecteur gradient est orthogonal à la courbe de niveau, dans le sens des valeurs croissantes de φ et de norme proportionnelle à la vitesse d'accroissement de φ dans cette direction. La contrainte vérifie une propriété analogue puisqu'elle est aussi différentiable. L'ensemble étudié est celui des valeurs x tel que ψ(x) est nul. Si x0 est élément de G, les points voisins de x0 dans G ont aussi une image nulle par ψ, autrement dit, l'espace tangent à G au point x0 est formé par les accroissements h de x0 qui ont une image par la différentielle de ψ nulle. La direction de l'espace tangent est le noyau de l'application différentielle de ψ. Une analyse par les fonctions coordonnées ψi exprime ce résultat en indiquant que l'espace tangent est l'intersection des hyperplans orthogonaux des gradients de ψi. Une analyse au point optimal x0 recherché indique, en approximation du premier ordre, qu'un déplacement h dans la direction de l'espace tangent à G ne peut pas accroître la valeur de φ. Ceci signifie que le déplacement h est nécessairement orthogonal au gradient de φ en x0. C'est ainsi que se traduit le théorème de Rolle, dans ce contexte. Géométriquement, cela signifie que la courbe de niveau bleue et la ligne rouge sont tangentes au point recherché. Analytiquement cela se traduit par le fait que le noyau de la différentielle de ψ en x0 est orthogonal au gradient de φ en ce point. Le problème à résoudre est de trouver le minimum suivant : Les fonctions φ et ψ ne sont pas nécessairement définies sur tout E mais au moins sur des ouverts de E. De plus, le domaine de définition de φ possède une intersection non vide avecG. La méthode des multiplicateurs de Lagrange se fonde sur un théorème. Théorème du multiplicateur de Lagrange — Si le point x0 est un extremum local de φ dans l'ensemble G, alors le noyau de la différentielle de ψ au point x0 est orthogonal au gradient de φ en ce point.1 Un corollaire met en évidence le multiplicateur. Pour cela, il est nécessaire d'équiper F du produit scalaire tel que sa base soit orthonormale, le symbole t signifie la transposée d'une l'application linéaire, elle définit une application du dual de F, ici identifié à F dans le dual de E, encore identifié à E : Corollaire 1 — Si le point x0 est un extremum local de φ dans l'ensemble G et si la différentielle de ψ au point x0 est surjective, il existe un vecteur λ0 de F tel que la somme de l'image de λ0 par la transposée de la différentielle de ψ au point x0 et du gradient de φ en ce point soit nulle : Sous forme de coordonnées, on obtient : Un deuxième corollaire est plus pragmatique, car il offre une méthode effective pour déterminer l'extremum. Il correspond à la méthode utilisée dans l'exemple introductif. Corollaire 2 — Si le point x0 est un extremum local de φ dans l'ensemble G et si la différentielle de ψ au point x0 est surjective, alors il existe un vecteur λ0 de F tel que la fonction L de ExF dans R admet un gradient nul en (x0, λ0) :2 Ces théorèmes possèdent quelques faiblesses, de même nature que celle du théorème de Rolle. La condition est nécessaire, mais pas suffisante. Un point de dérivée nulle pour Rolle ou vérifiant les hypothèses du théorème du multiplicateur de Lagrange n'est pas nécessairement un maximum ou un minimum. Ensuite, même si ce point est un extremum, il n'est que local. Si une solution x0 est trouvée, rien n'indique que cet extremum local est le meilleur. L'approximation linéaire ne précise pas si cet optimum est un maximum ou un minimum. Enfin, comme pour le cas du théorème de Rolle, si les domaines de définition ne sont pas ouverts, il est possible qu'un point frontière soit un optimum qui ne vérifie pas le théorème. Ainsi, sur la figure de gauche, f(a) et f(b) sont des minima, mais la dérivée n'est nulle ni en a ni en b. Si l'écriture condensée permet de mieux comprendre la structure du théorème, les notations développées sont plus utiles pour une résolution effective. Dans la pratique, on considère souvent une fonction φ de Rn dans R et m fonctions ψj, avec j variant de 1 à m, aussi de Rn dans R. L'entier m est nécessairement plus petit que n pour pouvoir appliquer les théorèmes du paragraphe précédent. On cherche à trouver un n-uplet (a1, ..., an) tel que : Pour cela, on définit la fonction L de Rn+m dans R par : Le deuxième corollaire indique que résoudre les équations suivantes offrent sur condition nécessaire pour élucider le problème d'optimisation (1). Le n-uplet (a1, ..., an) est une solution de (1) seulement s'il existe un m-uplet (α1,...,αm) tel que le n+m-uplet (a1, ..., an, α1,...,αm) soit solution des n + m équations : Cette méthode peut être généralisée aux problèmes d'optimisation incluant des contraintes d'inégalités (ou non linéaires) en utilisant les conditions de Kuhn-Tucker. Mais également sur des fonctions discrètes à maximiser ou minimiser sous contraintes, moyennant un changement d'interprétation, en utilisant la méthode des multiplicateurs d'Everett (ou de Lagrange généralisés), plus volontiers appelée méthode des pénalités. La méthode du multiplicateur de Lagrange permet de démontrer l'inégalité arithmético-géométrique5. On définit les applications φ et ψ de On remarque que l'ensemble G, composé des n-uplets de coordonnées positives et de somme égale à Une solution vérifie les équations : On en déduit l'existence d'une unique solution, obtenue pour tous les La moyenne géométrique est inférieure à la moyenne arithmétique, l'égalité n'ayant lieu que si les Le multiplicateur de Lagrange offre une démonstration alternative de l'inégalité arithmético-géométrique. Il existe un autre contexte, qui fait appel au multiplicateur de Lagrange. Considérons une chaînette soumis à la gravité et recherchons son équilibre statique. La chaînette est de longueur a et l'on suppose qu'elle est accrochée à deux points d'abscisses -t0 et t0 et d'ordonnée nulle en ces deux points. Si son ordonnée est notée x, elle suit une courbe y=x(t) sur l'intervalle [-t0, t0], dont on se propose de calculer l'équation. Dire qu'elle est à l'équilibre revient à dire que son potentiel Φ est minimal, où : Ici, α désigne une constante physique, en l'occurrence le produit de g la gravitation terrestre, par la densité linéaire de la chaînette, supposée constante. La formule donnant la longueur d'un arc en fonction d'un paramétrage est donnée dans l'article Longueur d'un arc. La chaînette n'est pas supposée être élastique, elle vérifie donc la contrainte Ψ, indiquant que sa longueur l0 n'est pas modifiée : Si C1K(I) désigne l'ensemble des fonctions de [-t0, t0] dans R, dérivables et de dérivées continues, nulles en -t0 et t0, le problème revient à rechercher la fonction x0 telle que : La similitude avec la situation précédente est flagrante. Pour pouvoir appliquer des multiplicateurs de Lagrange, il faut donner un sens au gradient de Φ et Ψ. Dans le cas où il existe deux fonctions de classe C2 de R3 dans R, notées φ et ψ telles que : L'équation d'Euler-Lagrange affirme que : Dans le cas particulier où les fonctions φ et ψ sont des fonctions de deux variables et ne dépendent pas de t, on obtient la formulation de Beltrami (cf l'article Équation d'Euler-Lagrange): Dire que les deux gradients sont colinéaires revient à dire qu'il existe un réel λ, le multiplicateur de Lagrange, tel que : La résolution de cette équation différentielle est une chaînette. La méthode du multiplicateur de Lagrange permet bien de résoudre la question posée6. L'exemple précédent montre que le contexte de l'équation d'Euler-Lagrange n'est pas loin de celui du multiplicateur de Lagrange. Si l'ensemble de départ de la fonction x(t) recherchée est un intervalle I ouvert et borné de R et l'ensemble d'arrivée E l'espace vectoriel euclidien, la généralisation est relativement aisée. On suppose l'existence d'une fonction Φ à minimiser, son ensemble de départ est un espace fonctionnel, c'est-à-dire un espace vectoriel de fonctions, de I dans E et son ensemble d'arrivée R. La fonction Φ est construite de la manière suivante : Le point sur le x indique la fonction gradient, qui à t associe le gradient de x au point t. La fonction φ est une fonction de RxE2 dans R de classe C2. L'optimisation est sous contrainte, donnée sous une forme analogue à la précédente. On suppose l'existence d'une fonction Ψ de RxE2 dans F, un espace euclidien. La fonction Ψ est encore définie à l'aide d'une fonction ψ de classe C2 de IxE2, mais cette fois dans F un espace euclidien: L'ensemble G est composée de fonctions deux fois dérivables de I dans E et dont l'image par Ψ est nulle. On suppose de plus que les valeurs des fonctions de G aux bornes de I sont fixes et, quitte à opérer une translation, on peut toujours supposer, sans perte de généralités, que ces fonctions sont nulles aux bornes de I. La seule tâche un peu délicate est de définir l'espace vectoriel W2,2(I,E) sur lequel opèrent Φ et Ψ. Pour définir un équivalent de gradient, cet espace comporte nécessairement un produit scalaire. Si l'on souhaite établir des théorèmes équivalents aux précédents les fonctions dérivées et dérivées seconde sont définies et l'espace est complet. Un espace munis d'un produit scalaire et complet est un Hilbert. Sa géométrie est, de fait, suffisamment riche pour étendre les résultats précédents. On note D l'espace des fonctions de I, à valeur dans E, de classe L'espace D* contient le Hilbert des fonctions de carrés intégrables L2(I,E). En effet une fonction f de L2(I,E) agit sur D par le produit scalaire <.,.>L défini par l'intégrale de Lebesgue : C'est dans L2(I,E) que nous cherchons le bon espace. Dans cet espace, l'intégration par parties permet de définir la dérivée de la fonction f de L2(I). Comme g est à support compact et que I est ouvert, aux bornes de I, la fonction g est nulle. Si f est dérivable au sens classique du terme, on bénéficie des égalités : Si la distribution dérivée de f est encore d'un élément de L2(I,E), on dit qu'elle est dérivable au sens de Sobolev. Si cette dérivée est encore dérivable au sens précédent, on dit qu'elle est deux fois dérivables au sens de Sobolev. On note W2,2(I,E) le sous-espace de L2(I,E) équipé du produit scalaire suivant <.,.>W : Les intégrales sont bien définies car elles correspondent au produit de deux élément de L2(I,E), il est ensuite simple de vérifier que l'espace est bien complet7. Enfin, si f est une fonction dérivable au sens des distributions, il existe un représentant de f continue8. Ainsi tout élément de W2,2(I,E) admet un représentant continu et dont la dérivée admet aussi un représentant continu. La difficulté est maintenant d'exprimer le gradient des fonctions Φ et Ψ. L'équation d'Euler-Lagrange cherche dans un premier temps à trouver des fonctions de classe C2 qui minimisent Φ. L'espace vectoriel sous-jacent est celui des fonctions d'un intervalle borné et de classe C2 et nulles aux bornes de l'intervalle. Sur cet espace, le calcul du gradient de Φ n'est guère complexe, il donne aussi une idée de la solution ainsi que de la méthode pour y parvenir. En revanche, ce calcul est insuffisant dans le cas présent. Avec le bon produit scalaire, l'espace des fonctions de classe C2 n'est pas complet, ce qui empêche de disposer de la bonne géométrie permettant de démontrer la méthode du multiplicateur de Lagrange. L'objectif est de généraliser un peu la démonstration pour permettre de disposer de l'égalité du gradient dans l'espace complet W2,2(I,E). Dans un premier temps, exprimons l'égalité qui définit la différentielle de Φ en un point x, qui représente une fonction de W2,2(I,E) : L'application DΦx est une application linéaire continue de W2,2(I,E) dans R, c'est-à-dire un élément du dual topologique de W2,2(I,E), que le produit scalaire permet d'identifier à W2,2(I,E). L'égalité précédente devient : Autrement dit, le gradient de Φ au point x est une fonction de L2(I,E) dans R. De fait, ce gradient s'exprime à l'aide de l'équation d'Euler-Lagrange : Si la fonction φ est en général choisie au sens usuel de la dérivation, la fonction x(t) est une fonction de W2,2(I,E). Le symbole d/dt doit être pris au sens de la dérivée d'une distribution, qui n'est ici nécessairement une fonction de carrée intégrable, définie presque partout. Pour Ψ, la logique est absolument identique, mais cette fois-ci, la fonction est à valeurs dans F. En conséquence, la dérivée partielle de ψ par rapport à sa deuxième ou troisième variable n'est plus une application linéaire de E dans R, mais une application linéaire de E dans F. Ainsi, la différentielle de Ψ au point, une fonction x de I dans E, est une application de I dansL(E,F) l'ensemble des applications linéaires de E dans F. La logique reste la même. Ce paragraphe est très proche du précédent dans le cas de la dimension finie. Le problème à résoudre est de trouver le minimum suivant : Théorème du multiplicateur de Lagrange — Si le point x0 est un extremum local de Φ dans l'ensemble G, alors le noyau de la différentielle de Ψ au point x0 est orthogonal au gradient de Φ en ce point. On obtient les mêmes corollaire, que l'on peut écrire : Corollaire — Si le point x0 est un extremum local de Φ dans l'ensemble G et si la différentielle de Ψ au point x0 est surjective, alors il existe un vecteur λ0 de F tel que la fonction L de W2,2(I,E)xF dans R admet un gradient nul en (x0, λ0) : Cette équation s'écrit encore : Le signe d/dt doit être pris au sens de la dérivée des distributions. On obtient une solution faible, c'est-à-dire une fonction x définie presque partout et dérivable dans un sens faible. En revanche, si une fonction x de classe C2 est solution du problème de minimisation, comme ses dérivées premières et secondes sont des représentants de ses dérivées au sens faible, L'équation précédente est encore vérifiée. On recherche la surface de plus grande aire, ayant une frontière de longueur égale à 2π. On remarque que la surface est nécessairement convexe, d'intérieur non vide. On considère une droite coupant la surface en deux. Cette droite est utilisée comme axe d'un repère orthonormal, dont les abscisses sont notées par la lettre t et les ordonnées par x. La frontière supérieure est paramétrable en une courbe x(t) et, si le repère est bien choisi, on peut prendre comme abscisse minimale -a et maximale a. On recherche alors une courbe x, définie entre -a et a tel que l'aire Asoit maximale : On sait de plus que la demi longueur de la frontière est égale à π : La recherche de la surface se traite aussi avec le multiplicateur de Lagrange. La même astuce que celle utilisée dans l'exemple introductif montre, avec les notations usuelles : On en déduit l'existence de valeurs λ et k tel que : En notant u = x - k, on obtient : On trouve l'équation d'un demi-cercle de rayon λ, la valeur λ est égale à 1 et k à 0.9Dimension finie [modifier]
Exemple introductif [modifier]

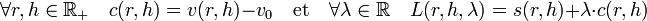


Deuxième exemple : l'isopérimétrie du triangle [modifier]






Notations et interprétation géométrique [modifier]
 , que l'on cherche à optimiser. On cherche un point a tel que φ(a) soit le plus petit possible. Soit ψ une fonction de E dans F, définissant la contrainte. L'ensemble sur lequel on travaille est G, correspondant aux points x tel que ψ(x) = 0.
, que l'on cherche à optimiser. On cherche un point a tel que φ(a) soit le plus petit possible. Soit ψ une fonction de E dans F, définissant la contrainte. L'ensemble sur lequel on travaille est G, correspondant aux points x tel que ψ(x) = 0.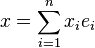

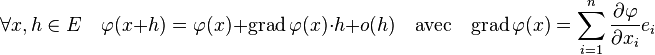
Théorèmes [modifier]
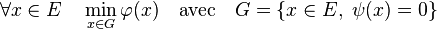

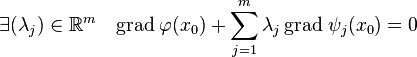

Écriture du problème [modifier]
![(1)quad varphi (a_1,cdots , a_n) = min_{(x_i) in G} varphi(x_1,cdots,x_n)quadtext{avec}quad G = {(x_i)in mathbb R^n, quad forall j in [1,m] ;psi_j (x_1,cdots, x_n)=0}](http://upload.wikimedia.org/math/9/b/a/9ba0f5f19d65952eb9d7a3b371cd8964.png)

![forall i in [1,n]quad frac {partial varphi}{partial x_i}(x_1,cdots, x_n) + sum_{j=1}^m lambda_j frac {partial psi_j}{partial x_i}(x_1,cdots, x_n) = 0 quad text{et}quad forall j in [1,m]quad psi_j(x_1,cdots, x_n) = 0](http://upload.wikimedia.org/math/9/f/d/9fd87191a3c724074f3d748818aa7207.png)
Application : inégalité arithmético-géométrique [modifier]
 dans
dans  par :
par :
 est un compact de
est un compact de  . Sur ce compact la fonction φ est continue, elle admet nécessairement un maximum. Les deux fonctions φ et ψ sont bien de classe
. Sur ce compact la fonction φ est continue, elle admet nécessairement un maximum. Les deux fonctions φ et ψ sont bien de classe  , il est donc possible d'utiliser le multiplicateur de Lagrange pour trouver ce maximum. Pour cela, on considère la fonction L :
, il est donc possible d'utiliser le multiplicateur de Lagrange pour trouver ce maximum. Pour cela, on considère la fonction L :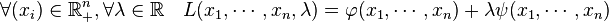
![forall i in [1,n] quad frac {partial L}{partial x_i} L(x_1,cdots x_n,lambda) = 0 Leftrightarrow prod_{k neq i} x_k = -lambdaquad text{et}quad sum_{i=1}^n x_i = s](http://upload.wikimedia.org/math/8/d/a/8da4e804b1eb6e4f9433ddca172319a4.png)
 égaux à
égaux à  et λ égal à
et λ égal à  . Ce qui s'exprime, en remplaçant s par sa valeur :
. Ce qui s'exprime, en remplaçant s par sa valeur :![forall (x_i) in mathbb R_+^{n} quad sqrt[n]{prod_{i=1}^n x_i} le frac{sum_{i=1}^n x_i}n](http://upload.wikimedia.org/math/7/8/1/78117f9776bf5a8021d8895f4187e99f.png)
 sont tous égaux.
sont tous égaux.Espace fonctionnel [modifier]
Exemple introductif : La chaînette [modifier]
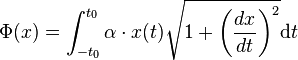
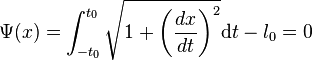

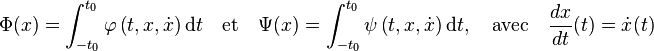
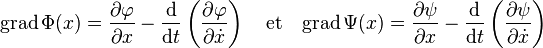

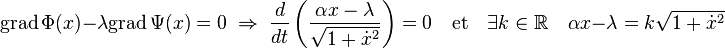
Espace de Sobolev [modifier]
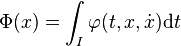

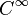 et à support compact et D* son dual topologique. L'espace D est muni de la norme de la borne supérieure et l'espace D* est celui des distributions. Ce premier couple n'est pas encore satisfaisant car D est trop petit et D* trop gros pour permettre de définir un bon produit scalaire, à l'origine d'une géométrie aussi simple que celle d'un Hilbert.
et à support compact et D* son dual topologique. L'espace D est muni de la norme de la borne supérieure et l'espace D* est celui des distributions. Ce premier couple n'est pas encore satisfaisant car D est trop petit et D* trop gros pour permettre de définir un bon produit scalaire, à l'origine d'une géométrie aussi simple que celle d'un Hilbert.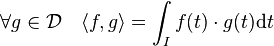
![langle dot f,grangle_L = int_I dot f(t)cdot g(t) mathrm dt = Big[f(t)cdot g(t)Big]_I - int_I f(t)cdot dot g(t) mathrm dt = -int_I f(t)cdotdot g(t) mathrm dt](http://upload.wikimedia.org/math/e/1/5/e15e646bc31575087fe9b3986184eb66.png)

Équation d'Euler-Lagrange [modifier]
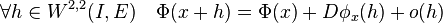

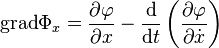
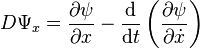
Théorèmes [modifier]
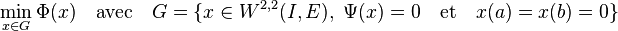


Application : Théorème isopérimétrique [modifier]



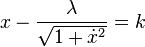
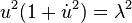
Voir aussi [modifier]
Notes [modifier]
Liens externes [modifier]
Références [modifier]
22:03 Publié dans Multiplicateur de Lagrange | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook










































 ; 10 000 pas.
; 10 000 pas.