Variables indépendantes et identiquement distribuées

Aller à :Navigation,rechercher

En statistique, des variables indépendantes et identiquement distribuées (iid) sont des variables aléatoires qui ont toutes la même loi de probabilité et sont mutuellement indépendantes.

En inférence statistique ou en apprentissage automatique, il est très courant de supposer que le tirage des échantillons d'apprentissage sont i.i.d. C'est une condition souvent nécessaire à l'application des théorèmes les plus courants. En particulier le théorème de la limite centrale dans sa forme classique stipule que la somme de variables aléatoires tendent vers unedistribution normale quand ces variable sont i.i.d.

Exemples [modifier]

Un exemple de tirage aléatoire i.i.d est celui du pile ou face. Chaque lancer de pièce suit la même loi de Bernoulli de paramètre p et est indépendant de ceux qui l'ont précédé ou vont lui succéder. Si p = 0.5 (pile et face ont la même chance d'apparition), et que nous avons obtenu 10 fois face lors des 10 tirages précédents, les chances d'obtenir pile et face lors du prochain tirage sont néanmoins égales.

Dans l'exemple précédent, le tirage ne serait plus i.i.d :

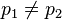• si on utilise alternativement deux pièces biaisées différemment () car dans ce cas les tirages ne suivent pas la même loi. Il restent néanmoins indépendants.
• si on choisit systématiquement la pièce ayant le plus de chance de donner face après chaque tirage pile (et que l'on prend les pièces au hasard après un tirage face), les tirages ne sont plus indépendants car conditionnées par le résultat du tirage précédent.

 

[Enrouler]

v · d · m

Probabilités et statistiques

Statistique descriptive • Statistique inférentielle

Échantillon • Variable qualitative nominale • Variable qualitative ordinale • Variable quantitative discrète • Variable quantitative continue • Estimateurs • Variable aléatoire • Théorème central limite

Moyenne • Médiane • Variance • Écart type • Distribution normale
Visualisation des données • Histogramme • Boîte à moustaches • Diagramme circulaire • Représentations graphiques de données statistiques

Test (statistique) • Test d'hypothèse • Hypothèse statistique • Hypothèse nulle • Statistiquement significatif • Valeur p • Loi de Student • Test de Student • Loi de Fisher • Test de Fisher • Loi du χ² •Test du χ² • Analyse de la variance • Régression linéaire • Corrélation • Corrélation de Spearman

Analyse des données • Statistique mathématique • Théorie des probabilités • Inégalités • Processus stochastiques • La mécanique statistique • Les statistiques et l'économie • Économétrie •Probabilité dans les jeux • Variables indépendantes et identiquement distribuées • R (logiciel)

•  Portail des probabilités et des statistiques

Catégories : Statistiques | Loi de probabilité | [+]

Source : http://fr.wikipedia.org/wiki/Variables_ind%C3%A9pendantes...