19/11/2010
Théorème de Schwarz
Théorème de Schwarz
|
|
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
Le théorème de Schwarz, également appelé théorème de Clairaut, peut s'énoncer ainsi : Théorème de Schwarz — Soit f, une fonction numérique de n variables, définie sur un ensemble ouvert U de ℝn. Si les dérivées partielles existent à l'ordre p et sontcontinues en un point x de U, alors le résultat d'une dérivation à l'ordre p ne dépend pas de l'ordre dans lequel se fait la dérivation par rapport aux p variables considérées. Dans le cas particulier des fonctions de deux variables x et y, on obtient : Le résultat ci-dessus peut tomber en défaut lorsque les hypothèses ne sont pas vérifiées. Considérons la fonction : Les dérivées sont : et Les dérivées partielles croisées d'ordre 2 en (0,0) sont Considérons la forme différentielle exacte suivante, où f est une fonction de classe C2 : Nous savons alors que : En appliquant le théorème de Schwarz nous en déduisons immédiatement la relation : (par dérivation et inversion de l'ordre de dérivation...)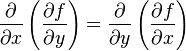
Un contre-exemple [modifier]

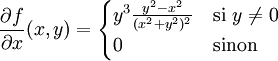
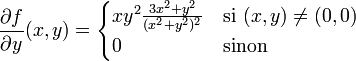
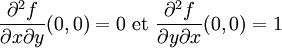
Application du théorème de Schwarz aux formes différentielles exactes [modifier]

 et
et 
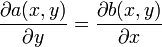
22:26 Publié dans Théorème de Schwarz | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook








































Les commentaires sont fermés.