D	L	M	M	J	V	S
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30	31

27/07/2010

La "taille" des ensembles : ordinaux, cardinaux

La "taille" des ensembles : ordinaux, cardinaux

Source : http://www.les-mathematiques.net/a/a/a/node3.php3

Définition [Définitions de base pour les ordinaux] On dit qu'un ensemble muni d'une relation d'ordre est bien ordonné si et seulement si toute partie non vide de cet ensemble admet un élément minimum. L'ordre est alors appelé un bon ordre. On appelle segment initial d'une partie bien ordonnée un ensemble de cette partie tel que étant donné un élément de cette partie, tous les éléments qui sont inférieurs à cet élément sont aussi dans la partie. On appelle segment initial engendré par l'ensemble des plus petits que ; cette partie est clairement un segment initial.
Un ensemble est dit transitif si tout élément de cet ensemble est inclus dans cet ensemble. C'est à dire que si , alors (non, il n'y a pas de faute de frappe!). Un ensemble est un ordinal s'il est transitif s'il est bien ordonné par , cette relation étant une relation d'ordre strict. On note l'ensemble des ordinaux.

Par exemple les ensembles suivants sont des ordinaux:

Proposition Les segments initiaux d'un ordinal sont soit lui-même, soit ses éléments.
Tout élément d'un ordinal est un ordinal.
Un ordinal n'appartient pas à lui-même.

Démonstration
Soit un segment initial d'un ordinal . Alors est un segment initial engendré par un certain ( est l'élément minimum de ); l'ensemble des éléments qui sont plus petits que étant les éléments qui appartiennent à (puisque c'est ainsi que l'on a défini la relation d'ordre), est donc le segment initial engendré par .
Facile...
Il suffit de voir que l'on a imposé que soit un ordre strict.

Proposition Etant donné deux ordinaux et , une et une seule des trois assertions suivantes est vérifiée:

.

Démonstration Il suffit de considérer l'intersection de et et d'examiner ses propriétés.

La relation est donc une relation d'ordre total sur la classe des ordinaux.

Proposition La relation est un bon ordre sur la classe des ordinaux.
Le plus petit élément de la classe des ordinaux plus grands que est .
L'union d'une classe d'ordinaux est un ordinal; il est plus grand que tous les ordinaux de cette classe, et il est plus petit que tous les autres ordinaux plus grands que tous ces ordinaux.

Démonstration
Il suffit de constater comme on l'a vu plus haut que le segment initial engendré par est .
Il est clair que doit appartenir à un tel élément, ainsi qu'être inclus dedans; réciproquement l'ensemble .
Facile.

Définition Etant donné un ordinal, est appelé le successeur de . On le note . est dit le prédécesseur de .

Propriété amusante:
La classe des ordinaux n'est pas un ensemble. En effet si un tel ensemble existe, alors tout élément de est un ordinal, et donc un ensemble d'ordinaux, et donc ; ce qui n'est pas possible pour un ordinal puisque est une relation d'ordre strict.

Définition On appelle morphisme d'ordre entre deux ensembles ou classes ordonnés et une application de vers telle que . Un morphisme d'ordre bijectif est appelé isomorphisme d'ordre. S'il existe un isomorphisme d'ordre entre deux ensembles ou classes alors on dit que ces ensembles ou classes sont isomorphes pour l'ordre.

Théorème S'il existe un isomorphisme d'ordre entre deux ordinaux et , alors et sont égaux (alors l'isomorphisme d'ordre est l'identité).

Théorème Pour tout ensemble ordonné il existe un et un seul isomorphisme d'ordre de vers un ordinal.

Théorème Toute relation de bon ordre dont le domaine n'est pas un ensemble est nécessairement isomorphe pour l'ordre à la classe des ordinaux.

Il est ensuite possible de montrer que s'il est vrai pour une certaine propriété à une seule variable libre que est vrai pour tout ordinal plus petit que , alors est vraie pour , alors on peut conclure que la propriété est vraie pour tout ordinal.

Il reste de nombreuses choses à justifier pour expliquer toutes les petites choses que l'on s'autorise en maths sans se prendre la tête trop; mais ces considérations dépassent mon propos...

**Figure:** Démonstration du théorème de Cantor-Bernstein.

Théorème [Théorème de Cantor-Bernstein] Soit et deux ensembles, une injection de dans , et une injection de dans ; alors il existe une bijection de dans .

Démonstration On considère l'ensemble des parties de telles que .
On montre que cet ensemble admet un élément maximal (car il est stable par réunion)
On montre que le maximum vérifie
On montre que la fonction qui à associe si et l'unique tel que si est une bijection

Définition [Définitions sur les ordres] Un ordre est une relation réflexive, antisymétrique, transitive.
Une relation d'ordre strict est une relation telle que définie par soit une relation d'ordre, et telle que pour tout .
Un élément d'une partie est un minimum de cette partie si et seulement si et si .
Un élément d'une partie est un élément minimal de si et seulement si et si et .
Un élément est dit minorant d'une partie si ; il n'est pas nécessaire que soit dans .
On définit de même maximum, élément minimal, majorant.
La figure illustre ces notions.

Un bon ordre est un ordre tel que toute partie non vide a un minimum.

**Figure:** Illustration de quelques notions sur les ordres. n'a pas de minorant, ni de plus petit élément; par contre il a un maximum, c'est le même élément que l'élément maximal unique. Bien noter toutefois qu'un élément maximal, même lorsqu'il est unique, n'est pas nécessairement un maximum.

Axiome [Axiome du choix, première version] Etant donné un ensemble , il existe une fonction qui à une partie non vide de associe un élément de cette partie.

Axiome [Axiome du choix, deuxième version] Un produit d'ensembles non vides est non vide.

On montre facilement que ces deux axiomes sont équivalents. Pour des applications amusantes de l'axiome du choix on pourra consulter .

Théorème [Théorème de Zermelo] non vide il existe une relation de bon ordre (i.e. telle que toute partie non vide admette un minimum).

Il est difficile de montrer ce théorème à partir de l'axiome du choix. La réciproque est par contre facile.

Définition [Ensemble inductif] Deux éléments sont dits comparables si l'un des deux est inférieur ou égal à l'autre.
On appelle chaine un ensemble totalement ordonné, c'est à dire tel que deux éléments soient toujours comparables.
Un ensemble ordonné est dit inductif si toute chaine admet un majorant.

Lemme [Lemme de Zorn] Tout ensemble non vide ordonné inductif admet un élément maximal.

Le lemme de Zorn est équivalent au théorème de Zermelo, lui même équivalent aux deux versions de l'axiome du choix. On peut montrer Zermelo à partir de Zorn en considérant l'ensemble des bons ordres sur des parties de , un couple étant inférieur à un couple , avec et des parties de et et des bons ordres sur respectivement et , si , , et si et avec , alors .

L'axiome du choix permet par exemple de démontrer l'existence d'une base pour tout espace vectoriel. L'axiome du choix est équivalent à l'existence d'une injection de dans ou de dans pour tous ensembles et ; la preuve de ce fait à partir de Zorn se fait facilement, en considérant les bijections entre des parties de et des parties de , par contre la réciproque est difficile.

L'axiome de fondation est l'assertion selon laquelle dans tout ensemble non vide il existe un élément d'intersection vide avec cet ensemble; l'axiome de fondation sera plus détaillé en .

Théorème [Consistance relative de et de ]

( désigne l'axiome du choix)

Si la théorie axiomatique de Zermelo-Fraenkel avec axiome de fondation est consistante, alors la théorie de Zermelo-Fraenkel avec axiome de fondation et axiome du choix est consistante.
Si la théorie axiomatique de Zermelo-Fraenkel est consistante, alors la théorie de Zermelo-Fraenkel avec axiome du choix est consistante.
D'autre part si la théorie de Zermelo-Fraenkel est consistante, alors la théorie de Zermelo-Fraenkel avec la négation de l'axiome du choix est consistante.
Enfin, si la théorie de Zermelo-Fraenkel avec axiome de fondation est consistante, alors la théorie de Zermelo-Fraenkel avec axiome de fondation et avec la négation de l'axiome du choix (i.e. en supposant qu'il existe un ensemble sur lequel on ne peut pas construire une relation de bon ordre) est consistante.

Démonstration Fortement non trivial. Je passe.

Il est aussi possible de remplacer la négation de l'axiome du choix par le fait que ne puisse pas être bien ordonné; une telle théorie est consistante si la théorie avec axiome de fondation est consistante.

On peut énoncer sans l'axiome du choix:
- un produit de groupes est non vide
- un produit dénombrable d'espaces métriques compacts est compact

Définition Deux ensembles sont dits équipotents s'il existe une bijection de l'un dans l'autre.

Il est évident qu'il s'agit là d'une relation d'équivalence.

L'axiome du choix permet de démontrer le théorème suivant:

Théorème Tout ensemble est équipotent à un ordinal.

Définition Etant donné un ensemble, on sait qu'il existe au moins un ordinal auquel cet ensemble est équipotent. Eventuellement il peut y en avoir plusieurs; le plus petit élément de ces ordinaux (au sens défini plus haut sur les ordinaux, c'est à dire la relation ) est appelé le cardinal de l'ensemble. On note usuellement le cardinal de , ou . On note la classe des cardinaux.

Théorème [Théorème de Cantor] Pour tout ensemble , on a .

Démonstration Supposons le contraire; alors il existe une surjection de dans . Posons l'ensemble des tels que ; il suffit alors de considérer le tel que . On constate que si , alors ; et vice-versa.

On notera que n'est pas un ensemble; sinon on pourrait construire un ensemble égal à , ce qui est impossible.

Définition [Somme de cardinaux] On note le cardinal de l'union disjointe de deux ensembles respectivement équipotents à et .
On notera que cette définition pose quelques petits problèmes de définition, pas difficiles à résoudre. L'addition de cardinaux est commutative et associative.
Une propriété importante est le fait que la somme des pour est le plus grand élément entre et les , sous réserve que l'un au moins de ses ensembles (ou l'un des ) soit infini.

Définition [Produit de cardinaux] On note le cardinal du produit cartésien de et de .

Là aussi il convient de vérifier que le produit de deux couples d'ensembles de mêmes cardinaux respectifs est le même. On peut en outre vérifier que la multiplication de cardinaux est associative et commutative, et distributive par rapport à l'addition. On notera que le produit de deux cardinaux est le plus grand de ces deux cardinaux.

Définition [Exponentiation de cardinaux] Etant donnés des cardinaux et on note le cardinal de l'ensemble des applications de dans .
On vérifiera facilement que la définition a bien un sens. On peut aussi montrer que $A^{B+C}=A^Btimes A^C$ et que ${A^B}^C=A^{Btimes C}$ .

De nombreuses manipulations plus approfondies sur les cardinaux requièrent l'axiome du choix.

Définition Un ordinal est dit fini si tout ordinal inclus dans cet ordinal admet un prédécesseur. On appelle aussi entier naturel un ordinal fini.

Moi ça m'amuse beaucoup de définir un entier naturel comme étant un ensemble incluant chacun de ses éléments, tel que pour toute partie de il existe tel que pour tout et pour tout élément de il existe incluant chacun de ses éléments, tel que pour toute partie de il existe tel que pour tout , et tel que . Si je me suis pas gouré.

On montre plein de choses bien agréables sur les ordinaux finis; ils sont stable par union, produit, exponentiation. On montre aussi que tout ordinal fini est un cardinal.

Définition Un cardinal est dit fini s'il est fini en tant qu'ordinal. Dans le cas contraire il est dit infini. On note la classe des cardinaux infinis.

Nous supposons maintenant l'axiome de la théorie des ensembles selon lequel il existe un ordinal infini. Un ordinal infini est, par définition, un ordinal qui n'est pas fini. Cet axiome de la théorie des ensembles est équivalent à l'axiome selon lequel la classe des ordinaux finis est un ensemble; ainsi, puisque la classe des ordinaux n'est pas un axiome, il existe un ordinal infini. On peut encore formuler cet axiome en disant qu'il existe un ordinal limite, au vu de la définition ci-dessous:

Définition Un ordinal différent du vide et sans prédécesseur est appelé un ordinal limite. C'est donc un ordinal non vide tel que tout élément plus petit que lui a un successeur aussi plus petit que lui.

Propriété: Un ordinal limite est l'union des ordinaux qui lui sont inférieurs.

Définition On appelle le minimum des ordinaux infinis. est donc un ordinal limite, c'est le plus petit, et c'est l'ensemble des ordinaux finis.
Un ensemble est dit fini si son cardinal est fini.
Un ensemble est dit dénombrable si son cardinal est inférieur ou égal à .
est un cardinal; on note $aleph_0={omega}$ et pour tout ordinal n'étant pas un ordinal limite, alors avec le prédécesseur de , est le plus petit ordinal plus grand que ; et si est un ordinal limite, alors est l'union des pour .

Propriété:
Un ensemble infini est un ensemble contenant une partie dénombrable infinie.
Un ensemble infini est un ensemble qui est en bijection avec l'une de ses parties propres.
est un cardinal.

suivant: monter: précédent:

C.Antonini_JF.Quint_P.Borgnat_J.Berard_E.Lebeau_E.Souche_A.Chateau_O.Teytaud

Les axiomes de la théorie des ensembles de Zermelo-Fraenkel

Source : http://www.les-mathematiques.net/a/a/a/node2.php3

Une classe est associée à une propriété d'une seul élément; c'est à dire que l'on se donne une assertion comportant une et une seule variable libre; un élément est dans la classe correspondante s'il vérifie l'assertion. Les formules comportant plusieurs variables libres sont appelées relations. Eventuellement on peut avoir une distinction entre des variables et des paramètres; dans ce cas on a une classe pour chaque valeur possible des paramètres.
La théorie des ensembles est basée sur un ensemble d'axiomes. Les objets de cette théorie sont appelés ensembles, et la classe des ensembles est appelée univers. Les axiomes de la théorie des ensembles de Zermelo-Fraenkel sont les suivants:

Axiome Axiome d'extensionalité:

( deux ensembles sont égaux si et seulement si ils contiennent exactement les mêmes éléments )

Axiome Axiome de l'union:

( une union d'ensembles est un ensemble )

Axiome Axiome de l'ensemble des parties:

( les parties d'un ensembles forment une partie. On note l'assertion )

Axiome Axiome du schéma de remplacement:
Etant donné une formule ${cal R}(x,y,z_0,...,z_n)$ de paramètres , définissant pour toute valeur des une fonction, alors:

$displaystyle forall z_0 ... forall z_n ( forall x forall y forall y' {cal R}(x,y,z_0,...,z_n)land E(x,y',z_0,...,z_n) rightarrow y=y')$

$displaystyle rightarrow forall t exists w forall v ( v in w iff exists u ( u in t land {cal R}(u,v,z_0,...,z_{n}) ))$

On ajoute usuellement un axiome supplémentaire à ces axiomes:

Axiome axiome de l'infini, qui affirme qu'il existe un ordinal infini. Nous verrons plus loin ce qu'est un ordinal, et ce qu'est un ordinal fini.

Théorème La consistance de ces axiomes n'est pas changée si on remplace l'axiome de l'infini par sa négation.

Démonstration Voir [12]...

On appelle paire l'ensemble . Ne pas confondre avec le couple , qui désigne en fait l'ensemble . On note de même l'ensemble , et ainsi de suite pour les -uplets ordonnés.
La différence entre ${x_0,...,x_n}$ et est que dans le premier cas l'ordre des termes n'influe pas, alors que dans le second elle influe. On démontre l'associativité et la commutativité de l'union. On notera l'ensemble des parties de l'ensemble .

On notera que toutes les opérations intuitives sur les ensembles sont possibles, enfin presque. On peut en tout cas utiliser les intersections, définir l'ensemble des éléments d'un ensemble donné qui vérifient une propriété donnée, on peut travailler sur l'ensemble des parties d'un ensemble, on peut travailler sur un produit cartésien d'ensembles, bref toutes ces choses sans lesquelles les maths prendraient vraiment la tête. On peut aussi montrer l'existence et l'unicité de l'ensemble vide.

suivant: La "taille" des ensembles monter: Théorie des ensembles - précédent: Théorie des ensembles - Index

C.Antonini_JF.Quint_P.Borgnat_J.Berard_E.Lebeau_E.Souche_A.Chateau_O.Teytaud

Théorème de Cantor Bernstein

Source : http://les-mathematiques.u-strasbg.fr/spip/article.php3?i...

Théorème de Cantor Bernstein

Par Guy Philippe
Le samedi 20 novembre 2004.

Voici une preuve constructive et très simple de ce théorème fondamental. Elle ne requière que peu de connaissance ( il suffit de savoir ce qu'est une injection ,une surjection et une bijection) et est donc accessible à tous. Rémi Saint-Romain avait indiqué les grandes lignes de la preuve. Guy Philippe a écrit et détaillé la démonstration.

L'axiome de fondation

Source : http://www.les-mathematiques.net/a/a/a/node6.php3

Axiome [Axiome de fondation] On appelle axiome de fondation l'axiome selon lequel pour tout ensemble non vide il existe tel que et .

Cet axiome entraîne, par exemple, qu'il n'existe pas d'ensemble tel que , ni d'ensemble tel que .

Théorème Si la théorie de Zermelo-Fraenkel est consistante, alors la théorie de Zaermelo-Fraenkel plus axiome de fondation est consistante.
Démonstration Dure!

Théorème Il n'existe pas de suite d'ensembles telle que $U_{n+1} in U_n$ pour tout .
Démonstration La preuve, facile, nécessite l'axiome de fondation.

Théorème Si l'on utilise l'axiome de fondation, alors un ensemble est un ordinal si et seulement si il est transitif et si deux éléments et de vérifient au moins une des assertions suivantes:

Démonstration La preuve est plus difficile, et je ne la donne pas ici car elle dépasse mon propos de simple brève introduction à la théorie des ensembles.

Bien sûr on peut montrer que si ces hypothèses sont vérifiées alors pour tout couple c'est l'une et une seule des assertions qui est vérifiée.

Théorème Si l'on utilise l'axiome de fondation, alors pour tout ensemble il existe un unique ensemble transitif contenant et inclus dans tout ensemble transitif incluant .
Démonstration Non triviale.

Définition On appelle fermeture transitive de l'ensemble transitif dont l'existence est garantie par le théorème .

Propriété:
La fermeture transitive de est la réunion de et de l'union des fermetures transitives des éléments de .

Définition Une relation est dite extensive si .
Un ensemble est dit extensif si est une relation extensive sur cet ensemble. C'est à dire que si deux éléments ont même intersection avec l'ensemble, alors ils sont égaux.

Propriétés:
Un ensemble transitive est extensif.
Un ensemble extensif est isomorphe à un ensemble transitif, et l'isomorphisme est unique (nécessitant l'axiome de fondation).

Il est possible de prouver que l'axiome de fondation est relativement consistant, c'est à dire que la théorie basée sur les axiomes de Zermelo-Fraenkel est consistante si et seulement si la théorie basée sur les mêmes axiomes plus l'axiome de fondation est consistante.

suivant: Résumé de théorie des monter: Théorie des ensembles - précédent: L'hypothèse du continu Index

C.Antonini_JF.Quint_P.Borgnat_J.Berard_E.Lebeau_E.Souche_A.Chateau_O.Teytaud

Résumé de théorie des ensembles

Source : http://www.les-mathematiques.net/a/a/a/node7.php3

En résumé on a les implications de consistance du schéma .

**Figure:** désigne la théorie de Zermelo-Fraenkel. désigne la même théorie mais privée de l'axiome de l'infini et muni de sa négation. désigne l'axiome du choix. désigne la négation de . désigne l'axiome selon lequel les parties de ne peuvent pas être bien ordonnes. désigne l'axiome de fondation. désigne l'axiome d'accessibilité. désigne l'hypothèse du continu, et l'hypothèse du continu généralisée. Une flèche relie une théorie à une théorie si est plus forte que , c'est-à-dire que tous les théorèmes de sont des théorèmes de . Notez bien que toutes les théories présentes sur la figure sont consistantes si et seulement si est consistante. Notez bien aussi que si est consistante, alors il est impossible de le prouver; mais que par contre si elle ne l'est pas, on dispose d'un algorithme théorique permettant en temps fini de le prouver...

suivant: Index monter: Théorie des ensembles - précédent: L'axiome de fondation Index

C.Antonini_JF.Quint_P.Borgnat_J.Berard_E.Lebeau_E.Souche_A.Chateau_O.Teytaud

Cas le plus général d'espace topologique

Source : http://www.les-mathematiques.net/a/a/b/node3.php3

Définition [Topologie] Une topologie sur l'ensemble est une partie vérifiant:
L'ensemble vide et sont dans
est stable par réunions arbitraires
est stable par intersections finies

Un tel couple est appelé espace topologique. Les éléments de sont appelés les ouverts de la topologie.
Une partie de est dite fermée si son complémentaire est ouvert.

Exemples:
La topologie discrète sur l'ensemble est la topologie ${cal T}_d = P(X)$
La topologie grossière sur l'ensemble est la topologie ${cal T}_g = { emptyset,X}$
Sur , la topologie usuelle est l'ensemble des tels que ou est cofini.

On verra aussi d'autres exemples en parties et .

Proposition Si est un espace topologique alors
et sont des fermés de
Une intersection quelconque de fermés est un fermé
Une union finie de fermés est un fermé

Démonstration: Immédiat, par passage au complémentaire.

Définition [Séparation par des ouverts] On dit que la partie et la partie sont séparées par des ouverts s'il existe deux ouverts et tels que et tels que .

suivant: Espaces métriques et espaces monter: Espaces topologiques précédent: Espaces topologiques Index

C.Antonini_JF.Quint_P.Borgnat_J.Bérard_E.Lebeau_E.Souche_A.Chateau_O.Teytaud

Analyse pour l'agrégation , Cours et exercices corrigés

Analyse pour l'agrégation , Cours et exercices corrigésH. Quefellec, C. Zuily

Scolaire / Universitaire (broché). Paru en 03/2007

POUR COMMANDER

Fiche détaillée : Analyse pour l'agrégation

Auteur	H. Quefellec , C. Zuily
Editeur	Dunod
Date de parution	mars 2007
Collection	Capes Agreg.
ISBN	2100508660
Illustration	Pas d'illustrations

Logique mathématique , T2 Fonctions récursives, théorème de Gödel, théorie des ensembles, théorie des modèles

Logique mathématique , T2 Fonctions récursives, théorème de Gödel, théorie des ensembles, théorie des modèlesRené Cori, Daniel Lascar

Scolaire / Universitaire (broché). Paru en 01/2003

Sommaire :

Ce deuxième tome est plus particulièrement consacré aux problèmes de récursivité et de formalisation de l’arithmétique, aux théorèmes de Gödel et à la théorie des ensembles ainsi qu’à la théorie des modèles.

Sommaire :
Récursivité. Formalisation de l’arithmétique. Théorèmes de Gödel. Théorie des ensembles. Un peu de théorie des modèles. Solutions des exercices.

26/07/2010

Endomorphismes remarquables d’un espace euclidien

Agrégation : leçon 126 en Maths Générales

E désigne un espace vectoriel de dimension fini muni d'un produit scalaire et de la norme associée.

I. Endomorphismes normaux

Rappel
Soit $fin mathcal{L}(E),;exists !;f^*inmathcal{L}(E)/forallquad(x,y)in E^2$
$<f(x),y>=<x,f^*(y)>$ $f^*$ est appelé l'adjoint de $f$ .
Soit $B$ une base de $E$ si $Mat_B(f)=M$ alors $Mat_B(f^*)=^tM$

Proposition 1 ([M]p357-358)

$Ker(f^*)=(Im(f))^{perp}$ et $Im(f^*)=(Ker(f))^{perp}$

$F$ sev de $E$ , $F$ stable par $f$ alors $F^{perp}$ stable par $f^*$

Définition 2

$finmathcal{L}(E)$ est dit normal si $f^* circ f = f circ f^*$
$Min M_n({mathbb R})$ est dit normal si $^tMM = M^tM$

Proposition 3 ([G]p254)

$f in mathcal{L}(E)$ normal ssi $|f(x)| = |f^*(x)|$

Théorème 4 ([C]p159)

$f in mathcal{L}(E)$ normal ssi il existe une base $B$ de $E$ orthonormée telle que $f$ soit presque diagonale dans cette base.
$begin{pmatrix}lambda_1& & & & & &ddots& & & & & &lambda_r& & & & & &boxed{rm{A_1}}& & & & & &ddots& & & & & &boxed{rm {A_s }}end{pmatrix}$ Avec $lambda_i in mathbb{R}$
Et $rm{A_i} = begin{pmatrix}a_i&-b_ib_1&a_iend{pmatrix}$ $(a_i,b_i)inmathbb{R}^2$

Lemme 5 ([C]p157)

Si $f$ endomorphisme normal, et si $F$ sous espace de $E$ stable par $f$ alors $F^{perp}$ stable par $f$ .

II. Endomorphismes symétriques

Définition 6

$f$ est dit symétrique ou autoadjoint si $f^*=f$ .

$f$ est dit antisymétrique si $f^*=-f$

Exemple :
Si $finmathcal{L}(E)$ , $fof^*$ est symétrique.

Remarque :
Si $f$ symétrique, alors $f$ est normal.
$mathcal{L}(E)=Sym(E)oplusAA(E)$ avec
$Sym(E)=lbrace finmathcal{L}(E),f^*=frbrace$ et $AA(E)=lbrace finmathcal{L}(E),f^*=-frbrace$

Proposition 7 ([G]p240)

$finmathcal{L}(E)$ autoadjoint ssi la matrice de $f$ dans une quelconque base orthonormée est symétrique.

Définition 8

$S_n(mathbb{R})=lbrace Min M_n(mathbb{R}),:^tM=Mrbrace$
$Min S_n(mathbb{R})$ est dite positive si $forall Xquad^tXMXge 0$
On note $S_n^+(mathbb{R})$ l'ensemble des telles matrices.
$Min S_n^+(mathbb{R})$ est dite définie positive si $forall; Xneq 0quad^tXMX>0$
On note $S_n^{++}(mathbb{R})$ l'ensemble des telles matrices.

Exemple :
$forall;Min M_n(mathbb{R})quad ^tMMinS_n^+(mathbb{R})$
$forall;Min GL_n(mathbb{R})quad ^tMMin S_n^{++}(mathbb{R})$

Proposition 9 ([M]p359)

Soit $psi:fin Sym(E)rightarrow psi_fin BL_S(E)$ tel que $psi_f(x,y)=<f(x),y>$
$psi$ est un isomorphisme d'espaces vectoriels de $Sym(E)$ vers $BL_S(E)$ l'ensemble des formes bilinéaires symétriques.

Théorème 10 ([G]p240)

Si $fin Sym(E)$ alors il existe une base orthonormée $B$ de $E$ , formée de vecteurs propres pour $f$ .
Si $Min S_n(mathbb{R}),exists; Cin M_n(mathbb{R}),; C$ orthogonale telle que :

$^tCMC=^{-1}CMC$ soit diagonale

Corollaire 11 ([G]p241)

Si $Min S_n^{++}(mathbb{R})$ , $Nin S_n^+(mathbb{R})$ alors il existe $Pin GL_n(mathbb{R})$ telle que

$^tPMP=I_nmbox{ et } ^tPNP$ soit diagonale

Application :
Si $Phi$ est une forme quadratique, il existe une base orthonormale dans laquelle la matrice de $Phi$ est diagonale.

Remarque :
On pourrait aussi réduire les endomorphismes antisymétriques par le Théorème 4.

III. Endomorphismes orthogonaux

Définition 12

$fin mathcal{L}(E)$ est orthogonal si et seulement si il vérifie l'une de ces quatre propositions équivalentes.

$fcirc f^*=f^*circ f=Id_E$

$forall (x,y)in E^2;<f(x),f(y)>=<x,y>$

$forall ; xin E |f(x)| = |x|$

l'image par $f$ d'une base orthonormée est une base orthonormée.

On note $O(E)$ l'ensemble des endomorphismes de $E$ qui sont aussi appelés isométries de $E$ .

Remarque :

$O(E)$ est un sous groupe de $GL(E)$

Si $fin O(E)$ , $f$ est normal.

$Min M_n(mathbb{R})$ est dite orthogonale si $^tMM=I_n$

Exemples :

Les symétries orthogonales sont des isométries.

Les matrices de permutations sont des isométries.

Les projections orthogonales ne sont pas des isométries.

Proposition 13 ([G]p252-253)

$fin mathcal{L}(E)$ est une isométrie ssi la matrice de $f$ dans toute base orthonormale est une matrice orthogonale.

Remarque :
Si $fin O(E)$ on a $(det(f))^2=1$
On note $SO(E)=lbrace fin O(E),; det(f)=1rbrace$ qui est un sous groupe distingué de $O(E)$
On définit de même $SO_n(mathbb{R})=lbrace Min O_n(mathbb{R}),mbox{det }M=1rbrace$

Proposition 14

$O(E)$ et $SO(E)$ sont des sous groupes compacts de $GL(E)$

Proposition 15 ([G]p252-253)

Si $fin O(E)$ il existe $B$ une base orthonormée telle que
$Mat_B(f)=begin{pmatrix}I_p& & & & &-I_q& & & & &boxed{R_1}& & & & &ddots& & & & &boxed{R_s}end{pmatrix}$ Avec $(p,q,s)in mathbb{N}^3/quad p+q+2s=n$
$Ri=begin{pmatrix} cos(theta_i)&-sin(theta_i)sin(theta_i)&cos(theta_i) end{pmatrix}$
$0<theta_1le ldotsle theta_s<pi$

Remarque :
$q$ pair $Leftrightarrow quad fin SO(E)$

Application :
$SO_n(mathbb{R})$ est connexe par arcs.

IV. Le groupe orthogonal

Théorème 16 ([MT]p18-19) - Décomposition polaire

Soit $phi:(O,S)in O_n(mathbb{R})times S_n^{++}(mathbb{R})rightarrow OSin GL_n(mathbb{R})$ est un homéomorphisme.

Application ([A]p138-140) :

$O_n(mathbb{R})$ sous groupe compact de $GL_n(mathbb{R})$

$SO_n(mathbb{R})$ sous groupe compact maximal de $SL_n(mathbb{R})$

$forall; Min M_n(mathbb{R})$ $d(M,O_n(mathbb{R})) = | sqrt{^tMM}-I_n |$

Corollaire 17

$forall M in GL_n(mathbb{R}),; exists (Omega_1,Omega_2)in(O_n(mathbb{R}))^2$ et $D$ diagonale à valeurs propres réelles positives telles que $M=Omega_1 DOmega_2$

Proposition 18 ([C]p?) - Décomposition d'Iwasawa

Si $Min GL_n(mathbb{R})$ alors il existe un unique couple $(O,T)$ avec $O$ orthogonale et $T$ triangulaire supérieure à coefficients diagonaux positifs tel que: $M=OT$

Proposition 19 ([B]2.7.5 et 8.2.5.2)

Soit $G$ un sous groupe compact de $GL_n(mathbb{R})$ , il existe une structure euclidienne $G$ -invariante sur $mathbb{R}^n$

Définition 18

$fin mathcal{L}(E)$ une symétrie orthogonale.
Si $dim(ker(f-Id_E))=n-1$ $f$ est appelé réflexion.
Si $dim(ker(f-Id_E))=n-2$ $f$ est appelé renversement.

Proposition 20 ([P]p142)

$Z(O_n(mathbb{R}))=lbrace pm I_nrbrace$

Si $n$ pair $Z(SO_n(mathbb{R}))=lbrace pm I_nrbrace$

Si $n$ impair $Z(SO_n(mathbb{R}))=lbrace I_nrbrace$

Proposition 21 ([P]p143)

$fin O(E)$ est le produit d'au plus $n$ réflexions.

Corollaire 22

$fin SO(E)$ est le produit d'un nombre pair de réflexions.

Proposition 23 ([P]p143)

Pour $nge3quad SO(E)$ est engendré par les renversements.

Application ([P]p148) :
$SO_3(mathbb{R})$ est simple.

Proposition 24 (([P]p150))

Soit $mathbb{P} SO_n(mathbb{R})=SO_n(mathbb{R})/Z(SO_n(mathbb{R}))$ .
Alors pour $n=3$ et $nge 5$ $mathbb{P} SO_n(mathbb{R})$ est simple.

Proposition 25 ([P]p152)

Tout automorphisme de $SO_3(mathbb{R})$ est intérieur.

Remarque [P] :

$SO_n(mathbb{R})$ est le groupe dérivé de $O_n(mathbb{R})$ et si $n>2$ c'est aussi celui de $SO_n(mathbb{R})$ .

$D(SO_2(mathbb{R}))=lbrace I_2rbrace$

$Min O_2(mathbb{R})$ alors $M=begin{pmatrix}a&-bb&aend{pmatrix}$ ou $M=begin{pmatrix}-a&bb&aend{pmatrix}$ avec $a^2+b^2=1$ .

$SO_2(mathbb{R})$ est commutatif est isomorphe à $mathbb{R}/2pimathbb Z$

On peut noter que le groupe $O_3(mathbb{R})$ est composé de :
$I_3$ , $-I_3$ , les rotations et les produits de 3 réflexions.

Proposition 26 ([MT]p125-127)

$SO_3(mathbb{R})approx mathbb P^3 mathbb{R}$

$Pi_1(SO_3(mathbb{R}))approxmathbb Z/2mathbb Z$

Bibliographie

[A]: M.Alessandri "Thèmes de géométrie"
[C]: M.Cognet "Algèbre bilinéaire"
[G]: X.Gourdon "Algèbre"
[MT]: R.Mneimné, F.Testard "Groupes de Lie Classiques"
[M]: D.Monasse "Cours MP-MP^*"
[P]: D.Perrin "Cours d'algèbre"

SOURCE : http://www.ilemaths.net/maths-agreg-endomorphismes-espace...

21/05/2010

Livre Mathématique discrète: outil pour l'informaticien

15/04/2010

Algèbre

Un article de Wikipédia, l'encyclopédie libre.

L'algèbre, mot d'origine arabe al-jabr (الجبر), est la branche des mathématiques qui étudie, d'une façon générale, les structures algébriques.

L'étude des structures algébriques peut être faite de manière unifiée dans la cadre de l'algèbre universelle.

L'étude épistémologique de l'algèbre a été introduite par Jules Vuillemin.

Pour la « structure d'algèbre », voir l'article : Algèbre sur un corps.

Sommaire

[masquer]

Histoire [modifier]

Article connexe : Chronologie de l'algèbre.

Antiquité [modifier]

Les anciens Babyloniens et Égyptiens savaient déjà résoudre des problèmes qui peuvent être traduits en équations du premier ou second degré.

Par exemple, le Papyrus Rhind (conservé au British Museum de Londres, il date de -1650, ère chrétienne) comporte l'énoncé suivant :

On doit diviser 100 miches de pain entre dix hommes comprenant un navigateur, un contremaître et un gardien, tous trois recevant double part. Que faut-il donner à chacun ?

Cependant, ils ne faisaient pas de l'algèbre, car ils n'effectuaient pas de calcul sur une inconnue (mathématiques).

Diophante, au III^e siècle de l'ère chrétienne, fut le premier à pratiquer l'algèbre en introduisant le concept d'inconnue en tant que nombre,^[1] et à ce titre peut être considéré comme "le père" de l'algèbre.

Monde arabo-musulman [modifier]

Page d'Algebra d'al-Khwarizmi

Le mot « algèbre » vient de l'arabe al-jabr (الجبر), qui est devenu algebra en latin et qui signifie « la réunion » (des morceaux), « la reconstruction » ou « la connexion » (en espagnol le mot algebrista désigne celui qui pratique le calcul algébrique mais aussi le rebouteux, celui qui sait réduire les fractures osseuses^[2]).

C'est un des premiers mots du titre en arabe d'un ouvrage du mathématicien d'origine persane Al-Khawarizmi qui reprend, dans la première partie du IX^e siècle, les travaux de Diophante d'Alexandrie (III^e siècle). Ce dernier avait imaginé de représenter une inconnue par un symbole nommé arithme. Le titre de cet ouvrage (Al-jabr wa'l-muqabalah) qui s'inscrivait dans l'époque d'essor des sciences et techniques islamiques (la culture de l'époque voulait que tout savoir soit traduit en arabe et disséminé dans tout l'Empire), a donné le mot moderne « algèbre ». Une large proportion des méthodes utilisées sont issues de résultats élémentaires de géométrie. Pour cette raison, on classe souvent ces premiers résultats dans la branche de l'algèbre géométrique.

Après un voyage dans le nord de l'Afrique, Léonard de Pise dit Fibonacci fut séduit par cette nouvelle façon d'écrire les chiffres (différente des chiffres romains) et par le système décimal. Dès son retour au pays, il est parmi les premiers à populariser les chiffres arabes et le système décimal en Europe et travaille sur sa fameuse suite.

XVI^e siècle : Europe [modifier]

François Viète

Le pape Gerbert d'Aurillac avait ramené d'Espagne vers l'an 1000 le zéro, invention indienne que les mathématiciens Al-Khawarizmi et Abu Kamil avaient eux-mêmes fait connaître dans tout l'Empire, et aussi à Cordoue.

Cette numération de position lance une ère de calcul algébrique, d'abord au moyen des algorithmes nommés ainsi en hommage à Al-Kawarizmi, qui remplacent peu à peu l'usage de l'abaque. Les mathématiciens italiens du XVI^e siècle (del Ferro, Tartaglia et Cardan) résolvent l'équation du 3^e degré (ou équation cubique). Ferrari, élève de Cardan, résout l'équation du 4^e degré (ou équation quartique), et la méthode est perfectionnée par Bombelli. À la fin du siècle, le Français Viète découvre que les fonctions symétriques des racines sont liées aux coefficients de l'équation polynomiale.

Jusqu'au XVII^e siècle, l'algèbre peut être globalement caractérisée comme la suite ou le début des équations et comme une extension de l'arithmétique ; elle consiste principalement en l'étude de la résolution des équations algébriques, et la codification progressive des opérations symboliques permettant cette résolution. C'est à François Viète (1540-1603) que l'on doit l'idée de noter les inconnues à l'aide de lettres .

Au XVII^e siècle, les mathématiciens utilisent progressivement des nombres « imaginaires », tels que l'une des racines carrées de -1, pour parvenir à calculer les racines non réelles de leurs équations. Cette « extension » des nombres réels (qui prendra le nom de nombres complexes) amène d'Alembert (en 1746) et Gauss (en 1799) à énoncer et démontrer le théorème fondamental de l'algèbre (ou théorème de d'Alembert-Gauss) :

Théorème — Toute équation polynomiale de degré n en nombres complexes a exactement n racines (en comptant chacune avec son éventuelle multiplicité).

Sous sa forme moderne, le théorème s'énonce :

Théorème — Le corps $_mathbb C$ des nombres complexes muni de l'addition et de la multiplication est algébriquement clos.

Le XIX^e siècle s'intéresse désormais à la calculabilité des racines, et en particulier à la possibilité de les exprimer par des formules générales à base de radicaux. Les échecs concernant les équations de degré 5 amènent le mathématicien Abel (après Vandermonde, Lagrange et Gauss) à approfondir les transformations sur l'ensemble des racines d'une équation. Évariste Galois (1811 - 1832), dans un mémoire fulgurant, introduit pour la première fois la notion de groupe (en étudiant le groupe des permutations des racines d'une équation polynomiale) et aboutit à l'impossibilité de la résolution par radicaux pour les équations de degré supérieur ou égal à 5.

Une étape décisive était franchie avec l'écriture des exposants fractionnaires. Celle-ci permettra à Euler d'énoncer sa célèbre formule $e i π = - 1$ .

Algèbre moderne [modifier]

Ernst Kummer

Dès lors, l'algèbre moderne entame un parcours fécond : Boole crée l'algèbre qui porte son nom, Hamilton invente les quaternions, et les mathématiciens anglais Cayley, Hamilton et Sylvester étudient les structures de matrices. L'algèbre linéaire, longtemps restreinte à la résolution de systèmes d'équations linéaires à 2 ou 3 inconnues, prend son essor avec le théorème de Cayley-Hamilton (« Toute matrice carrée à coefficients dans $_mathbb R$ ou $_mathbb C$ annule son polynôme caractéristique »). S'ensuivent les transformations par changement de base, la diagonalisation et la trigonalisation des matrices, et les méthodes de calcul qui nourriront, au XX^e siècle, la programmation des ordinateurs. Parallèlement, Kummer généralise les structures galoisiennes et étudie les structures de corps et d'anneau. Dedekind définit les idéaux (déjà entrevus par Gauss) qui permettront de généraliser et reformuler les grands théorèmes d'arithmétique. L'algèbre linéaire se généralise en algèbre multilinéaire et algèbre tensorielle.

Au début du XX^e siècle, sous l'impulsion de l'allemand Hilbert et du français Poincaré, les mathématiciens s'interrogent sur les fondements des mathématiques : logique et axiomatisation occupent le devant de la scène. Peano axiomatise l'arithmétique, puis les espaces vectoriels. La structure d'espace vectoriel et la structure d'algèbre sont approfondies par Artin en 1925, avec des corps de base autres que $_mathbb R$ ou $_mathbb C$ et des opérateurs toujours plus abstraits. On doit aussi à Artin, considéré comme le père de l'algèbre contemporaine, des résultats fondamentaux sur les corps de nombres algébriques. Les corps non commutatifs amènent à définir la structure de module sur un anneau et la généralisation des résultats classiques sur les espaces vectoriels.

L'école française « Nicolas Bourbaki », emmenée par Weil, Cartan et Dieudonné, entreprend de réécrire l'ensemble des connaissances mathématiques sur une base axiomatique : ce travail gigantesque commence par la théorie des ensembles et l'algèbre dans le milieu du siècle, et confirme l'algèbre comme langage universel des mathématiques. Paradoxalement, alors que le nombre de publications suit une croissance exponentielle à travers le monde, alors qu'aucun mathématicien ne peut prétendre dominer qu'une toute petite partie des connaissances, les mathématiques n'ont jamais autant paru unifiées qu'aujourd'hui.

Notations européennes modernes [modifier]

Les symboles + et - apparaissent en 1489 dans l'ouvrage Arithmétique de John Widmann (Leipzig)
Le signe = apparaît en 1557 chez Robert Recorde "parce que deux choses ne sauraient être plus égales que deux lignes parallèles".
Les signes < et > apparaissent en 1610 chez Thomas Harriot (1560-1621).
William Oughtred (1574-1660) introduit le signe de la multiplication × dans son Clavis Mathematica (1631). Il introduit aussi les termes de sinus, cosinus et tangente.
Le signe de la division / est utilisé par Johann Heinrich Rahn en 1659 et introduit en Angleterre par John Pell en 1668.

Voir aussi [modifier]

Sur les autres projets Wikimedia :

Algèbre sur Wikimedia Commons (ressources multimédia)
Algèbre sur Wiktionnaire (dictionnaire universel)
Algèbre sur Wikiversity (communauté pédagogique libre)
Algèbre sur Wikibooks (livres pédagogiques)

Notes et références [modifier]

↑ Diophante et l'algèbre pré-symbolique [archive], Luis RADFORD .
↑ Diccionario de la lengua española [archive] de la Real Academia Española

Bibliographie [modifier]

Adolf P. Youschkevitch, Les Mathématiques Arabes, VIIIe-XVe siècles, Ed. VRIN, Paris - 1976

Liens externes [modifier]

Sur Al-Khwarizmi, mathématicien (en anglais)
Les mathématiques.net : références et cours en ligne

Source : http://fr.wikipedia.org/wiki/Alg%C3%A8bre

30/01/2010

Le triangle de Reuleaux

Le 4 janvier 2010, par Serge Cantat

Chargé de Recherche à l'Université Rennes 1 (page web)

Le triangle de Reuleaux est une figure de géométrie plane élémentaire, mais intrigante, qui peut être présentée à des élèves de collège. Elle jouit de propriétés remarquables, qui sont parfois difficiles à établir et à généraliser.

Le triangle de Reuleaux

L’objet de ce mois-ci concerne la géométrie de certaines parties du plan. Commençons par la plus simple, le disque, représenté ci-dessous en jaune. Le diamètre du disque n’a pas d’importance dans ce qui suit, et nous choisirons nos unités de mesure pour qu’il soit égal à 1 Ce disque jaune est donc l’ensemble des points du plan situés à une distance du centre inférieure à 12 ; la courbe qui borde ce disque est un cercle de diamètre 1

La position exacte du centre n’a pas non plus d’importance pour la propriété suivante. Prenons deux droites parallèles qui ne coupent pas le disque et qui sont situées de part et d’autre du disque ; rapprochons-les de celui-ci, en les gardant toujours parallèles à la direction qu’elles avaient initialement, jusqu’à ce qu’elles viennent chacune toucher le disque en un point. L’écart entre les deux droites est alors égal au diamètre du disque, ceci quelques soient les droites initialement choisies. On dit que le disque et le cercle sont de largeur constante. Ce que nous allons voir, c’est qu’il existe beaucoup d’autres parties du plan de largeur constante.

Le premier exemple est le triangle de Reuleaux. Pour le définir, le plus simple est de partir d’un triangle équilatéral dont nous noterons A B etC les trois sommets. L’équilatéralité signifie que les distances AB BC et CA entre les sommets sont égales, et nous supposerons que cette distance entre sommets vaut 1 Ainsi, le cercle de centre A et de rayon 1 passe par les sommets B et C De même, le cercle de centre B et de rayon 1 passe par C et A et le cercle de centre C et de rayon 1 passe par A et B Traçons ces trois cercles. Ils bordent trois disques de rayon1 Le triangle de Reuleaux est l’intersection de ces trois disques ; ce n’est donc pas un triangle au sens usuel. Comme on le voit sur la figure présentée ci-dessous, le triangle de Reuleaux s’obtient en ajoutant trois lunules au triangle équilatéral ABC dont nous sommes partis.

Pour tracer un triangle de Reuleaux avec un compas, il n’est pas utile de suivre pas à pas la construction précédente. Écartez votre compas d’une unité, puis choisissez un point A dans le plan où vous plantez votre compas. Tracez un grand arc de cercle C1 Plantez alors votre compas en un point B situé sur cet arc C1 près de l’une des extrémités de celui-ci, et tracez maintenant un deuxième arc de cercle C2 en sorte que C2passe par A et vienne couper l’arc C1 en un point C Plantez maintenant votre compas au point C et tracer l’arc de cercle passant par A et BVous voyez surgir le triangle de Reuleaux. Si vous désirez faire apparaître le triangle équilatéral évoqué ci-dessus, il suffit de relier les sommetsA B et C avec une règle.

Les figures présentées ici ont été réalisées en suivant ce canevas à l’aide du matériel de CM1 de ma fille ainée.

Comme annoncé plus haut, la propriété remarquable du triangle de Reuleaux s’énonce ainsi : le triangle de Reuleaux est de largeur constante. En effet, lorsque deux droites parallèles viennent toucher le triangle de Reuleaux en se rapprochant de part et d’autre, l’une d’entre elles le touche en l’un des sommets A B ou C et la seconde le touche en un point de l’arc de cercle opposé ; ainsi, l’écart entre les deux droites est égal à 1 le rayon du cercle. Reformulons cette propriété : si l’on découpe un triangle de Reuleaux dans une plaque de granit et qu’on vient le serrer avec une clé anglaise, l’écart de la clé anglaise ne dépend pas de la position du triangle de Reuleaux. Autrement dit, une fois serrée, on peut tourner la pièce de granit sans changer l’écart de la clé et, ce faisant, la pièce reste en permanence en contact avec les bords de l’ustensile. Ou encore, si vous faites rouler le triangle de granit entre deux règles parallèles situées à une distance unité l’une de l’autre, le triangle de Reuleaux touchera en permanence le bord des deux règles.

Convexes de largeur constante

Nous voyons donc qu’il y a au moins deux parties du plan qui sont de largeur constante, le disque et le triangle de Reuleaux. Peut-on en construire d’autres ? La réponse est oui, mais avant de continuer il convient d’exclure certaines constructions sans intérêt. Si l’on évide un petit trou dans un triangle de Reuleaux ou dans un disque, on crée une nouvelle partie du plan dont la largeur est constante, mais pour la raison idiote qu’aucune modification n’a été effectuée au bord, là où la clé anglaise vient serrer la pièce de granit étudiée.

Avant de continuer nous allons donc introduire une définition utile. Nous dirons qu’une partie D du plan est convexe si elle satisfait la propriété suivante : quelque soit la paire de points A et B situés dans D la totalité du segment joignant A à B est contenue dans D

Le triangle de Reuleaux est convexe ; si on le perce, il ne l’est plus. D’autres exemples sont fournis sur la figure ci-contre. La partie jaune à gauche est convexe, tandis que la partie orange H en forme de haricot, ne l’est pas. La plus petite partie convexe qui contient H s’obtient en ajoutant la portion jaune bordée par H d’un côté et par un segment de l’autre ; la droite contenant ce segment vient toucher le bord de H en deux points distincts. Ce fait, à lui seul, montre que H ne peut pas être de largeur constante car si l’on serre H avec une clé anglaise dont un côté touche le bord de H en deux points, alors on ne peut plus tourner H sans agrandir l’écart de la clé.

Ainsi, lorsque D est une partie du plan de largeur constante alors, après avoir boucher les trous éventuels de D on obtient une partie convexe qui reste de largeur constante. De plus, le bord de cette partie ne contient aucun segment ; autrement dit, les droites parallèles qui viennent enserrer D de part et d’autre touchent chacune D en exactement un point.

L’étude des parties du plan de largeur constante se ramène donc à l’étude de celles qui sont convexes.

Pour les parties convexes du plan, on dispose d’une caractérisation moins poétique de de la propriété largeur constante à l’aide de plaques d’égouts. La forme d’une plaque d’égouts doit être telle qu’elle ne peut jamais tomber dans le trou qu’elle vient boucher. Si le trou a la forme d’un triangle de Reuleaux, d’un disque, ou de toute autre courbe de largeur constante, alors la plaque qui vient l’obstruer ne peut tomber : quel que soit l’orientation de la plaque, elle touchera les bords du trou sans pouvoir chuter sur la tête de l’ouvrier travaillant au fond. A l’inverse, la plaque verte ci-dessous n’est pas de largeur constante et, de fait, en tournant d’un quart de tour et en basculant, elle tomberait dans les égouts, son grand côté à la verticale et son petit côté à l’horizontal .

Il s’agit maintenant de construire de nouvelles parties convexes du plan qui sont de largeur constante, égale à 1 pour fixer les idées. Construire la partie ou la courbe qui l’encercle constituent le même problème. Nous chercherons donc à construire de telles courbes, et parlerons decourbes de largeur constante.

C’est encore le mécanicien Franz Reuleaux [1] qui nous apporte des exemples. On peut tout d’abord répéter une construction similaire en remplaçant le triangle équilatéral ABC utilisé ci-dessus par un polygone régulier ayant un nombre impair de côtés. Plutôt que de se livrer à un cours sur la construction de polygones réguliers, contentons nous de contempler un film délicieusement vintage.

On peut aussi reprendre la construction au compas que nous avons décrite en la généralisant au p’tit bonheur la chance. Pour cela on part d’un point A0 et l’on trace un petit arc de cercle C1 centré en A0 dont l’on note A1 et A2 les extrémités. On trace ensuite un arc de cercle centré en A1partant de A0 et s’approchant de A2 et un arc de cercle centré en A2 partant de A0 et s’approchant de A1 Deux nouvelles extrémités apparaissent et l’on répète le procédé à partir de celles-ci. En traçant un nombre impair d’arcs de cercles on peut ainsi tracer une courbe qui est la frontière d’une partie convexe de largeur constante. La figure ci-dessous illustre ce procédé. [2]

Nous disposons donc maintenant de nombreuses parties du plan qui sont de largeur constante. On peut déjà se féliciter : l’architecture en a profité, les pièces de monnaie, et les moteurs aussi. Le lecteur en verra apparaître au fil des illustrations de ce texte. Mon but maintenant est de mener le lecteur à un joli problème de mathématique encore ouvert de nos jours, et pour cela mieux vaut passer directement à la suite.

Buffon et Didon

Les courbes de largeur constante donnée ont un périmètre fixé ! Ainsi, le triangle de Reuleaux, comme toute courbe de largeur constante égale à 1, a le même périmètre que le disque de diamètre unité, il vaut Le film vintage mentionné ci-dessus illustre ceci aux alentours d’une minute et vingt seconde. Cette propriété remarquable peut être démontrée en faisant appel à un autre objet mathématique célèbre, l’aiguille de Buffon. Le problème de l’aiguille de Buffon est le suivant. Traçons des droites parallèles sur le sol en les espaçant régulièrement de sorte que la distance entre deux droites consécutives est constamment égale à une distance L fixée. Prenons maintenant une aiguille de longueur l plus petite que L ; ainsi, lorsque l’aiguille repose sur le plan, elle coupe au plus une des droites que nous avons tracées. Le problème proposé par Buffon en 1733 est le suivant : quelle est la probabilité que l’aiguille, lancée au hasard sur le plan, coupe l’une des droites tracées ? La réponse est

Ainsi, lorsque l’espace entre les droites parallèles est fixé à L=1 cette probabilité vaut (2)l Si l’on fait un grand nombre de lancers de l’aiguille sur le plan, le nombre des lancers pour lesquels l’aiguille intersecte l’une des droites du quadrillage sera donc approximativement égal à

(longueur de l'aiguille)

(nombre de lancers)

Ou encore, si l’on lance notre aiguille N fois et que l’on note I le nombre total d’intersections observées, alors

longueur de l'aiguille

l’égalité devenant exacte dans la limite d’un nombre infini de lancers. Ceci vaut en fait pour n’importe quelle courbe Z Supposons en effet qu’on veuille calculer la longueur d’une courbe Z tracée dans un plan. Prenons du fil de fer et tordons-le pour qu’il épouse la forme de la courbe ZAllons ensuite nous placer au-dessus d’un parquet dont les lattes sont toutes de largeur 1 Lançons le fil de fer sur le parquet et considérons le nombre de points d’intersection total entre la courbe en fil de fer et les droites qui bordent les lattes. Si la courbe Z est un segment de longueur inférieure à 1 nous observons à chaque fois 0 ou 1 intersection. Mais pour une courbe Z plus longue ou plus tordue, plusieurs points d’intersection peuvent être obtenus. Maintenant, effectuons N lancers et faisons la somme I de toutes les intersections observées. Alors, lorsque N tend vers l’infini, le rapport (2)(IN) tend vers la longueur de la courbe Z

Avec un peu d’imagination, nous pouvons maintenant inverser le lancer. La courbe Z est maintenant tracée au sol, immobile. C’est le plancher qu’on va lancer. Si cela vous inquiète, pensez à une grande feuille de papier calque rayée de droites parallèles faisant des bandes de largeur unité. Nous pouvons lancer le calque sur la courbe Z aléatoirement un grand nombre N de fois. Notons encore I le nombre total d’intersections observées entre les droites tracées sur le calque et la courbe Z Quand le nombre de lancers devient très grand, le rapport IN s’approche de(2) (Longueur de Z). [3]

Nous pouvons maintenant démontrer la propriété des courbes de largeur constante annoncée. Prenons une courbe de largeur constante égale à1 Lançons la sur un plan qui a été rayé de droites parallèles espacées d’une unité. Une fois sur le plan, la courbe ne peut être située dans une bande entre deux des droites sans toucher aucune de ces droites, car sinon sa largeur serait inférieure à la largeur de la bande, donc inférieure (strictement) à 1 Seuls deux cas peuvent donc se produire. Ou bien la courbe coupe une droite en deux points : elle est à cheval entre les deux bandes situées de part et d’autre de la droite. Ou bien la courbe est contenue dans une bande, mais touche les deux droites qui la délimitent. Ainsi, dans tous les cas, le nombre de points d’intersection de la courbe avec les droites tracées dans le plan est égal à 2 ; ceci quelque soit le lancer effectué. Si l’on effectue N lancers, le nombre total d’intersections est donc égal à 2N La formule de Buffon fournit alors

longueur d'une courbe de largeur constante 1

On retrouve le périmètre du disque de diamètre 1 (donc de rayon 12) : toutes les courbes de largeur constante égale à 1 partagent le même périmètre De même, le périmètre des courbes de largeur constante L est égal à L

Ceci, plus la solution du problème de Didon [4] nous apprend que le cercle est la courbe de largeur constante donnée qui enclôt l’aire la plus grande. Les triangles de Reuleaux admettent une caractérisation opposée :

Théorème de Blaschke et Lebesgue

Les courbes de largeur constante donnée qui entourent une aire minimale sont les triangles de Reuleaux.

Cette caractérisation des triangles de Reuleaux est dûe à Wilhelm Blaschke et Henri Lebesgue, elle date des années 1910, et est difficile à établir.

Nous pouvons maintenant contempler un joli film issu du site russe déjà cité par Étienne Ghys dans son article sur la machine à marcher. Il illustre élégamment les remarques précédentes et décrit

une autre construction de courbes de largeur constante ;
un moteur d’automobile utilisant le triangle de Reuleaux ;
un mécanisme utilisé pour les projecteurs cinématographiques.

Hexagones de Julius Pál

Si je n’ose présenter ici une preuve de la caractérisation des triangles de Reuleaux dûe à Blaschke et Lebesgue, je ne peux m’empêcher d’expliquer une jolie construction qui permet de comparer toute courbe de largeur constante à des triangles de Reuleaux qui lui sont proches et qui peut donc être utilisée pour démontrer le théorème de Blaschke et Lebesgue. Cette construction est dûe à un mathématicien hongrois, Julius Pál.

Pour la comprendre, commençons par un problème de nature différente qui tracasse pas mal de familles les dimanches d’été : pendant que grand-père se fait roussir la barbe au-dessus du barbecue, papa essaie de placer au milieu de la pelouse la table de jardin qu’il vient d’acheter. Au bout d’un quart d’heure de jurons, il rentre se servir un pastis en hurlant qu’à cause de cette satanée pelouse sa table ne sera jamais stable. Et pourtant. Pourtant, il suffit d’opérer comme suit. Plaçons la table au hasard sur la pelouse ; si elle est bancale, c’est que deux pieds de la table situés en diagonale sont sur le sol, tandis que chacun des deux autres pieds est soit sur le sol, soit décolé, suivant qu’on appuie ici ou là ; il y a donc deux diagonales distinctes, la diagonale d’appui et la diagonale bancale. Tournons maintenant la table progressivement d’un quart de tour. La position finale des diagonales a été inversée, la diagonale d’appui est devenue bancale et la diagonale bancale a maintenant les deux pieds sur terre. Ainsi, au cours de la rotation de la table d’un quart de tour, il y a au moins une position où les deux diagonales échangent leur rôle ; à ce moment là, les quatre pieds de la table touchent le sol simultanément et la table n’est plus bancale (en revanche, elle peut être légèrement penchée suivant l’inclinaison de la pelouse).

Appliquons ce principe de démonstration pour nos courbes de largueur constante. Nous allons montrer que toute courbe de largeur constante est inscrite dans un hexagone régulier dont les côtés sont tous tangents à la courbe. Chaque côté de l’hexagone touche donc la courbe en un unique point. Les hexagones réguliers sont ceux pour lesquels tous les côtés ont même longueur et tous les angles aux sommets sont égaux ; ces deniers valent 120 (soit un tiers de tour). Voici un tel hexagone, avec un triangle de Reuleaux inscrit à l’intérieur pour décorer.

Voici maintenant un hexagone régulier, à gauche et, à droite, un hexagone obtenu en faisant coulisser deux côtés parallèles de l’hexagone précédent. De la sorte, nous n’avons changé ni les angles aux sommets ni l’écart entre les côtés opposés ; pourtant, le nouvel hexagone n’est pas régulier.

Donnons nous une courbe P de largeur constante égale à 1 Choisissons deux droites parallèles L et L venant toucher la courbe en deux points opposés ; elles sont donc séparées l’une de l’autre d’une unité. Ce choix étant fait, il existe deux paires de droites qui font un angle de120 avec les deux premières et viennent enserrer la courbe P en des points opposés ; la distance entre ces droites est encore égale à 1 carP est de largeur constante. A priori, l’hexagone formé par ces 6 droites n’est pas régulier car, pour qu’il le soit, il faut que ses 6 côtés aient même longueur, ce qui n’est pas automatique. C’est toutefois un hexagone très spécial : les angles aux sommets valent bien 120 et l’écart entre deux côtés parallèles quelconques est égal à 1 Notons A B C D E et F les sommets successifs de cet hexagone (voir la figure ci-dessous).

On remarque alors que cet hexagone est régulier dès que la longueur AB est égale à la longueur DE Si ce n’est pas le cas, on peut donc supposer que AB est strictement plus grand (ou plus petit) que DE Faisons maintenant tourner progressivement cette construction en conservant l’appellation des sommets : la courbe P est fixe, mais les deux droites parallèles L et L font un demi tour, si bien que les six sommets tournent autour de P Une fois le demi tour complètement effectué, les sommets A et B ont été échangés avec les sommets D et E Si la longueur initiale AB est plus grande (ou plus petite) que DE c’est le contraire qui se produit après ce demi tour ; il y a donc bien un instant au cours de la rotation pour lequel AB=DE et pour cet instant l’hexagone ABCDEF est régulier, ce qu’il fallait démontrer.

La figure suivante représente une courbe de largeur constante (elle borde l’union des zones oranges et jaune), un hexagone régulier dans lequel elle est inscrite, et un triangle de Reuleaux qui lui est proche (il entoure la partie jaune et les trois portions vertes). Le lecteur curieux pourra consulter le chapitre 7 du livre [5] pour voir comment cette figure montre que les triangles de Reuleaux entourent une aire minimale.

Solides de Meissner

Quel est l’analogue du triangle de Reuleaux pour les solides convexes, c’est-à-dire pour les parties convexes de l’espace de dimension 3 ? Il s’agit d’abord de savoir comment transposer la propriété « de largeur constante » en dimension 3 Nous dirons donc qu’un solide S est de largeur constante si la largeur entre deux plans parallèles quelconques qui viennent serrer le solide est constante. Pour visualiser cette définition, il suffit de penser à une presse constituée de deux plaques reliées par un pas de vis : posons le solide S sur la plaque inférieure et manœuvrons la presse pour que la plaque supérieure vienne serrer le solide ; S est de largeur constante si la hauteur de la plaque supérieure ne doit pas dépendre de la position du solide S

Prenons une courbe de largeur constante qui possède un axe de symétrie, par exemple le triangle de Reuleaux, ou la pièce de fifty pence représentée ci-dessous, puis faisons tourner la courbe dans l’espace autour de son axe. Le solide entouré par cette surface est de largeur constante.

Une autre construction consiste à généraliser celle du triangle de Reuleaux. Prenons donc un tétraèdre régulier. C’est une pyramide dont toutes les faces sont des triangles équilatéraux. Les quatre sommets A B C et D sont donc tous à la même distance (disons d’une unité) les uns des autres. La sphère de centre A et de rayon 1 passe ainsi par B C et D L’intersection des quatre sphères de centre 1 centrées aux sommets forme un solide parfois appelé tétraèdre de Reuleaux. Le malheur, c’est qu’il n’est pas de largeur constante. Le bonheur, c’est qu’on peut modifier légèrement la construction pour qu’il le devienne. L’idée est dûe à Ernst Meissner et Friedrich Schilling : prenons l’un des côtés T du tétraèdre initial et prolongeons un peu les deux faces contenant ce côté. Elles viennent alors intersecter le tétraèdre de Reuleaux sur deux arcs de cercles C1 et C2 Retirons la partie située entre C1 et C2 et remplaçons-la par le nouveau morceau obtenu en faisant tourner l’arc de cercleC1 jusqu’à l’arc de cercle C2 autour de l’axe T On répète alors cette opération trois fois, soit avec trois côtés T T et T" qui bordent une face du tétraèdre soit avec trois côtés partant d’un même sommet. Nous obtenons deux solides différents, les deux solides de Meissner, qui sont de largeur constante. Pour contempler l’un de ces solides, le mieux est de se rendre sur la page créée par Cristof Weber, de l’université de Zurich.

Le problème ouvert que j’ai mentionné plus haut s’énonce ainsi :

Question

Les solides de largeur constante donnée dont le volume est minimum sont-ils exactement les solides de Meissner ?

Apparemment, la réponse n’est pas connue.

Notes

[1] Franz Reuleaux (1829-1905) est un mécanicien allemand du dix-neuvième siècle réputé qui a contribué à de nombreuses avancées en mécanique, cinématique, et ingénierie. Il fût parfois critiqué, paraît-il, pour avoir une approche un peu trop mathématique de la mécanique... L’ université Cornell, aux Etats-Unis, a créé un bâtiment en son honneur et lui dédie plusieurs sites web : site de la bibliothèque ; site du laboratoire de mathématique .

[2] Cette construction est un progrès véritable, puisqu’on peut

passer à la limite en utilisant une infinité d’arcs de cercles pour construire de nouvelles courbes de largeur constante ;
démontrer que toute courbe de largeur constante (égale à 1) peut être approchée par des courbes ainsi formées par des morceaux de cercles de rayon 1

[3] La formule de Cauchy et Crofton dit essentiellement la même chose : la somme (ou plutôt l’intégrale), sur l’ensemble des droites affines du plan, du nombre de points d’intersection entre les droites et une courbe Z fixée est égale à (une constante fixe fois) la longueur de la courbe. Il faut intégrer par rapport à une mesure sur l’espace des droites qui est invariante par rotations et translations ; le choix de la mesure détermine la constante.

[4] Voir le billet de Benoît Kloeckner sur l’inégalité isopérimétrique

[5] H. G. Eggleston : Convexity, Cambridge Tracts in Mathematics and Mathematical Physics, No. 47, (1958), Cambridge University Press

Source : http://images.math.cnrs.fr/Le-triangle-de-Reuleaux.html

Louis Bachelier

11 mars 1870 - 28 avril 1946

Le 15 octobre 2006, par Laurent Carraro et Pierre Crépel

(Cet article, écrit en 2006, est issu de la version papier d’Images des mathématiques.)

Incroyable destinée, pour un mathématicien contemporain, que celle de Bachelier, qui fut d’abord déconsidéré, qui obtint son premier poste fixe à l’université (de Besançon) à 57 ans, et ne devint célèbre que 20 ans après sa mort.

LOUIS Bachelier naquit au Havre, dans une famille habituée aux affaires bancaires et commerciales. Il fit des études sans éclat, puis soutint son doctorat sous la direction de Poincaré le 29 mars 1900, avec seulement la mention “honorable”, sous le titre “Théorie de la spéculation”. Ce travail, qui a pour objet l’application du calcul des probabilités aux opérations de la Bourse, est suivi de nombreux autres notes, mémoires et ouvrages originaux sur les probabilités, rédigés malgré la situation très précaire de leur auteur.

La thèse de Bachelier contient, et cela de trois façons différentes, la première théorie mathématique du mouvement brownien (cinq ans avant Einstein). Ainsi, en utilisant une terminologie moderne, le mouvement brownien est vu tour à tour comme le processus à accroissements indépendants et homogènes dont les trajectoires sont continues, comme le processus à temps continu limite de marches au hasard symétriques, et enfin comme le processus de Markov dont l’équation “forward” de Kolmogorov est l’équation de la chaleur. Bachelier procède à une étude “fine” des trajectoires du mouvement brownien trente ans avant Paul Lévy, à l’aide du principe de réflexion, de la propriété de Markov forte.

On peut interpréter cette thèse comme le confluent de deux traditions apparemment très éloignées :

La première, qui sert de ligne directrice mathématique à son auteur, est celle de la physique mathématique française de J. Fourier, de G. Lamé et évidemment de H. Poincaré. Bachelier tire d’ailleurs explicitement ses analogies (tel le rayonnement de la probabilité) de ces idées.
La seconde, ce sont les modèles de raisonnement tacites des spéculateurs en Bourse qu’on trouve, sous des expressions certes moins formalisées, dans la seconde moitié du XIXe siècle. Ainsi un ouvrage de Jules Regnault de 1863 renferme-t-il déjà, en termes plus “littéraires”, le cadre conceptuel de l’application du calcul des probabilités aux opérations de Bourse, notamment le fait que “l’écart pris sur un grand nombre d’opérations est en raison directe de la racine carrée du temps”.

Bachelier a été méprisé, fort peu lu et encore moins compris, et il en a beaucoup souffert : Gevrey et P. Lévy ont cru (à tort) qu’il s’était grossièrement trompé ; seul Kolmogorov a reconnu la profondeur de ses travaux, dans les années trente. Or, non seulement, sa thèse était remarquable, mais ses recherches ultérieures l’étaient quelquefois encore davantage et passèrent à peu près inaperçues, malgré un certain soutien de Poincaré.

Par exemple, son mémoire de 1906 donne-t-il les définitions de grandes classes de processus aléatoires apparus par la suite : processus à accroissements indépendants, processus de Markov, processus d’Ornstein-Uhlenbeck. Ces définitions apparaissent comme conséquences d’une théorie plus générale : celle des équations différentielles stochastiques que Bachelier développe ici, sans toute la rigueur à laquelle nous sommes habitués maintenant, à l’aide d’un vocabulaire issu des jeux de hasard. Deux fonctions jouent un rôle central dans son mémoire, la première, appelée espérance relative à une partie est le terme de “drift” de l’équation différentielle stochastique, alors que la seconde, appelée fonction d’instabilité relative à une partie, est évidemment le coefficient de diffusion de cette même équation. Bachelier raisonne plutôt en trajectoire : ses équations définissent bien un mouvement, en cela il fait penser à Langevin (1908), puis à Itō et Lévy, plus tard. L. Bachelier a en outre introduit une théorie intéressante de la “probabilité inverse” et de la “probabilité des causes”, c’est-à-dire de l’estimation statistique, qu’il a d’ailleurs reprise dans un traité de calcul des probabilités, aussi clair que remarquable, publié en 1912.

N.B. Pour toutes précisions, voir Courtault Jean-Michel & Kabanov Youri (dir.), Louis Bachelier. Aux origines de la finance mathématiqueBesançon, Presses de l’Université de Franc-Comtoises, 2002.

Références

Bachelier, L. (1900), Théorie de la spéculation, Annales de l’Ecole Normale Supérieure, 17, p. 21-86

Bachelier, L. (1906), Théorie des probabilités continues, Journal de mathématiques pures et appliquées, 2, p. 259-327

Bachelier, L. (1912), Calcul des probabilités, Gauthier-Villars, Paris

Gobet, E. (2004), Les mathématiques appliquées au coeur de la finance, Images des mathématiques.

Regnault, J. (1863), Calcul des chances et philosophie de la Bourse, Mallet-Bachelier, Paris

Source : http://images.math.cnrs.fr/Louis-Bachelier.html

Mandelbulb

Le 16 janvier 2010, par Jos Leys

Mathematical Imagery (page web)

... ou la quête de l’ensemble Mandelbrot en trois dimensions.

IL y a un mois, on voyait apparaître un peu partout sur internet des images d’une nouvelle famille d’ensembles fractals. C’est un groupe d’amateurs, enthousiastes d’images fractales, qui en ont fait la découverte en collaborant dans un forum. Une discussion en ligne sur le sujet du « vrai Mandelbrot 3D » a démarré en septembre et avait plus de 500 contributions vers la fin de novembre. Des dizaines de personnes ont participé en faisant des suggestions de modifications sur les formules et sur les techniques de visualisations, mais on doit attribuer l’idée pour le Mandelbulb, le « bulbe Mandelbrot » à Daniel White etPaul Nylander.

De quoi s’agit-il ?

De nombreux lecteurs connaissent probablement l’image de gauche qui est l’ensemble Mandelbrot en 2D. Pour chaque nombre complexe c, on considère la transformation du plan complexe définie par zz2+c. Partant de z0=0, on itère cette transformation, c’est-à-dire qu’on construit la suite zn avec zn+1=z2n+c. L’ensemble de Mandelbrot est l’ensemble des c qui sont tels que la suite zn ne tend pas vers l’infini quand l’entier n tend vers l’infini.

Prendre le carré du nombre complexe z revient à doubler l’argument et à élever au carré lemodule. On ajoute ensuite c. On obtient un nouveau point et on répète les mêmes opérations. Certains points vont rester près de l’origine, même après beaucoup d’itérations, et d’autres s’envolent vers l’infini. L’ensemble de Mandelbrot est donc la figure formée par les points c tels que l’origine 0 ne s’envole pas dans ce processus.

La figure est fractale : même élargie à l’extrême on voit des détails époustouflants (voir par exemple ce film, extrait de Dimensions, où on peut aussi voir l’effet de prendre le carré d’un nombre complexe sur une photo).

Il ne faut pas se limiter au carré d’un nombre complexe. Si on itère zzp+c, avec n’importe quel nombre p, on obtiendra aussi un ensemble de Mandelbrot. Voici les ensembles avec p=3, p=4 et p=8. Sur cette dernière image, remarquez les « bulbes » qui entourent la figure. Nous les rencontrerons à nouveau dans ce qui suit.

Depuis sa découverte en 1979 par Benoît Mandelbrot, de très nombreux amateurs ont créé des images fractales basées sur la simple formule d’itération que nous avons vue. Voilà donc une chose dont on a des millions de peintures, mais aucune sculpture !

Une question est devenue comme le Graal des amateurs de fractales : existe-t-il un équivalent en trois dimensions de l’ensemble Mandelbrot ?

L’ensemble Mandelbrot consiste d’une cardioïde entourée de cercles de toutes tailles, qui à leur tour sont entourés de différentes formes, comme des spirales, qui deviennent de plus en plus petites. Il y a des vrilles où poussent des copies minuscules de l’ensemble.

En trois dimensions, on imagine donc un corps principal muni de quelques sphères, et sur les sphères des sphères plus petites, etc. Il va de soi qu’on aimerait voir des vrilles où poussent des copies minuscules de l’ensemble qui à leur tour ont des vrilles microscopiques, etc.

Il faut dire tout de suite que personne n’a encore trouvé un tel objet mais, d’autre part, on n’a pas encore démontré qu’un tel objet n’existe pas. Cela donne la motivation aux amateurs de fractales de continuer leur quête !

Le « Bristorbrot »

Comment pourrait-on essayer de trouver un tel objet ? Voici un premier effort :

Pour l’ensemble de Mandelbrot, on a besoin de nombres complexes z=a+ib, avec i2=−1. On a donc :

z2=(a+ib)2=a2−b2+i2ab

On met la partie réelle a2−b2 sur l’axe x, et la partie imaginaire 2ab sur l’axe y. En trois dimensions il nous faudrait donc un nombre « supercomplexe » comme w=a+ib+jc, pour qu’on ait quelque chose à mettre sur une troisième axe z. Appelons les trois composantes simplement xyz.

Définissons ces nombres à trois composantes. On impose que i2=−1, j2=−1, ji=i, ij=−j. La multiplication de i et j n’est donc pas commutative. Si nous calculons w2=(a+ib+jc)2, on obtient

x=a2−b2−c2

y=2ab−bc

z=2ac+bc

Si on a c=0, on se trouve dans le plan xy et on a la même expression pour le carré que pour les nombres complexes habituels. Si on a b=0, on se trouve dans le plan xz et là encore on a la même expression. On peut donc s’attendre au fait qu’une itération ww2+c, où c est aussi un tel nombre « triplex », donne un objet 3D dont les coupes avec les plans xy et xz soient des ensembles de Mandelbrot.

C’est Doug Bristor, un programmeur anglais qui a proposé ce système en 1995 : voici ce que ça donne.

Voici les coupes à travers les plans xy (à gauche) et xz (à droite) :

Ici non plus, il ne faut pas se limiter à prendre le carré de ces nombres « triplex », on peut aussi dessiner des « Bristorbrot » de plus haut degré.

Si, dans zz2+c, c est une constante, on obtient un « ensemble de Julia ». Voici en dessous un ensemble de Julia selon Bristor de troisième degré.

Le système de Bristor est un bel effort mais on ne peut pas dire qu’on ait trouvé le Saint Graal !

Dessiner des objets fractals en 3D

Avant de revenir au Mandelbulb, parlons un peu des méthodes pour visualiser de tels objets 3D. Pour les fractales 2D il suffit de faire une itération pour chaque pixel de l’image. Si le point s’éloigne de l’origine il sera en dehors de l’ensemble et il reste à décider quelle couleur on donnera à ce pixel. On pourrait simplement colorer tous les pixels « en dehors » en blanc et les pixels « dedans » en noir, mais il y a beaucoup d’autres méthodes. On déclare un pixel comme « en dehors » si son module devient plus grand qu’un nombre qu’on a choisi à l’avance. Les méthodes pour colorer les pixels sont souvent basées sur le nombre d’itérations avant que le module ne devienne assez grand pour être déclaré « en dehors ».

Pour représenter un objet 3D, on doit penser à l’image comme un plan de projection. On choisit un point de vue virtuel et on tire des rayons de ce point de vue vers chaque point du plan de projection, donc vers chaque pixel de l’image. Pour chaque rayon, il faut maintenant découvrir si le rayon rencontre l’objet fractal et, si oui, à quel endroit sur le rayon.

Le plus simple serait de bouger un point sur un rayon vers le plan de projection à petits pas, faire l’itération à chaque pas, et s’arrêter quand l’itération du point sur le rayon nous dit qu’on est « dedans ». Le problème, évidemment, c’est qu’on ne sait pas a priori où se trouve l’objet fractal et on devrait prendre des pas infinitésimaux pour ne rien manquer (rappelez-vous que notre objet pourrait avoir des vrilles très fines) et on risque de prendre un grand nombre de pas inutiles si le rayon ne coupe même pas l’objet. Cela « coûte très cher » en temps de calcul.

Si par contre on connaît une estimation de la distance entre un point sur un rayon et l’objet fractal, on peut d’abord avancer avec un pas plus grand et ajuster les pas lorsqu’on s’approche de l’objet. Heureusement, on peut calculer une telle estimation, ce qui permet de dessiner les objets très rapidement. Vous trouverez les principes de deux méthodes en dépliant : la méthode « analytique » et une méthode développée parDavid Makin.

L’estimation de distance

Quand on a trouvé le point d’intersection d’un rayon avec l’objet, on doit encore colorer le pixel qui correspond à ce rayon. Heureusement, les fractales n’ont pas de couleur préférée, on peut donc choisir, mais ce sont bien des objets 3D dont la couleur va varier selon la lumière qui tombe sur ce point. Il faut aussi décider si le point est dans l’ombre ou pas. C’est pourquoi il faut savoir à quel endroit sur le rayon se trouve l’intersection, car cela va permettre de mettre en rapport la position du point et la position d’une source de lumière virtuelle. Pour faire tout cela correctement, il nous faut aussi la normale sur la surface fractale. Problème ! Les surfaces fractales n’ont pas de normale car elles sont a prioritrès irrégulières. On résout cela en trouvant quelques autres points d’intersection très près du point principal et en considérant la surface comme étant lisse localement. Avec les coordonnées de ces points on peut calculer un produit vectorielpour approximer une normale.

Cette technique de « raytracing » est assez rapide. Les images ci-dessous prennent environ une minute à calculer (taille 1000*1000 pixels) [2]. À noter qu’il est possible de programmer de tels algorithmes sur les processeurs de la carte graphique de l’ordinateur, ce qui permet de calculer ces images en une fraction d’une seconde !

Le « Mandelbulb »

Revenons sur la quête du Mandelbrot 3D.

Un point dans l’espace à trois dimensions est décrit par trois coordonnées xyz mais on peut aussi décrire la position du point par ses coordonnées sphériques. La position d’un point P à distance R de l’origine peut être décrit par deux angles t et p comme :

x=Rsin(p)cos(t)

y=Rsin(p)sin(t)

z=Rcos(p)

On obtient les angles par t=arctanxy et p=arctanzx2+y2 . [3]

Voici l’idée de Daniel White : comme le passage au carré consiste de doubler l’angle et à prendre le carré du module, on définit le « carré » d’un point en coordonnées sphériques comme

x=R2sin(2p)cos(2t), y=R2sin(2p)sin(2t), z=R2cos(2p).

ou plus généralement : x=Rqsin(qp)cos(qt), y=Rqsin(qp)sin(qt), z=Rqcos(qp). Cela permet donc d’effectuer une itérationwwq+c.

L’itération en détail

Voici ce qu’on obtient avec q=2.

Une déception ! L’objet ne ressemble même pas l’ensemble de Mandelbrot. Il est vrai qu’on repère quelques éléments fractals sur l’objet, comme les petits « arbres » sur le côté gauche mais si on veut trouver le fameux Graal, il va falloir chercher ailleurs, semble-t-il.

Mais pourquoi ne pas essayer ce que ça donne avec d’autres valeurs de q ? Essayons q=3 :

Cela va dans la bonne direction, c’est-à-dire que l’objet devient plus régulier. Alors on essaie q=4 :

En augmentant le degré il semble que de plus en plus de « bulbes » poussent sur l’objet. Prenons q=5 :

... et sautons vers q=8 :

C’est ce Mandelbulb de degré 8 qui est devenu le plus populaire mais rien ne nous empêche de dessiner le Mandelbulb de degré 16 :

Pour mieux apprécier les détails de l’objet, voici encore quelques vues de plus près :

L’animation en bas prouve que l’objet est bien fractal : c’est un zoom d’ordre 1012, ce qui veut dire que si la première image a la taille de la Terre, la dernière montre des détails d’un centième de millimètre...

Regardez aussi quelques autres images sur le site de l’auteur. On peut aussi admirer une image géante par Daniel White ici.

On n’a donc pas encore trouvé ce Saint Graal et la quête continue ; mais on a fait cette belle découverte du Mandelbulb en route. Si vous voulez participer et suivre quelles autres choses concoctent tous ces amateurs, il suffit de s’inscrire sur Fractalforums.com. Vous y serez le bienvenu !

Notes

[1] Jussi HARKONEN. On smooth fractal coloring techniques. (Master’s thesis)

[2] Les images de cet article ont été calculées avec le logiciel Ultrafractal sur un ordinateur à double cœur.

[3] Dans les algorithmes des logiciels, on utilise la fonction atan2(x,y) qui est équivalente à arctanxy, mais qui prend en compte les signes de x et yafin de mettre le résultat dans le bon quadrant.

Source : http://images.math.cnrs.fr/Mandelbulb.html

Images mathématiques

21/01/2010

Liens vers des sites de mathématiques

Academy of Sciences of the Czech Republic; American Institute of Mathematics; Argonne National Lab, Mathematics and Computer Science; AT&T Bell Laboratories Research; Australian CSIRO Math/Stat; Australian Mathematical Sciences Institute (AMSI); Basic Research Institute in the Mathematical Sciences; Budapest Semesters in Mathematics Program; CMU Center for Nonlinear Analysis; Center for Advanced Studies, Research and Development in Sardinia Applied Math Group; Center for Applied Mathematics and Theoretical Physics (U Maribor); CCM, The Center for Coputational Mathematics, University of Colorado, Denver; Center for Dynamical Systems and Nonlinear Studies; Centre for Engineering and Industrial Mathematics (U Wollongong); Centre for Experimental & Constructive Mathematics; Center for Gravitational Physics and Geometry; Centre Emile Borel; Centre for Industrial and Applied Mathematics (U South Australia); Centre for Innovation in Mathematics Teaching; Centro Internazionale Matematico Estivo; Centre International de Mathématiques Pures et Appliquées; Centre International de Recontres Mathématiques (CIRM); Centro de Investigación en Matemáticas A.C (Mexico); Centre de Mathématiques (École Polytechnique); Centre de Mathematiques Appliquees (École des Mines de Paris); Center for Mathematical Analysis, Geometry, and Dynamical Systems; Center for the Mathematical Sciences (UWisconsin); Centre de Recerca Matemàtica (Barcelona); Centre de recherches mathématiques (UMontréal); Center for Research in Scientific Computation (at NCSU); Center for Statistical and Mathematical Computing; Centrum voor Wiskunde en Informatica (CWI); Claremont Research Institute of Applied Mathematical Sciences (CRIAMS); The Clay Mathematics Institute (CMI); Collège de France, Sciences Mathématiques, Physiques et Naturelles; Computer Algebra Information Network; Cornell Center for Applied Mathematics; Courant Institute of NYU; CTI Centre for Mathematics and Statistics; Diffiety Instute of the Russian Academy of Natural Sciences; DIMACS; Euler Institute fot Discrete Mathematics and its Applications; The Euler International Mathematical Institute; Erwin Schrodinger Institute of Mathematical Physics; Euromath Center; EURHomogenization; The Fields Institute for Research in Mathematical Sciences; Fuzzy Logic Laboratory Linz; Geometry Center (UMinn); Groupe Fractales (INRIA); Indian Statistical Institute; Industrial Mathematics Institute (Linz); Institut de Mathématiques de Bordeaux; Institut des Hautes Etudes Scientifiques IHES; Institute for Advanced Study; Institute of Applied and Computational Mathematics; Institute for Computational Fluid Dynamics; Institute for Computer Applications in Science and Engineering; Institute of Cybernetics, Applied Math. Dept. (Estonia); Institute of Mathematics and Geometry (Faculty of Civil Engineering and Architecture) University of Innsbruck, Austria; Institut für Dynamische Systeme (Bremen); Institute for Experimental Mathematics (Essen); Institute for Mathematical Research (FIM, ETH-Zuerich); Institute for Studies in Theoretical Physics and Mathematics (IPM); Institut Fourier, Université Joseph Fourier; Institut Henri Poincare; Institute of Information Theory and Automation (Czech Academy of Sciences); Institute of Mathematical Sciences (India); Institut of Mathematics, University of Liege; Institut d'Informatique et de Mathématiques Appliquées de Grenoble; Institute for Mathematics and its Applications; Institut de Mathématiques Appliquées; Institute of Mathematics and Computer Science in Medicine (IMDM); Institut de Mathématique de Jussieu (Paris VI et Paris VII); Institute of Mathematics and Informatics (Bulgarian Academy of Sciences); Institute of Mathematics and Informatics Lithuania; Institute of Mathematics, Physics and Mechanics (Ljubljana); Institute of Mathematics of the Polish Academy of Sciences; Instituto de Matemática Pura e Aplicada (Brazil); Instituto de Matematicas y Estadistica (Uruguay); Institute of Mathematical Sciences Hong Kong; Instituto Nacional de Pesquisas Espaciais Brazil (applied math); Institute of Numerical Mathematics (RAS); Institute for Pure and Applied Mathematics at UCLA; Institut de Recherche Mathématique Avancée (IRMA); Institut de Recherche Mathematique de Rennes (IRMAR); Institut des sciences mathematiques (ISM); Institute of Statistical Mathematics (Japan); International Centre of Excellence for Education in Mathematics (ICE-EM); International Centre for Mathematical Sciences, Edinburgh; International Centre for Theoretical Physics; Isaac Newton Institute for Mathematical Sciences; Konrad-Zuse-Zentrum (Berlin); Laboratory for Computer Aided Mathematics (U Helsinki); Manchester Centre for Computational Mathematics; Mathematical Analysis Research Group; Mathematical Sciences Research Institute; Mathematics Institute of the Romanian Academy (IMAR); Mathematisches Forschungsinstitut Oberwolfach; Max-Planck Institut f"ur Mathematik, Bonn; Max-Planck Institut f"ur Mathematik in den Naturwissenschaften, Leipzig; Mittag-Leffler Institute; Pacific Institute for the mathematical sciences; pLab Project (Salzburg); Programme de Recherches Coordonnées, Mathématiques et Informatique; Research Centre of Applied Mathematics CIRAM (Bologna); Research Institute for Mathematical Sciences RIMS (Kyoto); Research Institute for Symbolic Computation (RISC-Linz); Steklov Institute of Mathematics, Russian Academy of Sciences; Steklov Mathematical Institute; Systems Analysis Laboratory (Helsinki UT); Tata Institute of Fundamental Research (India); University of Graz Institute of Mathematics; Unión Matemática Argentina; UMass Center for Geometry Analysis Numerics and Graphics; University of Minnesota Geometry Center; University of Nevada, Reno Mathematics Center; Virtual Institute of Mathematical Sciences; Visual Math Institute; Weierstraß-Institute for Applied Analysis and Stochastics (WIAS)
Magnet High Schools in Mathematics: Bronx High School of Science; Central Virginia Governor's School for Science and Technology; Illinois Mathematics and Science Academy; Massachusetts Academy of Mathematics and Science; Mississippi School for Mathematics and Science; Montgomery Blair High School; New Horizons Governor's School (VA); North Carolina School of Science and Mathematics; Oklahoma School of Science and Mathematics; Roanoke Valley Governor's School for Science and Technology (VA); Thomas Jefferson High School for Science and Technology

Les flottants au format double

suivant: Opérations sur les flottants monter: Les réels précédent: Virgule fixe et flottante. Index

Les flottants au format `double`

Cette section développe les notions de la section précédente pour les flottants machine, utilisables dans les langage de programmation usuels, elle peut être omise. La représentation d'un double en mémoire se compose de 3 parties : le bit de signe s = ±1 sur 1 bit, la mantisse M

[0, 2⁵²[ sur 52 bits, et l'exposant e

[0, 2¹¹[ sur 11 bits. Pour les nombres ``normaux'', l'exposant est en fait compris entre 1 et 2¹¹ - 2, le nombre représenté est le rationnel

(1 + $displaystyle {frac{{M}}{{2^{52}}}}$ )2^e+1-2¹⁰

Pour écrire un nombre sous cette forme, il faut d'abord chercher par quel multiple de 2 il faut le diviser pour obtenir un réel r dans [1, 2[, ce qui permet de déterminer l'exposant e. Ensuite on écrit la représentation en base 2 de r - 1

[0, 1[. Exemples :

-2
Signe négatif. Il faut diviser sa valeur absolue 2 par 2¹ pour être entre 1 et 2 dont e + 1 - 2¹⁰ = 1, l'exposant est e = 2¹⁰. On a alors r = 1, r - 1 = 0. Représentation
1 10000000000 00000000...0000
1.5=3/2
Signe positif, compris entre 1 et 2 dont l'exposant vérifie e + 1 - 2¹⁰ = 0 soit e = 2¹⁰ -1 = 2⁹ +2⁸ +2⁷ +2⁶ +2⁵ +2⁴ +2³ +2² +2¹ +2⁰. On a r - 1 = 1/2 = 2^-1. D'où la représentation
0 01111111111 10000000...0000
6.4=32/5
Positif. Il faut le diviser par 2² pour avoir 8/5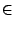 [1, 2[ donc e + 1 - 2¹⁰ = 2 soit e = 2¹⁰ + 1. Ensuite r = 3/5 qu'il faut écrire en base 2 (cf. section précédente), on écrit donc les 52 premiers éléments du développement avec une règle d'arrondi du dernier bit au nombre le plus proche. Ici le bit suivant le dernier 1001 est un 1, on arrondit donc à 1010. D'où la représentation
0 1000000001 100110011001...10011010

On observe que la représentation en base 2 de 6.4 a du être arrondie (car elle est infinie en base 2) bien qu'elle soit exacte (finie) en base 10. Seuls les entiers et les rationnels dont le dénominateur est une puissance de 2 peuvent être représentés exactement. Ceci entraine des résultats qui peuvent surprendre comme par exemple le fait que 0.3 - 3*0.1 n'est pas nul.

Des représentations spéciales (avec e = 0 ou e = 2¹¹ - 1) ont été introduites pour représenter ± (pour les flottants plus grands en valeur absolue que le plus grand flottant représentable), et pour représenter les nombres non nuls plus petits que le plus petit flottant représentable de la manière exposée ci-dessus (on parle de flottants dénormalisés), ainsi que le nombre NaN (Not a Number) lorsqu'une opération a un résultat indéfini (par exemple 0/0).

suivant: Opérations sur les flottants monter: Les réels précédent: Virgule fixe et flottante. Index

Retour à la page principale de mat249

Source : http://www-fourier.ujf-grenoble.fr/~parisse/mat249/mat249...

Source :

Séries entières

suivant: Série alternée monter: Développement de Taylor, séries précédent: La fonction exponentielle Index

Séries entières.

Les séries de type prendre la limite lorsque n tend vers l'infini du développement de Taylor en x=0 sont de la forme

$displaystyle sum_{{n=0}}^{infty}$ a_nxⁿ : = $displaystyle lim_{{ k rightarrow +infty}}^{}$ $displaystyle sum_{{n=0}}^{k}$ a_nxⁿ, a_n = $displaystyle {frac{{f^{[n]}(0)}}{{n!}}}$

On peut s'intéresser plus générallement à $sum_{{n=0}}^{infty}$ a_nxⁿ lorsque a_n est un complexe quelconque, c'est ce qu'on appelle une série entière, on peut aussi les voir comme des polynômes généralisés.

S'il existe un point x₀ tel que | a_nx₀ⁿ| est borné (ce sera le cas en particulier si la série converge en x₀), alors

| a_nxⁿ| = | a_nx₀ⁿ|| $displaystyle {frac{{x}}{{x_0}}}$ |ⁿ

M| $displaystyle {frac{{x}}{{x_0}}}$ |ⁿ

la série converge donc en x si | x| < | x₀| et on peut majorer le reste de la série au rang n par

| R_n|

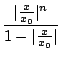
M $displaystyle {frac{{ vertfrac{x}{x_0}vert^n}}{{1-vertfrac{x}{x_0}vert}}}$

la vitesse de convergence est donc du même type que pour le théorème du point fixe (le nombre de termes à calculer pour trouver une valeur approchée avec k décimales dépend linéairement k, les constantes sont d'autant plus grandes que | x| est grand).

Théorème 5 S'il existe un rang n₀, un réel M > 0 et un complexe x₀ tels que pour n > n₀, on ait :

| a_nx₀|ⁿ

alors la série converge pour | x| < | x₀| et pour n

n₀, on a :

| R_n|

M $displaystyle {frac{{ vertfrac{x}{x_0}vert^n}}{{1-vertfrac{x}{x_0}vert}}}$

(3)

On en déduit qu'il existe un réel positif R 0 éventuellement égal à + tel que la série converge (la limite de la somme jusqu'à l'infini existe) lorsque | x| < R et n'existe pas lorsque | x| > R, ce réel est appelérayon de convergence de la série. Par exemple ce rayon vaut + pour l'exponentielle, le sinus ou le cosinus. Il est égal à 1 pour la série géométrique xⁿ (car elle diverge si | x| > 1 et converge si | x| < 1). On ne peut pas dire ce qui se passe génériquement lorsqu'on est à la limite, c'est-à-dire lorsque | x| = R (si R + ). Mais cela n'a en fait pas trop d'importance en pratique car même si la série converge, elle converge souvent trop lentement pour donner de bonnes approximations. En fait, la vitesse de convergence d'une série entière de rayon R + est en gros la même que celle d'une série géométrique de raison | x|/R.

Lorsque 2 séries ont un rayon de convergence non nul, alors on peut effectuer leur somme, leur produit comme des polynômes et la série somme/produit a un rayon de convergence au moins égal au plus petit des 2 rayons de convergence des arguments. On peut inverser une série entière non nulle en 0 en appliquant

(1 + x)^-1 = 1 - x + x² - x³ + ...

et on obtient une série entière de rayon de convergence non nul. On peut aussi composer deux séries entières g et f en gof (avec les règles de calcul de composition des polynômes) si f (0) = 0. On peut enfin dériver et intégrer une série entière terme à terme dans son rayon de convergence.

On dit qu'une fonction est développable en série entière en 0 si elle est égale à son développement de Taylor en 0 sommé jusqu'en l'infini dans un disque de centre 0 et de rayon non nul. Les fonctions exponentielle, sinus, cosinus sont donc développables en série entière en 0. La fonction tangente également car le dénominateur cosinus est non nul en 0, mais son rayon de convergence n'est pas l'infini et le calcul des a_n est assez complexe. La fonction (1 + x) est développable en séries entières pour tout avec un rayon de convergence 1 (ou l'infini pour entier positif).

(1 + x) = 1 +

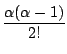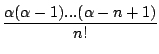x + $displaystyle {frac{{alpha (alpha-1)}}{{2!}}}$ x² + ... + $displaystyle {frac{{alpha (alpha-1) ... (alpha -n +1)}}{{n!}}}$ xⁿ + ...

Pour

= - 1, c'est la série géométrique de raison - x, en effet si | x| < 1 :

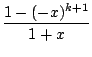
$displaystyle sum_{{n=0}}^{k}$ (- x)ⁿ = $displaystyle {frac{{1-(-x)^{k+1}}}{{1+x}}}$ $displaystyle rightarrow_{{krightarrow infty}}^{}$ $displaystyle {frac{{1}}{{1+x}}}$

En intégrant par rapport à x, on obtient que ln(1 + x) est développable en série entière en 0 de rayon de convergence 1 et

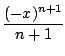
ln(1 + x) = $displaystyle sum_{{n=0}}^{infty}$ $displaystyle {frac{{(-x)^{n+1}}}{{n+1}}}$

On peut calculer de manière analogue le développement en série entière de arctan(x) en iintégrant celui de 1/(1 + x²), de même pour arccos(x) et arcsin(x) en intégrant celui de (1 - x²)^-1/2.

arctan(x) = $displaystyle sum_{{n=0}}^{infty}$ (- 1)ⁿ $displaystyle {frac{{x^{2n+1}}}{{2n+1}}}$ ,

On peut donc calculer ln, arctan, ... par ces formules, mais il faut répondre à la question où arrête-t-on la somme pour obtenir une précision donnée? Dans le cas de ln(1 + x), on pourrait répondre comme avec l'exponentielle en majorant la dérivée n + 1-ième, mais ce n'est plus faisable pour arctan, arcsin, arccos. On va donner un autre critère qui ne nécessite pas de calculer cette dérivée mais utilise l'alternance des signes dans la somme.

suivant: Série alternée monter: Développement de Taylor, séries précédent: La fonction exponentielle Index

Retour à la page principale de mat249

Source : http://www-fourier.ujf-grenoble.fr/~parisse/mat249/mat249...

Index - fourier.ujf-grenoble.fr

suivant: À propos de ce monter: Mat 249 précédent: Quelques références

Index

atan: Séries entières.
Bezout: Arithmétique des polynomes: Bézout
bit: Les flottants au format
complexe: Types composés.
contractante: Le point fixe
convexe: La méthode de Newton.
cos: La fonction exponentielle
determinant: Déterminant
diagonalisation: Réduction exacte des endomorphismes
division euclidienne: Entiers courts et longs
double: Les flottants au format
erreur: Erreur absolue, relative et | Erreurs d'arrondis du pivot
exp: La fonction exponentielle
exposant: Les flottants au format
expression: Types composés.
factorisation: Multiplicité des racines. | Factorisation dans . | Calcul approché des racines | Factorisation dans 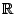| Factorisation exacte
flottant: Les flottants au format
fonction: Types composés.
Gauss: Le pivot de Gauss
integration: Intégration numérique
interpolation: Approximation polynomiale
inverse: Inverse
iterations inverses: Itérations inverses
ker: Noyau
lagrange: Approximation polynomiale | Approximation polynomiale
liste: Types composés.
ln: La fonction logarithme
LU: La méthode de factorisation
mantisse: Les flottants au format
matrice: Types composés.
multiplicite: Multiplicité des racines.
Newton: La méthode de Newton. | La méthode de Newton.
Newton-Cotes: Newton-Cotes
noyau: Noyau
ordre: Ordre d'une méthode
pivot: Le pivot de Gauss
point fixe: Le point fixe
point milieu: Les rectangles et les
polynome: Types composés.
polynome caracteristique: Polynome caractéristique
polynome minimal: Polynome minimal
puissance: Méthode de la puissance
quadrature: Intégration numérique
racine: Multiplicité des racines. | Calcul approché des racines
racines rationnelles: Factorisation exacte
rationnel: Entiers courts et longs
rectangle: Les rectangles et les
reduction: Réduction sous forme échelonnée
rref: Réduction sous forme échelonnée
sequence: Types composés.
serie alternee: Série alternée
serie entiere: Séries entières.
Simpson: Simpson
sin: La fonction exponentielle
squarefree: Multiplicité des racines.
Sturm: Factorisation dans
symbole: Types composés.
Taylor: Développement de Taylor, séries
trapeze: Les rectangles et les
vecteur: Types composés.; Source :; http://www-fourier.ujf-grenoble.fr/~parisse/mat249/mat249...

Erreur absolue, relative et propagation des erreurs

suivant: Types composés. monter: Les réels précédent: Erreurs Index

Erreur absolue, relative et propagation des erreurs.

On a vu précédemment que pour représenter un réel, on devait l'arrondir, ce qui introduit une erreur même si le réel est connu exactement (par exemple 1/10). Voyons comment se propagent les erreurs dans les opérations arithmétiques de base : on distingue l'addition, la multiplication et l'inversion. La soustraction se ramène à l'addition car le calcul de l'opposé n'introduit aucune erreur nouvelle. Pour l'addition, si |x - x₀|

$varepsilon_{0}^{}$ et si | y - y₀|

$varepsilon_{1}^{}$ alors par l'inégalité triangulaire ( | a + b|

| a| + | b|), on a :

|(x + y) - (x₀ + y₀)|

| x - x₀| + | y - y₀|

$displaystyle varepsilon_{0}^{}$ + $displaystyle varepsilon_{1}^{}$

on dit que les erreurs absolues s'additionnent.

Définition 1 L'erreur absolue est définie comme un majorant de la valeur absolue de la différence entre le nombre réel et son représentant double :

| x - x₀|

Mais comme il faut représenter x₀ + y₀ en machine, on doit ajouter une erreur d'arrondi, qui est proportionnelle à la valeur absolue de x₀ + y₀ d'où la notion d'erreur relative :

Définition 2 L'erreur relative est égale à l'erreur absolue divisée par la valeur absolue du nombre

| x - x₀|

| x₀|

Remarquons au passage que les erreurs de mesure expérimentales sont pratiquement toujours des erreurs relatives.

Donc lorsqu'on effectue une addition (ou une soustraction) de deux réels sur machine, on doit additionner les deux erreurs absolues sur les opérandes et ajouter une erreur d'arrondi (relative de 2^-53, à titre d'exercice, on pourra vérifier que cette erreur d'arrondi est majorée par l'erreur absolue de la somme x + y dès l'instant où x et y ont eux-même une erreur d'arrondi).

Lorsqu'on effectue une multiplication de deux nombres x, y dont les représentants x₀, y₀ sont non nuls, on a

$displaystyle leftvertvphantom{ frac{xy-x_0 y_0}{x_0 y_0} }right.$ $displaystyle {frac{{xy-x_0 y_0}}{{x_0 y_0}}}$ $displaystyle left.vphantom{ frac{xy-x_0 y_0}{x_0 y_0} }rightvert$ = $displaystyle leftvertvphantom{ frac{x}{x_0} frac{y}{y_0} -1) }right.$ $displaystyle {frac{{x}}{{x_0}}}$ $displaystyle {frac{{y}}{{y_0}}}$ - 1) $displaystyle left.vphantom{ frac{x}{x_0} frac{y}{y_0} -1) }rightvert$ = $displaystyle leftvertvphantom{ (frac{x}{x_0}-1)(frac{y}{y_0} -1)+(frac{x}{x_0}-1)+(frac{y}{y_0} -1) }right.$ ( $displaystyle {frac{{x}}{{x_0}}}$ -1)( $displaystyle {frac{{y}}{{y_0}}}$ -1) + ( $displaystyle {frac{{x}}{{x_0}}}$ -1) + ( $displaystyle {frac{{y}}{{y_0}}}$ - 1) $displaystyle left.vphantom{ (frac{x}{x_0}-1)(frac{y}{y_0} -1)+(frac{x}{x_0}-1)+(frac{y}{y_0} -1) }rightvert$

l'erreur relative est donc la somme des erreurs relatives et du produit des erreurs relatives (on peut souvent négliger le produit devant la somme). Il faut aussi y ajouter une erreur relative d'arrondi de 2^-53 surx₀y₀.

On observe que la multiplication est une opération posant moins de problèmes que l'addition, car on manipule toujours des erreurs relatives, par exemple si l'erreur relative sur deux doubles x et y non nuls est de 2^-53, alors l'erreur relative sur xy sera de

2^-53 +2^-53 +2^-106 +2^-53

3×2^-53

Lorsque l'erreur relative sur les données est grande devant 2^-53, l'erreur relative d'arrondi final est négligeable, on peut alors dire que les erreurs relatives s'additionnent pour un produit (c'est aussi vrai pour un quotient: exercice!). Par contre, si on additionne deux nombres dont le représentant de la somme est proche de 0, la somme des erreurs absolues peut devenir non négligeable par rapport à la somme des représentants, entrainant une erreur relative très grande. Par exemple si x est représenté par x₀ = 1 + 2^-52 avec une erreur d'arrondi de 2^-53 et y par y₀ = - 1 avec la même erreur d'arrondi, l'addition de x et yrenvoie 2^-52 avec une erreur absolue de 2*2^-53 (ici il n'y a pas d'arrondi lorsqu'on fait la somme). C'est une erreur relative de 1 (qui domine largement l'erreur d'arrondi) ce qui signifie que dans la mantisse, seul le premier bit sur les 52 a un sens, la perte de précision est très grande.

Une autre conséquence importante est que l'addition de réels sur machine n'est pas une opération associative, par exemple

(2.0^-53 +2.0^-53) + 1.0

1 + 2^-52

alors que

(2.0^-53 +1.0) + 2.0^-53

Si on a plusieurs termes à additionner, il faut commencer par additionner entre eux les termes les plus petits, pour que les petits termes ne soient pas absorbés un à un dans les erreurs d'arrondi (les petits ruisseaux font les grands fleuves).

Exercice : pour calculer la valeur numérique d'une dérivée de fonction, il vaut mieux calculer (f (x + h) - f (x - h))/(2h) que (f (x + h) - f (x))/h. Attention à ne pas prendre h trop petit, sinon x + h = x.

Remarquons néanmoins que les erreurs calculées ici sont des majorations des erreurs réelles (ou si on préfère l'erreur obtenue dans le pire des cas), statistiquement les erreurs sur les résultats sont moindres. Il est d'ailleurs souvent trop difficile de calculer la majoration rigoureuse de l'erreur pour des calculs complexes. Lorsqu'on doute de la précision d'un calcul, un test peu couteux consiste à refaire ce calcul en utilisant des flottants en précision plus grande et tester si le résultat varie en fonction du nombre de chiffres significatifs utilisés. On peut aussi faire varier légèrement les données et observer la sensibilité du résultat. Si on veut travailler en toute rigueur sans pour autant calculer les erreurs à priori, il faut utiliser un logiciel utilisant des intervalles pour représenter les réels (par exemple la bibliothèque C MPFI).

suivant: Types composés. monter: Les réels précédent: Erreurs Index

Retour à la page principale de mat249

Source : http://www-fourier.ujf-grenoble.fr/~parisse/mat249/mat249...

Cours, définitions, Vidéos, théorèmes, exercices, corrigés, livres sur les mathématiques, Livres Rares, Livres anciens de mathématiques

Recherchez sur le site (cours, livres, Agregation, etc.)

Liens utiles

Rechercher

Liens mathématiques divers

Livres en pdf

Cours

Documents Mathématiques

Décembre 2024

Notes récentes

Archives

Catégories

Derniers weblogs mis à jour

Liens Sites Amis

27/07/2010

La "taille" des ensembles : ordinaux, cardinaux

Source : http://www.les-mathematiques.net/a/a/a/node3.php3

Les axiomes de la théorie des ensembles de Zermelo-Fraenkel

Théorème de Cantor Bernstein

Théorème de Cantor Bernstein

L'axiome de fondation

L'axiome de fondation

Résumé de théorie des ensembles

Cas le plus général d'espace topologique

Analyse pour l'agrégation , Cours et exercices corrigés

Logique mathématique , T2 Fonctions récursives, théorème de Gödel, théorie des ensembles, théorie des modèles

26/07/2010

Endomorphismes remarquables d’un espace euclidien

I. Endomorphismes normaux

II. Endomorphismes symétriques

III. Endomorphismes orthogonaux

IV. Le groupe orthogonal

Bibliographie

21/05/2010

Livre Mathématique discrète: outil pour l'informaticien

15/04/2010

Algèbre

Algèbre

Un article de Wikipédia, l'encyclopédie libre.

Sommaire

Histoire [modifier]

Antiquité [modifier]

Monde arabo-musulman [modifier]

XVIe siècle : Europe [modifier]

Algèbre moderne [modifier]

Notations européennes modernes [modifier]

Articles connexes [modifier]

Voir aussi [modifier]

Notes et références [modifier]

Bibliographie [modifier]

Liens externes [modifier]

30/01/2010

Le triangle de Reuleaux

Le triangle de Reuleaux

Le 4 janvier 2010, par Serge Cantat

Chargé de Recherche à l'Université Rennes 1 (page web)

Le triangle de Reuleaux

Convexes de largeur constante

Buffon et Didon

Hexagones de Julius Pál

Solides de Meissner

Notes

Louis Bachelier

Louis Bachelier

11 mars 1870 - 28 avril 1946

Le 15 octobre 2006, par Laurent Carraro et Pierre Crépel

Références

Mandelbulb

Mandelbulb

Le 16 janvier 2010, par Jos Leys

Mathematical Imagery (page web)

Le « Bristorbrot »

Dessiner des objets fractals en 3D

Le « Mandelbulb »

Notes

Images mathématiques

21/01/2010

Liens vers des sites de mathématiques

Les flottants au format double

Les flottants au format double

XVI^e siècle : Europe [modifier]

Les flottants au format `double`