Endomorphismes remarquables d’un espace euclidien : Mathématique

D	L	M	M	J	V	S
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28

« Livre Mathématique discrète: outil pour l'informaticien | Page d'accueil | Logique mathématique , T2 Fonctions récursives, théorème de Gödel, théorie des ensembles, théorie des modèles »

26/07/2010

Endomorphismes remarquables d’un espace euclidien

Agrégation : leçon 126 en Maths Générales

E désigne un espace vectoriel de dimension fini muni d'un produit scalaire et de la norme associée.

I. Endomorphismes normaux

Rappel
Soit $fin mathcal{L}(E),;exists !;f^*inmathcal{L}(E)/forallquad(x,y)in E^2$
$<f(x),y>=<x,f^*(y)>$ $f^*$ est appelé l'adjoint de $f$ .
Soit $B$ une base de $E$ si $Mat_B(f)=M$ alors $Mat_B(f^*)=^tM$

Proposition 1 ([M]p357-358)

$Ker(f^*)=(Im(f))^{perp}$ et $Im(f^*)=(Ker(f))^{perp}$

$F$ sev de $E$ , $F$ stable par $f$ alors $F^{perp}$ stable par $f^*$

Définition 2

$finmathcal{L}(E)$ est dit normal si $f^* circ f = f circ f^*$
$Min M_n({mathbb R})$ est dit normal si $^tMM = M^tM$

Proposition 3 ([G]p254)

$f in mathcal{L}(E)$ normal ssi $|f(x)| = |f^*(x)|$

Théorème 4 ([C]p159)

$f in mathcal{L}(E)$ normal ssi il existe une base $B$ de $E$ orthonormée telle que $f$ soit presque diagonale dans cette base.
$begin{pmatrix}lambda_1& & & & & &ddots& & & & & &lambda_r& & & & & &boxed{rm{A_1}}& & & & & &ddots& & & & & &boxed{rm {A_s }}end{pmatrix}$ Avec $lambda_i in mathbb{R}$
Et $rm{A_i} = begin{pmatrix}a_i&-b_ib_1&a_iend{pmatrix}$ $(a_i,b_i)inmathbb{R}^2$

Lemme 5 ([C]p157)

Si $f$ endomorphisme normal, et si $F$ sous espace de $E$ stable par $f$ alors $F^{perp}$ stable par $f$ .

II. Endomorphismes symétriques

Définition 6

$f$ est dit symétrique ou autoadjoint si $f^*=f$ .

$f$ est dit antisymétrique si $f^*=-f$

Exemple :
Si $finmathcal{L}(E)$ , $fof^*$ est symétrique.

Remarque :
Si $f$ symétrique, alors $f$ est normal.
$mathcal{L}(E)=Sym(E)oplusAA(E)$ avec
$Sym(E)=lbrace finmathcal{L}(E),f^*=frbrace$ et $AA(E)=lbrace finmathcal{L}(E),f^*=-frbrace$

Proposition 7 ([G]p240)

$finmathcal{L}(E)$ autoadjoint ssi la matrice de $f$ dans une quelconque base orthonormée est symétrique.

Définition 8

$S_n(mathbb{R})=lbrace Min M_n(mathbb{R}),:^tM=Mrbrace$
$Min S_n(mathbb{R})$ est dite positive si $forall Xquad^tXMXge 0$
On note $S_n^+(mathbb{R})$ l'ensemble des telles matrices.
$Min S_n^+(mathbb{R})$ est dite définie positive si $forall; Xneq 0quad^tXMX>0$
On note $S_n^{++}(mathbb{R})$ l'ensemble des telles matrices.

Exemple :
$forall;Min M_n(mathbb{R})quad ^tMMinS_n^+(mathbb{R})$
$forall;Min GL_n(mathbb{R})quad ^tMMin S_n^{++}(mathbb{R})$

Proposition 9 ([M]p359)

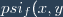Soit $psi:fin Sym(E)rightarrow psi_fin BL_S(E)$ tel que $psi_f(x,y)=<f(x),y>$
$psi$ est un isomorphisme d'espaces vectoriels de $Sym(E)$ vers $BL_S(E)$ l'ensemble des formes bilinéaires symétriques.

Théorème 10 ([G]p240)

Si $fin Sym(E)$ alors il existe une base orthonormée $B$ de $E$ , formée de vecteurs propres pour $f$ .
Si $Min S_n(mathbb{R}),exists; Cin M_n(mathbb{R}),; C$ orthogonale telle que :

$^tCMC=^{-1}CMC$ soit diagonale

Corollaire 11 ([G]p241)

Si $Min S_n^{++}(mathbb{R})$ , $Nin S_n^+(mathbb{R})$ alors il existe $Pin GL_n(mathbb{R})$ telle que

$^tPMP=I_nmbox{ et } ^tPNP$ soit diagonale

Application :
Si $Phi$ est une forme quadratique, il existe une base orthonormale dans laquelle la matrice de $Phi$ est diagonale.

Remarque :
On pourrait aussi réduire les endomorphismes antisymétriques par le Théorème 4.

III. Endomorphismes orthogonaux

Définition 12

$fin mathcal{L}(E)$ est orthogonal si et seulement si il vérifie l'une de ces quatre propositions équivalentes.

$fcirc f^*=f^*circ f=Id_E$

$forall (x,y)in E^2;<f(x),f(y)>=<x,y>$

$forall ; xin E |f(x)| = |x|$

l'image par $f$ d'une base orthonormée est une base orthonormée.

On note $O(E)$ l'ensemble des endomorphismes de $E$ qui sont aussi appelés isométries de $E$ .

Remarque :

$O(E)$ est un sous groupe de $GL(E)$

Si $fin O(E)$ , $f$ est normal.

$Min M_n(mathbb{R})$ est dite orthogonale si $^tMM=I_n$

Exemples :

Les symétries orthogonales sont des isométries.

Les matrices de permutations sont des isométries.

Les projections orthogonales ne sont pas des isométries.

Proposition 13 ([G]p252-253)

$fin mathcal{L}(E)$ est une isométrie ssi la matrice de $f$ dans toute base orthonormale est une matrice orthogonale.

Remarque :
Si $fin O(E)$ on a $(det(f))^2=1$
On note $SO(E)=lbrace fin O(E),; det(f)=1rbrace$ qui est un sous groupe distingué de $O(E)$
On définit de même $SO_n(mathbb{R})=lbrace Min O_n(mathbb{R}),mbox{det }M=1rbrace$

Proposition 14

$O(E)$ et $SO(E)$ sont des sous groupes compacts de $GL(E)$

Proposition 15 ([G]p252-253)

Si $fin O(E)$ il existe $B$ une base orthonormée telle que
$Mat_B(f)=begin{pmatrix}I_p& & & & &-I_q& & & & &boxed{R_1}& & & & &ddots& & & & &boxed{R_s}end{pmatrix}$ Avec $(p,q,s)in mathbb{N}^3/quad p+q+2s=n$
$Ri=begin{pmatrix} cos(theta_i)&-sin(theta_i)sin(theta_i)&cos(theta_i) end{pmatrix}$
$0<theta_1le ldotsle theta_s<pi$

Remarque :
$q$ pair $Leftrightarrow quad fin SO(E)$

Application :
$SO_n(mathbb{R})$ est connexe par arcs.

IV. Le groupe orthogonal

Théorème 16 ([MT]p18-19) - Décomposition polaire

Soit $phi:(O,S)in O_n(mathbb{R})times S_n^{++}(mathbb{R})rightarrow OSin GL_n(mathbb{R})$ est un homéomorphisme.

Application ([A]p138-140) :

$O_n(mathbb{R})$ sous groupe compact de $GL_n(mathbb{R})$

$SO_n(mathbb{R})$ sous groupe compact maximal de $SL_n(mathbb{R})$

$forall; Min M_n(mathbb{R})$ $d(M,O_n(mathbb{R})) = | sqrt{^tMM}-I_n |$

Corollaire 17

$forall M in GL_n(mathbb{R}),; exists (Omega_1,Omega_2)in(O_n(mathbb{R}))^2$ et $D$ diagonale à valeurs propres réelles positives telles que $M=Omega_1 DOmega_2$

Proposition 18 ([C]p?) - Décomposition d'Iwasawa

Si $Min GL_n(mathbb{R})$ alors il existe un unique couple $(O,T)$ avec $O$ orthogonale et $T$ triangulaire supérieure à coefficients diagonaux positifs tel que: $M=OT$

Proposition 19 ([B]2.7.5 et 8.2.5.2)

Soit $G$ un sous groupe compact de $GL_n(mathbb{R})$ , il existe une structure euclidienne $G$ -invariante sur $mathbb{R}^n$

Définition 18

$fin mathcal{L}(E)$ une symétrie orthogonale.
Si $dim(ker(f-Id_E))=n-1$ $f$ est appelé réflexion.
Si $dim(ker(f-Id_E))=n-2$ $f$ est appelé renversement.

Proposition 20 ([P]p142)

$Z(O_n(mathbb{R}))=lbrace pm I_nrbrace$

Si $n$ pair $Z(SO_n(mathbb{R}))=lbrace pm I_nrbrace$

Si $n$ impair $Z(SO_n(mathbb{R}))=lbrace I_nrbrace$

Proposition 21 ([P]p143)

$fin O(E)$ est le produit d'au plus $n$ réflexions.

Corollaire 22

$fin SO(E)$ est le produit d'un nombre pair de réflexions.

Proposition 23 ([P]p143)

Pour $nge3quad SO(E)$ est engendré par les renversements.

Application ([P]p148) :
$SO_3(mathbb{R})$ est simple.

Proposition 24 (([P]p150))

Soit $mathbb{P} SO_n(mathbb{R})=SO_n(mathbb{R})/Z(SO_n(mathbb{R}))$ .
Alors pour $n=3$ et $nge 5$ $mathbb{P} SO_n(mathbb{R})$ est simple.

Proposition 25 ([P]p152)

Tout automorphisme de $SO_3(mathbb{R})$ est intérieur.

Remarque [P] :

$SO_n(mathbb{R})$ est le groupe dérivé de $O_n(mathbb{R})$ et si $n>2$ c'est aussi celui de $SO_n(mathbb{R})$ .

$D(SO_2(mathbb{R}))=lbrace I_2rbrace$

$Min O_2(mathbb{R})$ alors $M=begin{pmatrix}a&-bb&aend{pmatrix}$ ou $M=begin{pmatrix}-a&bb&aend{pmatrix}$ avec $a^2+b^2=1$ .

$SO_2(mathbb{R})$ est commutatif est isomorphe à $mathbb{R}/2pimathbb Z$

On peut noter que le groupe $O_3(mathbb{R})$ est composé de :
$I_3$ , $-I_3$ , les rotations et les produits de 3 réflexions.

Proposition 26 ([MT]p125-127)

$SO_3(mathbb{R})approx mathbb P^3 mathbb{R}$

$Pi_1(SO_3(mathbb{R}))approxmathbb Z/2mathbb Z$

Bibliographie

[A]: M.Alessandri "Thèmes de géométrie"
[C]: M.Cognet "Algèbre bilinéaire"
[G]: X.Gourdon "Algèbre"
[MT]: R.Mneimné, F.Testard "Groupes de Lie Classiques"
[M]: D.Monasse "Cours MP-MP^*"
[P]: D.Perrin "Cours d'algèbre"

SOURCE : http://www.ilemaths.net/maths-agreg-endomorphismes-espace...

Les commentaires sont fermés.

Mathématique

Cours, définitions, Vidéos, théorèmes, exercices, corrigés, livres sur les mathématiques, Livres Rares, Livres anciens de mathématiques

Recherchez sur le site (cours, livres, Agregation, etc.)

Liens utiles

Rechercher

CODE PROMO

Liens mathématiques divers

Livres en pdf

Cours

Documents Mathématiques

Février 2025

Notes récentes

Archives

Catégories

Derniers weblogs mis à jour

Liens Sites Amis

26/07/2010

Endomorphismes remarquables d’un espace euclidien

Endomorphismes remarquables d’un espace euclidien

I. Endomorphismes normaux

II. Endomorphismes symétriques

III. Endomorphismes orthogonaux

IV. Le groupe orthogonal

Bibliographie