D	L	M	M	J	V	S
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30	31

21/01/2010

Arithmétique des polynomes: Bézout et applications

On considère les polynômes à une variable à coefficients dans ou ou . Les algorithmes de base déjà évoqués sont l'évaluation en un point (méthode de Horner), l'addition, la soustraction, la multiplication et la division euclidienne de A par B 0 :

A = BQ + R, deg(R) < deg(B)

A l'aide de la division euclidienne, on peut calculer le PGCD de deux polynômes par l'algorithme d'Euclide. Nous allons présenter l'algorithme d'Euclide étendu (ou de Bézout)

Théorème 7 Étant donnés 2 polynômes A et B, il existe deux polynômes U, V tels que

AU + BV = pgcd(A, B), deg(U) < deg(B),deg(V) < deg(A)

Algorithme :
On construit en fait 3 suites (U_n), (V_n) et (R_n) telles que :

AU_n + BV_n = R_n

on initialise U₀ = 1, V₀ = 0, R₀ = A et U₁ = 0, V₁ = 1, R₁ = B
on calcule les indices n + 2 en fonction de n et n + 1 en effectuant la division euclidienne de R_n par R_n+1

R_n = Q_nR_n+1 + R_n+2, U_n+2 = U_n - Q_nU_n+1, V_n+2 = V_n - Q_nV_n+1
on s'arrête au dernier reste non nul

Exemple :
A = x³ -1, B = x² + 1, les rangs 0 et 1 sont donnés ci-dessus. Au rang 2, Q₀ est le quotient euclidien de A par B (fonction quo) donc x, d'où

U₂ = 1, V₂ = - x, R₂ = - x - 1

Puis on divise x² + 1 par - x - 1, quotient - x + 1, donc

U₃ = x - 1, V₃ = 1 + x(- x + 1) = 1 + x - x², R₃ = 2

Preuve de l'algorithme :
On montre facilement par récurrence que la relation AU_n + BV_n = R_n est conservée. Comme R_n est la suite des restes, le dernier reste non nul est bien le pgcd de A et B. D'autre part, examinons les degrés des V_k. Supposons que deg(A) deg(B) (sinon on échange A et B). Au rang n = 0, V₀ = 0 donc V₂ = - Q₀V₁, aux rangs suivants le degré de Q_n est non nul (car le degré de R_n+1 est strictement inférieur au degré de R_n) On montre donc par récurrence que la suite des degrés de V_n est croissante et que :

deg(V_n+2) = deg(Q_n) + deg(V_n+1)

Comme deg(Q_n)=deg(R_n)-deg(R_n+1), on en déduit que

deg(V_n+2) + deg(R_n+1) = deg(V_n+1) + deg(R_n) = ... = deg(V₁) + deg(R₀) = deg(A)

Donc si n + 2 est le rang du dernier reste non nul, V_n+2 = V et degV=degA-degR_n+1 est donc strictement inférieur au degré de A (car R_n+1, l'avant-dernier reste non nul, est de degré plus grand ou égal à 1). On en déduit enfin que le degré de U est strictement inférieur au degré de B, car AU = R - BV, le degré de BV est strictement inférieur à celui de B plus celui de A.

L'identité de Bézout permet de résoudre plus générallement une équation du type

Au + Bv = C

où A, B, C sont trois polynômes donnés, à condition que C soit divisible par le pgcd de A et B. L'ensemble des solutions s'obtient à partir d'une solution particulière U, V de Bézout, notons c = C/gcd(A, B), on a alors

A(cU) + B(cV) = c gcd(A, B) = C

et l'ensemble des solutions est donné par u = cU - PB, v = cV + PA où P est un polynôme quelconque. Si le degré de C est plus petit que le degré de A plus le degré de B, il existe une solution ``priviligiée'', on prend pour u le reste de la division euclidienne de cU par B, v est alors le reste de la division euclidienne de cV par A pour des raisons de degré.

Exemple : si on veut résoudre

(x³ -1)u + (x² +1)v = 2x²

on multiplie U = x - 1 et V = 1 + x - x² par x² ce qui donne une solution

u = x²(x - 1), v = x²(1 + x - x²)

l'ensemble des solutions est de la forme

u + P(x² +1), v - P(x³ - 1)

et la solution priviligiée (de degrés minimaux) est

- x + 1 = rem(x²(x - 1), x² +1), x² - x + 1 = rem(x²(1 + x - x²), x³ - 1)

L'identité de Bézout intervient dans de nombreux problèmes en particulier la décomposition en éléments simples d'une fraction rationnelle. Si le dénominateur D d'une fraction se factorise en produit de 2 facteurs D = AB premiers entre eux, alors il existe deux polynômes u et v tels que N = Au + Bv, donc

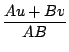$displaystyle {frac{{N}}{{D}}}$ = $displaystyle {frac{{Au+Bv}}{{AB}}}$ = $displaystyle {frac{{u}}{{B}}}$ + $displaystyle {frac{{v}}{{A}}}$

Si de plus N/D est une fraction propre (degré de N plus petit que celui de D), alors u/B et v/A sont encore des fractions propres (en calculant le reste de la division euclidienne pour u et v comme expliqué ci-dessus).

Par exemple :

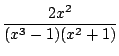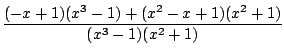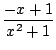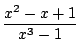
$displaystyle {frac{{2x^2}}{{(x^3-1)(x^2+1)}}}$ = $displaystyle {frac{{(-x+1)(x^3-1)+(x^2-x+1)(x^2+1)}}{{(x^3-1)(x^2+1)}}}$ = $displaystyle {frac{{-x+1}}{{x^2+1}}}$ + $displaystyle {frac{{x^2-x+1}}{{x^3-1}}}$

Les applications sont diverses, citons

le calcul de primitive de fraction rationnelles (et tout ce qui s'y ramène), par exemple

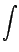
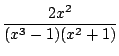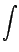
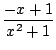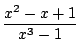
$displaystyle {frac{{2x^2}}{{(x^3-1)(x^2+1)}}}$ = = $displaystyle {frac{{-x+1}}{{x^2+1}}}$ + $displaystyle {frac{{x^2-x+1}}{{x^3-1}}}$

Puis on fait apparaitre la dérivée du dénominateur au numérateur pour éliminer les x, 2x = (x² + 1)'

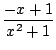
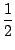
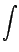
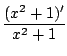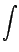
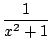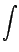
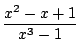
$displaystyle {frac{{-x+1}}{{x^2+1}}}$ = - $displaystyle {frac{{1}}{{2}}}$ $displaystyle {frac{{(x^2+1)'}}{{x^2+1}}}$ + $displaystyle {frac{{1}}{{x^2+1}}}$ + $displaystyle {frac{{x^2-x+1}}{{x^3-1}}}$

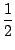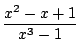
= - $displaystyle {frac{{1}}{{2}}}$ ln(x² +1) + arctan(x) + $displaystyle {frac{{x^2-x+1}}{{x^3-1}}}$

pour faire le calcul complet, il faut aussi décomposer la fraction restante (exercice!)
le calcul de transformée de Laplace inverse de fractions rationnelles, l'idée est la même, sauf qu'on remplace l'intégrale par la transformée de Laplace inverse (et les formules donnant la transformée inverse de 1/(x - p), 1/(x² + p²), p/(x² + p²) respectivement exp(px), sin(xp)/p, cos(px)) (calcul non exigible à l'examen)
le calcul du terme d'ordre n du développement de Taylor en 0 d'une fraction rationnelle. On décompose, et on se ramène à des séries dont le terme général est connu, comme (a + x)^-n. Par exemple pour connaitre le développement de 1/(x² - 3x + 2), on factorise le dénominateur 1/((x - 1)(x - 2)), on décompose

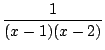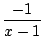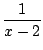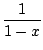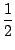
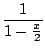
$displaystyle {frac{{1}}{{(x-1)(x-2)}}}$ = $displaystyle {frac{{-1}}{{x-1}}}$ + $displaystyle {frac{{1}}{{x-2}}}$ = $displaystyle {frac{{1}}{{1-x}}}$ - $displaystyle {frac{{1}}{{2}}}$ $displaystyle {frac{{1}}{{1-frac{x}{2}}}}$

et on développe, le terme d'ordre n est donc 1 - (1/2)ⁿ⁺¹.

Il faut néanmoins savoir factoriser un polynôme, ce dont nous parlerons dans la section suivante.

Exercice : Calculer l'intégrale

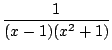
$displaystyle {frac{{1}}{{(x-1)(x^2+1)}}}$

en utilisant l'identité de Bézout pour décomposer la fraction rationnelle. Trouver à l'aide de cette décomposition le terme d'ordre n du développement de Taylor de la fraction à intégrer, vérifier avec un logiciel de calcul formel que les termes d'ordre 0 à 3 sont corrects.

Una autre application est l'élimination dans les systèmes polynomiaux, par exemple considérons le système de 2 équations à 2 inconnues (intersection d'une ellipse et d'un cercle) :

x² + y² -9 = 0, x² +2y² - 2xy - 7 = 0

En calculant les coefficients de Bézout des 2 polynômes en x x² + y² - 9 et x² +2y² - 2xy - 7 et en multipliant au besoin par le PPCM (plus grand commun multiple) des dénominateurs, on obtient à droite de l'équation de Bézout un polynôme ne dépendant que de y et qui s'annule aussi aux solutions du système, on peut alors résoudre en y (en factorisant) puis en x. Ici par exemple ce polynome est 5y⁴ -32y² + 4. Cette méthode se systématise, le polynome obtenu par élimination d'une variable est appelé résultant.

suivant: monter: précédent:

Retour à la page principale de mat249

Source : http://www-fourier.ujf-grenoble.fr/~parisse/mat249/mat249...

08/01/2010

Entre figures et espaces : le cas des diagrammes en géométrie finie

Le 12 novembre 2009, par Sébastien Gandon

Que représente une figure ? On cherche ici à montrer que la réponse à cette question n’est pas aussi simple qu’il y paraît. Nous sommes tous plus ou moins familiers avec les diagrammes de la géométrie classique, qui matérialisent une figure dans le plan ou dans l’espace. On sait peut-être moins que dans l’Antiquité, ces figures ... n’étaient dans rien. Ce n’est que bien plus tard, voici en gros un siècle, qu’on les a approchées comme partie d’un espace, espace vers lequel s’était déplacé une grande partie de l’effort mathématique. Ce qui est encore moins connu, c’est la manière dont des diagrammes semblables à ceux de la géométrie classique ont été utilisés, au début du XXe siècle, pour représenter ... des espaces. Il fallait pour cela que les mathématiciens s’intéressent aux géométries finies. Cet article est consacré à leur émergence et au rôle conceptuel qu’elles jouèrent dans l’histoire de la géométrie.

Introduction

EN histoire de la géométrie, on a souvent coutume d’opposer la géométrie qu’on dit « classique » —celle qui aurait été pratiquée depuis les Eléments d’Euclide jusqu’aux Fondements de la géométrie de Hilbert [1], publiés en 1899, et qui porte sur les propriétés des figures— à la géométrie dite « moderne » —celle qu’auraient inauguré les mêmes Fondements— et qui étudie les propriétés d’un espace. Dans cette perspective, les Éléments d’Euclide représentent le modèle d’une « géométrie des figures ». Certes, chez Euclide, les théorèmes sur le triangle, le cercle, etc. sont déduits, comme cela se passe chez Hilbert, à partir d’axiomes (les cinq « demandes » du livre I [2]). Mais on a mis en évidence depuis longtemps que les preuves euclidiennes comportaient des lacunes : certaines hypothèses, nécessaires dans les déductions, sont introduites par référence aux diagrammes et ne font l’objet ni d’axiomes, ni de propositions déduites de ces axiomes [3]. Les propriétés de l’espace dans lequel « vivent » et s’insèrent les figures étudiées ne sont ainsi complètement explicitées ni chez Euclide ni chez ses successeurs. En fait, cet « espace » n’est même abordé qu’indirectement, par le biais du fait que chaque figure peut être « enrichie » de diverses manières (les droites peuvent être prolongées, de nouveaux points introduits, etc.). Se permettre d’opérer de la sorte sur une figure, c’est dire qu’elle se trouve donc d’une certaine manière intrinsèquement liée à un « environnement », un plan par exemple. Mais Euclide n’élucide pas complètement les modalités de cette articulation. Ainsi, pour ne citer qu’un exemple, le simple fait que deux cercles « entrelacés » se coupent en deux points n’est prouvé nulle part !

C’est précisément sur ce point que la géométrie inaugurée par Hilbert se démarque des pratiques anciennes et c’est la raison pour laquelle on la qualifie de « moderne » : dans cette nouvelle manière de faire, la structure globale de l’espace est complètement donnée par un système d’axiomes. Tout ce qui peut être déduit des postulats est considéré comme un théorème, mais l’on s’interdit en revanche d’utiliser, dans les démonstrations, une information qui ne figurerait pas dans les axiomes ou qui ne pourrait pas être établie à partir d’eux. Hilbert a présenté dans les Fondements une liste de vingt postulats, répartis en cinq groupes [4], et l’ensemble des théorèmes de la géométrie d’Euclide s’en déduisent. À la différence des géomètres « classiques », au sens que nous avons introduit plus haut, Hilbert démontre ainsi, par exemple, le fait que deux cercles « entrelacés » se coupent en deux points. Ce trait trahit en fait une mutation fondamentale par rapport aux pratiques antérieures. Le géomètre hilbertien n’étudie plus tant les propriétés des figures qu’il ne s’intéresse à la structure des « modèles » du système axiomatique considéré. Un modèle, ici, c’est un ensemble d’objets (qu’on appelle « points », « droites ») et de relations (« être sur », « se couper », « être parallèle », etc.) qui satisfont tous les axiomes. Les points et les droites dans le plan, tels que les concevaient les mathématiciens grecs, obéissent à tous les postulats de Hilbert. Mais il en va de même des couples de nombres réels (l’interprétation de « points » dans la géométrie « cartésienne ») et des équations linéaires en x et en y (interprétant les « droites »). Ils n’ont certes en eux-mêmes rien à voir avec l’espace tel que notre intuition visuelle et tactile nous le présente, et tel aussi que les Grecs le concevaient, mais ils satisfont néanmoins à ces axiomes et ils constituent donc également un modèle du plan euclidien.

Dans cette nouvelle perspective, l’objet d’étude du géomètre n’est plus la figure ou ses propriétés, mais un espace. De plus, cet espace ne se présente pas comme ce « dans quoi » les figures étudiées se trouvent, c’est-à-dire comme un milieu toujours présent dont les propriétés resteraient à l’arrière-plan, mais comme un modèle abstrait d’un système axiomatique. Ces deux approches de la géométrie présentent des ressemblances (en un sens, Hilbert axiomatise bien la théorie d’Euclide), mais les différences entre elles sont essentielles. Les historiens des mathématiques parlent volontiers de la rupture hilbertienne. Pour reprendre une métaphore classique en histoire de la philosophie, on pourrait dire que les Fondements de la géométrie accomplissent une véritable révolution copernicienne : dans la géométrie classique, les propositions géométriques portent sur (tournent autour) des figures, considérées comme des objets s’insérant dans un espace donné antérieurement à la théorie ; dans la géométrie qui se situe dans la descendance de Hilbert, c’est l’inverse : le géomètre définit l’espace par un discours qui prend systématiquement la forme d’une axiomatique —le discours ici tourne autour de l’espace.

Mon propos dans ce qui suit n’est pas de remettre en cause la pertinence de l’opposition que je viens de décrire, mais de montrer que la division ne recoupe pas tout le champ des possibles. Plus précisément, je montrerai dans ce qui suit qu’il existe des cadres théoriques dans lesquels les mathématiciens ont utilisé des figures ou des diagrammes pour représenter des espaces —et, inversement, que dans ces contextes des espaces, définis axiomatiquement, ont pu être dessinés sur une feuille de papier. Ainsi, dans les géométries finies qui sont apparues au début du XXe siècle, les modèles des axiomatiques sont des figures, et les propriétés de ces figures expriment des caractéristiques de l’espace sous-jacent. Plutôt que de présenter un panorama chronologique de l’émergence de ces nouvelles géométries, je me servirai de la distinction entre figure et espace pour problématiser quelques étapes de cette histoire. Je donnerai tout d’abord quelques indications mathématiques préalables sur la notion de « configuration », qui a joué un rôle fondamental dans cette affaire. Je montrerai ensuite comment les géomètres du XIXe siècle en sont venus à distinguer deux notions de configuration : un concept « abstrait », combinatoire, d’une part, et un concept « concret », géométrique, de l’autre. Enfin, j’étudierai le début de l’article « Finite Projective Geometries » de Oswald Veblen (et de son collègue W. Bussey), véritable acte de naissance des géométries finies, pour montrer comment la substitution des espaces finis aux configurations nécessitent, pour être comprise, de remettre en question le caractère exclusif de la disjonction « figure versus espace ».

1- Préalable mathématique

Avant de définir le concept clé de configuration, donnons quelques indications sur la façon dont les mathématiciens définissent aujourd’hui la notion de structure d’incidence. Soit P un ensemble (fini) de « points », et D un ensemble (fini) de « droites » (j’expliquerai bientôt pourquoi je mets des guillemets) ; une structure d’incidence nous apprend sur quelles « droites » se trouve chacun des « points » de P , et quels « points » chacune des « droites » de D contient. Prenons un exemple. Admettons qu’on ait trois « points » AB et C et deux droites 1 et 2 (P=ABC et D=12) ; on peut définir la structure d’incidence I de cette manière : A et B sont sur les « droites » 1 et 2, C sur la « droite » 1 seulement. I peut être représentée par un tableau à double entrée, où les « X » indiquent que le « point » correspondant à la colonne se trouve sur la « droite » correspondant à la ligne :

I	A	B	C
1	X	X	X
2	X	X

Tous les tableaux à double entrée de ce type correspondent à une structure d’incidence possible définie sur ABC et 12. Certains correspondent à des situations géométriquement réalisables – mais d’autres non. Qu’est-ce à dire ? Reprenons pour exemple la structure que nous considérons : en géométrie euclidienne (comme dans la plupart des autres géométries), une droite est déterminée par deux points ; or dans la structure I , deux droites distinctes (1 et 2) passent par les deux mêmes points (A et B). Il est donc clair que nous ne pouvons pas représenter sur une figure, par des « vrais » points et des « vraies » droites, les conditions énoncées dans le tableau précédent. Au mieux, on peut proposer le genre de représentation que montre la figure 1, où (AB) correspond à la « droite » 2, mais où un arc de cercle correspond à la « droite » 1

$PNG - 7.9 ko$: Figure 1.

J’ai mis ci-dessus « points » et « droites » entre guillemets pour manifester le fait que les éléments de P et de D ne correspondaient pas nécessairement aux objets géométriques associés d’habitude à ces mots. Et j’ai enlevé les guillemets lorsque je parlais des entités géométriques usuelles. La notion de structure d’incidence est très générale, puisque n’importe quel tableau à double entrée en constitue une. Les mathématiciens ont été conduits à introduire des structures d’incidence plus particulières, qu’ils ont appelées « configurations », en imposant diverses contraintes supplémentaires sur la façon dont les points et les droites se croisaient. Une configuration (vrbk) désigne ainsi une structure d’incidence de v « points » et b « droites », telle que :

(i) il y a au plus une « droite » passant par deux « points » quelconques ;
(ii) il y a k « points » sur chaque « droite » et r « droites » sur chaque « point ». [5]

La structure I n’est ainsi pas une configuration car deux « droites » différentes passent par le même couple de « points » (ce qui contredit (i)). De plus, cette structure n’a ni le même nombre de « points » sur toutes les « droites », ni le même nombre de « droites » sur tous les « points » (ce qui contredit (ii)).

En revanche, la structure d’incidence qui comporte 4 « points » (P=ABCD ) et 6 « droites » (D=123456 ), dont chaque point est à l’intersection de trois droites et dont chaque droite contient deux points, est une configuration. On la qualifie comme ayant le genre (4362)ou encore4 3 2 6 [6]. On peut lui associer le tableau suivant, où on vérifie que chaque ligne comporte deux « X » et chaque colonne en contient trois :

	A	B	C	D
1	X		X
2	X			X
3	X	X
4		X	X
5		X		X
6			X	X

Comme nous venons de le voir, les éléments distingués —les « points » et les « droites »— ne sont pas ici, malgré leur nom, des objets géométriques. Le diagramme précédent est un tableau à double entrée, et il peut recevoir toutes les interprétations qu’une telle structure de données est habituellement susceptible de recevoir. Mais il se trouve ici, à la différence de ce qui se passait plus haut, qu’on peut donner un sens géométrique à la configuration en question. Dans la Fig. 2, si l’on ne considère que les points ABCD et les droites 1…6 chacun des quatre points ABCD est sur trois des six droites 1…6 et chacune de ces six droites contient deux des quatre points :

$PNG - 37.4 ko$: Figure 2. : Réalisation géométrique de la configuration(4362)

La figure 2 est le schéma d’un objet géométrique, et même d’un objet euclidien, si l’on entend par là que les « droites » sont représentées par des droites conformes à celles qu’Euclide considérait et non pas par des arcs de cercles comme dans la Fig. 1. Remarquons toutefois que l’objet est euclidien en un sens très particulier, puisque dans la configuration, beaucoup d’éléments considérés ordinairement comme faisant partie de la figure doivent être ignorés. Ainsi, les droites 1…6 ne contiennent que deux points ; tous les « autres » points, y compris les intersections des droites 1 et 52 et 43 et 6, ne comptent pas. De même, les « autres » droites passant par les points A…D (celles, par exemple, qui se trouvent à l’intérieur de l’angle de sommet A et de côtés 1 et 3) sont volontairement écartées. Nous reviendrons sur cet étrange aspect des configurations géométriques bientôt – faisons pour l’instant comme si l’on pouvait faire correspondre des figures euclidiennes à certaines configurations. La question qui se pose naturellement est de savoir si toutes les configurations peuvent recevoir une telle interprétation géométrique. Ce n’est pas le cas, comme le montre l’exemple de la configuration « symétrique » (7373), c’est-à-dire la configuration composée de 7 « points » et 7 « droites » et pour laquelle chaque « point » se trouve sur trois « droites » tandis que chaque « droite » est composée de trois « points ». Donnons la table d’incidence de la configuration :

	A	B	C	D	E	F	G
1	X	X	X
2	X					X	X
3	X			X	X
4			X	X		X
5		X		X			X
6			X		X		X
7		X			X	X

Il n’est pas possible de réaliser une telle configuration en prenant, pour éléments de P, des points et, pour éléments de D, des droites du plan ordinaire. Un beau théorème de Steinitz (1894) [7] montre cependant que chaque configuration de n « points » et n « droites » tels que chaque « point » se trouve sur trois « droites » et chaque « droite » est composée de trois « points » peut être tracée dans le plan ordinaire à l’aide de droites quasi toutes « normales », à l’exception de l’une d’entre elles au plus, qui doit être une ligne « quadratique » (une courbe de second degré coupée par une droite en au plus deux points). Ainsi la configuration 73, également appelée plan de Fano, peut être représentée comme suit :

$PNG - 25.1 ko$: Figure 3. : Le « plan de Fano » 73

Une des questions qui traverse l’histoire de la théorie des configurations est celle de distinguer les configurations du genre de 73 qui ne peuvent recevoir d’interprétation géométrique de celles auxquelles il est possible d’en associer une, comme celle représentée dans laFig. 2.

Il se présente également un autre problème, plus délicat à décrire. Revenons, pour l’introduire, à la notion de structure d’incidence, dont nous avons vu qu’elle était complètement spécifiée par une table d’incidence. Si nous intervertissons la ligne 1 et la ligne 2 dans la table d’incidence de la configuration à quatre points et six droites étudiée ci-dessus, nous obtenons une nouvelle structure d’incidence, différente de la première. Nous n’obtenons pas pour autant une configuration réellement nouvelle. Nous avons en effet simplement interverti le nom de la droite 1 et de la droite 2 — ce qui ne change rien à la nature de la configuration.

Il ne faudrait cependant pas croire que les configurations de genre (vrbk) ont des tables d’incidence qui s’obtiennent toutes les unes à partir des autres par des modifications de ce type. Il arrive (et c’est, en réalité, le cas le plus fréquent) que l’on trouve, pour un genre de configuration(vrbk) donné, plusieurs tables d’incidences que l’on ne peut pas transformer les unes dans les autres par une simple modification du nom des « points » et des « droites ». Dans ces cas, on a véritablement affaire à des configurations différentes. Je donne, pour illustrer ce phénomène, une représentation des trois configurations 93 (neuf points, neuf droites, trois droites par points, trois points par droites), exemple qui a pour avantage que les configurations sont toutes réalisables géométriquement dans le plan ordinaire :

$PNG - 70.1 ko$: 93(a)93(b)93(c)
Figure 4. : Les trois configurations 93. La seconde est la configuration de Pappus.

Il n’existe aucune possibilité de faire correspondre les lignes et les colonnes de la table d’incidence de 93(a) et de 93(b), de manière telle que, si la case déterminée par une ligne et une colonne dans la première table est occupée par un X, alors la case déterminée par l’image de la ligne et l’image de la colonne est également occupée par un X (et réciproquement). Il n’y a pas moyen, ici, de corréler un à un (on parle en termes plus techniques de relier « bijectivement ») les points et les droites des configurations de façon à laisser les relations d’incidence inchangées. La question de savoir combien de configurations différentes d’un certain type existent (problème dit de l’énumération des configurations) a joué un rôle très important dans le développement de la théorie. Et comme nous allons maintenant le voir, il n’est pas sans lien avec le problème de la distinction entre les configurations géométriquement réalisables et celles qui ne le sont pas.

2- Le concept de configuration : de Reye à Moore [8]

C’est, en 1876, dans la seconde édition de son Geometrie der Lage que Theodor Reye, mathématicien allemand de l’université de Strasbourg, présente une première définition générale du terme de configuration [9] :

Une configuration ni dans le plan consiste en n points et n droites tels que chacune des n droites passe par i des n points et que par chacun des n points passent i des n droites.

La définition est restrictive, dans la mesure où c’est seulement les configurations planaires « symétriques » (où points et droites jouent des rôles qui se font miroir) qui sont retenues. Mais surtout, Reye considère les configurations comme des objets géométriques. Une configuration d’un type donné n’est pas ici une (ou plus précisément un ensemble de) structure(s) d’incidence « abstraite », définie par une (une famille de) table(s) d’incidence : les points et les droites dont il est question dans les configurations sont pour Reye des points et des droites d’un plan —pour être précis, disons que les plans en question sont ordinaires à ceci près que deux droites quelconques s’y rencontrent toujours (on appelle de tels plans « projectifs »). Le géomètre affirme ainsi qu’il n’y a pas de configuration 83, parce qu’aucune interprétation ne peut être donnée à la structure dans un plan de ce type. Dans un texte ultérieur, intitulé Das Problem der Configurationen et publié en 1882 [10], Reye pose toutefois une question qui va mettre les mathématiciens sur la voie du concept « abstrait » :

Le problème des configurations est celui d’énumérer combien de configurations différentes il y a du genre ni et d’étudier leurs principales propriétés.

Reye, se référant aux résultats obtenus par Seligmann Kantor (un mathématicien allemand travaillant à Prague) en 1881 [11], affirme ainsi qu’il y a trois configurations 93(non « réductibles » les unes aux autres au sens évoqué plus haut) et dix configurations 103. À la fin de son article, Kantor construisait, c’est-à-dire dessinait, ces dix configurations. Pour Kantor comme pour Reye, une configuration est un objet géométrique, représentable par une figure que l’on peut construire sur le plan de la feuille en respectant certaines conventions qui sont celles de la géométrie ordinaire ou celle de la géométrie que nous avons évoquée plus haut sous le qualificatif de « projective ».

$PNG - 46.1 ko$: Figure 5. : La configuration de Desargues, une des configurations 103.

Six ans après, en 1887, un mathématicien italien, Vittorio Martinetti [12], découvre une méthode permettant de trouver le nombre de configurations symétriques n3 à partir du nombre des configurations (n−1)3. Son approche est purement « abstraite » : construire une configuration veut ici dire élaborer une table d’incidence, et, au lieu d’user des mots « points » et « droites », Martinetti emploie d’ailleurs les mots « nombre » et « colonnes ». Rien donc ne permet a priori d’affirmer l’identité entre les configurations au sens de Martinetti et les configurations au sens de Kantor. En réalité, les deux notions diffèrent. Heinrich Schröter, dans un article daté de 1888 [13], montre que s’il y a bien, comme Kantor le prétend, dix configurations 103, seules neuf sont géométriquement réalisables au sens que nous avons donné à l’expression dans cet article – une des figures dessinées par Kantor était en réalité fausse, dans la mesure où Kantor assimilait un angle proche d’un angle plat à un angle plat.

$PNG - 33.2 ko$: Figure 6. : La (fausse) configuration 103 de Kantor (tiré de Gropp 2004, 82).

Comme l’on voit, il n’est pas du tout évident de déterminer en quoi la figure est incorrecte.

Schröter tire la conclusion qui s’impose en distinguant les configurations géométriquement constructibles des configurations « combinatoirement » admissibles. À la fin de son article, il reprend l’approche abstraite de Martinetti, et ajoute :

On habille ce pur problème combinatoire, consistant à construire une configuration 103, d’un habit géométrique (ein geometrisches Gewand) lorsque l’on pose que les éléments sont des points et les colonnes des droites, et que l’on recherche donc une figure de dix points et de dix droites, telle que chacune des dix droites contienne trois des dix points et telle que, par chacun des dix points, passent trois des dix droites.

De la présentation qui précède, il ressort donc que la notion de configuration a d’abord été perçue comme un concept relevant de la géométrie (projective réelle) pour peu à peu s’abstraire en devenant un concept relevant de la « combinatoire ». Alors que chez Reye et Kantor, une configuration est un système d’éléments spatiaux dont on étudie les propriétés, chez Schröter, ce système est seulement « l’habit géométrique » d’une structure plus profonde, qui devrait pouvoir être décrite indépendamment de toutes considérations relatives à l’espace.

Mais Schröter ne donne aucune définition générale du concept abstrait de configuration, et on ne trouve pas chez lui la notion de structure d’incidence, telle que nous l’avons rencontrée dans la section 1. C’est le mathématicien américain E. H. Moore, dans un article intitulé Tactical Memoranda, daté de 1896, qui donne la première définition générale, sous-jacente dans le raisonnement de Schröter [14]. Moore se place dans le cadre très général d’un espace de dimension n (donc dans un cadre beaucoup plus général que celui que nous avons adopté dans la section 1, où nous nous sommes limités au plan). Si on laisse cet aspect de côté, sa caractérisation du concept de configuration revient, à quelques détails près, à celle que nous avons donnée à la section 1.

Moore définit d’abord le concept de structure d’incidence (p. 265) et celui, connexe, de table d’incidence. Il précise que la table fournit la caractérisation complète de la relation d’incidence, « qui n’est pas autrement définie ». Il poursuit, g et h désignant deux classes d’objets (par exemple des points et des droites), et ag désignant le nombre d’éléments de la classe g :

Ce système est appelé configuration tactique de rang n si, pour tout gh(g≠h), chaque objet de l’ensemble g est incident avec le même nombre, agh, disons, d’objets de l’ensemble h. J’inscris les nombres fondamentaux ag et agh d’une configuration de rang n dans le symbole matriciel carré (agh) (avec gh=12…n et la convention agg=ag) Ce symbole vaut en quelque sorte comme une notation de la configuration.

Une configuration « tactique » de rang 2 correspond donc à la notion de configuration donnée dans la section 1 (elle est en réalité un peu plus générale puisque seule la condition (ii) de la définition supra. est reprise). Et on retrouve l’usage de la notation tabulaire utilisée plus haut.

Pour bien comprendre comment Moore la généralise, prenons l’exemple de la configuration tridimensionnelle tétraèdre, qui peut se noter en utilisant une table de trois par trois ainsi 4 3 3 2 6 2 3 3 4 . La configuration tétraèdre (voir figure 7) est constituée de quatre points, six droites, quatre plans (les nombres apparaissant dans la diagonale de la table). Elle se caractérise par le fait que par chaque point passent trois droites et trois plans (première ligne), tandis que chaque droite est composée de deux points et passe par deux plans (seconde ligne) et que chaque plan contient trois points et trois droites (troisième ligne) [15].

$PNG - 35.3 ko$: Figure 7. Configuration tétraèdre

Adoptant le point de vue « abstrait » de Schröter, Moore reprend ainsi la distinction entre configurations géométriquement réalisables et celles qui ne le sont pas. Le mathématicien souligne par exemple (p. 266) que 73 n’est pas constructible dans le plan euclidien – il ne mentionne toutefois pas le résultat de Steinitz.

3- L’émergence des espaces finis

L’approche de Moore est « abstraite », donc en un sens déjà « moderne » si l’on entend par ce terme l’idée introduite au tout début de l’article : la configuration comme objet géométrique apparaît en effet seulement comme une interprétation de la structure combinatoire sous-jacente. J’aimerais montrer pourtant que cette « abstraction » n’est pas de même nature que celle introduite par Hilbert et sa méthode axiomatique.

En 1906, Veblen et Bussey, qui ont été élèves de Moore, publient un article fondateur, « Finite Projective Geometries », dans lequel sont élaborées, en suivant le modèle axiomatique hilbertien, les premières géométries finies (c’est-à-dire les premières géométries dans lesquelles le nombre de points et de droites et éventuellement de plans de l’espace considéré est fini). L’article de Moore y joue un rôle crucial mais ambigu. Dans la section 1 de leur article, intitulée « définition synthétique », les deux auteurs présentent une liste de cinq axiomes définissant un espace de dimension k. Je vais ici, pour plus de facilité, me restreindre au cas du plan dont je parlais plus haut, le plan projectif, celui où deux droites se coupent toujours, pour lequel, donc, k est égal à 2 :

I L’ensemble contient un nombre fini (2) de points. Il contient des sous-ensembles appelés droites, qui comportent chacun au moins trois points.
II Si A et B sont des points distincts, il y a une et une seule droite qui contienne A et B.
III Si ABC sont trois points n’appartenant pas tous à la même droite, et si une droite I contient un point D de la droite AB et un pointE de la droite BC, mais ne contient ni A, ni B, ni C, alors la droite I contient un point F de la droite CA.
IV Les points ne sont pas tous sur la même droite.

Soit donc un ensemble fini de « points » (le « plan ») et une famille de sous-ensembles (les « droites » du « plan »). L’axiome I stipule que les « droites » doivent contenir au moins trois « points », l’axiome II, que deux « points » déterminent une « droite », l’axiome IV que, quelle que soit la « droite » que l’on considère, il y a un « point » extérieur à cette « droite ». Enfin l’axiome III, légèrement plus compliqué, impose que si ABCest un « triangle », et si D est un « point » de (AB) et E un « point » de (BC), chacun distinct de AB et C, alors (DE) coupe (CA) en un point (voir figure 8).

$PNG - 27.7 ko$: Figure 8. L’axiome III de Veblen

Si les axiomes I, II et IV sont vérifiés dans le plan euclidien, le troisième ne l’est pas puisqu’il n’est pas compatible avec l’existence d’une droite parallèle à (CA) coupant (AB) en D et (BC) en E. En revanche, nous avons vu plus haut que pour la géométrie qu’on appelle « projective », deux droites coplanaires distinctes se coupent toujours en exactement un point.

Ces quatre postulats correspondent presque exactement aux axiomes qui permettent à Veblen et Young, dans leur manuel de géométrie projective de 1910 [16], de développer la totalité de la géométrie du plan projectif « ordinaire » (non fini). C’est sur cette base que Veblen et Bussey peuvent affirmer que leur théorie est une géométrie projective finie : mise à part la demande que le plan soit constitué d’un nombre fini de points, rien ne distingue leur théorie de la géométrie projective standard. Cette ressemblance justifie donc de considérer leur axiomatique comme une « géométrie ».

Bussey et Veblen montrent que la configuration 73 (le plan de Fano, considéré comme une structure combinatoire décrite par une table d’incidence, voir supra.) satisfait les axiomes de la géométrie projective. La configuration en question constitue donc un modèle parmi d’autres du système, et elle peut donc être considérée comme un plan projectif fini. Dans le reste de leur opuscule, les deux géomètres étudient de façon systématique les propriétés des espaces projectifs finis, en déployant toutes les ressources qu’offrent leur axiomatique et l’analogie qu’ils mettent en place avec la géométrie projective « ordinaire ». A priori, la démarche de Veblen et Bussey ne présente donc rien de méthodologiquement étrange. Dans le sillage de Hilbert, les deux mathématiciens étudient les modèles d’une structure axiomatique particulière.

Vu de plus près toutefois, leur travail prend un autre visage. Citons l’introduction de « Finite Projective Geometries » :

Par le biais du concept généralisé de géométrie tel qu’il ressort inévitablement des recherches récentes et profondes sur les fondements de cette science, est donnée, dans le §1 de cet article, une définition d’une classe de configurations tactiques qui inclut de nombreuses configurations bien connues, ainsi que plusieurs nouvelles. Le §2 développe une méthode qui permet de construire ces configurations et qui se révèle fournir toutes les configurations satisfaisant la définition. Dans les §§4-8, on montre que les configurations ont une théorie géométrique identique, dans la plupart de ses théorèmes généraux, à la géométrie projective ordinaire (…). Dans le §9, référence est faite aux autres définitions de certaines des configurations incluses dans la classe définie dans le § 1.

Veblen et Bussey se placent non seulement dans la filiation de « recherches récentes et profondes sur les fondements » de Hilbert, mais aussi dans celle des études sur les configurations développées durant toute la fin du XIXe siècle et dont le Tactical Memoranda de Moore propose une synthèse. La liste de postulats est présentée ici, non pas comme un système axiomatique particulier, mais comme la « définition d’une classe de configurations ». Et le paragraphe 9, final, dans lequel les auteurs renvoient à Moore, vise à expliciter les liens entre le concept d’espace projectif fini et les diverses structures combinatoires déjà connues –signalons, dans un langage un peu plus technique, la connexion la plus évidente : un plan projectif d’ordre [17] q peut être vu comme une configuration symétrique de q2+q+1 points et droites laquelle a pour propriétés que chaque point y est sur q+1 droites et chaque droite comporte q+1 points (on vérifie que le plan de Fano est un modèle du plan projectif d’ordre 2).

L’adoption du nouveau schéma hilbertien, loin donc de constituer une rupture radicale par rapport aux anciennes recherches, permet donc de reformuler les questions liées aux configurations dans un nouveau cadre, explicitement considéré comme « géométrique ». Mais la question se pose alors de comprendre en quel sens exactement on entend désormais ce qualificatif de « géométrique ».

Caractériser les recherches de Veblen et Bussey de « géométriques » ne signifie pas, bien entendu, qu’on les assimile à celles, pré-combinatoires, de Reye et Kantor. Les espaces projectifs ne sont pas des figures, comme les configurations l’étaient chez les deux précurseurs. Veblen et Bussey adoptent le point de vue « abstrait » de Moore : les configurations ne sont pour eux que des familles de structures d’incidence. Leur idée est cependant qu’il est possible d’appliquer à l’étude de ces systèmes d’éléments abstraits, des concepts et des méthodes issus de la géométrie. Plus précisément, ils conçoivent ces systèmes comme des modèles de la théorie projective finie.

Cette réintroduction de la géométrie dans la combinatoire se manifeste de façon particulièrement spectaculaire dans le traitement par Veblen et Bussey de la configuration 73. Le plan de Fano est la structure la plus simple satisfaisant les conditions I-IV. Or 73 était considéré par Moore comme l’exemple paradigmatique d’une configuration géométriquement impossible. En une dizaine d’années, l’illustration la plus simple d’une configuration non constructible dans un cadre euclidien ordinaire (ou projectif) devient l’exemple le plus simple et le plus répandu de ce qu’est un espace projectif fini.

Il y a ici une inversion extrêmement frappante : 73, qui en était venue à être conçue comme une configuration « abstraite » dénuée de tout contenu géométrique, devient l’illustration la plus simple de ce qu’est un plan projectif fini. La configuration dessinée dans la Fig. 3 ci-dessus passe du statut de figure fausse, reflétant l’impossibilité de construire une certaine structure sur le plan de la feuille, à celle d’une représentation, toujours sur le plan de la feuille, du plan projectif lui-même.

Bien entendu, c’est « le concept généralisé de géométrie, tel qu’il ressort inévitablement des recherches récentes et profondes sur les fondements de cette science », c’est-à-dire les Fondements de Hilbert, qui explique ce renversement (la configuration 73 est un modèle de l’axiomatique proposée). Mais il faut insister sur le fait que le nouveau cadre conceptuel reprend certains éléments présents dans la vieille notion de configuration.

D’une certaine façon, même lorsqu’une configuration est conçue comme un objet géométriquement réalisable, elle possède déjà une certaine indépendance, une certaine autonomie, par rapport à son plan d’inscription. Nous avions noté que la Fig. 2, celle de la configuration de quatre points et de six droites, pouvait difficilement être considérée comme une figure euclidienne, dans la mesure où, chez elle, certains éléments qui d’ordinaire seraient considérés comme faisant partie du schéma devaient en être exclus. Toujours dans le même ordre d’idées, j’ai choisi, dans la Fig. 1, de représenter la droite (AB) par un segment, et la « droite » (ABC) par un arc s’arrêtant à A et C, ceci pour signifier que le « devenir » de (AB) et de (ABC) dans le plan ne nous intéressait pas. Autrement dit, les configurations réalisables géométriquement ne s’insèrent pas dans leur environnement comme les figures « ordinaires » (bien entendu, je schématise ici : il y a de multiples types d’usage des figures chez les géomètres euclidiens).

Les configurations n’ont aucun hors-champ que l’on pourrait utiliser à discrétion pour introduire ce qui nous est nécessaire dans les démonstrations. Les relations d’incidence entre les points et les droites y sont fixées dès le début, et toute modification de ces relations détruit le système que l’on considère. Le regard qui parcourt une configuration géométrique n’est ainsi pas le même que celui qui étudie une figure euclidienne. L’attention est focalisée sur le nombre d’intersections – elle n’est pas tendue par la possibilité d’enrichir ou de diviser la figure.

Veblen et Bussey, en construisant leurs nouvelles géométries, ne font donc qu’accomplir ce mouvement d’autonomisation contenu en germe dans la notion de configuration. La tendance à détacher la figure de son inscription dans un espace atteint son apogée dans le concept de plan projectif fini : le plan de Fano n’est pas le dessin d’une figure sur une feuille – il est censé se substituer à la feuille sur laquelle on dessine.

Conclusion

Que Veblen et Bussey s’inscrivent dans le projet de refondre axiomatiquement la géométrie n’empêche pas leur travail de prolonger et radicaliser les premières recherches sur les configurations. L’étude des géométries finies est ainsi un bon belvédère pour observer et tenter de mesurer in concreto l’impact des Fondements de la géometrie sur la pratique des géomètres.

Veblen, comme Moore d’ailleurs [18], ont lu Hilbert très précisément, et, avec d’autres mathématiciens américains (les travaux de ce groupe sont connus étant ceux de l’« école postulationniste » [19] ), ils entreprennent d’appliquer la nouvelle méthode à des champs très différents (théorie algébriques, géométriques, etc).

Dans l’article sur la géométrie finie de 1906, l’utilisation du modèle hilbertien rencontre toutefois un mouvement d’abstraction déjà fort abouti – celui qui a mené les mathématiciens des configurations considérées comme des objets géométriques aux configurations combinatoires abstraites. Dans ce contexte, l’axiomatisation n’est pas seulement une étape supplémentaire vers l’abstraction – ironiquement, elle se présente même comme un mouvement inverse, comme un retour vers la géométrie.

La nouvelle approche permet en effet d’appliquer les concepts et les techniques géométriques à des situations et des problèmes purement combinatoires. Essayer de préciser l’impact des Fondements sur les mathématiciens américains travaillant sur les configurations permet donc de mesurer combien la révolution copernicienne que représente l’approche hilbertienne intègre des éléments qui appartiennent à un socle plus ancien.

Plus généralement, l’opposition souvent reprise entre géométrie de la figure et géométrie de l’espace a l’inconvénient de présupposer que le mode d’insertion de la figure dans un espace n’est pas vraiment un problème digne de l’attention de l’historien. Dans la perspective de la dichotomie entre espace et figure, soit on se concentre sur la figure, et dans ce cas, la question de la nature de l’espace dans lequel « vit » la figure ne peut par principe pas être explicitée ; soit on axiomatise l’espace sous-jacent, mais alors l’étude des triangles et des cercles, des courbes et des droites, devient secondaire et disparaît de l’horizon.

Or, il semble que le rapport entre la figure à son « environnement » (à son « support », et même à la matérialité de ce support) ait parfois été une question pour les mathématiciens (qu’ils précèdent Hilbert ou qu’ils le suivent). Elle devrait donc l’être aussi pour les historiens des mathématiques. La feuille sur laquelle le géomètre trace ses figures a des bords – n’est-il pas possible prendre en compte l’existence de ces limites dans la pratique géométrique elle-même [20] ?

Certaines sortes de « figures » (mais faut-il encore les appeler ainsi ?), les configurations, dans lesquelles les rapports à l’espace « environnant » sont comme suspendus, ont peu à peu été prises pour sujet d’étude par les géomètres au XIXème siècle – comment caractériser ces nouveaux objets ?

Enfin, les mathématiciens qui travaillent de nos jours en géométrie discrète et plus généralement en combinatoire utilisent abondamment des figures et même des stéréogrammes [21] pour représenter les espaces qu’ils considèrent – quel statut accorder à ces figures-espaces ? Ce qui précède doit être lu comme une invitation à poser ce genre de questions [22]

Notes

[1] Hilbert D., Les fondements de la géométrie (1899), trad. fr. P. Rossier, Gabay, 2000.

[2] Le premier axiome stipule que deux points déterminent une droite, le second que l’on peut prolonger continûment en ligne droite une droite limitée donnée, le troisième que l’on peut construire un cercle lorsque l’on dispose de son rayon et son centre, le quatrième que tous les angles droits sont égaux entre eux. Le cinquième axiome a toujours eu un statut particulier : il s’agit de l’axiome des parallèles, qui revient à demander que, par un point extérieur à une droite donnée, il ne passe qu’une et qu’une seule parallèle à cette droite.

[3] Il en va notamment ainsi des propositions qui mettent en jeu des considérations tenant à la continuité, au déplacement ou encore à l’« ordre » (c’est-à-dire à ce qui est relatif, par exemple, à la distinction entre intérieur et extérieur d’une courbe close, ou à l’opposition entre demi-plan droit et gauche, etc.).

[4] La formulation des axiomes varie selon les éditions. Mais la division en cinq groupes reste constante : les 7 axiomes « d’appartenance » posent des conditions sur les relations d’incidence entre points, droites et plans ; les 5 axiomes d’ordre donnent un sens à l’expression « être entre deux points » et à la notion de demi-plan ; l’axiome des parallèles reprend le contenu du postulat d’Euclide ; les 5 postulats de congruence définissent l’égalité entre les segments et entre les aires ; enfin Hilbert ajoute deux axiomes de continuité.

[5] Par souci de symétrie, on parle de « droite » sur un point comme on parlait de « point » sur une droite.

[6] Les nombres qui figurent dans la diagonale (qui va de gauche à droite en descendant) correspondent aux nombres de « points » et de « droites » de la configuration (4 « points » et 6 « droites ») ; les autres nombres indiquent le nombre de « points » situés sur chaque « droite » (2) et le nombre de « droites » rencontrant chaque « point » (3).

[7] E. Steinitz, Über die Construction der Configurationen n3, (1894), Dissertation, Breslau.

[8] Dans toute cette section, je reprends les conclusions de l’article très éclairant de H. Gropp, « Configurations between geometry and combinatorics », Discrete Applied Mathematics, (2004), 138, pp. 79-88, auquel je renvoie le lecteur pour plus de précisions.

[9] Th. Reye, Geometrie der Lage, (1867), C. Jümpler, Hannover, 2nd edition, 1876. La notion de configuration est historiquement liée au développement de la géométrie projective au XIXe siècle. Cela n’est pas surprenant, dans la mesure où la géométrie projective est progressivement devenue une théorie portant sur les relations d’intersection et d’appartenance (c’est-à-dire les relations d’incidence) entre les points, les droites et les plans dans l’espace. Mais ce n’est que relativement tardivement que, dans le contexte de ses recherches sur la théorie projective, Theodor Reye introduit cette première définition générale de la configuration.

[10] Th. Reye, “Das Problem der Configurationen”, (1882), Acta Mathematica, 1, pp. 93–96.

[11] S. Kantor, “Die Configurationen (3;3)10”, (1881) Sitzungsberichte der Akademie der Wissenschaften in Wien, 84, pp. 1291–1314.

[12] V. Martinetti, “Sulle le configurazione piani 3”,3 (1887), Annali di Matematica Pura ed Applicata, 15, 1887, pp. 1-26.

[13] H. Schröter, “Ueber die Bildungsweise und geometrische Construction der Configurationen”, (1889), Göttinger Nachrichten, pp.193–236. Pour de plus amples détails, voir Gropp 2004, 83-85.

[14] « Tactical Memoranda », American Journal of Mathematics, (1896), 18, pp.264-303. Moore explique que « sous le titre général de Tactical Memoranda », il « publiera une série d’articles concernant des sujets plus ou moins liés entre eux de Tactique ». Pour une définition de « tactique », Moore renvoie à Cayley (« On the Notion of Boundaries of Algebra », Quarterly Journal of Mathematics, 6, 1864, Collected Math. Papers, V). Un problème tactique est pour Cayley un problème de combinatoire.

[15] L’exemple est tiré de O. Veblen & J. W. Young, Projective Geometry, I, 1910, New York : Ginn and Company, pp. 38-40.

[16] Voir O., Veblen & J. W. Young, Projective Geometry, op. cit.… , pp.15-19.

[17] Lorsque sa dimension est supérieure ou égale à 3, un espace projectif peut toujours être défini à partir d’un espace vectoriel (le cas n=2 est rendu compliqué par l’existence de plans finis non arguésiens) – on peut donc alors associer à cet espace un corps, puisqu’un espace vectoriel se définit sur un corps. Veblen et Bussey explicitent ce point dans leur manuel de 1910 aussi bien que dans leur article de 1906. L’objet du §2 de « Finite Projective Geometries » est de montrer (en mettant de côté le cas des plans non arguésiens) qu’un espace projectif fini est associé à un corps fini, lequel a donc pour ordre un entier. L’ordre de l’espace projectif est alors l’ordre du corps sur lequel il est défini

[18] E. H. Moore, “On the foundations of mathematics”, Bulletin of the American Mathematical Society, (1903), 9, pp. 402-424.

[19] M. J. Scanlan, “Who were the American postulate theorists”, Journal of Symbolic Logic, (1991), 56, pp. 981-1002.

[20] J’ai discuté cette question dans « Pasch entre Klein et Peano : empirisme et idéalité en géométrie », Dialogue, (2005), 14, pp. 653-692.

[21] B. Polster, A Geometrical Picture Book, Springer, 1998

[22] Je remercie chaleureusement Karine Chemla pour l’aide qu’elle m’a apportée dans la construction de cet article.

Source : http://images.math.cnrs.fr/Entre-figures-et-espaces-le-ca...

INITIATION AUX MATHÉMATIQUES FINANCIÈRES

J.Azéma

Date: Février 2004

Introduction

Ces notes , destinées aux étudiants de la maitrise MASS de l'université Paris V , ne prétendent à aucune originalité. Elles ont pour but d'aider les étudiants de ce cursus, possèdant pour certains d'entre eux un bagage mathématique réduit ,à comprendre le début du remarquable petit livre de
Lamberton et Lapeyre intitulé "Introduction au calcul stochastique appliqué à la finance" Ed.Ellipses (97) ;la lecture des 40 premières pages de cet ouvrage est , bien entendu , fortement recommandée.

Le problème principal que nous nous poserons est celui de l'évaluation du prix d'une option (pricing) ; voici en gros de quoi il s'agit. Et tout d'abord de quoi il ne s'agit pas : on ne cherche en aucune façon à prédire l'évolution du cours d'une action ; ce travail est celui des analystes financiers qui auscultent le bilan de la firme , ses avantages ou ses handicaps vis à vis de la concurrence , regardent si elle est positionnée sur un marché porteur , etc...Cela fait, ils prodiguent à leurs clients ou publient dans la presse financière des conseils d'achat ou de vente.
Mais cette même action peut servir de support à des options d'achat (call) ou de vente (put) dont le fonctionnement peut être décrit de la manière suivante.
L'acheteur d'une option achète un droit à son émetteur ( en général un grand établissement financier) qu'il pourra ou non exercer à une date convenue à l'avance appelée date d'exercice. S'il s'agit d'un call, ( resp.d'un put), ce droit consiste en la possibilité pour le détenteur de l'option d'acheter, (resp.de vendre), l'action support à son émetteur à un prix, lui aussi déterminé à l'avance, appelé prix d'exercice.
Il est à noter

que l'acheteur de l'option paye immédiatement son dû , à savoir le prix de l'option, à son vendeur ; celui ci dipose donc de liquidités qu'il peut faire fructifier a sa guise jusqu'à la date d'exercice.
que si le détenteur de l'option peut choisir d'exercer ou non son droit, son vendeur est tenu de respecter le contrat en cas d'exercice de l'option.

Pour se rendre compte du caractère très spéculatif des marchés où se négocient les options , souvent appelés marchés dérivés, imaginons l'exemple suivant:
Au $1^{er}$ Otobbre 2000 ,l'action Michelin étant cotée 200F,la Société Générale émet des options d'achat sur ce support , au prix de 10F , la date d'exercice étant fixée au $1^{er}$ Octobre 2001 , et le prix d'exercice à 220F ; vous disposez d'une somme de 20.000F et avez toute confiance dans les perspectives de la société Michelin ; vous pouvez manifester cette confiance de 2 façons

soit acheter 100 actions Michelin
soit acheter a la Société Générale 2000 call sur Michelin

Si les dieux vous sont favorables, et que l'action gagne 20% en un an, elle cotera 240F à la date d'exercice ; dans le premier cas il ne se passe rien que de très banal : vous avez gagné 4000F ; mais dans le deuxième cas, vous pouvez acheter 2000 actions Michelin à la S.G. qui est tenue de vous les vendre au prix d'exercice (220F), puis les revendre en bourse 240F, ce qui vous procure une plus value de 40.000F ; si l'on déduit de cette somme votre dépense initiale,votre bénéfice est de 20.000F, soit 100%.
Mais ce petit miracle a une contrepartie : si l'action Michelin, contrairement à votre attente, perd 5% au cours de l'année, elle cotera 190F à la date d'exercice ; le droit que vous avez acquis (la possibilité de l'acheter a 220F) n'a plus aucune utilité et donc aucune valeur ; il ne vous reste plus qu'à jeter votre option à la corbeille et à constater, en gardant le sourire, que vous avez perdu la totalité de votre investissement initial de 20.000F
Le mécanisme de l'option de vente est exactement inverse : c'est un outil de spéculation à la baisse avec un risque de ruine en cas de hausse ; si vous achetez un put doté des memes caractéristiques, et si le cours de l'action support a perdu 20%, elle cote 160F à la date d'exercice ; vous achetez alors sur le marché boursier 2000 actions à 160F que vous revendez 220F à la Société Générale ; je vous laisse calculer votre bénéfice...
Ces options ont une autre fonction ; supposons qu'un fonds de pension américain détienne 30% du capital de Michelin et s'attende à une forte baisse du cours de l'action ; il peut, bien entendu , vendre sa participation avant la catastrophe annoncée, mais, pour des raisons fiscales, ou pour ne pas perdre son droit de regard sur la gestion de l'entreprise, il préfèrera souvent recourir à une stratégie de couverture des risques (hedging) fondée sur l'achat d'options de vente. En cas d'effondrement du marché, les gains procurés par la possession de ces put, amplifiés par l'effet de levier qui vient d'être décrit, permettront de compenser la perte provoquée par la chute des cours. Plus que le goût de la spéculation prêté aux anglo-saxons, c'est vraisemblablement ce souci de sécurité qui explique le développement spectaculaire des marchés dérivés constaté au cours des 20 dernières années aux Etats Unis.

Il reste à expliquer le rôle que jouent les mathématiques dans cet univers ; une étude statistique des cours de bourse conduit tout d'abord a une estimation de la loi de probabilité qui gouverne leur évolution ; répétons qu'il ne s'agit pas ici de formuler des prédictions ; pour prendre un exemple analogue , il s'agit , après observation d'un grand nombre de jets d'une pièce de monnaie , d'établir que la probabilité de tomber sur pile est (à peu près) 1/2 ; dans ces notes , nous supposerons ce problème résolu à l'aide des techniques classiques de la statistique des processus , et nous supposerons donc cette loi connue. La tâche qui incombe alors à l'équipe de probabilistes salariés par la Société Générale est de déterminer à quel prix vendre ses options (les 10F de notre exemple); vendues trop chères, personne n'en voudra, vendues trop bon marché , elles peuvent conduire à la faillite des établissements réputés indestructibles , (toujours ce dévastateur effet de levier) . Ce dernier point n'est pas une exagération : les faillites retentissantes (Baring , LTCB,etc..) qui ont récemment semé la panique sur les marchés financiers sont presque toutes dues a des spéculations malheureuses sur les marchés dérivés .

Nous nous bornerons, pour l'essentiel , à l'étude du modèle discret de Cox, Ross et Rubinstein dans lequel on suppose que le marché financier est réduit a un actif risqué (par exemple une action) et à un actif sans risque (par exemple un carnet d'épargne à taux fixe) . On fait en outre les hypothèses simplificatrices suivantes:

Le temps est discret (on ne s'intéresse par exemple au cours des actifs qu'à la clôture de la bourse chaque jour a 17H)
l'actif risqué n'a que 2 comportements possibles : son cours est multiplié chaque jour par une quantité aléatoire qui ne peut prendre que 2 valeurs fixées (par exemple, à chaque clôture ce cours est soit multiplié par 2 soit divisé par 3) .

Nous verrons plus loin les raisons mathématiques qui conduisent à faire cette dernière hypothèse (fort éloignée du comportement réel d'une action!)
En dépit de son caractère simpliste, l'étude de ce modèle est instructive pour plusieurs raisons ; tout d'abord les méthodes employées sont en tout point analogues à celles qui conduisent aux résultats de Black and Scholes et ceci dans un cadre élémentaire . On peut déjà y discerner le rôle fondamental joué par la théorie des martingales ainsi que les raisons d'un certain nombre de résultats assez surprenants du modèle de B. and S. , le fait que le prix d'une option dépende uniquement de la volatilité du marché et non pas de sa tendance (haussière ou baissière) par exemple.

Mais il va nous falloir faire un peu de mathématiques ; au travail!

Mathématiques Financières : l’essentiel

Retour

- Les 10 formules incontournables
  (Fin de période)

Marc ROMANO
Télécharger le fichier au format word (103 ko)

Sommaire

Rappels d'algèbre

Taux proportionnel - Taux équivalent

Taux proportionnel
Taux équivalent

Capitalisation - Actualisation

Valeur acquise par un capital placé pendant n périodes au taux i
Valeur actuelle d'un capital futur actualisé sur n périodes au taux i

Emprunts indivis - Annuités

Valeur future d'une suite d'annuités constantes
Annuité de constitution d'un capital futur
Valeur actuelle d'une suite d'annuités constantes
Annuité de remboursement d'un capital
Calcul du premier amortissement d'un emprunt
Calcul de l'amortissement d'un empruny, connaissant le précédent ou le suivant
Montant du capital remboursé après une annuité quelconque
Montant du capital restant à rembourser après une annuité quelconque

Rappels d’algèbre

- Retour au Sommaire

Taux proportionnel - Taux équivalent

- - Exemple : taux mensuel t proportionnel à un taux annuel de 12%
    
    Retour au Sommaire
  - Taux Proportionnel
    
    Taux équivalent
    
    Exemple : taux t mensuel équivalent à un taux i annuel de 12%
    
    (ou 0.9488%)
    
    Retour au Sommaire

Capitalisation - Actualisation

- - Valeur acquise par un capital de 10.000 F placé pendant 5 ans au taux annuel de 7 % :
    
    Même calcul, mais intérêts composés trimestriellement.
    
    Etape 1 : Détermination du taux trimestriel équivalent à 7% annuel
    
    Etape 2 : calcul de la valeur acquise d’un capital de 10000 F placé pendant 20 périodes (5 années de 4 trimestres) au taux de 1.706%
    
    On constate que, les taux étant équivalents, les valeurs futures sont strictement identiques, quelle que soit la période de composition choisie.
    
    Retour au Sommaire
    
    Combien faudrait-il placer aujourd’hui, sur un livret de Caisse d’Epargne à 4% par an, pour disposer de 100.000 F dans 8 ans ?
    
    Retour au Sommaire
  - Valeur acquise Vn par un capital Vo placé pendant n périodes à un taux i
    
    (1)
    
    Valeur actuelle Vo (actualisation) d’une valeur future Vn actualisée sur n périodes à un taux i
    
    (2)

Emprunts indivis - Annuités (fin de période)

- - Quelle sera la valeur totale d’une série de versements de 500 F par mois, versés en fin de période pendant 8 ans au taux de 5,15% par an ?
    
    Etape 1 : taux mensuel équivalent à 5,15% annuel
    
    Etape 2 : calcul de la valeur future
    
    Avec les mêmes données que l’exemple précédent (taux et durée), combien aurait-il fallu verser mensuellement pour obtenir un capital de 100.000 F au terme des 8 années ?
    
    Le calcul est direct (nous connaissons déjà le taux mensuel équivalent).
    
    Retour au Sommaire
    
    Une assurance vie propose deux formules en cas de décès :
  - Valeur future Vn d’une suite d’annuités a placées au taux i pendant n périodes
    
    (3)
    
    Problème corollaire : montant de l’annuité a pour constituer un capital Vn
    
    De la formule ci-dessus, on peut facilement déduire a en supposant Vn connu :
    
    (4)
    
    Valeur actuelle d’une suite d’annuités constantes de fin de période
    
    (5)

- - - Versement d’un capital unique de 500.000 F
    - Versement d’une rente annuelle de 50.000 F pendant 12 ans

- - En considérant un indice du coût de la vie de 2 % par an, laquelle des deux formules est la plus intéressante ?
    
    Il faut calculer la valeur actuelle des 12 versements annuels de 50.000 F. en appliquant la formule d’actualisation des annuités constantes :
    
    Il est donc beaucoup plus intéressant de choisir la rente annuelle pendant 12 ans (à condition que le bénéficiaire survive, lui).
    
    Prenons le même problème, mais avec un taux d’inflation de 8 %. Le calcul d’actualisation donne dans ce cas une Vo de 376.803,90 F. On aura donc intérêt à préférer le versement immédiat.
    
    Un ami vous demande de lui prêter 10.000 F, qu’il se propose de vous rembourser en 12 mensualités. Quel montant de mensualité devez-vous lui demander pour vous assurer un taux de 5 % ?
    
    Calcul du taux proportionnel mensuel à 5 % annuel :
    
    Calcul de l’annuité :
    
    Ce n’est pas encore de l’usure !
    
    Retour au Sommaire
    
    Soit un emprunt de 100.000 F remboursable en 10 annuités à 5 %, Calculez :
  - Problème corollaire : montant de l’annuité a connaissant Vo, le taux et la durée (problème de l’annuité de remboursement de crédit).
    
    (6)
    
    Calcul du premier amortissement d’un emprunt
    
    Rappel : une annuité de remboursement (a) comprend une partie d’amortissement du capital emprunté (A) et une partie d’intérêts sur le capital.
    
    (7)

- - 1. Le montant de l’annuité constante a
    2. Le montant de l’amortissement A₁ compris dans la première annuité
    3. Vérifiez que a - A₁ (autrement dit, la part des intérêts compris dans la première annuité) est égal à 5 % du capital emprunté.

- - Calcul de l’annuité constante a
    
    soit
    
    Calcul de la part en capital de la première annuité :
    
    Part des intérêts : soit très exactement 5 % du capital emprunté, ce qui est normal : dans la première annuité, la totalité du capital produit des intérêts pendant toute la première période.
    
    Retour au Sommaire
    
    Dans le même exemple que ci-dessus, quel est la répartition entre capital et intérêt des 2^ème, 3^ème et 4^ème annuités ?
    
    Connaissant A₁, on applique la formule : A₂=A₁(1+0,05), etc. Le montant des intérêts se déduit simplement en retranchant du montant de l’annuité l’amortissement du capital.
  - Calcul d’un amortissement connaissant le précédent ou le suivant
    
    (8)

Annuité	Part en Capital	Intérêts
A2	8.347,98	4.602,48
A3	8.765,38	4.184,64
A4	9.203,65	3.748,81

- - Toujours dans l’exemple ci-dessus, calculez le montant du capital remboursé après paiement de la 3^ème échéance.
    
    Vérification : Nous avons calculé tout à l’heure le montant des amortissements en capital des 4 premières échéances. On peut donc vérifier que la somme des amortissements des trois premières échéances est bien égale au montant calculé :
    
    7.950,46 + 8.347,98 + 8.765,38 =25.063,82.
    
    Compte tenu des arrondis successifs, l’écart d’1 centime n’est pas significatif.
    
    Retour au Sommaire
    
    Toujours sur le même exemple, quel est le capital restant à rembourser après paiement de la 3^ème échéance ?
    
    Vérification : Nous avons calculé le capital remboursé et le capital restant à rembourser après la troisième échéance. La somme de ces deux chiffres doit logiquement être égale au capital initial :
    
    74.936,20 + 25063,83 = 100.000,03
    
    Les centimes d’écart sont dus aux arrondis. Ils se régularisent normalement sur la dernière échéance de l’emprunt.
    
    Retour au Sommaire
    
    Source : http://www.ecogesam.ac-aix-marseille.fr/Resped/Gestion/mathfi/mathfin1.html#Taux Proportionnel
  - Retour au Sommaire
    
    Calcul du capital remboursé R_p après paiement de la p^ème annuité
    
    (9)
    
    Connaissant le calcul de A1 en fonction de Vo, il est possible de remplacer A1 par :
    
    Cette formule peut être simplifiée, en éliminant i, et devient :
    
    (9bis)
    
    Calcul du capital V_p restant à rembourser après paiement de la p^ème annuité
    
    (10)

06/01/2010

Construction de Z à partir de N

En supposant connues les propriétés élémentaires de l'ensemble et de l'addition des entiers naturels, nous allons donner une construction rigoureuse de et de l'addition des entiers relatifs. Dans cette construction, apparaîtra sous forme d'un quotient de par une relation d'équivalence. Ce paragraphe est aussi l'occasion de rappeler les notions de relation d'équivalence et d'ensemble quotient, notions centrales pour le reste du cours.

Définition Soit un ensemble. Une relation sur est un ensemble de couples d'éléments de . On écrit au lieu de . Une relation est une relation d'équivalence si elle est

a): réflexive (i.e. pour tout , on a )
b): symétrique (i.e. on a équivalence entre et quels que soient )
c): transitive (i.e. les conditions et impliquent que quels que soient )

Exemples 1 [1)] Soit

l'ensemble des villes de France. On définit une relation

sur

en déclarant que

signifie que

se trouvent dans la même région. Il est facile de vérifier qu'il s'agit d'une relation d'équivalence.

[2)] Soit et définissons par

Par exemple, on a

. La réflexivité et la symétrie de

résultent de la commutativité de l'addition des entiers positifs. Montrons que

est transitive. En effet, par définition, les conditions

équivalent aux équations

En rajoutant la première à la seconde on obtient

ou encore

Or on sait que la loi d'addition sur

est régulière c'est-à-dire qu'une égalité

implique

quels que soient

. Il s'ensuit que

c'est-à-dire que

. Notons que dans cette démonstration, nous avons utilisé l'associativité, la commutativité et la régularité des entiers naturels.

Définition Soit un ensemble et une relation d'équivalence sur . Pour , on pose

$displaystyle ^Roverline {x} = { x'in X ;vert ; x R x' ; } subset X$

et on appelle classe d'équivalence de par rapport à cette partie de . Par définition, l'ensemble est formé des classes $^Roverline {x}$ d'éléments . On appelle le quotient de par la relation d'équivalence . On définit l'application quotient (=la projection canonique) par $^Roverline {x}$ . Une partie de est un système de représentants pour si elle contient un élément de chaque classe d'équivalence et un seul.

Exemples 2 [1)] Dans l'exemple des villes de France (voir ci-dessus) la classe d'équivalence d'une ville

est formée de toutes les villes qui se trouvent dans la même région que

. En particulier deux classes

sont égales ssi

se trouvent dans la même région. Les éléments de

sont des ensembles de villes, deux villes étant regroupé dans un même ensemble ssi elles se trouvent dans la même région. On a donc une bijection

$displaystyle X/R stackrel{_sim}{rightarrow}{$ régions de France

la région où se trouve v

Il existe beaucoup de systèmes de représentants. Par exemple, l'ensemble

formé des capitales des régions en est un. L'ensemble

formé des villes les plus éloignées de la capitale dans leur région en est un autre.

[2)] Dans le cas de l'exemple et de la relation introduite ci-dessus on vérifie que si et seulement si l'une des deux conditions suivantes est remplie

il existe tel que et
il existe tel que et .

Ainsi, deux éléments appartiennent à une même classe d'équivalence si on peut passer de l'un à l'autre en ajoutant un même entier naturel aux deux coordonnées. Les classes sont donc des `parties diagonales' du plan

includegraphics[width=10.0cm height=10.0cm]{classesNN.eps}

Il y a beaucoup de systèmes de représentants. Par exemple

$displaystyle X_0 = {0}times{mbox{bf N}}cup {mbox{bf N}}times{0} = { ldots, (0,3), (0,2), (0,1), (0,0), (1,0), (2,0), ldots }$

en est un. On définit l'ensemble ${mbox{bf Z}}_{ax}$ (

axiomatique) comme étant l'ensemble quotient

Lemme [Propriété universelle de ] Soit un ensemble, une relation d'équivalence sur et une application constante sur les classes d'équivalence par rapport à (c'est-á-dire qu'on a à chaque fois que ). Alors il existe une application et une seule telle que. Réciproquement, toute application de la forme est constante sur les classes d'équivalence.

begin{picture}(14,8)(0,0) % multiput(0,0)(1,0){15}{ line(0,1){8}} % multi... ...3.5){makebox(0,0)[tl]{$ ;g $}} put(6,6.2){makebox(2,2){$ f $}} end{picture}

Remarque 3 Le lemme signifie que la règle

définit une application

si et seulement si on a

quels que soient

vérifiant

Démonstration. On pose . Il s'agit de vérifier que est indépendant du représantant de la classe . Or si en est un autre, c'est-à-dire que, alors par définition, on a et donc .

Exemple 4 Il existe une application $g: {mbox{bf Z}}_{ax} rightarrow {mbox{bf Z}}$ et une seule telle que

. En effet, si

alors

et donc

. L'application

est bijective : En effet, elle est surjective car si

, on a

. Elle est injective car si on a

, alors

c'est-à-dire que

et que

Lemme [Addition sur ${mbox{bf Z}}_{ax}$ ] Il existe une application

$displaystyle {mbox{bf Z}}_{ax} times {mbox{bf Z}}_{ax} rightarrow {mbox{bf Z}}_{ax}$

et une seule telle que

Démonstration. Il s'agit de montrer que si et . Nous laissons au lecteur le soin de cette vérification.

Définition Un groupe est un couple formé d'un ensemble et d'une application

appelée la loi du groupe telle que

a): la loi est associative (i.e. on a quels que soient )
b): la loi admet un élément neutre (i.e. il existe tel que quel que soit )
c): tout élément de admet un inverse pour la loi (i.e. on a )

Un groupe est commutatif si on a quels que soient .

Exemple 5 [1)] Si les conditons a) et b) sont vérifiées, alors l'élément neutre

est unique. En effet, soient

deux éléments neutres. Alors on a

(car

est neutre) et

(car

est neutre) et donc

[2)] Si les conditions a), b) et c) sont vérifiées, l'élément inverse de la conditon c) est unique. En effet, supposons que et sont deux éléments inverses à . Alors on a

On note $x^{-1}$ l'élement inverse de

Exemple 6 [1)] Le couple

vérifie a) et b) (pour

) mais non pas c) car l'équation

n'admet pas de solution

[2)] Le couple $({mbox{bf Z}}_{ax}, +)$ est un groupe. En effet, on vérifie facilement l'associativité. L'élément neutre est la classe de . L'inverse de la classe de est la classe de ! En effet, nous avons

Lemme [Propriété universelle de ${mbox{bf Z}}_{ax}$ ] Soit l'application

$displaystyle iota :{mbox{bf N}}rightarrow {mbox{bf Z}}_{ax}: , ;n rightarrow overline {(n,0)}.$

On a et si est une autre application de vers un groupe telle que , alors il existe une application $psi: {mbox{bf Z}}_{ax}rightarrow G$ et une seule telle que a) et b) quels que soient $x,x'in {mbox{bf Z}}_{ax}$ .

Remarque 7 On peut interpréter ce lemme en disant que ${mbox{bf Z}}_{ax}$ (et donc

) est le groupe universel contenant .

Démonstration. Il est immédiat que est additive. Supposons donnée une application comme dans l'énoncé. Définissons par $f((a,b))=phi(a)starphi(b)^{-1}$ . Montrons que induit une application ${mbox{bf Z}}_{ax}rightarrow G$ , Supposons que et donc que . Alors pour montrer que

$displaystyle phi(a)phi(b)^{-1} = phi(a') phi(b')^{-1}$

il suffit de montrer que

$displaystyle phi(a)phi(b)^{-1} phi(b) phi(b') = phi(a') phi(b')^{-1} phi(b) phi(b').$

En utilisant que nous sommes ramenés à montrer que

ce qui est clair car et . Montrons l'unicité de . En effet, si et vérifient les hypothèses, nous avons

En outre, si , alors et sont tous les deux inverses de où . Donc . Comme les et les , , forment un système de représentants des classes d'équivalence par rapport à , il s'ensuit que .

Source : http://www.les-mathematiques.net/b/a/d/node2.php3

Propriétés de l'intégrale de Riemann

Proposition Pour , on a

$displaystyle forall Xin S_{a,b}: s(f,X) le int_a^b f(x),rd x le S(f,X) ~. eqno{(sIS)}$

En particulier, on a

$displaystyle (b-a)inf f([a,b]) le int_a^b f(x),rd x le (b-a) sup f([a,b]) ~. eqno{(iIs)}$

Démonstration L'inégalité est conséquence immédiate de la définition de resp. . Pour montrer , il suffit de prendre .

Théorème [de Chasles] Soit . Alors,

et on a la relation de Chasles :

Démonstration Pour tout $Xin S_{a,c},~Yin S_{c,b}$ , on a évidemment $Xcup Yin S_{a,b}$ et . Ceci entraîne. Le même s'applique à . Ainsi l'intégrabilité sur et implique celle sur , et la relation de Chasles. Réciproquement, tout $Zin S_{a,b}$ qui contient se décompose en avec $Xin S_{a,c},~Yin S_{c,b}$ , et on a les mêmes relations pour les sommes de Darboux. Pour passer à et , on peut toujours supposer , quitte à l'ajouter, sans perte de généralité. On en déduit le théorème. (Exercice: détailler cette démonstration.)

Définition Pour , on définit

et pour

Remarque Avec ces conventions, la relation de Chasles est valable quel que soit l'ordre de (par exemple aussi pour ). C'est en effet la principale motivation pour ces définitions, ce qui laisse deviner l'utilité et importance de cette relation dans les applications.
Il convient d'être très vigilant concernant cette généralisation lorsqu'on utilise des inégalités (telles que celles de la Prop. ), qui ne sont généralement valables que pour.

Proposition est un sous-espace vectoriel du -espace vectoriel $R^{[a,b]}$ des fonctions de dans , et , est une forme linéaire sur . Autrement dit, et surtout

$displaystyle int_a^bp{a,f(x)+b,g(x)}dx = aint_a^b f(x)dx + bint_a^b g(x)dx ~.$

Démonstration Les sommes de Darboux ne sont pas linéaires (car et ne sont pas additives). Passons donc par les sommes de Riemann, dont la linéarité,, est évidente, ce qui donne, par passage à la limite , le résultat souhaité. (Exercice: détailler ceci...)

Proposition Pour , (), on a:

		(1)
		(2)
et	$displaystyle lrvertvert{int_a^b f(x)dx} le int_a^b vert f(x)vert dx ~.$	(3)

Démonstration (1): et .
(2): .

(3): on a , avec le (2) donc et .

Remarque La réciproque du (1) est évidemment fausse, n'implique pas . (Contre-exemple: sur .)

Remarque Dans le cas , , on a que est l'aire de l'épigraphe

$% latex2html id marker 4180 $displaystyle E = set{, (x,y)inR^2 mid xin[a,b] text{ et } 0le yle f(x) ,} ~. $$

Théorème [de la moyenne] Soit (fonction continue de ). Alors

$% latex2html id marker 4186 $displaystyle exists cin[a,b]:underbrace{ frac1{b-a}int_a^b f(x)dx }_{text{moyenne de $f$ sur $[a,b]$}} = f(c) $$

Démonstration étant continue, on a

D'après l'éq.

$displaystyle f(x_i) le frac1{b-a} int_a^b f(x)dx le f(x_s) ~.$

D'après le thm. des valeurs intermédiaires

appliqué à

(continue) entre

, on a $% latex2html id marker 4202 $ exists cinlr][{x_i,x_s}$$ (ou $lr][{x_s,x_i}$ ) tel que

$displaystyle f(c) = frac1{b-a} int_a^b f(x)dx ~.$

Source : http://www.les-mathematiques.net/a/d/a/node3.php3

Intégrale de Riemann

Le programme ne précise pas si la définition de l'intégrale de Riemann doit figurer dans le cours. Certains collègues commencent ce cours directement avec la définition de la primitive d'une fonction, et Ainsi, le théorème fondamental de l'analyse, qui établit le lien entre l'intégration et la dérivation, devient trivial.

A mon avis, ce cours est quand même l'occasion ou jamais de définir l'intégrale de Riemann. Même si on passe sur les détails, on peut donner les trois définitions de ce premier chapitre et évoquer l'interprétation géométrique qui est très liée à la définition des sommes de Darboux.

Subdivisions et sommes de Darboux

Définition Une subdivision d'ordre d'un intervalle est une partie finie $X={x_0,x_1,dots,x_n}subset[a,b]$ telle que

$displaystyle a=x_0<x_1<dots<x_{n-1}<x_n=b ~.$

On notera $S_{a,b}$ l'ensemble des subdivisions de

Exemple [subdivision équidistante] Lorsque avec $h=frac{b-a}n$ , on parle de la subdivision équidistante d'ordre de ; on la note parfois ${[a,b]}_n$ . Le nombre est le pas (uniforme) de cette subdivision.

Définition La somme de Darboux inférieure resp. supérieure de relativement à une subdivision $X={x_0,dots,x_n}$ sont définies par

$displaystyle s(f,X) := sum_{i=1}^n h_i, inf f(I_i)$ resp. $displaystyle S(f,X) := sum_{i=1}^n h_i, sup f(I_i) ~,$

où $h_i=x_i-x_{i-1}$ est la longueur du

sous-intervalle $I_i=[x_{i-1},x_i]$ .

Les sommes de Darboux sont des réels bien définis ssi la fonction est bornée, .

Sauf mention du contraire, dans tout ce qui suit, les fonctions considérées seront toujours bornées sur l'intervalle en question, sans que celà soit nécessairement dit explicitement.

Remarque Etudier l'interprétation géométrique des sommes de Darboux comme aire des rectangles de base $[x_{i-1},x_i]$ , encadrant l'épigraphe de de en-dessous resp. au-dessus.

includegraphics[width=10.0cm,height=8.0cm]{A1.eps}

Exercice Montrer qu'en ajoutant un point (entre $x_{i-1}$ et ) à , la somme de Darboux inférieure (resp. supérieure) croît (resp. décroît). En déduire qu'on a

$displaystyle forall X,Yin S_{a,b} : Xsubset Y impl s(f,X)le s(f,Y)$ et

Utiliser le résultat précédent et la subdivision

pour montrer que

$displaystyle forall X,Yin S_{a,b} : s(f,X)le S(f,Y) ~.$

Solution

Remarque Lorsque pour $X,Yin S_{a,b}$ , on dit que est plus fine que . (C'est une relation d'ordre partiel sur $S_{a,b}$ .)

Fonctions Riemann-intégrables, intégrale de Riemann

Définition La fonction est Riemann-intégrable sur ssi les deux nombres

$displaystyle s_a^b(f) := sup_{Xin S_{a,b}} s(f,X) ~,~~ S_a^b(f) := inf_{Xin S_{a,b}} S(f,X) ~.$

coïncident ; ce nombre est alors appellé l'intégrale de Riemann de

sur

(ou de

), et noté

.
L'ensemble des fonctions Riemann-intégrables

sur

est noté

Remarque L'existence de et est évidente: il suffit de constater que les ensembles $set{s(f,X);Xin S_{a,b}}$ et $set{S(f,X);Xin S_{a,b}}$ sont non-vides (prendre $set{a,b}in S_{a,b}$ ) et majorés resp. minorés d'après l'exercice précédent. On peut aussi montrer que et sont atteints lorsque le pas de la subdivision, $vert Xvert=maxvert x_i-x_{i-1}vert$ tend vers zéro. La taille de ce pas induit la structure d'une base de filtre sur $S_{a,b}$ , permettant de considérer la limite de et en .

Remarque Revenir sur l'interprétation géométrique de et , en considérant la limite de subdivisions de plus en plus fines.

Remarque La ``variable d'intégration'' dans est une ``variable muette'', elle peut être remplacée par n'importe quelle autre variable (qui n'intervient pas déjà ailleurs dans la même formule).

Donnons encore une propsition d'ordre plutôt technique, avant d'énoncer une condition d'intégrabilité suffisante dans tous les cas que nous allons rencontrer.

Proposition (Critère d'intégrabilité de Riemann.) Une fonction est Riemann-intégrable sur ssi pour tout il existe une subdivision $Xin S_{a,b}$ telle que.

Démonstration Par déf. de et , $% latex2html id marker 3726 $ forallveps>0,~ exists X',X''in S_{a,b}: S(f,X')-S_a^b(f)<veps/2$$ et . Avec , il vient que . Donc si , on a la subdivision souhaitée. Réciproquement, si une telle subdivision existe pour tout , alors et coïncident évidemment.

Théorème Toute fonction monotone ou continue sur un intervalle est Riemann-intégrable.

Démonstration Si est monotone, le et est atteint au bord de chaque sous-intervalle . On a donc $% latex2html id marker 3752 $ S(f,X)-s(f,X)=sum h_i,vert f(x_i)-f(x_{i-1})ve... ...vert sumvert f(x_i)-f(x_{i-1})vert=vert Xvert{text ·}vert f(b)-f(a)vert$$ . Il suffit donc de choisir le pas de la subdivision assez petit, , pour que ceci soit inférieur à un donné, d'où l'intégrabilité d'après le critère de Riemann.
Pour une fonction continue, la démonstration est admise dans le cadre de ce cours. A titre indicatif: $vert f(x_i)-f(x_{i-1})vert$ est à remplacer par $f(xi_i^{sup})-f(xi_i^{inf})$ , où $xi_i^{sup}, xi_i^{inf}$ sont les points de l'intervalle fermé et borné en lesquels la fonction continue atteint son maximum et minimum. On utilise maintenant le fait qu'une fonction continue sur y est uniformément continue, pour donné il existe (indépendant du point ) tel que. Donc, pour , on a . Ceci devient aussi petit que voulu, car on peut prendre des subdivisions équidistantes pour lesquelles , il suffit donc de prendre assez petit.
Pour montrer qu'une fonction continue est uniformément continue sur un intervalle borné , on peut utiliser que l'ensemble des boules ouvertes telles que, est un recouvrement ouvert de , dont on peut extraire un recouvrement fini d'après le théorème de Heine-Borel. Le minimum de ces correspond au de l'uniforme continuité (au pire pour au lieu de ).
(Pour une démonstration du théorème de Heine-Borel, voir ailleurs...)

Corollaire De même, une fonction (bornée!) continue sauf en un nombre fini de points, ou monotone sur chaque sous-intervalle d'une partition finie de , est Riemann-intégrable. (On peut en effet utiliser l'additivité des sommes de Darboux, pour $Xin S_{a,c},~Yin S_{c,b}$ qui entraîne celle de et de même pour .)

Remarque [fonction de Dirichlet] La fonction de Dirichlet,

$displaystyle {chi}_Q(x) = CASES{ 1 & xinQ 0 & xnotinQ}$

n'est pas Riemann-intégrable, car on a

$displaystyle forall Xin S_{a,b}:~ s(f,X)=0 ~,~~ S(f,X)=b-a ~.$

En effet, sur chaque $I=[x_{i-1},x_i]$ il existe un point irrationnel, donc

, mais aussi un point rationnel, d'où

. Ainsi

est somme des longeurs des sous-intervalles et donc égale à

Remarque Le pas uniforme des subdivisions équidistantes simplifie beaucoup l'expression des sommes de Darboux (exercice!).
On peut montrer que pour , on a

$displaystyle = lim_{ntoinfty} s(f,[a,b]_n) = lim_{ntoinfty} S(f,[a,b]_n)$

La réciproque est vraie si

est continue.

Sommes de Riemann

Les sommes de Darboux ne sont pas très utiles pour le calcul effectif d'une intégrale, par exemple à l'aide d'un ordinateur, car il est en général assez difficile de trouver les inf et sup sur les sous-intervalles. On considère plutôt

$displaystyle s_n(f)=SUM i1n (x_i-x_{i-1}), f(x_{i-1})$ ou $displaystyle S_n(f)=SUM i1n (x_i-x_{i-1}), f(x_i) ~.$

Plus généralement:

Définition Si vérifie $forall iinset{1,...,n}, xi_iin[x_{i-1},x_i]$ , on appelle une subdivision pointée et

$displaystyle S(f,X,xi)=SUM i1n (x_i-x_{i-1}), f(xi_i)$

la somme de Riemann associée à la subdivision pointée

. Si on pose de plus $Delta x_i=x_i-x_{i-1}$ , on a

c'est de là que vient la notation

Théorème Si , alors les sommes de Riemann tendent vers , independamment du choix des , lorsque la subdivision devient de plus en plus fine.

Démonstration Par définition, il est évident que . Soit et tel que . Alors on a aussi, quel que soit le choix des , et a fortiori pour tout . D'où le résultat.

Si est continue, atteint son minimum et maximum sur chaque $[x_{i_1},x_i]$ en un certain $xi_i^{min}$ et $xi_i^{max}$ . On obtient donc les sommes de Darboux comme cas particulier des sommes de Riemann, en associant à chaque des points $xi^{min},~xi^{max}$ tels que $s(f,X)=S(f,X,xi^{min}),~ S(f,X)=S(f,X,xi^{max})$ .

En particulier, lorsque la fonction est monotone, par exemple croissante, sur un sous-intervalle , alors $xi_i^{min}=x_{i-1}$ et $xi_i^{max}=x_i$ . Les sommes de Riemann et données en début de ce paragraphe coïncident donc avec les sommes de Darboux inférieure et supérieure pour une fonction croissante.

Source : http://www.les-mathematiques.net/a/d/a/node2.php3#SECTION...

05/01/2010

Cours de 6ème - quadrilatère

Quadrilatère

1°) Le losange :

Définition
Un losange est un quadrilatère qui a quatre côtés égaux .
Exemple :
Construire un losange ABCD tel AB= 3 cm
Propriété :
Les côtés opposés d'un losange sont parallèles .
Les diagonales d'un losange sont perpendiculaires et se coupent en leur milieu .
Exemple :
Construire un losange ABCD tel que AC = 5 cm .

2°) Le rectangle :
Définition :
Un rectangle est un quadrilatère qui a trois angles droits .
Exemple 1:
Construire un rectangle MNPQ tel que MN = 5 cm et NP = 4 cm .
Exemple 2 :
Construire un rectangle ABCD tel que AB = 4 cm et AC = 7 cm .

Propriétés :
Deux côtés opposés du rectangle sont parallèles et ont la même longueur .
Les diagonales d'un rectangle ont la même longueur et se coupent en leur milieu .

3°) Le carré :
Définition :
Un carré est à la fois un rectangle et un losange .
Exemple :
Construire un carré ABCD dans les cas suivant :
a) AB = 4 cm .
b) BD = 5 cm .

Source : http://194.2.124.18/monbru/index.html

Cours de 6ème - Repérage dans le plan

Repérages dans le plan

Définitions et exemples :

Le point A a pour abscisse + 2
Le point A a pour ordonnée + 3

+2 et + 3 sont les coordonnées du point ,
on dira que A a pour coordonnées ,
et on notera : A ( 2 ; 3 )

Les coordonnées des autres points sont :

B (4,2) ;C(-4,4) ;D(-1,3);

E(-2,-2) et F(-3,-4)

Source : http://194.2.124.18/monbru/index.html

Cours de 6ème - Les nombres décimaux

Les nombres décimaux

DEFINITION
Un nombre décimal comporte une virgule . La partie entière est située à gauche
de la virgule . La partie décimale est située à droite de la virgule .

Exemple :

1	,	3	4	6	5
Unités		Dixièmes	Centièmes	Millièmes	Dix-millièmes

1,3465 peut se lire une unité trois dixièmes quatre centièmes six millièmes et cinq dix-millièmes

Remarque : Convention d'écriture :
On supprime les zéros inutiles .
Exemple :
0 , 750 = 750 millièmes = 75 centièmes = 0 , 75

Source : http://194.2.124.18/monbru/index.html

Cours de 6ème - Triangle

Triangle

Définition :

a) Triangle isocèle

Un triangle isocèle est un triangle qui a deux côtés égaux.

b) Triangle équilatéral
·
Un triangle équilatéral est un triangle qui a ses trois côtés égaux.

c) Triangle rectangle
·
Un triangle rectangle est un triangle qui a un angle droit.

Source : http://194.2.124.18/monbru/index.html

Cours de 6ème - Symétrie Axiale

Symétrie Axiale

Figures symétriques:

Définition :

Deux figures symétriques par rapport à une droite d sont superposables par
pliage autour de la droite d.

Les figures ABCDE et A'B'C'D'E' sont symétriques par rapport à la droite d.
Cette droite d est appelée axe de symétrie

Propriété :
Deux figures symétriques ont les mêmes dimensions (longueurs, angles, aires).

Définition :

Une figure possède un axe de symétrie, si elle est sa propre symétrique dans la symétrie par rapport à cet axe.

La figure posséde un axe de symétrie . (axe en pointillé )

Points symétriques:

Définition :

Deux points A et A' sont symétriques par rapport à une droite (d) signifie que (d) est la médiatrice du segment [AA'].

(d) est la médiatrice du segment [AA'].
I est le milieu de [AA'].

Propriété :

Un point situé sur l'axe de symétrie (d) sera son propre symétrique.

Propriété :

La symétrie axiale conserve les longueurs : le symétrique d'un segment par rapport à une droite est un segment de même longueur ; et les angles :le symétrique d'un angle par rapport à une droite est un angle de même mesure.

Source : http://194.2.124.18/monbru/index.html

Cours de 6ème - Fractions

Fractions

Définitions

est une écriture fractionnaire du quotient de a par b.

a est le numérateur.
b est le dénominateur.
Lorsque le numérateur et le dénominateur sont des nombres entiers, l'écriture fractionnaire est appelée fraction.

Fractions égales
On ne change pas un nombre en écriture fractionnaire en multipliant ou en divisant son numérateur et son dénominateur par un même nombre non nul .

Soient a , b et k trois entiers , alors :

Multiplier un nombre à une fraction :

Pour multiplier un nombre à une fraction , on mutiplie ce nombre au numérateur ensuite on divise le résultat obtenu par le dénominateur .

Source :
http://194.2.124.18/monbru/index.html

Cours de 6ème - Droites parallèles et droites perpendiculaires :

Droites parallèles et droites perpendiculaires :

Définitions .

Deux droites sécantes sont deux droites qui ont un ( seul ) point commun. Sinon, elles sont parallèles. (d) et (d') sont deux droites parallèles .

Deux droites perpendiculaires sont deux droites ( sécantes ) qui forment un angle droit. (d) et (d') sont deux droites perpendiculaires .
Propriétés .

Si deux droites sont perpendiculaires à une même troisième, alors elles sont parallèles
. Les droites (d) et (d') sont perpendiculaires à la droite (d1), alors les droites (d) et (d') sont parallèles .

Si deux droites sont parallèles et si une troisième est perpendiculaire à l'une, alors elle est perpendiculaire à l'autre . Les droites (d) et (d') sont parallèles ,la droite (d1)est perpendiculaire à la droite (d) , alors les droites (d1) et (d') sont perpendiculaires .

Si deux droites sont parallèles à une même troisième, alors elles sont parallèles.

Les droites (d1) et (d2) sont parallèles à la droite (d3) , alors (d1) et (d2) sont parallèles.

source : http://194.2.124.18/monbru/index.html

Fractal Zoom Mandelbrot Corner

Vidéo

03/01/2010

Quelques informations sur les fractales

Retour à la page de présentation

Avertissement : la lecture de cette page est inutile si les fractales vous sont familières. Elle est fortement déconseillée aux mathématiciens, à moins qu’ils soient très indulgents pour l’aspect élémentaire et les approximations de ces explications.

Euclide et les fractales
	Euclide aurait certainement horrifié s’il avait connu les fractales, comme l’ont été beaucoup de ses successeurs, beaucoup plus proches de nous, qui ne voyaient là que des monstres mathématiques dont il convenait de se détourner ! Et pourtant... On obtient une image fractale en partant d’un objet graphique auquel on applique une certaine transformation qui ajoute un élément de complexité, puis en appliquant la même transformation au nouvel objet ainsi obtenu, ce qui accroît encore sa complexité... et en recommençant à l’infini ce processus d’itération. Bien entendu toutes les itérations n’engendrent pas des fractales. Prenons un segment de droite et effaçons-en une moitié, puis appliquons au demi-segment résultant la même opération : il est évident que pour un nombre d’itérations infini la figure tend vers un point. Rien de très passionnant. Si en revanche on prélève à ce segment son 1/3 central, puis qu’à chacun des deux segments résultants on enlève à nouveau leur 1/3 central, etc. on tend vers une figure, certes peu spectaculaire, mais dotée de propriétés mathématiques curieuses : la poussière de Cantor.

	En effet, imaginons qu’on « zoome » dans cette figure avec une loupe puis un microscope à des grossissements de plus en plus puissants. Quel que soit le grossissement on observera la même structure. On sera donc incapable, sur un détail, de décider quel est le grossissement auquel la poussière de Cantor aura été observée (dans l’illustration ci-dessus la résolution de l’écran limite l’observation des plus fins détails). Première propriété d’une image fractale : l’auto-similarité, ou invariance d’échelle.

	Légèrement plus spectaculaire est l’exemple de la « courbe » ou « flocon » de Koch. Cette « courbe » s’obtient en appliquant à chaque côté d’un triangle équilatéral une transformation un peu différente : on remplace le 1/3 central de chaque côté par 2 segments ayant la même longueur que celle qui a été prélevée. À la première itération on obtient une image proche d’une étoile de David, puis au fur et à mesure des itérations successives le résultat mime plus ou moins un flocon de neige. Là encore, à quelque grossissement qu’on examine la « courbe » on observera les mêmes détails... pour autant que le nombre d’itérations soit infini (ou, au moins, assez important).

	Ce type de courbe présente une particularité bien curieuse. La première intuition conduit à penser que, puisqu’on ajoute des détails de plus en plus petits au fur et à mesure des itérations successives, le périmètre de cette figure tend vers une valeur limite finie. En réalité, à la première itération la longueur l de chaque côté est remplacée par 4 l / 3 ; à la deuxième elle devient 16 l / 9... Autrement dit, à chaque itération la longueur est multipliée par 4 / 3, ce qui signifie que (contrairement à l’intuition première) la longueur d’une courbe de Koch tend vers l’infini pour un nombre d’itérations infini. Et pourtant cette courbe ne déborde à aucun moment des limites constituées à l’extérieur par le cercle circonscrit au triangle initial, et à l’intérieur par le cercle inscrit dans ce triangle ! Une autre propriété encore moins intuitive est relative à la dimension des objets fractals. Nous savons tous qu’un point est une figure de dimension 0 ; qu’une ligne droite est un objet de dimension 1 ; qu’une surface plane est un objet de dimension 2 ; qu’un volume est de dimension 3... qu’en est-il d’un objet fractal ? Il existe plusieurs méthodes mathématiques pour exprimer la dimension d’un objet. Sans entrer dans les détails on peut penser qu’un objet bizarre comme la courbe de Koch, qui a une longueur infinie tout en n’emplissant qu’une région très limitée du plan, doit avoir des propriétés très particulières. En fait on peut démontrer que sa dimension est égale à *log 4 / log 3. Presque tous les objets fractals ont des dimensions non entières.* Ceci est encore moins intuitif qu’une longueur infinie.

Les nombres complexes et les fractales
	Il existe toute une série d’objets fractals curieux qu’il est possible de construire à partir d’opérations simples de la géométrie euclidienne, comme les précédents (l’image en tête de page est une variante du tamis de Sierpinski, après 4 itérations). Certains sont des figures planes, d’autres déploient leur structure dans l’espace. Mais si l’on applique le procédé d’itération à des formules même très simples, utilisant lesnombres complexes, on entre dans un monde fabuleux de formes étranges et d’une beauté parfois étonnante. Rappelons qu’un nombre complexe a la structure générale suivante :
	z = x + yi
	où x et y sont des nombres réels et i est la racine carrée de -1 (opération qui était jugée impossible par les mathématiques anciennes, puisqu’avec les nombres réels un carré est toujours positif). x est la partie réelle du nombre et y est la partie imaginaire. On peut se demander comment on peut représenter graphiquement un fonction utilisant des nombres complexes puisqu’il n’est pas possible d’associer une image mentale concrète à un nombre aussi étrange que la racine carrée de -1. Le principe qui guide la réalisation de la plupart de ces images sur un ordinateur est en réalité très simple. Quand on gradue un axe de coordonnées on peut donner à chaque division de l’axe une valeur unité conventionnelle quelconque. Si l’on dit que la valeur qu’une division vaut i on aura d’un côté de l’origine la représentation des nombres i, 2i, 3i... et de l’autre côté -i, -2i, -3i... l’axe des x représente la partie réelle du résultat du calcul ; l’axe des y représente la partie imaginaire, et la luminosité ou la couleur de chaque point est fonction du nombre d’itérations nécessaires pour que le résultat réponde à une condition donnée. Prenons une expression aussi simple que

	c est un nombre complexe quelconque fixé au départ. On fait le calcul pour chacun des points z du plan complexe (chaque point a une coordonnée x réelle et une coordonnée y imaginaire). Seulement, petit détail, au lieu de faire le calcul une seule fois pour chaque point, on recommence en donnant à z la valeur z' trouvée dans le calcul précédent et l’on recommence encore en donnant à z la valeur z' trouvée par ce nouveau calcul... En bref on effectue un nombre d’itérations théoriquement infini lors du calcul de chacun des points, ce qui peut s’écrire

	en partant d’une valeur initiale z₍₀₎ égale aux coordonnées de chaque point du plan complexe. Il est intéressant de voir vers quelle valeur tend cette fonction pour chacun des points du plan complexe. On s’aperçoit que pour beaucoup de points (c’est-à-dire de valeurs initiales de z) la fonction diverge plus ou moins rapidement (la valeur de z' s’écarte de plus en plus de la valeur initiale). Au contraire pour certains points le résultat reste définitivement enfermé dans un intervalle limité : la fonction ne diverge pas, même pour un nombre infini d’itérations. l’ensemble des points pour lesquels la fonction ne diverge pas forme un ensemble appelé ensemble de Julia rempli (la zone noire au centre de la figure ; l’ensemble de Julia stricto sensu est la frontière de cette zone). Bien entendu il existe un nombre infini d’ensembles de Julia, puisqu’on peut donner à c n’importe quelle valeur. Selon la valeur de c l’ensemble de Julia peut dessiner des figures très banales ou, au contraire, des images extraordinairement complexes et souvent très esthétiques. Point fondamental ces ensembles de Julia sont des structures fractales.
	partie réelle de c = -0.0519... partie imaginaire = 0.688...
	Dans certains cas l’ensemble de Julia est continu (ou, plus rigoureusement, connexe) comme ci-dessus, mais dans d’autres il est fragmenté (non connexe) comme ci-dessous.
	partie réelle de c = -0.577... partie imaginaire = 0.478...
	Les points pour lesquels la valeur de z diverge ne font pas partie de l’ensemble de Julia rempli : ils sont situés à l’extérieur. Mais on peut obtenir des informations complémentaires en leur affectant une luminosité ou une couleur fonction du nombre d’itérations nécessaires pour observer la divergence. En d’autres termes cette couleur est une mesure de la vitesse avec laquelle la fonction diverge pour ce point. Autour de l’ensemble proprement dit, coloré en noir ici, on observe une série d’auréoles dessinant des figures parfois très intéressantes (voir ci-dessus et ci-dessous).
	Détail d’un ensemble de Julia (x 14.57)
	Si, au lieu de donner une valeur fixe et arbitraire à c on lui affecte pour tout point du plan complexe une valeur initiale c = z₍₀₎, on obtient un objet mathématique plus complexe appelé ensemble de Mandelbrot. l’ensemble de Mandelbrot est, là encore, l’objet noir au centre de l’image.
	Remarque : contrairement aux apparences l’ensemble de Mandelbrot est connexe, mais certains détails sont si ténus qu’ils ne sont pas visibles à la résolution de l’écran.
	Si l’explication précédente ne vous a pas parue claire, en voici une autre, strictement équivalente. Au lieu de calculer la fonction en donnant une valeur constante et arbitraire à c, considérons c comme une variable à laquelle nous attribuerons successivement les valeurs correspondant aux différents points du plan complexe (heureusement sur un écran d’ordinateur le nombre de points à calculer est limité par le nombre de pixels affichés). Pour chacune de ces valeurs itérons la fonction en partant de la valeurz₍₀₎=(0,0) et colorons chaque point c en utilisant la même recette que pour les ensembles de Julia. Nous obtenons l’ensemble de Mandelbrot. Pourquoi les deux explications sont-elles équivalentes ? Parce qu’à la première itération la valeur de z étant nulle, la valeur de z₍₁₎ est égale à0+c, c’est-à-dire c. Relisez maintenant la première explication et choisissez celle que vous préférez. Bien entendu, s’il y a une infinité d’ensembles de Julia, il n’existe qu’un seul ensemble de Mandelbrot pour la fonction

	Il y a, évidemment, une relation entre cet ensemble et les ensembles de Julia : l’ensemble de Mandelbrot est l’ensemble de tous les points cpour lesquels l’ensemble de Julia correspondant est connexe. Autrement dit, quand on prend pour c une valeur en dehors de la surface noire on obtient un ensemble de Julia « brisé ». Les ensembles de Mandelbrot et de Julia sont des objets fractals et en zoomant sur leur bordure on peut y voir, quel que soit le grossissement, des structures toujours aussi complexes et auto-similaires. c’est ainsi que l’ensemble de Mandelbrot possède à sa périphérie une multitude de ramifications qui se dilatent localement en mini-ensembles de Mandelbrot qui, à leur tour... Tous ces détails sont auto-similaires, ce qui ne veut pas dire qu’ils soient rigoureusement identiques entre eux (contrairement aux fractales plus vues plus haut, engendrées par des opérations géométriques simples). La série d’image suivante montre des grossissements de plus en plus forts révélant des mini-ensembles de Mandelbrot à la périphérie de l’ensemble central. Toutes les images, sauf la dernière, ont été traitées en niveau de bleu pour simplifier la reconnaissance des formes. Dans chacune un petit rectangle montre les limites de l’image suivante. En cliquant sur chaque image on visualise une image de taille 800x600. Le facteur d’agrandissement entre la première et la dernière image de la série est de 3 200 000 fois.
	Toutes les images peuvent être vues au format 800x600
	La fonction qui engendre les ensembles de Julia et de Mandelbrot est l’exemple le plus simple qu’on puisse trouver. Pourtant l’ensemble de Mandelbrot est considéré par certains comme l’objet mathématique le plus complexe connu. Toutes ses propriétés n’ont d’ailleurs pas encore été démontrées. On a pu établir que la dimension de sa bordure est 2, ce qui est la plus grande dimension fractale possible pour une structure de surface nulle (mais curieusement on n’a pas encore démontré que cette surface est nulle, bien que ceci paraisse intuitivement évident :Douady, communication personnelle ; 1996). Beaucoup d’amateurs d’images fractales utilisent d’autres fonctions. Certaines ne sont que des modifications plus ou moins complexes des formules de Julia et Mandelbrot ; d’autres sont totalement différentes. Le programme Fractint et d’autres programmes plus récents permettent de tester sans problème pratiquement toutes les fonctions nouvelles qu’on peut imaginer. Il reste un dernier détail : *comment tester si la fonction diverge pour un point donné du plan complexe ?* Je me limiterai encore aux ensembles de Julia et de Mandelbrot, mais le principe est applicable à beaucoup d’autres fonctions. Il consiste à vérifier que le module de zreste inférieur ou égal à une valeur de référence qui, pour les deux ensembles choisis comme exemple, est 2 (sur ce point nous ferons confiance aux mathématiciens). c’est la « valeur d’échappement » (bailout value en anglais). Le module d’un nombre complexe est une astuce mathématique parfaitement légitime pour se débarasser de i et retomber dans le domaine rassurant des nombres réels (au prix toutefois d’une certaine perte d’information). Si on appelle x la partie réelle et y la partie imaginaire d’un nombre complexe, le module est

	(remarquez que pour la vitesse du calcul il est plus facile de vérifier que le carré du module est <= 4, astuce utilisée par Fractint).

	Informations théoriques sur d’autres serveurs.
	Retour à la page de présentation
	Mon album de fractales
	Dernière mise à jour : 02/10/03 Source : http://fractals.iut.u-bordeaux1.fr/jpl/jpl1.html

Cours de tests paramétriques

Descriptif du cours

Auteurs :	Peggy Cénac, Florence Muri-Majoube
Domaine :	Mathématiques :: Statistique
Niveau :	Licence	Langue :	Français

Description :	Ce cours introduit les concepts nécessaires pour développer et appliquer les tests paramétriques.
Prérequis :
Mots clefs :	test ; paramétrique ; comparaison ; moyenne ; variance ; intervalle ; de ; confiance ; niveau ; puissance
Commentaire :

Documents associés

Cours de tests paramétriques

Par Peggy Cénac, Florence Muri-Majoube
Ce cours introduit les concepts nécessaires pour développer et appliquer les tests paramétriques.
Date d'envoi : 01-Jul-2007 17:21

Source : http://www.librecours.org/cgi-bin/course?callback=info&am...

La théorie des groupes et résolutions des équations algébriques

Descriptif du cours

Auteurs :	Serge Hublau
Domaine :	Mathématiques :: Histoire des mathématiques
Niveau :	Licence	Langue :	Français

Description :	Vulgarisation de la théorie des groupes, de la théorie de Galois et de leurs applications à la résolution par radicaux des équations polynomiales insistant sur l'aspect historique des fondements de la théorie de Galois
Prérequis :
Mots clefs :
Commentaire :

Documents associés

La théorie des groupes et résolutions des équations algébriques

Par Serge Hublau
Vulgarisation de la théorie des groupes, de la théorie de Galois et de leurs applications à la résolution par radicau...

Date d'envoi : 07-Dec-2004 17:04

PDF (2.20Mo)
PS (3.19Mo)

Tables des matières

Du nombre au groupe
Théorie des groupes
Groupes, anneaux, corps et morphismes
Groupes cycliques
Groupes diédraux
Groupes de permutations
Les homomorphismes de Sn vers Sn-1
Vers une classification des groupes
Les groupes et la géométrie
La résolution des équations algébriques
Le mémoire de Lagrange
Disquisitiones Arithmetica de Gauss
Les mémoires d'Abel
Les écrits mathématiques de Galois
La théorie de Galois à travers des exemples
Le groupe de Galois, vu comme un critère pour déterminer la résolubilité des équations par radicaux
Annexes
Bibliographie

Source : http://www.librecours.org/cgi-bin/course?callback=info&am...

L'histoire des logarithmes

Descriptif du cours

Auteurs :	Simon Trompler
Domaine :	Mathématiques :: Histoire des mathématiques
Niveau :	Licence	Langue :	Français

Description :	Les logarithmes: histoire de leur développement.
Prérequis :
Mots clefs :	histoire ; logarithme ; log
Commentaire :

Documents associés

L'histoire des logarithmes

Par Simon Trompler
Les logarithmes: histoire de leur développement.

Date d'envoi : 12-Jan-2004 14:45

PDF (265.25ko)
PS (768.18ko)

Tables des matières

Première partie: Les logarithmes. Histoire de leur développement
1. Avant Neper
2. John Napier ou Neper (1550-1617)
3. Aprés Neper
4. Les logarithmes et les courbes
5. Les logarithmes et le calcul infinitésimal
6. Les logarithmes des nombres négatifs et des imaginaires
7. l'oeuvre d'Euler
Deuxième partie: Compléments:
1. La période mésopotamienne
2. Archimède: l'Arénaire
3. John Napier (Neper)
4. L'appendiceau "constructio" de Napier
5. Les logarithmes de Huygens
6. La spirale géométrique
7. Mengoli
8. Correspondance entre Leibnitz et Bernouilli
9. Euler

Source : http://www.librecours.org/cgi-bin/course?callback=info&am...

Preuves formelles en Coq

par Loïc Pottier

Niveau : Master Langue : Français

Description :

Cours d'option en DEA de mathématiques, université de Nice-Sophia Antipolis, janvier 2003. Ce cours est inspiré du cours de DEA de Gilles Dowek, et du cours de DEA de Christine Paulin-Mohring et Benjamin Werner (DEA de programmation SPL, Paris).

Télécharger :

PDF (690.34ko)
PS (158.35ko)

Detail du cours

Tables des matières

Le langage de Coq
Les objets et la syntaxe
Les types
Les sortes
Les fonctions
Les formules logiques, leurs preuves, et l'isomorphisme de Curry-Howard
Le typage
Règles de typage informelles
Les règles du typage
Les contextes
Les jugements de typage
Les règles
Exemples
Quelques remarques sur les règles de typage des produits
Le calcul
La beta-réduction
La consistance
Logique intuitionniste et mathématiques constructives
Les définitions et la delta-réduction
La conversion
Exemple : les codages imprédicatifs
Les types inductifs
Exemples
Les entiers naturels
L'égalité de Leibniz
Raisonnement et calcul par cas : la construction Cases
La iota-réduction
Fonctions récursives : la construction Fix
Un exemple
Un exemple de récursion mutuelle
Le cas général
La iota-réduction, bis
Typage de Cases et Fix
Introduction au système Coq
Commandes élémentaires
Lancer coq depuis un shell
Obtenir le type d'un terme
Définir une constante
Obtenir la valeur d'une constante
Calculer
Fonctions récursives
Démontrer
pour tout A, A implique A
pour tout A, A implique non non A
Calcul des propositions
Calcul des prédicats
Exemples mathématiques
L'ensemble des parties est plus gros que l'ensemble

Source : http://www.librecours.org/cgi-bin/course?callback=info&am...

Modérateurs

Dimitri Ara, Romain Théret
Contact : logique AT librecours.org

Source : http://www.librecours.org/cgi-bin/domain?callback=info&am...

$displaystyle {frac{{-x+1}}{{x^2+1}}}$	=	- $displaystyle {frac{{1}}{{2}}}$ $displaystyle {frac{{(x^2+1)'}}{{x^2+1}}}$ + $displaystyle {frac{{1}}{{x^2+1}}}$ + $displaystyle {frac{{x^2-x+1}}{{x^3-1}}}$
	=	- $displaystyle {frac{{1}}{{2}}}$ ln(x² +1) + arctan(x) + $displaystyle {frac{{x^2-x+1}}{{x^3-1}}}$

Cours, définitions, Vidéos, théorèmes, exercices, corrigés, livres sur les mathématiques, Livres Rares, Livres anciens de mathématiques

Recherchez sur le site (cours, livres, Agregation, etc.)

Liens utiles

Rechercher

Liens mathématiques divers

Livres en pdf

Cours

Documents Mathématiques

Décembre 2024

Notes récentes

Archives

Catégories

Derniers weblogs mis à jour

Liens Sites Amis

21/01/2010

Arithmétique des polynomes: Bézout et applications

08/01/2010

Entre figures et espaces : le cas des diagrammes en géométrie finie

Entre figures et espaces : le cas des diagrammes en géométrie finie

Introduction

1- Préalable mathématique

2- Le concept de configuration : de Reye à Moore [8]

3- L’émergence des espaces finis

Conclusion

Notes

INITIATION AUX MATHÉMATIQUES FINANCIÈRES

INITIATION AUX MATHÉMATIQUES FINANCIÈRES

Mathématiques Financières : l’essentiel

06/01/2010

Construction de Z à partir de N

Propriétés de l'intégrale de Riemann

Intégrale de Riemann

05/01/2010

Cours de 6ème - quadrilatère

Cours de 6ème - Repérage dans le plan

Cours de 6ème - Les nombres décimaux

Cours de 6ème - Triangle

Cours de 6ème - Symétrie Axiale

Cours de 6ème - Fractions

Cours de 6ème - Droites parallèles et droites perpendiculaires :

Fractal Zoom Mandelbrot Corner

03/01/2010

Quelques informations sur les fractales

Quelques informations sur les fractales

Euclide et les fractales

Les nombres complexes et les fractales

Cours de tests paramétriques

Cours de tests paramétriques

Descriptif du cours

Documents associés

La théorie des groupes et résolutions des équations algébriques

La théorie des groupes et résolutions des équations algébriques

Descriptif du cours

Documents associés

Tables des matières

L'histoire des logarithmes

L'histoire des logarithmes

Descriptif du cours

Documents associés

Tables des matières

Preuves formelles en Coq

Description :

Télécharger :

Tables des matières

Modérateurs