21/11/2010
Triangle rectangle
Source : http://fr.wikipedia.org/wiki/Triangle_rectangle
Triangle rectangle
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Logique |
| Arithmétique |
| Probabilités |
| Statistiques |
Un triangle rectangle est un triangle dont l'un des angles est droit. On nomme alors hypoténuse le côté opposé à l'angle droit. De plus, on appellecathète chaque côté adjacent à l'angle droit.
Sommaire[masquer] |
Intérêt [modifier]
La connaissance des triangles rectangles et de leurs relations métriques permettent de travailler sur de nombreux problèmes. Par exemple :
- on peut décomposer tout triangle en deux triangles rectangles ;
- dans un repère orthonormé
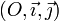 , si un point M se projette selon H sur l'axe
, si un point M se projette selon H sur l'axe 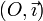 et selon I sur l'axe
et selon I sur l'axe 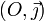 , alors OHM et OMI sont des triangles rectangles ;
, alors OHM et OMI sont des triangles rectangles ; - d'un point de vue vectoriel, un vecteur
 se décompose selon
se décompose selon
les vecteurs forment un triangle rectangle ;
forment un triangle rectangle ; - de manière générale, la trigonométrie concerne les relations dans le triangle rectangle.
Principales propriétés [modifier]
Aire [modifier]
Comme pour tout triangle, pour calculer l'aire d'un triangle rectangle, on multiplie base et hauteur correspondantes, et on divise le tout par deux. Si ABC est rectangle en A, chacun des côtés AB et AC peut être considéré comme une hauteur, la base étant alors l'autre côté de l'angle droit (AC et AB respectivement). L'aire "S" du triangle est donc égale à S = (AB * AC) / 2.
Par exemple, on a un triangle rectangle en A avec AB = 4cm, AC = 3cm, et l'hypoténuse BC = 5 cm. On a S = (4 * 3) / 2 = 6, donc l'aire du triangle rectangle est de 6cm².
Remarque : On pourrait bien sûr utiliser aussi le troisième côté, l'hypoténuse BC, comme base, et trouver le même résultat, mais la hauteur associée à BC devrait être calculée, elle n'est pas directement un côté.
Théorème de Pythagore [modifier]
Le Théorème de Pythagore précise que :
si un triangle ABC est rectangle en A, alors le carré de l'hypoténuse est égal à la somme des carrés des côtés adjacents, soit : BC2 = AC2 + AB2 Réciproquement, tout triangle ABC vérifiant l'égalité précédente est un triangle rectangle en A.
Ce théorème est une conséquence de la définition de la distance entre deux points à partir du carré scalaire de leur vecteur. En effet
puisque 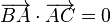 car les vecteurs
car les vecteurs  et
et 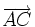 sont orthogonaux.
sont orthogonaux.
Voir l'article Théorème de Pythagore pour d'autres démonstrations.
Théorème de la médiane [modifier]
Pour un triangle rectangle, le théorème de la médiane s'énonce ainsi
si M est le milieu de l'hypoténuse, alors AM=½BC. On peut également dire que le point A est situé sur le cercle de diamètre [BC]. Réciproquement, si A est un point quelconque du cercle de diamètre [BC] alors le triangle ABC est rectangle en A
Il existe plusieurs démonstrations de ce théorème. Le sens direct peut se montrer de manière purement géométrique : par définition M est le milieu de [BC]. Le triangle rectangle ABC est un demi-rectangle ABCD. Un rectangle est un parallélogramme, donc ses diagonales se coupent en leur milieu, donc M, milieu de [BC], est aussi celui de [AD]. Les diagonales d'un rectangle sont de longueur égales, donc AD = BC et AM = AD / 2 = BC / 2 .
On peut aussi faire appel aux vecteurs :
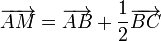 et
et  , d'où :
, d'où :  ,
,
Ces deux derniers vecteurs sont orthogonaux, donc : AM² = (AB² + AC²)/4
D'autre part, en appliquant le théorème de Pythagore au triangle ABC, on obtient : BC² = AB² + AC². Et finalement : AM = BC / 2
On peut également appliquer le théorème de l'angle au centre, qui permet en outre de démontrer la réciproque. Considérons le cercle circonscrit au triangle ABC et notons O son centre. D'après le théorème de l'angle au centre l'angle BOC est le double de l'angle BAC. Donc
Ainsi les points B, O et C sont alignés. Comme de plus BO=OC on voit que O est le milieu de [BC] donc O=M.
Réciproquement, si on sait que A est un point du cercle de diamètre [BC]. D'après le théorème de l'angle au centre, l'angle BAC est la moitié de l'angle BOC, donc il vaut π/2. Ainsi le triangle BAC est rectangle en A.
Ce théorème se généralise dans un triangle quelconque. Voir à ce propos l'article théorème de la médiane.
Centre de gravité [modifier]
Avec les notations précédentes (ABC rectangle en A et M le milieu de [BC]) : le centre de gravité G vérifie
(voir Triangle > Médianes et centre de gravité), et M se projette aux milieux de [AB] et de [AC] (ABM et ACM sont des triangles isocèles). Le point G se projette donc au tiers de [AB] et de [AC] :
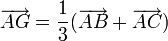 .
.
Autres propriétés [modifier]
Pour tout nombre entier n supérieur ou égal à 3, on peut toujours trouver un triangle rectangle dont la longueur d'un côté de l'angle droit est n et la longueur des deux autres côtés sont des nombres entiers. En effet :
- Si n est un nombre pair, n = 2k
Il suffit de prendre la longueur de l'autre côté de l'angle droit égal à k2 - 1. Le théorème de Pythagore nous donne alors une hypoténuse de longueur égale à k2+1. - Si n est un nombre impair, n = 2k + 1
Il suffit de prendre la longueur de l'autre côté de l'angle droit égal à 2k2 + 2k. Le théorème de Pythagore nous donne alors une hypoténuse de longueur égale à 2k2 + 2k + 1.
Voir aussi [modifier]
Articles connexes [modifier]
10:08 Publié dans Triangle rectangle | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook









































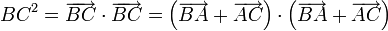
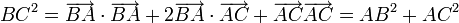



Les commentaires sont fermés.