21/11/2010
Théorème des quatre carrés de Lagrange
Source : http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_des_quatr...
Théorème des quatre carrés de Lagrange
Le théorème des quatre carrés de Lagrange, est également connu sous le nom de conjecture de Bachet ; il a été énoncé pour la première fois par Claude-Gaspard Bachet de Méziriac en 1621, dans les notes accompagnant sa traduction en latin du Diophante. C'est un cas particulier du Problème de Waring. Démontré en 1770 par le mathématicien françaisJoseph Louis Lagrange, il correspond à une équation diophantienne qui se résout avec les techniques de l'arithmétique modulaire. Il s'énonce de la façon suivante :
Plus formellement, pour tout entier positif n, il existe des entiers positifs a, b, c, d tels que :
Le mathématicien français Adrien-Marie Legendre améliora le théorème en 1798 en affirmant qu'un entier positif peut être exprimé comme la somme d'au plus trois carrés si et seulement s'il n'est pas de la forme
 .
.
Sa démonstration était incomplète, laissant une brèche qui fut comblée plus tard par le mathématicien allemand Carl Friedrich Gauss.
Le théorème des quatre carrés de Lagrange est un cas particulier du théorème du nombre polygonal de Fermat (en) et du problème de Waring.
La démonstration du théorème repose (en partie) sur l'identité des quatre carrés d'Euler :
Sommaire[masquer] |
Démonstration basée sur les quaternions d'Hurwitz [modifier]
Nous allons travailler sur l'ensemble des quaternions d'Hurwitz, également appelés entiers d'Hurwitz, qui sont des quaternions particuliers.
Quelques propriétés [modifier]
Les entiers d’Hurwitz [modifier]
Les entiers d’Hurwitz sont les nombres de la forme : a.(1 + i + j + k) / 2 + b.i + c.j + d.k avec  . Avec h = (1 + i + j + k) / 2, on peut écrire l’ensemble des entiers d’Hurwitz sous la forme
. Avec h = (1 + i + j + k) / 2, on peut écrire l’ensemble des entiers d’Hurwitz sous la forme ![mathbb{Z} [h,i,j,k]](http://upload.wikimedia.org/math/8/4/0/840ef30ae2eae5cbde635ada3b76039c.png)
On a alors la somme et le produit des deux entiers d’Hurwitz est un entier d’Hurwitz (les entiers d'Hurwitz forment un sous anneau de l'anneau formé par l'ensemble des quaternions, l'addition et la multiplication usuelles).
On rappelle que la norme d’un quaternion (et donc d’un entier d’Hurwitz) de la forme α = a + b.i + c.j + d.k est 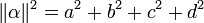
Il existe donc 24 nombres unités : 8 formés par 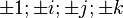 et 16 formés par
et 16 formés par 
Identité des quatre carrés d’Euler [modifier]
On démontre que si deux nombres s’écrivent sous forme de somme de quatre carrés, alors leur produit s’écrit aussi sous forme de somme de quatre carrés. On peut le démontrer, soit à partir de l’identité des quatre carrés d’Euler, soit en écrivant que la norme d’un produit est le produit des normes.
Division [modifier]
Les entiers d’Hurwitz obéissent à la propriété de la division selon laquelle, de la même manière qu’avec la division euclidienne :
Si a et b sont des entiers d’Hurwitz, b non nul, il existe un quotient q et un reste r tel que :
a=b.q+r avec 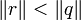 , q et r étant des entiers d’Hurwitz.
, q et r étant des entiers d’Hurwitz.
Les quaternions d'Hurwitz forment donc un anneau euclidien à gauche et à droite.
Par exemple :
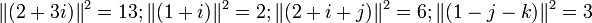
Comme 2 + 3i = (1 + i).(2 + i + j) + (1 − j − k),
2+3i divisé par 1+i admet comme couple (quotient,reste) le couple (2+i+j,1-j-k) Ce couple n’est pas unique puisque cette division admet aussi le couple (2+i+k,1+j-k)
On dira que a divise b (ou que a admet comme diviseur b) s’il existe q tel que a = b.q. q est alors unique.
Entier d’Hurwitz premier [modifier]
Un entier d’Hurwitz p est premier s’il n’admet comme diviseur que les nombre unités et p fois les nombres unités.
Or, si a divise b, 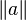 divise
divise  . Donc si
. Donc si  est premier, il ne peut exister d’entier divisant x ayant une norme différente de 1 ou de
est premier, il ne peut exister d’entier divisant x ayant une norme différente de 1 ou de  , donc x est un nombre d’Hurwitz premier.
, donc x est un nombre d’Hurwitz premier.
1+i est, par exemple, un entier d’Hurwitz premier, car  est premier.
est premier.
Algorithme d’Euclide [modifier]
On peut définir un algorithme d’Euclide dans ![mathbb{Z} [h,i,j,k]](http://upload.wikimedia.org/math/8/4/0/840ef30ae2eae5cbde635ada3b76039c.png) , de la même manière que dans
, de la même manière que dans  .
.
On peut ainsi trouver un plus grand diviseur commun à a et b (noté pgcd(a ,b)), c'est-à-dire celui ayant la plus grande norme. En toute rigueur, étant donné la non commutativité de cet ensemble, on doit définir un plus grand diviseur commun à droite, et un plus grand diviseur commun à gauche.
De même que dans  , on peut alors trouver u et v tels que pgcd(a,b)=a.u+b.v, avec u et v des entiers d’Hurwitz.
, on peut alors trouver u et v tels que pgcd(a,b)=a.u+b.v, avec u et v des entiers d’Hurwitz.
Propriété de la division d’un produit par un entier réel d’Hurwitz premier [modifier]
Si p est un entier réel d’Hurwitz premier (c'est-à-dire un nombre premier appartenant à  ) , et qui divise a.b, où a et b sont des entiers d’Hurwitz, alors p divise a ou p divise b.
) , et qui divise a.b, où a et b sont des entiers d’Hurwitz, alors p divise a ou p divise b.
Preuve
Supposons que p premier divise a.b mais ne divise pas a. Alors, un pgcd de a et p est 1, et il existe u et v tels que au+pv=1.
Alors en multipliant par b de chaque coté, on obtient bau+bpv=b. p divise ab donc bau, et p divise p donc bpv (comme p appartient à  , p commute avec les quaternions) .
, p commute avec les quaternions) .
Donc p divise b.
Théorème et lemme préliminaires [modifier]
Tout d’abord, remarquons que 0, 1 et 2 peuvent s’écrire sous forme de somme de 4 carrés (0 = 02 + 02 + 02 + 02;1 = 12 + 02 + 02 + 02 et 2 = 12 + 12 + 02 + 02).
Théorème [modifier]
Tout entier premier de  qui n’est pas un entier d’Hurwitz premier peut s’écrire sous forme de somme de quatre carrés.
qui n’est pas un entier d’Hurwitz premier peut s’écrire sous forme de somme de quatre carrés.
Preuve
Soit p remplissant les conditions précédentes. On peut donc écrire p sous la forme p = (a + bi + cj + dk)γ , avec  et
et 
On a alors le conjugué de p (égal à p puisque p appartient à  ) :
) : 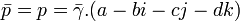
Alors 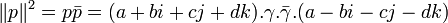
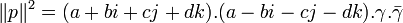 car
car 
Donc  avec (a2 + b2 + c2 + d2) et
avec (a2 + b2 + c2 + d2) et 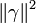 strictement supérieure à 1 et strictement inférieure à p.
strictement supérieure à 1 et strictement inférieure à p.
Étant donné que p est premier, la seule décomposition de p2 est donc p.p. On en déduit que (a2 + b2 + c2 + d2) = p.
Si a, b, c et d sont des entiers, p s’écrit comme somme de quatre carrés.
Si ce sont des demis-entiers, on peut alors trouver w tel que :
 et a + bi + cj + dk = w + a1 + b1i + c1j + d1k avec a1,b1,c1 et d1 des entiers pairs. On remarque que
et a + bi + cj + dk = w + a1 + b1i + c1j + d1k avec a1,b1,c1 et d1 des entiers pairs. On remarque que 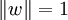
On a alors :
p = (a + bi + cj + dk)(a − bi − cj − dk)


Or comme a1,b1,c1 et d1 sont des entiers pairs, 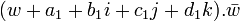 ne donnera que des entiers et sera donc de la forme A+Bi+Cj+Dk, avec A, B, C et D des entiers. De même pour son conjugué, d’où : p = (A + Bi + Cj + Dk)(A − Bi − Cj − Dk) = A2 + B2 + C2 + D2
ne donnera que des entiers et sera donc de la forme A+Bi+Cj+Dk, avec A, B, C et D des entiers. De même pour son conjugué, d’où : p = (A + Bi + Cj + Dk)(A − Bi − Cj − Dk) = A2 + B2 + C2 + D2
Donc p s’écrit comme somme de quatre carrés.
Lemme [modifier]
Soit p un entier premier impair, alors il existe l et m tels que p divise 1 + l2 + m2 (p, l et m appartenant à  )
)
Preuve
Soit p premier impair. Les différentes classes de congruence modulo p sont 0, 1, -1, ..., (p-1)/2, -(p-1)/2. Il y en a donc p.
 est équivalent à ( a
est équivalent à ( a  b ou a
b ou a  –b ) (modulo p). Les différents carrés modulo p sont donc 02,12,...,((p − 1) / 2)2. Il y en a donc 1 + (p − 1) / 2 = (p + 1) / 2.
–b ) (modulo p). Les différents carrés modulo p sont donc 02,12,...,((p − 1) / 2)2. Il y en a donc 1 + (p − 1) / 2 = (p + 1) / 2.
De même pour − 1 − m2, il y a (p + 1) / 2 éléments qui sont de cette forme, différents, modulo p. Supposons que ces deux ensembles soient disjoints. Alors il y aurait (p + 1) / 2 + (p + 1) / 2 = p + 1 éléments dans 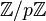 , ce qui est faux puisqu’il y en a p. Donc au moins un élément est simultanément de la forme l2 et de la forme − 1 − m2 modulo p, donc il existe l et m tel que
, ce qui est faux puisqu’il y en a p. Donc au moins un élément est simultanément de la forme l2 et de la forme − 1 − m2 modulo p, donc il existe l et m tel que  modulo p c'est-à-dire
modulo p c'est-à-dire 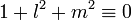 modulo p.
modulo p.
Il existe donc l et m tel que p divise 1 + l2 + m2.
Théorème des quatre carrés [modifier]
Tout entier de  peut s’écrire sous forme de somme de quatre carrés.
peut s’écrire sous forme de somme de quatre carrés.
Preuve
Soit p un entier impair premier. Il existe donc d’après le lemme précédant l et m entier tel que p divise 1 + l2 + m2. Donc p divise 1 + l2 + m2 = (1 + li + mj)(1 − li − mj).
Supposons que p soit un entier d’Hurwitz premier. Alors d’après un théorème précédant, p divise 1 + li + mj ou p divise 1 − li − mj. Or, ni  ni
ni  ne sont des entiers d’Hurwitz. Donc p n’est pas un entier d’Hurwitz premier.
ne sont des entiers d’Hurwitz. Donc p n’est pas un entier d’Hurwitz premier.
D’après le théorème précédant, p peut donc s’écrire sous forme de somme de quatre carrés.
Donc, si p est un entier impair premier, p peut donc s’écrire sous forme de somme de quatre carrés.
Si p=0, p=1 ou p=2, nous avons déjà vu que p peut s’écrire sous forme de somme de quatre carrés.
Si p est un entier, non premier, strictement supérieur à 2, alors p peut s’écrire sous forme de produit de nombre premiers. Ces nombres premiers peuvent s’écrire sous forme de carrés, et leur produits aussi, d’après la remarque sur l’identité des quatre carrés d’Euler. Donc p peut s’écrire sous forme de somme de quatre carrés.
Finalement, tout élément de  peut s’écrire sous forme de somme de quatre carrés.
peut s’écrire sous forme de somme de quatre carrés.
Fonctions arithmétiques [modifier]
Les fonctions arithmétiques permettent d'obtenir des résultats plus généraux. Si on pose r4(n) comme étant le nombre de façon de décomposer n sous forme d'une somme de 4 carrés, on obtient le résultat suivant:
 , pour | x | < 1.
, pour | x | < 1.
Moyennant l'utilisation des séries de Lambert, on en déduit le théorème suivant, dit théorème de Jacobi :
Par exemple, 1 n'est divisible que par lui-même, qui n'est pas congru à 0 modulo 4. Donc r4(1) = 8
3 des 8 formes sont :
1 = 12 + 02 + 02 + 02
1 = 02 + 12 + 02 + 02
1 = ( − 1)2 + 02 + 02 + 02
Articles connexes [modifier]
21:37 Publié dans Théorème des quatre carrés de Lagrange | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook










































![forall n in mathbb{N}^*, r_4(n) = 8 sum_{d|n, d notequiv 0[4]}{d}](http://upload.wikimedia.org/math/f/2/d/f2de8fa897b940dd87bfb7457bc12e72.png)
Les commentaires sont fermés.