Nombres p-adiques

Nombres p-adiques

Théorie des nombres
Algèbre -- Anneaux
Algèbre -- Corps
Analyse -- Topologie -- Vocabulaire général

  Comme les nombres réels sont construits à partir des nombres rationnels en complétant Q pour la topologie induite par la valeur absolue, les nombres p-adiques sont obtenus en complétant Q, mais pour une topologie différente, celle induite par la distance p-adique.  On fixe donc un premier p et on définit la norme p-adique de la façon suivante :

• Si n est un entier, la valuation p-adique de n, notée v_p(n), est l'exposant de p dans la décomposition en produit de facteurs premiers de n.
• Si r=a/b est un rationnel, on pose v_p(r)=v_p(a)-v_p(b). Ceci ne dépend pas du représentant a/b choisi pour la fraction r.
• On pose aussi v_p(0)=0.
• La norme p-adique d'un rationnel r est alors défini par :

|.|_p est une norme sur Q, avec des propriétés très différentes de la valeur absolue. Par exemple,

• Plus |r|_p est petit, plus une grande puissance de p divise r. Ainsi, un rationnel peut avoir une très grande valeur absolue, et une très petite distance p-adique. Ainsi :
• La distance p-adique définie sur Q par d_p(x,y)=|x-y|_p est une distance ultra-métrique :

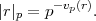
Définition : Le corps des nombres p-adiques, noté Q_p, est le complété de Q pour la norme p-adique.

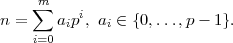  On peut encore décrire autrement les nombres p-adiques. Si n est un entier positif, il s'écrit de façon unique sous la formeLa suite (a_i) est définie par

• a₀ est l'entier de {0,...,p-1} qui est congru à n modulo p;
• a_j+1 est l'entier de {0,...,p-1} qui est congru àmodulo p.

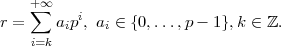Les nombres p-adiques sont ceux qui s'écriventCette série est convergente pour la distance p-adique. L'écriture précédente s'appelle décomposition de Hensel de r.  Finalement, l'ensemble des entiers p-adiques, noté Z_p, est l'ensemble des r de Q_p s'écrivant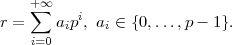C'est un sous-anneau de Q_p.Les nombres p-adiques ont été introduits par Hensel en 1897. Son idée était de pouvoir utiliser la théorie des séries entières en arithmétique. Depuis, toute une branche des mathématiques, l'analyse p-adique, s'est développée sur ses idées.

Version imprimable

 

Source : http://www.bibmath.net/dico/index.php3?action=affiche&...