02/12/2010
Crochet de Lie
Crochet de Lie
|
|
Cet article ne cite pas suffisamment ses sources (août 2007).
Si vous connaissez le thème traité, merci d'indiquer les passages à sourcer avec {{Référence souhaitée}} ou, mieux, incluez les références utiles en les liant aux notes de bas de page. (Modifier l'article)
|
Le crochet de Lie est une loi de composition interne [,] sur un espace vectoriel V, qui lui confère une structure d'algèbre de Lie. Le commutateur [u,v]=uv-vu de deux endomorphismesen constitue un des exemples les plus simples. Le nom de crochet de Lie, ou simplement crochet, est souvent employé pour le crochet de Lie de deux champs de vecteurs sur une variété différentielle.
Sommaire[masquer] |
Soit un espace vectoriel V sur un corps Un crochet de Lie vérifie : L'antisymétrie implique [x,x] = 0 pour tout corps pour lequel Si on combine la bilinéarité avec l'antisymétrie [λx + x',y] = − [y,λx + x'] on peut ne vérifier la linéarité que sur une seule composante:[λx + x',y] = λ[x,y] + [x',y]. Muni d'un crochet de Lie, un espace vectoriel devient une algèbre de Lie. Soit V une variété différentielle et X et Y deux champs de vecteurs sur V. On note X . f la dérivée de la fonction f dans la direction du champ X. Le crochet de Lie de X et Y est l'unique champ de vecteur, noté [X,Y], tel que, pour toute fonction f indéfiniment dérivable, On montre en effet qu'un champ de vecteurs Z peut être caractérisé par la façon dont il dérive les applications. On vérifie en outre que l'application [,] définit bien un crochet de Lie sur les champs de vecteurs. Voir pour les démonstrations l'article dérivée de Lie. Lorsque deux champs de vecteurs ont un crochet nul, on dit qu'ils commutent.Définition générale [modifier]
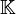 . Un crochet de Lie est une loi de composition interne sur V (c'est-à-dire que le crochet de Lie de deux vecteurs est encore un vecteur :
. Un crochet de Lie est une loi de composition interne sur V (c'est-à-dire que le crochet de Lie de deux vecteurs est encore un vecteur : ![forall x,yin V,quad [x,y]in V](http://upload.wikimedia.org/math/c/9/0/c90e2410e31abf79d4f6e106317124d8.png) ), vérifiant les propriétés suivantes :
), vérifiant les propriétés suivantes :
![forall x,x',yin V,lambda,muinmathbb K, [lambda x+mu x', y]=lambda[x,y]+mu [x',y],](http://upload.wikimedia.org/math/c/0/1/c01d118d897c2d3f49c20c718d51ae12.png)
![forall x,y,y'in V,lambda,muinmathbb K,[x,lambda y+mu y']=lambda[x,y]+mu [x,y']](http://upload.wikimedia.org/math/4/f/e/4fe65ba8376181cbed9147b7c0c055c0.png) .
.![forall xin V,quad [x,x]=0](http://upload.wikimedia.org/math/d/8/8/d88816febe6581ab9bb2e732129847f6.png)
![forall x,y,zin V, [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0](http://upload.wikimedia.org/math/c/6/c/c6c225e906d1dc76d5e14589e036be94.png) .
.
![forall x,yin V, [x,y]=-[y,x]](http://upload.wikimedia.org/math/e/e/e/eeeffe9a658fc19122b5102dad29c923.png) .
.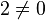 (corps de caractéristique différente de deux).
(corps de caractéristique différente de deux).Crochet de Lie de deux champs de vecteurs [modifier]
![[X,Y]cdot f = Xcdot (Ycdot f) -Y cdot (Xcdot f)](http://upload.wikimedia.org/math/8/7/2/87246955c4529cfe2065604eaff72625.png)
Bibliographie [modifier]
Voir aussi [modifier]
21:30 Publié dans Crochet de Lie | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook








































Les commentaires sont fermés.