Algèbre enveloppante : Mathématique

D	L	M	M	J	V	S
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30

« Crochet de Lie | Page d'accueil | Forme de Killing »

02/12/2010

Algèbre enveloppante

Cet article est une ébauche concernant l'algèbre.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

En mathématiques, on peut construire l'algèbre enveloppante U(L) d'une algèbre de Lie L. Il s'agit une algèbre associative unitaire qui permet de rendre compte de la plupart des propriétés de L.

Si A est une algèbre associative sur un corps K, on peut facilement la munir d'une structure d'algèbre de Lie, en posant [x,y]=xy-yx. On note l'algèbre de Lie ainsi obtenue A_L.

La construction d'une algèbre enveloppante répond au problème réciproque : à partir d'une algèbre de Lie, on construit une algèbre associative dont le commutateur correspond au crochet dont on était parti.

Construction [modifier]

Soit L une algèbre de Lie sur un corps K. Soit T(L) l'algèbre tensorielle de L. On construit U(L) à partir de T(L) en imposant les relations $xotimes y-yotimes x=[x,y]$ .

Plus formellement, on note I l'idéal bilatère engendré par les $xotimes y-yotimes x-[x,y]$ . U(L) est alors le quotient de T(L) par l'idéal I. L'injection canonique de L dans T(L) fournit alors un morphisme $iota:Lto U(L)$ .

Propriété universelle [modifier]

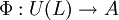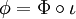On peut caractériser l'algèbre enveloppante de L par la propriété universelle suivante : U(L) est l'unique algèbre assocative telle que pour toute K-algèbre associative A et tout morphisme d'algèbre de Lie $phi : Lto A_L$ , il existe un unique morphisme d'algèbre associative $Phi:U(L)to A$ tel que $phi=Phicirc iota$ .

Autres propriétés [modifier]

L'intérêt premier de la construction de l'algèbre enveloppante est que toute représentation d'une algèbre de Lie L peut être vue comme un module sur U(L). Formellement, il y a uneéquivalence de catégories entre les représentations de L et les U(L)-modules.

Le théorème de Poincaré-Birkhoff-Witt permet de mieux comprendre la structure de l'algèbre enveloppante. Un corollaire important de ce théorème est que l'application $ι$ définie ci-dessus est injective.