02/12/2010
Groupe diédral
En mathématiques, le groupe diédral noté Dn, pour Groupe diédral
 , ou parfois D2n, est un groupe d'ordre 2n qui s'interprète notamment comme le groupe des isométries du plan conservant un polygone régulier à n côtés. Le groupe est constitué de n éléments correspondant aux rotationset n autres correspondant aux réflexions. Le groupe D1 est le groupe cyclique d'ordre 2, noté C2 ; le groupe D2 est le groupe de Klein à quatre éléments. Parmi les groupes diédraux Dn, ce sont les deux seuls à être abéliens.
, ou parfois D2n, est un groupe d'ordre 2n qui s'interprète notamment comme le groupe des isométries du plan conservant un polygone régulier à n côtés. Le groupe est constitué de n éléments correspondant aux rotationset n autres correspondant aux réflexions. Le groupe D1 est le groupe cyclique d'ordre 2, noté C2 ; le groupe D2 est le groupe de Klein à quatre éléments. Parmi les groupes diédraux Dn, ce sont les deux seuls à être abéliens.
Sommaire[masquer] |
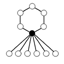
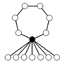
Le groupe Dn peut être défini par la suite exacte scindée suivante : où Cn est un groupe cyclique d'ordre n, C2 est cyclique d'ordre 2, la section étant donnée par l'action d'un relevé σ du générateur de C2, sur un générateur τ du groupe cyclique d'ordre n : Ce groupe est donc produit semi-direct de Cn par C2 suivant le morphisme ψ, où l'unité de C2 agit sur Cn comme l'application identique et l'autre élément de C2 agit sur Cn par inversion. Explicitement: Une présentation est alors : Plus explicitement les générateurs sont des σ, τ et les relations qu'ils vérifient sont de la forme : On peut ainsi dresser une liste complète des éléments du groupe : Une présentation alternative, où μ = τσ dans le système de générateurs de la présentation précédente, est : Plus explicitement les générateurs sont des σ, μ et les relations qu'ils vérifient sont de la forme : On voit ainsi que le groupe diédral admet un système de deux générateurs distincts tous deux d'ordre 2. Les groupes diédraux sont les seuls groupes finis possédant cette propriété1. Le groupe diédral d'ordre 2n peut aussi être vu comme le groupe d'automorphisme du graphe constitué seulement d'un cycle avec n sommets (si n ≥ 3). On peut définir de la façon suivante une représentation du groupe diédral Dn : avec On reconnaît que la matrice φ(τ) est une matrice de rotation d'angle Les graphes de cycles de groupes diédraux sont constitués d'un cycle à n éléments et de cycles à 2 éléments. Le sommet sombre dans les graphes de cycle ci-dessous de divers groupes diédraux représente l'élément identité, et les autres sommets sont les autres éléments du groupe. Un cycle est constitué des puissances successives de l'un ou l'autre élément connecté à l'élément identité. Présentation et définitions équivalentes [modifier]
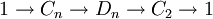
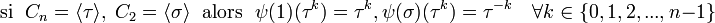 .
.
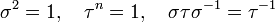 .
.

 .
.Interprétation géométrique [modifier]
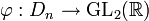
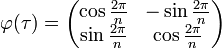 et
et  . Cette représentation est en fait à valeurs dans le groupe
. Cette représentation est en fait à valeurs dans le groupe 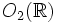 .
. , et la matrice φ(σ) une matrice de réflexion. Ces transformations laissent effectivement invariant le polygone régulier centré en l'origine à n côtés.
, et la matrice φ(σ) une matrice de réflexion. Ces transformations laissent effectivement invariant le polygone régulier centré en l'origine à n côtés.Graphe de cycle [modifier]
| D2 | D3 | D4 | D5 | D6 | D7 |
|---|
Le sous-ensemble des rotations Certaines propriétés des groupes diédraux Dn avec n ≥ 3 dépendent de la parité de n. Elles peuvent souvent facilement être déduites de la représentation géométrique de ce groupe. où D2n est l'ensemble de départ Dn*C2 celui d'arrivée, h et ε étant définis modulo 2, et k modulo n. Les générateurs des groupes diédraux sont choisis comme dans la première partie de l'article. Si n est impair, le groupe Dn admet 2 représentations irréductibles complexes de degré 1 : En revanche, si n est pair, il existe 4 représentations irréductibles de degré 1 : Les autres représentations irréductibles sont toutes de degré 2 ; elles sont en nombre où ω désigne une racine primitive ne de l'unité, et h parcourt les entiers compris entre 1 et n-1. On peut vérifier que deux telles représentations sont isomorphes seulement pour h1 et h2vérifiant h1+h2=n. On obtient alors le nombre annoncé de représentations irréductibles de degré 2 non isomorphes, et donc toutes les représentations irréductible du groupe diédral, par la formule liant le nombre de représentations irréductibles à l'ordre du groupe. En plus des groupes diédraux finis, on trouve le groupe diédral infini D∞. Tout groupe diédral est généré par une rotation r et une réflexion. Si la rotation est un multiple rationnel d’une rotation totale, alors il existe un entier n tel que rn soit l’identité, et on est en présence d’un groupe diédral fini d’ordre 2n. Mais si la rotation n’est pas un multiple rationnel d’une rotation totale, alors il n’existe pas de tel n et le groupe résultant a un nombre infinid’éléments ; on le note D∞. Il admet pour présentation et est isomorphe au produit semi-direct de Z par C2, ainsi qu’au produit libre C2 * C2. Il s’agit de l’automorphisme de groupes du graphe constitué d’un chemin infini vers les deux extrémités. De façon équivalente, il s’agit du groupe des isométries de Z. Pour tout groupe abélien H, le groupe diédral généralisé de H, noté Dih(H), est le produit semi-direct de H par C2, l'action de C2 sur H étant l'inversion, i.e. où φ(0) est l'application identité et φ(1) l'inversion des éléments. On obtient ainsi, si H et C2 sont tous deux notés additivement : pour tous h1, h2 dans H et t2 dans C2. (Si C2 est noté multiplicativement, ces deux formules se résument en (h1, t1) * (h2, t2) = (h1 + t1h2, t1t2) .) Le sous-groupe de Dih(H) constitué des éléments de la forme (h, 0) est un sous-groupe normal d'indice 2, isomorphe à H. Quant aux éléments de la forme (h, 1), chacun est son propre inverse. Les classes de conjugaison sont Ainsi, pour tout sous-groupe M de H, les éléments correspondants (m,0) forment aussi un sous-groupe normal de Dih(H) isomorphe à M, et l'on a : Exemples : Dih(H) est abélien si et seulement si le produit semi-direct est direct, c'est-à-dire si et seulement si chaque élément de H est son propre inverse, i.e. H est un 2-groupe abélien élémentaire : Dih(C2k) = C2k+1.Propriétés [modifier]
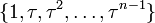 est un sous-groupe normal.
est un sous-groupe normal.

Représentations [modifier]

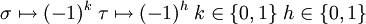
 si n est impair, respectivement
si n est impair, respectivement  si n est pair. On peut les définir comme suit :
si n est pair. On peut les définir comme suit :
Groupe diédral infini [modifier]


Groupe diédral généralisé [modifier]
Bibliographie [modifier]
Notes et références [modifier]
21:33 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook









































Les commentaires sont fermés.