02/12/2010
Groupe de Weyl
En mathématiques, et en particulier dans la théorie des algèbres de Lie, le groupe de Weyl d'un système de racines Le système de racines de Le groupe de Weyl d'un groupe de Lie semi-simple, d'une algèbre de Lie semi-simple, d'un groupe algébrique linéaire semi-simple, etc. est le groupe de Weyl du système de racines de ce groupe ou de cette algèbre. Enlever les hyperplans définis par les racines de La base du système de racine qui respecte le choix de Les groupes de Weyl sont des exemples des groupes de Coxeter. Ceci signifie qu'ils ont une sorte particulière de présentation dans laquelle chaque générateur Si G est un groupe algébrique linéaire semisimple sur un corps algébriquement clos (plus généralement un groupe déployé), et T est un tore maximal, le normalisateur N de T contient Tcomme sous-groupe d'indice fini et le groupe de Weyl W de G est isomorphe à N/T. Si B est un sous-groupe de Borel de G, i.e. un sous-groupe connexe résoluble maximal choisi pour contenir T, alors nous obtenons une décomposition de Bruhat ce qui provoque la décomposition de la variété de drapeaux G/B en cellules de Schubert (voir Grassmannienne).Groupe de Weyl
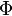 est le sous-groupe du groupe d'isométries du système de racines engendré par les réflexions orthogonales par rapport aux hyperplans orthogonaux aux racines.
est le sous-groupe du groupe d'isométries du système de racines engendré par les réflexions orthogonales par rapport aux hyperplans orthogonaux aux racines.Exemple [modifier]
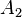 est constitué des sommets d'un hexagone régulier centré à l'origine. Le groupe complet des symétries de ce système de racines est par conséquent legroupe diédral d'ordre 12. Le groupe de Weyl est engendré par les réflexions à travers les droites bissectant les paires de côtés opposés de l'hexagone ; c'est le groupe diédral d'ordre 6.
est constitué des sommets d'un hexagone régulier centré à l'origine. Le groupe complet des symétries de ce système de racines est par conséquent legroupe diédral d'ordre 12. Le groupe de Weyl est engendré par les réflexions à travers les droites bissectant les paires de côtés opposés de l'hexagone ; c'est le groupe diédral d'ordre 6.Les chambres de Weyl [modifier]
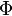 découpe l'espace euclidien en un nombre fini de régions ouvertes, appelées les chambres de Weyl. Celles-ci sont permutées par l'action sur le groupe de Weyl, et un théorème établit que cette action est simplement transitive. En particulier, le nombre de chambres de Weyl est égal à l'ordre du groupe de Weyl. Tout vecteur v différent de zéro divise l'espace euclidien en deux demi-espaces bordant l'hyperplan
découpe l'espace euclidien en un nombre fini de régions ouvertes, appelées les chambres de Weyl. Celles-ci sont permutées par l'action sur le groupe de Weyl, et un théorème établit que cette action est simplement transitive. En particulier, le nombre de chambres de Weyl est égal à l'ordre du groupe de Weyl. Tout vecteur v différent de zéro divise l'espace euclidien en deux demi-espaces bordant l'hyperplan  orthogonal à v, nommés
orthogonal à v, nommés  et
et 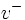 . Si v appartient à une certaine chambre de Weyl, aucune racine ne se trouve dans
. Si v appartient à une certaine chambre de Weyl, aucune racine ne se trouve dans  , donc chaque racine se trouve dans
, donc chaque racine se trouve dans  ou
ou 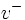 , et si
, et si  se trouve dans l'un d'eux, alors
se trouve dans l'un d'eux, alors  se trouve dans l'autre. Ainsi,
se trouve dans l'autre. Ainsi,  constitué d'exactement la moitié des racines de
constitué d'exactement la moitié des racines de 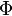 . Bien sûr,
. Bien sûr, 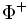 dépend de v, mais il ne change pas si v reste dans la même chambre de Weyl.
dépend de v, mais il ne change pas si v reste dans la même chambre de Weyl.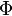 est l'ensemble des racines simples dans
est l'ensemble des racines simples dans 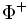 , i.e., les racines qui ne peuvent pas être écrites comme une somme de deux racines dans
, i.e., les racines qui ne peuvent pas être écrites comme une somme de deux racines dans 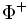 . Ainsi, les chambres de Weyl, l'ensemble
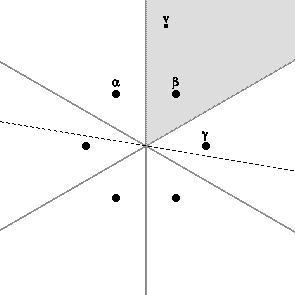
. Ainsi, les chambres de Weyl, l'ensemble 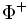 et la base en déterminent un autre, et le groupe de Weyl agit simplement transitivement dans chaque cas. L'illustration suivante montre les six chambres de Weyl d'un système de racines
et la base en déterminent un autre, et le groupe de Weyl agit simplement transitivement dans chaque cas. L'illustration suivante montre les six chambres de Weyl d'un système de racines 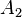 , un choix de v, l'hyperplan
, un choix de v, l'hyperplan  (indiqué par une droite en pointillé) et les racines positives
(indiqué par une droite en pointillé) et les racines positives  ,
,  , et
, et  . La base dans ce cas est (
. La base dans ce cas est (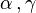 }.
}.Les groupes de Coxeter [modifier]
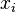 est d'ordre deux, et les relations autres que
est d'ordre deux, et les relations autres que  sont de la forme
sont de la forme  . Les générateurs sont les réflexions données par les racines simples et
. Les générateurs sont les réflexions données par les racines simples et 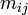 est 2, 3, 4 ou 6 dépendant si les racines i et jfont un angle de 90, 120, 135 ou 150 degrés, i.e., si dans le Diagramme de Dynkin, elles ne sont pas connectées, connectées avec une arête simple, connectées par une double arête ou connectées par une triple arête. La longueur d'un élément du groupe de Weyl est la longueur du mot le plus court représentant cet élément en termes de ces générateurs standards.
est 2, 3, 4 ou 6 dépendant si les racines i et jfont un angle de 90, 120, 135 ou 150 degrés, i.e., si dans le Diagramme de Dynkin, elles ne sont pas connectées, connectées avec une arête simple, connectées par une double arête ou connectées par une triple arête. La longueur d'un élément du groupe de Weyl est la longueur du mot le plus court représentant cet élément en termes de ces générateurs standards.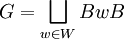
21:32 Publié dans Groupe de Weyl | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook








































Les commentaires sont fermés.