L’Académie norvégienne des sciences a remis le prix Abel 2011 au mathématicien américain John Milnor pour ses découvertes pionnières dans les domaines de la topologie, de la géométrie et de l’algèbre. Une contribution très large, donc, qui est récompensée par ce prix nommé d’après le mathématicien norvégien Niels Henrik.
17/04/2011
Puiseux series
Puiseux series
From Wikipedia, the free encyclopedia
(Redirected from Puiseux's theorem)
|
This article may be too technical for most readers to understand. Please improve this article to make it understandable to non-experts, without removing the technical details. Reason: The article should start by providing examples, definitions, and theorems in the setting of undergraduate-level complex analysis, which will make it useful to a fairly wide audience (engineers, physicists, mathematics undergraduates, etc.). Only after that should it provide the formulation informed by modern algebra (involving concepts such as "functor," "union of fields," "direct limit," etc.), which is useful only to a much narrower audience. (April 2011) |
In mathematics, Puiseux series are a generalization of formal power series, first introduced by Isaac Newton in 1676[1] and rediscovered by Victor Puiseux in 1850,[2] that allows for negative and fractional exponents of the indeterminate. The field of Puiseux series is a (functorial) construction which, for any field (of coefficients) K, gives a field
containing the field of formal Laurent series, and which is algebraically closed of characteristic 0 when K is so (a statement usually referred to as Puiseux's theorem or sometimes theNewton–Puiseux theorem). The Puiseux expansion is a generalization of the Laurent series expansion (hence also of the formal series expansion), initially defined for algebraic functions or (equivalently) branches of algebraic curves (a fact also referred to as Puiseux's theorem) and which can be generalized to various settings.
Contents[hide] |
[edit]Field of Puiseux series
If K is a field then we can define the field of Puiseux series with coefficients in K (or over K) informally as the set of formal expressions of the form
where n and k0 are a nonzero natural number and an integer respectively (which are part of the datum of f): in other words, Puiseux series differ from formal Laurent series in that they allow for fractional exponents of the indeterminate as long as these fractional exponents have bounded denominator (here n), and just as Laurent series, Puiseux series allow for negative exponents of the indeterminate as long as these negative exponents are bounded (here by k0). Addition and multiplication are as expected: one might define them by first “upgrading” the denominator of the exponents to some common denominator and then performing the operation in the corresponding field of formal Laurent series.
In other words, the field of Puiseux series with coefficients in K is the union of the fields K((T1 / n)) (where n ranges over the nonzero natural numbers), where each element of the union is a field of formal Laurent series over T1 / n (considered as an indeterminate), and where each such field is considered as a subfield of the ones with larger n by rewriting the fractional exponents to use a larger denominator (e.g., T1 / 2 is identified with T15 / 30 as expected).
This yields a formal definition of the field of Puiseux series: it is the direct limit of the direct system, indexed over the non-zero natural numbers n ordered by divisibility, whose objects are all K((T)) (the field of formal Laurent series, which we rewrite as
K((Tn)) for clarity),
with a morphism
being given, whenever m divides n, by .
[edit]Valuation and order
The Puiseux series over a field K form a valued field with value group (the rationals): the valuation v(f) of a series
as above is defined to be the smallest rational k / n such that the coefficient ck of the term with exponent k / n is non-zero (with the usual convention that the valuation of 0 is +∞). The coefficient ck in question is typically called the valuation coefficient of f.
This valuation in turn defines a (translation-invariant) distance (which is ultrametric), hence a topology on the field of Puiseux series by letting the distance from f to 0 be exp( − v(f)). This justifies a posteriori the notation
as the series in question does, indeed, converge to f in the Puiseux series field (this is in contrast to Hahn series which cannot be viewed as converging series).
If the base field K is ordered, then the field of Puiseux series over K is also naturally (“lexicographically”) ordered as follows: a non-zero Puiseux series f with 0 is declared positive whenever its valuation coefficient is so. Essentially, this means that any positive rational power of the indeterminate T is made positive, but smaller than any positive element in the base field K.
If the base field K is endowed with a valuation w, then we can construct a different valuation on the field of Puiseux series over K by letting the valuation
of be
where v = k / n is the previously defined valuation (ck is the first non-zero coefficient) and ω is infinitely large (in other words, the value group of is ordered lexicographically, where Γ is the value group of w). Essentially, this means that the previously defined valuation v is corrected by an infinitesimal amount to take into account the valuation w given on the base field.
[edit]Algebraic closedness of Puiseux series
One essential property of Puiseux series is expressed by the following theorem, attributed to Puiseux[2] (for ) but which was implicit in Newton's use of the Newton polygon as early as 1671[3] and therefore known either as Puiseux's theorem or as the Newton–Puiseux theorem[4]:
Theorem: if K is an algebraically closed field of characteristic zero, then the field of Puiseux series over K is the algebraic closure of the field of formal Laurent series over K.[5]
Very roughly, the proof proceeds essentially by inspecting the Newton polygon of the equation and extracting the coefficients one by one using a valuative form of Newton's method. Provided algebraic equations can be solved algorithmically in the base field K, then the coefficients of the Puiseux series solutions can be computed to any given order.
For example, the equation X2 − X = T − 1 has solutions
and
(one readily checks on the first few terms that the sum and product of these two series are 1 and T − 1 respectively): this is valid whenever the base field K has characteristic different from 2.
As the powers of 2 in the denominators of the coefficients of the previous example might lead one to believe, the statement of the theorem is not true in positive characteristic. The example of the Artin Schreier equation Xp − X = T − 1 shows this: reasoning with valuations shows that X should have valuation , and if we rewrite it as X = T − 1 / p + X1 then
, so
and one shows similarly that X1 should have valuation , and proceeding in that way one obtains the series
;
since this series makes no sense as a Puiseux series—because the exponents have unbounded denominators— the original equation has no solution. However, such Eisenstein equations are essentially the only ones not to have a solution, because, if K is algebraically closed of characteristic p>0, then the field of Puiseux series over K is the perfect closure of the maximal tamely ramified extension of K[4].
Similarly to the case of algebraic closure, there is an analogous theorem for real closure: if K is a real closed field, then the field of Puiseux series over K is the real closure of the field of formal Laurent series over K.[6] (This implies the former theorem since any algebraically closed field of characteristic zero is the unique quadratic extension of some real-closed field.)
There is also an analogous result for p-adic closure: if K is a p-adically closed field with respect to a valuation w, then the field of Puiseux series over K is also p-adically closed.[7]
[edit]Puiseux expansion of algebraic curves and functions
[edit]Algebraic curves
Let X be an algebraic curve[8] given by an affine equation F(x,y) = 0 over an algebraically closed field K of characteristic zero, and consider a point p on X which we can assume to be (0,0). We also assume that X is not the coordinate axis x=0. Then a Puiseux expansion of (the y coordinate of) X at p is a Puiseux series f having positive valuation such thatF(x,f(x)) = 0.
More precisely, let us define the branches of X at p to be the points q of the normalization Y of X which map to p. For each such q, there is a local coordinate t of Y at q (which is a smooth point) such that the coordinates x and y can be expressed as formal power series of t, say (since K is algebraically closed, we can assume the valuation coefficient to be 1) and : then there is a unique Puiseux series of the form (a power series in T1 / n), such that y(t) = f(x(t)) (the latter expression is meaningful since is a well defined power series in t). This is a Puiseux expansion of X at p which is said to be associated to the branch given by q(or simply, the Puiseux expansion of that branch of X), and each Puiseux expansion of X at p is given in this manner for a unique branch of X at p.[9][10]
This existence of a formal parametrization of the branches of an algebraic curve or function is also referred to as Puiseux's theorem: it has arguably the same mathematical content as the fact that the field of Puiseux series is algebraically closed and is a historically more accurate description of the original author's statement[11].
For example, the curve y2 = x3 + x2 (whose normalization is a line with coordinate t and map ) has two branches at the double point (0,0), corresponding to the points t=+1 and t=−1 on the normalization, whose Puiseux expansions are and respectively (here, both are power series because the x coordinate is étale at the corresponding points in the normalization). At the smooth point (-1,0) (which is t=0 in the normalization), it has a single branch, given by the Puiseux expansion y = − (x + 1)1 / 2 + (x + 1)3 / 2 (the x coordinate ramifies at this point, so it is not a power series).
The curve y2 = x3 (whose normalization is again a line with coordinate t and map ), on the other hand, has a single branch at the cusp point (0,0), whose Puiseux expansion is y = x3 / 2.
[edit]Analytic convergence
When , i.e. the field of complex numbers, the Puiseux expansions defined above are convergent in the sense that for a given choice of n-th root of x, they converge for small enough | x | , hence define an analytic parametrization of each branch of X in the neighborhood of p (more precisely, the parametrization is by the n-th root of x).
[edit]Generalization
The field of Puiseux series is not complete, but its completion can be easily described: it is the field of formal expressions of the form , where the support of the coefficients (that is, the set of e such that ) is the range of an increasing sequence of rational numbers that either is finite or tends to +∞. In other words, such series admit exponents of unbounded denominators, provided there are finitely many terms of exponent less than A for any given bound A. For example, is not a Puiseux series, but it is the limit of a Cauchy sequence of Puiseux series (Puiseux polynomials). However, even this completion is still not "maximally complete" in the sense that it admits non-trivial extensions which are valued fields having the same value group and residue field[12][13], hence the opportunity of completing it even more:
Hahn series are a further (larger) generalization of Puiseux series, introduced by Hans Hahn (in the course of the proof of his embedding theorem in 1907 and then studied by him in his approach to Hilbert's seventeenth problem), where instead of requiring the exponents to have bounded denominator they are required to form a well-ordered subset of the value group (usually or ). These were later further generalized by Anatoly Maltsev and Bernhard Neumann to a non-commutative setting (they are therefore sometimes known as Hahn-Mal'cev-Neumann series). Using Hahn series, it is possible to give a description of the algebraic closure of the field of power series in positive characteristic which is somewhat analogous to the field of Puiseux series.[14]
[edit]Notes
- ^ Newton (1960)
- ^ a b Puiseux (1850, 1851)
- ^ Newton (1736)
- ^ a b cf. Kedlaya (2001), introduction
- ^ cf. Eisenbud (1995), corollary 13.15 (p. 295)
- ^ Basu &al (2006), chapter 2 (“Real Closed Fields”), theorem 2.91 (p. 75)
- ^ Cherlin (1976), chapter 2 (“The Ax–Kochen–Ershof Transfer Principle”), §7 (“Puiseux series fields”)
- ^ We assume that X is irreducible or, at least, that it is reduced and that it does not contain the y coordinate axis.
- ^ Shafarevich (1994), II.5, p. 133–135
- ^ Cutkosky (2004), chapter 2, p. 3–11
- ^ Puiseux (1850), p. 397
- ^ Poonen, Bjorn (1993). "Maximally complete fields". Enseign. Math. 39: 87–106.
- ^ Kaplansky, Irving (1942). "Maximal Fields with Valuations". Duke Math. J. 9: 393–321.
- ^ Kedlaya (2001)
[edit]References
- Basu, Saugata; Pollack, Richard; Roy, Marie-Françoise (2006). Algorithms in Real Algebraic Geometry. Algorithms and Computations in Mathematics 10 (2nd ed.). Springer-Verlag. doi:10.1007/3-540-33099-2. ISBN 978-3-540-33098-1.
- Cherlin, Greg (1976). Model Theoretic Algebra Selected Topics. Lecture Notes in Mathematics 521. Springer-Verlag. ISBN 978-3-540-07696-4.
- Cutkosky, Steven Dale (2004). Resolution of Singularities. Graduate Studies in Mathematics 63. American Mathematical Society. ISBN 0821835556.
- Eisenbud, David (1995). Commutative Algebra with a View Toward Algebraic Geometry. Graduate Texts in Mathematics 150. Springer-Verlag. ISBN 3-540-94269-6.
- Kedlaya, Kiran Sridhara (2001). "The algebraic closure of the power series field in positive characteristic". Proc. Amer. Math. Soc. 129: 3461–3470. doi:10.1090/S0002-9939-01-06001-4
- Newton, Isaac (1671). The method of fluxions and infinite series; with its application to the geometry of curve-lines (translated from Latin and published by John Colson in 1736)
- Newton, Isaac (1960). "letter to Oldenburg dated 1676 Oct 24". The correspondence of Isaac Newton. II. Cambridge University press. pp. 126–127. ISBN 0521087228
- Puiseux, Victor Alexandre (1850). "Recherches sur les fonctions algébriques". J. Math. Pures Appl. 15: 365–480
- Puiseux, Victor Alexandre (1851). "Recherches sur les fonctions algébriques". J. Math. Pures Appl. 16: 228–240
- Shafarevich, Igor Rostislavovich (1994). Basic Algebraic Geometry (2nd ed.). Springer-Verlag. ISBN 3-540-54812-2.
- Puiseux series at MathWorld
- Puiseux's Theorem at MathWorld
- Puiseux series at PlanetMath
[edit]External links
Categories: Commutative algebra | Algebraic curves
08:08 Publié dans Puiseux series | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Chronologie de l'algèbre
Chronologie de l'algèbre
Aller à :Navigation,rechercher
Le tableau de cette page fournit une chronologie sommaire des mots clefs dans le développement de l'algèbre. Le découpage en grande période tient compte de l'avancée des mathématiques dans le monde gréco-latin, arabo-musulman, et européen. Il ne prétend pas rendre compte du mouvement général, Inde et Chine comprises, du développement d'ensemble des notions algébriques.
|
Année |
Évènement |
|
|
|
|
Les origines de l'algèbre. |
|
|
|
|
|
Vers le XVIIIe siècle av. J.-C. |
Les scribes babyloniens recherchent la solution d'une équation quadratique. Voir Tablette de Strasbourg |
|
Vers le XVIIIe siècle av. J.-C. |
La tablette Plimpton 322 écrite à Babylone en écriture Cunéiforme donne une table de triplets pythagoriciens. |
|
Vers le VIIIe siècle av. J.-C. |
Le mathématicien indien Baudhayana, dans son Baudhayana Sulba Sutra, découvre les triplets pythagoriciens de façon algébrique et une solution géométrique des équations linéaires et des équations quadratiques de la forme ax2 = c and ax2 + bx = c, enfin, il trouve deux ensembles de solutions entières et positives à un système d'équations diophantiennes. |
|
Vers le VIIe siècle av. J.-C. |
Le mathématicien indien Apastamba, dans son Apastamba Sulba Sutra, résout les équations linéaires générales et utilise les systèmes d'équations diophantiennes comportant jusqu'à cinq inconnues. |
|
Vers le IVe siècle av. J.-C. |
Dans le livre II de ses Éléments, Euclide donne une construction géométrique à la règle et au compas de la solution d'une équation quadratique pour des racines réelles et positives. La construction est un résultat de l'école de géométrie de Pythagore. |
|
Vers le IVe siècle av. J.-C. |
Une construction géométrique de la solution des équations cubiques est soulevée (le problème de la duplication du cube). Il est connu que celui-ci n'a pas de solution constructible à la règle et au compas. |
|
Vers 150 |
Le mathématicien grec Héron d'Alexandrie traite des équations algébriques dans ses trois volumes de mathématiques. |
|
|
|
|
De Diophante à Al-Khwarizmi, l'algèbre se dégage de la géométrie. |
|
|
|
|
|
Vers 200 |
Le mathématicien hellénistique Diophante qui vécut à Alexandrie, et souvent considéré comme le père de l'algèbre, écrit son fameux Arithmetica, un travail préfigurant la théorie des équations algébriques et la théorie des nombres. |
|
Vers 300 |
Des équations algébriques sont traitées dans le manuel chinois de mathématiques de Liu Hui Jiuzhang suanshu (The Nine Chapters on the Mathematical Art), qui contient la solution de systèmes linéaires utilisant la méthode de la fausse position, des solutions géométriques d'équations quadratiques et la recherche de matrices équivalentes selon la méthode de Sylvester-Gauss. |
|
Le mathématicien indien Aryabhata, dans son traité Aryabhatiya, obtient le nombre complet de solutions d'un système d'équations linéaires par des méthodes équivalentes aux méthodes modernes, et décrit la solution générale de telles équations. Il donne également des solutions d'équations différentielles. |
|
|
Vers 625 |
Le mathématicien chinois Wang Xiaotong trouve les solutions numériques d'une équation cubique. |
|
Le mathématicien indien Brahmagupta, dans son traité Brahma Sputa Siddhanta, invente la méthode du chakravala pour résoudre les équations quadratiques, dont l'équation de Pell, et donne des règles pour résoudre les équations linéaires et quadratiques. Il découvre que les équations du second degré ont deux racines, dont les négatives et les irrationnelles. |
|
|
Vers 800 |
Les califes abbassides al-Mansur, Haroun ar-Rachid, et Al-Mamun, ont fait traduire les travaux scientifiques des Grecs, des Babyloniens et des Indiens en langue arabe. Commence ainsi, au Moyen-Orient, une renaissance de la culture scientifique. Bagdad devient une nouvelle Alexandrie, particulièrement sous le règne d'Al-Mamun (809-833). À la suite d'un rêve où lui serait apparu Aristote, le calife a demandé à ce qu'on traduise tout ce qu'on connaissait des Grecs, y compris l'Almageste de Ptolémée et une version complète des éléments d'Euclide. Al-Mamun fit construire à Baghdad une « Maison de la Sagesse » (Bait al-hikma) afin de rivaliser avec l'ancien Museum d'Alexandrie. |
|
|
|
|
D'Al-Khawarizmi à Stevin, l'algèbre établit ses procédures. |
|
|
|
|
|
Le mot algèbre naît. Il dérive de l'opération qui consiste à diviser les deux membres d'une égalité par une même quantité (non nulle). Il ne peut être séparé qu'au prix d'une mutilation du terme « Al'muqabala », (transposition) aujourd'hui inusité, qui désigne la soustraction aux deux membres d'une même quantité. Ces deux termes forment le projet algorithmique décrit par Muḥammad ibn Mūsā al-Ḵwārizmī dans Al-Kitab al-Jabr wa-l-Muqabala (soit « La méthode de calcul par réduction et transposition » ou restauration et comparaison). On obtient ainsi la solution des équations linéaires. Al-Khwarizmi est souvent considéré comme le père de l'algèbre médiévale, car il dégage celle-ci de l'emprise géométrique. |
|
|
Vers 850 |
Le mathématicien persan Al-Mahani (en) conçoit l'idée de réduire géométriquement le problème de la duplication du cube à un problème algébrique. |
|
Vers 850 |
Le mathématicien indien Mahavira résout différentes équations paramétrées de degrés élevés. |
|
Vers 990 |
Le mathématicien persan Al-Karaji (ou al-Karkhi), dans son ouvrage l'Al-Fakhri, développe la méthode d'Al-Khwarizmi. Il définit les monômes x, x2, x3, ... et 1/x, 1/x2, 1/x3, ... Il donne des règles qui régissent le produit de ceux-ci. Il découvre la première solution des équations de la forme ax2n + bxn = c. |
|
Vers 1050 |
Le mathématicien chinois Jia Xian (en) trouve des solutions numériques d'équations de degrés élevés. |
|
Le mathématicien persan Omar Khayyam donne une classification complète des équations cubiques aux racines positives et une solution géométrique lorsqu'elles sont exprimables au moyen d'intersections de coniques. Le « fabricant de tentes » résout géométriquement des équations de degré 3. Mais croit impossible leur résolution algébrique générale. Il généralise les méthodes, déjà utilisées par Menechme, Archimede, et Al'hazan, à toutes les équations de degré 3 possédant des racines positives. |
|
|
Le mathématicien indien Bhaskara, dans son ouvrage Bijaganita (Algebra), reconnaît les racines carrées négatives, résout des équations quadratiques à plusieurs inconnues, des équations d'ordre supérieur comme celles de Fermat ainsi que les équations du second degré générales. |
|
|
Vers 1200 |
Sharaf al-Dīn al-Tūsī (1135-1213) écrit l'Al-Mu'adalat (Traité des Équations), qui fournit huit types d'équations cubiques aux solutions positives et cinq types éventuellement privés de telles solutions. Il utilise ce qui deviendra la « méthode de Ruffini et Horner », méthode d'analyse numérique pour approcher les racines. Il développe les concepts d'extremum . Il entrevoit le rôle du discriminant des équations cubiques et utilise pour la première fois la formule de Cardan due à Scipione del Ferro pour résoudre les équations de degré 3. Roshdi Rashed, affirme que Sharaf al-Din découvrit la dérivée du polynôme de degré 3 et comprit la nécessité de lier cette dérivée aux conditions de résolution de cette équation. |
|
Au XIIe siècle |
Une équipe de traducteurs sous la direction de Gondisalvius traduit les manuscrits arabes de la bibliothèque de Cordoue. parmi eux, se distingue nettement un des premiers algébristes occidentaux Jean Hispalensis. Dans le même mouvement, Jordan de Nemore introduit dans son Isagogue la notations des inconnus par des symboles. |
|
En 1202 |
L'algèbre arabe conquiert l'Europe au travers du livre du Pisan Leonardo Fibonacci et de son livre Liber Abaci. |
|
En 1299 |
Le mathématicien chinois Zhu Shijie résout les équations quadratiques, numériquement des quartiques et des équations avec plusieurs inconnues (au plus 4). Il donne le premier la méthode de développement des polynômes nommé Méthode de Horner. |
|
Vers 1400 |
Jamshīd al-Kāshī développe une première forme de la méthode de Newton Regula falsi. |
|
Vers 1400 |
Le mathématicien indien Madhava de Sangamagrama trouve la solution de fonctions transcendantales et d'équations différentielles par itération. |
|
Le mathématicien arabe Abū al-Hasan ibn Alī al-Qalasādī donne une première étape de notation symbolique. |
|
|
Vers 1500 |
Le mathématicien italien Scipione del Ferro, élève de Pacioli parvient pour la première fois à une résolution algébrique d'un grand type d'équations du troisième degré. Il ne les publie pas. |
|
Le mathématicien allemand Christoff Rudolff introduit la notation des racines carrées dans son ouvrage Die Coss. |
|
|
Vers 1530 |
Robert Recorde introduit le signe = et Michael Stifel développe une première forme de notation algébrique. |
|
Niccolo Fontana Tartaglia retrouve les formules de Scipione del Ferro. |
|
|
Cardan, aidé de son secrétaire Ludovico Ferrari, publie dans son Ars magna les formules qu'il a achetées à Tartaglia sous le sceau du secret ainsi que celles recueillies dans un carnet du défunt Scipione del Ferro. Ferrari donne la solution des équations de degré 4. |
|
|
Rafaelle Bombelli donne une formulation des nombres complexes et les règles de calculs effectifs. Une racine carrée de -1 apparaît sous la forme piu di meno. |
|
|
Le mathématicien néerlandais Stevin rédige un manuel de seize pages pour populariser l'art de compter avec les nombres décimaux. Il écrit les puissances du dixième cernées d'un exposant. Il donne la première écriture des vecteurs. |
|
|
|
|
|
De Viète à Gauss, l'algèbre triomphe des équations polynomiales. |
|
|
|
|
|
Le mathématicien français François Viète ouvre une nouvelle période de l'algèbre en faisant opérer les calculs sur des lettres, voyelles pour désigner les inconnues et consonnes pour les paramètres. C'est l'algèbre nouvelle. Par cet acte fondateur, il inaugure la période qui voit triompher le formalisme dans la résolution des équations algébriques. Par ailleurs, il donne le développement du binôme de Newton, résout une équation de degré 45[réf. nécessaire] et introduit l'usage des parenthèses In artem analyticam isagoge. |
|
|
Période de diffusion de l'algèbre nouvelle grâce aux éditions de François Viète par Marin Ghetaldi, Alexander Anderson et Van Schooten. |
|
|
Le mathématicien anglais Thomas Harriot introduit, dans une publication posthume, les symboles > et <. La même année William Oughtred donne pour la première fois le symbole multiplié. |
|
|
Le philosophe et mathématicien français René Descartes renomme les inconnus x,y,z et les paramètres a,b,c et étend l'usage de l'algèbre aux longueurs et au plan, créant avec Pierre de Fermat la géométrie analytique. |
|
|
Le philosophe et mathématicien français Blaise Pascal nomme ordonnée la coordonnée portée sur le second axe du plan. |
|
|
Le philosophe et mathématicien allemand Gottfried Leibniz développe le maniement du calcul symbolique par des règles qu'il nomme characteristica generalis. Il définit les courbes algébriques et nomme abscisse la première coordonnée. Enfin, il résout les systèmes linéaires en usant - sans justification théorique - de matrices et de déterminants. |
|
|
Vers 1680 |
Isaac Newton développe le calcul formel sur les séries entières, et calcule lescontacts des branches d'une courbe algébrique par la méthode du polygone qui porte son nom. |
|
Le mathématicien japonais Kowa Seki, dans sa Méthode de résolution des problèmes cachés, découvre les premières version du déterminant. Il résout des équations de degré 4 et 5 et donne les formules de résolution des équations cubiques. |
|
|
Le mathématicien suisse Leonhard Euler donne la résolution des équations cubiques de façon achevée. |
|
|
L'encyclopédiste français Jean le Rond D'Alembert donne la première preuve du théorème fondamental de l'algèbre. |
|
|
Le mathématicien français Gabriel Cramer, dans son traité Introduction à l'analyse des courbes algébriques, établit la règle de Cramer et étudie les courbes algébriques, des systèmes qu'on nommera matriciels à l'aide de « déterminants ». |
|
|
Le mathématicien français Bézout publie ses travaux sur le degré des équations et la théorie des équations algébriques. Donnant une première preuve reliant le degré et l'intersection. |
|
|
Le mathématicien italien Paolo Ruffini démontre partiellement l'impossibilité de résoudre par radicaux toutes les équations de degré cinq. |
|
|
Le mathématicien allemand Gauss donne un démonstration rigoureuse du théorème de d'Alembert. Il commence la publication des disquisitiones qui contiennent la première preuve de la loi de réciprocité quadratique dans la partie IV)1 . |
|
|
Le mathématicien suisse Argand publie la première représentation plane des nombres complexes et utilise des mesures algébriques. |
|
|
Le mathématicien français Gergonne introduit le symbole marquant l'inclusion. |
|
|
vers 1820 |
Le mathématicien français Adrien-Marie Legendre donne par son symbole la caractérisation des résidus de carrés dans les anneaux de congruence. |
|
Le mathématicien français Jean-Victor Poncelet fonde la géométrie projective. |
|
|
Le mathématicien norvégien Niels Henrik Abel donne un exemple d'équation de degré cinq insoluble par radicaux. Il introduit la notion de nombres algébriques (publié en 1826) |
|
|
Le mathématicien allemand Möbius introduit le calcul barycentrique oublié depuis le Suisse Paul Guldin et Archimède. |
|
|
Gauss donne une construction rigoureuse des nombres complexes. |
|
|
|
|
|
|
|
|
La Théorie de Galois, développée par le mathématicien français Évariste Galois ouvre le champ d'une nouvelle ère, celle des structures. Des prémisses de la théorie des groupes sont à rechercher chez Hudde (1659), Saunderson (1740) Le Sœur (1748) et Waring (1762- 1782), Lagrange (1770 - 1771) etVandermonde (1770). Mais Évariste Galois signe véritablement l'apparition de la notion de groupe dans son travail, mal reconnu, où se trouvent les conditions nécessaires et suffisantes pour qu'une équation soit résoluble par radicaux. |
|
|
Le baron français Cauchy établit une première théorie des déterminants. Il diagonalise les endomorphismes symétriques réels dans des cas simples. |
|
|
Le géomètre français Michel Chasles introduit le terme de birapport, d'homothétie et d'homographie, notions oubliées depuis Girard Desargues. |
|
|
Le mathématicien allemand Hermann Grassmann définit le premier une notion d'algèbre, méconnue à son époque, mais qui aura l'heur d'être comprise quelques vingt ans plus tard par Sophus Lie. À la même date, l'irlandais William Rowan Hamilton définit des espaces de vecteurs. La notion d'espace vectoriel sera clairement définie par l'Allemand Möbius et par l'Italien Giuseppe Peano 40 ans plus tard. |
|
|
Énoncé de la conjecture diophantienne d'Eugène Charles Catalan. |
|
|
Publication par Liouville des travaux d'Évariste Galois (Liouville, Vol. XI). |
|
|
Le mathématicien allemand Ernst Kummer parvient à démontrer le théorème de Fermat pour tous les nombres premiers réguliers et dégage la théorie des idéaux premiers, il approfondit la décomposition des groupes. |
|
|
Publication par le mathématicien irlandais George Boole des lois de la pensée où l'analyse logique est automatisée via une structure d'algèbre. |
|
|
Vers 1850 |
Les mathématiciens anglais Arthur Cayley et James Joseph Sylvester introduisent le terme de matrices. |
|
Le mathématicien allemand Richard Dedekind introduit les termes d'anneaux et de corps dans son livre Lehrbuch des Algebra. |
|
|
Le mathématicien français Victor Puiseux développe ses séries, permettant ainsi une meilleure approche des singularités d'une courbe et l'étude de branches conjuguées 2. Un lemme de préparation de Karl Weierstrass, publié en 1895, justifiera ultérieurement cette approche. |
|
|
Le mathématicien français Liouville montre l'existence d'une infinité de nombres transcendants. |
|
|
Le mathématicien allemand Leopold Kronecker confirme les résultats de Niels Abel et d'Évariste Galois. Les travaux de Arthur Cayley font de même l'année suivante. |
|
|
Démonstration par le mathématicien allemand Gustav Roch du théorème de Riemann-Roch reliant le degré et le genre d'une courbe algébrique dans une première version analytique. |
|
|
Les mathématiciens allemands Siegfried Heinrich Aronhold et Alfred Clebsch travaillent sur les théories de l'invariant. Ils sont à l'origine de la vision algébrique des théories de Riemann, et donc les ancêtres de la cohomologie algébrique. |
|
|
Le mathématicien français Camille Jordan montre l'invariance à ordre près de la suite des groupes quotients dans la décomposition des groupes. Son travail se prolonge par ceux de Eugen Netto (1882) et de Von Dyck (1882) qui définit les groupes dans leur sens actuel. |
|
|
Le mathématicien allemand Felix Klein, dans son programme d'Erlangen, met l'étude des groupes au centre de la définition des différentes géométries. |
|
|
Le mathématicien français Charles Hermite démontre la transcendance de e. Théorème d'Hermite-Lindemann. |
|
|
Le mathématicien allemand Max Noether donne des théorèmes d'existence de courbes algébriques dans certains faisceaux de courbes. L'anglais William Kingdon Clifford étudie les algèbres qui portent son nom et seront un des objets féconds du siècle suivant. |
|
|
Le mathématicien allemand Cantor jette les bases de la théorie des ensembles et des cardinaux. Il montre que les nombres algébriques sont en fait dénombrables. |
|
|
Le mathématicien allemand Ferdinand Georg Frobenius donne la première démonstration correcte du théorème de Cayley-Hamilton. Il enrichit, par ailleurs, la théorie de la réduction et des algèbres (associatives). |
|
|
Vers 1880 |
Le mathématicien français Émile Picard étudie les surfaces algébriques, les générateurs des complexes linéaires et les groupes de diviseurs qui portent son nom. |
|
Les mathématiciens anglais William Burnside, norvégien Ludwig Sylow (82), américain Leonard Eugene Dickson (91), allemand Otto Hölder, français Emile Mathieu et allemand Heinrich Weber complètent la théorie des groupes linéaires et des groupes finis. |
|
|
Les mathématiciens italiens Castelnuovo et Federigo Enriques collaborent sur les surfaces, les classent en cinq types, et découvrent les théorèmes qui portent leur nom sur les systèmes linéaires. |
|
|
L'étude systématique des groupes s'amplifie avec le mathématicien norvégien Sophus Lie, l'allemand Issai Schur et le français Elie Cartan. Ce dernier introduit la notion de groupe algébrique. |
|
|
L'étude des groupes discrets se poursuit avec Felix Klein, Sophus Lie, Henri Poincaré, Émile Picard, en liaison avec la monodromie. |
|
|
Le mathématicien français Elie Cartan publie sa thèse sur les groupes de transformations. Il s'intéressera ultérieurement aux algèbres associatives et aux espaces symétriques. |
|
|
Le mathématicien allemand Holder montre l'isomorphisme des groupes quotients entrant dans les tours de décompositions. |
|
|
Le mathématicien italien Giuseppe Peano introduit le symbole d'appartenance ainsi qu'une première version de l'écriture des quantificateurs. Leur forme définitive sera donnée par David Hilbert. Il donne plus de 40000 définitions dans une langue qu'il veut universelle. |
|
|
|
|
|
De David Hilbert à Kurt Gödel, l'algèbre des structures complexes. |
|
|
|
|
|
Le mathématicien allemand David Hilbert donne une première approche du corps de classe. Dans sa conférence 1900, lors du deuxième congrès international de mathématiques tenu à Paris, il présente les 21 problèmes de Hilbert, dont une partie porte sur la théorie de la démonstration et l'algèbre. On retiendra notamment le troisième qui débouche sur le paradoxe de Banach-Tarski, le cinquième, le huitième (qui demeure ouvert), le quinzième (qui appelle la théorie de l'intersection). Ils sont de natures plus ou moins profondes, mais ils ont fortement influé sur les mathématiques du siècle. |
|
|
Les travaux concernant les automorphismes des groupes de grande dimension sont poursuivis par Moore, William Burnside et vulgarisés par Leonard Eugene Dickson3. |
|
|
Le rôle des groupes simples est développé par le Français Camille Jordan. Des critères de non-simplicité le sont par l'Allemand Otto Hölder, qui classifie 200 groupes non triviaux. On atteint avec l'Américain Frank Nelson Cole le nombre de 660, avec l'Anglais William Burnside 1092 (2001 de nos jours par l'Américain Gary Lee Miller) 4. |
|
|
Le mathématicien allemand Anton Suschkewitsch et le Français Jean-Armand De Seguier (1862-1935)5 fondent la théorie des semi-groupes. |
|
|
Vers 1910 |
Les travaux de Walther von Dyck, l'Allemand Max Dehn (1900-1910), le Danois Jakob Nielsen 6 complètent la théorie des groupes. |
|
Le mathématicien français Albert Châtelet travaille sur les automorphismes des groupes abéliens. |
|
|
Collaboration des mathématiciens anglais J.E. Littlewood et G. H. Hardy avec le mathématicien indien S. Ramanujan. |
|
|
Le mathématicien français Gaston Julia décrit les formes binaires non quadratiques. L'allemand Erich Hecke étudie l'équation fonctionnelle de la fonction zêta de Dedekind, manie les fonctions thêta et certains caractères de fonctions L nommés d'après son nom. |
|
|
Création des algèbres de Von Neumann. |
|
|
Hermann Weyl développe ses travaux sur les groupes compacts. |
|
|
Travaux de l'anglo-canadien Coxeter en combinatoire et en théorie des groupes permettant d'unifier les groupes décrits par Hermann Weyl. |
|
|
Le mathématicien japonais Teiji Takagi7 livre les premiers résultats fondamentaux sur le corps de classe. |
|
|
Louis Mordell a démontré que l'ensemble des points rationnels d'une courbe elliptique forme un groupe abélien de type fini. Il est à l'origine de la conjecture de Mordell-Weyl, qu'établira Gerd Faltings en 1983. |
|
|
Heinz Hopf démontre que toute variété Riemannienne de dimension 3 de courbure constante est globalement isométrique à un espace euclidien, sphérique ou hyperbolique. Il donne une nouvelle démonstration au théorème de Poincaré-Hopf. Les notions qu'il introduit marquent la naissance des Algèbres de Hopf. |
|
|
Le mathématicien allemand Helmut Hasse publie sa théorie des corps de nombres algébriques. Son compatriote Richard Brauer commence à développer le travail dans les algèbres qui portent son nom. |
|
|
Le mathématicien autrichien Artin publie la théorie de la loi de réciprocité générale. |
|
|
Le mathématicien français André Weil étudie l'arithmétique des courbes algébriques. |
|
|
La mathématicienne allemande Emmy Noether fixe la théorie des hypercomplexes ou algèbres associatives. |
|
|
Parution de la Moderne Algebra de Van der Warden. Le mathématicien hollandais résout le quinzième problème de Hilbert en définissant une vraie théorie de l'intersection dans le groupe des diviseurs d'une variété algébrique. |
|
|
Vers 1930 |
Le mathématicien anglais Raymond Paley démontre l'existence de matrices de Hadamard d'ordre q+1 lorsque q est une puissance d'un nombre premier congrue à 3 modulo 4. Il fonde ainsi la conjecture d'Hadamard. |
|
Le mathématicien allemand Wolfgang Krull développe la théorie des idéaux maximaux. |
|
|
Le mathématicien français Claude Chevalley étudie les corps de classe des corps finis et les corps locaux. Il introduit les adèles et les idèles. Son camarade André Weil fonde ce qui deviendra la Cohomologie Galoisienne. |
|
|
Naissance de Nicolas Bourbaki sous l'impulsion d'André Weil, d'Henri Cartan, de Claude Chevalley, de Jean Delsarte8, de Jean Dieudonné, de Charles Ehresmann, de René de Possel et de Szolem Mandelbrojt |
|
|
Le mathématicien polonais Tarski poursuit les travaux de logique à propos de la complétude de l'algèbre et des théorèmes de transfert. Il montre l'indécidabilité de la théorie des groupes. C'est le théorème de Tarski. Il retrouve ainsi les résultats non publiés du très cosmopolite Kurt Gödel (1931). |
|
|
Le mathématicien russe Andreï Kolmogorov définit son travail topologique en terme cohomologique. |
|
|
Oscar Zariski définit la topologie de Zariski sur les variétés algébriques. |
|
|
|
|
|
De Bourbaki à Andrew Wiles, l'algèbre de la cohomologie, des catégories et des schémas. |
|
|
|
|
|
Travaux du mathématiciens français Pierre Samuel sur la multiplicité. |
|
|
Les Américains Samuel Eilenberg et Saunders Mac Lane fondent la notion de catégorie. |
|
|
Le mathématicien américain John Tate donne une nouvelle forme de cohomologie. |
|
|
Les séminaires Cartan, rue d'Ulm, conduisent le mathématicien français Henri Cartan et Samuel Eilenberg à la publication de Homological Algebra (1956). L'étude chomologique du corps de classe conjoint les efforts des mathématiciens français Claude Chevalley, de Jean-Louis Koszul et de Jean-Pierre Serre. |
|
|
Publication des livres de Pierre Samuel. |
|
|
La conjecture de Shimura-Taniyama-Weil annonce que toute courbe elliptique est associée à une forme modulaire de même fonction L. Une version faible est annoncée par le mathématicien japonais Yutaka Taniyama. Elle est reformulée par André Weil dans les années 1960. |
|
|
Le mathématicien ukrainien Oscar Zariski utilise les surfaces qui portent son nom pour obtenir des surfaces non rationnelles mais unirationnelles. Le problème de l'unirationnalité demeure ouvert même pour des surfaces simples 9. |
|
|
Vers 1960 |
L'Américain John Griggs Thompson accomplit des progrès décisifs dans la classification des groupes finis. |
|
Vers 1960 |
Le mathématicien japonais Kunihiko Kodaira achève ses travaux par un renouvellement de la classification des surfaces algébriques. |
|
Le mathématicien anglais David Mumford rénove dans le langage des schémas les points de vue de Kodeira sur la classification des surfaces dans l'American Journal of Mathematics ; notamment en caractéristique p. |
|
|
Le mathématicien français Yves Hellegouarch étudie les propriétés de courbes elliptiques associées à des contre-exemples au dernier théorème de Fermat. Il fonde l'étude des formes modulaires. |
|
|
Le mathématicien français Alexandre Grothendieck développe et pousse à son terme la théorie des catégories et des schémas. |
|
|
Énoncé par le mathématicien canadien Robert Langlands du Programme de Langlands qui permet de lier la généralisation des fonctions L de Dirichlet dans le cas des groupes de Galois non-abéliens aux représentation cuspidale automorphes. Travail initialisé par Israel Gelfand. |
|
|
Vers 1980 |
Le mathématicien français Alain Connes résout une grande part des problèmes soulevés par la théorie des algèbres de Von Neumann, notamment la classification des facteurs de type III. Pour cela, il sera récompensé parla médaille Fields en 1982. |
|
Vers 1980 |
Le mathématicien russe Yuri Manin établit une part de la conjecture de Mordell et, avec Iskovskikh, un contre exemple à la conjecture de Lüroth. |
|
Gerd Faltings montre le Théorème de Faltings précédemment connu sous le nom de conjecture de Mordell. Il donne des résultats sur le nombre de solutions d'une équation diophantienne. |
|
|
Le mathématicien russe Vladimir Drinfeld donne forme au groupe quantique et généralise la notion d'algèbre de Hopf. |
|
|
Les travaux du mathématicien anglais Andrew Wiles, rectifiés par Richard Taylor montrent une grande partie de la conjecture de Shimura-Taniyama-Weil. Ils étendent ainsi les classes de courbes où la conjecture de Birch et Swinnerton-Dyer est vérifiée et font tomber le Dernier théorème de Fermat. |
|
|
Le mathématicien français Laurent Lafforgue démontre une partie des conjectures de Langlands. |
|
|
Démonstration de la conjecture de Shimura-Taniyama-Weil par Christophe Breuil, Brian Conrad, Fred Diamond, et Richard Taylor. |
|
|
Le mathématicien russe Vladimir Voevodsky développe la notion d'homotopie pour les variétés algébriques ainsi que la cohomologie motivique, faisant tomber conjecture de Milnor. |
|
|
Une matrice de Hadamard d'ordre 428 a été donnée le 21 juin 2004 par Hadi Kharaghani et Behruz Tayfeh-Rezaie. Le plus petit ordre multiple de 4 pour lequel aucune matrice de Hadamard n'est connue est actuellement 668. |
Notes et références[modifier]
- ↑ La loi de réciprocité quadratique [archive] sur le site DynaMaths
- ↑ [1] Une approche des séries de Puiseux
- ↑ [2] la page Wikipédia anglaise de Leonard Dickson
- ↑ [3] [archive] le site contemporain de Gary Miller
- ↑ [4] [archive] une trace de De Seguier au travers de la biographie de Paul Dubreil (de) sur le site Chronomaths de Serge Mehl
- ↑ [5] la page Wikipédia anglaise de Jakob Nielson
- ↑ [6] [archive] Un livre en allemand sur la naissance de l'école algébriste japonaise
- ↑ [7] la page de Wikipédia allemande de Jean Delsarte
- ↑ [8] [archive] Un exemple d'étude de surface de Zariski
Catégories : Algèbre | Histoire des mathématiques | [+]
Source : http://fr.wikipedia.org/wiki/Chronologie_de_l'alg%C3%A8bre
08:03 Publié dans Algèbre, Histoire des mathématiques | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
04/04/2011
Lettres grecques en mathématiques financières
Lettres grecques en mathématiques financières
Source : http://fr.wikipedia.org/wiki/Lettres_grecques_en_math%C3%...
Livres de mathématiques financières
Les lettres grecques ou grecques ou grecs sont les instruments de base de la gestion financière des options. Elles découlent des principaux modèles d'évaluation d'option, notamment de celui de Black et Scholes.
Ces indicateurs calculent l'impact sur le prix de l'option d'une variation des paramètres qui le forment :
- le prix du sous-jacent (ou spot)
 ,
, - le prix d'exercice fixé par l'option
 ,
, - la volatilité implicite
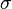 ,
, - le temps
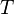 ,
, - le taux d'intérêt (ou interest rate)
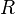 .
.
 , la loi normale centrée réduite.
, la loi normale centrée réduite.
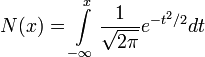 , la fonction de répartition de la loi normale centrée réduite.
, la fonction de répartition de la loi normale centrée réduite.
Sommaire[masquer] |
Définitions[modifier]
En reprenant les notations expliquées dans le modèle de Black et Scholes et en notant 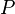 la prime de l'option, on a les dérivées suivantes.
la prime de l'option, on a les dérivées suivantes.
Le delta[modifier]
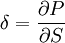
δCall = N(d1)
δPut = δCall − 1 = N(d1) − 1
Le delta d'une option mesure la sensibilité de son prix à une variation donnée du cours du sous-jacent.
La prime d'un call est une fonction croissante du prix du sous-jacent,  , alors que celle d'un put en est une fonction décroissante,
, alors que celle d'un put en est une fonction décroissante,  . En effet, plus le prix du sous-jacent est élevé, plus la probabilité que le call soit dans la monnaie est grande. Symétriquement, plus le prix du sous-jacent est bas, plus la probabilité que le put soit dans la monnaie est grande. Ainsi, lorsqu'une option a un delta égal (en valeur absolue) à ou proche de 0,5, on dit qu'elle est à la monnaie.
. En effet, plus le prix du sous-jacent est élevé, plus la probabilité que le call soit dans la monnaie est grande. Symétriquement, plus le prix du sous-jacent est bas, plus la probabilité que le put soit dans la monnaie est grande. Ainsi, lorsqu'une option a un delta égal (en valeur absolue) à ou proche de 0,5, on dit qu'elle est à la monnaie.
En outre, 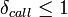 et
et  . On le comprend en prenant le cas extrême d'un call de prix d'exercice nul, sur un sous-jacent qui ne peut pas avoir un prix négatif. La prime de cette option sera toujours égale au prix du sous-jacent :
. On le comprend en prenant le cas extrême d'un call de prix d'exercice nul, sur un sous-jacent qui ne peut pas avoir un prix négatif. La prime de cette option sera toujours égale au prix du sous-jacent : 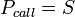 . Sa dérivée par rapport au prix du sous-jacent sera donc égale à 1.
. Sa dérivée par rapport au prix du sous-jacent sera donc égale à 1.
Un raisonnement symétrique permet de comprendre pourquoi le delta d'un put est supérieur à -1.
Le delta d'un portefeuille d'options est la somme des deltas de chacune des options qui le composent.
Le gamma[modifier]
article principal : gamma

Le gamma représente la convexité du prix d'une option en fonction du cours du sous-jacent. Il indique si le prix de l'option a tendance à évoluer plus ou moins vite que le prix du sous-jacent. Par analogie, on peut comparer le delta à la vitesse et le gamma à l'accélération.
Une autre lecture du gamma est le sens d'évolution du delta en fonction du prix du sous-jacent. Un gamma positif indique que prix du sous-jacent et delta évoluent dans le même sens, alors qu'un gamma négatif montre le contraire.
Comme  et
et 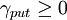 , on dit qu'un acheteur de call ou de put sera long de gamma, ou que son portefeuille sera gamma positif, et qu'un vendeur sera court (short) de gamma, ou gamma négatif. Toutes choses égales par ailleurs, le gamma est maximum lorsque l'option est à la monnaie (i.e. lorsque son delta est égal à 0.5). Un portefeuille comportant des positions acheteuses (dites longues) et vendeuses (dites courtes) d'options à différents prix d'exercice (sur un même sous-jacent) verra donc la valeur de son gamma évoluer, voire changer de signe, en fonction des évolutions du prix du sous-jacent.
, on dit qu'un acheteur de call ou de put sera long de gamma, ou que son portefeuille sera gamma positif, et qu'un vendeur sera court (short) de gamma, ou gamma négatif. Toutes choses égales par ailleurs, le gamma est maximum lorsque l'option est à la monnaie (i.e. lorsque son delta est égal à 0.5). Un portefeuille comportant des positions acheteuses (dites longues) et vendeuses (dites courtes) d'options à différents prix d'exercice (sur un même sous-jacent) verra donc la valeur de son gamma évoluer, voire changer de signe, en fonction des évolutions du prix du sous-jacent.
Le gamma d'un portefeuille d'options est la somme des gammas de chacune des options qui le composent.
Le gamma est une fonction décroissante de la maturité.
NB: Pour le call, le delta est nécessairement positif (au pire nul) : une option d'achat vaut d'autant plus cher que le cours du sous-jacent est élevé. Par ailleurs, le delta du call est nécessairement compris entre 0 et 1.
Pour le put, le delta est nécessairement négatif (au pire nul) : une option de vente à un prix fixe vaut d'autant plus cher que le cours du sous-jascent est bas. Par un raisonnement symétrique au précédent on peut montrer que le delta du put est strictement compris entre -1 et 0.
Le thêta[modifier]
Le thêta est le coût (ou le gain) du temps qui passe sur un portefeuille d'options. Il évalue combien le passage du temps influe sur la valeur d'une option. Une position longue d'options (gamma positive) sera thêta negative. Le trader devra veiller tous les jours à payer son thêta journalier en profitant de sa position longue en gamma. On préfèrera donc être long d'une option qui soit suffisamment volatile, ainsi en rebalancant la position, on pourra payer le temps qui passe en tradant le gamma.
Pour un call européen sur une action ne versant pas de dividendes :

Pour un put européen sur une action ne versant pas de dividendes :

Le rhô[modifier]
Il est le taux de variation de la valeur de la prime en fonction du taux d'intérêt.

- ρcall = KTe − rTN(d2)
- ρput = − KTe − rTN( − d2)
Le véga[modifier]
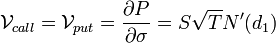
Le véga mesure de la sensibilité à la volatilité implicite (voir modèle Black-Scholes). Représenté par la lettre nu minuscule car le nom « véga » n'est pas lui-même un nom de lettre grecque.
Comme  et
et  , on dit qu'un acheteur de call ou de put sera long de véga, ou que son portefeuille sera véga positif, et qu'un vendeur sera court (short) de véga, ou véga négatif.
, on dit qu'un acheteur de call ou de put sera long de véga, ou que son portefeuille sera véga positif, et qu'un vendeur sera court (short) de véga, ou véga négatif.
Contrairement au gamma et au thêta, le véga est une fonction croissante de la maturité. Ainsi une augmentation parallèle de la volatilité aura-t-elle plus d'impact sur les options dont la date d'échéance est éloignée que sur celles dont elle est proche. Une position généralement appreciée des traders et des market makers est alors d'avoir une position globalement gamma positive (sensible aux grands mouvements de marché) et véga négative, qui consiste à acheter des options courtes et à vendre des options longues.
Utilisation[modifier]
Des indicateurs de risques[modifier]
Les grecques sont avant tout des indicateurs des risques pris par celui qui a acheté ou vendu des options. Elles détaillent ces risques par origine : le prix du sous-jacent, la volatilité implicite, le temps et le taux d'intérêt.
Elles vont donc permettre de gérer chacun de ces paramètres finement, que ce soit au niveau du trading, ou au niveau des services de contrôle des risques dans les structures où ils existent.
Des outils de gestion pour le trader[modifier]
La stratégie de gestion d'options la plus courante est appelée gestion en delta neutre. Elle consiste à éliminer à chaque instant le risque lié au prix du sous-jacent.
Prenons l'exemple d'un trader qui vend à l'instant t0 n calls identiques, de delta δ0. Le delta de son portefeuille est alors de 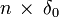 . Voulant immuniser son portefeuille contre les variations de prix du sous-jacent, il va annuler ce delta. La solution la plus simple en général est alors d'acheter (car dans le cas d'un call,
. Voulant immuniser son portefeuille contre les variations de prix du sous-jacent, il va annuler ce delta. La solution la plus simple en général est alors d'acheter (car dans le cas d'un call,  ) une quantité
) une quantité 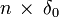 de sous-jacent. En effet, par définition, le delta du sous-jacent est égal à 1.
de sous-jacent. En effet, par définition, le delta du sous-jacent est égal à 1.
Seulement, au cours de la vie de cette option, son delta va évoluer, notamment parce que le prix du sous-jacent aura changé. À l'instant t1, le delta δ1 sera différent de δ0 et donc la couverture du portefeuille ne sera plus optimale : le trader devra ajuster celle-ci en rachetant ou en vendant un peu plus de sous-jacent.
Prendre en compte le gamma permet d'optimiser cette gestion. Lorsque le gamma est positif, le delta augmente quand le prix du sous-jacent monte. Situation confortable pour l'opérateur qui doit vendre du sous-jacent lors des hausses marché, et en racheter lors des baisses. Ces allers-retours sur le sous-jacent sont utilisés pour regagner le coût du passage du temps (on dit souvent : payer le thêta). En revanche, si le gamma est négatif, il doit mener les opérations inverses, et les allers-retours doivent perdre moins que ce que fait gagner le thêta.
En outre, plus le gamma est important, plus les interventions pour neutraliser le delta seront fréquentes, ce qui peut poser un problème dans un environnement où les coûts de transaction sont élevés. À l'inverse, si le gamma de l'option est nul, le trader peut conserver une position fixe tout au long de la durée de vie de l'option.
Une gestion en delta neutre peut être un moyen de parier sur la volatilité : le portefeuille étant théoriquement immunisé contre les variations de prix du sous-jacent, sa valeur va principalement évoluer en fonction de la volatilité implicite.
Voir aussi[modifier]
- Le modèle de Black et Scholes
- Dérivée
- Option (finance), call, put, straddle, warrant
- Mathématiques financières
- Évaluation d'option
Liens externes[modifier]
- les Grecques, Les Grecques expliquées sur warrant-invest.com
07:43 Publié dans Mathématiques financières | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Mathématiques financières sur Wikipedia
Mathématiques financières
Source : http://fr.wikipedia.org/wiki/Math%C3%A9matiques_financi%C...
Livres de mathématiques financières :
Les mathématiques financières sont une branche des mathématiques appliquées ayant pour but la modélisation, la quantification et la compréhension des phénomènes régissant lesmarchés financiers. Elles utilisent principalement des outils issus de l'actualisation, de la théorie des probabilités, du calcul stochastique, des statistiques et du calcul différentiel.
L'actualisation et l'utilisation des probabilités remontent à plusieurs siècles. Louis Bachelier, par sa thèse intitulée Théorie de la spéculation en 1900, est considéré comme le fondateur des mathématiques financières. La théorie moderne des marchés financiers remonte au MEDAF et à l'étude du problème d'évaluation des options dans les années 1950-1970.
Sommaire[masquer] |
Nature aléatoire des marchés[modifier]
L'observation empirique du cours des actifs financiers montre que ceux-ci ne sont pas déterminés de façon certaine par leur histoire. En effet, les nombreuses opérations d'achat ou de vente ne sont pas prévisibles, font souvent intervenir des éléments n'appartenant pas à l'historique et modifient le cours de l'actif. Celui-ci est donc souvent représenté par un processus stochastique. Benoit Mandelbrot a établi par des considérations statistiques qu'un modèle aléatoire ordinaire, par exemple gaussien, ne pouvait convenir. L'aléa reste cependant souvent modélisé par un mouvement brownien1, bien que des modèles plus élaborés (par exemple, le modèle de Bates) tiennent compte de la non-continuité des cours (présence de sauts dus à des chocs boursiers), ou de la non-symétrie des mouvements à la baisse et à la hausse.
Hypothèse de non arbitrage[modifier]
L'une des hypothèses fondamentales des modèles usuels est qu'il n'existe aucune stratégie financière permettant, pour un coût initial nul, d'acquérir une richesse certaine dans une date future. Cette hypothèse est appelée absence d'opportunités d'arbitrage. Elle est justifiée théoriquement par l'unicité des prix caractérisant un marché en concurrence pure et parfaite. Pratiquement, il existe des arbitrages qui disparaissent très rapidement du fait de l'existence d'arbitragistes, acteurs sur les marchés dont le rôle est de détecter ce type d'opportunités et d'en profiter. Ceux-ci créent alors une force qui tend à faire évoluer le prix de l'actif vers son prix de non-arbitrage.
Hypothèse de complétude des marchés[modifier]
Une autre hypothèse, beaucoup plus remise en question, est que tout flux à venir peut être répliqué exactement, et quel que soit l'état du monde, par un portefeuille d'autres actifs bien choisis. Les modèles ne comprenant pas les hypothèses de non arbitrage et de complétude des marchés sont dits modèles de marchés imparfaits.
Probabilité risque-neutre[modifier]
Une des conséquences des hypothèses de non arbitrage et de complétude des marchés est l'existence et l'unicité à équivalence près d'une mesure de probabilité dite probabilité martingale ou « probabilité risque-neutre » telle que le processus des prix actualisés des actifs ayant une source de risque commune est une martingale sous cette probabilité. Cette probabilité peut s'interpréter comme celle qui régirait le processus de prix des sous-jacents de ces actifs si l'espérance du taux de rendement de ceux-ci était le taux d'intérêt sans risque (d'où le terme risque-neutre: aucune prime n'est attribuée à la prise de risque).
Un processus stochastique est une martingale par rapport à un ensemble d'information si son espérance en date t conditionnelle à l'information disponible en date s < t est égale à la valeur du processus en date s, c'est-à-dire qu'un processus A(u) est une martingale si l'espérance conditionnelle de A(t) par rapport a la filtration F(s) est A(s) (i.e : ![mathbb{E}left[A_t|mathcal{F}_sright]=A_s](http://upload.wikimedia.org/math/f/2/3/f23b63c07f72e3fc4b9be0147672843f.png) ).
).
Le problème d'évaluation des produits dérivés[modifier]
L'évaluation (on dit aussi pricing ou, à tort, « valorisation » qui signifie « augmenter la valeur ») des produits dérivés se ramène souvent au calcul du prix aujourd'hui d'un actif dont on ne connaît le prix qu'à une date future. Il se ramène donc au calcul d'une espérance conditionelle. Le modèle Black-Scholes est un exemple de solution analytique au problème d'évaluation des options d'achat (call) ou de vente (put) d'un actif sous jacent. Dans le cas d'un call, le problème s'écrit :
 ,
,
où St est le cours de l'actif, K est le prix d'exercice (ou Strike), r(s) est le taux d'intérêt instantané sans risque à la date s, t est la date « d'aujourd'hui », T est la maturité de l'option, c’est-à-dire la date à laquelle la décision d'exercice peut être prise.
La formule de Black et Scholes est un exemple de solution analytique à ce problème, sous des hypothèses restrictives sur la dynamique du sous-jacent. Voir aussi option.
Une obligation convertible peut s'évaluer comme un lot comprenant une option d'achat et une obligation classique.
Taux d'intérêt et dérivés de taux d'intérêt[modifier]
Les modèles simples supposent que le taux d'intérêt, c'est-à-dire le loyer de l'argent est constant. Cette hypothèse est centrale, car sous l'hypothèse d'absence d'opportunités d'arbitrage, un portefeuille non risqué rapporte ce taux d'intérêt. Or cette approximation n'est évidemment plus admissible dès que le cours de l'actif est essentiellement lié au niveau du taux d'intérêt (par exemple, le cours des obligations à taux variable, des swaptions...) ne peuvent être expliqués par un modèle à taux d'intérêt fixe.
On modélisera donc le taux d'intérêt par un processus aléatoire, auquel on demandera:
- d'être au mieux compatible avec l'ensemble des courbes des taux observables
- d'avoir des propriétés réalistes, comme de ne pas autoriser des taux négatifs, de rendre compte de l'effet de retour à la moyenne (mean reversion), ...
Les travaux de Vasicek ont permis d'exhiber un processus, dérivé du processus d'Ornstein-Uhlenbeck, cohérent, dont le loyer de l'argent ne dépend que du taux instantané (overnight) mais autorisant des taux négatifs. Des modèles plus élaborés (processus CIR, ...), faisant partie de la famille dite des modèles affines de taux court, ont permis de remédier à cette lacune, mais ne satisfont pas vraiment les spécialistes du fait de la difficulté d'interprétation financière des paramètres de diffusion et de leur incapacité à épouser exactement la courbe des taux zéro-coupon spot. Heath, Jarrow et Morton ont proposé une famille de modèles cohérents, dont la dynamique ne dépend que d'une fonction facilement interprétable (la volatilité du taux forward), et capables de rendre compte de n'importe quelle courbe de taux donnée. Des modèles dits de marché (BGM ou Libor Forward) connaissent un certain succès dans l'explication du prix des caps et des floors.
Toutefois, à la différence du marché des dérivés d'options où le modèle de Black et Scholes, plus ou moins arrangé pour le débarrasser de ses imperfections (volatilité constante, taux d'intérêt constant, ...) occupe une place prépondérante, aucun modèle de taux ne fait l'unanimité des spécialistes. Les taux d'intérêts sont en effet soumis à des pressions exogènes très importantes, qui rendent caduques très rapidement toutes les calibrations possibles. À l'heure actuelle, les publications et les recherches à ce sujet sont abondantes.
Dérivés de crédit[modifier]
Les dérivés de crédit sont des produits dérivés dont les flux dépendent d'événements de crédits intervenant sur un sous-jacent. Ces produits servent à prévenir la dégradation de la qualité de signature d'une contrepartie, c'est-à-dire son aptitude à assumer ses obligations de paiement ("CDS"'ou Credit default swap, "CLN" ou "Credit linked Notes"). Ils peuvent servir également à améliorer la qualité de signature d'une partie d'un panier d'actifs ("CDOs" ou "Collateralized debt obligations" ).
Dérivés climatiques[modifier]
Les dérivés climatiques sont des produits financiers dont les flux dépendent d'un événement totalement indépendant de la structure des marchés financiers, lié à un événement climatique. Par exemple, un produit peut assurer à son détenteur une rente dans le cas où la température relevée en un lieu fixé par contrat dépasse ou reste en dessous d'une température de référence considérée comme normale. Ces produits — récents — ont pour vocation de permettre à des entreprises touristiques ou agricoles de se prémunir contre des aléas climatiques. Ils s'apparentent donc à des produits d'assurance, négociés directement sur les marchés financiers.
Notes et références[modifier]
Voir aussi[modifier]
Articles connexes[modifier]
Liens externes[modifier]
- (fr) Cours d'introduction aux mathématiques financières : Calculs Stochastiques pour la finance
- (fr)Cours du Dea de Probabilité, option finance du professeur Nicole El Karoui.
Bibliographie[modifier]
- Pierre Bonneau, Mathématiques financières, Coll. Economie, Paris, Dunod, 1980.
- Jean-Marcel Dalbarade, Mathématiques des marchés financiers, Ed. Eska, 2005, ISBN 2-7472-0846-X.
- Benoît Mandelbrot & Richard Hudson, Une approche fractale des marchés, éditions Odile Jacob, 2005
07:42 Publié dans Mathématiques financières | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Mathématiques financières Thierry Rolando, Jean-Claude Fink Etude (broché). Paru en 03/2006
07:40 Publié dans Mathématiques financières | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Mathématiques financières Edith Ginglinger, J.M. Hasquenoph Essai (poche). Paru en 01/2006
07:39 Publié dans Mathématiques financières | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Algèbre linéaire Rémi Goblot Etude (broché). Paru en 09/2005
07:37 Publié dans Algèbre, Algèbre linéaire | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Algèbre : travaux dirigés Jean-Pierre Lecoutre, Philippe Pilibossian Scolaire / Universitaire (broché). Paru en 08/2009
07:36 Publié dans Algèbre | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Algèbre L3 , Cours complet avec 700 tests et exercices corrigés Aviva Szpirglas Scolaire / Universitaire (broché). Paru en 08/2009
07:34 Publié dans Algèbre | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Algèbre , Les structures et les morphismes vus par les problèmes Roland Groux, Philippe Soulat Manuel (livre CDROM). Paru en 09/2008
07:33 Publié dans Algèbre | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
26/03/2011
Le mathématicien John Milnor, prix Abel 2011
Le mathématicien John Milnor, prix Abel 2011
A 80 ans, le découvreur des "sphères exotiques" à sept dimensions est récompensé pour l'ensemble de ses travaux.
- Agrandir la fonteRétrécir la fonte
- Imprimer
- Envoyer
- Partager
- Traduire
- Réagir
 Le mathématicien John Milnor, prix Abel 2011. (Abel Prize Foundation)
Le mathématicien John Milnor, prix Abel 2011. (Abel Prize Foundation)Aujourd’hui âgé de 80 ans, John Milnor, de l’Université Stony Brook de New-York, s’est notamment distingué par la découverte des «sphères exotiques» à sept dimensions en 1956. Ses travaux ont créé un champ nouveau d’investigation en mathématiques, la topologie différentielle.
John Milnor avait déjà été récompensé par la médaille Fields en 1962 –la plus haute distinction pour un mathématicien, remise avant ses 40 ans- et le prix Wolf en 1968
Le prix Abel (doté de 750.000 euros) est remis depuis 2003. Il compense l’absence des mathématiques parmi les prix Nobel.
C.D.
Sciences et Avenir.fr
25/03/11
13:15 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Algèbre de Boole
Algèbre de Boole
Source : http://www.arcanapercipio.com/lessons/algebre_de_boole/al...
Alors voilà...
"Une proposition peut être vraie OU fausse, mais ne peut pas être vraie ET fausse".
Non, non, et non, cette phrase n'est pas extraite des Mémoires du Seigneur de la Palice. Cette dépotante évidence est signée... Aristote [~384~322] !
Et oui ! Parfaitement, M'sieurs Dames ! De la Logique aristotélicienne ! De la Sagesse 100% grecque ! De la vraie Philosophie péripatéticienne et deux fois millénaire... Un minimum de respect, donc.
Comment ça, "vérité de comptoir" ? Douteriez-vous du très haut intérêt de ce genre de désarmante tautologie ? Et pourtant ! Avec sa jugeote pour seul diplôme, un certain George Boole a bâti sur ce truisme les axiomes d'une algèbre assez révolutionnaire dont les théories, lorsqu'elles se marieront aux technologies de l'électronique près d'un siècle plus tard, donneront naissance à une machine assez prometteuse appelée ordinateur.
 Truisme, axiomes, tautologie... No panic ! L'algèbre de Boole, quand on saitla prendre, est d'une logique déconcertante. Nul besoin, donc, à l'évocation de Boole, de flipper.
Truisme, axiomes, tautologie... No panic ! L'algèbre de Boole, quand on saitla prendre, est d'une logique déconcertante. Nul besoin, donc, à l'évocation de Boole, de flipper.
Arcana Percipio vous propose aujourd'hui un circuit touristique inédit, un voyage initiatique depuis les Mathématiques les plus abstraites jusqu'aux tripes électroniques de votre puce préférée.
Allez, roule Boole !
L'algèbre booléenne
Boole, qui est-ce ?

 George Boole nait en 1815 à Lincoln, Angleterre.
George Boole nait en 1815 à Lincoln, Angleterre.
A ses débuts, le petit Boole verse plutôt dans le Latin, son premier amour, et c'est plus âgé qu'il se tourne vers les Mathématiques. Totalement autodidacte, son étude sur les équations différentielles lui vaut une chaire à l'université de Cork.
En 1854, sa publication " An investigation into the Laws of Thought, on Which are founded the Mathematical Theories of Logic and Probabilities" parvient à marier de manière éclatante les mathématiques à la logique, discipline qu'il arrache de fait aux philosophes de l'époque.
An investigation into the Laws of Thought, on Which are founded the Mathematical Theories of Logic and Probabilities" parvient à marier de manière éclatante les mathématiques à la logique, discipline qu'il arrache de fait aux philosophes de l'époque.
Honoré à Oxford, Boole devient membre de la "Royal Society" la même année, mais meurt précocement, en 1864, des suites des théories de Madame Boole sur la meilleure manière de guérir une grippe.
Les lois de la pensée
Pour un non-cartésien comme l'auteur de cette page, le meilleur moyen d'approcher Boole, c'est encore de l'attaquer par derrière, l'air de rien, en faisant mine de s'amuser avec quelques dessins. Quels dessins ? Des dessins de parties, ou pour parler doctoralement, de sous-ensembles. Nous allons donc procéder de la sorte, entremêlant de façon parfaitement naïve algèbre de Boole et théorie des ensembles.
Normalement, ça ne fait pas mal.
Les parties de Boole
A la source de l'inspiration de Boole, l'intime conviction que l'algèbre traditionnelle, celle qu'il baptise lui-même "l'algèbre d'école", n'est rien d'autre que l'application aux nombres de schémas de pensée plus fondamentaux par lesquels l'esprit humain manipule, combine et redéfinit ses concepts logiques (que Boole appelle classes) selon les lois immuables de la pensée ("the laws of thought").
De manière fort simple, nous pourrions définir une classe comme l'ensemble de tous les éléments partageant un même nom ou une même caractéristique, comme par exemple "les êtres humains", "les rivières", "les cornets à piston", "les jours de grève à la SNCF", etc.
Ceci convenu, en imaginant deux classes A et B quelconques, Boole définit trois opérations fondamentales de l'esprit susceptible de s'exercer sur elles:
Bêtes deux sommes
Attention ! Bien que leur nom et leur symbole nous y poussent, ne confondons pas la somme et le produit logiques avec la somme et le produit arithmétiques, tels que nous les connaissons. Les premiers s'exercent sur des classes, les seconds sur des nombres.
Produit de première urgence
En absence de toute parenthèses explicites, le produit logique est prioritaire sur la somme logique.
Ainsi, (A.B)+C peut donc également s'écrire A.B+C.
- La SOMME LOGIQUE (logical sum), que nous noterions A + B, définissant la classe des éléments obéissant à l'une ou l'autre des définitions des classes A et B;
- La COMPLÉMENTATION (negation), que nous noterions A (ou B), définissant la classe des éléments n'obéissant pas à la définition de la classe A (ou B).
Mais ne nous emballons pas et appuyons-nous pour continuer sur l'exemple des deux classes suivantes:
- La classe A définie comme "les chasseurs",
- La classe B définie comme "les myopes".
Partant de ces deux simples définitions, nous pouvons très facilement, par le jeu de notre seule pensée, définir quatre autres classes:
- La classe A.B définie comme "les chasseurs myopes",
- La classe A+B définie comme "les chasseurs et les myopes".
- La classe A définie comme "les non-chasseurs",
- La classe B définie comme "les non-myopes".
Il existe un moyen très visuel de traduire ces concepts un peu abstraits: il consiste à considérer les classes de Boole comme des ensembles. Dès lors, les opérations fondamentales de Boole prennent des noms plus familiers à nos souvenirs scolaires:
- La somme logique de deux classes se traduit par l'union (∪) entre les deux ensembles correspondants,
- Le produit logique par l'intersection (∩),
- La complémententation par... le complément.
Survolez les différentes classes ou expressions afin de visualiser leur équivalent graphique.
Comme nous manipulons ici des ensembles plutôt que des classes, nous prendrons la précaution préalable de définir E comme l'ensemble référentiel, celui contenant tous les autres.
Les évidences booléennes
Avec un poil de curiosité mathématique, nous pourrions facilement constater que ces opérations fondamentales obéissent à quelques propriétés plus ou moins classiques mais si foncièrement évidentes qu'indémontrables.
Ce sont les axiomes de l'algèbre booléenne.
 Ainsi, en reprenant nos deux classes exemples A ("les chasseurs") et B ("les myopes") et en y ajoutant pour l'occasion une troisième classe C définie comme "les buveurs excessifs", on ne peut nier que:
Ainsi, en reprenant nos deux classes exemples A ("les chasseurs") et B ("les myopes") et en y ajoutant pour l'occasion une troisième classe C définie comme "les buveurs excessifs", on ne peut nier que:
- A + B = B + A et A . B = B . A, c'est la commutativité;
- (A + B) + C = A + (B + C) et (A . B) . C = A . (B . C) , c'est l'associativité;
- (A + B) . C = (A . C) + (B . C) mais aussi (A . B) + C = (A + C) . (B + C), c'est la distributivité;
Avec un effort de curiosité supplémentaire, nous pourrions même sans trop de problème imaginer l'existence de deux classes "remarquables", notons les "0" et "1" qui, quelle que soit la classe A, vérifieraient toujours:
- A + 0 = A
Dans l'esprit de Boole, cet élément 0 correspondait à une sorte de classe impossible, mais sur nos petits dessins à nous, on l'assimilera à l'élément vide {Ø}. - A . 1 = A
Pour Boole, cet élément 1 symbolisait la classe universelle, un espèce de grand Tout. Moins ambitieux, nous l'assimilerons sur nos dessins à E, la totalité du référentiel.
Un bon mathématicien dirait alors de 0 et 1 qu'ils sont éléments neutres: 0 à l'égard de la somme logique (+), et 1 à l'égard du produit logique (.).
Et le lascar en profiterait sans doute pour pour nous asséner un dernier axiome bien senti, tout aussi évident que les autres, qu'il appellerait axiome de la complémentation et qui dirait, de manière bien moins poétique qu'Aristote, que:
- A + A = 1, également appelé "loi du tiers exclu",
- A . A = 0, également appelé "principe de contradiction".
Comme pour nous rassurer, ces cinq axiomes fondamentaux de l'algèbre de Boole sont tous confirmés par nos modestes petits dessins. Nous verrons par la suite pourquoi ceci (nos dessins) explique si bien cela (l'algèbre de Boole).
Bon ! Maintenant, quelques minutes d'intense phosphorage neuronal...
Ça risque de secouer un brin...
Les théorèmes de l'algèbre booléenne
A partir des lois booléennes fondamentales et évidentes que nous venons de détailler, il est tout à fait possible, à l'aide de raisonnements logiques appelés démonstrations, d'établir quelques autres propositions utiles que nous appellerons théorèmes de l'algèbre de Boole:
- Théorème de l'unicité du complément: pour toute classe A, il existe une et une seule classe A telle que:
A + A = 1 et A . A = 0
- Théorèmes de l'involution: A = A
- Théorèmes d'absorption: A + A . B = A et A .(A + B) = A
- Théorème de la redondance: A . B + A . C = A . B + A . C + B . C
Ajoutons à cette liste deux théorèmes importants, dits THÉORÈMES DE MORGAN, fruits des travaux du mathématicien anglais Augustus de Morgan [1806-1871], qui annoncent que:
- le complément d'une somme logique est égal au produit logique des compléments: A + B = A . B
- le complément d'un produit logique est égal à la somme logique des compléments: A . B = A + B
Attention ! Purs littéraires s'abstenir...
Ces théorèmes de Morgan illustrent une particularité fascinante de l'algèbre booléenne: le PRINCIPE DE DUALITÉ (duality). Selon ce principe, pour toute égalité E vérifiée dans l'algèbre de Boole, il existe une égalité E*, appelée duale, qui se trouve également vérifiée. Celle-ci, qui plus est, se retrouve quasi immédiatement à partir de E puisqu'il suffit en effet:
- de permuter les opérateurs (+) et (.)
- de permuter les constantes 0 et 1
La confiance règne...
L'algèbre de Boole à facettes
Avouons-le bien volontiers: George Boole ne nous a pas légué "clef en main" cette théorie toute en formules simples et définitives. D'autres esprits illustres ont repris, approfondi et mis en ordre ces idées novatrices dont il eût néanmoins l'intuition géniale de jeter les premiers fondements. Citons, entre autres, l'anglais Augustus De Morgan [1806-1871], et les américains Charles Peirce [1839-1914] et Edward Huntington [1874-1952].
Aujourd'hui, en termes très mathématiques, on appelle algèbre de Boole (E, +, ., , 0, 1) la donnée d'un ensemble E non vide, muni de deux lois de composition interne (+ et .) commutatives et associatives, d'une application unaire ( ) et de deux éléments privilégiés (0 et 1), toutes ces données vérifiant les différents axiomes vus plus haut.
Soupir...
Pour 99% de la population, cette très jolie phrase provoquera nausées, maux de tête voire un petit raffermissement du quadriceps. Les initiés y verront au contraire le formidable canevas à une foule d'applications plus ou moins évidentes: théorie des ensembles, logique des prédicats, calcul des aléas technologiques et, ce qui nous intéressera ici plus particulièrement, technologie des composants électroniques.
Partis très loin dans des sphères très abstraites, tentons de revenir à très petits pas vers notre pécé préféré...
L'algèbre du tout ou rien
De manière rassurante, entrevoir l'immense intérêt de l'algèbre de Boole pour nos petites machines réclamera un petit effort préalable de... simplification. Et imaginer pour cela un univers booléen minimaliste, c'est-à-dire réduit à ses deux seuls éléments remarquables: "0" et "1".
Et là, miracle ! Ce cas très particulier et plutôt minimaliste de l'algèbre de Boole ouvre grand les portes sur d'inattendus horizons: à savoir, tous les domaines où règne la loi du tout ou rien, tous ces univers où toute variable ne peut prendre que deux états différents et complémentaires. Bref, les univers chamarrés de l'ALGÈBRE BINAIRE (binary algebra).
Si, pour vous aussi, la théorie est un tunnel, il semble bien que nous en voyons le bout...
Boole, au coeur de nos vies
Vrai / Faux
Dans cette algèbre booléenne que nous venons de décrire, avoir dénommé "0" et "1" nos deux éléments remarquables était pure convention d'écriture. D'ailleurs, appliqués à la théorie des ensemble, nous avons vu que ces derniers avaient pris des noms autrement plus explicites: ensemble vide (pour "0") et référentiel complet (pour "1").
Ramenés à un univers booléen minimaliste où ces deux valeurs, seules possibles, sont également complémentaires, pourquoi ne pas envisager de les rebaptiser "vrai" et "faux" ? Le "non-vrai" étant forcément "faux", et le "non-faux" obligatoirement "vrai", avouez que ces deux adjectifs colleraient plutôt bien à la "philosophie" booléenne.
Par ailleurs, l'algèbre binaire mettant en jeu des variable ne pouvant prendre que l'une ou l'autre de ces deux valeurs, il devient réalisable, pour chacun de nos trois opérateurs fondamentaux, de consigner en trois petits tableaux l'ensemble de tous les résultats possibles mettant en jeu deux variables:
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
Pas vraiment normande, notre nouvelle algèbre booléenne...
Dans ce nouveau contexte très manichéen, les résultats produits par chacun de nos opérateurs de base peuvent se résumer à trois phrases désarmantes de bon sens:
- Pour la somme logique: si A + B est "vrai", alors A est "vrai" OU B est "vrai",
- Pour le produit logique: si A . B est "vrai", alors A est "vrai" ET B est "vrai",
- Pour la complémentation: le NON "faux" est "vrai" et le NON "vrai" est "faux".
Avouez que nous avons trouvé là des noms beaucoup plus familiers pour nos trois opérateurs booléens fondamentaux. Nous les utiliserons donc dorénavant pour désigner ces derniers, mais plutôt dans leur version anglaise:
Quand et est ou
Méfions-nous quand même des subtilités de la langue; ainsi, par exemple, lorsque nous évoquons "les Hommes et les Femmes", nous ne faisons généralement pas référence aux hermaphrodites, mais bel et bien à toute personne, qu'elle soit hommeou femme. Bref, derrière nos "et" se cachent parfois de parfaits "ou".
Et maintenant, si je vous dis: "je sortirai s'il fait beau ou s'il pleut et que j'ai mon parapluie", et que j'appelle (A) la proposition "il fait beau" et (B) la proposition "j'ai mon parapluie", alors je peux très simplement exprimer mes chances de sortie par la délicieuse expression: A + A.B, digne des plus belles pages de la littérature française.
Tout cela pour vous montrer à quel point, nous, créatures pourtant si subtiles, ne cessons de jongler, sans nous en rendre compte, avec des concepts parfaitement booléens.
Sans surprise, nous appellerons VARIABLE BOOLÉENNE (boolean variables), ou encore VARIABLE LOGIQUE (logical variables), toute variable obéissant à cette algèbre binaire pour laquelle seules deux valeurs différentes et complémentaires sont possibles.
Celles-ci, comme nous l'avons vu, seront généralement notées "1" et "0", mais parfois aussi "vrai" (true) et "faux" (false).
Boole, détecteur de mensonge
On / Off
Bon, bon, bon... Nous en voyons que le précédent chapitre n'a pas du tout convaincus du très haut intérêt de l'algèbre de Boole. Pour ceux-là, nous allons donc sortir la très grosse artillerie, à savoir: une simple pile, quelques fils conducteurs et une ampoule en état de marche.
Tout va bientôt s'éclairer...
En un point donné de tout circuit électrique, deux situations très simples peuvent se produire: soit le courant "passe", soit il ne "passe pas": une simple ampoule nous l'apprendra brillamment.
Afin de symboliser ces deux états très différents, nous pourrions utiliser les termes très suggestifs de "lumière/obscurité", "on/off" ou, pourquoi pas, "1/0".
Etudions maintenant quelques montages électriques de niveau cours élémentaire:
Cliquez sur les différents interrupteurs du montage afin de voir la conséquence sur l'ampoule.
Pense-bête: contacter Varta, Duracel et toute l'industrie de la pile pour leur proposer un espace d'affichage sur le générateur de cette spectaculaire animation.
Et là, divine suprise, nous remarquons ébahis que:
- Pour le montage en parallèle: l'ampoule brille si l'interrupteur A OU l'interrupteur B est en position fermée. Ce que pourrions exprimer par: Lumière = A + B,
- Pour le montage en série: l'ampoule brille si l'interrupteur A ET l'interrupteur B sont en position fermée, soit: Lumière = A . B.
Juste le temps de nous remettre de la vive émotion causée par cette révélation et profitons encore un instant du matériel grâcieusement prêté par le club des électriciens amateurs pour constater que nos axiomes booléens se vérifient parfaitement dans ce petit monde conducteur:
Cliquez sur les différents interrupteurs du montage afin de vérifier la lumineuse pertinence des axiomes booléens.
Vous voila rassuré(e): tout ce que nous avons appris sur l'algèbre booléenne n'est donc pas complètement vain puisqu'elle semble, en effet, trouver certaines applications très lumineuses et très concrètes.
Bon, il est vrai que le rapport est encore ténu entre ces montages pour grands débutants en génie électrique et le concentré de technologie que constitue une puce savante.
Le chemin est encore long, mais il est désormais un poil éclairé !
Heu, à ce propos... Nous allons entrer dans un nouveau tunnel de théorie... Mais promis, la lumière sera encore plus vive de l'autre côté.
Fonctions booléennes
Prenez un mathématicien normalement constitué, donnez lui pour s'amuser quelques variables usagées et attendez. Tôt ou tard, la créature toute excitée viendra vous embrumer l'esprit avec des fonctions !
Et oui. Tout comme en algèbre "classique", il est tout à fait envisageable de combiner entre elles plusieurs variables booléennes à l'aide de nos opérateurs fondamentaux (OR, AND, NOT) pour former des fonctions.
Sans surprise, une telle fonction sera baptisée FONCTION BOOLÉENNE (boolean function), ou encore, FONCTION LOGIQUE (logical function).
Fonctions logiques à deux variables:
OR, NOR, XOR et consorts...
Binaire²
L'épithète "binaire" doit être ici compris comme qualifiant une opération mettant en jeu deux variables, tout comme notre opérateur NOT est un opérateur unaire.
Tous ces opérateurs sont néanmoins des opérateurs de l'algèbre binaire (dans le sens où toute variable ne peut prendre que deux valeurs), ce qui n'arrange rien à la lisibilité de cette note...
A ce stade, nous avons déjà repéré deux opérateurs binaires fondamentaux: le "OR" et le "AND", de par le fait qu'ils correspondaient à des raisonnements logiques très familiers à notre esprit humain et, cadeau bonus, qu'ils décrivaient parfaitement les montages parallèle et série d'un circuit électrique.
Mais ce ne sont pas les seuls !
Pour nous en persuader, nous allons construire un petit tableau original - comme seule l'algèbre binaire peut nous permettre d'en concevoir - afin de lister toutes les fonctions possibles pouvant mettre en jeu deux variables booléennes.
Evidemment, ça va être pénible... mais on y a mis un peu de couleur...
| Fonctions booléennes à deux variables | ||||||||||||||||||||||||||||||||
Quelles que soient les valeurs de A et B, cette fonction renvoie toujours la valeur 0. Il s'agit donc de la fonction constante: F(A, B) = 0
Intérêt discutable... |
Cette fonction, qui ne renvoie 1 que si A et B sont égaux à 1, nous la connaissons fort bien: il s'agit de notre produit logique, alias AND:
F(A, B) = A . B = A AND B |
|||||||||||||||||||||||||||||||
Fonction sans grande correspondance dans le langage parlé, mais que les spécialistes appellent inhibition:
F(A, B) = A . B |
Fonction pour laquelle la variable B ne sert pas à grand chose... Bref, la fonction unaire:
F(A, B) = A |
|||||||||||||||||||||||||||||||
Fonction inhibition comparable à la fonction ci-dessus
F(A, B) = A . B |
Fonction qui ressemble fort à la fonction ci-dessus, A endossant cette fois le rôle de la variable croupion.
F(A, B) = B |
|||||||||||||||||||||||||||||||
Fonction très intéressante, qui ne donne 1 que si les variables A et B sont de valeur différente. Nous l'appellerons fonction d'anticoïncidence, ou XOR:
F(A, B) = A . B + A . B = A XOR B |
Cette fonction là aussi, nous la connaissons déjà fort bien; c'est notre fonction OR, alias somme logique:
F(A, B) = A + B = A OR B |
|||||||||||||||||||||||||||||||
Autre fonction intéressante,complémentaire de notre fonction OR et que nous appellerons donc pour la peine fonction NOR (Not-OR):
F(A, B) = A + B = A . B = A NOR B |
Fonction ô combien remarquable, qui ne prend la valeur 1 que si A et B sont de même valeur. Bref, une fonction de coïncidence, également appelée XNOR:
F(A, B) = A . B + A . B = A XNOR B |
|||||||||||||||||||||||||||||||
Fonction pour laquelle A ne sert pas à grand chose puisque ne renvoie de fait que le complément de B. Il s'agit donc de notre fonction NOT, appliquée à B:
F(A, B) = B |
|
|||||||||||||||||||||||||||||||
Ici aussi, c'est notre fonction NOT qui se cache derrière une façade binaire, la variable B ne servant strictement à rien:
F(A, B) = A |
|
|||||||||||||||||||||||||||||||
Fonction complémentaire de notre opérateur AND, et qu'il serait donc logique d'appeler NAND:
F(A, B) = A . B = A + B = A NAND B |
Fonction somme toute optimiste, donnant 1 quels que soient les valeurs de A et B. Bref, la fonction constante:
F(A, B) = 1 |
|||||||||||||||||||||||||||||||
Parfait ! Nous n'allons pas revenir sur la beauté parfaite de notre "OR" et de notre "AND", mais attardons-nous quelques instants sur certains de ces autres opérateurs aux noms étranges...
XOR (eXclusive OR)

Le XOR, alias "ou exclusif", qui correspond à la fonction booléenne F(A, B) =A.B + A.B est un peu un "ou" version "fromage ou dessert", dans le sens où A XOR B sera "vrai" si A est "vrai" ou B est "vrai", mais pas les deux ! Cela lui vaut ses noms, sans doute plus parlants, d'opérateur d'anticoïncidence, voire, également, de comparateur de différence.
Son symbole est ⊕ et ses caractéristiques principales sont:
- Commutativité: A ⊕ B = B ⊕ A,
- Associativité: (A ⊕ B) ⊕ C = A ⊕ (B ⊕ C),
- Comportement vis-à-vis des éléments neutres: A ⊕ 0 = A et A ⊕ 1 = A,
- A ⊕ A = 0 (pas d'idempotence) et A ⊕ A = 1.
NOR (Not OR)
Comme son nom l'indique assez bien, l'opérateur NOR, noté ↓, est le complément de l'opérateur OR, c'est-à-dire A + B.
Même si cet opérateur n'a pas d'équivalent simple dans le langage parlé, son intérêt en électronique est un tout petit peu essentiel et nous allons donc expliciter quelques unes de ses propriétés:
- Commutativité: A ↓ B = B ↓ A,
- Pas d'associativité: (A ↓ B) ↓ C ≠ A ↓ (B ↓ C),
- Inversion: A ↓ 0 = A.
XNOR (eXclusive Not OR)
Booléennement parlant, XNOR est le complément de l'opérateur XOR que nous venons de voir. Vous ne serez donc pas étonné(e) d'apprendre que son petit nom soit opérateur de coïncidence, ou encore,comparateur d'identité puisque A XNOR B ne sera "vrai" que si A et B ont même valeur.
Ses principales propriétés sont:
- Commutativité: A XNOR B = B XNOR A,
- Associativité: (A XNOR B) XNOR C = A XNOR (B XNOR C),
- Comportement vis-à-vis des éléments neutres: A XNOR 0 = A et A XNOR 1 = A,
- A XNOR A = 1 (pas d'idempotence) et A XNOR A = 0.
NAND (Not AND)
L'opérateur NAND ("ET-NON"), noté ↑, est simple à assimiler puisqu'il agit comme le complément de l'opérateur AND. En clair, A ↑ B ne donnera "faux" que si A et B sont simultanément "vrai".
A l'image du NOR, le NAND n'a pas d'équivalent direct dans le langage parlé, mais son importance est tout aussi fondamentale en électronique et voici pourquoi nous allons nous intéresser à ses passionnantes propriétés:
- Commutativité: A ↑ B = B ↑ A,
- Pas d'associativité: (A ↑ B) ↑ C ≠ A ↑ (B ↑ C),
- Inversion: A ↑ 1 = A.
Fonctions booléennes à N variables
Nous venons d'étudier le cas très particulier et très simple des fonctions booléennes à deux variables. Bien évidemment, vous vous doutez qu'une fonction logique peut mettre en jeu un nombre quelconque de variables booléennes.
Ainsi, la fonction F(A, B, C) = A.B + A.C est un exemple pris tout à fait au hasard de fonction logique à trois variables.
Cartes sur table
Comme nous l'avons déjà mis en pratique, la grande particularité des fonctions booléennes est qu'elles peuvent être explorées de manière exhaustive. En effet, chaque variable de ces fonctions ne pouvant prendre que deux valeurs différentes, il devient tout à fait faisable de récapituler tous les cas possibles dans un tableau que l'on appelle alors TABLE DE VÉRITÉ (truth table).
Ainsi, si nous reprenons notre fonction booléenne définie par F(A, B, C) = A.B + A.C, nous pouvons sans trop de problème mettre au point sa table de vérité:
| A | B | C | F(A, B, C) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | ? |
Cette table comporte une colonne par variable mise en jeu par la fonction, plus une colonne terminale où l'on consigne, pour chaque combinaison des variables, la valeur prise alors par la fonction.
Canon Boole
Supposons un instant que nous ayons sous les yeux une table de vérité toute faite, sans aucune définition algébrique de la fonction associée:
| A | B | C | F(A, B, C) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Et bien cette table de vérité peut nous permettre de retrouver une définition polynômiale de la fonction F.
En effet, nous savons qu'en algèbre binaire, si nous avons une expression:
X + Y + Z + .... = 1, alors on peut dire que
X = 1 OU Y = 1 OU Z = 1...
Il est par conséquent tout à fait envisageable de définir notre fonction F comme la somme logique des différentes lignes pour lesquelles F = 1.
Conséquence toute naturelle de tout cela: deux fonctions logiques F et F' seront égales si et seulement si leur table de vérité sont identiques.
Ainsi, dans notre exemple, on peut écrire: F(A, B, C) = A.B.C + A.B.C + A.B.C + A.B.C + A.B.C
Aucune absence tolérée
Pour qu'un produit logique de N variables mérite le qualificatif de minterme, chacune de ses N variables ou son complément doit apparaître dans le produit.
Ainsi, A.C ou B.C ne sont pas des mintermes des variables A, B, C.
En groscursussien, les différents monômes de la fonction (c'est-à-dire les produits logiques A.B.C, A.B.C, A.B.C, A.B.C et A.B.C) sont appelés des MINTERMES (minterms), et la fonction F, qui se trouve alors exprimée sous la forme d'unesomme logique de mintermes est dite se trouver sous sa FORME CANONIQUE DISJONCTIVE (disjunctive canonical form), ou également première forme canonique.
Par ailleurs, dans notre univers booléen, nous pouvons également définir le complément de F comme la somme des mintermes égaux à 0. Nous avons donc aussi:
F(A, B, C) = A.B.C + A.B.C + A.B.C
Et puisque nous savons parfaitement que A = A et aussi que, grâce à ce qu'a fait Morgan, A+B = A.B, nous pouvons donc également écrire F sous la forme:
| F(A, B, C) = | A.B.C + A.B.C + A.B.C | = (A + B + C) . (A + B + C) . (A + B + C) |
De la même manière que pour le minterme, pour qu'une somme logique de N variables mérite le qualificatif de maxterme, chacune de ces N variables ou son complément doit apparaître dans la somme.
Les termes A+B+C, A+B+C et A+B+C, sommes logiques de toutes les variables de F (ou de leur complément) sont appelés MAXTERMES (maxterms) de la fonction, et cette écriture de F sous la forme de produits de maxtermes est appelée FORME CANONIQUE CONJONCTIVE (conjunctive canonical form), ou aussi parfois deuxième forme canonique.
Que vous ayez ou non compris cette histoire de canon, vous aurez de toute façon noté qu'une fonction logique peut être exprimée algébriquement de différentes façons.
Et ceci n'est pas une bonne nouvelle pour nos neurones...
Vocaboolaire de base
L'art de faire simple
La plupart du temps, une fonction logique nous sera proposée sous une forme développée plus ou moins alambiquée qu'il sera très souvent possible de fortement simplifier.
Pour ce faire, trois pistes à explorer:
Méthode algébrique
Génération spontanée
En algèbre booléenne, rien de plus simple que de faire apparaître le terme C dans le produit A.B puisque, sachant que C+C=1, on peut écrire:
A.B = A.B.(C+C) = A.B.C + A.B.C
Ceci est une règle de l'algèbre binaire: Il faut parfois savoir complexifier une expression pour mieux la simplifier ensuite.
Nous l'avons vu ensemble, l'algèbre booléenne dispose d'un véritable arsenal d'axiomes et théorèmes bien définitifs qui peuvent nous permettre de simplifier une fonction logique.
Bien souvent, la solution passe par de judicieux développements afin de faire apparaître des termes qui, par factorisations non moins habiles, vont s'annuler sur le principe que A + 1 = A ou A . 0 = 0.
Attention toutefois: la simplification algébrique demande un minimum de rigueur et de zénitude. Si vous êtes du genre à facilement oublier un A en route ou prêt(e) à tout abandonner quand retentit le jingle annonçant l'arrivée d'un pote sur MSN, envisagez peut-être directement le plan B...
Comment simplifiez-vous la fonction logique F(A, B) = (A + B) . (A + B) ?
Formes canoniques
L'annonce ne vous surprendra pas deux fois: la table de vérité d'une fonction logique à N variables comportera 2N lignes.
Dès lors, trois scénarii possibles:
Ce n'est pas parce que vous aurez exprimé votre fonction sous une forme canonique plutôt simple que celle-ci sera obligatoirement l'expression la plus simplifiée de la fonction. Très souvent, une phase de simplification algébrique permettra d'achever complètement la simplification.
- Ou la table de vérité révèle un petit nombre de cas pour lesquels la fonction est égale à 1. Dans ce cas, il sera sensé d'exprimer la fonction dans sa forme canonique disjonctive;
- Ou la table de vérité révèle un petit nombre de cas pour lesquels la fonction est égale à 0, et il sera alors pertinent d'exprimer la fonction dans sa forme canonique conjonctive, en complémentant la somme des mintermes égaux à 0;
- Ou la table de vérité ne révèle aucune prépondérance nette de résultats égaux à 0 ou 1, et on devra se résoudre à faire appel à Maurice...
Diagramme de Karnaugh
Le DIAGRAMME DE KARNAUGH (Karnaugh map) est une méthode simple et ingénieuse afin de trouver à coup sûr la forme la plus simple d'une fonction logique donnée, à partir de sa table de vérité.
A vrai dire, le diagramme de Karnaugh d'une fonction n'est ni plus ni moins que la table de vérité de celle-ci, mais mise en forme de telle manière que soient géographiquement proches les mintermes logiquement proches.
Comme le fait d'expliquer textuellement le principe de ce diagramme conduirait à une somme faramineuse de lignes totalement imbitables, nous allons plutôt illustrer nos dires par un exemple bien senti.
Soit l'anodine fonction logique F telle que F(A, B, C, D) = A + A.B + A.B.C + A.B.C.D.
Amusons-nous à développer sa table de vérité.
| A | B | C | D | F(A, B, C, D) |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Voilà ! On s'est bien poilé et nous avons, conformément à nos attentes, obtenu une table de vérité à 16 lignes.
Nous allons maintenant transformer ce tableau à seize lignes en un tableau à seize cases. Pour ce faire, nous allons répartir tous les mintermes de nos variables groupées deux à deux, mais en prenant soin de scrupuleusement respecter cette règle: il faut impérativement que le passage d'une case à une case adjacente ne traduise le changement d'état que d'une seule variable.
Normalement, nous devrions obtenir quelque chose qui ressemble à ça:
| C.D | C.D | C.D | C.D | |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 0 | 0 | 1 |
A chaque case de notre nouveau tableau correspond un minterme de la table de vérité; il est donc normal de retrouver dans notre table de Karnaugh tous les résultats possibles pour la fonction F, et donc, le même nombre de "1" et de "0".
Nous allons dès lors pouvoir procéder aux simplifications.
Pour ce faire, nous allons localiser les cases adjacentes marquées à "1" en nombre égal à une puissance de deux, c'est-à-dire les groupes de 1, 2, 4, 8, 16.... cases "1" adjacentes, en recherchant bien sûr les regroupements les plus importants. On ne garde ensuite, parmi les mintermes concernés par le regroupement, que la ou les variable(s) logique(s) commune(s) à toutes les cases.
| C.D | C.D | C.D | C.D | |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 0 | 0 | 1 |
Premier regroupement: parmi les huit cases formées par les deux premières lignes, seule la variable B est commune aux mintermes.
Notez qu'on ne peut inclure la troisième ligne dans notre premier regroupement, car nous aurions alors douze cases, douze n'étant pas une puissance de deux.
| C.D | C.D | C.D | C.D | |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 0 | 0 | 1 |
Deuxième regroupement: parmi les huit cases formées par les deuxième et troisième lignes, seule la variable A est commune aux mintermes.
Comme vous le constatez pour notre deuxième ligne, une ou plusieurs case(s) peut(vent) tout à fait servir à plusieurs regroupements.
| C.D | C.D | C.D | C.D | |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 0 | 0 | 1 |
Troisième regroupement: parmi les huit cases formées par la première et la dernière colonne, seule la variable C est commune aux mintermes.
Remarquez que les lignes / colonnes situées aux extrémités doivent être considérées comme adjacentes. Et cela est après tout fort logique, puisqu'une seule variable change d'état de l'une à l'autre.
Parfait ! Aucun autre regroupement n'étant possible, on recopie les mintermes n'ayant servi à aucun regroupement - ici, aucun - et on récupère les fruits de nos regroupements successifs, pour finalement obtenir:
F = B + A + C
...ce qui constitue quand même, vous êtes maintenant connaisseur(se), une fort belle simplification !
Bien évidemment, nous aurions pu parvenir au même résultat avec beaucoup moins d'efforts et un zeste de réflexion, en remarquant que la table de vérité ne recensait que deux cas où la fonction s'annulait, cas correspondant au monôme A.B.C.
Dès lors, on pouvait se remémorer le théorème de l'involution puis avoir une pensée pour Morgan pour noter que:
| F(A, B, C) = | A.B.C |
= A + B + C
|
Evidemment, vous vous doutez que la méthode de Karnaugh devient franchement hostile dès lors que le nombre de variables logiques excède quatre, puisqu'il faut dès lors faire appel à une table en 3D, du moins si l'on veut continuer d'obéir à l'obligation de ne changer qu'une seule variable d'état lors du passage d'une case à une autre.
Inutile également de préciser qu'au delà de six variables logiques, la méthode de Karnaugh devient inapplicable sans très très haute faculté d'abstraction. Il faut alors se replier vers d'autres méthodes de simplification, telle la méthode de Quine-Mac Cluskey, que nous n'aborderons pas ici car nous ne voudrions pas abuser de votre gentille attention.
Bon ! Autant le dire tout de suite, le "machin" ci-dessus en est encore à une béta pré-version 0.0 sûrement buggée jusqu'à la moëlle. Bref, un truc absolument pas fiable qui, à l'heure où sont écrites ces lignes, pourrit consciencieusement la vie de son auteur qui se mord les doigts de s'être réveillé un matin avec la lubie de créer un truc de ce style.
13:13 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
25/03/2011
E8 (mathématiques)
E8 (mathématiques)
En mathématiques,  est le plus grand groupe de Lie complexe de type exceptionnel. Son algèbre de Lie est notée
est le plus grand groupe de Lie complexe de type exceptionnel. Son algèbre de Lie est notée  .
.
E8 est de rang 8 et de dimension 248. Il est simplement connexe et son centre est trivial.
La structure E8 a été découverte en 1887 par le mathématicien norvégien Sophus Lie pour étudier la symétrie et jusqu’ici personne ne pensait que cet objet mathématique pourrait être compris, considère Jeffrey Adams, responsable de l’équipe Atlas of Lie Groups and Représentations qui réunit 18 mathématiciens et programmeurs dans le monde, dont Fokko du Cloux et Marc van Leeuwen.
Sommaire[masquer]
|
Formes réelles[modifier]
En plus du groupe de Lie complexe E8, de dimension complexe 248 (donc de dimension réelle 496), il existe trois formes réelles de ce groupe, toutes de dimension réelle 248. Les plus simples sont les formes compactes  et déployées
et déployées  (non-compacte maximale ou encore split en anglais) et il en existe une troisième, notée
(non-compacte maximale ou encore split en anglais) et il en existe une troisième, notée  .
.
Constructions[modifier]
On peut construire la forme compacte du groupe E8 comme le groupe d'automorphismes de l'algèbre de lie  correspondante. Cette algèbre possède
correspondante. Cette algèbre possède  comme sous-algèbre de dimension 120 et on peut se servir de celle-ci pour décomposer la représentation adjointe comme
comme sous-algèbre de dimension 120 et on peut se servir de celle-ci pour décomposer la représentation adjointe comme
où  est l'une des deux représentations spinorielles, de type Majorana-Weyl du groupe
est l'une des deux représentations spinorielles, de type Majorana-Weyl du groupe  dont
dont 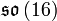 est l'algèbre de Lie.
est l'algèbre de Lie.
Si on appelle  un jeu de générateurs pour
un jeu de générateurs pour 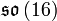 et
et  les 128 composantes de
les 128 composantes de  alors on peut écrire explicitement les relations définissant
alors on peut écrire explicitement les relations définissant  comme
comme
ainsi que
![left[J_{ij}, Q_aright] = frac14 left(gamma_igamma_j - gamma_jgamma_iright)_{ab}Q_b,](http://upload.wikimedia.org/math/b/f/1/bf123d341c9502ae0e5452733a8004ea.png) ,
,
qui correspond à l'action naturelle de  sur le spineur
sur le spineur  . Le commutateur restant (qui est bien un commutateur et non pas un anticommutateur) est défini entre les composantes du spineur comme
. Le commutateur restant (qui est bien un commutateur et non pas un anticommutateur) est défini entre les composantes du spineur comme
![left[Q_a, Q_bright] = gamma^{[i}_{ac}gamma^{j]}_{cb}J_{ij},](http://upload.wikimedia.org/math/5/1/6/51632689c8006bf6f240719672da191c.png) .
.
À partir de ces définitions on peut vérifier que l'identité de Jacobi est satisfaite.
Géométrie[modifier]
La forme réelle compacte de E8 peut être vue comme le groupe d'isométrie d'une variété riemannienne de dimension 128 appelée plan projectif octooctonionique. Ce nom vient de ce qu'il peut être construit en utilisant une algèbre qui est construite comme produit tensoriel des octonions avec eux-mêmes. Ce type de construction est analysé en détail par Hans Freudenthal et Jacques Tits dans leur construction du carré magique.
En physique[modifier]
Dans le cadre des théories de grande unification en physique des particules, le groupe E8 est parfois considéré comme groupe de jauge candidat dans la mesure où il contient d'une façon naturelle une série d'autres groupes de grande unifications souvent considérés. On peut le voir sous la succession d'inclusions
Par ailleurs, le groupe E8 apparait fréquemment en théorie des cordes et en supergravité. Dans la théorie des cordes hétérotiques une formulation fait apparaître  (sous forme compacte) comme groupe de jauge. Par ailleurs, lorsque la supergravité maximale est compactifiée sur un tore de dimension 8 alors la théorie résultante en dimension trois possède unesymétrie globale E8 (c'est-à-dire la forme déployée, ou maximalement non-compacte). Il a été par la suite suggéré[réf. nécessaire] qu'une version discrète, notée
(sous forme compacte) comme groupe de jauge. Par ailleurs, lorsque la supergravité maximale est compactifiée sur un tore de dimension 8 alors la théorie résultante en dimension trois possède unesymétrie globale E8 (c'est-à-dire la forme déployée, ou maximalement non-compacte). Il a été par la suite suggéré[réf. nécessaire] qu'une version discrète, notée  , de ce groupe serait une symétrie, appelée dans ce contexte U-dualité, de la théorie M.
, de ce groupe serait une symétrie, appelée dans ce contexte U-dualité, de la théorie M.
En novembre 2007, un physicien américain, Antony Garrett Lisi, dépose sur le site de publications scientifiques ArXiv un article très discuté sur une théorie unificatrice des forces basé sur le groupe E8.
Algèbre[modifier]
Diagramme de Dynkin[modifier]

Système de racines[modifier]
Dans la base formée par les racines simples  , le système de racines de E8 est formé d'une part de toutes les permutations de
, le système de racines de E8 est formé d'une part de toutes les permutations de
qui constitue le système de racines de  et possède
et possède  éléments (il faut rajouter les 8 générateurs du Cartan pour obtenir 120 qui est la dimension de
éléments (il faut rajouter les 8 générateurs du Cartan pour obtenir 120 qui est la dimension de  ).
).
Par ailleurs on doit ajouter à cela les 128 poids de la représentation spinorielle  de
de 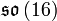 . Toujours dans la même base, ceux-ci sont représentés par les vecteurs
. Toujours dans la même base, ceux-ci sont représentés par les vecteurs
tels que la somme de toutes les coordonnées soit paire. Ils sont au nombre de  .
.
On obtient donc  racines, toutes de multiplicité 1. Par abus de langage on considère aussi parfois le vecteur nul comme une racine associée à la sous-algèbre de Cartan. Comme E8 est de rang 8, la racine nulle est alors de multiplicité 8. Ainsi au final on a bien décrit les 248 générateurs de l'algèbre
racines, toutes de multiplicité 1. Par abus de langage on considère aussi parfois le vecteur nul comme une racine associée à la sous-algèbre de Cartan. Comme E8 est de rang 8, la racine nulle est alors de multiplicité 8. Ainsi au final on a bien décrit les 248 générateurs de l'algèbre  .
.
Matrice de Cartan[modifier]
Représentations[modifier]
 se distingue des autres algèbres de Lie de dimension finie par le fait que sa plus petite représentation non-triviale est la représentation adjointe.
se distingue des autres algèbres de Lie de dimension finie par le fait que sa plus petite représentation non-triviale est la représentation adjointe.
La représentation fondamentale de E8 est de dimension 248.
Décodage du groupe  [modifier]
[modifier]
Le 19 mars 2007, l'Institut américain des mathématiques (AIM) a annoncé que des chercheurs américains et européens et après quatre ans d'efforts et plus d'un siècle après sa découverte sont parvenus à décoder l'E8, l'une des structures mathématiques les plus complexes et les plus grandes. Le noyau dur du groupe de chercheurs est formé de sept mathématiciens, cinq Américains et deux Français : Jeffrey Adams de l'Université du Maryland, Dan Barbasch de Université Cornell, John Stembridge de l'Université du Michigan, Peter Trapa de l'Université de l'Utah, Marc van Leeuwen de l'Université de Poitiers, David Vogan du Massachusetts Institute of Technology et Fokko du Cloux de l'Université de Lyon1.
Selon Peter Sarnak, professeur de mathématiques à l'Université Princeton et président du comité scientifique de AIM, le décodage de ce groupe pourrait ouvrir la porte à d'autres innovations dans le domaine de la programmation informatique.
« Cette percée est importante non seulement pour faire avancer les connaissances mathématiques de base mais aussi pour faciliter les calculs par ordinateur permettant de résoudre des problèmes complexes, [...]. Le décodage de cette structure appelée E8 pourrait aussi très bien avoir des applications en mathématiques et physique qu'on ne découvrira pas avant plusieurs années. »
— Peter Sarnak, Le Monde, 19 mars 2007
Parmi les objets sous-jacents aux groupes de Lie, on trouve toutes sortes de figures géométriques telles que les sphères, les cônes, les cylindres dans l’espace à trois dimensions. Mais les choses se corsent lorsque l’on étudie ces objets dans des espaces de dimensions supérieures. « Comprendre et classer les structures  a été critique pour comprendre des phénomènes dans de nombreux domaines des mathématiques incluant l’algèbre, la géométrie, la théorie des nombres ainsi que la physique et la chimie », commente Peter Sarnak, professeur de mathématique à l’université de Princeton et président du comité scientifique de l’AIM.
a été critique pour comprendre des phénomènes dans de nombreux domaines des mathématiques incluant l’algèbre, la géométrie, la théorie des nombres ainsi que la physique et la chimie », commente Peter Sarnak, professeur de mathématique à l’université de Princeton et président du comité scientifique de l’AIM.
Ces calculs ont nécessité de nouvelles techniques mathématiques et des capacités de calcul des ordinateurs qui n'existaient pas il y a encore peu d'années, précisent les chercheurs. L’opération a pris 77 heures et a nécessité un supercalculateur doté de 200 Go de mémoire vive, et a produit un résultat de l’ordre de 60 Go dont la taille peut être comparée à 60 fois celle du génome humain. L’équipe attendait donc de trouver un supercalculateur capable d’effectuer les calculs lorsque Noam Elkies, un mathématicien de l’université Harvard a mis en évidence un moyen de découper le projet en éléments plus simples. Chaque élément produit un sous-ensemble du résultat et leur réunion permet de donner la solution complète au problème. À l’été 2006, trois membres de l’équipe, dont Fokko du Cloux, ont décomposé le programme en plusieurs éléments. Les calculs ont été réalisés sur une machine de l’université de Washington.
L’ordre de grandeur et la nature du calcul est à rapprocher du projet de séquençage du génome humain, indique le communiqué de presse diffusé par AIM. Alors que l’ensemble des informations du génome représente un volume de 1 Go, le résultat de l’E8 est environ 60 fois plus important avec des données hautement compressées. Écrit sur un papier, ce résultat couvrirait un espace équivalent à la taille de Manhattan.
Quelques chiffres sur le calcul de  [modifier]
[modifier]
Quelques idées sur la taille du résultat final1 :
- Le résultat du calcul E8 est une matrice de 453 060 lignes et colonnes.
- La matrice comporte 205 263 363 600 éléments,
- Si chaque élément de cette matrice était écrit sur une surface de 2,5 cm2, la matrice aurait une dimension d’un carré de plus de 10 km de côté.
- Nombre de polynômes distincts : 1 181 642 979,
- nombre de coefficients dans les polynômes distincts : 13 721 641 221,
- plus grand coefficient : 11 808 808,
- polynôme ayant le plus grand coefficient : 152 q22 + 3472 q21 + 38 791 q20 + 293 021 q19 + 1 370 892 q18 + 4 067 059 q17 + 7 964 012 q16 + 11 159 003 q15 + 11 808 808 q14 + 9 859 915 q13 + 6 778 956 q12 + 3 964 369 q11 + 2 015 441 q10 + 906 567 q9 + 363 611 q8 + 129 820 q7 + 41 239 q6 + 11 426 q5 + 2 677 q4 + 492 q3 + 61 q2 + 3 q,
- valeur de ce polynôme pour q=1 : 60 779 787,
- polynôme ayant la plus grande valeur (lorsque q=1) découvert jusqu'à présent (mai 2007) : 1 583 q22 + 18 668 q21 + 127 878 q20 + 604 872 q19 + 2 040 844 q18 + 4 880 797 q17 + 8 470 080 q16 + 11 143 777 q15 + 11 467 297 q14 + 9 503 114 q13 + 6 554 446 q12 + 3 862 269 q11 + 1 979 443 q10 + 896 537 q9 + 361 489 q8 + 129 510 q7 + 41 211 q6 + 11 425 q5 + 2 677 q4 + 492 q3 + 61 q2 + 3 q,
- valeur pour ce polynôme pour q=1 : 62 098 473.
Notes et références[modifier]
- AIM math: Representations of E8 [archive]
Voir aussi[modifier]
Articles connexes[modifier]
- Groupe de Lie
- Algèbre de Lie
- Système de racines
- Diagramme de Dynkin
Liens externes[modifier]
- [pdf] Théorie de A. Garrett Lisi sur l'utilisation de E8 pour réunifier les différentes forces physiques et la physique quantique
- (fr) Groupe de Lie E8 : une clé pour la théorie des supercordes ?
- (en) Taille de certaines lignes de calcul du groupe E8
- (fr) Une solution mathématique aux dimensions démesurées Article de Techno-science.net
- [pdf] Représentation graphique de E8
- (fr) Garrett Lisi sur la théorie du Tout Conférence TED 2008 (VOST FR) www.ted.com
- Portail des mathématiques
11:34 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Algèbre enveloppante
Algèbre enveloppante
|
|
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
En mathématiques, on peut construire l'algèbre enveloppante  d'une algèbre de Lie
d'une algèbre de Lie  . Il s'agit une algèbre unitaire qui permet de rendre compte de la plupart des propriétés de
. Il s'agit une algèbre unitaire qui permet de rendre compte de la plupart des propriétés de  .
.
Sommaire[masquer] |
Algèbres de Lie[modifier]
Soit K un corps commutatif de caractéristique différente de 2. Une algèbre de Lie  sur K est un espace vectoriel muni d'une apllication bilinéaire
sur K est un espace vectoriel muni d'une apllication bilinéaire ![(x,y) mapsto [x,y]](http://upload.wikimedia.org/math/7/5/e/75e87350f83275e11f126171780fd7ca.png) de
de  dans
dans  qui vérifie les propriétés suivantes :
qui vérifie les propriétés suivantes :
![forall x in mathfrak{g}, [x,x]=0](http://upload.wikimedia.org/math/f/3/2/f3223a3fe063412bb2f5033ba34850f5.png) ;
;![forall x,y,z in mathfrak{g}, [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0](http://upload.wikimedia.org/math/6/7/d/67d115952cf9c1c691b6053868febb0d.png)
Tout espace vectoriel V peut être muni d'une structure d'algèbre de Lie, en posant ![forall x,y in V, [x,y]=0](http://upload.wikimedia.org/math/8/6/9/8697bab9adc96fe793676eb0843e4edc.png) . Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne. Un autre exemple, fondamental pour ce qui suit, est le suivant. Soit V un espace vectoriel sur K. L'espace vectoriel End(V) des endomorphismes de V peut être muni d'une structure d'algèbre de Lie, en posant :
. Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne. Un autre exemple, fondamental pour ce qui suit, est le suivant. Soit V un espace vectoriel sur K. L'espace vectoriel End(V) des endomorphismes de V peut être muni d'une structure d'algèbre de Lie, en posant : ![[u,v]=ucirc v-vcirc u](http://upload.wikimedia.org/math/e/c/e/ecea3c23938418479a1064ef02f67bb2.png) . On note également
. On note également  l'algèbre de Lie ainsi obtenue. Lorsque V est de dimension finie n,
l'algèbre de Lie ainsi obtenue. Lorsque V est de dimension finie n,  s'identifie aux matrices de taille
s'identifie aux matrices de taille  à coefficient dans K. On la note alors
à coefficient dans K. On la note alors 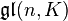 .
.
La construction d'une algèbre enveloppante répond au problème réciproque : à partir d'une algèbre de Lie  , peut-on construire une algèbre associative dont le commutateur correspond au crochet de Lie de
, peut-on construire une algèbre associative dont le commutateur correspond au crochet de Lie de  ?
?
L'algèbre enveloppante[modifier]
Construction[modifier]
A partir de l'algèbre de Lie  , on peut construire le produit tensoriel
, on peut construire le produit tensoriel  et plus généralement
et plus généralement  . On note par convention
. On note par convention  . On considère alors l'algèbre tensorielle de
. On considère alors l'algèbre tensorielle de  , définie par
, définie par  . On note σ l'application canonique de
. On note σ l'application canonique de  dans
dans  . L'algèbre tensorielle satisfait une propriété universelle : pour toute application linéaire τ de
. L'algèbre tensorielle satisfait une propriété universelle : pour toute application linéaire τ de  dans une algèbre avec unité A, il existe un unique morphisme d'algèbre
dans une algèbre avec unité A, il existe un unique morphisme d'algèbre  tel que
tel que 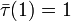 et
et  .
.
Pour construire l'algèbre enveloppante, il faut encore tenir compte de la structure d'algèbre de Lie de  . On veut donc forcer
. On veut donc forcer  à être égal à [X,Y]. Plus formellement, soit J l'idéal bilatère engendré par les
à être égal à [X,Y]. Plus formellement, soit J l'idéal bilatère engendré par les ![Xotimes Y-Yotimes X-[X,Y]](http://upload.wikimedia.org/math/e/f/a/efa058d8548e9c2c9d27cf84332bdfff.png) , pour
, pour  . L'algèbre enveloppante
. L'algèbre enveloppante  est alors le quotient de
est alors le quotient de  par l'idéalJ. L'injection canonique de
par l'idéalJ. L'injection canonique de  dans
dans  passe au quotient et fournit alors un morphisme
passe au quotient et fournit alors un morphisme 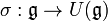 .
.
Notons  l'image de
l'image de 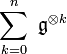 dans
dans  . Lorsque l'algèbre de Lie
. Lorsque l'algèbre de Lie  est de dimension finie,
est de dimension finie,  est un sous-espace vectoriel de dimension finie de
est un sous-espace vectoriel de dimension finie de  . Dans tous les cas, on a la filtration suivante :
. Dans tous les cas, on a la filtration suivante :  .
.
Exemple Considérons l'algèbre de Lie abélienne K, de dimension 1. Dans ce cas, le crochet de Lie est identiquement nul. L'idéal J est alors engendré par les vecteurs  , pour
, pour  . On vérifie alors dans ce cas que
. On vérifie alors dans ce cas que ![U(K) cong K[T]](http://upload.wikimedia.org/math/0/c/9/0c96d59ae426e695ac9de9520e7472a9.png) (l'algèbre des polynômes en une indéterminée).
(l'algèbre des polynômes en une indéterminée).
Propriété universelle[modifier]
Comme pour l'algèbre tensorielle, on peut caractériser l'algèbre enveloppante de  par une propriété universelle :
par une propriété universelle :
Propriété universelle de l'algèbre enveloppante — Soit  une application linéaire de
une application linéaire de  dans une algèbre associative avec unité A telle que
dans une algèbre associative avec unité A telle que
![varphi([X,Y])=varphi(X)varphi(Y)-varphi(Y)varphi(X)](http://upload.wikimedia.org/math/3/e/9/3e97049ebe943b16508bcef76c30c203.png) , pour tout
, pour tout  . Alors il existe un unique morphisme d'algèbre
. Alors il existe un unique morphisme d'algèbre  tel que
tel que  et
et  .
.
Remarque L'unicité provient du fait que  est engendrée par 1 et
est engendrée par 1 et  . L'existence s'obtient à partir de la propriété universelle de l'algèbre tensorielle.
. L'existence s'obtient à partir de la propriété universelle de l'algèbre tensorielle.
Cette propriété universelle a une conséquence importante en théorie des représentations, à savoir toute représentation de  dans un espace vectoriel V s'étend de manière unique en un morphisme d'algèbre entre
dans un espace vectoriel V s'étend de manière unique en un morphisme d'algèbre entre  et End(V).
et End(V).
Théorème de Poincaré-Birkhoff-Witt et ses conséquences[modifier]
Le théorème de Poincaré-Birkhoff-Witt(PBW) donne une base de l'algèbre enveloppante et ainsi permet de mieux en comprendre la structure. Pour en simplifier un peu l'énoncé, nous le donnons pour une algèbre de Lie de dimension finie.
Théorème de Poincaré-Birkhoff-Witt — L'application  est injective. Soit
est injective. Soit  une base de
une base de  . Alors les monômes
. Alors les monômes  ,
,  , forment une base de
, forment une base de  .
.
Voici quelques conséquences importantes de PBW :
- Soit
 une sous-algèbre de Lie de
une sous-algèbre de Lie de  . Alors
. Alors 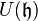 s'identifie à une sous-algèbre associative de
s'identifie à une sous-algèbre associative de  .
. - Supposons que
 soit la somme directe de deux sous-algèbres :
soit la somme directe de deux sous-algèbres :  . Alors l'algèbre
. Alors l'algèbre  est isomorphe au produit tensoriel
est isomorphe au produit tensoriel  .
. - Soit Kn l'algèbre de Lie abélienne de dimension n. Alors U(Kn) est isomorphe à l'algèbre de polynômes
![K[T_1,ldots,T_n]](http://upload.wikimedia.org/math/2/0/4/20496667b52257abfbda4b3696b1f9c5.png) .
. - Soit V un espace vectoriel. Tout morphisme d'algèbre de
 dans End(V) donne par restriction une représentation de
dans End(V) donne par restriction une représentation de  dans V. En tenant compte de la remarque de la partie précédente, cela fournit une équivalence de catégories entre la catégorie des représentations de
dans V. En tenant compte de la remarque de la partie précédente, cela fournit une équivalence de catégories entre la catégorie des représentations de  et celle des représentations de l'algèbre
et celle des représentations de l'algèbre  .
.
Dans certains cas, il est possible de décrire explicitement l'algèbre enveloppante. Soit G un groupe de Lie réel, d'algèbre de Lie  . Notons
. Notons  le complexifié de
le complexifié de  . Soit
. Soit  . On construit alors l'opérateur différentiel
. On construit alors l'opérateur différentiel  sur
sur  par :
par :
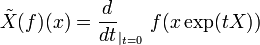 , pour
, pour  et
et  . L'opérateur
. L'opérateur  est un exemple d'opérateur différentiel invariant à gauche (i.e. commutant avec les translations à gauche par des vecteurs de G). Notons D(G) l'ensemble des opérateurs différentiels invariants à gauche. On a donc une application
est un exemple d'opérateur différentiel invariant à gauche (i.e. commutant avec les translations à gauche par des vecteurs de G). Notons D(G) l'ensemble des opérateurs différentiels invariants à gauche. On a donc une application  . Cette application s'étend en une application de
. Cette application s'étend en une application de  dans D(G). Cette application définit par propriété universelle un morphisme d'algèbre de
dans D(G). Cette application définit par propriété universelle un morphisme d'algèbre de  dans D(G). Ce morphisme est un fait unisomorphisme. Ainsi l'algèbre enveloppante de
dans D(G). Ce morphisme est un fait unisomorphisme. Ainsi l'algèbre enveloppante de  s'identifie avec l'algèbre des opérateurs différentiels invariants à gauche sur G.
s'identifie avec l'algèbre des opérateurs différentiels invariants à gauche sur G.
Exemple Regardons le cas simple de l'algèbre de Lie  . Le groupe de Lie
. Le groupe de Lie  a pour algèbre de Lie
a pour algèbre de Lie  , qui a pour complexifié
, qui a pour complexifié  . Ici
. Ici  est l'espace usuel des fonctions
est l'espace usuel des fonctions  à valeurs dans
à valeurs dans  . Ainsi, pour
. Ainsi, pour  , l'opérateur
, l'opérateur  est donné par
est donné par  . Autrement dit, l'opérateur est donné par
. Autrement dit, l'opérateur est donné par 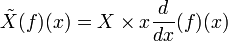 . D'autre part, un opérateur différentiel
. D'autre part, un opérateur différentiel 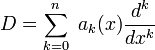 sur G est invariant à gauche si et seulement si
sur G est invariant à gauche si et seulement si  . Ainsi, on a
. Ainsi, on a 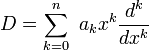 , ce qui identifie
, ce qui identifie  avec
avec ![mathbb{C}[T]](http://upload.wikimedia.org/math/5/d/a/5da3c864653f85dd225b9b00e48bd866.png) , qui est isomorphe à
, qui est isomorphe à  comme nous l'avons déjà remarqué.
comme nous l'avons déjà remarqué.
Représentation adjointe[modifier]
L'algèbre de Lie  agit sur elle-même via la représentation adjointe
agit sur elle-même via la représentation adjointe  définie par ad(X)(Y) = [X,Y], pour
définie par ad(X)(Y) = [X,Y], pour  . Cette représentation s'étend en une représentation de
. Cette représentation s'étend en une représentation de  sur son algèbre enveloppante, via la formule
sur son algèbre enveloppante, via la formule  , pour
, pour  et
et  . Cette représentation laisse stable les sous-espaces
. Cette représentation laisse stable les sous-espaces  et donc aussi les quotients
et donc aussi les quotients  . Lorsque
. Lorsque  est de dimension finie,
est de dimension finie,  est aussi de dimension finie. Cela fournit donc toute une famille de représentations de dimension finie de
est aussi de dimension finie. Cela fournit donc toute une famille de représentations de dimension finie de  .
.
L'algèbre symétrique[modifier]
Un autre quotient de l'algèbre tensorielle joue un rôle important : l'algèbre symétrique. Soit I l'idéal bilatère de  engendré par les vecteurs
engendré par les vecteurs  . L'algèbre symétrique
. L'algèbre symétrique  est l'algèbre quotient
est l'algèbre quotient  . C'est une algèbre associative et commutative. On note toujours σ l'application canonique de
. C'est une algèbre associative et commutative. On note toujours σ l'application canonique de  dans
dans  . Comme pour l'algèbre enveloppante, l'algèbre symétrique satisfait une propriété universelle :
. Comme pour l'algèbre enveloppante, l'algèbre symétrique satisfait une propriété universelle :
Propriété universelle de l'algèbre symétrique — Soit C une algèbre associative et commutative, avec unité. Pour toute application linéaire 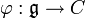 , il existe un unique morphisme d'algèbre
, il existe un unique morphisme d'algèbre  tel que
tel que  et
et  .
.
Les deux algèbres symétrique et enveloppante sont reliées par une application de symétrisation. En effet, on construit une application  comme suit :
comme suit :
 où
où  désigne le groupe des permutations de n éléments. En fait, l'application Sym est un isomorphisme linéaire de
désigne le groupe des permutations de n éléments. En fait, l'application Sym est un isomorphisme linéaire de  sur
sur  (la structure d'algèbre n'est pas conservée en général car
(la structure d'algèbre n'est pas conservée en général car  n'est pas commutative lorsque l'algèbre de Lie
n'est pas commutative lorsque l'algèbre de Lie  n'est pas abélienne).
n'est pas abélienne).
Structure d'anneau de l'algèbre enveloppante[modifier]
On suppode dans cette partie que le corps de base K est de caractéristique nulle.
Généralités[modifier]
L'algèbre enveloppante  est en particulier un anneau. L'étude de cette structure d'anneau est fondamentale en théorie des représentations. L'anneau U est sans diviseur de zéro (autrement dit le produit de deux éléments non nuls de U est également non nul). L'anneau U est noethérien : toute suite croissante d'idéaux est stationnaire. Cependant U n'est pasartinien : par exemple, l'idéal bilatère engendré par
est en particulier un anneau. L'étude de cette structure d'anneau est fondamentale en théorie des représentations. L'anneau U est sans diviseur de zéro (autrement dit le produit de deux éléments non nuls de U est également non nul). L'anneau U est noethérien : toute suite croissante d'idéaux est stationnaire. Cependant U n'est pasartinien : par exemple, l'idéal bilatère engendré par  contient l'idéal engendré par
contient l'idéal engendré par  , qui contient l'idéal engendré par
, qui contient l'idéal engendré par  , etc.
, etc.
Centre de l'algèbre enveloppante[modifier]
Le centre de l'algèbre enveloppante est  . En fait, comme
. En fait, comme  engendre
engendre  , on a aussi
, on a aussi  . Même lorsque l'algèbre de Lie
. Même lorsque l'algèbre de Lie  a un centre trivial, l'algèbre enveloppante peut avoir un centre non trivial (voire gros).
a un centre trivial, l'algèbre enveloppante peut avoir un centre non trivial (voire gros).
Exemple Soit  l'algèbre de Lie des marices complexes de taille
l'algèbre de Lie des marices complexes de taille  , de trace nulle. Une base de
, de trace nulle. Une base de  est donnée par les matrices suivantes :
est donnée par les matrices suivantes :

Le vecteur suivant est un élément du centre  :
:  . Plus précisement, on peut démontrer que
. Plus précisement, on peut démontrer que ![Z(U(mathfrak{g}))=mathbb{C}[Omega]](http://upload.wikimedia.org/math/b/c/e/bce008597faaac0cedbfe906b9608620.png) . Autrement dit, le vecteur Ω engendre l'algèbre
. Autrement dit, le vecteur Ω engendre l'algèbre  . Ceci est un cas particulier d'un résultat de Harish-Chandra et d'un résultat de Chevalley sur le centre des algèbres enveloppantes desalgèbres de Lie semi-simples.
. Ceci est un cas particulier d'un résultat de Harish-Chandra et d'un résultat de Chevalley sur le centre des algèbres enveloppantes desalgèbres de Lie semi-simples.
L'algèbre  joue un rôle fondamental en théorie des représentations. En effet, le lemme de Schur affirme que tout opérateur qui commute à une représentation irréductible d'une algèbre de Lie complexe est une homothétie. D'après ce qui précède, si (π,V) est une représentation irréductible de l'algèbre de Lie complexe
joue un rôle fondamental en théorie des représentations. En effet, le lemme de Schur affirme que tout opérateur qui commute à une représentation irréductible d'une algèbre de Lie complexe est une homothétie. D'après ce qui précède, si (π,V) est une représentation irréductible de l'algèbre de Lie complexe  , alors l'opérateur π(Z) associé à n'importe quel vecteur Z de
, alors l'opérateur π(Z) associé à n'importe quel vecteur Z de  commute à tous les π(X),
commute à tous les π(X),  . Donc π(Z) est une homothétie. Ceci est vrai pour tout Z dans le centre de l'algèbre enveloppante. On obtient ainsi un caractère du centre, c'est-à-dire un morphisme d'algèbre de
. Donc π(Z) est une homothétie. Ceci est vrai pour tout Z dans le centre de l'algèbre enveloppante. On obtient ainsi un caractère du centre, c'est-à-dire un morphisme d'algèbre de  dans
dans  , que l'on appelle le caractère infinitésimal de la représentation π. Ainsi l'étude des caractères du centre de l'algèbre enveloppante fournit des informations importantes pour l'étude des représentations irréductibles de
, que l'on appelle le caractère infinitésimal de la représentation π. Ainsi l'étude des caractères du centre de l'algèbre enveloppante fournit des informations importantes pour l'étude des représentations irréductibles de  .
.
Idéaux de l'algèbre enveloppante[modifier]
Toute représentation de  s'étend canoniquement en une représentation de
s'étend canoniquement en une représentation de  , c'est-à-dire un morphisme d'algèbre
, c'est-à-dire un morphisme d'algèbre  . Le noyau de π est un idéal de
. Le noyau de π est un idéal de  . D'autre part, si la représentation (π,V) est irréductible (ou même seulement cyclique), il existe un vecteur v de V tel que l'application
. D'autre part, si la représentation (π,V) est irréductible (ou même seulement cyclique), il existe un vecteur v de V tel que l'application  , soit surjective. La représentation V s'identifie alors avec le quotient de
, soit surjective. La représentation V s'identifie alors avec le quotient de  par le noyau de cette application. Ces deux faits montrent l'importance de comprendre les idéaux de
par le noyau de cette application. Ces deux faits montrent l'importance de comprendre les idéaux de  .
.
Références[modifier]
- N. Bourbaki, Groupes et algèbres de Lie
- Jacques Dixmier, Algèbres enveloppantes Éditions Jacques Gabay, Paris, 1996. ISBN 2-87647-014-4
- James E. Humphreys, Introduction to Lie Algebras and Representation Theory, Second printing, revised. Graduate Texts in Mathematics, 9. Springer-Verlag, New York, 1978. ISBN 0-387-90053-5
- Nathan Jacobson, Lie algebras, Republication of the 1962 original. Dover Publications, Inc., New York, 1979. ISBN 0-486-63832-4
- Anthony Knapp, Representation theory of semisimple groups: an overview based on examples, Princeton University Press, 2001. Reprint of the 1986 original. ISBN 0-691-09089-0
Voir aussi[modifier]
11:32 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Représentation d'algèbre de Lie
Représentation d'algèbre de Lie
|
|
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
Source : http://fr.wikipedia.org/wiki/Repr%C3%A9sentation_d'alg%C3...
Livres : Représentation d'algèbre de Lie
En mathématiques, une représentation d'une algèbre de Lie est une façon d'écrire cette algèbre comme une algèbre de matrices, ou plus généralement d'endomorphismes d'un espace vectoriel, avec le crochet de Lie donné par le commutateur.
Sommaire[masquer] |
Algèbres de Lie[modifier]
Soit K un corps commutatif de caractéristique différente de 2. Une algèbre de Lie  sur K est un espace vectoriel muni d'une apllication bilinéaire
sur K est un espace vectoriel muni d'une apllication bilinéaire ![(x,y) mapsto [x,y]](http://upload.wikimedia.org/math/7/5/e/75e87350f83275e11f126171780fd7ca.png) de
de  dans
dans  qui vérifie les propriétés suivantes :
qui vérifie les propriétés suivantes :
![forall x in mathfrak{g}, [x,x]=0](http://upload.wikimedia.org/math/f/3/2/f3223a3fe063412bb2f5033ba34850f5.png) ;
;![forall x,y,z in mathfrak{g}, [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0](http://upload.wikimedia.org/math/6/7/d/67d115952cf9c1c691b6053868febb0d.png)
Tout espace vectoriel V peut être muni d'une structure d'algèbre de Lie, en posant ![forall x,y in V, [x,y]=0](http://upload.wikimedia.org/math/8/6/9/8697bab9adc96fe793676eb0843e4edc.png) . Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne. Un autre exemple, fondamental pour ce qui suit, est le suivant. Soit V un espace vectoriel sur K. L'espace vectoriel End(V) des endomorphismes de V peut être muni d'une structure d'algèbre de Lie, en posant :
. Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne. Un autre exemple, fondamental pour ce qui suit, est le suivant. Soit V un espace vectoriel sur K. L'espace vectoriel End(V) des endomorphismes de V peut être muni d'une structure d'algèbre de Lie, en posant : ![[u,v]=ucirc v-vcirc u](http://upload.wikimedia.org/math/e/c/e/ecea3c23938418479a1064ef02f67bb2.png) . On note également
. On note également  l'algèbre de Lie ainsi obtenue. Lorsque V est de dimension finie n,
l'algèbre de Lie ainsi obtenue. Lorsque V est de dimension finie n,  s'identifie aux matrices de taille
s'identifie aux matrices de taille 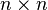 à coefficient dans K. On la note alors
à coefficient dans K. On la note alors 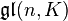 .
.
Une sous-algèbre de Lie de  est un sous-espace vectoriel
est un sous-espace vectoriel  de
de  stable par le crochet de Lie, i.e. tel que
stable par le crochet de Lie, i.e. tel que ![forall x,y in mathfrak{h}, [x,y] in mathfrak{h}](http://upload.wikimedia.org/math/f/4/3/f43e3feae72d881ec0c5811b4c166016.png) .
.
Exemples
- Si
 est une algèbre de Lie abélienne alors tout sous-espace vectoriel de
est une algèbre de Lie abélienne alors tout sous-espace vectoriel de  est automatiquement une sous-algèbre de Lie.
est automatiquement une sous-algèbre de Lie. - Le sous-espace vectoriel de
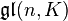 formé des matrices de trace nulle est une sous-algèbre de Lie de
formé des matrices de trace nulle est une sous-algèbre de Lie de 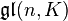 car tr(AB) = tr(BA) pour toutes matrices A et B. Cette sous-algèbre est notée
car tr(AB) = tr(BA) pour toutes matrices A et B. Cette sous-algèbre est notée  .
.
Un idéal d'une algèbre de Lie  est un sous-espace vectoriel
est un sous-espace vectoriel  de
de  tel que
tel que ![forall xin mathfrak{g}, yin mathfrak{h}, [x,y] in mathfrak{h}](http://upload.wikimedia.org/math/7/4/c/74c078f25ba2a4b38726a906c20aac88.png) . Tout idéal d'une algèbre de Lie est en particulier une sous-algèbre de Lie (mais la réciproque est fausse).
. Tout idéal d'une algèbre de Lie est en particulier une sous-algèbre de Lie (mais la réciproque est fausse).
Exemples
- Si
 est une algèbre de Lie abélienne alors tout sous-espace vectoriel de
est une algèbre de Lie abélienne alors tout sous-espace vectoriel de  est automatiquement un idéal.
est automatiquement un idéal. - La sous-algèbre de Lie
 de
de 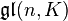 est un idéal.
est un idéal.
Un morphisme entre deux algèbres de Lie  et
et  est une application linéaire
est une application linéaire  telle que
telle que ![forall x,y in mathfrak{g}, varphi([x,y])=[varphi(x),varphi(y)]](http://upload.wikimedia.org/math/3/b/e/3be01a86f4f2f1c4d2431f784e4347f4.png) . Le noyau d'un morphisme d'algèbres de Lie est alors un idéal de l'algèbre de Lie source et l'image une sous-algèbre de Lie de l'algèbre de Lie but. Un isomorphisme entre deux algèbres de Lie est morphisme d'algèbre de Lie qui est un isomorphisme d'espace vectoriel.
. Le noyau d'un morphisme d'algèbres de Lie est alors un idéal de l'algèbre de Lie source et l'image une sous-algèbre de Lie de l'algèbre de Lie but. Un isomorphisme entre deux algèbres de Lie est morphisme d'algèbre de Lie qui est un isomorphisme d'espace vectoriel.
Exemples
- Si
 est une sous-algèbre de Lie de
est une sous-algèbre de Lie de  alors l'inclusion de
alors l'inclusion de  dans
dans  est un morphisme d'algèbre de Lie, de noyau nul et d'image
est un morphisme d'algèbre de Lie, de noyau nul et d'image  .
. - Si
 est un idéal de
est un idéal de  alors il existe une unique structure d'algèbre de Lie sur l'espace vectoriel quotient
alors il existe une unique structure d'algèbre de Lie sur l'espace vectoriel quotient  telle que la projection canonique
telle que la projection canonique  soit un morphisme d'algèbre de Lie. Le noyau de p est alors
soit un morphisme d'algèbre de Lie. Le noyau de p est alors  et son image
et son image  . L'algèbre de Lie
. L'algèbre de Lie 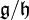 ainsi définie s'appelle l'algèbre de Lie quotient de
ainsi définie s'appelle l'algèbre de Lie quotient de  sur
sur  . Par exemple l'algèbre de Lie quotient
. Par exemple l'algèbre de Lie quotient  est isomorphe à l'algèbre de Lie abélienne K.
est isomorphe à l'algèbre de Lie abélienne K.
Représentations[modifier]
Définitions[modifier]
Une représentation de l'algèbre de Lie  dans un espace vectoriel V est la donnée d'un morphisme
dans un espace vectoriel V est la donnée d'un morphisme  . Autrement dit, π est une application linéaire qui vérifie également
. Autrement dit, π est une application linéaire qui vérifie également ![forall x,y in mathfrak{g}, pi([x,y])=pi(x)circpi(y)-pi(y)circpi(x)](http://upload.wikimedia.org/math/0/0/8/0080e112135e13fa673bfb501e2b8780.png) . On note (π,V) cette représentation ou simplement V lorsqu'il n'y a pas d'ambiguité possible sur π. On dit aussi que V est un
. On note (π,V) cette représentation ou simplement V lorsqu'il n'y a pas d'ambiguité possible sur π. On dit aussi que V est un  -module ou simplement un module. On note parfois
-module ou simplement un module. On note parfois  au lieu de π(x)(v) l'action de l'élément
au lieu de π(x)(v) l'action de l'élément  sur le vecteur
sur le vecteur  .
.
Une représentation (π,V) est dite fidèle si le morphisme π est injectif. Dans ce cas, l'algèbre de Lie  peut être vue comme une sous-algèbre de Lie de
peut être vue comme une sous-algèbre de Lie de  .
.
Une sous-représentation d'une représentation (π,V) de  est la donnée d'un sous-espace vectoriel W de V stable par l'action de
est la donnée d'un sous-espace vectoriel W de V stable par l'action de  , i.e. tel que
, i.e. tel que  . En particulier, pour qu'une droite vectorielle D engendrée par un vecteur v soit stable il faut et il suffit que v soit un vecteur propre commun à tous les endomorphismes π(x). Une représentation (π,V) est irréductible si elle n'admet aucune sous-représentation propre, c'est-à-dire autre que les sous-espaces {0} et V. En particulier toute représentation (π,V) de dimension 1 est irréductible, car dans ce cas les seuls sous-espaces vectoriels de V sont précisement {0} et V. Soit V' une sous-représentation de (π,V). La représentation quotientest la représentation
. En particulier, pour qu'une droite vectorielle D engendrée par un vecteur v soit stable il faut et il suffit que v soit un vecteur propre commun à tous les endomorphismes π(x). Une représentation (π,V) est irréductible si elle n'admet aucune sous-représentation propre, c'est-à-dire autre que les sous-espaces {0} et V. En particulier toute représentation (π,V) de dimension 1 est irréductible, car dans ce cas les seuls sous-espaces vectoriels de V sont précisement {0} et V. Soit V' une sous-représentation de (π,V). La représentation quotientest la représentation  de
de  dans l'espace quotient V / V' définie par
dans l'espace quotient V / V' définie par  .
.
Un morphisme entre deux représentations (π,V) et (π',V') d'une même algèbre de Lie  est la donnée d'une application linéaire
est la donnée d'une application linéaire  qui commute à l'action de
qui commute à l'action de  , c'est-à-dire telle que
, c'est-à-dire telle que  . Lorque
. Lorque  est un isomorphisme d'espace vectoriel, on dit que les deux représentations sont isomorphes. L'ensemble de tous les morphismes entre les représentations (π,V) et (π',V') forme un espace vectoriel, noté
est un isomorphisme d'espace vectoriel, on dit que les deux représentations sont isomorphes. L'ensemble de tous les morphismes entre les représentations (π,V) et (π',V') forme un espace vectoriel, noté  .
.
Le lemme de Schur est un résultat important pour la compréhension de cet espace  . En voici l'énoncé :
. En voici l'énoncé :
Lemme de Schur —
- Soient V et V' deux représentations irréductibles d'une algèbre de Lie
 . Soit
. Soit  . Alors
. Alors  est soit l'application nulle soit un isomorphisme. En particulier, si V et V' ne sont pas isomorphes,
est soit l'application nulle soit un isomorphisme. En particulier, si V et V' ne sont pas isomorphes,  .
. - Supposons ici que le corps K soit algébriquement clos. Soit V une représentation irréductible de dimension finie de
 . Alors tout morphisme
. Alors tout morphisme  est un multiple de l'identité. En d'autres termes,
est un multiple de l'identité. En d'autres termes,  .
.
Remarques
- Le premier point du lemme de Schur résulte du fait que
 est une sous-représentation de V et
est une sous-représentation de V et  une sous-représentation de V'.
une sous-représentation de V'. - Le deuxième point du lemme de Schur résulte du fait que tout endomorphisme d'un espace vectoriel de dimension finie admet au moins une valeur propre λ sur un corps algébriquement clos. Par conséquent
 est un morphisme de V dans V qui n'est pas un isomorphisme. D'après le premier point, il s'agit donc de l'application nulle, i.e.
est un morphisme de V dans V qui n'est pas un isomorphisme. D'après le premier point, il s'agit donc de l'application nulle, i.e.  . Ce résultat est encore valable en dimension infinie mais nécessite la puissance du théorème spectral.
. Ce résultat est encore valable en dimension infinie mais nécessite la puissance du théorème spectral. - Le deuxième point du lemme de Schur est faux pour un corps non algébriquement clos. Supposons par exemple
 . Considérons la représentation (π,V) donnée par la formule
. Considérons la représentation (π,V) donnée par la formule 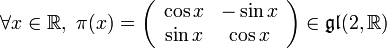 . On vérifie que (π,V) est une représentation irréductible de l'algèbre de Lie abélienne
. On vérifie que (π,V) est une représentation irréductible de l'algèbre de Lie abélienne  . Considérons y = 45o et posons
. Considérons y = 45o et posons  . Comme l'algèbre de Lie
. Comme l'algèbre de Lie  est abélienne,
est abélienne,  est un morphisme de V dans V. On peut d'ailleurs vérifier que
est un morphisme de V dans V. On peut d'ailleurs vérifier que  est bien un isomorphisme. Cependant
est bien un isomorphisme. Cependant  n'est pas un multiple de l'identité. Remarquons à ce propos que
n'est pas un multiple de l'identité. Remarquons à ce propos que  n'a pas de valeurs propres réelles (ce qui explique pourquoi la preuve du deuxième point du lemme n'est pas valable dans ce cas).
n'a pas de valeurs propres réelles (ce qui explique pourquoi la preuve du deuxième point du lemme n'est pas valable dans ce cas).
Exemples[modifier]
- Une représentation d'une algèbre de Lie abélienne
 est une application linéaire à valeurs dans un sous-espace commutatif de l'espace des endomorphismes d'un espace vectoriel V. Par exemple, si V est de dimension fini, on peut représenter
est une application linéaire à valeurs dans un sous-espace commutatif de l'espace des endomorphismes d'un espace vectoriel V. Par exemple, si V est de dimension fini, on peut représenter  par des matrices diagonales (qui commutent entre elles).
par des matrices diagonales (qui commutent entre elles). - La représentation triviale de
 dans un espace vectoriel V est la représentation π définie par
dans un espace vectoriel V est la représentation π définie par  .
. - Si
 , on définit la représentation naturelle de
, on définit la représentation naturelle de  comme la représentation
comme la représentation  définie par
définie par 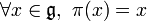 . Plus généralement la représentation naturelle d'une sous-algèbre de Lie
. Plus généralement la représentation naturelle d'une sous-algèbre de Lie  de
de 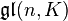 est définie comme l'inclusion de
est définie comme l'inclusion de  dans
dans 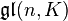 . Elle est donc à valeurs dans Kn.
. Elle est donc à valeurs dans Kn. - La représentation adjointe d'une algèbre de Lie
 est la représentation
est la représentation  définie par
définie par ![forall x in mathfrak{g}, ad(x): y in mathfrak{g} mapsto [x,y] in mathfrak{g}](http://upload.wikimedia.org/math/8/8/f/88ff3fa6e010a55f36d8b87327a5fd4f.png) .
. - Soit
 l'algèbre de Lie abélienne de dimension 1, définie sur
l'algèbre de Lie abélienne de dimension 1, définie sur  . Considérons l'espace
. Considérons l'espace  . On définit une représentation de
. On définit une représentation de  dans V par la formule
dans V par la formule  , où
, où  .
.
Constructions de représentations[modifier]
- Somme directe : soient (π,V) et (π',V') deux représentations de
 . On définit la représentation somme directe
. On définit la représentation somme directe  dans l'espace vectoriel
dans l'espace vectoriel 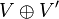 par la formule
par la formule  . Dans ce cas,
. Dans ce cas,  et
et  sont des sous-représentations de
sont des sous-représentations de 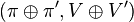 .
. - Produit tensoriel : soient (π,V) et (π',V') deux représentations de
 . On définit la représentation produit tensoriel
. On définit la représentation produit tensoriel  dans l'espace vectoriel
dans l'espace vectoriel 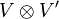 par la formule
par la formule 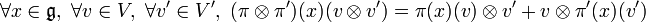 .
. - Contragrédiente : soit (π,V) une représentation de
 . On définit la représentation contragrédiente π * dans l'espace vectoriel dual V * par la formule
. On définit la représentation contragrédiente π * dans l'espace vectoriel dual V * par la formule  .
. - Espace des morphismes : soient (π,V) et (π',V') deux représentations de
 . Nous avons vu comment définir l'espace vectoriel
. Nous avons vu comment définir l'espace vectoriel  des morphimes de V dans V'. On définit une représentation encore notée π de
des morphimes de V dans V'. On définit une représentation encore notée π de  sur cet espace par la formule
sur cet espace par la formule  .
. - Restriction à une sous-algèbre de Lie : soit (π,V) une représentation de
 . Soit
. Soit  une sous-algèbre de Lie de
une sous-algèbre de Lie de  . Alors
. Alors  est une représentation de
est une représentation de  , appelée la restriction de (π,V) à
, appelée la restriction de (π,V) à  . On la note parfois
. On la note parfois  par abus de notations.
par abus de notations.
Une représentation de  est indécomposable si elle n'est pas isomorphe à la somme directe de deux sous-représentations propres. En particulier, toute représentation irréductible est indécomposable, mais la réciproque est fausse. Une représentation est semi-simple (ou complétement réductible) si elle est isomorphe à une somme directe de sous-représentations irréductibles (éventuellement en nombre infini). Une représentation indécomposable et semi-simple est nécessairement irréductible.
est indécomposable si elle n'est pas isomorphe à la somme directe de deux sous-représentations propres. En particulier, toute représentation irréductible est indécomposable, mais la réciproque est fausse. Une représentation est semi-simple (ou complétement réductible) si elle est isomorphe à une somme directe de sous-représentations irréductibles (éventuellement en nombre infini). Une représentation indécomposable et semi-simple est nécessairement irréductible.
Exemples:
- Soit
 l'algèbre de Lie abélienne de dimension 1 sur le corps
l'algèbre de Lie abélienne de dimension 1 sur le corps  . On définit une représentation π de
. On définit une représentation π de  dans
dans  par la formule
par la formule  . Cette représentation n'est pas irréductible. Par exemple la droite D1 engendrée par le vecteur
. Cette représentation n'est pas irréductible. Par exemple la droite D1 engendrée par le vecteur 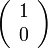 est stable, tout comme la droiteD2 engendrée par le vecteur
est stable, tout comme la droiteD2 engendrée par le vecteur  . Il s'agit donc de deux sous-représentations de π, irréductibles car de dimension 1. Or on a
. Il s'agit donc de deux sous-représentations de π, irréductibles car de dimension 1. Or on a  . Donc la représentation π est semisimple.
. Donc la représentation π est semisimple. - Avec les notations de l'exemple précédent, on peut aussi considérer la représentation π' dans
 définie par la formule
définie par la formule  . A nouveau la droiteD1 est un sous-espace stable. Donc la représentation π' n'est pas irréductible. Plus généralement, on peut vérifier que D1 est la seule droite stable et donc la seule sous-représentation de π'. Ainsi π' est indécomposable.
. A nouveau la droiteD1 est un sous-espace stable. Donc la représentation π' n'est pas irréductible. Plus généralement, on peut vérifier que D1 est la seule droite stable et donc la seule sous-représentation de π'. Ainsi π' est indécomposable. - Gardons toujours les mêmes notations. On définit la représentation π'' de
 dans
dans  par la formule
par la formule  . On peut vérifier qu'il n'y a pas de droites stables par la représentation π''. En d'autres termes, π'' est irréductible.
. On peut vérifier qu'il n'y a pas de droites stables par la représentation π''. En d'autres termes, π'' est irréductible.
Ces trois exemples traduisent le fait qu'une matrice réelle peut être soit diagonalisable, soit trigonalisable mais pas diagonalisble, ou ne possède pas de valeurs propres réelles. On voit ainsi que la notion de représentation d'une algèbre de Lie généralise la notion classique de réduction des endomorphismes.
Lien avec les représentations de l'algèbre enveloppante[modifier]
L'algèbre enveloppante d'une algèbre de Lie[modifier]
Soit A une algèbre associative avec unité. Alors il existe sur A une structure d'algèbre de Lie pour laquelle le crochet de Lie est donné par la formule ![forall a,b in A, [a,b]=ab-ba](http://upload.wikimedia.org/math/3/6/e/36ed7366f61db225948e1e425e1a1074.png) . On note parfois AL cette algèbre de Lie. Ainsi toute algèbre associative fournit une algèbre de Lie. Nous avons vu que
. On note parfois AL cette algèbre de Lie. Ainsi toute algèbre associative fournit une algèbre de Lie. Nous avons vu que  est un exemple de cette construction. Peut-on donner une réciproque à ce résultat ? Peut-on construire une algèbre associative à partir d'une algèbre de Lie. Cette idée conduit à la notion d'algèbre enveloppante d'une algèbre de Lie.
est un exemple de cette construction. Peut-on donner une réciproque à ce résultat ? Peut-on construire une algèbre associative à partir d'une algèbre de Lie. Cette idée conduit à la notion d'algèbre enveloppante d'une algèbre de Lie.
Soit  une algèbre de Lie sur K. Soit
une algèbre de Lie sur K. Soit  l'algèbre tensorielle de
l'algèbre tensorielle de  . Soit J l'idéal bilatère de
. Soit J l'idéal bilatère de  engendré par les tenseurs
engendré par les tenseurs ![x otimes y - y otimes x - [x,y] in T(mathfrak{g})](http://upload.wikimedia.org/math/2/5/7/25730dde99f61e92ddf418741d424129.png) pour tous x ety de
pour tous x ety de  . L'algèbre enveloppante de
. L'algèbre enveloppante de  est l'algèbre associative unitaire définie comme le quotient
est l'algèbre associative unitaire définie comme le quotient  . On la note
. On la note  . La composition
. La composition 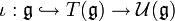 s'appelle l'application canonique de
s'appelle l'application canonique de  dans son algèbre enveloppante. En tant qu'algèbre,
dans son algèbre enveloppante. En tant qu'algèbre,  est engendrée par 1 et l'image
est engendrée par 1 et l'image  . De plus, ι est un morphisme d'algèbre de Lie de
. De plus, ι est un morphisme d'algèbre de Lie de  dans
dans  . L'algèbre enveloppante d'une algèbre de Lie satisfait la propriété universelle suivante :
. L'algèbre enveloppante d'une algèbre de Lie satisfait la propriété universelle suivante :
Propriété universelle de l'algèbre enveloppante — Soit A une algèbre associative avec une unité. Soit  un morphisme d'algèbres de Lie de
un morphisme d'algèbres de Lie de  dans AL. Alors il existe un unique morphisme d'algèbres associatives Φ de
dans AL. Alors il existe un unique morphisme d'algèbres associatives Φ de  dans A tel que Φ(1) = 1 et
dans A tel que Φ(1) = 1 et 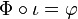 .
.
Exemple:
- Si
 est une algèbre de Lie abélienne, alors son algèbre enveloppante s'identifie à son algèbre symétrique
est une algèbre de Lie abélienne, alors son algèbre enveloppante s'identifie à son algèbre symétrique  , qui elle même s'identifie (après choix d'une base) à une algèbre de polyômes. En particulier,
, qui elle même s'identifie (après choix d'une base) à une algèbre de polyômes. En particulier,  est isomorphe à l'algèbre des polynômes à une indeterminée K[X].
est isomorphe à l'algèbre des polynômes à une indeterminée K[X].
Représentations d'une algèbre de Lie vs Représentations de son algèbre enveloppante[modifier]
Soit (π,V) une représentation de  . Comme
. Comme  est une algèbre associative avec unité, la propiété universelle de
est une algèbre associative avec unité, la propiété universelle de  implique qu'il existe un unique morphisme d'algèbres
implique qu'il existe un unique morphisme d'algèbres  telle que
telle que 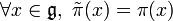 . Cette opération permet donc de passer d'une représentation d'une algèbre de Lie à un morphisme d'algèbres associatives. Réciproquement, tout morphisme d'algèbres associatives
. Cette opération permet donc de passer d'une représentation d'une algèbre de Lie à un morphisme d'algèbres associatives. Réciproquement, tout morphisme d'algèbres associatives  donne par restriction à
donne par restriction à  un morphisme d'algèbres de Lie, c'est-à-dire à une représentation de
un morphisme d'algèbres de Lie, c'est-à-dire à une représentation de  . Ce principe s'interprète comme une équivalence de catégories entre la catégorie des représentations d'une algèbre de Lie donnée et la catégorie des représentations de son algèbre enveloppante.
. Ce principe s'interprète comme une équivalence de catégories entre la catégorie des représentations d'une algèbre de Lie donnée et la catégorie des représentations de son algèbre enveloppante.
Ce nouveau point de vue est important car il permet de considérer de nouveaux objets fondamentaux. Le premier d'entre eux est l'annulateur d'une représentation. Soit (π,V) une représentation de  . Notons encore par la lettre π la représentation de
. Notons encore par la lettre π la représentation de  qu'il s'en déduit. Alors l'annulteur de V est l'ensemble
qu'il s'en déduit. Alors l'annulteur de V est l'ensemble  . C'est un idéal bilatère de
. C'est un idéal bilatère de  car π est un morphisme d'algèbre. Tout idéal qui est l'annulateur d'une représentation irréductible de
car π est un morphisme d'algèbre. Tout idéal qui est l'annulateur d'une représentation irréductible de  s'appelle un idéal primitif.
s'appelle un idéal primitif.
Soit (π,V) une représentation de  . Notons encore par la lettre π la représentation de
. Notons encore par la lettre π la représentation de  qu'il s'en déduit. Pour tout v dans V, l'ensemble
qu'il s'en déduit. Pour tout v dans V, l'ensemble  définit une sous-représentation non nulle de V. Lorsque V est irréductible, on a donc
définit une sous-représentation non nulle de V. Lorsque V est irréductible, on a donc  . Plus généralement, une représentation V est dite cyclique s'il existe
. Plus généralement, une représentation V est dite cyclique s'il existe  tel que
tel que  . Le vecteur v est appelé un vecteur cyclique. Une représentation V est irréductible si et seulement si tout vecteur non nul de V est cyclique. Une représentation Vest dite de type fini s'il existe un nombre fini de vecteurs
. Le vecteur v est appelé un vecteur cyclique. Une représentation V est irréductible si et seulement si tout vecteur non nul de V est cyclique. Une représentation Vest dite de type fini s'il existe un nombre fini de vecteurs  de V tels que
de V tels que  . Une représentation irréductible est donc de type finie. Soit V une représentation cyclique et soit v un vecteur cyclique. On définit alors une application
. Une représentation irréductible est donc de type finie. Soit V une représentation cyclique et soit v un vecteur cyclique. On définit alors une application  par la formule
par la formule  . Le noyau de
. Le noyau de  est l'annulateur de v, noté Ann(v). Il s'agit d'un idéal à gauche de
est l'annulateur de v, noté Ann(v). Il s'agit d'un idéal à gauche de  . Comme V est cyclique, l'image de
. Comme V est cyclique, l'image de  est égale à tout V. On en déduit donc que
est égale à tout V. On en déduit donc que  . Ainsi toute représentation cyclique (et en particulier toute représentation irréductible) apparaît comme un quotient de l'algèbre enveloppante de
. Ainsi toute représentation cyclique (et en particulier toute représentation irréductible) apparaît comme un quotient de l'algèbre enveloppante de  . De plus, lorsque V est irréductible l'idéal Ann(v)est maximal. Ainsi la classification des représentations irréductibles de
. De plus, lorsque V est irréductible l'idéal Ann(v)est maximal. Ainsi la classification des représentations irréductibles de  est équivalente à la classification des idéaux à gauche maximaux de son algèbre enveloppante.
est équivalente à la classification des idéaux à gauche maximaux de son algèbre enveloppante.
Exemple Considérons l'algèbre de Lie commutative  . Identifions son algèbre enveloppante avec l'anneau de polynômes
. Identifions son algèbre enveloppante avec l'anneau de polynômes ![mathbb{C}[X]](http://upload.wikimedia.org/math/6/d/d/6ddcc166f3aa1cea808fa816f33ec673.png) . Cet anneau est principal et donc ses idéaux sont engendrés par un unique polynôme. De plus, si un polynôme P(X) peut se décomposer sous la forme P(X) = Q(X)(X − a), alors l'idéal (P) engendré par P est contenu dans l'idéal (X −a) engendré par X − a. Le théorème de d'Alembert-Gauss implique alors que les idéaux maximaux de
. Cet anneau est principal et donc ses idéaux sont engendrés par un unique polynôme. De plus, si un polynôme P(X) peut se décomposer sous la forme P(X) = Q(X)(X − a), alors l'idéal (P) engendré par P est contenu dans l'idéal (X −a) engendré par X − a. Le théorème de d'Alembert-Gauss implique alors que les idéaux maximaux de ![mathbb{C}[X]](http://upload.wikimedia.org/math/6/d/d/6ddcc166f3aa1cea808fa816f33ec673.png) sont les idéaux de la forme (X − a), pour a décrivant tout
sont les idéaux de la forme (X − a), pour a décrivant tout  . Le quotient
. Le quotient ![mathbb{C}[X]/(X-a)](http://upload.wikimedia.org/math/1/5/5/155462b2e946c4c988602a2a27055577.png) correspondant est alors isomorphe à
correspondant est alors isomorphe à  et l'action de
et l'action de ![mathbb{C}[X]](http://upload.wikimedia.org/math/6/d/d/6ddcc166f3aa1cea808fa816f33ec673.png) est donnée par
est donnée par  et
et 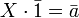 . Regardons à présent le quotient
. Regardons à présent le quotient ![mathbb{C}[X]/(P)](http://upload.wikimedia.org/math/7/6/1/761213716fa77688fbb80916637c12d6.png) où P(X) = (X − a)(X − b). Si
où P(X) = (X − a)(X − b). Si 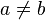 , le quotient est une représentation semi-simple, somme directe des deux représentations irréductibles
, le quotient est une représentation semi-simple, somme directe des deux représentations irréductibles ![mathbb{C}[X]/(X-a)](http://upload.wikimedia.org/math/1/5/5/155462b2e946c4c988602a2a27055577.png) et
et ![mathbb{C}[X]/(X-b)](http://upload.wikimedia.org/math/6/0/2/602a28d49033d8f2b7f339929ae9489a.png) . La situation est fondamentalement différente lorsque a = b. Dans ce cas, le quotient est un espace vectoriel de dimension 2 sur lequel l'opérateur donné par la multiplication par X − a est nilpotent d'indice 2. En termes de représentation de l'algèbre de Lie
. La situation est fondamentalement différente lorsque a = b. Dans ce cas, le quotient est un espace vectoriel de dimension 2 sur lequel l'opérateur donné par la multiplication par X − a est nilpotent d'indice 2. En termes de représentation de l'algèbre de Lie  , ce quotient correspond à la représentation donnée par la formule
, ce quotient correspond à la représentation donnée par la formule  , qui est indécomposable mais pas irréductible.
, qui est indécomposable mais pas irréductible.
Induction[modifier]
Soit  une algèbre de Lie. Soit
une algèbre de Lie. Soit  une sous-algèbre de Lie de
une sous-algèbre de Lie de  . Soit (π,V) une représentation de
. Soit (π,V) une représentation de  . Nous avons vu que nous pouvons obtenir une représentation de
. Nous avons vu que nous pouvons obtenir une représentation de  par restriction. La notion d'algèbre enveloppante va donner un moyen simple de considérer le problème réciproque. Soit donc (π',V') une représentation de
par restriction. La notion d'algèbre enveloppante va donner un moyen simple de considérer le problème réciproque. Soit donc (π',V') une représentation de  , que l'on voit comme une représentation de son algèbre enveloppante
, que l'on voit comme une représentation de son algèbre enveloppante 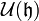 . Une conséquence du théorème de Poincaré-Birkhoff-Witt est que
. Une conséquence du théorème de Poincaré-Birkhoff-Witt est que 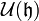 apparaît comme une sous-algèbre de
apparaît comme une sous-algèbre de  . D'autre part,
. D'autre part,  fournit une représentation de
fournit une représentation de  en faisant agir
en faisant agir  par multiplication à gauche sur les tenseurs. On construit alors la représentation
par multiplication à gauche sur les tenseurs. On construit alors la représentation  . On l'appelle la représentation induite de
. On l'appelle la représentation induite de  à
à  par (π',V').
par (π',V').
Lien avec les représentations des groupes de Lie[modifier]
Dans cette partie, le corps K est  (ou
(ou  ). Un groupe de Lie G est une variété différentielle réelle (ou complexe) munie de deux applications
). Un groupe de Lie G est une variété différentielle réelle (ou complexe) munie de deux applications  et
et  lisses (ou holomorphes) telles que
lisses (ou holomorphes) telles que 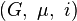 soit un groupe. Le corps K lui-même est un groupe de Lie commutatif. Le groupe GL(n,K) des matrices inversibles de taille n est un autre exemple de groupes de Lie. Un morphisme de groupes de Lie est un morphisme de groupes différentiable (ou holomorphe). Une représentation de dimension finie du groupe de LieG est un morphsime de G dans GL(n,K).
soit un groupe. Le corps K lui-même est un groupe de Lie commutatif. Le groupe GL(n,K) des matrices inversibles de taille n est un autre exemple de groupes de Lie. Un morphisme de groupes de Lie est un morphisme de groupes différentiable (ou holomorphe). Une représentation de dimension finie du groupe de LieG est un morphsime de G dans GL(n,K).
Les groupes de Lie sont reliés aux algèbres de Lie. En effet, l'espace tangent à un groupe de Lie G en l'identité est une algèbre de Lie de dimension finie, appelée algèbre de Lie du groupe G et notée  . Par exemple, l'algèbre de Lie de K est K lui-même ; l'algèbre de Lie de GL(n,K) est
. Par exemple, l'algèbre de Lie de K est K lui-même ; l'algèbre de Lie de GL(n,K) est 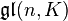 . Comme l'algèbre de Lie du groupe de Lie G est l'espace tangent en l'identité, elle ne dépend en fait que de la composante connexe de l'identité. Ainsi par exemple, le groupe
. Comme l'algèbre de Lie du groupe de Lie G est l'espace tangent en l'identité, elle ne dépend en fait que de la composante connexe de l'identité. Ainsi par exemple, le groupe  des matrices réelles de déterminant strictement positif a la même algèbre de Lie que
des matrices réelles de déterminant strictement positif a la même algèbre de Lie que  . Par contre, à isomorphisme près, il existe un unique groupe de Lie connexe et simplement connexe ayant une algèbre de Lie (de dimension finie) donnée.
. Par contre, à isomorphisme près, il existe un unique groupe de Lie connexe et simplement connexe ayant une algèbre de Lie (de dimension finie) donnée.
Comme tout morphisme 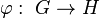 entre groupes de Lie est par hypothèse différentiable, il induit une application entre les algèbres de Lie sous-jacentes
entre groupes de Lie est par hypothèse différentiable, il induit une application entre les algèbres de Lie sous-jacentes 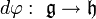 . Cette application
. Cette application  est en fait un morphisme d'algèbres de Lie. En particulier, pour H = GL(n,K), toute représentation d'un groupe de Lie G donne naissance à une représentation de dimension finie de son algèbre de Lie
est en fait un morphisme d'algèbres de Lie. En particulier, pour H = GL(n,K), toute représentation d'un groupe de Lie G donne naissance à une représentation de dimension finie de son algèbre de Lie  . Réciproquement, toute représentation de dimension finie d'une algèbre de Lie
. Réciproquement, toute représentation de dimension finie d'une algèbre de Lie  provient d'une représentation de l'unique groupe de Lie simplement connexe ayant pour algèbre de Lie
provient d'une représentation de l'unique groupe de Lie simplement connexe ayant pour algèbre de Lie  .
.
Remarque Il existe des notions plus fortes de représentations de groupes de Lie permettant d'étendre la théorie à la dimension infinie, tout en conservant un analogue de ce dernier résultat. Il s'agit par exemple de représentations admissibles et de la notion de  -modules.
-modules.
Catégorie de modules[modifier]
Soit  une algèbre de Lie. L'ensemble de tous les
une algèbre de Lie. L'ensemble de tous les  -modules (ou de manière équivalente de toutes les représentations de
-modules (ou de manière équivalente de toutes les représentations de  ) forme une catégorie, notée
) forme une catégorie, notée  . Cette catégorie estabélienne. En particulier, on peut considérer des suites exactes de modules. Une suite exacte dans
. Cette catégorie estabélienne. En particulier, on peut considérer des suites exactes de modules. Une suite exacte dans  est la donnée de trois modules M, N, P et de deux morphismes
est la donnée de trois modules M, N, P et de deux morphismes  injectif et
injectif et  surjectif. On note
surjectif. On note 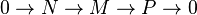 une telle suite. Un module P est projectif si toute suite exacte
une telle suite. Un module P est projectif si toute suite exacte 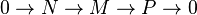 est scindée, c'est-à-dire s'il existe un morphisme
est scindée, c'est-à-dire s'il existe un morphisme  tel que
tel que  . Une définition équivalente est la suivante : le module P est projectif si pour tout morphisme surjectif
. Une définition équivalente est la suivante : le module P est projectif si pour tout morphisme surjectif  et tout morphisme
et tout morphisme  il existe un unique morphisme
il existe un unique morphisme  tel que
tel que  . De manière duale, un module I est injectif si toute suite exacte
. De manière duale, un module I est injectif si toute suite exacte  est scindée. Une définition équivalente est la suivante : le module I est injectif si pour tout morphisme injectif
est scindée. Une définition équivalente est la suivante : le module I est injectif si pour tout morphisme injectif  et tout morphisme
et tout morphisme  il existe un unique morphisme
il existe un unique morphisme  tel que
tel que  .
.
Comme tout module est aussi un module sur l'anneau  , on peut reprendre les notions générales de modules sur un anneau. Un module M est de longueur fini s'il existe une suite finie de sous-modules
, on peut reprendre les notions générales de modules sur un anneau. Un module M est de longueur fini s'il existe une suite finie de sous-modules  telle que les quotients successifs Mi + 1 / Mi soient des modules irréductibles. Une telle suite s'appelle unesuite de Jordan-Hölder de M. Pour un module de longueur finie, la classe d'isomorphismes des quotients ne dépend que du module M. En particulier, l'entier n ne dépend que du module M et est appelé la longueur du module M. Par exemple, tout module irréductible est de longueur 1, toute somme directe de deux modules irréductibles est de longueur 2.
telle que les quotients successifs Mi + 1 / Mi soient des modules irréductibles. Une telle suite s'appelle unesuite de Jordan-Hölder de M. Pour un module de longueur finie, la classe d'isomorphismes des quotients ne dépend que du module M. En particulier, l'entier n ne dépend que du module M et est appelé la longueur du module M. Par exemple, tout module irréductible est de longueur 1, toute somme directe de deux modules irréductibles est de longueur 2.
Un module M est artinien si toute suite décroissante de sous-modules  est stationnaire. Par exemple, tout module de dimension finie est artinien. Un module M est noethérien si toute suite croissante de sous-modules
est stationnaire. Par exemple, tout module de dimension finie est artinien. Un module M est noethérien si toute suite croissante de sous-modules  est stationnaire. Comme l'algèbre enveloppante
est stationnaire. Comme l'algèbre enveloppante  est un anneau noethérien, un module M est noethérien si et seulement s'il est de type fini. Un module est de longueur fini si et seulement s'il est noethérien et artinien.
est un anneau noethérien, un module M est noethérien si et seulement s'il est de type fini. Un module est de longueur fini si et seulement s'il est noethérien et artinien.
Exemple: Un module de dimension finie est toujours noethérien et artinien, et est donc toujours de longueur fini. Ceci n'est plus valable en dimension infinie, même pour une algèbre de Lie abélienne. Supposons par exemple que  . Considérons le module
. Considérons le module ![L=mathbb{C}[X]](http://upload.wikimedia.org/math/6/0/2/602bd4aa8a8bd385bddbcbb0c0ab6e71.png) où l'action de
où l'action de  est donnée par la multiplication par le scalaire z. L'action de
est donnée par la multiplication par le scalaire z. L'action de ![mathcal{U}(mathbb{C})=mathbb{C}[X]](http://upload.wikimedia.org/math/a/5/7/a57221d1077e5e9e886a8d7f281ef765.png) est donc donnée par la multiplication à gauche. Ainsi tout idéal à gauche est un sous-module de L. Notons (P) l'idéal engendré par le polynôme P. Soit
est donc donnée par la multiplication à gauche. Ainsi tout idéal à gauche est un sous-module de L. Notons (P) l'idéal engendré par le polynôme P. Soit  une suite infinie de nombre complexes. On a alors la suite décroissante suivante :
une suite infinie de nombre complexes. On a alors la suite décroissante suivante :  . C'est une suite non stationnaire de sous-modules, dont les quotients successifs sont des modules irréductibles (car de dimension 1). Ainsi L n'est pas artinien et n'est pas de longueur finie. Notons que L est noethérien car c'est un module de type fini (en fait cyclique, engendré par le polynôme constant 1).
. C'est une suite non stationnaire de sous-modules, dont les quotients successifs sont des modules irréductibles (car de dimension 1). Ainsi L n'est pas artinien et n'est pas de longueur finie. Notons que L est noethérien car c'est un module de type fini (en fait cyclique, engendré par le polynôme constant 1).
Une sous-catégorie pleine de  est artinienne (respectivement noethérienne) si tous ses objets sont des modules artiniens (respectivement noethériens). Dans une sous-catégorie pleine de
est artinienne (respectivement noethérienne) si tous ses objets sont des modules artiniens (respectivement noethériens). Dans une sous-catégorie pleine de  artinienne et noethérienne tout objet est de longueur finie. Une sous-catégorie pleine de
artinienne et noethérienne tout objet est de longueur finie. Une sous-catégorie pleine de  a assez de projectifs si pour tout objet M de la sous-catégorie il existe un module projectif P dans la sous-catégorie et un morphisme surjectif de P sur M. Elle a assez d'injectifs si pour tout objet M de la sous-catégorie il existe unmodule injectif I dans la sous-catégorie et un morphisme injectif de M dans I.
a assez de projectifs si pour tout objet M de la sous-catégorie il existe un module projectif P dans la sous-catégorie et un morphisme surjectif de P sur M. Elle a assez d'injectifs si pour tout objet M de la sous-catégorie il existe unmodule injectif I dans la sous-catégorie et un morphisme injectif de M dans I.
Références[modifier]
- N. Bourbaki, Éléments de mathématique, Groupes et algèbres de Lie, Chapitre 1, Springer, 2007 (ISBN 978-3-540-35335-5)
- Jacques Dixmier, Algèbres enveloppantes, Jacques Gabay, 1996 (ISBN 2-87647-014-4)
- Brian Hall, Lie Groups, Lie Algebras, and Representations, Springer, 2003 (ISBN 978-0-387-40122-5)
- James Humphreys, Introduction to Lie Algebras and Representation Theory, Second printing, revised. Graduate Texts in Mathematics, 9. Springer, 1978 (ISBN 0-387-90053-5)
- Nathan Jacobson, Lie algebras, Republication of the 1962 original, Dover, 1979 (ISBN 0-486-63832-4)
Voir aussi[modifier]
11:30 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Groupe de Lie
Groupe de Lie
|
|
Cet article ne cite pas suffisamment ses sources (septembre 2009).
Si vous connaissez le thème traité, merci d'indiquer les passages à sourcer avec {{Référence souhaitée}} ou, mieux, incluez les références utiles en les liant aux notes de bas de page. (Modifier l'article)
|
Source : http://fr.wikipedia.org/wiki/Groupe_de_Lie
En mathématiques, un groupe de Lie est un groupe qui est continu, c'est-à-dire que chaque élément du groupe peut être approché d'aussi près que l'on veut par une suite d'autres éléments du groupe. Un groupe de Lie est en fait un peu plus qu'un groupe continu : il est en plus lisse[pas clair], et on peut faire du calcul différentiel dessus. Ces groupes sont nommés ainsi en l'honneur du mathématicien norvégien Sophus Lie, qui les introduisit afin d'étudier certaines propriétés des équations différentielles.
Sommaire[masquer] |
Histoire[modifier]
Sophus Lie lui-même considérait que la théorie des groupes continus était née lors de l'hiver 1873-1874, mais le biographe Hawkins suggère que la théorie est née des recherches effectuées par Lie durant les quatre années précédentes (de 1869 à 1873).
Une partie des idées initiales de Lie furent développées en collaboration avec Felix Klein, qu'il rencontrait quotidiennement durant les jours d'octobre des années 1869 à 1872, à Berlin d'abord, puis Paris, Gőttingen et Erlangen.
Les résultats de Lie furent publiés dans des journaux norvégiens lors de la décennie 1870, et son œuvre gagna rapidement le reste de l'Europe. En 1884, un jeune mathématicien allemand, Friedrich Engel travailla avec Lie à la création d'un exposé systématique de la théorie des groupes continus, lequel fut publié en trois volumes sous le titre Theorie der Transformationsgruppen, en 1888, 1890 et 1893.
Un développement important de la théorie fut ensuite réalisé par Wilhelm Killing. La généralisation par Elie Cartan, mena à la classification des algèbres de Lie semi-simples et aux travaux d'Hermann Weyl sur les représentations des groupes de Lie compacts.
La théorie des groupes de Lie fut exposée méthodiquement dans le langage mathématique moderne par Claude Chevalley.
Définitions[modifier]
Une structure algébrique G est un groupe de Lie réel ou complexe lorsque :
- G est une variété différentiable réelle ou complexe ;
- G, munie de deux fonctions G×G
 G (multiplication) et G
G (multiplication) et G G (inversion), est un groupe (c'est-à-dire possède une loi associative — pas forcément commutative — avec un élément neutre, chaque élément ayant un symétrique) ;
G (inversion), est un groupe (c'est-à-dire possède une loi associative — pas forcément commutative — avec un élément neutre, chaque élément ayant un symétrique) ; - les applications de multiplication et d'inversion sont différentiables ou holomorphes.
Il est également possible de définir un groupe de Lie comme une variété différentielle munie d'opérations de groupe seulement continues. Cette définition est équivalente à la précédente et est une interprétation du 5e problème de Hilbert.
La dimension d'un groupe de Lie est définie comme sa dimension en tant que variété.
Il existe également une notion analogue de Groupe de Lie p-adique lorsque la variété différentielle sous-jacente est remplacée par un ensemble analytique p-adique. Ce sera le cas, par exemple, du groupe des points p-adiques d'un groupe algébrique.
Premiers exemples simples[modifier]
Un exemple simple est le groupe des matrices de rotation 2×2, noté SO(2, ) :
) : 
Il est paramétré par un seul angle λ : sa variété est donc unidimensionnelle (un cercle). C'est bien un groupe car l'inverse d'un élément de paramètre λ est donné par l'élément de paramètre −λ et le produit des éléments de paramètres λ et μ est donné par l'élément de paramètre λ+μ.
À l'inverse,  n'est pas un groupe continu, car il n'y a aucun élément entre 1 et 2.
n'est pas un groupe continu, car il n'y a aucun élément entre 1 et 2.
Propriétés[modifier]
Types de groupes de Lie[modifier]
Les groupes de Lie sont classables selon leur propriétés algébriques (abélien, simple, semisimple, résoluble, nilpotent), ou bien topologiques (connexe, simplement connexe, compact).
Ils sont également usuellement classés en quatre types, représentés dans le tableau d'exemples plus bas :
- Groupes de Lie réels, basés sur le groupe
 .
. - Groupes de Lie complexes, basés sur le groupe
 .
. - Groupes de Lie quaternioniques, basés sur le groupe des quaternions
 .
. - Groupes de Lie exceptionnels.
Homomorphismes et isomorphismes[modifier]
Si G et H sont deux groupes de Lie (tous deux réels ou complexes), alors un homomorphisme de groupes de Lie f : G H est un homomorphisme de groupe qui est également unefonction différentiable ou holomorphe (il suffit en fait que f soit continue).
H est un homomorphisme de groupe qui est également unefonction différentiable ou holomorphe (il suffit en fait que f soit continue).
La composition de deux homomorphismes de groupes de Lie est un homomorphisme de groupes de Lie et la classe de tous les groupes de Lie est une catégorie dont les flèches sont les homomorphismes de groupes de Lie. Deux groupes de Lie sont dits isomorphes s'il existe entre eux un homomorphisme bijectif dont la réciproque est également un homomorphisme.
La classe des groupes de Lie réels ou complexes de dimension n identifiés à isomorphisme près est un ensemble.
Algèbre de Lie associée à un groupe de Lie[modifier]
Il est possible d'associer naturellement à tout groupe de Lie G une algèbre de Lie. Il existe deux manières équivalentes d'introduire cette algèbre de Lie. L'une consiste à introduire un espace de champs de vecteurs sur G, la seconde consiste à munir l'espace tangent en l'élément neutre d'un crochet de Lie, dérivant de l'expression locale de la loi interne de G.
Comme algèbre de champs de vecteurs[modifier]
G désigne un groupe de Lie réel ou complexe de dimension n. Pour g un élément de G, l'application Lg : G G définie par Lg(f) = gf est un difféomorphisme de la variété réelle ou complexe sous-jacente à G. Un champ de vecteurs X sur G est dit invariant à gauche lorsque pour tout couple d'élément g et h de G, on a : dLg(Xh) = Xgh (où on note Xa la valeur du champ de vecteurs X au point a).
G définie par Lg(f) = gf est un difféomorphisme de la variété réelle ou complexe sous-jacente à G. Un champ de vecteurs X sur G est dit invariant à gauche lorsque pour tout couple d'élément g et h de G, on a : dLg(Xh) = Xgh (où on note Xa la valeur du champ de vecteurs X au point a).
Pour toute variété différentielle réelle ou complexe M, l'espace vectoriel réel ou complexe des champs de vecteurs sur M, noté I(M), est muni d'une structure naturelle d'algèbre de Lie réelle ou complexe, dont le crochet est le crochet de champs de vecteurs. La naturalité signifie exactement que tout morphisme f:M N entre variétés induit un morphisme d'algèbres de Lie f* : I(N)
N entre variétés induit un morphisme d'algèbres de Lie f* : I(N)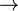 I(M). En particulier, pour M = N = G, on dispose d'automorphismes (Lg)* de l'algèbre de Lie I(G). L'ensemble des points fixes communs à tous ces automorphismes (Lg)* est une sous-algèbre de Lie de I(G), notée g. Ses éléments sont les champs de vecteurs invariants à gauche sur G.
I(M). En particulier, pour M = N = G, on dispose d'automorphismes (Lg)* de l'algèbre de Lie I(G). L'ensemble des points fixes communs à tous ces automorphismes (Lg)* est une sous-algèbre de Lie de I(G), notée g. Ses éléments sont les champs de vecteurs invariants à gauche sur G.
Comme espace tangent[modifier]
Soit TeG l'espace tangent en e à G, e désignant l'élément neutre de G. L'application  (où Xe est la valeur de X en l'élément neutre) est un isomorphisme linéaire. La structure d'algèbre de Lie de g se transporte donc, via cet isomorphisme, en une structure d'algèbre de Lie sur l'espace vectoriel TeG
(où Xe est la valeur de X en l'élément neutre) est un isomorphisme linéaire. La structure d'algèbre de Lie de g se transporte donc, via cet isomorphisme, en une structure d'algèbre de Lie sur l'espace vectoriel TeG
Cette structure peut se définir directement. Supposons donnée f une carte locale de G en l'élément neutre e avec f(e)=0, alors, l'application produit lue dans la carte locale f est au second ordre près :
f(f-1(a).f-1(b))=a+b+B(a,b)+...
où B est une forme bilinéaire antisymétrique. La structure d'algèbre de Lie sur TeG est donnée par :
- [X,Y] = B(X,Y).
Application exponentielle[modifier]
Dans la première présentation, tout vecteur X de g est par définition un champ de vecteurs invariant à gauche sur G. L'invariance à gauche implique que son flot est globalement défini. L'exponentielle de X est définie comme l'image au temps 1 de l'élément neutre e de G. Plus précisément, il existe une unique fonction  dont la dérivée est donnée par :
dont la dérivée est donnée par :
et telle que c(0) = e.
Elle possède la propriété remarquable suivante :
pour tous s et t.
Si l'on note, pour v = Xe, ev = c(1), une reparamétrisation incluant la variable t montre que :
![c(t) = e^{tv}qquad [eq.3]](http://upload.wikimedia.org/math/f/9/6/f960208fb71afe952ce33fea615c5a97.png) .
.
On peut alors vérifier :
 .
.
Cette fonction est également appelée fonction exponentielle et relie l'algèbre de Lie g au groupe de Lie G. Elle définit un difféomorphisme entre un voisinage de 0 dans g et un voisinage de e dans G. Toutefois, en général, l'application exponentielle n'est pas surjective, ni injective.
Un sous-groupe à un paramètre de G est une application différentiable c  G vérifiant l'identité eq.2 ci-dessus. À tout sous-groupe à un paramètre c est associé un unique élément Xde g vérifiant : c(t) = etv.
G vérifiant l'identité eq.2 ci-dessus. À tout sous-groupe à un paramètre c est associé un unique élément Xde g vérifiant : c(t) = etv.
Classification algébrique des groupes de Lie[modifier]
Plusieurs groupes de Lie peuvent partager la même algèbre de Lie associée. Cependant, à toute algèbre de Lie g correspond un groupe de Lie simplement connexe G, unique à isomorphisme près. De plus cet isomorphisme est uniquement déterminé par l'isomorphisme d'algèbre de Lie associé. Tout groupe de Lie connexe dont l'algèbre de Lie est isomorphe àg se réalise comme quotient de G par un sous-groupe normal discret.
Un groupe de Lie connexe est simple, semisimple, résoluble, nilpotent ou abélien si et seulement si son algèbre de Lie associée possède la propriété de même nom. En particulier, la classification des algèbres de Lie semi-simples donne une classification des groupes de Lie simplement connexes et semi-simples.
Exemples[modifier]
Groupes de Lie réels (groupes de Lie classiques)[modifier]
| Groupe de Lie | Description | Propriétés | Algèbre de Lie | Description | Dimension |
|---|---|---|---|---|---|
 |
Espace euclidien muni de l'addition | Abélien ; Simplement connexe, non compact |  |
Le crochet de Lie est nul | n |
 |
Nombres réels non nuls munis de la multiplication | Abélien ; Non connexe, non compact |  |
Le crochet de Lie est nul | 1 |
 |
Nombres réels strictement positifs munis de la multiplication | Abélien ; Simplement connexe, non compact |  |
Le crochet de Lie est nul | 1 |
 |
Nombres complexes de module 1 munis de la multiplication | Abélien ; Connexe, non simplement connexe, compact |  |
Le crochet de Lie est nul | 1 |
 |
Groupe général linéaire :matrices réelles n×ninversibles | Non connexe, non compact |  |
Matrices n×n, le crochet de Lie étant le commutateur | n² |
 |
matrices réelles n×n à déterminant positif | Simplement connexe, non compact |  |
Matrices n×n, le crochet de Lie étant le commutateur | n² |
 |
Groupe spécial linéaire : matrices réelles de déterminant 1 | Simplement connexe, non compact si n > 1 |  |
Matrices carrées de trace nulle, le crochet de Lie étant le commutateur | n²-1 |
 |
Groupe orthogonal : matrices orthogonales réelles | Non connexe, compact |  |
Matrices antisymétriques carrées réelles, le crochet de Lie étant le commutateur ;  est isomorphe à est isomorphe à  et et  muni du produit vectoriel muni du produit vectoriel |
n(n - 1)/2 |
 |
Groupe spécial orthogonal : matrices orthogonales réelles de déterminant 1 | Simple et semisimple pour n=3 et n≥5 ; Connexe, compact, non simplement connexe pour n≥2 | 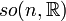 |
Matrices antisymétriques carrées réelles, le crochet de Lie étant le commutateur | n(n - 1)/2 |
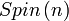 |
Groupe Spin | Simple et semisimple pour n=3 et n≥5 ; Simplement connexe, compact | 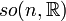 |
Matrices antisymétriques carrées réelles, le crochet de Lie étant le commutateur | n(n - 1)/2 |
 |
Groupe symplectique :matrices symplectiquesréelles | Simple, semisimple ; Non compact |  |
Matrices réelles satisfaisant JA + ATJ = 0 où J est la matrice antisymétrique standard | n(2n + 1) |
 |
Groupe unitaire : matrices unitaires n×n complexes | Non simplement connexe, compact ; Isomorphe à S1 pour n=1 |  |
Matrices carrées complexes A vérifiant A=-A*, le crochet de Lie étant le commutateur | n² |
 |
Groupe spécial unitaire : matrices unitaires complexesn×n de déterminant 1 | Simple et semisimple pour n≥2 ; Simplement connexe, compact |  |
Matrices carrées complexes de traces nulles A vérifiantA=-A*, le crochet de Lie étant le commutateur | n²-1 |
 |
Quaternions de module 1 munis de la multiplication, également noté  |
Simple, semisimple ; Simplement connexe, compact ; Topologiquement une sphère, isomorphe à  et et  |
 |
Quaternions de partie réelle nulle, le crochet de Lie étant leproduit vectoriel ; Isomorphe aux vecteurs réels de dimension 3, également isomorphe à  et et  |
3 |
 |
Groupe compact symplectique : matrices unitaires n×n quaternioniques | Simple, semisimple ; Compact, simplement connexe |  |
Matrices quaternioniques carrées A vérifiant A=-A*, le crochet de Lie étant le commutateur | n(2n + 1) |
Groupes de Lie complexes[modifier]
Les dimensions sont données sur  . (Tout groupe ou algèbre de Lie complexe peut être vu comme un groupe ou une algèbre de Lie réel de dimension double.)
. (Tout groupe ou algèbre de Lie complexe peut être vu comme un groupe ou une algèbre de Lie réel de dimension double.)
| Groupe de Lie | Description | Propriétés | Algèbre de Lie | Description | Dimension |
|---|---|---|---|---|---|
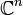 |
Espace euclidien muni de l'addition | Abélien ; Simplement connexe, non compact | 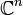 |
Le crochet de Lie est nul | n |
 |
Nombres complexes non nuls munis de la multiplication | Abélien ; Non simplement connexe, non compact |  |
Le crochet de Lie est nul | 1 |
 |
Groupe général linéaire : matricescomplexes n×n inversibles | Simplement connexe, non compact ; Isomorphe à pour n=1 pour n=1 |
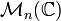 |
Matrices n×n, le crochet de Lie étant le commutateur | n² |
 |
Groupe spécial linéaire : matrices complexes de déterminant 1 | Simple, semisimple ; Simplement connexe, non compact pour n≥2 |  |
Matrices carrées de trace nulle, le crochet de Lie étant le commutateur | (n²-1) |
 |
Groupe orthogonal : Matrices orthogonalescomplexes | Non connexe, non compact pour n≥2 |  |
matrices antisymétriques carrées complexes, le crochet de Lie étant le commutateur | n(n-1) |
 |
Groupe spécial orthogonal : matrices orthogonales complexes de déterminant 1 | Simple et semisimple pour n=3 et n≥5 ; Non simplement connexe, non compact pour n≥2 |  |
Matrices antisymétriques carrées complexes, le crochet de Lie étant le commutateur | n(n-1) |
 |
Groupe symplectique : matrices symplectiques complexes | Simple et semisimple ; Non compact |  |
Matrices complexes satisfaisant JA+ATJ=0 où J est la matrice antisymétrique standard | 2n(2n+1) |
Groupes de Lie quaternioniens[modifier]
Les dimensions sont données sur  .
.
| Groupe de Lie | Description | Propriétés | Algèbre de Lie | Description | Dimension |
|---|---|---|---|---|---|
 |
Quaternions non nuls munis de la multiplication | Simplement connexe, non compact | 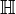 |
Quaternions, le crochet de Lie étant le commutateur | 1 |
Groupes de Lie exceptionnels[modifier]
On répertorie cinq groupes de Lie dits exceptionnels, notés respectivement E6, E7, E8, F4 et G2.
Voir aussi[modifier]
Articles connexes[modifier]
- Espace homogène
- Action de groupe de Lie
- Action hamiltonienne
- Représentation
- Représentation coadjointe
- Application moment
- E8 (mathématiques)
- Groupe algébrique (l'analogue algébrique des groupes de Lie, ce sont des variétés algébriques munies d'une structure de groupe).
- Groupe classique
Sites externes[modifier]
- Site du Projet Atlas de résolution des représentations des groupes de Lie (National Science Foundation, American Institute of Mathematics)
Bibliographie[modifier]
- Rached Mneimné et Frédéric Testard, Introduction à la théorie des groupes de Lie classiques [détail des éditions]
- Roger Godement, Introduction à la théorie des groupes de Lie, Springer, 2004 (ISBN 978-3-540-20034-5)
- (en) John M. Lee, Introduction to smooth manifolds, Springer, 2002
- (en) Ivan Kolář, Peter Michor (de) et Jan Slovák, Natural operations in differential geometry, Springer, 1993
- Bourbaki, Éléments de mathématique, Groupes et algèbres de Lie, Springer, 2006-2007
- (en) Sigurdur Helgason (de), Differential geometry, Lie groups and symmetric spaces, Academic Press, 1978
11:29 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Algèbre de Lie
Algèbre de Lie
Source : http://fr.wikipedia.org/wiki/Alg%C3%A8bre_de_Lie
En mathématiques, une algèbre de Lie, nommée en l'honneur du mathématicien Sophus Lie, est un espace vectoriel qui est muni d'un crochet de Lie, c'est-à-dire d'une loi de composition interne bilinéaire, antisymétrique et qui vérifie l'identité de Jacobi. Une algèbre de Lie est un cas particulier d'algèbre sur un corps.
Sommaire[masquer] |
Définitions, exemples et premières propriétés[modifier]
Définition[modifier]
Soit  un corps commutatif.
un corps commutatif.
Une algèbre de Lie sur  est un espace vectoriel
est un espace vectoriel  sur
sur  muni d'une application bilinéaire
muni d'une application bilinéaire ![(x,y) mapsto [x,y]](http://upload.wikimedia.org/math/7/5/e/75e87350f83275e11f126171780fd7ca.png) de
de 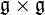 dans
dans  qui vérifie les propriétés suivantes:
qui vérifie les propriétés suivantes:
![forall x in mathfrak{g}, [x,x]=0](http://upload.wikimedia.org/math/f/3/2/f3223a3fe063412bb2f5033ba34850f5.png) ;
;![forall x,y,z in mathfrak{g}, [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0](http://upload.wikimedia.org/math/6/7/d/67d115952cf9c1c691b6053868febb0d.png)
Le produit [x,y] est appelé crochet de Lie (ou simplement crochet) de x et y. Puisque le crochet est une fonction bilinéaire alternée de x,y, on a aussi l'identité [x,y] = − [y,x] pour tousx,y dans  . L'identité (2) ci-dessus est appelée l'identité de Jacobi.
. L'identité (2) ci-dessus est appelée l'identité de Jacobi.
Une sous-algèbre de Lie de  est un sous-espace vectoriel de
est un sous-espace vectoriel de  stable pour le crochet de Lie. Toute sous-algèbre de Lie de
stable pour le crochet de Lie. Toute sous-algèbre de Lie de  est munie de manière évidente d'une structure d'algèbre de Lie sur
est munie de manière évidente d'une structure d'algèbre de Lie sur  .
.
Remarque : contrairement aux algèbres tensorielles (et aux algèbres de Clifford, dont les algèbres extérieures), les algèbres de Lie ne sont pas unitaires, ni associatives.
Quelques exemples classiques d'algèbres de Lie[modifier]
- Tout espace vectoriel E peut être muni d'une structure d'algèbre de Lie, en posant
![forall x,y in E, [x,y]=0](http://upload.wikimedia.org/math/4/7/b/47b2e0b6393e77c2e6376834f8c87276.png) . Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne.
. Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne. - On peut, à partir de (A, * ), une algèbre associative sur un corps, construire une algèbre de Lie, de la façon suivante : on pose
![forall x,y in A, [x,y]=x*y-y*x](http://upload.wikimedia.org/math/5/9/7/59711ef28af13f749a361b567295a858.png) (c'est lecommutateur des deux éléments x et y). Il est facile de vérifier que l'on définit ainsi sur A une structure d'algèbre de Lie.
(c'est lecommutateur des deux éléments x et y). Il est facile de vérifier que l'on définit ainsi sur A une structure d'algèbre de Lie.- Inversement, toute algèbre de Lie
 est contenue dans une algèbre associative, appelée algèbre enveloppante, dans laquelle le crochet de Lie coïncide avec le crochet défini ci-dessus. L'algèbre enveloppante est beaucoup plus grande que l'algèbre de départ.
est contenue dans une algèbre associative, appelée algèbre enveloppante, dans laquelle le crochet de Lie coïncide avec le crochet défini ci-dessus. L'algèbre enveloppante est beaucoup plus grande que l'algèbre de départ.
- Inversement, toute algèbre de Lie
- Comme exemple concret de la situation ci-dessus, considérons
 , l'espace des matrices
, l'espace des matrices 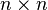 à coefficients dans
à coefficients dans  . C'est une algèbre associative pour le produit matriciel usuel. On peut donc également lui donner une structure d'algèbre de Lie, avec le crochet [A,B] = AB − BA. On note
. C'est une algèbre associative pour le produit matriciel usuel. On peut donc également lui donner une structure d'algèbre de Lie, avec le crochet [A,B] = AB − BA. On note  cette algèbre, lorsque l'on considère sa structure d'algèbre de Lie.
cette algèbre, lorsque l'on considère sa structure d'algèbre de Lie. - Bien évidemment, tout sous-espace vectoriel de
 stable par le crochet est une algèbre de Lie. Ainsi, on peut vérifier que l'ensemble des matrices de trace nulle est une algèbre de Lie, que l'on note
stable par le crochet est une algèbre de Lie. Ainsi, on peut vérifier que l'ensemble des matrices de trace nulle est une algèbre de Lie, que l'on note  .
.- En fait, le théorème d'Ado montre que toute algèbre de Lie de dimension finie peut être vue comme une sous-algèbre de
 .
.
- En fait, le théorème d'Ado montre que toute algèbre de Lie de dimension finie peut être vue comme une sous-algèbre de
- Un autre exemple fondamental, plus géométrique, est le suivant. Soit M une variété différentielle. Alors l'espace vectoriel formé par les champs de vecteurs sur M possède une structure naturelle d'algèbre de Lie, sans être une algèbre.
- En particulier, l'ensemble des vecteurs de Killing d'une variété forme une algèbre de Lie, qui correspond au groupe d'isométries de la variété considérée.
- L'espace euclidien tri-dimensionnel
 avec le produit vectoriel comme crochet de Lie est une algèbre de Lie.
avec le produit vectoriel comme crochet de Lie est une algèbre de Lie.
Morphismes et idéaux[modifier]
Un morphisme d'algèbre de Lie  est une application linéaire φ qui respecte le crochet de Lie, c'est-à-dire telle que
est une application linéaire φ qui respecte le crochet de Lie, c'est-à-dire telle que
![forall a,b in mathfrak{g}, phi([a,b])=[phi(a),phi(b)]](http://upload.wikimedia.org/math/7/9/f/79fe9d02198bb8da7ba2c3fe5df52add.png) .
.
Un idéal de  est un sous-espace vectoriel
est un sous-espace vectoriel  tel que
tel que ![forall ginmathfrak{g}, forall hin mathfrak{h}, [g,h]inmathfrak{h}](http://upload.wikimedia.org/math/9/f/e/9fe5cc6e32f7a61a988f42d549cb43b3.png) . C'est en particulier une sous-algèbre de Lie. Si une algèbre de Lie n'admet pas d'idéal non trivial, elle est dite simple.
. C'est en particulier une sous-algèbre de Lie. Si une algèbre de Lie n'admet pas d'idéal non trivial, elle est dite simple.
Si  est un idéal de
est un idéal de  , on peut former le quotient de
, on peut former le quotient de  par
par  : c'est l'espace vectoriel quotient
: c'est l'espace vectoriel quotient 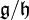 , muni du crochet défini par
, muni du crochet défini par ![[g+mathfrak{h},g'+mathfrak{h}] = [g,g']](http://upload.wikimedia.org/math/8/2/d/82d29f5c4eb7af6feb2661af74a7bd29.png) . La projection
. La projection 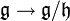 est alors un morphisme d'algèbres de Lie.
est alors un morphisme d'algèbres de Lie.
Une représentation d'une algèbre de Lie  est un morphisme
est un morphisme 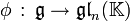 . Autrement dit, c'est une application linéaire telle que φ([g,h]) = φ(g)φ(h) − φ(h)φ(g).
. Autrement dit, c'est une application linéaire telle que φ([g,h]) = φ(g)φ(h) − φ(h)φ(g).
Le morphisme  défini par ad(g)(h) = [g,h] définit une représentation de
défini par ad(g)(h) = [g,h] définit une représentation de  , appelée représentation adjointe. L'identité de Jacobi exprime précisément le fait que ad respecte le crochet. Le noyau de cette représentation est le centre
, appelée représentation adjointe. L'identité de Jacobi exprime précisément le fait que ad respecte le crochet. Le noyau de cette représentation est le centre ![Z(mathfrak{g})={ginmathfrak{g}forall hinmathfrak{g} [g,h]=0}](http://upload.wikimedia.org/math/a/f/e/afe7160b530a847134d5f4291027ee9c.png) de l'algèbre de Lie
de l'algèbre de Lie  .
.
Relation avec les groupes de Lie et les groupes algébriques[modifier]
Les algèbres de Lie sont naturellement associées aux groupes de Lie. Si G est un groupe de Lie et 1 son élément neutre, alors l'espace tangent en 1 à G est une algèbre de Lie ; la construction exacte de cette algèbre est détaillée dans la section correspondante de l'article Groupe de Lie. La même construction est valable pour les groupes algébriques. On note en général en petites lettres gothiques l'algèbre de Lie associée à un groupe de Lie, ou à un groupe algébrique. Ainsi, comme on l'a déjà vu,  désigne l'ensemble des matrices carrées de taille n et
désigne l'ensemble des matrices carrées de taille n et 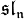 désigne l'ensemble des matrices carrées de taille n de trace nulle. De la même façon,
désigne l'ensemble des matrices carrées de taille n de trace nulle. De la même façon,  désigne l'ensemble des matrices carrées A de taille n antisymétriques, etc. Dans tous ces exemples, le crochet de Lie n'est rien d'autre que le commutateur : [A,B]=AB-BA.
désigne l'ensemble des matrices carrées A de taille n antisymétriques, etc. Dans tous ces exemples, le crochet de Lie n'est rien d'autre que le commutateur : [A,B]=AB-BA.
Si φ est un morphisme de groupes entre deux groupes de Lie G et H, et si l'on suppose φ différentiable, alors sa différentielle en l'identité sera un morphisme entre les algèbres de Lie  et
et  de G et H. En particulier, à une représentation de G différentiable, on associe une représentation de
de G et H. En particulier, à une représentation de G différentiable, on associe une représentation de  .
.
La classification des algèbres de Lie est utilisée de façon cruciale pour l'étude des groupes de Lie, des groupes algébriques et de leurs représentations.
Classification[modifier]
Si 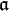 et
et 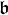 sont deux sous-algèbres de Lie d'une algèbre de Lie
sont deux sous-algèbres de Lie d'une algèbre de Lie  , notons
, notons ![[mathfrak{a},mathfrak{b}]](http://upload.wikimedia.org/math/c/5/2/c528d5c197e3f72db0a9bbc760333ee4.png) le sous-espace vectoriel engendré par les éléments de la forme [a,b] pour
le sous-espace vectoriel engendré par les éléments de la forme [a,b] pour  et
et 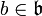 .
.
Algèbres de Lie nilpotentes[modifier]
Une algèbre de Lie est dite nilpotente lorsque toute suite de commutateurs ![[[[g_1,g_2],g_3],dots,g_n]](http://upload.wikimedia.org/math/4/8/a/48ab7757f1f2f8ed370a0f9d8acecd13.png) finit par être nulle, lorsque n devient suffisamment grand.
finit par être nulle, lorsque n devient suffisamment grand.
Plus précisément, définissons Ci par  et
et ![C_{i+1}=[C_i,mathfrak{g}]](http://upload.wikimedia.org/math/3/b/2/3b21f80fad4a73cdcc2c55569abfd0d0.png) .
.
S'il existe un i tel que Ci=0, on dit que  est nilpotente. Cette notion est à mettre en parallèle avec celle de groupe nilpotent. Il est facile de voir que toute algèbre de Lie abélienne est nilpotente.
est nilpotente. Cette notion est à mettre en parallèle avec celle de groupe nilpotent. Il est facile de voir que toute algèbre de Lie abélienne est nilpotente.
L'algèbre  des matrices triangulaires strictes, c'est-à-dire de la forme
des matrices triangulaires strictes, c'est-à-dire de la forme  fournit un exemple d'algèbre de Lie nilpotente.
fournit un exemple d'algèbre de Lie nilpotente.
Le théorème d'Engel affirme que toute sous-algèbre nilpotente de  est en fait simultanément trigonalisable et donc conjuguée à une sous-algèbre de
est en fait simultanément trigonalisable et donc conjuguée à une sous-algèbre de  .
.
Algèbres de Lie résolubles[modifier]
Définissons par récurrence Di par 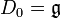 et Di + 1 = [Di,Di]
et Di + 1 = [Di,Di]
S'il existe un i tel que Di=0, on dit que  est résoluble. Comme dans le cas des algèbres nilpotentes, cette notion correspond à celle de groupe résoluble. Il est facile de voir que toute algèbre de Lie nilpotente est résoluble.
est résoluble. Comme dans le cas des algèbres nilpotentes, cette notion correspond à celle de groupe résoluble. Il est facile de voir que toute algèbre de Lie nilpotente est résoluble.
Un exemple d'algèbre de Lie résoluble est donné par l'algèbre 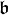 des matrices triangulaires supérieures dans
des matrices triangulaires supérieures dans  .
.
Le théorème de Lie montre que, si  est algébriquement clos et de caractéristique nulle, alors toute sous-algèbre de Lie résoluble de
est algébriquement clos et de caractéristique nulle, alors toute sous-algèbre de Lie résoluble de  est conjuguée à une sous-algèbre de
est conjuguée à une sous-algèbre de 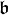
Algèbres de Lie semi-simples et réductives[modifier]
On dit qu'une algèbre de Lie  est semi-simple lorsqu'elle ne contient pas d'idéal résoluble non trivial.
est semi-simple lorsqu'elle ne contient pas d'idéal résoluble non trivial.  est dite réductive lorsque sa représentation adjointe est semi-simple.
est dite réductive lorsque sa représentation adjointe est semi-simple.
Lorsque 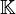 est de caractéristique nulle, et que
est de caractéristique nulle, et que  est de dimension finie, la semi-simplicité de
est de dimension finie, la semi-simplicité de  est équivalente à la non-dégénerescence de la forme de Killing K(x,y) définie par K(x,y) = tr(ad(x)ad(y)), où tr désigne la trace. Par ailleurs,
est équivalente à la non-dégénerescence de la forme de Killing K(x,y) définie par K(x,y) = tr(ad(x)ad(y)), où tr désigne la trace. Par ailleurs,  est réductive si et seulement si
est réductive si et seulement si ![[mathfrak{g},mathfrak{g}]](http://upload.wikimedia.org/math/3/f/1/3f1683bcf0fa96e29329efca70a1d284.png) est semi-simple.
est semi-simple.
On peut montrer que, sous les mêmes hypothèses, toute algèbre de Lie semi-simple est en fait une somme directe d'algèbres de Lie simples.
Les algèbres de Lie simples de dimension finie sur le corps  des nombres complexes sont classifiées par les diagrammes de Dynkin. Il y a donc 4 familles d'algèbres de Lie simples (ou 3 si on considère Bn et Dn comme une même famille) et 5 algèbres de Lie exceptionnelles, correspondant chacune à un diagramme de Dynkin différent.
des nombres complexes sont classifiées par les diagrammes de Dynkin. Il y a donc 4 familles d'algèbres de Lie simples (ou 3 si on considère Bn et Dn comme une même famille) et 5 algèbres de Lie exceptionnelles, correspondant chacune à un diagramme de Dynkin différent.
- À un diagramme de Dynkin de type
 correspond l'algèbre de Lie
correspond l'algèbre de Lie 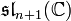 .
.
- À un diagramme de Dynkin de type
 correspond l'algèbre de Lie
correspond l'algèbre de Lie 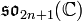 .
.
- À un diagramme de Dynkin de type
 correspond l'algèbre de Lie
correspond l'algèbre de Lie  .
.
- À un diagramme de Dynkin de type
 correspond l'algèbre de Lie
correspond l'algèbre de Lie  .
.
- Les algèbres de Lie exceptionnelles, correspondant aux diagrammes de Dynkin restants (de type E6, E7, E8, F4 et G2) n'ont pas d'interprétation aussi simple.
L'algèbre de Lie  est, elle, réductive et son algèbre de Lie dérivée est
est, elle, réductive et son algèbre de Lie dérivée est 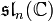 .
.
Les algèbres de Lie semi-simples de dimension finie sur le corps  des nombres réels sont classifiées par les involutions d'algèbres de Lie complexe ou, de façon équivalente, par lesinvolutions de systèmes de racines. Ceci correspond à la notion d'algèbre de Lie symétrique. Comme classe d'algèbre de Lie simple réelle, on peut citer:
des nombres réels sont classifiées par les involutions d'algèbres de Lie complexe ou, de façon équivalente, par lesinvolutions de systèmes de racines. Ceci correspond à la notion d'algèbre de Lie symétrique. Comme classe d'algèbre de Lie simple réelle, on peut citer:
- Les algèbres de Lie compactes. Ce sont les algèbres de Lie de groupes compacts. Il y en a exactement une qui correspond à chaque algèbre de Lie complexe.
- Les algèbres de Lie complexes vues comme algèbres de Lie réelles.
- Les autres peuvent être classées en familles AI, AII, AIII, BI, CI, CII, DI, DIII et en algèbres exeptionelles
EI, EII, EIII, EIV (de type E6) EV, EVI, EVII (de type E7) EVIII, EIX (de type E8) FI, FII (de type F4) et GI (de type G2) suivant la notation d'Helgason1)
Dimension infinie[modifier]
Il n'y a pas de classification générale des algèbres de Lie de dimension infinie mais plusieurs classes de telles algèbres ont été étudiées.
- Une algèbre de Kac-Moody est une algèbre de Lie définie abstraitement en termes de générateurs et relations codés par une matrice de Cartan généralisée non nécessairement définie positive. Elles peuvent donc être de dimension infinie. Leur classification générale est encore hors de portée mais plusieurs sous-types sont connus
- Une algèbre de Kac-Moody affine possède la propriété que tous les sous-diagrammes de Dynkin de son diagramme de Dynkin correspondent à des sous-algèbres de Lie de dimension finie. Sa matrice de Cartan généralisée est alors de corang 1. Les algèbres de Kac-Moody affines ont été classifiées par Victor G. Kac. Elles sont très utilisées enphysique théorique dans l'étude des théories conformes des champs et en particulier dans l'étude des modèles WZW.
- Une algèbre de Kac-Moody hyperbolique possède un diagramme de Dynkin connexe avec la propriété que si on lui retire une racine, on obtient une algèbre de Lie semi-simple de dimension finie ou bien une algèbre de Kac-Moody affine. Elles ont été également classifiées et sont de rang 10 au maximum. Leur matrice de Cartan généralisée est non dégénérée et de signature Lorentzienne (c’est-à-dire avec exactement une direction négative).
- algèbre de Kac-Moody généralisée ou algèbre de Borcherds: c'est un type d'algèbre de Lie généralisant le concept d'algèbre de Kac-Moody dont la matrice de Cartan généralisée peut posséder des racines simples nommées imaginaires pour lesquelles l'élément diagonal de la matrice de Cartan généralisée est négatif. Elles ont été introduite par Richard Ewen Borcherds dans le cadre de l'étude de la conjecture monstrous moonshine.
Généralisation[modifier]
Il existe différentes sortes de généralisations des algèbres de Lie, on citera les superalgèbres de Lie, les groupes quantiques, les algèbres de Leibniz, les algèbres pré-Lie.
Références[modifier]
- Bourbaki, Groupes et algèbres de Lie
- Dixmier, Jacques Algèbres enveloppantes Éditions Jacques Gabay, Paris, 1996. ISBN 2-87647-014-4
- Humphreys, James E. Introduction to Lie Algebras and Representation Theory, Second printing, revised. Graduate Texts in Mathematics, 9. Springer-Verlag, New York, 1978. ISBN 0-387-90053-5
- Jacobson, Nathan, Lie algebras, Republication of the 1962 original. Dover Publications, Inc., New York, 1979. ISBN 0-486-63832-4
- S. Helgason, Differential Geometry and Symmetric Spaces [archive]
Voir aussi[modifier]
11:28 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
10/03/2011
La figure et le monde, archéologie de la géométrie, Peuples paysans sans écriture et premières civilisations Olivier Keller Etude (broché). Paru en 08/2006
20:08 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Le dossier Pythagore , Du chamanisme à la mécanique quantique Pierre Brémaud Essai (broché). Paru en 09/2010
20:07 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Byrne , Six books of Euclid Werner Oechslin Guide en anglais (broché). Paru en 05/2010
20:06 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook








































![d_{1} = frac{1}{sigma sqrt{T}} left[ ln left( frac{S}{K} right) + left( r + frac{1}{2}sigma^2 right)T right]](http://upload.wikimedia.org/math/a/2/1/a212752c107bcd1d6d2d0c5a0d0056ee.png)











![left[J_{ij}, J_{kell}right] = delta_{jk}J_{iell} - delta_{jell}J_{ik} - delta_{ik}J_{jell} + delta_{iell}J_{jk},](http://upload.wikimedia.org/math/f/8/d/f8ddba45c26b81da3205c690d5648aeb.png)




![c'(t) = X[c(t)]qquad [eq.1]](http://upload.wikimedia.org/math/2/2/1/221d26faae62a0bbd5bd41a335944438.png)
![c(s + t) = c(s).c(t)qquad [eq.2]](http://upload.wikimedia.org/math/b/c/e/bce93f16e470559e54834d2b3f18bf49.png)



