13/02/2011
Apprendre la mathématique Jeu éducatif
09:05 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Mathématique pour économistes et gestionnaires Louis Esch Etude (broché). Paru en 04/2010 Livre
09:03 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Analyse mathématique et océanographie Roger Lewandowski (donnée non spécifiée). Paru en 10/1997 Livre
09:02 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Statistique mathématique
Source : http://fr.wikipedia.org/wiki/Statistique_math%C3%A9matiqueStatistique mathématique
![]() Pour les articles homonymes, voir Statistique.
Pour les articles homonymes, voir Statistique.
|
|
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
Les statistiques, dans le sens populaire du terme, traitent des populations. En statistique descriptive, on se contente de décrire un échantillon à partir de grandeurs comme la moyenne, la médiane, l'écart type, la proportion, la corrélation, etc. C'est souvent la technique qui est utilisée dans les recensements. Dans un sens plus large, la théorie statistique est utilisée en recherche dans un but inférentiel. Le but de l'inférence statistique est de dégager le portrait d'une population donnée, à partir de l'image plus ou moins floue constituée à l'aide d'un échantillon issu de cette population. Dans un autre ordre d'idées, il existe aussi la statistique « mathématique » où le défi est de trouver des estimateurs judicieux (non biaisées et efficients). L'analyse des propriétés mathématiques de ces estimateurs sont au cœur du travail du mathématicien spécialiste de la statistique. La statistique mathématique repose sur la théorie des probabilités. Des notions comme la mesurabilité ou la convergence en loi y sont souvent utilisées. Mais il faut distinguer la statistique en tant que discipline et la statistique en tant que fonction des données. Une fois les bases de la théorie des probabilités acquises, il est possible de définir une statistique à partir d'une fonction S mesurable à n arguments. Lorsque les valeurs La loi de S(X) dépend uniquement de la loi de X et de la forme de S. La fonction de répartition d'une variable aléatoire réelle X (cette définition s'étend naturellement aux variables aléatoires à valeurs dans des espaces de dimension quelconque) associe à une valeur x la probabilité qu'une réalisation de X soit plus petite de x : F(x) = Prob(X < x) Lorsqu'on dispose de n réalisations de X, on peut construire la fonction de répartition empirique de X ainsi (on note x(k) la kème valeur ordonnées des de même, la distribution empirique peut se définir (pour tout borélien B) comme : Le Théorème de Glivenko-Cantelli assure la convergence de la fonction de distribution empirique vers la fonction de distribution original lorsque la taille n de l'échantillon augmente vers l'infini. Ces deux fonctions empirique n'étant pas continues, on leur préfère souvent des estimateurs par noyau, qui ont les mêmes propriétés de convergence. On définit usuellement plusieurs types de statistiques suivant la forme de S : L'intérêt de cette différenciation est que chaque catégorie de statistique va avoir des caractéristiques propres. Les estimateurs par noyau, et les moments empiriques d'une loi sont les M-statistiques. Le moment empirique d'ordre k d'une loi calculé à partir d'un échantillon Il s'agit d'un estimateur de E(Xk). Le moment centré d'ordre k est E((X − E(X))k). La variance est le moment centré d'ordre 2. Considérons une population d'où l'on extrait un échantillon d'effectif n de façon purement aléatoire dont les éléments sont xi. Dans ce cas, la statistique descriptive qui estime la moyenne de la population est la moyenne empirique La statistique qui estime la dispersion autour de la moyenne est la variance empirique La loi de probabilité associée à cette population possède une moyenne μ et une variance σ2 qui sont estimés par m et s2. Le problème est que, si on avait choisi un autre échantillon, on aurait trouvé des valeurs différentes pour ces estimations. Ceci conduit à considérer les éléments, la moyenne empirique et la variance empirique comme des variables aléatoires. Ces variables suivent une loi de probabilité donnée. Une fois qu'on connait ces lois de probabilité, il est possible de construire les tests statistiques voulus pour étudier les paramètres d'intérêt ( μ et σ2 pour cet exemple). Sous la condition d'indépendance entre les observations, on peut calculer la moyenne (ou espérance) et la variance de la moyenne empirique. On obtient : Ces résultats s’interprètent directement en termes d’estimation. Le problème d’estimation est relié aux intervalles de confiance. L’idée est de fournir une estimation d’un paramètre accompagnée d’une idée de sa précision liée aux fluctuations échantillonnales. Voici un exemple bien spécifique d’intervalle de confiance pour la moyenne. Pour décrire le principe, considérons un exemple assez artificiel qui présente l’avantage de la simplicité : l’estimation de la moyenne (m) d’une population supposée normale dont nous connaîtrions l’écart-type (σ). D’après le paragraphe précédent, la moyenne empirique suit également une loi normale dont l’écart-type est divisé par le facteur Puisque les tables de probabilités de la loi normale sont connues, nous pouvons déterminer qu’un intervalle centré autour de la moyenne empirique aura x % de chance de contenir la vraie moyenne. En pratique, x est souvent fixé à 95. Lorsqu’on fixe x (à 95 par exemple), on détermine la longueur de l’intervalle de confiance simplement par connaissance de la loi normale. Voici l’intervalle de confiance à 95 % pour ce cas très précis. voir aussi loi de Student. Une hypothèse statistique concerne les paramètres issue d'une ou plusieurs populations. On ne peut pas la vérifier mais seulement la rejeter lorsque les observations paraissent en contradiction avec elle. Nous concluerons que la valeur observée (à partir de l'échantillon) est très peu probable dans le cadre de l'hypothèse (qui concerne la population). La première étape consiste à édicter l'hypothèse nulle. Souvent cette hypothèse sera ce qu'on croit faux. Exemple d'hypothèses nulles : Les deux moyennes issues de deux populations sont égales La corrélation entre deux variables est nulle Il n'y a pas de lien entre l'âge et l'acuité visuelle etc. L'hypothèse nulle concerne les paramètres (valeurs vraies) de la population. Pour chaque test statistique, il y a une mesure ou statistique précise (selon le paramètre qui nous intéresse) qui suit une loi de probabilité connue. Cette statistique peut être vue comme une mesure entre ce qu'on observe dans l'échantillon et ce qu'on postule dans la population (hypothèse nulle). Plus cette mesure sera grande, plus sa probabilité d'occurrence sera petite. Si cette probabilité d'occurrence est trop petite, on aura tendance à rejeter l'hypothèse nulle et donc conclure que l'hypothèse nulle est fausse. Se dit des tests qui présupposent que les variables à étudier suivent une certaine distribution décrite par des paramètres. De nombreux tests paramétriques concernent des variables qui suivent la loi normale. Les tests t pour échantillons indépendants ou appariés, les ANOVA, la régression multiple, etc. Voici l'exemple d'un test qui utilise la loi du χ². Cependant, une multitude de tests utilisent cette loi de probabilité: (Mc Nemar, tests d'adéquation de modèles,tests d'adéquation à une distribution etc...) Exemple : On se demande si un échantillon extrait d'une population correspond raisonnablement à une loi de probabilité hypothétique. L'échantillon d'effectif n est divisé en k classes d'effectifs ni comme pour la construction d'un histogramme, avec une différence : il est possible d'utiliser des classes de largeur variable, c'est même recommandé pour éviter qu'elles soient trop petites. Avec cette précaution, le théorème de la limite centrale dans sa version multidimensionnelle indique que le vecteur des effectifs (n1,...,nk) se comporte approximativement comme un vecteur gaussien. La loi de probabilité étant donnée d'autre part, elle permet d'assigner à chaque classe une probabilité pi. Dans ces conditions l'expression qui représente d'une certaine manière la distance entre les données empiriques et la loi de probabilité supposée, suit une loi de probabilité de χ2 à k − 1 degrés de liberté. Les tables de χ2 permettent de déterminer s'il y a lieu de rejeter l'hypothèse en prenant le risque, fixé à l'avance, de se tromper. Si on considère le cas d'une loi de probabilité dont les paramètres (en général moyenne et écart-type) sont inconnus, la minimisation du χ2 par rapport à ces paramètres fournit une estimation de ceux-ci. Statistique[modifier]
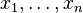 sont des réalisations d'une même variable aléatoire X, on note :
sont des réalisations d'une même variable aléatoire X, on note :
Fonctions de répartition[modifier]
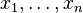 et on pose arbitrairement
et on pose arbitrairement  et
et  ) :
) :![F^*_n(x) = {kover n},, forall xin ]x_{(k)},x_{(k+1)}]](http://upload.wikimedia.org/math/b/e/8/be897bb86ca1ce37f497a43c6ecdc5da.png)
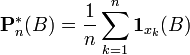
Types de statistiques[modifier]
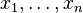 est :
est :
Exemple de statistiques : Moyenne et variance[modifier]


![E[m] = mu qquad qquad V[m] = sigma^2 / n](http://upload.wikimedia.org/math/0/6/a/06aab144fa9f73e5b3112353aec8d972.png)
L'écart-type de la moyenne empirique vaut σ / √n. Si n devient grand, le théorème de la limite centrale enseigne que la moyenne empirique suit une loi normale caractérisée par la moyenne μ et cet écart-type. Ce résultat reste valable quelle que soit la taille de l'échantillon lorsque la loi de probabilité assignée à la population est normale. Dans ce dernier cas, particulièrement important en pratique, on montre également que (n-1) s2 / σ2 suit une loi de χ2 à n-1 degrés de liberté.Estimation[modifier]
 .
.![[m - {{1.96 sigma}over sqrt n} ; m + {{1.96 sigma}over sqrt n}]](http://upload.wikimedia.org/math/7/e/5/7e5cfae70b4f1ddbbd8036eb1907b0e6.png)
Tests d'hypothèses[modifier]
Notion générale de test d'hypothèse statistique[modifier]
Test paramétrique[modifier]
Test du χ²[modifier]

Références[modifier]
Voir aussi[modifier]
Sommaire[masquer] |
09:01 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Morphologie mathématique
Source : http://fr.wikipedia.org/wiki/Morphologie_math%C3%A9matiqueMorphologie mathématique
|
|
Cet article est une ébauche concernant les mathématiques.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
La morphologie mathématique est une branche des mathématiques présentant des liens forts avec l'algèbre, la théorie des treillis, latopologie et les probabilités. Le développement de la morphologie mathématique a été inspiré par des problèmes de traitement d'images, domaine qui constitue son principal champ d'application. Elle fournit en particulier des outils de filtrage, segmentation, quantification et modélisation d'images. Une des idées de base de la morphologie mathématique est d'étudier ou de traiter un ensemble à l'aide d'un autre ensemble, appelé élément structurant, qui sert de sonde. A chaque position de l'élément structurant, on regarde s'il touche ou s'il est inclus dans l'ensemble initial. En fonction de la réponse, on construit un ensemble de sortie. On obtient ainsi des opérateurs de base qui sont relativement intuitifs. Des propriétés que l'on retrouve souvent dans les opérateurs morphologiques sont : Ceci implique en particulier une perte d'information ; bien utilisés, ces opérateurs permettent d'éliminer des structures ne respectant pas certains critères, comme par exemple de largeur ou de volume. La morphologie mathématique s'intéresse aussi aux ensembles et aux fonctions aléatoires. Le principal domaine d'application de la morphologie mathématique est le traitement d'images. Elle fournit, en particulier, des outils de filtrage, de segmentation et de quantification. Depuis son apparition, en 1964, elle connaît un succès grandissant et désormais contribue à garnir la boite à outils de tout traiteur d'images. La morphologie mathématique a été inventée en 1964 par Georges Matheron et Jean Serra dans les laboratoires de Mines ParisTech. Son développement a toujours été fortement motivé par des applications industrielles. Dans un premier temps, il s'est agi de répondre à des problèmes dans le domaine de l'exploitation minière, mais très vite ses champs d'applications se sont diversifiés : biologie, imagerie médicale, sciences des matériaux, vision industrielle, multimédia, télédétection et géophysique constituent quelques exemples de domaines dans lesquels la morphologie mathématique a apporté une contribution importante. La morphologie mathématique reste un domaine actif de recherche. En témoignent les nombreuses publications scientifiques sur le sujet, ainsi que les symposiums internationaux sur la morphologie mathématique qui ont lieu tous les deux ou trois ans. Quelques exemples de thèmes de recherche actuels: La morphologie mathématique peut être développée dans le cadre abstrait de la théorie des treillis. Cependant, une présentation plus pratique, visant un utilisateur potentiel d'outils de traitement d'images, plutôt qu'un mathématicien, est ici adoptée. Plaçons nous dans L'élément structurant joue en quelque sorte le rôle de modèle local, ou de sonde. Il est promené partout sur l'image à traiter, et à chaque position on étudie sa relation avec l'image binaire, considérée comme un ensemble. Ces relations peuvent être du type « est inclus dans l'ensemble », ou « touche l'ensemble », par exemple. Les éléments structurants les plus classiquement utilisés sont la croix, constituée de l'origine et des quatre points les plus proches, et le carré, constitué de l'origine et des huit points les plus proches. Ces deux éléments structurants correspondent respectivement à deux définitions possibles du voisinage ou de la connexité de l'image. On introduit aussi le symétrique d'un ensemble, noté Si B est symétrique, on a Soit X un sous-ensemble de E. La dilatation morphologique avec l'élément structurant B est définie comme la somme de Minkowski: 1 Une autre formulation plus intuitive est : La dilatation morphologique n'est, en général, pas inversible. L'opération qui en quelque sorte tente de produire l'inverse de la dilatation est l'érosion morphologique: La dilatation et l'érosion sont les opérateurs de base de la morphologie mathématique. Pratiquement tous les autres peuvent être définis à l'aide de ceux-ci, en utilisant des compositions de fonctions et des opérations ensemblistes. On peut aussi prendre deux éléments structurants A et B pour définir des transformations. Si on demande en chaque point x à A d'être à l'extérieur de l'ensemble et à B à l'intérieur on obtient la transformation en tout ou rien (hit or miss transform en anglais) : où Ac désigne le complémentaire de l'ensemble A. Cette transformation permet de détecter certaines configurations précises de pixels. En ajoutant le résultat de la transformation à l'ensemble initial on obtient un épaississement: en enlevant le résultat de l'ensemble initial on obtient un amincissement: En prenant des suites d'amincissements, on peut réduire progressivement l'ensemble initial (comme si on l'épluchait). De cette façon on peut calculer différents types de squelettes, dont des squelettes homotopiques. La composition d'une dilatation morphologique avec l'érosion par le même élément structurant ne produit pas, en général, l'identité, mais deux autres opérateurs morphologiques, l'ouverture morphologique: et la fermeture morphologique: L'ouverture peut être caractérisée géométriquement: elle donne l'union de tous les Bx inclus dans X. Ainsi, la forme de l'élément structurant permet de choisir les structures qui peuvent le contenir. La fermeture est le dual de l'ouverture: la fermeture du complémentaire d'un ensemble est égale au complémentaire de l'ouverture de cet ensemble. La fermeture et l'ouverture sont des opérations croissantes et idempotentes, deux propriétés qui définissent les filtres morphologiques. La fermeture est extensive ( Une image à niveaux de gris peut être modélisée comme une fonction de L'ouverture et la fermeture de fonctions s'obtiennent comme dans le cas ensembliste : L'ouverture et la fermeture morphologiques constituent déjà des outils intéressants de filtrage d'images. Cependant, ils peuvent modifier le contour des objets, propriété qui peut être malvenue. Les opérateurs par reconstruction et plus généralement les nivellements, introduits plus loin, permettent de pallier cet inconvénient. Epaississements et amincissements ne sont pas, en général, des opérateurs croissants. Par conséquent, leur application aux fonctions (en pratique, aux images à niveaux de gris) n'est pas triviale. Plusieurs extensions ont été proposées dans la littérature. La détection de contours représente une tâche importante en traitement d'images. La morphologie mathématique propose des outils non-linéaires de détection de contours, comme le gradient et le laplacien morphologiques. Le gradient morphologique, aussi appelé gradient de Beucher du nom de son inventeur, est défini par: Il correspond, en quelque sorte, à la version morphologique du module du gradient euclidien. Le laplacien morphologique est construit de façon analogue: où I correspond à l'opérateur identité. Segmenter une image à niveaux de gris consiste à produire une partition du support de l'image, de façon à ce que les régions de la partition correspondent avec les objets présents dans l'image. Les filtres morphologiques constituent une aide précieuse dans un processus de segmentation. En particulier, les nivellements permettent de filtrer les images tout en préservant les contours importants, ce qui simplifie l'opération de segmentation proprement dite. Dans certains cas, un filtrage important peut de lui-même produire une partition pertinente. Mais l'outil morphologique le plus connu en segmentation d'images est la ligne de partage des eaux. Il existe plusieurs algorithmes de segmentation par ligne de partage des eaux. L'idée de base consiste à simuler une inondation de l'image, vue comme un relief topographique où le niveau de gris correspond à l'altitude. Les frontières entre régions de la partition ont alors tendance à se placer sur les lignes de crête. Typiquement, on applique cet opérateur au gradient de l'image (norme du gradient euclidien, ou gradient morphologique) que l'on cherche à segmenter, et par conséquent les frontières se placent de façon privilégiée sur les lignes de gradient élevé. Plusieurs algorithmes de calcul de ligne de partage des eaux ont une complexité linéaire en fonction du nombre de pixels de l'image, ce qui les place parmi les méthodes de segmentation les plus rapides. En français En anglais![]() Pour les articles homonymes, voir Morphologie.
Pour les articles homonymes, voir Morphologie.Aperçu général[modifier]
Bref historique[modifier]
Opérateurs de base[modifier]
Cas ensembliste[modifier]
 , souvent utilisé comme modélisation du support des images binaires à deux dimensions, même si tout ce qui est présenté dans cette section reste valable dans
, souvent utilisé comme modélisation du support des images binaires à deux dimensions, même si tout ce qui est présenté dans cette section reste valable dans  , où d est un entier strictement positif. Soit B un sous-ensemble de E, appelé élément structurant. Si x est un élément de E, alors nous noterons Bx l'ensemble Btranslaté de x :
, où d est un entier strictement positif. Soit B un sous-ensemble de E, appelé élément structurant. Si x est un élément de E, alors nous noterons Bx l'ensemble Btranslaté de x :
 :
:
 .
.Dilatation et érosion[modifier]



Transformation en tout ou rien[modifier]


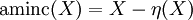
Ouverture et fermeture[modifier]
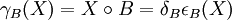
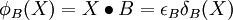
 ), et l'ouverture est anti-extensive(
), et l'ouverture est anti-extensive( ).
).Extension aux fonctions[modifier]
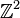 dans
dans  . Soit f une fonction appartenant à cet ensemble. On a alors :
. Soit f une fonction appartenant à cet ensemble. On a alors :



Exemple d'utilisation : détection de contours[modifier]


Opérateurs connexes, nivellements[modifier]
Segmentation[modifier]
Ensembles aléatoires[modifier]
Quantification[modifier]
Notes[modifier]
On gagne alors la dualité entre érosion et dilatation, mais on perd l'adjonction. Il faut alors modifier les définitions de l'ouverture et de la fermeture morphologiques en conséquence. Lorsque l'élément structurant est symétrique, cette distinction n'a pas d'importance.
Bibliographie[modifier]
Articles connexes[modifier]
Liens externes[modifier]
Sommaire[masquer] |
09:00 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Table des symboles mathématiques
Source : http://fr.wikipedia.org/wiki/Table_des_symboles_math%C3%A...Table des symboles mathématiques
|
|
Cette page contient des caractères spéciaux.
Si certains caractères de cet article s’affichent mal (carrés vides, points d’interrogation, etc.), consultez la page d’aide Unicode.
|
En mathématiques, certains symboles sont fréquemment utilisés. Le tableau suivant représente une aide pour ceux qui ne sont pas habitués à ces symboles. Dans la table, sont précisés pour chaque symbole, le nom, la prononciation et la branche des mathématiques dans laquelle le symbole est principalement utilisé. En plus, la quatrième colonne contient une définition informelle et la dernière donne un court exemple apportant une explication sur l'utilisation du symbole. Du fait de leur utilisation répandue, il existe un grand nombre de façons différentes de représenter certains symboles. Ce tableau ne saurait prétendre à l'exhaustivité. D'autres symboles sont définis par Unicode dans les plages suivantes:Logique[modifier]
Autres branches[modifier]
Autres symboles mathématiques[modifier]
Liens externes[modifier]
Sommaire[masquer] |
| Symbole (TeX) | Symbole (utf8) | Nom | Signification | Exemples |
|---|---|---|---|---|
| Prononciation | ||||
| Branche | ||||
 |
⇒ | Implication |  signifie « si A est vraie, alors B est vraie aussi ; si A est fausse alors on ne peut rien dire de la vérité de B ». signifie « si A est vraie, alors B est vraie aussi ; si A est fausse alors on ne peut rien dire de la vérité de B ».Parfois, on utilise 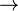 au lieu de au lieu de  |
 est vraie, mais est vraie, mais  est fausse (puisque x=−2 est aussi une solution). est fausse (puisque x=−2 est aussi une solution). |
| « implique » ou « si... alors » | ||||
| Logique | ||||
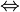 |
⇔ | Équivalence logique |  signifie : « A est vraie quand B est vraie et A est fausse quand B est fausse ». signifie : « A est vraie quand B est vraie et A est fausse quand B est fausse ». |
 |
| « si et seulement si » ou « équivaut à » | ||||
| Logique | ||||
 |
∧ | Conjonction logique |  est vraie si et seulement si A et B sont vraies (donc fausse si A ou B ou A et B sont fausses) est vraie si et seulement si A et B sont vraies (donc fausse si A ou B ou A et B sont fausses) |
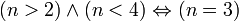 , si n est un entier naturel , si n est un entier naturel |
| « et » | ||||
| Logique | ||||
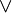 |
∨ | Disjonction logique |  est vraie quand A ou B (ou les deux) sont vraies et fausse quand les deux sont fausses. est vraie quand A ou B (ou les deux) sont vraies et fausse quand les deux sont fausses. |
 , si n est un entier naturel , si n est un entier naturel |
| « ou » | ||||
| Logique | ||||
 |
¬ | Négation logique |  est vraie quand A est fausse et fausse quand A est vraie est vraie quand A est fausse et fausse quand A est vraie |
  |
| « non » | ||||
| Logique | ||||
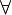 |
∀ | Quantificateur universel |  signifie : « P(x) est vraie pour tout x ». signifie : « P(x) est vraie pour tout x ». |
 |
| « Quel que soit », « pour tout » | ||||
| Logique | ||||
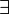 |
∃ | Quantificateur existentiel |  signifie : « il existe au moins un x tel que P(x) soit vraie » signifie : « il existe au moins un x tel que P(x) soit vraie » |
 (5 répond en effet à la question) (5 répond en effet à la question) |
| « il existe au moins un ... tel que » | ||||
| Logique |
| Symbole (TeX) | Symbole (utf8) | Nom | Signification | Exemples |
|---|---|---|---|---|
| Prononciation | ||||
| Branche | ||||
 |
! | Factorielle | n! est le produit : 1 × 2 × ... × n. | 6! = 1 × 2 × 3 × 4 × 5 × 6 = 720 |
| Factorielle (de) n. | ||||
| Combinatoire | ||||
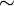 |
~ | Relation d'équivalence | ||
| « ... est équivalent à ... » | ||||
| Théorie des ensembles | ||||
| Équivalence | an ~ bn signifie que les suites an et bn sont équivalentes | sin(1/n) ~ 1/n (lorsque n tend vers l'infini) | ||
| « ... est équivalent à ... » | ||||
| Analyse | ||||
| Distribution de probabilité | X ~ D, signifie : « la variable aléatoire X a la distribution de probabilité D » | X ~ N(0,1), la distribution ou loi normale | ||
| « ... a la distribution de probabilité ... » | ||||
| Statistiques | ||||
 |
= | Égalité | x = y signifie : « x et y désignent le même objet mathématique » | 1 + 2 = 6 − 3 |
| « est égal à » | ||||
| toute branche | ||||
 |
≠ | Non-égalité | 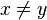 signifie : « x et y ne désignent pas le même objet mathématique » signifie : « x et y ne désignent pas le même objet mathématique » |
2 ≠ 3 |
| « n'est pas égal à », « est différent de » |
||||
| toute branche | ||||
 |
≡ | Congruence | ||
| « identique à », « congru à » |
||||
| Arithmétique modulaire | ||||
 |
∝ | Proportionnalité |  signifie : « x est proportionnel à y » signifie : « x est proportionnel à y » |
si y=2x, alors 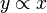 |
| « est proportionnel à » | ||||
| toute branche | ||||
: = |
:= :⇔ |
Définition | x: = y signifie : « x est défini comme étant un autre nom de y » signifie : « P est définie comme étant logiquement équivalente à Q » signifie : « P est définie comme étant logiquement équivalente à Q » |
 (cosinus hyperbolique) (cosinus hyperbolique) (OU exclusif) (OU exclusif) |
| « est défini comme » | ||||
| le second est très peu utilisé | ||||
| {,} | { , } | Ensemble en extension | {a,b,c} désigne l'ensemble dont les éléments sont a, b et c |  (ensemble des entiers naturels) (ensemble des entiers naturels) |
| « L'ensemble des ... » | ||||
| Théorie des ensembles | ||||
| { / } {;} {} |
{ / } { ; } { } |
Construction d'ensemble en compréhension | {x / P(x)} désigne l'ensemble de tous les x qui vérifient P(x). {x / P(x)} est le même ensemble que {x;P(x)} ou encore que {xP(x)} |
 |
| « L'ensemble de tous les ... qui vérifient ... » | ||||
| Théorie des ensembles | ||||
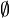 {} |
∅ {} |
Ensemble vide | {} et 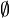 désignent l'ensemble vide, l'ensemble qui n'a pas d'élément désignent l'ensemble vide, l'ensemble qui n'a pas d'élément |
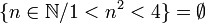 |
| « Ensemble vide » | ||||
| Théorie des ensembles | ||||
 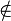 |
∈ ∉ |
Appartenance (ou non) à un ensemble |  signifie : « a est un élément de l'ensemble S » signifie : « a est un élément de l'ensemble S » signifie : « a n'est pas élément de S » signifie : « a n'est pas élément de S » |
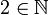  |
| « appartient à », « est élément de », « est dans ». « n'appartient pas », « n'est pas élément de », « n'est pas dans » |
||||
| Théorie des ensembles | ||||
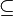 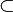 |
⊆ ⊂ |
Sous-ensemble | 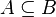 signifie : « tout élément de A est aussi un élément de B » signifie : « tout élément de A est aussi un élément de B »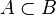 a généralement la même signification que a généralement la même signification que 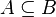 . Signalons toutefois que pour certains, les canadiens français notamment, le symbole . Signalons toutefois que pour certains, les canadiens français notamment, le symbole 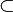 représente l'inclusion stricte représente l'inclusion stricte 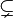 . . |
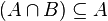  |
| « est un sous-ensemble (une partie) de ... », « est inclus dans... » | ||||
| Théorie des ensembles | ||||
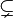 |
⊈ | Sous-ensemble strict, partie stricte |  signifie signifie 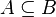 et et 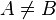 (ou (ou 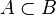 et et 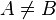 quand quand 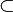 représente l'inclusion au sens large). représente l'inclusion au sens large). |
 |
| « est un sous-ensemble strict de ... », « est strictement inclus dans... » | ||||
| Théorie des ensembles | ||||
  |
⊇ ⊃ |
Sur-ensemble |  est une autre façon d'écrire est une autre façon d'écrire 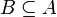 . . est une autre façon d'écrire est une autre façon d'écrire 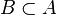 |
 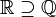 |
| « est un sur-ensemble de ... », « contient... » | ||||
| Théorie des ensembles | ||||
 |
⊋ | Sur-ensemble strict |  a le même sens que a le même sens que  . . |
 |
| « est un sur-ensemble strict de ... », « contient strictement... » | ||||
| Théorie des ensembles | ||||
 |
∪ | Réunion |  désigne l'ensemble qui contient tous les éléments de A et de B et seulement ceux-là désigne l'ensemble qui contient tous les éléments de A et de B et seulement ceux-là |
 |
| « Réunion de ... et de ... », « ... union ... » | ||||
| Théorie des ensembles | ||||
 |
⋂ | Intersection |  désigne l'ensemble des éléments qui appartiennent à la fois à A et à B, c'est-à-dire les éléments qu'ont les ensembles A et B en commun désigne l'ensemble des éléments qui appartiennent à la fois à A et à B, c'est-à-dire les éléments qu'ont les ensembles A et B en commun |
 |
| « Intersection de ... et de ... », « ... inter ... » | ||||
| Théorie des ensembles | ||||
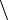 |
Différence |  désigne l'ensemble de tous les éléments de A qui n'appartiennent pas à B désigne l'ensemble de tous les éléments de A qui n'appartiennent pas à B |
 |
|
| « différence de ... et ... », « ... moins ... », « ... privé de ... » | ||||
| Théorie des ensembles | ||||
| () [] {} |
( ) [ ] { } |
Fonction application ; regroupement | f(x) désigne l'image de l'élément x par la fonction f Regroupement: les opérations placées à l'intérieur sont effectuées en premier |
Si f est définie par f(x) = x2, alors f(3) = 32 = 9 (8/4)/2 = 2/2 = 1, mais 8/(4/2) = 8/2 = 4 |
| « de » | ||||
| toute branche | ||||
 |
→ | Fonction |  signifie que la fonction va de X dans Y, ou a pour ensemble de définition X et pour ensemble d'arrivée Y, ou a pour origine X et pour but Y. signifie que la fonction va de X dans Y, ou a pour ensemble de définition X et pour ensemble d'arrivée Y, ou a pour origine X et pour but Y. |
Considérons la fonction  définie par f(x) = x2 définie par f(x) = x2 |
| « de ... vers », « de ... dans », « de ... sur ... » | ||||
| toute branche | ||||
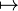 |
↦ | Fonction |  signifie que la variable x a pour image f(x) signifie que la variable x a pour image f(x) |
Au lieu d'écrire que f est définie par f(x) = x2, nous pouvons écrire " Soit la fonction  " " |
| « est envoyé sur », « a pour image » | ||||
| toute branche | ||||
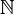 |
ℕ | Ensemble des entiers naturels | 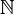 représente représente  |
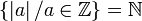 |
| « N » | ||||
| Nombre | ||||
 |
ℕ* | « N privé de zéro » |  |
|
 |
ℤ | Ensemble des entiers relatifs |  représente représente 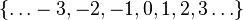 |
 |
| « Z » | ||||
| Nombre | ||||
 |
ⅅ | Ensemble des nombres décimaux |  représente représente  |
  |
| « D » | ||||
| Nombre | ||||
 |
ℚ | Ensemble des nombres rationnels |  représente représente 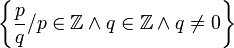 |
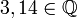  |
| « Q » | ||||
| Nombre | ||||
 |
ℚ+ | 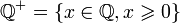 |
||
 |
ℝ | Ensemble des nombres réels |  représente l'ensemble des limites des suites de Cauchy de représente l'ensemble des limites des suites de Cauchy de  |
  (i étant le nombre complexe tel que i2= − 1) (i étant le nombre complexe tel que i2= − 1) |
| « R » | ||||
| Nombre | ||||
 |
ℂ | Ensemble des nombres complexes |  représente représente  |
 |
| « C » | ||||
| Nombre | ||||
  |
< > |
Comparaison | x < y signifie que x est strictement inférieur à y (ou x est inférieur à y). x > y signifie que x est strictement supérieur à y (ou x est supérieur à y). |
 |
| « est strictement inférieur à », « est strictement supérieur à » | ||||
| Relation d'ordre | ||||
  |
≤ ou ⩽ ≥ ou ⩾ |
Comparaison |  signifie que x est inférieur ou égal à y. signifie que x est inférieur ou égal à y. signifie que x est supérieur ou égal à y. signifie que x est supérieur ou égal à y. |
 |
| « est inférieur ou égal à » ; « est supérieur ou égal à » | ||||
| Relation d'ordre | ||||
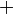 |
+ | Addition | 4 + 6 = 10 signifie que si quatre est ajouté à six, alors la somme ou le résultat est égal à dix. | 43 + 65 = 108 2 + 7 = 9 |
| « plus » | ||||
| Arithmétique | ||||
 |
- | Soustraction | 9 - 4 = 5 signifie que si quatre est ôté (retranché) de neuf, alors le résultat est égal à 5. Le signe moins peut aussi être placé immédiatement à gauche d'un nombre pour le rendre négatif. Par exemple, 5 + (-3) = 2 signifie que si cinq et le nombre négatif moins trois, sont ajoutés, alors le résultat est égal à deux. | 87 - 36 = 51 |
| « moins » | ||||
| Arithmétique | ||||
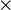 |
× | Multiplication | 3 × 2 = 6 signifie que si trois est multiplié par deux, alors le produit est égal à six. | 23 × 11 = 253 |
| « fois » | ||||
| Arithmétique | ||||
 |
÷ | Division | 8 ÷ 4 = 2 signifie que huit divisé par quatre est égal à deux. | 100 ÷ 4 = 25 |
| « divisé par » | ||||
| Arithmétique | ||||
 |
/ | fraction |  représente la fraction neuf quarts. / peut être aussi utilisé pour représenter la division. représente la fraction neuf quarts. / peut être aussi utilisé pour représenter la division. |
 |
| « sur » | ||||
| Arithmétique Nombre | ||||
 et et 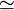 |
≈ ou ≃ | Approximation |  à 10-3 près signifie qu'une valeur approchée de e à 10-3 près est 2,718. à 10-3 près signifie qu'une valeur approchée de e à 10-3 près est 2,718. |
 à 10-7 près. à 10-7 près. |
| « approximativement égal à » | ||||
| Nombre réel | ||||
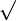 |
√ | Racine carrée |  représente le nombre réel positif dont le carré est égal à x. représente le nombre réel positif dont le carré est égal à x. |
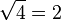  |
| « Racine carrée de ... » | ||||
| Nombre | ||||
 |
∞ | Infini |  et et  sont des éléments de la droite réelle achevée. sont des éléments de la droite réelle achevée.  apparaît dans les calculs de limites. apparaît dans les calculs de limites.  est un point adjoint au plan complexe pour le rendre isomorphe à une sphère (sphère de Riemann) est un point adjoint au plan complexe pour le rendre isomorphe à une sphère (sphère de Riemann) |
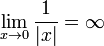 |
| « Infini » | ||||
| Nombre | ||||
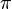 |
π | π | π est le rapport de la circonférence d'un cercle à son diamètre. | 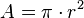 est l'aire d'un disque de rayon r est l'aire d'un disque de rayon r |
| « Pi » | ||||
| Géométrie euclidienne | ||||
 |
ϕ ou φ | « nombre d'or » | 
|
|
| e | e | « e » | e est la base des logarithmes naturels. | exp(1) = e ≈ 2,718 |
 |
| | | Valeur absolue oumodule d'un nombre complexe ou cardinal d'un ensemble |  désigne la valeur absolue de x (ou le module de x). désigne la valeur absolue de x (ou le module de x).| A | désigne le cardinal de l'ensemble A et représente, lorsque A est fini, le nombre d'éléments de A. |
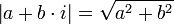 |
| « Valeur absolue de... », « module de ... » ; « cardinal de ... » | ||||
| Nombre ou Théorie des ensembles | ||||
 |
∑ | Somme | 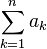 se lit « somme de ak pour k de 1 à n », et représente a1 + a2 + ... + an se lit « somme de ak pour k de 1 à n », et représente a1 + a2 + ... + an |
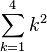 = 12 + 22 + 32 + 42 = 30 |
| « Somme de ... pour ... de ... à ... » | ||||
| Arithmétique | ||||
 |
∏ | Produit | 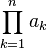 se lit « produit de ak pour k de 1 à n », et représente : a1·a2·...·an se lit « produit de ak pour k de 1 à n », et représente : a1·a2·...·an |
 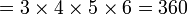 |
| « Produit de .. pour .. de .. à .. » | ||||
| Arithmétique | ||||
 |
∫,∬,∭,∮,∯ ou ∰ | Intégrale |  se lit « Intégrale de a à b de f de x dx », et représente l'aire algébrique du domaine délimité par la courbe représentative de f, l'axe des abscisses et les droites d'équation x = a et x = b se lit « Intégrale de a à b de f de x dx », et représente l'aire algébrique du domaine délimité par la courbe représentative de f, l'axe des abscisses et les droites d'équation x = a et x = b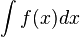 se lit « intégrale de f de x dx, et représente une primitive de f se lit « intégrale de f de x dx, et représente une primitive de f |
  (C désignant une constante) (C désignant une constante) |
| « Intégrale (de .. à ..) de .. d-.. » | ||||
| Analyse | ||||
 |
 |
Partie entière |  se lit « Partie entière de x», et représente la partie entière inférieure de x se lit « Partie entière de x», et représente la partie entière inférieure de x |
  |
| « Partie entière de .. » | ||||
| Nombre | ||||
 |
 |
Partie entière par excès |  se lit « Partie entière par excès de x », et représente l'entier supérieur à x se lit « Partie entière par excès de x », et représente l'entier supérieur à x |
  |
| « Partie entière par excès de .. » | ||||
| Nombre |
| Plage | Nom officiel du bloc |
|---|---|
2000 – 206F |
Ponctuation générale |
2070 – 209F |
Exposants et indices |
20D0 – 20FF |
Signes combinatoires pour symboles |
2150 – 218F |
Formes numérales |
2190 – 21FF |
Flèches |
2200 – 22FF |
Opérateurs mathématiques |
2300 – 23FF |
Signes techniques divers (2336 – 237A = symboles APL) |
25A0 – 25FF |
Formes géométriques |
2600 – 26FF |
Symboles divers |
2700 – 27BF |
Casseau |
27C0 – 27EF |
Divers symboles mathématiques - A |
27F0 – 27FF |
Supplément A de flèches |
2900 – 297F |
Supplément B de flèches |
2980 – 29FF |
Divers symboles mathématiques-B |
2A00 – 2AFF |
Opérateurs mathématiques supplémentaires |
2B00 – 2BFF |
Divers symboles et flèches |
3000 – 303F |
Symboles et ponctuation Chinois, japonais et coréen (CJC) |
10100 – 1013F |
Nombres égéens |
1D400 – 1D7FF |
Symboles mathématiques alphanumériques |
08:59 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Modèle mathématique
Modèle mathématique
![]() Pour les articles homonymes, voir modèle (homonymie).
Pour les articles homonymes, voir modèle (homonymie).
|
|
Cet article ne cite pas suffisamment ses sources (septembre 2010).
Si vous connaissez le thème traité, merci d'indiquer les passages à sourcer avec {{Référence souhaitée}} ou, mieux, incluez les références utiles en les liant aux notes de bas de page. (Modifier l'article)
|
Un modèle mathématique est une traduction de la réalité pour pouvoir lui appliquer les outils, les techniques et les théories mathématiques, puis généralement, en sens inverse, la traduction des résultats mathématiques obtenus en prédictions ou opérations dans le monde réel. Le mot modélisation est aussi très utilisé dans le monde du graphisme, où l'on modélise des objets en 3D ou en 2D. Un modèle se rapporte toujours à ce qu’on espère en déduire. Un même objet, par exemple une souris, ne sera pas modélisé de la même façon selon que l'on s'intéresse à De même, un modèle n'est jamais parfait, ni totalement représentatif de la réalité : le choix des paramètres et des relations qui les lient éclaire la finalité. Au sein d’un même modèle, le choix des valeurs des paramètres peut permettre d’appréhender divers aspects, ou encore des réalités différentes. Même lorsque le but est fixé, il y a souvent plusieurs modèles possibles dont chacun présente des avantages spécifiques. Dans toute modélisation, il y a un choix a priori de l’environnement mathématique servant à décrire l’ensemble des phénomènes. La formulation s'identifie rarement aux manifestations physiques réelles. Ainsi en physique, il est commode d'utiliser un espace tridimensionnel euclidien, ou un espace « courbe », ou un espace à 4, 5, 11 ou 26 dimensions, ou un espace de Hilbert, etc. Bien qu'il soit généralement possible de montrer une grande proximité de ces différentes représentations, elles s'avèrent toutefois plus ou moins bien adaptées à la situation considérée. Ces formulations théoriques restent des modèles utiles pour appréhender la réalité, mais ils s'en distinguent. Par exemple, lorsqu'un physicien déclare que « l'univers est en expansion », il faut bien comprendre qu'il affirme implicitement que « par rapport à mon cadre mathématique, tout ce passe comme si... ». Un autre physicien peut affirmer que « l'univers n'est pas en expansion » : ils peuvent être parfaitement d'accord si les formulations mathématiques sont distinctes. La même remarque s'applique à d'autres domaines, en particulier aux modèles économiques et comptables dont les résultats et les décisions qui en découlent ont des conséquences économiques et fiscales importantes : l'archétype de la modélisation économique étant le cadastre fiscal et les bases de la taxation immobilière, dont tout le monde sait bien qu'elles sont « fausses », c’est-à-dire qu'elle ne reflètent qu'imparfaitement la valeur réelle qui est censée servir de référence. Tout ceci sans ignorer la réalité : bien qu'un modèle de génie civil pour la construction d'un pont garantisse la robustesse de l'ouvrage, il n'est pas exclu qu'il finisse par s'écrouler (par contre, si le modèle indique que telle variante est trop faible, il serait insensé de la réaliser ...). La modélisation peut s'exercer Ces modèles mathématiques sont utilisés pour anticiper des événements ou des situations, comme prévoir le temps avec la météo, estimer les prix potentiels des actifs financiers avec les modèles d'évaluation en finance, ou prévenir les épidémies. On parle de modèles prédictifs, dans lesquels des variables connues, dites « explicatives », vont être utilisées pour déterminer des variables inconnues, dites « à expliquer ». Dans ce cas, les modèles servent à représenter des données historiques. On parle de modèles descriptifs. L'objectif est de rendre compte, de manière interprétable, d'une masse d'informations. L'archétype de ces modèles est la comptabilité : elle décrit de manière simplifiée les événements économiques réels en leur affectant un compte, c'est-à-dire une « étiquette » censée les caractériser. Ces comptes sont ensuite agrégés pour présenter de manière standard la situation économique des entreprises et des pays. Les deux types de modèles sont parfaitement liés : une bonne prédiction suppose au moins la prédiction de la situation passée et actuelle, c’est-à-dire une bonne description. Inversement, une bonne description serait parfaitement vaine si elle ne servait pas au moins de diagnostic, ou de carte, pour identifier la conduite à tenir. Un même modèle mathématique peut se trouver applicable à de nombreuses situations, n'ayant pas forcément un rapport évident. Par exemple, des générateurs de paysages sont capables de créer des formes réalistes d'objets aussi différents que des montagnes, des arbres, des rochers, de l'herbe, des coquillages ou des flocons de neige, avec un seul modèle général, alors même que les processus de croissance et de constructions de ses objets sont très divers. Si, au lieu de créer un nouveau modèle, on est capable de rapprocher un problème d'un ancien modèle connu, on obtient immédiatement une masse de données très utile. Une grande partie du travail est donc de reconnaître qu'un modèle connu s'applique, ou à étendre les propriétés connues d'une classe particulièrement utile de modèle (propriété qu'on pourra ensuite utiliser plus largement). En préliminaire, il est important de comprendre que la complexité mathématique n'est pas un critère suffisant pour juger si un modèle est pertinent ou non : il existe des classes de modèles qui font appel à des outils mathématiques complexes, tels la recherche opérationnelle ou la théorie des jeux ; d'autres classes, la comptabilité par exemple, sont d'un abord mathématique enfantin (additions, soustractions). Mais, à résultat comparable, c'est bien sûr le modèle le plus simple qui est préférable. Un modèle est pertinent Il n'est pas question dans un article si court de présenter une méthodologie applicable à toutes les situations (s'il en existe une !), mais quelques points essentiels. 1. Le point de départ est toujours une question qu'on se pose sur une situation future et/ou si complexe qu'on n'y trouve pas la réponse de manière évidente. 2. Pour trouver la réponse, il est nécessaire de limiter le champ du problème en recherchant les données qu'on imagine avoir un lien direct avec la question. Trop limiter fait courir le risque de ne pas modéliser un phénomène qui a du poids dans le contexte, mais trop ouvrir entraîne une dispersion des moyens et une accumulation de données non pertinentes qu'il faudra écarter en justifiant les choix. Cette étape est la plus délicate pour la qualité du modèle : elle est soumise aux a priori du modélisateur, à ses manques de connaissances — parfois de méthode — et aux moyens dont il dispose (temps, argent, accès aux données). Au cours de cette étape, on choisit le type de modèle général qu'on va utiliser, notamment en fonction des données dont on pense disposer. 3. Il faut ensuite construire le modèle : C'est là qu'interviennent les outils mathématiques et informatiques, qui permettent un filtrage et une construction avec un minimum de subjectivité en un minimum de temps. 4. Le « substrat » restant constitue le modèle, ensemble de règles ou d'équations. Il faut décrire ces règles le plus complètement possible : leur importance relative, les données en entrée et en sortie, les outils mathématiques utilisés, les étapes par lesquelles il faut passer, les points de contrôle. 5. La dernière étape consiste à valider le modèle : en appliquant aux données filtrées les règles du modèle, retrouve-t-on la situation initiale ? Si l'écart est trop important, il est nécessaire de se reposer la question des limites que l'on a fixées, ou de la pertinence des outils utilisés pour la modélisation. Il s'agit essentiellement d'outils statistiques et de probabilités, de calculs différentiels (équation aux dérivées partielles et ordinaires). Plus précisément,Généralités[modifier]
Multiplicité de buts[modifier]
Multiplicité des modélisations[modifier]
Typologie de modèle : selon le sens de la modélisation[modifier]
Les qualités d'un modèle[modifier]
Comment créer un modèle ?[modifier]
Les principaux domaines d'applications[modifier]
Les outils mathématiques les plus courants[modifier]
Voir aussi[modifier]
Liens externes[modifier]
Sommaire[masquer] |
08:59 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Physique mathématique
Physique mathématique
|
|
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
La physique mathématique est un domaine de recherche commun à la physique et aux mathématiques s'intéressant au développement des méthodes mathématiques spécifiques aux problèmes physiques ou plus généralement à l'application des mathématiques à la physique, et, à l'opposé, aux développement mathématiques que suscitent certains domaines de recherche en physique. Elle inclut notamment l'étude des systèmes dynamiques, des algèbres aux symétries particulières, des méthodes de décomposition en séries et des méthodes de résolution d'équations différentielles. Au XVIIe siècle, le mathématicien et physicien Isaac Newton a développé de nouveaux outils de mathématiques pour résoudre des problèmes de physique (dont la question du mouvement des objets). Suivirent James Clerk Maxwell, Lord Kelvin, William Rowan Hamilton. David Hilbert développa la théorie des espaces de Hilbert pour résoudre les équations intégrales, théorie qui se trouve au centre aujourd'hui de la mécanique quantique. La relativité générale d'Einstein utilise les connaissances mathématiques en géométrie différentielle, géométrie riemannienne et géométrie lorentzienne. Introduction historique[modifier]
08:58 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Espérance mathématique
L'espérance mathématique d'une variable aléatoire est l'équivalent en probabilité de la moyenne d'une série statistique en statistiques. Elle se note E(X) et se lit espérance de X. C'est une valeur numérique permettant d'évaluer le résultat moyen d'une expérience aléatoire. Elle permet par exemple de mesurer le degré d'équité d'un jeu de hasard; elle est alors égale à la somme des gains (et des pertes) pondérés par la probabilité du gain (ou de la perte). Lorsque l'espérance est égale à 0, le jeu est dit équitable. Soit Si C'est notamment le cas quand le nombre de valeurs possibles est fini, par exemple Dans ce cas la famille Exemple de calcul pour la roulette française : en jouant un numéro plein, le joueur a 1 chance sur 37 (les numéros vont de 0 à 36) de repartir avec 35 fois sa mise initialenote 1. Son espérance de gain est donc : Ce résultat indique qu'en moyenne, il perd 2,7 % de sa mise à chaque partie au profit du casino. X étant une variable aléatoire réelle, une fonction f supposée régulière définit une nouvelle variable aléatoire Variable aléatoire continue: En particulier, il est intéressant de considérer la variable aléatoire à valeurs complexes Il s'agit de la fonction caractéristique d'une variable aléatoire. L'exponentielle se développe en série : ou, si la densité de probabilité est une fonction suffisamment régulière : Définition — qui signifie que Propriété — En général, l'opérateur espérance ne respecte pas les fonctions de variable aléatoire, c'est-à-dire qu'en général: Une inégalité célèbre à ce propos est l'inégalité de Jensen pour des fonctions convexes (ou concaves). On utilise souvent comme estimateur de l'espérance la moyenne empirique, qui est un estimateur: On considère fréquemment l'espérance comme le centre de la variable aléatoire, c'est-à-dire la valeur autour de laquelle se dispersent les autres valeurs. Mais ce point de vue n'est plus valable lorsque la loi est dissymétrique. Pour s'en persuader il suffit d'étudier le cas d'une loi géométrique, une loi particulièrement dissymétrique. Si X représente le nombre de lancers nécessaires pour obtenir le chiffre 1 avec un dé cubique, on démontre que E(X) = 6 ce qui veut dire qu'il faut en moyenne 6 lancers pour obtenir le chiffre 1. Pourtant, la probabilité que 5 essais ou moins suffisent vaut près de 0,6 et la probabilité que 7 lancers ou plus soient nécessaires est de 0,33. Les valeurs de X ne se répartissent donc pas équitablement de part et d'autre de l'espérance. Dans certains cas, les indications de l'espérance mathématique ne coïncident pas avec un choix rationnel. Imaginons par exemple qu'on vous fasse la proposition suivante : si vous arrivez à faire un double six avec deux dés, vous gagnez un million d'euros, sinon vous perdez 10 000 euros. Il est probable que vous refuserez de jouer. Pourtant l'espérance de ce jeu vous est très favorable : la probabilité de tirer un double 6 est de 1/36; on obtient donc : à chaque partie vous gagnez en moyenne 18 000 euros. Le problème tient justement sur ce « en moyenne » : si les gains sont extrêmement importants, ils n'interviennent que relativement rarement, et pour avoir une garantie raisonnable de ne pas finir ruiné, il faut donc avoir suffisamment d'argent pour participer à un grand nombre de parties. Si les mises sont trop importantes pour permettre un grand nombre de parties, le critère de l'espérance mathématique n'est donc pas approprié. Ce sont ces considérations et de risque de ruine qui conduisirent, à partir de son « paradoxe de Saint Petersbourg », le mathématicien Daniel Bernoulli à introduire en 1738 l'idée d'aversion au risque qui conduit à assortir l'espérance mathématique d'une prime de risque pour son application dans les questions de choix. Plutôt que de passer par une notion de prime, on peut directement établir une fonction d'utilité, associant à tout couple {gain, probabilité} une valeur. L'espérance mathématique constitue alors la plus simple des fonctions d'utilité, appropriée dans le cas d'un joueur neutre au risque disposant de ressources au moins très grandes à défaut d'infinies. Émile Borel adopta cette notion d'utilité pour expliquer qu'un joueur ayant peu de ressources choisisse rationnellement de prendre un billet de loterie chaque semaine : la perte correspondante n'est en effet pour lui que quantitative, tandis que le gain - si gain il y a - sera qualitatif, sa vie entière en étant changée. Une chance sur un million de gagner un million peut donc valoir dans ce cas précis bien davantage qu'un euro.Espérance mathématique
Définition[modifier]
 une variable aléatoire de l' espace probabilisé
une variable aléatoire de l' espace probabilisé  vers
vers  (ou un espace mesurable
(ou un espace mesurable 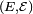 ). Son espérance est définie par:
). Son espérance est définie par: (où
(où  est la probabilité image).
est la probabilité image).
Si la loi de probabilité de  admet une densité
admet une densité  , alors:
, alors:
 est une variable aléatoire discrète prenant les valeurs sur un espace de valeurs dénombrables
est une variable aléatoire discrète prenant les valeurs sur un espace de valeurs dénombrables 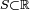 , et qu'elle a une fonction de masse
, et qu'elle a une fonction de masse  , l'espérance prend la forme:
, l'espérance prend la forme:
 avec les probabilités
avec les probabilités  . Dans ce cas l'espérance devient:
. Dans ce cas l'espérance devient:
 est sommable et la convergence absolue assure que la division de la série ne dépend pas de la manière de numéroter les termes.
est sommable et la convergence absolue assure que la division de la série ne dépend pas de la manière de numéroter les termes.Exemple[modifier]

Généralisation: espérance d'une fonction d'une variable aléatoire réelle[modifier]
 notée f(X) dont l'espérance, lorsqu'elle existe, s'écrit en remplaçantk par f(k) ou x par f(x) dans les formules précédentes (théorème de transfert).
notée f(X) dont l'espérance, lorsqu'elle existe, s'écrit en remplaçantk par f(k) ou x par f(x) dans les formules précédentes (théorème de transfert).
Variable aléatoire discrète: ![mathbb E[f(X)] = sum_{k=-infty}^{+infty} f(k) mathbb P_X(k)](http://upload.wikimedia.org/math/0/8/7/087d15a2cc548365fdbc4e4fd08fef45.png)
![mathbb E[f(X)] = int_{-infty}^{+infty} f(x) p_X(x) dx](http://upload.wikimedia.org/math/e/1/8/e1828c50e62af051e6a69aa5214591c6.png)
 (où
(où  ) dont l'espérance mathématique est [la valeur en θ de] la transformée de Fourier inverse de la densité de probabilité :
) dont l'espérance mathématique est [la valeur en θ de] la transformée de Fourier inverse de la densité de probabilité :![phi_X(theta) = mathbb Eleft[e^{i theta X}right],](http://upload.wikimedia.org/math/a/6/2/a62080b8497ae043b0cbc5d0669915c0.png)
![phi_X(theta) = mathbb Eleft[sum_{k=0}^infty {(i theta X)^k over {k !}}right]](http://upload.wikimedia.org/math/5/8/e/58e0db6a4e0d73bb3ea56a0fa99feaf8.png)
![phi_X(theta) = sum_{k=0}^infty {(i theta)^k over {k !}} mathbb Eleft[X^kright]](http://upload.wikimedia.org/math/6/1/2/612ed082421e38d4bb0d97f91ee51433.png)
Propriétés[modifier]
Propriétés élémentaires[modifier]
 et
et  sont des variables aléatoires tels que
sont des variables aléatoires tels que  presque sûrement, alors
presque sûrement, alors  .
.
 et
et 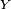 (qui doivent être définies sur le même espace probabiliste) et pour deux nombres réels
(qui doivent être définies sur le même espace probabiliste) et pour deux nombres réels  et
et  :
:
 . L'égalité est vraie pour des variables X et Y indépendantes. L'absence de la multiplicativité amène à étudier les covariances et corrélation.
. L'égalité est vraie pour des variables X et Y indépendantes. L'absence de la multiplicativité amène à étudier les covariances et corrélation.Loi de l'espérance itérée[modifier]

 est une fonction de y (en fait une variable aléatoire). L'espérance itérée vérifie
est une fonction de y (en fait une variable aléatoire). L'espérance itérée vérifie

Espérance d'une fonctionnelle[modifier]
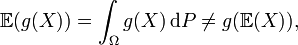
Estimation[modifier]
Caractère central[modifier]
En particulier, si X et 2a - X ont même loi de probabilité, c'est-à-dire si la loi de probabilité est symétrique par rapport à a, alors E(X) = a.Interprétation et applications[modifier]
Espérance mathématique et choix rationnel[modifier]
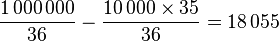
Incidence de la prime de risque[modifier]
Applications particulières (économie, assurance, finance, jeux)[modifier]
Notion d'utilité probabiliste[modifier]
Notes et références[modifier]
Notes[modifier]
Références[modifier]
Liens externes[modifier]
Sommaire[masquer] |
08:58 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Fondements des mathématiques
La fondation, ou les fondements, des mathématiques sont les principes sur lesquels est établie cette science. Le logicisme a été prôné notamment par Gottlob Frege et Bertrand Russell. La mathématique pure présente deux caractéristiques : la généralité de son discours –- la considération des particuliers existants est exclue -- et la déductibilité du discours mathématique –- les inférences qui structurent le discours mathématique sont des implications formelles (elles affirment non pas les propositions elles-mêmes, mais la nécessité de leur connexion) --. En ce que le discours mathématique ne prétend qu’à une vérité formelle, il est possible de réduire les mathématiques à la logique, les lois logiques étant les lois du « vrai ». Par exemple, la définition logique du nombre, loin d’être réduite à l’opération concrète de dénombrement d’objets, consiste en la référence à l’égalité numérique de deux classes (deux classes ont le même nombre s’il est possible d’instaurer entre leurs éléments respectifs une relation bijective). Le logicisme a rencontré néanmoins, à ses débuts, de réelles difficultés en tant qu’il s'engage ontologiquement par rapport aux classes. La théorie des classes avait conduit à desparadoxes logiques maintenant résolus mais qui avaient mis au jour la nécessité de clarifier les axiomes. Le formalisme soutenu par David Hilbert : les mathématiques se présentent comme une pure construction de l’esprit. La tâche des mathématiciens est de déduire des théorèmes à partir d’axiomes qui ne sont ni vrais ni faux. La validité ne repose plus que sur la structure des énoncés, et non sur la nature de ce dont ils parlent. La vérité des mathématiques est réduite à leur cohérence interne, la non contradiction des propositions. Le débat sur cette conception formaliste a été relancé par le théorème d'incomplétude de Gödel qui affirme que tout système formel cohérent et récursif contenant l'arithmétique, possède une proposition valide (ou disons « vraie ») qui n’est ni démontrable, ni réfutable. L’intuitionnisme défendu de manière paradigmatique par Brouwer : les mathématiques ont un fondement intuitif. Sans l’intuition, la logique s’avère stérile. Défendre une conception intuitionniste a des conséquences importantes. Ainsi, selon la logique intuitionniste, on ne peut pas éliminer la double négation (ce que fait la logique classique) : « non non p » ne se réduit pas à « p ». Il s’ensuit que « non p ou p » n'est pas un théorème. Ces refus sont justifiés par le fait qu'en logique intuitionniste « q implique r » signifie que « d'une démonstration de q je peux construire une démonstration de r », or l'affirmation « non non p implique p» ne permet pas de construire une démonstration de p à partir d'une démonstration de « non nonp ». Brouwer concevait l'intuitionnisme comme un positionnement philosophique sur les mathématiques et a acueilli avec scepticisme sa formalisation donnée ultérieurement par Arend Heyting[réf. nécessaire]. L’œuvre de Hilbert est très représentative de la crise des fondements qui s’est produite en mathématiques pendant le XIXe et au début du xxe siècle. Hilbert, comme d’autres logiciens et mathématiciens de son temps, s’est rendu compte que la géométrie euclidienne était incomplète, pas au sens où l’axiome des parallèles n’y est pas déductible, mais parce que tous les géomètres depuis Euclide se servent dans leurs preuves d’axiomes qui n’avaient jamais été explicités. À la suite des travaux de Pasch, Hilbert a donné une formulation presque complète de la géométrie euclidienne, dans son livre Les Fondements de la géométrie, pour laquelle aucun axiome géométrique n’était laissé dans l’ombre. Ce programme de fondation de la géométrie n’était cependant pas achevé pour deux raisons. D’une part, les règles de raisonnement admises étaient encore laissées dans l’ombre.[réf. nécessaire] D’autre part, un des axiomes de la géométrie, relatif à la continuité de l’espace, posait des problèmes d’interprétation associés à ceux de la définition des nombres réels et de la théorie des ensembles de Cantor. L’analyse, que l’on peut aussi appeler calcul infinitésimal, ou calcul différentiel et intégral, repose maintenant sur la définition de l’ensemble des nombres réels. Depuis les découvertes de Newton et Leibniz, il avait fallu sortir du cadre des Éléments d'Euclide. Les mathématiciens du XIXe siècle, notamment Cauchy et Weierstrass, pour l'analyse proprement dite, puis Dedekind et Cantor ont donné une formulation précise de principes qui permettent de raisonner avec rigueur et exactitude sur les nombres réels. Ceux-ci sont définis par Dedekind comme des ensembles de nombres rationnels. Peano a donné des axiomes et des méthodes formelles pour développer d’une façon logiquement rigoureuse l’arithmétique et celle-ci suffit pour fonder la théorie des nombres rationnels. La théorie des ensembles de Cantor, qui n'était pas vraiment formalisée, semblait cependant le cadre idéal, paradisiaque selon l’expression de Hilbert, pour fonder l’analyse et plus généralement les mathématiques. Frege, de son côté avait donné des règles formelles précises et explicites pour une théorie logique qui devait permettre de fonder les mathématiques. On pouvait espérer une base solide. Mais cette base n'a pas tardé à montrer ses faiblesses. La découverte du paradoxe de Burali-Forti (l'ensemble de tous les ordinaux est bien ordonné, ce bon ordre est supérieur à tous les ordinaux, donc à son propre ordinal), puis celle du paradoxe de Russell, proche sur le principe mais nettement plus simple (l'ensemble des ensembles qui ne s'appartiennent pas à eux-mêmes est un ensemble, il ne peut ni s'appartenir, ni ne pas s'appartenir à lui-même), montrent l'incohérence de ces deux théories (Russell a donné son paradoxe initialement pour la théorie de Frege). Des solutions pour éviter ces paradoxes furent rapidement trouvées. L'une, initiée par Russell, et développée dans les Principia Mathematica, stratifie les prédicats grâce à la notion detype : on ne peut plus écrire qu'un ensemble appartient à lui-même. L'autre, initiée par Zermelo, restreint la définition des ensembles par compréhension, c'est-à-dire par une propriété de ses éléments : la propriété de ne pas appartenir à soi-même ne définit plus un ensemble. Mais pouvait-on s'assurer que l'on ne puisse pas dériver de nouveaux paradoxes dans ces théories ? Pour répondre à la crise des fondements des mathématiques, Hilbert avait conçu un programme dont il établit les prémisses en 1900 dans l'introduction à sa célèbre liste de problèmes, le second problème étant justement celui de la cohérence de l'arithmétique. Il développe ce programme avec ses collaborateurs, parmi lesquels Bernays et Ackermann, essentiellement dans les années 1920. L'idée est grossièrement la suivante. Tant que l'on manipule le fini, les mathématiques sont sûres. L'arithmétique élémentaire (en un sens qui doit se préciser) est sûre. Pour justifier l'utilisation d'objets abstraits ou idéaux, en particulier infinis, il suffit de montrer que la théorie qui les utilise est cohérente, mais bien sûr cette cohérence doit elle-même être démontrée par des moyens finitaires. On peut alors affirmer l'existence de ces objets. C'est la position formaliste (à ne pas confondre avec le finitisme qui considère que seules les constructions directement finitaires ont un sens). Le système dans lequel on pourrait formaliser les mathématiques finitaires n'est pas clair. À l'époque, il semble que Hilbert pensait, sans l'avoir explicitement formalisé, à un système plus faible que l'arithmétique de Peano, l'arithmétique primitive récursive : toutes les définitions de fonctions récursives primitives sont dans le langage, la récurrence est restreinte aux formules sans quantificateurs (disons aux égalités pour faire simple), donc très immédiate. Peu importe en fait : le second théorème d'incomplétude de Gödel, montre que l'on ne pourra même pas prouver dans la théorie arithmétique en question sa propre cohérence, et donc certainement pas celle de théories plus fortes qui assureraient la fondation des mathématiques. Le programme de Hilbert n'est donc pas réalisable, en tout cas pas sans une révision drastique. Des logiciens comme Gentzen, et Gödel lui-même, ont pensé à rétablir ce programme en étendant la notion de méthodes finitaires, celles-ci ne pouvant cependant pas être définies une fois pour toutes par une théorie toujours à cause du second théorème d'incomplétude. Ainsi Gentzen a donnée en 1936 une preuve de cohérence de l'arithmétique de Peano dans un système forcément plus fort, où l'on raisonne par induction sur un ordre bien fondé (dénombrable mais plus grand que l'ordre des entiers), mais où l'induction est cependant restreinte à des formules sans quantificateurs, donc plus "immédiate". Si l'intérêt mathématique des méthodes mise en œuvre par Gentzen ne fait aucun doute, l'interprétation de ses preuves de cohérence, en tant que preuves "absolues" (ce sont bien sûr indubitablement des preuves de cohérence relative) reste très discutable. Il reste que, malgré son échec, le programme de Hilbert a joué un rôle décisif dans le développement de la logique mathématique moderne. Il ne faudrait pas confondre formalisme, et méthode formelle. La méthode formelle est essentielle pour comprendre les mathématiques contemporaines. Définir une théorie formelle, c'est : Définir une théorie de façon formelle est essentiel pour en donner des propriétés : cohérence ou incohérence, complétude ou incomplétude etc. Tant qu’on a pas formalisé une théorie, on ne sait pas exactement si une formule appartient ou non à la théorie. Les règles de déduction de la logique traditionnelle sont désormais complètement connues et formalisées au sein de la logique mathématique. Toutes les connaissances mathématiques peuvent être prouvées avec ces règles et des axiomes convenablement choisis. C'est probablement dans cette catégorie que l'on doit classer les mathématiques à rebours d'Harvey Friedman. Les mathématiques actuelles sont basées sur la notion d' ensemble. En fait, tout objet mathématique ou presque peut être défini comme un ensemble. Par exemple, « 23 » peut être défini comme un certain ensemble qui contient 23 éléments. (voir à ce sujet l'article sur la construction des entiers naturels). Avec de telles définitions, ou d’autres semblables, toutes les connaissances mathématiques peuvent être prouvées à l’intérieur d’une théorie des ensembles. Leurs axiomes peuvent être considérés comme les principaux fondements des mathématiques (avec les règles de déduction du calcul des prédicats au premier ordre). Plusieurs systèmes d’axiomes ont été proposés : Parmi les mathématiciens, certains se contentent des axiomes ZF, et refusent l'axiome du choix (C), car ils considèrent que certaines de ses implications sont contre-intuitives. Certains mathématiciens refusent même ZF et la logique classique qui en est la base, car ils considèrent que tout doit être construit explicitement; c'est la raison pour laquelle on les appelleconstructivistes ou intuitionnistes.Fondements des mathématiques
Les points de vue sur la nature des mathématiques[modifier]
Le logicisme[modifier]
Le formalisme[modifier]
L'intuitionnisme[modifier]
Les fondements de la géométrie[modifier]
Les fondements de l’analyse et la théorie des ensembles[modifier]
Le programme de Hilbert[modifier]
La méthode formelle[modifier]
Les théories des ensembles[modifier]
De même,  peut être construit à partir d'ensembles comme suit :
peut être construit à partir d'ensembles comme suit :


D'autres formalismes[modifier]
Bibliographie[modifier]
Voir aussi[modifier]
Références[modifier]
Sommaire[masquer] |
08:50 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
12/02/2011
Réalisations des complexes motiviques de Voevodsky
| HAL : hal-00437302, version 2 |
| arXiv : 0911.5611 |
|
|
| Fiche détaillée |  Récupérer au format Récupérer au format |
| Versions disponibles : | v1 (30-11-2009) | v2 (07-02-2011) |
| Réalisations des complexes motiviques de Voevodsky |
| Florence Lecomte 1Nathalie Wach 1 |
| (30/11/2009) |
|
|
| Over a number field k, we construct realizations of Voevodsky motivic complexes, realizations as presented by Fontaine and Perrin-Riou [FPR94]. Our realization functors are defined from the category of motivic complexes constructed by Voevodsky and are obtained as cohomological functors which are, up to some limits, representable. The De Rham realization is represented by the De Rham motivic complex defined in [LW09]. We obtain integral Betti and l-adic realizations. Our realization functors are related by comparison arrows, which become isomorphisms when restricted to the category of geometrical motives. Furthermore, on geometrical motives, the realizations are endowed with Bondarko's weight filtration [Bo09], the Hodge realization is constructed and all these realizations coincide rationally with those defined by A. Huber [H00]. |
| 1 : | Institut de Recherche Mathématique Avancée (IRMA) |
| CNRS : UMR7501 – Université de Strasbourg | |
| Domaine | : | Mathématiques/Théorie des nombres Mathématiques/Géométrie algébrique Mathématiques/K-théorie et homologie |
| motifs : réalisations |
| Liste des fichiers attachés à ce document : | ||||||||||
|
|
|
|
| hal-00437302, version 2 | |
| http://hal.archives-ouvertes.fr/hal-00437302/fr/ | |
| oai:hal.archives-ouvertes.fr:hal-00437302 | |
| Contributeur : Nathalie Wachwach@math.unistra.fr | |
| Soumis le : Lundi 7 Février 2011, 15:50:45 | |
| Dernière modification le : Lundi 7 Février 2011, 16:33:17 | |
Source :
21:39 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Asymptotics of prediction in functional linear regression with functional outputs
| HAL : hal-00422679, version 3 |
| arXiv : 0910.3070 |
|
|
| Fiche détaillée |  Récupérer au format Récupérer au format |
| Versions disponibles : | v1 (16-10-2009) | v2 (29-10-2009) | v3 (10-02-2011) |
| Asymptotics of prediction in functional linear regression with functional outputs |
| Christophe Crambes 1André Mas 1 |
| (08/10/2009) |
|
|
| We study prediction in the functional linear model with functional outputs : $Y=SX+varepsilon $ where the covariates $X$ and $Y$ belong to some functional space and $S$ is a linear operator. We provide the asymptotic mean square prediction error with exact constants for our estimator which is based on functional PCA of the input and has a classical form. As a consequence we derive the optimal choice of the dimension $k_{n}$ of the projection space. The rates we obtain are optimal in minimax sense and generalize those found when the output is real. Our main results hold with no prior assumptions on the rate of decay of the eigenvalues of the input. This allows to consider a wide class of parameters and inputs $Xleft( cdot right) $ that may be either very irregular or very smooth. We also prove a central limit theorem for the predictor which improves results by Cardot, Mas and Sarda (2007) in the simpler model with scalar outputs. We show that, due to the underlying inverse problem, the bare estimate cannot converge in distribution for the norm of the function space |
| 1 : | Institut de Mathématiques et de Modélisation de Montpellier (I3M) |
| CNRS : UMR5149 – Université Montpellier II - Sciences et Techniques du Languedoc | |
| Domaine | : | Mathématiques/Statistiques Statistiques/Théorie |
| Liste des fichiers attachés à ce document : | ||||||||||
|
|
|
|
| hal-00422679, version 3 | |
| http://hal.archives-ouvertes.fr/hal-00422679/fr/ | |
| oai:hal.archives-ouvertes.fr:hal-00422679 | |
| Contributeur : André Masmas@math.univ-montp2.fr | |
| Soumis le : Jeudi 10 Février 2011, 09:10:20 | |
|
Dernière modification le : Jeudi 10 Février 2011, 09:15:19
Source : http://hal.archives-ouvertes.fr/INSMI/hal-00422679/fr/ |
|
21:38 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
300 défis mathématiques Mohammed Aassila Scolaire / Universitaire (broché). Paru en 09/2001 Livre
21:34 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Annales des olympiades internationales de mathématiques P. Bourgade Scolaire / Universitaire (broché). Paru en 04/2005 Livre
21:33 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Olympiades internationales de mathématiques M. Aassila Etude (broché). Paru en 06/2003
21:31 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Olympiades de mathématiques réflexes et stratégies T.B. Soulami Essai (broché). Paru en 11/2007
21:29 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
En passant par hasard les probabilites de tous les jours Gilles Pagès broché. Paru en 12/1999
21:27 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
101 quizz qui banquent Gilles Pagès, Ed. Vuibert, 2010
21:22 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Au nom de l'infini (Loren Graham et Jean-Michel Kantor, Ed. Belin, 2010)
21:21 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Agenda http://www.sciencesmaths-paris.fr/
Agenda
Février 2011
09-02-2011 - Le cours de Caucher Birkar
Cliquez ici pour connaître les dates des séances, le lieu et le résumé du cours.22-02-2011 - Le cours de Sergiu Klainerman
Cliquez ici pour connaître les dates, salles et pour tout savoir sur ce cours.28-02-2011 - Séminaire IHP-Fondation SMP
Cliquez ici pour en savoir plus.Mars 2011
07-03-2011 - Séminaire d'analyse IHP-FSMP
Cliquez ici pour en savoir plus.
21:19 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook




















































 |
| 



