25/03/2011
E8 (mathématiques)
E8 (mathématiques)
Pour les articles homonymes, voir E8.
En mathématiques, 
est le plus grand groupe de Lie complexe de type exceptionnel. Son algèbre de Lie est notée 
.
E8 est de rang 8 et de dimension 248. Il est simplement connexe et son centre est trivial.
La structure E8 a été découverte en 1887 par le mathématicien norvégien Sophus Lie pour étudier la symétrie et jusqu’ici personne ne pensait que cet objet mathématique pourrait être compris, considère Jeffrey Adams, responsable de l’équipe Atlas of Lie Groups and Représentations qui réunit 18 mathématiciens et programmeurs dans le monde, dont Fokko du Cloux et Marc van Leeuwen.
Sommaire[masquer]
|
Formes réelles[modifier]
En plus du groupe de Lie complexe E8, de dimension complexe 248 (donc de dimension réelle 496), il existe trois formes réelles de ce groupe, toutes de dimension réelle 248. Les plus simples sont les formes compactes 
et déployées 
(non-compacte maximale ou encore split en anglais) et il en existe une troisième, notée 
.
Constructions[modifier]
On peut construire la forme compacte du groupe E8 comme le groupe d'automorphismes de l'algèbre de lie correspondante. Cette algèbre possède 
comme sous-algèbre de dimension 120 et on peut se servir de celle-ci pour décomposer la représentation adjointe comme
où 
est l'une des deux représentations spinorielles, de type Majorana-Weyl du groupe 
dont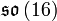 
est l'algèbre de Lie.
Si on appelle 
un jeu de générateurs pour 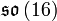et 
les 128 composantes de alors on peut écrire explicitement les relations définissant comme
![left[J_{ij}, J_{kell}right] = delta_{jk}J_{iell} - delta_{jell}J_{ik} - delta_{ik}J_{jell} + delta_{iell}J_{jk},](http://upload.wikimedia.org/math/f/8/d/f8ddba45c26b81da3205c690d5648aeb.png)
ainsi que
![left[J_{ij}, Q_aright] = frac14 left(gamma_igamma_j - gamma_jgamma_iright)_{ab}Q_b,](http://upload.wikimedia.org/math/b/f/1/bf123d341c9502ae0e5452733a8004ea.png)
,
qui correspond à l'action naturelle de 
sur le spineur 
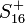. Le commutateur restant (qui est bien un commutateur et non pas un anticommutateur) est défini entre les composantes du spineur comme
![left[Q_a, Q_bright] = gamma^{[i}_{ac}gamma^{j]}_{cb}J_{ij},](http://upload.wikimedia.org/math/5/1/6/51632689c8006bf6f240719672da191c.png)
.
À partir de ces définitions on peut vérifier que l'identité de Jacobi est satisfaite.
Géométrie[modifier]
La forme réelle compacte de E8 peut être vue comme le groupe d'isométrie d'une variété riemannienne de dimension 128 appelée plan projectif octooctonionique. Ce nom vient de ce qu'il peut être construit en utilisant une algèbre qui est construite comme produit tensoriel des octonions avec eux-mêmes. Ce type de construction est analysé en détail par Hans Freudenthal et Jacques Tits dans leur construction du carré magique.
En physique[modifier]
Dans le cadre des théories de grande unification en physique des particules, le groupe E8 est parfois considéré comme groupe de jauge candidat dans la mesure où il contient d'une façon naturelle une série d'autres groupes de grande unifications souvent considérés. On peut le voir sous la succession d'inclusions
Par ailleurs, le groupe E8 apparait fréquemment en théorie des cordes et en supergravité. Dans la théorie des cordes hétérotiques une formulation fait apparaître 
(sous forme compacte) comme groupe de jauge. Par ailleurs, lorsque la supergravité maximale est compactifiée sur un tore de dimension 8 alors la théorie résultante en dimension trois possède unesymétrie globale E8 (c'est-à-dire la forme déployée, ou maximalement non-compacte). Il a été par la suite suggéré[réf. nécessaire] qu'une version discrète, notée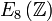 
, de ce groupe serait une symétrie, appelée dans ce contexte U-dualité, de la théorie M.
En novembre 2007, un physicien américain, Antony Garrett Lisi, dépose sur le site de publications scientifiques ArXiv un article très discuté sur une théorie unificatrice des forces basé sur le groupe E8.
Algèbre[modifier]
Diagramme de Dynkin[modifier]
Système de racines[modifier]
Dans la base formée par les racines simples , le système de racines de E8 est formé d'une part de toutes les permutations de
qui constitue le système de racines de et possède 
éléments (il faut rajouter les 8 générateurs du Cartan pour obtenir 120 qui est la dimension de 
).
Par ailleurs on doit ajouter à cela les 128 poids de la représentation spinorielle de 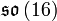. Toujours dans la même base, ceux-ci sont représentés par les vecteurs
tels que la somme de toutes les coordonnées soit paire. Ils sont au nombre de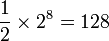 
.
On obtient donc 
racines, toutes de multiplicité 1. Par abus de langage on considère aussi parfois le vecteur nul comme une racine associée à la sous-algèbre de Cartan. Comme E8 est de rang 8, la racine nulle est alors de multiplicité 8. Ainsi au final on a bien décrit les 248 générateurs de l'algèbre .
Matrice de Cartan[modifier]
Représentations[modifier]
se distingue des autres algèbres de Lie de dimension finie par le fait que sa plus petite représentation non-triviale est la représentation adjointe.
La représentation fondamentale de E8 est de dimension 248.
Décodage du groupe [modifier]
Le 19 mars 2007, l'Institut américain des mathématiques (AIM) a annoncé que des chercheurs américains et européens et après quatre ans d'efforts et plus d'un siècle après sa découverte sont parvenus à décoder l'E8, l'une des structures mathématiques les plus complexes et les plus grandes. Le noyau dur du groupe de chercheurs est formé de sept mathématiciens, cinq Américains et deux Français : Jeffrey Adams de l'Université du Maryland, Dan Barbasch de Université Cornell, John Stembridge de l'Université du Michigan, Peter Trapa de l'Université de l'Utah, Marc van Leeuwen de l'Université de Poitiers, David Vogan du Massachusetts Institute of Technology et Fokko du Cloux de l'Université de Lyon1.
Selon Peter Sarnak, professeur de mathématiques à l'Université Princeton et président du comité scientifique de AIM, le décodage de ce groupe pourrait ouvrir la porte à d'autres innovations dans le domaine de la programmation informatique.
« Cette percée est importante non seulement pour faire avancer les connaissances mathématiques de base mais aussi pour faciliter les calculs par ordinateur permettant de résoudre des problèmes complexes, [...]. Le décodage de cette structure appelée E8 pourrait aussi très bien avoir des applications en mathématiques et physique qu'on ne découvrira pas avant plusieurs années. »
— Peter Sarnak, Le Monde, 19 mars 2007
Parmi les objets sous-jacents aux groupes de Lie, on trouve toutes sortes de figures géométriques telles que les sphères, les cônes, les cylindres dans l’espace à trois dimensions. Mais les choses se corsent lorsque l’on étudie ces objets dans des espaces de dimensions supérieures. « Comprendre et classer les structures a été critique pour comprendre des phénomènes dans de nombreux domaines des mathématiques incluant l’algèbre, la géométrie, la théorie des nombres ainsi que la physique et la chimie », commente Peter Sarnak, professeur de mathématique à l’université de Princeton et président du comité scientifique de l’AIM.
Ces calculs ont nécessité de nouvelles techniques mathématiques et des capacités de calcul des ordinateurs qui n'existaient pas il y a encore peu d'années, précisent les chercheurs. L’opération a pris 77 heures et a nécessité un supercalculateur doté de 200 Go de mémoire vive, et a produit un résultat de l’ordre de 60 Go dont la taille peut être comparée à 60 fois celle du génome humain. L’équipe attendait donc de trouver un supercalculateur capable d’effectuer les calculs lorsque Noam Elkies, un mathématicien de l’université Harvard a mis en évidence un moyen de découper le projet en éléments plus simples. Chaque élément produit un sous-ensemble du résultat et leur réunion permet de donner la solution complète au problème. À l’été 2006, trois membres de l’équipe, dont Fokko du Cloux, ont décomposé le programme en plusieurs éléments. Les calculs ont été réalisés sur une machine de l’université de Washington.
L’ordre de grandeur et la nature du calcul est à rapprocher du projet de séquençage du génome humain, indique le communiqué de presse diffusé par AIM. Alors que l’ensemble des informations du génome représente un volume de 1 Go, le résultat de l’E8 est environ 60 fois plus important avec des données hautement compressées. Écrit sur un papier, ce résultat couvrirait un espace équivalent à la taille de Manhattan.
Quelques chiffres sur le calcul de [modifier]
Quelques idées sur la taille du résultat final1 :
- Le résultat du calcul E8 est une matrice de 453 060 lignes et colonnes.
- La matrice comporte 205 263 363 600 éléments,
- Si chaque élément de cette matrice était écrit sur une surface de 2,5 cm2, la matrice aurait une dimension d’un carré de plus de 10 km de côté.
- Nombre de polynômes distincts : 1 181 642 979,
- nombre de coefficients dans les polynômes distincts : 13 721 641 221,
- plus grand coefficient : 11 808 808,
- polynôme ayant le plus grand coefficient : 152 q22 + 3472 q21 + 38 791 q20 + 293 021 q19 + 1 370 892 q18 + 4 067 059 q17 + 7 964 012 q16 + 11 159 003 q15 + 11 808 808 q14 + 9 859 915 q13 + 6 778 956 q12 + 3 964 369 q11 + 2 015 441 q10 + 906 567 q9 + 363 611 q8 + 129 820 q7 + 41 239 q6 + 11 426 q5 + 2 677 q4 + 492 q3 + 61 q2 + 3 q,
- valeur de ce polynôme pour q=1 : 60 779 787,
- polynôme ayant la plus grande valeur (lorsque q=1) découvert jusqu'à présent (mai 2007) : 1 583 q22 + 18 668 q21 + 127 878 q20 + 604 872 q19 + 2 040 844 q18 + 4 880 797 q17 + 8 470 080 q16 + 11 143 777 q15 + 11 467 297 q14 + 9 503 114 q13 + 6 554 446 q12 + 3 862 269 q11 + 1 979 443 q10 + 896 537 q9 + 361 489 q8 + 129 510 q7 + 41 211 q6 + 11 425 q5 + 2 677 q4 + 492 q3 + 61 q2 + 3 q,
- valeur pour ce polynôme pour q=1 : 62 098 473.
Notes et références[modifier]
- AIM math: Representations of E8 [archive]
Voir aussi[modifier]
Articles connexes[modifier]
- Groupe de Lie
- Algèbre de Lie
- Système de racines
- Diagramme de Dynkin
Liens externes[modifier]
- [pdf] Théorie de A. Garrett Lisi sur l'utilisation de E8 pour réunifier les différentes forces physiques et la physique quantique
- (fr) Groupe de Lie E8 : une clé pour la théorie des supercordes ?
- (en) Taille de certaines lignes de calcul du groupe E8
- (fr) Une solution mathématique aux dimensions démesurées Article de Techno-science.net
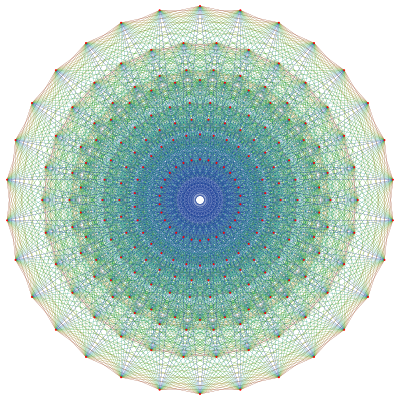
- [pdf] Représentation graphique de E8
- (fr) Garrett Lisi sur la théorie du Tout Conférence TED 2008 (VOST FR) www.ted.com
Portail des mathématiques
11:34 | Lien permanent | Commentaires (0) | 
| 
del.icio.us | 
| 
Digg | 
Facebook
Les commentaires sont fermés.