Algèbre enveloppante : Mathématique

D	L	M	M	J	V	S
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30

« Représentation d'algèbre de Lie | Page d'accueil | E8 (mathématiques) »

25/03/2011

Algèbre enveloppante

Cet article est une ébauche concernant l'algèbre.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Pour les articles homonymes, voir Algèbre (homonymie).

Source : http://fr.wikipedia.org/wiki/Alg%C3%A8bre_enveloppante

Livres : Algèbre enveloppante

En mathématiques, on peut construire l'algèbre enveloppante $U(mathfrak{g})$ d'une algèbre de Lie $mathfrak{g}$ . Il s'agit une algèbre unitaire qui permet de rendre compte de la plupart des propriétés de $mathfrak{g}$ .

Sommaire

[masquer]

Algèbres de Lie[modifier]

Article détaillé : Algèbre de Lie.

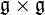Soit K un corps commutatif de caractéristique différente de 2. Une algèbre de Lie $mathfrak{g}$ sur K est un espace vectoriel muni d'une apllication bilinéaire $(x,y) mapsto [x,y]$ de $mathfrak{g}timesmathfrak{g}$ dans $mathfrak{g}$ qui vérifie les propriétés suivantes :

$forall x in mathfrak{g}, [x,x]=0$ ;
$forall x,y,z in mathfrak{g}, [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0$

Tout espace vectoriel $V$ peut être muni d'une structure d'algèbre de Lie, en posant $forall x,y in V, [x,y]=0$ . Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne. Un autre exemple, fondamental pour ce qui suit, est le suivant. Soit V un espace vectoriel sur K. L'espace vectoriel End(V) des endomorphismes de V peut être muni d'une structure d'algèbre de Lie, en posant : $[u,v]=ucirc v-vcirc u$ . On note également $mathfrak{gl}(V)$ l'algèbre de Lie ainsi obtenue. 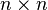Lorsque V est de dimension finie n, $mathfrak{gl}(V)$ s'identifie aux matrices de taille $ntimes n$ à coefficient dans K. 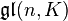On la note alors $mathfrak{gl}(n,K)$ .

La construction d'une algèbre enveloppante répond au problème réciproque : à partir d'une algèbre de Lie $mathfrak{g}$ , peut-on construire une algèbre associative dont le commutateur correspond au crochet de Lie de $mathfrak{g}$ ?

L'algèbre enveloppante[modifier]

Construction[modifier]

A partir de l'algèbre de Lie $mathfrak{g}$ , on peut construire le produit tensoriel $mathfrak{g} otimes mathfrak{g}$ et plus généralement $mathfrak{g}^{otimes n} = underbrace{mathfrak{g} otimes cdots otimes mathfrak{g}}_{n}$ . On note par convention $mathfrak{g}^{otimes 0}=K$ . On considère alors l'algèbre tensorielle de $mathfrak{g}$ , définie par $T(mathfrak{g})=K oplus mathfrak{g} oplus mathfrak{g}^{otimes 2} oplus cdots= sum_{n=0}^{infty} mathfrak{g}^{otimes n}$ . On note $σ$ l'application canonique de $mathfrak{g}$ dans $T(mathfrak{g})$ . 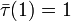L'algèbre tensorielle satisfait une propriété universelle : pour toute application linéaire $τ$ de $mathfrak{g}$ dans une algèbre avec unité A, il existe un unique morphisme d'algèbre $bar{tau}$ tel que $bar{tau}(1)=1$ et $tau = bar{tau} circ sigma$ .

Pour construire l'algèbre enveloppante, il faut encore tenir compte de la structure d'algèbre de Lie de $mathfrak{g}$ . On veut donc forcer $Xotimes Y-Yotimes X$ à être égal à $[X, Y]$ . Plus formellement, soit J l'idéal bilatère engendré par les $Xotimes Y-Yotimes X-[X,Y]$ , pour $X, Y in mathfrak{g}$ . L'algèbre enveloppante $U(mathfrak{g})$ est alors le quotient de $T(mathfrak{g})$ par l'idéalJ. 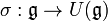L'injection canonique de $mathfrak{g}$ dans $T(mathfrak{g})$ passe au quotient et fournit alors un morphisme $sigma : mathfrak{g} rightarrow U(mathfrak{g})$ .

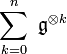Notons $U^n(mathfrak{g})$ l'image de $sum_{k=0}^n mathfrak{g}^{otimes k}$ dans $U(mathfrak{g})$ . Lorsque l'algèbre de Lie $mathfrak{g}$ est de dimension finie, $U^n(mathfrak{g})$ est un sous-espace vectoriel de dimension finie de $U(mathfrak{g})$ . Dans tous les cas, on a la filtration suivante : $U(mathfrak{g})=cup_{k=0}^{infty} U^k(mathfrak{g})$ .

Exemple Considérons l'algèbre de Lie abélienne K, de dimension 1. Dans ce cas, le crochet de Lie est identiquement nul. L'idéal J est alors engendré par les vecteurs $Xotimes Y - Yotimes X$ , pour $X, Y in K$ . On vérifie alors dans ce cas que $U(K) cong K[T]$ (l'algèbre des polynômes en une indéterminée).

Propriété universelle[modifier]

Comme pour l'algèbre tensorielle, on peut caractériser l'algèbre enveloppante de $mathfrak{g}$ par une propriété universelle :

Propriété universelle de l'algèbre enveloppante — Soit $varphi$ une application linéaire de $mathfrak{g}$ dans une algèbre associative avec unité A telle que

$varphi([X,Y])=varphi(X)varphi(Y)-varphi(Y)varphi(X)$ , pour tout $X, Y in mathfrak{g}$ . Alors il existe un unique morphisme d'algèbre $tilde{varphi} : U(mathfrak{g}) mapsto A$ tel que $tilde{varphi}(1)=1$ et $varphi = tilde{varphi} circ sigma$ .

Remarque L'unicité provient du fait que $U(mathfrak{g})$ est engendrée par 1 et $sigma(mathfrak{g})$ . L'existence s'obtient à partir de la propriété universelle de l'algèbre tensorielle.

Cette propriété universelle a une conséquence importante en théorie des représentations, à savoir toute représentation de $mathfrak{g}$ dans un espace vectoriel V s'étend de manière unique en un morphisme d'algèbre entre $U(mathfrak{g})$ et $E n d (V)$ .

Théorème de Poincaré-Birkhoff-Witt et ses conséquences[modifier]

Le théorème de Poincaré-Birkhoff-Witt(PBW) donne une base de l'algèbre enveloppante et ainsi permet de mieux en comprendre la structure. Pour en simplifier un peu l'énoncé, nous le donnons pour une algèbre de Lie de dimension finie.

Théorème de Poincaré-Birkhoff-Witt — L'application $sigma : mathfrak{g} mapsto U(mathfrak{g})$ est injective. Soit $X_1, ldots, X_n$ une base de $mathfrak{g}$ . Alors les monômes $X_1^{j_1}cdots X_n^{j_n}$ , $j_kgeq 0$ , forment une base de $U(mathfrak{g})$ .

Voici quelques conséquences importantes de PBW :

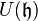Soit $mathfrak{h}$ une sous-algèbre de Lie de $mathfrak{g}$ . Alors $U(mathfrak{h})$ s'identifie à une sous-algèbre associative de $U(mathfrak{g})$ .
Supposons que $mathfrak{g}$ soit la somme directe de deux sous-algèbres : $mathfrak{g}=mathfrak{a} oplus mathfrak{b}$ . Alors l'algèbre $U(mathfrak{g})$ est isomorphe au produit tensoriel $U(mathfrak{a}) otimes U(mathfrak{b})$ .
Soit $K n$ l'algèbre de Lie abélienne de dimension n. Alors $U (K n)$ est isomorphe à l'algèbre de polynômes $K[T_1,ldots,T_n]$ .
Soit V un espace vectoriel. Tout morphisme d'algèbre de $U(mathfrak{g})$ dans $E n d (V)$ donne par restriction une représentation de $mathfrak{g}$ dans V. En tenant compte de la remarque de la partie précédente, cela fournit une équivalence de catégories entre la catégorie des représentations de $mathfrak{g}$ et celle des représentations de l'algèbre $U(mathfrak{g})$ .

Dans certains cas, il est possible de décrire explicitement l'algèbre enveloppante. Soit G un groupe de Lie réel, d'algèbre de Lie $mathfrak{g}_0$ . Notons $mathfrak{g}$ le complexifié de $mathfrak{g}_0$ . Soit $Xin mathfrak{g}_0$ . On construit alors l'opérateur différentiel $tilde{X}$ sur $C^{infty}(G)$ par :

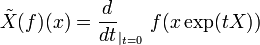$tilde{X}(f)(x)=frac{d}{dt}_{|_{t=0}} f(xexp(tX))$ , pour $fin C^{infty}(G)$ et $xin G$ . L'opérateur $tilde{X}$ est un exemple d'opérateur différentiel invariant à gauche (i.e. commutant avec les translations à gauche par des vecteurs de G). Notons D(G) l'ensemble des opérateurs différentiels invariants à gauche. On a donc une application $Xin mathfrak{g}_0 mapsto tilde{X}in D(G)$ . Cette application s'étend en une application de $mathfrak{g}$ dans D(G). Cette application définit par propriété universelle un morphisme d'algèbre de $U(mathfrak{g})$ dans D(G). Ce morphisme est un fait unisomorphisme. Ainsi l'algèbre enveloppante de $mathfrak{g}$ s'identifie avec l'algèbre des opérateurs différentiels invariants à gauche sur G.

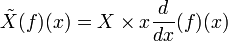Exemple Regardons le cas simple de l'algèbre de Lie $mathbb{C}$ . Le groupe de Lie $mathbb{R}^*$ a pour algèbre de Lie $mathbb{R}$ , qui a pour complexifié $mathbb{C}$ . Ici $C^{infty}(G)$ est l'espace usuel des fonctions $C^{infty}$ à valeurs dans $mathbb{C}$ . Ainsi, pour $Xin mathbb{R}$ , l'opérateur $tilde{X}$ est donné par $tilde{X}(f)(x)=xXf'(x)$ . Autrement dit, l'opérateur est donné par $tilde{X}(f)(x)=Xtimes xfrac{d}{dx}(f)(x)$ . D'autre part, un opérateur différentiel 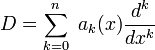$D=sum_{k=0}^n a_k(x)frac{d^k}{dx^k}$ sur G est invariant à gauche si et seulement si $a_k(x)=a_ktimes x^k$ . Ainsi, on a 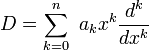$D=sum_{k=0}^n a_kx^kfrac{d^k}{dx^k}$ , ce qui identifie $D(mathbb{R}^*)$ avec $mathbb{C}[T]$ , qui est isomorphe à $U(mathfrak{mathbb{C}})$ comme nous l'avons déjà remarqué.

Représentation adjointe[modifier]

L'algèbre de Lie $mathfrak{g}$ agit sur elle-même via la représentation adjointe $ad : mathfrak{g} rightarrow mathfrak{gl}(mathfrak{g})$ définie par $a d (X)(Y) = [X, Y]$ , pour $X, Yin mathfrak{g}$ . Cette représentation s'étend en une représentation de $mathfrak{g}$ sur son algèbre enveloppante, via la formule $ad(X)(u)=Xotimes u-uotimes X$ , pour $Xin mathfrak{g}$ et $uin U(mathfrak{g})$ . Cette représentation laisse stable les sous-espaces $U^n(mathfrak{g})$ et donc aussi les quotients $U_{n+1}(mathfrak{g})=U^{n+1}(mathfrak{g})/U^n(mathfrak{g})$ . Lorsque $mathfrak{g}$ est de dimension finie, $U_n(mathfrak{g})$ est aussi de dimension finie. Cela fournit donc toute une famille de représentations de dimension finie de $mathfrak{g}$ .

L'algèbre symétrique[modifier]

Un autre quotient de l'algèbre tensorielle joue un rôle important : l'algèbre symétrique. Soit I l'idéal bilatère de $T(mathfrak{g})$ engendré par les vecteurs $Xotimes Y-Yotimes X$ . L'algèbre symétrique $S(mathfrak{g})$ est l'algèbre quotient $T(mathfrak{g})/I$ . C'est une algèbre associative et commutative. On note toujours $σ$ l'application canonique de $mathfrak{g}$ dans $S(mathfrak{g})$ . Comme pour l'algèbre enveloppante, l'algèbre symétrique satisfait une propriété universelle :

Propriété universelle de l'algèbre symétrique — Soit C une algèbre associative et commutative, avec unité. Pour toute application linéaire 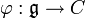$varphi : mathfrak{g} rightarrow C$ , il existe un unique morphisme d'algèbre $tilde{varphi} : S(mathfrak{g}) rightarrow C$ tel que $tilde{varphi}(1)=1$ et $varphi = tilde{varphi} circ sigma$ .

Les deux algèbres symétrique et enveloppante sont reliées par une application de symétrisation. En effet, on construit une application $Sym : S(mathfrak{g}) rightarrow U(mathfrak{g})$ comme suit :

$Sym(X_1cdots X_n) = frac{1}{n!} displaystylesum_{sin mathfrak{S}_n} X_{s(1)}cdots X_{s(n)},$ où $mathfrak{S}_n$ désigne le groupe des permutations de n éléments. En fait, l'application Sym est un isomorphisme linéaire de $S(mathfrak{g})$ sur $U(mathfrak{g})$ (la structure d'algèbre n'est pas conservée en général car $U(mathfrak{g})$ n'est pas commutative lorsque l'algèbre de Lie $mathfrak{g}$ n'est pas abélienne).

Structure d'anneau de l'algèbre enveloppante[modifier]

On suppode dans cette partie que le corps de base K est de caractéristique nulle.

Généralités[modifier]

L'algèbre enveloppante $U=U(mathfrak{g})$ est en particulier un anneau. L'étude de cette structure d'anneau est fondamentale en théorie des représentations. L'anneau U est sans diviseur de zéro (autrement dit le produit de deux éléments non nuls de U est également non nul). L'anneau U est noethérien : toute suite croissante d'idéaux est stationnaire. Cependant U n'est pasartinien : par exemple, l'idéal bilatère engendré par $mathfrak{g}$ contient l'idéal engendré par $mathfrak{g}^{otimes 2}$ , qui contient l'idéal engendré par $mathfrak{g}^{otimes 3}$ , etc.

Centre de l'algèbre enveloppante[modifier]

Le centre de l'algèbre enveloppante est $Z(U(mathfrak{g}))={uin U(mathfrak{g}) : uv=vu, forall vin U(mathfrak{g})}$ . En fait, comme $mathfrak{g}$ engendre $U(mathfrak{g})$ , on a aussi $Z(U(mathfrak{g}))={u in U(mathfrak{g}) : uX=Xu, forall X in mathfrak{g}}={u in U(mathfrak{g}) : ad(X)(u)=0, forall X in mathfrak{g}}$ . Même lorsque l'algèbre de Lie $mathfrak{g}$ a un centre trivial, l'algèbre enveloppante peut avoir un centre non trivial (voire gros).

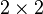Exemple Soit $mathfrak{g}=mathfrak{sl}(2,mathbb{C})$ l'algèbre de Lie des marices complexes de taille $2times 2$ , de trace nulle. Une base de $mathfrak{g}$ est donnée par les matrices suivantes :

$H=left(begin{array}{cc} 1 & 0 0 & -1 end{array}right), E=left(begin{array}{cc} 0 & 1 0 & 0end{array}right), F=left(begin{array}{cc} 0 & 0 1 & 0end{array}right).$

Le vecteur suivant est un élément du centre $Z(U(mathfrak{g}))$ : $Omega=frac{1}{2}Hotimes H+Eotimes F+Fotimes E$ . Plus précisement, on peut démontrer que $Z(U(mathfrak{g}))=mathbb{C}[Omega]$ . Autrement dit, le vecteur $Ω$ engendre l'algèbre $Z(U(mathfrak{g}))$ . Ceci est un cas particulier d'un résultat de Harish-Chandra et d'un résultat de Chevalley sur le centre des algèbres enveloppantes desalgèbres de Lie semi-simples.

L'algèbre $Z(U(mathfrak{g}))$ joue un rôle fondamental en théorie des représentations. En effet, le lemme de Schur affirme que tout opérateur qui commute à une représentation irréductible d'une algèbre de Lie complexe est une homothétie. D'après ce qui précède, si $(π, V)$ est une représentation irréductible de l'algèbre de Lie complexe $mathfrak{g}$ , alors l'opérateur $π(Z)$ associé à n'importe quel vecteur Z de $Z(U(mathfrak{g}))$ commute à tous les $π(X)$ , $X in mathfrak{g}$ . Donc $π(Z)$ est une homothétie. Ceci est vrai pour tout Z dans le centre de l'algèbre enveloppante. On obtient ainsi un caractère du centre, c'est-à-dire un morphisme d'algèbre de $Z(U(mathfrak{g}))$ dans $mathbb{C}$ , que l'on appelle le caractère infinitésimal de la représentation $π$ . Ainsi l'étude des caractères du centre de l'algèbre enveloppante fournit des informations importantes pour l'étude des représentations irréductibles de $mathfrak{g}$ .

Idéaux de l'algèbre enveloppante[modifier]

Toute représentation de $mathfrak{g}$ s'étend canoniquement en une représentation de $U(mathfrak{g})$ , c'est-à-dire un morphisme d'algèbre $pi : U(mathfrak{g}) rightarrow End(V)$ . Le noyau de $π$ est un idéal de $U(mathfrak{g})$ . D'autre part, si la représentation $(π, V)$ est irréductible (ou même seulement cyclique), il existe un vecteur v de V tel que l'application $pi :uin U(mathfrak{g}) mapsto pi(u)(v)in V$ , soit surjective. La représentation V s'identifie alors avec le quotient de $U(mathfrak{g})$ par le noyau de cette application. Ces deux faits montrent l'importance de comprendre les idéaux de $U(mathfrak{g})$ .

Références[modifier]

N. Bourbaki, Groupes et algèbres de Lie
Jacques Dixmier, Algèbres enveloppantes Éditions Jacques Gabay, Paris, 1996. ISBN 2-87647-014-4
James E. Humphreys, Introduction to Lie Algebras and Representation Theory, Second printing, revised. Graduate Texts in Mathematics, 9. Springer-Verlag, New York, 1978. ISBN 0-387-90053-5
Nathan Jacobson, Lie algebras, Republication of the 1962 original. Dover Publications, Inc., New York, 1979. ISBN 0-486-63832-4
Anthony Knapp, Representation theory of semisimple groups: an overview based on examples, Princeton University Press, 2001. Reprint of the 1986 original. ISBN 0-691-09089-0

Voir aussi[modifier]

Portail des mathématiques

Catégorie : Algèbre de Lie | [+]

Les commentaires sont fermés.

Mathématique

Cours, définitions, Vidéos, théorèmes, exercices, corrigés, livres sur les mathématiques, Livres Rares, Livres anciens de mathématiques

Recherchez sur le site (cours, livres, Agregation, etc.)

Liens utiles

Rechercher

CODE PROMO

Liens mathématiques divers

Livres en pdf

Cours

Documents Mathématiques

Novembre 2024

Notes récentes

Archives

Catégories

Derniers weblogs mis à jour

Liens Sites Amis

25/03/2011

Algèbre enveloppante

Algèbre enveloppante

Sommaire

Algèbres de Lie[modifier]

L'algèbre enveloppante[modifier]

Construction[modifier]

Propriété universelle[modifier]

Théorème de Poincaré-Birkhoff-Witt et ses conséquences[modifier]

Représentation adjointe[modifier]

L'algèbre symétrique[modifier]

Structure d'anneau de l'algèbre enveloppante[modifier]

Généralités[modifier]

Centre de l'algèbre enveloppante[modifier]

Idéaux de l'algèbre enveloppante[modifier]

Références[modifier]

Voir aussi[modifier]