Représentation d'algèbre de Lie

 

Aller à :Navigation,rechercher

Cet article est une ébauche concernant l'algèbre. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Source : http://fr.wikipedia.org/wiki/Repr%C3%A9sentation_d'alg%C3...

Livres : Représentation d'algèbre de Lie

En mathématiques, une représentation d'une algèbre de Lie est une façon d'écrire cette algèbre comme une algèbre de matrices, ou plus généralement d'endomorphismes d'un espace vectoriel, avec le crochet de Lie donné par le commutateur.

Sommaire

 [masquer]

• 1 Algèbres de Lie
• 2 Représentations
  • 2.1 Définitions
  • 2.2 Exemples
  • 2.3 Constructions de représentations
• 3 Lien avec les représentations de l'algèbre enveloppante
  • 3.1 L'algèbre enveloppante d'une algèbre de Lie
  • 3.2 Représentations d'une algèbre de Lie vs Représentations de son algèbre enveloppante
  • 3.3 Induction
• 4 Lien avec les représentations des groupes de Lie
• 5 Catégorie de modules
• 6 Références
• 7 Voir aussi

Algèbres de Lie[modifier]

Article détaillé : Algèbre de Lie.

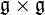Soit K un corps commutatif de caractéristique différente de 2. Une algèbre de Lie  sur K est un espace vectoriel muni d'une apllication bilinéaire  de  dans qui vérifie les propriétés suivantes :

1. ;
2. 

Tout espace vectoriel V peut être muni d'une structure d'algèbre de Lie, en posant . Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne. Un autre exemple, fondamental pour ce qui suit, est le suivant. Soit V un espace vectoriel sur K. L'espace vectoriel End(V) des endomorphismes de V peut être muni d'une structure d'algèbre de Lie, en posant : . On note également  l'algèbre de Lie ainsi obtenue. Lorsque V est de dimension finie n, s'identifie aux matrices de taille 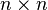 à coefficient dans K. On la note alors .

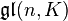Une sous-algèbre de Lie de  est un sous-espace vectoriel  de  stable par le crochet de Lie, i.e. tel que .

Exemples

• Si  est une algèbre de Lie abélienne alors tout sous-espace vectoriel de  est automatiquement une sous-algèbre de Lie.
• Le sous-espace vectoriel de 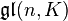 formé des matrices de trace nulle est une sous-algèbre de Lie de  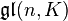car tr(AB) = tr(BA) pour toutes matrices A et B. Cette sous-algèbre est notée .

Un idéal d'une algèbre de Lie  est un sous-espace vectoriel  de  tel que . Tout idéal d'une algèbre de Lie est en particulier une sous-algèbre de Lie (mais la réciproque est fausse).

Exemples

• Si  est une algèbre de Lie abélienne alors tout sous-espace vectoriel de  est automatiquement un idéal.
• La sous-algèbre de Lie  de 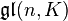 est un idéal.

Un morphisme entre deux algèbres de Lie  et  est une application linéaire 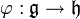 telle que . Le noyau d'un morphisme d'algèbres de Lie est alors un idéal de l'algèbre de Lie source et l'image une sous-algèbre de Lie de l'algèbre de Lie but. Un isomorphisme entre deux algèbres de Lie est morphisme d'algèbre de Lie qui est un isomorphisme d'espace vectoriel.

Exemples

• Si  est une sous-algèbre de Lie de  alors l'inclusion de  dans  est un morphisme d'algèbre de Lie, de noyau nul et d'image .
• Si  est un idéal de  alors il existe une unique structure d'algèbre de Lie sur l'espace vectoriel quotient 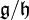 telle que la projection canonique  soit un morphisme d'algèbre de Lie. Le noyau de p est alors  et son image 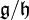. L'algèbre de Lie  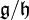ainsi définie s'appelle l'algèbre de Lie quotient de  sur . Par exemple l'algèbre de Lie quotient  est isomorphe à l'algèbre de Lie abélienne K.

Représentations[modifier]

Définitions[modifier]

Une représentation de l'algèbre de Lie  dans un espace vectoriel V est la donnée d'un morphisme . Autrement dit, π est une application linéaire qui vérifie également . On note (π,V) cette représentation ou simplement V lorsqu'il n'y a pas d'ambiguité possible sur π. On dit aussi que V est un -module ou simplement un module. On note parfois  au lieu de π(x)(v) l'action de l'élément  sur le vecteur .

Une représentation (π,V) est dite fidèle si le morphisme π est injectif. Dans ce cas, l'algèbre de Lie  peut être vue comme une sous-algèbre de Lie de .

Une sous-représentation d'une représentation (π,V) de  est la donnée d'un sous-espace vectoriel W de V stable par l'action de , i.e. tel que . En particulier, pour qu'une droite vectorielle D engendrée par un vecteur v soit stable il faut et il suffit que v soit un vecteur propre commun à tous les endomorphismes π(x). Une représentation (π,V) est irréductible si elle n'admet aucune sous-représentation propre, c'est-à-dire autre que les sous-espaces {0} et V. En particulier toute représentation (π,V) de dimension 1 est irréductible, car dans ce cas les seuls sous-espaces vectoriels de V sont précisement {0} et V. Soit V' une sous-représentation de (π,V). La représentation quotientest la représentation  de  dans l'espace quotient V / V' définie par .

Un morphisme entre deux représentations (π,V) et (π',V') d'une même algèbre de Lie  est la donnée d'une application linéaire  qui commute à l'action de , c'est-à-dire telle que . Lorque  est un isomorphisme d'espace vectoriel, on dit que les deux représentations sont isomorphes. L'ensemble de tous les morphismes entre les représentations (π,V) et (π',V') forme un espace vectoriel, noté .

Le lemme de Schur est un résultat important pour la compréhension de cet espace . En voici l'énoncé :

Lemme de Schur — 

• Soient V et V' deux représentations irréductibles d'une algèbre de Lie . Soit . Alors  est soit l'application nulle soit un isomorphisme. En particulier, si V et V' ne sont pas isomorphes, .
• Supposons ici que le corps K soit algébriquement clos. Soit V une représentation irréductible de dimension finie de . Alors tout morphisme  est un multiple de l'identité. En d'autres termes, .

Remarques

• Le premier point du lemme de Schur résulte du fait que  est une sous-représentation de V et  une sous-représentation de V'.
• Le deuxième point du lemme de Schur résulte du fait que tout endomorphisme d'un espace vectoriel de dimension finie admet au moins une valeur propre λ sur un corps algébriquement clos. Par conséquent  est un morphisme de V dans V qui n'est pas un isomorphisme. D'après le premier point, il s'agit donc de l'application nulle, i.e. . Ce résultat est encore valable en dimension infinie mais nécessite la puissance du théorème spectral.
• Le deuxième point du lemme de Schur est faux pour un corps non algébriquement clos. Supposons par exemple . Considérons la représentation (π,V) donnée par la formule 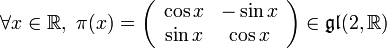. On vérifie que (π,V) est une représentation irréductible de l'algèbre de Lie abélienne . Considérons y = 45^o et posons . Comme l'algèbre de Lie  est abélienne,  est un morphisme de V dans V. On peut d'ailleurs vérifier que  est bien un isomorphisme. Cependant n'est pas un multiple de l'identité. Remarquons à ce propos que  n'a pas de valeurs propres réelles (ce qui explique pourquoi la preuve du deuxième point du lemme n'est pas valable dans ce cas).

Exemples[modifier]

• Une représentation d'une algèbre de Lie abélienne  est une application linéaire à valeurs dans un sous-espace commutatif de l'espace des endomorphismes d'un espace vectoriel V. Par exemple, si V est de dimension fini, on peut représenter  par des matrices diagonales (qui commutent entre elles).
• La représentation triviale de  dans un espace vectoriel V est la représentation π définie par .
• Si , on définit la représentation naturelle de  comme la représentation  définie par 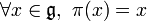. Plus généralement la représentation naturelle d'une sous-algèbre de Lie  de 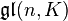 est définie comme l'inclusion de  dans 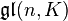. Elle est donc à valeurs dans Kⁿ.
• La représentation adjointe d'une algèbre de Lie  est la représentation  définie par .
• Soit  l'algèbre de Lie abélienne de dimension 1, définie sur . Considérons l'espace . On définit une représentation de  dans V par la formule , où .

Constructions de représentations[modifier]

• Somme directe : soient (π,V) et (π',V') deux représentations de . On définit la représentation somme directe  dans l'espace vectoriel 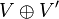 par la formule . Dans ce cas,  et  sont des sous-représentations de .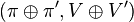
• Produit tensoriel : soient (π,V) et (π',V') deux représentations de . On définit la représentation produit tensoriel  dans l'espace vectoriel 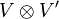 par la formule .
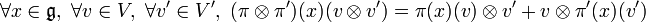• Contragrédiente : soit (π,V) une représentation de . On définit la représentation contragrédiente π ^* dans l'espace vectoriel dual V ^* par la formule .
• Espace des morphismes : soient (π,V) et (π',V') deux représentations de . Nous avons vu comment définir l'espace vectoriel  des morphimes de V dans V'. On définit une représentation encore notée π de  sur cet espace par la formule .
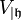• Restriction à une sous-algèbre de Lie : soit (π,V) une représentation de . Soit  une sous-algèbre de Lie de . Alors  est une représentation de , appelée la restriction de (π,V) à . On la note parfois  par abus de notations.

Une représentation de  est indécomposable si elle n'est pas isomorphe à la somme directe de deux sous-représentations propres. En particulier, toute représentation irréductible est indécomposable, mais la réciproque est fausse. Une représentation est semi-simple (ou complétement réductible) si elle est isomorphe à une somme directe de sous-représentations irréductibles (éventuellement en nombre infini). Une représentation indécomposable et semi-simple est nécessairement irréductible.

Exemples:

• Soit  l'algèbre de Lie abélienne de dimension 1 sur le corps . On définit une représentation π de  dans  par la formule . Cette représentation n'est pas irréductible. Par exemple la droite D₁ engendrée par le vecteur 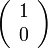 est stable, tout comme la droiteD₂ engendrée par le vecteur . Il s'agit donc de deux sous-représentations de π, irréductibles car de dimension 1. Or on a . Donc la représentation π est semisimple.
• Avec les notations de l'exemple précédent, on peut aussi considérer la représentation π' dans  définie par la formule . A nouveau la droiteD₁ est un sous-espace stable. Donc la représentation π' n'est pas irréductible. Plus généralement, on peut vérifier que D₁ est la seule droite stable et donc la seule sous-représentation de π'. Ainsi π' est indécomposable.
• Gardons toujours les mêmes notations. On définit la représentation π'' de  dans  par la formule . On peut vérifier qu'il n'y a pas de droites stables par la représentation π''. En d'autres termes, π'' est irréductible.

Ces trois exemples traduisent le fait qu'une matrice réelle peut être soit diagonalisable, soit trigonalisable mais pas diagonalisble, ou ne possède pas de valeurs propres réelles. On voit ainsi que la notion de représentation d'une algèbre de Lie généralise la notion classique de réduction des endomorphismes.

Lien avec les représentations de l'algèbre enveloppante[modifier]

L'algèbre enveloppante d'une algèbre de Lie[modifier]

Article détaillé : Algèbre enveloppante.

Soit A une algèbre associative avec unité. Alors il existe sur A une structure d'algèbre de Lie pour laquelle le crochet de Lie est donné par la formule . On note parfois A_L cette algèbre de Lie. Ainsi toute algèbre associative fournit une algèbre de Lie. Nous avons vu que  est un exemple de cette construction. Peut-on donner une réciproque à ce résultat ? Peut-on construire une algèbre associative à partir d'une algèbre de Lie. Cette idée conduit à la notion d'algèbre enveloppante d'une algèbre de Lie.

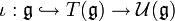Soit  une algèbre de Lie sur K. Soit  l'algèbre tensorielle de . Soit J l'idéal bilatère de  engendré par les tenseurs  pour tous x ety de . L'algèbre enveloppante de  est l'algèbre associative unitaire définie comme le quotient . On la note . La composition  s'appelle l'application canonique de  dans son algèbre enveloppante. En tant qu'algèbre,  est engendrée par 1 et l'image . De plus, ι est un morphisme d'algèbre de Lie de  dans . L'algèbre enveloppante d'une algèbre de Lie satisfait la propriété universelle suivante :

Propriété universelle de l'algèbre enveloppante —  Soit A une algèbre associative avec une unité. Soit  un morphisme d'algèbres de Lie de  dans A_L. Alors il existe un unique morphisme d'algèbres associatives Φ de  dans A tel que Φ(1) = 1 et .

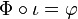Exemple:

• Si  est une algèbre de Lie abélienne, alors son algèbre enveloppante s'identifie à son algèbre symétrique , qui elle même s'identifie (après choix d'une base) à une algèbre de polyômes. En particulier,  est isomorphe à l'algèbre des polynômes à une indeterminée K[X].

Représentations d'une algèbre de Lie vs Représentations de son algèbre enveloppante[modifier]

Soit (π,V) une représentation de . Comme  est une algèbre associative avec unité, la propiété universelle de  implique qu'il existe un unique morphisme d'algèbres  telle que 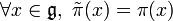. Cette opération permet donc de passer d'une représentation d'une algèbre de Lie à un morphisme d'algèbres associatives. Réciproquement, tout morphisme d'algèbres associatives  donne par restriction à  un morphisme d'algèbres de Lie, c'est-à-dire à une représentation de . Ce principe s'interprète comme une équivalence de catégories entre la catégorie des représentations d'une algèbre de Lie donnée et la catégorie des représentations de son algèbre enveloppante.

Ce nouveau point de vue est important car il permet de considérer de nouveaux objets fondamentaux. Le premier d'entre eux est l'annulateur d'une représentation. Soit (π,V) une représentation de . Notons encore par la lettre π la représentation de  qu'il s'en déduit. Alors l'annulteur de V est l'ensemble . C'est un idéal bilatère de  car π est un morphisme d'algèbre. Tout idéal qui est l'annulateur d'une représentation irréductible de  s'appelle un idéal primitif.

Soit (π,V) une représentation de . Notons encore par la lettre π la représentation de  qu'il s'en déduit. Pour tout v dans V, l'ensemble  définit une sous-représentation non nulle de V. Lorsque V est irréductible, on a donc . Plus généralement, une représentation V est dite cyclique s'il existe  tel que . Le vecteur v est appelé un vecteur cyclique. Une représentation V est irréductible si et seulement si tout vecteur non nul de V est cyclique. Une représentation Vest dite de type fini s'il existe un nombre fini de vecteurs  de V tels que . Une représentation irréductible est donc de type finie. Soit V une représentation cyclique et soit v un vecteur cyclique. On définit alors une application  par la formule . Le noyau de  est l'annulateur de v, noté Ann(v). Il s'agit d'un idéal à gauche de . Comme V est cyclique, l'image de  est égale à tout V. On en déduit donc que . Ainsi toute représentation cyclique (et en particulier toute représentation irréductible) apparaît comme un quotient de l'algèbre enveloppante de . De plus, lorsque V est irréductible l'idéal Ann(v)est maximal. Ainsi la classification des représentations irréductibles de  est équivalente à la classification des idéaux à gauche maximaux de son algèbre enveloppante.

Exemple Considérons l'algèbre de Lie commutative . Identifions son algèbre enveloppante avec l'anneau de polynômes . Cet anneau est principal et donc ses idéaux sont engendrés par un unique polynôme. De plus, si un polynôme P(X) peut se décomposer sous la forme P(X) = Q(X)(X − a), alors l'idéal (P) engendré par P est contenu dans l'idéal (X −a) engendré par X − a. Le théorème de d'Alembert-Gauss implique alors que les idéaux maximaux de  sont les idéaux de la forme (X − a), pour a décrivant tout . Le quotient  correspondant est alors isomorphe à  et l'action de  est donnée par  et 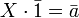. Regardons à présent le quotient  où P(X) = (X − a)(X − b). Si 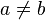, le quotient est une représentation semi-simple, somme directe des deux représentations irréductibles  et . La situation est fondamentalement différente lorsque a = b. Dans ce cas, le quotient est un espace vectoriel de dimension 2 sur lequel l'opérateur donné par la multiplication par X − a est nilpotent d'indice 2. En termes de représentation de l'algèbre de Lie , ce quotient correspond à la représentation donnée par la formule , qui est indécomposable mais pas irréductible.

Induction[modifier]

Soit  une algèbre de Lie. Soit  une sous-algèbre de Lie de . Soit (π,V) une représentation de . Nous avons vu que nous pouvons obtenir une représentation de  par restriction. La notion d'algèbre enveloppante va donner un moyen simple de considérer le problème réciproque. Soit donc (π',V') une représentation de , que l'on voit comme une représentation de son algèbre enveloppante 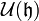. Une conséquence du théorème de Poincaré-Birkhoff-Witt est que  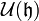apparaît comme une sous-algèbre de . D'autre part,  fournit une représentation de  en faisant agir  par multiplication à gauche sur les tenseurs. On construit alors la représentation . On l'appelle la représentation induite de  à  par (π',V').

Lien avec les représentations des groupes de Lie[modifier]

Dans cette partie, le corps K est  (ou ). Un groupe de Lie G est une variété différentielle réelle (ou complexe) munie de deux applications  et lisses (ou holomorphes) telles que 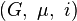 soit un groupe. Le corps K lui-même est un groupe de Lie commutatif. Le groupe GL(n,K) des matrices inversibles de taille n est un autre exemple de groupes de Lie. Un morphisme de groupes de Lie est un morphisme de groupes différentiable (ou holomorphe). Une représentation de dimension finie du groupe de LieG est un morphsime de G dans GL(n,K).

Les groupes de Lie sont reliés aux algèbres de Lie. En effet, l'espace tangent à un groupe de Lie G en l'identité est une algèbre de Lie de dimension finie, appelée algèbre de Lie du groupe G et notée . Par exemple, l'algèbre de Lie de K est K lui-même ; l'algèbre de Lie de GL(n,K) est 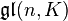. Comme l'algèbre de Lie du groupe de Lie G est l'espace tangent en l'identité, elle ne dépend en fait que de la composante connexe de l'identité. Ainsi par exemple, le groupe  des matrices réelles de déterminant strictement positif a la même algèbre de Lie que . Par contre, à isomorphisme près, il existe un unique groupe de Lie connexe et simplement connexe ayant une algèbre de Lie (de dimension finie) donnée.

Comme tout morphisme 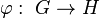 entre groupes de Lie est par hypothèse différentiable, il induit une application entre les algèbres de Lie sous-jacentes 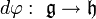. Cette application  est en fait un morphisme d'algèbres de Lie. En particulier, pour H = GL(n,K), toute représentation d'un groupe de Lie G donne naissance à une représentation de dimension finie de son algèbre de Lie . Réciproquement, toute représentation de dimension finie d'une algèbre de Lie  provient d'une représentation de l'unique groupe de Lie simplement connexe ayant pour algèbre de Lie .

Remarque Il existe des notions plus fortes de représentations de groupes de Lie permettant d'étendre la théorie à la dimension infinie, tout en conservant un analogue de ce dernier résultat. Il s'agit par exemple de représentations admissibles et de la notion de 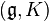-modules.

Catégorie de modules[modifier]

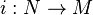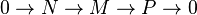Soit  une algèbre de Lie. L'ensemble de tous les -modules (ou de manière équivalente de toutes les représentations de ) forme une catégorie, notée . Cette catégorie estabélienne. En particulier, on peut considérer des suites exactes de modules. Une suite exacte dans  est la donnée de trois modules M, N, P et de deux morphismes  injectif et  surjectif. On note  une telle suite. Un module P est projectif si toute suite exacte  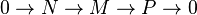est scindée, c'est-à-dire s'il existe un morphisme  tel que . Une définition équivalente est la suivante : le module P est projectif si pour tout morphisme surjectif 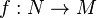 et tout morphisme  il existe un unique morphisme  tel que . De manière duale, un module I est injectif si toute suite exacte  est scindée. Une définition équivalente est la suivante : le module I est injectif si pour tout morphisme injectif 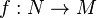 et tout morphisme  il existe un unique morphisme  tel que .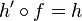

Comme tout module est aussi un module sur l'anneau , on peut reprendre les notions générales de modules sur un anneau. Un module M est de longueur fini s'il existe une suite finie de sous-modules  telle que les quotients successifs M_{i + 1} / M_i soient des modules irréductibles. Une telle suite s'appelle unesuite de Jordan-Hölder de M. Pour un module de longueur finie, la classe d'isomorphismes des quotients ne dépend que du module M. En particulier, l'entier n ne dépend que du module M et est appelé la longueur du module M. Par exemple, tout module irréductible est de longueur 1, toute somme directe de deux modules irréductibles est de longueur 2.

Un module M est artinien si toute suite décroissante de sous-modules  est stationnaire. Par exemple, tout module de dimension finie est artinien. Un module M est noethérien si toute suite croissante de sous-modules  est stationnaire. Comme l'algèbre enveloppante  est un anneau noethérien, un module M est noethérien si et seulement s'il est de type fini. Un module est de longueur fini si et seulement s'il est noethérien et artinien.

Exemple: Un module de dimension finie est toujours noethérien et artinien, et est donc toujours de longueur fini. Ceci n'est plus valable en dimension infinie, même pour une algèbre de Lie abélienne. Supposons par exemple que . Considérons le module  où l'action de  est donnée par la multiplication par le scalaire z. L'action de  est donc donnée par la multiplication à gauche. Ainsi tout idéal à gauche est un sous-module de L. Notons (P) l'idéal engendré par le polynôme P. Soit une suite infinie de nombre complexes. On a alors la suite décroissante suivante : . C'est une suite non stationnaire de sous-modules, dont les quotients successifs sont des modules irréductibles (car de dimension 1). Ainsi L n'est pas artinien et n'est pas de longueur finie. Notons que L est noethérien car c'est un module de type fini (en fait cyclique, engendré par le polynôme constant 1).

Une sous-catégorie pleine de  est artinienne (respectivement noethérienne) si tous ses objets sont des modules artiniens (respectivement noethériens). Dans une sous-catégorie pleine de  artinienne et noethérienne tout objet est de longueur finie. Une sous-catégorie pleine de  a assez de projectifs si pour tout objet M de la sous-catégorie il existe un module projectif P dans la sous-catégorie et un morphisme surjectif de P sur M. Elle a assez d'injectifs si pour tout objet M de la sous-catégorie il existe unmodule injectif I dans la sous-catégorie et un morphisme injectif de M dans I.

Références[modifier]

• N. Bourbaki, Éléments de mathématique, Groupes et algèbres de Lie, Chapitre 1, Springer, 2007 (ISBN 978-3-540-35335-5)
• Jacques Dixmier, Algèbres enveloppantes, Jacques Gabay, 1996 (ISBN 2-87647-014-4)
• Brian Hall, Lie Groups, Lie Algebras, and Representations, Springer, 2003 (ISBN 978-0-387-40122-5)
• James Humphreys, Introduction to Lie Algebras and Representation Theory, Second printing, revised. Graduate Texts in Mathematics, 9. Springer, 1978 (ISBN 0-387-90053-5)
• Nathan Jacobson, Lie algebras, Republication of the 1962 original, Dover, 1979 (ISBN 0-486-63832-4)

 

Voir aussi[modifier]

• Représentation de groupe
• Représentation d'un groupe de Lie
• Représentations d'un groupe fini

•  Portail des mathématiques

Catégories : Algèbre de Lie | Théorie des représentations des groupes de Lie | [+]