Pour compléter le livre de Cédric Villani "Théorème Vivant" Chapitre 2 p17 Amortissement Landau

Amortissement LANDAU 

"En physique, l’amortissement Landau, du nom de son découvreur¹, le physicien russe Lev Davidovich Landau, est le phénomène d'amortissement (décroissance exponentielle en fonction du temps) des oscillations longitudinale...."

Lire la suite : 

http://fr.wikipedia.org/wiki/Amortissement_Landau

LIVRE Vorlesungen über Gastheorie BOLTZMANN, LUDWIG

Vorlesungen über Gastheorie

BOLTZMANN, LUDWIG

 

Détails bibliographiques

 

Titre : Vorlesungen über Gastheorie

Éditeur : Leipzig: J.A. Barth, 1896, Leipzig

Date d'édition : 1896

Reliure : Hardcover

Edition : First Edition

Description :

2 vols. FIRST EDITION. 8 vo. Orig. printed cloth, gilt top edges. viii, 204; x, 265, (4, pub. ads) pp. Figs. in the text. The first volume with the stamps of Zeiss Bibliothek in a number of places. Minor discoloration on lower spine and lower front cover of vol. one from removed taped label with partial loss of printed letters on the front cover and to the edge of the brown front pastedown; otherwise a clean, very good set in the original binding. "In 1872, the Austrian physicist Ludwig Boltzmann (1844-1906) derived the transport equation for distribution of velocity among the molecules of a gas. This equation, which is so important in the kinetic theory of gases, had been previously derived by Maxwell, but the form in which Boltzmann derived it led him immediately to the concept of entropy as related to the probability of various velocity distributions among an assembly of gas molecules. This major contribution and many others that Boltzmann made to the kinetic theory of gases were summarized in his masterpiece of theoretical physics, 'Vorlesungen über Gastheorie'. This work can rightly be considered the peak of development achieved in the modern kinetic theory of gases." (Stanitz, Sources of Science & Technology, no.79). N° de réf. du libraire 000047

 

EN SAVOIR PLUS ou Commander

An Introduction to the Theory of the Boltzmann Equation Stewart Harris - broché

An Introduction to the Theory of the Boltzmann Equation

Stewart Harris - broché

EAN	978-0486438313
Editeur	Dover Pubns
Hauteur	21.59 cm
Langues	English
Largeur	1.91 cm
Longueur	14.61 cm
Poids	0.11 kg
Divers
Détails Techniques	- Illustrations : Non - Publisher's note : This introductory graduate-level course for students of physics and engineering features detailed presentations of Boltzmann's equation, including applications using both Boltzmann's equation and the model Boltzmann equations developed within the text. It emphasizes physical aspects of the theory and offers a practical resource for researchers and other professionals. 1971 edition.
Nombre de pages	221

Pour commander

En savoir plus

 

LIVRE Stochastic Numerics for the Boltzmann Equation, Springer Series in Computational Mathematics Serge J. Rjasanow, Wolfgang Wagner - relié

Stochastic Numerics for the Boltzmann Equation, Springer Series in Computational Mathematics

Serge J. Rjasanow, Wolfgang Wagner - relié

EAN	978-3540252689
Editeur	Springer Verlag
Hauteur	23.50 cm
Langues	English
Largeur	1.91 cm
Longueur	15.24 cm
Poids	0.50 kg
Divers
Détails Techniques	- Illustrations : Non
Nombre de pages	256

 

En savoir plus

Commander

 

 

 

 

Direct Methods for Solving the Boltzmann Equation and Study of Nonequilibrium Flows, Fluid Mechanics and Its Applications V. V. Aristov - relié - janvier 2001

Direct Methods for Solving the Boltzmann Equation and Study of Nonequilibrium Flows, Fluid Mechanics and Its Applications

V. V. Aristov - relié - janvier 2001

EAN	978-0792368311
Date de parution	janvier 2001
Editeur	Kluwer Academic Pub
Hauteur	24.13 cm
Langues	English
Largeur	1.91 cm
Longueur	15.88 cm
Poids	0.61 kg
Divers
Détails Techniques	- Illustrations : Non
Nombre de pages	294

 

Pour commander

En savoir plus

LIVRE The lattice boltzmann equation Sauro Succi (Auteur) - relié. Paru en 06/2001

Auteur	Sauro Succi
Editeur	Oxford Press Libri
Date de parution	juin 2001
ISBN	0198503989
EAN	978-0198503989

 

En savoir plus

Commander

 

Pour compléter le livre de Cédric Villani "Théorème Vivant" Chapitre 1 p14 L'équation de Boltzmann

Équation de Boltzmann

"L'équation de Boltzmann (1872) est une équation intégro-différentielle de la théorie cinétique qui décrit l'évolution d'un gaz peu dense hors d'équilibre. Elle permet notamment de démontrer lethéorème H, et d'étudier la relaxation du gaz d'un état d'équilibre local¹ vers l'équilibre global caractérisé par la distribution de Maxwell des vitesses.

La première solution analytique complète..."

Lire la suite : http://fr.wikipedia.org/wiki/%C3%89quation_de_Boltzmann

 

 

VIDEO Cédric Villani - La meilleure et la pire des erreurs de Poincaré

Cédric Villani - La meilleure et la pire des... par CIJM

Courbe elliptique

"En mathématiques, une courbe elliptique est un cas particulier de courbe algébrique, munie entre autres propriétés d'une addition géométrique sur ses points.

Les courbes elliptiques ont de nombreuses applications dans des domaines très différents des mathématiques : elles interviennent ainsi en mécanique classique dans la description du mouvement des toupies, en théorie des nombres dans la preuve du dernier théorème de Fermat, en cryptologie dans le problème de la factorisation des entiers ou pour fabriquer des codes performants.

Contrairement à ce que son nom pourrait laisser croire, l'ellipse n'est pas une courbe elliptique. Le nom des courbes elliptiques vient historiquement de leur association avec les intégrales elliptiques, elles-mêmes appelées ainsi car elles servent en particulier à calculer la longueur d'arcs d'ellipses.

À l'aide d'un choix adapté de coordonnées, une courbe elliptique peut être représentée dans un plan par une équation cubique de la forme :

Les coefficients , , 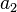,  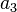et  sont des éléments du corps  sur lequel est définie la courbe, mais ils ne sont pas déterminés par la courbe..."

Lire la suite :

http://fr.wikipedia.org/wiki/Courbe_elliptique

Grigori Perelman par Cédric Villani 25.10.10

"Grigori Perelman naît le 13 juin 1966 à Leningrad,

l’actuelle Saint-Pétersbourg. Sa mère, intellectuelle

juive, avait renoncé à une carrière de mathématicienne pour se consacrer à l’éducation de ses deux

enfants, Grigori et Lena, tous deux devenus mathématiciens.

À cette époque, les mathématiques constituaient l’un des rares

moyens d’accéder à des trésors bannis par le gouvernement

dans d’autres domaines : le raisonnement logique, la..."

Lire la suite : 

http://cedricvillani.org/wp-content/uploads/2012/10/perel...

 

 

Création d'un portail mathématique pour l'industrie italienne

La naissance d'un "Portail Mathématique pour l'Industrie Italienne" a été annoncée à la fin du mois de juin lors du congrès biennale de la Société Italienne de Mathématique Appliquée et Industrielle (SIMAI) à Turin. Son objectif est de faire connaitre au monde de l'entreprise l'offre mathématique potentiellement utile au monde industriel. Ci-dessous est reporté un entretien de Roberto Natalini, directeur...

Lire la suite :

http://www.bulletins-electroniques.com/actualites/71448.htm

Enquête internationale sur la mathématique et les sciences

Enquête internationale sur la mathématique et les sciences

« Le Québec a de quoi être fier de ses élèves! » - Josée Bouchard

LBR.ca - QUÉBEC, le 11 décembre 2012 - La Fédération des commissions scolaires du Québec (FCSQ) est très heureuse de souligner la réussite des élèves québécois à l'enquête internationale sur la mathématique et les sciences (TEIMS) dont les résultats ont été dévoilés aujourd'hui.

C'est en mathématique de 2^e secondaire que les élèves du Québec se sont le plus illustrés avec d'excellents résultats. La performance mérite d'être soulignée puisque les élèves ont non seulement amélioré leurs résultats par rapport aux enquêtes précédentes (2003 et 2007), mais ils se sont classés les premiers au Canada et ont obtenu des résultats nettement supérieurs à la...

Lire la suite : 

http://www.lbr.ca/index.php?pageID=5&idA=19809

NIELS HENRIK ABEL MEMORIAL Publie A L'Occasion Du Centenaire De Sa Naissance. HOLST, Elling STORMER, Carl & SYLOW, L. [Editors]

NIELS HENRIK ABEL MEMORIAL Publie A L'Occasion Du Centenaire De Sa Naissance.

HOLST, Elling STORMER, Carl & SYLOW, L. [Editors]

Détails bibliographiques

 

Titre : NIELS HENRIK ABEL MEMORIAL Publie A ...

Éditeur : Jacob Dybwad [&] Gauthier-Villars [&] B.G. Teubner [&] Williams & Norgate, 1902.

Date d'édition : 1902

Reliure : Hardcover

Edition : 1st Edition

Description :

1st edn. 4to. Rebound in recent gilt lettered blue buckram cloth (Fine). Pp. variously paginated (new endpapers with original printed card covers bound in; no inscriptions), illus with b&w plates and folding facsimile sheets. N° de réf. du libraire 22502

 

EN SAVOIR PLUS 

Commander

Niels Henrik ABEL LIVRE 1881 Oeuvres complètes. Nouvelle edition publiee aux frais de l'Etat Norvegien par MM. L. Sylow et S. Lie. Tome premier + Tome second., 2 Volumes (so complete), Abel, Niels Henrik.

 

Oeuvres complètes. Nouvelle edition publiee aux frais de l'Etat Norvegien par MM. L. Sylow et S. Lie. Tome premier + Tome second., 2 Volumes (so complete),

Abel, Niels Henrik.

 

 

Détails bibliographiques

 

Titre : Oeuvres complètes. Nouvelle edition publiee ...

Éditeur : Grondahl & Son, Christiana

Date d'édition : 1881

Reliure : Hardcover

 

Description :

VIII, 621 S.; 1 Bl., 338 S., 2 Bl., Originalausgabe! Original (French) Edition from 1881! Rückentitel in Deutsch: "Abels Werke I, II". Lexikon bedeutender Mathematiker, S. 9. Abel, Niels Henrik (1802-1829) lieferte grundlegende Arbeiten zur Auflösungstheorie algebraischer Gleichungen, über elliptische Funktionen und zur Reihenlehre, starb als 27jähriger vor Antritt einer Anstellung als PD an der Berliner Universität an Tuberkulose. Sprache: fr Gewicht in Gramm: 3320 4°, marmoriertes Halbleinen mit Rückentitel, Bibliotheks-Exemplar (ordnungsgemäß entwidmet) mit kleinem Rückenschild, Stempel auf Vortitel, Kanten leicht berieben, insgesamt sehr gutes und innen sauberes Exemplar, N° de réf. du libraire 62366

 

EN SAVOIR PLUS

 

 

 

 

 

Grigori Perelman face à la conjecture de Poincaré (French Edition) (ISBN 10: 2100508687 / ISBN 13: 9782100508686 ) O'Shea, Donal

Grigori Perelman face à la conjecture de Poincaré (French Edition)

(ISBN 10: 2100508687 / ISBN 13: 9782100508686 )

O'Shea, Donal

Détails bibliographiques

 

Titre : Grigori Perelman face à la conjecture de ...

Éditeur : DUNOD

Date d'édition : 2007

Reliure : PAPERBACK

Etat du livre : New

Description :

2100508687 Thematic: Scientifiques et techniques. Language: French. Format: Poche. Ed: DUNOD (06/13/2007) Weight: 502g. / 1.11lbs Great Customer Service! Shipped by courier tracking. N° de réf. du libraire 9782100508686

 

Jules Henri POINCARE Thèses présentées a la Faculté des sciences de Paris pour obtenir le grade de docteur des sciences mathématiques. 1re These. Sur les propriétés des fonctions définies par les équations aux différences partielles. 2e These

 

Thèses présentées a la Faculté des sciences de Paris pour obtenir le grade de docteur des sciences mathématiques. 1re These. Sur les propriétés des fonctions définies par les équations aux différences partielles. 2e These. Propositions données par la Faculté. Soutenues le 1er aout 1879, devant la commission d'examen.

POINCARÉ, Jules Henri.

Détails bibliographiques

 

Titre : Thèses présentées a la Faculté des sciences ...

Éditeur : Gauthier-Villars, Paris

Date d'édition : 1879

Edition : First edition

Description :

A fine copy, with the original printed wrappers, of Poincaré's thesis for his doctorate in science from the University of Paris. "Poincaré's doctoral thesis [was] on differential equations (not on methods of solution, but on existence theorems), which led to one of his most celebrated contributions to mathematics-the properties of automorphic functions" (Boyer & Merzbach, History of Mathematics, p. 675). "The theory of differential equations and its applications to dynamics was clearly at the center of Poincaré’s mathematical thought; from his first (1878) to his last (1912) paper, he attacked the theory from all possible angles and very seldom let a year pass without publishing a paper on the subject" (DSB XI: 56)."Poincaré's thesis, which was examined by Bouquet, Bonnet and Darboux, concerned the study of integrals of first-order partial differential equations in the neighbourhood of a singular point. It was his second paper of the theory of differential equations and, as Hadamard remarked, it contained a strong pointer towards his future success with the topic and its applications to celestial mechanics: ‘Even Poincaré 's thesis contained a remarkable result which was destined later to provide him with a powerful tool in his researches in celestial mechanics.’ "Looked at in the context of the theory of differential equations already in existence at the time, Poincaré's thesis was the natural convergence of two streams of thought. On the one hand, Cauchy, and later Kovalevskaya, had applied Cauchy’s method of majorants to obtain results about the solutions of partial differential equations in the neighbourhood of an ordinary point, while on the other, Briot and Bouquet. and later Fuchs, using similar methods, had studied the solutions of ordinary differential equations in the neighbourhood of a singular point. Poincare followed both Cauchy, by considering the solutions of partial differential equations, and Briot and Bouquet, by considering these solutions in the neighbourhood of a singular point" (June Barrow-Green, Poincaré and the three-body problem, Vol. 2, p. 44). "The development of mathematics in the nineteenth century began under the shadow of a giant, Carl Friedrich Gauss; it ended with the domination by a genius of similar magnitude, Henri Poincaré. Both were universal mathematicians in the supreme sense, and both made important contributions to astronomy and mathematical physics. Poincaré remains the most important figure in the theory of differential equations and the mathematician who after Newton did the most remarkable work in celestial mechanics" (DSB XI: 52). Large 4to (262 x 210 mm), pp [iv] 93 [3], bound in a fine recent half cloth binding over marbled boards, gilt morocco title label to spine, original brown printed wrappers with bound (small hole to the front wrapper, paper flaw?), a fine copy copy. N° de réf. du libraire 2928

 

Pour commander

 

En savoir plus

 

Henri POINCARÉ LIVRE de 1890 Sur le problème des trois corps et les équations de la dynamique. (In: Acta Mathematica, vol. 13)

Sur le problème des trois corps et les équations de la dynamique. (In: Acta Mathematica, vol. 13)

POINCARÉ, Henri

Détails bibliographiques

 

Titre : Sur le problème des trois corps et les ...

Éditeur : F.&G. Beijer, Stockholm

Date d'édition : 1890

Reliure : Couverture rigide

Etat du livre : Très bon

Edition : Edition originale

Description :

Demi reliure à coins en basane de l'époque, dos lisse portant le titre doré. Un volume in quarto (26,4x21,3 cm) de xii / 270-(2) / 174 / (2) pages Reliure légèrement frottée. Marge de la page 155 fendillée Les 174 dernières pages sont occupées par le mémoire primé d'Appell «Sur les Intégrales Fonctions de multiplicateurs et une demande au Développement". Première et seule édition de ce traité fondamental de Poincaré. Henri Poincaré est le dernier mathématicien universel. Il a crée une branche importante des mathématiques (la topologie). De part ses travaux, précédent le mémoire d'Einstien, certains le considèrent comme le père de la relativité restreinte. Le "problème des trois corps" est le traité fondateur de la théorie du chaos. Dans ce mémoire, Poincaré tente de répondre au problème posé par le roi Oscar II de Suède et de Norvège. Il s'agissait de décrire le système formé par N corps célestes dont les mouvements sont régis par la loi de l'attraction universelle. Cela aurait permis de savoir si le système solaire est stable ou non. Ce problème est d'une grande compléxité, et Poincaré n'y répond que partiellement : il traite le cas d'un système à trois corps. Il y développe de nouveaux outils (section de Poincaré), démontre la stabilité d'un système à trois corps avec l'un de masse nulle (correspond en gros à un système soleil, terre, lune) et y découvre un système extrèmement sensible aux conditions initiales : une variation minime dans la position initiale de la trajectoire peut modifier radicalement son comportement à long terme. C'est la découverte des phénomènes chaotiques dans les systèmes dynamiques. 1152 g. N° de réf. du libraire 538

 

Poincare, Henri Leçons de mécanique céleste professées a la Sorbonne [Tome I, Tome II, Tome III] (Lessons of Celestial Mechanics)

Leçons de mécanique céleste professées a la Sorbonne [Tome I, Tome II, Tome III] (Lessons of Celestial Mechanics)

Poincare, Henri

 

Description :

Paris: Gauthier-Villars, 1905-1910. First Edition. 3 volumes in 4, vi, 365, [3]; [4], 165, [3]; [4], 136, [2], + 2 ad.; [4], 472. Illustrated with text figures and two folding world maps in Vol. III. 10x6½, original grey printed wrappers. First edition of a work fundamental to celestial mechanics. Poincaré was one of the greatest mathematical minds of the 19th century; his work on the "three-body problem" (the gravitational interplay of three masses) leads some to credit him as a co-discoverer of the special theory of relativity, along with Einstein and Lorentz. The present is one of two of Poincaré's major works on the subject. With the inkstamp of Paul Berg. Scarce, no copies appear in ABPC for the past 20 years. Some light wear and staining/darkening to spines, back wrapper of Vol. III chipped at edges, minor splitting at joints, but overall very good or better with clean pages partially unopened. Another one of those sets you just have to hold in your hands and stare at sometimes. L1516. N° de réf. du libraire 000234

 

En savoir plus

 

POUR COMMANDER