D	L	M	M	J	V	S
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30

« La figure et le monde, archéologie de la géométrie, Peuples paysans sans écriture et premières civilisations Olivier Keller Etude (broché). Paru en 08/2006 | Page d'accueil | Groupe de Lie »

25/03/2011

Algèbre de Lie

Alg%C3%A8bre_de_Lie

Livres : Algèbre de Lie

http://fr.wikipedia.org/wiki/Alg%C3%A8bre_de_Lie http://fr.wikipedia.org/wiki/Alg%C3%A8bre_de_LieAlgèbre de Lie

Pour les articles homonymes, voir Algèbre (homonymie).

En mathématiques, une algèbre de Lie, nommée en l'honneur du mathématicien Sophus Lie, est un espace vectoriel qui est muni d'un crochet de Lie, c'est-à-dire d'une loi de composition interne bilinéaire, antisymétrique et qui vérifie l'identité de Jacobi. Une algèbre de Lie est un cas particulier d'algèbre sur un corps.

Sommaire

[masquer]

Définitions, exemples et premières propriétés[modifier]

Définition[modifier]

Soit $mathbb{K}$ un corps commutatif.

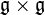Une algèbre de Lie sur $mathbb{K}$ est un espace vectoriel $mathfrak{g}$ sur $mathbb{K}$ muni d'une application bilinéaire $(x,y) mapsto [x,y]$ de $mathfrak{g}timesmathfrak{g}$ dans $mathfrak{g}$ qui vérifie les propriétés suivantes:

$forall x in mathfrak{g}, [x,x]=0$ ;
$forall x,y,z in mathfrak{g}, [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0$

Le produit $[x, y]$ est appelé crochet de Lie (ou simplement crochet) de $x$ et $y$ . Puisque le crochet est une fonction bilinéaire alternée de $x, y$ , on a aussi l'identité $[x, y] = - [y, x]$ pour tous $x, y$ dans $mathfrak{g}$ . L'identité (2) ci-dessus est appelée l'identité de Jacobi.

Une sous-algèbre de Lie de $mathfrak{g}$ est un sous-espace vectoriel de $mathfrak{g}$ stable pour le crochet de Lie. Toute sous-algèbre de Lie de $mathfrak{g}$ est munie de manière évidente d'une structure d'algèbre de Lie sur $mathbb{K}$ .

Remarque : contrairement aux algèbres tensorielles (et aux algèbres de Clifford, dont les algèbres extérieures), les algèbres de Lie ne sont pas unitaires, ni associatives.

Quelques exemples classiques d'algèbres de Lie[modifier]

Tout espace vectoriel $E$ peut être muni d'une structure d'algèbre de Lie, en posant $forall x,y in E, [x,y]=0$ . Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne.
On peut, à partir de $(A, * )$ , une algèbre associative sur un corps, construire une algèbre de Lie, de la façon suivante : on pose $forall x,y in A, [x,y]=x*y-y*x$ (c'est lecommutateur des deux éléments x et y). Il est facile de vérifier que l'on définit ainsi sur $A$ une structure d'algèbre de Lie.
Inversement, toute algèbre de Lie $mathfrak{g}$ est contenue dans une algèbre associative, appelée algèbre enveloppante, dans laquelle le crochet de Lie coïncide avec le crochet défini ci-dessus. L'algèbre enveloppante est beaucoup plus grande que l'algèbre de départ.
Comme exemple concret de la situation ci-dessus, considérons $mathcal{M}_n(mathbb{K})$ , l'espace des matrices $n times n$ à coefficients dans $mathbb{K}$ . C'est une algèbre associative pour le produit matriciel usuel. On peut donc également lui donner une structure d'algèbre de Lie, avec le crochet $[A, B] = A B - B A$ . On note $mathfrak{gl}_n(mathbb{K})$ cette algèbre, lorsque l'on considère sa structure d'algèbre de Lie.
Bien évidemment, tout sous-espace vectoriel de $mathfrak{gl}_n(mathbb{K})$ stable par le crochet est une algèbre de Lie. Ainsi, on peut vérifier que l'ensemble des matrices de trace nulle est une algèbre de Lie, que l'on note $mathfrak{sl}_n(mathbb{K})$ .
En fait, le théorème d'Ado montre que toute algèbre de Lie de dimension finie peut être vue comme une sous-algèbre de $mathfrak{gl}_n(mathbb{K})$ .
Un autre exemple fondamental, plus géométrique, est le suivant. Soit $M$ une variété différentielle. Alors l'espace vectoriel formé par les champs de vecteurs sur $M$ possède une structure naturelle d'algèbre de Lie, sans être une algèbre.
En particulier, l'ensemble des vecteurs de Killing d'une variété forme une algèbre de Lie, qui correspond au groupe d'isométries de la variété considérée.
L'espace euclidien tri-dimensionnel $mathbb{R}^3$ avec le produit vectoriel comme crochet de Lie est une algèbre de Lie.

Morphismes et idéaux[modifier]

Un morphisme d'algèbre de Lie $mathfrak{g}$ est une application linéaire $φ$ qui respecte le crochet de Lie, c'est-à-dire telle que

$forall a,b in mathfrak{g}, phi([a,b])=[phi(a),phi(b)]$ .

Un idéal de $mathfrak{g}$ est un sous-espace vectoriel $mathfrak{h}$ tel que $forall ginmathfrak{g}, forall hin mathfrak{h}, [g,h]inmathfrak{h}$ . C'est en particulier une sous-algèbre de Lie. Si une algèbre de Lie n'admet pas d'idéal non trivial, elle est dite simple.

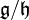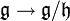Si $mathfrak{h}$ est un idéal de $mathfrak{g}$ , on peut former le quotient de $mathfrak{g}$ par $mathfrak{h}$ : c'est l'espace vectoriel quotient $mathfrak{g}/mathfrak{h}$ , muni du crochet défini par $[g+mathfrak{h},g'+mathfrak{h}] = [g,g']$ . La projection $mathfrak{g}to mathfrak{g}/mathfrak{h}$ est alors un morphisme d'algèbres de Lie.

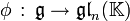Une représentation d'une algèbre de Lie $mathfrak{g}$ est un morphisme $phi,:,mathfrak{g}to mathfrak{gl}_n(mathbb{K})$ . Autrement dit, c'est une application linéaire telle que $φ([g, h]) = φ(g)φ(h) - φ(h)φ(g)$ .

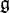Le morphisme $ad:mathfrak{g}tomathfrak{gl(g)}$ défini par $a d (g)(h) = [g, h]$ définit une représentation de $mathfrak{g}$ , appelée représentation adjointe. L'identité de Jacobi exprime précisément le fait que ad respecte le crochet. Le noyau de cette représentation est le centre $Z(mathfrak{g})={ginmathfrak{g}forall hinmathfrak{g} [g,h]=0}$ de l'algèbre de Lie $mathfrak g$ .

Relation avec les groupes de Lie et les groupes algébriques[modifier]

Les algèbres de Lie sont naturellement associées aux groupes de Lie. Si $G$ est un groupe de Lie et 1 son élément neutre, alors l'espace tangent en 1 à $G$ est une algèbre de Lie ; la construction exacte de cette algèbre est détaillée dans la section correspondante de l'article Groupe de Lie. La même construction est valable pour les groupes algébriques. On note en général en petites lettres gothiques l'algèbre de Lie associée à un groupe de Lie, ou à un groupe algébrique. Ainsi, comme on l'a déjà vu, 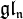$mathfrak{gl_n}$ désigne l'ensemble des matrices carrées de taille n et 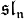$mathfrak{sl_n}$ désigne l'ensemble des matrices carrées de taille n de trace nulle. De la même façon, $mathfrak{so_n}$ désigne l'ensemble des matrices carrées A de taille n antisymétriques, etc. Dans tous ces exemples, le crochet de Lie n'est rien d'autre que le commutateur : [A,B]=AB-BA.

Si $φ$ est un morphisme de groupes entre deux groupes de Lie $G$ et $H$ , et si l'on suppose $φ$ différentiable, alors sa différentielle en l'identité sera un morphisme entre les algèbres de Lie $mathfrak{g}$ et $mathfrak{h}$ de $G$ et $H$ . En particulier, à une représentation de $G$ différentiable, on associe une représentation de $mathfrak{g}$ .

La classification des algèbres de Lie est utilisée de façon cruciale pour l'étude des groupes de Lie, des groupes algébriques et de leurs représentations.

Classification[modifier]

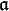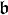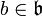Si $mathfrak{a}$ et $mathfrak{b}$ sont deux sous-algèbres de Lie d'une algèbre de Lie $mathfrak{g}$ , notons $[mathfrak{a},mathfrak{b}]$ le sous-espace vectoriel engendré par les éléments de la forme $[a, b]$ pour $ainmathfrak{a}$ et $binmathfrak{b}$ .

Algèbres de Lie nilpotentes[modifier]

Une algèbre de Lie est dite nilpotente lorsque toute suite de commutateurs $[[[g_1,g_2],g_3],dots,g_n]$ finit par être nulle, lorsque n devient suffisamment grand.

Plus précisément, définissons $C i$ par $C_0=mathfrak{g}$ et $C_{i+1}=[C_i,mathfrak{g}]$ .

S'il existe un i tel que $C i$ =0, on dit que $mathfrak{g}$ est nilpotente. Cette notion est à mettre en parallèle avec celle de groupe nilpotent. Il est facile de voir que toute algèbre de Lie abélienne est nilpotente.

L'algèbre $mathfrak n$ des matrices triangulaires strictes, c'est-à-dire de la forme $left(begin{matrix} 0 & star & cdots & star \ vdots & ddots & star& vdots \ vdots & 0 & ddots & star \ 0 & cdots & cdots & 0 \ end{matrix}right)$ fournit un exemple d'algèbre de Lie nilpotente.

Le théorème d'Engel affirme que toute sous-algèbre nilpotente de $mathfrak{gl}_n(mathbb K)$ est en fait simultanément trigonalisable et donc conjuguée à une sous-algèbre de $mathfrak n$ .

Algèbres de Lie résolubles[modifier]

Définissons par récurrence $D i$ par 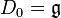$D_0=mathfrak{g}$ et $D i + 1 = [D i, D i]$

S'il existe un i tel que $D i$ =0, on dit que $mathfrak{g}$ est résoluble. Comme dans le cas des algèbres nilpotentes, cette notion correspond à celle de groupe résoluble. Il est facile de voir que toute algèbre de Lie nilpotente est résoluble.

Un exemple d'algèbre de Lie résoluble est donné par l'algèbre 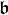$mathfrak b$ des matrices triangulaires supérieures dans $mathfrak{gl}_n(mathbb K)$ .

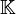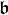
Le théorème de Lie montre que, si $mathbb K$ est algébriquement clos et de caractéristique nulle, alors toute sous-algèbre de Lie résoluble de $mathfrak{gl}_n(mathbb K)$ est conjuguée à une sous-algèbre de $mathfrak b$

Algèbres de Lie semi-simples et réductives[modifier]

Article détaillé : algèbre semi-simple.

On dit qu'une algèbre de Lie $mathfrak{g}$ est semi-simple lorsqu'elle ne contient pas d'idéal résoluble non trivial. $mathfrak{g}$ est dite réductive lorsque sa représentation adjointe est semi-simple.

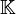Lorsque $mathbb K$ est de caractéristique nulle, et que $mathfrak{g}$ est de dimension finie, la semi-simplicité de $mathfrak{g}$ est équivalente à la non-dégénerescence de la forme de Killing $K (x, y)$ définie par $K (x, y) = t r (a d (x) a d (y))$ , où tr désigne la trace. Par ailleurs, $mathfrak{g}$ est réductive si et seulement si $[mathfrak{g},mathfrak{g}]$ est semi-simple.

On peut montrer que, sous les mêmes hypothèses, toute algèbre de Lie semi-simple est en fait une somme directe d'algèbres de Lie simples.

Les algèbres de Lie simples de dimension finie sur le corps $mathbb C$ des nombres complexes sont classifiées par les diagrammes de Dynkin. Il y a donc 4 familles d'algèbres de Lie simples (ou 3 si on considère $B n$ et $D n$ comme une même famille) et 5 algèbres de Lie exceptionnelles, correspondant chacune à un diagramme de Dynkin différent.

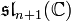À un diagramme de Dynkin de type $A_n (ngeq 1)$ correspond l'algèbre de Lie $mathfrak{sl}_{n+1}(mathbb{C})$ .

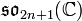À un diagramme de Dynkin de type $B_n (ngeq 2)$ correspond l'algèbre de Lie $mathfrak{so}_{2n+1}(mathbb{C})$ .

À un diagramme de Dynkin de type $C_n (ngeq 3)$ correspond l'algèbre de Lie $mathfrak{sp}_{2n}(mathbb{C})$ .

À un diagramme de Dynkin de type $D_n (ngeq 4)$ correspond l'algèbre de Lie $mathfrak{so}_{2n}(mathbb{C})$ .

Les algèbres de Lie exceptionnelles, correspondant aux diagrammes de Dynkin restants (de type E₆, E₇, E₈, F₄ et G₂) n'ont pas d'interprétation aussi simple.

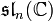L'algèbre de Lie $mathfrak{gl}_{n}(mathbb{C})$ est, elle, réductive et son algèbre de Lie dérivée est $mathfrak{sl}_{n}(mathbb{C})$ .

Les algèbres de Lie semi-simples de dimension finie sur le corps $mathbb R$ des nombres réels sont classifiées par les involutions d'algèbres de Lie complexe ou, de façon équivalente, par lesinvolutions de systèmes de racines. Ceci correspond à la notion d'algèbre de Lie symétrique. Comme classe d'algèbre de Lie simple réelle, on peut citer:

Les algèbres de Lie compactes. Ce sont les algèbres de Lie de groupes compacts. Il y en a exactement une qui correspond à chaque algèbre de Lie complexe.

Les algèbres de Lie complexes vues comme algèbres de Lie réelles.

Les autres peuvent être classées en familles AI, AII, AIII, BI, CI, CII, DI, DIII et en algèbres exeptionelles

EI, EII, EIII, EIV (de type $E 6$ ) EV, EVI, EVII (de type $E 7$ ) EVIII, EIX (de type $E 8$ ) FI, FII (de type $F 4$ ) et GI (de type $G 2$ ) suivant la notation d'Helgason¹)

Dimension infinie[modifier]

Il n'y a pas de classification générale des algèbres de Lie de dimension infinie mais plusieurs classes de telles algèbres ont été étudiées.

Une algèbre de Kac-Moody est une algèbre de Lie définie abstraitement en termes de générateurs et relations codés par une matrice de Cartan généralisée non nécessairement définie positive. Elles peuvent donc être de dimension infinie. Leur classification générale est encore hors de portée mais plusieurs sous-types sont connus
- Une algèbre de Kac-Moody affine possède la propriété que tous les sous-diagrammes de Dynkin de son diagramme de Dynkin correspondent à des sous-algèbres de Lie de dimension finie. Sa matrice de Cartan généralisée est alors de corang 1. Les algèbres de Kac-Moody affines ont été classifiées par Victor G. Kac. Elles sont très utilisées enphysique théorique dans l'étude des théories conformes des champs et en particulier dans l'étude des modèles WZW.
- Une algèbre de Kac-Moody hyperbolique possède un diagramme de Dynkin connexe avec la propriété que si on lui retire une racine, on obtient une algèbre de Lie semi-simple de dimension finie ou bien une algèbre de Kac-Moody affine. Elles ont été également classifiées et sont de rang 10 au maximum. Leur matrice de Cartan généralisée est non dégénérée et de signature Lorentzienne (c’est-à-dire avec exactement une direction négative).
algèbre de Kac-Moody généralisée ou algèbre de Borcherds: c'est un type d'algèbre de Lie généralisant le concept d'algèbre de Kac-Moody dont la matrice de Cartan généralisée peut posséder des racines simples nommées imaginaires pour lesquelles l'élément diagonal de la matrice de Cartan généralisée est négatif. Elles ont été introduite par Richard Ewen Borcherds dans le cadre de l'étude de la conjecture monstrous moonshine.

Généralisation[modifier]

Il existe différentes sortes de généralisations des algèbres de Lie, on citera les superalgèbres de Lie, les groupes quantiques, les algèbres de Leibniz, les algèbres pré-Lie.

Références[modifier]

Bourbaki, Groupes et algèbres de Lie
Dixmier, Jacques Algèbres enveloppantes Éditions Jacques Gabay, Paris, 1996. ISBN 2-87647-014-4
Humphreys, James E. Introduction to Lie Algebras and Representation Theory, Second printing, revised. Graduate Texts in Mathematics, 9. Springer-Verlag, New York, 1978. ISBN 0-387-90053-5
Jacobson, Nathan, Lie algebras, Republication of the 1962 original. Dover Publications, Inc., New York, 1979. ISBN 0-486-63832-4

↑ S. Helgason, Differential Geometry and Symmetric Spaces [archive]

Voir aussi[modifier]

Groupe de Lie

[enrouler] v · d · m Algèbre linéaire générale
Vecteur • Scalaire • Combinaison linéaire • Espace vectoriel • Matrice
Famille de vecteurs	Famille génératrice • Famille libre (indépendance linéaire) • Base • Théorème de la base incomplète • Rang • Colinéarité
Sous-espace	Sous-espace vectoriel • Somme d'ensembles • Somme directe • Sous-espace supplémentaire • Dimension • Codimension • Droite • Plan •Hyperplan
Morphisme et notions relatives	Application linéaire • Noyau • Conoyau • Lemme des noyaux • Pseudo-inverse • Théorème de factorisation • Théorème du rang • Équation linéaire • Système d'équations linéaires • Élimination de Gauss-Jordan • Forme linéaire • Espace dual • Orthogonalité • Base duale •Endomorphisme linéaire • Valeur propre, vecteur propre et espace propre • Spectre • Projecteur • Symétrie • Matrice diagonalisable •Diagonalisation • Endomorphisme nilpotent
En dimension finie	Espace vectoriel de dimension finie • Trace • Déterminant • Polynôme caractéristique • Polynôme d'endomorphisme • Théorème de Cayley-Hamilton • Polynôme minimal d'un endomorphisme • Invariants de similitude • Réduction d'endomorphisme • Réduction de Jordan •Décomposition de Dunford • Décomposition de Frobenius
Enrichissements de structure	Norme • Produit scalaire • Forme quadratique • Espace vectoriel topologique • Orientation • Algèbre sur un corps • Algèbre de Lie • Complexe différentiel
Développements	Théorie des matrices • Représentation de groupe • Analyse fonctionnelle • Algèbre multilinéaire • Module sur un anneau

Portail des mathématiques

Catégorie : Algèbre de Lie | [+]

Algèbre de Lie

Pour les articles homonymes, voir Algèbre (homonymie).

Sommaire

[masquer]