02/12/2010
Transformation géométrique
Catégorie:Transformation géométrique
Articles dans la catégorie « Transformation géométrique »
| Outils : Arborescence de la catégorie (graphique) Recherches : Recherche interne • avec CatScan (requêtes simples) |
Cette catégorie contient les 45 pages suivantes.
21:38 Publié dans Transformation géométrique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Transformation géométrique
On appelle transformation géométrique, toute bijection d'une partie d'un ensemble géométrique dans lui-même. On peut tenter une ou des classifications de ces transformations. D'abord selon la dimension de l'ensemble géométrique ; on distinguera donc principalement les transformations planes et les transformations dans l'espace. On peut aussi classer les transformations d'après leurs éléments conservés : Chacune de ces classes contient la précédente.Transformation géométrique
![]() Pour les articles homonymes, voir Transformation.
Pour les articles homonymes, voir Transformation.
| image de départ | isométrie | similitude |
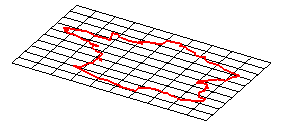 |
 |
 |
| transformation affine | transformation homographique | inversions |
Et enfin, englobant les précédentes :
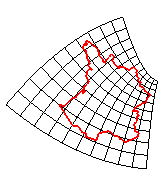 |
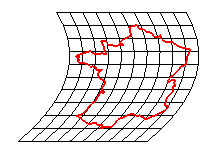 |
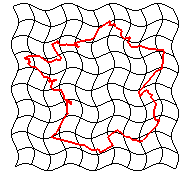 |
 |
| transformation conforme | transformation équivalente | difféomorphisme | homéomorphisme |
On crée alors des groupes et des sous-groupes de transformations. L'étude de la géométrie est en grande partie l'étude de ces transformations. Il existe aussi des transformations qui ne sont pas définies dans le plan ou l'espace tout entier. Parmi celles-ci on peut citer les inversions, les homologies qui sont des transformations homographiquesClassification non exhaustive des transformations selon leur degré de complexité [modifier]
21:37 Publié dans Transformation géométrique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Transformation géométrique
Catégorie:Transformation géométrique
Articles dans la catégorie « Transformation géométrique »
| Outils : Arborescence de la catégorie (graphique) Recherches : Recherche interne • avec CatScan (requêtes simples) |
Cette catégorie contient les 45 pages suivantes.
21:37 Publié dans Transformation géométrique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Transformation géométrique
Catégorie:Transformation géométrique
Articles dans la catégorie « Transformation géométrique »
| Outils : Arborescence de la catégorie (graphique) Recherches : Recherche interne • avec CatScan (requêtes simples) |
Cette catégorie contient les 45 pages suivantes.
21:35 Publié dans Transformation géométrique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Groupe diédral
En mathématiques, le groupe diédral noté Dn, pour Groupe diédral
 , ou parfois D2n, est un groupe d'ordre 2n qui s'interprète notamment comme le groupe des isométries du plan conservant un polygone régulier à n côtés. Le groupe est constitué de n éléments correspondant aux rotationset n autres correspondant aux réflexions. Le groupe D1 est le groupe cyclique d'ordre 2, noté C2 ; le groupe D2 est le groupe de Klein à quatre éléments. Parmi les groupes diédraux Dn, ce sont les deux seuls à être abéliens.
, ou parfois D2n, est un groupe d'ordre 2n qui s'interprète notamment comme le groupe des isométries du plan conservant un polygone régulier à n côtés. Le groupe est constitué de n éléments correspondant aux rotationset n autres correspondant aux réflexions. Le groupe D1 est le groupe cyclique d'ordre 2, noté C2 ; le groupe D2 est le groupe de Klein à quatre éléments. Parmi les groupes diédraux Dn, ce sont les deux seuls à être abéliens.
Sommaire[masquer] |
Le groupe Dn peut être défini par la suite exacte scindée suivante : où Cn est un groupe cyclique d'ordre n, C2 est cyclique d'ordre 2, la section étant donnée par l'action d'un relevé σ du générateur de C2, sur un générateur τ du groupe cyclique d'ordre n : Ce groupe est donc produit semi-direct de Cn par C2 suivant le morphisme ψ, où l'unité de C2 agit sur Cn comme l'application identique et l'autre élément de C2 agit sur Cn par inversion. Explicitement: Une présentation est alors : Plus explicitement les générateurs sont des σ, τ et les relations qu'ils vérifient sont de la forme : On peut ainsi dresser une liste complète des éléments du groupe : Une présentation alternative, où μ = τσ dans le système de générateurs de la présentation précédente, est : Plus explicitement les générateurs sont des σ, μ et les relations qu'ils vérifient sont de la forme : On voit ainsi que le groupe diédral admet un système de deux générateurs distincts tous deux d'ordre 2. Les groupes diédraux sont les seuls groupes finis possédant cette propriété1. Le groupe diédral d'ordre 2n peut aussi être vu comme le groupe d'automorphisme du graphe constitué seulement d'un cycle avec n sommets (si n ≥ 3). On peut définir de la façon suivante une représentation du groupe diédral Dn : avec On reconnaît que la matrice φ(τ) est une matrice de rotation d'angle Les graphes de cycles de groupes diédraux sont constitués d'un cycle à n éléments et de cycles à 2 éléments. Le sommet sombre dans les graphes de cycle ci-dessous de divers groupes diédraux représente l'élément identité, et les autres sommets sont les autres éléments du groupe. Un cycle est constitué des puissances successives de l'un ou l'autre élément connecté à l'élément identité. Présentation et définitions équivalentes [modifier]
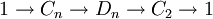
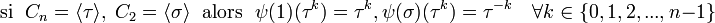 .
.
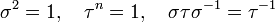 .
.

 .
.Interprétation géométrique [modifier]
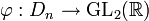
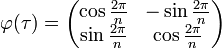 et
et  . Cette représentation est en fait à valeurs dans le groupe
. Cette représentation est en fait à valeurs dans le groupe  .
. , et la matrice φ(σ) une matrice de réflexion. Ces transformations laissent effectivement invariant le polygone régulier centré en l'origine à n côtés.
, et la matrice φ(σ) une matrice de réflexion. Ces transformations laissent effectivement invariant le polygone régulier centré en l'origine à n côtés.Graphe de cycle [modifier]
| D2 | D3 | D4 | D5 | D6 | D7 |
|---|
Le sous-ensemble des rotations Certaines propriétés des groupes diédraux Dn avec n ≥ 3 dépendent de la parité de n. Elles peuvent souvent facilement être déduites de la représentation géométrique de ce groupe. où D2n est l'ensemble de départ Dn*C2 celui d'arrivée, h et ε étant définis modulo 2, et k modulo n. Les générateurs des groupes diédraux sont choisis comme dans la première partie de l'article. Si n est impair, le groupe Dn admet 2 représentations irréductibles complexes de degré 1 : En revanche, si n est pair, il existe 4 représentations irréductibles de degré 1 : Les autres représentations irréductibles sont toutes de degré 2 ; elles sont en nombre où ω désigne une racine primitive ne de l'unité, et h parcourt les entiers compris entre 1 et n-1. On peut vérifier que deux telles représentations sont isomorphes seulement pour h1 et h2vérifiant h1+h2=n. On obtient alors le nombre annoncé de représentations irréductibles de degré 2 non isomorphes, et donc toutes les représentations irréductible du groupe diédral, par la formule liant le nombre de représentations irréductibles à l'ordre du groupe. En plus des groupes diédraux finis, on trouve le groupe diédral infini D∞. Tout groupe diédral est généré par une rotation r et une réflexion. Si la rotation est un multiple rationnel d’une rotation totale, alors il existe un entier n tel que rn soit l’identité, et on est en présence d’un groupe diédral fini d’ordre 2n. Mais si la rotation n’est pas un multiple rationnel d’une rotation totale, alors il n’existe pas de tel n et le groupe résultant a un nombre infinid’éléments ; on le note D∞. Il admet pour présentation et est isomorphe au produit semi-direct de Z par C2, ainsi qu’au produit libre C2 * C2. Il s’agit de l’automorphisme de groupes du graphe constitué d’un chemin infini vers les deux extrémités. De façon équivalente, il s’agit du groupe des isométries de Z. Pour tout groupe abélien H, le groupe diédral généralisé de H, noté Dih(H), est le produit semi-direct de H par C2, l'action de C2 sur H étant l'inversion, i.e. où φ(0) est l'application identité et φ(1) l'inversion des éléments. On obtient ainsi, si H et C2 sont tous deux notés additivement : pour tous h1, h2 dans H et t2 dans C2. (Si C2 est noté multiplicativement, ces deux formules se résument en (h1, t1) * (h2, t2) = (h1 + t1h2, t1t2) .) Le sous-groupe de Dih(H) constitué des éléments de la forme (h, 0) est un sous-groupe normal d'indice 2, isomorphe à H. Quant aux éléments de la forme (h, 1), chacun est son propre inverse. Les classes de conjugaison sont Ainsi, pour tout sous-groupe M de H, les éléments correspondants (m,0) forment aussi un sous-groupe normal de Dih(H) isomorphe à M, et l'on a : Exemples : Dih(H) est abélien si et seulement si le produit semi-direct est direct, c'est-à-dire si et seulement si chaque élément de H est son propre inverse, i.e. H est un 2-groupe abélien élémentaire : Dih(C2k) = C2k+1.Propriétés [modifier]
 est un sous-groupe normal.
est un sous-groupe normal.

Représentations [modifier]

 si n est impair, respectivement
si n est impair, respectivement  si n est pair. On peut les définir comme suit :
si n est pair. On peut les définir comme suit :
Groupe diédral infini [modifier]


Groupe diédral généralisé [modifier]
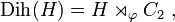
Bibliographie [modifier]
Notes et références [modifier]
21:33 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Groupe de Weyl
En mathématiques, et en particulier dans la théorie des algèbres de Lie, le groupe de Weyl d'un système de racines Le système de racines de Le groupe de Weyl d'un groupe de Lie semi-simple, d'une algèbre de Lie semi-simple, d'un groupe algébrique linéaire semi-simple, etc. est le groupe de Weyl du système de racines de ce groupe ou de cette algèbre. Enlever les hyperplans définis par les racines de La base du système de racine qui respecte le choix de Les groupes de Weyl sont des exemples des groupes de Coxeter. Ceci signifie qu'ils ont une sorte particulière de présentation dans laquelle chaque générateur Si G est un groupe algébrique linéaire semisimple sur un corps algébriquement clos (plus généralement un groupe déployé), et T est un tore maximal, le normalisateur N de T contient Tcomme sous-groupe d'indice fini et le groupe de Weyl W de G est isomorphe à N/T. Si B est un sous-groupe de Borel de G, i.e. un sous-groupe connexe résoluble maximal choisi pour contenir T, alors nous obtenons une décomposition de Bruhat ce qui provoque la décomposition de la variété de drapeaux G/B en cellules de Schubert (voir Grassmannienne).Groupe de Weyl
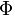 est le sous-groupe du groupe d'isométries du système de racines engendré par les réflexions orthogonales par rapport aux hyperplans orthogonaux aux racines.
est le sous-groupe du groupe d'isométries du système de racines engendré par les réflexions orthogonales par rapport aux hyperplans orthogonaux aux racines.Exemple [modifier]
 est constitué des sommets d'un hexagone régulier centré à l'origine. Le groupe complet des symétries de ce système de racines est par conséquent legroupe diédral d'ordre 12. Le groupe de Weyl est engendré par les réflexions à travers les droites bissectant les paires de côtés opposés de l'hexagone ; c'est le groupe diédral d'ordre 6.
est constitué des sommets d'un hexagone régulier centré à l'origine. Le groupe complet des symétries de ce système de racines est par conséquent legroupe diédral d'ordre 12. Le groupe de Weyl est engendré par les réflexions à travers les droites bissectant les paires de côtés opposés de l'hexagone ; c'est le groupe diédral d'ordre 6.Les chambres de Weyl [modifier]
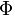 découpe l'espace euclidien en un nombre fini de régions ouvertes, appelées les chambres de Weyl. Celles-ci sont permutées par l'action sur le groupe de Weyl, et un théorème établit que cette action est simplement transitive. En particulier, le nombre de chambres de Weyl est égal à l'ordre du groupe de Weyl. Tout vecteur v différent de zéro divise l'espace euclidien en deux demi-espaces bordant l'hyperplan
découpe l'espace euclidien en un nombre fini de régions ouvertes, appelées les chambres de Weyl. Celles-ci sont permutées par l'action sur le groupe de Weyl, et un théorème établit que cette action est simplement transitive. En particulier, le nombre de chambres de Weyl est égal à l'ordre du groupe de Weyl. Tout vecteur v différent de zéro divise l'espace euclidien en deux demi-espaces bordant l'hyperplan  orthogonal à v, nommés
orthogonal à v, nommés  et
et 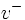 . Si v appartient à une certaine chambre de Weyl, aucune racine ne se trouve dans
. Si v appartient à une certaine chambre de Weyl, aucune racine ne se trouve dans  , donc chaque racine se trouve dans
, donc chaque racine se trouve dans  ou
ou 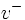 , et si
, et si 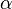 se trouve dans l'un d'eux, alors
se trouve dans l'un d'eux, alors  se trouve dans l'autre. Ainsi,
se trouve dans l'autre. Ainsi,  constitué d'exactement la moitié des racines de
constitué d'exactement la moitié des racines de 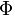 . Bien sûr,
. Bien sûr, 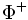 dépend de v, mais il ne change pas si v reste dans la même chambre de Weyl.
dépend de v, mais il ne change pas si v reste dans la même chambre de Weyl.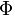 est l'ensemble des racines simples dans
est l'ensemble des racines simples dans 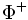 , i.e., les racines qui ne peuvent pas être écrites comme une somme de deux racines dans
, i.e., les racines qui ne peuvent pas être écrites comme une somme de deux racines dans 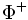 . Ainsi, les chambres de Weyl, l'ensemble
. Ainsi, les chambres de Weyl, l'ensemble 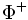 et la base en déterminent un autre, et le groupe de Weyl agit simplement transitivement dans chaque cas. L'illustration suivante montre les six chambres de Weyl d'un système de racines
et la base en déterminent un autre, et le groupe de Weyl agit simplement transitivement dans chaque cas. L'illustration suivante montre les six chambres de Weyl d'un système de racines  , un choix de v, l'hyperplan
, un choix de v, l'hyperplan  (indiqué par une droite en pointillé) et les racines positives
(indiqué par une droite en pointillé) et les racines positives 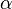 ,
,  , et
, et 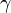 . La base dans ce cas est (
. La base dans ce cas est (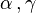 }.
}.Les groupes de Coxeter [modifier]
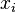 est d'ordre deux, et les relations autres que
est d'ordre deux, et les relations autres que  sont de la forme
sont de la forme  . Les générateurs sont les réflexions données par les racines simples et
. Les générateurs sont les réflexions données par les racines simples et 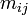 est 2, 3, 4 ou 6 dépendant si les racines i et jfont un angle de 90, 120, 135 ou 150 degrés, i.e., si dans le Diagramme de Dynkin, elles ne sont pas connectées, connectées avec une arête simple, connectées par une double arête ou connectées par une triple arête. La longueur d'un élément du groupe de Weyl est la longueur du mot le plus court représentant cet élément en termes de ces générateurs standards.
est 2, 3, 4 ou 6 dépendant si les racines i et jfont un angle de 90, 120, 135 ou 150 degrés, i.e., si dans le Diagramme de Dynkin, elles ne sont pas connectées, connectées avec une arête simple, connectées par une double arête ou connectées par une triple arête. La longueur d'un élément du groupe de Weyl est la longueur du mot le plus court représentant cet élément en termes de ces générateurs standards.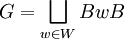
21:32 Publié dans Groupe de Weyl | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Forme de Killing
Dans la théorie des algèbres de Lie, la forme de Killing est une forme bilinéaire symétrique naturellement associée à toute algèbre de Lie. Elle reflète un certain nombre de propriétés des algèbres de Lie (semi-simplicité, résolubilité…). Soit g une K-algèbre de Lie, où K désigne un corps (commutatif). La représentation adjointe définit pour tout vecteur x de g un endomorphisme K-linéaire ad(x) du K-espace vectoriel g : Si g est de dimension finie, il existe une forme bilinéaire symétrique B définie par : où Tr désigne l'opérateur trace. Cette forme est appelée forme de Killing de g. La forme de Killing est l'unique forme bilinéaire symétrique sur g, invariante sous l'action des automorphismes de la K-algèbre de Lie g et vérifiant l'identité remarquable : Curieusement, la forme de Killing a été définie par Henri Cartan, tandis que la matrice de Cartan a été définie par Wilhelm Killing (en).Forme de Killing
Définition [modifier]

![Bleft([x,y],zright)=Bleft(x,[y,z]right)](http://upload.wikimedia.org/math/5/3/5/5358cbdd3d95b2f7f83b373ba0cd8c6f.png) .
.Voir aussi [modifier]
21:31 Publié dans Forme de Killing | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Algèbre enveloppante
Algèbre enveloppante
|
|
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
En mathématiques, on peut construire l'algèbre enveloppante U(L) d'une algèbre de Lie L. Il s'agit une algèbre associative unitaire qui permet de rendre compte de la plupart des propriétés de L. Si A est une algèbre associative sur un corps K, on peut facilement la munir d'une structure d'algèbre de Lie, en posant [x,y]=xy-yx. On note l'algèbre de Lie ainsi obtenue AL. La construction d'une algèbre enveloppante répond au problème réciproque : à partir d'une algèbre de Lie, on construit une algèbre associative dont le commutateur correspond au crochet dont on était parti. Soit L une algèbre de Lie sur un corps K. Soit T(L) l'algèbre tensorielle de L. On construit U(L) à partir de T(L) en imposant les relations Plus formellement, on note I l'idéal bilatère engendré par les On peut caractériser l'algèbre enveloppante de L par la propriété universelle suivante : U(L) est l'unique algèbre assocative telle que pour toute K-algèbre associative A et tout morphisme d'algèbre de Lie Construction [modifier]
![xotimes y-yotimes x=[x,y]](http://upload.wikimedia.org/math/b/d/2/bd2240aecf197b2db0010dfee8f15c66.png) .
.![xotimes y-yotimes x-[x,y]](http://upload.wikimedia.org/math/e/4/8/e4819d4c89717203131bdeddfc38bd8a.png) . U(L) est alors le quotient de T(L) par l'idéal I. L'injection canonique de L dans T(L) fournit alors un morphisme
. U(L) est alors le quotient de T(L) par l'idéal I. L'injection canonique de L dans T(L) fournit alors un morphisme  .
.Propriété universelle [modifier]
 , il existe un unique morphisme d'algèbre associative
, il existe un unique morphisme d'algèbre associative 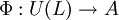 tel que
tel que 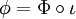 .
.Autres propriétés [modifier]
21:30 Publié dans Algèbre enveloppante | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Crochet de Lie
Crochet de Lie
|
|
Cet article ne cite pas suffisamment ses sources (août 2007).
Si vous connaissez le thème traité, merci d'indiquer les passages à sourcer avec {{Référence souhaitée}} ou, mieux, incluez les références utiles en les liant aux notes de bas de page. (Modifier l'article)
|
Le crochet de Lie est une loi de composition interne [,] sur un espace vectoriel V, qui lui confère une structure d'algèbre de Lie. Le commutateur [u,v]=uv-vu de deux endomorphismesen constitue un des exemples les plus simples. Le nom de crochet de Lie, ou simplement crochet, est souvent employé pour le crochet de Lie de deux champs de vecteurs sur une variété différentielle.
Sommaire[masquer] |
Soit un espace vectoriel V sur un corps Un crochet de Lie vérifie : L'antisymétrie implique [x,x] = 0 pour tout corps pour lequel Si on combine la bilinéarité avec l'antisymétrie [λx + x',y] = − [y,λx + x'] on peut ne vérifier la linéarité que sur une seule composante:[λx + x',y] = λ[x,y] + [x',y]. Muni d'un crochet de Lie, un espace vectoriel devient une algèbre de Lie. Soit V une variété différentielle et X et Y deux champs de vecteurs sur V. On note X . f la dérivée de la fonction f dans la direction du champ X. Le crochet de Lie de X et Y est l'unique champ de vecteur, noté [X,Y], tel que, pour toute fonction f indéfiniment dérivable, On montre en effet qu'un champ de vecteurs Z peut être caractérisé par la façon dont il dérive les applications. On vérifie en outre que l'application [,] définit bien un crochet de Lie sur les champs de vecteurs. Voir pour les démonstrations l'article dérivée de Lie. Lorsque deux champs de vecteurs ont un crochet nul, on dit qu'ils commutent.Définition générale [modifier]
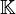 . Un crochet de Lie est une loi de composition interne sur V (c'est-à-dire que le crochet de Lie de deux vecteurs est encore un vecteur :
. Un crochet de Lie est une loi de composition interne sur V (c'est-à-dire que le crochet de Lie de deux vecteurs est encore un vecteur : ![forall x,yin V,quad [x,y]in V](http://upload.wikimedia.org/math/c/9/0/c90e2410e31abf79d4f6e106317124d8.png) ), vérifiant les propriétés suivantes :
), vérifiant les propriétés suivantes :
![forall x,x',yin V,lambda,muinmathbb K, [lambda x+mu x', y]=lambda[x,y]+mu [x',y],](http://upload.wikimedia.org/math/c/0/1/c01d118d897c2d3f49c20c718d51ae12.png)
![forall x,y,y'in V,lambda,muinmathbb K,[x,lambda y+mu y']=lambda[x,y]+mu [x,y']](http://upload.wikimedia.org/math/4/f/e/4fe65ba8376181cbed9147b7c0c055c0.png) .
.![forall xin V,quad [x,x]=0](http://upload.wikimedia.org/math/d/8/8/d88816febe6581ab9bb2e732129847f6.png)
![forall x,y,zin V, [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0](http://upload.wikimedia.org/math/c/6/c/c6c225e906d1dc76d5e14589e036be94.png) .
.
![forall x,yin V, [x,y]=-[y,x]](http://upload.wikimedia.org/math/e/e/e/eeeffe9a658fc19122b5102dad29c923.png) .
.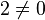 (corps de caractéristique différente de deux).
(corps de caractéristique différente de deux).Crochet de Lie de deux champs de vecteurs [modifier]
![[X,Y]cdot f = Xcdot (Ycdot f) -Y cdot (Xcdot f)](http://upload.wikimedia.org/math/8/7/2/87246955c4529cfe2065604eaff72625.png)
Bibliographie [modifier]
Voir aussi [modifier]
21:30 Publié dans Crochet de Lie | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Classification de Bianchi
La classification de Bianchi est une classification des algèbres de Lie réelles de dimension 3, donnée par Luigi Bianchi.Classification de Bianchi
Classification de Bianchi [modifier]
| Type | Description | Exemple | Groupe de Lie | Matrice |
|---|---|---|---|---|
| Type I | Abélienne | R³, muni d'un crochet nul | R³ comme groupe additif | M = 0 |
| Type II | Nilpotente et unimodulaire | H³, l'algèbre de Heisenberg | Le Groupe de Heisenberg de dimension 3 | M nilpotente non nulle |
| Type III | Résoluble et pas unimodulaire | Rx... | RxG : Produit direct du groupe additif R et du groupe G des matrices triangulaires supérieures de déterminant 1 | M a une unique valeur propre nulle |
| Type IV | Résoluble et pas unimodulaire | M est une matrice non semi-simple possédant une unique valeur propre, qui est non nulle. | ||
| Type V | Résoluble et non unimodulaire | M est une matrice semi-simple possédant une unique valeur propre. | ||
| Type VI | Résoluble et non unimodulaire | M a deux valeurs propres réelles distinctes non nulles et de somme non nulle. | ||
| Type VI0 | Résoluble et unimodulaire | so(1,1) | SO(1,1) | M possède deux valeurs propres réelles distinctes de somme nulle. |
| Type VII | Résoluble et unimodulaire | M a des valeurs propres non réelles et non imaginaires pures. | ||
| Type VII0 | Résoluble et unimodulaire | Groupe des isométries directes du plan euclidien | M ne possède que des valeurs propres imaginaires pures non nulles. | |
| Type VIII | Semisimple et unimodulaire | sl2(R) | SL2(R) | Irréalisable |
| Type IX | Semisimple et unimodulaire | o3(R) ou su2(C) | SO3(R) ou SU2(C) | Irréalisable |
En cosmologie, cette classification est utilisée pour les espace-temps homogènes de dimension 3+1. L'univers de Friedmann-Lemaître-Robertson-Walker est isotrope, ce qui est un cas particulier du type I, V et IX décrit ci-dessus. Le cas général correspond à univers homogène, mais dont l'expansion est anisotrope, c'est-à-dire dont le taux d'expansion est différent suivant trois directions orthogonales . Le type IX de la classification de Bianchi (la Métrique de Kasner est un cas particulier) révèle une dynamique particulièrement complexe de l'expansion. Celle-ci se faisant par la succession d'époques de type expansion anisotrope (avec deux directions en expansion, une en contraction) qui sont séparées par des périodes où les taux d'expansion dans les trois directions changent de façon brutale et relativement chaotique.Intérêt pour la cosmologie [modifier]
Références [modifier]
21:29 Publié dans Classification de Bianchi | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Bialgèbre de Lie
Bialgèbre de Lie
|
|
Cet article est une ébauche concernant les mathématiques.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
En mathématiques, une bialgèbre de Lie est une algèbre de Lie munie d'une application (appelée coproduit ou cocommutateur) telle que l'application duale δ * soit un crochet de Lie, et telle que δ soit un cocycle : Remarque importante : Une bialgèbre de Lie n'est pas a proprement parler une bialgèbre. En effet, on exige en général d'une bialgèbre que son algèbre sous-jacente soit unitaire etassociative.
![delta([X,Y]) = left( operatorname{ad}_X otimes 1 + 1 otimes operatorname{ad}_X right) delta(Y) - left( operatorname{ad}_Y otimes 1 + 1 otimes operatorname{ad}_Y right) delta(X)](http://upload.wikimedia.org/math/1/0/2/10207876644736180447ff35d551f701.png)
21:27 Publié dans Bialgèbre de Lie | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Algèbre de Lie
En mathématiques, une algèbre de Lie, nommée en l'honneur du mathématicien Sophus Lie, est un espace vectoriel qui est muni d'un crochet de Lie, c'est-à-dire d'une loi de composition interne bilinéaire, antisymétrique et qui vérifie l'identité de Jacobi. Une algèbre de Lie est un cas particulier d'algèbre sur un corps.Algèbre de Lie
Sommaire[masquer] |
Soit Une algèbre de Lie sur Le produit [x,y] est appelé crochet de Lie (ou simplement crochet) de x et y. Puisque le crochet est une fonction bilinéaire alternée de x,y, on a aussi l'identité [x,y] = − [y,x] pour tousx,y dans Une sous-algèbre de Lie de Remarque : contrairement aux algèbres tensorielles (et aux algèbres de Clifford, dont les algèbres extérieures), les algèbres de Lie ne sont pas unitaires, ni associatives. Un morphisme d'algèbre de Lie Un idéal de Si Une représentation d'une algèbre de Lie Le morphisme Les algèbres de Lie sont naturellement associées aux groupes de Lie. Si G est un groupe de Lie et 1 son élément neutre, alors l'espace tangent en 1 à G est une algèbre de Lie ; la construction exacte de cette algèbre est détaillée dans la section correspondante de l'article Groupe de Lie. La même construction est valable pour les groupes algébriques. On note en général en petites lettres gothiques l'algèbre de Lie associée à un groupe de Lie, ou à un groupe algébrique. Ainsi, comme on l'a déjà vu, Si φ est un morphisme de groupes entre deux groupes de Lie G et H, et si l'on suppose φ différentiable, alors sa différentielle en l'identité sera un morphisme entre les algèbres de Lie La classification des algèbres de Lie est utilisée de façon cruciale pour l'étude des groupes de Lie, des groupes algébriques et de leurs représentations. Si Une algèbre de Lie est dite nilpotente lorsque toute suite de commutateurs Plus précisément, définissons Ci par S'il existe un i tel que Ci=0, on dit que L'algèbre Le théorème d'Engel affirme que toute sous-algèbre nilpotente de Définissons par récurrence Di par S'il existe un i tel que Di=0, on dit que Un exemple d'algèbre de Lie résoluble est donné par l'algèbre Le théorème de Lie montre que, si On dit qu'une algèbre de Lie Lorsque On peut montrer que, sous les mêmes hypothèses, toute algèbre de Lie semi-simple est en fait une somme directe d'algèbres de Lie simples. Les algèbres de Lie simples de dimension finie sur le corps L'algèbre de Lie Les algèbres de Lie semi-simples de dimension finie sur le corps EI, EII, EIII, EIV (de type E6) EV, EVI, EVII (de type E7) EVIII, EIX (de type E8) FI, FII (de type F4) et GI (de type G2) suivant la notation d'Helgason1) Il n'y a pas de classification générale des algèbres de Lie de dimension infinie mais plusieurs classes de telles algèbres ont été étudiées. Il existe différentes sortes de généralisations des algèbres de Lie, on citera les superalgèbres de Lie, les groupes quantiques, les algèbres de Leibniz, les algèbres pré-Lie.Définitions, exemples et premières propriétés [modifier]
Définition [modifier]
 un corps.
un corps. est un espace vectoriel
est un espace vectoriel  sur
sur  muni d'une application bilinéaire
muni d'une application bilinéaire ![(x,y) mapsto [x,y]](http://upload.wikimedia.org/math/7/5/e/75e87350f83275e11f126171780fd7ca.png) de
de 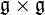 dans
dans  qui vérifie les propriétés suivantes:
qui vérifie les propriétés suivantes:
![forall x in mathfrak{g}, [x,x]=0](http://upload.wikimedia.org/math/f/3/2/f3223a3fe063412bb2f5033ba34850f5.png) ;
;![forall x,y,z in mathfrak{g}, [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0](http://upload.wikimedia.org/math/6/7/d/67d115952cf9c1c691b6053868febb0d.png)
 . L'identité (2) ci-dessus est appelée l'identité de Jacobi.
. L'identité (2) ci-dessus est appelée l'identité de Jacobi. est un sous-espace vectoriel de
est un sous-espace vectoriel de  stable pour le crochet de Lie. Toute sous-algèbre de Lie de
stable pour le crochet de Lie. Toute sous-algèbre de Lie de  est munie de manière évidente d'une structure d'algèbre de Lie sur
est munie de manière évidente d'une structure d'algèbre de Lie sur  .
.Quelques exemples classiques d'algèbres de Lie [modifier]
![forall x,y in E, [x,y]=0](http://upload.wikimedia.org/math/4/7/b/47b2e0b6393e77c2e6376834f8c87276.png) . Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne.
. Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne.![forall x,y in A, [x,y]=x*y-y*x](http://upload.wikimedia.org/math/5/9/7/59711ef28af13f749a361b567295a858.png) (c'est lecommutateur des deux éléments x et y). Il est facile de vérifier que l'on définit ainsi sur A une structure d'algèbre de Lie.
(c'est lecommutateur des deux éléments x et y). Il est facile de vérifier que l'on définit ainsi sur A une structure d'algèbre de Lie. est contenue dans une algèbre associative, appelée algèbre enveloppante, dans laquelle le crochet de Lie coïncide avec le crochet définit ci-dessus. L'algèbre enveloppante est beaucoup plus grande que l'algèbre de départ.
est contenue dans une algèbre associative, appelée algèbre enveloppante, dans laquelle le crochet de Lie coïncide avec le crochet définit ci-dessus. L'algèbre enveloppante est beaucoup plus grande que l'algèbre de départ. , l'espace des matrices
, l'espace des matrices 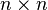 à coefficients dans
à coefficients dans  . C'est une algèbre associative pour le produit matriciel usuel. On peut donc également lui donner une structure d'algèbre de Lie, avec le crochet [A,B] = AB − BA. On note
. C'est une algèbre associative pour le produit matriciel usuel. On peut donc également lui donner une structure d'algèbre de Lie, avec le crochet [A,B] = AB − BA. On note  cette algèbre, lorsque l'on considère sa structure d'algèbre de Lie.
cette algèbre, lorsque l'on considère sa structure d'algèbre de Lie. stable par le crochet est une algèbre de Lie. Ainsi, on peut vérifier que l'ensemble des matrices de trace nulle est une algèbre de Lie, que l'on note
stable par le crochet est une algèbre de Lie. Ainsi, on peut vérifier que l'ensemble des matrices de trace nulle est une algèbre de Lie, que l'on note  .
. .
. avec le produit vectoriel comme crochet de Lie est une algèbre de Lie.
avec le produit vectoriel comme crochet de Lie est une algèbre de Lie.Morphismes et idéaux [modifier]
 est une application linéaire φ qui respecte le crochet de Lie, c'est-à-dire telle que
est une application linéaire φ qui respecte le crochet de Lie, c'est-à-dire telle que![forall a,b in mathfrak{g}, phi([a,b])=[phi(a),phi(b)]](http://upload.wikimedia.org/math/7/9/f/79fe9d02198bb8da7ba2c3fe5df52add.png) .
. est un sous-espace vectoriel
est un sous-espace vectoriel  tel que
tel que ![forall ginmathfrak{g}, forall hin mathfrak{h}, [g,h]inmathfrak{h}](http://upload.wikimedia.org/math/9/f/e/9fe5cc6e32f7a61a988f42d549cb43b3.png) . C'est en particulier une sous-algèbre de Lie. Si une algèbre de Lie n'admet pas d'idéal non trivial, elle est dite simple.
. C'est en particulier une sous-algèbre de Lie. Si une algèbre de Lie n'admet pas d'idéal non trivial, elle est dite simple. est un idéal de
est un idéal de  , on peut former le quotient de
, on peut former le quotient de  par
par  : c'est l'espace vectoriel quotient
: c'est l'espace vectoriel quotient 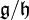 , muni du crochet défini par
, muni du crochet défini par ![[g+mathfrak{h},g'+mathfrak{h}] = [g,g']](http://upload.wikimedia.org/math/8/2/d/82d29f5c4eb7af6feb2661af74a7bd29.png) . La projection
. La projection 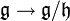 est alors un morphisme d'algèbres de Lie.
est alors un morphisme d'algèbres de Lie. est un morphisme
est un morphisme 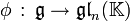 . Autrement dit, c'est une application linéaire telle que φ([g,h]) = φ(g)φ(h) − φ(h)φ(g).
. Autrement dit, c'est une application linéaire telle que φ([g,h]) = φ(g)φ(h) − φ(h)φ(g). défini par ad(g)(h) = [g,h] définit une représentation de
défini par ad(g)(h) = [g,h] définit une représentation de  , appelée représentation adjointe. L'identité de Jacobi exprime précisément le fait que ad respecte le crochet. Le noyau de cette représentation est le centre
, appelée représentation adjointe. L'identité de Jacobi exprime précisément le fait que ad respecte le crochet. Le noyau de cette représentation est le centre ![Z(mathfrak{g})={ginmathfrak{g}forall hinmathfrak{g} [g,h]=0}](http://upload.wikimedia.org/math/a/f/e/afe7160b530a847134d5f4291027ee9c.png) de l'algèbre de Lie
de l'algèbre de Lie 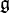 .
.Relation avec les groupes de Lie et les groupes algébriques [modifier]
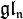 désigne l'ensemble des matrices carrées de taille n et
désigne l'ensemble des matrices carrées de taille n et 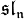 désigne l'ensemble des matrices carrées de taille n de trace nulle. De la même façon,
désigne l'ensemble des matrices carrées de taille n de trace nulle. De la même façon,  désigne l'ensemble des matrices carrées A de taille n antisymétriques, etc. Dans tous ces exemples, le crochet de Lie n'est rien d'autre que le commutateur : [A,B]=AB-BA.
désigne l'ensemble des matrices carrées A de taille n antisymétriques, etc. Dans tous ces exemples, le crochet de Lie n'est rien d'autre que le commutateur : [A,B]=AB-BA. et
et  de G et H. En particulier, à une représentation de G différentiable, on associe une représentation de
de G et H. En particulier, à une représentation de G différentiable, on associe une représentation de  .
.Classification [modifier]
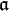 et
et 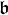 sont deux sous-algèbres de Lie d'une algèbre de Lie
sont deux sous-algèbres de Lie d'une algèbre de Lie  , notons
, notons ![[mathfrak{a},mathfrak{b}]](http://upload.wikimedia.org/math/c/5/2/c528d5c197e3f72db0a9bbc760333ee4.png) le sous-espace vectoriel engendré par les éléments de la forme [a,b] pour
le sous-espace vectoriel engendré par les éléments de la forme [a,b] pour  et
et 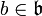 .
.Algèbres de Lie nilpotentes [modifier]
![[[[g_1,g_2],g_3],dots,g_n]](http://upload.wikimedia.org/math/4/8/a/48ab7757f1f2f8ed370a0f9d8acecd13.png) finit par être nulle, lorsque n devient suffisamment grand.
finit par être nulle, lorsque n devient suffisamment grand. et
et ![C_{i+1}=[C_i,mathfrak{g}]](http://upload.wikimedia.org/math/3/b/2/3b21f80fad4a73cdcc2c55569abfd0d0.png) .
. est nilpotente. Cette notion est à mettre en parallèle avec celle de groupe nilpotent. Il est facile de voir que toute algèbre de Lie abélienne est nilpotente.
est nilpotente. Cette notion est à mettre en parallèle avec celle de groupe nilpotent. Il est facile de voir que toute algèbre de Lie abélienne est nilpotente. des matrices triangulaires strictes, c'est-à-dire de la forme
des matrices triangulaires strictes, c'est-à-dire de la forme  fournit un exemple d'algèbre de Lie nilpotente.
fournit un exemple d'algèbre de Lie nilpotente. est en fait simultanément trigonalisable et donc conjuguée à une sous-algèbre de
est en fait simultanément trigonalisable et donc conjuguée à une sous-algèbre de  .
.Algèbres de Lie résolubles [modifier]
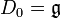 et Di + 1 = [Di,Di]
et Di + 1 = [Di,Di] est résoluble. Comme dans le cas des algèbres nilpotentes, cette notion correspond à celle de groupe résoluble. Il est facile de voir que toute algèbre de Lie nilpotente est résoluble.
est résoluble. Comme dans le cas des algèbres nilpotentes, cette notion correspond à celle de groupe résoluble. Il est facile de voir que toute algèbre de Lie nilpotente est résoluble.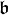 des matrices triangulaires supérieures dans
des matrices triangulaires supérieures dans  .
.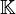 est algébriquement clos et de caractéristique nulle, alors toute sous-algèbre de Lie résoluble de
est algébriquement clos et de caractéristique nulle, alors toute sous-algèbre de Lie résoluble de  est conjuguée à une sous-algèbre de
est conjuguée à une sous-algèbre de 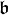
Algèbres de Lie semi-simples et réductives [modifier]
 est semi-simple lorsqu'elle ne contient pas d'idéal résoluble non trivial.
est semi-simple lorsqu'elle ne contient pas d'idéal résoluble non trivial.  est dite réductive lorsque sa représentation adjointe est semi-simple.
est dite réductive lorsque sa représentation adjointe est semi-simple.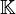 est de caractéristique nulle, et que
est de caractéristique nulle, et que  est de dimension finie, la semi-simplicité de
est de dimension finie, la semi-simplicité de  est équivalente à la non-dégénerescence de la forme de Killing K(x,y) définie par K(x,y) = tr(ad(x)ad(y)), où tr désigne la trace. Par ailleurs,
est équivalente à la non-dégénerescence de la forme de Killing K(x,y) définie par K(x,y) = tr(ad(x)ad(y)), où tr désigne la trace. Par ailleurs,  est réductive si et seulement si
est réductive si et seulement si ![[mathfrak{g},mathfrak{g}]](http://upload.wikimedia.org/math/3/f/1/3f1683bcf0fa96e29329efca70a1d284.png) est semi-simple.
est semi-simple. des nombres complexes sont classifiées par les diagrammes de Dynkin. Il y a donc 4 familles d'algèbres de Lie simples (ou 3 si on considère Bn et Dn comme une même famille) et 5 algèbres de Lie exceptionnelles, correspondant chacune à un diagramme de Dynkin différent.
des nombres complexes sont classifiées par les diagrammes de Dynkin. Il y a donc 4 familles d'algèbres de Lie simples (ou 3 si on considère Bn et Dn comme une même famille) et 5 algèbres de Lie exceptionnelles, correspondant chacune à un diagramme de Dynkin différent.
 correspond l'algèbre de Lie
correspond l'algèbre de Lie 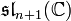 .
.
 correspond l'algèbre de Lie
correspond l'algèbre de Lie 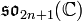 .
.
 correspond l'algèbre de Lie
correspond l'algèbre de Lie  .
.
 correspond l'algèbre de Lie
correspond l'algèbre de Lie  .
.
 est, elle, réductive et son algèbre de Lie dérivée est
est, elle, réductive et son algèbre de Lie dérivée est 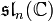 .
. des nombres réels sont classifiées par les involutions d'algèbres de Lie complexe ou, de façon équivalente, par lesinvolutions de systèmes de racines. Ceci correspond à la notion d'algèbre de Lie symétrique. Comme classe d'algèbre de Lie simple réelle, on peut citer:
des nombres réels sont classifiées par les involutions d'algèbres de Lie complexe ou, de façon équivalente, par lesinvolutions de systèmes de racines. Ceci correspond à la notion d'algèbre de Lie symétrique. Comme classe d'algèbre de Lie simple réelle, on peut citer:
Dimension infinie [modifier]
Généralisation [modifier]
Références [modifier]
Voir aussi [modifier]
21:26 Publié dans Algèbre de Lie | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
ABSTRACT ALGEBRA ON LINE
ABSTRACT ALGEBRA ON LINE
This site contains many of the definitions and theorems from the area of mathematics generally called abstract algebra. It is intended for undergraduate students taking an abstract algebra class at the junior/senior level, as well as for students taking their first graduate algebra course. It is based on the books Abstract Algebra, by John A. Beachy and William D. Blair, and Abstract Algebra II, by John A. Beachy.
The site is organized by chapter. The page containing the Table of Contents also contains an index of definitions and theorems, which can be searched for detailed references on subject area pages. Topics from the first volume are marked by the symbol ![]() and those from the second volume by the symbol
and those from the second volume by the symbol ![]() . To make use of this site as a reference, please continue on to the Table of Contents.
. To make use of this site as a reference, please continue on to the Table of Contents.
- TABLE OF CONTENTS (No frames)
-
TABLE OF CONTENTS (Frames version)
Interested students may also wish to refer to a closely related site that includes solved problems: the
- OnLine Study Guide for Abstract Algebra.
REFERENCES
Abstract Algebra, Second Edition, by John A. Beachy and William D. Blair
ISBN 0-88133-866-4, © 1996, 427 pages
Waveland Press, P.O. Box 400, Prospect Heights, Illinois, 60070, Tel. 847 / 634-0081
Abstract Algebra II
This set of lecture notes was expanded into the following text.
Introductory Lectures on Rings and Modules, by John A. Beachy
ISBN 0-521-64407-0, © 1999, 238 pages
Cambridge University Press, London Mathematical Society Student Texts #47
In addition to the Table of Contents, this page contains an index of definitions and theorems, so it can be searched for detailed references on subject area pages. Topics from the first volume are marked by the symbol
Click here for the version with frames.
The site is maintained by John Beachy as a service to students.
email: beachy@math.niu.edu | John Beachy's homepage | About this document
TABLE OF CONTENTS
 Integers
Integers
 Functions
Functions
 Groups
Groups
 Polynomials
Polynomials
 Rings
Rings Fields
Fields
 Structure of Groups
Structure of Groups Galois Theory
Galois Theory
 Unique Factorization
Unique Factorization
 Modules
Modules Structure of Noncommutative Rings
Structure of Noncommutative Rings
 Ideal Theory of Commutative Rings
Ideal Theory of Commutative Rings
INDEX
Index of Definitions
- abelian group
- action, of a group
- algebraic element
- algebraic extension
- algebraic numbers
- alternating group
- annihilator, of a module
- Artinian module
- Artinian ring
- ascending central series
- associated prime ideal
- automorphism, of a group
- automorphism, of a ring
- bicommutator, of a module
- bilinear function
- bimodule
- center of a group
- centralizer, of an element
- characteristic, of a ring
- codomain, of a function
- commutative ring
- commutator
- completely reducible module
- composite number
- composition, of functions
- composition series, for a group
- composition series, for a module
- congruence class of integers
- congruence, modulo n
- congruence, of polynomials
- conjugate, of a group element
- constructible number
- coset
- cycle of length k
- cyclic group
- cyclic module
- cyclic subgroup
- cyclotomic polynomial
- Dedekind domain
- degree of a polynomial
- degree of an algebraic element
- degree of an extension field
- derived subgroup
- dense subring
- dihedral group
- disjoint cycles
- division ring
- divisor, of a polynomial
- divisor, of an integer
- divisor, of zero
- direct product, of groups
- direct product, of modules
- direct sum, of modules
- direct sum, of rings
- domain, of a function
- equivalence class
- equivalence classes defined by a function
- equivalence relation
- essential submodule
- Euclidean domain
- Euler's phi-function
- even permutation
- extension field
- factor, of a polynomial
- factor, of an integer
- factor group
- factor ring
- faithful module
- field
- finite extension field
- finite group
- finitely generated module
- fixed subfield
- formal derivative
- fractional ideal
- free module
- Frobenius automorphism
- function
- Galois field
- Galois group of a polynomial
- general linear group
- generator, of a cyclic group
- greatest common divisor, of integers
- greatest common divisor, of polynomials
- greatest common divisor, in a principal ideal domain
- group
- group algebra
- group ring
- holomorph (of the integers mod n)
- homomorphism, of groups
- homomorphism, of modules
- homomorphism, of rings
- ideal
- idempotent element, of a ring
- image, of a function
- index of a subgroup
- injective module
- inner automorphism, of a group
- integer
- integral closure
- integral domain
- integral extension
- integrally closed domain
- invariant subfield
- inverse function
- invertible element, in a ring
- irreducible element, in a ring
- irreducible polynomial
- isomorphism, of groups
- isomorphism, of rings
- Jacobson radical, of a module
- kernel, of a group homomorphism
- kernel, of a ring homomorphism
- Krull dimension
- leading coefficient
- least common multiple, of integers
- left ideal
- Legendre symbol
- linear action
- localization at a prime ideal
- maximal ideal
- maximal submodule
- minimal polynomial
- minimal submodule
- module
- Moebius function
- monic polynomial
- multiple, of an integer
- multiplicity, of a root
- nil ideal
- nil radical
- nilpotent element, of a ring
- nilpotent ideal
- Noetherian module
- Noetherian ring
- normal extension
- normal subgroup
- normalizer, of a subgroup
- one-to-one function
- onto function
- odd permutation
- orbit
- order of a group
- order of a permutation
- p-group
- partition of a set
- perfect extension
- permutation
- permutation group
- primary ideal
- primitive polynomial
- principal left ideal
- product, of polynomials
- projective module
- polynomial
- prime ideal, of a commutative ring
- prime ideal, of a noncommutative ring
- prime module
- prime number
- prime ring
- primitive ideal
- primitive ring
- principal ideal
- principal ideal domain
- quadratic residue
- quaternions
- radical, for modules
- radical, of an ideal
- radical extension
- regular element
- relatively prime integers
- right ideal
- ring
- ring of differential operators
- root of a polynomial
- root of unity
- semidirect product
- semiprime ideal
- semiprime ring
- semiprimitive ring
- semisimple Artinian ring
- simple extension
- semisimple module
- separable polynomial
- separable extension
- simple group
- simple ring
- simple extension
- simple module
- skew field
- small submodule
- socle of a module
- solvable by radicals
- split homomorphism
- splitting field
- stabilizer
- subfield
- subgroup
- subring
- Sylow subgroup
- symmetric group
- tensor product
- torsion module
- torsionfree module
- transcendental element
- transposition
- unique factorization domain
- unit, of a ring
- von Neumann regular ring
- well-ordering principle
- zero divisor
Index of Theorems
- An algebraic extension of an algebraic extension is algebraic(6.2.10)
- Artin-Wedderburn theorem(11.3.2)
- Artin's lemma(8.3.4)
- Baer's criterion for injectivity(10.5.9)
- Burnside's theorem(7.2.8)
- Cauchy's theorem(7.2.10)
- Cayley's theorem(3.6.2)
- Characteristic of an integral domain(5.2.10)
- Characterization of completely reducible modules(10.2.9)
- Characterization of completely reducible rings(10.5.6)
- Characterization of constructible numbers(6.3.6)
- Characterization of Dedekind domains(12.1.6)
- Characterization of equations solvable by radicals(8.4.6)
- Characterization of finite fields(6.5.2)
- Characterization of finite normal separable extensions(8.3.6)
- Characterization of free modules(10.2.3)
- Characterization of integral elements(12.2.2)
- Characterization of internal direct products(7.1.3)
- Characterization of invertible functions(2.1.8)
- Characterization of the Jacobson radical(11.2.10)
- Characterization of linear actions(7.9.5)
- Characterization of nilpotent groups(7.8.4)
- Characterization of Noetherian modules(10.3.3)
- Characterization of normal subgroups(3.8.7)
- Characterization of projective modules(10.2.11)
- Characterization of semisimple Artinian rings(11.3.4)
- Characterization of prime ideals(11.1.3)
- Characterization of semidirect products(7.9.6)
- Characterization of semiprime ideals(11.1.7)
- Characterization of semisimple modules(10.5.3)
- Characterization of subgroups(3.2.2)
- Characterization of subrings(5.1.3)
- Chinese remainder theorem, for integers(1.3.6)
- Chinese remainder theorem, for rings(5.7.9)
- Class equation(7.2.6)
- Class equation (generalized)(7.3.6)
- Classification of cyclic groups(3.5.2)
- Classification of groups of order less than sixteen
- Classification of groups of order pq(7.4.6)
- Cohen's theorem(12.4.1)
- Computation of Euler's phi-function(1.4.8)
- Construction of extension fields(4.4.8)
- Correspondence between roots and linear factors(4.1.11)
- Dedekind's theorem on reduction modulo p
- Properties of Dedekind domains(12.1.4)
- Degree of a tower of finite extensions(6.2.4)
- DeMoivre's theorem(A.5.2)
- The direct product of nilpotent groups is nilpotent(7.8.2)
- Disjoint cycles commute(2.3.4)
- Division algorithm for integers(1.1.3)
- Division algorithm for polynomials(4.2.1)
- Eisenstein's irreducibility criterion(4.3.6)
- Endomorphisms of indecomposable modules(10.4.6)
- Existence of finite fields(6.5.7)
- Existence of greatest common divisors (for integers)(1.1.6)
- Existence of greatest common divisors (for polynomials)(4.2.4)
- Existence of greatest common divisors, in a principal ideal domain(9.1.6)
- Existence of irreducible polynomials(6.5.12)
- Existence of maximal submodules(10.1.8)
- Existence of quotient fields(5.4.4)
- Existence of splitting fields(6.4.2)
- Existence of tensor products(10.6.3)
- Euclidean algorithm for integers
- Euclidean algorithm for polynomials(Example 4.2.3)
- Euclid's lemma characterizing primes(1.2.5)
- Euclid's theorem on the infinitude of primes(1.2.7)
- Euler's theorem(1.4.11)
- Euler's theorem(Example 3.2.12)
- Euler's criterion(6.7.2)
- Every Euclidean domain is a principal ideal domain(9.1.2)
- Every field of characteristic zero is perfect(8.2.6)
- Every finite extension is algebraic(6.2.9)
- Every finite separable extension is a simple extension(8.2.8)
- Every finite field is perfect(8.2.7)
- Every PID is a UFD(9.1.12)
- Finite integral domains are fields(5.1.8)
- Every finite p-group is solvable(7.6.3)
- Finitely generated torsion modules over a PID(10.3.9)
- Finitely generated torsionfree modules over a PID(10.7.5)
- First isomorphism theorem(7.1.1)
- Fitting's lemma for modules(10.4.5)
- Frattini's argument(7.8.5)
- Fundamental theorem of algebra(8.3.10)
- Fundamental theorem of arithmetic(1.2.6)
- Fundamental theorem of finitely generated modules over a PID(10.7.5)
- Fundamental theorem of Galois theory(8.3.8)
- Fundamental theorem of finite abelian groups(7.5.4)
- Fundamental homomorphism theorem for groups(3.8.8)
- Fundamental homomorphism theorem for rings(5.2.6)
- F[x] is a principal ideal domain(4.2.2)
- On Galois groups(8.4.3, 8.4.4)
- Galois groups of cyclotomic polynomials(8.5.4)
- Galois groups over finite fields(8.1.7)
- Galois groups and permutations of roots(8.1.4)
- Gauss's lemma(4.3.4)
- When the group of units modulo n is cyclic(7.5.11)
- Hilbert basis theorem(10.3.7)
- Hilbert's nullstellensatz(12.4.9)
- Hopkin's theorem(11.3.5)
- Ideals in the localization of an integral domain(5.8.11)
- Impossibility of trisecting an angle(6.3.9)
- Incomparability, lying-over, and going up(12.2.9)
- Insolvability of the quintic(8.4.8)
- Irreducibility of cyclotomic polynomials(8.5.3)
- Irreducible ideals are primary(12.3.6)
- Irreducible polynomials over R(A.5.7)
- Jacobson density theorem(11.3.7)
- Jordan-Holder theorem for groups(7.6.10)
- Jordan-Holder theorem for modules(10.4.2)
- Kronecker's theorem(4.4.8)
- Krull's theorem(12.4.6)
- Krull-Schmidt theorem(10.4.9)
- Lagrange's theorem(3.2.10)
- Lasker-Noether decomposition theorem(12.3.10)
- Maschke's theorem(10.5.8)
- Maximal subgroups in nilpotent groups(7.8.5)
- Moebius inversion formula(6.6.6)
- The multiplicative group of a finite field is cyclic(6.5.10)
- Nakayama's lemma(11.2.8)
- The nil radical is nilpotent (in Noetherian rings)(12.4.3)
- Number of irreducible polynomials over a finite field(6.6.9)
- Number of roots of a polynomial(4.1.12)
- Order of a permutation(2.3.8)
- Order of the Galois group of a polynomial(8.1.6)
- Partial fractions(Example 4204)
- Every p-group is abelian(7.2.9)
- Every permutation is a product of disjoint cycles(2.3.5)
- The polynomial ring over a UFD is a UFD(9.2.6)
- The ring of power series is Noetherian(12.4.2)
- Prime and maximal ideals(5.3.9)
- Prime ideals in a principal ideal domain(5.3.10)
- Generalized principal ideal theorem(12.4.7)
- Quadratic reciprocity law(6.7.3)
- Rational roots(4.3.1)
- Remainder theorem(4.1.9)
- Schur's lemma(10.1.11)
- Second isomorphism theorem(7.1.2)
- Simplicity of PSL(2,F)(7.7.9)
- Simplicity of the alternating group(7.7.4)
- The smallest nonabelian simple group(7.10.7)
- On solvable groups(7.6.7, 7.6.8)
- Splitting fields are unique(6.4.5)
- Structure of simple extensions(6.1.6)
- Subgroups of cyclic groups(3.5.1)
- Sylow's theorems(7.4.1, 7.4.4)
- When the symmetric group is solvable(7.7.2)
- Unique factorization of integers(1.2.6)
- Unique factorization of polynomials(4.2.9)
- Wedderburn's theorem(8.5.6)
- Source : http://www.math.niu.edu/~beachy/aaol/contents.html#index
07:32 Publié dans ABSTRACT ALGEBRA ON LINE | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
GALOIS THEORY
GALOIS THEORY
Excerpted from Beachy/Blair, Abstract Algebra, 2nd Ed., © 1996Chapter 8
- 8.1 The Galois group of a polynomial
- 8.2 Multiplicity of roots
- 8.3 The fundamental theorem of Galois theory
- 8.4 Solvability by radicals
- 8.5 Cyclotomic polynomials
- 8.6 Computing Galois groups
Forward | Back | Table of Contents | About this document
The Galois group of a polynomial
To study solvability by radicals of a polynomial equation f(x) = 0, we let K be the field generated by the coefficients of f(x), and let F be a splitting field for f(x) over K. Galois considered permutations of the roots that leave the coefficient field fixed. The modern approach is to consider the automorphisms determined by these permutations. We note that any automorphism of a field F must leave its prime subfield fixed.8.1.1. Proposition. Let F be an extension field of K. The set of all automorphisms  : F -> F such that
: F -> F such that  (a) = a for all a in K is a group under composition of functions.
(a) = a for all a in K is a group under composition of functions.
8.1.2. Definition. Let F be an extension field of K. The set
{ 
 Aut(F) |
Aut(F) |  (a) = a for all a
(a) = a for all a  K }
K }
8.1.3. Definition. Let K be a field, let f(x)  K[x], and let F be a splitting field for f(x) over K. Then Gal(F/K) is called the Galois group of f(x) over K, or the Galois group of the equation f(x) = 0 over K.
K[x], and let F be a splitting field for f(x) over K. Then Gal(F/K) is called the Galois group of f(x) over K, or the Galois group of the equation f(x) = 0 over K.
8.1.4. Proposition. Let F be an extension field of K, and let f(x)  K[x]. Then any element of Gal(F/K) defines a permutation of the roots of f(x) that lie in F.
K[x]. Then any element of Gal(F/K) defines a permutation of the roots of f(x) that lie in F.
8.1.5. Lemma. Let f(x)  K[x] be a polynomial with no repeated roots and let F be a splitting field for f(x) over K. If
K[x] be a polynomial with no repeated roots and let F be a splitting field for f(x) over K. If  : K -> L is a field isomorphism that maps f(x) to g(x)
: K -> L is a field isomorphism that maps f(x) to g(x)  L[x] and E is a splitting field for g(x) over L, then there exist exactly [F:K] isomorphisms
L[x] and E is a splitting field for g(x) over L, then there exist exactly [F:K] isomorphisms  : F -> E such that
: F -> E such that  (a) =
(a) =  (a) for all a in K.
(a) for all a in K.
8.1.6. Theorem. Let K be a field, let f(x)  K[x], and let F be a splitting field for f(x) over K. If f(x) has no repeated roots, then |Gal(F/K)| = [F:K].
K[x], and let F be a splitting field for f(x) over K. If f(x) has no repeated roots, then |Gal(F/K)| = [F:K].
8.1.7. Corollary. Let K be a finite field and let F be an extension of K with [F:K] = m. Then Gal(F/K) is a cyclic group of order m.
Multiplicity of roots
8.2.1. Definition. Let f(x) be a polynomial in K[x], and let F be a splitting field for f(x) over K. If f(x) has the factorizationf(x) = (x - r1)m1 (x - r2)m2 · · · (x - rt)mt
over F, then we say that the root ri has multiplicity mi.If mi=1, then ri is called a simple root.
8.2.2. Definition. Let f(x)  K[x], with f(x) =
K[x], with f(x) = 
 ak xk. The formal derivative f'(x) of f(x) is defined by the formula
ak xk. The formal derivative f'(x) of f(x) is defined by the formula
f'(x) = 
 k ak xk-1,
k ak xk-1,
8.2.3. Proposition. The polynomial f(x) in K[x] has no multiple roots if and only if gcd(f(x),f'(x)) = 1.
8.2.4. Proposition. Let f(x) be an irreducible polynomial over the field K. Then f(x) has no multiple roots unless chr(K) = p  0 and f(x) has the form
0 and f(x) has the form
f(x) = a0 + a1 xp + a2 x2p + · · · + an xnp.
8.2.5. Definition. A polynomial f(x) over the field K is called separable if its irreducible factors have only simple roots.An algebraic extension field F of K is called separable over K if the minimal polynomial of each element of F is separable.
The field F is called perfect if every polynomial over F is separable.
8.2.6. Theorem. Any field of characteristic zero is perfect. A field of characteristic p>0 is perfect if and only if each of its elements has a pth root.
8.2.7. Corollary. Any finite field is perfect.
8.2.8. Theorem. Let F be a finite extension of the field K. If F is separable over K, then it is a simple extension of K.
The fundamental theorem of Galois theory
8.3.1. Proposition. Let F be a field, and let G be a subgroup of Aut(F). Then{ a  F |
F |  (a) = a for all
(a) = a for all 
 G }
G }
8.3.2. Definition. Let F be a field, and let G be a subgroup of Aut (F). Then
{ a  F |
F |  (a) = a for all
(a) = a for all 
 G }
G }
8.3.3. Proposition. If F is the splitting field over K of a separable polynomial and G = Gal(F/K), then FG = K.
8.3.4. Lemma. [Artin] Let G be a finite group of automorphisms of the field F, and let K = FG. Then
[F:K]  | G |.
| G |.
8.3.6. Theorem. The following conditions are equivalent for an extension field F of K:
- (1) F is the splitting field over K of a separable polynomial;
- (2) K = FG for some finite group G of automorphisms of F;
- (3) F is a finite, normal, separable extension of K.
Example. 8.3.1. The Galois group of GF(pn) over GF(p) is cyclic of order n, generated by the automorphism  defined by
defined by  (x) = xp, for all x in GF(pn). This automorphism is usually known as theFrobenius automorphism of GF(pn).
(x) = xp, for all x in GF(pn). This automorphism is usually known as theFrobenius automorphism of GF(pn).
8.3.8. Theorem. [Fundamental Theorem of Galois Theory] Let F be the splitting field of a separable polynomial over the field K, and let G = Gal(F/K).
- (a) There is a one-to-one order-reversing correspondence between subgroups of G and subfields of F that contain K:
- (i) If H is a subgroup of G, then the corresponding subfield is FH, and
H = Gal(F/FH).
-
(ii) If E is a subfield of F that contains K, then the corresponding subgroup of G is H = Gal(F/E), and
E = FH.
- (i) If H is a subgroup of G, then the corresponding subfield is FH, and
- (b) For any subgroup H of G, we have
[F:FH] = | H | and [FH:K] = [G:H].
- (c) Under the above correspondence, the subgroup H is normal if and only if the subfield E = FH is a normal extension of K. In this case,
Gal(E/K)
 Gal(F/K) / Gal(F/E).
Gal(F/K) / Gal(F/E).
 (E)
(E)  E for all
E for all in Gal(F/K). In the context of the fundamental theorem, we say that two intermediate subfields E1 and E2 are conjugate if there exists
in Gal(F/K). In the context of the fundamental theorem, we say that two intermediate subfields E1 and E2 are conjugate if there exists 
 Gal(F/K) such that
Gal(F/K) such that  ( E1 ) = E2. We now show that the subfields conjugate to an intermediate subfield E correspond to the subgroups conjugate to Gal(F/E). Thus E is a normal extension if and only if it is conjugate only to itself.
( E1 ) = E2. We now show that the subfields conjugate to an intermediate subfield E correspond to the subgroups conjugate to Gal(F/E). Thus E is a normal extension if and only if it is conjugate only to itself.
8.3.9. Proposition. Let F be the splitting field of a separable polynomial over the field K, and let E be a subfield such that K  E
E  F, with H = Gal(F/E). If
F, with H = Gal(F/E). If 
 Gal(F/K), then
Gal(F/K), then
Gal(F/ (E)) =
(E)) =  H
H  -1.
-1.
Solvability by radicals
In most results in this section we will assume that the fields have characteristic zero, in order to guarantee that no irreducible polynomial has multiple roots. When we say that a polynomial equation is solvable by radicals, we mean that the solutions can be obtained from the coefficients in a finite sequence of steps, each of which may involve addition, subtraction, multiplication, division, or taking nth roots. Only the extraction of an nth root leads to a larger field, and so our formal definition is phrased in terms of subfields and adjunction of roots of xn-a for suitable elements a.8.4.1. Definition. An extension field F of K is called a radical extension of K if there exist elements u1, u2, ... , um in F such that
- (i) F = K (u1, u2, ... , um), and
-
(ii) u1n1
 K and uini
K and uini  K ( u1, ... , ui-1 ) for i = 2, ... , m and n1, n2, ... , nm
K ( u1, ... , ui-1 ) for i = 2, ... , m and n1, n2, ... , nm  Z.
Z.
 K[x], the polynomial equation f(x) = 0 is said to be solvable by radicals if there exists a radical extension F of K that contains all roots of f(x).
K[x], the polynomial equation f(x) = 0 is said to be solvable by radicals if there exists a radical extension F of K that contains all roots of f(x).
8.4.2. Proposition. Let F be the splitting field of xn - 1 over a field K of characteristic zero. Then Gal(F/K) is an abelian group.
8.4.3. Theorem. Let K be a field of characteristic zero that contains all nth roots of unity, let a  K, and let F be the splitting field of xn-a over K. Then Gal(F/K) is a cyclic group whose order is a divisor of n.
K, and let F be the splitting field of xn-a over K. Then Gal(F/K) is a cyclic group whose order is a divisor of n.
8.4.4. Theorem. Let p be a prime number, let K be a field that contains all pth roots of unity, and let F be an extension of K. If [F:K] = |Gal(F/K)| = p, then F = K(u) for some u  F such that up
F such that up  K.
K.
8.4.5. Lemma. Let K be a field of characteristic zero, and let E be a radical extension of K. Then there exists an extension F of E that is a normal radical extension of K.
8.4.6. Theorem. Let f(x) be a polynomial over a field K of characteristic zero. The equation f(x) = 0 is solvable by radicals if and only if the Galois group of f(x) over K is solvable.
Theorem 7.7.2 shows that Sn is not solvable for n  5, and so to give an example of a polynomial equation of degree n that is not solvable by radicals, we only need to find a polynomial of degree n whose Galois group over Q is Sn.
5, and so to give an example of a polynomial equation of degree n that is not solvable by radicals, we only need to find a polynomial of degree n whose Galois group over Q is Sn.
8.4.7. Lemma. Any subgroup of S5 that contains both a transposition and a cycle of length 5 must be equal to S5 itself.
8.4.8. Theorem. There exists a polynomial of degree 5 with rational coefficients that is not solvable by radicals.
Cyclotomic polynomials
8.5.1. Definition. Let n be a positive integer, and let be the complex number
be the complex number  = cos
= cos  + i sin
+ i sin  , where
, where  = 2
= 2  / n. The polynomial
/ n. The polynomial
 n (x) =
n (x) =  k (x -
k (x -  k),
k),
8.5.2. Proposition. Let n be a positive integer, and let  n(x) be the nth cyclotomic polynomial. The following conditions hold:
n(x) be the nth cyclotomic polynomial. The following conditions hold:
- (a) deg (
 n (x)) =
n (x)) =  (n);
(n); -
(b) xn - 1 =
 d | n
d | n  d (x);
d (x); -
(c)
 n (x) is monic, with integer coefficients.
n (x) is monic, with integer coefficients.
 n(x) is irreducible over Q, for every positive integer n.
n(x) is irreducible over Q, for every positive integer n.
8.5.4. Theorem. For every positive integer n, the Galois group of the nth cyclotomic polynomial  n(x) over Q is isomorphic to Zn×.
n(x) over Q is isomorphic to Zn×.
Example. 8.5.2. A regular n-gon is constructible if and only if  (n) is a power of 2. If p is an odd prime, and
(n) is a power of 2. If p is an odd prime, and  (p) is a power of 2, then p must have the form p = 2k + 1, where k is a power of 2. Such primes are called Fermat primes. The only known examples are 3, 5, 17, 257, and 65537. This implies, for example, that a regular 17-gon is constructible.
(p) is a power of 2, then p must have the form p = 2k + 1, where k is a power of 2. Such primes are called Fermat primes. The only known examples are 3, 5, 17, 257, and 65537. This implies, for example, that a regular 17-gon is constructible.
A set that satisfies all the axioms of a field except for commutativity of multiplication is called a division ring or skew field.
8.5.6. Theorem. [Wedderburn] Any finite division ring is a field.
Computing Galois groups
8.6.1. Definition. Let G be a group acting on a set S. We say that G acts transitively on S if for each pair of elements x,y in S there exist an element g in G such that y = gx.If G is a subgroup of the symmetric group Sn, then G is called a transitive group if it acts transitively on the set { 1, 2, ... , n }.
8.6.2. Proposition. Let f(x) be a separable polynomial over the field K, with roots r1 , ... , rn in its splitting field F. Then f(x) is irreducible over K if and only if Gal(F/K) acts transitively on the roots of f(x).
8.6.3. Lemma. Let p be a prime number, and let G be a transitive subgroup of Sp. Then any nontrivial normal subgroup of G is also transitive.
8.6.4. Lemma. Let p be a prime number, and let G be a solvable, transitive subgroup of Sp. Then G contains a cycle of length p.
8.6.5. Proposition. Let p be a prime number, and let G be a solvable, transitive subgroup of Sp. Then G is a subgroup of the normalizer in Sp of a cyclic subgroup of order p.
Let f(x) be a polynomial of degree n over the field K, and assume that f(x) has roots r1, r2, ... , rn in its splitting field F. The element  of F defined by
of F defined by
 =
=  (ri - rj)2,
(ri - rj)2,
 i < j
i < j  n, is called the discriminant of f(x).
n, is called the discriminant of f(x).
It can be shown that the discriminant of any polynomial f(x) can be expressed as a polynomial in the coefficients of f(x), with integer coefficients. This requires use of elementary symmetric functions, and lies beyond the scope of what we have chosen to cover in the book.
We have the following properties of the discriminant:
- (i)

 0 if and only if f(x) has distinct roots;
0 if and only if f(x) has distinct roots; -
(ii)

 K;
K; -
(iii) If

 0, then a permutation
0, then a permutation 
 Sn is even if and only if it leaves unchanged the sign of
Sn is even if and only if it leaves unchanged the sign of
 (ri-rj) .
(ri-rj) .
 , and let F be its splitting field over K. Then every permutation in Gal(F/K) is even if and only if
, and let F be its splitting field over K. Then every permutation in Gal(F/K) is even if and only if  is the square of some element in K.
is the square of some element in K.
We now restrict our attention to polynomials with rational coefficients. The next lemma shows that in computing Galois groups it is enough to consider polynomials with integer coefficients. Then a powerful technique is to reduce the integer coefficients modulo a prime and consider the Galois group of the reduced equation over the field GF(p).
8.6.7. Lemma. Let f(x) = xn + an-1 xn-1 + · · · + a1 x + a0  Q[x], and assume that
Q[x], and assume that
ai = bi / d for d, b0, b1, ... , bn-1  Z.
Z.
Then dn f(x/d) is monic with integer coefficients, and has the same splitting field over Q as f(x).
If p is a prime number, we have the natural mapping  : Z[x] -> Zp[x] which reduces each coefficient modulo p. We will use the notation
: Z[x] -> Zp[x] which reduces each coefficient modulo p. We will use the notation  ( f(x) ) = fp(x).
( f(x) ) = fp(x).
Theorem [Dedekind]. Let f(x) be a monic polynomial of degree n, with integer coefficients and Galois group G over Q, and let p be a prime such that fp(x) has distinct roots. If fp(x) factors in Zp[x] as a product of irreducible factors of degrees n1, n2, ... , nk, then G contains a permutation with the cycle decomposition
(1,2, ... ,n1) (n1+1, n1+2, ... , n1+n2) · · · (n-nk+1, ... ,n),
relative to a suitable ordering of the roots.
07:30 Publié dans GALOIS THEORY | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Un cours de DEA sur la théorie de Galois
07:26 Publié dans Un cours de DEA sur la théorie de Galois | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Théorie de Galois
En mathématiques et plus précisément en algèbre, la théorie de Galois est l'étude des extensions de corps commutatifs, par le biais d'une correspondance avec des groupes de transformations sur ces extensions, les groupes de Galois. Cette méthode féconde, qui constitue l'exemple historique, a essaimé dans bien d'autres branches des mathématiques, avec par exemple la théorie de Galois différentielle, ou la théorie de Galois des revêtements. Cette théorie est née de l'étude par Évariste Galois des équations algébriques. L'analyse de permutations des racines permet d'expliciter une condition nécessaire et suffisante de résolubilité par radicaux. Ce résultat est connu sous le nom de théorème d'Abel-Ruffini. Les applications sont très variées. Elles s'étendent de la résolution de vieilles conjectures comme la détermination des polygonesconstructibles à la règle et au compas démontrée par le théorème de Gauss-Wantzel à la géométrie algébrique à travers, par exemple, lethéorème des zéros de Hilbert.Théorie de Galois
Sommaire[masquer] |
La théorie de Galois voit ses origines dans l'étude des équations algébriques. Elle se ramène à l'analyse des équations polynomiales. Une approche par des changements de variables et des substitutions a permis à des mathématiciens comme Al-Khwarizmi1 (783 850), Tartaglia (1499 1557), Cardano2 (1501 1576) ou Ferrari (1522 1565) de résoudre tous les cas jusqu'au degré quatre. Cette approche ne permet pas d'aller plus loin et deux siècles seront nécessaires pour apporter de nouvelles idées. Gauss (1777 1855) utilise les polynômes cyclotomiques3 pour apporter une contribution à un problème ouvert depuis l'antiquité: celui de la construction à la règle et au compas de polygones réguliers. Il construit en particulier l'heptadécagone, polygone régulier à 17 côtés. Son approche, typiquement galoisienne bien avant la découverte de la théorie, lui vaut le surnom de prince des mathématiciens. Son travail est complété par Wantzel4 (1814 1848), qui donne une condition nécessaire et suffisante de constructibilité des polygones réguliers et démontre l'impossibilité de la trisection de l'angle et de la duplication du cube. Dans le cas général, l'équation quintique n'admet pas de solution par radicaux. C'est la raison pour laquelle une démarche à l'aide de substitutions et changements de variables devient stérile. Lagrange5 (1736 1813) et Vandermonde6(1735 1796) utilisent la notion de permutation à la fin du xviiie siècle et pressentent l'importance de cet outil dans le cadre de l'équation polynomiale. Ruffini7 (1765 1822) est le premier à prévoir l'impossibilité de la solution générale et que la compréhension du phénomène réside dans l'étude des permutations des racines. Sa démonstration reste néanmoins peu rigoureuse et partielle. Le mathématicien norvégien Abel (1802 1829) publie une démonstration8 en 1824 qui finit par convaincre la communauté scientifique. Elle ne propose pas à l'époque de condition nécessaire et suffisante de résolubilité. En étudiant le problème de l'équation algébrique, Galois (1811 1832) met en évidence les premiers éléments de la théorie qui porte maintenant son nom. Ses écrits sont perdus ou tombent dans l'oubli. Un mémoire9 est finalement retrouvé par Liouville (1809 1882) qui le présente à l'Académie des sciences en 1843. Les travaux de Galois accèdent alors in extremis à la postérité. Galois, pour la première fois dans l'histoire des mathématiques, met en évidence une structure abstraite qu'il appelle groupe. À la différence de ses prédécesseurs, il n'étudie pas une incarnation particulière comme les permutations de Lagrange ou les groupes cycliques de Gauss, mais une structure générale définie par un ensemble et une loi. Cette démarche, particulièrement novatrice, est à l'origine de l'algèbre moderne. Liouville en parle dans les termes suivants : « Cette méthode, vraiment digne de l'attention des géomètres, suffirait seule pour assurer à notre compatriote un rang dans le petit nombre des savants qui ont mérité le titre d'inventeur. »10 L'apport majeur de Galois, c'est-à-dire l'utilisation d'une structure algébrique comme outil fondamental, est rapidement compris par la communauté mathématique. Cauchy (1789 1855)publie vingt-cinq articles sur les groupes dont un sur son célèbre théorème11. Cayley (1821 1895) donne la première définition abstraite d'un groupe12. Enfin, Jordan (1838 1922) diffuse largement les idées de Galois. Son livre13 de 1870 présente les travaux de Galois comme une théorie générale sur des groupes, dont le théorème sur la résolution des équations n'est qu'une application. En France, la théorie de Galois est identifiée à celle des groupes à cette époque. D'autres structures sont mises en évidence, particulièrement en Allemagne. Indépendamment des travaux de Galois, Kummer (1810 1893) étudie14 des anneaux et découvre l'ancêtre de la notion d'idéal. Kronecker (1823 1891) et Dedekind (1831 1916) développent les prémisses de la théorie des anneaux et des corps15. Kronecker établit le pont entre les écoles française et allemande. Il donne la définition moderne de groupe de Galois à partir d'automorphismes de corps. À la fin du xixe siècle, Weber (1842 1913) réalise une synthèse16 des différents travaux. La théorie de Galois est alors pour la première fois identifiée avec celle des corps commutatifs. Un nouvel axe d'analyse enrichit la théorie de Galois. En 1872, Klein (1849 1925) se fixe comme objectif de classifier les différentes géométries de l'époque. Il dégage, dans son célèbre programme d'Erlangen, le principe général qu'une géométrie est définie par un espace et un groupe opérant sur cet espace, appelé groupe des isométries. Un pont est ainsi établi entre la théorie des groupes et la géométrie. Ces premiers groupes correspondent à des groupes de Lie et n'appartiennent pas directement à ceux de la théorie de Galois. En 1877 Klein remarque17 que le groupe des isométries laissant invariant l'icosaèdre est isomorphe au groupe de Galois d'une équation quintique. La théorie de Galois s'étend à la géométrie algébrique. Les groupes de Galois prennent alors la forme de revêtements aussi appelés revêtement de Galois. David Hilbert (18621943) étudie les corps de nombres quadratiques et apporte une contribution majeure à la théorie en démontrant18 son célèbre théorème des zéros. Ce théorème possède aussi une interprétation géométrique sur les variétés algébriques. La théorie est maintenant enrichie d'une nouvelle branche: la théorie de Galois géométrique. Elle s'avère particulièrement féconde. Les travaux de Hilbert ouvrent d'autres branches de la théorie de Galois. Le théorème des zéros permet l'étude des premiers groupes de Galois d'ordre infini. Son théorème d'irréductibilité ouvre la problématique inverse. Elle s'énonce de la manière suivante : si G est un groupe alors est-il le groupe de Galois d'une extension? Enfin les travaux de Picard (1856 1941) et Vessiot (1865 1952) ouvrent une autre voie pour l'étude des groupes de Galois d'ordre infini, la théorie de Galois différentielle. Les travaux de Hilbert ont ouvert l'étude des cas où le groupe de Galois est d'ordre infini et commutatif. Ce vaste sujet prend le nom de théorie des corps de classes. Elle est maintenant achevée et est souvent considérée comme un des plus beaux succès des mathématiques du siècle. La formalisation définitive19 de la théorie de Galois est donnée par Artin. L'adjonction de l'algèbre linéaire permet une exposition plus claire et concise. La théorie utilise maintenant toutes les grandes structures de l'algèbre, les groupes, les anneaux, les corps et les espaces vectoriels. Elle dispose maintenant de ramifications importantes en géométrie algébrique. Elle est la base d'une quantité majeure des grandes réalisations mathématiques du xxe siècle. L'alliance de la géométrie et de l'algèbre est presque systématiquement utilisée. On peut citer par exemple les travaux des mathématiciens Jean-Pierre Serre (Médaille Fields 1954) et Grothendieck (Médaille Fields 1966) avec une refonte de la géométrie algébrique, Faltings(Médaille Fields 1986) pour ses travaux sur les modules de Galois démontrant le théorème de Mordell ou Laurent Lafforgue (Médaille Fields 2002) sur le Programme de Langlands, une généralisation de la théorie des corps de classes. Le petit théorème de Fermat nous indique que si a est un entier et p un nombre premier alors: Il est possible de démontrer ce théorème en remarquant que Fp le quotient de l'ensemble des nombres entiers par son idéal engendré par p est un corps, car p est un nombre premier. (Fp*, .) est un groupe fini de cardinal p -1. Le théorème de Lagrange assure que tout élément de ce groupe à la puissance p -1 est égal à l'unité, ce qui démontre le théorème. Conclusion : Ce cas est particulièrement aisé car la structure du corps est simple. Il illustre néanmoins le fait qu'une structure de corps est un outil utile en théorie algébrique des nombres. D'autres théorèmes d'arithmétique modulaire comme la loi de réciprocité quadratique demandent une compréhension beaucoup plus profonde de la structure des corps. C'est la raison pour laquelle la démonstration ne put être trouvée malgré leurs efforts par Euler (1707 1783) ou Lagrange et qu'il fallut attendre Gauss et ses polynômes cyclotomiques pour conclure. Soit L l'ensemble des éléments de la forme a + b.√2 où a et b sont des rationnels. Montrons que L est un corps : L est clairement stable pour l'addition et le passage à l'opposé, et est donc un groupe additif. Il est stable pour la multiplication et le passage à l'inverse des éléments non nuls, en effet: Ces deux dernières propositions montrent que L est un sous-corps des nombres réels. L est aussi un espace vectoriel de dimensiondeux sur les nombres rationnels, car il possède pour base 1 et √2. Un tel corps s'appelle une extension quadratique. Montrons que L ne contient pas la racine cubique de deux : Soit l un élément de L, alors de l 2 est une combinaison linéaire à coefficients rationnels de 1 et √2 car ces deux éléments forment une base et l 2 est un élément de L. il existe donc deux rationnels α etβ tel que l'égalité suivante est vraie: Et pour tout élément l de L il existe un polynôme de degré inférieur ou égal à deux ayant pour racine l. Or, le plus petit degré du polynôme non nul à coefficients rationnels qui annule la racine cubique de deux est trois, et la proposition est démontrée. Conclusion : Wantzel a démontré que les nombres constructibles à la règle et au compas sont soit dans une extension quadratique, soit dans une extension quadratique dont les coefficients sont pris dans une extension quadratique et ainsi de suite. On parle alors de tour d'extension quadratique. Il est possible de démontrer par un raisonnement analogue à celui présenté ici que la racine cubique de deux n'est pas élément d'une tour d'extension quadratique. Voilà pourquoi la duplication du cube est impossible. Le choix judicieux de corps particuliers est la clé de la résolution de cette antique conjecture. Considérons un exemple d'équation du troisième degré : Détermination d'un élément du groupe de Galois : Le polynôme P[X] est un polynôme irréductible à coefficients rationnels. La théorie de Galois nous indique qu'il existe un corps L qui est une extension des rationnels contenant toutes les racines deP[X]. Cette extension est de dimension six. De plus, il existe un sous-corps K de L tel que L est de dimension trois sur K et j la première racine cubique de l'unité est élément de K. Le groupe de Galois de L sur K est l'ensemble des automorphismes de corps de L laissant invariant tout élément de K. La théorie de Galois nous indique que ce groupe a trois éléments, soit g un élément du groupe différent de l'identité. Diagonalisation de g : Le théorème de Lagrange nous assure que g3 est égal à l'identité. Si l est un élément non nul de L, alors l, g(l) et g2(l) forment une base de L sur K. Considérant g comme opérateur linéaire, son polynôme caractéristique est X3 - 1 et ses valeurs propres sont 1, j et j2. Il existe une base (u, v, w) de L sur K constituée de vecteurs propres, car le nombre de valeurs propres est égal à la dimension de L sur K. On a donc g(u)=j·u, g(v)=j2·v et g(w)=w. De plus, 1 + j + j2 = 0. Détermination de l'image des racines par g : Soit x1, une racine de P[X]. L'image d'une racine par g est une racine, en effet: On en déduit que x1, g(x1) et g2(x1) sont les trois racines de P. On peut repésenter x1 comme somme de vecteurs propres de g:x1 = u + v + w (léger abus de notation: w sera en l'occurrence 0, ne formant plus une base comme ci-dessus). Les trois égalités suivantes sont alors vérifiées: Calcul des valeurs des racines : Il suffit d'utiliser les relations entre coefficients et racines pour montrer que : On en déduit que u 3 et v 3 vérifient l'équation X2 + X + 1 = 0. Ce qui permet de conclure que x1 est égal à 2 cos(2π/9), 2 cos(8π/9) ou 2 cos(14π/9). Conclusion : Le groupe de Galois, permet la résolution de l'équation cubique par une diagonalisation d'un endomorphisme. La méthode est généralisable si et seulement si le groupe de Galois possède de bonnes propriétés, en fait s'il est résoluble. Ces exemples ont un point commun, ce sont les propriétés des structures algébriques qui permettent de trouver les solutions. Pour le premier exemple, la propriété démontrée par Lagrange sur les groupes (et donc les groupes multiplicatifs des corps) finis permet de conclure. Dans le deuxième exemple, ce sont les propriétés associées sur la dimension d'un l'espace vectoriel qui sont utilisées. Dans le troisième cas, sont utilisés les propriétés des corps et de leurs extensions, des groupes avec le théorème de Lagrange et celle des espaces vectoriels avec les propriétés de réduction d'endomorphisme dans le cas où le polynôme minimal est scindé. La théorie de Galois offre une richesse dans les structures algébriques permettant de résoudre nombre de cas très différents et dans des domaines éloignés. La théorie algébrique des nombres est l'étude des nombres racines d'un polynôme à coefficients entiers, appelés nombres algébriques. La théorie de Galois est ici essentielle car elle offre la structure la plus adéquate d'analyse, à savoir l'extension finie la plus petite contenant les nombres étudiés. Un sous-ensemble joue un rôle particulier : celui des entiers algébriques, ils correspondent à la généralisation des entiers dans l'extension. L'étude de cet ensemble ajoute à la théorie de Galois de nombreuses propriétés issues de la théorie des anneaux. Les entiers algébriques jouent un rôle important pour la résolution d'équations d'arithmétique modulaire ou diophantiennes. On peut citer comme application de la théorie de Galois à ce domaine, le théorème de Gauss-Wantzel qui détermine tous les polygones réguliers constructibles à la règle et au compas. La Théorie de Kummer s'applique aux équations diophantiennes et permet de valider le grand théorème de Fermat pour presque tous les entiers inférieurs à cent. Enfin, dans le cadre de l'arithmétique modulaire, la loi de réciprocité d'Artin généralise la loi de réciprocité quadratique de Gauss et résout le neuvième problème de Hilbert. La cryptographie est la discipline qui s'attache à protéger un message. Le cadre théorique maintenant le plus utilisé consiste à définir unalgorithme qui, associé à une clef permet de créer un nouveau message dit cryptogramme signifiant qu'il est chiffré. Le message chiffré est simple à déchiffrer, c'est-à-dire simple à transformer en message d'origine avec une clef et difficile sans celle-ci pour la personne qui s'efforce alors de le décrypter. Dans une partie des théories modernes de cryptographie, les lettres du message sont choisies dans un corps fini. Le cadre est donc celui de la théorie de Galois. Il est naturel que les outils associés soient ceux de la théorie. L'arithmétique modulaire (cf par exemple l'algorithme RSA) est très largement employée. Si les techniques simples reposent sur des résultats élémentaires comme le théorème de Bézout, le théorème des restes chinoisou l'exponentiation modulaire, les développements actuels utilisent des outils plus subtils comme les courbes elliptiques (cf une clé privée inviolable ?). La problématique de la théorie des équations algébriques est celle qui donna naissance à la théorie de Galois. Elle complète le théorème d'Abel-Ruffini en proposant une condition nécessaire et suffisante pour l'existence d'une expression par radicaux des racines d'un polynôme. Elle permet néanmoins d'aller plus loin. Le théorème de Kronecker-Weber explicite précisément la structure des extensions rationnelles associées aux polynômes ayant des racines s'exprimant par radicaux. Il devient alors possible de résoudre explicitement toutes les équations de cette nature. Elle possède pour champs d'application tous les corps, offrant un outil puissant à l'arithmétique modulaire. Beaucoup de lois de réciprocité, de même nature que celle démontrée par Gauss dans le cas quadratique sont ainsi démontrables grâce à la théorie de Galois. Abel puis Hermite (1822 1902) ont travaillé sur une autre approche : les fonctions elliptiques. Elles permettent, par exemple, d'exprimer les racines de toute équation polynomiale. La théorie géométrique de Galois intégre cette notion à travers les courbes elliptiques. Le grand théorème de Fermat a été démontré à l'aide de méthodes de cette nature. Il existe une théorie de Galois un peu particulière traitant des équations différentielles polynomiales. Cette théorie prend le nom de théorie de Galois différentielle. Elle étudie une famille particulière de corps appelée extension différentielle. Ces corps possèdent des groupes de Galois. La résolution d'une équation algébrique correspond aussi à l'analyse du groupe associé et permet la résolution d'une équation différentielle. Le corps commutatif est l'objet de la théorie de Galois. C'est donc naturellement la structure centrale de la théorie. La technique la plus importante de construction correspond à l'extension, c'est-à-dire à un corps qui contient le corps d'origine. À partir d'un corps de base, souvent le plus petit, celui engendré par l'unité, qui est un corps cyclique (construit à partir d'un groupe cyclique d'ordre un nombre premier) ou celui des rationnels une nouvelle structure est créée. Cette méthode permet la création d'une zoologie décrivant les différentes propriétés de la structure. Un corps peut ainsi être par exemple algébrique, simple, parfait, quadratique,séparable, cyclotomique ou algébriquement clos. Il existe des théorèmes importants, comme celui de l'élément primitif ou celui de Wedderburn qui assurent que tout corps fini est commutatif. Une extension possède une structure d'espace vectoriel sur son corps de base. Cette structure est importante à deux titres: Elle permet de classifier l'étude des différents corps, ceux de dimension finie dit encore extension finie et les autres. De même qu'en algèbre linaire, le premier cas est infiniment plus simple que l'autre. Elle est ensuite un outil qui permet la démonstration de nombreuses propriétés en adjoignant à la théorie les théorèmes d'algèbres linéaires. On peut citer par exemple le théorème de Gauss-Wantzel dont la démonstration se trouve dans le paragraphe applications des tours d'extension quadratique ou le théorème d'Abel-Ruffini qui utilise une diagonalisationd'endomorphisme. Le cas de dimension infinie est largement plus complexe, il est partiellement traité dans la théorie des corps de classe. Un outil important de la théorie est le polynôme formel. Et la structure d'anneau est celle de l'ensemble des polynômes. Il est utilisé par exemple pour construire des extensions. Une extension est ainsi souvent le quotient de l'anneau des polynômes par un idéal engendré par un polynôme irréductible. Un polynôme joue un rôle particulier dans la théorie: le polynôme minimal qui est le polynôme unitaire de plus petit degré qui possède pour racine un élément donné. Ainsi, une extension est algébrique si tous les éléments possèdent un polynôme minimal, quadratique si le polynôme minimal de tout élément est de degré inférieur ou égal à deux, séparable si aucun polynôme minimal n'a de racine multiple, cyclotomique si l'extension est engendrée par une racine d'un polynôme cyclotomique. Un corps est parfait si toute extension est séparable. La théorie algébrique des nombres utilise aussi souvent des sous-ensembles d'une extension ne disposant que d'une structure d'anneau, comme par exemple les entiers algébriques. Cette structure est l'apport majeur du mathématicien portant le nom de la théorie. Le groupe de Galois est le groupe des automorphismes d'une extension laissant invariant le corps de base. Sous certaines conditions relativement générales, le corps est entièrement caractérisé par son groupe de Galois. Une extension satisfaisant ces conditions est dite galoisienne. En particulier, si la structure d'espace vectoriel est de dimension finie, alors le groupe d'une extension abélienne a pour ordre la dimension du groupe. Comme il est largement plus simple d'étudier un groupe fini qu'une structure de corps, l'analyse du groupe est une puissante méthode pour comprendre le corps. Le groupe de Galois est à l'origine de nombreux théorèmes. On peut citer le théorème fondamental de la théorie, le théorème d'Abel-Ruffini ou celui de Kronecker-Weber. Le terme de classique est largement utilisé, même s'il ne possède pas de définition précise. On le trouve par exemple, sur la page de présentation d'un membre de l'Académie des sciences : Jean-Pierre Ramis. Il est aussi utilisé largement par Daniel Bertrand professeur à l'université de Paris VI. Il désigne en général la théorie recouvrant les extensions algébriques finies et séparables. la théorie traite essentiellement des extensions normales et donc galoisiennes. Les résultats principaux sont le théorème de l'élément primitif et le théorème fondamental de la théorie de Galois. Ce cadre permet par exemple la démonstration du théorème d'Abel-Ruffini de Gauss-Wantzel ou de Kronecker-Weber, il est utilisé dans la classification des corps finis. L'étendue de cette théorie couvre l'état de la science à l'époque de Weber c'est-à-dire la fin du xixe siècle, même si maintenant elle est très généralement présenté avec le formalisme d'Artin. Cela correspond un peu au cas de la dimension finie pour l'algèbre linéaire. La théorie de Galois classique traite le cas des extensions algébriques finies. Toutefois, elle ne s'avère pas assez puissante pour traiter aussi celui des extensions algébriques infinies. Pour cela une étude algébrique ne s'avère pas suffisante, il faut y ajouter l'utilisation de propriétés topologiques. Une extension algébrique est dite galoisienne si elle est séparable et normale. Son groupe de Galois peut alors être défini comme dans le cas classique, mais on y ajoute une topologie qui en fait un groupe topologique compact. Dans le cas d'une extension finie, cette topologie est discrète, de sorte que la seule information contenue dans le groupe de Galois est de nature algébrique. Dans ce cadre, il existe un analogue au théorème fondamental de la théorie de Galois, qui donne une correspondance entre les sous-groupes fermés du groupe de Galois et les extensions intermédiaires de corps. Il est en général difficile de déterminer le groupe de Galois d'une extension donnée, mais la question réciproque est tout aussi intéressante: soit un groupe donné, y a-t-il une extension sur un corps donné qui possède ce groupe comme groupe de Galois? Si oui la ou les préciser. C'est à cette question que la théorie inverse cherche à répondre. Dans le cas des groupes finis, un premier résultat montre que si n est un entier strictement positif alors il existe une extension du corps des rationnels ayant pour groupe de Galois legroupe symétrique d'ordre n. Par exemple, le corps de décomposition du polynôme rationnel Xn - X - 1 admet pour groupe de Galois le groupe symétrique d'ordre n. Le théorème de Cayley et le théorème fondamental de la théorie de Galois permet d'en déduire que, pour tout groupe fini G, il existe une extension d'un corps de nombres (c'est-à-dire une extension finiedes nombres rationnels) ayant G pour groupe de Galois. De façon plus précise la théorie inverse cherche à répondre à trois questions : Malgré d'importants progrès durant les trente dernières années du xxe siècle, en 2006 les trois questions restent très largement ouvertes. Certaines fonctions obtenues par addition, multiplication, division et composition de fonctions élémentaires (polynômes, exponentielle et logarithme par exemple) n'admettent aucuneprimitive qui puisse s'obtenir de la même manière. C'est le cas par exemple de la fonction gaussienne d'expression x ↦ exp(−x2/2). Ce fait est généralisé par la théorie de Galois différentielle, qui permet de déterminer, dans un ensemble des fonctions élémentaires, celles qui admettent une primitive élémentaire. Cette théorie étudie des corps particuliers appelés corps différentiels. Ce sont les corps K munis d'une dérivation δ, c'est-à-dire d'une application vérifiant la propriété suivante : Cette branche traite d'une famille de corps, il est donc naturel de la considérer comme un cas particulier de la théorie de Galois. Cependant l'analogie va plus loin et à bien des égards, cette théorie ressemble à la théorie classique. La différence principale est que, dans ce contexte, le groupe de Galois n'est plus un groupe fini mais en général un groupe algébrique.Histoire [modifier]
Genèse [modifier]
Gauss et les polynômes cyclotomiques [modifier]
Théorème d'Abel-Ruffini [modifier]
Évariste Galois [modifier]
Structures algébriques [modifier]
Théories de Galois [modifier]
Apports du XXe siècle [modifier]
Exemples [modifier]
Petit théorème de Fermat [modifier]

Duplication du cube [modifier]
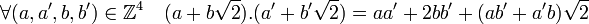


Équation cubique [modifier]
![P[X]=0 quad avec quad P[X]=X^3-3X+1;](http://upload.wikimedia.org/math/f/f/8/ff8d27380fe47a3187dffab0b36de1a4.png)
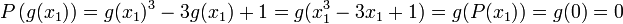
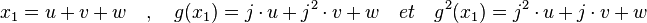
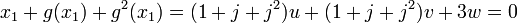 , donc
, donc 
 , donc
, donc 
 , donc
, donc 
Synthèse [modifier]
Applications [modifier]
Théorie algébrique des nombres [modifier]
Cryptographie [modifier]
Théorie des équations algébriques [modifier]
Géométrie algébrique [modifier]
Les structures utilisées [modifier]
Corps commutatifs [modifier]
Espace vectoriel [modifier]
Anneau [modifier]
Groupe [modifier]
Topologie [modifier]
Théories de Galois [modifier]
Théorie classique [modifier]
Théorie de Galois infinie [modifier]
Théorie géométrique [modifier]
Théorie inverse [modifier]
Théorie différentielle [modifier]

Théorie des corps de classes [modifier]
Notes et références [modifier]
Voir aussi [modifier]
Bibliographie [modifier]
Liens externes [modifier]
07:25 Publié dans Théorie de Galois | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Corps (mathématiques)
En mathématiques, et plus précisément en algèbre, un corps est une structure algébrique. De manière informelle, un corps est un ensemble dans lequel il est possible d'effectuer des additions, des soustractions, des multiplications et des divisions. Des exemples élémentaires de corps sont le corps des nombres rationnels (noté La théorie des corps est appelée, par certains, théorie de Galois[réf. nécessaire] ; cependant, la théorie de Galois désigne en général une méthode d'étude qui s'applique en particulier aux corps commutatifs et aux extensions de corps, qui forment l'exemple historique, mais s'étend aussi à bien d'autres domaines, par exemple l'étude des équations différentielles (théorie de Galois différentielle), ou des revêtements. Autrement dit, la théorie de Galois est une branche de la théorie des corps.Corps (mathématiques)
![]() Pour les articles homonymes, voir Corps.
Pour les articles homonymes, voir Corps. ), le corps des nombres réels (noté
), le corps des nombres réels (noté  ), le corps des nombres complexes (noté
), le corps des nombres complexes (noté  ) et le corps
) et le corps  des congruences modulo p où p est un nombre premier. L'exemple le plus simple de corps non commutatif (parfois appelés anneau à division, suivant l'anglais) est celui des quaternions.
des congruences modulo p où p est un nombre premier. L'exemple le plus simple de corps non commutatif (parfois appelés anneau à division, suivant l'anglais) est celui des quaternions.
Sommaire[masquer] |
Jusqu'au xixe siècle, les ensembles de nombres ont paru tellement naturels que l'on ne s'est jamais préoccupé de leur donner un nom, ni même de définir avec précision leur structure1. Cependant, avec la naissance de l'étude des nombres algébriques, il est apparu d'autres ensembles de nombres que les rationnels, les réels et les complexes. Il est devenu nécessaire de préciser la structure de corps, puis la notion d'entiers sur ce corps et enfin la notion d'anneau. C'est à l'école allemande que l'on doit le développement de ces notions. C'est Richard Dedekind qui définit pour la première fois la structure de corps (Körper en allemand)2 et c'est la raison pour laquelle un corps quelconque est souvent nommé K ou Un corps est un ensemble K muni de deux lois internes notées en général + et × vérifiant les axiomes suivants : On parle alors du corps Les premiers corps étudiés étant des ensembles de nombres (rationnels, réels, complexes, algébriques), la multiplication y était commutative. C'est la raison pour laquelle, initialement, dans la définition d'un corps, la multiplication devait être commutative. Actuellement, la tendance est plutôt de ne pas exiger la commutativité de la multiplication3 ou du moins de préciser la nature des corps étudiés4 ; on appelle alors corps commutatif un corps dont la multiplication est commutative. Les corps non commutatifs sont parfois appelés corps gauches ou anneaux à division. Cette terminologie est inspirée de l'anglais où un corps commutatif est appelé field (champ) et un corps non nécessairement commutatif division ring(anneau à division). Exemples de corps : Un sous-corps d'un corps K est une partie non vide L de K, stable par S'il existe un entier naturel n non nul tel que Par exemple le corps Ce sont les corps dont le nombre d'éléments est fini. L'étude des corps finis est tardive dans l'étude des corps. On démontre qu'un corps fini est toujours commutatif, de cardinal égal à la puissance d'un nombre premier. Il est en fait possible de dresser la liste de tous les corps finis (à isomorphisme près). Le plus petit corps fini est celui des booléens, dont voici les tables d'addition et de multiplication :Fragments d'histoire [modifier]
 . En 1910, Ernst Steinitz fonde la théorie axiomatique des corps. La structure de corps s'insère dans une hiérarchie comprenant le monoïde, le groupe, l'anneau, et donne lieu à la définition de l'espace vectoriel, et de l'algèbre.
. En 1910, Ernst Steinitz fonde la théorie axiomatique des corps. La structure de corps s'insère dans une hiérarchie comprenant le monoïde, le groupe, l'anneau, et donne lieu à la définition de l'espace vectoriel, et de l'algèbre.Définition et exemple [modifier]

 .
.
 est un corps commutatif ;
est un corps commutatif ; est un corps commutatif ;
est un corps commutatif ; est un corps commutatif ;
est un corps commutatif ; est un corps non commutatif ;
est un corps non commutatif ; , où p est un nombre premier, est un corps commutatif.
, où p est un nombre premier, est un corps commutatif. et
et  , telle que L munie des lois induites soit un corps.
, telle que L munie des lois induites soit un corps.Caractéristique [modifier]
 (avec n termes) est nul, on appelle caractéristique du corps le plus petit entier positif non nul vérifiant cette propriété. S'il n'existe pas d'entier non nul vérifiant cette propriété, on dit que le corps est de caractéristique nulle (parfois aussi grande que l'on veut).
(avec n termes) est nul, on appelle caractéristique du corps le plus petit entier positif non nul vérifiant cette propriété. S'il n'existe pas d'entier non nul vérifiant cette propriété, on dit que le corps est de caractéristique nulle (parfois aussi grande que l'on veut). est de caractéristique nulle alors que le corps
est de caractéristique nulle alors que le corps  est de caractéristique p. On démontre qu'un corps possède toujours pour caractéristique soit 0 soit un nombre premier.
est de caractéristique p. On démontre qu'un corps possède toujours pour caractéristique soit 0 soit un nombre premier.Corps finis [modifier]
| + | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
| x | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
Les corps finis les plus connus sont les corps de congruences modulo un nombre premier comme dans le cas ci-dessus, mais il en existe une infinité d’autres, comme par exemple ceux-ci, respectivement à quatre et neuf éléments, dont nous donnons ci-dessous les « tables de Pythagore », successivement pour la première loi de composition dite « addition », puis pour la deuxième dite « multiplication ». Nous désignons dans chaque cas comme a l’élément neutre de la première loi de composition, b celui de la deuxième. Quatre éléments :
| + | a | b | c | d |
| a | a | b | c | d |
| b | b | a | d | c |
| c | c | d | a | b |
| d | d | c | b | a |
| x | a | b | c | d |
| a | a | a | a | a |
| b | a | b | c | d |
| c | a | c | d | b |
| d | a | d | b | c |
Neuf éléments :
| + | a | b | c | d | e | f | g | h | i |
| a | a | b | c | d | e | f | g | h | i |
| b | b | c | a | e | f | d | h | i | g |
| c | c | a | b | f | d | e | i | g | h |
| d | d | e | f | g | h | i | a | b | c |
| e | e | f | d | h | i | g | b | c | a |
| f | f | d | e | i | g | h | c | a | b |
| g | g | h | i | a | b | c | d | e | f |
| h | h | i | g | b | c | a | e | f | d |
| i | i | g | h | c | a | b | f | d | e |
| x | a | b | c | d | e | f | g | h | i |
| a | a | a | a | a | a | a | a | a | a |
| b | a | b | c | d | e | f | g | h | i |
| c | a | c | b | g | i | h | d | f | e |
| d | a | d | g | c | f | i | b | e | h |
| e | a | e | i | f | g | b | h | c | d |
| f | a | f | h | i | b | d | e | g | c |
| g | a | g | d | b | h | e | c | i | f |
| h | a | h | f | e | c | g | i | d | b |
| i | a | i | e | h | d | c | f | b | g |
L'ensemble Plus généralement, un anneau unitaire est un ensemble A muni de deux lois + et ×, et vérifiant les axiomes suivants : Si l'anneau A est intègre, c’est-à-dire si ou encore, l'anneau est presque un corps car il ne lui manque plus que l'inversibilité pour la multiplication. Exemple : Un anneau intègre (unitaire) est un corps si et seulement si {0} et A (les idéaux triviaux) sont les seuls idéaux. Un anneau intègre (unitaire) A est un corps si et seulement si tout A-module est libre. Partant du corps L'étude des polynômes à coefficient dans un corps commutatif et la recherche de leurs racines a développé considérablement la notion de corps. Si f est un polynôme de degré n sur un corps commutatif K, l'équation f(x) = 0 est une équation algébrique dans K. Si, de plus, f est un polynôme irréductible, l'équation est dite irréductible. Lorsque n ≥ 2, trouver les solutions d'une telle équation demande de se placer dans un corps plus grand que K, une extension de corps. Par exemple, l'équation x2 − 2 = 0 est irréductible dans Un corps de rupture d'un polynôme est, par exemple, un corps minimal contenant K et une racine de f. Le corps de décomposition de f est le plus petit corps contenant K ainsi que toutes les racines de f. L'étude des corps de décomposition d'un polynôme et du groupe de permutations de ses racines forme la branche des mathématiques que l'on appelle la théorie de Galois. On retrouve la théorie des corps dans l'étude de certaines fonctions comme les fonctions rationnelles ou les fonctions elliptiques.Corps et anneau [modifier]
 n'est pas un corps car la plupart des éléments de
n'est pas un corps car la plupart des éléments de 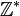 ne sont pas inversibles : par exemple, il n'existe pas d'entier relatif n tel que 2n = 1 donc 2 n'est pas inversible.
ne sont pas inversibles : par exemple, il n'existe pas d'entier relatif n tel que 2n = 1 donc 2 n'est pas inversible.
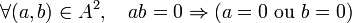 ,
,
 est le corps des fractions de
est le corps des fractions de 
Corps et espace vectoriel [modifier]
 , il est naturel de s'intéresser à
, il est naturel de s'intéresser à  , ensemble des n-uplet de réels. On est amené à le munir d'une addition et d'une multiplication par un réel. La structure ainsi définie (une addition interne munissant l'ensemble d'une structure de groupe et une multiplication externe possédant des propriétés de distributivité et d'associativité) est appelée espace vectoriel sur
, ensemble des n-uplet de réels. On est amené à le munir d'une addition et d'une multiplication par un réel. La structure ainsi définie (une addition interne munissant l'ensemble d'une structure de groupe et une multiplication externe possédant des propriétés de distributivité et d'associativité) est appelée espace vectoriel sur  . Il est alors naturel de définir ce que pourrait être un espace vectoriel sur un corps K quelconque.
. Il est alors naturel de définir ce que pourrait être un espace vectoriel sur un corps K quelconque.Corps et équation algébrique [modifier]
 mais possède des racines dans
mais possède des racines dans  ou mieux dans
ou mieux dans ![mathbb Q[sqrt 2]](http://upload.wikimedia.org/math/d/b/5/db51c502f6ea3908be57943d0ba5af9a.png) . L'équation x2 + 1 = 0 ne possède pas de solution dans
. L'équation x2 + 1 = 0 ne possède pas de solution dans  mais en possède dans
mais en possède dans  ou mieux dans
ou mieux dans ![mathbb Q[i]](http://upload.wikimedia.org/math/2/8/3/2830a273d48073b03c768cce92401ea7.png) .
.Propriétés [modifier]
 un corps commutatif. Alors tout polynôme de degré n admet au plus n zéros (ou racines) dans
un corps commutatif. Alors tout polynôme de degré n admet au plus n zéros (ou racines) dans  .
.
 un corps commutatif. Alors tout sous-groupe fini de
un corps commutatif. Alors tout sous-groupe fini de  est un groupe cyclique.
est un groupe cyclique.Autres champs d'étude [modifier]
Structures additionnelles [modifier]
Voir aussi [modifier]
Notes et références [modifier]
Liens internes [modifier]
Sources [modifier]
07:24 Publié dans Corps (mathématiques) | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
01/12/2010
Analogues de la factorielle
Analogues de la factorielle
En mathématiques, de nombreuses fonctions analogues à la fonction factorielle ont été définies ; cette page recense les variantes les plus fréquemment rencontrées.
Sommaire[masquer] |
Primorielle [modifier]
La fonction primorielle est similaire à la fonction factorielle, mais ne prend en compte que le produit des nombres premiers.
Multifactorielles [modifier]
Afin d'alléger l'écriture, une notation courante est d'utiliser plusieurs points d'exclamation pour noter une fonction multifactorielle, le produit d'un facteur sur deux (n!!), sur trois (n!!!) ou plus.
n!!, la double factorielle de n, est définie de façon récurrente par :
Par exemple :
Certaines identités découlent de la définition :
Il faut faire attention de ne pas interpréter n!! comme la factorielle de n!, qui serait écrite (n!)! et est un nombre largement plus grand. Certains mathématiciens ont suggéré la notation alternative n!2 pour la double factorielle et d'une façon similaire n!n pour les autres multifactorielles, mais cet usage ne s'est pas répandu.
La double factorielle est la variante la plus commune, mais il est possible de définir de façon similaire la triple factorielle, etc. De façon générale, la ke factorielle, notée n!(k), est définie de façon récurrente par :
Hyperfactorielle [modifier]
L'hyperfactorielle de n, notée H(n), est définie par :
Pour n = 1, 2, 3, 4,... les valeurs de H(n) sont 1, 4, 108, 27 648,... (suite A002109 de l’OEIS).
La fonction hyperfactorielle est similaire à la fonction factorielle, mais produit de plus grands nombres. Sa croissance est en revanche comparable.
Superfactorielle [modifier]
Neil Sloane et Simon Plouffe ont défini la superfactorielle en 1995 comme le produit des n premières factorielles :
Par exemple, la superfactorielle de 4 est :
La suite des superfactorielles débute (depuis n = 0) par :
L'idée fut étendue en 2000 par Henry Bottomley à la superduperfactorielle, produit des n premières superfactorielles, débutant (depuis n = 0) par :
puis, par récurrence, à n'importe quelle factorielle de niveau supérieur, où la factorielle de niveau m de n est le produit des n premières factorielles de niveau m-1, c’est-à-dire, en notant f(n,m) la factorielle de n de niveau m :
où f(n,0) = n pour n > 0 et f(0,m) = 1.
Superfactorielle (définition alternative) [modifier]
Clifford Pickover, dans son livre Keys to Infinity (1995), définit la superfactorielle de n, notée n$ ($ étant un signe factoriel ! portant un S superposé), comme :
 ,
,
ou, en utilisant la notation de Knuth :
 .
.
Les premiers éléments de la suite des superfactorielles sont :
Sous-factorielle [modifier]
La fonction sous-factorielle, notée !n, sert à calculer le nombre de permutations possible de n objets distincts de manière à ce qu'aucun objet ne se trouve à sa place.
Par exemple, il existe !n façon de glisser n lettres dans n enveloppes affranchies et adressées de manière à ce qu'aucune des lettres ne soit dans la bonne enveloppe.
Il existe différentes façons de calculer la sous-factorielle
Où Γ est la fonction gamma incomplète et e la base du logarithme népérien.
Où [x] désigne l'entier le plus proche de x
Les premières valeurs de cette fonction sont :
- !1 = 0
- !2 = 1
- !3 = 2
- !4 = 9
- !5 = 44
- !6 = 265
- !7 = 1854
- !8 = 14833
- !9 = 133496
- !10 = 1334961
- !11 = 14684570
- !12 = 176214841
- !13 = 2290792932
22:42 Publié dans Analogues de la factorielle | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Mathématiques discrètes
Mathématiques discrètes
|
|
Cet article est une ébauche concernant les mathématiques.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
Les mathématiques discrètes, parfois appelées mathématiques finies, sont l'étude des structures mathématiques fondamentalement discrètes, dans le sens où la notion de continuité n'est pas exigée ou supportée. La plupart des objets étudiés en mathématiques discrètes, si ce n'est pas la totalité, sont des ensembles dénombrables comme celui des entiers.
Les mathématiques discrètes sont devenues populaires ces dernières décennies du fait de leurs applications dans l'informatique. Les notations et les concepts des mathématiques discrètes sont utilisés pour exprimer ou étudier des problèmes et des objets en algorithmique et en programmation.
Les mathématiques discrètes incluent habituellement une partie de :
- la théorie des nombres ;
- la combinatoire ;
- la théorie des graphes ;
- la théorie de l'information ;
- la théorie des langages ;
- la théorie de la calculabilité et de la complexité.
22:40 Publié dans Mathématiques discrètes | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook












































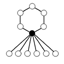
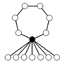
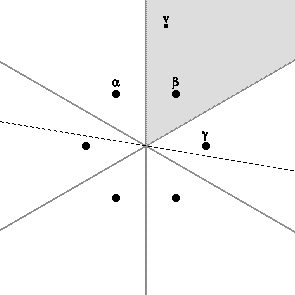









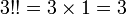
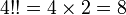
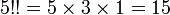
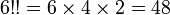
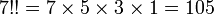


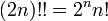
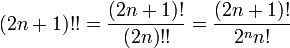

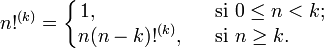
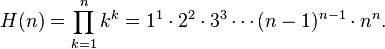




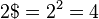

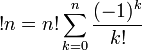
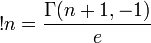
![!n = left [ frac {n!}{e} right ]](http://upload.wikimedia.org/math/b/c/6/bc6b78cafc03ee3a79b30031c1d705a4.png)

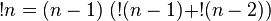
 avec
avec  et
et  suite
suite