D	L	M	M	J	V	S
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30

Source : http://fr.wikipedia.org/wiki/Andrew_Wiles

Andrew Wiles

Sir Andrew John Wiles

Sir Andrew John Wiles (né le 11 avril 1953 à Cambridge, Angleterre) est un mathématicien britannique, professeur à l'université de Princeton, aux États-Unis. Il est surtout connu pour sa démonstration du dernier théorème de Fermat en 1994, résolvant ainsi l'un des problèmes les plus connus de l'histoire des mathématiques.

Sommaire

[masquer]

Biographie [modifier]

Il entre à Clare College en 1974 pour y préparer un Ph.D. en mathématiques sur les lois de réciprocité et la conjecture de Birch et Swinnerton-Dyer, qu'il obtient en 1979. Il devient professeur à l'Université de Princeton au New Jersey en 1982.

En ce qui concerne la démonstration du dernier théorème de Fermat, l'odyssée de Wiles commence en 1985 quand Ken Ribet, partant d'une idée de Gerhard Frey, démontre que ce théorème résulterait de la conjecture de Shimura-Taniyama-Weil qui affirme que toute courbe elliptiqueest paramétrable par une forme modulaire. Bien que moins familière que le théorème de Fermat, elle est la plus significative, car elle touche au cœur de la théorie des nombres.

Cependant, personne n'a la moindre piste de travail pour la démontrer. Travaillant dans le plus grand secret pendant huit ans, et faisant part de ses idées et progrès à Nicholas Katz, un collègue de Princeton, Wiles démontre la conjecture de Shimura-Taniyama-Weil et, par conséquent, le théorème de Fermat. Comme toute démonstration de cette ampleur, elle est un tour de force riche en nouvelles idées.

Pour dévoiler sa démonstration, Wiles s'y prend de manière quasi théâtrale. Il annonce trois conférences (les 21, 22 et 23 juin 1993) sans en donner l'objet, ce qu'il ne fait que lors de la dernière en précisant que le grand théorème de Fermat est un corollaire de ses principaux résultats. Il agit ainsi pour s'assurer que la paternité de sa démonstration ne lui soit pas disputée après coup.

Dans les mois qui suivent, le manuscrit de sa démonstration circule auprès d'un petit nombre de mathématiciens. Plusieurs critiques sont émises contre la démonstration que Wiles a présentée en 1993, presque toutes de l'ordre du détail et résolues rapidement, sauf une, qui met en évidence une lacune. Avec l'aide de Richard Taylor, Wiles réussit à contourner le problème soulevé, en octobre 1994. Son travail met ainsi fin à une recherche qui a duré plus de 300 ans.

Il est aussi l'auteur d'autres travaux importants en théorie des nombres. Avec John Coates (qui fut son directeur de thèse), il a obtenu plusieurs résultats sur la conjecture de Birch et Swinnerton-Dyer et a collaboré avec Barry Mazur sur les extensions cyclotomiques.

Il est fait Chevalier commandeur de l'Ordre de l'Empire britannique (KBE) en 2000¹.

Bibliographie [modifier]

Simon Singh, Le Dernier Théorème de Fermat, Hachette Littératures collection Pluriel Sciences

Notes et références [modifier]

↑ London Gazette : n° 55710, p. 34 [archive], 31-12-1999

Lien externe [modifier]

(en) Biographie
(en) Le texte de la preuve du dernier théorème de Fermat (pdf de 10 Mo)

Source : http://fr.wikipedia.org/wiki/Diophante

Diophante d'Alexandrie

(Redirigé depuis Diophante)

Page couverture de l'édition de 1670des Arithmetica, principal ouvrage de Diophante d'Alexandrie.

Diophante d'Alexandrie (env. 200/214 - env. 284/298) était un mathématicien grec. Surtout connu pour son étude des équations diophantiennes, il est surnommé le « père de l'algèbre ».

Sommaire

[masquer]

Biographie [modifier]

Page 81 de l'édition de 1670 des Arithmétiques de Diophante.

Peu de choses sont connues de sa vie. Il vécut à Alexandrie et mourut à 84 ans. Diophante était probablement un babylonien hellène. Son œuvre est en partie perdue.

Il est connu pour son étude des équations à variables rationnelles ( $in mathbb{Q}$ ) et les équations diophantiennes furent nommées en son honneur. Son nom donne l'adjectif diophantien, souvent utilisé en théorie des nombres pour décrire un problème qui s'y rapporte.

Son ouvrage le plus important est son Arithmétique, qui influença les mathématiciens arabes et plus tard ceux de la Renaissance.

Diophante a aussi écrit un traité sur les nombres polygonaux, le plus ancien de cette science ; il ne nous en reste que 10 livres sur 13¹. Six d'entre eux ont été publiés en latin et annotés par Claude-Gaspard Bachet en 1621, en latin et grec et annotés par Pierre de Fermat à Toulouse en1670 (après sa mort), et ont été traduits en français par Simon Stevin et Albert Girard en 1625 (après la mort de Stevin).

Diophante s'intéresse notamment aux problèmes suivants :

Page 61 de l'édition de 1670 des Arithmetica de Diophante. Elle contient, en caractères d'imprimerie, la note de Pierre de Fermat à propos de son grand théorème.

résolution d'équations quadratiques (du type ax²=bx+c).
détermination de valeurs faisant de 2 expressions linéaires des carrés (ex: trouver x tel que 10x+9 et 5x+4 sont tous deux des carrés).
décomposition d'un nombre en somme de 2 carrés. Il semble que Diophante sache d'expérience que les entiers de la forme 4n+3 ne s'écrivent pas comme la somme de 2 carrés.
partage d'un carré en 2 carrés : il explique notamment comment partager 16 en somme de 2 carrés : (16/5)²+(12/5)². C'est en marge de ce problème que Fermat inscrit sur son exemplaire des Arithmetica sa fameuse note, selon laquelle il est impossible de partager un cube en 2 cubes, un bicarré en 2 bicarrés, et plus généralement une puissance quelconque sauf le carré, en 2 puissance de même exposant. Il faudra attendre 1995 pour avoir une démonstration de ce résultat par Andrew Wiles.

Son épitaphe [modifier]

Mais il est également connu pour son épitaphe : problème, attribué à Métrodore (vers 500), permettant de trouver l'âge de Diophante d'Alexandrie à sa mort. Ce problème partage la vie de Diophante en parties inégales représentées par des fractions et permet de calculer la durée de sa vie, soit 84 ans. Voici le problème en abrégé : L'enfance de Diophante occupa un sixième de toute sa vie. Le douzième fut pris par son adolescence. Après une nouvelle période équivalente au septième de sa vie, il se maria. Cinq ans plus tard, il eut un fils. La vie de ce fils fut exactement une demie de celle de son père. Diophante mourut quatre ans après la mort de son fils.

Une version de ce problème a été composée en alexandrins par H. Eutrope :

Passant, sous ce tombeau repose Diophante.
Ces quelques vers tracés par une main savante
Vont te faire connaître à quel âge il est mort.
Des jours assez nombreux que lui compta le sort,
Le sixième marqua le temps de son enfance ;
Le douzième fut pris par son adolescence.
Des sept parts de sa vie, une encore s'écoula,
Puis s'étant marié, sa femme lui donna
Cinq ans après un fils qui, du destin sévère
Reçut de jours hélas ! deux fois moins que son père.
De quatre ans, dans les pleurs, celui-ci survécut.
Dis, si tu sais compter, à quel âge il mourut.

La réponse revient à résoudre l'équation suivante : x/6 + x/12 + x/7 + 5 + x/2 + 4 = x. On trouve x = 84 ans, âge auquel Diophante mourut.

Annexes [modifier]

Bibliographie [modifier]

Voir aussi la bibliographie des Irem (France).

Arithmétique (vers 250). Tome 3 ; éd. et tr. Roshdi Rashed. Paris : les Belles Lettres, 1984. (Collection des Universités de France). ccvi-264p. ISBN 2-251-00375-4.
Arithmétique. Tome 4 ; éd. et tr. Roshdi Rashed. Paris : les Belles Lettres, 1984. (Collection des Universités de France). cxxxiv-322p. ISBN 2-251-00376-2.
Cet article comprend des extraits du Dictionnaire Bouillet. Il est possible de supprimer cette indication, si le texte reflète le savoir actuel sur ce thème, si les sources sont citées, s'il satisfait aux exigences linguistiques actuelles et s'il ne contient pas de propos qui vont à l'encontre des règles de neutralité de Wikipédia.

Notes et références [modifier]

↑ Les quatre derniers ont été retrouvés en 1968 dans une bibliothèque à Meshed, une ville au nord-est de l'Iran L. Radford Diophante et l'algèbre pré-symbolique Bulletin AMQ 1991 lire [archive]

Liens externes [modifier]

(en) J. J. O'Connor et E. F. Robertson, Diophantus
Épitaphe de diophante

Catégories : Mathématicien de la Grèce antique | Scientifique de la Rome antique | [+]

Source : http://fr.wikipedia.org/wiki/Th%C3%A9orie_des_corps_de_cl...

Théorie des corps de classes

Cet article est une ébauche concernant l'algèbre.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

En mathématiques, la théorie des corps de classes est une branche majeure de la théorie algébrique des nombres qui a pour objet la classification des extensions abéliennes, c'est-à-dire galoisiennes et de groupe de Galois commutatif, d'un corps donné. Plus précisément, il s'agit de décrire et de construire ces extensions en termes de propriétés arithmétiques du corps de base lui-même.

La plupart des résultats centraux ont été démontrés dans la période s'étendant entre 1900 et 1950. La théorie a été nommée ainsi en rapport avec les idées, conjectures et résultats de ses débuts, tel que le corps de classes de Hilbert, et s'organisa vers 1930.

De nos jours, le terme est généralement utilisé comme synonyme de l'étude de toutes les extensions abéliennes des corps de nombres algébriques (et plus généralement des corps globaux), mais aussi des corps de nombres p-adiques (et plus généralement des corps locaux).

Une autre ligne importante est la recherche de générateurs explicites pour les corps de classes de corps de nombres algébriques, c'est-à-dire de générateurs donnés par les valeurs defonctions transcendantes. C'est le Kronecker Jugendtraum (rêve de jeunesse de Kronecker). Il n'est encore réalisé que pour de rares cas, notamment celui du corps des rationnels (théorème de Kronecker-Weber, où les générateurs sont des racines de l'unité, c'est-à-dire des valeurs de la fonction exponentielle), et des corps quadratiques imaginaires (cas des corps à multiplication complexe, où les générateurs sont des valeurs de fonctions elliptiques).

Sommaire

[masquer]

Formulation en langage contemporain [modifier]

En langage moderne, il existe une extension abélienne maximale A de K, qui sera de degré infini sur K; et associée à A, un groupe de Galois G qui sera un groupe profini, donc ungroupe topologique compact, et aussi abélien. Nous nous intéressons à la description de G en termes de K.

Le résultat fondamental de la théorie des corps de classes établit que le groupe G est naturellement isomorphe à la complétion profinie du groupe des classes d'idèles (en) de K. Par exemple, lorsque K est le corps des nombres rationnels, le groupe de Galois G est (naturellement isomorphe à) un produit infini du groupe des unités des entiers p-adique pris sur tous les nombres premiers p, et l'extension abélienne maximale correspondante des rationnels est le corps engendré par toutes les racines de l'unité. Ceci était connu comme le théorème de Kronecker-Weber, originellement énoncé par Kronecker.

Pour une description du cas général, voir l'article détaillé : formation de classes.

En pratique, le programme prend la forme suivante. Étant donné un corps K et fixée une clôture séparable K^sep de K, on cherche à associer à toute extension finie abélienne L de Kincluse dans K^sep un groupe topologique C(L) et un homomorphisme continu de groupes N_L_/K de C(L) dans C(K) de manière que :

L'application qui à L associe N_L_/K(C(L)) est une bijection entre extensions finies abéliennes de K incluse dans K^sep et sous-groupes ouverts d'indice fini de C(K).
Pour chaque extension finie abélienne L/K incluse dans K^sep, on a un isomorphisme de groupes r_L_/K de Gal(L/K) dans C(K)/N_L_/K(C(L)), appelé application de réciprocité.

La théorie du corps de classes a été décrite pour une famille variée de corps, parmi lesquels les corps de nombres algébriques et les corps de nombres p-adiques.

L'exemple le plus simple est celui des corps finis. Si K est un corps fini de cardinal q, on pose 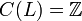$C(L)=Z,$ et N_L_/K est égal à la multiplication par le degré [L/K] de L/K, pour toute extension finie L de K incluse dans K^sep. On a un homomorphisme de groupes de $Z,$ dans Gal(K^sep/K) injectif et d'image dense, qui envoie 1 sur le Frobenius de K, c'est-à-dire sur l'automorphisme $varphi_K : x mapsto x^q,$ . Si σ est un élément de Gal(L/K), il existe un unique n dans $Z/[L:K]Z,$ tel que φ_Kⁿ prolonge σ. L'application de réciprocité est définie par $sigma mapsto n,$ .

Théorie du corps de classes local [modifier]

Il s'agit de la partie de la théorie concernant les corps locaux. Dans ce qui suit, on se restreint aux corps locaux dont le corps résiduel est fini.

Si K est un corps local de corps résiduel fini, il existe un homomorphisme de groupes topologiques, injectif et d'image dense, du groupe multiplicatif de K sur le groupe de Galois de l'extension abélienne maximale de K. Cet homomorphisme, appelé le symbole d'Artin (en), est défini de la façon suivante : à chaque élément premier de K est associé un automorphisme qui, restreint à toute sous-extension abélienne non ramifiée, est l'automorphisme de Frobenius de cette extension, et le symbole d'Artin se factorise à travers les groupes de normes associées aux sous-extensions finies. Il y a alors une correspondance de Galois des sous-extensions de l'extension abélienne maximale de K avec les sous-groupes (fermés pour la topologie de Krull) du groupe de Galois de cette extension, et donc, via le symbole d'Artin, avec les sous-groupes du groupe multiplicatif de K.

Le cas particulier le plus frappant est celui du groupe des unités : il est associé à l'extension non ramifiée maximale de K.

Corps de classes global [modifier]

Pour K un corps de nombres, la correspondance du corps de classes s'énonce comme la collection des correspondances locales en toutes les places non archimédiennes de K, à l'aide des idèles (en).

Historique [modifier]

La généralisation prit place dans un projet historique à long terme impliquant les formes quadratiques, les lois de réciprocité (en), les travaux de Kummer et de Kronecker/Hensel sur les idéaux et ses achèvements, la théorie de la cyclotomie, les extensions de Kummer, les conjectures de Hilbert et les démonstrations par de nombreux mathématiciens (Takagi, Hasse,Artin, Furtwängler (en) et d'autres). Le théorème d'existence de Takagi crucial était connu en 1920 et tous les autres résultats principaux vers 1930. La propriété de principalisation est une des dernières conjectures classiques à avoir été démontrée.

Dans les années 1930 et ultérieurement, l'usage des extensions infinies et de la théorie de Krull sur leurs groupes de Galois a été considérée comme de plus en plus utile. Elle se mélange avec la dualité de Pontryagin pour donner une formulation plus claire mais plus abstraite du résultat central, la loi de réciprocité d'Artin (en). Elle est aussi basée sur la théorie d'Iwasawa.

Après que les résultats furent reformulés en termes de cohomologie galoisienne, avec la notion de formation de classes, ce domaine subit une relative stagnation. Le programme de Langlands lui donna une impulsion nouvelle, dans sa forme de « théorie non abélienne des corps de classes (en) » , bien que cette description puisse être à présent considérée comme restrictive si elle est confinée à la question de savoir comment les idéaux premiers se décomposent dans les extensions galoisiennes générales.

Références [modifier]

(en) Georges Gras, Class Field Theory : From Theory to Practice [détail des éditions]
(en) Jürgen Neukirch, Algebraic number theory [détail des éditions]
(en) Jürgen Neukirch, Alexander Schmidt, Kay Wingberg Cohomology of number fields [détail des éditions]
Jean-Pierre Serre, Corps locaux [détail des éditions]

Liens externes [modifier]

(en) Page de J. S. Milne, professeur émérite à l'Université du Michigan
Un texte sur cette théorie sur le blog de Maurice Mischler, de l'université de Lausanne

Portail des mathématiques

Catégories : Théorie des corps de classes | Théorie de Galois | [+]

Source : http://fr.wikipedia.org/wiki/Conjecture_de_Dubner

Conjecture de Dubner

Selon Harvey Dubner :

Si un p-jumeau est un nombre premier ayant un jumeau, alors tout nombre pair supérieur à 4208 est la somme de deux p-jumeaux.¹

Cette conjecture a été vérifiée par logiciel pour tous les nombres pairs jusqu'à 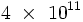$4 times 10^{11}$

Si cette conjecture était démontrée, cela prouverait à la fois la conjecture de Goldbach (tout nombre pair est la somme de deux nombres premiers) et la conjecture des nombres premiers jumeaux (il existe une infinité de nombres premiers jumeaux).

Sommaire

[masquer]

Généralisation [modifier]

L'intérêt de la conjecture de Dubner par rapport à la conjecture de Goldbach, c'est qu'elle est plus exigeante, dans la mesure où les nombres premiers jumeaux sont plus rares que les nombres premiers.

Si on considère comme miraculeuse la conjecture de Goldbach, la conjecture de Dubner l'est encore plus.

En généralisant encore, voici quatre nouvelles conjectures dérivées, encore plus exigeantes :

Nommons min-jumeau le plus petit d'une paire de nombres premiers jumeaux, et max-jumeau le plus grand d'une paire de nombres premiers jumeaux.

Tout nombre pair (assez grand) est la somme de deux min-jumeaux.
Tout nombre pair (assez grand) est la somme de deux max-jumeaux.
Tout nombre pair (assez grand) est la somme d'un min-jumeau et d'un max-jumeau, avec min-jumeau>max-jumeau.
Tout nombre pair (assez grand) est la somme d'un min-jumeau et d'un max-jumeau, avec min-jumeau<max-jumeau.

Sources [modifier]

Harvey Dubner, "Twin Prime Conjectures", Journal of Recreational Mathematics, Vol.30(3), 1999-2000
Jean-Paul Delahaye, "Nombres premiers inévitables et pyramidaux", Pour la science n°296, juin 2002, pages 98 à 102

Articles connexes [modifier]

Liens externes [modifier]

Notes [modifier]

↑ Les deux nombres ne sont pas jumeaux entre eux, mais chacun dispose d'un jumeau.

Portail des mathématiques

Catégories : Arithmétique | Nombre premier | Conjecture | [+]

Source : http://fr.wikipedia.org/wiki/Conjecture_des_nombres_premi...

Nombres premiers jumeaux

(Redirigé depuis Conjecture des nombres premiers jumeaux)

En mathématiques, deux nombres premiers jumeaux sont deux nombres premiers qui ne diffèrent que de 2. Hormis pour la paire (2, 3), cette distance de 2 est la plus petite distance possible entre deux nombres premiers. Les plus petits nombres premiers jumeaux sont 3 et 5, 5 et 7, 11 et 13.

Au 15 janvier 2007, les plus grands nombres premiers jumeaux connus sont 2003663613 × 2¹⁹⁵⁰⁰⁰±1, qui possèdent 58 711 chiffres en écriture décimale et furent découverts par Éric Vautier dans le cadre des projets de calcul distribué Twin Prime Search et PrimeGrid¹.

La conjecture des nombres premiers jumeaux stipule qu'il existe une infinité de nombres premiers jumeaux ; les observations numériques et des raisonnements heuristiquesjustifient la conjecture, mais aucune démonstration n'en a encore été faite.

Sommaire

[masquer]

Définition [modifier]

Soit $(p, q)$ un couple de nombres entiers tel que $p$ et $q$ soient tous les deux des nombres premiers et $p < q$ . On dit que $(p, q)$ forme un couple de nombres premiers jumeaux si $q = p + 2$ .

Liste des premiers nombres premiers jumeaux [modifier]

L'ensemble des nombres premiers jumeaux jusqu'à 1000 :

(3, 5)	(5, 7)	(11, 13)	(17, 19)	(29, 31)
(41, 43)	(59, 61)	(71, 73)	(101, 103)	(107, 109)
(137, 139)	(149, 151)	(179, 181)	(191, 193)	(197, 199)
(227, 229)	(239, 241)	(269, 271)	(281, 283)	(311, 313)
(347, 349)	(419 , 421)	(431 , 433)	(461 , 463)	(521 , 523)
(569 , 571)	(599 , 601)	(617 , 619)	(641 , 643)	(659 , 661)
(809 , 811)	(821 , 823)	(827 , 829)	(857 , 859)	(881 , 883)

Quelques propriétés [modifier]

Le couple $(2,3)$ est le seul couple de nombres premiers consécutifs.
En omettant le couple $(2,3)$ , 2 est la plus petite distance possible entre deux nombres premiers ; deux nombres premiers jumeaux sont ainsi deux nombres impairs consécutifs.
Tout couple de nombres premiers jumeaux (à l'exception du couple $(3,5)$ ) est de la forme $(6 n - 1,6 n + 1)$ pour un certain entier $n$ . En effet, toute série de trois nombres entiers naturels consécutifs comporte au moins un multiple de 2 (éventuellement deux) et un seul multiple de 3 ; ces deux multiples sont confondus entre les deux nombres premiers jumeaux.
Il est possible de démontrer que, pour tout entier 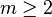$m ge 2$ , le couple $(m, m + 2)$ est constitué de nombres premiers jumeaux si et seulement si $4[(m-1)! + 1] + m equiv 0 mod m(m+2)$ . Cette caractérisation modulaire et factorielle des nombres premiers jumeaux a été découverte par P. A. Clement en1949².
La série des inverses de nombres premiers jumeaux est convergente vers la constante de Brun, au contraire de la série des inverses de nombres premiers. Cette propriété fut démontrée par Viggo Brun en 1919³.

Record [modifier]

Le 15 janvier 2007, deux projets de calcul distribué, Twin Prime Search et PrimeGrid, ont découvert le plus grand couple de nombres premiers jumeaux actuellement connu (c’est-à-dire en janvier 2007). Le découvreur est le français Éric Vautier¹.

Le couple record est 2003663613 × 2¹⁹⁵⁰⁰⁰±1 ; les deux nombres possèdent 58 711 chiffres en écriture décimale.

Conjecture des nombres premiers jumeaux [modifier]

La conjecture des nombres premiers jumeaux affirme qu'il existe une infinité de nombres premiers jumeaux:

Il existe une infinité de nombres premiers p tels que p + 2 soit aussi premier.

Bien que la plupart des chercheurs en théorie des nombres pensent que cette conjecture est vraie, elle n'a jamais été démontrée. Ils se basent sur des observations numériques et des raisonnements heuristiques utilisant la distribution probabiliste des nombres premiers.

En 1849, Alphonse de Polignac émit une conjecture plus générale : la conjecture de De Polignac dont le cas n = 2 correspond à la conjecture des nombres premiers jumeaux.

Il existe également une version plus forte de cette conjecture : la conjecture de Hardy-Littlewood, qui fournit une loi de distribution des nombres premiers jumeaux et qui s'inspire duthéorème des nombres premiers.

La conjecture des nombres premiers jumeaux est un cas particulier de la conjecture de Schinzel.

Résultats partiels [modifier]

En 1940, Paul Erdős démontra l'existence d'une constante c < 1 et d'une infinité de nombres premiers p tels que :

p' - p < c ln(p)

où p' désigne le nombre premier suivant immédiatement p.

Ce résultat fut plusieurs fois amélioré ; en 1986, Maier montra qu'une constante c < 0,25 pouvait être atteinte.

En 2003, Goldston et Yildirim ont démontré que, pour tout c > 0, il existe une infinité de nombres premiers p tels que p' - p < c ln(p).

En 1966, J.R. Chen a démontré l'existence d'une infinité de nombres premiers p tels que p + 2 soit le produit d'au plus deux facteurs premiers (un tel nombre, produit d'au plus deux facteurs premiers, est dit 2-presque-premier).

Son approche fut celle de la théorie du crible, qu'il utilisa pour traiter de façon similaire la conjecture des nombres premiers jumeaux et la conjecture de Goldbach.

La conjecture de Hardy-Littlewood [modifier]

Il existe aussi une généralisation de la conjecture des nombres premiers jumeaux, connue sous le nom de conjecture de Hardy - Littlewood, en rapport avec la distribution des premiers jumeaux, par analogie avec le théorème des nombres premiers. Soit π₂(x) le nombre de nombres premiers p ≤ x tels que p + 2 soit aussi premier.

On note C₂ le nombre obtenu de la façon suivante :

$C_2 = prod_{pge 3} frac{p(p-2)}{(p-1)^2} approx 0,6601618158468695739278121100145 ...$

(ici le produit s'étend à l'ensemble des nombres premiers p ≥ 3). C₂ est appelé constante des nombres premiers jumeaux⁴

Alors la conjecture de Hardy-Littlewood s'énonce de la façon suivante :

$pi_2(x) sim 2 C_2 int_2^x {dt over (ln t)^2}$

(ce qui signifie que le quotient des deux expressions tend vers 1 quand x tend vers l'infini).

Comme le second membre à une limite infinie quand x tend vers l'infini, cette conjecture démontrerait que le nombre de nombres premiers jumeaux est bien infini.

Cette conjecture peut être justifiée (mais pas démontrée) en supposant que 1/ln(t) est la fonction de densité de la distribution des nombres premiers, une hypothèse suggérée par le théorème des nombres premiers. Cette conjecture est un cas particulier d'une conjecture plus générale appelée conjecture des n-uplets premiers de Hardy-Littlewood⁵ utilisée dans les recherches sur la conjecture de Goldbach.

Notes et références [modifier]

↑ ^a et b (en) [pdf] Twin Prime Search, Communiqué officiel de la découverte du 15 janvier 2007 [archive]
↑ (en) P.A. Clement, Congruences for sets of primes, American Mathematical Monthly n° 56 (1949), pp. 23-25
↑ Viggo Brun, La série 1/5 + 1/7 + 1/11 + 1/13 + 1/17 + 1/19 + 1/29 + 1/31 + 1/41 + 1/43 + 1/59 + 1/61 + ... où les dénominateurs sont "nombres premiers jumeaux" est convergente ou finie, Bulletin des Sciences Mathématiques n°43 (1919), pp. 100-104 et 124-128
↑ Cette constante est parfois appelée constante de Shah-Wilson et son double nommée constante des nombres premiers jumeaux d'après Weisstein, Eric W. "Twin Primes Constant." From MathWorld--A Wolfram Web Resource [archive]
↑ d'après Weisstein, Eric W. "Twin Prime Conjecture." From MathWorld--A Wolfram Web Resource. [archive]

Voir aussi [modifier]

Articles connexes [modifier]

Liens externes [modifier]

(en) Twin Primes (Chris Caldwell)
(en) Introduction to Twin Primes and Brun's Constant (Xavier Gourdon, Pascal Sebah)
(en) Site de Primegrid. Projet de calcul réparti utilisant BOINC afin de rechercher des nombres premiers jumeaux
Liste des 10001 premières paires de nombres premiers jumeaux (p,p+2), présentées par leur moyenne p+1

Portail des mathématiques

Catégorie : Nombre premier | [+]

Source : http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_des_quatr...

Théorème des quatre carrés de Lagrange

Le théorème des quatre carrés de Lagrange, est également connu sous le nom de conjecture de Bachet ; il a été énoncé pour la première fois par Claude-Gaspard Bachet de Méziriac en 1621, dans les notes accompagnant sa traduction en latin du Diophante. C'est un cas particulier du Problème de Waring. Démontré en 1770 par le mathématicien françaisJoseph Louis Lagrange, il correspond à une équation diophantienne qui se résout avec les techniques de l'arithmétique modulaire. Il s'énonce de la façon suivante :

Tout entier positif peut s'exprimer comme la somme d'au plus quatre carrés.

Plus formellement, pour tout entier positif n, il existe des entiers positifs a, b, c, d tels que :

$n = a^2 + b^2 + c^2 + d^2,!$

Le mathématicien français Adrien-Marie Legendre améliora le théorème en 1798 en affirmant qu'un entier positif peut être exprimé comme la somme d'au plus trois carrés si et seulement s'il n'est pas de la forme

$4^{k}(8m + 7),!$ .

Sa démonstration était incomplète, laissant une brèche qui fut comblée plus tard par le mathématicien allemand Carl Friedrich Gauss.

Le théorème des quatre carrés de Lagrange est un cas particulier du théorème du nombre polygonal de Fermat (en) et du problème de Waring.

La démonstration du théorème repose (en partie) sur l'identité des quatre carrés d'Euler :

$begin{array}{rcl} (x_1^2 + y_1^2 + z_1^2 + t_1^2)(x_2^2 + y_2^2 + z_2^2 + t_2^2)& = & (x_1x_2 + y_1y_2 + z_1z_2 + t_1t_2)^2\ & & quad + (x_1y_2 - y_1x_2 + t_1z_2 - z_1t_2)^2 \ & & quadquad + (x_1z_2 - z_1x_2 + y_1t_2 - t_1y_2)^2 \ & & quadquadquad + (x_1t_2 - t_1x_2 + z_1y_2 - y_1z_2)^2 end{array}$

Sommaire

[masquer]

Démonstration basée sur les quaternions d'Hurwitz [modifier]

Nous allons travailler sur l'ensemble des quaternions d'Hurwitz, également appelés entiers d'Hurwitz, qui sont des quaternions particuliers.

Quelques propriétés [modifier]

Les entiers d’Hurwitz [modifier]

Les entiers d’Hurwitz sont les nombres de la forme : $a .(1 + i + j + k) / 2 + b . i + c . j + d . k$ avec $(a,b,c,d) in mathbb{Z}^4$ . Avec $h = (1 + i + j + k) / 2$ , on peut écrire l’ensemble des entiers d’Hurwitz sous la forme $mathbb{Z} [h,i,j,k]$

On a alors la somme et le produit des deux entiers d’Hurwitz est un entier d’Hurwitz (les entiers d'Hurwitz forment un sous anneau de l'anneau formé par l'ensemble des quaternions, l'addition et la multiplication usuelles).

On rappelle que la norme d’un quaternion (et donc d’un entier d’Hurwitz) de la forme $α = a + b . i + c . j + d . k$ est 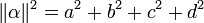$|alpha|^2=a^2+ b^2+ c^2+ d^2$

Il existe donc 24 nombres unités : 8 formés par 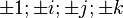$pm 1 ; pm i ; pm j ; pm k$ et 16 formés par $(pm 1 pm i pm j pm k)/2$

Identité des quatre carrés d’Euler [modifier]

On démontre que si deux nombres s’écrivent sous forme de somme de quatre carrés, alors leur produit s’écrit aussi sous forme de somme de quatre carrés. On peut le démontrer, soit à partir de l’identité des quatre carrés d’Euler, soit en écrivant que la norme d’un produit est le produit des normes.

Division [modifier]

Les entiers d’Hurwitz obéissent à la propriété de la division selon laquelle, de la même manière qu’avec la division euclidienne :

Si a et b sont des entiers d’Hurwitz, b non nul, il existe un quotient q et un reste r tel que :

a=b.q+r avec 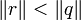$| r|<|q|$ , q et r étant des entiers d’Hurwitz.

Les quaternions d'Hurwitz forment donc un anneau euclidien à gauche et à droite.

Par exemple :

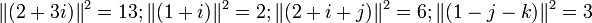
$| (2+3i) |^2=13 ; | (1+i) |^2=2 ; | (2+i+j) |^2=6 ; | (1-j-k) |^2=3$

Comme $2 + 3 i = (1 + i).(2 + i + j) + (1 - j - k)$ ,

2+3i divisé par 1+i admet comme couple (quotient,reste) le couple (2+i+j,1-j-k) Ce couple n’est pas unique puisque cette division admet aussi le couple (2+i+k,1+j-k)

On dira que a divise b (ou que a admet comme diviseur b) s’il existe q tel que a = b.q. q est alors unique.

Entier d’Hurwitz premier [modifier]

Un entier d’Hurwitz p est premier s’il n’admet comme diviseur que les nombre unités et p fois les nombres unités.

Or, si a divise b, 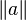$|a|$ divise $|b|$ . Donc si $|x|^2$ est premier, il ne peut exister d’entier divisant x ayant une norme différente de 1 ou de $|x|$ , donc x est un nombre d’Hurwitz premier.

1+i est, par exemple, un entier d’Hurwitz premier, car $|1+i|^2=2$ est premier.

Algorithme d’Euclide [modifier]

On peut définir un algorithme d’Euclide dans $mathbb{Z} [h,i,j,k]$ , de la même manière que dans $mathbb{N}$ .

On peut ainsi trouver un plus grand diviseur commun à a et b (noté pgcd(a ,b)), c'est-à-dire celui ayant la plus grande norme. En toute rigueur, étant donné la non commutativité de cet ensemble, on doit définir un plus grand diviseur commun à droite, et un plus grand diviseur commun à gauche.

De même que dans $mathbb{N}$ , on peut alors trouver u et v tels que pgcd(a,b)=a.u+b.v, avec u et v des entiers d’Hurwitz.

Propriété de la division d’un produit par un entier réel d’Hurwitz premier [modifier]

Si p est un entier réel d’Hurwitz premier (c'est-à-dire un nombre premier appartenant à $mathbb{N}$ ) , et qui divise a.b, où a et b sont des entiers d’Hurwitz, alors p divise a ou p divise b.

Preuve

Supposons que p premier divise a.b mais ne divise pas a. Alors, un pgcd de a et p est 1, et il existe u et v tels que au+pv=1.

Alors en multipliant par b de chaque coté, on obtient bau+bpv=b. p divise ab donc bau, et p divise p donc bpv (comme p appartient à $mathbb{N}$ , p commute avec les quaternions) .

Donc p divise b.

Théorème et lemme préliminaires [modifier]

Tout d’abord, remarquons que 0, 1 et 2 peuvent s’écrire sous forme de somme de 4 carrés ( $0 = 0 2 + 0 2 + 0 2 + 0 2;1 = 1 2 + 0 2 + 0 2 + 0 2$ et $2 = 1 2 + 1 2 + 0 2 + 0 2$ ).

Théorème [modifier]

Tout entier premier de $mathbb{N}$ qui n’est pas un entier d’Hurwitz premier peut s’écrire sous forme de somme de quatre carrés.

Preuve

Soit p remplissant les conditions précédentes. On peut donc écrire p sous la forme $p = (a + b i + c j + d k)γ$ , avec $|gamma|ne 1$ et $|gamma|ne p$

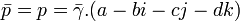
On a alors le conjugué de p (égal à p puisque p appartient à $mathbb{N}$ ) : $bar p =p=bar gamma.(a-bi-cj-dk)$

Alors 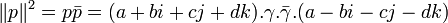$|p|^2=pbar p=(a+bi+cj+dk).gamma. bar gamma .(a-bi-cj-dk)$

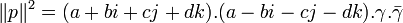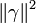$|p|^2=(a+bi+cj+dk). (a-bi-cj-dk). gamma. bar{gamma}$ car $gamma. bar{gamma}=|gamma|^2 in mathbb{N}$

Étant donné que p est premier, la seule décomposition de $p 2$ est donc $p . p$ . On en déduit que $(a 2 + b 2 + c 2 + d 2) = p$ .

Si a, b, c et d sont des entiers, p s’écrit comme somme de quatre carrés.

Si ce sont des demis-entiers, on peut alors trouver w tel que :

$w=(pm 1 pm i pm j pm k)/2$ et $a + b i + c j + d k = w + a 1 + b 1 i + c 1 j + d 1 k$ avec $a 1, b 1, c 1$ et $d 1$ des entiers pairs. On remarque que $|w|=1$

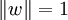
On a alors :

$p = (a + b i + c j + d k)(a - b i - c j - d k)$

$p=( w + a_1 + b_1 i + c_1 j + d_1 k)( bar w + a_1 - b_1 i - c_1 j - d_1 k)$

$p=( w + a_1 + b_1 i + c_1 j + d_1 k) bar w w( bar w + a_1 - b_1 i - c_1 j - d_1 k)$

Or comme $a 1, b 1, c 1$ et $d 1$ sont des entiers pairs, 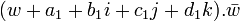$( w+a_1 +b_1 i+c_1 j+d_1 k). bar w$ ne donnera que des entiers et sera donc de la forme A+Bi+Cj+Dk, avec A, B, C et D des entiers. De même pour son conjugué, d’où : $p = (A + B i + C j + D k)(A - B i - C j - D k) = A 2 + B 2 + C 2 + D 2$

Donc p s’écrit comme somme de quatre carrés.

Lemme [modifier]

Soit p un entier premier impair, alors il existe l et m tels que p divise $1 + l 2 + m 2$ (p, l et m appartenant à $mathbb{N}$ )

Preuve

Soit p premier impair. Les différentes classes de congruence modulo p sont 0, 1, -1, ..., (p-1)/2, -(p-1)/2. Il y en a donc p.

$a^2 equiv b^2$ est équivalent à ( a $equiv$ b ou a $equiv$ –b ) (modulo p). Les différents carrés modulo p sont donc $02,1 2,...,((p - 1) / 2) 2$ . Il y en a donc $1 + (p - 1) / 2 = (p + 1) / 2$ .

De même pour $- 1 - m 2$ , il y a $(p + 1) / 2$ éléments qui sont de cette forme, différents, modulo p. Supposons que ces deux ensembles soient disjoints. Alors il y aurait $(p + 1) / 2 + (p + 1) / 2 = p + 1$ éléments dans 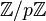$mathbb{Z}/pmathbb{Z}$ , ce qui est faux puisqu’il y en a p. 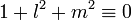Donc au moins un élément est simultanément de la forme $l 2$ et de la forme $- 1 - m 2$ modulo p, donc il existe l et m tel que $l^2 equiv -1-m^2$ modulo p c'est-à-dire $1+l^2+m^2 equiv 0$ modulo p.

Il existe donc l et m tel que p divise $1 + l 2 + m 2$ .

Théorème des quatre carrés [modifier]

Tout entier de $mathbb{N}$ peut s’écrire sous forme de somme de quatre carrés.

Preuve

Soit p un entier impair premier. Il existe donc d’après le lemme précédant l et m entier tel que p divise $1 + l 2 + m 2$ . Donc p divise $1 + l 2 + m 2 = (1 + l i + m j)(1 - l i - m j)$ .

Supposons que p soit un entier d’Hurwitz premier. Alors d’après un théorème précédant, p divise $1 + l i + m j$ ou p divise $1 - l i - m j$ . Or, ni $frac{1}{p}+frac{li}{p}+frac{mj}{p}$ ni $frac{1}{p}-frac{li}{p}-frac{mj}{p}$ ne sont des entiers d’Hurwitz. Donc p n’est pas un entier d’Hurwitz premier.

D’après le théorème précédant, p peut donc s’écrire sous forme de somme de quatre carrés.

Donc, si p est un entier impair premier, p peut donc s’écrire sous forme de somme de quatre carrés.

Si p=0, p=1 ou p=2, nous avons déjà vu que p peut s’écrire sous forme de somme de quatre carrés.

Si p est un entier, non premier, strictement supérieur à 2, alors p peut s’écrire sous forme de produit de nombre premiers. Ces nombres premiers peuvent s’écrire sous forme de carrés, et leur produits aussi, d’après la remarque sur l’identité des quatre carrés d’Euler. Donc p peut s’écrire sous forme de somme de quatre carrés.

Finalement, tout élément de $mathbb{N}$ peut s’écrire sous forme de somme de quatre carrés.

Fonctions arithmétiques [modifier]

Les fonctions arithmétiques permettent d'obtenir des résultats plus généraux. Si on pose $r 4 (n)$ comme étant le nombre de façon de décomposer $n$ sous forme d'une somme de 4 carrés, on obtient le résultat suivant:

$sum_{n=0}^{infty}{r_4(n)x^n} = left( sum_{n=0}^{infty}{x^{n^2}} right)^4$ , pour

| x | < 1

.

Moyennant l'utilisation des séries de Lambert, on en déduit le théorème suivant, dit théorème de Jacobi :

$forall n in mathbb{N}^*, r_4(n) = 8 sum_{d|n, d notequiv 0[4]}{d}$

Par exemple, 1 n'est divisible que par lui-même, qui n'est pas congru à 0 modulo 4. Donc $r 4 (1) = 8$

3 des 8 formes sont :

$1 = 1 2 + 0 2 + 0 2 + 0 2$

$1 = 0 2 + 1 2 + 0 2 + 0 2$

$1 = ( - 1) 2 + 0 2 + 0 2 + 0 2$

Articles connexes [modifier]

Portail des mathématiques

Catégories : Équation diophantienne | Théorème d'algèbre | Joseph-Louis Lagrange | Arithmétique modulaire | [+]

Source : http://fr.wikipedia.org/wiki/Probl%C3%A8me_de_Waring

Problème de Waring

En théorie des nombres, le problème de Waring, proposé en 1770 par Edward Waring, demande si, pour tout entier naturel k, il existe un entier naturel s tel que tout entier soit la somme d'au plus s puissances k^e d'entiers. La réponse affirmative fut apportée par David Hilbert en 1909. Ce sujet est parfois décrit comme le théorème de Hilbert-Waring.

Pour chaque k, nous notons le plus petit s par g(k). Nous avons g(1) = 1. Quelques calculs montrent que 7 requiert 4 carrés, 23 requiert 9 cubes, et 79 requiert 19 puissances quatrièmes. Waring conjectura que ces valeurs étaient les meilleures possibles.

Le théorème des quatre carrés de Lagrange de 1770 affirme que chaque nombre naturel est la somme d'au plus quatre carrés ; puisque trois carrés ne sont pas suffisants, ce théorème établit g(2) = 4. Ce théorème fut conjecturé par Fermat en 1640 et sa première mention date de 1621.

Au fil des années, divers résultats sur les valeurs de g furent établis, en utilisant des techniques de démonstration de plus en plus sophistiquées et complexes. Par exemple, Liouvillemontra que g(4) vaut au plus 53. Hardy et Littlewood démontrèrent que tous les nombres suffisamment grands sont la somme d'au plus 19 puissances quatrièmes.

L'égalité g(3) = 9 fut établie entre 1909 et 1912 par Wieferich et A. J. Kempner, l'égalité g(4) = 19 en 1986 par R. Balasubramanian, F. Dress et J.-M. Deshouillers, l'égalité g(5) = 37 en 1964 par Chen Jingrun et l'égalité g(6) = 73 en 1940 par Pillai.

Toutes les autres valeurs de g sont connues aujourd'hui, grâce au travail de Dickson, Pillai, Rubugunday et Niven. Leur énoncé contient deux cas et il est conjecturé que le second cas ne peut jamais se produire ; dans le premier cas, la formule se lit

g(k) = E((3/2)^k) + 2^k - 2 pour k ≥ 6.

Sommaire

[masquer]

Les majorations provisoires [modifier]

Avant que soient trouvées les valeurs exactes de g(n), des majorations avaient été déterminées. En voici quelques unes, pour n de 3 à 8.

Majoration de g(3) [modifier]

17 (Maillet, 1895)
13 (A. Fleck, 1906)
9 (Wieferich, 1909), valeur exacte.

Majoration de g(4) [modifier]

53 (J. Liouville, 1859)
47 (S. Réalis, 1878)
45 (É. Lucas, 1878)
41 (É. Lucas, 1878)
39 (A. Fleck, 1906)
38 (E. Landau, 1907)
37 (A. Wieferich, 1909)
35 (L. E. Dickson, 1933)
22 (H.E. Thomas, 1973)
21 (R. Balasubramanian, 1979)
20 (R. Balasubramanian, 1985)
19 (R. Balasubramanian, F. Dress, J.-M. Deshouillers, 1986), valeur exacte

Majoration de g(5) [modifier]

192 (A. Fleck, 1906)
59 (A. Wieferich, 1909)
58 (Baer, 1913)
54 (L.E. Dickson, 1933)
37 (Chen Jingrun, 1965), valeur exacte.

Majoration de g(6) [modifier]

970, (A.J. Kempner, 1912)
478 (Baer, 1913)
183 (James, 1934)
73 (K.C.S. Pillai, 1940), valeur exacte.

Majoration de g(7) [modifier]

3806 (A. Wieferich, 1909)
322 (James, 1934)
143, valeur exacte.

Majoration de g(8) [modifier]

36 119 (A. Hurwitz, 1908)
31 353 (A.J. Kempner, 1912)
595 (James, 1934)
279, valeur exacte.

Bibliographie [modifier]

W. J. Ellison: Waring's problem. American Mathematical Monthly, volume 78 (1971), pp. 10-76. (Exposé, contenant une formule précise pour g(k) et une version simplifiée de la preuve d'Hilbert)
Hans Rademacher et Otto Toeplitz, The Enjoyment of Mathematics (1933) (ISBN 0-691-02351-4). (Contient une preuve du théorème de Lagrange, accessible aux étudiants)

Portail des mathématiques

Catégorie : Équation diophantienne | [+]

Source : http://fr.wikipedia.org/wiki/M%C3%A9daille_Fields

Médaille Fields

Médaille Fields

Nom original	Fields Medal
Description	Prix récompensant une contribution majeure en mathématiques
Organisateur	Union mathématique internationale
Date de création	1936
Actuel récipiendaire	Elon Lindenstrauss Ngô Bảo Châu Stanislav Smirnov Cédric Villani
Site officiel	http://www.mathunion.org/

La médaille Fields est la plus prestigieuse récompense pour la reconnaissance de travaux en mathématiques, souvent comparée par les médias au prix Nobel¹, à tort car elle en diffère sur certains aspects essentiels (distinction de travaux exceptionnels, limite d'âge, récompense financière modeste), ce qui fait du prix Abel un meilleur équivalent du prix Nobel (récompense plutôt d'une œuvre dans son ensemble)². Son but est d'apporter un soutien aux mathématiciens jeunes qui ont déjà apporté des contributions majeures. Elle est attribuée tous les quatre ans au cours du congrès international des mathématiciens à, au plus, quatre mathématiciens devant avoir moins de 40 ans au 1^er janvier de l'année en cours. Les lauréats se voient attribuer chacun une médaille et un prix de 15 000 dollars canadiens (soit un peu plus de 10 000 euros)³.

John Charles Fields (1863-1932) proposa la création de cette médaille en 1923 lors d'une réunion internationale à Toronto. À sa mort, en 1932, il lègue ses biens à la science afin de financer la médaille. À l'origine, seules deux médailles étaient décernées tous les quatre ans. La Seconde Guerre mondiale a interrompu l'attribution de cette distinction jusqu'en 1950. La décision de passer à quatre lauréats au plus date de 1966.

Sommaire

[masquer]

Liste des lauréats [modifier]

1936 : Lars Ahlfors ( Finlande), Jesse Douglas ( États-Unis)
1950 : Laurent Schwartz ( France), Atle Selberg ( Norvège)
1954 : Jean-Pierre Serre (), Kunihiko Kodaira ( Japon)
1958 : René Thom (), Klaus Roth ( Royaume-Uni)
1962 : Lars Hormander ( Suède), John Milnor ()
1966 : Michael Atiyah (), Paul Cohen (), Alexandre Grothendieck (), Stephen Smale ()
1970 : Alan Baker (), Heisuke Hironaka (), Sergueï Novikov ( Union soviétique), John Griggs Thompson ()
1974 : Enrico Bombieri ( Italie), David Mumford ()
1978 : Pierre Deligne ( Belgique), Charles Fefferman (), Gregori Margulis (), Daniel Quillen ()
1982 : Alain Connes (), William Thurston (), Shing-Tung Yau ()
1986 : Simon Donaldson (), Gerd Faltings ( Allemagne), Michael Freedman ()
1990 : Vladimir Drinfeld (⁴), Vaughan Frederick Randal Jones ( Nouvelle-Zélande), Shigefumi Mori (), Edward Witten ()
1994 : Jean-Christophe Yoccoz (), Pierre-Louis Lions (), Efim Zelmanov ( Russie), Jean Bourgain ()
1998 : Richard Ewen Borcherds ( Afrique du Sud), William Timothy Gowers (), Maxim Kontsevich (), Curtis McMullen ()
2002 : Laurent Lafforgue (), Vladimir Voevodsky ()
2006 : Wendelin Werner (), Andreï Okounkov (), Grigori Perelman [médaille déclinée] (), Terence Tao ( Australie)
2010 : Cédric Villani (), Ngô Bảo Châu ( Viêt Nam,), Elon Lindenstrauss ( Israël), Stanislav Smirnov ()

Circonstances inhabituelles [modifier]

En 1966, Alexandre Grothendieck a boycotté la cérémonie devant lui remettre une médaille Fields, tenue à Moscou, pour protester contre les actions militaires soviétiques mises en place en Europe de l’Est⁵.

En 1970, Sergueï Novikov, en raison des restrictions mises en place à son encontre par le gouvernement soviétique, fut incapable de voyager pour se rendre au congrès à Nice pour recevoir sa médaille.

En 1978, Gregori Margulis, en raison des restrictions mises en place à son encontre par le gouvernement soviétique, fut incapable de voyager pour se rendre au congrès à Helsinki pour recevoir sa médaille. La récompense fut reçue en son nom par Jacques Tits, qui dit à cette occasion : « Je ne peux pas ne pas exprimer ma profonde déception — sans doute partagée par beaucoup de monde ici — due à l'absence de Margulis à cette cérémonie. En raison du sens symbolique de cette ville d'Helsinki, j'ai vraiment eu l'espoir grandissant que j'aurais au moins la chance de rencontrer un mathématicien que j'ai seulement connu à travers son travail et pour qui j'ai le plus grand respect et la plus grande admiration⁶. »

En 1982, le congrès aurait dû se tenir à Varsovie mais fut reprogrammé l'année suivante, en raison de l'instabilité politique du pays. Les récompenses furent annoncées à la neuvième Assemblée Générale de l'IMU plus tôt dans l'année et remises lors du congrès de Varsovie en 1983.

En 1998, au CIM, Andrew Wiles fut présenté par le président du comité de la médaille Fields, Yuri Manin (en), avec la première plaque d'argent de l'IMU en reconnaissance de sa démonstration du dernier théorème de Fermat. Don Zagier fit référence à la plaque comme une « médaille Fields de poids ». Pour expliquer cette récompense, il est fréquemment mis en avant le fait que Wiles avait dépassé l'âge limite de la médaille Fields (40 ans⁷). Pourtant, bien que Wiles ait déjà légèrement dépassé l'âge limite en 1994, il avait alors été pressenti favori pour gagner la médaille ; ce ne fut finalement pas envisageable car un trou dans la démonstration fut trouvé à l'été 1993, qui ne fut comblé par Wiles qu'en 1995⁸^,⁹.

En 2003, un autre équivalent du Prix Nobel pour les mathématiques a été créé en Norvège, le prix Abel. Le premier prix a été attribué au Français Jean-Pierre Serre, déjà plus jeune lauréat de la médaille Fields en 1954.

En 2006, Grigori Perelman, lauréat pour sa démonstration de la conjecture de Poincaré, refusa la médaille Fields¹⁰ et n'assista pas au congrès¹¹.

Un même problème, savoir si une variété homotopiquement équivalente à une sphère de dimension n est ou non une sphère de dimension n (voir Conjecture de Poincaré), a vu l'attribution de trois médailles Fields, la première en 1966 à Stephen Smale, la deuxième en 1986 à Michael Freedman, la troisième vingt ans plus tard à Grigori Perelman.

Classement par pays [modifier]

États-Unis	13
France	11
URSS (3) / Russie (6)	9
Royaume-Uni	5
Japon	3
Belgique	2
Afrique du Sud	1
Finlande	1
Israël	1
Italie	1
Norvège	1
Nouvelle-Zélande	1
Suède	1
Allemagne	1
Australie	1
Vietnam	1

Classement par institutions [modifier]

À leur nomination, les médaillés Fields travaillaient dans les institutions suivantes¹² :

Université de Princeton	13
Université de Paris (y compris, après séparation, Université Paris-Sud (3) et Université Paris-Dauphine(1))	7
Université de Cambridge	4
Université d'Harvard	4
Institut des Hautes Études Scientifiques	4
Université d'Oxford	3
Massachusetts Institute of Technology	2
Université de Californie à Berkeley	2
Université de Moscou	2
Université de Stanford	2
École Normale Supérieure de Lyon	1
Université de Californie à Los Angeles	1
Université de Californie à San Diego	1
Université de Genève	1
Université de Jérusalem	1
Université de Kharkov	1
Université de Kyoto	1
Université de Londres	1
Université de Nancy	1
Université de Pise	1
Université Rutgers	1
Université de Stockholm	1
Université de Strasbourg	1
Université du Wisconsin	1

La médaille [modifier]

Revers de la médaille Fields.

La médaille a été dessinée par le sculpteur canadien R. Tait McKenzie (en)¹³.

Sur l'avers, un portrait de profil d'Archimède et une citation en latin du poète Manilius http://fr.wikipedia.org/wiki/Marcus_Manilius, Astronomica, IV, v. 392 http://www.filosofico.net/manilioastronomica.htm : « Transire suum pectus mundoque potiri » (mot à mot : « traverser ton propre coeur (= franchir tes limites) et te rendre maître de l'univers (par la connaissance »).

Sur le revers, l'inscription latine :

CONGREGATI

EX TOTO ORBE

MATHEMATICI

OB SCRIPTA INSIGNIA

TRIBUERE

Traduction : « Les mathématiciens s'étant rassemblés du monde entier ont remis cette récompense en raison de remarquables écrits. »

Dans l'arrière-plan, une représentation de la tombe d'Archimède, avec la gravure de son théorème « De la sphère et du cylindre » (une sphère et un cylindre circonscrit de mêmes hauteur et diamètre, travail duquel il était le plus fier) derrière un rameau.

La tranche porte le nom du lauréat.

Dans les arts [modifier]

Dans le film Un conte de Noël, le personnage joué par Hippolyte Girardot est médaillé Fields. Il est amusant de noter que c'est Cédric Villani, qui depuis a obtenu lui-même la médaille Fields en 2010, qui a couvert de formules le tableau sur lequel est censé écrire Hippolyte Girardot.
Dans le film Will Hunting, le personnage fictif Gerald Lambeau aurait reçu la médaille Fields pour des travaux en combinatoire.
Dans le film Un homme d'exception, John Forbes Nash se plaint de ne pas avoir reçu la médaille Fields.
Dans la série télévisée Eureka, Nathan Stark dit avoir reçu la médaille Fields.
Dans la série télévisée Numb3rs, le mathématicien fictif Charlie Eppes explique à Megan Reeves l'inexistence d'un prix Nobel des mathématiques.

Notes et références [modifier]

↑ Alfred Nobel ne s'est jamais expliqué des motifs justifiant l'absence des mathématiques parmi les disciplines récompensées par un Prix Nobel.
↑ Mathématiques : quelle pérennité pour le prestige français ? [archive] Intervention de Michel Brouédans l'émission de Science publique du 1^er septembre 2010 (8 min 10 dans le podcast)
↑ (en) Eric W. Weisstein, Fields Medal [archive], MathWorld. (page consultée le 24 août 2010)
↑ Vladimir Drinfeld est parfois considéré comme ukrainien mais l'indépendance ukrainienne fut proclamée le 24 août 1991.
↑ (en) Allyn Jackson, « As If Summoned from the Void: The Life of Alexandre Grothendieck », dansNotices of the American Mathematical Society, vol. 51, n^o 10, novembre 2004, p. 1196-1212[ [pdf]texte intégral [archive] (page consultée le 24 août 2010) ], p. 1198
↑ (en) John J. O'Connor et Edmund F. Robertson, « Gregori Margulis [archive] », MacTutor History of Mathematics archive, Université de St Andrews.(page consultée le 24 août 2010)
↑ (en) Andrew John Wiles [archive], Encyclopædia Britannica (page consultée le 24 août 2010)
↑ (en) Andrew J. Wiles awarded the "IMU silver plaque" [archive], Medieninformation Nr. 183, 18 août 1998, Université technique de Berlin (page consultée le 24 août 2010)
↑ (en) Allyn Jackson, « Borcherds, Gowers, Kontsevich, and McMullen Receive Fields Medals », dans Notices of the American Mathematical Society, vol. 45, n^o 10, novembre 1998, p. 1358-1360[ [pdf]texte intégral [archive] (page consultée le 24 août 2010) ], p. 1360
↑ (en) « Maths genius turns down top prize », dans BBC News, 22 août 2006 [ texte intégral [archive](page consultée le 24 août 2010) ]
↑ (en) Justin Mullins, « Prestigious Fields Medals for mathematics awarded », dans New Scientist, 31 août 2006 [ texte intégral [archive] (page consultée le 24 août 2010) ]
↑ http://www.infoplease.com/ipa/A0192505.html#axzz0xhlSGy2N [archive]
↑ (en) The Fields Medal [archive] (site officiel)

Voir aussi [modifier]

Sur les autres projets Wikimédia :

Médaille Fields sur Wikinews(actualités libres)

Lien externe [modifier]

(en) Site officiel

[Dérouler] v · d · m Lauréats de la médaille Fields

Catégories : Distinction en mathématiques | Médaille Fields | [+]

Source : http://fr.wikipedia.org/wiki/Recherche_math%C3%A9matique

Recherche mathématique

La recherche mathématique est une branche de la recherche scientifique.

Sommaire

[masquer]

Domaines de recherche [modifier]

Centres internationaux de recherche [modifier]

Revues, publications [modifier]

Récompenses en mathématiques [modifier]

Portail des mathématiques

Catégories : Recherche en mathématiques | Liste en rapport avec les mathématiques | [+]

Source : http://fr.wikipedia.org/wiki/Math%C3%A9maticien

Mathématicien

Cet article ne cite pas suffisamment ses sources (avril 2010).

Si vous connaissez le thème traité, merci d'indiquer les passages à sourcer avec {{Référence souhaitée}} ou, mieux, incluez les références utiles en les liant aux notes de bas de page. (Modifier l'article)

Cet article est une ébauche concernant l'épistémologie.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Pierre-Simon Laplace

Un mathématicien est au sens restreint un chercheur en mathématiques, par extension toute personne faisant des mathématiques la base de son activité principale. Ce terme recouvre une large palette de compétences et de pratiques très différentes, avec néanmoins en commun un vocabulaire et un formalisme spécifiques, ainsi qu'une exigence de rigueur propre à cette discipline.

Le terme générique mathématicien peut se décliner pour des domaines plus restreints, comme algébriste, analyste, arithméticien, géomètre,probabiliste, statisticien, logicien etc.

Un mathématicien est véritablement reconnu s'il est admis qu'il a contribué significativement au développement de la science mathématique.

Les personnes mettant en oeuvre les résultats mathématiques pour les profits d'une autre discipline ou activité ne sont pas pour autant considérées comme mathématiciens.

Sommaire

[masquer]

Sur le sens du mot mathématicien [modifier]

On trouve essentiellement deux usages différents de ce mot : le mathématicien peut désigner une personne travaillant activement dans la recherche mathématique¹, ce qui donne la plupart du temps lieu, de nos jours, à des publications dans des revues à comité de lecture. Ainsi sont classés Henri Poincaré ou Andrew Wiles, par exemple. D'un autre côté, le mathématicien peut désigner une personne versée dans les mathématiques², ou qui a travaillé dans un domaine connexe (enseignement des mathématiques ne donnant pas lieu à de la recherche, épistémologie, pédagogie, ou même par des oeuvres de vulgarisation scientifique). Ainsi peuvent être classés Denis Guedj ou Stella Baruk.

Activités essentielles d'un mathématicien [modifier]

Il n'y a pas de définition précise ou de restriction a priori de l'activité d'un mathématicien³, en dehors de l'objectif d'un apport à sa discipline.

Le travail principal d'un mathématicien peut ainsi prendre pour objectif la résolution des problèmes ouverts et la vérification des conjectures. Dans ce contexte, le terme problème est à distinguer des exercices que posent les professeurs aux élèves, et dont les solutions sont déjà connues. Les problèmes peuvent se poser lors de modélisations en physique, en économie, en informatique, etc. ou lors de tentatives de généralisations de découvertes antérieures.

Ces travaux peuvent nécessiter un élargissement ou un approfondissement des résultats déjà acquis dans un domaine des mathématiques, mais également consister en la recherche de liens entre des domaines différents.

La découverte et la caractérisation d'un domaine d'étude nouveau peuvent également être un résultat de l'activité d'un mathématicien.

Les mathématiciens s'imposent une rigueur méthodologique qui peut faire paraître singulière leur discipline. Le formalisme et l'exposition rigoureuse des travaux, y compris des étapes intermédiaires, sont des points estimés nécessaires à l'acceptation des résultats obtenus. Le travail de vérification, ou de réfutation le cas échéant, des résultats présentés par d'autres mathématiciens fait également partie de l'activité d'un mathématicien. Pour certains exposés particulièrement complexes ou difficiles, ces vérifications peuvent nécessiter la contribution de plusieurs mathématiciens travaillant de manière concertée.

Emplois dans le monde contemporain [modifier]

Les mathématiciens se spécialisent souvent dans différentes branches des mathématiques. On distingue parfois les mathématiques pures des mathématiques appliquées. Cette distinction n'est cependant ni formalisée, ni de compréhension commune à l'ensemble des mathématiciens.

L'usage grandissant des mathématiques dans de nombreuses disciplines et techniques offre aux mathématiciens des opportunités d'emploi diverses. Ils sont parfois employés par des entreprises privées ou étatiques, ou comme professeurs dans un cadre universitaire, souvent en complément de leurs travaux de recherche. En tant que spécialistes de leur discipline, ou d'une partie des mathématiques, certains mathématiciens sont intégrés dans des équipes multidisciplinaires travaillant sur un sujet plus vaste (physique, informatique, modélisations, ...).

Distinctions et prix [modifier]

Il n'existe pas de prix Nobel pour les mathématiciens. La médaille Fields est cependant considérée par beaucoup comme une distinction de même valeur et à ce titre parfois appelée prix Nobel des mathématiques. Notons cependant que ce prix est réservé aux mathématiciens de moins de 40 ans⁴.

Parmi les autres distinctions prestigieuses figurent notamment :

le prix Abel
le prix Nevanlinna
le prix Wolf
le prix Fermat
le prix Loève
le prix Clay (parfois nommé prix du millénaire)
le prix Crafoord
le prix Carl-Friedrich-Gauss pour les mathématiques appliquées
le prix Pólya et la médaille De Morgan, décernés par la London Mathematical Society

Titres particuliers [modifier]

Le Prince des mathématiciens : surnom donné à Carl Friedrich Gauss eu égard à l'ampleur de sa contribution aux mathématiques.

Données démographiques [modifier]

Un annuaire mondial de mathématiciens, publié par l'Union mathématique internationale, est accessible sur le site de l'Union.

A cet usage, l'Union Mathématique Internationale a précisé la définition du mathématicien retenue :

On appelle mathématicien actif toute personne qui a publié dans les 4 dernières années au moins 2 articles référencés dans les 3 grandes bases de données bibliographiques, à savoir ZentraleBlatt fürtabon Mathematik, Mathematical Reviews et Referatnyi Zhurnal.

Restrictive, mais opératoire, cette définition permet un dénombrement des mathématiciens en activité.

En France, une autre définition considère comme mathématicien toute personne employée au titre des mathématiques par l'université ou un organisme de recherche; en ce sens, il existe entre 3 500 et 4 000 mathématiciens en France, dont la très grande majorité (environ 3 200) sont à l'université, la plupart étant également actifs au sens de la définition précédente.

Selon Alain Connes, David Hilbert et Henri Poincaré sont les derniers mathématiciens à avoir une maîtrise complète de la recherche de leur époque⁵. Selon leurs dires, il y aurait entre 15 000 et 20 000 mathématiciens.

Bien que la majorité des mathématiciens reconnus soient des hommes, la profession s'est féminisée, en particulier depuis la Seconde Guerre mondiale. Cette féminisation, moins forte en mathématiques pures qu'en mathématiques appliquées, marque cependant le pas depuis plusieurs années, en particulier en haut de l'échelle : parmi les 75 mathématiciens admis à l'Institut universitaire de France depuis sa fondation, on ne compte aucune femme.

Notes et références [modifier]

↑ Qu'est-ce qu'un mathématicien ? [archive] Entretien avec André Lichnerowicz
↑ Mathématicien [archive] sur le site du TLFI
↑ Un mathématicien est une machine à transformer le café en théorèmes. Paul Erdös
↑ Voir à ce sujet les péripéties concernant Andrew Wiles dans le paragraphe Circonstances inhabituelles de l'article sur la médaille Fields.
↑ Alain Connes, triangles de pensée, Éditions Odile Jacob, p.127.

Bibliographie [modifier]

Didier Nordon, Les obstinations d'un mathématicien. Regards sur la science pour la science, Belin, 2003.
Pierre Lecomte , Le mathématicien et ses esclaves, Éditions de l'Université de Liège, 2009.
Paul Lévy, Quelques aspects de la pensée d'un mathématicien. Librairie scientifique et technique, A. Blanchard, 1970.
Eric Temple Bell, Les grands mathématiciens, texte traduit par Ami Gandillon, Payot, 1961.
Encyclopédie méthodique: dictionnaire des jeux mathématiques, contenant l'analyse, les recherches, les calculs, les probabilités les tables numériques, publiés par plusieurs célèbres mathématiciens, relativement aux jeux de hasard et de combinaisons, et suite du Dictionnaire des jeux, Chez H. Agasse, 1798
Histoire des mathématiques, dans laquelle on rend compte de leurs progrès depuis leur origine jusqu'à nos jours; où l'on expose le tableau & le développement des principales découvertes, les contestations qu'elles ont fait naître & les principaux traits de la vie des mathématiciens les plus..., Jean-Étienne Montucla, Bibliothèque interuniversitaire (Nancy), Chez Ch. Ant. Jombert, 1758.

Voir aussi [modifier]

Articles connexes [modifier]

Sur les autres projets Wikimédia :

Mathématicien sur Wikimedia Commons (ressources multimédia)
Mathématicien sur le Wiktionnaire(dictionnaire universel)
Mathématicien sur Wikisource(bibliothèque universelle)
Mathématicien sur Wikiquote (recueil de citations)

Liste de statisticiens

Portail des mathématiques

Catégories : Mathématicien | Mathématicienne | Recherche en mathématiques | [+]

Mathématique

Cours, définitions, Vidéos, théorèmes, exercices, corrigés, livres sur les mathématiques, Livres Rares, Livres anciens de mathématiques

Recherchez sur le site (cours, livres, Agregation, etc.)

Liens utiles

Rechercher

CODE PROMO

Liens mathématiques divers

Livres en pdf

Cours

Documents Mathématiques

Novembre 2024

Notes récentes

Archives

Catégories

Derniers weblogs mis à jour

Liens Sites Amis

22/11/2010

Andrew Wiles

Andrew Wiles

Sommaire

Biographie [modifier]

Bibliographie [modifier]

Notes et références [modifier]

Lien externe [modifier]

Diophante d'Alexandrie

Diophante d'Alexandrie

Sommaire

Biographie [modifier]

Son épitaphe [modifier]

Annexes [modifier]

Bibliographie [modifier]

Notes et références [modifier]

Liens externes [modifier]

21/11/2010

Théorie des corps de classes

Théorie des corps de classes

Sommaire

Formulation en langage contemporain [modifier]

Théorie du corps de classes local [modifier]

Corps de classes global [modifier]

Historique [modifier]

Références [modifier]

Liens externes [modifier]

Conjecture de Dubner

Conjecture de Dubner

Sommaire

Généralisation [modifier]

Sources [modifier]

Articles connexes [modifier]

Liens externes [modifier]

Notes [modifier]

Nombres premiers jumeaux

Nombres premiers jumeaux

Sommaire

Définition [modifier]

Liste des premiers nombres premiers jumeaux [modifier]

Quelques propriétés [modifier]

Record [modifier]

Conjecture des nombres premiers jumeaux [modifier]

Résultats partiels [modifier]

La conjecture de Hardy-Littlewood [modifier]

Notes et références [modifier]

Voir aussi [modifier]

Articles connexes [modifier]

Liens externes [modifier]

Théorème des quatre carrés de Lagrange

Théorème des quatre carrés de Lagrange

Sommaire

Démonstration basée sur les quaternions d'Hurwitz [modifier]

Quelques propriétés [modifier]

Les entiers d’Hurwitz [modifier]

Identité des quatre carrés d’Euler [modifier]

Division [modifier]

Entier d’Hurwitz premier [modifier]

Algorithme d’Euclide [modifier]

Propriété de la division d’un produit par un entier réel d’Hurwitz premier [modifier]

Théorème et lemme préliminaires [modifier]

Théorème [modifier]

Lemme [modifier]

Théorème des quatre carrés [modifier]