20/11/2010
Histoire des mathématiques
L’histoire des mathématiques s'étend sur plusieurs millénaires et dans de nombreuses régions du globe allant de la Chine à l’Amérique centrale. Jusqu'au xviie siècle, le développement des connaissances mathématiques s’effectue essentiellement de façon cloisonnée dans divers endroits du globe. À partir du xixe et surtout au xxe siècle, le foisonnement des travaux de recherche et la mondialisation des connaissances mènent plutôt à un découpage de cette histoire en fonction des domaines de mathématiques.Histoire des mathématiques
L'os d'Ishango datant de plus de 20 000 ans avant notre ère est généralement cité pour être la première preuve de la connaissance des premiers nombres premiers et de la multiplication[réf. nécessaire], mais cette interprétation reste sujette à discussions[réf. nécessaire]. Il est dit que les mégalithes en Égypte au Ve millénaire avant notre ère ou en Angleterre au IIIe millénaire incorporeraient des idées géométriques comme les cercles, les ellipses et les triplets pythagoriciens[réf. nécessaire]. En 2 600 avant notre ère, les constructions égyptiennes attestent d'une connaissance précise et réfléchie de la géométrie[réf. nécessaire]. L'ethnomathématiques est un domaine de recherche à la frontière de l'anthropologie, de l'ethnologie et des mathématiques qui vise entre autres à comprendre l'essor des mathématiques dans les premières civilisations à partir des objets, instruments, peintures, et autres documents retrouvés. On attribue généralement le début de l'écriture à Sumer, dans le bassin du Tigre et de l'Euphrate ou Mésopotamie. Cette écriture, dite cunéiforme, naît du besoin d'organiser l'irrigation 1et le commerce. Conjointement à la naissance de l'écriture naissent les premières mathématiques utilitaires (économie, calculs de surface). Le premier système numérique positionnel apparaît : le système sexagésimal. Pendant près de deux mille ans, les mathématiques vont se développer dans la région de Sumer, Akkad puis Babylone. Les tablettes datant de cette période sont constituées de tables numériques et de modes d'emploi. C'est ainsi qu'à Nippur (à une centaine de kilomètres de Bagdad), ont été découvertes au xixe siècle des tablettes scolaires datant de l'époque paléo-Babylonienne (2000 av. J.-C.)2. On sait donc qu'ils connaissaient les quatre opérations mais se sont lancés dans des calculs plus complexes avec une très grande précision, comme des algorithmes d'extraction de racines carrées3, racines cubiques, la résolution d'équations du second degré. Comme ils faisaient les divisions par multiplication par l'inverse, les tables d'inverse jouaient un grand rôle. On en a retrouvé avec des inverses pour des nombres à six chiffres sexagésimaux, ce qui indique une très grande précision 4. On a également retrouvé des tablettes sur lesquelles figurent des listes de carrés d'entier, des listes de cubes et une liste souvent interprétée comme celle de triplets pythagoriciens5 suggérant qu'ils connaissaient la propriété des triangles rectangles plus de 1 000 ans avant Pythagore. Des tablettes ont aussi été retrouvées décrivant des algorithmes pour résoudre des problèmes complexes 6. Ils étaient capables d'utiliser des interpolations linéaires pour les calculs des valeurs intermédiaires ne figurant pas dans leurs tableaux. La période la plus riche concernant ces mathématiques est la période de Hammurabi (xviiie siècle av. J.-C.). Vers 1000 av. J.-C., on observe un développement du calcul vers l'astronomie mathématique7. Les meilleures sources sur les connaissances mathématiques en Égypte antique sont le Papyrus Rhind (seconde période intermédiaire, xxe siècle av. J.-C.) qui développe de nombreux problèmes de géométrie, et le Papyrus de Moscou (1850 avant J.-C.) et le rouleau de cuir. À ces documents s'ajoutent trois autres papyrus et deux tablettes de bois ; le manque de documents ne permet pas d'attester ces connaissances8. Les Égyptiens ont utilisé les mathématiques principalement pour le calcul des salaires, la gestion des récoltes, les calculs de surface et de volume et dans leurs travaux d'irrigation et de construction (voir Sciences Égyptiennes). Ils utilisaient un système d'écriture des nombres additionnel (numération égyptienne). Ils connaissaient les quatre opérations, étaient familiers du calcul fractionnaire (basé uniquement sur les inverses d'entiers naturels) et étaient capables de résoudre des équations du premier degré par la méthode de la fausse position. Ils utilisaient une approximation fractionnaire de π9. Les équations ne sont pas écrites, mais elles sous-tendent les explications données. La source principale la plus ancienne de nos connaissances sur les mathématiques chinoises provient du manuscrit de Zhoubi Suanjing ou Les neuf chapitres sur l'art mathématique, daté du ier siècle, mais regroupant des résultats probablement plus anciens. On y découvre que les Chinois avaient développé des méthodes de calcul et de démonstration qui leur étaient propres : arithmétique, fractions, extraction des racines carrées et cubiques, mode de calcul de l'aire du disque, volume de la pyramide et méthode du pivot de Gauss. Leur développement des algorithmes de calcul est remarquablement moderne. Mais on trouve aussi, sur des os de moutons et de bœufs, des gravures prouvant qu'ils utilisaient un système décimal positionnel (numération chinoise). Ils sont aussi à l'origine d'abaques les aidant à calculer. Les mathématiques chinoises avant notre ère sont principalement tournées vers les calculs utilitaires. Elles se développent ensuite de manière propre entre le ier et le viie siècle après J.-C. puis entre le xe et le xiiie siècle. La civilisation maya s'étend de 2600 avant J.-C. jusqu'à 1500 ans après J.-C. avec un apogée à l'époque classique du iiie siècle au ixe siècle. Les mathématiques sont principalement numériques et tournées vers le comput calendaire et l'astronomie. Les Mayas utilisent un système de numération positionnel de base vingt (numération maya). Les sources mayas sont issues principalement des codex (écrits autour duxiiie siècle). Mais ceux-ci ont été en grande majorité détruits par l'Inquisition et il ne reste de nos jours que quatre codex (celui de Dresde, deParis, de Madrid et Grolier) dont le dernier est peut-être un faux. La civilisation Inca (1400-1530) a développé un système de numération positionnel en base 10 (donc similaire à celui utilisé aujourd'hui). Ne connaissant pas l'écriture10, ils utilisaient des quipus pour « écrire » les statistiques de l'État. Un quipu est un encordage dont les cordes présentent trois types de nœuds symbolisant respectivement l'unité, la dizaine et la centaine11. Un agencement des nœuds sur une corde donne un nombre entre 1 et 999 ; les ajouts de cordes permettant de passer au millier, au million, etc. La civilisation de la vallée de l'Indus développa un usage essentiellement pratique des mathématiques : système décimal de poids et mesures et régularité des proportions dans la confection de briques. Les sources écrites les plus anciennes concernant les mathématiques indiennes sont les sulba-sutras (de 800 av. J.-C. jusqu'à 200). Ce sont des textes religieux écrits en sanscrit réglementant la taille des autels de sacrifice. Les mathématiques qui y sont présentées sont essentiellement géométriques et sans démonstration. On ignore s'il s'agit de la seule activité mathématique de cette époque ou seulement les traces d'une activité plus générale. Les Indiens connaissaient le théorème de Pythagore, savaient construire de manière exacte la quadrature d'un rectangle (construction d'un carré de même aire) et de manière approchée celle du cercle. On voit apparaître aussi des approximations fractionnaires de π et de racine carrée de deux. Vers la fin de cette période, on voit se mettre en place les neuf chiffres du système décimal. Il faut ensuite attendre l'époque jaïniste (ve siècle après J.-C.) pour voir naître de nouveaux textes mathématiques. Les mathématiciens de cette époque commencent une réflexion sur l'infini, développent des calculs sur des nombres de la forme À la différences des mathématiques égyptiennes et mésopotamiennes connues par des papyrus ou des tablettes d'argiles antiques remarquablement bien conservées, les mathématiques grecques ne sont pas parvenues jusqu'à nous grâce à des traces archéologiques. On les connait grâce aux copies, traductions et commentaires de leurs successeurs. La grande nouveauté des mathématiques grecques est qu'elles quittent le domaine de l'utilitaire pour rentrer dans celui de l'abstraction. Les mathématiques deviennent une branche de la philosophie. De l'argumentation philosophique découle l'argumentation mathématique. Il ne suffit plus d'appliquer, il faut prouver et convaincre : c'est la naissance de la démonstration. L'autre aspect de ces nouvelles mathématiques concerne leur objet d'étude. Au lieu de travailler sur des méthodes, les mathématiques étudient des objets, des représentations imparfaites d'objets parfaits, on ne travaille pas sur un cercle mais sur l'idée d'un cercle. Les grandes figures de ces nouvelles mathématiques sont Thalès (-625 – -547), Pythagore (-580 – -490) et l'école pythagoricienne, Hippocrate(-470 – -410) et l'école de Chios, Eudoxe de Cnide (-408 – -355) et l'école de Cnide, Théétète d'Athènes (-415 – -369) puis Euclide. Il est probable que cette école grecque des mathématiques ait été influencée par les apports mésopotamiens et égyptiens. Ainsi Thalèsvoyagea en Égypte, et il a pu rapporter en Grèce des connaissances en géométrie. Il travailla sur les triangles isocèles et les triangles inscrits dans un cercle. Selon l'école pythagoricienne, « tout est nombre ». Les deux branches d'étude privilégiées sont l'arithmétique et la géométrie. La recherche d'objets parfaits conduit les Grecs à n'accepter d'abord comme nombres que les nombres rationnels matérialisés par la notion de longueurs commensurables : deux longueurs sont commensurables s'il existe une unité dans laquelle ces deux longueurs sont entières. L'échec de cette sélection matérialisée par l'irrationalité de la racine carrée de deux les conduit à n'accepter que les nombres constructibles à la règle et au compas. Ils se heurtent alors aux trois problèmes qui vont traverser l'histoire : la quadrature du cercle, la trisection de l'angle et la duplication du cube. En arithmétique, ils mettent en place la notion de nombre pair, impair, parfait et figuré. Cet idéalisation des nombres et le souci de les relier à des considérations géométriques est probablement lié au système de numération grecque assez peu pratique : si le système est décimal, il est additif et se prête donc assez peu facilement aux calculs numériques. En géométrie, ils étudient les polygones réguliers avec un penchant pour le pentagone régulier. Hippocrate de Chios cherchant à résoudre le problème mis en place par Pythagore découvre la quadrature des lunules et perfectionne le principe de la démonstration en introduisant la notion de problèmes équivalents. Eudoxe de Cnide travaille sur la théorie des proportions acceptant ainsi de manipuler des rapports de nombres irrationnels. Il est probablement à l'origine de la formalisation de laméthode d'exhaustion pour le calcul par approximations successives d'aires et de volumes. Théétète travaille sur les polyèdres réguliers. La synthèse la plus importante des mathématiques grecques vient des Éléments d’Euclide. Les objets géométriques doivent être définis : il ne s'agit plus d'objets imparfaits mais de l'idée parfaite des objets. Dans ses Éléments, Euclide se lance dans la première formalisation de la pensée mathématique. Il définit les objets géométriques (droites, cercles, angles), il définit l'espace par une série d'axiomes, il démontre par implication les propriétés qui en découlent et fait le lien formel entre nombre et longueur. Cet ouvrage restera dans le cursus mathématique universitaire européen jusqu'au xixe siècle. Après Euclide, d'autres grands noms éclairent les mathématiques grecques. Archimède qui perfectionne les méthodes d'Eudoxe, et Apollonius de Perge dont le traité sur les coniquesest considéré comme un classique de la géométrie grecque. Dans l'antiquité tardive, les mathématiques sont représentées par l'école d'Alexandrie. Diophante étudiera les équations dites diophantiennes, et sera appelé le "père de l'algèbre". Durant la période allant de 800 à 1500 après J.C., c'est dans les régions conquises par les musulmans que se développent le plus les mathématiques. La langue arabe devient langue officielle des pays conquis. Un vaste effort de recueils et de commentaires de textes est entrepris. S'appuyant d'une part sur les mathématiques grecques, d'autre part sur les mathématiques indiennes et chinoises que leur relations commerciales leur permettent de connaître, les mathématiciens musulmans vont considérablement enrichir les mathématiques, développant l'embryon de ce qui deviendra l'algèbre, répandant le système décimal indien avec les chiffres improprement appelés chiffres arabes et développant des algorithmes de calculs. Parmi les nombreux mathématiciens musulmans, on peut citer Al-Khwarizmi et son ouvrage al-jabr. On assiste à un développement important de l'astronomie et de la trigonométrie. Le rôle du Moyen Âge fut essentiel pour l'extension du domaine des nombres. C'est durant le Moyen Âge que l'application de l'algèbre au commerce amena en Orient l'usage courant des nombres irrationnels, un usage qui se transmettra ensuite à l'Europe. C'est aussi durant le Moyen Âge, mais en Europe, que pour la première fois des solutions négatives furent acceptées dans des problèmes. C'est enfin peu après la fin du Moyen Âge que l'on considéra les quantités imaginaires, qui permettaient de mettre en évidence des solutions réelles de certaines équations du troisième degré. Dès le xiie siècle est entreprise en Italie une traduction des textes arabes et, par là-même, la redécouverte des textes grecs12. Tolède, ancien centre culturel de l'Espagne musulmane, devient, suite à la Reconquista, l'un des principaux centres de traduction, grâce au travail d'intellectuels comme Gérard de Crémone ou Adélard de Bath. L'essor économique et commercial que connaît alors l'Europe, avec l'ouverture de nouvelles routes commerciales notamment vers l'Orient musulman, permet également aux milieux marchands de se familiariser avec les techniques transmises par les Arabes. Ainsi, Léonard de Pise, avec son Liber abaci en 1202, contribue largement à faire redécouvrir les mathématiques à l'Europe. Parallèlement au développement des sciences, se concentre une activité mathématique en Allemagne, en Italie et en Pologne aux xive siècle et xve siècle. On assiste à un développement important de l'école italienne avec Scipione del Ferro, Tartaglia, Cardan, Ferrari, Bombelli, école principalement tournée vers la résolution des équations. Cette tendance est fortement liée au développement dans les villes italiennes de l'enseignement des mathématiques non plus dans un but purement théorique tel qu'il pouvait l'être dans le Quadriviummais à des fins pratiques, notamment destinée aux marchands. Cet enseignement se diffuse dans des botteghe d'abbaco ou « écoles d'abbaques » où des maestri enseignent l'arithmétique, la géométrie et les méthodes calculatoires à de futurs marchands à travers des problèmes récréatifs, connus grâce à plusieurs « traités d'abbaque » que ces maîtres nous ont laissés13. Les nombres complexes apparaissent lors des travaux de Scipione del Ferro, à l'occasion de la résolution des équations de degrés trois. Repris par Tartaglia, et publiés par Cardan, ils trouvent une première forme avec Bombelli. Ferrari résout les équations du quatrième degré. Jusqu'à la fin du xvie siècle, la résolution de problèmes demeure cependant rhétorique. Le calcul symbolique apparaît en 1591 lors de la publication de l’Isagoge de François Viète avec l'introduction de notations spécifiques pour les constantes et les variables (ce travail popularisé et enrichi par Harriot, Fermat et Descartes modifiera entièrement le travail algébrique en Europe). Les mathématiques portent leur regard sur des aspects physiques et techniques. Fils de deux pères, Isaac Newton et Gottfried Leibniz, le calcul infinitésimal fait entrer les mathématiques dans l'ère de l'analyse (dérivée, intégrale, équation différentielle). L'univers mathématiques du début du xviiie siècle est dominé par la figure de Leonhard Euler 14 et par ses apports tant sur les fonctions que sur la théorie des nombres, tandis que Joseph-Louis Lagrange éclaire la seconde moitié de ce siècle. Le siècle précédent avait vu la mise en place du calcul infinitésimal ouvrant la voie au développement d'un nouveau domaine mathématique : l'analyse algébrique dans laquelle, aux opérations algébriques classiques, viennent s'ajouter deux opérations nouvelles, la différentiation et l'intégration (introductio in analysin infinitorum - Euler-1748). Le calcul infinitésimal se développe et s'applique aussi bien aux domaines physiques (mécanique, mécanique céleste, optique, cordes vibrantes) qu'aux domaines géométriques (étude de courbes et de surfaces).Leonhard Euler, dans Calculi différentialis (1755) et Institutiones calculi integralis (1770) essaie de mettre au point les règles d'utilisation des infiniment petits et développe des méthodes d'intégration et de résolution d'équations différentielles. Jean le Rond d'Alembert puis Joseph-Louis Lagrange lui emboîtent le pas. En 1797, Sylvestre-François Lacroix publie Traité du calcul différentiel et intégral qui se veut une synthèse des travaux d'analyse du xviiie siècle. La famille Bernoulli contribue au développement de la résolution des équations différentielles. La fonction devient un objet d'étude à part entière. On s'en sert dans des problèmes d'optimisation. On la développe en séries entières ou asymptotiques(Taylor, Stirling, Euler, Maclaurin, Lagrange), mais sans se préoccuper de leur convergence. Leonhard Euler élabore une classification des fonctions. On tente de les appliquer à des réels négatifs ou à des complexes 15. Le théorème fondamental de l'algèbre (existence de racines éventuellement complexes à tout polynôme) resté sous forme de conjecture depuis deux siècles est remis en avant dans l'utilisation de la décomposition des fractions en éléments simples nécessaire pour le calcul intégral. Successivement, Euler (1749), le chevalier de Foncenex (1759) et Lagrange (1771) tentent des démonstrations algébriques mais se heurtent à la partie transcendante du problème (tout polynôme de degré impair sur R possède une racine réelle) qui nécessiterait l'utilisation du théorème des valeurs intermédiaires16.. La démonstration de D'Alembert, publiée en 1746 dans les annales de l'académie de Berlin, est la plus achevée mais présente encore quelques trous et des obscurités. Gauss, en 1799, qui critique D'Alembert sur ces points n'est d'ailleurs pas exempté des mêmes reproches. Il faut à un moment faire intervenir un résultat d'analyse fort que le siècle ne connaît pas. De plus, l'obstacle se situe dans la question des points de branchement: on retrouve ici une question déjà débattue lors de la polémique sur les logarithmes des nombres négatifs que tranchera Euler. La seconde et la troisième démonstration de Gauss ne souffrent pas de ces reproches mais on n'est plus au xviiie siècle... En arithmétique, Euler démontre le petit théorème de Fermat et en donne une version élargie aux nombres composés (1736-1760). Il infirme la conjecture de Fermat sur la primalité des nombres de la forme Durant ce siècle, les mathématiciens continuent de s'intéresser aux résolutions algébriques des équations. Le premier essai systématique sur la résolution des équations algébriques était l'œuvre de Tschirnhaus en 1683. Euler lui-même, dans deux essais, ne va pas au-delà de son devancier et en 1762, Bezout introduit la notion de racine de l'unité. Entre 1770 et 1772, on peut citer trois grands mémoires plus originaux : celui de Waring, celui d'Alexandre-Théophile Vandermonde (1771) sur la résolubilité par radicaux des équations xn − 1 = 0(équation cyclotomique) qui est un précurseur dans l'utilisation des permutations des racines21 et celui de Lagrange (1770) qui rassemble toutes les méthodes de résolutions déjà tentées mais va introduire les résolvantes de Lagrange et démontrer, dans un langage où la notion de groupe n'existe pas encore, le théorème de Lagrange: l'ordre d'un sous-groupe d'un groupe fini divise l'ordre du groupe. Ces deux derniers mathématiciens mettent en évidence l'importance des racines et de leurs permutations mais il faut attendre le siècle suivant pour voir naitre la notion de groupe de permutations. La géométrie analytique se développe et s'étend de l'étude des courbes à celle des surfaces. Euler étudie l'équation générale du second degré à trois variables et présente une classification des solutions. Alexis Clairaut étudie les courbes gauches (1729). Gabriel Cramer publie en 1750 un traité sur les courbes algébriques. La grande figure de la géométrie du XVIIIe reste Gaspard Monge22. Celui-ci développe la géométrie différentielle avec l'étude des tangentes et crée une nouvelle discipline: la géométrie descriptive. Leonhard Euler développe le calcul trigonométrique, met en place les formules de calcul de la géométrie sphérique et replace les fonctions circulaires dans l'ensemble général des fonctions, les développant en séries entières ou en produits infinis et découvrant une relation entre les fonctions circulaires et les fonctions exponentielles Le siècle voit l'apparition de quelques théoriciens de la logique. Leonhard Euler met au point une méthode de représentation figurée des déductions syllogistiques (diagramme d'Euler), Jean-Henri Lambert travaille sur la logique des relations 22. C'est aussi le siècle qui s'attaque aux premiers exemples de ce qui va devenir la théorie des graphes. Euler résout en 1736 le problème des ponts de Königsberg, et, en 1766, énonce le théorème des circuits eulériens: un p-graphe admet un circuit eulérien si et seulement si le nombre de ses sommets de degré impair est 0 ou 2. Il s'attaque au problème du cavalier en 1759 mais ne publie rien jusqu'en 1766. Il s'agit d'un cas particulier de graphes hamiltoniens. Le problème du cavalier est connu depuis fort longtemps. Vers 840, al-Adli ar-Rumi en donne une solution. Le poête Rudrata en parlait aussi dans le Kavyalankara, un texte indou. Mais le siècle est fécond aussi en conjectures qui resteront des énigmes pendant plus d'un siècle : le problème de Goldbach, le problème de Waring23, ... Le siècle voit aussi Legendre s'échiner pendant des années sur les intégrales elliptiques. Malheureusement pour lui, même s'il fait l'admiration d'Euler en ce domaine, la solution de la question allait lui échapper au profit d'Abel. Le xviiie siècle est aussi celui de l'encyclopédie dans laquelle Jean le Rond d'Alembert fait un état des lieux des mathématiques de ce siècle. Durant la période Edo (1603 - 1887), au Japon, se développe une mathématique sans influence de la mathématique occidentale mais inspirée de la mathématique chinoise, travaillant sur des problèmes d'essence géométrique. Des énigmes géométriques sont posées et résolues sur des tablettes en bois appelées Sangaku. L'histoire mathématique du xixe siècle est riche. Trop riche pour qu'en un essai de taille raisonnable on puisse couvrir la totalité des travaux de ce siècle. Aussi ne doit-on attendre de cette partie que les points saillants des travaux de ce siècle. Le xixe siècle vit apparaître plusieurs théories nouvelles et l'accomplissement des travaux entrepris au siècle précédent. Le siècle est dominé par la question de la rigueur. Celle-ci se manifeste en analyse avec Cauchy et la sommation des séries. Elle réapparaît à propos de la géométrie. Elle ne cesse de se manifester en théorie des fonctions et particulièrement sur les bases du calcul différentiel et intégral au point de voir disparaître totalement ces infiniments petits qui avaient pourtant fait le bonheur du siècle précédent. Mais plus encore, le siècle marque la fin de l'amateurisme mathématique: les mathématiques étaient jusque là surtout le fait de quelques particuliers suffisamment fortunés soit pour étudier eux-mêmes soit pour entretenir quelques génies. Au xixe siècle, tout cela prend fin : Les mathématiciens deviennent des professionnels appointés. Le nombre de ces professionnels ne cesse de croître et avec ce nombre, les mathématiques prennent une importance jamais atteinte, comme si la société tout entière prenait enfin conscience du formidable outil. Les applications, en germe dans le siècle précédent, se développent rapidement dans tous les domaines, laissant croire que la science peut tout. D'ailleurs, certains succès sont là pour en attester. N'a-t-on pas découvert une nouvelle planète uniquement par le calcul ? N'a-t-on pas expliqué la création du système solaire ? Le domaine de la physique, science expérimentale par excellence est complètement envahi par les mathématiques: la chaleur, l'électricité, le magnétisme, la mécanique des fluides, la résistance des matériaux et l'élasticité, la cinétique chimique sont à leur tour mathématisés au point que le bon vieux cabinet de curiosité du xviiie siècle finissant est remplacé par un tableau noir. Et le vaste champ de la science s'étend encore et encore. Certes, on ne dit plus ce presque lieu commun du xviiie siècle que les sciences mathématiques seront bientôt achevées et qu'il faudra "fermer la mine", à la place on se met à rêver à la machine de Leibniz qui répondrait à toutes les questions. On va même jusqu'à quantifier le hasard ou l'incertain, histoire de se rassurer. Cournot veut appliquer le calcul des probabilités en matière judiciaire pour arriver à cette stupéfiante, et combien rassurante, conclusion qu'il y a moins de deux pour cent d'erreurs judiciaires ! Les mathématiques s'insinuent jusqu'à la structure intime de la matière: plusieurs théories de la lumière et les prémisses de la théorie de la relativité chez Lorentz qui complète la théorie électromagnétique de Maxwell. La tendance à la rigueur, commencée au début du xixe siècle, ne verra son accomplissement qu'au début du xxe siècle par la remise en cause de bien des a priori.Préhistoire [modifier]
De Sumer à Babylone [modifier]
Égypte [modifier]
Chine [modifier]
Civilisations précolombiennes [modifier]
Inde [modifier]
 qu'ils nomment première racine carrée, seconde racine carrée, troisième racine carrée. De cette époque, datent l'Aryabhata (499), du nom de son auteur, écrit en sanscrit et en vers, et les traités d'astronomie et de mathématiques de Brahmagupta (598-670) . Dans le premier, on y trouve des calculs de volume et d'aire, des calculs de sinus qui donne la valeur de la demi-corde soutenue par un arc, la série des entiers, des carrés d'entiers, des cubes d'entiers. Une grande partie de ces mathématiques sont orientées vers l'astronomie. Mais on trouve aussi des calculs de dettes et recettes où l'on voit apparaître les premières règles d'addition et de soustraction sur les nombres négatifs. Mais c'est à Brahmagupta semble-t-il que l'on doit les règles opératoires sur le zéro en tant que nombre et la règle des signes.
qu'ils nomment première racine carrée, seconde racine carrée, troisième racine carrée. De cette époque, datent l'Aryabhata (499), du nom de son auteur, écrit en sanscrit et en vers, et les traités d'astronomie et de mathématiques de Brahmagupta (598-670) . Dans le premier, on y trouve des calculs de volume et d'aire, des calculs de sinus qui donne la valeur de la demi-corde soutenue par un arc, la série des entiers, des carrés d'entiers, des cubes d'entiers. Une grande partie de ces mathématiques sont orientées vers l'astronomie. Mais on trouve aussi des calculs de dettes et recettes où l'on voit apparaître les premières règles d'addition et de soustraction sur les nombres négatifs. Mais c'est à Brahmagupta semble-t-il que l'on doit les règles opératoires sur le zéro en tant que nombre et la règle des signes.Grèce antique [modifier]
Civilisation islamique [modifier]
Occident [modifier]
Durant le Moyen Âge [modifier]
Durant la renaissance européenne [modifier]
Au xviie siècle [modifier]
Le xviiie siècle [modifier]
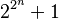 (nombre de Fermat)17. Il s'intéresse à la répartition des nombres premiers et prouve que la série des inverses des nombres premiers est divergente18. Laconjecture de Bachet (tout nombre est somme de 4 carrés au plus) est démontrée par Lagrange en 1770. C'est aussi Lagrange qui démontre en 1771 le théorème de Wilson (si p est premier, il divise (p-1)! + 1). Il développe la technique de décomposition en fractions continues et démontre l'infinité des solutions de l'équation de Pell-Fermat19. Legendre publie en 1798 sa Théorie des nombres qui rassemble un grand nombre de résultats d'arithmétique20.La loi de réciprocité quadratique conjecturée par Euler et Legendre ne sera démontrée que le siècle suivant.
(nombre de Fermat)17. Il s'intéresse à la répartition des nombres premiers et prouve que la série des inverses des nombres premiers est divergente18. Laconjecture de Bachet (tout nombre est somme de 4 carrés au plus) est démontrée par Lagrange en 1770. C'est aussi Lagrange qui démontre en 1771 le théorème de Wilson (si p est premier, il divise (p-1)! + 1). Il développe la technique de décomposition en fractions continues et démontre l'infinité des solutions de l'équation de Pell-Fermat19. Legendre publie en 1798 sa Théorie des nombres qui rassemble un grand nombre de résultats d'arithmétique20.La loi de réciprocité quadratique conjecturée par Euler et Legendre ne sera démontrée que le siècle suivant.Japon [modifier]
xixe siècle [modifier]
|
Gottlob Frege.jpg
|
Euler, dont on a commencé la publication des travaux (prévus sur cinquante ans !), s'était déjà attaqué à bien des domaines : acoustique, optique, résistance des matériaux, mécanique des fluides, élasticité, mais ces domaines étaient encore naissants. C'est Fourier, dont le premier mémoire est refusé par l'Académie des sciences de Paris, qui attaque le premier la théorie de la chaleur faisant usage de ce qui va devenir les séries de Fourier. Vers la même époque, les années 1820, Fresnel s'occupe d'optique ainsi que Bessel qui va introduire lesfonctions de Bessel. La mécanique des fluides, qui en était quasiment au stade laissé par Euler et d'Alembert, le stade des fluides parfaits, fait des progrès avec Henri Navier et George Gabriel Stokes qui s'attaquent aux fluides incompressibles puis compressibles introduisant la viscosité. L'électricité, fait ses débuts sous l'influence de Gauss, d'Ohm, de Biot, de Savartet d'Ampère mais c'est surtout le génie de Maxwell qui va embrasser la théorie dans l'une des plus belles théories du siècle, la théorie électromagnétique, qui prétend unifier l'ensemble des travaux sur l'électricité, l'optique et le magnétisme. En résistance des matériaux, les progrès sont plus modestes. On peut citer notamment Barré de Saint-Venant, Yvon Villarceau,Aimé-Henry Résal et son fils Jean Résal mais il faudra attendre le siècle suivant pour que l'élasticité fasse de décisifs progrès, d'autant qu'on ignore encore bien des propriétés du béton et plus encore le béton armé. Vers la fin du siècle, on en connaît suffisamment pour que certains se lancent dans des réalisations monumentales en acier, tels Eiffel. Trois grands problèmes éclaireront le siècle : la loi de réciprocité quadratique, la répartition des nombres premiers et le grand théorème de Fermat. Le xixe siècle offre des progrès considérables sur ses trois questions grâce aux développements d'une véritable théorie prenant le nom d'arithmétique ou de théorie des nombres et s'appuyant sur des outils abstraits et sophistiqués. sous la seule justification du développement en série de Taylor de 1/(1+x). Les mathématiciens croient encore, pour peu de temps, que la somme infinie de fonctions continues est continue, et (pour plus longtemps) que toute fonction continue admet une dérivée... Mais déjà le siècle est écoulé et, au congrès international de mathématique qui se tient, en cette année 1900, à Paris, David Hilbert présente une liste de 23 problèmes non résolus de première importance pour le siècle d'après. Ces problèmes couvrent une grande partie des mathématiques et vont prendre une part importante dans l'histoire mathématique du xxe siècle. Ce paragraphe donne un ensemble de livres de première importance, soit par leur contenu historiquement important soit pour la synthèse qu'ils constituent sur un domaine donné. L'ordre choisi est alphabétique sur le nom des auteurs. Le xxe siècle aura été un siècle extraodinairement fécond du point de vue mathématique. Trois grands théorèmes dominent tous les autres : d'une part le théorème de Gödel ; d'autre part la démonstration de la conjecture de Tanyama-Shimura qui entraîna la démonstration du grand théorème de Fermat ; enfin la démonstration des conjectures de Weil par Pierre Deligne. De nouveaux domaines de recherche sont nés ou se sont développés : les systèmes dynamiques, suite aux travaux de Poincaré, les probabilités, la topologie, la géométrie différentielle, la logique, la géométrie algébrique, suite aux travaux de Grothendieck, ...Revues de mathématiques [modifier]
Mécanique [modifier]
Physique mathématique [modifier]
Théorie des nombres [modifier]
Logique [modifier]
Géométrie [modifier]
Algèbre [modifier]
Probabilité et statistiques [modifier]
Théorie des graphes [modifier]
Analyse réelle [modifier]

 . Karl Weierstrass construit
. Karl Weierstrass construit  à partir de la notion d'« agrégats » tandis que Richard Dedekind crée
à partir de la notion d'« agrégats » tandis que Richard Dedekind crée  de la notion de coupure de l'ensemble des rationnels.
de la notion de coupure de l'ensemble des rationnels.
Analyse complexe [modifier]
 .Il démontre les inégalités "de Cauchy" qui seront intensément utilisées, dans la théorie des équations différentielles notamment.
.Il démontre les inégalités "de Cauchy" qui seront intensément utilisées, dans la théorie des équations différentielles notamment.
Perspectives [modifier]
Les livres du siècle [modifier]
xxe siècle [modifier]
La communauté mathématique explose [modifier]
Algèbre [modifier]
Mécanique [modifier]
Analyse [modifier]
Théorie des groupes [modifier]
Topologie [modifier]
Équations différentielles [modifier]
Théorie des nombres [modifier]
Graphes [modifier]
Analyse complexe [modifier]
Logique et théorie des ensembles [modifier]
Probabilités [modifier]
Analyse numérique [modifier]
Paradoxes apparents et curiosités [modifier]
Notes et références [modifier]
Voir aussi [modifier]
Liens internes [modifier]
Liens externes [modifier]
Bibliographie [modifier]
10:07 Publié dans Histoire des mathématiques | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Recherche par termes mathématiques
Cliquez sur le nom pour voir les notes afférentes :
Algèbre (mathématiques élémentaires)
Analyse (mathématiques élémentaires)
Antoine Gombaud, chevalier de Méré
Argument de la diagonale de Cantor
Arithmétique (mathématiques élémentaires)
Base naturelle des logarithmes
Calcul des prédicats du premier ordre
Calcul intégral (mathématiques élémentaires)
Calcul numérique d'une intégrale
Centre de gravité (mathématiques élémentaires)
Cohérence des axiomes de l'arithmétique formelle
Compétition de factorisation RSA
Construction à la règle et au compas
Construction des anneaux de polynômes
Construction des entiers naturels
Construction des entiers relatifs
Construction des nombres complexes
Construction des nombres rationnels
Construction des nombres réels
Construction des objets courants
Construire des tables trigonométriques
Coupe pentagonale de la pyramide à base carrée
Développement décimal de l'unité
Décomposition en produit de facteurs premiers
Démonstrations du petit théorème de Fermat
Démonstration automatique de théorèmes
Démonstration de l'irrationalité de e
Dimension d'un espace vectoriel
Distributivité (mathématiques élémentaires)
Écrire les figures de la géométrie
Équations aux dérivées partielles
Équation (mathématiques élémentaires)
Équation aux dérivées partielles
Équation différentielle linéaire
Équation différentielle linéaire d'ordre un
Équation différentielle ordinaire
Espace localement connexe par arcs
Fonction (mathématiques élémentaires)
Fonction linéaire (mathématiques élémentaires)
Fonction polynôme (mathématiques élémentaires)
Géométrie (mathématiques élémentaires)
Identité remarquable (mathématiques élémentaires)
Inéquation (mathématiques élémentaires)
Indépendance en probabilité élémentaire
Jeu de stratégie combinatoire abstrait
Liste d'associations statistiques académiques
Liste des articles de mathématiques
Liste des articles de technique de calcul
Liste des éléments remarquables d'un triangle
Liste des fonctions mathématiques
Liste de logiciels de mathématiques
Livre I des Éléments d'Euclide
Logique (mathématiques élémentaires)
Mathématiques de la relativité générale
Méthode des différences finies
Nicolaï Ivanovitch Lobatchevsky
Nombre décimal (mathématiques élémentaires)
Nombre premier (mathématiques élémentaires)
Opération sur des correspondances
Point d'accumulation (mathématiques)
Primitives de fonctions circulaires réciproques
Primitives de fonctions exponentielles
Primitives de fonctions hyperboliques
Primitives de fonctions hyperboliques réciproques
Primitives de fonctions irrationnelles
Primitives de fonctions logarithmes
Primitives de fonctions rationnelles
Primitives de fonctions trigonométriques
Probabilité (mathématiques élémentaires)
Produit de convolution de Dirichlet
Proportionnalité (mathématiques élémentaires)
Puissance d'un point par rapport à un cercle
Puissance (mathématiques élémentaires)
Relations entre coefficients et racines
Représentations graphiques de données statistiques
Série statistique à deux variables
Schéma d'axiomes de compréhension
Statistiques élémentaires continues
Statistiques élémentaires discrètes
Statistique (mathématiques élémentaires)
Statistique de Maxwell-Boltzmann
Symétrie (transformation géométrique)
Table des symboles mathématiques
Table de constantes mathématiques
Théorème des facteurs invariants
Théorème d'incomplétude de Gödel
Théorème des accroissements finis
Théorème des milieux (mathématiques élémentaires)
Théorème des valeurs intermédiaires
Théorème de la limite monotone
Théorème fondamental de l'arithmétique
Théorème fondamental du calcul différentiel et intégral
Théorie axiomatique des ensembles
Trigonométrie classique et formules
Usage des lettres en mathématiques
Valeur propre, vecteur propre et espace propre
Variables aléatoires élémentaires
Vocabulaire élémentaire des probabilités
Vocabulaire multilingue mathématique
09:57 Publié dans Recherche par termes mathématiques | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Définitions des termes mathématiques
lettre A
lettre B
lettre C
lettre D
lettre E
lettre F
lettre G
lettre H
lettre I
lettre Î
lettre J
lettre K
lettre L
lettre M
lettre N
lettre O
lettre P
lettre Q
lettre R
lettre S
lettre T
lettre U
lettre V
lettre W
lettre Y
lettre Z
Source : http://www.ilemaths.net/encyclopedie/definitions-TOUT.php
09:54 Publié dans Définitions des termes mathématiques | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
MULTIPLICATIONS PAR 9 ET PAR 11 SANS CHRONO
|
MULTIPLICATIONS PAR 9 ET PAR 11 SANS CHRONO
|
|
|
Source : http://www.neroucheffmichel.be/html/X9X11SChrono/x11x9.html
09:49 Publié dans MULTIPLICATIONS PAR 9 ET PAR 11 SANS CHRONO | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
A KAHUN MATHEMATICAL FRAGMENT

A KAHUN MATHEMATICAL FRAGMENTJohn A.R. Legon[Based on the author's article in Discussions in Egyptology 24 (1992), p.21-24] |
|
The significance of the numbers written in hieratic in column 12 of the fragment (see fig. 1) was in fact first recognised by Moritz Cantor [4], who noticed that |
  |
|
To explain why only ten terms in the series were actually recorded, when there was enough space on the papyrus for the scribe to write down several more terms if he had wanted to, Gillings wrote: "we may surmise that he was checking his progression totals, and when he reached 100, he thought he had finished at 110. Or he may just have got tired of the interminable subtractions" [5]. In support of his theory, Gillings believed that the working in the adjacent column 11 of the text was a check multiplication for the thirteenth term of the series, and a stumbling block to the view that the series was intended to contain only ten terms. But in fact, the working is exactly of the form that we should expect for the Egyptian method of computing an arithmetical progression, when ten terms are required. This is proven by the other surviving example of a calculation of this type, in problem 64 in the Rhind Papyrus [6]. Since Cantor also failed to explain the significance of column 11, however, it is now necessary to describe how the calculation was carried out. Given a quantity of 100 which has to be divided into ten shares in arithmetical progression, these shares will have nine differences between them, and the interval between the smallest and largest of the shares will equal nine times the common difference. The largest share can be found by adding half the total interval to the average share. This calculation was performed by the scribe by multiplying half the common difference by the number of differences; and hence in column 11 of Kahun IV.3, for the common difference of "3 '6, the scribe multiplies '3 '12 by 9 with a result of 3 "3 '12. This is added to the average share which is simply 100/10 equals 10; and hence as shown at the top of column 12, the largest share will be Now to explain why the common difference of "3 '6 was selected, it will be noted that the smallest share is about equal to half the largest share; and it seems very likely that an approximation to this simple relationship was the scribe's objective. The problem was thus to distribute a quantity of 100 into 10 shares in arithmetical progression, such that the smallest share should be equal to half the largest share. The scribe seems to have realized that the smallest and largest shares then had to represent one-third and two-thirds of their sum, which should amount to twice the average share, or just 20; and that the correct values for these shares was therefore 6 "3 and 13 '3. But in this case, the common difference between the shares had to equal one-ninth of 6 "3 or "3 '18 '54, which was an awkward quantity to deal with. The calculation was made easier by rounding up the common difference to "3 '6, with slight error so far as any practical distribution was concerned. In problem 64 of the Rhind Papyrus, by way of comparison, it was required to divide 10 hekat of barley between ten men with a common difference equal to the Horus-eye fraction of '8 hekat. The largest share which resulted thus arbitrarily amounted to more than three times the smallest share. Problem 40 in the Rhind Papyrus deals with the distribution of loaves in arithmetical progression such that the two smallest shares amount to 1/7 of the three largest shares - a requirement which was apparently devised to make use of the chance property of a previously constructed progression. The Kahun fragment provides the only existing example where a distribution of shares in arithmetical progression appears to have been determined by a specific relationship between the smallest and largest shares. |
|
[1]. F.Ll. Griffith, Hieratic Papyri from Kahun and Gurob, 2 vols. (London, 1897). Vol.1, 16; vol.2, pl.VIII. [2]. H. Schack-Schackenburg, ZÄS 37 (1899), 78-9; ZÄS 38 (1900), 138-9. [3]. R.J. Gillings, Mathematics in the Time of the Pharaohs, (Cambridge, Mass., 1972), 176-180. [4]. M. Cantor, 'Die mathematischen Papyrusfragmente von Kahun',Orientalistische Litteratur-Zeitung vol.1 no.10 (1898), 306-8. [5]. Gillings op.cit., 80. [6]. T.E. Peet, The Rhind Mathematical Papyrus (Liverpool, 1923), 107-8. See also G. Robins and C.C.D. Shute, The Rhind Mathematical Papyrus (London, 1987), 42-3.
|
09:46 Publié dans A KAHUN MATHEMATICAL FRAGMENT | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Papyrus Kahun
Papyrus Kahun
|
|
Cet article est une ébauche concernant le mobilier archéologique et les monuments d’Égypte antique et lamédecine.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
Les papyrus de Kahun auraient été écrits vers la fin de la XIIe dynastie égyptienne. Ils reproduisent des traités plus anciens et comprennent, entre autres, un traité de gynécologie et untraité de mathématiques.
Bibliographie [modifier]
- Le livre de Sylvia Couchoud, Mathématiques Égyptiennes. Recherches sur les connaissances mathématiques de l’Égypte pharaonique (éditions Le Léopard d’Or, 1993), a peu à dire sur le contenu arithmétique des papyrus de Kahun en tant que tel ; de même celui, plus solide, de Caveing cité infra. On consultera beaucoup plus profitablement l'analyse de Annette Imhausen, Ägyptische Algorithmen. Eine Untersuchung zu den mittelägyptischen mathematischen Aufgabentexten (Wiesbaden, Harrassowitz, 2003), p. 33-175.
- Le tome 2 de Collier & Quirke (p. 72-96) présente la transcription, la traduction et une analyse succincte de ces papyrus mathématiques, aux soins d'A. Imhausen et James ("Jim") Ritter. A leur bibliographie p. 96, ajouter Maurice Caveing, Essai sur le savoir mathématique dans la Mésopotamie et l'Égypte ancienne (s.l., Presses Universitaires de Lille, 1993), p. 370-372.
- F. L. Griffith, Hieratic Papyri from Kahun and Gurob (Principally of the Middle Kingdom), I-II, Quaritch, London, 1898
Présentation et traduction dans le tome 1, fac-similé des textes hiéroglyphiques et copies autographes dans le tome 2
- Mark Collier, Stephen Quirke, The UCL Lahun Papyri, I-III, Archeopress, Oxford, 2002, 2004 et 2006
Lettres dans le tome 1, textes de contenu littéraire et mathématique dans le 2, documents divers dans le 3 ; textes hiéroglyphiques, transcription et traduction, avec reproduction complète des papyrus dans le CD-ROM attaché à chaque tome
- Richard Gillings, Mathematics in the Time of the Pharaohs, pages 176-180, MIT, Cambridge, Mass, 1972, (ISBN 0-486-24315-X)
- John Legon, A Kahun mathematical fragment, in Discussions in Egyptology 24 (1992), p.21-24.
- Gay Robins, Charles Shute, The Rhind Mathematical Papyrus, pages 41-43, British Museum, Dover reprint, 1987, (ISBN 0-486-26407-6).
Liens externes [modifier]
- John Legon: A Kahun Mathematic Fragment
- Math-History-List
- MathOrigins.com
- History of Egyptian fractions
- Medical Papyrus, UCL wbsite
- The Kahun Gynaecological Papyrus
- Planetmath
- Source :
09:44 Publié dans Papyrus Kahun | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Egyptian fraction
|
(view preamble | get metadata)
|
|
Cross-references: link, connected, theory, translation, point, products, even, bodies, entire, subtraction, addition, clear, implication, algorithm, lifting, consequence, group, simple, key,Arabic numerals, Liber Abaci, Fibonacci, base, region, place, Calculus, infinite, parabola, geometric series, minor, Greek letter, alphabets, mapping, AD, order, Egyptian Mathematical Leather Roll, Hultsch-Bruins method, project, code, multiples, production, Rhind Mathematical Papyrus, algebra, degree, variable, remainder arithmetic, efficiency, Reisner Papyrus,geometry, area, length, proof, partitions, expression, integer, quotients and remainders, multiplication, division, primary, denominators, aliquot part, numerators, sides, additive, arithmetic,operations, contained, right, unit fractions, line, sound, onto, numbers, least common multiple, classes, scaling, solution, divisor, remainders, quotients, unity, foundations, closed, open,egyptian fraction, volume, series, measures, weights, numeration system, finite, term, binary, units, fractions
There are 74 references to this entry.
This is version 159 of Egyptian fraction, born on 2007-12-02, modified 2010-11-05.
Object id is 10080, canonical name is EgyptianFraction2.
Accessed 15189 times total.
Classification:
| AMS MSC: | 01A16 (History and biography :: History of mathematics and mathematicians :: Egyptian) |
| 01A20 (History and biography :: History of mathematics and mathematicians :: Greek, Roman) | |
| 01A30 (History and biography :: History of mathematics and mathematicians :: Islam ) | |
|
01A35 (History and biography :: History of mathematics and mathematicians :: Medieval)
Source : http://planetmath.org/encyclopedia/EgyptianFraction2.html |
09:42 Publié dans Egyptian fraction | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
The Rhind Mathematical Papyrus
AN366139001 © The Trustees of the British Museum Department: Ancient Egypt & Sudan Registration number: 1865,0218.3 BM/Big number: 10058 Additional IDs Bibliographic reference Object types Title (series) Description Acquisition date Exhibition History Noticed a mistake? Have some extra information about this object? Please contact us To bookmark this page select "Bookmark this page" or "Add to favourites" from the web browser menu. Source : http://www.britishmuseum.org/research/search_the_collecti...The Rhind Mathematical Papyrus

BS.10058
Strudwick N 2006 p.118
papyrus (scope note | all objects)
The Rhind Mathematical Papyrus
Materials
papyrus (scope note | all objects)
Place (findspot)
Found/Acquired Thebes, According to Budge’s original introduction to the facsimile of the papyrus, from a chamber in the ruins of a building near the Ramesseum. (all objects)
Period/Culture
Second Intermediate (all objects)
Papyrus; Hieratic text: "Rhind Mathematical Papyrus".
Inscriptions
Inscription Type: inscription
Inscription Script: hieratic
Inscription Position: both sides
Inscription Language:
Dimensions
Length: 216 centimetres (frame)
Width: 43 centimetres (frame)
Length: 199.5 centimetres (Papyrus)
Width: 32 centimetres (Papyrus)
Condition
Papyrus Survey: Condition Details: Papyrus Black ink Red ink Checked for loan to Vienna 1994 Checked for loan to Paris 1997 Checked for loan to Japan Star Objects 2004 Checked for loan to Cornwall 2008 Mount Details: Sandwich: glass Sandwich: board Frame: wood Object Priority: A Mount Priority: A Overall Condition: A Curatorial condition comment: fair
Curator's comments
Strudwick N 2006
Several documents have survived that yield some insights into the ancient Egyptians' approach to mathematics. The best-known and longest is the Rhind Mathematical Papyrus, acquired by the Scottish lawyer A.H. Rhind in Thebes in about 1858. Budge's original introduction to the facsimile of the papyrus indicates that these fragments were found in a chamber of a ruined building near the Ramesseum. The two sections in the British Museum were linked by a now missing section about 18 cm long; the original may have been cut in half by modern robbers to increase its sale value. Fragments which partly fill this gap were identified in 1922, in the collection of the New York Historical Society, which had acquired them from Edwin Smith. Smith also acquired a surgical papyrus of about the same date as the Rhind Papyrus, suggesting that these two documents could have come from a cache of early New Kingdom manuscripts.
The papyrus is probably a mathematics textbook, used by scribes (the principal literate section of the populace) to learn to solve particular mathematical problems by writing down appropriate examples. The text includes eighty-four problems: tables of divisions, multiplications, and handling of fractions; geometry, including volumes and areas; and miscellaneous problems.
The papyrus is extremely important as a historical document, since the scribe, Ahmose, dated it in year 33 of Apophis, the penultimate king of the Hyksos Fifteenth Dynasty. The other side of the papyrus mentions 'year 11' without a king's name, but with a reference to the capture of the city of Heliopolis. The late Second Intermediate Period context suggests this may refer to conflict between the Egyptians and the Hyksos before the beginning of the New Kingdom. Most scholars believe this refers to year 11 of the Theban ruler Ahmose, which would add to the evidence that Ahmose did not campaign against the Hyksos rulers until the middle or later parts of his reign.
Published: G. Robins and C. Shute, The Rhind Mathematical Papyrus : an ancient Egyptian text (BM press 1987).
A. B. Chace, The Rhind mathematical papyrus : free translation and commentary with selected photographs, transcriptions, transliterations, and literal translations (National Council of Teachers of Mathematics 1979 [reprint]).
A. Imhausen, Ägyptische Algorithmen : eine Untersuchung zu den mittelägyptischen mathematischen Aufgabentexten (Harrassowitz, 2003).
Pharaonen Und Fremde Catalogue (Vienna 1994): No.134
Nicholson and Shaw, Ancient Egyptian Materials and Technology (Cambridge 2000), p. 240;
N. Strudwick, Masterpieces of Ancient Egypt, London 2006, pp. 118-9.
1865
Acquisition name
Purchased from David Bremner (biographical details | all objects)
Previous owner/ex-collection Alexander Henry Rhind (all objects)
Exhibited:
21 Aug-11 Oct 2008. Truro, Royal Museum of Cornwall, 'Masters of Mathematics'.
January to May in BM as part of History of the World objects
09:40 Publié dans The Rhind Mathematical Papyrus | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Papyrus de Moscou
Papyrus de Moscou
|
|
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
Le papyrus de Moscou, aussi appelé papyrus Golenischev d'après le nom de son découvreur, Golenishchev, est un papyrus contenant des résultats mathématiques. Avec le papyrus Rhind, c'est un des deux fameux papyrus mathématiques égyptiens. Le papyrus mathématique de Moscou est le plus ancien, tandis que le papyrus Rhind est le plus grand. Au xxie siècle, il fait partie de la collection du musée des Beaux-Arts Pouchkine de Moscou.
D’environ 5,40 m de long et d’une largeur qui varie entre 4 et 7 cm, il comporte, selon l’étude faite en 1930 par l'orientaliste soviétique Vassili Vassilievitch Struve, 25 problèmes avec leurs solutions, dont les plus intéressants sont ceux traitant de la surface d'une demi-sphère et du volume d'une pyramide tronquée (voir géométrie dans l'Égypte antique). La paléographie du texte hiératique permet de le dater probablement de la XIe dynastie (vers -2000).
Le Papyrus de Moscou offre un exemple historique d'une étude mathématique où le système unaire a été utilisé[réf. nécessaire].
09:38 Publié dans Papyrus de Moscou | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Papyrus Rhind
Le papyrus Rhind est un célèbre papyrus de la deuxième période intermédiaire qui aurait été écrit par le scribe Ahmès. Son nom vient de l'Écossais Henry Rhind qui l'acheta en 1858 à Louxor, mais aurait été découvert sur le site de la ville de Thèbes. Au xxie siècle, il est conservé au British Museum ( à Londres). Avec le Papyrus de Moscou, il est une des sources les plus importantes concernant les mathématiques dans l'Égypte antique. Ahmès indique que son papyrus est, en partie, une copie de résultats plus anciens remontant au Moyen Empire (vers -2000). Il contient 87 problèmes résolus d'arithmétique, d'algèbre, de géométrie et d'arpentage, sur plus de 5 m de longueur et 32 cm de large. Il est rédigé enécriture hiératique.Papyrus Rhind
Sommaire[masquer] |
Ces problèmes permettent de comprendre les techniques de multiplication et de division chez les Égyptiens. Voir Mathématiques dans l'Égypte antique#Résolutions d'équations L'arpentage, mesures des distances et les problèmes géométriques qui lui sont liés sont également abordés : aires planes (du trapèze en particulier), volumes de greniers à grains, calcul de pyramides. Les sections R57, R58, R59a et R59b, sont consacrées aux problèmes relatifs à la pente, inclinaison (terme égyptien "skd" avec un point sous le "k") d'une pyramide. Cette inclinaison, qui concerne la ligne de plus grande pente des faces, est exprimée en palmes, unité de longueur qui vaut le septième d'une coudée (voir Mathématiques dans l'Égypte antique). L'examen du contenu de ces sections montre qu'il s'agit, en palmes , de 7 fois la cotangente de l'angle que forme la ligne de plus grande pente avec l'horizontale. Pour le triangle égyptien, elle vaut (3 / 4) x 7 = 21/4 = 5 + 1/4 palmes. Comme ces quatre sections du papyrus, illustrées par un dessin de pyramide, concernent toutes la valeur de 5 + 1/4 palmes, elles attestent qu'il s'agit du triangle égyptien 3, 4, 5 dans ces problèmes de pyramides1. Le papyrus Rhind atteste donc, de façon indirecte par l'inclinaison mais incontestable par la valeur numérique donnée, que la géométrie de la pyramide utilise le triangle égyptien. La pyramide de Khéphren est construite ainsi (voir Mathématiques dans l'Égypte antique). Dans les problèmes 48 et 50, Ahmes étudie le rapport liant l'aire d'un disque à son diamètre en cherchant à ramener l'aire de la circonférence à celle d'un carré équivalent : le papyrus Rhind précise en effet une première approche de la quadrature du cercle (construction d'un carré de même aire qu'un cercle donné) : c'est le carré de côté 8d/9 où d est le diamètre du cercle. En d'autres termes, l'aire d'un cercle de diamètre 9 unités est sensiblement égal à l'aire d'un carré de 8 unités de côté. Cette égalité se traduit par : donc Cette approximation par la quadrature du cercle permit donc aux égyptiens de se passer de la constante π, constante qu'ils connurent seulement à laBasse époque et offrant des résultats moins justes qu'au problème du papyrus Rhind décrit ci-dessus.Algorithmes de multiplication et division (problèmes 1 à 23) [modifier]
Résolution d'équations par la méthode de fausse position (problèmes 24 à 34) [modifier]
Les problèmes d'arpentage (problèmes 41 à 60) [modifier]

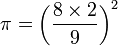 . Ainsi, notre actuel nombre π serait le carré de 16/9, soit : π = 256/81 = 3 + 1/9 + 1/27 + 1/81 = 3,160.
. Ainsi, notre actuel nombre π serait le carré de 16/9, soit : π = 256/81 = 3 + 1/9 + 1/27 + 1/81 = 3,160.Notes [modifier]
Bibliographie [modifier]
Voir aussi [modifier]
Articles connexes [modifier]
Liens externes [modifier]
09:37 Publié dans Papyrus Rhind | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Mathématiques dans l'Égypte antique
Les mathématiques en Égypte antique étaient fondées sur un système décimal. Chaque puissance de dix était représentée par un hiéroglyphe particulier. Le zéro était inconnu. Toutes les opérations étaient ramenées à des additions. Pour exprimer des valeurs inférieures à leur étalon, les Égyptiens utilisaient un système simple de fractions unitaires. Pour déterminer la longueur d'un champ, sa surface ou encore mesurer un butin, les Égyptiens utilisaient trois systèmes de mesure différents, mais tous obéissaient aux règles décrites ci-dessus. Les rares documents mathématiques découverts à ce jour ne donnent qu'une vague idée de l'étendue des connaissances des anciens Égyptiens dans ce domaine. Toutefois, il est certain qu'ils parvenaient à proposer des résolutions de problèmes apparentés à des équations du premier et du second degré. Ils connaissaient les suites numériques et le calcul de volumes et de surfaces avait également atteint un certain degré de complexité.Mathématiques dans l'Égypte antique
Si l'on a souvent sous-estimé les connaissances scientifiques des anciens Égyptiens, c'est sans doute à cause du peu de documents dont nous disposons. Les plus anciens sont les inscriptions contenues sur les murs de quelques temples ou tombes, comme celles de la tombe de Metjen (IVe dynastie) qui montrent que les Égyptiens savaient à cette époque calculer correctement la surface d'un rectangle. Les ostraca1 apportent également quelques témoignages de l'art des mathématiques égyptiennes. Le plus remarquable est sans doute celui retrouvé à Saqqarah sur lequel figure une courbe avec abscisse et ordonnée. Daté de 2750 ans avant notre ère, il montre que dès cette première génération de bâtisseurs, les Égyptiens avaient suffisamment de connaissances mathématiques pour élaborer ce type de problème. Enfin viennent les papyri. Plus fragiles, ils ont moins résisté au temps et ceux qui sont parvenus jusqu'à nous sont, de fait, postérieur aux pyramides. Seule une poignée d'entre eux traite de mathématiques. Citons par exemple le papyrus de Berlin ou celui de Moscou, découvert en 1893 par l'égyptologue russe Vladimir Golenischev et conservé au musée des Beaux-Artsde Moscou. Daté de la fin du Moyen Empire (1850 ans av. J.-C.) et rédigé en écriture hiéroglyphique, il contient vingt-cinq problèmes mathématiques. Mais le papyrus mathématique le mieux conservé, le plus complet et le plus prestigieux est sans nul doute le papyrus Rhind, du nom de son premier propriétaire l'Écossais Alexander Henry Rhind, qui l'acheta peu après sa découverte à Thèbes en 1857. Rédigé en écriture hiératique et daté du début du xvie siècle , c'est une copie d'un document plus ancien. Il présente une suite de quatre-vingt-sept problèmes mathématiques, accompagnés de leurs solutions. Les Égyptiens de l'Antiquité utilisaient un système de numération décimal, mais dans lequel le zéro n'existait pas. Chaque ordre de grandeur (unités, dizaines, centaines, etc.) possédait un signe répété le nombre de fois nécessaire. C'était donc un système additionnel. Plusieurs systèmes coexistaient selon le type de mesure désirée. Pour mesurer des longueurs, il existait deux systèmes. Le premier était basé sur la grande coudée ou coudée royale (meh ni-sout). Cette coudée représentait la distance entre le bout du majeur et la pointe du coude et mesurait à peu près 0,5 mètre. Cette unité était très utilisée pour mesurer les largeurs, longueurs de pièces d'une construction ou des salles d'un temple, mais aussi la hauteur d'une crue. Cent coudées constituent un khet. Le deuxième système, le système oncial, était lui basé sur la coudée sacrée (meh djeser). Elle mesurait à peu près 0,7 mètre. Elle était principalement utilisée dans la décoration des tombes, temples et palais. Pour les surfaces, l'unité de mesure était l'aroure. Elle représentait un carré de 1 khet (100 coudées) de côté. On nommait coudée de terre (meh) une bande d'une coudée sur cent. L'aroure était utilisée pour mesurer des terres, et construire un cadastre précis après chaque crue. Pour mesurer des volumes, l'unité de mesure était l'hekat. Les mesures s'effectuaient grâce à un sac de cuir de vingt hekat. Les Égyptiens avaient réussi à établir une correspondance de ce système avec celui des longueurs : il y avait équivalence entre le cube de la coudée royale et trente hekat. L'hekat était utilisé pour mesurer les récoltes de grain. Pour mesurer un poids, l'unité de mesure était le deben. À l'Ancien Empire, son poids variait selon le type du produit pesé (or, cuivre...), mais au Nouvel Empire, ce système se simplifia et ne garda qu'un étalon unique (d'environ 91 grammes). De petits cylindres en pierre servaient à la mesure et matérialisaient cet étalon. Cette unité servait à mesurer l'importance d'un butin ou d'un poids de métaux précieux utilisés pour une décoration. Les scribes se servaient des premières fractions dyadiques, à savoir 1/2, 1/4, 1/8, 1/16, 1/32 et 1/64 pour faire des calculs. Celles-ci étaient représentées par l'Œil d'Horus, une représentation de l'œil gauche d'Horus perdu puis retrouvé. Seth le lui ôta par jalousie et le découpa en plusieurs morceaux, Thot en retrouva six morceaux (représentant les six fractions donc) mais il manquait 1/64 pour faire l'unité. Thot y ajouta alors « le liant magique » permettant à l'œil de recouvrer son unité. Les scribes opéraient donc leurs calculs en approximant 63/64 à 1. La composition de deux fractions susnommées leur permettait d'en créer de nouvelles (par exemple 1/2 et 1/4 pour avoir 3/4). Les parties du dessin, stylisées, sont utilisées comme hiéroglyphes pour noter, dans les textes sur les volumes de grains, les fractions correspondantes (voir Œil Oudjat). Dans les papyrus mathématiques, les fractions sont notées en écrivant les nombres explicitement, mais, dans les sections R37 et R38 du papyrus Rhind, qui comportent chacune des vérifications différentes, les deux dernières de R37 et la dernière de R38 sont proposées sous forme de volumes de grains en hekat et écrites dans la notation de l'œil Oudjat, de même que le calcul de R64 2. Les Égyptiens connaissaient les quatre opérations, pratiquaient le calcul fractionnaire, étaient capables de résoudre des équations du premier degré par la méthode de la fausse position et de résoudre certaines équations du second degré. Le papyrus Rhind explique comment calculer l'aire d'un cercle en utilisant une approximation fractionnaire de pi : 4x(8/9)x(8/9)=3,16. Le papyrus de Moscou, quant à lui, explique entre autres comment calculer le volume d'une pyramide tronquée et la surface d'une demi-sphère, montrant que les anciens Égyptiens avaient de bonnes connaissances en géométrie. Bien qu'aucune explication ne soit fournie par les papyrus mathématiques, le système additionnel de la numération égyptienne rend toutes naturelles les opérations d'addition et de soustraction. L'addition de deux nombres consistait à compter le nombre de symboles total correspondant à une même grandeur. Si le nombre de cette grandeur dépassait dix, le scribe remplaçait ces dix symboles par le symbole de la grandeur supérieure.Brève histoire des mathématiques dans l'Égypte antique [modifier]
Numération égyptienne [modifier]
Les unités de mesure [modifier]
Les fractions [modifier]
L'Œil d'Horus ou Œil Oudjat [modifier]
Connaissances arithmétiques [modifier]
Addition et soustraction [modifier]
|
+
|
nous donne
|
Soit :
|
Finalement, le résultat est :
|
La technique de multiplication en Égypte antique reposait sur la décomposition d'un des nombres (généralement le plus petit) en une somme et la création d'une table de puissance pour l'autre nombre. Très souvent, cette décomposition s'effectuait suivant les puissances de deux. Mais celle-ci pouvait varier en fonction de la complexité de l'opération. Le plus petit nombre pouvait ainsi être décomposé alternativement suivant les puissances de deux, les dizaines et les fractions fondamentales telles que 2/3, 1/3, 1/10 etc. La technique de division en Égypte antique reposait sur le même principe que la multiplication, en ce sens où des tables constituées de puissances de deux successives, de fractions fondamentales et de dizaines étaient utilisées pour résoudre le problème. Le carré d'une valeur appliqué au calcul d'une surface peut sans aucun problème être assimilé à une simple multiplication. Par contre, les racines carrées, dont il est assuré qu'elles furent connues des anciens Égyptiens, n'ont laissé aucun document nous permettant de comprendre la technique d'extraction opérée par eux. L'énoncé du problème mathématique du papyrus 6619 de Berlin (voir § Équations du second degré) contient la racine carrée de 1 + 1/2 + 1/16, soit 1 + 1/4 ; ainsi que la racine carrée de 100, c'est-à-dire 10. À en juger par les exemples connus d'extraction d'une racine carrée, il semble que le scribe ne connaissait que les radicaux simples, résultant en entiers ou en peu de fractions. Toutefois, l'absence d'opérations dans les problèmes traités indique que le scribe devait avoir à sa disposition des tables contenant le résultat des racines carrées usuelles. Le papyrus Kahun et le papyrus de Moscou contiennent des applications aux racines carrées, mais il est notable que le plus important papyrus mathématique, le papyrus Rhind, n'en contient aucune. Si la réputation des scribes en matière de mathématiques est, d'ordre général, inférieure à celle des Babyloniens ou des Grecs, la géométrie, au regard des prouesses techniques réalisées très tôt dans leur histoire, fut leur domaine de prédilection et il ne fait aucun doute aujourd'hui que cette science associée à l'architecture, fit la grande réputation des Égyptiens. C'est l'une des raisons pour lesquelles leur pays accueillit en pèlerinage les savants de la Grèce antique. Les égyptiens réussirent ainsi à calculer la surface d'un disque sans connaitre le nombre pi, avec une erreur de seulement 0,6%. Ils pouvaient calculer les volumes de pyramides et de cylindres et l'aire d'une sphère. certains problèmes figurant sur les papyrimathématiques du Moyen Empire préfigurent même les théorèmes de Thalès et de Pythagore. Le papyrus Rhind et le papyrus de Moscou contiennent différents problèmes que de nombreux auteurs ont assimilé à des problèmes algébriques de résolutions d'équations à une inconnue (voire deux inconnues), du premier et du second degré. Loin de faire l'unanimité, ce rapprochement met au moins l'accent sur une méthode efficace de résolution présageant l'utilisation de variables et d'inconnues. Le scribe égyptien ne pose jamais les problèmes sous forme d'équations algébriques (il ne connait pas d'opérateurs mathématiques tels que +, -, x ou %, ni la notion d'inconnue posée par une lettre telle que x). Cependant, la technique utilisée pour résoudre ces problèmes s'apparentent bien souvent aux méthodes de résolution modernes d'équations. L'inconnue dont la valeur est à déterminer est toujours désignée par la quantité ‘ḥ‘ (‘ḥ‘w au pluriel).Multiplication [modifier]
Division [modifier]
Carré et racine carrée [modifier]
Connaissances géométriques [modifier]
Résolutions d'équations [modifier]
Recherches d'une quantité (les problèmes ‘ḥ‘w) [modifier]
| Problème ‘ḥ‘ posé par le scribe | Transcription du problème en langage algébrique moderne |
| Calcul d'une quantité (‘ḥ‘) à déterminer telle que | |
| si elle est traitée 2 fois avec elle-même, il en vient 9 | X + 2X = 9 |
| Quelle est donc la quantité qui s'exprime ainsi ? | que vaut X ? |
| Tu dois faire en sorte de calculer le total de cette quantité | |
| avec sa deuxième (quantité). Le résultat est 3. | X + 2X = 3X |
| Avec ces 3 tu dois trouver 9. | 3X = 9 |
| Le résultat est 3 fois. | 9/3 = 3 |
| Vois c'est 3 qui s'exprime ainsi. | X = 3 |
| Tu trouveras cela correct | Vérification de l'énoncé avec le résultat. 3 + 2x3 = 9 |
Une seconde technique consistait à résoudre les problèmes par la méthode de la fausse position. C'est-à-dire que l'on attribuait à la quantité inconnue une valeur quelconque. Le résultat donné par cette valeur était évidemment faux, mais pouvait être corrigé par la règle de proportionnalité inhérente aux équations linéaires. C'est bien cette propriété, fondée sur une méthode empirique, qui fut utilisée ici. Une quantité (‘ḥ‘) à laquelle on ajoute ses 1/4 devient 15 (Soit X + 1/4X = 15). Première étape : une valeur aléatoire est donnée à cette quantité, en l'occurrence 4. Le scribe calcule donc 4 + 1/4x4, dont le résultat ne sera évidemment pas 15 :
| ✔ | 1 | 4 |
| ✔ | 1/4 | 1 |
|
|
||
| 1 + 1/4 | 5 | |
Le résultat est 5. Deuxième étape : le résultat n'est pas 15 mais 5. Quel est donc le rapport entre ces deux résultats ?
| ✔ | 1 | 5 |
| ✔ | 2 | 10 |
|
|
||
| 3 | 15 | |
Le rapport vaut 3. Par conséquent la relation entre notre valeur aléatoire 4 et la quantité ‘ḥ‘ vérifiant l'égalité posée dans le problème est 4x3 = ‘ḥ‘. Troisième étape : calcul de 4x3
| 1 | 3 | |
| 2 | 6 | |
| ✔ | 4 | 12 |
|
|
||
| 4 | 12 | |
Le résultat est 12. Quatrième étape : le scribe vérifie l'exactitude de sa solution par la vérification de l'égalité (soit 12 + 1/4x12 = 15)
| ✔ | 1 | 12 |
| ✔ | 1/4 | 3 |
|
|
||
| 1 + 1/4 | 15 | |
La quantité ‘ḥ‘ vaut bien 12 et ses 1/4 ajoutés à elle-même font un total de 15. Certains énoncés posent le problème de la recherche d'une ou plusieurs quantités dont la somme des carrés est connue. Le papyrus 6619 de Berlin offre un très bon exemple du type de résolution par fausse position proposé par les anciens Égyptiens, sous la forme d'un système équivalent à deux équations à deux inconnues. Le problème est de trouver les aires de deux carrés différents dont la somme est égale à l'aire d'un carré de 100 coudées², le rapport des côtés de ces deux carrés étant de 1 pour (1/2 + 1/4). Posons X la longueur du côté du petit carré, et Y la longueur du côté du grand carré. Par conséquent, l'énoncé serait traduit en langage algébrique moderne par X² + Y² = 100 et X/Y = 1/2 + 1/4. Le scribe ne différencie pas deux variables. Les côtés des deux carrés étant liés par la relation 1 pour 1/2 + 1/4, il décide d'affecter la valeur 1 au côté du plus grand carré, et 1/2 + 1/4 au côté du plus petit. C'est la méthode de la fausse position déjà étudiée ci-dessus. Il calcule donc les aires des deux carrés : (1/2 + 1/4) ² et 1². Il obtient un total de 1 + 1/2 + 1/16. L'aire totale des deux carrés est donc de 1 + 1/2 + 1/16. Il en déduit le côté du carré équivalent à cette surface en extrayant la racine carrée de 1 + 1/2 + 1/16. Il vient 1 + 1/4. Or le côté du carré de départ est 10 (racine carrée de 100 effectuée par le scribe). Le rapport de 10 sur (1 + 1/4) est de 8. Ce ratio va nous permettre de réajuster les valeurs prises par fausse position : 1 x 8 et (1/2 + 1/4) x 8, soit 8 et 6. nous avons bien 6² + 8² = 100. La surface d'un carré de 10 coudées de côté est donc équivalente à la surface totale de deux carrés dont les côtés sont respectivement de 6 et de 8 coudées. Les rares papyrus mathématiques découverts jusqu'à présent ont révélé que les Égyptiens avaient de très bonnes notions sur les suites et qu'ils savaient résoudre des problèmes à l'aide des suites arithmétiques ou géométriques. Une suite arithmétique est une suite de nombres dont chacun des termes s'obtient à partir du précédent en lui additionnant (ou en lui soustrayant) toujours la même valeur. Cette valeur est appelée en langage mathématique moderne, la raison. Par exemple, la suite {1; 3; 5; 7; 9} est une suite arithmétique de cinq termes dont la raison est 2.Équations du second degré [modifier]
Suites arithmétiques et géométriques [modifier]
Suites arithmétiques [modifier]
| 1 1/2 1/16 | ||
| 1 1/4 1/8 1/16 | ||
| 1 1/4 1/16 | ||
| 1 1/8 1/16 | ||
| 1 1/16 | ||
| 1/2 1/4 1/8 1/16 | ||
| 1/2 1/4 1/16 | ||
| 1/2 1/8 1/16 | ||
| 1/2 1/16 | ||
| 1/4 1/8 1/16 | ||
|
|
||
| 10 | ||
Le problème consiste à partager 10 héqat de blé entre 10 hommes. On peut désigner leurs parts respectives par H1, H2, H3, H4, H5, H6, H7, H8, H9 et H10. Les 10 héqat de blé représentent le total des parts à distribuer. Nommons le S. Soit N le nombre de parts. Chaque homme ne possèdera pas la même quantité d'héqat. Pris dans l'ordre, chacun obtiendra 1/8 d'héqat de plus que son prédécesseur. Soit H2 = H1 + 1/8, H3 = H2 + 1/8 et ainsi de suite, le dernier individu ayant la plus grande part. 1/8 représente la raison de la suite donc R = 1/8. Le scribe détermine en premier lieu la valeur moyenne de héqat que l'on distribuera à chaque homme, soit S/N = 10/10 = 1. Ensuite, il calcule le nombre de différences effectuées sur l'ensemble des 10 individus. Il y en a N-1 = 10-1, soit 9. Il vient R/2 = 1/16, puis R/2 * (N-1) = 1/16 * 9 = 1/2 + 1/16. Le plus grand terme est donné par R/2 * (N-1) + S/N = 1/2 + 1/16 + 1. On a donc les dix parts suivantes :
| H10 = 1 + 1/2 + 1/16. | ||
| H9 = H10 - 1/8 = 1 + 1/4 + 1/8 + 1/16 | ||
| H8 = H9 - 1/8 = 1 + 1/4 + 1/16 | ||
| H7 = H8 - 1/8 = 1 + 1/8 + 1/16 | ||
| H6 = H7 - 1/8 = 1 + 1/16 | ||
| H5 = H6 - 1/8 = 1/2 + 1/4 + 1/8 + 1/16 | ||
| H4 = H5 - 1/8 = 1/2 + 1/4 + 1/16 | ||
| H3 = H4 - 1/8 = 1/2 + 1/8 + 1/16 | ||
| H2 = H3 - 1/8 = 1/2 + 1/16 | ||
| H1 = H2 - 1/8 = 1/4 + 1/8 + 1/16 | ||
|
|
||
| Total = 10 | ||
Par une méthode empirique, le scribe a donc retrouvé la propriété des suites arithmétiques et appliqué les formules suivantes : puis Une suite géométrique est une suite de nombres dont chacun des termes s'obtient à partir du précédent en le multipliant toujours par la même valeur. Par exemple, la suite {1; 3; 9; 27; 81} est une suite géométrique de cinq termes dont la raison est 3. Ce type de suite fut usité, mais les documents manquent et il est impossible de se faire une idée précise quant aux connaissances que pouvaient en avoir le scribe. Les méthodes demultiplication et de division employées par les Égyptiens sont fondées sur les puissances de deux, autrement dit une suite géométrique de raison 2, et sur les fractions 1/2, 1/4, 1/8 ... c'est-à-dire une suite géométrique de raison 1/2. Par ailleurs, le papyrus Rhind nous fournit l'unique exemple de problème basé sur l'application des suites géométriques. Somme d'une suite géométrique de cinq termes, tels que le premier terme vaut 7 et le multiplicateur de chaque terme (la raison) vaut 7. Application à l'inventaire d'une maison :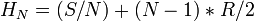

Suites géométriques [modifier]
| ✔ | 1 | 2801 |
| ✔ | 2 | 5602 |
| ✔ | 4 | 11204 |
|
|
||
| 7 | 19607 | |
| Maisons | 7 | |
| Chats | 49 | |
| Souris | 343 | |
| Malt | 2401 (le scribe a noté 2301 par erreur) | |
| Héqat | 16807 | |
|
|
||
| 19607 | ||
Index des termes mathématiques égyptiens [modifier]
Notes [modifier]
Sources [modifier]
Liens internes [modifier]
Liens externes [modifier]
09:36 Publié dans Mathématiques dans l'Égypte antique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
2-POLYNOMES (Troisième partie : Fonctions Polynômes- Polynômes sur R et C)
2-POLYNOMES (Troisième partie : Fonctions Polynômes- Polynômes sur R et C)
Retour a la page de garde
Les étudiants trouveront des notes détaillées sur le web, correspondant au cours LM125 du premier semestre.
Liens : http://www.edu.upmc.fr/maths/math1/lm125/prive/UeL/mathem...
(Nous suivons mot à mot le chapitre :http://www.edu.upmc.fr/maths/math1/lm125/prive/UeL/mathem...)
Fonctions Polynômes
Plan du cours :
A- Fonctions Polynômes
Introduction, notion de fonction polynôme
Racines d’un polynôme
Multiplicité
Polynômes scindés
Méthode de Horner
---------------------------------
B- Polynômes à coefficients réels ou complexes
Degré du polynôme dérivé
Formule de Taylor pour un polynôme à coefficients réels ou complexes
Ordre de multiplicité d'une racine
Existence de racines : Théorème de d'Alembert
Polynômes irréductibles dans C[X]
Polynômes irréductibles dans R[X]
Formule d'interpolation de Lagrange
Introduction
Les fonctions numériques de la forme![]() , où k est un entier positif ou nul et
, où k est un entier positif ou nul et ![]() des nombres réels, sont bien connues ainsi que toutes leurs propriétés. C'est un exemple d'une situation générale qui va être exposée dans cette ressource.
des nombres réels, sont bien connues ainsi que toutes leurs propriétés. C'est un exemple d'une situation générale qui va être exposée dans cette ressource.
Definition
![]() Contexte :
Contexte :
Pour l'étude de la notion de fonction polynôme, on se place dans le contexte suivant : on considère un corps K et l’ensemble des polynômes à une indéterminée K[X]
|
Définition d'une fonction polynôme, associée à un polynôme P appartenant à K[X] Soit . x |
L'expression ![]() a bien un sens et est bien un élément de K.
a bien un sens et est bien un élément de K.
En effet, x étant un élément de K, ![]() en est aussi un (le produit est une loi interne dans l'anneau K), ainsi que
en est aussi un (le produit est une loi interne dans l'anneau K), ainsi que ![]() .
.
Exemple
Par exemple soit ![]() appartenant à
appartenant à![]() .
.
Alors![]() .
.
Racine d’un polynôme
Définitions et exemples
|
Théorème - définition : Racine d'un polynôme de Soit a un élément de K et P un élément de i. ii. Le polynôme Si l'une de ces conditions est vérifiée, on dit que a est racine de P (ou est un "zéro" de P). |
Preuve de l'équivalence : i. ![]() ii. :
ii. :
Soit a un élément de K ; la division euclidienne dans ![]() de P par le polynôme
de P par le polynôme ![]() donne :
donne :
![]() ,
, ![]() avec
avec ![]() ou
ou ![]()
Ces deux conditions sur le reste R se traduisent par le fait que ce reste est un polynôme constant ; on note r cette constante qui est un élément de K. D'après les règles de calcul sur les fonctions polynômes, on obtient l'égalité : ![]() .
.
D'où ![]() . L'équivalence est alors immédiate.
. L'équivalence est alors immédiate.
Conséquence immédiate :
Il résulte clairement de la définition que tout polynôme de degré 1 admet une racine (et une seule).
![]() Exemples :
Exemples :
1. Soit le polynôme de ![]() ,
, ![]() . En utilisant l'une ou l'autre des conditions du théorème, il est immédiat que les réels 3 et
. En utilisant l'une ou l'autre des conditions du théorème, il est immédiat que les réels 3 et ![]() sont les racines de P.
sont les racines de P.
2. Soit le polynôme de ![]() ,
, ![]() . Visiblement, on peut mettre X en facteur dans le polynôme P, et par conséquent le réel 0 est une racine de P.
. Visiblement, on peut mettre X en facteur dans le polynôme P, et par conséquent le réel 0 est une racine de P.
D'autre part, un simple calcul prouve que ![]() . Donc 1 est une racine de P. Le polynôme P est donc divisible par
. Donc 1 est une racine de P. Le polynôme P est donc divisible par ![]() .
.
Comme les polynômes X et ![]() sont premiers entre eux, le polynôme P est divisible
sont premiers entre eux, le polynôme P est divisible
par ![]() .
.
|
Théorème : Si un polynôme est divisible par deux polynômes premiers entre eux, il est divisible par leur produit. La démonstration de cette propriété est basée sur la propriété de Bézout.
|
On a donc ![]() .
.
Comme le polynôme ![]() n'a pas de racines réelles, on a toutes les racines de P dans R.
n'a pas de racines réelles, on a toutes les racines de P dans R.
Remarque importante
La terminologie " racine dans le corps K " est essentielle. En effet, le corps K joue un rôle fondamental. Soit par exemple le polynôme ![]() :
:
- Considéré comme élément de
 , il n'a pas de racines. Sinon il existerait un réel a tel que
, il n'a pas de racines. Sinon il existerait un réel a tel que  , ce qui est contraire à la structure de corps ordonné de R.
, ce qui est contraire à la structure de corps ordonné de R. - Considéré comme élément de
 , il a deux racines : i et
, il a deux racines : i et  .
.
On peut introduire le vocabulaire suivant :
|
Définition : Racine d'un polynôme dans un sur-corps du corps de ses coefficients Soient K et M deux corps tels que M contienne K. Soit P un élément de Si a est un élément de M tel que |
Si l'on reprend l'exemple précédent en introduisant ce vocabulaire, on peut dire que le polynôme ![]() n'a pas de racines dans R mais qu'il a deux racines dans C.
n'a pas de racines dans R mais qu'il a deux racines dans C.
Ordre de multiplicité d’une racine
Sur les deux exemples précédents, il est possible de faire la remarque suivante : on sait d'avance que si a est une racine dans K d'un polynôme P de ![]() , le polynôme Pest divisible par
, le polynôme Pest divisible par ![]() , mais il peut être divisible par une puissance de
, mais il peut être divisible par une puissance de ![]() strictement supérieure à 1.
strictement supérieure à 1.
C'est le cas dans l'exemple 1 mais pas dans l'exemple 2.
Cela nous conduit à l'introduction de la notion d'ordre de multiplicité d'une racine d'un polynôme.
|
Définition de l'ordre de multiplicité d'une racine Soit a une racine dans K de P, où P est un polynôme non nul de |
Un tel entier existe bien car l'ensemble des entiers k tels que divise P est non vide ; il contient l'entier 1 puisque a est racine de P (théorème précédent), et cet ensemble est fini car majoré par le degré de P. Donc il a un plus grand élément (propriété de N).
On peut traduire cette définition de la manière suivante :
|
Corollaire Un entier n est l'ordre de multiplicité de la racine a d'un polynôme P si et seulement si il existe un polynôme Q appartenant à |
Vocabulaire : Une racine d'ordre 1, est dite aussi racine simple.
Une racine d'ordre 2 (respectivement 3), est dite aussi racine double (respectivement racine triple).
![]() Exemples :
Exemples :
· Si l'on reprend le polynôme de l'exemple 1, ![]() ,
,
on observe que ![]() est une racine réelle d'ordre 1, et que 3 une racine réelle d'ordre 2.
est une racine réelle d'ordre 1, et que 3 une racine réelle d'ordre 2.
· Si l'on reprend le polynôme de l'exemple 2, ![]() ,
,
on voit que 0 et 1 sont toutes les deux des racines simples de P dans R.
Il résulte du corollaire la proposition suivante :
|
Proposition Soit P un polynôme non nul de Alors il existe un polynôme Q, élément de
|
Preuve : elle est immédiate, à partir des définitions ou propriétés suivantes :
· Définition d'une racine et de son ordre de multiplicité
· Les polynômes de la forme ![]() et
et ![]() avec a et b distincts, k et l étant des entiers positifs, sont premiers entre eux.
avec a et b distincts, k et l étant des entiers positifs, sont premiers entre eux.
· Un polynôme, divisible par des polynômes premiers entre eux deux à deux, est divisible par leur produit.
|
Corollaire (très important) Un polynôme non nul, de degré n, a au plus n racines (si l'on convient de compter une racine d'ordre r comme l'équivalent de r racines simples). |
Ceci est une conséquence immédiate de la proposition et des propriétés du degré du produit des polynômes.
Illustration : Pour un polynôme du troisième degré dans ![]() , les possibilités de racines dans K sont les suivantes :
, les possibilités de racines dans K sont les suivantes :
aucune racine (par exemple ![]() dans
dans ![]() )
)
une racine simple (par exemple ![]() dans
dans ![]() )
)
trois racines simples (par exemple ![]() dans
dans ![]() )
)
une racine simple et une racine double (par exemple ![]() dans
dans ![]() )
)
une racine triple (par exemple ![]() dans
dans ![]() )
)
Remarque : la démonstration du premier exemple est basée sur le fait que ![]() n'appartient pas à Q. La justification est tout à fait semblable à celle que l'on fait pour montrer que
n'appartient pas à Q. La justification est tout à fait semblable à celle que l'on fait pour montrer que ![]() n'appartient pas à Q.
n'appartient pas à Q.
Polynômes scindés
Le cas particulier où le polynôme P satisfait à la condition de la proposition, avec un polynôme Q constant, est très intéressant. Il est abordé dans cette partie.
|
Définition : Polynôme scindé dans un corps K. Un polynôme P non nul appartenant à où |
Il est clair que le rôle joué par le corps est très important.
Par exemple, le polynôme ![]() est scindé dans R.
est scindé dans R.
Quant au polynôme ![]() , il n'est pas scindé dans R mais il l'est dans C.
, il n'est pas scindé dans R mais il l'est dans C.
On a très facilement la propriété suivante :
|
Proposition Deux polynômes P et Q de |
Relations entre coefficients et racines d'un polynôme de K[X] scindé sur K
On peut trouver des relations entre les coefficients d'un polynôme scindé et ses racines.
Par exemple si l'on a un polynôme de degré 2 scindé dans ![]() , on peut l'écrire
, on peut l'écrire
![]()
où ![]() et
et ![]() sont les racines de P non nécessairement distinctes.
sont les racines de P non nécessairement distinctes.
Alors, en effectuant les calculs on obtient : ![]() .
.
D'où les relations :

Ceci est un exemple de la situation générale qui est explicitée dans le théorème suivant.
|
Théorème : Relations entre coefficients et racines Soit
(en écrivant r fois chaque racine multiple d'ordre r). Alors pour tout p,
En particulier : |
Exemple : Dans le cas d'un polynôme de degré 3, scindé sur K, en notant ![]() ses trois racines distinctes ou non, on a :
ses trois racines distinctes ou non, on a :
, et
Nous ne donnerons pas la démonstration dans le cas général, Nous avons déjà vu le cas d'un polynôme de degré 2. Les formules, dans le cas d'un polynôme de degré 3 se démontrent de la même façon. Nous pouvons donner le résultat.
Si ![]() , on a :
, on a :
![]()
![]()
![]()
![]() Remarques sur les sommes
Remarques sur les sommes ![]()
La notation  peut paraître complexe. En fait on peut l'expliciter. On prend tous les produits possibles de p racines (on note
peut paraître complexe. En fait on peut l'expliciter. On prend tous les produits possibles de p racines (on note ![]() un tel produit en les ordonnant dans l'ordre croissant de leurs indices) et on fait la somme de tous ces produits.
un tel produit en les ordonnant dans l'ordre croissant de leurs indices) et on fait la somme de tous ces produits.
Pour être sûr d'avoir tous " les produits possibles " il est nécessaire d'écrire ces produits en suivant un classement.
La méthode est explicitée sur l'exemple suivant : ![]() . Pour écrire
. Pour écrire ![]() il faut écrire tous les produits
il faut écrire tous les produits ![]() , avec
, avec ![]() . Ils sont présentés dans le tableau suivant :
. Ils sont présentés dans le tableau suivant :

La somme ![]() est obtenue en faisant la somme de tous les produits de la colonne de droite.
est obtenue en faisant la somme de tous les produits de la colonne de droite.
Les sommes  sont appelées les fonctions symétriques élémentaires des racines.
sont appelées les fonctions symétriques élémentaires des racines.
Intérêt : Toute fonction symétrique des racines s'exprime à l'aide des ![]() donc des coefficients du polynôme. C'est la base de la théorie de Galois.
donc des coefficients du polynôme. C'est la base de la théorie de Galois.
Fonction symétrique des racines
Soit ![]() une expression polynômiale par rapport aux n variables
une expression polynômiale par rapport aux n variables ![]() .
.
On dit que c'est une fonction symétrique si pour toute permutation s de l'ensemble ![]() (s est donc une bijection de
(s est donc une bijection de ![]() dans lui-même) l'égalité suivante est satisfaite :
dans lui-même) l'égalité suivante est satisfaite :
![]()
Exemple : ![]()
Il ne peut être question ici de dépasser cette définition quasi intuitive car cela nécessiterait des outils mathématiques hors du cadre de cette ressource.
(ce paragraphe n’est pas au programme car nécessite la connaissance des Espaces Vectoriels –On admettra le résultat)
|
Proposition : Etude de Soit K un corps infini. Soit P est un polynôme de
Alors P est le polynôme nul. Cela signifie que l'application |
Preuve : Elle est basée sur la remarque précédente et se fait grâce à un raisonnement par l'absurde.
Supposons que le polynôme P ne soit pas nul. On peut alors considérer son degré, soit n.
Il résulte de ce qui précède que P a au plus n racines.
Or l'hypothèse faite signifie que tout élément de K est racine de P. Si K est infini, P aurait une infinité de racines, d'où la contradiction.
Comme l'application ![]() est linéaire, cela signifie que son noyau est réduit à zéro, et donc qu'elle est injective.
est linéaire, cela signifie que son noyau est réduit à zéro, et donc qu'elle est injective.
Autrement dit, lorsque K est infini, l'égalité des fonctions polynômes associées à deux polynômes équivaut à l'égalité des deux polynômes.
![]() Conséquence sur les notations
Conséquence sur les notations
Cela permet alors de simplifier les notations. La fonction polynôme ![]() peut être notée
peut être notée ![]() sans aucune ambiguïté.
sans aucune ambiguïté.
C'est en particulier le cas lorsque le corps K est égal à R ou C.
Remarque : Le cas des polynômes à coefficients dans R ou dans C n'est pas étudié en détail dans cette ressource qui est consacrée aux propriétés générales.
Attention, cette propriété est fausse si le corps K n'est pas fini comme le prouve l'exemple suivant.
Soit le corps ![]() .
.
|
|
|
On a le résultat général suivant : Soit n un entier supérieur ou égal à 2. L'anneau quotient Comme 2 est un nombre premier, cela donne le résultat. |
Le corps ![]() a deux éléments qui sont notés
a deux éléments qui sont notés ![]() et
et ![]() .
.
Soit P le polynôme de ![]() défini par :
défini par : ![]() .
.
Alors ![]() et
et ![]() . Donc :
. Donc : ![]() . Donc la fonction polynôme
. Donc la fonction polynôme ![]() est nulle ce qui n'est évidemment pas le cas du polynôme P.
est nulle ce qui n'est évidemment pas le cas du polynôme P.
Méthodes de Horner
Pour calculer la valeur prise par une fonction polynôme en un point x de K, il y a plusieurs méthodes.
Une méthode très "performante" est la méthode de Hörner.
Elle consiste à calculer ![]() , avec
, avec  , en utilisant la forme suivante :
, en utilisant la forme suivante :
![]() ,
,
ce qui nécessite n multiplications et n additions, nombre d'opérations très inférieur à celui obtenu en faisant les calculs comme ils se présentent.
Pour s'en convaincre, on peut considérer l'exemple suivant :
Soit l'élément ![]() de
de ![]() et x un nombre réel.
et x un nombre réel.
On écrit ![]() sous la forme :
sous la forme : ![]() .
.
Pour calculer ![]() , avec x élément de R, on a donc besoin de 3 multiplications et de 3 additions par la méthode de Hörner, mais de 5 multiplications et de 3 additions en calculant directement.
, avec x élément de R, on a donc besoin de 3 multiplications et de 3 additions par la méthode de Hörner, mais de 5 multiplications et de 3 additions en calculant directement.
De plus, cette méthode est très facilement programmable.
Deuxième Partie : Polynômes coefficients réels ou complexes
Degré du polynôme dérivé
|
Proposition : Degré du polynôme dérivé d'un polynôme à coefficients réels ou complexes Soit P un polynôme non nul de degré n, · Si · Si |
Cela est immédiat à partir de la définition du degré d'un polynôme et du polynôme dérivé.
Remarque importante :
La considération des degrés permet de démontrer grâce à une récurrence que si P est un polynôme de degré n, ![]() est le polynôme nul. On aura un résultat plus général dans la proposition suivante
est le polynôme nul. On aura un résultat plus général dans la proposition suivante
Formule de Taylor pour un polynôme à coefficients réels ou complexes
Rappel sur la notation des fonctions polynômes :
On sait que dans le cas de polynômes à coefficients dans un corps infini, la fonction polynôme de K dans K, ![]() , est entièrement déterminée par le polynôme P. Cela permet de simplifier les notations et en particulier lorsque l'on considère des polynômes à coefficients réels ou complexes, elle pourra être notée
, est entièrement déterminée par le polynôme P. Cela permet de simplifier les notations et en particulier lorsque l'on considère des polynômes à coefficients réels ou complexes, elle pourra être notée ![]() sans aucune ambiguïté.
sans aucune ambiguïté.
La formule de Taylor pour les polynômes est démontrée ici uniquement par des moyens algébriques. Elle est extrêmement utile dans l'étude des racines d'un polynôme.
|
Proposition : Formule de Taylor pour les polynômes Soit i. Si ii. Pour tout h de K, on a :
|
Démonstration :
i. Une démonstration par récurrence immédiate justifie la propriété.
ii. si ![]() est un élément de
est un élément de ![]() , l'opération de substitution d'un polynôme dans un autre permet d'écrire :
, l'opération de substitution d'un polynôme dans un autre permet d'écrire :![]()
On obtient ainsi un élément de ![]() . Il existe donc des éléments
. Il existe donc des éléments ![]() de
de ![]() tels que
tels que ![]() . Soit k,
. Soit k, ![]() . En dérivant k fois le polynôme
. En dérivant k fois le polynôme ![]() sous la forme
sous la forme ![]() , on obtient (par une récurrence simple)
, on obtient (par une récurrence simple) ![]() et par conséquent, en prenant la valeur en 0 de la fonction polynôme associée, on a
et par conséquent, en prenant la valeur en 0 de la fonction polynôme associée, on a ![]() .
.
La formule peut aussi être formulée de la manière suivante :
Si a est un élément de K, on a  .
.
Il suffit de prendre  et de substituer
et de substituer  à X dans l'égalité
à X dans l'égalité
 pour obtenir ce résultat
pour obtenir ce résultat
Ordre de multiplicité d'une racine
Ce théorème permet de donner une caractérisation, très intéressante dans la pratique, de l'ordre de multiplicité d'une racine.
Rappel ordre de multiplicité
On va donner une caractérisation de l'ordre de multiplicité d'une racine, à l'aide des polynômes dérivés.
|
Théorème : Caractérisation de l'ordre de multiplicité d'une racine, à l'aide des polynômes dérivés Un élément a de K est racine d'ordre k d'un polynôme
|
La démonstration est basée sur la formule suivante déduite de la formule de Taylor pour les polynômes :

Existence de racines : Théorème de d'Alembert
Un des problèmes qui se pose concernant les racines d'un polynôme est celui de l'existence de racines. C'est un problème difficile.
Pour les polynômes à coefficients dans C, le théorème de d'Alembert répond entièrement à la question. Il est fondamental, mais sa démonstration n'est pas élémentaire.
Il en existe plusieurs, utilisant soit des propriétés d'analyse soit des propriétés algébriques, dans les deux cas puissantes et nécessitant des notions qui sont hors du niveau où est placé ce cours.
Nous l'admettrons donc.
Il va permettre de caractériser tous les polynômes irréductibles de ![]() et de
et de ![]() .
.
|
Théorème de d'Alembert-Gauss Tout polynôme non constant de |
Remarque historique : Ce résultat a d'abord été énoncé par d'Alembert puis démontré beaucoup plus tard par Gauss.
|
Définition d'un corps algébriquement clos On dit qu'un corps K est algébriquement clos si et seulement si tout polynôme non constant à coefficients dans K admet au moins une racine dans K. |
Il résulte du théorème de d'Alembert que le corps C est algébriquement clos. Par contre, le corps R ne l'est pas. Revoir l'exemple de ![]() pour s'en convaincre.
pour s'en convaincre.
Polynômes irréductibles dans C[X]
On suppose connues les propriétés générales des polynômes irréductibles de ![]() où K est un corps quelconque. Il n'y a pas, dans le cas général, de caractérisation des polynômes irréductibles. L'objet des deux paragraphes qui suivent est d'étudier ce problème dans les cas particuliers de
où K est un corps quelconque. Il n'y a pas, dans le cas général, de caractérisation des polynômes irréductibles. L'objet des deux paragraphes qui suivent est d'étudier ce problème dans les cas particuliers de ![]() et de
et de ![]() .
.
Le théorème suivant résulte immédiatement du théorème de d'Alembert :
|
Théorème : Caractérisation des polynômes irréductibles dans Les polynômes irréductibles de |
En effet, soit P un polynôme à coefficients complexes de degré supérieur ou égal à 2. Il est donc non constant et, d'après le théorème de d'Alembert, il admet au moins une racine complexe a. D'après la caractérisation des racines, cela signifie qu'il est divisible par le polynôme ![]() . Il n'est donc pas irréductible.
. Il n'est donc pas irréductible.
En intégrant ce résultat dans le théorème général de factorisation des polynômes en produit de polynômes irréductibles, on obtient :
|
Théorème : Factorisation en éléments irréductibles dans Tout polynôme non constant de |
Exemple : ![]() avec
avec ![]() .
.
Polynômes irréductibles dans R[X]
Le résultat de l'étude précédente permet d'obtenir la caractérisation des polynômes irréductibles sur ![]() .
.
L'outil essentiel, pour ce faire, est l'inclusion évidente :
![]()
En préliminaire, on établit la propriété suivante, très utile dans la pratique.
|
Proposition : Racine complexe d'un polynôme à coefficients réels Soit P un polynôme non constant à coefficients réels. On suppose que ce polynôme, considéré comme élément de Alors |
Preuve : Il est clair, comme les coefficients de P sont réels et compte tenu des propriétés de la conjugaison dans C, que pour tout x complexe
![]()
![]()
Alors la caractérisation des racines d'un polynôme et de leur ordre de multiplicité à l'aide des dérivées de ce polynôme prouve le résultat.
|
Corollaire 1 : Description des racines d'un élément de Soit P un polynôme à coefficients réels. Ses racines, dans C, sont · soit réelles · soit non réelles, conjuguées deux à deux, une racine et sa conjuguée ayant le même ordre de multiplicité. |
On en déduit un résultat très pratique :
|
Corollaire 2 Tout polynôme à coefficients réels de degré impair a au moins une racine réelle. |
Ici, il est justifié par des propriétés purement algébriques. On peut aussi le démontrer avec des outils d'analyse en étudiant les variations de la fonction polynôme associée.
Cela conduit au théorème suivant :
|
Théorème : Factorisation en facteurs irréductibles dans Soit P un polynôme non constant appartenant à où les polynômes
Une telle décomposition est unique. |
Preuve
D'après le résultat du corollaire, la décomposition en facteurs irréductibles de P, considéré comme un élément de ![]() , est de la forme
, est de la forme
où les ![]() sont des nombres réels et les
sont des nombres réels et les ![]() des nombres complexes non réels.
des nombres complexes non réels.
Or : ![]() .
.
On a ![]() ; on obtient donc un nombre réel. De même, on a
; on obtient donc un nombre réel. De même, on a ![]() qui est aussi un nombre réel.
qui est aussi un nombre réel.
Donc le polynôme ![]() s'écrit
s'écrit ![]() avec
avec ![]() et
et ![]() réels. De plus ce polynôme n'a pas de racines réelles ce que l'on peut caractériser en disant que son discriminant
réels. De plus ce polynôme n'a pas de racines réelles ce que l'on peut caractériser en disant que son discriminant ![]() est négatif.
est négatif.
Ce polynôme est donc un polynôme irréductible dans ![]() (sinon il serait divisible par un polynôme de degré 1 ce qui équivaudrait à l'existence d'une racine réelle).
(sinon il serait divisible par un polynôme de degré 1 ce qui équivaudrait à l'existence d'une racine réelle).
On obtient donc une décomposition de P en un produit de polynômes à coefficient réels, irréductibles dans ![]() :
:

A cause de l'unicité d'une telle décomposition, c'est la décomposition en facteurs irréductibles dans ![]() de P.
de P.
Remarque : on a l'égalité : ![]() .
.
![]() Exemple :
Exemple :
Soit le polynôme ![]() et cherchons sa décomposition en facteurs irréductibles dans
et cherchons sa décomposition en facteurs irréductibles dans ![]() . Si on le considère comme un polynôme à coefficients complexes, il vient que i est racine de P d'ordre de multiplicité égal à 2. En effet,
. Si on le considère comme un polynôme à coefficients complexes, il vient que i est racine de P d'ordre de multiplicité égal à 2. En effet,
![]()
![]() , d'où
, d'où ![]()
![]() , d'où
, d'où ![]()
Donc ![]() est aussi racine d'ordre 2 de
est aussi racine d'ordre 2 de ![]() dans C. Donc
dans C. Donc ![]() est divisible
est divisible
dans ![]() par
par ![]() . Il existe donc
. Il existe donc ![]() dans
dans ![]() tel que :
tel que :
![]() (considération de degré).
(considération de degré).
On calcule ![]() , soit par la méthode des coefficients indéterminés, soit par division euclidienne de
, soit par la méthode des coefficients indéterminés, soit par division euclidienne de ![]() par
par ![]() , et l'on obtient :
, et l'on obtient :
![]()
Le polynôme ![]() est irréductible dans
est irréductible dans ![]() (son discriminant est
(son discriminant est ![]() , donc strictement négatif), donc
, donc strictement négatif), donc ![]() est la décomposition de
est la décomposition de ![]() en facteurs irréductibles dans
en facteurs irréductibles dans ![]() .
.
Remarque : La décomposition en facteurs irréductibles de ![]() dans
dans ![]() est
est
![]() .
.
Ce théorème permet d'obtenir une description complète des polynômes irréductibles
dans ![]() :
:
|
Théorème : Caractérisation des polynômes irréductibles dans Les polynômes irréductibles de |
Remarque : Attention ! Une conséquence immédiate de ce résultat est qu'un polynôme à coefficients réels qui n'a pas de racine n'est pas forcément irréductible.
L'exemple suivant en est une illustration.
Exemple : Soit ![]() .
.
· Ce polynôme n'a pas de racines réelles : en effet s'il en avait une, soit a, ce réel vérifierait l'égalité ![]() , ce qui est absurde dans R.
, ce qui est absurde dans R.
· Mais ce polynôme n'est pas irréductible puisqu'il n'est pas de l'un des deux types précédents.
Donc on sait d'avance que ce polynôme est le produit de deux polynômes de degré égal à 2, sans racines réelles.
· Pour trouver sa factorisation en facteurs irréductibles, on a (au moins) trois méthodes possibles :
On peut utiliser la remarque qui vient d'être faite, l'écrire sous la forme du produit de deux polynômes de degré égal à 2 avec des coefficients indéterminés, développer et identifier les coefficients. Cela aboutit à un système linéaire qu'il faut résoudre. Cette méthode est efficace, mais lourde du point de vue des calculs.
On pourrait aussi chercher sa décomposition dans ![]() , puis regrouper les termes correspondant à des racines conjuguées (en suivant le principe de la démonstration théorique).
, puis regrouper les termes correspondant à des racines conjuguées (en suivant le principe de la démonstration théorique).
On peut aussi procéder de la manière suivante : on considère que c'est le début du développement du carré de la somme ![]() , le double produit manquant.
, le double produit manquant.
Alors : ![]() , soit
, soit ![]() .
.
C'est la décomposition cherchée.
Remarque : La décomposition en facteurs irréductibles est unique, donc tous les moyens mathématiquement corrects sont bons pour la déterminer.
Formule d'interpolation de Lagrange
Pour terminer cette ressource, nous allons donner la formule d'interpolation de Lagrange qui permet de caractériser un polynôme par la valeur de la fonction polynôme qui lui est associée en un certain nombre de points. (très utile en mathématiques appliquées pour les calculs et les approximations).
On suppose que le corps K est égal à R ou C.
|
Théorème : Formule d'interpolation de Lagrange Etant donnés n points
|
Preuve : elle se décompose en deux parties : l'unicité et l'existence.
· Unicité : S'il existait deux polynômes ![]() et
et ![]() satisfaisant au problème donné,
satisfaisant au problème donné,
avec ![]() , le polynôme non nul
, le polynôme non nul ![]() , serait de degré strictement inférieur à n et aurait au moins n racines, les
, serait de degré strictement inférieur à n et aurait au moins n racines, les ![]() , ce qui serait absurde.
, ce qui serait absurde.
· Existence : On vérifie que le polynôme

est solution du problème posé.
Exemple : Si l'on considère le cas ![]() et
et ![]() , on retrouve le résultat (bien connu) que par deux points distincts il passe une et une seule droite.
, on retrouve le résultat (bien connu) que par deux points distincts il passe une et une seule droite.
Remarque :
Si tous les ![]() sont nuls, le seul polynôme tel que pour tout k,
sont nuls, le seul polynôme tel que pour tout k, ![]() ,
, ![]() est le polynôme nul (cf. la démonstration de l'unicité).
est le polynôme nul (cf. la démonstration de l'unicité).
Source : http://www.ann.jussieu.fr/~berco/LM125/LM125-Lecon-4.htm
09:35 Publié dans Fonctions Polynômes | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Algorithme d'Euclide
L'algorithme d'Euclide est un algorithme permettant de déterminer le plus grand commun diviseur (P.G.C.D.) de deux entiers dont on ne connaît pas la factorisation. Il est déjà décrit dans le livre VII des Éléments d'Euclide. Dans la tradition grecque, en comprenant un nombre entier comme une longueur, un couple d'entiers comme un rectangle, leur PGCD est la longueur du côté du plus grand carré permettant de carreler entièrement ce rectangle. L'algorithme décompose ce rectangle en carrés, de plus en plus petits, par divisions euclidiennes successives, de la longueur par la largeur, puis de la largeur par le reste, jusqu'à un reste nul. Dans le rectangle de dimensions L=21 par l=15 ci-dessous, par exemple, on peut glisser un carré de côté 15 mais il reste un rectangle de côtés 15 et 6, dans lequel on peut glisser deux carrés de côté 6 mais il reste un rectangle de côtés 6 et 3 que l'on peut carreler entièrement de carrés de côté 3. Les carrés de côté 6 ou 15 peuvent aussi se carreler en carrés de côté 3. Le rectangle entier peut se carreler en carrés de côté 3. Il n'existe pas de carré plus grand permettant un tel carrelage. Cet algorithme repose sur la structure d'anneau euclidien de l'anneau L'algorithme est effectif à condition de disposer d'un algorithme effectif de division euclidienne. La possibilité de disposer d'un tel algorithme rend de nombreux autres calculs effectifs, notamment, en algèbre linéaire, le calcul de facteurs invariants.Algorithme d'Euclide
 des entiers relatifs, plus particulièrement sur la propriété de division euclidienne. Il se généralise donc à bien d'autres anneaux, en particulier les anneaux de polynômes à coefficients dans un corps. L'algorithme se généralise pour permettre le calcul des coefficients de Bezout.
des entiers relatifs, plus particulièrement sur la propriété de division euclidienne. Il se généralise donc à bien d'autres anneaux, en particulier les anneaux de polynômes à coefficients dans un corps. L'algorithme se généralise pour permettre le calcul des coefficients de Bezout.
Sommaire[masquer] |
Puisque l'algorithme a pour objet le calcul d'un PGCD, il est possible de se restreindre aux entiers positifs, un PGCD de deux entiers relatifs étant égal au PGCD de leurs valeurs absolues. Soient deux entiers naturels a et b, dont on cherche le PGCD. Le cas où a ou b est nul ne nécessite aucun algorithme ; on l'exclut. Une suite d'entiers (an)n est définie par récurrence de pas 2, plus précisément par divisions euclidiennes successives ; la suite est initialisée par a0 = a, a1 = b, puis propagée par la règle de récurrence : tant que an+1 est non nul, an+2 est défini comme le reste de la division euclidienne de an par an+1. On commence donc par calculer le reste de la division de a par b, qu'on note r ; puis on remplace a par b, puis b par r, et on réapplique le procédé depuis le début. On obtient ainsi une suite, qui vaut 0 à un certain rang ; le PGCD cherché est le terme précédent de la suite. Il est intéressant de noter que si a < b, la première itération de la boucle a pour effet de "permuter a et b". Plus précisément : dans ce cas, la division euclidienne de a par b s'écrit a = b.0 + a donc a2 = a, si bien que la suite produite par l'algorithme appliqué au couple (a, b) commence par a, suivie de la suite produite par l'algorithme appliqué au couple (b, a). Calculons, par exemple, le PGCD de 1071 et de 1029 à l'aide de l'algorithme d'Euclide : 1071 = 1029 × 1 + 42 1029 = 42 × 24 + 21 42 = 21 × 2 + 0 Il faut prendre le dernier reste avant le zéro, donc PGCD(1071 ; 1029) = 21 Voici différents exemples d'implémentations de l'algorithme d'Euclide en programmation. Fonction PGCD(a:nombre, b:nombre):nombre ou sous forme condensée: ou en utilisant une boucle, sans rappeler la fonction dans elle-même (algorithme ressemblant plus à l'organigramme à flèche présent sur l'article): Au début, Euclide a formulé le problème de façon géométrique : comment trouver une « unité de mesure » commune pour deux longueurs de segments. Il procède par soustractions répétées de la longueur du plus court segment sur la longueur du plus long. Cela correspond à une adaptation de la méthode naïve de calcul de la division euclidienne, telle que décrite dans l'article consacré. La définition même de la suite (an) par division euclidienne montre que, pour tout n tel que an + 1 est non nul, il existe un entier qn + 2 tel que : avec de plus Soit N + 1 l'indice de ce dernier reste non nul. Il faut montrer que aN + 1 est bien le PGCD cherché. La relation précédente s'écrit donc ici aN + 1 est donc un diviseur commun de a et b que divise tout autre diviseur commun ; c'est bien le PGCD. Le théorème de Lamé stipule que le nombre d'étape de l'algorithme d'Euclide exécuté sur deux entiers est borné (supérieurement) par cinq fois le nombre de chiffres nécessaire à écrire (en base 10) le plus petit de ces deux entiers. On peut en fait être légèrement plus précis : le nombre d'étapes de l'algorithme d'Euclide exécuté sur deux entiers a et b, avec Comme le nombre de chiffres de l'écriture de b en base 10 est ln(b) / ln(10) et que la quantité De plus, cette majoration est la meilleure possible, puisqu'elle est atteinte quand a et b sont deux nombres de Fibonacci consécutifs. L'identité de Bézout assure l'existence de deux entiers u et v tels que : au + bv = aN + 1 = PGCD(a,b). L'algorithme d'Euclide convenablement adapté permet de calculer de tels coefficients. Pour cela, on introduit deux suites (un) et (vn) telles que pour tout n, on ait la relation : aun + bvn = an. Si de telles suites existent, les termes uN + 1,vN + 1 constitueront une paire de coefficients de Bezout pour a et b. On peut choisir u0 = 1,v0 = 0 puis u1 = 0,v1 = 1, puis la relation de récurrence de pas 2 entre les an montre : an + 2 = an − qn + 2an + 1 = aun + bvn − qn + 2(aun + 1 + bvn + 1) = a(un − qn + 2un + 1) + b(vn − qn + 2vn + 1) On peut ainsi définir (un) par la relation de récurrence de pas 2 : un + 2 = un − qn + 2un + 1 et l'initialisation précédente, et (vn) par vn + 2 = vn − qn + 2vn + 1 et l'initialisation précédente ; et on obtient bien la relation annoncée pour tout n. L'algorithme étendu s'implémente comme l'algorithme classique ; il suffit de rajouter des variables correspondant aux coefficients u et v à calculer, et de faire une multiplication et une soustraction supplémentaires, pour calculer chacun des deux nouveaux coefficients, à chaque étape. Les quotients successifs qui apparaissent quand l'algorithme d'Euclide est appliqué aux données a et b, sont précisément les nombres qui apparaissent dans la représentation sous forme de fraction continue de a/b. Considérons l'exemple de a = 1071 et b = 1029 utilisé ci-dessus. Voici le calcul avec les quotients soulignés (successivement 1, 24 et 2): De cela on tire : Dans l'égalité précédente, le second membre s'appelle la fraction continue ou continuée du quotient 1071/1029. On peut en déduire les 3 approximations suivantes de la fraction, classées par ordre de précision croissante : Cette méthode peut également être utilisée pour des nombres réels a et b ; comme dans le cas de deux entiers, la suite de quotients calculés représente la « décomposition en fraction continue » de a/b et fournit une suite d'approximations successives, de qualité croissante, du quotient a/b. Dans le cas où ce quotient est irrationnel, l'algorithme d'Euclide ne se termine pas et la suite des approximations obtenues est donc elle-même infinie ! nota : La décomposition en fraction continuée (et la série d'approximations successives correspondante) peut être appliquée, non seulement à un nombre réel quelconque, mais également à une fonction : cette démarche consiste à rechercher les approximants de Padé, dont on peut définir le principe comme suit : Au voisinage d'un point, le développement ensérie de Taylor d'une fonction donnée fournit un polynôme qui réalise une approximation de la fonction. Mais on peut également chercher une fraction rationnelle qui satisfasse les mêmes conditions que la partie polynomiale du développement de Taylor : l'égalité des dérivées de la fonction et de son approximation, jusqu'à un certain ordre donné. La comparaison de ces deux types de développements permet de très intéressants développements, comme la démonstration de l'irrationalité de ζ(3).Remarque préliminaire [modifier]
Description de l'algorithme [modifier]
Exemple [modifier]
Exemples d'implémentations [modifier]
Pseudocode [modifier]
Si b=0 alors
| Retourner a
Sinon
| r egal au reste de la division entière (modulo) de a par b
| Retourner PGCD(b, r)
Python [modifier]
def PGCD(a, b):
if b == 0:
return a
else:
return PGCD(b, a % b)
C [modifier]
int PGCD(int a, int b)
{
if (b == 0)
return a;
else
return PGCD(b, a % b);
}
int PGCD(int a, int b)
{
return (b) ? PGCD(b, a%b) : a;
}
int PGCD(int a, int b)
{
int r;
while ((r = a % b) != 0)
{
a = b;
b = r;
}
return b;
}
Remarque historique [modifier]
Démonstration de sa finitude et de son exactitude [modifier]

 . La suite d'entiers naturels (an) est donc strictement décroissante à partir du rang 1, et donc vaut 0 à un certain rang. L'existence d'un dernier reste non nul est ainsi établie.
. La suite d'entiers naturels (an) est donc strictement décroissante à partir du rang 1, et donc vaut 0 à un certain rang. L'existence d'un dernier reste non nul est ainsi établie.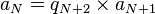 , qui montre que aN+ 1 divise aN. Écrivant ensuite
, qui montre que aN+ 1 divise aN. Écrivant ensuite  , on en déduit que aN + 1 divise aussi aN − 1 ; puis, de même, et par récurrence, que aN + 1 divise tous les termes de la suite an ; en particulier les premiers termes a et b. aN + 1 est donc bien un diviseur commun de a et b. Réciproquement, tout diviseur commun de a et b divisera aussi
, on en déduit que aN + 1 divise aussi aN − 1 ; puis, de même, et par récurrence, que aN + 1 divise tous les termes de la suite an ; en particulier les premiers termes a et b. aN + 1 est donc bien un diviseur commun de a et b. Réciproquement, tout diviseur commun de a et b divisera aussi 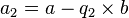 , et à nouveau par récurrence, divisera tous les termes de la suite (an) ; donc en particulier aN + 1.
, et à nouveau par récurrence, divisera tous les termes de la suite (an) ; donc en particulier aN + 1.Le théorème de Lamé [modifier]
 , est borné par la partie entière de
, est borné par la partie entière de  , où ln désigne le logarithme naturel et
, où ln désigne le logarithme naturel et  est le nombre d'or.
est le nombre d'or. est inférieure à 5 (elle vaut environ 4,78497), on retrouve bien le théorème de Lamé.
est inférieure à 5 (elle vaut environ 4,78497), on retrouve bien le théorème de Lamé.Algorithme étendu aux coefficients de Bézout [modifier]
Description [modifier]
Commentaires [modifier]
Fractions continues [modifier]
 .
.
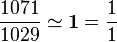
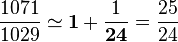

Voir aussi [modifier]
Liens externes [modifier]
09:33 Publié dans Algorithme d'Euclide | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Mathématiques sur diffusion.ens.fr
mathématiques
Source : http://www.diffusion.ens.fr/index.php?res=themes&idth...
09:31 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Probabilité dans les jeux
Les probabilités et les jeux concernent à la fois le jeu de hasard pur et le jeu de hasard raisonné. Le mathématicien Pascal est très connu pour avoir théorisé les jeux mais par la suite von Neumann (théorie des jeux) et Kolmogorov apportèrent des éléments beaucoup plus importants. En informatique, Tesauro utilisa l'observation de nombreuses parties de backgammon afin de développer un logiciel d'auto apprentissage basé sur ce jeu. Probabilité dans les jeux
09:26 Publié dans Probabilité dans les jeux | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Variables indépendantes et identiquement distribuées
En statistique, des variables indépendantes et identiquement distribuées (iid) sont des variables aléatoires qui ont toutes la même loi de probabilité et sont mutuellement indépendantes. En inférence statistique ou en apprentissage automatique, il est très courant de supposer que le tirage des échantillons d'apprentissage sont i.i.d. C'est une condition souvent nécessaire à l'application des théorèmes les plus courants. En particulier le théorème de la limite centrale dans sa forme classique stipule que la somme de variables aléatoires tendent vers unedistribution normale quand ces variable sont i.i.d. Un exemple de tirage aléatoire i.i.d est celui du pile ou face. Chaque lancer de pièce suit la même loi de Bernoulli de paramètre p et est indépendant de ceux qui l'ont précédé ou vont lui succéder. Si p = 0.5 (pile et face ont la même chance d'apparition), et que nous avons obtenu 10 fois face lors des 10 tirages précédents, les chances d'obtenir pile et face lors du prochain tirage sont néanmoins égales. Dans l'exemple précédent, le tirage ne serait plus i.i.d : Variables indépendantes et identiquement distribuées
Exemples [modifier]
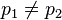 ) car dans ce cas les tirages ne suivent pas la même loi. Il restent néanmoins indépendants.
) car dans ce cas les tirages ne suivent pas la même loi. Il restent néanmoins indépendants.
09:25 Publié dans Variables indépendantes et identiquement distribué | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
19/11/2010
Théorie des probabilités
La théorie des probabilités est l'étude mathématique des phénomènes caractérisés par le hasard et l'incertitude. Les objets centraux de la théorie des probabilités sont les variables aléatoires, les processus stochastiques, et lesévénements: ils traduisent de manière abstraite des événements non déterministes ou des quantités mesurées qui peuvent parfois évoluer dans le temps d'une manière apparemment aléatoire. En tant que fondement mathématique desstatistiques, la théorie des probabilités est essentielle à la plupart des activités humaines qui nécessitent une analyse quantitative d'un grand nombre de mesures. Les méthodes de la théorie des probabilités s'appliquent également à la description de systèmes complexes dont on ne connait qu'en partie l'état, comme en mécanique statistique. Une grande découverte de la physique du vingtième siècle fut la nature probabiliste de phénomènes physiques à une échelle microscopique, décrite par la mécanique quantique.Théorie des probabilités
Sommaire[masquer] |
La théorie mathématique des probabilités trouve ses origines dans l'analyse de jeux de hasard par Gerolamo Cardano au seizième siècle, et par Pierre de Fermat et Blaise Pascal au dix-septième siècle. Bien qu'un simple pile ou face ou un lancer de dés soit un événement aléatoire, en les répétant de nombreuses fois on obtient une série de résultats qui va posséder certaines propriétés statistiques, que l'on peut étudier et prévoir. Deux résultats mathématiques fondamentaux à ce propos sont la loi des grands nombres et le théorème de la limite centrale. Initialement, la théorie des probabilités considérait surtout les événements discrets, et ses méthodes étaient principalement combinatoires. Mais des considérations analytiques ont forcé l'introduction de variables aléatoires continues dans la théorie. Cette idée prend tout son essor dans la théorie moderne des probabilités, dont les fondations ont été posées parAndreï Nikolaevich Kolmogorov. Kolmogorov combina la notion d'univers, introduite par Richard von Mises et la théorie de la mesure pour présenter son système d'axiomes pour la théorie des probabilités en 1933. Très vite, son approche devint la base incontestée des probabilités modernes. La théorie discrète des probabilités s'occupe d'événements dans le cadre d'un univers fini ou dénombrable. Exemples: lancer de dés, expériences avec des paquets de cartes, et marche aléatoire. Définition classique: Initialement, la probabilité d'un événement était définie comme le nombre de cas favorables pour l'événement, divisé par le nombre total d'issues possibles à l'expérience aléatoire. Par exemple, si l'événement est obtenir un nombre pair en lançant le dé, sa probabilité est donnée par Définition moderne : La définition moderne commence par un ensemble appelé univers, qui correspond à l'ensemble des issues possibles à l'expérience dans la définition classique. Il est noté On définit ensuite un événement comme un ensemble d'issues, c'est-à-dire un sous-ensemble de Ω. La probabilité d'un évènement E est alors définie de manière naturelle par : Ainsi, la probabilité de l'univers est 1, et la probabilité de l'événement impossible (l'ensemble vide) est 0. Pour revenir à l'exemple du lancer de dés, on peut modéliser cette expérience en se donnant un univers Ω = {1;2;3;4;5;6} correspondant aux valeurs possibles du dé, et une fonction fqui à chaque La théorie des probabilités continue s'occupe des événements qui se produisent dans un univers continu (par exemple la droite réelle). Définition classique: La définition classique est mise en échec lorsqu'elle est confrontée au cas continu (cf. paradoxe de Bertrand). Définition moderne Si l'univers est la droite réelle La fonction de répartition doit satisfaire les propriétés suivantes : Si Pour un ensemble Si la densité de probabilité existe, on peut alors la réécrire : Tandis que la densité de probabilité n'existe que pour les variables aléatoires continues, la fonction de répartition existe pour toute variable aléatoire (y compris les variables discrètes) à valeurs dans Ces concepts peuvent être généralisés dans les cas multidimensionnel sur La probabilité d'un événement donné A, Historique [modifier]
Théorie des probabilités discrète [modifier]
 , puisque trois faces sur six ont un nombre pair.
, puisque trois faces sur six ont un nombre pair.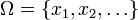 . Ensuite, on a besoin d'une fonction f définie sur Ω, qui va associer à chaque élément de Ω sa probabilité, satisfaisant donc les propriétés suivantes :
. Ensuite, on a besoin d'une fonction f définie sur Ω, qui va associer à chaque élément de Ω sa probabilité, satisfaisant donc les propriétés suivantes :
![f(x)in[0,1]mbox{ pour tout }xin Omega](http://upload.wikimedia.org/math/0/e/7/0e77ec055bf042c11b977174cb518c4d.png)
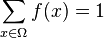

 associe
associe  .
.Théorie des probabilités continue [modifier]
 , alors on admet l'existence d'une fonction appelée fonction de répartition
, alors on admet l'existence d'une fonction appelée fonction de répartition 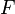 , qui donne
, qui donne  pour une variable aléatoire X. Autrement dit, F(x) retourne la probabilité que X soit inférieur ou égal à x.
pour une variable aléatoire X. Autrement dit, F(x) retourne la probabilité que X soit inférieur ou égal à x.
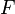 est une fonction croissante et continue à droite.
est une fonction croissante et continue à droite.
 est dérivable, alors on dit que la variable aléatoire X a une densité de probabilité
est dérivable, alors on dit que la variable aléatoire X a une densité de probabilité 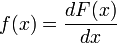 .
.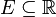 , la probabilité que la variable aléatoire X soit dans
, la probabilité que la variable aléatoire X soit dans 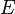 est définie comme :
est définie comme :
 .
. et d'autres univers continus.
et d'autres univers continus.Principes fondamentaux [modifier]
 , est représentée par un nombre compris entre 0 et 1. L'événement impossible a une probabilité de 0 et l'événement certain a une probabilité de 1. Il faut savoir que la réciproque n'est pas vraie. Un événement qui a une probabilité 0 peut très bien se produire dans le cas où un nombre infini d'événements différents peut se produire. Ceci est détaillé dans l'article Ensemble négligeable.
, est représentée par un nombre compris entre 0 et 1. L'événement impossible a une probabilité de 0 et l'événement certain a une probabilité de 1. Il faut savoir que la réciproque n'est pas vraie. Un événement qui a une probabilité 0 peut très bien se produire dans le cas où un nombre infini d'événements différents peut se produire. Ceci est détaillé dans l'article Ensemble négligeable.
| Évènement | Probabilité |
|---|---|
| probabilité de A | ![mathbb{P}(A)in[0,1],](http://upload.wikimedia.org/math/e/8/0/e80064214aea988389b07fc8d173b9cd.png) |
| probabilité de ne pas avoir A |  |
| probabilité d'avoir A ou B |  |
| probabilité conditionnelle de A, sachant B |
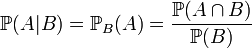 |
| probabilité d'avoir A et B | 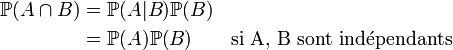 |
Certaines distributions peuvent être un mélange de distributions discrètes et continues, et donc n'avoir ni densité de probabilité ni fonction de masse. La distribution de Cantor constitue un tel exemple. L'approche moderne des probabilités résout ces problèmes par l'utilisation de la théorie de la mesure pour définir un espace probabilisé et aboutir aux axiomes des probabilités développés par Kolmogorov Un espace probabilisé comporte trois parties: Dans cette optique, pour des événements deux à deux disjoints (c'est-à-dire, d'intersection deux à deux vide) A1, A2, A3…, la probabilité de leur union apparaît comme la somme de leurs probabilités, ou, avec les notations mathématiques, C'est le troisième et dernier axiome des probabilités. Par exemple, et toujours pour un dé à 6 faces, la probabilité de tirer un 1 ou un 2 En plus de permettre une meilleure compréhension et une unification des théories discrètes et continues des probabilités, l'approche de la théorie de la mesure nous permet aussi de parler de probabilités en dehors de Certaines variables aléatoires sont fréquemment rencontrées en théorie des probabilités car on les retrouve dans de nombreux processus naturels ; leur loi a donc une importance particulière. Les lois discrètes les plus fréquentes sont la loi uniforme discrète, la loi de Bernoulli, ainsi que les lois binomiale, de Poisson et géométrique. Les lois uniforme continue,normale, exponentielle et gamma sont parmi les plus importantes lois continues. En théorie des probabilités, il y a plusieurs notions de convergence pour les variables aléatoires. En voici une liste: Un processus stochastique est un processus aléatoire qui dépend du temps. Un processus stochastique est donc une fonction de deux variables : le temps et la réalisation ω d'une certaine expérience aléatoire. Quelques exemples d'utilisation des processus stochastiques incluent le mouvement brownien, les fluctuations du marché boursier, ou la reconnaissance vocale. En temps discret, ces processus sont aussi connus sous le nom de Séries temporelles et servent entre autres en économétrie. Parmi les processus stochastiques, les chaînes de Markov constituent l'exemple le plus simple et sans doute celui qui a le plus d'applications pratiques. Une chaîne de Markov est un processus stochastique possédant la propriété markovienne. Dans un tel processus, la prédiction du futur à partir du présent ne nécessite pas la connaissance du passé. Il suffit alors de connaître l'état de la chaîne à un instant t pour savoir comme elle évoluera au temps t+1, il n'est pas nécessaire de connaître tout le passé entre 0 et t pour prévoir l'évolution de la chaîne. Une chaîne en temps discret est une séquence X1, X2, X3, ... de variables aléatoires. La valeur Xn étant l'état du processus au moment n. Si la distribution de probabilité conditionnellede Xn+1 sur les états passés est une fonction de Xn seulement, alors de façon mathématique: où x est un état quelconque du processus, Cette propriété de Markov s'oppose à la notion d'hystérésis où l'état actuel dépend de l'histoire et non seulement de l'état actuel. Ces chaînes de Markov ou des modèles de Markov cachés interviennent dans l'étude de la marche aléatoire et ont de nombreux champs d'application: filtre anti-spam, mouvement brownien, hypothèse ergodique, théorie de l'information,reconnaissance des formes, algorithme de Viterbi utilisé en téléphonie mobile, etc... Citons entre autres comme cas particuliers de chaînes de Markov la marche aléatoire qui sert en particulier à l'étude de la diffusion ou du jeu de pile ou face. Une marche aléatoire est une chaîne de Markov où la probabilité de transition ne dépend que de x-y. Autrement dit une chaîne de Markov où l'on a: P(Xn + 1 = x | Xn = y) = f(x − y). Un jeu de pile ou face où l'on jouerait 1 à chaque lancer est un exemple de marche aléatoire. Si on a y après n lancers,P(Xn + 1 = x | Xn = y) = 1 / 2 si (x-y)=+1 ou -1 et 0 sinon. (on a une chance sur deux de gagner 1 et une chance sur deux de perdre 1) Les équations différentielles stochastiques sont une forme d'équation différentielle incluant un terme de bruit blanc. Ces équations différentielles stochastiques remplacent les équations différentielles ordinaires lorsque l'aléatoire entre en jeu. Au premier ordre par exemple: Pour faire une analogie avec la physique, μ(X(t)) est la vitesse moyenne au point X(t) et σ est lié au coefficient de diffusion (voir à ce propos l'exemple donné dans lemme d'Itô). Lelemme d'Itô et l'intégrale d'Itô permettent alors de passer de ces équations stochastiques à des équations aux dérivées partielles classiques ou à des équations intégrales. Par exemple en utilisant le lemme d'Itô on obtient pour la probabilité de se trouver à l'instant t au point x: Ce lemme est particulièrement important car il permet de faire le lien entre l'étude d'équations stochastiques et les équations aux dérivées partielles qui relèvent de l'analyse. Ce lemme permet entre autres d'obtenir les équation de Fokker-Planck en physique et de traiter le mouvement brownien par des équations aux dérivées partielles classiques ou de modéliser les cours de la bourse en Mathématiques financières.  est la réunion de A et B.
est la réunion de A et B.  est l'intersection de A et de B.
est l'intersection de A et de B.  est appelé la probabilité conditionnelle de A sachant B. C'est la probabilité d'avoir A quand on sait que l'on a B. Par exemple, pour un dé à 6 faces la probabilité d'avoir un 2 (A) quand on sait que le résultat est pair (B) est égal à
est appelé la probabilité conditionnelle de A sachant B. C'est la probabilité d'avoir A quand on sait que l'on a B. Par exemple, pour un dé à 6 faces la probabilité d'avoir un 2 (A) quand on sait que le résultat est pair (B) est égal à  car la probabilité d'avoir à la fois un 2 et un nombre pair est égal à 1/6 et la probabilité d'avoir un nombre pair est égal à 1/2. Ici on remarque que
car la probabilité d'avoir à la fois un 2 et un nombre pair est égal à 1/6 et la probabilité d'avoir un nombre pair est égal à 1/2. Ici on remarque que  car on a toujours un nombre pair quand on a 2.
car on a toujours un nombre pair quand on a 2.La théorie des probabilités aujourd'hui [modifier]
 : C'est une tribu sur les événements Ω. Cet ensemble contient tous les résultats possibles de l'événement au sens large. Par exemple pour un dé à 6 faces il contient la possibilité d'avoir un 1 ou un 2: {1, 2}, la possibilité de ne rien sortir comme résultat: l'ensemble vide
: C'est une tribu sur les événements Ω. Cet ensemble contient tous les résultats possibles de l'événement au sens large. Par exemple pour un dé à 6 faces il contient la possibilité d'avoir un 1 ou un 2: {1, 2}, la possibilité de ne rien sortir comme résultat: l'ensemble vide 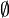 , la possibilité de sortir n'importe quel face du dé {1, 2, 3, 4, 5, 6}. En général en probabilité on se contente de prendre la tribu borélienne. À titre d'exemple la tribu borélienne pour le résultat d'un dé à 4 faces est donné (celle pour le dé à 6 faces est encore plus grande mais suit le même principe):
, la possibilité de sortir n'importe quel face du dé {1, 2, 3, 4, 5, 6}. En général en probabilité on se contente de prendre la tribu borélienne. À titre d'exemple la tribu borélienne pour le résultat d'un dé à 4 faces est donné (celle pour le dé à 6 faces est encore plus grande mais suit le même principe):
 : Cette mesure ou probabilité est la probabilité de réaliser l'un des éléments de
: Cette mesure ou probabilité est la probabilité de réaliser l'un des éléments de  . Cette probabilité est comprise entre 0 et 1 pour tous les éléments de
. Cette probabilité est comprise entre 0 et 1 pour tous les éléments de  , c'est lepremier axiome des probabilités. Par exemple pour un dé a 6 faces: la probabilité d'avoir {1} est 1/6, la probabilité de Ω={1, 2, 3, 4, 5, 6}, tirer n'importe laquelle des 6 faces, est 1 (ceci est aussi toujours le cas, c'est le deuxième axiome des probabilités), la probabilité de l'ensemble vide ø est 0. Ceci est toujours le cas, c'est également une conséquence des axiomes des probabilités.
, c'est lepremier axiome des probabilités. Par exemple pour un dé a 6 faces: la probabilité d'avoir {1} est 1/6, la probabilité de Ω={1, 2, 3, 4, 5, 6}, tirer n'importe laquelle des 6 faces, est 1 (ceci est aussi toujours le cas, c'est le deuxième axiome des probabilités), la probabilité de l'ensemble vide ø est 0. Ceci est toujours le cas, c'est également une conséquence des axiomes des probabilités.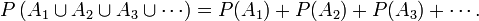
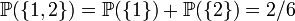
 , notamment dans la théorie des processus stochastiques. Par exemple pour l'étude du mouvement brownien, la probabilité est définie sur un espace de fonctions.
, notamment dans la théorie des processus stochastiques. Par exemple pour l'étude du mouvement brownien, la probabilité est définie sur un espace de fonctions.Lois de probabilité [modifier]
Convergence de variables aléatoires [modifier]
 converge en loi vers la variable aléatoire
converge en loi vers la variable aléatoire  si et seulement si la suite des mesures images
si et seulement si la suite des mesures images  converge étroitement vers la mesure image μX. En particulier dans le cas réel, il faut et il suffit que les fonctions de répartition convergent simplement vers la fonction de répartition de X en tout point de continuité de cette dernière.
converge étroitement vers la mesure image μX. En particulier dans le cas réel, il faut et il suffit que les fonctions de répartition convergent simplement vers la fonction de répartition de X en tout point de continuité de cette dernière. converge en probabilité vers
converge en probabilité vers  ssi
ssi  ,
,  . Cette convergence implique la convergence en loi.
. Cette convergence implique la convergence en loi. converge presque sûrement vers
converge presque sûrement vers  ssi
ssi  . Elle implique la convergence en probabilité, donc la convergence en loi.
. Elle implique la convergence en probabilité, donc la convergence en loi. :
:  converge dans
converge dans  vers
vers  ssi
ssi  . Elle implique aussi la convergence en probabilité.
. Elle implique aussi la convergence en probabilité.Le calcul stochastique [modifier]
Chaîne de Markov [modifier]

 est la probabilité d'avoir A quand on sait que l'on a B par exemple ici la probabilité d'avoir une certaine valeur pour Xn + 1 quand on connaît la valeur de Xn. L'identité ci-dessus est la propriété de Markov pour le cas particulier d'une chaîne en temps discret. La probabilité P(Xn + 1 = x | Xn = y) est appelée la probabilité de transition de x à y ; c'est la probabilité d'aller de x à y au temps n et a une importance particulière pour l'étude de ces chaînes. Nous considérons ici uniquement des chaînes de Markov en temps discret mais il faut savoir qu'il existe une généralisation en temps continu.
est la probabilité d'avoir A quand on sait que l'on a B par exemple ici la probabilité d'avoir une certaine valeur pour Xn + 1 quand on connaît la valeur de Xn. L'identité ci-dessus est la propriété de Markov pour le cas particulier d'une chaîne en temps discret. La probabilité P(Xn + 1 = x | Xn = y) est appelée la probabilité de transition de x à y ; c'est la probabilité d'aller de x à y au temps n et a une importance particulière pour l'étude de ces chaînes. Nous considérons ici uniquement des chaînes de Markov en temps discret mais il faut savoir qu'il existe une généralisation en temps continu.Équations différentielles stochastiques [modifier]


Voir aussi [modifier]
Articles connexes [modifier]
Liens externes [modifier]
22:52 Publié dans Théorie des probabilités | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
JOURNAL OF NONCOMMUTATIVE GEOMETRY
The Journal of Noncommutative Geometry covers the noncommutative world in all its aspects. It is devoted to publication of research articles which represent major advances in the area of noncommutative geometry and its applications to other fields of mathematics and theoretical physics. Topics covered include in particular: DOI: 10.4171/JNCG Source : http://www.ems-ph.org/journals/journal.php?jrn=jncgJOURNAL OF NONCOMMUTATIVE GEOMETRY
The Journal of Noncommutative Geometry is covered in:
Mathematical Reviews (MR), Current Mathematical Publications (CMP), MathSciNet, Zentralblatt für Mathematik, Zentralblatt MATH Database, Science Citation Index Expanded (SCIE), CompuMath Citation Index (CMCI), Current Contents/Physical, Chemical & Earth Sciences (CC/PC&ES), ISI Alerting Services, Journal Citation Reports/Science Edition, Web of Science.
22:46 Publié dans JOURNAL OF NONCOMMUTATIVE GEOMETRY | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Documents d'Alain Connes
Documents
Ouvrages
Derniers articles publiés
Anciens articles récemment mis à disposition
Liste exhaustive des articles à disposition
Articles de synthèse
Cours au Collège de France
Autres conférences
Documents divers
22:44 Publié dans Documents d'Alain Connes | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Szolem Mandelbrojt Collège de France
Professeurs disparus |
22:43 Publié dans Szolem Mandelbrojt, Szolem Mandelbrojt Collège de France | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook














































































 ; 10 000 pas.
; 10 000 pas.