20/11/2010
Algorithme d'Euclide
L'algorithme d'Euclide est un algorithme permettant de déterminer le plus grand commun diviseur (P.G.C.D.) de deux entiers dont on ne connaît pas la factorisation. Il est déjà décrit dans le livre VII des Éléments d'Euclide. Dans la tradition grecque, en comprenant un nombre entier comme une longueur, un couple d'entiers comme un rectangle, leur PGCD est la longueur du côté du plus grand carré permettant de carreler entièrement ce rectangle. L'algorithme décompose ce rectangle en carrés, de plus en plus petits, par divisions euclidiennes successives, de la longueur par la largeur, puis de la largeur par le reste, jusqu'à un reste nul. Dans le rectangle de dimensions L=21 par l=15 ci-dessous, par exemple, on peut glisser un carré de côté 15 mais il reste un rectangle de côtés 15 et 6, dans lequel on peut glisser deux carrés de côté 6 mais il reste un rectangle de côtés 6 et 3 que l'on peut carreler entièrement de carrés de côté 3. Les carrés de côté 6 ou 15 peuvent aussi se carreler en carrés de côté 3. Le rectangle entier peut se carreler en carrés de côté 3. Il n'existe pas de carré plus grand permettant un tel carrelage. Cet algorithme repose sur la structure d'anneau euclidien de l'anneau L'algorithme est effectif à condition de disposer d'un algorithme effectif de division euclidienne. La possibilité de disposer d'un tel algorithme rend de nombreux autres calculs effectifs, notamment, en algèbre linéaire, le calcul de facteurs invariants.Algorithme d'Euclide
 des entiers relatifs, plus particulièrement sur la propriété de division euclidienne. Il se généralise donc à bien d'autres anneaux, en particulier les anneaux de polynômes à coefficients dans un corps. L'algorithme se généralise pour permettre le calcul des coefficients de Bezout.
des entiers relatifs, plus particulièrement sur la propriété de division euclidienne. Il se généralise donc à bien d'autres anneaux, en particulier les anneaux de polynômes à coefficients dans un corps. L'algorithme se généralise pour permettre le calcul des coefficients de Bezout.
Sommaire[masquer] |
Puisque l'algorithme a pour objet le calcul d'un PGCD, il est possible de se restreindre aux entiers positifs, un PGCD de deux entiers relatifs étant égal au PGCD de leurs valeurs absolues. Soient deux entiers naturels a et b, dont on cherche le PGCD. Le cas où a ou b est nul ne nécessite aucun algorithme ; on l'exclut. Une suite d'entiers (an)n est définie par récurrence de pas 2, plus précisément par divisions euclidiennes successives ; la suite est initialisée par a0 = a, a1 = b, puis propagée par la règle de récurrence : tant que an+1 est non nul, an+2 est défini comme le reste de la division euclidienne de an par an+1. On commence donc par calculer le reste de la division de a par b, qu'on note r ; puis on remplace a par b, puis b par r, et on réapplique le procédé depuis le début. On obtient ainsi une suite, qui vaut 0 à un certain rang ; le PGCD cherché est le terme précédent de la suite. Il est intéressant de noter que si a < b, la première itération de la boucle a pour effet de "permuter a et b". Plus précisément : dans ce cas, la division euclidienne de a par b s'écrit a = b.0 + a donc a2 = a, si bien que la suite produite par l'algorithme appliqué au couple (a, b) commence par a, suivie de la suite produite par l'algorithme appliqué au couple (b, a). Calculons, par exemple, le PGCD de 1071 et de 1029 à l'aide de l'algorithme d'Euclide : 1071 = 1029 × 1 + 42 1029 = 42 × 24 + 21 42 = 21 × 2 + 0 Il faut prendre le dernier reste avant le zéro, donc PGCD(1071 ; 1029) = 21 Voici différents exemples d'implémentations de l'algorithme d'Euclide en programmation. Fonction PGCD(a:nombre, b:nombre):nombre ou sous forme condensée: ou en utilisant une boucle, sans rappeler la fonction dans elle-même (algorithme ressemblant plus à l'organigramme à flèche présent sur l'article): Au début, Euclide a formulé le problème de façon géométrique : comment trouver une « unité de mesure » commune pour deux longueurs de segments. Il procède par soustractions répétées de la longueur du plus court segment sur la longueur du plus long. Cela correspond à une adaptation de la méthode naïve de calcul de la division euclidienne, telle que décrite dans l'article consacré. La définition même de la suite (an) par division euclidienne montre que, pour tout n tel que an + 1 est non nul, il existe un entier qn + 2 tel que : avec de plus Soit N + 1 l'indice de ce dernier reste non nul. Il faut montrer que aN + 1 est bien le PGCD cherché. La relation précédente s'écrit donc ici aN + 1 est donc un diviseur commun de a et b que divise tout autre diviseur commun ; c'est bien le PGCD. Le théorème de Lamé stipule que le nombre d'étape de l'algorithme d'Euclide exécuté sur deux entiers est borné (supérieurement) par cinq fois le nombre de chiffres nécessaire à écrire (en base 10) le plus petit de ces deux entiers. On peut en fait être légèrement plus précis : le nombre d'étapes de l'algorithme d'Euclide exécuté sur deux entiers a et b, avec Comme le nombre de chiffres de l'écriture de b en base 10 est ln(b) / ln(10) et que la quantité De plus, cette majoration est la meilleure possible, puisqu'elle est atteinte quand a et b sont deux nombres de Fibonacci consécutifs. L'identité de Bézout assure l'existence de deux entiers u et v tels que : au + bv = aN + 1 = PGCD(a,b). L'algorithme d'Euclide convenablement adapté permet de calculer de tels coefficients. Pour cela, on introduit deux suites (un) et (vn) telles que pour tout n, on ait la relation : aun + bvn = an. Si de telles suites existent, les termes uN + 1,vN + 1 constitueront une paire de coefficients de Bezout pour a et b. On peut choisir u0 = 1,v0 = 0 puis u1 = 0,v1 = 1, puis la relation de récurrence de pas 2 entre les an montre : an + 2 = an − qn + 2an + 1 = aun + bvn − qn + 2(aun + 1 + bvn + 1) = a(un − qn + 2un + 1) + b(vn − qn + 2vn + 1) On peut ainsi définir (un) par la relation de récurrence de pas 2 : un + 2 = un − qn + 2un + 1 et l'initialisation précédente, et (vn) par vn + 2 = vn − qn + 2vn + 1 et l'initialisation précédente ; et on obtient bien la relation annoncée pour tout n. L'algorithme étendu s'implémente comme l'algorithme classique ; il suffit de rajouter des variables correspondant aux coefficients u et v à calculer, et de faire une multiplication et une soustraction supplémentaires, pour calculer chacun des deux nouveaux coefficients, à chaque étape. Les quotients successifs qui apparaissent quand l'algorithme d'Euclide est appliqué aux données a et b, sont précisément les nombres qui apparaissent dans la représentation sous forme de fraction continue de a/b. Considérons l'exemple de a = 1071 et b = 1029 utilisé ci-dessus. Voici le calcul avec les quotients soulignés (successivement 1, 24 et 2): De cela on tire : Dans l'égalité précédente, le second membre s'appelle la fraction continue ou continuée du quotient 1071/1029. On peut en déduire les 3 approximations suivantes de la fraction, classées par ordre de précision croissante : Cette méthode peut également être utilisée pour des nombres réels a et b ; comme dans le cas de deux entiers, la suite de quotients calculés représente la « décomposition en fraction continue » de a/b et fournit une suite d'approximations successives, de qualité croissante, du quotient a/b. Dans le cas où ce quotient est irrationnel, l'algorithme d'Euclide ne se termine pas et la suite des approximations obtenues est donc elle-même infinie ! nota : La décomposition en fraction continuée (et la série d'approximations successives correspondante) peut être appliquée, non seulement à un nombre réel quelconque, mais également à une fonction : cette démarche consiste à rechercher les approximants de Padé, dont on peut définir le principe comme suit : Au voisinage d'un point, le développement ensérie de Taylor d'une fonction donnée fournit un polynôme qui réalise une approximation de la fonction. Mais on peut également chercher une fraction rationnelle qui satisfasse les mêmes conditions que la partie polynomiale du développement de Taylor : l'égalité des dérivées de la fonction et de son approximation, jusqu'à un certain ordre donné. La comparaison de ces deux types de développements permet de très intéressants développements, comme la démonstration de l'irrationalité de ζ(3).Remarque préliminaire [modifier]
Description de l'algorithme [modifier]
Exemple [modifier]
Exemples d'implémentations [modifier]
Pseudocode [modifier]
Si b=0 alors
| Retourner a
Sinon
| r egal au reste de la division entière (modulo) de a par b
| Retourner PGCD(b, r)
Python [modifier]
def PGCD(a, b):
if b == 0:
return a
else:
return PGCD(b, a % b)
C [modifier]
int PGCD(int a, int b)
{
if (b == 0)
return a;
else
return PGCD(b, a % b);
}
int PGCD(int a, int b)
{
return (b) ? PGCD(b, a%b) : a;
}
int PGCD(int a, int b)
{
int r;
while ((r = a % b) != 0)
{
a = b;
b = r;
}
return b;
}
Remarque historique [modifier]
Démonstration de sa finitude et de son exactitude [modifier]

 . La suite d'entiers naturels (an) est donc strictement décroissante à partir du rang 1, et donc vaut 0 à un certain rang. L'existence d'un dernier reste non nul est ainsi établie.
. La suite d'entiers naturels (an) est donc strictement décroissante à partir du rang 1, et donc vaut 0 à un certain rang. L'existence d'un dernier reste non nul est ainsi établie.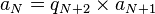 , qui montre que aN+ 1 divise aN. Écrivant ensuite
, qui montre que aN+ 1 divise aN. Écrivant ensuite  , on en déduit que aN + 1 divise aussi aN − 1 ; puis, de même, et par récurrence, que aN + 1 divise tous les termes de la suite an ; en particulier les premiers termes a et b. aN + 1 est donc bien un diviseur commun de a et b. Réciproquement, tout diviseur commun de a et b divisera aussi
, on en déduit que aN + 1 divise aussi aN − 1 ; puis, de même, et par récurrence, que aN + 1 divise tous les termes de la suite an ; en particulier les premiers termes a et b. aN + 1 est donc bien un diviseur commun de a et b. Réciproquement, tout diviseur commun de a et b divisera aussi 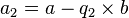 , et à nouveau par récurrence, divisera tous les termes de la suite (an) ; donc en particulier aN + 1.
, et à nouveau par récurrence, divisera tous les termes de la suite (an) ; donc en particulier aN + 1.Le théorème de Lamé [modifier]
 , est borné par la partie entière de
, est borné par la partie entière de  , où ln désigne le logarithme naturel et
, où ln désigne le logarithme naturel et  est le nombre d'or.
est le nombre d'or. est inférieure à 5 (elle vaut environ 4,78497), on retrouve bien le théorème de Lamé.
est inférieure à 5 (elle vaut environ 4,78497), on retrouve bien le théorème de Lamé.Algorithme étendu aux coefficients de Bézout [modifier]
Description [modifier]
Commentaires [modifier]
Fractions continues [modifier]
 .
.
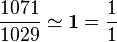
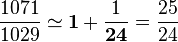

Voir aussi [modifier]
Liens externes [modifier]
09:33 Publié dans Algorithme d'Euclide | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook










































Les commentaires sont fermés.