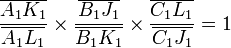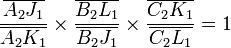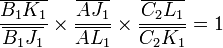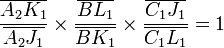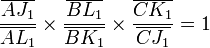08/12/2010
Droite (mathématiques)
Droite (mathématiques)
![]() Pour les articles homonymes, voir Droite.
Pour les articles homonymes, voir Droite.
|
|
Cet article ou cette section concernant les mathématiques doit être recyclé.
Une réorganisation et une clarification du contenu est nécessaire. Discutez des points à améliorer en page de discussion.
|
Pour les Anciens, la droite, en mathématiques et surtout en géométrie, était un objet allant de soi, si évident que l'on négligeait de préciser de quoi l'on parlait. L'un des premiers à formaliser la notion de droite fut le Grec Euclide dans ses Éléments. Avec le développement du calcul algébrique et du calcul vectoriel, d'autres définitions vinrent s'ajouter. Mais c'est la naissance des géométries non euclidiennes qui a conduit à la découverte de nouveaux types de droites, et, par là-même, nous a forcés à éclaircir et approfondir ce concept.
Sommaire[masquer] |
« La ligne droite est le plus court chemin pour aller d'un point à un autre »1. Cette définition simple suffit à certaines applications concrètes. Elle permet par exemple au jardinier de tracer ses lignes de semis : en tendant une corde entre deux piquets, il matérialise une ligne tirée au cordeau. Une autre image habituelle est celle du fil à plomb1. C'est-à-dire, dans les deux cas, un fil tendu dont on néglige l'épaisseur. Cette définition est celle d'un segment. Une droite, à la différence d'un segment, est illimitée des deux côtés. Différentes limitations de cette définition ont conduit les mathématiciens à lui en préférer d'autres. Par exemple, si on assimilie la Terre à une sphère, le chemin le plus court entre deux points n'est plus une ligne droite, mais un arc de cercle. Cependant, à l'échelle d'un être humain, ce cercle est si grand qu'une ligne droite en est une bonne approximation2. La notion de « chemin le plus court » est étudiée sous le nom de géodésique. Dans ses éléments, Euclide définit les objets relevant de la géométrie (point, droite, plan, angle) et leur affecte un certain nombre de propriétés (postulats). À l'aide de ces éléments de base, il essaie de construire, par des démonstrations rigoureuses, l'ensemble des autres propriétés. Pour Euclide : Il part d'une droite finie qu'il définit comme un segment. Il a besoin d'un postulat pour la prolonger au-delà de ses extrémités, d'un autre pour en prouver l'existence (Par deux points distincts passe une droite) et d'un autre appelé le cinquième postulat d'Euclide pour traiter des positions relatives des droites ( Si une droite coupe deux autres droites, de telle façon que la somme des angles intérieurs du même côté soit plus petite que deux droits, ces droites, prolongées à l'infini, se rencontreront du côté où les angles sont plus petits que deux droits.) dont plusieurs versions équivalentes peuvent être données. L'approche d'Euclide est féconde, elle permet de démontrer de nombreux théorèmes considérés comme élémentaires au regard des mathématiques au sens moderne du terme. On peut citer le théorème de Thalès, le théorème de Pythagore ou encore le problème de Napoléon. La définition axiomatique d'Euclide apparait trop pauvre pour résoudre plusieurs familles de problèmes. On peut citer historiquement ceux associés à la construction à la règle et au compas, par exemple la trisection de l'angle, la duplication du cube ou encore la construction d'un polygone régulier. Une approche algébrique est utilisée pour pallier cette faiblesse. À l'aide de la notion de polynôme cyclotomique, Gauss réalise une percée majeure dans ce domaine en 1801 qu'il publie dans son livre Disquisitiones arithmeticae. Les progrès de la physique engendrent une nouvelle branche des mathématiques, initialement appelée calcul infinitésimal et maintenant calcul différentiel. Elle obtient comme premier succès la compréhension de la mécanique céleste. Une fois encore, la modélisation d'Euclide est insuffisante pour formaliser convenablement ce domaine. Une nouvelle construction est alors proposée, elle se fonde sur des structures algébriques. Les groupes abéliens et les corps sont utilisées pour définir un espace vectoriel puis unespace affine. En géométrie vectorielle, une droite est un sous-espace vectoriel de dimension 1. On peut la nommer également droite vectorielle. Si v est un vecteur non nul, la droite vectorielle engendrée par v est l'ensemble des vecteurs w pour lesquels il existe un scalaire (un réel pour un espace vectoriel sur R) k tel que w = kv. On dit alors que les vecteurs v et w sont colinéaires. En géométrie affine, une droite est un sous-espace affine de dimension 1. Si A est un point et v un vecteur non nul, la droite affine engendrée par A et v est l'ensemble des points M pour lesquels il existe un scalaire k tel que On peut aussi définir la droite passant par les points distincts A et B comme l'ensemble des barycentres des points A et B. La notion de droite est alors largement généralisée. L'espace vectoriel peut être un ensemble fini comme pour les codes linéaires utilisés dans la théorie de l'information, ou enarithmétique. Une droite est alors elle aussi un ensemble fini de points. L'espace vectoriel peut être une extension de corps comme dans le cadre de la théorie de Galois, l'ensemble desnombres rationnels dans le corps des réels possède les propriétés géométrique d'une droite. En analyse, et particulièrement en analyse fonctionnelle une droite est un ensemble de fonctions. Par exemple les primitives d'une fonction continue réelle de la variable réelle forment une droite. L'approche algébrique permet d'enrichir très largement la géométrie et offre des réponses satisfaisantes à bon nombre de problèmes. En revanche une vielle conjecture reste ouverte : comment démontrer le cinquième postulat d'Euclide. Proclos l'exprime de la manière suivante: Dans un plan, par un point distinct d'une droite d, il existe une unique droite parallèle à d. Déjà, les grecs savaient qu'une sphère semble pouvoir définir une géométrie, les droites seraient alors les grands cercles de la sphère. En revanche, la connexion entre une sphère et la définition d'une géométrie reste à cette époque hors de portée. David Hilbert apporte un élément de réponse. La construction d'Euclide n'est pas entièrement rigoureuse. Il manque en effet, quinze axiomes pour bâtir les fondements d'un système logique à même de supporter la géométrie euclidienne. Une telle formalisation existe, on parle par exemple d'axiomes de Hilbert. La réponse à la question que pose le cinquième postulat est donc de l'ordre de la logique. La base axiomatique d'Euclide constituée des quatre premiers postulats est trop faible pour garantir le cinquième. Si l'approche de Hilbert permet de résoudre cette question, elle est peu opérationnelle pour bâtir la théorie de la géométrie euclidienne. On utilise en général la base axiomatique dePeano pour construire l'ensemble des entiers naturels puis les différentes structures algébriques utilisées. L'intérêt des travaux de Hilbert sur cette question est donc surtout de l'ordre de la logique et peu géométrique. Bien avant de comprendre la dimension logique de la problématique et dans le courant du XIXe, sont nées d'autres géométries dans lesquelles la droite n'avait plus les mêmes propriétés que dans la géométrie euclidienne : les géométries non euclidiennes. En géométrie projective, des droites parallèles se coupent en un point impropre et par deux points ne passe qu'une seule droite. En géométrie hyperbolique, par un point donné, non situé sur une droite donnée, il passe au moins deux droites qui ne coupent pas la droite donnée. En géométrie elliptique, deux droites sont toujours sécantes. Un exemple classique de géométrie elliptique est la géométrie sur une sphère où le plus court chemin pour aller d'un point à un autre est une partie d'un grand cercle. Une droite est alors définie comme un grand cercle. Deux droites distinctes se coupent alors en deux points diamétralement opposés qui n'en forment qu'un pour cette géométrie. On retrouve la propriété : par deux points distincts passe une seule droite. De plus on peut aussi définir une droite comme un cercle de rayon infini. Cette définition est incompatible avec celle issue de l'algèbre linéaire. Dans ce contexte, on parle en général de géodésique pour éviter une confusion. Si l'espace vectoriel est muni d'une base, ou l'espace affine d'un repère, la droite peut être caractérisée par des équations. Une droite affine est l'ensemble des points M de coordonnées (x ; y) tels que Dans cette famille de droites, on rencontre m représente la pente de la droite. En dimension n, la droite passant par Ce système d'équations s'appelle un système d'équations paramétrées de la droite. Cas particulier de l'espace (dimension 3), en :Point de vue concret [modifier]
L'approche d'Euclide [modifier]
Définition formelle [modifier]
Applications [modifier]
Approche algébrique [modifier]
Motivations [modifier]
Géométrie vectorielle [modifier]
Géométrie affine [modifier]
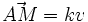 . Le vecteur v est appelé vecteur directeur de la droite.
. Le vecteur v est appelé vecteur directeur de la droite.Applications [modifier]
Logique et géométrie [modifier]
Motivation [modifier]
Rôle de Hilbert [modifier]
Géométries non euclidiennes [modifier]
Géométrie analytique [modifier]
Espace affine de dimension 2 [modifier]
 , où
, où  . Un vecteur directeur de la droite est le vecteur de coordonnées ( − b;a). L'équation précédente est appelée équation cartésienne de la droite.
. Un vecteur directeur de la droite est le vecteur de coordonnées ( − b;a). L'équation précédente est appelée équation cartésienne de la droite.
Espace affine de dimension n [modifier]
 et de vecteur
et de vecteur  est l'ensemble des points
est l'ensemble des points  pour lesquels il existe un scalaire k tel que
pour lesquels il existe un scalaire k tel que
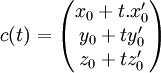
Annexes [modifier]
Articles connexes [modifier]
Bibliographie [modifier]
Notes et références [modifier]
08:20 Publié dans Droite (mathématiques) | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
La quatrième relation
On peut aujourd'hui munir la géométrie du symbolisme spécifique cherché par Leibniz. Et ce symbolisme nous montre que la géométrie euclidienne repose sur quatre relations inséparables. Or de ces quatre relations nous continuons, vingt cinq siècles après Euclide, à n'en comprendre que trois ! Un sujet de réflexion aussi inédit que curieux.
Présentation Leibniz pensait que lorsque on saurait trouver une écriture opératoire pour les figures de la Géométrie, elle constituerait un Art d'Inventer comparable à celui qui venait de se produire dans l'Algèbre grâce à l'introduction par Viète d'une écriture opératoire pour les équations. Or ce projet qui fut jugé utopique autrefois peut être réalisé aujourd'hui. Il est présenté sur ce site avec les nouvelles perspectives qu'il ouvre effectivement pour la géométrie. Le contexte historique En 1591 Viète publie l'Isagoge. Dans ce livre il montre qu'il est possible en algèbre de calculer avec les lettres exactement comme on calculait auparavant avec les nombres. L'introduction de ce symbolisme marque une véritable révolution en mathématique. Là où Diophante est obligé d'énoncer « Partager un nombre donné tel que 100 par exemple en deux nombres dont la différence est donnée telle que 40 par exemple », il suffit dorénavant de dire : « Résoudre le système x+y=100 et x-y=40 ». De plus il permet de traiter directement la forme générale qui est « Résoudre le système x+y=a et x-y=b ». Les avantages du symbolisme ainsi introduit sont donc considérables. Ils viennent de ce que les énoncés rhétoriques d'antan ont été remplacés par une écriture opérationnelle à la fois réductrice et visuelle. Le livre a un grand succès et très rapidement l'algèbre prend un essor fulgurant. Chacun tient à cœur d'y apporter des améliorations. Par exemple Descartes est le premier à affecter les notations x et y aux inconnues. Dans la foulée il montre aussi que les droites, les cercles et autres lignes mathématiques peuvent être elles aussi représentées par des équations et c'est le début de l'analytique. Leibniz [1646–1716] apporte lui aussi sa contribution à l'édifice en posant les bases du calcul différentiel. Mais il a un projet beaucoup plus ambitieux qui est de trouver pour la géométrie la même écriture opératoire que celle que Viète vient de proposer pour l'algèbre, car il pense que l'analytique de Descartes n'est pas la bonne approche. Il donne à sa recherche le nom d'Analysis Situs. Par les descriptions extrêmement précises qu'il en fait dans ses notes nous comprenons à présent que cette écriture devait tenir à la fois des vecteurs et des complexes (voir la Note1). Mais en l'absence de ces connaissances indispensables il ne put pas mener son projet à bien. L'audace de Descartes autrefois L'introduction du symbolisme introduit par Viète permet alors une découverte qui est fondamentale. Dans son ouvrage La Géométrie publié en 1637 Descartes écrit "Il faut que je dise quelque chose sur la nature des équations" et il compare les deux équations (x-2)(x-3)(x-4)=0 et (x-2)(x-3)(x-4)(x+5)=0. Or comme à cette époque les nombres négatifs n'existent pas encore il est obligé d'admettre que ces deux équations différentes admettent pourtant les mêmes racines. Cette disparité qui n'était pas visuelle tant que les nouvelles notations n'avaient pas été introduites, devient désormais inacceptable et Descartes prend la décision de dire qu'il considère la seconde équation comme « une équation dans laquelle il y a quatre racines, à savoir trois vraies qui sont 2,3,4 et une fausse qui est 5 », et par la suite il traite absolument de la même façon les racines vraies et les racines fausses (Voir la Note2 ). C'est une innovation absolument remarquable car à cette époque elle va à l'encontre du sens commun. Elle consiste finalement à dire que parmi les quatre sommes u+v, u-v, v+u et v-u que l'on peut écrire avec deux nombres naturels u et v, où pour fixer les idées on suppose u>v, la quatrième doit être aussi bien acceptée que les trois autres. Or ce faisant il se met à dos toute la communauté mathématique. Comment peut on imaginer un segment qui ait la longueur fausse 5 ? Et puisque x+5=0 c'est à dire x=0-5 comment peut on imaginer qu'on puisse enlever 5 à 0 ? Plusieurs années après, en 1670, Pascal, dans les Pensées écrit ironiquement « Trop de vérité nous étonne. J'en sais qui ne peuvent comprendre que, qui de zéro ôte quatre, reste zéro ». (Voir la Note3 ) Et cette opposition se poursuit longtemps encore puisque en 1806 le grand mathématicien Carnot s'élève toujours contre cette possibilité. Dans un mémoire écrit à cette date il insère une Digression sur la Nature des Quantités dites Négatives où il écrit : « Il y a des personnes qui regardent les quantités négatives isolées comme moindre que 0; mais cette opinion ne paraît nullement soutenable; car pour obtenir une pareille quantité, il faudrait pouvoir ôter quelque chose de rien, ce qui est absurde . » Et plus loin il trouve complètement farfelu que le produit de deux nombres moins que rien tels -4 et -5 puisse ensuite être supérieur à celui des deux nombres 2 et 3 qui leur sont pourtant supérieurs. (Voir la Note4 ) Maintenant que nous avons le recul nécessaire, nous savons comme l'innovation de Descartes fut fructueuse. En effet elle ouvrait la voie à toutes les extensions qui suivirent, celle des réels, puis des complexes, puis des quaternions.., extensions qui devinrent les fondements de toutes les merveilleuses mathématiques que nous avons aujourd'hui. Or par les réticences que cette innovation rencontra non seulement au début, mais aussi sur de nombreuses années, nous mesurons l'audace de Descartes qui, pour une simple raison d'harmonie, eut le courage d'aller à l'encontre de ce "trop de vérité" que lui reprocha Pascal. Le conservatisme des mathématiciens d'aujourd'hui. Les développements que nous allons présenter dans les pages suivantes vont être d'une ressemblance étonnante avec l'exemple précédent. Le symbolisme introduit par Viète permettait d'écrire les équations de l'algèbre au lieu de les présenter sous la forme rhétorique qu'elles avaient avant lui. Pareillement le symbolisme que nous allons proposer va permettre d'écrire les figures de la géométrie au lieu de les décrire rhétoriquement comme le faisait Euclide il y a 25 siècles ... et comme le font encore les collégiens d'aujourd'hui, stagnation tout à fait unique dans l'histoire de la science .(voir Note 5) Mais surtout, par la visualisation simplificatrice qu'il donnait dorénavant aux opérations de l'algèbre, le symbolisme de Viète fit apparaître dans nos calculs sur les nombres cette anomalie que Descartes trouva inacceptable, et qui consistait à dire que sur les quatre sommes u+v, u-v, v+u et v-u seules les trois premières avaient un sens. Pareillement la visualisation simplificatrice de notre symbolisme permettra d'écrire les relations fondamentales de la géométrie sous la forme de quatre égalités de même premier membre où les seconds membres seront (u,v), (u,-v), (v,u) et (v,-u), et nous poserons qu'il est inacceptable de dire que seules les trois premières ont un sens. L'analogie continue malheureusement pour l'étape suivante. Comme on l'a vu les nombres négatifs furent d'emblée considérés autrefois comme absurdes car on ne leur trouvait pas de signification quand on essayait de les traduire avec les nombres alors connus. Et pareillement la quatrième relation qui va apparaître dans la géométrie euclidienne est aussi considérée comme absurde par les mathématiciens d'aujourd'hui car pour le moment on ne lui trouve pas de signification quand nous essayons de la traduire avec les nombres que nous connaissons. Dans les pages suivantes nous allons donc montrer ce qu'aurait probablement été ce symbolisme auquel Leibniz aspirait. Sa validité n'est pas mise en cause comme le montre par exemple la citation ci dessus d'une correspondance de Monsieur Kahane, membre de la section mathématique de l'Académie des Sciences. Ensuite la quatrième relation que les notations introduites sont les seules à faire apparaître nous place sur le seuil d'une extension prometteuse pour la géométrie euclidienne. Mais il reste à trouver le grand nom qui aura l'autorité et surtout l'audace de Descartes pour oser franchir ce seuil, et il n'y en a pas encore eu pour le moment. Raymond Pouzergues Notes (1) Les lecteurs intéressés par ces conceptions de Leibniz pourront les lire dans l'excellent ouvrage de Louis Couturat "La Logique de Leibniz " consultable sur Gallica [cliquer ici]. On y trouve son rejet de l'analytique car "la géométrie analytique n'exprime les faits géométriques que d'une manière détournée et compliquée " [p399], son ambition que l' écriture des figures à laquelle il aspire permette de calculer de façon qu'on puisse "exprimer par ce calcul toute la nature et la définition de la figure " [p392], la forme que doit avoir cette écriture telle que "dans le calcul géométrique les lettres ou symboles quelconques ne représentent plus des grandeurs ni des nombres comme en algèbre mais des points et des combinaisons de points " [p 410] et enfin son pressentiment des nombres complexes identifiables comme on le sait avec les similitudes du plan puisque " la théorie de la similitude est par suite le fondement de la véritable analyse de situation" [p411] (2) On peut consulter le texte entier au Livre III de son oeuvre: La Géométrie dont malheureusement on ne peut pas trouver le texte intégral sur Gallica. (3) On trouve cette citation dans les Pensées de Pascal l'Homme sans Dieu Chapitre I [La pléiade p 1109] (4) Le texte complet de cette Digression sur la Nature des Quantités dites Négatives se trouve dans Mémoire de Carnot [ cliquer ici ] à partir de la page 96. Il est vraiment surprenant. (5) Le véritable essor de chacune de nos connaissances se fait à partir du moment où nous lui trouvons une écriture dédiée. Ce fut non seulement le cas pour l'algèbre, l'analyse et de nombreuses autres branches des mathématiques, mais aussi pour les relations de la physique, les formules de la chimie et même les partitions de la musique. Or nous n'avons jamais franchi le pas en géométrie. En effet lorsque on lit un énoncé rhétorique tel que " Si une sécante rencontre deux autres droites en faisant des angles alternes-internes égaux alors ces deux droites sont paralléles" [Euclide- proposition 27 du Livre I], force nous est de constater qu'on peut le trouver encore tel quel dans le livre de n'importe lequel de nos collégiens d'aujourd'hui. Cette stagnation dans ce qui est probablement la plus ancienne de nos connaissances est tout à fait surprenant, et ce qui est plus surprenant encore c'est que Leibniz semble avoir été le seul dans l'histoire des mathématiques à en prendre conscience.
Les bivecteurs Dans cette page nous allons montrer ce qu'aurait probablement été l'Analysis Situs de Leibniz s'il avait réussi à la mettre au point. Nous nous contenterons d'une description générale qui suffira à en donner un aperçu. L'intuition de Leibniz était qu'il fallait d'abord disposer d'un outil qui prenne en compte non seulement la longueur comme le fait le segment, mais aussi la situation c'est à dire la direction et le sens. Il anticipait ainsi le vecteur dont la théorie allait être élaborée au XIX° siècle. Nous la supposerons connue. Rappelons qu'un même vecteur v est représenté par l'ensemble des flèches de même longueur, de même direction et de même sens. Comme nous allons principalement travailler avec eux les notations telles que AB, CD….désigneront toujours des vecteurs. Dans les autres cas nous expliciterons cas par cas les ensembles eux aussi définissables par deux points en mentionnant par exemple : soit la droite AB, soit le segment AB, soit la longueur AB, soit le diamètre AB, etc etc. Ensuite l'intuition de Leibniz était de fonder son Analysis Situs sur la similitude. Par suite nous conviendrons Si ( AB,AC)=(A'B',A'C') cela signifie que c'est la même similitude directe qui fait passer de AB à AC et de A'B' à A'C'. On dit alors que les triangles ABC et A'B'C' sont directement semblables. Et si (AB,AC)=)A'B',A'C'( c'est que les similitudes qui font passer de AB à AC et de A'B' à A'C' sont inverses l'une de l'autre. On dit alors que les triangles ABC et A'B'C' sont inversement semblables. Ces notations purement géométriques auraient effectivement pu être trouvées par Leibniz et elles respectent bien sa volonté que « …les lettres ou symboles quelconques ne représenteront plus des grandeurs ni des nombres comme en algèbre, mais des points et des combinaisons de points ». Alors iI est remarquable de constater qu'elles suffisent pour pouvoir retrouver tous les résultats de la géométrie euclidienne. _________________________________ Egalités des bivecteurs Nous appellerons bivecteurs ces couples de vecteurs. En se basant sur les propriétés des triangles semblables auxquels ils sont associés il est possible de donner les propriétés de toutes les égalités qu'ils permettent d'écrire. Mais aujourd'hui nous disposons d'un moyen beaucoup plus commode en identifiant chaque vecteur à son affixe complexe. Ainsi si u, v, u', v' sont respectivement des vecteurs ou bien les affixes complexes des vecteurs OA,OB,OA',OB' alors l'égalité (OA,OB)=(OA',OB') c'est à dire (u,v)=(u',v') correspond tout simplement à l'égalité complexe des rapports v/u=v'/u'. Les triangles OAB et OA'B' sont directement semblables. Et de même l'égalité (OA,OB)=)OA',OB'( c'est à dire (u,v)=)u',v'( correspond à l'égalité du rapport v/u avec le conjugué du rapport v'/u'. Et cette fois ci les triangles OAB et OA'B' sont dits inversement semblables. Nous conserverons la même appellation que pour les complexes en disant que le bivecteur )u,v( est le conjugué du bivecteur (u,v). Addition des bivecteurs L'ensemble des bivecteurs peut être muni d'une addition par la convention suivante: (u,v) + (u',v') = (OA,OB)+(OA',OB') = (OA,OB)+(OB,OC)= (OA,OC) c'est la relation que nous appelons en France relation de Chasles c'est à dire (u,v) + (v,w) = (u,w) qui, avec les nombres complexes s'écrit (v/u).(w/v) = w/u - cette addition donne à l'ensemble des bivecteurs une structure de groupe commutatif d'élément neutre le bivecteur nul (u,u)=0 - comme (u,v)+(v,u)=(u,u)=0 le bivecteur (v,u) est l'opposé du bivecteur (u,v). Propriétés des bivecteurs La correspondance avec les rapports de nombres complexes permet d'obtenir directement toutes les propriétés nécessaires dans les calculs utilisant les bivecteurs. Signalons en quelques unes: - On a (-u,-v)=(u,v) et (-u,v)=(u,-v) ce qui permet de convenir d'une forme canonique pour les bivecteurs en ne les faisant jamais commencer par un vecteur précédé du signe -. - Si (u,v)=(u',v') alors (u,u')=(v,v') ou bien (v,u)=(v',u') ou bien …. - Quel que soit un nombre k réel alors (u,v) = (ku,kv) - Quels que soient k et h alors (u,v) = (u',v') donne (u,v) = (ku+hu',kv+hv') - Quels que soient les réels k,h,p,q alors (u,v) = )u',v'( donne (ku+hv,pu+qv) = )ku'+hv',pu'+qv'( et ainsi de suite. ... Nous dirons que les égalités de la forme (u,v)=)u',v'( sont des égalités mixtes. Elles vont jouer un rôle prépondérant car elles font intervenir la symétrie cette relation à laquelle les chercheurs, à travers la chiralité, accordent une grande importance pour la compréhension de notre univers. Les trois relations fondamentales De la même façon que l'étude des nombres commence par la considération de ceux qui sont les plus simples, nous allons chercher quelles sont les égalités mixtes les plus simples qu'il est possible d'écrire. Pour être non triviales elles doivent évidemment comprendre au moins deux vecteurs. En tenant compte de la forme canonique et des équivalences posées au paragraphe précédent on obtient alors quatre et seulement quatre relations qui sont (u,v)=)u,v( ; (u,v)=)v,u( ; (u,v)=)u,-v( et enfin (u,v)=)v,-u( L'égalité (u,v)=)u,v( impose que le complexe v/u soit égal à son conjugué c'est-à-dire que ce rapport soit réel. Par suite si (u,v)=)u,v( alors les vecteurs u et v sont colinéaires. L'égalité (u,v)=)v,u( impose que le produit de v par son conjugué soit égal au produit de u par son conjugué, c'est-à-dire que leurs normes sont égales. Par suite si (u,v)=)v,u( alors les vecteurs u et v sont isométriques. L'égalité (u,v)=)u,-v( impose que le complexe v/u soit opposé à son conjugué, c'est-à-dire que ce rapport soit un imaginaire pur. Par suite si (u,v)=)u,-v( alors les vecteurs u et v sont orthogonaux. Si nous laissons pour le moment de coté la quatrième relation qui sera traitée à la page suivante nous observons que les trois égalités mixtes les plus simples que nous pouvons écrire avec les bivecteurs correspondent justement aux relations qu'Euclide a donné pour bases à la géométrie euclidienne. Les trois relations fondamentales L'axiomatisation d'Euclide manquait de rigueur. En 1930 David Hilbert a fait paraître la dernière version d'un livre qui fait autorité en la matière "Les Fondements de la Géométrie" dans lequel il montre que celle-ci est toute entière déterminée par la seule donnée de 21 axiomes. Il les répartit en axiomes d'appartenance, d'ordre, de continuité et enfin seulement trois axiomes relationnels : le parallélisme des droites, la congruence des segments et la congruence des angles. Mais comme il ne se sert de cette dernière que pour démontrer les cas d'égalité des triangles quelconques, il aurait pu la remplacer par la relation de perpendicularité, puis s'en servir pour démontrer les cas d'égalité des triangles rectangles et passer ensuite aux triangles quelconques. Ainsi il est indifférent de remplacer la relation concernant la congruence des angles par la relation de perpendicularité.
Ainsi, au contraire d'Euclide et de Hilbert qui se sont seulement laissés guider par l'intuition, c'est par une démarche systématique que les bivecteurs font apparaître les trois relations fondamentales de la géométrie. Ensuite, de même qu'en arithmétique les chiffres permettent d'écrire tous les nombres, ces relations fondamentales vont nous permettre d'écrire toutes les figures de la géométrie. Par exemple l'ensemble des points M situés sur la droite passant par les deux points distincts A et B est défini par la relation (MA,MB)=)MA,MB(, et l'ensemble des points du plan situés sur le cercle de diamètre AB est défini par la relation (MA,MB)=)MA,BM( ces deux relations pouvant d'ailleurs prendre de multiples formes différentes. Enfin une écriture opératoire pour les figures de la géométrie. Les bivecteurs permettent " d'écrire " les figures élémentaires de la géométrie au lieu de les décrire rhétoriquement comme nous le faisons encore maintenant et ce depuis Euclide en énonçant par exemple " On appelle triangle isocèle ABC de sommet A un triangle tel que ....". Dorénavant: le triangle isocèle ABC de sommet A s'écrit (AB,AC)=)AC,AB( le triangle rectangle ABC de sommet A s'écrit (AB,AC)=)AB,CA( le triangle équilatéral ABC s'écrit (AB,AC)=(BC,BA) le triangle rectangle isocèle de sommet A s'écrit (AB,AC)=(AC,BA) le quadrangle harmonique ABCD s'écrit ( AC,DA)=(BC,BD) ........... Ensuite, de même que tous les nombres peuvent s'écrire à l'aide d'un ou de plusieurs chiffres, toutes les figures de la géométrie pourront s'écrire à l'aide d'une ou de plusieurs relations. Et si on convient d'appeler figures élémentaires celles qui s'écrivent au moyen d'une seule relation, on peut s'apercevoir que leur nombre est déjà assez conséquent puisqu'il résulte, en exceptant les vecteurs nuls, de toutes les combinaisons qu'il est possible d'écrire avec huit lettres différentes ou non dans des égalités mixtes ou non. Le grand intérêt de cette notation est évidemment que chaque "écriture" est non seulement succinte mais que pourtant elle contient en elle-même l'ensemble des propriétés de la figure qu'elle définit. Par exemple l'écriture textuelle « quadrangle harmonique » contient 20 lettres et ne nous donne aucune information sur la figure qu'elle désigne, à part que c'est un quadrangle. Il nous faut donc "apprendre" ces propriétés si nous voulons les connaitre. Par contre l'écriture (AC,DA)=(BC,BD) ne contient que 8 lettres et, malgré cette concision, en appliquant les règles de calculs sur les bivecteurs, on peut en déduire absolument toutes les propriétés du quadrangle harmonique. Donnons un exemple. Soit I le milieu de AB alors: (AC,DA) = (BC,BD) = (AC+BC,BD+DA) = (2 IC,BA) = ( 2 IC, 2 IA) = (IC, IA) de même : (AC,DA) = (BC,BD) = (AC-BC, DA-BD) = (AB,2 DI ) = (2 AI, 2 DI) = (AI,DI) = (IA,ID) Il en résulte que les trois triangles BCD, IAD, et ICA sont directement semblables d'où plusieurs propriétés concernant les angles et les longueurs de la figure. Par exemple en considérant la proportionnalité des cotés on en déduit: Dans un quadrangle harmonique les produits des cotés opposés sont égaux. ou encore Dans un quadrangle harmonique le produit des diagonales est égal au demi produit des cotés. ou encore puisque (AC,DA)=(BC,BD) est équivalent à )AC,DA(=)BC,BD( par soustraction membres à membres on obtient (AC,DA)-)AC,DA(=(BC,BD)-)BC,BD( c'est à dire: (AC,AD) - )AC,AD( = (BC,BD) - )BC,BD( il est facile de voir que cette relation permet d'énoncer: Dans un quadrangle harmonique les quatre sommets sont sur un même cercle etc etc . Conclusion Si Leibniz avait pu mettre son Analysis Situs au point il est probable que leur pratique ultérieure aurait évidemment introduit à la longue de nombreux raccourcis de démonstrations. Il est d'ores et déjà facile d'en trouver quelques uns. Mais ce n'est pas le but ici. En fait ses espérances étaient beaucoup plus ambitieuses. En effet en plus d'une approche complètement différente de la géométrie, et d'une écriture fonctionnelle de ses figures, il considérait que son Analysis Situs devait surtout être un Art d'Inventer, c'est à dire permettre des découvertes impossibles avec les autres approches. C'est ce que nous allons voir dans la page suivante.
l'Anoptrie Apparition de l'Anoptrie. Dans la page précédente, en cherchant quelles sont les égalités mixtes les plus simples qu'il soit possible d'écrire, nous avons vu qu'on obtient quatre et seulement quatre relations qui sont (u,v)=)u,v( ; (u,v)=)v,u( ; (u,v)=)u,-v( et enfin (u,v)=)v,-u(. Nous ne nous sommes intéressés qu'aux trois premières. Si nous explicitons la quatrième relation avec les complexes elle se traduit par ||u||²+||v||²=0 . Par suite nous trouvons absurde de vouloir la prendre en considération. On se trouve exactement dans la même situation que ceux qui autrefois n'accordaient de sens qu'aux sommes u+v, u-v, v+u et trouvaient absurde qu'on puisse vouloir considérer v-u. L'audace de Descartes en posant l'existence de nombres faux, a été de mettre cette quatrième opération sur le même pied d'égalité que les trois autres. Nous allons faire comme lui et mettre cette quatrième relation sur le même pied d'égalité que les trois autres. Nous l'appellerons Anoptrie ( formé sur le privatif a et la racine grecque optos=visible). Mais comme elle n'est pas accessible par l'écriture classique des complexes, nous utiliserons son écriture bivectorielle avec les seules règles de calcul qui ont été vues à la page précédente. Premières propriétés de l'anoptrie Nous dirons donc que deux vecteurs u et v sont anoptriques lorsqu'ils seront liés par la relation (u,v)=)v,-u(. Cette relation n'est pas réflexive mais elle est symétrique ce qui se voit facilement. Quant à la transitivité, si u est anoptrique à v et si v est anoptrique à w alors: (u,v)=)-v,u( et (v,w)=)w,-v( implique par addition que (u,w)=) w,u( L'anoptrie n'est pas transitive, mais nous obtenon ce résultat intéressant: Si deux vecteurs u et w sont anoptriques à un même vecteur v alors ils sont isométriques entre eux . Triangles anoptriques Intéressons nous à présent aux figures élémentaires du plan qui font intervenir l'anoptrie. Exercice I On sait que dans un triangle rectangle ABC la médiane AI partage ce triangle en deux triangles isocèles, et que dans un triangle isocèle ABC la médiane AI partage ce triangle en deux triangles rectangles. Cherchons alors quelle peut bien être la propriété de la médiane AI d'un triangle anoptrique ABC de sommet A ? (AB,AC)=)AC,BA( cad (AB+AC,AB+CA)=)AC+BA,AC+AB( cad (2 AI , CB)=)BC, 2 AI( cad (AI,CI)=)IC,AI( cad (IA,IC)=)IC,AI( Il en résulte que le triangle AIC est lui aussi anoptrique de sommet I. Et comme la démonstration est évidemment la même quand on travaille avec le triangle AIB on peut énoncer : Théorème : la médiane d'un triangle anoptrique partage ce triangle en deux triangles qui sont eux aussi anoptriques. Exercice II Dans un triangle isocèle les deux triangles formés par la médiane sont inversement semblables, et dans un triangle rectangle ces deux triangles sont isocèles. Qu'en est il pour le triangle anoptrique ABC de médiane AI ? (AB,AC)=)AC,BA( cad (AB,CB)=)AC, AB+AC( cad (AB,2 IB)=)AC, 2 AI( cad (BA,BI)=)AC,AI( Les deux triangles BAI et ACI sont inversement semblables. Enonçons Théorème : la médiane au sommet d'un triangle anoptrique le partage en deux triangles inversement semblables. Exercice III Dans un triangle isocèle les angles à la base sont égaux, dans un triangle rectangle ils sont complémentaires. Etudions ceux qui sont à la base d'un triangle anoptrique ABC. (AB,AC)=)AC,BA( cad (BA,BC)=)CA,CA+BA( Posons D tel que BA = AD on obtient : (BA,BC) = )CA, CD( = )CA,CB( + )CB,CD( Comme C n'est pas aligné avec A,B et D l'angle de CB avec CD est quelconque. Par conséquent: Théorème: En général il n'existe pas de relation particulière entre les angles à la base d'un triangle anoptrique Exercice IV Dans les triangles habituels la somme des trois angles du triangle est égale à l'angle plat. En est il de même pour un triangle anoptrique ABC de médiane AI. (AB,AC)=)AC,BA( cad (CA, CA+AB)=)AB, AB+AC( cad (CA,CB)=)AB, 2 AI( (AB,AC)+(BC,BA)+(CA,CB) = )AB,2 AI(+)2 AI, AC(+)AC,BA( = )AB,BA( cqfd Théorème: Comme pour tous les autres triangles de la géométrie euclidienne, la somme des angles d'un triangle anoptrique est égale à un angle plat. On arrive alors à une géométrie étonnante. Exemple I Considérons le triangle ABC anoptrique de sommet A on a donc (AB,AC) = )AC,BA( c'est-à-dire que pour les longueurs qui se trouvent dans cette relation on a : Par conséquent les deux cotés relatifs au sommet d'un triangle anoptrique sont égaux, or nous avons vu que les angles à la base de ce triangle ne sont pas égaux! Enonçons: Un triangle anoptrique est un triangle qui a deux cotés égaux, mais ses angles à la base ne sont pas égaux. Exemple II Nous avons vu que la médiane AI d'un triangle anoptrique ABC partage ce triangle en deux triangles inversement semblables BAI et ACI. Leurs cotés sont donc proportionnels et en particulier AI/CI=IB/IA c'est-à-dire IA² = IB x IC et comme I est le milieu de BC on a IA = IB = IC. Enonçons: Le pied de la médiane d'un triangle anoptrique est équidistant des trois sommets du triangle mais ce triangle n'est pas rectangle. Conclusion Continuons à comparer la découverte des négatifs avec la découverte de l'anoptrie. En travaillant, grâce aux notations introduites par Viète, sur les nombres négatifs qu'il appelait des nombres "faux", Descartes arrivait à des résultats qui lui paraissaient sûrement étranges. Il pouvait par exemple énoncer: Dans le nouvel ensemble que nous venons d'obtenir il existe deux catégories de nombres entiers qui ont pour produit 6. Ce sont d'une part les couples de nombres "vrais" à savoir (1,6) et (2,3), et d'autre part des couples de nombres "faux" à savoir (-1,-6) et (-2,-3). De même en travaillant, grâce aux bivecteurs, dans notre nouvelle géométrie, nous pouvons énoncer des résultats ici encore étranges. Par exemple Dans la nouvelle géométrie que nous venons d'obtenir il existe deux catégories de triangles qui ont deux cotés égaux. Ce sont d'une part les triangles isocèles qui ont leurs angles à la base égaux, et d'autre part les triangles anoptriques qui n'ont pas les angles à la base égaux. Ou encore Dans la nouvelle géométrie que nous venons d'obtenir il existe deux catégories de triangles qui sont inscriptibles dans un cercle ayant leur base pour diamètre. Ce sont d'une part les triangles rectangles qui ont leurs angles à la base complémentaires, et d'autre part les triangles anoptriques qui n'ont pas leurs angles à la base complémentaires. Notre stupéfaction est alors au moins égale à celle de Carnot dans sa Digression sur la Nature des Quantités dites Négatives. Il y énonce tout un tas de bizarreries qui nous font sourire aujourd'hui, mais qui pouvaient effectivement paraître étonnantes dans les débuts. Or il y avait quand même déjà 170 ans que Descartes avait introduit les nombres négatifs! Pareillement l'anoptrie va offrir tout un tas de bizarreries dont nous ne venons de donner qu'un échantillon et qui par la suite participeront aux fondements de la géométrie euclidienne étendue à laquelle elle va donner naissance.
Objections On trouvera ci dessous une compilation des objections et des questions qui m'ont été faites depuis la première présentation en 1988 de cette conception au congrés de géométrie organisé par les IREM de Montpellier où elle figure dans les actes de ce colloque sous le titre: Les bivecteurs et les complexes Les bivecteurs ne sont qu'une écriture différente des nombres complexes. Introduire une notation nouvelle ne fait que compliquer inutilement les choses! Les bivecteurs sont aux nombres complexes ce que les entiers relatifs sont aux entiers naturels. Dans leur partie commune on peut effectivement les confondre. Mais les relatifs permettent de donner un sens à des expressions telles que 3-5 alors qu'elle n'a pas de sens dans l'ensemble des naturels. Quelles possibilités les bivecteurs offrent ils de plus que les complexes ? Le premier exemple est que les bivecteurs donnent un sens à l'anoptrie alors que ce n'est pas le cas des complexes. Pareillement les relatifs donnaient un sens à la soustraction 3-5 ce que ne permettaient pas les nombres naturels. Mais l'étude des bivecteurs montrera d'autres extensions impossibles avec les complexes. Par exemple, au contraire des complexes, ils peuvent s'étendre à l'espace oridinaire. Pour cette extension on convient que deux bivecteurs de l'espace seront égaux ssi, en plus des conditions déjà posées, les plans qu'ils définissent sont parallèles. On définit ensuite l'addition de deux bivecteurs quelconques (PQ,PR) et (P'Q',P'R') de la façon suivante: soient O et B deux points distincts sur l'intersection des plans PQR et P'Q'R'; alors dans le plan PQR on construit (OA,OB)=(PQ,PR) et dans le plan P'Q'R' on construit (OB,OC)=(P'Q',P'R'). L'addition de ces deux bivecteurs est alors définie par: (PQ,PR)+(P'Q',P'R') = (OA,OB)+(OB,OC)=(OA,OC) L'huis clos des nombres Vous dites que, selon la prémonition de Leibniz, les bivecteurs sont un outil purement géométrique qui ne fait pas intervenir le nombre. Or les vecteurs sont munis d'une loi de composition externe sur un ensemble qui est R par exemple? Oui. Et on s'est autorisé à écrire 2 AB au lieu de AB+AB. Mais à part quelques simplifications de ce genre il est facile de voir que la multiplication des vecteurs par un réel n'est ni nécessaire ni souhaitable. Pour que deux vecteurs soient égaux il faut que leurs normes soient égales. Pour que deux bivecteurs soient égaux il faut que le rapport de leurs normes soient égales. Or ces normes sont bien des réels? La norme est une connaissance qui permet de savoir si un vecteur est plus grand ou plus petit qu'un autre. Or dans la géométrie telle que nous la construisons cette connaissance est inutile. Il faut simplement savoir si deux vecteurs sont isomètriques ou non. Même chose pour les rapports des normes. Le vocabulaire nécessaire pour traduire ces propriétés manque. Le nom de norme est donc utilisé à défaut d'autre mais effectivement il est incorrect. Pourquoi ce parti pris contre le nombre ? Parce que, pour reprendre une image de Platon, le nombre nous maintient dans une espèce de caverne numérique, une espèce de huis clos. Il n'engendre que ce qu'il est programmé à engendrer. Seule la géométrie réussit à nous en sortir. Par exemple les entiers naturels de l'antiquité n'engendraient que des rationnels. C'est par la géométrie que nous avons pu aller plus loin grâce à la célèbre démonstration d'Hippase de Metaponte qui, en utilisant le thèorème de Pythagore, a montré que la mesure de la diagonale du carré unitaire ne pouvait pas être rationnelle. De même dans l'analytique de Descartes deux droites parallèles ne pouvaient pas se couper. Et c'est en utilisant la géométrie pure que Poncelet a découvert la géométrie projective qui allait plus tard ouvrir la voie à toutes les géométries non euclidiennes. Aussi, essayer de faire des découvertes en géométrie en passant par les nombres, comme nous le faisons actuellement, aurait consisté pour Poncelet a essayer de découvrir sa géométrie projective en utilisant l'analytique. C'était impossible. Actuellement l'anoptrie n'est pas acceptée pour la seule raison que si nous l'abordons avec notre notation actuelle des complexes elle est "vide" (voir note 1). Observons que si ce critère avait été appliqué à la géométrie projective en l'abordant avec l'outil numérique dont on disposait à l'époque, c'est à dire l'analytique de Descartes, elle aurait subi le même sort. Heureusement elle était assez élémentaire pour pouvoir être visualisée par les projections. Aussi elle fut prise en considération et quelques années après les coordonnées projectives permirent de lui apporter l'outil qu'il lui fallait. Car si le nombre est un mauvais maître il est par contre un excellent serviteur. C'est quand même rassurant de savoir que vous ne bannissez pas complètement le nombre ! Bien évidemment. Mais les exemples qui viennent d'être donnés montrent que le nombre est pour ainsi dire " interprétatif " et qu'il n'est pas " créatif ". - C'était donc une erreur dans l'antiquité de rejeter l'existence des irrationnels pour la raison qu'ils ne s'exprimaient pas comme des rapports d'entiers naturels les seuls nombres alors connus. Ces exemples et sans doute bien d'autres encore montrent que les nombres opèrent chaque fois dans un ensemble dont ils nous empêchent de sortir c'est à dire en quelque sorte pour reprendre l'image de Platon à l'intérieur d'une espèce de "caverne numérique".(voir note 3) Les lacunes actuelles Pour en revenir à votre développement il est plein de lacunes. Par exemple dire que l'équation (MA,MB) = )MA,BM( est celle du cercle de diamètre AB est inexact car dans cette équation le point M ne peut être ni en A ni en B ? Oui. Le cas des vecteurs nuls est une singularité à prendre en compte. Mais elle ne suffit pas à invalider l'utilisation des bivecteurs de même que le cas des dénominateurs nuls n'invalide pas les calculs avec les fractions. Observons d'ailleurs que les transformations autorisées avec les bivecteurs permettent presque toujours de contourner ces singularités. Par exemple ici, en posant I milieu du segment AB, la relation devient (2 MI,BA)=)BA,2 MI( qui autorise les positions de M en A ou en B. Votre exposé n'est pas cohérent non plus car vous dites par exemple que deux vecteurs AB et CD sont isomètriques quand ils vérifient la relation (AB,CD)=)CD,AB(. Mais ensuite vous dites que si (AB,CD)=)CD,BA( ils ne sont pas isomètriques, et quelques lignes plus loin qu'ils sont isomètriques. C'est proprement incompréhensible ! Oui c'est vrai. Cette confusion vient du fait que nous faisons les premiers pas avec la quatrième relation. De même Descartes semait lui aussi la confusion en parlant de nombre "vrai" 5 et de nombre " faux" 5. Il faut réaliser que dans la géométrie basée sur les quatre relations il va y avoir désormais une analogie complète entre les directions et les isométries. Cette analogie permet de clarifier les choses. Par exemple si, au lieu d'être des êtres d'un espace à trois dimensions, nous étions des êtres d'un espace à une seule dimension nous n'aurions pas conscience de l'orthogonalité. Alors nous dirions que les vecteurs MA et MB tels que (MA,MB)=)MA,MB( sont liés par une colinéarité "vraie", et que si (MA,MB)=)MA,BM( ils sont liés par une colinéarité "fausse". On observerait alors la même confusion. Mais comme nous ne sommes pas des êtres de dimension un et que nous concenvons les angles droits nous disons que cette colinéarité "fausse" est tout simplement l'orthogonalité. C'est un aveuglement semblable qui nous empêche de distinguer ce que sont l'isomètrie "vraie" et l'isomètrie "fausse" et ces deux appellations ressemblantes sont effectivement trompeuses car elles sont aussi différentes entre elles que la colinéarité et l'orthogonalité. Par exemple à cause de sa propriété involutive l'orthogonalité est en quelque sorte une anti-colinéarité. De même l'anoptrie, elle aussi involutive, est une espèce d'anti-isomètrie. Notre conservatisme irrémissible La géométrie euclidienne a été étudiée depuis des millénaires et on sait tout sur elle depuis longtemps. Il est utopique de croire pouvoir "trouver quoi que ce soit que des milliers de spécialistes internationaux n'aient pas encore trouvé en dépit de décennies de labeur acharné " [Jean Pierre Demailly] Ce serait utopique si quelqu'un découvrait que les développements présentés ici sont erronés ou bien ont déjà été proposés. Or ce n'est pas le cas. La géométrie euclidienne est aujourd'hui une vieille lune. Les mathématiciens sont tous d'accord pour dire que son étude n'offre plus d'intérêt et leurs préoccupations vont dorénavant vers les géométries non euclidiennes.[Jean Dieudonné] C'est un fait que les mathématiciens d'aujourd'hui poursuivent leurs recherches vers d'autres géométries. Mais voici sur ce sujet les avis autorisés de deux grands noms. Dans son livre La Science et l'Hypothèse écrit en 1902, Henri Poincarré écrit:Que doit on penser de cette question: "La Géométrie Euclidienne est elle vraie?" Elle n'a aucun sens. Autant demander si le système métrique est vrai et les anciennes mesures fausses; si les coordonnées cartésiennes sont vraies et les coordonnées polaires fausses. Une géométrie ne peut pas être plus vraie qu'une autre; elle peut seulement être plus commode. Or la géométrie euclidienne est et restera la plus commode" Et Einstein dans un discours qu'il prononça devant l'Académie des Sciences de Berlin le 27 janvier 1921 et qui a été édité en français chez Gauthier-Villard en 1953 sous le titre La Géométrie et l'Expérience, déclara : « De toutes les autres géométries axiomatiques concevables, la Géométrie Euclidienne se distingue par la simplicité. Et comme la géométrie axiomatique pure ne contient pas d'énoncés sur la réalité accessible à l'expérience, mais seulement la géométrie axiomatique en liaison avec des propositions physiques, il devrait être possible et raisonnable, quelle que soit la nature de la réalité, de conserver la Géométrie Euclidienne » . Impossible d'être plus clair: quelle que soit la nature de la réalité il est raisonnable de conserver la Géométrie Euclidienne ! Ce qui compte dans une notion mathématique nouvelle c'est son utilité. Or l'anoptrie est inutile. C'est effectivement une des conceptions possibles des mathématiques où on distingue deux attitudes fondamentalement différentes: celle des maths pures et celle des maths appliquées. Les maths pures s'intéressent à la connaissance pour la connaissance. L'anoptrie ne se justifie pour le moment que sous ce dernier point de vue par l'harmonie absolument parfaite avec laquelle elle s'intègre aux trois autres relations fondamentales. C'est vrai que pour le moment nous ne la comprenons pas et par conséquent nous ne lui trouvons pas d'utilité. Mais au lieu de la rejeter nous devrions chercher à lui trouver son interprétation géométrique, ce qui peut effectivement demander beaucoup de temps. Souvenons nous qu'il s'est écoulé plus de deux siècles entre la découverte des complexes et la compréhension de leur signification géométrique. Pourquoi les scientifiques ne vous suivent ils pas ? Les raisons qu'ils donnent viennent d'ètre exposées ci dessus. On voit qu'elles sont aussi réfutables que l'étaient autrefois, la raison de "vérité" donnée par Pascal ou la raison "d'absurdité" donnée par Carnot pour s'opposer aux nombres négatifs c'est à dire pour refuser exactement de la même façon de mettre sur le même pied d'égalité les quatre opérations u+v,u-v,v+u et v-u. Le manque de curiosité des scientifiques devant la quatrième relation est par conséquent décevant à moins d'accepter l'explication qu'en donne Jean François Revel dans son livre La Connaissance Inutile publié en 1988 où il écrit: « Les idées qui nous intéressent le plus ne sont pas les idées nouvelles, ce sont les idées habituelles. L'essor de la science depuis le XVII° siècle nous incite à prêter à la nature humaine un congénital appétit de connaissances et une insatiable curiosité pour les faits. Or, l'histoire nous l'enseigne, si l'homme déploie, en effet, une intense activité intellectuelle, c'est pour construire de vastes systèmes explicatifs aussi verbeux qu'ingénieux, qui lui procurent le calme de l'esprit dans l'illusion d'une compréhension globale, plutôt que pour explorer humblement les réalités et s'ouvrir à des informations inconnues. La science, pour naître et se développer, a dû et doit encore lutter contre cette tendance primordiale, autour d'elle et dans son propre sein : l'indifférence au savoir » Pour pouvoir parler d'indifférence encore faudrait-il que de grands mathématiciens aient été mis au courant. Dés le début, dans les années quatre vingt, j'ai informé quelques grands noms des mathématiques. Monsieur Dieudonné m'a répondu que la "géométrie pure était une vieille lune". Monsieur Demailly que "la géométrie euclidienne avait été étudiée depuis des siècles voire des millénaires". Monsieur Cartan, qui fut le plus aimable puisqu'il m'a même accordé une entrevue, transforma devant moi la relation (u,v)=)v,-u( en ||u||²+||v||²=0 et il me déclara sur le champ qu'il était "absurde" de vouloir aller plus loin. Quand aux autres grands noms actuels comme Monsieur Connes (voir note 4) ou Monsieur Gromov ils ne m'ont pas donné leurs avis soit parce qu'ils n'ont pas d'autres raisons que celles données plus haut, soit, plus probablement, parce qu'ils sont effectivement indifférents à cette idée nouvelle . Mais enfin réalisez vous de quelle suffisance vous faites preuve en vous opposant à des avis aussi illustres ? Bien sûr que j'en ai conscience. Et c'est même la raison pour laquelle j'ai laissé dormir pendant des dizaines d'années au fond de mes tiroirs ces conceptions qui remontent maintenant à presque trente ans! Mais rien n'y fait et constamment elles reviennent à la charge. Je suis exactement dans la position de ce berger d'il y a cinq ou six mille ans qui fut le premier à observer que dans le ciel certains astres se mettent parfois à reculer. Les plus grandes autorités de l'époque pouvaient bien lui affirmer que l'univers tournait autour de la terre, et lui n'être que le plus humble et le plus insignifiant des hommes, chaque fois qu'il regardait le ciel il devait se dire que le géocentrisme n'était pas la bonne explication. Il n'y avait aucune suffisance dans cette attitude. De même, dans la simplicité de l'anoptrie et dans l'harmonie avec laquelle elle s'intègre aux trois autres relations de la géométrie, il y a une force de conviction qui l'emporte sur toutes les objections aussi augustes soient elles. L'universalité de cette conception. Une force de conviction devrait s'imposer à tout le monde. Oui. Mais en pratique on observe que ce n'est pas le cas. Par exemple quand Galilée a montré que des satellites tournaient autour de Jupiter, c'était une force de conviction suffisante pour prouver que l'univers n'était pas géocentrique. Et pourtant elle n'a pas convaincu. Ici la force de conviction vient des trois observations manifestes suivantes: D'abord le vecteur qui prend en compte toutes les informations données par un couple de points montre de façon évidente que le segment sur lequel Euclide a fondé notre géométrie était un outil trop rudimentaire. Ensuite nous savons maintenant, d'après les travaux de Félix Klein exposés dans le Programme d'Erlangen, que la similitude est la transformation caractéristique de la géométrie euclidienne. Il en résulte que l'outil spécifique de cette géométrie ne peut être que le bivecteur. Enfin ces bivecteurs permettent d'écrire quatre relations élémentaires, pas une de plus et pas une de moins. L'intuition d'Euclide et de Hilbert a pris pour base les trois qui nous sont perceptibles. Penser que la géométrie va se limiter à ces trois relations pour la seule raison que nous ne comprenons pas la quatrième est manifestement très prétentieux. Quoi qu'il en soit c'est seulement la reconnaissance par les autres mathématiciens qui importe ! Effectivement. Mais l'universalité de cette notion nouvelle procure une satisfaction indépendante. C'est sans doute ce que voulait dire Platon quand il écrit que " la Géométrie est une merveille qui manifeste son caractère divin à l'homme capable de la concevoir " [Epinomis §990]. En effet nous savons aujourd'hui que notre univers est constitué d'une infinité de galaxies. Il n'y a aucune raison pour que nous soyons les seuls êtres vivants dans cette multitude. Et de même il est presque sûr que de nombreuses civilisations y ont atteint un stade de développement semblable ou supérieur au notre avec, comme nous l'avons fait, une convention de notation c'est à dire d'écriture pour leur langage et pour leurs nombres. Alors, parmi ces civilisations, celles qui auront cherché à se munir d'une écriture pour la géométrie auront forcément abouti elles aussi aux bivecteurs puisque nous avons vu qu'il est impossible de passer outre. Elles auront abouti aux mêmes observations que celles que nous avons faites. Et parmi elles certaines auront éclairci le mystère de l'anoptrie. Quant à nous, par aveuglement volontaire, nous allons continuer pendant longtemps encore à considérer la géométrie comme étant ce mouton à trois pattes qu'Euclide nous a construit il y a vingt cinq siècles, et que D Hilbert vient de rafistoler il y a moins d'un siècle. Conclusion Je voudrais maintenant remercier ceux qui auront eu la patience de lire ces pages jusqu'à ces dernières lignes. Et, contrairement à l'usage, qu'on me permette de terminer par la citation d'une profession de foi qu'Einstein jugea si importante qu'il en fit la conclusion de son livre L'Evolution des Idées en Physique écrit en collaboration avec Infeld. La voici: " Sans la croyance qu'il est possible de saisir la réalité avec nos constructions théoriques, sans la croyance en l'harmonie interne de notre monde, il ne pourrait pas y avoir de science. Cette croyance est et restera toujours le motif fondamental de toute création scientifique. A travers tous nos efforts, dans chaque lutte dramatique entre les conceptions anciennes et les conceptions nouvelles, nous reconnaissons l'éternelle aspiration à comprendre, la croyance toujours ferme en l'harmonie de notre monde, continuellement raffermie par les obstacles qui s'opposent à notre compréhension". Tout y est : l'erreur de nous fier à notre expérience pour découvrir la réalité alors que celle ci ne peut être saisie que par une construction théorique (voir note 6); la lutte inévitable entre les conceptions anciennes et les conceptions nouvelles, lutte si traditionnelle qu'il la qualifie de dramatique; les obstacles qui s'opposent à notre compréhension et qui viennent non seulement de notre fausse perception des choses mais aussi de notre conservatisme obstiné; enfin et surtout l'impérieuse nécessité de faire confiance à l'harmonie de notre monde, ce fil d'Ariane qui ne nous a jamais fait défaut et auquel pourtant nous refusons perpétuellement de nous fier. Maintenant, comme dit l'expression populaire, il ne faut pas essayer de marcher plus vite que la musique. Un jour, pas forcément proche, (deux millénaires entre le pressentiment de l'héliocentrisme par les pythagoriciens, et la défense acharnée de Galilée !) nos autorités savantes réaliseront que la géométrie mérite elle aussi son écriture dédiée. Ils retrouveront alors l'écriture bivectorielle dont le support est la similitude car, comme Leibniz le pressentait, et comme on le sait maintenant il est impossible de passer outre pour la géométrie euclidienne ( voir note 7). Ensuite, de même que l'écriture introduite par Viète a rendu inacceptable l'absence des nombres négatifs (voir note 8), de même l'écriture bivectorielle rendra insupportable l'absence de la relation (u,v)=)v,-u(. Les portes de la Géométrie Euclidienne enfin complète s'ouvriront alors. Il suffit donc tout simplement d'attendre. Cagnes sur mer le 15 avril 2010 Notes: (1) - Dans une correspondance qu'il m'a adressée le 3 mars 2000, Monsieur Jean Pierre Demailly, académicien expert de la Géométrie Complexe, m'écrit " ...il y a isomorphisme entre classes d'équivalence des bivecteurs et nombres complexes non nuls avec votre loi d'addition des bivecteurs et la multiplication sur le groupe des complexes non nuls. Par conséquent la notion d'anoptrie est vide..." . Cette foi absolue dans la nécessité pour une vérité mathématique de pouvoir se traduire par les nombres que nous connaissons se retrouve chez tous mes correspondants. (2) - Les exemples donnés ici ne pouvaient effectivement pas se traduire avec les notations numériques alors connues mais par contre ils étaient suffisamment élémentaires pour être visualisables: l'irrationnalié apparaissait de fait dans la diagonale du carré unitaire, les nombres négatifs dans la nécessité de donner une abscisse à tous les points de la droite, et une simple projection rendait "visible" l'intersection de deux droites parallèles. L'anoptrie n'a plus cette élémentarité et par suite ne bénéficie d'aucun apport intuitif. Son seul argument est l'harmonie avec laquelle elle s'intègre aux trois autres relations, cette harmonie qu'Einstein demande constamment de prendre comme principe directeur mais qui laisse de marbre les autres scientifiques. (3) - Ce mythe célèbre de Platon débute le Livre VII de La République. Il y décrit l'humanité confinée dans une caverne qu'elle considère comme le véritable univers. En ne tenant pour vrai que ce que nos nombres nous rendent visible nous faisons penser aux savants de cette caverne qui n'y tiennent pour vrai que les ombres visibles sur les parois et pour lesquels la science consiste à avoir ".. la vue la plus fine pour saisir le passage des ombres contre la paroi, le plus de capacité pour tirer de ces observations des conjectures sur ce qui doit arriver.." . (4) - L'indifférence de Monsieur Connes est la plus surprenante car dans une interview qu'il donna au journaliste Olivier Postel Vinay pour La Recherche, il déclare "Fondamentalement je pense qu'on ne peut pas du tout exclure la possibilité qu'en fin de compte les lois fondamentales soient incroyablement simples, bien plus simples que tout ce qu'on peut imaginer aujourd'hui" , et aussi "Je suis prèt à parier qu'on s'apercevra un jour que la réalité matérielle se situe en fait à l'intérieur de la réalité mathématique" justement deux particularités de l'anoptrie, son extrème simplicité et le fait qu'elle n'est pour le moment qu'une réalité mathématique. (5) - L'héliocentrisme avait été pressenti par les Pythagoriciens vers 600 avant notre ère et Plutarque au début de notre ère en parle longuement. Quant aux nombres négatifs plusieurs mathématiciens avaient commencé à les utiliser avant Descartes (voir note 8) (6) - Dans son livre Comment je vois le monde, Einstein affirme que, tout physicien qu'il soit, c'est par les mathématiques que nous découvrirons les concepts et les principes de l'univers: " Je suis convaincu que la construction exclusivement mathématique nous permet de trouver les concepts et les principes les reliant entre eux" et dans Conceptions Scientifiques il écrit " Nous constatons maintenant avec évidence combien sont dans l'erreur les théoriciens de la connaissance qui croient que la théorie vient par induction de l'expérience" (7) Dans son célèbre programme d'Erlangen Félix Klein écrit "Les propriétés géométriques sont caractérisées par leur invariance relativement aux transformations du groupe principal" sachant qu'il appelle groupe principal "les déplacements de l'espace, ses transformations avec similitude et celles par symétrie" c'est à dire les similitudes directes et indirectes dont les déplacements et les symétries ne sont que des cas particuliers. (8) En fait si on en juge par la Kleine Enzyklopädie der Mathématik publiée par l'Institut de Bibliographie de Leipzig [p33] " En Inde vers 700 après Jésus Christ les calculs avec les nombres négatifs étaient déjà complètement connus" et c'est effectivement le symbolisme introduit par Viète qui a rendu leur absence inacceptable. Addenda: Dans l'impossibilité d'accèder aux moyens de diffusion classiques il ne me reste que le recours de déposer un pli cacheté à l'Académie des Sciences, que je motiverai en signalant l'indifférence de la communauté mathématique. Conformément aux statuts ce pli ne sera ouvert que dans cent ans. Mais il n'est même pas sûr que ce délai soit suffisant quand on réalise que pour les nombres négatifs, beaucoup moins révolutionnaires, et malgré le grand nom de Descartes, ils étaient encore refusés par Carnot 170 ans après.


- de noter (AB,AC) la similitude directe qui fait passer du vecteur AB au vecteur AC,
- de noter )AB,AC( la similitude indirecte qui fait passer du vecteur AB au vecteur AC.
On sait que ces deux similitudes ont le même rapport. Elles ne diffèrent que par leur angle qui est celui de AB avec AC pour la première et celui de AC avec AB pour la seconde.


de la
Géométrie Euclidienne

- Un triangle ABC où les vecteurs AB et AC sont isométriques s'appelle triangle isocèle de sommet A.
- Un triangle ABC où les vecteurs AB et AC sont orthogonaux s'appelle un triangle rectangle de sommet A.
- De même un triangle ABC où les vecteurs AB et AC seront anoptriques s'appellera triangle anoptrique ABC de sommet A.
et de même
(AB,AC)=)AC,BA( cad (BA+AC,BA)=)CA+BA, CA( cad (BC,BA)=)2 AI, AC(
d'où par addition
AC/AB = AB/AC cad AB² = AC ² cad AB = AC
" De nouveaux outils pour les démonstrations géométrique"
- C'était donc une erreur à la Renaissance de rejeter l'existence des nombres négatifs pour la raison qu'ils ne pouvaient pas mesurer des longueurs dont on croyait que c'était la mission obligatoire pour les nombres.
- Cela aurait été une erreur de refuser l'intersection des droites paralléles pour la raison qu'elle était impossible dans l'analytique de Descartes.
- Et pareillement je pense que c'est une erreur de la part de Messieurs Cartan ou Demailly pour ne citer qu'eux de refuser l'anoptrie pour la raison qu'elle ne peut pas s'interprèter avec les nombres que nous connaissons (voir note 2)
08:19 Publié dans La quatrième relation | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Merveilleux Pappus
|
Merveilleux Pappus
Introduction Depuis l'Antiquité les hommes pensent que la géomètrie est une science essentielle pour notre compréhension de l'univers, car dans cet univers les éléments géométriques abondent. En effet les corps célestes sont sphériques, les orbites sont elliptiques, les rayons lumineux non perturbés sont rectilignes, les galaxies ont souvent la forme de spirales, les déplacements des étoiles sur la voute céleste sont des cercles parfaits, et tout à l'avenant. De plus, autre mystère très étonnant de l'univers, la plupart des êtres vivants qui le peuplent ont une configuration presque parfaitement symétrique, en commençant par le plus important d'entre eux : l'homme. Le premier miracle de la Géométrie Aussi est il normal de penser que la progression de notre connaissance est conditionnée par celle que nous pouvons avoir en géomètrie et Platon, qui le pressentit , la mettait en tête de toutes les connaissances. Voilà pourquoi il écrivit au fronton de son Académie " Nul n'entre ici s'il n'est géomètre ". Plus tard la communion d'efforts des premiers chercheurs de ces temps reculés a été synthétisée par Euclide dans ses fameux Eléments. Il y a rappelé toutes les connaissances géomètriques de son temps. Mais surtout il a montré que cet ensemble prodigieux de résultats repose sur un tout petit nombre de principes qu'il a appelés des "axiomes". Et finalement , en dehors des considérations d'appartenance, d'ordre et de continuité, il apparaît que ces axiomes se ramènent exclusivement à trois relations: le parallélisme, l'isomètrie et l'orthogonalité. C'est à proprement parler un miracle, le premier miracle de la géométrie. Le second miracle de la Géomètrie. Puis un jour l'homme s'est aperçu que le parallelisme vient d'un cécité particulière de notre nature humaine, semblable à celle qui nous empêche par exemple de déceler les ultra violets dans les couleurs. Cette cécité géométrique nous empêche de voir une droite particulière du plan que nous avons appelée droite de l'infini. Dès que celle ci fut découverte, la distinction plane entre droites sécantes et droites parallèles tomba, et tout couple de droites eut désormais un point d'intersection. Ce fut une simplification considérable. Et il en fut de même avec l'orthogonalite. Elle cessa elle aussi d'avoir son statut particulier et les angles droits devinrent des angles comme les autres. La géométrie d'Euclide, avec tous ses axiomes, apparut dés lors comme un cas particulier de cette nouvelle géométrie beaucoup plus simple, qui prit le nom de Géométrie projective. Ce fut le second miracle de la géomètrie. Le troisième miracle de la Géométrie Cette géométrie regroupa de nombreux résultats qui avaient jusque là paru distincts. Parmi les théorèmes qui échappèrent à ce regroupement émergent deux thèorèmes fondamentaux qui portent le nom de Pappus et de Desargues lequel est aussi appelé: Théorème des triangles homologiques. Or un grand mathématicien, Federigo Enriques , écrivit dans un livre qui fait référence "Leçons de Géomètrie Projective", qu' "en se servant du théorème des triangles homologiques ..on pourrait déduire tous les théorèmes de géomètrie projective plane ". (voir page 46 de son livre ) . Et quelques temps avant un autre grand mathématicien, David Hilbert avait montré que le Théorème de Desargues peut se déduire de celui de Pappus alors que le contraire n'est pas possible. Il résulte alors de ces deux observations que le seul théorème de Pappus est le générateur de tous les théorèmes de géomètrie projective plane et par suite de tous les théorèmes de géométrie euclidienne puisque celle ci est contenue dans la géométrie projective, et nous avons vu par exemple qu'il démontre effectivement la belle propriété del'hexagramme mystique de Pascal, à la base de tout le contenu de ce site. C'est le troisième miracle de la géomètrie. Voilà la raison qui fait du théorème de Pappus un théorème tout à fait exceptionnel. ________________________________
Présentation du Théorème de Pappus. C'est à la Proposition 139 du Livre VII de son oeuvre: La Collection Mathématique, que le mathématicien Pappus, dans les premiers siècles de notre ère, énonce le théorème qui porte désormais son nom. Depuis cet exposé, il y a bien longtemps, la figure traditionnellement attachée à ce théorème est la suivante.
et l'énoncé du Thèorème de Pappus est alors: Si les points A',B',C' sont alignés, de même que A",B",C" alors il en est de même de A,B,C On voit comme ce thèorème est d'une grande élégance car il minimalise les hypothèses nécessaires, et il ne fait intervenir que des alignements de points. Mais il est dommage que nous lui conservions encore dans sa représentation graphique la disposition qui fut adoptée par Pappus à l'origine. En effet cette disposition suggère ce que l'on pourrait appeler une symétrie binaire avec une figure en quelques sorte symétrique autour de ABC qui semble jouer un rôle privilégié. Or en fait la particularité du Théorème de Pappus est une symétrie ternaire, où la droite ABC ne joue pas un rôle différent de celui des deux autres droites A'B'C' et A"B"C", et où les neuf droites de la figure n'ont pas la répartition 3+2+2+2 , suggérée par la représentation ci dessus ( les trois droites en gras, et leurs six liaisons) mais la répartition bien plus symétrique 3+3+3 de la figure ci dessous, où les notations sont absolument les mêmes que dans la première figure et où seule la disposition adoptée est différente.
La différence est que dans cette représentation on voit très bien la symétrie ternaire. On peut alors dire: - des trois alignements de points ABC, A'B'C', A"B"C", deux d'entre eux impliquent le troisième, défini sans ambiguïté par les deux premiers. mais on peut dire aussi - des trois convergences de droites abc, a'b'c', a"b"c", deux d'entre elles impliquent la troisième, définie sans ambiguïté par les deux premières .
Les deux Thèrèmes de Pappus On obtient alors deux théorèmes que les Géomètres appellent duaux l'un de l'autre . Donnons leur énoncés en convenant par exemple d'appeler droite PQ la droite qui passerait par les deux points P et Q, et d'appeler point pq le point qui serait l'intersection des deux droites p et q. Théorème 1: Soient B,B',B",C,C',C" six points d'un plan. Si les droites B'C', BC" et B"C sont concourantes, de même que les droites B"C", B'C et BC' alors les droites BC, B"C' et B'C" sont aussi concourantes. Théorème 2: Soient b,b',b",c,c',c" six droites d'un plan. Si les points b'c', bc" et b"c sont alignés, de même que les points b"c",b'c et bc' alors les points bc,b"c' et b'c" sont aussi alignés. ce dernier théorème est justement le Théorème de Pappus ou non seulement A,B,C sont présentés comme des intersections de droites mais aussi A',B',C' et A",B",C" ce qui rétablit les rôles symétriques de ces trois alignements. passons ensuite à sa démonstration |
|
Desargues par Pappus Maintenant que nous connaissons le Théorème de Pappus, utilisons le par exemple pour démontrer le Théorème de Desargues, puisque d'après D Hilbert c'est possible, alors que le contraire ne l'est pas. La figure est dessinée ci dessous et on y a coloré en jaune les deux triangles particuliers qui donnent aussi l'appellation de Triangles homologiques à ce théorème.
La démonstration de Desargues , donnée autrefois par Hilbert, se fait alors en appliquant trois fois Pappus:
|
|
Interprétation spatiale de Desargues Il est bien regrettable que le théorème fondamental ne soit pas celui de Desargues car son interprétation spatiale est très simple. En effet il est tout simplement la projection plane de la figure constituée par cinq plans quelconques de l'espace (au sens projectif bien entendu, c'est à dire sans possibilité de parallélismes)
Si on appelle O le point d'intersection de trois quelconques d'entre eux, alors les deux autres se coupent suivant une droite d, et ces deux plans coupent les trois premiers suivant deux triangles ABC et A'B'C' qui sont dits homologiques, et dont les cotés correspondants se coupent évidemment sur la droite d, c'est à dire sont alignés, ce qui constitue justement l'information apportée par le théorème de Desargues. On réalise l'intérèt qu'il y aurait à avoir une interprétation semblable pour le Théorème de Pappus dont la démonstration serait ainsi libérée de tout théorème plan "antérieur", comme le Théorème de Ménélaüs qui est généralement utilisé. A défaut d'avoir trouvé cette démonstration dans les ouvrages mathématiques que j'ai consultés, en voici une de mon cru, que je remplacerai volontiers par toute autre meilleure qui me sera proposée.
Interprétation spatiale de Pappus Soient dans l'espace trois droites d,d',d" dont aucune n'est coplanaire avec une autre.
Soit M1 un point de d. La droite d1d'intersection des plans P(M1,d') et P(M1,d"), existe toujours par hypothèse et rencontre par construction les trois droites d,d',d". Soient M1,M1',M1" ces points de rencontre. Soit M2 un autre point de d, et d2 la droite pareillement construite qui rencontre les trois droites d,d',d". Soient M2,M2' ,M2" ces points de rencontre. Quels que soient M1 et M2 les droites d1 et d2 ne sont jamais sécantes sinon les points M1,M1',M1",M2,M2',M2" seraient coplanaires c'est à dire aussi les droites d,d',d" ce qui est contraire à l'hypothèse. Soit M3 un autre point de d, et d3 la droite pareillement construite qui rencontre les trois droites d,d',d". Soient M3,M3' ,M3" ces points de rencontre.
Considérons alors la projection plane de ces points M à partir d'un centre de projection O pour le moment arbitraire. Dans cette projection plane les droites concourantes M1M3',M1"M2',M2M3" continuent à concourir au point que nous avons appelé I. Ensuite choisissons pour O un point situé sur une droite OJ du réseau R1 . Cette droite rencontre donc d,d',d", c'est à dire que vues de O ces trois droites, à savoir M1M2, M2'M3',M1"M3" sont vues concourantes en J. Mais alors l'appartenance de O à une droite du réseau R1 implique que O est situé sur (S) et donc que par O il passe aussi une droite du réseau R2, c'est à dire une droite OK qui rencontre d1,d2,d3. Par suite il en résulte qu'on voit aussi , à partir de O, ces trois droites ,à savoir M1M1",M2M2',M3'M3" concourir en K. Comme nous l'avons vu en commençant, ces deux convergences de droites qui en impliquent une troisième sont une des formes du Théorème de Pappus, ce que nous voulions justement démontrer. Quant à la figure d'accompagnement, avec ses neuf droites, on choisira à son gré, selon la remarque faite au début de cette page, l'une des deux suivantes:
Conclusion
Source : http://hexamys.free.fr/pappus.htm |
08:12 Publié dans Merveilleux Pappus | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Théorème de Pappus
Théorème de Pappus
Sommaire[masquer] |
Introduction [modifier]
Le théorème de Pappus est un résultat de géométrie présentant deux particularités :
D'abord, parmi tous les théorèmes de géométrie, c'est celui qui demande les hypothèses minimales. Il porte sur deux triplets de points arbitraires respectivement pris sur deux droites coplanaires quelconques. Il ne demande donc comme connaissance que celle de l'alignement de trois points et ne nécessite par exemple ni métrique, ni orthogonalité… On dit qu'il est un théorème de géométrie projective.
Ensuite, ce théorème est le générateur de tous les théorèmes de géométrie euclidienne par l'enchaînement suivant
- D'après un résultat obtenu par D. Hilbert, le théorème de Pappus permet de démontrer le théorème des triangles homologiques.
- Dans Leçons de géométrie projective du célèbre géomètre F. Enriqués, on lit : …en se servant du théorème des triangles homologiques […] on pourrait déduire tous les théorèmes de géométrie projective plane. (voir page 46 de son livre)
- Enfin la géométrie projective contient la géométrie euclidienne comme cas particulier.
On trouvera tous les détails sur ces développements dans les références données en fin d'article. Cette particularité remarquable explique que certains auteurs aient conféré le statut d'axiome à ce théorème, voir axiomes de plans projectifs.
Énoncé du théorème [modifier]
Dans un plan, soient A1, B1, C1 trois points distincts alignés sur une droite (d) , et soient A2, B2, C2 trois autres points distincts alignés sur une autre droite 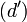 alors les points
alors les points
- A intersection de (B2C1) avec (C2B1)
- B intersection de (A2C1) avec (C2A1)
- C intersection de (A2B1) avec (B2A1)
sont alignés.
Il s'agit d'un théorème de géométrie projective donc les points considérés peuvent être propres ou impropres. Dans le cas où tous les points sont propres, on obtient une configuration du type ci-contre.
Remarques :
si l'on note (Δ) la droite portant les points A,B,C alors les assertions suivantes sont équivalentes (en géométrie projective) :
-- les trois droites (d), 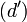 et (Δ) sont concourantes ;
et (Δ) sont concourantes ;
-- les trois droites (A1A2) (B1B2) (C1C2) sont concourantes ;
-- les six droites « croisillons » (B2C1) (C2B1) (A2C1) (C2A1) (A2B1) (B2A1) sont tangentes à une même conique.
-- Les deux droites (d) et 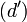 peuvent être considérées comme une conique dégénérée : pour l'hexagramme A1B2C1A2B1C2, le théorème de Pappus-Pascal affirme l'alignement des points A, B et C.
peuvent être considérées comme une conique dégénérée : pour l'hexagramme A1B2C1A2B1C2, le théorème de Pappus-Pascal affirme l'alignement des points A, B et C.
Démonstration à l'aide des applications projectives [modifier]
On construit les points O intersection de (d) et (d'), D intersection de (A1B2) et (A2C1) et E intersection de (A1C2) et (C1B2)
On considère la projection centrale p de la droite (A1B2) sur la droite (d) de centre A2
- A1 a pour image A1
- C a pour image B1
- D a pour image C1
- B2 a pour image O
On considère la projection centrale q de la droite (d) sur la droite (B2C1) de centre C2
- A1 a pour image E
- B1 a pour image A
- C1 pour image C1
- O a pour image B2
Par l'application projective q o p de la droite (A1B2) sur la droite (B2C1)
- A1 a pour image E
- C a pour image A
- D a pour image C1
- B2 a pour image B2
Si on regarde maintenant la projection centrale r de la droite (A1B2) sur la droite (B2C1) de centre B
- A1 a pour image E
- D a pour image C1
- B2 a pour image B2
Or, une application projective d'une droite sur une autre est entièrement déterminée par l'image de trois points distincts. Les transformations q o p et r coïncident sur A1, D et B2. Elles sont donc égales et r(C) = A. Les points A, B et C sont donc alignés.
Démonstration à l'aide du théorème de Ménélaüs [modifier]
Dans le cas où aucun point n'est impropre et à condition qu'il existe un triangle de référence, dont les côtés soient interceptés par cinq droites du problème, on peut caractériser l'alignement de cinq triplets de points grâce au théorème de Ménélaüs et en déduire simplement que les trois points A, Bet C sont alignés. Deux triangles de référence peuvent être choisis à cette fin :
- le triangle J1K1L1 (en bleu sur la figure) dont les sommets sont les intersections des droites (A2B1), (B2C1) et (A1C2),
- le triangle J2K2L2 (en rouge sur la figure) dont les sommets sont les intersections des droites (A1B2), (B1C2) et (A2C1).
Dans le triangle J1K1L1 (s'il existe) :
- la droite (A1C1) intercepte les trois côtés en A1, B1, C1
- la droite (A2C2) intercepte les trois côtés en A2, B2, C2
- la droite (B1C2) intercepte les trois côtés en B1, A, C2
- la droite (A2C1) intercepte les trois côtés en A2, B, C1
- la droite (A1B2) intercepte les trois côtés en A1, C, B2
D'après Ménélaüs, ces alignements se traduisent par les égalités suivantes :
En multipliant membre à membre ces cinq égalités, il reste après simplification :
ce qui prouve d'après la réciproque de Ménélaüs l'alignement des trois points A, B et C.
Une démonstration analogue peut être faite dans le triangle J2K2L2. Dans ce cas, les trois droites (B1C2), (A2C1) et (A1B2) (en rouge sur la figure) échangent leur rôle avec les trois droites (B2C1), (A1C2) et (A2B1) (en bleu sur la figure). Cette fois-ci, les trois premières droites délimitent le triangle de référence tandis que les trois dernières interceptent les côtés du triangle de référence. Les droites (A1C1) et (A2C2) (en vert sur la figure) sont conservées pour intercepter le triangle.
Il existe un moyen pratique de trouver les deux triangles de référence. On peut représenter la ligne brisée A1, B2, C1, A2, B1 et C2 sous la forme d'un circuit hexagonal. Les côtés opposés de ce circuit hexagonal ont pour intersection les 3 points A, B, C et les deux triangles de référence sont les deux triangles bâtis sur l'hexagone.
On peut illustrer sur une autre configuration, avec quelle facilité le circuit hexagonal permet de trouver les deux triangles de référence. Définissons cette fois-ci :
- A comme l'intersection de (A1B2) avec (C1C2)
- B comme l'intersection de (A1A2) avec (B1C2)
- C comme l'intersection de (C1A2) avec (B1B2)
Le circuit hexagonal est alors A1, A2, C1, C2, B1 et B2 et les deux triangles de référence sont alors :
- le triangle J1K1L1 (en bleu sur la figure) dont les sommets sont les intersections des droites (A1B2), (B1C2) et (A2C1),
- le triangle J2K2L2 (en rouge sur la figure) dont les sommets sont les intersections des droites (A2B1), (B2C1) et (A1C2).
Notions connexes [modifier]
- Le Théorème d'Hessenberg qui fait le lien entre le théorème de Pappus et le théorème de Desargues.
- Le théorème de Pappus-affine dans le plan affine.
- L'Hexagramme de Pascal dont la configuration de Pappus est une version dégénérée (la conique est une bidroite).
- Enfin il est indispensable de rappeler que la configuration de Pappus est un bel exemple de Dualité (géométrie projective).
Théorème ou axiome? [modifier]
Tout dépend dans quelle géométrie on se situe. Si on travaille dans un contexte de géométrie euclidienne, cette propriété n'est qu'un théorème découlant d'axiomes plus puissants.
En revanche, dans un contexte de géométrie projective, si on travaille dans un plan projectif pappusien, c'est un de nos axiomes de construction de ce plan. Si on travaille dans un plan projectif homogène, c'est un théorème qui découle d'un autre ensemble d'axiomes.
Sources [modifier]
- Leçons de géométrie projective de F. Enriqués
- Petite encyclopédie de mathématiques Ed. Didier
- Enfin un site où sont donnés de nombreux développements sur le Thèorème de Pappus:Merveilleux Pappus
08:11 Publié dans Théorème de Pappus | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Prix Abel
Le prix Abel est une récompense décernée annuellement à des mathématiciens par l'Académie norvégienne des sciences et des lettres.Prix Abel
![]() Pour les articles homonymes, voir Abel (homonymie).
Pour les articles homonymes, voir Abel (homonymie).
Sommaire[masquer] |
En 2001, le gouvernement norvégien a annoncé qu'à l'occasion du bicentenaire de la naissance du mathématicien norvégien Niels Henrik Abel (1802) serait créé un nouveau prix pour les mathématiciens. Ce prix est inspiré du prix Nobel, qui n'existe pas en mathématiques. Même si la médaille Fields a souvent été comparée au prix Nobel, elle en diffère sur certains aspects essentiels (elle distingue des travaux exceptionnels accomplis par un mathématicien avant l'âge de 40 ans ; récompense financière modeste), ce qui fait du prix Abel un meilleur équivalent du prix Nobel (récompense plutôt d'une œuvre dans son ensemble)1. Le prix est décerné par l'Académie norvégienne des sciences et des lettres. Le comité de sélection est composé de cinq mathématiciens internationaux. Le prix est décerné en novembre par le Roi de Norvège et vaut 6 millions de couronnes norvégiennes, c'est-à-dire environ 730 000 euros. La Norvège a donné pour le prix une dotation initiale de 200 millions decouronnes norvégiennes (environ 25 millions d'euros). (en) Site officielCréation [modifier]
Le prix [modifier]
Liste des lauréats [modifier]
![]() France, Collège de France)
France, Collège de France)
![]() Royaume-Uni, Université d'Édimbourg) et Isadore Singer (
Royaume-Uni, Université d'Édimbourg) et Isadore Singer (![]() États-Unis, MIT)
États-Unis, MIT)
![]() Hongrie /
Hongrie / ![]() États-Unis, Courant Institute of Mathematical Sciences de New York)
États-Unis, Courant Institute of Mathematical Sciences de New York)
![]() Suède, Institut royal de technologie de Stockholm)
Suède, Institut royal de technologie de Stockholm)
![]() Inde /
Inde / ![]() États-Unis, National Academy of Sciences)
États-Unis, National Academy of Sciences)
![]() Belgique /
Belgique / ![]() France, Collège de France) et John Griggs Thompson (
France, Collège de France) et John Griggs Thompson (![]() États-Unis, Université de Floride)
États-Unis, Université de Floride)
![]() Russie /
Russie / ![]() France, Institut des hautes études scientifiques)
France, Institut des hautes études scientifiques)
![]() États-Unis, Université du Texas)
États-Unis, Université du Texas)Notes et références [modifier]
Lien externe [modifier]
| Lauréats du prix Abel | |
|---|---|
| Serre (2003) · Atiyah et Singer (2004) · Lax (2005) · Carleson (2006) · Varadhan (2007) · Tits et Thompson (2008) · Gromov (2009) · Tate (2010) | |
07:55 Publié dans Prix Abel | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Louis-François Benoiston de Châteauneuf
Louis-François Benoiston de Châteauneuf, né à le 22 mars 1776 à Paris où il est mort le 2 mai 1856, est un économiste, statisticien et démographe français, également historien et homme de lettres.Louis-François Benoiston de Châteauneuf
Sommaire[masquer] |
Après des études à l'École de médecine et au Val-de-Grâce, il effectue plusieurs campagnes en tant que chirurgien militaire. De retour à Paris en 1810, il obtient un poste administratif au ministère des Finances, ce qui lui permet de se consacrer à des travaux historiques et littéraires. Guidé par le mathématicien Siméon Denis Poisson, il entreprend en même temps les premières recherches statistiques auxquelles il doit sa réputation. Il se lie avec Louis René Villermé, avec qui il est chargé d'une mission d'étude en 1832. L'année suivante, les deux hommes sont élus membres de l'Académie des sciences morales et politiques. En 1835 et 1837, l'Académie confie à Benoiston de Châteauneuf deux enquêtes d'observation sur l'état économique et moral de la population. Les résultats en sont compilés sous forme de mémoires et de communications mais ne sont pas plus amplement diffusés en cette époque où lascience statistique en est encore à ses premiers essors. Balzac, qui mentionne Benoiston de Châteauneuf à deux reprises dans sa Comédie humaine, a parlé de lui comme « l'un des plus courageux savants qui se soient voués aux arides et utiles recherches de la statistique1 ». Biographie [modifier]
Publications [modifier]
Notes et références [modifier]
Source biographique [modifier]
07:54 Publié dans Louis-François Benoiston de Châteauneuf | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Théorème de Bayes
Le théorème de Bayes est un résultat de base en théorie des probabilités, issu des travaux du révérend Thomas Bayes et retrouvé ensuite indépendamment par Laplace. Dans son unique article, Bayes cherchait à déterminer ce que l’on appellerait actuellement la distribution a posteriori de la probabilité p d’une loi binomiale. Ses travaux ont été édités et présentés à titre posthume (1763) par son ami Richard Price dans Un essai pour résoudre un problème dans la théorie des risques (An Essay towards solving a Problem in the Doctrine of Chances). Les résultats de Bayes ont été repris et étendus par le mathématicien français Laplace dans un essai de 1774, lequel n’était apparemment pas au fait du travail de Bayes. Le résultat principal (la Proposition 9 de l’essai) obtenu par Bayes est le suivant : en considérant une distribution uniforme du paramètre binomial p et une observation m d'une loi binomiale Ses résultats préliminaires, en particulier les propositions 3, 4 et 5 impliquent le résultat que l’on appelle théorème de Bayes (énoncé plus bas) mais il ne semble pas que Bayes se soit concentré ou ait insisté sur ce résultat. Ce qui est « bayésien » (au sens actuel du mot) dans la Proposition 9, c’est que Bayes ait présenté cela comme une probabilité sur le paramètre p. Cela revient à dire qu’on peut déterminer, non seulement des probabilités à partir d’observations des issues d’une expérience, mais aussi les paramètres relatifs à ces probabilités. C’est le même type de calcul analytique qui permet de déterminer par inférence les deux. En revanche, si l’on en croit une interprétation fréquentiste, il ne peut pas exister de probabilité de distribution du paramètre pet par conséquent, on ne peut raisonner sur p qu’avec un raisonnement d’inférence non-probabiliste.Théorème de Bayes
 , où m est donc le nombre d’issues positives observées et n le nombre d’échecs observés, la probabilité que p soit entre a et b sachant m vaut :
, où m est donc le nombre d’issues positives observées et n le nombre d’échecs observés, la probabilité que p soit entre a et b sachant m vaut :
Sommaire[masquer] |
Le théorème de Bayes est utilisé dans l’inférence statistique pour mettre à jour ou actualiser les estimations d’une probabilité ou d’un paramètre quelconque, à partir des observations et des lois de probabilité de ces observations. Il y a une version discrète et une version continue du théorème. En théorie des probabilités, le théorème de Bayes énonce des probabilités conditionnelles : étant donné deux évènements A et B, le théorème de Bayes permet de déterminer la probabilité de A sachant B, si l’on connaît les probabilités : Ce théorème élémentaire (originellement nommé « de probabilité des causes ») a des applications considérables. Pour aboutir au théorème de Bayes, on part d’une des définitions de la probabilité conditionnelle : en notant soit le théorème de Bayes. Chaque terme du théorème de Bayes a une dénomination usuelle. Le terme P(A) est la probabilité a priori de A. Elle est « antérieure » au sens qu’elle précède toute information sur B. P(A) est aussi appelée la probabilité marginale de A. Le termeP(A|B) est appelée la probabilité a posteriori de A sachant B (ou encore de A sous condition B) . Elle est « postérieure », au sens qu’elle dépend directement de B. Le terme P(B|A), pour un B connu, est appelé la fonction de vraisemblance de A. De même, le terme P(B) est appelé la probabilité marginale ou a priori de B. On améliore parfois le théorème de Bayes en remarquant que afin de réécrire le théorème ainsi : où AC est le complémentaire de A. Plus généralement, si {Ai} est une partition de l’ensemble des possibles, pour tout Ai de la partition. Voyez aussi le théorème des probabilités totales. I. J. Good reprend une idée d’Alan Turing : les probabilités deviennent plus faciles à manier si au lieu de raisonner sur une probabilité p, on travaille sur une quantité construite de la façon suivante : Ev(p) = ln (p/(1-p)) ou Ev(p) = log (p/(1-p)) qu’il nomme weight of evidence, terme auquel on peut donner différentes traductions : « poids de témoignage », « valeur de plausibilité », etc. Ce qui est intéressant à en retenir est ceci : En calculs de fiabilité, où il faut manier des probabilités très grandes (1-ε) et très petites (ε), travailler en termes d’evidences permet une visualisation bien plus claire des classes de sécurité : une évidence de -70 dB correspond à une probabilité de 10-7, etc. On peut également travailler en gardant en toutes circonstances le même nombre de décimales et sans manipuler d’exposants, ce qui améliore la lisibilité des calculs. Il existe aussi une version du théorème pour les distributions continues, qui se déduit simplement de la densité jointe des observations et des paramètres, produit de la vraisemblance par la densité a priori sur les paramètres, par application de la définition des lois et des densités conditionnelles. La forme continue du théorème de Bayes peut aussi s'interpréter comme indiquant que la distribution a posteriori s’obtient en multipliant la distribution a priori, par la vraisemblance, et en effectuant une normalisation (du fait qu'il s'agit d'une densité de probabilité). En calcul bayésien, on prend donc l'habitude de travailler avec des signes de proportionnalité plutôt que des égalités pour diminuer la complexité des expressions puisque les constantes manquantes se retrouvent par intégration (en principe). Les techniques de simulation de type Monte Carloet MCMC n'utilisent d'ailleurs pas ces constantes de normalisation. L’exemple le plus connu est le suivant : si l’on observe K numéros de séries d’appareils, que le plus grand est S, et qu’on les suppose numérotés à partir de 1, quelle est la meilleure estimation du nombre N d’appareils existants ? On démontre[réf. nécessaire] que le meilleur estimateur simple est N = S.(K − 1) / (K − 2), et surtout que la précision de cette estimation croît très vite, même avec de petites valeurs de K. Autre exemple possible : supposons qu’une proportion p inconnue d’électeurs vote « oui » avec p ∈ [0,1]. On tire de la population un échantillon de n électeurs parmi lesquels un nombre x a voté « oui ». La fonction de vraisemblance vaut donc : En multipliant cela par la fonction de densité de probabilité a priori de p et en normalisant, on calcule la distribution de probabilité a posteriori de p, ce qui injecte l'information des nouvelles données du sondage. Ainsi, si la probabilité a priori de p est uniforme sur l'intervalle [0,1], alors la probabilité a posteriori aura la forme d'unefonction bêta. la constante étant différente de celle de la fonction de vraisemblance. La fonction bêta se retrouve avec une grande régularité dans ces questions d’estimation. Le calcul de la variation d’entropie entre l’ancienne et la nouvelle distribution permet de quantifier exactement, en bits, l’information obtenue. Les règles de la théorie mathématique des probabilités s’appliquent à des probabilités en tant que telles, pas uniquement à leur application en tant que fréquences relatives d’évènements aléatoires. On peut décider de les appliquer à des degrés de croyance en certaines propositions. Ces degrés de croyance s’affinent au regard d’expériences en appliquant le théorème de Bayes. Le Théorème de Cox-Jaynes justifie aujourd’hui très bien cette approche, qui n’eut longtemps que des fondements intuitifs et empiriques. À titre d’exemple, imaginons deux urnes remplies de boules. La première contient dix (10) boules noires et trente (30) blanches ; la seconde en a vingt (20) de chaque. On tire sans préférence particulière une des urnes au hasard et dans cette urne, on tire une boule au hasard. La boule est blanche. Quelle est la probabilité qu'on ait tiré cette boule dans la première urne sachant qu'elle est blanche? Intuitivement, on comprend bien qu'il est plus probable que cette boule provienne de la première urne, que de la seconde. Donc, cette probabilité devrait être supérieure à 50 %. La réponse exacte vient du théorème de Bayes. Soit H1 l’hypothèse « On tire dans la première urne. » et H2 l’hypothèse « On tire dans la seconde urne. ». Comme on tire sans préférence particulière, P(H1) = P(H2) ; de plus, comme on a certainement tiré dans une des deux urnes, la somme des deux probabilités vaut 1 : chacune vaut 50 %. Notons 'D' l’information donnée « On tire une boule blanche. » Comme on tire une boule au hasard dans une des urnes, la probabilité de D sachant/sous l’hypothèse H1 vaut : De même si l’on considère H2, La formule de Bayes dans le cas discret nous donne donc. Avant que l’on regarde la couleur de la boule, la probabilité d’avoir choisi la première urne est une probabilité a-priori, P(H1) soit 50 %. Après avoir regardé la boule, on révise notre jugement et on considère P(H1|D), soit 60 %, ce qui confirme notre intuition première. Qui croire, et avec quelle probabilité? Cette approche bayésienne est utilisée par les centres anti-poison pour détecter le plus vite possible et avec le maximum de précision le type d’empoisonnement dont souffre probablement un patient. Un problème régulièrement soulevé par l’approche bayésienne est le suivant : si une probabilité de comportement (délinquance, par exemple) est fortement dépendante de certains facteurs sociaux, culturels ou héréditaires, alors : Les faux positifs sont une difficulté inhérente à tous les tests : aucun test n’est parfait. Parfois, le résultat sera positif à tort, ce que l’on nomme parfois risque du premier ordre ou risque alpha. Par exemple, quand on teste une personne pour savoir si elle est infectée par une maladie, il y a un risque généralement infime que le résultat soit positif alors que le patient n’a pas contracté la maladie. Le problème alors n’est pas de mesurer ce risque dans l’absolu (avant de procéder au test), il faut encore déterminer la probabilité qu’un test positif le soit à tort. Nous allons montrer comment, dans le cas d’une maladie très rare, le même test par ailleurs très fiable peut aboutir à une nette majorité de positifs illégitimes. Imaginons un test extrêmement fiable : Imaginons que la maladie ne touche qu’une personne sur mille, soit avec une probabilité 0,001. Cela peut paraître peu mais dans le cas d’une maladie mortelle, c’est considérable. Nous avons toutes les informations nécessaires pour déterminer la probabilité qu’un test soit positif à tort, ce qui peut causer un surdiagnostic. Désignons par A l’évènement « Le patient a contracté la maladie » et par B l’évènement « Le test est positif ». La seconde forme du théorème de Bayes dans le cas discret donne alors : Sachant que le test est positif, la probabilité que le patient soit sain vaut donc environ : (1 − 0,019) = 0,981. Du fait du très petit nombre de malades, Si le traitement est très lourd, coûteux ou dangereux pour un patient sain, il peut être alors opportun de faire subir à tous les patients positifs un test complémentaire (qui sera sans doute plus précis et plus coûteux, le premier test n’ayant servi qu’à écarter les cas les plus évidents). On a tout de même réussi avec le premier test à isoler une population vingt fois moindre qui contient pratiquement tous les malades. En procédant à d’autres tests, on peut espérer améliorer la fiabilité du test. Le théorème de Bayes nous montre que dans le cas d’une probabilité faible de la maladie recherchée, le risque d’être déclaré positif à tort a un impact très fort sur la fiabilité. Le dépistage d'une maladie rare telle que le cancer peut causer le surdiagnostic.Le théorème de Bayes en Statistique [modifier]

 la probabilité que A et B aient tous les deux lieu. En divisant de part et d’autre par P(B), on obtient :
la probabilité que A et B aient tous les deux lieu. En divisant de part et d’autre par P(B), on obtient :
Autres écritures du théorème de Bayes [modifier]
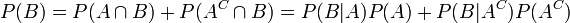
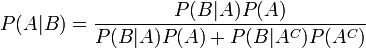

La démarche d’I. J. Good [modifier]
Théorème de Bayes pour des densités de probabilité [modifier]
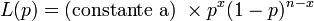

Inférence bayésienne [modifier]
Exemples [modifier]
De quelle urne vient la boule ? [modifier]

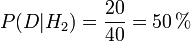

Pronostics contradictoires [modifier]
Aspects sociaux, juridiques et politiques [modifier]
« Faux positifs » médicaux [modifier]

Références [modifier]
Différentes versions de l’essai original, en anglais [modifier]
Commentaires en anglais [modifier]
Autres références [modifier]
Articles connexes [modifier]
07:53 Publié dans Théorème de Bayes | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Thomas Bayes
Thomas Bayes
| Thomas Bayes | |
|---|---|
| Naissance | vers 1702 Londres (Angleterre) |
| Décès | 17 avril 1761 Tunbridge Wells (Angleterre) |
| Domicile | Angleterre |
| Nationalité | |
| Champs | Mathématiques |
| Diplômé | Université d'Édimbourg |
| Célèbre pour | Théorème de Bayes |
| modifier |
|
Thomas Bayes (env. 1702, Londres - 17 avril 1761) est un mathématicien britannique et pasteur de l'Église presbytérienne, connu pour avoir formulé le théorème de Bayes. Ses découvertes en probabilités ont été résumées dans son Essais sur la manière de résoudre un problème dans la doctrine des risques (Essay Towards Solving a Problem in the Doctrine of Chances - 1763) publié à titre posthume dans les comptes-rendus de l'Académie royale de Londres (the Philosophical Transactions of the Royal Society of London). On lui connaît deux publications de son vivant : Né à Londres, il est mort à Tunbridge Wells, dans le Kent. Sa dépouille repose dans le cimetière de Bunhill Fields à Londres.
On lui doit en particulier une loi importante des probabilités, la règle de Bayes (posthume, 1763), très utilisée en classification automatique. Un exemple parmi d'autres est la lutte contre le pourriel, par la méthode dite d'inférence bayésienne.
Liens externes en anglais [modifier]
07:51 Publié dans Thomas Bayes | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
07/12/2010
Distributions dans le sillage de Laurent Schwartz Par Nicole Berline,Claude Sabbah
18:22 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Problèmes choisis de mathématiques supérieures Par Hervé Gianella,R. Krust,F. Taieb,Nicolas Tosel
18:14 Publié dans Problèmes choisis de mathématiques supérieures | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Matlab: aide-mémoire Par Kermit Sigmon
18:12 Publié dans Matlab: aide-mémoire | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Programmer avec Maple V Par M. B. Monagan,Waterloo Maple Software Inc.,K. O. Geddes,K. M. Heal,G. Labahn,S. M. Vorkoetter
18:11 Publié dans Programmer avec Maple V | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Sophus Lie: une pensée audacieuse Par Arild Stubhaug
18:10 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
LIVRE Essentials of mathematica
06:57 Publié dans LIVRE Essentials of mathematica, Livres | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
LIVRE Riemannian geometry
06:51 Publié dans Livres, Riemannian geometry | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
LIVRE Geometry of quantum states
06:49 Publié dans Geometry of quantum states, Livres | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
06/12/2010
Combinatorial Commutative Algebra and Applications
Winfried Bruns (Universität Osnabrück), Alicia Dickenstein (University of Buenos Aires, Argentina), Takayuki Hibi (Nagoya University), Allen Knutson (Cornell University), and Bernd Sturmfels (University of California, Berkeley) Important: Airline travel reimbursement restrictions If you are applying for funding, the funding deadline is Thu, Sep 23 2010 The Institute is committed to the principles of Equal Opportunity and Affirmative Action. Source : http://www.msri.org/web/msri/scientific/workshops/show/-/...
• Register
• Registration: Please register by the deadline of Mon, Dec 03 2012 if possible.
• Funding: Students, recent Ph.D.'s, women, and minorities are particularly encouraged to apply. Funding awards are made typically 6 weeks before the workshop begins. Requests received after the funding deadline are considered only if additional funds become available. Please see Travel funding rules
• Lodging information
• Visa information
• Directions to MSRI
or by regular mail to:
Mathematical Sciences Research Institute
17 Gauss Way, Berkeley, CA
94720-5070.
USA
21:43 Publié dans Combinatorial Commutative Algebra and Applications | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
L'Algorithme de Génération des Premiers
Version [pdf ] (1.07 Mo, 12 pages) L'Algorithme de Génération des Premiers (AGP)
Article déposé le 19 avril 2010. Toute reproduction pour publication ou à des fins commerciales, de la totalité ou d'une partie de l'article, devra impérativement faire l'objet d'un accord préalable avec l'éditeur (ENS Ulm). Toute reproduction à des fins privées, ou strictement pédagogiques dans le cadre limité d'une formation, de la totalité ou d'une partie de l'article, est autorisée sous réserve de la mention explicite des références éditoriales de l'article.
Une version courte de cet article a été publiée par la Revue Tangente (n°108, 2006). CultureMATH remercie la Revue Tangente d'avoir autorisé la publication de cette version complétée.
|
SOMMAIRE Avant propos 1. Du crible d'Eratosthène à l'AGP 2. Les lois mathématiques de l’AGP Théorème de "stabilisation" Conclusion : l’ordre plutôt que le chaos Bibliographie
Tableau : Algorithme de Génération de Premiers
Version courte de l'article en anglais - The Prime-Generating Algorithm |
1. Du crible d'Eratosthène à l'AGP
Le fameux crible d’Eratosthène vieux de plus de 2000 ans sera néanmoins un excellent moyen de comparaison pour introduire l’AGP. Rappelons son principe. Il est basé sur le fait qu’un nombre entier est premier s’il n’est pas divisible par tous les nombres qui lui sont strictement inférieurs à l’exclusion de 1. Si on cherche par exemple les nombres premiers inférieurs à cent, on opère ainsi : on place les nombres de 2 à 100 dans un tableau. On entoure le nombre 2 qui est premier, puis on barre les multiples stricts de 2 du tableau. On entoure le plus petit nombre non barré qui est 3. 3 est premier puisqu’il n’est pas divisible par les nombres qui lui sont inférieurs et qui se résument à 2. On entoure le nombre 3 et on barre tous les multiples stricts de 3. Le plus petit nombre non barré est 5 qui est premier car il n’est divisible ni par 2 ni par 3, ni par 4, et ainsi de suite. On obtient par ce procédé tous les nombres premiers inférieurs à cent. Le crible nous fait toucher du doigt qu’un nombre est premier en fonction de ceux qui l’ont précédé. Ainsi 5 est premier en fonction de la non divisibilité par 2 ou par 3. Ce qui explique d’ailleurs le mal que l’on a pour trouver les grands nombres premiers. A titre de comparaison élémentaire, si un nombre est pair cela ne dépend pas des nombres pairs qui l’ont précédé. Pour autant, si le crible permet de trouver les nombres premiers, il n’a pas la vocation d’expliquer leur répartition. Tout au contraire, il met en évidence que les nombres premiers apparaissent dans le tableau dans une succession qui ne laisse deviner aucun ordre et aucune loi, et c’est bien ce problème qui a tant intrigué, voire fasciné, les mathématiciens depuis plus de 2000 ans.
Dans le remarquable livre de Gilles Godefroy L’aventure des nombres, nous avons eu l’attention attiré par un chapitre intitulé : Connaître un ensemble par son complémentaire. Gilles Godefroy exprime d’abord l’idée qu’il est difficile d’exhiber des nombres premiers arbitrairement grands alors qu’on peut obtenir sans peine des nombres composés aussi grands soient - ils. Gilles Godefroy poursuit « Nous voyons ici poindre une idée, implicite chez Euclide comme chez Cantor : on peut étudier un ensemble au moyen de son complémentaire, montrer l’existence d’objets qui jouissent de certaines propriétés en étudiant les objets qui n’ont pas ces propriétés. Le crible d’Eratosthène, qui exhibe les nombres premiers comme étant ceux qui ne sont pas composés reflète d’ailleurs cette dissymétrie. » [1]
En effet, le crible se contente d’éliminer les composés pour faire apparaître les premiers. Avant de présenter notre algorithme (AGP) qui se propose plus précisément d’étudier les propriétés des nombres composés pour connaître leur complémentaire, les premiers, passons une dernière fois "au crible" le fameux crible! Quand on barre les multiples de trois on constate que des nombres ont déjà été barrés. Ce sont bien entendu les multiples communs à deux et à trois. Cette simple remarque met en évidence ceci : en prenant successivement tous les multiples des nombres premiers on décrit N tout entier, mais on ne réalise pas une partition de l'ensemble des entiers naturels N. Ce sera l’une des différences essentielles entre le crible et l’AGP. L’AGP réalise, lui, une partition de N ce qui offre un avantage considérable pour les problèmes de dénombrements. L’autre différence que nous allons bientôt constater est que dans le crible tous les nombres non premiers sont impitoyablement barrés. Dans l’AGP, au contraire les nombres non premiers sont tous écrits et jouent tous leur rôle dans la constitution de l’algorithme. Mais il est temps à présent de décrire l’AGP.
La première caractéristique de cet algorithme est d’abord d’utiliser le théorème fondamental de l’arithmétique qui dit que tout nombre entier s’écrit de manière unique comme produit de nombres premiers. Aucun résultat important sur les nombres premiers ne peut se dispenser de cette propriété essentielle. Ainsi le succès de la fonction zêta de Riemann dans l’étude de la répartition des nombres premiers, vient du fait qu’elle rend compte, dans sa définition même, de la décomposition des entiers en facteurs premiers.
La longueur d’un entier est le nombre de premiers qui entrent dans la décomposition de cet entier en produit de facteurs premiers. Exemples : la décomposition de 12 contient trois facteurs premiers (12= 2x2x3). Ainsi la longueur de 12 est 3. De même la longueur de 5 est 1.
Il est très facile d’exprimer le théorème fondamental de l’arithmétique en terme de longueur. En effet, appelons Er l’ensemble des entiers de longueur r, pour tout entier r. Dire que tout nombre est produit de manière unique de nombres premiers se traduit en disant que N est la réunion des Er, et que les Er forment une partition de N puisque Ei ∩ Ej = ∅ pour i ≠ j.
E1 est donc l’ensemble des nombres premiers. Mais c’est un ensemble qui se construit pas à pas comme on va le voir. 2 étant le plus petit nombre premier, observons que les ensembles Er ont un plus petit élément qui est 2r. C’est donc le plus petit nombre de longueur r.
Considérons à présent les intervalles Ir définis par : Ir = [2r ; 2r+1[ pour tout entier r. Tout entier de cet intervalle est strictement inférieur au plus petit entier de longueur r+1. Il en résulte que la longueur maximum des entiers de Ir est r. Cette longueur est atteinte par 2r. Nous admettrons provisoirement que les longueurs des entiers de Irprennent toutes les valeurs de 1 à r. Observons que les intervalles Ir forment une partition de N et que par conséquent il en est de même des ensembles Ir ∩ Ei lorsque ivarie de 1 à r.
L’algorithme AGP consiste à écrire successivement ces ensembles en commençant par r = 0, l’algorithme commençant vraiment pour r = 1 puisque 1 n’est pas premier. Comme ces ensembles forment une partition de N, nous allons être amenés à réécrire les nombres entiers selon notre loi algorithmique.
Tableau 1 : Algorithme de Génération de Premiers
| Longueurs des entiers | ||||||
| Intervalles Ir | 1 | 2 | 3 | 4 | 5 | ... |
| Io = [20 ; 21 [ | 1 |
|||||
| I1 = [21 ; 22 [ |
2 3 |
|||||
| I2 = [ 22 ; 23 [ | 5
7 |
2×3 2×2 |
||||
| I3 = [ 23 ; 24 [ | 11 13 |
2×5
2×7 3×5 3×3 |
2×2×2 2×2×3 |
|||
| I4 = [ 24 ; 25 [ |
17 19 23 29 31 |
2×11 2×13 3×7 5×5 |
2×3×3 2×2×5 2×3×5 2×2×7 3×3×3 |
2×2×2×2 2×2×2×3 |
||
| I5 = [ 25 ; 26 [ |
37 41 43 47 53 59 61 |
2×31
2×29 2×23 2×19 2×17 3×19 3×17 3×13 3×11 5×11 5×7 7×7 |
2×2×11 2×2×13 2×2×7 3×3×5 3×3×7 2×5×5 |
2×2×2×5
2×2×2×7 2×2×3×3 2×2×3×5 2×3×3×3 |
2×2×2×2×2
2×2×2×2×3 |
|
| ... |
Générés par 2 ; 3 ; 5 ; 7 ; 11 et 13 |
Stabilisé à 5 entiers Générés par 2 ; 3 ; 5 et 7 |
Stabilisé à 2 entiers Générés par 2 et 3 |
|||
On pourrait présenter de manière imagée l’algorithme ainsi : chaque intervalle Ir est un train. La locomotive est représentée par les nouveaux nombres premiers ; les wagons sont formés à l’aide des anciens. Le wagon de queue du train I4 est formé par les premiers de l’intervalle I1 à savoir 2 et 3. De plus le wagon de queue comportera toujours deux éléments quelque soit l’intervalle (dans I1000 les nombres de longueur mille sont au nombre de 2). L’avant dernier wagon de I4 (les nombres de longueur 3) est formé des premiers qui se trouvent dans I1 et I2. Le nombre d’entiers de ce wagon est cinq et on peut montrer qu’il est stabilisé. C'est-à-dire que le nombre d’entiers de l’avant dernier wagon (les entiers de longueur 4) du train suivant I5 est aussi égal à cinq comme on peut l’observer sur le Tableau 1. Plus les trains sont longs plus il y a de wagons comportant un nombre stabilisé d’entiers. Ainsi on montre que dans I100 les trente-six derniers wagons ont un nombre d’entiers stabilisé (voir ci-dessous le théorème dit de « stabilisation »).
2. Les lois mathématiques de L’AGP
On donne ici une série de théorèmes qui expliquent le fonctionnement de l’AGP. Le théorème de « stabilisation » (théorème 4) nous paraît le plus important.
Soit l’intervalle Ir = [2r ; 2r+1[. On désigne par Lr,m les entiers de Ir de longueur m. L’entier m varie donc de 1 à r.
Théorème 1
A) Les nombres premiers q qui sont dans la décomposition des entiers de Lr,m sont tels que q < 2 r - m + 2.
B) Pour tout q premier vérifiant la condition q < 2 r - m + 2 il existe au moins un entier de Lr,m , avec 2 ≤ m ≤ r, qui contient q comme facteur.
Preuve A)
Si q ≥ 2 r - m + 2 alors 2m-1q ≥ 2r+1.
Or 2m-1q est le plus petit entier de longueur m qui contient q. Donc il n’y a aucun entier de Lr,m contenant q.
On a donc nécessairement q < 2 r - m + 2 .
Pour démontrer B nous avons besoin du lemme suivant :
Lemme
Pour tout réel x ≥ 2 on peut toujours trouver un nombre premier compris entre x et 2x.
Preuve
Rappelons que le postulat de Bertrand assure que pour tout entier n > 1 on peut toujours trouver un nombre premier compris entre n et 2n.[3]
Soit x réel, x ≥ 2 et E(x) la partie entière de x. On a E(x) > 1 et d’après Bertrand il existe un nombre premier p tel que E(x) < p < 2 E(x) qui entraîne E(x) + 1 ≤ p < 2E(x).
Comme E(x) ≤ x < E(x) +1. On déduit x < E(x) + 1 ≤ p < 2 E(x) ≤ 2x ce qui prouve notre assertion.
Preuve B)
Soit q < 2 r - m + 2.
Si 2 r - m + 1 ≤ q < 2 r - m + 2 alors 2 r ≤ 2 m - 1 q < 2 r - 1.
Donc pour 2 ≤ m ≤ r il existe bien au moins un entier de Lr,m qui contient q comme facteur.
Si q < 2 r - m + 1 alors 2 r - m + 1 / q > 1 et 2 r - m + 2 /q > 2.
Donc d’après le lemme précédent, il existe un nombre premier p entre 2 r - m + 2 /q et 2 r - m + 3 /q.
On en déduit pour 2 ≤ m ≤ r que 2 m - 2 pq est dans Ir et ce nombre est bien un entier de longueur m qui contient q comme facteur.
En d’autres termes les entiers de longueur m telle que 2 ≤ m ≤ r d’un intervalle Ir sont « engendrés » par tous les nombres premiers inférieurs ou égaux à ceux de l’intervalle I r - m +1. (On dira que des nombres premiers engendrent une collection H de nombres entiers si tous ces premiers se trouvent dans la décomposition des entiers de H et s’il n’y en a pas d’autres).
Pour bien comprendre ce résultat il est utile de reprendre le tableau précédent de notre algorithme correspondant à l’intervalle I4 = [ 24 ; 25[ :
Tableau 2
| L4,1 | L4,2 | L4,3 | L4,4 |
| 17 | 2×11 | 2×3×3 | 2×2×2×2 |
| 19 | 2×13 | 2×2×5 | 2×2×2×3 |
| 23 | 3×7 | 2×3×5 | |
| 29 | 5×5 | 2×2×7 | |
| 31 | 3×3×3 |
On a dit que les entiers de Lr,m sont engendrés par les nombres premiers qui vérifient q < 2 r - m + 2.
Donc en faisant r = 4 on a L4,m qui est engendré par les q < 2 6 - m :
Pour m = 4 on a L4,4 engendrés par les premiers q < 2² soit q = 2 et q = 3.
Pour m = 3 on a L4,3 engendrés par les premiers q < 23 soit q = 2 , q = 3, q = 5, q = 7.
Pour m = 2 on a L4,2 engendrés par les premiers q < 24 soit q = 2 et q = 3, q = 5, q = 7, q = 11 , q = 13.
Ce que l’on vérifie aisément avec le tableau de I4.
Théorème 2
Les nombres premiers qui engendrent Lr,m avec 2 ≤ m ≤ r sont les mêmes que ceux qui engendrent Lr+n,m+n, avec n entier relatif tel que n ≥ 2 - m.
Preuve
Les premiers qui engendrent Lr,m avec 2 ≤ m ≤ r sont les premiers q tels que q < 2 r - m + 2 .
Les premiers qui engendrent Lr+n,m+n avec 2 ≤ m+ n ≤ r + n (qui équivaut à n ≥ 2 - m sous l’hypothèse 2 ≤ m ≤ r) sont les premiers tels que q < 2 r+n - (m+n) + 2, c'est-à-dire q < 2 r - m + 2.
Ce sont donc les mêmes que ceux qui engendrent Lr,m.
Par exemple, on voit dans le Tableau 1 donnant le début de l’algorithme : les entiers de L4,3 sont 2×3×3 ; 2×2×5 ; 2×3×5 ; 2×2×7 ; 3×3×3, et ceux de L3,2 sont 2×5 ; 2×7 ; 5×5 ; 3×3.
Ces deux collections d’entiers sont engendrés par les mêmes premiers 2 ; 3 ; 5 et 7 tels que q < 23.
Théorème 3
Pour m ≥ (r+1)ln2 / ln3 tous les entiers de Lr,m sont pairs.
Preuve
En effet, 3m est le plus petit entier de longueur m qui n’est pas pair. Donc pour 3m ≥ 2r+1 tout entier de Lr,m est pair, ce qui est vrai pour m ≥ (r+1)ln2 / ln3.
Théorème 4 (dit de "stabilisation")
Pour r entier et pour m ≥ (r+1)ln2 / ln3 on a card( Lr,m)= card( Lr + n, m + n) pour tout entier n.
Preuve
D’après le Théorème 3, pour m ≥ (r+1)ln2 / ln3 les entiers de Lr,m sont pairs.
Dans ce cas, on en déduit que pour tout n, m + n ≥ (r+1)ln2 / ln3 + n.
Comme ln2 / ln3 < 1 on a n ln2 / ln3 < n et finalement m + n ≥ (r + n + 1)ln2 / ln3 qui prouve toujours d’après le théorème 3 que les entiers de Lr + n, m + n sont pairs.
Montrons à présent que, lorsque les entiers de Lr,m sont pairs, card (Lr,m)= card (Lr + 1, m+1).
Si q1.q2…qm est un élément de Lr,m alors 2q1.q2…qm est dans Lr + 1, m+1.
Et si n’ est un élément de Lr + 1, m+1 , comme il est pair, il est de la forme 2 q'1.q'2…q'm et q'1.q'2…q'm est élément de Lr,m.
Donc les entiers de Lr + 1, m+1 sont tous les entiers 2n tels que n soit entier de Lr,m.
On a donc card (Lr,m)= card (Lr + 1, m+1).
On en déduit par itération : card( Lr,m)= card( Lr + n, m + n) pour tout entier n.
Par exemple pour I100 on trouve m ≥ (101)ln2 / ln3 , soit m ≥ 64.
Il y a donc 36 longueurs d’entiers dans I100 dont le cardinal est stabilisé. En d’autres termes, pour employer l’image ferroviaire précédente, pour r ≥ 100 les 36 derniers wagons d’entiers de Ir auront toujours le même cardinal.
Théorème 5
Pour n ≥ (r+1)ln2 / (ln3 - ln2) le nombre des entiers de Lr+n,1+n se stabilise.
Preuve
En effet, un raisonnement analogue à celui des théorèmes 3 et 4 conduit à la majoration 3n+1 ≥ 2r + n +1 qui donne le résultat annoncé.
Théorème 6
Pour m ≥ (r+1)ln2 / ln (p) il n’y a aucun entier dans Lr,m dont tous les termes sont supérieurs ou égaux à p, un nombre premier.
Preuve
En effet, pm est le plus petit entier de longueur m dont tous les facteurs sont supérieurs ou égaux à p.
Donc pour pm ≥ 2r +1 , il n’y a aucun entier dans Lr,m dont tous les facteurs premiers sont supérieurs ou égaux à p. Soit pour m ≥ (r+1)ln2 / ln (p).
Remarque : si on désigne par m0 le plus petit entier m qui vérifie la majoration précédente, on peut en déduire que pour m < m0 il existe au moins un entier de Lr,m dont tous les facteurs premiers sont supérieurs ou égaux à p.
À titre d’exemple plaçons-nous dans I4. Pour p = 5 on trouve : m ≥ 2,15… ce qui donne m = 3 pour le plus petit entier vérifiant cette condition.
On se rapportera au Tableau 2 ci-dessus. Pour m = 2 on en déduit qu’il existe au moins un nombre dont tous les termes sont supérieurs ou égaux à 5, ce que confirme le nombre 5×5.
Toujours dans I4 et pour p = 7 on trouve : m ≥ 1,78 soit m ≥ 2. Nous laissons au lecteur le soin de trouver ce qu’il en résulte pour m.
Conclusion : l’ordre plutôt que le chaos
L’AGP a permis de révéler une structure. Les intervalles Ir apparaissent dans cet algorithme comme la cellule de fabrication d’une collection de nombres premiers Prqui n’interviennent jamais dans la formation des entiers de Ir et a fortiori dans les intervalles précédents. En revanche ils vont servir à engendrer les intervalles suivants : les entiers de longueur 2 de Ir+1, les entiers de longueur 3 de Ir+2 et ainsi de suite jusqu’à une longueur n dont le cardinal va se stabiliser. Par ailleurs chaque intervalle Ircomprend exactement r longueurs d’entiers qui sont engendrés de r à 2 respectivement par P1 ; P1 ∪ P2 ; ... ; P1 ∪ P2 …∪ Pr-1. Si bien que l’intervalle Ir apparaît aussi comme l’historique des nombres premiers construits avant lui. Il y a là un véritable mouvement d’horlogerie qui montre davantage l’ordre que le chaos. Si l’on considère la suite des nombres premiers donnés dans les tables, elle semble être régie par le hasard. Cela provient du fait, à notre avis, que la suite ordonnée des nombres entiers donne la priorité à la structure additive de N. Dans notre algorithme qui donne la priorité à la structure multiplicative qui définit les nombres premiers, un ordre nouveau apparaît avec des lois d’une rigoureuse précision. On voit que ce n’est plus le nombre premier seul, qu’il faut considérer mais la collection de ceux qui sont contenus dans chaque intervalle Ir. Ramener l’étude des nombres premiers de N à ceux des intervalles Ir, telle est la voie que nous proposons. L’encadrement entre des puissances de deux est essentiel. Il suffit de construire un algorithme avec comme encadrement des puissances de trois pour constater qu’il n’offre pas d’intérêt. On voit aussi que l’algorithme offre des perspectives dans le domaine du dénombrement et du même coup on retrouve le grand problème de la répartition des nombres premiers. L’étude des entiers de longueur 2, mis en évidence dans l’AGP, concerne les problèmes de cryptographie. Les nombres premiers de Mersenne ont une place privilégiée dans l’AGP. En effet le plus grand nombre de chaque intervalle Ir est 2r+1 - 1 et par conséquent tous les nombres premiers de Mersenne seront à cette place, ce qui n’est peut-être pas anodin. C’est sur ces perspectives que nous terminons cet article.
Bibliographie commentée
Jacques Bienvenu, "L'algorithme de génération des premiers (AGP)", Revue Tangente, n°108, 2006
Chris Caldwell, Site Web "The primes pages", http://primes.utm.edu/.
Un site fameux et très complet sur les nombres premiers.
Jean-Paul Delahaye, Merveilleux nombres premiers. Voyage au cœur de l'arithmétique. Éditions Belin/Pour la science, Paris, 2000.
Incontournable référence.
Gilles Godefroy, L’aventure des nombres, Editions Odile Jacob, 1997.
Une réflexion profonde sur la notion et l’histoire des nombres.
Andrew Grandville, "Nombres premiers et chaos quantique", 2002. En ligne http://smf4.emath.fr/Publications/Gazette/2003/97/smf_gaz...
Cet article fascinant et accessible porte sur des recherches récentes.
Edouard Lucas, Théorie des nombres, Gauthier-Villars, 1891, réédition Jacques Gabay, 1991.
Ouvrage historiquement très intéressant dans lequel on observe que toutes les questions ouvertes sur les nombres premiers posées en 1891 n’ont toujours pas été résolues.
M. Mendes France, G. Tenenbaum, Les nombres premiers. Que sais-je? vol. 571. Presses Universitaires de France, 1997.
Un classique.
[3] Le postulat conjecturé Joseph Bertrand en 1845 a été démontré pour la première fois en 1850 par Pafnouti Tchebychev. Une démonstration relativement simple a été publiée par Paul Erdös en 1932. Voir à ce sujet l'article de Wikipedia http://fr.wikipedia.org/wiki/Postulat_de_Bertrand
21:37 Publié dans L'Algorithme de Génération des Premiers | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Imparité rythmique
Article déposé le 20 octobre 2010. Toute reproduction pour publication ou à des fins commerciales, de la totalité ou d'une partie de l'article, devra impérativement faire l'objet d'un accord préalable avec l'éditeur (ENS Ulm). Toute reproduction à des fins privées, ou strictement pédagogiques dans le cadre limité d'une formation, de la totalité ou d'une partie de l'article, est autorisée sous réserve de la mention explicite des références éditoriales de l'article. Imparité rythmique
Version [pdf] (157 ko, 9 pages)
Dans un article récent Marc Chemillier a étudié deux exemples de structure mathématique associés à des répertoires musicaux de sociétés africaines de tradition orale. L'un de ces exemples concerne une structure rythmique asymétrique utilisée entre autres par les Pygmées Aka, un peuple de chasseurs-cueilleurs vivant dans la forêt tropicale, au sud-ouest de la République centrafricaine, dans la vallée de la Lobaye. L'ethnomusicologue Simha Arom a observé que ces rythmes africains ont un aspect asymétrique caractéristique, obtenu en combinant des durées successives de 2 et 3 unités. Considérons par exemple la suite de durées 32222322222 et représentons la sur un cercle (voir la Figure 1 ci-dessous extraite de l'article "Mathématiques de la musique d'Afrique centrale" de Marc Chemillier) pour signifier qu'elle est répétée plusieurs fois. La propriété, appelée imparité rythmique, exprime le fait qu'on ne peut couper le cercle en deux parties égales faites de durées successives.
Motivation
|
Figure 1
 |
Notons R l'ensemble des mots rythmiques et ε le mot rythmique de longueur nulle. Soit δ la permutation de R définie par δ(ε)=ε et δ(au)=ua,a∈{2,3},u∈R. Lesconjugués d'un mot rythmique m sont les mots de la forme δk(m) pour tout entier k. Le préfixe de longueur λ d'un mot rythmique m=x0x1…xl-1, l≥λ, est le mot x0x1…xλ-1. Le mot xixi+1…xj-1, 0≤i<j≤l, est le préfixe de longueur j-i du mot conjuguéδi(m). Un mot rythmique m de hauteur h est donc impair si et seulement si tout préfixe de tout conjugué de m est de hauteur différente de h/2. La caractérisation suivante affirme que l'on peut tester l'imparité rythmique en examinant seulement les préfixes d'une longueur fixe. La longueur de m est 2l+1=9 et sa hauteur est 2h=24. Chaque préfixe de longueur l=4 d'un conjugué de m a une hauteur égale à h-2=10 ou h-1=11. Il s'ensuit que m est impair d'après le lemme.
Un mot rythmique est une séquence finie m=x0x1…xl-1 dont chaque terme xi est égal à l'entier 2 ou 3. L'entier l est la longueur de m et l'entier h=∑0≤i<lxi est la hauteurde m. Le mot rythmique m est impair s'il n'existe aucun sous-mot xixi+1…xj-1, 0≤i<j≤l, de hauteur égale à h/2. Il est évident qu'un mot rythmique est impair si sa hauteur est un entier impair. Nous proposons quelques caractérisations et une construction des mots rythmiques impairs de hauteur paire.
1. Énoncé des résultats de base
1.1 Test de l'imparité rythmique
Lemme 1 Un mot rythmique m de hauteur paire égale à 2h est impair si et seulement si les deux conditions suivantes sont réalisées :
- La longueur de m est impaire, soit 2l+1.
- Les préfixes de longueur l des conjugués de m ont une hauteur égale à h-2 ou h-1.
Exemple Le mot rythmique m= 332323323 engendre par répétition le rythme mokongo des pygmées Aka. Chacun des conjugués, listés ci-dessous en appliquant itérativement δ, engendre le même rythme.
332323323, 323233233, 232332333, 323323332, 233233323, 332333232, 323332323, 233323233, 333232332
1.2 Appariement d'un mot rythmique
À partir de maintenant les opérations arithmétiques sur les indices d'un mot m=x0x1…xl-1 seront effectuées mod l. Soit un entier d tel que 0<d≤l/2. Un appariement de m à distance d est une partition du sous-ensemble d'indices {i:0≤i<l,xi=3} en paires d'indices de la forme {j,j+d}.
Théoreme 1 Un mot rythmique m de hauteur paire est impair si et seulement si les deux conditions suivantes sont réalisées :
- La longueur de m est impaire, soit 2l+1.
- Le mot m admet un appariement à distance l.
Exemple (suite) Répartissons les valeurs successives de m le long d'un cercle trigonométrique (la première lettre de m figure le plus à droite). Les trois cordes représentent un appariement à distance 4.
|
Figure 2
 |
Preuve du Théorème 1
2. Applications
2.1 Lecture par sauts
Soit un mot m=x0x1…xl-1 et un entier p premier avec l. Notons m(p) le mot de longueur l obtenu en lisant les lettres de m de façon circulaire en partant de l'indice 0 et en sautant à chaque fois p indices plus loin pour lire la prochaine lettre. Formellement, si l'on pose m(p)=y0y1…yl-1, on a
yi=xip, 0≤i<l (1)
en calculant chaque produit ip mod(l).
Puisque p est premier avec l il existe un entier q tel que qp=1 mod(l). On a alors
yiq=xiqp=xi,0≤i<l (2)
Il s'ensuit que m(p)(q)=m (3)
Corollaire 1 Un mot rythmique m de hauteur paire est impair si et seulement si les deux conditions suivantes sont réalisées :
- La longueur de m est impaire, soit 2l+1.
- Le mot m(l) admet un appariement à distance 1.
Remarque Posons mʹ=m(l). On retrouve le mot m en appliquant la relation (3) avec q=-2, soit m=mʹ(-2).
Exemple (suite) On vérifie que mʹ=m(4)=323322333. Le mot mʹ admet l'appariement A={{2,3},{6,7},{8,0}} à distance 1, qui est représenté ci-dessous. On vérifie que m=mʹ(-2) (lecture circulaire de mʹ par sauts successifs de 2 positions vers la gauche).
|
Figure 3
 |
Posons les définitions suivantes pour un mot rythmique mʹ de longueur impaire qui admet un appariement A à distance 1 (unique d'après la propriété précédente). Un sous-mot réductible de mʹ est un sous-mot égal à 33 dont les indices forment une paire appartenant à A. Le mot mʹ est bien apparié si chaque occurrence de 3 apparaît dans un sous-mot réductible. La réduction d'un mot mʹ bien apparié est le mot binaire (sur l'alphabet {0,1}) obtenu en remplaçant chaque occurrence de 2 par 0 et chaque sous-mot réductible par 1. De façon générale on vérifie facilement que si un mot rythmique mʹ de longueur impaire admet un appariement à distance 1 sans être bien apparié alors δ(mʹ) est bien apparié. Nous venons de voir comment associer un mot binaire à un mot rythmique impair de hauteur paire. Nous allons maintenant faire le chemin inverse. Soient deux entiers positifs p et q. Nous désirons énumérer l'ensemble R=R(2p+1,2q) des mots rythmiques impairs de hauteur paire comprenant 2p+1 occurrences de 2 et2q occurrences de 3. Ce n'est pas l'énumération complète de R qui nous intéresse car deux mots conjugués engendrent le même rythme par répétition. Il importe plutôt d'énumérer les classes de conjugaison contenues dans R en fournissant un représentant dans chacune d'entre elles. Disons de façon générale qu'un ensemble de mots C {em représente} un ensemble de mots M si C contient un élément et un seul de chaque classe de conjugaison incluse dans M. Il s'agit donc de construire un ensemble de mots qui représente R. Nous allons voir que ce problème peut se ramener à celui de la construction d'un ensemble de mots qui représente l'ensemble B=B(2p+1,q) des mots binaires (sur l'alphabet {0,1}) contenant 2p+1 occurrences de 0 et q occurrences de 1. Soit un mot b∈B. Remplaçons chaque occurrence de 0 par 2 et chaque occurrence de 1 par le mot 33. Nous obtenons ainsi un mot mʹ dans l'ensemble A=A(2p+1,2q)des mots rythmiques admettant un appariement à distance 1 et contenant 2p+1 occurrences de 2 et 2q occurrences de 3. Considérons la fonction f:B→A définie parf(b)=mʹ. Le mot m=mʹ(-2) appartient à R d'après le corollaire 1 et la remarque qui suit. Considérons la fonction g:A→R définie par g(mʹ)=m. La composée h=g∘f associe à tout mot b∈B un mot h(b)∈R. Corollaire 2 Si C est un ensemble de mots qui représente B alors h(C) représente R. Exemple L'ensemble B(3,3), qui contient quatre classes de conjugaison, est représenté par C={000111,001011,001101,010101} (le minimum lexicographique a été choisi dans chaque classe de conjugaison). Le tableau ci-dessous reprend une partie de la table 2 d'un article de Marc Chemillier et Charlotte Truchet [1]. Il détaille la construction d'un mot rythmique impair de hauteur 24 pour chaque élément b∈C.
Preuve du corollaire 1
2.2 Réduction d'un mot rythmique bien apparié
Propriété 1 Si un mot rythmique de longueur impaire admet un appariement à distance 1 alors cet appariement est unique.
Preuve de la Propriété 1
2.3 Construction des mots rythmiques impairs de hauteur paire
| b | m' | m = m'(-2) | |
| 1 | 000111 | 222333333 | 233323332 |
| 2 | 001011 | 223323333 | 233323323 |
| 3 | 001101 | 223333233 | 233323233 |
| 4 | 010101 | 233233233 | 233233233 |
Remarques Le mot rythmique de la ligne numéro 1 engendre le rythme mokongo. Celui de la ligne 2 engendre le rythme mokongo rétrograde. Celui de la ligne 3 n'est pas utilisé dans un rythme connu. Le mot rythmique 4 a une période égale à 3 ; il engendre le même rythme que 233. Le théorème 1 donne une caractérisation facile à vérifier de l'imparité rythmique. La section 2.3 établit une bijection entre l'ensemble de mots rythmiques R(2p+1,2q) et l'ensemble de mots binaires B(2p+1,q), dont la compréhension est très simple. Cependant la construction donnée dans cette section manque de naturel en requérant de calculer le mot mʹ(-2) à partir d'un mot binaire mʹ appartenant à B(2p+1,q). Nous préférons la construction suivante d'un mot rythmique impair. Pour la décrire convenons de dire que, pour un nombre impair positif 2p+1, le nombre p en est lamoitié. Partons d'un mot rythmique impair de longueur 2p+1 ne contenant que des occurences du symbole 2 réparties sur un cercle. Plaçons une occurence du symbole 3 n'importe où sur le cercle sauf en un point où l'on a déjà placé une occurence de 2. En parcourant le cercle à partir de cette occurence de 3 sautons par dessus un nombre d'occurences de 2 égal à la moitié du nombre de symboles écrits initialement (la moitié est ici égale à p) et plaçons alors une nouvelle occurence de 3. On peut recommencer la même opération en écrivant sur le cercle une nouvelle occurence de 3 et, après avoir sauté la moitié des occurences déjà placées (la moitié est maintenant égale à p+1), en écrivant une nouvelle occurence de 3. Et ainsi de suite en prenant la précaution de sauter successivement au dessus de p+2, p+3, … occurences déjà placées avant d'écrire une seconde occurence de 3. La validité de la construction peut se vérifier à partir du théorème 1. Elle est simple en exigeant seulement de sauter au dessus de symboles déjà écrits en les comptant jusqu'à la moitié de ces symboles. Un principe semblable pourrait-il avoir été utilisé dans la construction originale des rythmes des pygmées Aka ? Il faut signaler ici que Marc Chemillier a déjà décrit une construction des rythmes impairs en appliquant successivement, à partir du couple de mots (ε,ε), deux transformations a:(u,v)↦(3u,3v) et b:(u,v)↦(v,2u), où (u,v) est un couple de mots. Si la transformation b est appliquée un nombre impair de fois et si (u,v) est le couple de mots final, alors uv est un mot rythmique impair. Est-il possible de relier cette transformation aux méthodes introduites dans cette note ?
Preuve du Corollaire 2
Conclusion
Bibliographie
[2] Marc Chemillier, "Mathématiques de la musique d'Afrique centrale", CultureMATH, 2009
21:36 Publié dans Imparité rythmique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Urnes aléatoires, populations en équilibre et séries génératrices
Article déposé le 28 novembre 2010. Validation scientifique : Grégory Ginot (ENS Ulm) - Editeur : Eric Vandendriessche. Toute reproduction pour publication ou à des fins commerciales, de la totalité ou d'une partie de l'article, devra impérativement faire l'objet d'un accord préalable avec l'éditeur (ENS Ulm). Toute reproduction à des fins privées, ou strictement pédagogiques dans le cadre limité d'une formation, de la totalité ou d'une partie de l'article, est autorisée sous réserve de la mention explicite des références éditoriales de l'article. Urnes aléatoires, populations en équilibre et séries génératrices
Version [pdf] (284 ko, 15 pages)
Le but de cet article est de présenter un objet étudié en probabilités : les urnes aléatoires. Une urne aléatoire est une boite opaque, contentant des boules de deux couleurs, disons rouge et bleu. Sur la boite on a inscrit une règle d'évolution, sous la forme suivante : α, β, γ et δ sont des entiers fixés, et on suppose qu'avant le premier tirage, le nombre de boules de chaque couleur présentes dans la boite est connu. On cherche alors comment la composition de cette urne évoluera au fil des tirages. Le nombre de boules présentes dans l'urne après n tirages forme deux suites de variables aléatoires que l'on appelle une chaîne de Markov, c'est-à-dire que seule la valeur de la suite à l'instant n influe sur la loi de la (n+1)ième variable aléatoire. Insistons sur le fait que dans notre règle d'évolution, on a supposé que la boule tirée est remise dans l'urne. Un des intérêts des urnes aléatoires est qu'elles donnent des modèles, simples à comprendre et à utiliser, pour simuler des phénomènes divers, en physique, en biologie... On peut par exemple s'intéresser à l'évolution d'un gaz dans deux chambres reliées l'une à l'autre par un trou, pour savoir s'il est possible que tout le gaz rentre dans la première chambre. C'est dans ce but qu'Ehrenfest a introduit l'urne qui porte son nom, afin de démontrer certains paradoxes de la thermodynamique qui annonçait qu'une telle évolution était impossible, le gaz devant forcément s'équilibrer entre les deux chambres. L'urne évolue ainsi : lorsqu'on tire une boule d'une couleur, on la remplace par une boule de l'autre couleur. Le lien avec le modèle est le suivant. On suppose que l'écoulement dans les chambres se fait une molécule après l'autre. Les boules rouges représentent les molécules présentes dans la chambre de gauche, et les bleues celles de la chambre de droite. A chaque étape, une molécule au hasard parmi toutes les molécules présentes change de chambre. On retrouve bien le problème d'Ehrenfest. Nous pouvons également citer la modélisation d'évolutions de populations. Des modèles déterministes, comme la suite de Fibonacci, que nous expliciterons en Section 2.3. sont connus depuis bien longtemps. Les urnes aléatoires permettent d'obtenir d'autres types de modèles, aléatoires, comme l'urne de Pólya que nous présenterons en Section 3.2, qui permet par exemple de modéliser l'évolution d'une population dans laquelle deux versions d'un même gène coéxistent. Pour cette urne, les boules rouges représentent alors des individus possédant l'une des versions de ce gène, et les boules bleues ceux possédantl'autre version. La boule que l'on tire est alors considérée comme un descendant possédant l'une des deux versions du gène. On ajoute donc dans l'urne une boule de la même couleur que celle que nous avons piochée, et remise. Afin de calculer la probabilité pour qu'après n étapes, il y ait un certain nombre de boules rouges dans l'urne, nous aurons besoin d'une notion très utile en combinatoire, celle de série génératrice. L'idée est d'associer une fonction à une suite, de telle sorte que des égalités sur les quantités de la suite (comme des formules de récurrence) se transforment en équations fonctionnelles (équation différentielle, équation du second degré, etc.). On utilise alors des résultats d'analyse afin de déterminer cette fonction, pour ainsi remonter à la suite inconnue. D'une certaine manière, la série génératrice (la fonction associée) "retient" toute l'information contenue dans la suite, y compris pour les très grandes valeurs, alors qu'en combinatoire, la plupart des raisonnements se font à entier n fixé. Cette "connaissance" des grandes valeurs nous permet alors d'appliquer les relations connues à toute la suite à la fois, et donc d'obtenir une information supplémentaire. De plus les outils d'analyse permettent une écriture très simple de certaines relations compliquées. Nous commencerons par présenter les séries génératrices, que nous appliquerons tout d'abord au calcul de la fameuse suite de Fibonacci. Ensuite nous reviendrons aux urnes aléatoires en général, avant d'appliquer les résultats présentés au cas de l'urne de Pólya. Présentons maintenant ce qu'est une série génératrice. On a déjà expliqué qu'il s'agissait d'une fonction associée à une suite permettant notamment deux opérations : connaissant la fonction, on doit pouvoir retrouver la suite, et les relations connues sur les suites doivent pouvoir se traduire sur la fonction. Nous définissons la série génératrice associée à la suite (an)n∈ N comme : Cette fonction est bien définie pour z assez petit, pourvu que (an)n∈ N ne croisse pas trop vite. Par exemple, si an≤An pour tout n, la limite de (∑k=0nakzk)n∈ N existe pour tout ∣z∣<1A. Donc dans ce cas, la série génératrice est bien définie, et on peut calculer avec. Nous devons pour commencer vérifier que les séries génératrices caractérisent les suites auxquelles elles sont associées de manière non équivoque, c'est-à-dire que si deux séries génératrices sont égales, alors les suites associées le sont aussi. Prenons deux suites (an)n∈N et (bn)n∈ N. Si nous avons : Par conséquent, à chaque fonction est associée au plus une série génératrice, mais cette preuve nous donne davantage : connaissant une fonction qui est une série génératrice, nous pouvons calculer la suite de termes associée en utilisant la méthode précédente. Par exemple, pour f(z)=11+z2, nous avons : Nous pourrions bien sûr itérer ce processus pour obtenir pour tout entier n : Une autre propriété intéressante de ces séries est leur comportement intuitif vis-à-vis des opérations usuelles. Notamment, si l'on pose : Par conséquent, fʹ est la série génératrice associée à la suite ((n+1)an+1)n∈N, f+g est celle associée à (an+bn)n∈N, et fg à (∑k=0nakbn-k)n∈N. Intéressons-nous maintenant à la détermination de séries génératrices remarquables, qui nous permettrons de calculer par la suite les développements des fonctions que nous obtiendrons. Les séries génératrices que nous aurons à développer par la suite pourront être exprimées comme somme de fonctions plus simples de la forme z→1(1-z)i. Par conséquent nous allons déterminer quelles sont les suites associées à ces fonctions. Nous commençons par calculer le développement de z→11-z. Soit gn la fonction définie (pour ∣z∣<1) comme suit : Dès lors nous pouvons écrire, pour a,b,c∈ R : Nous allons généraliser un peu plus notre propos, et développer fp:z→1(1-z)p. Pour cela procédons par récurrence. On sait que pour p=1, tous les coefficients sont égaux à 1. Pour p=2, remarquons que f2=f1ʹ. Par conséquent, il suffit de dériver l'écriture de f1 en série génératrice pour obtenir : La suite de Fibonacci a été introduite au XIIIe siècle par Leonardo Fibonacci. Cette suite peut représenter, par exemple, l'évolution d'une population de lapins qui se reproduisent de la manière suivante. Un jeune couple de lapins met un mois à devenir adulte, et tout couple de lapins adultes donne naissance à un nouveau couple chaque mois. On note fn le nombre de couples de lapins présents au début du nième mois, et on suppose qu'au premier mois, on ne possède qu'un unique couple de jeunes lapins. Nous commençons par déterminer la formule de récurrence. Le nombre de couples de lapins naissant le (n+2)ième mois est égal au nombre de couples âgés de plus d'un mois présents. Or il y a fn+1-fn couples qui sont nés au (n+1)ième mois qui sont donc des jeunes qui ne se reproduisent pas. Chacun des fn couples âgés d'au moins un mois donne alors naissance à un nouveau couple. On a en définitive : Cette suite est très connue en raison de son lien avec le nombre d'or Φ=1+52. En particulier on remarque que le rapport fn+1fn tend vers Φ quand n tend vers l'infini, comme nous le montrerons ci-dessous. Soit ψ la série génératrice associée à la suite de Fibonacci, qui est définie par : Nous utilisons alors la relation de récurrence pour calculer explicitement ψ. En effet, en écrivant fn+2=fn+1+fn dans la formule précédente, nous obtenons : On vient d'appliquer à la série génératrice la relation de récurrence que nous connaissions pour la suite. Cela se traduit par une égalité fonctionnelle, particulièrement simple dans ce cas particulier, qui nous permet de déterminer ψ : Ce n'est malheureusement pas une forme que l'on sait facilement développer en série entière. Nous allons donc la décomposer en éléments simples. Commençons par déterminer les solutions de z2+z-1=0. On obtient ω1=5-12=1Φ et ω2=-1+52=-Φ, où on a posé Φ=1+52 le nombre d'or. On écrit alors : En utilisant les calculs du paragraphe précédent et en déterminant la série génératrice associée à ψ, nous obtenons alors pour fn : On en déduit une expression explicite pour la suite de Fibonacci ne nécessitant pas le calcul des n premiers termes pour donner fn+1. En particulier, on obtient bien, grâce à un petit calcul, que limn→+∞fn+1fn=Φ. Commençons par nous intéresser à une urne aléatoire générale. Rappelons que la règle est la suivante : si on a tiré une boule rouge, on ajoute α boules rouges et β bleues à l'urne, et si on a tiré une boule bleue, on en ajoute γ rouges et δ bleues. On note a0 et b0 le nombre (déterministe) de boules respectivement rouges et bleues présentent à l'instant 0, et an et bn le nombre (aléatoire) de boules de chaque couleur présentes dans l'urne après n étapes. Nous cherchons quelle est la probabilité pour une urne donnée d'arriver après n étapes à une configuration avec a boules rouges et b boules bleues. Pour cela nous avons besoin de déterminer le nombre d'"histoires" possibles pour l'urne conduisant à une configuration avec a boules rouges et b boules bleues en n étapes. Une "histoire" est donnée par la suite des boules tirées, chacune étant supposées distinctes. Par exemple, pour l'urne de Pólya partant d'une boule rouge et d'une boule bleue, il existe deux histoires menant à deux boules rouges et deux boules bleues après deux étapes : celle où on a d'abord tiré la boule rouge et celle où on a d'abord tiré la boule bleue. Il existe également deux histoires menant à trois boules rouges et une bleue selon la boule rouge tirée à la deuxième étape, l'"ancienne" ou la "nouvelle".
- Regarder sa couleur et la remettre dans l'urne.
- Si la boule est rouge, ajouter α boules rouges (α pouvant être négatif, dans ce cas on retirera des boules rouges) et β boules bleues.
- Si la boule est bleue, ajouter γ boules rouges et δ boules bleues (là encore, δ peut être positif ou négatif).
- Recommencer à la première étape
2. Série génératrice
2.1 Propriétés des séries génératrices
alors pour z=0 nous avons a0=b0. Soustrayons a0=b0, et divisons par z nous avons :
a1+a2z+a3z2+...=b1+b2z+b3z2+...
Ce qui nous permet de voir que a1=b1, en faisant tendre z vers 0. En réitérant le processus nous obtenons bien que les suites (an)n∈N et (bn)n∈N sont identiques.
a0=f(0)=1a1=limz→01z(f(z)-a0)=limz→0-z1+z2=0a2=limz→01z(-z1+z2-0)=limz→0-11+z2=-1a3=limz→01z(-11+z2+1)=limz→0z1+z2=0⋯
mais cette formule nous demande de calculer tous les termes jusqu'au rang n - 1 pour connaître le nième terme, alors que nous souhaiterions connaître une formule valable quel que soit l'entier n. Notons que (an)n∈N ne dépend que des valeurs de f pour z proche de 0. On pourra par conséquent toujours supposer que z est assez petit, et restreindre f à une fonction définie sur un voisinage de 0.
f(z)=a0+a1z+a2z2+... et g(z)=b0+b1z+b2z2+...,
on a alors (pour des z assez petits) :
fʹ(z)=a1+2a2z+3a3z2+...
f(z)+g(z)=(a0+b0)+(a1+b1)z+(a2+b2)z2+...
f(z)g(z)=(a0+a1z+a2z2+...)(b0+b1z+b2z2+...)=a0b0+(a1b0+a0b1)z+(a2b0+a1b1+a0b2)z2+⋯
2.2 Calcul des coefficients de fonctions "utiles"
On remarque que
zgn(z)-gn(z)=z+z2+...+zn+1-(1+z+...+zn)=zn+1-1.
Par conséquent gn(z)=zn+1-1z-1. En faisant tendre n vers +∞, nous obtenons alors :
limn→+∞gn(z)=11-z
Ce qui nous donne en définitive l'égalité suivante valable pour ∣z∣<1 :
1+z+z2+...=11-z
autrement dit, la suite associée à la fonction z↦11-z est la suite constante égale à 1.
donc par conséquent le nième coefficient associé à cette fonction s'écrira a(-b)ncn+1.
De manière générale, on remarque que fp+1=1pfpʹ. On obtient ainsi par récurrence que, pour tout n∈N :
fp(z)=1+(p1)z+(p+12)z2+(p+23)z3+...
Soit par conséquent, le nième coefficient associé à fp est égal à
(n+p-1n)=(n+p-1p-1).
Nous allons maintenant appliquer ces résultats une première fois à la suite de Fibonacci.
2.3 La suite de Fibonacci
2.3.1 Génération de la suite
Les conditions initiales sont données par f0=0 et f1=1.
2.3.2 Construction et calcul de la série génératrice
ψ(z)=f0+f1z+f2z2+...=f0+f1z+(f2z2+f3z3+f4z4+⋯)=z+((f0+f1)z2+(f1+f2)z3+(f2+f3)z4+⋯)=z+z2(f0+f1z+f2z2+...)+z(f0+f1z+f2z2+...)=z+zψ(z)+z2ψ(z).
En réduisant au même dénominateur il vient :
ψ(z)=-(a+b)z+(-aΦ+bΦ)z2+z-1=-zz2+z-1,
d'où on tire le système :
{a+b=1bΦ-aΦ=0
soit a=11+Φ2 et b=Φ21+Φ2.
fn=a1ω1n+1+b1ω2n+1=11+Φ2(Φn+1+(-1)n+1Φn-1)
3. Urne aléatoire
Les urnes aléatoires ont été introduites il y a plus de trois siècles, et les premiers résultats ont été démontrés par Jacob Bernouilli et Laplace [Flajolet, Dumas et Puyhaubert, 2006]. Par la suite de nombreuses urnes particulières ont été introduites pour modéliser certains problèmes, parmi lequelles les urnes d'Ehrenfest, Friedman ou encore Pólya sont certainement les plus connues. Nous allons maintenant utiliser les outils que nous venons de développer pour étudier l'urne de Pólya. Comme l'approche que nous avons choisi s'étend sans grandes difficultés à de très nombreux types d'urnes, nous nous placerons pour commencer dans un cadre général. Nous laissons à la curiosité du lecteur l'application des résultats obtenus ici à d'autres urnes aléatoires, comme l'urne d'Ehrenfest, ou bien d'autres [1].
3.1 Série génératrice associée à l'urne aléatoire
Figure I Arbre des "histoires" d'une urne de Pólya |
La figure I montre que pour l'urne de Pólya, après 2 étapes, chacune des compositions possibles est donnée par deux histoires. On remarquera que l'on distingue bien dans la deuxième étape le choix de la première boule rouge et celui de la deuxième dans la partie gauche du tableau, et de même dans la partie droite pour ce qui est des boules bleues. Toutes les histoires possibles de longueur n sont équiprobables. Par conséquent, si on note hn(a,b) le nombre d'histoires de longueur n menant à une urne composée de aboules rouges et b boules bleues et hn le nombre total d'histoires de longueur n, alors on a : Nous allons calculer hn(a,b) grâce à la notion de série génératrice. Comme la quantité hn(a,b) croit très vite quand n croit, nous allons utiliser une série génératrice exponentielle, associée à hn(a,b)n!, où n!=1×⋯×n, qui croira donc à un rythme bien plus acceptable. Il y a néanmoins un autre problème, nous avons trois quantités à retenir simultanément : le nombre de boules rouges, le nombre de boules bleues, et le nombre d'étapes que nous avons effectué. Néanmoins, après n étapes, l'urne ne peut être que dans un nombre fini d'états différents, par conséquent, la somme suivantea : Ceci nous permet donc d'introduire la série génératrice exponentielle associée à l'urne comme la fonction de trois variables x,y,z suivante : Comme nous l'avons vu précédemment, connaître cette fonction nous permet de remonter aux coefficients, en considérant tout d'abord (x,y) comme des paramètres de notre fonction de la variable z. Pour x=y=1, la fonction z↦H(1,1,z) est intéressante en elle-même. En effet, hn est la somme des hn(a,b) pour tous les couples (a,b) possibles (le nombre d'histoires de longueur n est bien égal à la somme sur tous les états possibles du nombre d'histoires de longueur n menant à un état donné). Par conséquent, comme H(1,1,z) est la somme de tous les termes hn(a,b)znn!, pour a,b,n entiers, en commençant par faire les sommes par rapport à a et b à entier n fixé, on obtient que H(1,1,z) s'écrit comme la somme des hnznn!. Autrement dit, nous venons de prouver que la fonction z↦H(1,1,z) est la série génératrice exponentielle associée à la suite (hn). Afin d'établir une égalité fonctionnelle pour H, il va nous falloir utiliser une représentation astucieuse de notre urne aléatoire, utilisant des équations aux dérivées partielles. Nous pouvons remarquer que dans la série génératrice précédente, une urne avec a boules rouges et b boules bleues est représentée par le monôme xayb. Or si on définit les fonctions suivantes : Lorsqu'on réalise un tirage de cette urne, on crée a histoires pour lesquelles on a tiré une boule rouge et b pour lesquelles c'est une boule bleue qui est tirée. Par conséquent, à une fonction uavb, on associe a fonctions ua+αvb+β et b fonctions ua+γvb+δ. Cela revient à appliquer l'opérateur aux dérivées partielles suivant à notre fonction : En effet on a D(uavb)=aua+αvb+β+bua+γvb+δ. Par conséquent l'évolution de l'urne est gouvernée par cet opérateur, que l'on associe à l'urne. On peut se servir de celui-ci pour réécrire la série génératrice associée à l'urne. La série génératrice que nous cherchons est obtenue en itérant la dérivation associée à l'urne. Supposons que nous commencions avec a0 boules rouges et b0 boules bleues. L'état est représenté par ua0vb0. Les états accessibles après une étape, (comptés avec le nombre de manières possibles pour arriver à chacun d'entre eux) sont représentés par D(ua0vb0). Après deux étapes, c'est D(D(ua0vb0))=D2(ua0vb0) qui code la somme des états accessibles, puis D3(ua0vb0) après trois étapes, etc... On peut alors réécrire la série génératrice en regroupant tous les termes associés à zn. Grâce à l'opérateur D, nous pouvons alors écrire : Ceci nous donne un moyen d'obtenir une équation fonctionnelle satisfaite par H. Pour cela, appliquons l'opérateur D à l'égalité ci-dessus. H vérifie par conséquent l'équation aux dérivées partielles suivante : Pour résoudre cette équation différentielle on va chercher un couple de fonctions (X(z),Y(z)) qui se comportent, lorsqu'on les dérive par rapport à z, de la même manière que u et v lorsqu'on leur applique D. Autrement dit on veut que, pour tout choix de (a,b)∈N, on ait : Or on sait que : Maintenant, si les équations différentielles suivantes sont vérifiées par un couple de fonctions (Xx,Yy) satisfaisant la condition initiale Xx(0)=x,Yy(0)=y, alors on a : Nous venons d'obtenir une méthode générale permettant de calculer les valeurs de hn(a,b). Grâce à cette formule, si on est capable de résoudre le système d'équations différentielles précédent pour une urne aléatoires, alors on est capable de calculer la probabilité d'arriver dans un état donné en un certain nombre d'étapes. Nous allons maintenant appliquer les résultats obtenus au cas de l'urne de Pólya. Rappelons que l'urne de Pólya permet d'étudier l'évolution d'une population de deux espèces. Elle a été introduite par Pólya [Pólya, 1930] et été étudiée maintes fois par la suite. [Tautu,1986] en donne un bref aperçu historique. L'urne est définie avec les quantités suivantes : α=1,β=0,γ=0 et δ=1, autrement dit, quand on tire une boule d'une couleur, on en ajoute une de la même couleur. Le système associé à l'urne est alors le suivant : En d'autres termes, au produit de deux séries génératrices de coefficients (an) et (bn) est associé la suite (a0bn+a1bn-1+⋯+anb0). Dans notre cas, la série entière de zHx,y(z)=H(x,y,z) (nous considérons de nouveau x et y comme des paramètres) possède les coefficients suivants : Ceci nous permet par conséquent de calculer le nombre d'histoires de longueur n menant à un état particulier de l'urne : Finalement, toutes les histoires étant équiprobables, si on note an le nombre de boules rouges présentes dans l'urne à l'instant n et bn le nombre de boules bleues présentes à cet instant, nous obtenons les probabilités suivantes, qui nous permettent de déterminer l'évolution de toute urne (on utilisera le fait que le nombre total de boules à l'instantn est connu, an+bn=a0+b0+n, par conséquent nous pouvons nous intéresser au seul nombre de boules rouges, celui de boules bleues s'en déduit) : Nous pouvons maintenant interpréter les résultats obtenus. Commençons par une observation. On remarque que si a0=b0=1, c'est-à-dire que l'on commence avec une boule rouge et une boule bleue dans l'urne, alors toutes les urnes possibles au temps n ont exactement la même probabilité d'apparaître. Mais cette propriété n'est pas vraie quel que soit le nombre de boules avec lequel nous débutons : par exemple, si nous étudions une urne dans laquelle il y a au départ deux boules de chaque couleur, soit a0=b0=2, nous obtenons grâce à un calcul rapide : Ainsi, dans ce cas, on voit clairement que tous les états possibles au temps n ne sont pas équiprobables. En particulier, une urne qui possède une moitié de boules rouges apparaît avec la probabilité 3(n+4)22(n+3)(n+2)(n+1) à l'étape n alors qu'une urne ne possédant que deux boules rouges à l'étape n n'apparaît qu'avec la probabilité6(n+3)(n+2).
est finie quel que soit l'entier n. C'est un polynôme en deux variables x et y. Si x et y sont maintenant pensés comme des paramètres, la connaissance de cette quantité (dépendant de n) pour tout couple (x,y) nous permettra de remonter au polynôme puis aux coefficients. Étudions donc la série génératrice exponentielle associée à ces quantités :Hx,y(z)=(∑a,bh0(a,b)xayb)+(∑a,bh1(a,b)xayb)z1+(∑a,bh2(a,b)xayb)z22+⋯.
3.1.1 Représentation d'une urne aléatoire par une dérivation
v:x,y↦y,
on a xayb=ua(x,y)vb(x,y). On dit alors que l'urne contenant a boules rouges et b boules bleues est codée par la fonction uavb.
3.1.2 Système différentiel associé à l'urne
D(H)(u,v,z)=∑n=0+∞Dn+1(uavb)znn!=∑n=0+∞Dn+1(uavb)∂zzn+1(n+1)!=∂z∑n=1+∞Dn(uavb)znn!=∂zH.
Donc en choisissant successivement a=1,b=0 et a=0,b=1, il vient que X et Y vérifient en particulier le couple d'équations différentielles suivant :
{X.=Xα+1YβY.=XγYδ+1
Or H(x,y,z)=∑n=0+∞Dn(ua0vb0)(x,y)znn!, donc on a :
H(x,y,z)=∑n=0+∞Dn(ua0vb0)(Xx(0),Yy(0))dfracznn!=∑n=0+∞∂z(Xxa0Yyb0)(0)znn!=(Xx(z)a0Yy(z)b0)
3.2 L'urne de Pólya
qui se résout immédiatement en Xx(t)=x1-xt,Yy(t)=y1-yt. On a alors :
H(x,y,z)=(x1-xz)a0(y1-yz)b0.
On peut alors développer H en séries entières pour calculer hn(a,b). Pour cela nous commencerons par rappeler que :
(x1-xz)a0=x+(a0a0-1)x2z+(a0+1a0-1)x3z2+⋯
On doit maintenant réaliser le produit des deux développements suivants pour obtenir le développement en séries génératrices de notre urne. Rappelons que :
(a0+a1z+a2z2+...)(b0+b1z+b2z2+...)=a0b0+(a1b0+a0b1)z+(a2b0+a1b1+a0b2)z2+⋯
Or rappelons que ces coefficients s'écrivent également (c.f. Section 3.1, la définition de H(x,y,z) :
1n!(hn(0,n+2)yn+2+hn(1,n+1)xyn+1+⋯+hn(n+1,1)xn+1y).
De plus, en se souvenant que la série génératrice exponentielle associée à cette suite est H(1,1,z)=1(1-z)a0+b0, on obtient l'égalité :
hnn!=(n+a0+b0-1a0+b0-1).
Figure II Distribution des probabilités d'apparition d'une urne après 30 tours en fonctions des conditions initiales |
Sur la figure II, nous avons représenté la probabilité de posséder a boules rouges pour une urne de Pólya ayant subi 30 étapes d'évolution, à partir de toutes les situations initiales possibles avec 10 boules, de 1 rouges et 9 bleues à 9 rouges et 1 bleues. Chacune de ces distributions de probabilités est "piquée" au voisinage de la proportion de boules qu'il contient. Autrement dit, une urne de Pólya favorise dans le futur les configurations qui possèdent un nombre moyen de boules voisin du sien. Ainsi une urne de Pólya commençant avec une proportion r de boules rouges parmi ses boules rend plus probable les compositions d'urnes pour lesquelles cette proportion est conservée. En particulier, si on commence avec 13 de boules rouges dans l'urne, on a de fortes chances que ce rapport soit conservé pour toujours. Ce phénomène s'accentue quand le nombre total de boules augmente, autrement dit, plus le nombre initial de boules est grand, plus il est difficile de modifier le ratio de boules rouges présentes dans l'urne. Or une urne aléatoire vérifie une propriété remarquable : si à un moment donné nous regardons dans l'urne le nombre de boules de chaque couleur et que nous replaçons ensuite le couvercle, et recommençons à faire évoluer cette urne, alors l'urne se comporte comme si on avait dès le début commencé avec la composition que nous venons de découvrir. Cette propriété s'appelle la propriété de Markov. L'urne évolue à partir du temps n exactement comme si on avait à l'instant intial commencé avec an boules rouges et bn boules bleues. Revenons à l'urne de Pólya. On vient de voir que si la composition initiale est de une boule rouge et une boule bleue, alors à un instant donné toutes les compositions de l'urne sont équiprobables. Mais alors le ratio de boules rouges dans l'urne est une variable aléatoire choisie uniformément au hasard. Or si on repart ensuite d'un instant donné, ce ratio aura tendance à se conserver ! Par conséquent, le ratio de boules rouges tend vers une constante, mais cette constante est aléatoire de loi uniforme. Autrement dit, si on trace le graphe représentant l'évolution du nombre de boules rouges présentes dans l'urne au cours du temps, on obtient pour chaque réalisation de l'expérience une courbe proche d'une droite linéaire, mais dont la pente est aléatoire, et varie de telle façon qu'à un temps donné, sa distribution sur l'axe des ordonnées varie selon une loi uniforme (à entier n fixé, les probabilités d'atteindre chacun des points (n,k) pour 1≤k≤n+1 sont égales). On a représenté sur la figure III l'évolution du nombre de boules rouges de 11 réalisations d'urnes de Pólya, entre les instants 0 et 500. On remarquera l'allure de droite de ces courbes, ainsi que leur caractère uniforme.
Figure III 11 réalisations d'urnes de Pólya au cours du temps, partant d'une boule rouge et d'une boule bleue |
L'urne de Pólya modélise donc une population autostable, pour laquelle tout équilibre à un instant donné tend à être conservé à l'infini, avec une probabilité d'autant plus grande que le nombre d'individus est grand, cet équilibre restant toutefois aléatoire. Nous pourrions préciser quelle est la probabilité, partant d'une situation donné, que ces populations s'éloigne de manière significative de leur équilibre, c'est ce dont s'occupe la théorie des grandes déviations. De nombreuses autres questions peuvent encore se poser sur le comportement à l'infini de telles urnes. On a vu dans cet article comment nous pouvions utiliser des séries génératrices pour calculer certaines quantités (suite récurrente d'ordre 2, comme la suite de Fibonacci, probabilité pour une variable aléatoire d'avoir une valeur donnée, nombres d'objets de taille n dans un ensemble...). Le nombre d'application possibles ne s'arrête certainement pas ici. Il y a encore de nombreux cas pour lesquels cette méthode se révèle l'une des plus aisée, comme pour le calcul des nombres de Catalan, qui comptent le nombre d'arbres planaires à n branches (ou bien le nombre de parenthèsages de longueur n). Dans ce cas la résolution de la relation de récurrence se transforme en la résolution d'une équation du second degré. Un autre exemple est le nombre tn de triplets d'entiers naturels de somme égale à n (pour celui-ci nous avons déjà fait tous les calculs dans la Section 2.2, il suffit de considérer le développement de z↦1(1-z)3 de deux manières distinctes), et encore bien d'autres. En ce qui concerne les urnes aléatoires en général, il est possible de s'intéresser de plus près au système différentiel que nous leur avons associé, comme dans l'article [Flagolet, Dumas et Puyhaubert 2006]. Ainsi il devient possible d'étudier le comportement à long terme de certaines classes d'urnes aléatoires. Dans ce cas, il apparait que les proportions de boules rouges et bleues peuvent se comporter de manière bien plus étrange que dans le cas de l'urne de Pólya.
Conclusion
Bibliographie
Philippe Flajolet, Philippe Dumas, and Vincent Puyhaubert (2006). "Some exactly solvable models of urn process theory", Proceedings of Fourth Colloquium on Mathematics and Computer Science, vol. AG, p. 59–118.
Norman L. Johnson and Samuel Kotz (1977). Urns models and their application, John Wiley & Sons, New York-London-Sydney.
Pierre-Simon Laplace (1819). Théorie analytique des probabilités, Oeuvres complètes, Tome 7, Réédition 1886
Georges Pólya (1930). "Sur quelques points de la théorie des probabilités", Annales de l'institut Henri Poincaré, tome1, n° 2, p. 117-161
P. Tautu (1986). Stochastic spatial processes in biology : A concise historical survey, Lecture Notes in Math., vol. 1212, Springer-Verlag, Berlin and New York.
19:32 Publié dans Urnes aléatoires, populations en équilibre | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook