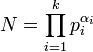05/12/2010
Nombre double de Mersenne
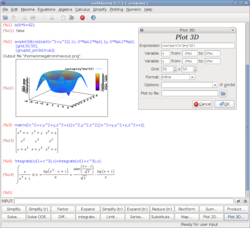
En mathématiques, un nombre double de Mersenne est un nombre de Mersenne de la forme où n est un entier positif. Les premiers petits nombres doubles de Mersenne sont : Un nombre double de Mersenne qui est premier est appelé un nombre premier double de Mersenne. Puisque un nombre de Mersenne Nombre double de Mersenne



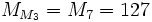

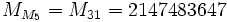
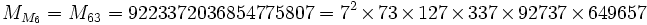
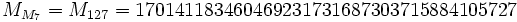
 ne peut être premier que si n est premier (condition necessaire mais pas suffisante), (voir nombre de Mersenne pour une démonstration de ceci), un nombre double de Mersenne
ne peut être premier que si n est premier (condition necessaire mais pas suffisante), (voir nombre de Mersenne pour une démonstration de ceci), un nombre double de Mersenne  est premier seulement si
est premier seulement si  est premier. Les premières valeurs de n pour lesquelles ceci est vrai sont n = 2, 3, 5, 7, 13, 17, 19, 31. De celles-ci,
est premier. Les premières valeurs de n pour lesquelles ceci est vrai sont n = 2, 3, 5, 7, 13, 17, 19, 31. De celles-ci,  est connu pour être premier pour n = 2, 3, 5, 7; pour n = 13, 17, 19, et 31, des facteurs explicites ont été trouvés. Si un autre nombre premier double de Mersenne est un jour trouvé, il serait presque certainement le plus grand nombre premier jamais connu.
est connu pour être premier pour n = 2, 3, 5, 7; pour n = 13, 17, 19, et 31, des facteurs explicites ont été trouvés. Si un autre nombre premier double de Mersenne est un jour trouvé, il serait presque certainement le plus grand nombre premier jamais connu.
13:07 Publié dans Nombre double de Mersenne | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Définitions concernant les suites aliquotes
Définitions concernant les suites aliquotes
Retour à page d'accueil
La fonction σ
Soit n un entier naturel.σ(n) est la somme de tous les diviseurs de n. C’est une fonction largement étudiée en théorie des nombres.
Par exemple, σ(10) = 1 + 2 + 5 + 10 = 18
Cliquer ici pour en savoir plus sur La fonction σ.
La fonction σ'
Soit n un entier naturel.σ'(n) est la somme des parties aliquotes de n, c'est-à-dire la somme de ses diviseurs hormis lui-même.
σ'(n) = σ(n) - n
Par exemple, σ'(10) = 1 + 2 + 5 = 8
Les suites aliquotes
Une suite aliquote s’obtient en prenant un nombre entier n de départ et en itérant à chaque étape avec la fonction σ’.Exemple : La suite aliquote de départ 10 est la suivante : 10 → 8 → 7 → 1
En effet, σ'(10) = 8, σ'(8) = 7 et σ'(7) = 1.
Les antécédents aliquotes
Soient n et N des entiers naturels.Si σ'(N) = n, alors N est un antécédent aliquote de n.
Deux cas sont possibles :
Soit l’entier n peut avoir 0 antécédents aliquotes : il s’agit alors d’un nombre intouchable dont Erdös a démontré qu’il en existe une infinité. Ces nombres sont référencés par Neil Sloan (suite A005114). La suite de ces nombres commence ainsi : 2, 5, 52, 88, 96, …
Soit l’entier n peut avoir un ou plusieurs antécédents aliquotes. La suite d’entiers donnant pour chaque entier naturel son nombre d’antécédents aliquotes est référencée par Neil Sloan : A048138. Elle commence ainsi : 0, 1, 1, 0, 2, 1, 2, 1, 1, 1, 1, 2, 2, 2, 2, 2, 1, 2, 2 …
Pour déterminer le nombre d’antécédents aliquotes d’un nombre entier n, il faut à priori tester des nombres entiers N compris entre 1 et (n-1)² inclus. Le lecteur comprendra pourquoi en réfléchissant 5 minutes. Mais en prenant quelques précautions, on peut se contenter de tester des entiers entre 1 et n3/2/2.5. Cela représente un gain de temps inestimable. Nous présentons ici cette méthode de détermination du nombre d’antécédents aliquotes de chaque entier naturel compris entre 1 et le n désiré, méthode qui est pour l'instant la plus rapide que nous ayons trouvée.
Remonter une suite aliquote à l’envers :
Nous avons fait quelques tentatives pour remonter des suites aliquotes à l’envers. Cela est très intéressant, surtout dans le cas particulier des nombres impairs. En effet : si la conjecture de Goldbach est vraie, alors une des conséquences est qu'on peut remonter une suite aliquote à l'envers d’autant d’étapes que l’on veut et de manière strictement monotone ! Pour en savoir plus, cliquer ici : remonter une suite aliquote à l'envers.Signalons encore que notre intuition nous fait sentir que les suites aliquotes qui démarrent sur un nombre intouchable semblent fondamentales, car elles ne peuvent être des parties de suites aliquotes plus longues !
Dernière modification : Septembre 2010
13:06 Publié dans Définitions concernant les suites aliquotes | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Suite aliquote
Suite aliquote
En arithmétique, une suite aliquote est une suite d'entiers dans laquelle chaque nombre est la somme des diviseurs propres1 de son prédécesseur. Quand la suite atteint 1, elle s'arrête car 1 ne possède pas de diviseur propre.
Ainsi la suite commençant à 10 se comporte de la manière suivante :
- u0 = 10
- les diviseurs propres de 10 sont 1, 2 et 5.
- u1 = 1 + 2 + 5 = 8
- les diviseurs propres de 8 sont 1, 2 et 4
- u2 = 1 + 2 + 4 = 7
- 7 ne possède qu'un diviseur propre 1
- u3 = 1
Sommaire[masquer] |
Cas particuliers [modifier]
L'étude des suites aliquotes met en évidence les cas particuliers suivants
- si u0 est un nombre premier alors u1 = 1 et la suite s'arrête.
- si u0 est un nombre parfait alors la suite est constante
- si u0 est un nombre amical, alors u1 est son nombre amical associé et la suite boucle sur ces deux valeurs
- si u0 est un nombre sociable alors la suite boucle sur tous les nombres sociables associés à u0
Relation de récurrence [modifier]
La suite est définie par la relation de récurrence suivante : pour tout entier n, si un est différent de 1
- un + 1 = f(un)
où f est définie de la manière suivante : si N est un entier différent de 1 dont la décomposition en facteurs premiers est
On remarque que f est définie par
- f(N) = s(N) − N
où s est la fonction diviseur d'ordre 1
Observations et conjectures [modifier]
Toutes les suites aliquotes dont le premier terme est un nombre inférieur ou égal à 100 ont été étudiées et s'arrêtent à 1, sauf les suites constantes commençant par les nombres parfaits 6 et 28. La suite la plus longue est alors obtenue pour un premier terme égal à 30.
Une conjecture importante, due à Catalan, stipule qu'une suite aliquote, ou bien se termine à 1, ou bien finit par être constante sur un nombre parfait, ou périodique sur une famille denombres sociables.
Cette conjecture ne fait pas l'unanimité. En effet, parmi les suites dont le premier terme est un nombre inférieur ou égal à 1000, 5 suites n'ont toujours pas pu être explorées jusqu'à leur terme. Ce sont les suites commençant par 276, 552, 564, 660 et 966. Ces nombres sont appelés les« cinq de Lehmer »2. Il existe de même 12 nombres (les douze de Godwin) compris entre 1000 et 2000 pour lesquels les suites aliquotes associées ne sont pas connues.
Il existe des suites aliquotes atteignant des termes astronomiques comme la suite démarrant à 3630 atteignant un nombre à 100 chiffres pour se terminer plus tard à 13. Hendrick Lenstra a démontré que l'on pouvait toujours trouver une suite aliquote croissante sur n termes consécutifs, quelle que soit la valeur de n.
La quantité a, elle aussi, été étudiée. La famille des
a, elle aussi, été étudiée. La famille des  n'est pas bornée mais Jean-Luc Garambois conjecture que la moyenne des
n'est pas bornée mais Jean-Luc Garambois conjecture que la moyenne des converge vers(π2 − 6) / 6.
converge vers(π2 − 6) / 6.
On peut prouver, grâce à la relation de récurrence, que la suite ne change de parité que si l'un des termes s'écrit a2 ou 2a2.
Bibliographie [modifier]
- Jean-Paul Delahaye, Les inattendus mathématiques, Nombres amiables et suites aliquotes
Sites internet [modifier]
Notes et références [modifier]
- Les diviseurs propres de l'entier naturel n non nul, sont les diviseurs positifs de n strictement inférieurs à n
- Jean-Paul Delahaye, Les inattendus mathématiques, Nombres amiables et suites aliquotes. (ISBN 2842450736)
- (en) Manuel Benito, Wolfgang Creyaufmüller, Juan Varona et Paul Zimmermann , Aliquot sequence 3630 ends after reaching 100 digits [archive]
13:02 Publié dans Suite aliquote | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Séminaire Institut de Recherche Mathématique Avancée
| Séminaire Quantique - Lundi 06-12-2010 (11:00) - Salle de séminaires IRMA Hidekazu Furusho (Nagoya U) : Tree Hopf algebra and motivic Hopf algebra
Séminaire GT3 - Lundi 06-12-2010 (14:00) - Salle de séminaires IRMA Albert Marden (Minnesota) : Holomorphic plumbing coordinates for Teichmüller and compactified moduli space. ABSTRACT: Start with one or two Riemann surfaces which have Séminaire Arithmétique et géométrie algébrique - Lundi 06-12-2010 (14:00) - Salle de séminaires 309 G. Christol (Jussieu) : la fonction rayon de convergence : un exemple éclairant Le but de l'exposé est d'illustrer une conjecture récente de Baldassarri Séminaire Géométrie symplectique et applications - Lundi 06-12-2010 (15:30) - Salle de séminaires IRMA Klaus Niederkruger (Université Paul Sabatier, Toulouse) : Remplissages faibles en géométrie de contact (collaboration avec P. Ghiggini et P. Massot) De façon intuitive il faut penser à des variétés de contact comme des bords de variétés Séminaire Calcul stochastique - Mercredi 08-12-2010 (11:00) - Salle de séminaires IRMA Pierre Patie (Bruxelles) : Quelques résultats sur la fonctionnelle exponentielle des processus de Lévy. La fonctionnelle exponentielle des processus de Lévy joue un rôle prépondérant dans de nombreux champs des mathématiques appliquées et a suscité un vif intérêt ces deux dernières décennies. Nous commencerons par un survol des résultats connus sur la loi de cette variable aléatoire. Ensuite, nous montrerons que, lorsque le processus de Lévy est spectralement négatif, la loi la fonctionnelle exponentielle est absolument continue avec une densité indéfiniment différentiable qui s’exprime à l'aide d’une série entière. Séminaire Doctorants - Jeudi 09-12-2010 (16:00) - Salle de séminaires IRMA Jean Gutt : Profondeur
Séminaire Calcul stochastique - Vendredi 10-12-2010 (11:15) - Salle de séminaires IRMA Christian Selinger (Luxembourg) : Regularized Laplacian on smooth Wasserstein space above the unit circle. The space of probability measures on Riemannian manifolds endowed with the Wasserstein distance has recently been identified as an infinite-dimensional Riemannian manifold. Furthermore geodesic equations and second order calculus on this space have been developed. In continuity of these ideas we propose a Zeta function regularized Laplacian for the space of smooth positive densities on the unit circle and show links to the Wasserstein diffusion constructed by Sturm/von Renesse. Groupe de travail Arithmétique et géométrie algébrique - Vendredi 10-12-2010 (13:30) - Salle de séminaires 309 Auguste Hoang Duc (IRMA) : Représentations attachées aux formes modulaires
Séminaire Quantique - Lundi 13-12-2010 (11:00) - Salle de séminaires IRMA Greg Kuperberg (U.C. Davis) : Buildings, spiders, and geometric Satake Louis Kauffman is a special description of the Jones polynomial Séminaire Equations aux dérivées partielles - Lundi 13-12-2010 (14:00) - A confirmer Pierre Morel (Statistical and Plasma Physics Laboratory, Bruxelles) : turbulence girocinétique : diagnostiques et modèles pour sa description numérique Attention, jour inhabituel Séminaire Géométrie symplectique et applications - Lundi 13-12-2010 (15:30) - Salle de séminaires IRMA Juan-Carlos Alvarez-Paiva (Lille) : Inégalités isosystoliques en géométrie de contact et une question de Viterbo. Il y a dix ans C. Viterbo demanda si le volume d'un corps convexe Séminaire Statistiques - Mardi 14-12-2010 (14:00) - Salle de séminaire 418 Christian Derquenne (EDF) : Analyse factorielle et classification automatique en présence de données manquantes
Séminaire Calcul stochastique - Vendredi 17-12-2010 (11:15) - Salle de séminaires IRMA Alano Ancona (Orsay) : Critères de régularité fine (à la Dynkin) pour des opérateurs de Schrödinger.
Séminaire GT3 - Lundi 03-01-2011 (14:00) - Salle de séminaires IRMA Constantin Vernicos (Montpellier) : Géométrie de Hilbert des polytopes convexes
Séminaire Géométrie symplectique et applications - Lundi 10-01-2011 (15:30) - Salle de séminaires IRMA Alexandru Oancea (IRMA) : A préciser
Séminaire Statistiques - Mardi 11-01-2011 (14:00) - Salle de séminaire 418 Bruno Lecoutre (Université de Rouen) : à préciser
Séminaire Equations aux dérivées partielles - Mardi 11-01-2011 (14:00) - Salle de séminaires 309 Victorita Dolean (Laboratoire Dieudonné, Université de Nice) : Methodes de preconditionnement pour des systemes d'EDPs en utilisant des outils algebriques
Séminaire Théorie des représentations et analyse harmonique - Jeudi 13-01-2011 (14:00) - Salle de séminaires 309 Tilmann Wurzbacher (Université de Bochum) : Paires de Howe symplectiques Résumé: Une paire d'actions hamiltoniennes est appelée Séminaire Calcul stochastique - Vendredi 14-01-2011 (11:15) - Salle de séminaires IRMA Peter Imkeller (Université Humboldt, Berlin) : Titre annoncé ultérieurement.
Colloquium Mathématique - Vendredi 14-01-2011 (16:30) - Salle de conférences IRMA Patrick Popescu-Pampu (Université de Lille) : Le zoo des singularités de surfaces complexes Nous nous promènerons dans le zoo des singularités Séminaire Géométrie symplectique et applications - Lundi 17-01-2011 (15:30) - Salle de séminaires IRMA Ana Rechtman (Northwestern University) : A préciser
Séminaire Statistiques - Mardi 18-01-2011 (14:00) - Salle de séminaire 418 Astrid Jullion (Arlenda, Belgique) : Adaptatifs Bayésiens P-splines modèles : application à des données provenant d’études de pharmacocinétique et de tomographie par émission de positrons Au cours d’essais cliniques, l’évolution de la concentration d’un produit dans un organe au cours du temps fait souvent l’objet d’analyse. Différents produits et organes peuvent être considérés : on peut par exemple analyser l’évolution de la concentration d’un médicament dans le plasma au cours du temps ou encore observer l’évolution du niveau de radioactivité dans différentes régions du cerveau lors d’un scanner TEP (tomographie par émission de positrons). L’objectif de cette présentation est la modélisation de telles évolutions qui sont appelées, de façon générique, des courbes pharmacocinétiques (courbe PC). Groupe de travail IREM - Mardi 18-01-2011 (14:00) - Salle de conférences IRMA Thomas Catherine (IREM) : Formation de formateurs
Conférence IREM - Mercredi 19-01-2011 (15:00) - Salle de conférences IRMA Rutger Noot (IRMA) : titre non communiqué à ce jour
Séminaire Calcul stochastique - Vendredi 21-01-2011 (11:15) - Salle de séminaires IRMA Jérémie Unterberger (Institut Élie Cartan, Nancy) : Chemins rugueux, algèbres de Hopf et renormalisation: une approche physico-algébrique du calcul stochastique fractionnaire. L'article fondateur de L. Coutin et Z. Qian (2002) a montré la difficulté de définir l'aire de Lévy, et partant -- suivant la théorie de l'intégration due à T. Lyons, dite théorie des chemins rugueux ou rough paths -- un calcul stochastique pour le brownien fractionnaire d'indice de Hurst inférieur à 1/4. De manière générale, le problème consiste à définir les intégrales itérées de chemins -- déterministes ou aléatoires -- de faible régularité Hölder. Nous apportons en un certain sens une réponse générale à cette question grâce à une algorithmique algébrique. Nous apportons également des constructions explicites dans le cas du brownien fractionnaire, montrant que le problème s'interprète en réalité comme un problème de théorie quantique des champs et se résout en tant que tel. Celles-ci permettront sans doute en retour d'attaquer des problèmes ouverts liés au calcul stochastique et aux équations différentielles stochastiques. Séminaire GT3 - Lundi 24-01-2011 (14:00) - Salle de séminaires IRMA Suhyoung Choi (KAIST- Seoul) : Convex real projective n-orbifolds with radial ends and their deformations Abstract .--- A real projective orbifold is an n-dimensional orbifold modeled on Séminaire Géométrie symplectique et applications - Lundi 24-01-2011 (15:30) - Salle de séminaires IRMA V. Zvonilov : A préciser
Séminaire Statistiques - Mardi 25-01-2011 (13:30) - Salle de séminaire 418 Jean Pierre Gauchi (INRA) : La X-optimalité : un critère de plans d'expériences pour des modèles de régression non linéaire. Attention, l'heure n'est pas habituelle Séminaire Equations aux dérivées partielles - Mardi 25-01-2011 (14:00) - Salle de séminaires 309 Claus Dieter Munz (IAG, Université de Stuttgart) : A confirmer
Séminaire GT3 - Lundi 31-01-2011 (14:00) - Salle de séminaires IRMA Gwenael Massuyeau : Invariants des variétés de dimension trois et groupe de Torelli d'une surface Il s'agira d'un exposé de survol sur ce thème. Séminaire Géométrie symplectique et applications - Lundi 31-01-2011 (15:30) - Salle de séminaires IRMA Cédric Bounya (IRMA) : A préciser
Séminaire Statistiques - Mardi 01-02-2011 (14:00) - Salle de séminaire 418 Abdallah Elamine (IRMA) : Régression linéaire locale pour des données fonctionnelles Dans ce travail, on s'intéresse à la régression non paramétrique locale pour des données fonctionnelles. Tout d'abord, on propose un estimateur de l'opérateur de régression. La Colloquium Mathématique - Vendredi 04-02-2011 (16:00) - Salle de conférences IRMA Pierre Parent (Bordeaux) : à préciser
Séminaire Quantique - Lundi 07-02-2011 (11:00) - Salle de séminaires IRMA Takuya Sakasai (Tokyo Institute of Technology) : Homology cylinders in knot theory This is a joint work with Hiroshi Goda (Tokyo University of Agriculture and Technology). Séminaire GT3 - Lundi 07-02-2011 (14:00) - Salle de séminaires IRMA Chloé Perin : TBA
Séminaire Géométrie symplectique et applications - Lundi 07-02-2011 (15:30) - Salle de séminaires IRMA Lev Birbrair (Fortaleza) : Metric Properties of Complex Algebraic Surfaces
Séminaire Statistiques - Mardi 08-02-2011 (14:00) - Salle de séminaire 418 Cédric Heuchenne (HEC-Management School of the University of Liège) : à préciser
Séminaire GT3 - Lundi 14-02-2011 (14:00) - Salle de séminaires IRMA Takuya Sakasai (Tokyo) : Lagrangian mapping class groups from group homological point of view Abstract: Séminaire GT3 - Lundi 28-02-2011 (14:00) - Salle de séminaires IRMA Yukio Matsumoto (Tokyo) : TBA
Séminaire Statistiques - Samedi 05-03-2011 (14:00) - Salle de séminaire 418 Stéphane Loisel (ISFA - Université de Lyon) : à préciser
Séminaire Géométrie symplectique et applications - Lundi 07-03-2011 (15:30) - Salle de séminaires IRMA Sheila Margherita Sandon (Université de Nantes) : A préciser
Séminaire Statistiques - Mardi 08-03-2011 (14:00) - Salle de séminaire 418 Laurent Gardes (INRIA - Université de Grenoble) : Méthode SIR Régularisée et étude d'images hyperspectrales
Cours Géométrie symplectique et applications - Lundi 14-03-2011 (15:30) - Salle de séminaires IRMA Stéphane Guillermou (Institut Fourier, Grenoble) : A préciser
Séminaire Statistiques - Mardi 22-03-2011 (14:00) - Salle de séminaire 418 Yuri Goegebeur (University of Southern Denmark) : à préciser
Séminaire Géométrie symplectique et applications - Lundi 28-03-2011 (15:30) - Salle de séminaires IRMA Alexander Ritter (Cambridge University) : A préciser
|
Dernière mise à jour le 8-04-2010
10:45 | Lien permanent | Commentaires (3) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
CM2 La division
Poser une division
Nous avons vu comment additionner, soustraire, ou multiplier des grands nombres. Voyons maintenant la division et prenons l'exemple de la division de 1458 par 6. On place d'abord les deux nombres dans un dessin comme ci dessous.

Avec le premier chiffre du nombre à gauche, on compte : "en 1 combien de fois 6?". Si le résultat est plus grand que 1, on divise le résultat par 6. Sinon, on se repose la même question mais en utilisant les 2 premiers chiffres du nombre à gauche, ce qui donne : "en 14 combien de 6? ". On effectue cette petite division.

En 14 il y a 2 fois 6 donc on écrit 2 dans la case de droite puis on effectue la multiplication avec le 6, on écrit le résultat sous le 14 et on effectue une soustraction.

Ensuite on abaisse le chiffre à droite du 14 et on effectue la même opération avec le nombre obtenu (25). En 25 combien de fois 6? 4 fois, 4 fois 6 = 24 et 25 - 24 = 1.

On effectue ensuite les mêmes opérations après avoir abaissé le 8.

Lorsqu'il n'y a plus de chiffre à abaisser, on peut alors lire dans la case de droite le quotient de la division et en bas dans la case de gauche le reste. Ici le quotient vaut 243 et le reste est nul.
Poser une division avec résultat décimal
Lorsque le reste de la division n'est pas nul, on peut continuer la division afin d'obtenir un résultat décimal avec autant de chiffres que l'on veut après la virgule. Par exemple pour la division suivante on trouve un quotient de 176 et un reste de 2.

Pour continuer le calcul on ajoute un zéro après le premier nombre, et on l'abaisse. On place également une virgule à droite du résultat.

Ensuite on continue le calcul aussi longtemps que l'on veut en ajoutant à chaque fois un zéro supplémentaire et en l'abaissant.

Poser une division avec des grands nombres
Il n'a pas pas de différence lorsque l'on divise par un grand nombre. Les calculs sont juste un petit peu plus difficiles à effectuer.

10:41 Publié dans CM2, Division | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Problèmes : CM2
Problèmes : CM2
(Exercice de maths (mathématiques) n°12602 - merci de citer ce numéro dans toute correspondance)  Autres exercices de maths (mathématiques) sur le même thème
Autres exercices de maths (mathématiques) sur le même thème
Problèmes : CM2

 Débutants
Débutants
Exercice de maths (mathématiques) 'Problèmes : CM2' créé le 11-11-2006 par bridg avec Le générateur de tests - créez votre propre test!
Voir les statistiques de réussite de ce test de maths (mathématiques)
Je dispose d'une somme. Je calcule que pour m'acheter 4 livres il me manque 5€50. Sachant que chaque livre coûte 14€50, calculez la somme que j'ai en poche.€
Le chargement d'un camion est composé de 35 caisses pesant chacune 54,5Kg et de 40 caisses pesant 35Kg. Quelle masse peut-on ajouter pour que la charge de ce camion atteigne 5 tonnes? tonne
Pour l'achat à crédit d'un meuble valant 10 600€, il faut verser 3850€ à la commande et payer le reste en 15 mensualités. Quel est le montant d'une mensualité? €
Un instituteur achète 25 livres de grammaire et 12 dictionnaires à 22,50€ l'un. Il dépense 482,50€. Combien coûte un livre de grammaire? €
Une secrétaire va à la poste, elle achète 36 timbres à 2€70, 28 timbres à 4,50€ et 14 timbres à un autre tarif. Elle paye 317€. Quel est le prix de chacun des 14 timbres? €
Quelle est la largeur d'un terrain rectangulaire de basket dont la surface est de 312,50m² et la longueur 25m ? m
Combien remplira t-on de verres de 8cL chacun avec 6 packs de 3 bouteilles, chaque bouteille contenant 75cL ? verres (par défaut)
Combien vais-je payer un billet d'avion coûtant 412€ si je bénéficie d'une réduction de 25%? €
10:39 Publié dans CM2, Problèmes : CM2 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Freemat
FreeMat is a free environment for rapid engineering and scientific prototyping and data processing. It is similar to commercial systems such as MATLAB from Mathworks, and IDL from Research Systems, but is Open Source. FreeMat is available under the GPL license. We are pleased to announce the release of FreeMat 4.0 . This version brings major feature improvements and changes to the internals of FreeMat. Here is a list of changes: Internal changes: Source : http://freemat.sourceforge.net/Home
Latest News - 2009-10-09 - FreeMat 4.0 Released
10:37 Publié dans FreeMat | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
FreeMat
FreeMat
| FreeMat | |
| Développeur | Samit Basu |
|---|---|
| Dernière version | v4.0 (9 octobre 2009) [+/−] |
| Environnement | Multiplate-forme (Linux, Mac OS X,Windows) |
| Langue | anglais |
| Type | Calcul numérique |
| Licence | GNU GPL |
| Site Web | freemat.sourceforge.net |
| modifier |
|
FreeMat est un environnement de calcul informatisé et un langage de programmation, sous forme d'un logiciel libre, relativement compatible au niveau des sources avec MATLAB et GNU Octave. Il supporte nombre des fonctions de MATLAB et quelques fonctionnalités d'IDL. Il s'interface facilement avec du code externe en C, C++, et Fortran, offre la possibilité de développement d'algorithmes distribués parallèles (via MPI). Et il possède quelques capacités de rendu volumique et de visualisation 3D.Liens externes [modifier]
10:35 Publié dans FreeMat | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Manuel Maxima
Node:Top, Next:Introduction à MAXIMA, Previous:(dir), Up:(dir)
MAXIMA est un programme de calcul formel assez complet.
Il a été réalisé en COMMON LISP par William F. Schelter, à partir de la version originale de Macsyma réalisée au MIT et qui fut distribuée par le Department of Energy. Le DOE ayant accordé la permission à W. Schelter d'en faire des copies dérivées, et en particulier de le distribuer sous license publique GNU (voyez le fichier COPYING inclus dans la distribution), les fichiers de MAXIMA peuvent désormais être redistribués selon les termes de la licence publique GNU.
Traduction française : André Jaccomard, Armand Osselet, Daniel Duparc et Michel Lavaud.
Dernière mise à jour : 1er mai 2003. La version la plus récente de ce document peut être obtenue sur le site web de l'association AsTeX, http://www.univ-orleans.fr/EXT/ASTEX
Infrastructure de MAXIMA
- Introduction à MAXIMA: Exemple de sessions MAXIMA.
- Aide: Demander de l'aide depuis une session MAXIMA.
- Ligne de commande: Syntaxe de la ligne de commande de MAXIMA.
- Opérateurs: Opérateurs utilisés dans les expressions de MAXIMA.
- Expressions: Expressions dans MAXIMA.
- Simplification: Simplifier les expressions.
- Tracé de courbe: Sorties graphiques 2D et 3D.
- Entrée et sortie: Fichiers en entrée et sortie.
- Virgule flottante: Routines numériques de bas niveau.
- Contextes: Ensemble des faits admis.
Assistance pour des domaines spécifiques des mathématiques
- Polynômes: Formes standards pour les polynômes, et fonctions opérant sur eux.
- Constantes: Constantes numériques.
- Logarithmes: Manipulation d'expressions impliquant les logarithmes.
- Trigonométrie: Manipulation d'expressions contenant des fonctions trigonométriques et trigonométriques inverses.
- Fonctions spéciales: Fonctions spéciales
- Polynômes orthogonaux: Polynômes orthogonaux et fonctions spéciales
- Limites: Limites d'expressions.
- Différentiation: Calcul différentiel.
- Intégration: Calcul intégral.
- Equations: Définir et résoudre des équations.
- Equations différentielles: Définir et résoudre des équations différentielles.
- Calcul numérique: Intégration numérique, transformée de Fourier, etc.
- Statistiques: Fonctions statistiques.
- Tableaux et tables: Créer et travailler avec des tableaux.
- Matrices et algèbre linéaire: Opérations sur les matrices.
- Affine:
- Tenseur: Ensemble de manipulation de tenseur indiciel.
- Ctenseur: Manipulation de tenseur composant.
- Séries: Séries puissance et de Taylor.
- Théorie des nombres: Théorie des nombres.
- Symétries:
- Groupes: Algèbre abstraite.
Ressources avancées et programmation
- Environnement d'exécution: Personnalisation de l'environnement de MAXIMA.
- Options diverses: Options ayant un effet global sur MAXIMA.
- Règles et modèles: Concordances définies par l'utilisateur et règles de simplification.
- Listes: Manipulation des listes Lisp.
- Définition de fonction: Définir des fonctions.
- Flot du programme: Définir des programmes MAXIMA.
- Débogage: Déboguer des programmes MAXIMA.
Index
- Index des fonctions et variables: Index.
--- Liste détaillée des noeuds ---
Introduction
- Introduction à MAXIMA:
Aide
- Introduction à l'aide:
- Lisp et Maxima:
- Ramasse-miettes:
- Documentation:
- Définitions pour l'aide:
Ligne de commande
- Introduction à la ligne de commande:
- Définitions pour la ligne de commande:
Opérateurs
- NARY:
- NOFIX:
- OPERATOR:
- POSTFIX:
- PREFIX:
- Définitions pour les opérateurs:
Expressions
- Introduction aux expressions:
- Affectation:
- Complexes:
- Inégalités:
- Syntaxe:
- Définitions pour les expressions:
Simplification
- Définitions pour simplification:
Tracé de courbe
- Définitions pour le tracé de courbe:
Entrée et sortie
- Introduction aux entrées/sorties:
- Fichiers:
- PLAYBACK:
- Définitions pour les entrées/sorties:
Virgule flottante
- Définitions pour virgule flottante:
Contexte
- Définitions pour les contextes:
Polynômes
- Introduction aux polynômes:
- Définitions pour les polynômes:
Constantes
- Définitions pour les constantes:
Logarithmes
- Définitions pour les logarithmes:
Trigonométrie
- Introduction à la trigonométrie:
- Définitions pour la trigonométrie:
Fonctions spéciales
- Introduction aux fonctions spéciales:
- GAMALG:
- SPECINT:
- Définitions pour les fonctions spéciales:
Polynômes orthogonaux
- Introduction aux polynômes orthogonaux:
- Définitions pour les polynômes orthogonaux:
Limites
- Définitions pour les limites:
Différentiation
- Définitions pour la différentiation:
Intégration
- Introduction à l'intégration:
- Définitions pour l'intégration:
Equations
- Définitions pour les équations:
Equations différentielles
- Définitions pour les équations différentielles:
Calcul numérique
- Introduction au calcul numérique:
- DCADRE:
- ELLIPT:
- FOURIER:
- NDIFFQ:
- Définitions pour le calcul numérique:
Statistiques
- Définitions pour les statistiques:
Tableaux et tables
- Définitions pour les tableaux et les tables:
Matrices et algèbre linéaire
- Introduction aux matrices et à l'algèbre linéaire:
- DOT:
- Vecteurs:
- Définitions pour les matrices et l'algèbre linéaire:
Affine
- Définitions pour affine:
Tenseur
- Introduction aux tenseurs:
- Définitions pour les tenseurs:
Ctenseur
- Introduction aux Ctenseurs:
- Définitions pour les Ctenseurs:
Séries
- Introduction aux séries:
- Définitions pour les séries:
Théorie des nombres
- Définitions pour la théorie des nombres:
Symétries
- Définitions pour les symétries:
Groupes
- Définitions pour les groupes:
Environnement d'exécution
- Introduction à l'environnement d'exécution:
- Interruptions:
- Définitions pour l'environnement d'exécution:
Options diverses
- Introduction à diverses options:
- SHARE:
- Définitions pour diverses options:
Règles et modèles
- Introduction aux règles et modèles:
- Définitions pour les règles et les modèles:
Listes
- Introduction aux listes:
- Définitions pour les listes:
Définition de fonction
- Introduction à la définition de fonction:
- Fonction:
- Macros:
- Optimisation:
- Définitions pour la définition de fonction:
Flot du programme
- Introduction au flot du programme:
- Définitions pour le flot du programme:
Débogage
- Définitions pour le débogage:
Node:Introduction à MAXIMA, Next:Aide, Previous:Top, Up:Top
Source : http://www.univ-orleans.fr/EXT/ASTEX/astex/doc/fr/maxima/...
10:21 Publié dans Manuel Maxima | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Documentation Maxima



Nouveau: Vincent Obaton propose un aide-mémoire très pratique pour maxima.
|
Documents |
Langue |
Auteur |
Version |
Format |
Action |
|
Aide-Mémoire pour Maxima |
Français |
août 2009 |
|
||
|
Aide-Mémoire de Maxima |
Français |
Yves Lemaire |
26/01/2003 |
|
|
|
Découverte de Maxima |
Français |
? |
1.0 |
|
|
|
html |
|||||
|
tm ( texmacs ) |
|||||
|
Introduction à Maxima |
Français |
H Hand, traduction de M Gosse |
1.1 |
|
|
|
html |
|||||
|
tm ( texmacs ) |
|||||
|
FAQ de Maxima |
Français |
Michel Gosse |
0.93 |
|
|
|
tm ( texmacs) |
|||||
|
html |
|||||
|
Manuel de Maxima |
Français |
A Jaccomard, |
3/05/2003 |
|
|
|
ps.tgz |
|||||
|
html |
|||||
|
Manuel de Maxima |
Anglais |
W Schleter |
1.0 |
|
|
|
ps.tgz |
|||||
|
html |
|||||
|
The Maxima Book |
Anglais |
De Souza, Fateman, Moses, Yapp |
10/02/2003 |
|
|
|
Introduction à Maxima |
Français |
Marc Gilg |
0.1.0 |
|
|
|
tm ( texmacs) (tar.gz) |
|||||
|
html |
|||||
| A Maxima Guide for Calculus students | Anglais | Moses Glasner |
2/01/2004 | Télécharger |
 Source : http://michel.gosse.free.fr/documentation/index.html
Source : http://michel.gosse.free.fr/documentation/index.html
10:20 Publié dans Documentation Maxima | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Maxima, a Computer Algebra System
Maxima is a system for the manipulation of symbolic and numerical expressions, including differentiation, integration, Taylor series, Laplace transforms, ordinary differential equations, systems of linear equations, polynomials, and sets, lists, vectors, matrices, and tensors. Maxima yields high precision numeric results by using exact fractions, arbitrary precision integers, and variable precision floating point numbers. Maxima can plot functions and data in two and three dimensions. The Maxima source code can be compiled on many systems, including Windows, Linux, and MacOS X. The source code for all systems and precompiled binaries for Windows and Linux are available at the SourceForge file manager. Maxima is a descendant of Macsyma, the legendary computer algebra system developed in the late 1960s at the Massachusetts Institute of Technology. It is the only system based on that effort still publicly available and with an active user community, thanks to its open source nature. Macsyma was revolutionary in its day, and many later systems, such as Maple and Mathematica, were inspired by it. The Maxima branch of Macsyma was maintained by William Schelter from 1982 until he passed away in 2001. In 1998 he obtainedpermission to release the source code under the GNU General Public License (GPL). It was his efforts and skill which have made the survival of Maxima possible, and we are very grateful to him for volunteering his time and expert knowledge to keep the original DOE Macsyma code alive and well. Since his passing a group of users and developers has formed to bring Maxima to a wider audience. We are constantly updating Maxima, to fix bugs and improve the code and the documentation. We welcome suggestions and contributions from the community of Maxima users. Most discussion is conducted on the Maxima mailing list. Source : http://maxima.sourceforge.net/News RSS
10:18 Publié dans Maxima, a Computer Algebra System | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Maxima
Maxima
| Maxima | |
 |
|
|
wxMaxima
|
|
| Développeur | William Schelter et coll. |
|---|---|
| Dernière version | 5.20.1 (14 décembre 2009) [+/-] |
| Environnement | GNU/Linux, Mac OS X, Windows |
| Type | Logiciel de calcul formel |
| Licence | GNU GPL |
| Site Web | maxima.sf.net |
| modifier |
|
Maxima est un logiciel libre de calcul formel, descendant sous licence GNU GPL du package Macsyma, le logiciel de calcul symbolique développé à l’origine pour les besoins du Département de l'Énergie américain.
Sommaire[masquer] |
Fonctionnalités [modifier]
Cette descendance fut initialisée par William Schelter en 1982 qui le maintint jusqu'à sa mort, en 2001. Depuis cette année, une communauté de développeurs tient régulièrement le programme à jour. En 1998, elle réussit à appliquer la licence GNU GPL pour libérer le code du programme et lui permettre de continuer son développement.
Maxima permet de faire du calcul sur les polynômes, les matrices, de l’intégration, de la dérivation, du calcul de séries, de limites, résolutions de systèmes, d’équations différentielles, etc. En plus du Macsyma distribué officiellement, il comporte le module SYM de manipulations de fonctions symétriques et de calculs de résolvantes écrit par Annick Valibouze. Ce module n'a pas son équivalent dans les autres systèmes de calcul formel (Magma, Mathematica, Maple, ...)
Les possibilités d'extension de Maxima sont très riches.
Son langage de programmation est inspiré de LISP, son langage sous-jacent. Il est ainsi recommandable pour l'enseignement de la programmation à des scientifiques utilisateurs potentiels du calcul formel. Il est aussi possible de développer dans son LISP sous-jacent utilisable sous Maxima en interprété (pour le débuggage) mais aussi, et c'est ce qui en fait l'intérêt, en compilable. L'interfaçage avec Maxima est très aisé.
Ses possibilités graphiques sont plus limitées que celles de Mathematica et de Maple, mais ses capacités dans le domaine du calcul symbolique sont les plus étendues du monde du logiciel libre, et n’ont pas à rougir face aux logiciels commerciaux.
Pour des besoins de publication, il peut formater ses formules en TeX et il existe un mode Emacs pour un affichage impeccable des formules.
Calculs numériques [modifier]
Comme tous les programmes de calcul formel, Maxima est spécialisé dans les manipulations de symboles. Cependant, il sait également produire des résultats numériques sous forme d'entiers et de fractions de taille variable, seulement limités par la taille de la mémoire centrale de l'ordinateur hôte, ou bien encore de réels à virgule flottante de précision arbitrairement grande (bfloat pour big floats).
Pour les calculs utilisant intensivement les nombres à virgule flottante et les grands tableaux, Maxima peut générer le code correspondant dans d'autres langages de programmation, tels Fortran, code qui s'exécutera d'autant plus efficacement.
Voir aussi [modifier]
Articles connexes [modifier]
- Mathematica et Maple : deux concurrents propriétaires
- Yacas : autre logiciel libre de calcul formel
Liens externes [modifier]
- (en) Site officiel
- (en) Accueil du projet Maxima sur SourceForge.net
- (en) wxMaxima, un GUI multiplate-forme
- (fr) Manuel
- (fr) Documentation Maxima
10:16 Publié dans Maxima | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Maple
Maple
![]() Pour les articles homonymes, voir Maple (homonymie).
Pour les articles homonymes, voir Maple (homonymie).![]() Cet article a pour sujet le logiciel de calcul formel Maple. Pour une définition du mot « maple », voir l’article maple du Wiktionnaire.
Cet article a pour sujet le logiciel de calcul formel Maple. Pour une définition du mot « maple », voir l’article maple du Wiktionnaire.
| Maple | |
| Développeur | Waterloo Maple Inc. (Maplesoft) |
|---|---|
| Dernière version | 14.00 (avril 2010) [+/−] |
| Environnement | Multi-plate-forme |
| Type | Logiciel de calcul formel |
| Licence | Propriétaire |
| Site Web | www.maplesoft.com/products/maple/ |
| modifier |
|
Maple est un logiciel propriétaire de calcul formel édité par la société canadienne Maplesoft. La dernière version est la version 14, disponible depuis le 29 avril 20101.
Sommaire[masquer] |
Maple a été initialement développé au sein du Symbolic Computation Group de l'Université de Waterloo en Ontario (Canada) à partir de 1981. La première version publique date de 1985 (version 3.3). Le logiciel permet aussi bien de travailler sur des quantités numériques (entières, réelles, complexes) qu'avec des polynômes, fonctions, séries. Maple réalise des dérivations, intégrations, résolutions de systèmes d'équations linéaires, inversions de matrices, développements asymptotiques et résolutions d'équations différentielles sous forme symbolique, c'est-à-dire en gardant des inconnues dans la résolution. Le système Maple offre aussi de nombreuses fonctionnalités en arithmétique des nombres et en combinatoire. Maple est un système interprété, c'est-à-dire que l'utilisateur tape une ligne de commande suivie d'un terminateur, ce qui provoque une évaluation (calcul ou résolution) et le système retourne un résultat. Maple représente les objets sous la forme d'un graphe acyclique orienté. Il est cependant également possible d'écrire des programmes (dans un langage très proche de celui des lignes de commandes) qui ne seront pas compilés, mais interprétés à leur appel, et d'enrichir ainsi le système avec de nouvelles commandes. Il est ensuite possible de : Maple offre un mode console et un mode graphique. Il est disponible sur la majorité des systèmes d'exploitation (GNU/Linux, Macintosh, Windows). En France, Maple est le logiciel de calcul formel le plus utilisé dans l'enseignement[réf. nécessaire], notamment dans les classes préparatoires aux grandes écoles[réf. nécessaire]. Le code suivant donne la solution de l'équation différentielle du second ordre y'' − 3y = x vérifiant les conditions initiales y(0) = 1 et y'(0) = 2 :Principe [modifier]
Exemple d'instruction [modifier]
dsolve({diff(y(x),x,x)-3*y(x)=x,y(0)=1,D(y)(0)=2},y(x));Notes et références [modifier]
Voir aussi [modifier]
Articles connexes [modifier]
Liens externes [modifier]
10:15 Publié dans Maple | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
04/12/2010
Mathematica
Mathematica
| Mathematica | |
| Développeur | Wolfram Research |
|---|---|
| Dernière version | 7 (18 novembre 2008) [+/−] |
| Environnements | Multiplate-forme (liste détaillée) |
| Type | Logiciel de calcul formel |
| Licence | Propriétaire |
| Site Web | Page d'accueil de Mathematica |
| modifier |
|
Mathematica est un logiciel propriétaire de calcul formel édité par Wolfram Research, la société de Stephen Wolfram. Wolfram commence à travailler sur le logiciel en 1986 et en sort la première version en 1988. Il est disponible sur de nombreuses plateformes et supporte un large choix d'opérations. Le système de Mathematica est formé d'un noyau, qui réalise les calculs et peut être exécuté sur une autre machine que celle de l'utilisateur, et d'une interface interactive pour entrer les données. Celle-ci attend des entrées de l'utilisateur exprimées dans le langage de Mathematica, selon une syntaxe définie, et affiche le résultat des calculs sous forme de texte simple, de formules, ou d'images. En France et en Suisse, le logiciel est avec Maple présent dans l'enseignement supérieur. L'entreprise a mis en service en site internet dit intelligent, basé entre autres sur Mathematica: Wolfram|Alpha. Il est ainsi possible d'utiliser les ressources de Mathematica gratuitement.Voir aussi [modifier]
Articles connexes [modifier]
Liens externes [modifier]
07:54 Publié dans Mathematica | Lien permanent | Commentaires (1) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Randomness and Recurrence in Dynamical Systems
Double-Click Image to Enlarge Catalog Code: CAM-31 This book, part of the MAA's oldest book series, makes the ideas of randomness and recurrence in dynamical systems comprehensible for undergraduates and beginning graduate students. It fills the gap between undergraduate teaching and current mathematical research, bringing out relevant results with a minimum of measure theory. Author Rodney Nillsen develops new techniques of proof and adapts known proofs to make the material accessible to students with a background only in elementary analysis. Forward Index of Symbols The curious phenomenon of the leading significant digit (p. 180): Suppose we have a collection of positive numbers, perhaps arising from a set of data. Assuming the data is random, we might expect that the leading digits of the numbers in the data would occur with an approximately equal frequency. So, it may come as a very surprising fact that this is often not the case. Back in the days when electronic calculators did not exist, arithmetical calculations were carried out using books of logarithmic tables. It seems to have been Simon Newcomb, the professor of mathematics and astronomy at Johns Hopkins University, who observed in 1881 that the pages near the front of books of logarithms were more used than the pages towards the back. He wrote: "That the ten digits do not occur with equal frequency must be evident to any one making use of logarithmic tables, and noticing how much faster the first pages wear out than the last ones. The first significant digit is oftener 1 than any other digit, and the frequency diminishes up to 9." Rodney Nillsen (University of Wollongong, in New South Wales, Australia) received his undergraduate education at the University of Tasmania and postgraduate education at Flinders University of South Australia. A member of the MAA, he is interested in harmonic analysis, functional analysis, differential equations, and measure theory. He is the author of Differential Spaces and Invariant Linear Forms (1994). Source : http://www.maa.org/pubs/CAM-31.html
Randomness and Recurrence in Dynamical Systems
Rodney Nillsen
ISBN: 978-0-88385-043-5
357 pp., Hardbound, 2010
List Price: $52.95
Member Price: $42.95
Series: Carus Mathematical Monographs, #31
• Emphasizes interpretations of results, concepts, and connections to other areas of inquiry;
• Includes exercises, investigations, and more than 60 figures to explain proofs;
• Sets the mathematical ideas in historical context;
• Suggests areas for further study.
Table of Contents
Preface
Background Ideas and Knowledge
Irrational Numbers and Dynamical Systems
Probability and Randomness
Recurrence
Averaging in Time and Space
Index of Subjects
Excerpt
About the Author
07:53 Publié dans Randomness and Recurrence in Dynamical Systems | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Calculus: Modeling and Application, 2nd Edition
Calculus: Modeling and Application, 2nd Edition, by David A. Smith and Lawrence C. Moore of Duke University, responds to advances in technology that permit the integration of text and student activities into a unified whole. In this approach, students can use mathematics to structure their understanding of and investigate questions in the world around them, to formulate problems and find solutions, then to communicate their results to others. This interactive textbook covers two semesters of single-variable calculus. Its features include use of real-world contexts for motivation, guided discovery learning, hands-on activities (including built-in applets), a problem-solving orientation, encouragement of teamwork, written responses to questions, tools for self-checking of results, intelligent use of technology, and high expectation of students. Calculus: Modeling and Application is available through License Agreement subscription. Schools that adopt the text will be charged each semester on a sliding scale based on the number of students expected to be using the text. CDs of the text, which schools can mount on their servers and/or replicate for their students, will be provided to adopters. The Firefox Browser, and MathML fonts, both free downloads, are needed to run the text. To order your subscription to the course, fill out our License Agreement and order form. Once both forms are filled out, fax them to the attention of Mary Anne Rice at: (301) 206-9789. You may also print out the license agreement and the order form and mail both to: MAA, PO Box 91112, Washington, DC 20090-1112. Source : http://calculuscourse.maa.org/Calculus: Modeling and Application, 2nd Edition
by David A. Smith and Lawrence C. Moore

For more information contact: Carol Baxter: cbaxter@maa.org, (202) 319-8479, or Mary Anne Rice at: 1-800-331-1622.
07:51 Publié dans Calculus: Modeling and Application, 2nd Edition | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Mathematics Magazine
Mathematics Magazine:
Guidelines for Authors
What do you like to read? What kind of writing can grab the interest of an undergraduate mathematics major? How can Mathematics Magazine serve to remind us all why we chose to study mathematics in the first place? If you keep these questions firmly in mind, you will be well on the way to meeting our editorial guidelines.
General information
Mathematics Magazine is an expository journal of undergraduate mathematics. In this section, we amplify our meaning of these words.Articles submitted to the Magazine should be written in a clear and lively expository style. The Magazine is not a research journal; papers in a terse "theorem-proof" style are unsuitable for publication. The best contributions provide a context for the mathematics they deliver, with examples, applications, illustrations, and historical background. We especially welcome papers with historical content, and ones that draw connections among various branches of the mathematical sciences, or connect mathematics to other disciplines.
Every article should contain interesting mathematics. Thus, for instance, articles on mathematical pedagogy alone, or articles that consist mainly of computer programs, would be unsuitable.
The Magazine is an undergraduate journal in the broad sense that its intended audience is teachers of collegiate mathematics and their students. One goal of the Magazine is to provide stimulating supplements for undergraduate mathematics courses, especially at the upper undergraduate level. Another goal is to inform and refresh the teachers of these courses by revealing new connections or giving a new perspective on history. We also encourage articles that arise from undergraduate research or pose questions to inspire it. In writing for the Magazine, make your work attractive and accessible to non-specialists, including well-prepared undergraduates.
Writing and revising
Mathematics Magazine is responsible first to its readers and then to its authors. A manuscript's publishability therefore depends as much on the quality of exposition as the mathematical significance. Our general advice is simple: Say something new in an appealing way, or say something old in a refreshing, new way. But say it clearly and directly, assuming a minimum of background. Our searchable database of past pieces from the Magazine and the College Mathematics Journal can help you check the novelty of your idea.Make your writing vigorous, expressive, and informal, using the active voice. Give plenty of examples and minimize computation. Help the reader understand your motivation and share your insights. Illustrate your ideas with visually appealing graphics, including figures, tables, drawings, and photographs.
First impressions are vital. Choose a short, descriptive, and attractive title; feel free to make it funny, if that would draw the reader in. Be sure that the opening sentences provide a welcoming introduction to the entire paper. Readers should know why they ought to invest time reading your work.
Our referees are asked to give detailed suggestions on style, as well as check for mathematical accuracy. In practice, almost every paper requires a careful revision by the author, followed by further editing in our office. To shorten this process, be sure to read your own work carefully, possibly after putting it away for a cooling-off period.
Provide a generous list of references to invite readers—including students—to pursue ideas further. Bibliographies may contain suggested reading along with sources actually referenced. In all cases, cite sources that are currently and readily available.
Since 1976, the Carl B. Allendoerfer Prize has been awarded annually to recognize expository excellence in the Magazine. In addition to these models of style, many useful references are available. Some are listed at the end of these guidelines.
Style and format
We assume that our authors are at least sometime-readers of the Magazine, with some knowledge of its traditions. If so, they know that most papers are published either as Articles or as Notes. Articles have a broader scope than Notes and usually run longer than 2000 words. Notes are typically shorter and more narrowly focused. Articles should be divided into a few sections, each with a carefully chosen title. Notes, being shorter, usually need less formal sectioning. Footnotes and subsectioning are almost never used in the Magazine.In addition to expository pieces, we accept a limited number of Math Bites, poems, cartoons, Proofs Without Words, and other miscellanea.
List references either alphabetically or in the order cited in the text, adhering closely to the Magazine's style for capitalization, use of italics, etc.
We recommend using simple, unadorned LaTeX in the preparation of your manuscript. Whatever technology you use, your manuscript should be generously spaced, with the title, author, and author's address at the top of the first page. Templates with further stylistic details are posted at our website in a variety of formats. Number the pages, but number only those equations that you refer to in the text. WhetherLaTeX is used or not, we hope for some electronic version of every article accepted.
Simple LaTeX template files are available for Articles and Notes. These templates do not approximate the appearance of Articles and Notes, but illustrate the desired format for submission to the Magazineand offer advice about style, as well as technical help. Using them requires only the most rudimentary knowledge of TeX or LaTeX. They are available in .pdf and .tex formats. Click on the appropriate filename(s) to obtain copies. (mmnote.tex, mmnote.pdf, mmartic.tex, mmartic.pdf ) For more information or to request hard copies, send email to maaservice@pmds.com. For technical information about preparing manuscripts and figures, see the general guidelines for MAA authors (this is a pdf file).
If you wish to provide any electronic complement to your article, including such things as color illustrations, Java applets, or animations, supply the URL of your draft site. If your article is accepted, complements will be hosted on this site.
In the interest of respecting the time of our referees, we recommend a referee's appendix, not for publication, but to guide the referee. Please expand on statements such as, "A simple calculation shows... ." It is often appropriate to suppress such things in exposition, but a referee might find the additional information a time-saver.
For initial submission, graphical material may be interspersed with text. Each figure should be numbered, and referenced by number in the text. Authors themselves are responsible for providing images of suitable quality. If a piece is to appear in the Magazine, separate copies of all illustrations must be supplied, both with and without added lettering. We hope authors will be able to provide electronic versions of all figures, preferably in a PostScript format.
Submitting manuscripts
Please submit new manuscripts by email to Editor Walter Stromquist at mathmag@maa.org. A brief message with an attached PDF file is preferred. Word processor and DVI files can also be considered. Alternatively, manuscripts may be mailed to:Mathematics Magazine
132 Bodine Rd.
Berwyn, PA 19312-1027
If possible, please include an email address for further correspondence.
References
- R.P. Boas, Can we make mathematics intelligible? Amer. Math. Monthly 88 (1981), 727--731.
- Paul Halmos, How to write mathematics, Enseign. Math. 16 (1970), 123--152. Reprinted in Halmos, Selecta, expository writings, Vol. 2, Springer, New York, 1983, 157--186.
- Andrew Hwang, Writing in the age of Latex, AMS Notices 42 (1995), 878--882.
- D.E. Knuth, T. Larrabee, and P.M. Roberts, Mathematical Writing, MAA Notes #14, 1989.
- Steven G. Krantz, A Primer of Mathematical Writing, American Mathematical Society, 1997.
- N. David Mermin, Boojums All the Way Through, Cambridge Univ. Pr., Cambridge, UK, 1990.
07:50 Publié dans Mathematics Magazine | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Mathematics Magazine
Mathematics Magazine
| Mathematics Magazine | |
| Pays | États-Unis |
|---|---|
| Langue(s) | Anglais |
| Périodicité | Bimensuel |
| Genre | Revue mathématique |
| Diffusion | 10 000 ex. (2008) |
| Date de fondation | 1947 |
| Éditeur | Washington, D.C. |
|
|
|
| ISSN | 0025-570X |
| Site Web | http://www.maa.org/pubs/mathmag.html |
Mathematics Magazine est une publication bimensuelle de référence de la Mathematical Association of America. Elle cible un public constitué d'enseignants en mathématiques et de leurs étudiants. C'est cependant une revue de mathématiques plutôt que de pédagogie. Au lieu d'articles adoptant un style lapidaire « théorème-preuve » répandu dans les revues de recherche, les articles fournissent un cadre au sujet, avec des exemples, des applications, des illustrations, et le contexte historique1. La diffusion payée en 2008 était de 9 500 et le tirage total était de 10 0002.
Notes et références [modifier]
- Mathematics Magazine: Guidelines for Authors [archive], June 2, 2008
- « Statement of Ownership, Management, and Circulation », dans Mathematics Magazine, vol. 81, no 4, October 2008, p. 316
07:49 Publié dans Mathematics Magazine | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
03/12/2010
CM2 : Additions et soustractions de nombres décimaux
Exemple : 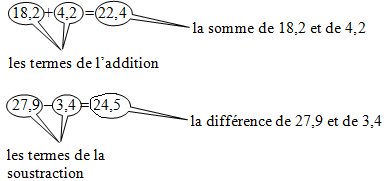
II. Calculer une somme, une différence
a) Poser une addition, une soustraction
Exemple : 
b) A l'aide d'une calculatrice
Exemple : A l'aide d'une calculatrice, calculer : 137,9 + 23,5
On tape : 137.9 + 23.5 =
La calculatrice affiche 161.4
On écrit : 137,9 + 23,5 = 161,4
III. Propriétés
Exemple :
7 + 72 + 3 + 28
= (72 + 28) + (7 + 3)
= 100 + 10
= 110
Remarque :
Regrouper les termes permet d'obtenir des opérations plus faciles à calculer.  Dans une soustraction, l'ordre des termes a de l'importance et on ne peut pas regrouper des termes.
Dans une soustraction, l'ordre des termes a de l'importance et on ne peut pas regrouper des termes.
Exemples :
| 100 - 40 - 15 | 100 - (40 - 15) |
| = 60 - 15 | = 100 - 25 |
| = 45 | = 75 |
IV. Ordre de grandeur d'une somme, d'une différence
Exemple :
Donnons un ordre de grandeur de la somme 2 037,82 + 4 984,75 :
2 037,82 est proche de 2 000.
4 984,75 est proche de 5 000.
Donc un ordre de grandeur de 2 037,82 + 4 984,75 est 2 000 + 5 000, c'est-à-dire 7 000.
Donc : 2 037,82 + 4 984,75 est proche de 7 000.
Exemple :
Donnons un ordre de grandeur de la différence 4 987,87 - 1 824,59 :
4 987,87 est proche de 5 000.
1 824,59 est proche de 2 000.
Donc un ordre de grandeur de 4 987,87 - 1 824,59 est 5 000 - 2 000, soit 3 000.
Donc 4 987,87 - 1 824,59 est proche de 3 000.
Remarque :
Un ordre de grandeur peut servir à prévoir ou à vérifier un résultat.
Exemple :
On a vu qu'un ordre de grandeur de 4 987,87 - 1 824,59 est 3 000.
En posant la soustraction, on trouve : 4 987,87 - 1 824,59 = 3 163,28.
3 163,28 est un nombre proche de 3 000. Le résultat est cohérent.
V. Lien entre addition et soustraction
La différence entre deux nombres est le nombre qu'il faut ajouter à l'un pour obtenir l'autre.
Exemple :
La différence 7 - 2 est le nombre qu'il faut ajouter à 2 pour obtenir 7.
7 - 2 = 5 signifie que 2 + 5 = 7
A une addition, on peut faire correspondre deux soustractions : 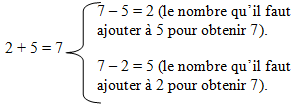
A une soustraction, on peut faire correspondre une addition et une soustraction :
VI. Calcul avec les durées
On utilise la base sexagésimale (de base soixante) pour mesurer le temps :  Dans une heure, il y a 60 minutes : 1 h = 60 min
Dans une heure, il y a 60 minutes : 1 h = 60 min  Dans une minute, il y a 60 secondes : 1 min = 60 s
Dans une minute, il y a 60 secondes : 1 min = 60 s
Exemple 1 :
Combien de temps dure une séance de cinéma qui commence à 15 h 25 et qui finit à 18 h 05 ?
Méthode 1 : On pose la soustraction : 
Méthode 2 :
De 15 h 25 à 16 h s'écoulent 35 min.
De 16 h à 18 h 05 sécoulent 2 h 05 min.35 min + 2 h 05 min = 2 h 40 min
Méthode 3 :
De 15 h 25 à 18 h 25 s'écoulent 3 h.
La séance finit à 18 h 05, soit 20 min avant 18 h 25.
3 h - 20 min = 2 h 40 min.
La séance dure donc 2 h 40 min.
Exemple 2 :
A quelle heure notre train doit-il arriver s'il est parti à 11 h 50 et que la durée du voyage est 4 heures et 20 minutes ? 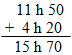
Or, 70 min = 1 h 10 min, donc :
15 h 00 + 70 min = 15 h 00 + 1 h 10 min = 16 h 10 min
Notre train va donc arriver à 16 h 10.
Source : http://www.le-precepteur.net/cm2/mathematiques/additions/...
22:07 Publié dans Additions et soustractions de nombres décimaux | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Réviser les quatre opérations
Calcul
Objectif : Réviser les quatre opérations
1 - Pose et effectue les opérations suivantes.
7860,4 X 5,26 = .........................................
1310 : 56 = ......................................... (au dixième près)
14000 : 456 = ......................................... (au dixième près)
2 - Observe les produits suivants puis complète les deux derniers sans poser les calculs.
57,8 X 6,25 = 361,25 5,78 X 62,5 = ................
578 X 0,625 = ................
3 - Additionne en lignes et en colonnes.
|
45,6 |
3025 |
34 |
21,8 |
|
|
326 |
28,73 |
35,8 |
827 |
|
|
42 |
651 |
396 |
42,45 |
|
|
567,52 |
17,6 |
5,62 |
257 |
|
|
|
|
|
|
|
4 - Calcule en ligne.
365 - 47,4 = .…………… 70643 X 6 = .……………
5 – Complète les opérations à trous.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
5 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
• |
• |
• |
|
|
|
|
6 |
7 |
, |
• |
|
|
|
|
|
|
|
|
|
2 |
6 |
1 |
• |
|
|
+ |
8 |
• |
0 |
, |
4 |
5 |
|
|
|
|
|
|
|
• |
• |
7 |
• |
|
|
|
+ |
|
5 |
• |
, |
1 |
3 |
• |
|
|
|
|
|
• |
• |
• |
• |
|
|
|
|
|
• |
7 |
6 |
, |
8 |
• |
7 |
|
|
|
|
|
• |
7 |
0 |
7 |
2 |
2 |
|
6 - Calcule mentalement
47 - 25 = ........................................................ 429 - 18 = ...................................................
85 - 17 = ........................................................ 47 X 10 = ...................................................
104 X 1000 = ................................................ 15 X 30 = ...................................................
12 X 400 = .................................................... 4 X 46 = .....................................................
7 + 3,5 = .......................................................... 24,7 + 10,2 = ...............................................
Corrigé
1 - Pose et effectue les opérations suivantes.
7860,4 X 5,26 = 41 345,704
1310 : 56 = 23,3 (au dixième près)
14000 : 456 = 30,7 (au dixième près)
2 - Observe les produits suivants puis complète les deux derniers sans poser les calculs.
57,8 X 6,25 = 361,25 5,78 X 62,5 = 361,25
578 X 0,625 = 361,25
3 - Additionne en lignes et en colonnes.
|
45,6 |
3025 |
34 |
21,8 |
3126,4 |
|
326 |
28,73 |
35,8 |
827 |
1217,53 |
|
42 |
651 |
396 |
42,45 |
1131,45 |
|
567,52 |
17,6 |
5,62 |
257 |
847,74 |
|
981,12 |
3722,33 |
471,42 |
1148,25 |
6323,12 |
4 - Calcule en ligne.
365 - 47,4 = 317,6 70 643 X 6 = 423 858
5 – Complète les opérations à trous.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
5 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
8 |
7 |
4 |
|
|
|
|
6 |
7 |
, |
3 |
|
|
|
|
|
|
|
|
|
2 |
6 |
1 |
2 |
|
|
+ |
8 |
5 |
0 |
, |
4 |
5 |
|
|
|
|
|
|
|
4 |
5 |
7 |
1 |
|
|
|
+ |
|
5 |
9 |
, |
1 |
3 |
7 |
|
|
|
|
|
5 |
2 |
2 |
4 |
|
|
|
|
|
9 |
7 |
6 |
, |
8 |
8 |
7 |
|
|
|
|
|
5 |
7 |
0 |
7 |
2 |
2 |
|
6 - Calcule mentalement
47 - 25 = 22 429 - 18 = 411
85 - 17 = 68 47 X 10 = 470
104 X 1000 = 104 000 15 X 30 = 450
12 X 400 = 4 800 4 X 46 = 184
7 + 3,5 = 10,5 24,7 + 10,2 = 34,9
22:04 Publié dans Réviser les quatre opérations | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook