03/12/2010
ENSEIGNER AUTREMENT LE CONCEPT DE CARRÉ EN CE2
Cet article a été rédigé en réponse à l’appel à contribution n° 5 MathemaTICE a publié deux autres articles de Francine Dubreucq : Nous proposons, dans cet article, d’exposer comment nous avons travaillé sur le carré dans une classe de CE2. Le concept de carré évolue au cours de la scolarité. Le mot ’’carré’’ appartient d’abord au monde sensible. En effet, dans les tâches d’observation et de tri d’objets à l’école maternelle, l’enfant devra reconnaître la forme carrée parmi d’autres formes. Puis le mot ’’carré’’ change de statut. L’enfant devra être capable de décrire, de reproduire ou de tracer un carré sur son cahier. Nous nous intéressons à ce changement de statut. Nous faisons l’hypothèse qu’un logiciel de géométrique dynamique est un agent favorable à cette évolution. Nous analyserons comment les contraintes du logiciel entraînent la structuration des connaissances géométriques. Le titulaire de la classe [1] a introduit les notions de perpendiculaires et de parallèles en prenant comme support les situations Ermel, trait sur trait et droites penchées pareil. D’une part, il a mené conjointement un travail en arts sur les oeuvres de Mondrian, Kandinsky et Vasarely et sur les notions de mathématiques qu’elles recèlent. D’autre part, le projet de classe consiste en la création d’un répertoire de jeux du monde. Les élèves cherchent des informations sur Internet sur différents jeux. Le jeu de marelle demande un plateau de jeu dont la base est représentée par trois carrés concentriques. Nous avons choisi de travailler sur ces carrés avec un logiciel de géométrie dynamique pour diffuser le plateau de jeu accompagnant les règles du jeu. Le plateau de jeu est présenté en annexe 2. La dévolution du problème a été faite par le titulaire dans l’environnement papier. Nous présentons la première séance d’introduction du logiciel TracenPoche (TeP) dans la classe de CE2. Nous ne parlerons pas précisément des conditions [2] Nous avons choisi de tracer d’abord le grand carré. Nous sommes dans une phase d’initiation instrumentale. Du point de vue mathématiques, à notre niveau d’enseignement, le segment est un trait qui s’arrête. Les connaissances mathématiques sont faibles. Par contre, le tracé du segment avec TeP nécessite des connaissances instrumentales importantes. Le processus cognitif fait appel à la représentation iconique du segment, tout en plaçant l’élève sur le mode de l’action. Il est à souligner, qu’à ce moment précis, se passe la compréhension de la validation d’un point. La tâche dans l’environnement informatique est de tracer le segment [AB] sachant que les points A et B ont été placés. Un élève doit comprendre la signification de l’affichage rouge. Cette tâche est nouvelle dans l’environnement informatique et ne repose pas sur une technique ancienne de l’environnement papier. Certains élèves expriment la couleur rouge comme celle de l’interdit. Ils vont valider la position de l’extrémité du segment et un point C sera malencontreusement tracé. Il faudra l’intervention du maître pour expliquer ce qui s’est passé. D’autres expliquent rapidement « C’est rouge, tu cliques ». Nous devons évoquer également les différences entre la tâche dans l’environnement papier et dans l’environnement numérique. Pour tracer le segment [AB], l’élève place le point A, puis il prend la règle pour tracer le ’’trait’’ et enfin il place le point B à la fin du ’’trait’’. Par contre, dans l’environnement numérique, l’élève place le point A, puis le point B et enfin, en utilisant le bouton ’’segment’’, il relie les points A et B. Ces chronologies différentes n’ont pas soulevé de difficulté. La connaissance mathématique est importante. Il n’est pas facile de visualiser la perpendiculaire à une droite passant par un point de cette dernière et encore moins de la tracer avec l’équerre. Le tracé avec TeP se fait sans difficulté. La représentation des boutons de TeP permet aux élèves de trouver la perpendiculaire. Ils reconnaissent le symbole de perpendicularité. En activant le bouton perpendiculaire, le logiciel favorise le passage au mode symbolique. Même si cette étape est difficile du point de vue mathématique, il semble important de faire formuler les élèves. Cela permet de passer par le langage mathématique. Le rapport entre les tâches mathématiques et instrumentales est maximal. Nous avons remarqué que les élèves ont été surpris par notre formulation. Lorsqu’on leur demande « Trace la droite, qui est perpendiculaire à (AB) et qui passe par le point A » dans l’environnement papier, ils doivent effectivement prendre leurs instruments de géométrie et leur crayon pour tracer. Ils sont dans le mode de l’action. Dans l’environnement TeP, ils veulent faire de même, à savoir tracer une droite. Il faut préciser aux élèves que c’est le logiciel qui va dessiner la droite, mais il ne le fera que sur notre ordre. Il est donc nécessaire de préciser ce que l’on demande au logiciel. Cette verbalisation est essentielle : elle permet d’utiliser le vocabulaire géométrique. L’utilisation de TeP aide à exprimer leur action avec les mots. Le choix a été fait de proposer un tracé sur papier et sur TeP sous forme de « symbiose instrumentale », définie par T. Assude. Les tâches dans l’environnement papier et dans l’environnement TeP sont imbriquées. Les procédures acquises dans une situation sont appliquées dans l’autre situation. C’est la présence du cercle qui assure la conservation des longueurs. Cette contrainte donnée sur le papier est exigeante. Elle repose sur l’équidistance des points du cercle au centre du cercle. Les élèves n’utilisent pas le compas pour le report des longueurs. Les connaissances mathématiques sont maximales. Cette difficulté étant surmontée, les élèves n’éprouvent aucune difficulté à utiliser TeP : ils reconnaissent le bouton de tracé du cercle. Pourtant, ils ne parviennent pas au mode symbolique : ils expliquent avec les doigts ce qu’ils vont faire. Les enfants se placent sur le mode iconique : ils placent le curseur sur le point A, et lorsqu’ils le valident comme étant le centre du cercle, ce dernier grandit au fur et à mesure du déplacement. Les traits de construction ne leur posent pas de problème. L’imbrication entre les tâches nouvelles et anciennes est importante. En effet, les élèves de CE2 n’utilisent habituellement pas le report des longueurs avec le compas. Cette tâche est nouvelle dans l’environnement papier. Pourtant, ils ont tracé de nombreux cercles au cours de cette année scolaire. Le tracé est donc une tâche ancienne. Un groupe propose de tracer le point D à une distance égale sans mesurer. Cette technique n’est pas proposée dans l’environnement papier. On peut donc en déduire que le changement de cadres induit des comportements différents. L’enseignant permettra cette découverte en utilisant la zone d’analyse pour vérifier l’égalité des longueurs. Pour la tâche dans l’environnement papier, il n’y a pas de difficulté. On pourrait dire alors que les connaissances mathématiques sont minimales. Les élèves placent le point D à l’intersection du cercle et de la droite. Par contre, la tâche dans l’environnement TeP est difficile. C’est la conservation de la forme lors du déplacement qui pose problème. Les élèves placent le point D de la même manière que sur le papier. Il faut que l’enseignant intervienne pour montrer que le point D ne se déplace pas en même temps que le carré. Le langage permet de surmonter cette difficulté : l’enseignant demande de décrire la position de D. Il aide à formuler la solution. On est dans la zone proximale de développement décrite par Vygotski : l’enfant ne peut pas trouver seul. Cependant avec l’aide d’un adulte, il parvient à formuler que le point D est à l’intersection du cercle et de la droite. On peut alors dire que les connaissances mathématiques deviennent intéressantes. C’est la tâche dans l’environnement instrumental qui déclenche la nécessité de le formuler. On peut noter que la tâche dans l’environnement numérique implique de comprendre la tâche mathématique. TeP propose des lettres dans l’ordre alphabétique. Il propose donc C pour le troisième point que nous avons tracé. Un enseignant et un groupe d’élèves ont donc construit un carré ABDC qu’ils ont nommé ABCD... Toutes les connaissances instrumentales ont été introduites. Il s’agit donc de réinvestir ce qui a été construit. Les élèves ont choisi la méthode qu’ils souhaitaient. Les connaissances mathématiques sont maximales : un quadrilatère qui a quatre angles droits et quatre côtés de même longueur est un carré. Pourtant les élèves utiliseront d’autres propriétés selon la construction qu’ils vont choisir : un quadrilatère qui a trois côtés de même mesure et deux angles droits ou un quadrilatère qui a quatre côtés de même mesure et un angle droit est un carré. La connaissance instrumentale est maximale : l’élève doit utiliser toutes les potentialités du logiciel qu’il connaît. On se retrouvera avec un quadrilatère qui a trois angles droits et trois côtés consécutifs de même longueur. La figure est proposée en annexe 1. Il s’agit pour l’élève de savoir tracer un carré, puis de reconnaître que le quadrilatère obtenu est un carré. Selon les méthodes de construction utilisées, le quadrilatère a des propriétés, mais il n’a pas quatre angles droits ni quatre côtés de même longueur. Or c’est le seul critère que les élèves connaissent. On n’est plus dans la géométrie perceptive mais dans la géométrie instrumentale : c’est le recours aux instruments de tracé et de mesure qui permet de conclure. La connaissance mathématique est maximale. Les élèves doivent changer de point de vue. Ils ne peuvent pas vérifier l’égalité des longueurs en utilisant une règle graduée, ni contrôler les angles droits en utilisant leur équerre. Comme ils ont déjà utilisé la zone « analyse », ils proposent facilement l’accès à cette zone. La connaissance instrumentale est maximale. Il est indispensable que l’outil utilisé réponde positivement aux exigences mathématiques. Les élèves connaissent deux formulations pour expliquer la présence d’un angle droit : soit l’angle est droit, soit les droites sont perpendiculaires. Il n’est pas possible d’utiliser la formule angle (...) du logiciel. D’une part, les élèves parlent de l’angle droit sans le nommer Les enfants concluent que l’utilisation de TeP est facile quand on leur a montré. Nous avons filmé une classe avec des élèves qui manipulent TeP avec une certaine aisance. Les élèves ont découvert une autre manière de faire de la géométrie. Ils ont compris qu’il ne suffit pas de faire un beau dessin, mais qu’il faut s’appuyer sur des connaissances géométriques. Ils ont évidemment travaillé sur leur cahier. La présence du logiciel n’exclut pas le travail dans l’environnement papier, il est un complément indispensable. Le logiciel de géométrie semble être le catalyseur pour favoriser les échanges entre les agents (élèves ou professeur). Il modifie leurs positions. Il modifie également le rapport au savoir mathématique. Il serait intéressant de comprendre comment se fait cette évolution sur un échantillon d’élèves plus important et sur une échelle temporelle plus longue. Enfin, il met en valeur l’évolution des connaissances. Le concept de carré a évolué au cours de cette séance. Le carré est un dessin, qui évolue vers un dessin sur lequel sont présentes des propriétés géométriques. C’est ainsi que le dessin deviendra la figure mathématique. En effet la construction avec le le logiciel de GD favorise la compréhension de ce qu’est un carré. Dans l’environnement papier, l’élève sait qu’il a dessiné un carré, il n’éprouve pas le besoin de vérifier. Dans l’environnement numérique, environnement nouveau dans le cadre des mathématiques, il accepte de le faire. La nouveauté facilite ce changement de position. On pourrait ainsi y voir le tremplin nécessaire pour éviter la rupture entre la géométrie instrumentée et la géométrie déductive introduite au collège. Cette modification de l’espace géométrique de travail passe par une genèse instrumentale qu’il conviendrait d’analyser ultérieurement. Il faudrait réfléchir à l’articulation entre la composante d’instrumentalisation (relative à l’artefact, à la découverte et à la sélection des commandes et à la personnalisation de l’objet) d’une part, et à la composante d’instrumentation (relative à l’émergence et à l’évolution des schèmes pour la réalisation d’un type de tâches) d’autre part.
I Expérience :
II Analyse de l’expérience :
Première partie : les élèves doivent tracer un segment.
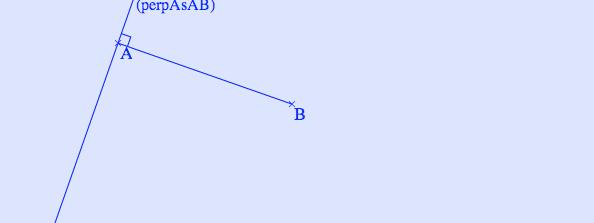
Deuxième partie : les élèves doivent tracer la perpendiculaire à (AB) passant par A.
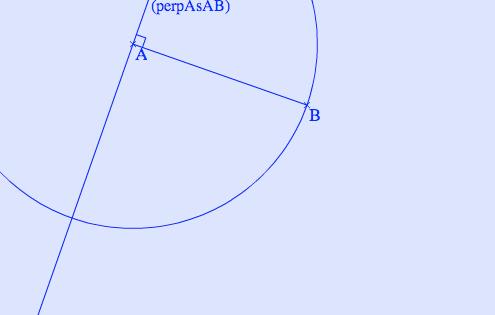
Troisième partie : le tracé de D situé à la même distance que B par rapport à A.
Quatrième partie : Placer le point D (erreur sur la lettre proposée par TeP, non corrigée)
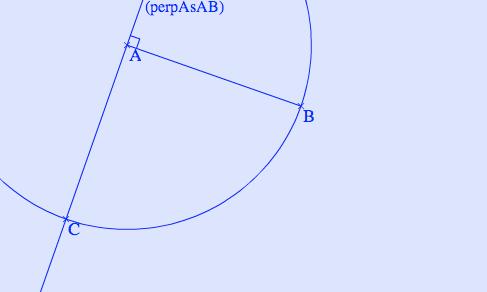
Cinquième partie : placer le point C
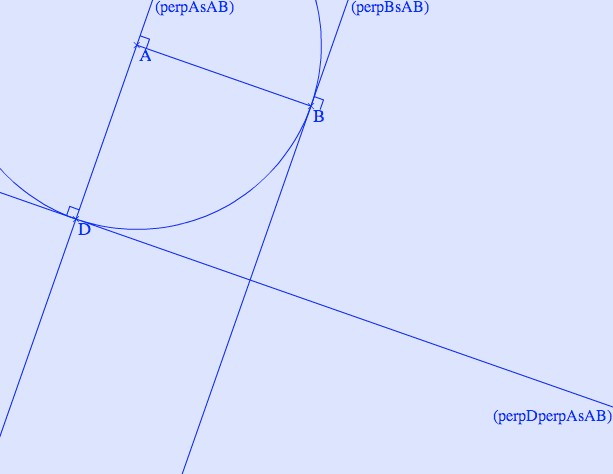
Sixième partie : enlever les traits de construction
 Il n’y a pas de connaissances mathématiques. Il n’y a que des connaissances instrumentales. Les enfants confondent « rendre invisible » et « effacer un trait de construction ». Un groupe va effacer toute la figure. Il hésitera à prendre de nouvelles initiatives. Puis il rend invisible le cercle. Ce dernier disparaît, mais, avant de poursuivre, les élèves se posent la question de savoir si les points de ce cercle vont également disparaître. Nous pouvons remarquer que cette tâche est nouvelle et contraire à ce que les élèves doivent faire dans l’environnement papier. Les élèves n’ont pas été gênés par cette contradiction. Cette situation-problème a permis aux élèves d’échanger sur ce qui s’est passé : la plupart des droites et segments sont invisibles. Ils se sont posés la question de savoir comment faire pour avoir un carré. Ils ont utilisé le bouton ’’segment’’ sans difficulté pour reconstruire les droites effacées.
Il n’y a pas de connaissances mathématiques. Il n’y a que des connaissances instrumentales. Les enfants confondent « rendre invisible » et « effacer un trait de construction ». Un groupe va effacer toute la figure. Il hésitera à prendre de nouvelles initiatives. Puis il rend invisible le cercle. Ce dernier disparaît, mais, avant de poursuivre, les élèves se posent la question de savoir si les points de ce cercle vont également disparaître. Nous pouvons remarquer que cette tâche est nouvelle et contraire à ce que les élèves doivent faire dans l’environnement papier. Les élèves n’ont pas été gênés par cette contradiction. Cette situation-problème a permis aux élèves d’échanger sur ce qui s’est passé : la plupart des droites et segments sont invisibles. Ils se sont posés la question de savoir comment faire pour avoir un carré. Ils ont utilisé le bouton ’’segment’’ sans difficulté pour reconstruire les droites effacées. Septième partie : vérifier que la figure construite est un carré
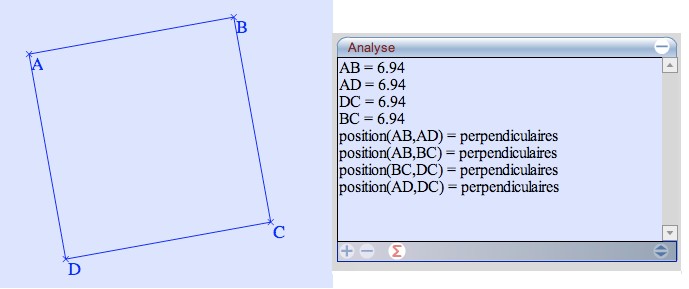
![]() ; d’autre part, la réponse proposée est 90 degrés. Il est donc indispensable d’aider les élèves à formuler quelles sont les droites perpendiculaires pour travailler sur la zone ’’analyse’’. Une élève formulait « c’est compliqué » en étant dans la zone analyse. Puis elle a enchaîné « Il faut sans arrêt enlever et remettre le cadenas ». En effet, le symbole ’’(’’ s’écrit en minuscule, tandis que AB doit être en majuscule.
; d’autre part, la réponse proposée est 90 degrés. Il est donc indispensable d’aider les élèves à formuler quelles sont les droites perpendiculaires pour travailler sur la zone ’’analyse’’. Une élève formulait « c’est compliqué » en étant dans la zone analyse. Puis elle a enchaîné « Il faut sans arrêt enlever et remettre le cadenas ». En effet, le symbole ’’(’’ s’écrit en minuscule, tandis que AB doit être en majuscule. III Conclusion :
Annexes :
Annexe 1 : figure obtenue à l’issue de la première séance

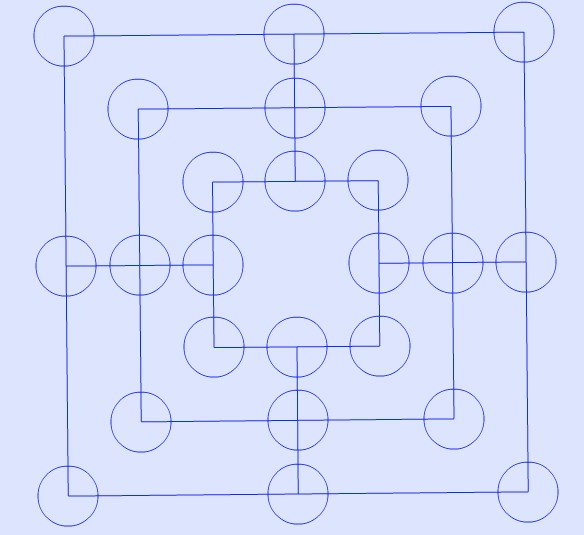
Annexe 2 : plateau de jeu
Bibliographie :
 RÉAGIR À CET ARTICLE
RÉAGIR À CET ARTICLE
 À LIRE AUSSI ICI
À LIRE AUSSI ICI
22:01 Publié dans ENSEIGNER AUTREMENT LE CONCEPT DE CARRÉ EN CE2 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Coloriage de cartes
Coloriage de cartes
Mots en couleurs (petit intermède)
|
A noir, E blanc, I rouge, U vert, O bleu : voyelles, |
Le principe
En 1852, Francis Guthrie, cartographe britannique, observe qu'en utilisant uniquement quatre couleurs, n'importe quelle carte géographique peut être coloriée de façon à ce que deux pays ayant une frontière commune soient de couleur distincte. Ce qu'il n'arrive pas à déterminer c'est si cette propriété est vraie pour toutes les cartes possibles et imaginables. Il s'intéresse alors aux mathématiques et pose la question au grand logicien Augustus de Morgan : quatre couleurs suffisent-elles ? De Morgan ne trouve pas la réponse. La renommée du problème va grandissant et la simplicité de l'énoncé contraste avec la difficulté pour y répondre. Cela a attisé la curiosité d'éminents mathématiciens et de nombreux amateurs.
Finalement, ce théorème des quatre couleurs a été résolu par Kenneth Appel et Wolfgang Haken en 1976, soit un siècle après avoir été énoncé.
De nombreux concepts théoriques fondamentaux de la théorie des graphes ont découlé des tentatives de résolution de ce problème.
La carte de France sans aide
Dans le jeu proposé, on choisit une couleur en cliquant dans la pastille colorée adéquate.
Ensuite on clique département à colorer qu'il soit blanc ou d'une couleur quelconque.
Si la couleur est acceptable, c'est à dire différente de celle des départements voisins, elle est déposée, sinon un petit bip indique l'erreur et Il faut alors choisir une autre couleur.
On efface un département avec la pastille blanche.
La carte de France avec aide
On colorie la carte comme précédemment
En cliquant sur le bouton AIDE, dès le début, la carte est coloriée complètement.
En cliquant sur le bouton AIDE, en cours de jeu, l'ordinateur essaie de terminer le coloriage en tenant compte des couleurs données si cela est possible.
Le coloriage est alors effectué par étapes. Il faudra peut-être cliquer sur le bouton CONTINUER pour terminer le coloriage.
On peut à tout moment modifier la couleur d'une région.
La carte de France avec coloriage automatique
Cette fois, la carte est coloriée automatiquement.L'algorithme utilisé est le suivant :
-Ordonner les départements selon l'ordre décroissant du nombre de voisins ;
-Parcourir cette liste en attribuant à la première région non colorée, la première couleur compatible avec celle des voisins ;
-Si impossibilité, reculer pas à pas en essayant une nouvelle couleur.
Le coloriage doit pouvoir se terminer.
![]()
21:57 Publié dans Coloriage de cartes | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Le découpage de Dudeney
Le découpage de Dudeney
L'animation
Henry Dudeney (1857-1930) découvrit une ingénieuse transformation de polygones suspendus. Il en exposa un modèle en acajou devant la Royal Society de Londres en 1905. Il s'agit de transformer 4 pièces groupées d'un triangle équilatéral en un carré de même aire.L'animation flash ci-dessous montre la transformation.
Prenons un triangle équilatéral ABC de côté BC=2 pour simplifier. Son aire est (1/2)(2)(2/2) =
Le carré de même aire aura donc un côté mesurantc'est à dire racine quatrième de 3 (ou racine de (racine de 3)).
Sur la figure ci-dessous, nous allons montrer que le côté du carré est [RS].
Nous allons vérifier que sa mesure est bien.
Construction :

Soient D et R les milieux des côtés [AB] et [AC].
Soit O le symétrique de A par rapport à (BC).Nous avons OA = 2(2
/2) = 2
.
OB = AB =2 Symétrie de O et de A par rapport à (BC)Traçons le cercle de centre O passant par B.
OP = OB = 2
Soit Q le milieu de [AP]
Traçons le cercle de centre Q passant par A.OA = 2
donc AP = 2 + 2
et QP = 1 +
= O1Q
OQ = QP - OP = 1 +- 2 =
- 1
Soit (OO1) la parallèle à (BC) passant par O.
I milieu de [OO1], alors
OI est la longueur désirée soit.
Avec Pythagore on a :
O1Q2 = OQ2 + OO12
OO12 = O1Q2 - OQ2
OO12 = (+ 1 )2 - (
- 1 )2
OO12 = 4
Donc OO1 =2
Finalement
OI =On construit le cercle de centre R de rayon OI qui coupe (BC) en S.
Nous obtenons ainsi les 4 polygones ADFR, BDFS, SGG, HGRC
RS = OI
De D on trace (DF) perpendiculaire à (RS).
Pour finir, on construit au compas RG = FS,
puis la perpendiculaire (GH) à (RS).
permettant de réaliser le triangle de Dudeney.Remarque
Quand on transforme le triangle, on obtient un quadrilatère convexe (les angles plats sur les côtés sont conservés par rotation de 180°) ;
ce quadrilatère a par construction 4 angles droits. Il s'agit donc d'un rectangle.
Ce rectangle a même aire que le triangle initial :(le découpage conserve l'aire).
Un côté de ce rectangle (jaune + bleu) mesure RS. En effet c'est RF + RG = RF + FS = RS
Le calcul précédent, RS =, montre que l'aire du rectangle est égale à RS² .
Ce rectangle est donc bien un carré.
Etant donnés deux polygones dont les aires sont identiques il existe un découpage de l'un en un nombre fini de polygones qui permet de recouvrir exactement le second sans chevauchement.
Le principe général de base consiste à découper chacune des deux figures en triangles.
En effet
Pour tout couple de triangles de même aire, il existe un découpage permettant de passer de l'un à l'autre et vice versa.Pour la démonstration, voir
http://bayledes.free.fr/decoupage/index.htmlSource :
http://therese.eveilleau.pagesperso-orange.fr/
21:54 Publié dans L'animation, Le découpage de Dudeney | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Groupe orthogonal
Groupe orthogonal
En mathématiques, plus précisément en algèbre linéaire, le groupe orthogonal d'une forme quadratique q est le groupe de ses automorphismes orthogonaux, muni de la loi decomposition. Si E est l'espace vectoriel sous-jacent, un automorphisme orthogonal pour q est un automorphisme f de l'espace vectoriel E (i.e. une application linéaire bijective de E dansE) laissant q invariante, c'est-à-dire vérifiant :
Le cas le plus étudié est (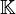 étant le corps des scalaires et n un entier naturel) :
étant le corps des scalaires et n un entier naturel) :
Le groupe orthogonal correspondant, noté  ou
ou  , s'identifie au groupe des matrices orthogonales et possède un sous-groupe particulier, le groupe spécial orthogonal.
, s'identifie au groupe des matrices orthogonales et possède un sous-groupe particulier, le groupe spécial orthogonal.
Sommaire[masquer] |
Généralités [modifier]
Le groupe orthogonal est compact, en effet on est en dimension finie et il est borné car tous les endomorphismes orthogonaux sont unitaires et fermé car c'est l'image réciproque du singleton identité par l'application continue  .
.
L'identité est un automorphisme orthogonal. L'ensemble des automorphismes orthogonaux est stable par composition et inversion. C'est donc un sous-groupe du groupe des automorphismes de E ; on l'appelle le groupe orthogonal associé à la forme quadratique q. Il est noté O(E,q).
Pour  , lorsque la forme quadratique q s'écrit : q(x) =
, lorsque la forme quadratique q s'écrit : q(x) =  xk2, on appelle matrices orthogonales les matrices des automorphismes orthogonaux. Une matrice M est donc orthogonale si et seulement si tMM = In, où tM est la matrice transposée de M. Par définition, le groupe orthogonal de degré n du corps
xk2, on appelle matrices orthogonales les matrices des automorphismes orthogonaux. Une matrice M est donc orthogonale si et seulement si tMM = In, où tM est la matrice transposée de M. Par définition, le groupe orthogonal de degré n du corps 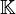 est le groupe des matrices orthogonales n ×n à coefficients dans
est le groupe des matrices orthogonales n ×n à coefficients dans 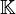 , muni de la multiplication matricielle. Il est habituellement noté
, muni de la multiplication matricielle. Il est habituellement noté  ou
ou  . C'est un sous-groupe du groupe général linéaire
. C'est un sous-groupe du groupe général linéaire 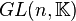 .
.
Toute matrice orthogonale a un déterminant égal à 1 ou -1. Les matrices orthogonales n × n de déterminant 1 forment un sous-groupe invariant de  appelé le groupe spécial orthogonal et noté
appelé le groupe spécial orthogonal et noté 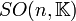 ou
ou 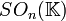 . Si la caractéristique de
. Si la caractéristique de 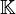 est 2, alors les groupes orthogonal et spécial orthogonal coïncident. Dans le cas contraire, l’indice de
est 2, alors les groupes orthogonal et spécial orthogonal coïncident. Dans le cas contraire, l’indice de 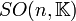 dans
dans  est 2.
est 2.
 et
et 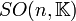 sont des groupes algébriques, car la condition que leurs matrices soient orthogonales, c’est-à-dire que leur transposée soit leur inverse, peut s’exprimer comme un ensemble d’équations polynomiales dans les éléments de ces matrices.
sont des groupes algébriques, car la condition que leurs matrices soient orthogonales, c’est-à-dire que leur transposée soit leur inverse, peut s’exprimer comme un ensemble d’équations polynomiales dans les éléments de ces matrices.
Nombres réels [modifier]
Sur le corps  des nombres réels,
des nombres réels,  et
et  sont généralement simplement notés
sont généralement simplement notés 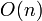 et
et  quand aucune confusion n’est possible. Ils forment deuxgroupes de Lie compacts de dimension
quand aucune confusion n’est possible. Ils forment deuxgroupes de Lie compacts de dimension  .
. 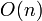 possède deux composantes connexes,
possède deux composantes connexes,  étant celle contenant la matrice identité.
étant celle contenant la matrice identité.
Géométriquement, 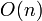 est isomorphe au groupe des isométries de
est isomorphe au groupe des isométries de  laissant invariant l’origine.
laissant invariant l’origine.  est isomorphe au groupe des isométries directes, ou rotations de
est isomorphe au groupe des isométries directes, ou rotations de  laissant l’origine invariante.
laissant l’origine invariante.
 est isomorphe (en tant que groupe de Lie) au cercle S1, formé des nombres complexes de module 1, muni de la multiplication. Cet isomorphisme lie le nombre complexe
est isomorphe (en tant que groupe de Lie) au cercle S1, formé des nombres complexes de module 1, muni de la multiplication. Cet isomorphisme lie le nombre complexe  à la matrice orthogonale
à la matrice orthogonale
Le groupe  est souvent appelé groupe des rotations (vectorielles) dans l'espace (tridimensionnel).
est souvent appelé groupe des rotations (vectorielles) dans l'espace (tridimensionnel).
En termes de topologie algébrique, pour n > 2, le groupe fondamental de  est le groupe cyclique d’ordre 2 et le groupe Spin Spin(n) est son revêtement universel. Pour n=2, le groupe fondamental est le groupe cyclique infini et son revêtement universel correspond à la droite des réels.
est le groupe cyclique d’ordre 2 et le groupe Spin Spin(n) est son revêtement universel. Pour n=2, le groupe fondamental est le groupe cyclique infini et son revêtement universel correspond à la droite des réels.
L’algèbre de Lie associée aux groupes de Lie 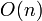 et
et  est formée des matrices n×n antisymétriques. Elle est généralement notée
est formée des matrices n×n antisymétriques. Elle est généralement notée 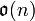 ou
ou  .
.
Nombres complexes [modifier]
Sur le corps  des nombres complexes,
des nombres complexes, 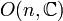 et
et  (là aussi notés
(là aussi notés 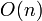 et
et  quand aucune confusion n’est possible) sont des groupes de Lie complexes de dimension
quand aucune confusion n’est possible) sont des groupes de Lie complexes de dimension  sur
sur  (le double sur
(le double sur  ).
). 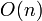 possède deux composantes connexes,
possède deux composantes connexes,  étant celle contenant la matrice identité. Pour
étant celle contenant la matrice identité. Pour  , ces groupes ne sont pas compacts.
, ces groupes ne sont pas compacts.
Pour n > 2, le groupe fondamental de  est le groupe cyclique d’ordre 2, tandis que le groupe fondamental de
est le groupe cyclique d’ordre 2, tandis que le groupe fondamental de  est le groupe cyclique infini.
est le groupe cyclique infini.
L’algèbre de Lie associée aux groupes de Lie 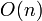 et
et  est formée des matrices complexes n×n antisymétriques.
est formée des matrices complexes n×n antisymétriques.
Voir aussi [modifier]
21:50 Publié dans Groupe orthogonal | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Groupe symplectique
En mathématiques, le terme groupe symplectique est utilisé pour désigner deux familles différentes de groupes linéaires. On les note Sp(2n, E) et Sp(n), ce dernier étant parfois nommé groupe compact symplectique pour le distinguer du premier. Cette notation ne fait pas l’unanimité et certains auteurs en utilisent d’autres, différant généralement d’un facteur 2. La notation utilisée dans cet article est en rapport avec la taille des matrices représentant les groupes.Groupe symplectique
Sommaire[masquer] |
Le groupe symplectique de degré 2n sur un corps E, noté Sp(2n, E), est le groupe des matrices symplectiques 2n×2n à coefficients dans E, muni de la multiplication matricielle. Comme toutes les matrices symplectiques ont pour déterminant 1, le groupe symplectique est un sous-groupe du groupe spécial linéaire SL(2n, E). De façon plus abstraite, le groupe symplectique peut être défini comme l’ensemble des transformations linéaires d’un espace vectoriel de dimension 2n sur E préservant une forme non-dégénérée, antisymétrique et bilinéaire. Si n = 1, la condition symplectique sur une matrice est satisfaite si et seulement si son déterminant est tel que Sp(2, E) = SL(2, E). Pour n>1, d’autres conditions s’y ajoutent. Typiquement, le corps E est le corps des nombres réels L’algèbre de Lie de Sp(2n, E) est donnée par l’ensemble des matrices 2n×2n réelles ou complexes A satisfaisant : où AT est la transposée de A et J est la matrice antisymétrique Le groupe symplectique Sp(n) est le sous-groupe de GL(n, C’est-à-dire que Sp(n) est simplement le groupe unitaire quaternionique U(n, Sp(n) est un groupe de Lie de dimension n(2n + 1). Il est compact, connexe et simplement connexe. L’algèbre de Lie de Sp(n) est donnée par l’ensemble des matrices quaternioniquesn×n satisfaisant où La relation entre les groupes Sp(2n, L’algèbre de Lie complexe Cn est juste l’algèbre sp(2n, Comparaison des groupes symplectiques :Sp(2n,E) [modifier]
 ou des nombres complexes
ou des nombres complexes  . Dans ce cas, Sp(2n, E) est un groupe de Lie réel ou complexe, de dimension réelle ou complexe n(2n + 1). Ces groupes sont connexes mais pas compacts. Sp(2n,
. Dans ce cas, Sp(2n, E) est un groupe de Lie réel ou complexe, de dimension réelle ou complexe n(2n + 1). Ces groupes sont connexes mais pas compacts. Sp(2n,  ) est simplement connexe tandis que Sp(2n,
) est simplement connexe tandis que Sp(2n,  ) possède un groupe fondamental isomorphe à Z.
) possède un groupe fondamental isomorphe à Z.
Sp(n) [modifier]
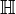 ) (
) (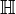 étant l’ensemble des matrices quaternioniques inversibles) préservant la forme hermitienne standard sur
étant l’ensemble des matrices quaternioniques inversibles) préservant la forme hermitienne standard sur  :
:
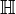 ). Il est d’ailleurs parfois appelé groupe hyperunitaire. Sp(n) n’est pas un groupe symplectique au sens de la section précédente : il ne préserve pas une forme antisymétrique sur
). Il est d’ailleurs parfois appelé groupe hyperunitaire. Sp(n) n’est pas un groupe symplectique au sens de la section précédente : il ne préserve pas une forme antisymétrique sur  (en fait, une telle forme n’existe pas).
(en fait, une telle forme n’existe pas).
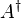 est la transposée conjuguée de A.
est la transposée conjuguée de A.Relations entre les groupes symplectiques [modifier]
 ), Sp(2n,
), Sp(2n,  ) et Sp(n) est la plus évidente au niveau de leur algèbre de Lie. Les algèbres de Lie de ces trois groupes, considérés comme groupes de Lie réels, partagent la même complexification. Dans la classification des algèbres de Lie simples de Cartan, cette algèbre est notée Cn.
) et Sp(n) est la plus évidente au niveau de leur algèbre de Lie. Les algèbres de Lie de ces trois groupes, considérés comme groupes de Lie réels, partagent la même complexification. Dans la classification des algèbres de Lie simples de Cartan, cette algèbre est notée Cn. ) des groupes de Lie complexes Sp(2n,
) des groupes de Lie complexes Sp(2n,  ). Cette algèbre possède deux formes réelles différentes :
). Cette algèbre possède deux formes réelles différentes :
 ), qui est l’algèbre de Lie de Sp(2n,
), qui est l’algèbre de Lie de Sp(2n,  ).
).
| Matrices | Groupe de Lie | Dim/ | Dim/ | Compact | π1 | |
|---|---|---|---|---|---|---|
Sp(2n,  ) ) |
 |
réel | n(2n + 1) | – |  |
|
Sp(2n,  ) ) |
 |
complexe | 2n(2n + 1) | n(2n + 1) | 1 | |
| Sp(n) | 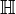 |
réel | n(2n + 1) | – | x | 1 |
21:37 Publié dans Groupe symplectique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Groupe fondamental
Groupe fondamental
![]() Pour les articles homonymes, voir Groupe de Poincaré.
Pour les articles homonymes, voir Groupe de Poincaré.
|
|
Des informations de cet article ou section devraient être mieux reliées aux sources mentionnées dans la bibliographie.
Améliorez sa vérifiabilité en les associant par des références.
|
En mathématiques, et plus spécifiquement en topologie algébrique, le groupe fondamental, ou groupe de Poincaré, est un invariant topologique. Le groupe fondamental d'un espace topologique pointé (X, p) est, par définition, l'ensemble des classes d'homotopie de lacets (arcs fermés) de X d'origine et d'extrémité p. C'est un groupe dont la loi de composition interneest induite par la concaténation des arcs. L'examen des groupes fondamentaux permet de prouver que deux espaces ne peuvent être homéomorphes, ou topologiquement équivalents. Le groupe fondamental permet de classifier les revêtements d'un espace connexe par arcs, à un isomorphisme près. Une généralisation des groupes fondamentaux est la suite des groupes d'homotopie supérieurs. Pour cette raison, le groupe fondamental est aussi appelé premier groupe d'homotopie1. Le groupe fondamental fut introduit par Henri Poincaré dans la douzième section de son article intitulé Analysis Situs, paru en 1895 et annoncé dans une note aux Comptes-rendus de l'Académie des Sciences, parue en 18922.
Sommaire[masquer] |
Tout d'abord, familiarisons-nous avec l'idée du groupe fondamental à travers l'exemple du tore bidimensionnel (qu'on peut se représenter comme étant la surface d'un donut ou d'une bouée). On fixe sur le tore un point de départ p. À partir de ce point, on peut construire des lacets, i.e des courbes fermées, qui partent du point p, se promènent sur le tore et qui reviennent au point de départ. Imaginons que les lacets soient faits à partir de caoutchouc comme un élastique et qu'il soit ainsi possible de les étirer, les déformer de telle manière que le point de départ et le point d'arrivée soient toujours p et que les lacets se déplacent toujours sur le tore. Une telle déformation s'appelle une homotopie : on dit que deux lacets qui peuvent s'obtenir l'un à partir de l'autre par une homotopie sont homotopiquement équivalents. Ce sont les lacets à déformation près qui nous intéressent : on regroupe donc les lacets dans des classes d'homotopie. Le groupe fondamental du tore est l'ensemble des différentes classes d'homotopie des lacets. Dans la figure ci-contre, les lacets a et b ne sont pas homotopiquement équivalents : on ne peut obtenir l'un en déformant continûment le second sans le « déchirer » à un moment, ils représentent deux éléments distincts du groupe fondamental. On obtient d'autres classes d'homotopie en faisant tourner les lacets plusieurs fois autour du trou. Comme son nom l'indique, le groupe fondamental n'est pas un simple ensemble, il est muni d'une structure degroupe : la loi de composition interne est celle qui à deux lacets associe un troisième lacet obtenu en parcourant le premier puis le second à la même vitesse (il n'y a pas de problèmes de définition puisque les lacets commencent et terminent avec le même point p). L'élément neutre du groupe fondamental est la classe d'homotopie du lacet qui reste au point p. On obtient un élément inverse en parcourant les lacets d'une classe d'homotopie dans le sens contraire. Soit X un espace topologique. Un arc continu est une application continue γ : [0 1] → X. Soit p un point fixé dans X. Un lacet basé en p est un arc continu vérifiant de plus γ(0) = γ(1) = p. Deux lacets γ0 et γ1 sont dits homotopes s'il existe une homotopie de l'un vers l'autre, c'est-à-dire une application continue H : [0 1]2 → X telle que : La dernière condition exprime que pour x fixé entre 0 et 1 γx(t) = H(t,x) est un lacet basé en p. Autrement dit, deux lacets sont dits homotopes si l'on peut passer continument de l'un à l'autre, à l'image de la figure de droite (le point p est situé en A sur la figure) . Le fait d'être homotopes est une relation d'équivalence entre lacets (basés en p). On peut considérer l'ensemble E(p) des lacets (basés en p) de X et l'ensemble quotient π1(X,p) de E(p)par la relation d'homotopie. On notera [γ] la classe d'équivalence d'un lacet γ (aussi appelée classe d'homotopie)3. Intuitivement (si l'espace X est métrisable et localement compact) une classe d'homotopie de lacets est une composante connexe par arcs de l'espace E(p) muni de la topologie de la convergence compacte-ouverte. π1(X,p) est l'ensemble des classes d'équivalence d'homotopie [γ] de lacets basés en p. C'est donc l'ensemble des composantes connexes par arcs deE(p). On souhaite donner une structure de groupe à cet ensemble π1(X,p). Si f et g sont deux lacets de X (basés en p), leur concaténation est le laceth défini par : Intuitivement, c'est le lacet qui parcourt f puis g (chacun à vitesse double, pour arriver à parcourir le lacet en un temps unité). On notera fg le concaténé de f et de g. On peut prouver que la classe d'homotopie [fg] ne dépend que de la classe d'homotopie de f, et de celle de g. Ainsi, on peut définir une loi de composition interne sur l'ensemble π1(X,p) des classes d'homotopie des lacets basés en p de X, par [f][g] = [fg]. On peut alors prouver que l'on obtient une structure de groupe sur l'ensemble π1(X,p) : la loi est associative car les lacets (fg)h et f(gh) sont homotopes, l'élément neutre est la classe d'homotopie [γ] du lacet trivial γ défini par γ(t) = p pour tout t. L'inverse d'un lacet f est simplement le même lacet, mais parcouru dans l'autre sens (c'est-à-dire, défini par f − 1(t) = f(1 −t)) Le groupe ainsi obtenu est appelé groupe fondamental3 (ou groupe de Poincaré) de X basé en p, et est noté π1(X,p). Examinons le cas particulier où l'espace topologique X est connexe par arcs. Deux groupes fondamentaux basés en deux points p et q (π1(X,p) et π1(X,q)) sont isomorphes. En effet, il existe un chemin γ allant de p à q. On peut donc définir l'application suivante qui réalise visiblement un isomorphisme du groupe fondamental π1(X,q) vers le groupe fondamental π1(X,p) dont l'isomorphisme réciproque est l'application : Ainsi, si X est connexe par arcs, par abus de langage, on parle du groupe fondamental (à un isomorphisme non unique près) de l'espace topologique X, sans préciser le point base4, que l'on note π1(X) = π1(X,p). Cependant, l'isomorphisme entre les groupes π1(X,p) et π1(X,q) n'est pas unique et dépend du choix d'un chemin entre p et q . Ainsi on doit se souvenir que le groupe fondamental varie lorsque le point base varie dans l'espace X, les groupes restant toujours isomorphes. Si X n'est pas connexe par arcs, les groupes fondamentaux de deux composantes connexes, sont différents. Par abus de langage, on parle néanmoins du groupe fondamental d'une composante connexe par arcs, sans préciser le point base, mais on doit se souvenir que le groupe fondamental varie lorsque le point base varie dans la composante connexe par arcs, les groupes restant toujours isomorphes. À l'inverse, un autre invariant d'un espace topologique, non nécessairement connexe par arcs, le premier groupe d'homologie, ne dépend pas du choix d'un point base ni du choix d'une composante connexe par arcs. Si le groupe fondamental (en un point) est abélien, ce qui est le cas de celui des groupes de Lie ou des espaces simplement connexes, il s'identifie naturellement au groupe d'homologie de la composante connexe du point. Un espace topologique connexe par arcs dont le groupe fondamental est trivial est dit simplement connexe . Soit E un espace euclidien de dimension n, où n est un entier strictement positif. On dispose de la propriété suivante : Si p est un élément de C, l'objectif est de montrer que π1(C,p) est le groupe trivial, ou encore que tout lacet γ basé en p est homotope au point p, c'est-à-dire au lacet constant valant p. Pour cela on définit une application H : [0 1]2 → C définie par : L'application H est manifestement continue, comme γ(x) et p sont deux éléments de C, pour toutes valeurs de t H(t,x) est élément de C car C est convexe. L'application H définit bien une homotopie entre le lacet constant et γ. Le terme de cercle désigne ici un espace homéomorphe à l'ensemble des points situées à une distance constante non nulle d'un point c d'un plan euclidien. Ainsi, l'ensemble des nombres complexes de module 1 ou encore R/Z sont des cercles. Le cercle est noté ici S1 et est identifié aux nombres complexes de module 1. Intuitivement, ce résultat est évident. On considère ici π1(S1,1), c'est-à-dire que le point de base est 1. Si le chemin considéré fait n tours dans le sens trigonométrique, on a envie de lui associer par l'isomorphisme de groupe μ de Z dans π1(S1,1) qui, à la valeur m, associe une classe de lacets qui fait m tours, dans le sens trigonométrique si m est positif, et dans le sens inverse sinon. Pour construire l'isomorphisme μ, on définit les lacets em de la manière suivante : On définit μ comme l'application qui à m associe [em]. Intuitivement, il semble clair que μ est un isomorphisme. La non trivialité du groupe fondamental du cercle est à l'origine de plusieurs démonstrations de théorèmes non triviaux. Un exemple est celui de Borsuk-Ulam qui indique qu'une application continue de la sphère dans le plan possède toujours deux points antipodaux ayant même image. Ce résultat est la clé de la démonstration du théorème du sandwich au jambon qui indique qu'il existe toujours un plan qui divise deux parties de volumes égaux trois solides bornés et mesurables. Si X et Y sont deux espaces connexes par arcs, l'espace topologique produit XxY est aussi connexe par arcs. Si (p, q) est un point du produit, le groupe fondamental de XxY que l'on note π1(XxY,(p,q)) est bien défini. On dispose de la propriété suivante : Les propositions précédentes permettent d'établir que le produit S1 par lui-même, généralement appelé tore de dimension 2, admet un groupe fondamental isomorphe à Z2. Plus généralement, le groupe fondamental du tore de dimension n est isomorphe à Zn. Une question naturelle est celle de la compatibilité du groupe fondamental vis à vis d'une application continue f. Soit X et Y deux espaces topologiques tel que X soit connexe par arc et fune application continue de X dans Y. La fonction f assure non seulement la connexité de Y, mais aussi sa connexité par arcs de f(X). De plus la fonction f transforme un lacet de X en un lacet de Y. Soit α un lacet de X, l'application foα est bien un lacet de Y. Ce lacet est généralement noté f * (α). La fonction f induit une application f * des lacets de X dans les lacets de Y. Cette application est compatible avec la relation d'équivalence que définit l'homotopie ainsi qu'avec la loi de composition du groupe fondamental. Si α1 et α2 sont deux lacets ayant mêmes extrémités p, la loi de concaténation s'applique. Si les deux lacets sont homotopes, et si H(t, x) est une homotopie, alors l'application foH(t, x) est une homotopie entre f * (α1) et f * (α2)., ce qui montre que l'application f * est définie sur le groupe π1(X,p) à valeurs dans le groupe π1(Y,f(p)). Pour montrer cette proposition, il suffit de remarquer que : Si Z est un autre espace topologique et g une fonction continue de Y dans Z, alors les morphismes se composent : Il suffit de remarquer que l'application (IdX)* est l'identité du groupe π1(X,p) pour conclure que : L'isomorphisme n'est en général pas unique. Un exemple d'application des morphismes précédents est le théorème du point fixe de Brouwer. En dimension deux, il se démontre simplement à l'aide de l'étude d'une fonction continue permettant de bâtir un morphisme de groupes fondamentaux. Une définition est utile8 : Cette définition permet d'exprimer la proposition suivante, équivalente au théorème du point fixe de Brouwer en dimension 2 : Soit B2 le disque et S1 sa frontière. Supposons qu'une telle rétraction, notée F, de B2 dans S1 existe. On note InjS, l'injection canonique deS1 dans B2 et IdS l'application identité de S1. On dispose des égalités : L'application (IdS) * est le morphisme identité du groupe fondamental du cercle. L'application (InjS) * est le morphisme du groupe fondamental du cercle dans le groupe fondamental du disque, qui est trivial. L'image de cette application est donc réduite à l'élément neutre. L'image par le morphisme F* du groupe fondamental du disque dans le groupe fondamental du cercle est réduite à l'élément neutre. Ce résultat est en contradiction avec le fait que l'image de (IdS) * , qui est le groupe fondamental du cercle, est non triviale car isomorphe à Z. Le théorème de Brouwer indique que toute fonction continue f du disque dans lui-même admet un point fixe. S'il n'en avait pas, il serait aisé de construire une rétraction continue. On considérerait le segment passant par x et f(x) illustré sur la figure (si x est un élément du disque). Ce segment traverse le disque en un point, plus proche de x que de f(x). Si ce point est l'image par F du point x, alors F est la rétraction recherchée9. Une description plus précise est disponible dans l'article détaillé : Deux espaces X et Y sont dits homotopiquement équivalents s'il existe deux applications f : X → Y et g : Y → X, telles que Par conséquent, un espace homotopiquement équivalent à un point est simplement connexe. Un tel espace est dit contractile. On montre que : le premier groupe d'homologie (d'un espace connexe par arcs) est isomorphe à l'abélianisé du groupe fondamental (en un point quelconque de l'espace). Il y a équivalence entre les sous-groupes à conjugaison près du groupe fondamental et les revêtements à isomorphisme près. Dans cette équivalence, les sous-groupes normaux correspondent aux revêtements galoisiens. En théorie des revêtements, on montre que si l'espace admet un revêtement simplement connexe (en particulier si l'espace est semi-localement simplement connexe c'est-à-dire si l'espace n'est pas trop "sauvage", par exemple s'il est localement contractile) son groupe fondamental est isomorphe au groupe des automorphismes d'un de ses revêtements universels. Calculer le groupe fondamental d'un espace topologique qui n'est pas simplement connexe est un exercice difficile, car il faut prouver que certains lacets ne sont pas homotopes. Lethéorème de van Kampen, également appelé théorème de Seifert-Van Kampen, permet de résoudre ce problème lorsque l'espace topologique peut être décomposé en des espaces plus simples dont les groupes fondamentaux sont déjà connus. Ce théorème permet de calculer le groupe fondamental d'un éventail très large d'espaces. En termes abstraits, ce théorème dit que si deux sous-espaces, tous les deux ouverts ou tous les deux fermés, de X contiennent le point p et ont une intersection connexe par arcs, le groupe fondamental de la réunion des deux espaces pointés en p est la somme amalgamée (dans la catégorie des groupes) des groupes fondamentaux des deux espaces, en p, somme amalgamée le long du groupe fondamental de leur intersection. Si X est un espace topologique, on définit le cône de X comme l'espace quotient Si f est une application continue entre deux espaces topologiques Exemple : Si f est l'application de degré 2 dans le cercle Le théorème du cône affirme que le groupe fondamental de C(f) est isomorphe au quotient de π1(Y) par le normalisé du sous-groupe de π1(Y) image de f. Application : les espaces projectifs (réels) En théorie des nœuds, on cherche à distinguer les différents nœuds (ceux qui ne sont pas homotopiques). Le groupe fondamental du complémentaire d'un nœud fournit un invariant des nœuds, qui permet de distinguer certains d'entre eux. Une catégorie est appelée un groupoïde si les objets et les flèches forment un ensemble (c'est une "petite catégorie") et si toutes les flèches sont inversibles (sont des isomorphismes). Les groupoïdes forment une catégorie dont les morphismes sont les foncteurs entre groupoïdes. Les groupes sont des groupoïdes (avec un seul objet). Soit G un groupoïde, on définit la relation d'équivalence À chaque espace topologique on va associer de façon fonctorielle un groupoïde πX. Soit X un espace topologique, on prend pour ensemble d'objets πX l'ensemble sous-jacent à X. Les flèches de source x et de but y sont les classes d'homotopie des chemins (= arcs continus) de x vers y. La relation d'homotopie est compatible avec la composition des chemins et définit donc un groupoïde πX appelé le groupoïde fondamental de X. Le théorème de Van Kampen s'exprime également simplement en utilisant les groupoïdes fondamentaux. Soit G un groupoïde, et x un objet de G (on dit aussi un point de G). La loi de composition entre les flèches de G(x,x) restreinte à ce sous-groupoïde est une loi de groupe. On noteπ1(G,x) ce groupe. Remarque : π1 ne définit pas un foncteur de la catégorie des groupoïdes vers la catégorie des groupes. Le groupe fondamental est défini par π1(X,x0) = π1(πX,x0) Le groupe fondamental est en fait le premier groupe d'homotopie, d'où l'indice 1 dans la notation π1(X). Dans la théorie des revêtements d'un espace X, on définit la fibre d'un revêtement Cette définition alternative ouvre la voie à la généralisation en géométrie algébrique, où la définition donnée précédemment en termes de lacets de base p ne s'applique pas naturellement. Dans cette généralisation, les revêtements étant remplacés par les morphismes étales : le groupe fondamental de l'espace pointé (X,p) est le groupe des automorphismes du foncteur fibre qui, à un morphisme étale Cette théorie permet d'expliquer le lien entre la théorie de Galois des revêtements des surfaces de Riemann (groupe d'automorphismes…) et la théorie de Galois des corps de fonctions. Lien externe en anglais :Définition intuitive à travers l'exemple du tore [modifier]
Définition [modifier]
Classe d'équivalence de lacets [modifier]
![forall t in [0,1], , H(t,0) = gamma_0(t)](http://upload.wikimedia.org/math/b/5/8/b5892f539a11f90d57098f18f05b42af.png)
![forall t in [0,1], , H(t,1) = gamma_1(t)](http://upload.wikimedia.org/math/3/3/d/33df61e4386ad0ac403ca9ccb5f2a206.png)
![forall x in [0,1], , H(0,x) = p = H(1,x)](http://upload.wikimedia.org/math/f/7/7/f7750bc468227bdf71fbf12b466023a7.png) .
.Structure de groupe [modifier]
![h(t)=left{begin{matrix} f(2t), & mbox{si }tin[0,1/2] \ g(2t-1), & mbox{si } tin[1/2,1]end{matrix}right.](http://upload.wikimedia.org/math/9/e/4/9e4213e4185f171d69986db1eaf2b3a4.png)
Point base [modifier]
![[alpha] mapsto [gamma] [alpha] [gamma]^{-1}](http://upload.wikimedia.org/math/f/a/1/fa16429899f6fdced664161e133c5981.png)
![[alpha] mapsto [gamma]^{-1} [alpha] [gamma]](http://upload.wikimedia.org/math/a/b/f/abf7783fbcedf110cb95bf5c19c9e20e.png)
Espaces simplement connexes [modifier]
Exemples [modifier]
Convexes d'un espace euclidien [modifier]
![forall t,x in [0,1]quad H(t,x)= tp + (1-t)gamma(x)](http://upload.wikimedia.org/math/2/2/8/228256d843bcbac96035f24b53923f59.png)
Cercle [modifier]
![e_m : [0,1] rightarrow mathbb S^1quad e_m(t) = exp(2ipi mt)](http://upload.wikimedia.org/math/9/9/5/995265c0011c7f3bd7ea43bb26a4af1f.png)
Espace produit [modifier]
Autres exemples [modifier]
 , le groupe fondamental de la sphère
, le groupe fondamental de la sphère  de l'espace euclidien
de l'espace euclidien  est également trivial. Autrement dit, les sphères de dimension supérieure ou égale à 2 sont simplement connexes.
est également trivial. Autrement dit, les sphères de dimension supérieure ou égale à 2 sont simplement connexes.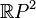 est isomorphe à
est isomorphe à  (voir plus bas).
(voir plus bas). , est isomorphe au groupe libre à deux générateurs F2. Les deux générateurs sont ici des lacets partant de p et faisant chacun le tour d'un des points a ou b.
, est isomorphe au groupe libre à deux générateurs F2. Les deux générateurs sont ici des lacets partant de p et faisant chacun le tour d'un des points a ou b.Fonction continue et morphisme [modifier]
Morphisme de groupes fondamentaux induit par une fonction continue [modifier]
![forall gamma in pi_1(X,p),;forall t in [0,1] quad f_*(gamma)(t) = fcircgamma (t)](http://upload.wikimedia.org/math/e/d/f/edf21cce99f87f27037acdf3b4c126b2.png)


Application : théorème du point fixe de Brouwer en dimension 2 [modifier]
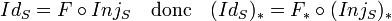
Degré d'une application du cercle dans lui-même
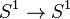 [modifier]
[modifier]Autres théorèmes [modifier]
Équivalence d'homotopie et espaces contractiles [modifier]
 est homotope à IdX et
est homotope à IdX et  est homotope à IdY.
est homotope à IdY.Propriétés [modifier]
Lien avec le premier groupe d'homologie [modifier]
Groupe fondamental et théorie des revêtements [modifier]
Méthodes de calcul et applications [modifier]
Théorème de van Kampen [modifier]
 .
.
Théorème du cône et groupe fondamental des espaces projectifs [modifier]
 où I désigne le segment [O;1]. Si X est un cercle, on obtient une partie d'un cône de révolution. Le groupe fondamental du cône d'un espace connexe par arc est trivial, autrement dit, si X est connexe par arcs, C(X) est simplement connexe. On a une inclusion canonique
où I désigne le segment [O;1]. Si X est un cercle, on obtient une partie d'un cône de révolution. Le groupe fondamental du cône d'un espace connexe par arc est trivial, autrement dit, si X est connexe par arcs, C(X) est simplement connexe. On a une inclusion canonique  .
. , on définit le cône de l'application f : C(f) comme l'espace obtenu en recollant
, on définit le cône de l'application f : C(f) comme l'espace obtenu en recollant  et
et  le long de X.
le long de X.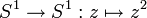 , on obtient
, on obtient  . Le cône de f est le plan projectif réel.
. Le cône de f est le plan projectif réel.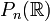 pour
pour  ont des groupes fondamentaux isomorphes à
ont des groupes fondamentaux isomorphes à 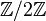 .
.Groupe fondamental des graphes, des surfaces et des polyèdres [modifier]
 et une seule relation (
et une seule relation ( 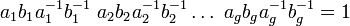 , on peut aussi choisir la présentation
, on peut aussi choisir la présentation  ). L'entier g est uniquement déterminé par la surface et est appelé genre de la surface.
). L'entier g est uniquement déterminé par la surface et est appelé genre de la surface.Théorie des nœuds [modifier]
Généralisations [modifier]
Groupoïde fondamental (ou groupoïde de Poincaré) [modifier]
 si l'ensemble G(x,y) des morphismes de x vers y est non vide. Elle définit un groupoïde quotient noté π0(G). π0 définit un foncteur (composantes connexes) de la catégorie des groupoïdes vers la catégorie des ensembles.
si l'ensemble G(x,y) des morphismes de x vers y est non vide. Elle définit un groupoïde quotient noté π0(G). π0 définit un foncteur (composantes connexes) de la catégorie des groupoïdes vers la catégorie des ensembles.Groupes d'homotopie supérieurs [modifier]
Groupe fondamental et géométrie algébrique [modifier]
 au point p comme l'ensemble
au point p comme l'ensemble 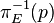 qui est aussi noté E(p). La correspondance
qui est aussi noté E(p). La correspondance  définit un foncteur de la catégorie des revêtements de base (X; p), dans la catégorie des ensembles. Le groupe fondamental peut être défini de manière abstraite comme le groupe des automorphismes du foncteur fibre, qui, à un revêtement de base (X,p), associe E(p).
définit un foncteur de la catégorie des revêtements de base (X; p), dans la catégorie des ensembles. Le groupe fondamental peut être défini de manière abstraite comme le groupe des automorphismes du foncteur fibre, qui, à un revêtement de base (X,p), associe E(p). , associe la fibre E(p) au point p. Cette généralisation est due à Alexandre Grothendieck et Claude Chevalley.
, associe la fibre E(p) au point p. Cette généralisation est due à Alexandre Grothendieck et Claude Chevalley.Bibliographie (en français) [modifier]
Notes et références [modifier]
Liens externes [modifier]
21:36 Publié dans Groupe fondamental | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Formulaire de géométrie classique
Formulaire de géométrie classique
Ce formulaire de géométrie classique récapitule diverses formules reliant algébriquement des mesures de longueur, d'aire ou de volumepour des figures de géométrie euclidienne.
Sommaire[masquer] |
| Nom | Représentation | Périmètre  | Aire intérieure 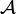 | Relations supplémentaires |
|---|---|---|---|---|
| Carré |  |
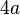 |
 |
 |
| Rectangle |  |
 |
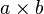 |
 |
| Triangle | 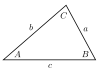 |
 |
 |
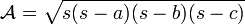
où |
| Triangle équilatéral |  |
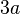 |
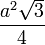 |
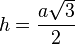 |
| Triangle isocèle rectangle |
 |
 |
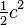 |
 |
| Losange |  |
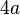 |
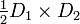 |
 |
| Parallélogramme |  |
 |
 |
|
| Trapèze |  |
 |
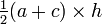 |
|
| Disque |  |
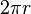 |
 |
|
| Ellipse |  |
(non algébrique) | 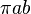 |
(voir ci-dessous) |
La lettre π désigne la constante d'Archimède qui vaut environ 3,14.
Autres relations [modifier]
- Théorème de Pythagore
- Dans un triangle ABC rectangle en C, les longueurs des côtés sont reliées par la formule :

- Théorème de Thalès
- Dans un triangle ABC non plat, si une droite parallèle à (BC) coupe (AB) en D et coupe (AC) en E alors les égalités suivantes sont vérifiées :

Figures de l'espace [modifier]
| Nom | Représentation | Aire de la surface | Volume intérieur | Relations supplémentaires |
|---|---|---|---|---|
| Cube |  |
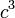 |
 |
|
| Pavé droit | 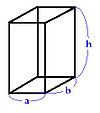 |
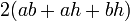 |
 |
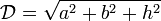 |
| Prisme droit |  |
|||
| Cylindre droit |  |
extrémités :
|
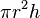 |
|
| Pyramide | 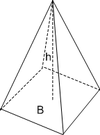 |
 |
||
| Tétraèdre régulier | 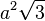 |
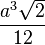 |
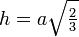 |
|
| Cône de révolution | 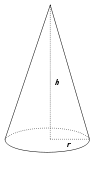 |
base : πr2
|
 |
|
| Sphère |  |
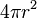 |
 |
|
| Calotte sphérique | 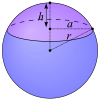 |
base :
|
 |
 |
| Ellipsoïde | (non algébrique) | 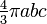 |
||
| Tore ouvert |  |
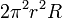 |
21:29 Publié dans Formulaire de géométrie classique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Géométrie symplectique
La géométrie symplectique est un domaine actif de la recherche mathématique, né de la volonté d'une formulation mathématique naturelle à la mécanique classique. Elle est à la rencontre de la géométrie différentielle et des systèmes dynamiques. En mathématiques, elle trouve des applications en géométrie algébrique, en géométrie riemannienne et engéométrie de contact. Formellement, elle est définie comme l'étude des « 2-formes différentielles fermées non dégénérées » — appelées formes symplectiques — sur les variétés différentielles1.Géométrie symplectique
Sommaire[masquer] |
L'adjectif symplectique fut introduit par le mathématicien Hermann Weyl (9 novembre 1885 – 8 décembre 1955) pour désigner le groupe symplectique Sp(2n), le groupe des automorphismes linéaires réels de Cn conjuguant la multiplication par i à elle-même. Ce groupe était appelé « groupe du linéaire complexe » et une confusion était possible avec le groupe des automorphismes linéaires complexes. Hermann Weyl justifie son choix : The name “complex group” formerly advocated by me in allusion to line complexes, as these are defined by the vanishing of antisymmetric bilinear forms, has become more and more embarrassing through collision with the word “complex” in the connotation of complex number. I therefore propose to replace it by the corresponding Greek adjective “symplectic”. — Hermann Weyl, The classical Groups. Their Invariants and Representations Plus exactement, l'adjectif « symplectique » est basé sur la racine grecque συµπλεκτικoς, traduction de la racine latine de complexus. La racine latine a donné le nom de complexité d'où dérive « nombre complexe », ce nom latin traduit l'idée d'entrelacement. En histoire naturelle, l'adjectif symplectique désigne « être entrelacé avec un autre corps ». Par extension, l'adjectif symplectique a été utilisé dans l'appellation de forme symplectique et de variété symplectique (voir définitions ci-dessous). Le cadre de la géométrie symplectique a permis de donner un nouveau regard sur la mécanique classique. Elle permet une étude du comportement global d'un système mécanique, de traiter les symétries et leurs conséquences et d'étudier des questions qualitatives comme par exemple l'existence de trajectoires périodiques ou le caractère chaotique ou stable d'une évolution. En mécanique, la position d'un ensemble de points matériels ou plus généralement d'un objet en mouvement est traditionnellement repérée par un certain nombre de coordonnées curvilignes Pour prendre en compte les vitesses, il est nécessaire d'ajouter aux coordonnées de position n nouvelles variables Bien sûr, il n'est en général pas possible de calculer explicitement toutes les trajectoires possibles et même un tel calcul ne donne pas forcément une bonne idée globale du comportement du système étudié. Pour comprendre ce comportement on peut essayer de suivre le déplacement d'un sous-ensemble de l'espace des phases, on a alors accès à des informations globales et qualitatives. Dans toute la suite on suppose que le système évolue en suivant les lois de la mécanique de Newton pour des forces dérivant d'un potentiel (ce qui signifie en simplifiant qu'il n'y a pas de frottements). On peut se demander quel type de géométrie est adapté à cette étude des trajectoires dans l'espace des phases. La géométrie euclidienne est la plus familière mais elle n'est pas adaptée car les droites ne sont pas conservées lors de l'évolution d'un système mécanique. Ainsi dans l'exemple du pendule simple on constate que si l'on part de configurations alignées cette propriété se perd en route. Il y a pire, un segment de droite n'est même pas envoyé sur une courbe de même longueur. Dans la suite on verra que la géométrie pertinente est la géométrie symplectique. Le théorème de Liouville affirme que lorsqu'un système mécanique évolue, le volume de toute partie de l'espace des phases est préservé. Voici comment on définit le volume d'une partie de l'espace des phases qui est de dimension 2n. Si la partie est définie par les conditions : alors le volume est Dans le cas où n = 1 on retrouve la définition de l'aire d'un rectangle. Si la partie dont on veut calculer le volume est plus compliquée, on la découpe en un très grand nombre de parties telles que plus haut et on fait la somme des volumes. Lorsque le nombre de rectangle tend vers l'infini et que leur réunion tend vers la partie initiale on trouve le volume. Ainsi dans le cas du pendule simple, on a conservation de l'aire de toute partie de l'espace des phases que l'on suit lors de l'évolution du système. Le théorème de Liouville affirme que l'évolution d'un système mécanique préserve le volume dans l'espace des phases. On peut donc penser que la structure géométrique de l'espace des phases est celle du volume des objets mais on va voir dans le paragraphe suivante qu'il existe une géométrie plus subtile. Le théorème de Poincaré est un raffinement du théorème de Liouville. Pour l'énoncer il faut introduire quelques notations. Pour tout i compris entre 1 et n, on note πi la projection de l'espace des phases sur le plan des (qi,pi). C'est donc la fonction qui à Le théorème de Poincaré affirme que pour toute surface S dans l'espace des phases, la somme des aires des projections pii(S) est conservée par l'évolution du système. %Todo dessin de la projection d'une surface Une structure symplectique sur un ensemble est un mécanisme d'attribution d'un nombre à toute surface dans l'ensemble et qui vérifie certaines conditions sur lesquelles on reviendra plus loin. Le fait d'associer à chaque surface S de l'espace des phases la somme des aires de ses projections πi(S) est un exemple de telle structure qu'on appelle structure symplectique canonique de l'espace des phases. Le théorème de Poincaré affirme donc que l'évolution d'un système mécanique préserve la structure symplectique canonique de l'espace des phases. On peut montrer que le théorème de Poincaré implique celui de Liouville. Pendant très longtemps, personne n'a su si le théorème de Poincaré permettait d'avoir vraiment plus d'information sur l'évolution des formes dans l'espace des phases que le théorème de Liouville. Enfin, en 1985, Mikhaïl Gromov a démontré le théorème suivant : pour tout système mécanique à n degrés de liberté, la boule ne peut jamais évoluer en un ensemble dont tous les points vérifient Or une telle évolution serait possible si seul le théorème de Liouville était vrai et pas le théorème de Poincaré. Ce théorème de Gromov est un théorème difficile et qui a de nombreuses conséquences, il a révolutionné le domaine de la géométrie symplectique. Le deuxième argument confortant l'idée que la géométrie symplectique est la géométrie naturelle des espaces de phases est la facilité avec laquelle elle permet d'intégrer les questions de symétrie et leurs conséquences dans la théorie. La présence de symétries dans un système mécanique a toujours pour conséquence la conservation de certaines quantités calculées à partir des positions et vitesses des objets étudiés. Ainsi lorsqu'un système est invariant par translation dans une direction, la quantité de mouvement dans cette direction est conservée. Lorsque le système est invariant par rotation autour d'un axe, le moment cinétique par rapport à cet axe est conservé. Dans la formulation Newtonnienne de la mécanique classique, il semble impossible d'énoncer un théorème général qui engloberait les exemples cités ainsi que des situations possédant des symétries plus compliquées. Le théorème de Noether affirme que dès que l'on a un groupe à un paramètre de transformations qui préserve un système mécanique il existe une quantité conservée lors de l'évolution de ce système. En fait l'énoncé complet donne une formule pour cette quantité en fonction des transformations et du système considérés. Dans la formulation lagrangienne de la mécanique on peut démontrer ce théorème en un dizaine de lignes. Dans la formulation hamiltonienne en termes de géométrie symplectique la démonstration ne fait qu'une ligne et l'énoncé se généralise au cas de groupe de transformations à un nombre quelconque de paramètres qui ne commutent pas nécessairement entre elles. Le nombre de quantités conservées est alors égal au nombre de paramètres du groupe de transformations. Une des conséquences de l'existence de quantités conservées est qu'elle contraint le système mécanique étudié à rester dans certaines régions de l'espace des phases définies par les conditions initiales. Lorsqu'on a autant de quantités conservées que de degrés de liberté on dit que le système mécanique est intégrable et la situation devient très simple, c'est ce qu'affirme le théorème d'Arnold-Liouville : pour presque toute énergie de départ il existe des coordonnées Bien sûr la plupart des systèmes mécaniques ne sont pas intégrables mais certains sont proches d'être intégrables, on peut alors essayer de comprendre dans quelle mesure leur comportement s'éloigne de celui d'un système intégrable, c'est l'objet de la théorie des perturbations qui fait elle aussi un grand usage de la structure symplectique des espaces de phases. Des connaissances élémentaires en géométrie différentielle sont nécessaires pour aborder les aspects techniques de la géométrie symplectique. L'introduction ici présentée donne un entr'aperçu des résultats fondamentaux qui se veut abordable. La géométrie symplectique partage de nombreux points communs avec la géométrie de Riemann, qui étudie les variétés différentielles dotées de tenseurs bilinéaires non dégénérés symétriques. Par contre, les variétés symplectiques n'ont pas d'invariants locaux telle que la courbure. C'est une conséquence du théorème de Darboux qui établit que deux variétés symplectiques sont localement isomorphes. La question de savoir quelles variétés admettent des structures symplectiques n'est pas encore complètement résolue. Chaque variété de Kähler est également une variété symplectique. Au cours des années 1970, les experts du domaine étaient incertains quant à la question de savoir si des variétés symplectiques compactes autres que celles de Kähler existaient, mais depuis plusieurs exemples ont peu être construits (le premier est dû à William Thurston). La plupart des variétés symplectiques ne sont pas de Kähler et n'ont donc pas de structure complexe intégrable compatible avec la forme symplectique. Mikhaïl Gromov a remarqué cependant que les variétés symplectiques possèdent de nombreuses structures quasi-complexes qui vérifient tous les axiomes d'une variété complexe à l'exception du fait que les fonctions de transition n'y sont pas holomorphes. Gromov développa le fait qu'il existe de telles structures pour fonder une théorie des courbes pseudoholomorphes, qui permit de grandes avancées dans la recherche géométrique symplectique, et notamment la découverte d'une classe d'invariants connus sous le nom d'invariants de Gromov-Witten, en coopération avec Edward Witten, qui jouent un rôle clé dans lathéorie des cordes. La géométrie euclidienne concerne les espaces affines euclidiens E : à ces derniers sont associées une distance naturelle, appelée distance euclidienne, unique invariant pour l'actiondiagonale du groupe des isométries affines de E sur E2, et une notion d'angle. Les distances et angles définis par un ensemble de points de E sont préservés sous l'action d'une isométrie. En oubliant la notion de distance, il est loisible de s'intéresser uniquement au volume euclidien. Il est bien connu qu'un isomorphisme linéaire affine préservant le volume est de déterminant +1 ou -1. Malheureusment, en dimension n, on perd ainsi toute information sur les configurations d'au plus n-1 points. La géométrie symplectique linéaire apparaît comme une géométrie intermédiaire, dans laquelle on perd la notion de distance, tout en conservant une notion d'aire orientée, et donc un invariant associé à 3 points. À trois points A, B et C d'un espace vectoriel réel E doit être associée une aire a(ABC). Pour des raisons d'additivité et de monotonicité des aires, cette quantité doit s'écrire : où Cette forme est dite non-dégénérée lorsque, pour tout vecteur Un isomorphisme linéaire ou affine de E est dit symplectique lorsqu'il préserve la forme symplectique ω. L'ensemble des isomorphismes linéaires symplectiques de Cn forme un groupe, appelé le groupe symplectique, noté Sp(n) ou Sp(2n) suivant les auteurs. C'est un groupe de Lie classique connexe non compact de dimension n(n-1)/2. Il contient le groupe unitaire U(n) comme rétracte par déformation forte : ces deux groupes ont donc le même type d'homotopie. La classification des ellipsoïdes dans un espace euclidien de dimension 2n modulo les isométries est donnée par 2n invariants, qui sont leurs diamètres respectifs. Par opposition, comme observé par Hofer et Zehnder2, la classification des ellipsoïdes d'un espace symplectique modulo les applications affines symplectiques est donné par n invariants. Les variétés différentielles s'obtiennent par des recollements d'ouverts d'espaces vectoriels réels de dimension finie suivant des difféomorphismes. Un intérêt porté sur des structures particulières peut conduire à imposer des restrictions sur la nature de ces recollements. L'objet d'étude de la géométrie symplectique est les 2-formes différentielles fermées non dégénérées. Une telle forme différentielle est appelée forme symplectique. Sur une variété différentielle M, on se donne une forme antilinéaire non dégénérée ωx, et on demande à ce que la collection Une variété munie d'une forme symplectique est appelée variété symplectique. Une fois les objets d'étude définis, on a coutume de s'intéresser aux relations qu'ils peuvent entretenir entre eux. Un difféomorphisme L'ensemble des difféomorphismes symplectiques de (M,ω) forment un groupe, appelé groupe des difféomorphismes symplectiques, et notéSymp(M,ω). Son étude a un intérêt de premier plan. L'un des principaux résultats élémentaires de la géométrie symplectique est le théorème de Darboux : localement, deux variétés symplectiques de même dimension sont isomorphes. Dit autrement, aucun invariant local n'existe. Sur ce point, et pas le moindre, la géométrie symplectique s'oppose complètement à la géométrie riemannienne : Cette dichotomie résume bien l'opposition entre la souplesse de la géométrie riemannienne contre la rigidité de la géométrie symplectique. Cette rigidité se retrouve à bien d'autres niveaux (rigidité des symplectomorphismes, théorème de rigidité de Gromov, ...). Les espaces de phases étudiés jusqu'à maintenant étaient assez simples car nous étions partis d'espaces de configurations assez simples. Cependant, dans l'exemple du pendule simple, il eut été plus logique de considérer que la variable q1 vivait dans une cercle et pas dans une droite. Plus généralement, on peut imaginer des espaces de configuration arbitrairement compliqués, par exemple si un point est astreint à se déplacer sur une surface ayant une forme sophistiquée. Quelle que soit la complexité de l'espace de configuration on peut toujours lui associer un espace des phases appelé fibré cotangent de l'espace de configuration et qui est toujours muni d'une structure symplectique canonique. Les théorèmes de Liouville, Poincaré, Noether et Liouville-Arnold restent vrais et on peut donner des analogues du théorème de Gromov dans ce cadre plus général. On peut vouloir aller plus loin dans la généralisation et étudier tous les espaces munis d'une structure symplectique. Pour cela il faut revenir un peu plus en détail sur la définition d'une structure symplectique. À partir de maintenant on considère un variété M de dimension 2n, c'est-à-dire un ensemble qui peut localement être paramétré par 2n nombres. Comme expliqué plus haut, une structure symplectique sur M est une application qui, à toute surface dans M, associe un nombre et qui vérifie en plus deux propriétés. La première est que cette structure doit permettre d'associer un volume à toute partie de dimension 2n de M en procédant comme expliqué dans le paragraphe sur le théorème de Poincaré. La deuxième condition est que le nombre associé à toute surface sans bord est nul. Le passage des espaces de phases aux variétés symplectiques générales est une grande généralisation mais on peut montrer qu'une variété symplectique ressemble toujours localement à un espace de phases. C'est le théorème de Darboux : au voisinage de n'importe quel point, toute variété symplectique peut être paramétré par un espace de phase de sorte que toute surface assez petite se voit attribuer le même nombre par la structure symplectique donnée et par la structure symplectique de l'espace des phases. La question de savoir quels ensembles admettent au moins une structure symplectique est difficile. On connaît de nombreux exemples, des conditions nécessaires, d'autres qui sont suffisantes mais aucune caractérisation complète. De même, une fois l'existence acquise on ne sait que très rarement combien de structures symplectiques réellement différentes cohabitent sur un même ensemble. L'étude de la géométrie symplectique est née du constat que l'évolution d'un système mécanique préserve la structure symplectique canonique de l'espace des phases. Plus généralement on peut chercher à comprendre l'ensemble des transformations qui préservent une structure symplectique donnée. De telles transformations sont appelées symplectomorphismes et sont toujours très nombreuses, elles forment un ensemble de dimension infinie appelé groupe des symplectomorphismes. Pour comprendre la forme de cet ensemble, on cherche à le comparer à des ensembles plus petits que l'on comprend mieux. Les premiers résultats significatifs dans ce domaine sont dus à Gromov dans la foulée de son théorème de non-tassement. La géométrie symplectique est née de la formalisation hamiltonienne des lois de la mécanique classique. Cette formulation est née par la somme successive des travaux de Newton, deLagrange, et de Hamilton, du XVIIe au xixe. Mais ce n'est que dans les années 1960 que les outils de la géométrie symplectique ont pu être formalisés, sous l'impulsion de Vladimir Arnold, et avec la participation active de Mikhaïl Gromov et Jean-Marie Souriau. En 1666, Newton révolutionne simultanément la physique et les mathématiques en énonçant la loi d'attraction universelle. Cette loi permet de décrire le mouvement relatif d'une planète autour de son étoile. Encore aujourd'hui, malgré l'avènement de la relativité générale, cette loi est toujours utilisée aujourd'hui dans la détection des exoplanètes. Une planète, à l'instar de la Terre, subit la force attractive du Soleil, et son évolution est décrite par l'équation différentielle : Le problème du mouvement relatif de deux corps en interaction mututelle est devenu un exercice classique incontournable du premier cycle universitaire. Newton lui-même en a donné une solution correcte dans les propositions 57 à 65 de ses Principia. La planète décrit par rapport à l'étoile un mouvement elliptique dont l'étoile est l'un des foyers. Six constantes sont nécessaires pour décrire ce mouvement : Toutefois, cette description oublie la présence d'autres planètes. Le problème à De 1808 à 1811, Joseph-Louis Lagrange, alors professeur de mathématiques à l' École polytechnique, s'intéresse au problème de la stabilité des planètes du système solaire. Compte-tenu du nombre de corps considérés, le problème est de taille ; il s'est depuis complexifié au fur et à mesure des avancées dans les observations astronomiques. Grossièrement, la méthode de Lagrange consiste à effectuer des petites perturbations sur le mouvement d'une planète, autrement dit, sur les six constantes d'intégration. Cette perturbation varie dans le temps suivant une loi moyennant les forces subies : Les calculs n'étaient pas justifiés. Poincaré montre la divergence des séries utilisées par les astronomes dans Méthodes nouvelles de la mécanique céleste. Il faudra attendre la seconde moitié du xxe siècle pour que les outils nécessaires soient introduits. La véritable révolution apportée par Lagrange est d'avoir introduit une fonctionnelle d'énergie, aujourd'hui notée L et appelée Lagrangien, dont les points critiques sont les trajectoires du mouvement. L'intérêt croissant vis-a-vis des structures symplectiques durant les dernières décennies s'explique par les besoins de la physique du xxe siècle. Le passage de la mécanique classique à la mécanique quantique est à ce jour encore mal compris. La question de fonder de sérieuses bases mathématiques est un défi qui a conduit les mathématiciens à s'interroger à nouveau sur la dynamique hamiltonienne (la mécanique classique, des systèmes dynamiques de points matériels à l'optique géométrique). Le regard porté à la lumière de la géométrie différentielle ne pouvait être que nouveau. Dans la continuation des travaux de Lagrange et de Hamilton, pour établir l'existence d'orbites périodiques dans le problème des trois corps, Henri Poincaré se ramène à l'étude d'une application préservant l'aire sur un anneau Les résultats furent démontrés dans les années 1920 par George David Birkhoff ; ils sont aujourd'hui considérés comme les premiers travaux sur la géométrie symplectique - s'ils peuvent être considérés comme tels. Le théorème de Birkhoff affirme l'existence de points fixes pour un difféomorphisme de l'anneau Le théorème de Birkhoff préfigure la conjecture d'Arnold, énoncée au début des années 1960. Cette conjecture s'efforce de trouver un minorant du nombre d'orbites périodiques pour un difféomorphisme symplectique sur une variété symplectique compacte. En 1983 Conley et Zehnder démontrent la conjecture pour le tore par une étude variationnelle. Inspiré de ces travaux, Andreas Floer démontre en partie la conjecture pour une large classe de variétés symplectiques compactes, étendue par la suite par Weinstein. Les méthodes utilisées ont contribué à la mise en place de l'homologie de Floer. La formulation de cette homologie représente un des aspects les plus puissants mis en place ces dernières décennies. Brièvement, et du moins sous certaines hypothèses, l'homologie de Floer consiste à compter des orbites périodiques d'une isotopie hamiltonienne et, modulo translation, des cylindres reliant ces orbites répondant à une EDP elliptique. L'ellipticité joue un rôle central. Le théorème KAM figure parmi les résultats les plus cités en dynamique hamiltonienne. Il étudie la stabilité des systèmes mécaniques complètement intégrables. Le nom du théorème est l'abréviation des trois mathématiciens qui ont contribué à sa démonstration : Kolmogorov, Arnold et Moser. Il justifie dans le langage actuel des mathématiques les résultats de Lagrange. Une autre investigation importante concerne l'introduction des capacités symplectiques. Ce sont des invariants symplectiques vérifiant de bonnes conditions de normalisation et d'homogénéité. Leur classification reste totalement incomprise à ce jour. Il existe un grand nombre de capacités introduites3 : le rayon de Gromov, lié au théorème de non-plongement de Gromov ; les capacités d'Ekeland-Hofer et de Hofer-Zehnder, utilisant des études variationnelles sur la dynamique hamiltonienne ; ou encore un grand nombre de capacités dites spectrales dont l'introduction a été initiée par Claude Viterbo. L'utilisation de ces capacités a permis une preuve partielle de la conjecture de Weinstein (évoquée plus haut), et une preuve du théorème de rigidité de Gromov. L'usage d'une généralisation des courbes holomorphes a porté de forts développements en géométrie symplectique. La géométrie symplectique s'est constituée comme domaine d'étude à part entière dès la fin des années 1960. Ce nouveau souffle dans la recherche mathématique a introduitparallèlement d'autres disciplines, la quantification géométrique et la Théorie des champs symplectique.Étymologie, histoire de la terminologie [modifier]
(Le nom « groupe complexe » que j'ai précédemment évoqué en allusion à la droite complexe, est devenu de plus en plus embarrassant par l'usage de « complexe » dans l'expression « nombre complexe ». Je propose donc de le remplacer par l'adjectif grec correspondant « symplectique ».)Motivations [modifier]
Mécanique classique et formalisme hamiltonien [modifier]
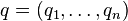 . Le nombre n est appelé nombre de degrés de liberté du système. Par exemple, un pendule astreint à rester dans un plan est repéré par un seul paramètre q1, à savoir l'angle que fait sa tige avec la verticale définie par le champ de gravité. Les positions occupées par deux masses ponctuelles en interaction (par exemple une planète et une étoile) sont repérées par six paramètres, trois pour chaque masse. L'ensemble des différentes valeurs
. Le nombre n est appelé nombre de degrés de liberté du système. Par exemple, un pendule astreint à rester dans un plan est repéré par un seul paramètre q1, à savoir l'angle que fait sa tige avec la verticale définie par le champ de gravité. Les positions occupées par deux masses ponctuelles en interaction (par exemple une planète et une étoile) sont repérées par six paramètres, trois pour chaque masse. L'ensemble des différentes valeurs  que les coordonnées peuvent prendre dans toutes les positions possibles du système est appelé espace de configuration. Les lois de Newton de la mécanique affirment (entre autres choses) qu'un système mécanique évolue d'une façon déterministe qui peut être prévue si on connait la position et la vitesse d'un point à l'instant initial.
que les coordonnées peuvent prendre dans toutes les positions possibles du système est appelé espace de configuration. Les lois de Newton de la mécanique affirment (entre autres choses) qu'un système mécanique évolue d'une façon déterministe qui peut être prévue si on connait la position et la vitesse d'un point à l'instant initial. . Dans le premier exemple, p1 serait la vitesse angulaire du pendule et dans le deuxième, on aurait les composantes de la vitesse des deux planètes. L'ensemble des valeurs
. Dans le premier exemple, p1 serait la vitesse angulaire du pendule et dans le deuxième, on aurait les composantes de la vitesse des deux planètes. L'ensemble des valeurs  que peuvent prendre les différents paramètres est appelé espace des phases du système. Les trajectoires du système se tracent dans cet espace.
que peuvent prendre les différents paramètres est appelé espace des phases du système. Les trajectoires du système se tracent dans cet espace.Théorème de Liouville [modifier]

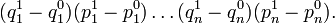
Théorème de Poincaré [modifier]
 associe (qi,pi).
associe (qi,pi).Théorème de non-tassement de Gromov [modifier]

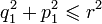 pour un r strictement plus petit que 1.
pour un r strictement plus petit que 1.Symétries en mécanique [modifier]
Théorème de Noether [modifier]
Systèmes hamiltoniens intégrables [modifier]
 et des nombres
et des nombres 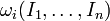 tels que
tels que
Systèmes presque intégrables [modifier]
Présentation générale [modifier]
Géométrie symplectique linéaire [modifier]
 est une forme bilinéaire. Comme une transposition sur les points A, B, C change l'orientation du triangle ABC, la forme ω doit être antisymétrique au sens où, pour tous vecteurs u et v :
est une forme bilinéaire. Comme une transposition sur les points A, B, C change l'orientation du triangle ABC, la forme ω doit être antisymétrique au sens où, pour tous vecteurs u et v : , il existe un vecteur v vérifiant :
, il existe un vecteur v vérifiant : 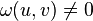 . Par définition, une forme symplectique sur E désigne une forme bilinéaire antisymétrique non dégénérée. Une telle forme est unique à isomorphisme linéaire près ; et son existence implique que la dimension de E soit paire, disons 2n. Le modèle standard est l'espace Cn regardé comme espace vectoriel réel, avec comme forme symplectique la partie imaginaire de la métrique hermitienne standard.
. Par définition, une forme symplectique sur E désigne une forme bilinéaire antisymétrique non dégénérée. Une telle forme est unique à isomorphisme linéaire près ; et son existence implique que la dimension de E soit paire, disons 2n. Le modèle standard est l'espace Cn regardé comme espace vectoriel réel, avec comme forme symplectique la partie imaginaire de la métrique hermitienne standard.Géométrie symplectique [modifier]
 ait une certaine régularité en x. L'application
ait une certaine régularité en x. L'application  est un exemple de 2-forme différentielle, qu'on exige fermée : tous champs de vecteurs X, Y, et Z vérifient :
est un exemple de 2-forme différentielle, qu'on exige fermée : tous champs de vecteurs X, Y, et Z vérifient :![Xcdotomega(Y,Z)+Ycdot omega(Z,X)+Zcdot omega(X,Y)=omega([X,Y],Z)+omega([Y,Z],X)+omega([Z,X],Y)](http://upload.wikimedia.org/math/c/a/f/cafb42aa9353df8939a401fa92557f92.png) .
.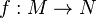 s'appelle difféomorphisme symplectique lorsque f préserve les formes symplectiques ω. De manière plus explicite, la différentielle
s'appelle difféomorphisme symplectique lorsque f préserve les formes symplectiques ω. De manière plus explicite, la différentielle  est un isomorphisme linéaire symplectique. Le lecteur mal à l'aise avec la géométrie différentielle comprendra les choses ainsi : au premier ordre, f est un isomorphisme symplectique linéaire.
est un isomorphisme linéaire symplectique. Le lecteur mal à l'aise avec la géométrie différentielle comprendra les choses ainsi : au premier ordre, f est un isomorphisme symplectique linéaire.
Variétés symplectiques [modifier]
Définition et théorème de Darboux [modifier]
Existence et classification [modifier]
Symplectomorphismes [modifier]
Interactions [modifier]
Histoire [modifier]
Genèse de la géométrie symplectique [modifier]
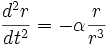
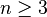 corps est autrement plus ardu. Il résiste encore aujourd'hui à trois siècles d'histoire. Aucune solution analytique n'est connue, excepté pour le problème à trois corps, pour lequel on sait déterminer certaines solutions dites "homographiques".
corps est autrement plus ardu. Il résiste encore aujourd'hui à trois siècles d'histoire. Aucune solution analytique n'est connue, excepté pour le problème à trois corps, pour lequel on sait déterminer certaines solutions dites "homographiques".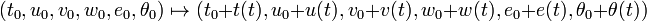
Histoire de la géométrie symplectique [modifier]
![S^1times [-1,1]](http://upload.wikimedia.org/math/1/0/d/10d35873f5d7303c9ab88ab2ac4cdcdb.png) . Cette application s'est avérée par la suite d'une grande utilité dans l'étude des flots de champs de vecteurs. Elle est aujourd'hui connue sous le nom d'application de retour de Poincaré.
. Cette application s'est avérée par la suite d'une grande utilité dans l'étude des flots de champs de vecteurs. Elle est aujourd'hui connue sous le nom d'application de retour de Poincaré.![S^1times [-1,1]](http://upload.wikimedia.org/math/1/0/d/10d35873f5d7303c9ab88ab2ac4cdcdb.png) , qui préserve la mesure de Lebesgue, et qui induit un difféomorphisme croissant sur
, qui préserve la mesure de Lebesgue, et qui induit un difféomorphisme croissant sur 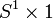 et un difféomorphisme décroissant sur
et un difféomorphisme décroissant sur  . En réalité, ils portaient davantage sur la préservation du volume. Mais en dimension 2, une mesure est essentiellement une forme d'aire, donc une forme symplectique. La dimension 2 reflète mal les particularités propres à la géométrie symplectique.
. En réalité, ils portaient davantage sur la préservation du volume. Mais en dimension 2, une mesure est essentiellement une forme d'aire, donc une forme symplectique. La dimension 2 reflète mal les particularités propres à la géométrie symplectique.Annexes [modifier]
Bibliographie [modifier]
Notes et références [modifier]
Voir aussi [modifier]
Articles connexes [modifier]
Liens externes [modifier]
21:28 Publié dans Géométrie symplectique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Les « harmonies cachées » de Cédric Villani, médaille Fields 2010
Le 26 août dernier, le mathématicien Cédric Villani recevait la prestigieuse médaille Fields, équivalent du prix Nobel pour cette discipline. Auteur de près d'une cinquantaine de publications, ce chercheur a bien voulu répondre aux questions de Futura-Sciences.
Après avoir enseigné à l'École normale supérieure de Lyon, Cédric Villani est aujourd'hui professeur à l'université de Lyon et assume par ailleurs la charge de directeur de l'institut Henri Poincaré depuis 2009. En compagnie de Ngo Bao Chau, un autre mathématicien français, de l'Israélien Elon Lindenstrauss et du Russe Stanislav Smirnov, il s'est vu attribuer la médaille Fields 2010.
Ce prix prestigieux récompense les travaux de Cédric Villani sur l'équationde Boltzmann et le transport optimal. En 2009, le mathématicien avait expliqué cette question dans un dossier de Futura-Sciences, l'abordant en termes simples et en remontant l'histoire de ce problème séculaire. Cédric Villani revient pour nous sur son travail original et nous fait part de ses réflexions sur la recherche française.


Cédric Villani maîtrise l'équation de Boltzmann mais aussi l'art de nouer une lavallière. Par ailleurs, il aime les araignées (et aussi, paraît-il, les marsupilamis). © Pierre Maraval
Futura-Sciences : Tout comme pour Pierre-Louis Lions, qui fut votre directeur de thèse, l'équation de Boltzmann occupe une place importante dans vos travaux : en quoi est-ce un bon problème ?
Cédric Villani : On trouve de tout dans l'équation de Boltzmann, et d'ailleurs les directions que j'ai le plus explorées ne sont pas les mêmes que celles explorées par Pierre-Louis Lions. L'équation de Boltzmann est un carrefour entre la mécanique des fluides (variations des caractéristiques des gaz), la physique statistique (grands systèmes de particules) et la théorie de l'information (augmentation de l'entropie). Cet assemblage lui confère une connotation unique et une richesse théorique qui va bien au-delà de son importance pratique. Dans mon cas les deux questions qui ont le plus retenu mon attention sont la régularité induite par les interactions à longue portée et la production d'entropie. Le premier problème est lié à des questions fondamentales de régularisation pour des équations dégénérées, le second mêle la mécanique des fluides, la théorie de l'information et diverses inégalités développées au départ en théorie quantique des champs ou enélasticité... On touche bien ici l'universalité des mathématiques et la richesse des problèmes issus de la physique.
FS : Quelle intuition vous a permis de mettre en relation l'équation de Boltzmann et le transport optimal ?
Cédric Villani : La relation entre l'équation de Boltzmann et le transport optimal est bien antérieure à mes travaux ! C'est le chercheur japonais Hiroshi Tanaka qui a compris, dans les années 1970, que la distance du transport optimal (techniquement parlant, la distance quadratique) ne peut que décroître le long des solutions de l'équation de Boltzmann spatialement homogène à interactions maxwelliennes (un modèle où les particules interagissent par des forces inversement proportionnelles à la puissance 5 de la distance). En d'autres termes, vous prenez deux solutions de cette équation, chacune associée à un profil de vitesses qui évolue au cours dutemps : à mesure que le temps passe il est de plus en plus facile de transporter le premier profil de vitesses vers le second profil.
C'est par Giuseppe Toscani (Pavie) que j'ai entendu parler pour la première fois de cette contribution de Tanaka et il se trouve que Yann Brenier, qui m'encadrait à l'École normale supérieure, était spécialiste du problème de transport optimal. Il m'a proposé de co-organiser un petit colloque consacré à ce problème de transport ; c'est là que j'ai rencontré Felix Otto, qui était en train de développer un formalisme révolutionnaire pour le transport optimal, basé sur la géométrie différentielle. J'ai été tout de suite frappé par le formalisme et je l'ai bien intégré. Quelques semaines plus tard, je me suis rendu compte en lisant un cours de Michel Ledoux (Toulouse) qu'un certainthéorème mentionné dans ce cours pouvait se démontrer par un chemin alternatif basé sur la vision géométrique de Otto.
C'était le point de départ de mon premier article avec Otto, qui reste à ce jour le plus cité de tous mes articles car il établit un pont entre deux domaines distincts de l'analyse. Dans la suite de mes travaux, ma culture de l'équation de Boltzmann et des phénomènes de transport m'a permis d'explorer le transport optimal de manière originale et efficace, mais comme vous le voyez, en fait d'intuition il y a surtout beaucoup de hasard et d'opportunités à saisir, le principal étant de rester curieux et ouvert d'esprit !
FS : Pensez-vous que vos travaux trouveront une application à l'étude des équations de Navier-Stokes ?
Cédric Villani : J'en doute fort ! En tout cas certainement pas Navier-Stokes incompressible, dont le lien avec Boltzmann est très indirect. Pour tout dire, le problème de la régularité de Navier-Stokes incompressible a beau être mis à prix pour un million de dollars, il me laisse de marbre, il ne rentre pas dans ma sensibilité mathématique.
FS : Quelles sont les conséquences de vos recherches pour les autres sciences ?
Cédric Villani : Mes recherches sont en interaction avec la physique, l'économie ou d'autres sciences. Quelques-uns de mes collaborateurs ont récemment publié un article où ils explorent les conséquences économiques d'un problème de géométrie différentielle relié à la régularité des solutions du transport optimal. Plus près de moi, récemment j'ai pu convaincre l'un de mes collaborateurs, spécialiste de simulations numériques, que l'un de ses codes donnait des résultats aberrants. L'une des raisons était que le comportement était en contradiction avec un de mes résultats théoriques. Ces conséquences sont modestes et je suis clairement un mathématicien, cependant j'ai très régulièrement l'occasion de discuter avec des physiciens ou de faire des exposés devant des parterres de physiciens, voire de leur suggérer des pistes de recherche.
FS : Quel est votre guide dans vos recherches ? Avez-vous un but particulier que vous souhaiteriez atteindre ?
Cédric Villani : Ce qui guide mes recherches : la curiosité, la conviction qu'il y a quelque chose d'intéressant à comprendre, des harmonies cachées... Un certain nombre de problèmes me tiennent particulièrement à cœur, surtout ceux qui sont liés à beaucoup d'autres questions. La régularité des solutions de l'équation de Boltzmann en est un. Il y a un certain problème de caractérisation de la courbure de Ricci qui me tient beaucoup à cœur, et puis d'autres pistes à explorer en physique des plasmas et des galaxies.... Je ne vais pas tous les citer !
FS : Que pensez-vous de la « déraisonnable efficacité des mathématiques », dont parlait Wigner ?
Cédric Villani : C'est un mystère sur lequel se sont extasiés Einstein, Poincaré et bien d'autres. On ne peut que constater cette efficacité, je n'aurai pas la prétention de l'expliquer. Il est incroyable que le monde, si complexe et incompréhensible qu'il puisse paraître, soit ainsi fait qu'on puisse isoler certaines caractéristiques abstraites fondamentales qui permettent de le comprendre, ou au moins de comprendre certains de ses aspects.


En conférence. © Doppler Institute
FS : Selon vous, vaut-il mieux parler en mathématiques de découverte ou d'invention ?
Cédric Villani : Il s'agit de découvertes, je ne le pense qu'ainsi ! La plupart de mes contributions marquantes ont consisté à mettre à jour des liens que personne, moi compris, ne soupçonnait. L'une, récente, est un lien entre la théorie de Kolmogorov-Arnold-Moser des systèmes mécaniques « presque intégrables » et la théorie non linéaire de l'amortissement Landau en physique des plasmas. Je n'en suis toujours pas revenu de la série de coïncidences qui m'a mené à trouver ce lien, j'aurais été bien en peine de l'imaginer. Bien sûr ce n'est qu'une impression personnelle… En fait il est impossible de trancher le vieux débat découverte-invention par des arguments scientifiques, cela relève de la conviction philosophique.
FS : Comment voyez-vous l'avenir de la recherche en France ?
Cédric Villani : L'avenir sera beau si quelques ajustements sont réussis. Plusieurs facteurs contribuent à une grande inquiétude ambiante actuellement : les mutations des institutions (Agence nationale de la recherche, AERES, réforme du CNRS, loi d'autonomie des universités), le poids accru sur la scène internationale d'indicateurs inadaptés (classement de Shanghai, impact factor), la chute des effectifs dans les filières scientifiques qui rend critique la situation des « petites » universités, nombreuses en France. Là-dessus est arrivé le très maladroit discours de Nicolas Sarkozy en janvier 2009 qui a mis le feu aux poudres, à un moment où la recherche avait besoin plus que jamais de se sentir en confiance.
Cependant les nouvelles institutions ne marchent pas mal : à l'usage, l'ANR est un bon pourvoyeur de moyens, même si à mon avis elle fait la part bien trop belle aux projets et devrait laisser plus de place à l'improvisation. L'AERES joue bien son rôle, au moins en mathématiques pour ce que j'en ai vu. Quant à la loi d'autonomie des universités, elle est très délicate à mettre en œuvre mais je pense qu'elle sera très bénéfique si le dispositif est simplifié et que l'on ne reste pas prisonnier des lourdeurs administratives. Ensuite ce sera aux chercheurs de s'organiser dans les universités pour mettre en place pouvoirs et contre-pouvoirs, et garantir la compétitivité sur la scène internationale. Si nous n'y arrivons pas, nous ne pourrons nous en prendre qu'à nous-mêmes !
Une caractéristique de la recherche française est le poids de nombreuses institutions assez spécifiques et très performantes : grandes écoles, CNRS, Inria, etc. La bonne articulation de ces organismes avec les universités (lieu naturel où se fait la recherche) est un défi majeur qui permettra de valoriser nos atouts. Tout le monde gagnera à renforcer les liens entre la recherche et les écoles d'ingénieurs, ainsi d'ailleurs que les liens entre la recherche et les entreprises (débat délicat car il ne faut en aucun cas sacrifier l'indépendance de la recherche).
De manière générale, on pourrait beaucoup gagner en efficacité en assouplissant l'administration, les contrôles, les évaluations, etc. Il faut parfois respecter l'esprit des textes plutôt que leur lettre ; cela demande du bon sens, de la souplesse et de l'intelligence administrative, et la réaffirmation du principe selon lequel l'administration doit se mettre au service du chercheur et non l'inverse. Nous avons de gros progrès à faire en ce sens, même si la situation française est considérablement meilleure qu'au niveau européen, où je pense que tout est à refaire. Dans l'ensemble les problèmes sont assez bien identifiés, je suis confiant en notre capacité à les résoudre.
Source : http://www.futura-sciences.com/fr/news/t/mathematiques-1/...
07:36 Publié dans Les « harmonies cachées » de Cédric Villani | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Skander Belhaj, un mathématicien aux multiples talents
Source : http://www.leaders.com.tn/article/skander-belhaj-un-mathe... C’est aux Editions Universitaires Européennes que le jeune chercheur tunisien Skander Belhaj vient de publier un nouvel ouvrage issu de ses travaux de thèse et intitulé Algèbre matricielle rapide en calcul formel et calcul numérique : Calcul rapide sur les matrices structurées.Originaire de Metouia où il est né en 1978, Skander est passé par les rangs de la mythique Sadkia où il obtient son Baccalauréat de Mathématiques en 1996. Les Mathématiques, un domaine dont il ne devait plus se séparer alignant une maîtrise, un DEA et une thèse élaborée sous la co-direction du Professeur Mohamed Jaoua du temps où ce dernier présidait le LAMSIN (Laboratoire de Modélisation Mathématique et Numérique dans la Science de l'Ingénieur) à l’Ecole Nationale des Ingénieurs de Tunis et du Professeur Henri Lombardi de l’Université de Franche-Comté à Besançon en France.
C’est aux Editions Universitaires Européennes que le jeune chercheur tunisien Skander Belhaj vient de publier un nouvel ouvrage issu de ses travaux de thèse et intitulé Algèbre matricielle rapide en calcul formel et calcul numérique : Calcul rapide sur les matrices structurées.Originaire de Metouia où il est né en 1978, Skander est passé par les rangs de la mythique Sadkia où il obtient son Baccalauréat de Mathématiques en 1996. Les Mathématiques, un domaine dont il ne devait plus se séparer alignant une maîtrise, un DEA et une thèse élaborée sous la co-direction du Professeur Mohamed Jaoua du temps où ce dernier présidait le LAMSIN (Laboratoire de Modélisation Mathématique et Numérique dans la Science de l'Ingénieur) à l’Ecole Nationale des Ingénieurs de Tunis et du Professeur Henri Lombardi de l’Université de Franche-Comté à Besançon en France.
Les travaux du Docteur Skander Belhaj portent sur la conception des algorithmes rapides via les outils d’algèbre matricielle et leurs applications au traitement d’image. Il a notamment travaillé sur l’amélioration de quelques algorithmes rapides sur les matrices structurées en calcul formel et numérique, objet de son nouvel ouvrage.
Skander Belhaj est également assistant de l’enseignement supérieur depuis 2007 à l’Université de Jendouba et a été élu Directeur du Département des Méthodes Quantitatives à la Faculté des Sciences Juridiques, Economiques et de Gestion de Jendouba en Février 2010. Une charge administrative qu’il assume en plus de ses activités de recherche et d’enseignement reconnues à l’échelle internationale puisqu’il est reviewer et editor de plusieurs revues scientifiques internationales (Journal of Mathematics Research., International Journal of Numerical Methods and Applications, Journal of Statistics and Mathematics, etc.).
Déjà père de famille depuis plusieurs années malgré son jeune âge, Skander avoue se sentir au tout début du long chemin périlleux de la recherche scientifique. « Je dois encore travailler, travailler et travailler », dit-il. On peut lui faire confiance, et les 4700 universitaires qui sont membres du groupe Facebook « Enseignants et chercheurs tunisiens » dont il est l’administrateur, peuvent témoigner de son dynamisme et de sa volonté de faire de ce groupe une communauté où les chercheurs tunisiens, jeunes et moins jeunes, peuvent exposer et partager leurs questionnements et leurs problématiques de recherche.
Anissa BEN HASSINE
07:33 Publié dans Skander Belhaj, un mathématicien aux multiples tal | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
SMS 2011 - Overview
In recent decades, metric-measure spaces have emerged as a fruitful source of mathematical questions in their own right, and as indispensable tools for addressing classical problems in geometry, topology, dynamical systems and partial differential equations. The purpose of the 2011 summer school is to lead young scientists to the research frontier concerning the analysis and geometry of metric-measure spaces, by exposing them to a series of mini-courses featuring leading researchers who will present both the state-of-the-art and the exciting challenges which remain. In geometry and topology, metric-measure spaces arise naturally as non-smooth limits of smooth objects, such as Riemannian manifolds. Here the limit may be taken in the coarse sense of Gromov-Hausdorff convergence, which allows the formation of singularities and dimensional collapse, among other phenomena. Such limits arise under dynamical processes including curvature flows, as in Perelman's proof of the Poincaré and Geometrization Conjectures for 3-manifolds. Moreover, the limit of the normalized Riemannian volume need not bear any relation to the limiting metric, hence it is natural to equip the limiting metric space with a limiting measure. Most results in geometry rely on curvature bounds, such as upper bounds on sectional curvatures or lower bounds on Ricci curvature. Nonsmooth analogues of sectional curvature bounds can be constructed using comparisons with triangles in model spaces, after Cartan, Alexandrov, and Topagonov, but notions of Ricci curvature have proved elusive in a metric-measure setting. Recently, two quite different definitions for Ricci curvature lower bounds have emerged from the theory of optimal transportation. Both respect (measured) Gromov-Hausdorff convergence, and depend crucially on the measure and a putative dimension (which need not coincide with the topological or geometric dimension), as well as the metric. These quite different approaches have led to some striking conclusions --- including Bishop, Myers, Sobolev, log-Sobolev, Talagrand and Poincaré inequalities in metric-measure settings, sometimes with sharp constants. In order for students to appreciate the latest breakthroughs, the summer school aims to provide a broad view of the developments in geometry of and analysis on metric measure spaces in recent years, as well as to touch on important advances in related areas. Among these are notions of differentiability, function spaces (Lipschitz, BV, Sobolev), Hausdorff measure and dimension, fundamental inequalities (Sobolev, Poincaré, isoperimetric, Gaussian), heat kernel estimates and probabilistic aspects, convergence of metric measure spaces, Ricci curvature lower bounds, optimal transportation, curvature flows, quasi-conformal mappings and geometric measure theory Source : SMS 2011 - Overview
07:09 Publié dans SMS 2011 - Overview | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Canadian Journal of Mathematics déc. 1996
07:07 Publié dans Canadian Journal of Mathematics déc. 1996 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Canadian Journal of Mathematics juin 1980
07:06 Publié dans Canadian Journal of Mathematics juin 1980 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Mathematisches Institut georg-august-universität Göttingen, seminars summer
07:04 Publié dans Mathematisches Institut georg-august-universität G | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Kurt Gödel und die mathematische Logik, Volume 5 Par Werner DePauli-Schimanovich
07:00 Publié dans Kurt Gödel und die mathematische Logik | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Théorie des nombres, Volume 1 Par Adrien Marie Legendre
06:56 Publié dans Théorie des nombres, Théorie des nombres, Volume 1 Par Adrien Marie Leg | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Nombres premiers et décomposition en produit de facteurs premiers
Théorie des nombres -- Nombres premiers Source : http://www.bibmath.net/dico/index.php3?action=affiche&...
Théorie des nombres -- Factorisation
Un nombre entier p positif supérieur strict à 1 est dit premier s'il n'admet que 2 diviseurs positifs : 1 et p (remarquons que 1 n'est pas premier). Dans le cas contraire, cet entier est dit composé.
Ex : 7 est premier. 24 est composé : 2 divise 24.
Ex : 24=23×3.
06:53 Publié dans Nombres premiers et décomposition en produit | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Nombres p-adiques
Théorie des nombres
Algèbre -- Anneaux
Algèbre -- Corps
Analyse -- Topologie -- Vocabulaire général
|.|p est une norme sur Q, avec des propriétés très différentes de la valeur absolue. Par exemple,
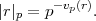


| Définition : Le corps des nombres p-adiques, noté Qp, est le complété de Q pour la norme p-adique. |
Source : http://www.bibmath.net/dico/index.php3?action=affiche&...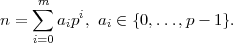 La suite (ai) est définie par
La suite (ai) est définie par
Les nombres p-adiques sont ceux qui s'écrivent modulo p.
modulo p.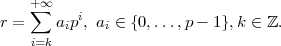 Cette série est convergente pour la distance p-adique. L'écriture précédente s'appelle décomposition de Hensel de r. Finalement, l'ensemble des entiers p-adiques, noté Zp, est l'ensemble des r de Qp s'écrivant
Cette série est convergente pour la distance p-adique. L'écriture précédente s'appelle décomposition de Hensel de r. Finalement, l'ensemble des entiers p-adiques, noté Zp, est l'ensemble des r de Qp s'écrivant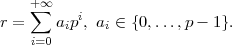 C'est un sous-anneau de Qp.
C'est un sous-anneau de Qp. Les nombres p-adiques ont été introduits par Hensel en 1897. Son idée était de pouvoir utiliser la théorie des séries entières en arithmétique. Depuis, toute une branche des mathématiques, l'analyse p-adique, s'est développée sur ses idées.
Les nombres p-adiques ont été introduits par Hensel en 1897. Son idée était de pouvoir utiliser la théorie des séries entières en arithmétique. Depuis, toute une branche des mathématiques, l'analyse p-adique, s'est développée sur ses idées.
06:51 Publié dans Nombres p-adiques | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Adhérence (mathématiques)
En topologie, l'adhérence d'une partie d'un espace topologique est le plus petit ensemble fermé contenant cette partie. On retrouve cette notion particulièrement dans la convergence de suites dans les espaces métriques avec la notion de valeur d'adhérence.Adhérence (mathématiques)
![]() Pour les articles homonymes, voir Adhérence.
Pour les articles homonymes, voir Adhérence.
Sommaire[masquer] |
En topologie, l'adhérence d'une partie X d'un espace topologique E est le plus petit ensemble fermé de E qui contienne X. L'existence d'un tel fermé est claire : il existe au moins un fermé contenant X, à savoir l'espace E lui-même ; d'autre part, l'intersection de tous les fermés contenant X est un fermé contenant X, et est le plus petit ayant cette propriété. L'adhérence de X est aussi appelée fermeture de X et se note souvent On dit d'un point x de E qu'il est adhérent à X lorsque tout voisinage de x rencontre X. L'adhérence de X est égale à l'ensemble des points qui lui sont adhérents. En effet : Intuitivement, l'adhérence d'une partie X contient tous les points de l'espace qui sont dans X ou qui sont trop près de X pour que l'on puisse y « bricoler » localement sans toucher à X. Dans un espace métrique (la topologie est issue d'une distance sur l'espace considéré), l'adhérence d'un ensemble X de E est l'ensemble contenant toutes les limites de suitesconvergentes dans E et formées des éléments de X. Caractère archimédien de L'adhérence d'un intervalle de Assez souvent on parle de On dit qu'une partie X d'un espace topologique E est dense lorsque son adhérence est l'espace E tout entier. Une telle partie se caractérise donc par le fait que tout ouvert non vide en contient un point. Ainsi, le caractère archimédien de Un point x de X est dense si {x} est dense. On l'appelle parfois aussi point générique. Intuitivement, les parties denses d'un espace sont donc des parties qui sont très grosses : on ne peut pas les éviter. Dans un espace métrique, on définit des boules ouvertes et des boules fermées, et la tentation est grande d'utiliser Néanmoins, c'est faux en général ; voyons l'exemple le plus simple : soit un ensemble E, avec au moins deux éléments. On définit une métrique dessus ainsi : la distance entre deux points distincts est 1. La boule ouverte de rayon 1 centrée en un point est donc ce point. La boule fermée de rayon 1 centrée en un point est donc l'espace entier. L'adhérence de la boule ouverte de rayon 1 centrée en un point est le point. Si dans le cadre d'espaces vectoriels sur Considérons l'ensemble Dans ce cas, l'adhérence de {0} est l'espace NB : en géométrie algébrique, ce genre de situation est très courant, car l'espace de base, le spectre d'anneau, vérifie souvent ce genre de propriétés ; en fait, cet exemple esthoméomorphe à Définitions [modifier]
 .
.Caractérisations [modifier]
Ensemble des points adhérents [modifier]
 , car celui-ci serait alors un voisinage de x ne rencontrant pas X ; donc il appartient à
, car celui-ci serait alors un voisinage de x ne rencontrant pas X ; donc il appartient à 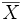 .
.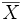 . Puisque x est dans U, x n'est pas dans
. Puisque x est dans U, x n'est pas dans 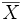 .
.Espaces métriques et suites [modifier]
Exemples [modifier]
 : l'ensemble des réels
: l'ensemble des réels  est l'adhérence de l'ensemble des rationnels
est l'adhérence de l'ensemble des rationnels  . En effet, tout ouvert contenant un irrationnel contient un rationnel. Tout irrationnel est donc dans l'adhérence de
. En effet, tout ouvert contenant un irrationnel contient un rationnel. Tout irrationnel est donc dans l'adhérence de  .
. , c'est l'intervalle fermé de mêmes bornes : l'adhérence de
, c'est l'intervalle fermé de mêmes bornes : l'adhérence de ![]-infty,a[](http://upload.wikimedia.org/math/1/c/5/1c5b9412c130c8defab790b16ed84156.png) est l'intervalle
est l'intervalle ![]-infty,a]](http://upload.wikimedia.org/math/8/0/8/808c7c08c83f0fc314006726dbc75c22.png) .
.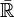 comme adhérence de
comme adhérence de  , mais cette notion veut simplement dire qu'on étend la notion de convergence aux valeurs infinies : ainsi la suite des entiers converge dans
, mais cette notion veut simplement dire qu'on étend la notion de convergence aux valeurs infinies : ainsi la suite des entiers converge dans  vers
vers  . Cela permet de donner un sens différent à la notion de divergence : ce qui diverge n'admet pas de limite, fût elle infinie. C'est le concept de droite réelle achevée.
. Cela permet de donner un sens différent à la notion de divergence : ce qui diverge n'admet pas de limite, fût elle infinie. C'est le concept de droite réelle achevée.Densité [modifier]
 fait que
fait que  est dense dans
est dense dans  .
.Pièges [modifier]
Boules ouvertes et boules fermées [modifier]
 dans ce cadre. Il est vrai que dans un certain nombre de cas, cela marche bien, notamment les
dans ce cadre. Il est vrai que dans un certain nombre de cas, cela marche bien, notamment les  avec la distance usuelle, et plus généralement pour la distance
avec la distance usuelle, et plus généralement pour la distance 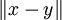 dans un espace vectoriel normé...
dans un espace vectoriel normé... ou
ou  normés de dimension finie, les propriétés de l'adhérence restent assez intuitives, il faut aussi se méfier des caractéristiques des espaces de dimension infinie.
normés de dimension finie, les propriétés de l'adhérence restent assez intuitives, il faut aussi se méfier des caractéristiques des espaces de dimension infinie.Un point c'est petit [modifier]
 des entiers naturels. On y définit une topologie (via des fermés) de la façon suivante :
des entiers naturels. On y définit une topologie (via des fermés) de la façon suivante :
 tout entier, ce qui signifie qu'on ne peut pas mettre le point 0 de côté pour travailler au voisinage d'un autre point. C'est un point dense/générique.
tout entier, ce qui signifie qu'on ne peut pas mettre le point 0 de côté pour travailler au voisinage d'un autre point. C'est un point dense/générique. par simple substitution des nombres premiers aux entiers non nuls.
par simple substitution des nombres premiers aux entiers non nuls.Voir aussi [modifier]
06:49 Publié dans Adhérence (mathématiques) | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
02/12/2010
Glossaire de topologie
Ceci est un glossaire de quelques termes utilisés en topologie. Ce glossaire est divisé en deux parties. La première traite des concepts généraux, et la seconde liste différents types d'espaces topologiques. Dans ce glossaire, tous les espaces sont supposés topologiques.Glossaire de topologie
Sommaire[masquer] |
Accessible : voir l'axiome de séparation T1. Adhérence Base ou base d'ouverts Base de voisinages : voir Système fondamental de voisinages. Boule Cauchy : voir Suite de Cauchy. Compact : voir les axiomes de recouvrement. Complet Complètement de Hausdorff : voir l'axiome de séparation T2½. Complètement normal : voir l'axiome de séparation T5. Complètement régulier : voir l'axiome de séparation T3½. Composante connexe Connexe, connexe par arcs : voir les notions de connexité. Continu Contractile : voir les notions de connexité. Convergent Dense Dérivé Discontinu Discret Distance Engendrée : voir Topologie engendrée. Espace de Fréchet Espace de Hausdorff : voir l'axiome de séparation T2. Espace de Kolmogorov : voir l'axiome de séparation T0. Espace de Tychonoff : voir l'axiome de séparation T3½. Espace métrique Espace polonais Espace topologique Faiblement normal : voir les axiomes de séparation. Fermé Fermeture : voir Adhérence. Filtre : Un filtre sur un ensemble E est un ensemble non vide de parties non vides de E qui est stable par sur-parties et intersections finies. Dans un espace topologique, les voisinages d'un point forment un filtre. Fin Fonctionnellement séparés Fréchet : voir l'axiome de séparation T1, ou le type d'espace vectoriel topologique dit de Fréchet. Frontière Fσ : Une partie d'un espace topologique est un Fσ si c'est une réunion dénombrables de fermés. Gδ : Une partie d'un espace topologique est un Gδ si c'est une intersection dénombrables d'ouverts. Grossière : voir Topologie grossière. Hausdorff : : voir l'axiome de séparation T2 ou Séparé. Homéomorphisme Homogène Homotopie Induite : voir Topologie induite. Intérieur Isolé : voir Point isolé. Kolmogorov : voir l'axiome de séparation T0 ou Espace de Kolmogorov. Limite Lindelöf : voir l'axiome de recouvrement Espace de Lindelöf. Localement : voir Propriété locale. Maigre Métrique : voir Espace métrique. Métrisable Moins fine : voir Topologie moins fine. Normal : voir les axiomes de séparation. Ouvert Paracompact : voir les axiomes de recouvrement. Parfait Parfaitement normal : voir les axiomes de séparation. Partition de l'unité Plus fine : voir Topologie plus fine. Point d'accumulation Point isolé Polonais : voir Espace polonais. Prébase Produit : voir Topologie produit. Quasi-compact : voir les axiomes de recouvrement. Quotient Raffinement Rare Recouvrement Relativement compact Régulier : voir l'axiome de séparation T3. Séparable Séparant Séparé : voir l'axiome de séparation T2. Simplement connexe : voir les notions de connexité. Sous-recouvrement Système fondamental de voisinages Suite de Cauchy T0, T1, T2, T2½, T3, T3½, T4, T5 : voir les axiomes de séparation. Topologie Topologie discrète Topologie engendrée Topologie grossière Topologie induite Topologie moins fine Topologie plus fine Topologie produit C'est la topologie la moins fine rendant continues toutes les projections Topologie quotient Topologique : voir Espace topologique. Totalement discontinu : voir les notions de connexité. Tychonoff : voir l'axiome de séparation T3½ ou Complètement régulier. Uniformisable : dont la topologie est induite par une structure d'espace uniforme ; voir l'axiome de séparation T3½ ou Complètement régulier. Valeur d'adhérence Voisinage Les espaces topologiques peuvent être qualifiés de différentes manières en termes de séparation, de recouvrements ou de connexité. Certains des termes employés ici peuvent avoir été définis autrement dans la littérature ancienne (voir l'histoire des axiomes de séparation). T0 ou de Kolmogorov : dans lequel pour tout couple de points distincts, il existe un voisinage de l'un qui ne contient pas l'autre. T1 ou accessible ou de Fréchet : dont tous les singletons sont fermés. T2 ou de Hausdorff ou séparé : dans lequel deux points distincts admettent toujours des voisinages disjoints. T2½ ou complètement de Hausdorff : dans lequel deux points distincts admettent toujours des voisinage fermés disjoints. Régulier : séparé et dont tout point admet une base de voisinages fermés. Complètement régulier ou de Tychonoff : séparé et uniformisable, ou encore : sous-espace d'un compact. Faiblement normal : complètement régulier et dans lequel deux ouverts disjoints quelconques ont deux voisinages fermés disjoints dont l'un est à base dénombrable. Normal : séparé et dans lequel deux fermés disjoints quelconques possèdent toujours des voisinages disjoints. Le lemme d'Urysohn garantit alors que ces deux fermés sontfonctionnellement séparés. Complètement normal : dont tout sous-espace est normal. Parfaitement normal : séparé et dont tout fermé est le lieu d'annulation d'une fonction continue réelle. Les axiomes de recouvrement traitent de l'existence de raffinements ou de sous-recouvrements particuliers pour un recouvrement quelconque de l'espace considéré. Paracompact : espace séparé dont tout recouvrement ouvert admet un raffinement localement fini. Lindelöf : dont tout recouvrement ouvert admet un sous-recouvrement dénombrable. Quasi-compact : dont tout recouvrement ouvert admet un sous-recouvrement fini. Compact : quasi-compact et séparé. σ-compact ou sigma-compact : recouvert par une famille dénombrable de parties compactes. Localement compact : séparé, et dont chaque point admet un système fondamental de voisinages compacts. Séquentiellement compact : dans lequel toute suite admet au moins une valeur d'adhérence. Les hypothèses de connexité décrivent la cohésion de l'espace ou de certains voisinages, ou l'existence de déformations (homotopies) entre certaines applications continues vers l'espace considéré. Connexe : qui n'est pas l'union disjointe de deux ouverts non vides. Localement connexe : dont chaque point admet un système fondamental de voisinages connexes. Totalement discontinu : dont les seules parties connexes sont les singletons. Connexe par arcs : dont tout couple de points (x,y) est relié par un chemin (ou arc), c'est-à-dire une application continue Localement connexe par arcs : dont chaque point admet un système fondamental de voisinages connexes par arcs. Simplement connexe : connexe par arcs et dans lequel toute application continue Contractile : pour lequel l'application identité de X est homotope à une application constante.Généralités [modifier]
A [modifier]
B [modifier]
C [modifier]
D [modifier]
 satisfaisant les propriétés suivantes :
satisfaisant les propriétés suivantes :
 .
.E [modifier]
F [modifier]
L'ensemble vide et l'espace sont donc des fermés. L'union de deux fermés est un fermé et l'intersection d'une famille quelconque de fermés est un fermé.G [modifier]
H [modifier]
 est une application continue
est une application continue ![H : Xtimes [0,1] to Y](http://upload.wikimedia.org/math/e/9/0/e90fbf798237734541171ebfcd412898.png) telle que
telle que  . Les applications f et g sont alors dites homotopes.
. Les applications f et g sont alors dites homotopes.I [modifier]
K [modifier]
L [modifier]
M [modifier]
N [modifier]
O [modifier]
P [modifier]
Q [modifier]
R [modifier]
 est un recouvrement dont chaque élément est inclus dans un élément de
est un recouvrement dont chaque élément est inclus dans un élément de  .
.S [modifier]
 de voisinages de ce point tel que tout autre voisinage de ce point contient un élément de
de voisinages de ce point tel que tout autre voisinage de ce point contient un élément de  .
.T [modifier]
 de parties d'un ensemble est celle dont les ouverts sont les réunions quelconques d'intersections finies d'éléments de
de parties d'un ensemble est celle dont les ouverts sont les réunions quelconques d'intersections finies d'éléments de  . L'ensemble
. L'ensemble constitue une prébase de la topologie engendrée.
constitue une prébase de la topologie engendrée.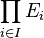 est la topologie engendrée par les
est la topologie engendrée par les  où un nombre fini d'éléments Ui sont des ouverts des espaces topologiques correspondants et les autres sont les espaces Ei correspondants.
où un nombre fini d'éléments Ui sont des ouverts des espaces topologiques correspondants et les autres sont les espaces Ei correspondants.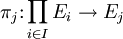 .
. une relation d'équivalence sur E, la topologie quotient sur l'ensemble quotient
une relation d'équivalence sur E, la topologie quotient sur l'ensemble quotient  est l'ensemble des parties de
est l'ensemble des parties de  dont lespréimages sont des ouverts de E. C'est la topologie la plus fine rendant continue la projection canonique, qui à tout élément de E associe sa classe d'équivalence..
dont lespréimages sont des ouverts de E. C'est la topologie la plus fine rendant continue la projection canonique, qui à tout élément de E associe sa classe d'équivalence..U [modifier]
V [modifier]
Propriétés d'espaces topologiques [modifier]
Axiomes de séparation [modifier]
Axiomes de recouvrement [modifier]
Connexité [modifier]
![p:[0,1]to X](http://upload.wikimedia.org/math/c/2/9/c2908a2ef3893f387f5f8042ee82d2b9.png) telle que p(0) = x et p(1) = y.
telle que p(0) = x et p(1) = y. est homotope à une application constante.
est homotope à une application constante.
21:39 Publié dans Glossaire, Glossaire de topologie | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook








































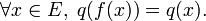
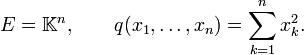

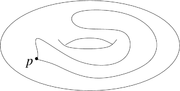


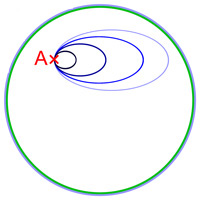



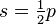 (
(





