03/12/2010
Groupe orthogonal
Groupe orthogonal
En mathématiques, plus précisément en algèbre linéaire, le groupe orthogonal d'une forme quadratique q est le groupe de ses automorphismes orthogonaux, muni de la loi decomposition. Si E est l'espace vectoriel sous-jacent, un automorphisme orthogonal pour q est un automorphisme f de l'espace vectoriel E (i.e. une application linéaire bijective de E dansE) laissant q invariante, c'est-à-dire vérifiant :
Le cas le plus étudié est (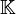 étant le corps des scalaires et n un entier naturel) :
étant le corps des scalaires et n un entier naturel) :
Le groupe orthogonal correspondant, noté  ou
ou  , s'identifie au groupe des matrices orthogonales et possède un sous-groupe particulier, le groupe spécial orthogonal.
, s'identifie au groupe des matrices orthogonales et possède un sous-groupe particulier, le groupe spécial orthogonal.
Sommaire[masquer] |
Généralités [modifier]
Le groupe orthogonal est compact, en effet on est en dimension finie et il est borné car tous les endomorphismes orthogonaux sont unitaires et fermé car c'est l'image réciproque du singleton identité par l'application continue  .
.
L'identité est un automorphisme orthogonal. L'ensemble des automorphismes orthogonaux est stable par composition et inversion. C'est donc un sous-groupe du groupe des automorphismes de E ; on l'appelle le groupe orthogonal associé à la forme quadratique q. Il est noté O(E,q).
Pour  , lorsque la forme quadratique q s'écrit : q(x) =
, lorsque la forme quadratique q s'écrit : q(x) =  xk2, on appelle matrices orthogonales les matrices des automorphismes orthogonaux. Une matrice M est donc orthogonale si et seulement si tMM = In, où tM est la matrice transposée de M. Par définition, le groupe orthogonal de degré n du corps
xk2, on appelle matrices orthogonales les matrices des automorphismes orthogonaux. Une matrice M est donc orthogonale si et seulement si tMM = In, où tM est la matrice transposée de M. Par définition, le groupe orthogonal de degré n du corps 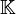 est le groupe des matrices orthogonales n ×n à coefficients dans
est le groupe des matrices orthogonales n ×n à coefficients dans 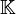 , muni de la multiplication matricielle. Il est habituellement noté
, muni de la multiplication matricielle. Il est habituellement noté  ou
ou  . C'est un sous-groupe du groupe général linéaire
. C'est un sous-groupe du groupe général linéaire 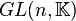 .
.
Toute matrice orthogonale a un déterminant égal à 1 ou -1. Les matrices orthogonales n × n de déterminant 1 forment un sous-groupe invariant de  appelé le groupe spécial orthogonal et noté
appelé le groupe spécial orthogonal et noté 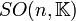 ou
ou 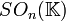 . Si la caractéristique de
. Si la caractéristique de 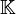 est 2, alors les groupes orthogonal et spécial orthogonal coïncident. Dans le cas contraire, l’indice de
est 2, alors les groupes orthogonal et spécial orthogonal coïncident. Dans le cas contraire, l’indice de 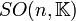 dans
dans  est 2.
est 2.
 et
et 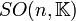 sont des groupes algébriques, car la condition que leurs matrices soient orthogonales, c’est-à-dire que leur transposée soit leur inverse, peut s’exprimer comme un ensemble d’équations polynomiales dans les éléments de ces matrices.
sont des groupes algébriques, car la condition que leurs matrices soient orthogonales, c’est-à-dire que leur transposée soit leur inverse, peut s’exprimer comme un ensemble d’équations polynomiales dans les éléments de ces matrices.
Nombres réels [modifier]
Sur le corps  des nombres réels,
des nombres réels,  et
et  sont généralement simplement notés
sont généralement simplement notés 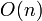 et
et  quand aucune confusion n’est possible. Ils forment deuxgroupes de Lie compacts de dimension
quand aucune confusion n’est possible. Ils forment deuxgroupes de Lie compacts de dimension  .
. 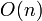 possède deux composantes connexes,
possède deux composantes connexes,  étant celle contenant la matrice identité.
étant celle contenant la matrice identité.
Géométriquement, 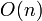 est isomorphe au groupe des isométries de
est isomorphe au groupe des isométries de  laissant invariant l’origine.
laissant invariant l’origine.  est isomorphe au groupe des isométries directes, ou rotations de
est isomorphe au groupe des isométries directes, ou rotations de  laissant l’origine invariante.
laissant l’origine invariante.
 est isomorphe (en tant que groupe de Lie) au cercle S1, formé des nombres complexes de module 1, muni de la multiplication. Cet isomorphisme lie le nombre complexe
est isomorphe (en tant que groupe de Lie) au cercle S1, formé des nombres complexes de module 1, muni de la multiplication. Cet isomorphisme lie le nombre complexe  à la matrice orthogonale
à la matrice orthogonale
Le groupe  est souvent appelé groupe des rotations (vectorielles) dans l'espace (tridimensionnel).
est souvent appelé groupe des rotations (vectorielles) dans l'espace (tridimensionnel).
En termes de topologie algébrique, pour n > 2, le groupe fondamental de  est le groupe cyclique d’ordre 2 et le groupe Spin Spin(n) est son revêtement universel. Pour n=2, le groupe fondamental est le groupe cyclique infini et son revêtement universel correspond à la droite des réels.
est le groupe cyclique d’ordre 2 et le groupe Spin Spin(n) est son revêtement universel. Pour n=2, le groupe fondamental est le groupe cyclique infini et son revêtement universel correspond à la droite des réels.
L’algèbre de Lie associée aux groupes de Lie 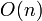 et
et  est formée des matrices n×n antisymétriques. Elle est généralement notée
est formée des matrices n×n antisymétriques. Elle est généralement notée 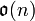 ou
ou  .
.
Nombres complexes [modifier]
Sur le corps  des nombres complexes,
des nombres complexes, 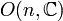 et
et  (là aussi notés
(là aussi notés 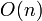 et
et  quand aucune confusion n’est possible) sont des groupes de Lie complexes de dimension
quand aucune confusion n’est possible) sont des groupes de Lie complexes de dimension  sur
sur  (le double sur
(le double sur  ).
). 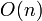 possède deux composantes connexes,
possède deux composantes connexes,  étant celle contenant la matrice identité. Pour
étant celle contenant la matrice identité. Pour  , ces groupes ne sont pas compacts.
, ces groupes ne sont pas compacts.
Pour n > 2, le groupe fondamental de  est le groupe cyclique d’ordre 2, tandis que le groupe fondamental de
est le groupe cyclique d’ordre 2, tandis que le groupe fondamental de  est le groupe cyclique infini.
est le groupe cyclique infini.
L’algèbre de Lie associée aux groupes de Lie 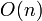 et
et  est formée des matrices complexes n×n antisymétriques.
est formée des matrices complexes n×n antisymétriques.
Voir aussi [modifier]
21:50 Publié dans Groupe orthogonal | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook








































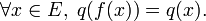
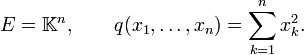

Les commentaires sont fermés.