11/12/2010
Nombre surréel et pseudo-réel
En mathématiques, les nombres surréels sont les éléments d'un corps1 qui inclut tous les nombres réels, ainsi que tous les ordinaux transfinis et leurs inverses, respectivement plus grands et plus petits que n'importe quel nombre réel positif. Les nombres surréels ont été introduits par John Conway et popularisés par Donald Knuth en 1974 dans son livre Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness (Les nombres surréels : comment deux ex-étudiants se mirent aux mathématiques pures et trouvèrent le bonheur total)2. Les nombres pseudo-réels, également introduits par Knuth, sont une sur-classe des nombres surréels, construit avec des conditions plus faibles que ces derniers.Nombre surréel et pseudo-réel
Sommaire[masquer] |
La construction des nombres surréels est similaire à la construction des nombres réels via les coupures de Dedekind, mais utilise le concept de récurrence transfinie. Elle repose sur la construction de nouveaux nombres représentés grâce à deux ensembles de nombres déjà construits, L et R (pour left et right, gauche et droite), éventuellement vides. Le nouveau nombre ainsi construit, noté Soient L et R deux ensembles de nombres surréels tels que : Alors, Étant donné un nombre surréel Pour éviter l'inflation d'accolades, on abrégera On constate qu'il s'agit d'une définition récurrente ; ce point sera explicité plus tard. Pour que la définition ci-dessus ait un sens, il est nécessaire de définir une relation binaire (notée ≤) sur les nombres surréels. Soient deux nombres surréels Là encore, cette définition est récurrente. Cette relation ne définit qu'un pré-ordre car elle n'est pas antisymétrique (on peut avoir Il s'agit d'une relation d'équivalence et l'ordre induit par Il est possible de montrer que ces opérations sont bien définies sur les nombres surréels. On peut les généraliser sans ambiguïté aux classes d'équivalence définie plus haut par : Finalement, on peut montrer que ces opérations sur les classes d'équivalence définissent un corps ordonné, avec la mention qu'elles ne forment pas un ensemble, mais une classe propre. Il est possible de montrer qu'il s'agit du plus grand corps ordonné, c'est-à-dire que tout corps ordonné peut y être plongé ; en particulier, ce corps est réel clos. À partir de maintenant, on ne fera plus la distinction entre un nombre surréel et sa classe d'équivalence et on appellera directement cette dernière nombre surréel. On l'a vu, les deux définitions précédentes utilisent le principe de récurrence. Il est possible d'utiliser la récurrence ordinaire, mais il est plus intéressant de prendre en compte larécurrence transfinie. Il est également nécessaire de créer un nombre surréel afin d'initier la récurrence ; Désignons par Nn, pour un ordinal n, l'ensemble des nombres surréels créés à l'étape n de la récurrence, en prenant Les nombres surréels créés en un nombre fini d'étapes (par un raisonnement de récurrence ordinaire, donc) sont assimilés aux rationnels dyadiques (c'est-à-dire les nombres p / 2n où p et n sont entiers). On définit de proche en proche : Mais aussi de nouveaux objets qui ne sont pas des ordinaux, comme On peut montrer que On obtient les nombres pseudo-réels (pseudo-real numbers selon la terminologie de Knuth) au lieu des nombres surréels si on enlève la condition qu'aucun élément de l'ensemble de droite ne peut être inférieur où égal à un élément quelconque de l'ensemble de gauche. Les nombres surréels forment un sous-ensemble des nombres pseudo-réels. Ces nombres pseudo-réels peuvent s'interpréter comme les valeurs de certains jeux. Ils sont à la base de la théorie des jeux combinatoires initiée par John Conway.Nombres surréels [modifier]
Présentation [modifier]
 , sera plus grand que tout nombre de L et plus petit que tout nombre de R, selon un ordre qui sera défini plus loin. Pour que cela soit possible, on impose une restriction sur L et R : il faut que chaque nombre de L soit plus petit que chaque nombre de R.
, sera plus grand que tout nombre de L et plus petit que tout nombre de R, selon un ordre qui sera défini plus loin. Pour que cela soit possible, on impose une restriction sur L et R : il faut que chaque nombre de L soit plus petit que chaque nombre de R.Définition [modifier]
 et tout
et tout  ,
, 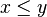
 est un nombre surréel.
est un nombre surréel. , on appelle XL et XR l'ensemble de gauche et l'ensemble de droite de X, respectivement.
, on appelle XL et XR l'ensemble de gauche et l'ensemble de droite de X, respectivement. en
en  ,
, 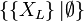 en
en  et
et 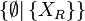 en
en 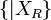 .
.Ordre [modifier]
 et
et  .
.  si et seulement si pour tout
si et seulement si pour tout 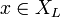 , on ne rencontre jamais
, on ne rencontre jamais  et si pour tout
et si pour tout  , on n'a jamais
, on n'a jamais  .
. et
et 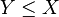 sans que X = Y, c'est le cas par exemple avec
sans que X = Y, c'est le cas par exemple avec 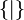 et
et 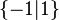 ). Pour contourner ce problème, on définit une nouvelle relation sur les nombres surréels :
). Pour contourner ce problème, on définit une nouvelle relation sur les nombres surréels : .
.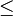 sur les classes d'équivalences est un ordre total, une classe d'équivalence pouvant alors être considérée comme un nombre unique.
sur les classes d'équivalences est un ordre total, une classe d'équivalence pouvant alors être considérée comme un nombre unique.Opérations [modifier]

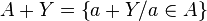 et
et 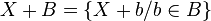 .
.
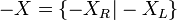
 .
.
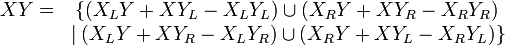
 .
.
Construction [modifier]
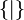 peut être défini grâce à l'ensemble vide et répond à cette fonction.
peut être défini grâce à l'ensemble vide et répond à cette fonction. . On appelle date de naissance d'un nombre surréel Xle plus petit ordinal n tel que
. On appelle date de naissance d'un nombre surréel Xle plus petit ordinal n tel que 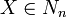 .
.Exemples [modifier]

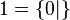 et
et 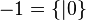
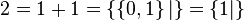 et
et 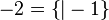
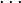
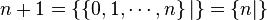 .
.

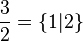

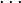
 qui est plus grand que n'importe quel nombre entier
qui est plus grand que n'importe quel nombre entier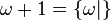
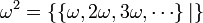

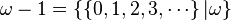


 qui est strictement positif mais inférieur à tout
qui est strictement positif mais inférieur à tout  , pour n entier positif.
, pour n entier positif.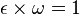 .
.Nombres pseudo-réels [modifier]
Voir aussi [modifier]
Liens externes [modifier]
Bibliographie [modifier]
Notes et références [modifier]
11:45 Publié dans Nombre surréel et pseudo-réel | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
08/12/2010
Les métamorphoses du calcul , Une étonnante histoire de mathématiques
19:29 Publié dans Les métamorphoses du calcul, Livres | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Dans la jungle des nombres premiers
19:27 Publié dans Dans la jungle des nombres premiers | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Histoire des nombres
19:25 Publié dans Histoire des nombres, Livres | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
La beauté des mathématiques
19:24 Publié dans La beauté des mathématiques | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Nicolas Bourbaki : histoire d'un génie des mathématiques qui n'a jamais existé
19:22 Publié dans Livres, Nicolas Bourbaki : histoire d'un génie des mathéma | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Hasard et complexité en mathématiques : la quête d'oméga
19:20 Publié dans Hasard et complexité en mathématiques : la quête d, Livres | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Mathématiques et physique
Mathématiques et physiqueBernard Diu
19:18 Publié dans Livres, Mathématiques et physique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Les systèmes complexes , Mathématiques et biologie
19:17 Publié dans Les systèmes complexes , Mathématiques et biologie, Livres | Lien permanent | Commentaires (1) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Les énigmes mathématiques du 3ème millénaire
19:15 Publié dans Les énigmes mathématiques du 3ème millénaire, Livres | Lien permanent | Commentaires (1) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Les inattendus mathématiques , Art, casse-tête, paradoxes
19:13 Publié dans Les inattendus mathématiques , Art, casse-tête, pa, Livres | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Jacques-Louis Lions , Un mathématicien d'exception
19:12 Publié dans Jacques-Louis Lions , Un mathématicien d'exception, Livres | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Un mathématicien aux prises avec le siècle
19:10 Publié dans Livres, Un mathématicien aux prises avec le siècle | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Evariste Galois, mathématicien humaniste et révolutionnaire
19:08 Publié dans Evariste Galois, mathématicien humaniste et révolu | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Ecole d’été 2011
MODULES DE COURBES ET THEORIE DE GROMOV-WITTEN 20 juin - 8 juillet 2011 Les deux premières semaines auront comme thème les modules des courbes (première semaine) et la théorie de Gromov-Witten (deuxième semaine). Les cours seront adaptés à un public large de mathématiciens plus ou moins expérimentés venant d’horizons très divers. Ces deux semaines auront une structure similaire : au cours des après-midi pendant toute la semaine il se déroulera un seul cours principal sur le thème de la semaine. Parallèlement, dans les séances du matin, nous avons programmé trois mini-cours par semaine introduisant des sujets de recherche majeurs. Le programme des après-midi laissera le temps aux discussions, aux exercices et aux séminaires organisés par les étudiants. Cours de l’après-midi : Carel FABER (tbc) et Dimitri ZVONKINE : Les espaces de modules des courbes stables. Mini-cours du matin : Cours de l’après-midi : Barabara FANTECHI : Théorie de Gromov-Witten Mini-cours du matin : Comité scientifique : Barbara FANTECHI (SISSA), Rahul PANDHARIPANDE (Princeton), Yongbin RUAN (University of Michigan). Lieu : Amphi Chabauty situé au rez-de-chaussée de l’Institut Fourier. Organisateurs : Samuel Boissière (Université de Nice), Alessandro Chiodo (Université de Grenoble), Laurent Manivel (Université de Grenoble). Cette école est financée par l’Institut Fourier, le CNRS, GRIFGA, et le projet ANR "Des nouvelles symétries pour la théorie de Gromov-Witten". Source : Ecole d’été 2011
Première semaine
![]() Gavril FARKAS
Gavril FARKAS ![]() Ravi VAKIL
Ravi VAKIL ![]() Rahul PANDHARIPANDE
Rahul PANDHARIPANDEDeuxième semaine
![]() Alessandro CHIODO et Yongbin RUAN
Alessandro CHIODO et Yongbin RUAN ![]() Tom COATES (tbc) et Alessio CORTI (tbc)
Tom COATES (tbc) et Alessio CORTI (tbc) ![]() Davesh MAULIK
Davesh MAULIKTroisième semaine
CONFERENCE SUR LA THÉORIE DE GROMOV-WITTEN
09:45 Publié dans Ecole d’été 2011 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Théorie des nombres algébriques
Théorie des nombres algébriques
Prof. Eva Bayer Fluckiger
Christian Wuthrich
Master en Mathématiques
Semestre d'hiver 2005/6
- Voici une version préliminaire d'un polycopié pour le cours. Je tiens à remercier Sébastien Nobs pour avoir pris les notes. Elles ne sont pas encore entièrement corrigées. ps - pdf
- Rappels (Prerequis pour le cours) : ps - pdf
- Littérature (une liste de références pour le cours) : ps - pdf
- Exercices série 1 : ps - pdf; Corrigée ps - pdf
- Exercices série 2 : ps - pdf; Corrigée ps - pdf
- Exercices série 3 : ps - pdf; Corrigée ps - pdf
- Exercices série 4 : ps - pdf; Corrigée ps - pdf
- Exercices série 5 : ps - pdf; Corrigée ps - pdf
- Exercices série 6 : ps - pdf; Corrigée ps - pdf
- Exercices série 7 : ps - pdf; Corrigée ps - pdf
- Exercices série 8 : ps - pdf; Corrigée ps - pdf
- Exercices série 9 : ps - pdf; Corrigée ps - pdf
- Exercices série 10 : ps - pdf; Corrigée ps - pdf
- Exercices série 11 (modifiée): ps - pdf Corrigée ps - pdf
- Exercices série 12 : ps - pdf Corrigée ps - pdf
- Résumé des exercices ps - pdf
- La liste complète de tous les exercices et toutes les solution ps - pdf
-
Lien divers :
- La page de J. S. Milne contient les notes d'un cours sur la théorie des nombres algébriques.
- Le cours de William Stein se trouve ici.
- Le Number Theory Web et
- les directories de Google contiennent beaucoup de lien vers des pages intéressantes.
- Des biographies de mathématiciens.
09:44 Publié dans Théorie des nombres algébriques | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Décomposition de Dunford
En mathématiques, la décomposition de Dunford s'inscrit dans la problématique de la réduction d'endomorphisme. Cette approche consiste à décomposer l'espace vectoriel en une somme directe de sous-espaces stables où l'expression de l'endomorphisme est plus simple. Ce n'est pas une réduction dans le sens où elle n'est pas maximale. C'est-à-dire qu'il est parfois possible de pousser la décomposition en sous-espaces vectoriels stables plus petits. Elle suppose comme hypothèses que l'espace vectoriel est de dimension finie et que le polynôme minimal est scindé, c'est-à-dire qu'il s'exprime comme produit de polynômes du premier degré. C'est toujours le cas si le corps est algébriquement clos, comme par exemple celui des nombres complexes. Dans le cas ou la propriété n'est pas vérifiée, alors il est possible d'étendre le corps à sa clôture algébrique, et l'espace vectoriel à ce nouveau corps et dans ce contexte d'appliquer la décomposition de Dunford. Le corps des nombres réels se voit par exemple très généralement étendre pour permettre une application de cette décomposition. La décomposition de Dunford prouve que tout endomorphisme est la somme d'un endomorphisme diagonalisable et d'un endomorphisme nilpotent, les deux endomorphismes commutant et étant uniques. Cette décomposition est largement appliquée. Elle permet un calcul matriciel souvent rapide. C'est néanmoins souvent sous la forme de la réduction de Jordan qu'elle est utilisée.Décomposition de Dunford
Sommaire[masquer] |
Le théorème de diagonalisabilité permet de déterminer la structure de u quand il admet un polynôme annulateur scindé à racines simples. La décomposition de Dunford s'applique à un cas plus général. Théorème de la décomposition de Dunford — Soit u un endomorphisme d'un espace vectoriel E. Si u admet un polynôme minimal scindé, alors il peut s'écrire sous la forme u=d+n avec d un endomorphisme diagonalisable et n un endomorphisme nilpotent tels que d et n commutent (c'est-à-dire dn=nd). De plus d et n sont des polynômes en u et sont uniques. L'idée initiale de cette approche est donnée par la proposition suivante, démontrée dans l'article sur les polynômes d'endomorphismes dans le paragraphe sur les polynômes minimaux : Or, si le polynôme minimal est scindé, il peut s'écrire sous la forme: Si l'on note Ces considérations permettent de démontrer la décomposition de Dunford. Elle permettent de plus de démontrer les propriétés suivantes : Un résultat notoire de l'approche par les polynômes d'endomorphismes réside dans le fait que la connaissance du polynôme minimal permet de définir une algorithmique fournissant à la fois les projecteurs sur les espaces caractéristiques mais aussi la composante diagonale et nilpotente de l'endomorphisme. En dimension finie le théorème de Cayley-Hamilton assure que χu(u) = 0 où χu désigne le polynôme caractéristique de u. Si χu est scindé alors u est décomposable. C'est en particulier le cas pour tout endomorphisme d'un espace de dimension finie sur un corps algébriquement clos ( La décomposition de Dunford, combinée avec la décomposition de Frobenius permet d'obtenir la réduction de Jordan en dimension finie. En effet, d et n commutent donc les sous-espaces propres de d sont stables par n. La restriction de n au sous-espace propre admet une matrice formée de blocs de Jordan nilpotents ce qui donne, en ajoutant λIp, des blocs de Jordan pour d+n dans une base adaptée. Ainsi on obtient une matrice diagonale par blocs formée de blocs de Jordan en utilisant l'union de ces bases.Théorème [modifier]
Démonstration [modifier]
Via les sous-espaces caractéristiques [modifier]
 une décomposition en facteurs de degré supérieur ou égal à 1 et premiers deux à deux du polynôme minimal
une décomposition en facteurs de degré supérieur ou égal à 1 et premiers deux à deux du polynôme minimal  d'un endomorphisme u. Alors la suite des noyaux
d'un endomorphisme u. Alors la suite des noyaux  est une décomposition de l'espace E en somme directe de sous-espaces stables par l'endomorphisme.
est une décomposition de l'espace E en somme directe de sous-espaces stables par l'endomorphisme.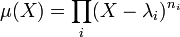
 le noyau de l'endomorphisme
le noyau de l'endomorphisme  , alors le paragraphe précédent nous indique que la suite
, alors le paragraphe précédent nous indique que la suite 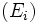 forme une somme directe de l'espace E de sous-espaces non réduits à 0 et stables par l'endomorphisme. On appelle ces sous-espaces les sous-espaces caractéristiques. Nous avons alors les trois propriétés suivantes:
forme une somme directe de l'espace E de sous-espaces non réduits à 0 et stables par l'endomorphisme. On appelle ces sous-espaces les sous-espaces caractéristiques. Nous avons alors les trois propriétés suivantes:
 est la somme d'une homothétie de rapport
est la somme d'une homothétie de rapport  et d'un endomorphisme nilpotent d'ordre
et d'un endomorphisme nilpotent d'ordre 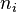 .
.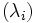 est la suite des valeurs propres (i.e. le spectre de u). Les sous-espaces propres associés sont inclus dans les sous-espaces caractéristiques.
est la suite des valeurs propres (i.e. le spectre de u). Les sous-espaces propres associés sont inclus dans les sous-espaces caractéristiques.
Via les projecteurs [modifier]
Cas d'applications [modifier]
 notamment).
notamment).Réduction de Jordan [modifier]
09:42 Publié dans Décomposition de Dunford | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Décomposition de Frobenius
On considère un K-espace vectoriel E de dimension finie et un endomorphisme u de cet espace. La décomposition de Frobenius est la décomposition de l'espace E en somme directe de sous-espaces cycliques. Cette décomposition fait apparaitre les facteurs invariants de l'endomorphisme u. Combinée avec la décomposition de Dunford (dans un ordre ou dans l'autre), on obtient la réduction de Jordan. Contrairement à ces dernières, la décomposition de Frobenius peut s'effectuer sur un corps quelconque, on ne suppose pas ici que K est algébriquement clos.Décomposition de Frobenius
Sommaire[masquer] |
Soit x un vecteur de E, l'ensemble Soit x un vecteur de E, l'ensemble Soit La dimension de Sx est égale au degré du polynôme πu,x. Pour tout vecteur x de E, le polynôme conducteur πu,x divise le polynôme minimal πu de u. On dira que x est u-maximum lorsque πu,x = πu. La décomposition de Frobenius est basée sur les deux résultats non triviaux suivants : En procédant par récurrence, on parvient alors à la : Il existe une suite de vecteurs Les polynômes Deux endomorphismes sont semblables ssi ils ont les mêmes facteurs invariants. Les endomorphismes induits par u ont des propriétés spécifiques, ce sont des endomorphismes cycliques dont il ne reste plus qu'à étudier les propriétés spécifiques. On dit que u est un endomorphisme cyclique ssi il existe un élément x de E tel que Sx = E. On peut caractériser les endomorphismes cycliques de plusieurs manières : un endomorphisme u de E est cyclique si et seulement siPolynôme conducteur [modifier]
![I_x={Pin K[X]mid P(u)(x)=0}](http://upload.wikimedia.org/math/a/8/d/a8d881ed5da882b9531e475451512abb.png) est un idéal non nul de K[X], il est donc engendré par un unique polynôme normalisé πu,x appelépolynôme conducteur de u en x, ou parfois polynôme minimal local de u en x.
est un idéal non nul de K[X], il est donc engendré par un unique polynôme normalisé πu,x appelépolynôme conducteur de u en x, ou parfois polynôme minimal local de u en x.Sous-espace cyclique [modifier]
![S_x={P(u)(x)mid Pin K[X]}](http://upload.wikimedia.org/math/9/b/0/9b0380de53edf0c2394f073ec285e463.png) est un sous-espace vectoriel de E stable par u appelé sous-espace u-cyclique engendré par x, ou encore clôture u-stable de x.
est un sous-espace vectoriel de E stable par u appelé sous-espace u-cyclique engendré par x, ou encore clôture u-stable de x.![Pin K[X]](http://upload.wikimedia.org/math/4/f/a/4facb36da11821b818abd66b424a6a76.png) , on a
, on a 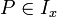 si et seulement si
si et seulement si  . Ainsi le polynôme conducteur πu,x est le polynôme minimal de l'endomorphisme induit par u sur le sous-espace Sx.
. Ainsi le polynôme conducteur πu,x est le polynôme minimal de l'endomorphisme induit par u sur le sous-espace Sx.Vecteurs u-maximums [modifier]
Décomposition de Frobenius [modifier]
 de E telle que
de E telle que

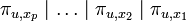
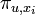 ne dépendent pas du choix des vecteurs xi, ce sont les facteurs invariants de u. Le polynôme minimal
ne dépendent pas du choix des vecteurs xi, ce sont les facteurs invariants de u. Le polynôme minimal 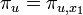 et le polynôme caractéristique
et le polynôme caractéristique  .
.Endomorphisme cyclique [modifier]
Applications [modifier]
Références [modifier]
Voir aussi [modifier]
09:34 Publié dans Décomposition de Frobenius | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Module sur un anneau
En mathématiques, au sein des structures algébriques, « un module est à un anneau ce qu'un espace vectoriel est à un corps »1 : pour un espace vectoriel, l'ensemble des scalairesforme un corps tandis que pour un module, cet ensemble est seulement muni d'une structure d'anneau (unitaire, mais non nécessairement commutatif). Une partie des travaux en théorie des modules consiste à retrouver les résultats spectaculaires de la théorie des espaces vectoriels, quitte pour cela à travailler avec des anneaux plus maniables, comme les anneaux principaux. Par ailleurs, la notion de module sur un anneau généralise celle d'idéal.Module sur un anneau
Sommaire[masquer] |
Certaines propriétés vraies pour les espaces vectoriels ne sont plus vraies pour les modules. Par exemple l'existence d'une base n'y est plus assurée, et on ne peut pas nécessairement y développer de théorie de la dimension, même dans un module engendré par un nombre fini d'éléments. Les modules ne sont pas une généralisation inutile. Ils apparaissent naturellement dans beaucoup de situations algébriques ou géométriques. Un exemple simple est un module sur l'anneau des fonctions infiniment différentiables sur un ouvert : il est naturel de ne pas pouvoir y faire de division, puisqu'il vaut mieux éviter de diviser par 0. De la même façon, il est naturel de considérer un module sur l'anneau des polynômes à une ou plusieurs variables. Si A est un anneau (unitaire), et (M , +) un groupe commutatif. Si de plus, M est muni d'une loi externe alors (M, + , Ce qui a été défini ici est un A-module à gauche, car, dans la loi externe, les éléments de A sont placés à gauche. On pourra définir de même un A-module à droite. Il est important de remarquer que les structures de module à gauche et à droite ne diffèrent pas uniquement par leur écriture : si les deux premiers axiomes sont les mêmes, le troisième s'écrit Par contre, le petit raisonnement ci-dessus montre que, si l'on "inverse" la loi de A, un module à droite peut être vu comme un module à gauche. Plus précisément, notons Aop l'anneau "opposé" à A, c'est-à-dire le groupe abélien A muni de la multiplication définie par aopbop = ba, si aop et bop désignent a et b vus comme éléments de Aop. Alors, si M est un A-module à gauche, M peut être vu comme un Aop-module à droite, où l'action de Aop est définie par a.m = m.aop. Ceci justifie que dans la suite, on puisse se restreindre à l'étude des modules à gauche. Cette loi est la seule qui munisse un groupe abélien d'une structure de Le premier axiome montre que, pour Réciproquement, la donnée d'un morphisme d'anneau unitaire Un tel morphisme A Ceci est une généralisation de ce que l'on trouve en représentation des groupes, où l'on définit une représentation d'un groupe G vers un espace vectoriel sur un corps K comme un morphisme de l'algèbre du groupe K[G] vers End(V), autrement dit, où l'on donne une structure de K[G]-module à V. Soit E un A-module à gauche, et M une partie de E. On dit que M est un sous-module (à gauche) si les conditions suivantes sont respectées : Autrement dit, un sous-module est une partie linéairement stable. Exemples Une application linéaire f entre deux modules M et N sur un même anneau A est une fonction qui conserve la structure de module, i.e qui vérifie : Autrement dit, une application linéaire est un morphisme de modules. Si f est bijective, on dit de plus que f est un isomorphisme. Si les modules de départ et d'arrivée M et N sont identiques, on dit que f est un endomorphisme. Si f est à la fois un endomorphisme et un isomorphisme, on dit que c'est un automorphisme. Le noyau d'une application linéaire f est l'ensemble des éléments x de M qui vérifient f(x) = 0. C'est un sous-module de M et il est noté Ker f. On peut également définir l'image d'une application linéaire Im f = f(M) qui est un sous-module de N. Comme dans le cas des groupes ou des anneaux, un morphisme de A-modules Si on considère une famille de module ( Le module ainsi défini s'appelle le module produit. Les projections Soit C'est un sous-module de Si M est un module, et Dans ce cas, la somme On dit qu'un A-module est de type fini s'il est engendré sur A par un nombre fini d'éléments. On a alors On dit qu'un module est de présentation finie s'il est le quotient d'un An par un sous-module de type fini. Un module de présentation finie est en particulier de type fini. La réciproque est vraie lorsque A est noethérien. Pour un module M de présentation finie, tout homomorphisme surjectif On dit qu'un A-module est libre s'il possède une base sur A (voir Module libre). Si M est de type fini et libre, il existe alors un isomorphisme entre M et An, où n est le cardinal de la base. Les modules sont un outil indispensable pour passer de propriétés géométriques à des propriétés fonctionnelles, ou ressemblant à des propriétés fonctionnelles. Ainsi, au lieu de voir unevariété différentiable comme une partie d'un espace concret ou abstrait, on va plutôt considérer une classe de fonctions sur cette variété et déclarer que cette classe est la classe des fonctions différentiables sur la variété -- il faudra satisfaire des conditions appropriées de compatibilité. On pourra ainsi traduire les propriétés géométriques de la variété par des propriétés algébriques de la classe de fonctions que nous avons déclarées comme fonctions différentiables. Mieux que des fonctions, on peut considérer des champs sur une variété différentiable. Le cas le plus simple est celui des champs tangents différentiables à une variété. Pensons par exemple aux champs de vecteurs tangents à la sphère unité dans un espace de dimension 3. Il s'agit bien d'un module sur l'anneau des fonctions différentiables sur la sphère : si on multiplie un champ différentiable tangent à la sphère par une fonction différentiable, on trouve bien un champ différentiable. Ce module est engendré par la restriction à la sphère des projections tangentes des champs constants égaux aux vecteurs de base de l'espace - cela nous fait trois champs. Mais on peut montrer que ces trois champs ne sont pas indépendants, et on peut même montrer qu'il n'existe aucun choix de deux champs tangents qui pourraient engendrer le module des champs tangents à la sphère et différentiables. On a là l'exemple le plus simple d'un module de type fini, c'est-à-dire engendré par un nombre fini de ses éléments, mais qui ne possède pas de base. La correspondance systématique entre objet géométrique et objet de nature fonctionnelle est dominante en géométrie algébrique. En effet, si V est l'ensemble des solutions communes d'un système d'équations polynomiales en n variables, on peut étudier l'ensemble des polynômes qui s'annulent sur V; ce sera un idéal de l'anneau des polynômes à n variables, et donc en particulier, un module sur cet anneau. Il est possible de retrouver nombre de propriétés géométrique de V en étudiant les propriétés de cet idéal: points singuliers, dimension, recherche de droites incluses dans V, et ainsi de suite. Cette faculté d'exprimer les propriétés d'objets géométriques au moyen d'espaces de fonctions sur ces objets est à la base de la géométrie non commutative: les espaces de fonctions sur des objets géométriques usuels sont des anneaux commutatifs pour la multiplication (et même souvent des algèbres, c'est-à-dire des anneaux munis également d'une structure compatible d'espace vectoriel). La démarche de la géométrie non commutative consiste à explorer ce que seraient des objets géométriques sur lesquels vivraient des "fonctions" formant un anneau ou une algèbre non commutative, et c'est pour cette raison que le cas des anneaux non commutatifs et des modules sur des anneaux non commutatifs est très important actuellement.Comparaison avec la structure d'espace vectoriel [modifier]
Définitions [modifier]
Module à gauche, module à droite [modifier]
 de A × M dans M vérifiant, pour tous éléments a et b de A et x, y de M :
de A × M dans M vérifiant, pour tous éléments a et b de A et x, y de M :
 (distributivité de
(distributivité de  par rapport à l'addition dans M)
par rapport à l'addition dans M)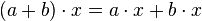 (distributivité de
(distributivité de  par rapport à l'addition dans A)
par rapport à l'addition dans A)


 ) est un A-module à gauche.
) est un A-module à gauche.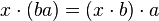 . Si l'on transcrivait naïvement cette égalité en écrivant les éléments de A gauche, on obtiendrait
. Si l'on transcrivait naïvement cette égalité en écrivant les éléments de A gauche, on obtiendrait 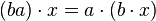 , ce qui, si A n'est pas commutatif, ne revient pas au même que l'axiome qui donne la structure de module à gauche.
, ce qui, si A n'est pas commutatif, ne revient pas au même que l'axiome qui donne la structure de module à gauche.Exemples [modifier]
 -module.
-module. -module pour la loi externe définie par :
-module pour la loi externe définie par : avec n termes x
avec n termes x
 l'opposé de
l'opposé de 
 -module. Il y a donc équivalence entre la notion de
-module. Il y a donc équivalence entre la notion de  -module et celle de groupe abélien.
-module et celle de groupe abélien.
 qui confère à M une structure de End(M)-module .
qui confère à M une structure de End(M)-module . à n dimensions est un module à gauche sur
à n dimensions est un module à gauche sur 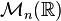 via la multiplication matricielle.
via la multiplication matricielle.
 sur un corps
sur un corps 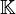 peut être considéré comme un module sur l'anneau principal
peut être considéré comme un module sur l'anneau principal ![mathbb K[X]](http://upload.wikimedia.org/math/1/1/c/11cf18672fa8c102e5d2ec8bdfe203c8.png) , et par ce biais la majeure partie des propriétés de l'algèbre linéaire peut être démontrée2.
, et par ce biais la majeure partie des propriétés de l'algèbre linéaire peut être démontrée2.
Cette structure de module est la suivante : étant donné 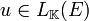 fixé, pour tout
fixé, pour tout ![left( p, x right) in mathbb K[X]times E](http://upload.wikimedia.org/math/4/f/e/4fe3999552e4b77d3dcb48d887246383.png) , on pose
, on pose 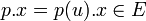 , avec
, avec 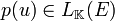 car cet ensemble a une structure d'algèbre sur
car cet ensemble a une structure d'algèbre sur 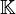 .
.Lien avec la théorie des représentations [modifier]
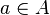 , l'application
, l'application 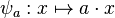 est un endomorphisme du groupe M. Les trois axiomes suivants traduisent quant à eux le fait que l'application
est un endomorphisme du groupe M. Les trois axiomes suivants traduisent quant à eux le fait que l'application  est un morphisme (unitaire) de l'anneau A dans l'anneau des endomorphismes de M, noté End(M).
est un morphisme (unitaire) de l'anneau A dans l'anneau des endomorphismes de M, noté End(M).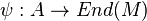 fournit à M une structure de A-module (à gauche) via la loi
fournit à M une structure de A-module (à gauche) via la loi  . Une structure de A-module est donc équivalente à la donnée d'un morphisme
. Une structure de A-module est donc équivalente à la donnée d'un morphisme  .
. End(M) est appelé une représentation de A sur le groupe abélien M. Une représentation est dite fidèle si elle est injective. En termes de module, cela signifie que si pour tout
End(M) est appelé une représentation de A sur le groupe abélien M. Une représentation est dite fidèle si elle est injective. En termes de module, cela signifie que si pour tout 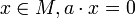 , alors a = 0.
, alors a = 0.Sous-module [modifier]
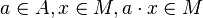
 , tout sous-groupe est aussi un sous-module.
, tout sous-groupe est aussi un sous-module.Applications linéaires [modifier]

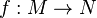 donne lieu à un isomorphisme
donne lieu à un isomorphisme 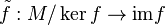 , défini par
, défini par 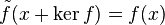
Opérations sur les modules [modifier]
Produits de modules [modifier]
 sur un même anneau A, on peut munir l'ensemble produit
sur un même anneau A, on peut munir l'ensemble produit 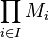 d'une structure de module en définissant les lois suivantes :
d'une structure de module en définissant les lois suivantes :
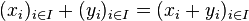

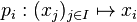 sont alors des applications linéaires surjectives. Un exemple important de produit de modules est celui où tous les modules facteurs sont identiques à un même module M ; leur produit MI n'est alors autre que l'ensemble des applications de I dans M.
sont alors des applications linéaires surjectives. Un exemple important de produit de modules est celui où tous les modules facteurs sont identiques à un même module M ; leur produit MI n'est alors autre que l'ensemble des applications de I dans M.Somme directe de modules [modifier]
 une famille de A-modules, on note leur produit
une famille de A-modules, on note leur produit 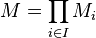 . L'ensemble E des éléments de M dont toutes les composantes sauf un nombre fini sont nulles est appelé somme directe externe de la famille de modules
. L'ensemble E des éléments de M dont toutes les composantes sauf un nombre fini sont nulles est appelé somme directe externe de la famille de modules  et il est noté :
et il est noté :
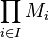 . Dans le cas où I est fini, la somme directe E et le produit M sont évidemment confondus.
. Dans le cas où I est fini, la somme directe E et le produit M sont évidemment confondus.Intersection et somme de sous-modules [modifier]
 est une collection de sous-modules de M, on dit que la famille est en somme directe si :
est une collection de sous-modules de M, on dit que la famille est en somme directe si :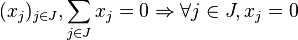
 , appelée somme directe interne, est isomorphe à la somme directe externe et elle est également notée
, appelée somme directe interne, est isomorphe à la somme directe externe et elle est également notée  .
.Propriétés de finitude [modifier]
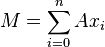 .
.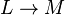 avec L de type fini admet un noyau de type fini3.
avec L de type fini admet un noyau de type fini3.Applications des modules [modifier]
Notes et références [modifier]
Voir aussi [modifier]
09:32 Publié dans Module sur un anneau | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Propriétés métriques des droites et plans
En géométrie euclidienne, c'est-à-dire dans le plan et l'espace muni d'une distance et d'un produit scalaire, les droites et les plans possèdent des propriétés métriques permettant de les caractériser grâce à un point et un vecteur, dit normal. On peut aussi calculer la distance qui les sépare d'un point donné ou bien calculer celle qui sépare deux droites ou deux plans. On peut aussi calculer l'angle formé par deux droites ou deux plans. Dans cet article, on a muni le plan ou l'espace d'un repère orthonormal dans lequel sont exprimées toutes les coordonnées. Toute droite du plan y possède une équation du type ux + vy + h = 0 où (u , v) est différent de (0 , 0) et tout plan de l'espace possède une équation de la forme ux + vy + wz + h = 0 où (u, v, w) est différent de (0, 0, 0).Propriétés métriques des droites et plans
Sommaire[masquer]
|
Soit M(x,y) un point de la droite D dont une équation dans un repère orthonormal est donnée par : et M0(x0,y0) un point spécifique de D, On a : En retranchant (2) à (1) on obtient : En notant La droite d'équation ux + vy + h = 0 est donc orthogonale au vecteur Soit un point M(x,y) et un vecteur La droite D, passant par M0(x0,y0) et orthogonale à Soit H la projecté de M(x,y) sur D avec La droite perpendiculaire à D et passant par M étant orientée suivant la direction du vecteur En valeur absolue : Pour v non nul, la droite D d'équation ux + vy + h = 0 possède une équation sous la forme mx + b = y avec et La pente d'une droite est le réel L'angle α représente l'angle entre l'axe des abscisses et la droite D. Dans le repère L'équation (1) s'écrit : Soit D et D' deux droites d'équations L'angle formé par les deux droites est connu par sa tangente : le plan Soit On calculera La distance MH est donnée par Le plan étant défini par l'équation ux + vy + wz + h = 0, les droites perpendiculaires au plan sont toutes les droites ayant comme vecteur directeur dans le cas où aucun des réels, u, v, w, n'est nul. Si un seul des des réels est nul , par exemple u= 0, le système devient : Si deux réels sont nuls, par exemple u=v=0, le système devient : Soient la droite (D0) passant par M0(x0,y0,z0) et de direction le vecteur Si les vecteurs L'aire de la base du solide est donnée par La distance entre les deux droites est alors égale à Si les vecteurs sont colinéaires alors les deux droites sont parallèles et la distance qui les sépare correspond à la distance qui sépare le point M1 de la droite D0. Soit M(x,y,z) un point du plan P dont l'équation dans un repère orthonormé est donnée par : Pour M0(x0,y0,z0) un point spécifique de P on obtient : En retranchant (2bis) à (1bis) on obtient : En notant Le plan P d'équation ux + vy + wz + h = 0 est donc orthogonal au vecteur Soit un point Le plan P, passant par M0(x0,y0,z0) et orthogonal à Soit H la projeté de M(x,y,z) sur P avec La droite perpendiculaire à P et passant par M étant orientée suivant la direction du vecteur En valeur absolue : Soitent (P) et (P') deux plans d'équations L'angle géométrique (P,P') est déterminé à l'aide de l'angle des vecteurs normaux L'angle de plus grande pente est l'angle le plus grand formé entre un plan et le plan horizontal. De façon imagée on peut définir l'angle de plus grande pente comme l'angle formé entre la trajectoire d'une bille cirulant librement sur un plan et le plan horizontal. Etant donné l'équation d'un plan horizontal : L'angle de plus grande pente est donné par : Les plan (P) et (P') sont perpendiculaires si les vecteurs normaux Soient un point M0(x0,y0,z0) et deux vecteurs Ce qui donne, en représentant le produit mixte de ces trois vecteurs sous la forme d'un déterminant : Son équation est : que l'on peut écrire sous la forme ux + vy + wz + h = 0 Soient deux points M1(x1,y1,z1),M2(x2,y2,z2) et un vecteur Le point M appartient au plan passant par M1(x1,y1,z1),M2(x2,y2,z2) et de direction Son équation est : Soient M1(x1,y1,z1),M2(x2,y2,z2),M3(x3,y3,z3), trois points non alignés. Par analogie avec ce qui précède, l'équation du plan passant par ces trois points est :La droite dans le plan euclidien [modifier]
Vecteur normal à une droite [modifier]
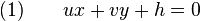


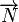 , le vecteur de coordonnées (u, v), on exprime (1) comme suit :
, le vecteur de coordonnées (u, v), on exprime (1) comme suit :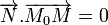
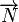 . Le vecteur
. Le vecteur 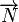 est appelé un vecteur normal à la droite D.
est appelé un vecteur normal à la droite D.Droite passant par un point et orthogonale à un vecteur non nul donné [modifier]
 non nul. Le point M appartient à la droite D, passant par M0(x0,y0) et orthogonale à
non nul. Le point M appartient à la droite D, passant par M0(x0,y0) et orthogonale à  , si et seulement si :
, si et seulement si :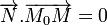
 , a donc pour équation :
, a donc pour équation :
Distance algébrique d'un point M(x,y) à une droite d'équation ux + vy + h = 0 [modifier]
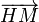 orthogonal à D.
orthogonal à D. , on montre que la distance algébrique entre M et D est donnée par :
, on montre que la distance algébrique entre M et D est donnée par :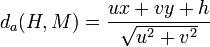
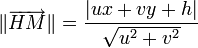
Droite et pente [modifier]
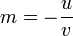
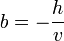

Équation normale d'une droite [modifier]
 ,notons
,notons 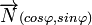 un vecteur unitaire normal à la droite D, orienté de O vers D, la valeur
un vecteur unitaire normal à la droite D, orienté de O vers D, la valeur  représente alors l'angle
représente alors l'angle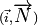 . On note d'autre part p la distance entre l'origine O du repère et la droite D.
. On note d'autre part p la distance entre l'origine O du repère et la droite D.
Angles de deux droites [modifier]
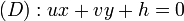

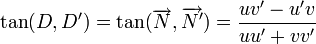
La droite dans l'espace euclidien [modifier]
Distance d'un point M à une droite quelconque D de l'espace [modifier]
Cas où la droite est définie par l'intersection de deux plans [modifier]
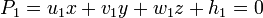

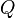 perpendiculaire à
perpendiculaire à  appartient au faisceau de plans
appartient au faisceau de plans 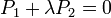
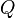 sera perpendiculaire à
sera perpendiculaire à  pour
pour 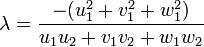
 les projections orthogonales du point
les projections orthogonales du point  respectivement sur
respectivement sur 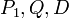 , on en déduit
, on en déduit 
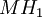 et
et  comme détaillé au chapitre "Distance algébrique d'un point à un plan" ci dessous.
comme détaillé au chapitre "Distance algébrique d'un point à un plan" ci dessous.Cas où la droite est définie par un point M0 et un vecteur
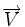 non nul [modifier]
non nul [modifier]
Droites orthogonales à un plan [modifier]
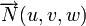 . Une droite D passant par le point M0(x0,y0,z0) et perpendiculaire à [P]:ux + vy + wz + h = 0 a pour équations :
. Une droite D passant par le point M0(x0,y0,z0) et perpendiculaire à [P]:ux + vy + wz + h = 0 a pour équations :
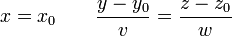

Distance entre deux droites quelconque de l'espace [modifier]
 et (D1) la droite passant par M1(x1,y1,z1) et de direction
et (D1) la droite passant par M1(x1,y1,z1) et de direction 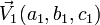
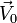 et
et 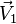 sont indépendants, le volume du solide construit sur
sont indépendants, le volume du solide construit sur  est égal à | k | . Ce réel se calcule grâce au produit mixte :
est égal à | k | . Ce réel se calcule grâce au produit mixte :
 tel que
tel que 

Le plan dans l'espace euclidien [modifier]
Vecteur orthogonal à un plan [modifier]
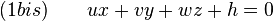

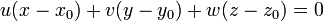
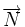 , le vecteur de coordonnées (u,, v , w), on exprime (1bis) comme suit :
, le vecteur de coordonnées (u,, v , w), on exprime (1bis) comme suit :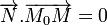
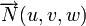 et ce vecteur est appelé un vecteur normal au plan P.
et ce vecteur est appelé un vecteur normal au plan P.Plan passant par un point et orthogonal à un vecteur non nul donné [modifier]
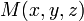 et un vecteur
et un vecteur 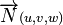 non nul. Le point M appartient au plan P, passant par
non nul. Le point M appartient au plan P, passant par  et orthogonal à
et orthogonal à 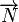 , si et seulement si :
, si et seulement si :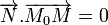
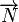 , a donc pour équation : :
, a donc pour équation : :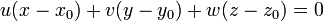
Distance algébrique d'un point M(x,y,z) à un plan P d'équation ux + vy + wz + h = 0 [modifier]
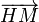 orthogonal à P.
orthogonal à P. , on montre que la distance algébrique entre M et P est donnée par :
, on montre que la distance algébrique entre M et P est donnée par :

Angles de deux plans [modifier]
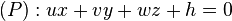

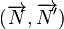
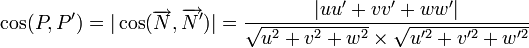
Cas particulier : Angle de plus grande pente [modifier]

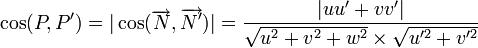
Plans perpendiculaires [modifier]
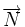 et
et  sont orthogonaux. Ce qui implique
sont orthogonaux. Ce qui implique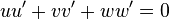
Équation de plan et déterminant [modifier]
Plan défini par un point et deux vecteurs non colinéaires [modifier]
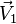 et
et  non colinéaires. Un point M (x, y, z) appartient au plan P passant par M0(x0,y0,z0) et de directions
non colinéaires. Un point M (x, y, z) appartient au plan P passant par M0(x0,y0,z0) et de directions 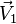 et
et  si et seulement si il existe deux réels λ et μ tels que
si et seulement si il existe deux réels λ et μ tels que 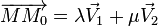 . Cette égalité exprime que
. Cette égalité exprime que 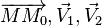 sont coplanaires.
sont coplanaires.

Plan défini par deux points et un vecteur [modifier]
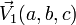 non colinéaire à
non colinéaire à  .
.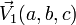 si et seulement si les trois vecteurs :
si et seulement si les trois vecteurs : sont coplanaires, donc :
sont coplanaires, donc :

Plan défini par trois points non alignés [modifier]

Annexes [modifier]
Liens internes [modifier]
08:37 Publié dans Propriétés métriques des droites et plans | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook