08/12/2010
Propriétés métriques des droites et plans
En géométrie euclidienne, c'est-à-dire dans le plan et l'espace muni d'une distance et d'un produit scalaire, les droites et les plans possèdent des propriétés métriques permettant de les caractériser grâce à un point et un vecteur, dit normal. On peut aussi calculer la distance qui les sépare d'un point donné ou bien calculer celle qui sépare deux droites ou deux plans. On peut aussi calculer l'angle formé par deux droites ou deux plans. Dans cet article, on a muni le plan ou l'espace d'un repère orthonormal dans lequel sont exprimées toutes les coordonnées. Toute droite du plan y possède une équation du type ux + vy + h = 0 où (u , v) est différent de (0 , 0) et tout plan de l'espace possède une équation de la forme ux + vy + wz + h = 0 où (u, v, w) est différent de (0, 0, 0).Propriétés métriques des droites et plans
Sommaire[masquer]
|
Soit M(x,y) un point de la droite D dont une équation dans un repère orthonormal est donnée par : et M0(x0,y0) un point spécifique de D, On a : En retranchant (2) à (1) on obtient : En notant La droite d'équation ux + vy + h = 0 est donc orthogonale au vecteur Soit un point M(x,y) et un vecteur La droite D, passant par M0(x0,y0) et orthogonale à Soit H la projecté de M(x,y) sur D avec La droite perpendiculaire à D et passant par M étant orientée suivant la direction du vecteur En valeur absolue : Pour v non nul, la droite D d'équation ux + vy + h = 0 possède une équation sous la forme mx + b = y avec et La pente d'une droite est le réel L'angle α représente l'angle entre l'axe des abscisses et la droite D. Dans le repère L'équation (1) s'écrit : Soit D et D' deux droites d'équations L'angle formé par les deux droites est connu par sa tangente : le plan Soit On calculera La distance MH est donnée par Le plan étant défini par l'équation ux + vy + wz + h = 0, les droites perpendiculaires au plan sont toutes les droites ayant comme vecteur directeur dans le cas où aucun des réels, u, v, w, n'est nul. Si un seul des des réels est nul , par exemple u= 0, le système devient : Si deux réels sont nuls, par exemple u=v=0, le système devient : Soient la droite (D0) passant par M0(x0,y0,z0) et de direction le vecteur Si les vecteurs L'aire de la base du solide est donnée par La distance entre les deux droites est alors égale à Si les vecteurs sont colinéaires alors les deux droites sont parallèles et la distance qui les sépare correspond à la distance qui sépare le point M1 de la droite D0. Soit M(x,y,z) un point du plan P dont l'équation dans un repère orthonormé est donnée par : Pour M0(x0,y0,z0) un point spécifique de P on obtient : En retranchant (2bis) à (1bis) on obtient : En notant Le plan P d'équation ux + vy + wz + h = 0 est donc orthogonal au vecteur Soit un point Le plan P, passant par M0(x0,y0,z0) et orthogonal à Soit H la projeté de M(x,y,z) sur P avec La droite perpendiculaire à P et passant par M étant orientée suivant la direction du vecteur En valeur absolue : Soitent (P) et (P') deux plans d'équations L'angle géométrique (P,P') est déterminé à l'aide de l'angle des vecteurs normaux L'angle de plus grande pente est l'angle le plus grand formé entre un plan et le plan horizontal. De façon imagée on peut définir l'angle de plus grande pente comme l'angle formé entre la trajectoire d'une bille cirulant librement sur un plan et le plan horizontal. Etant donné l'équation d'un plan horizontal : L'angle de plus grande pente est donné par : Les plan (P) et (P') sont perpendiculaires si les vecteurs normaux Soient un point M0(x0,y0,z0) et deux vecteurs Ce qui donne, en représentant le produit mixte de ces trois vecteurs sous la forme d'un déterminant : Son équation est : que l'on peut écrire sous la forme ux + vy + wz + h = 0 Soient deux points M1(x1,y1,z1),M2(x2,y2,z2) et un vecteur Le point M appartient au plan passant par M1(x1,y1,z1),M2(x2,y2,z2) et de direction Son équation est : Soient M1(x1,y1,z1),M2(x2,y2,z2),M3(x3,y3,z3), trois points non alignés. Par analogie avec ce qui précède, l'équation du plan passant par ces trois points est :La droite dans le plan euclidien [modifier]
Vecteur normal à une droite [modifier]
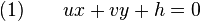


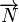 , le vecteur de coordonnées (u, v), on exprime (1) comme suit :
, le vecteur de coordonnées (u, v), on exprime (1) comme suit :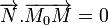
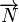 . Le vecteur
. Le vecteur 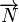 est appelé un vecteur normal à la droite D.
est appelé un vecteur normal à la droite D.Droite passant par un point et orthogonale à un vecteur non nul donné [modifier]
 non nul. Le point M appartient à la droite D, passant par M0(x0,y0) et orthogonale à
non nul. Le point M appartient à la droite D, passant par M0(x0,y0) et orthogonale à  , si et seulement si :
, si et seulement si :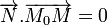
 , a donc pour équation :
, a donc pour équation :
Distance algébrique d'un point M(x,y) à une droite d'équation ux + vy + h = 0 [modifier]
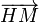 orthogonal à D.
orthogonal à D. , on montre que la distance algébrique entre M et D est donnée par :
, on montre que la distance algébrique entre M et D est donnée par :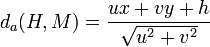
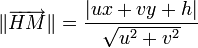
Droite et pente [modifier]
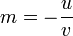
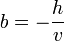

Équation normale d'une droite [modifier]
 ,notons
,notons 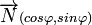 un vecteur unitaire normal à la droite D, orienté de O vers D, la valeur
un vecteur unitaire normal à la droite D, orienté de O vers D, la valeur  représente alors l'angle
représente alors l'angle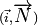 . On note d'autre part p la distance entre l'origine O du repère et la droite D.
. On note d'autre part p la distance entre l'origine O du repère et la droite D.
Angles de deux droites [modifier]
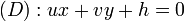

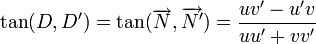
La droite dans l'espace euclidien [modifier]
Distance d'un point M à une droite quelconque D de l'espace [modifier]
Cas où la droite est définie par l'intersection de deux plans [modifier]
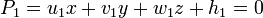

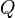 perpendiculaire à
perpendiculaire à 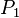 appartient au faisceau de plans
appartient au faisceau de plans 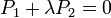
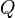 sera perpendiculaire à
sera perpendiculaire à 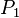 pour
pour 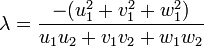
 les projections orthogonales du point
les projections orthogonales du point  respectivement sur
respectivement sur 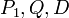 , on en déduit
, on en déduit 
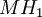 et
et  comme détaillé au chapitre "Distance algébrique d'un point à un plan" ci dessous.
comme détaillé au chapitre "Distance algébrique d'un point à un plan" ci dessous.Cas où la droite est définie par un point M0 et un vecteur
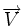 non nul [modifier]
non nul [modifier]
Droites orthogonales à un plan [modifier]
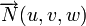 . Une droite D passant par le point M0(x0,y0,z0) et perpendiculaire à [P]:ux + vy + wz + h = 0 a pour équations :
. Une droite D passant par le point M0(x0,y0,z0) et perpendiculaire à [P]:ux + vy + wz + h = 0 a pour équations :
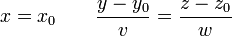

Distance entre deux droites quelconque de l'espace [modifier]
 et (D1) la droite passant par M1(x1,y1,z1) et de direction
et (D1) la droite passant par M1(x1,y1,z1) et de direction 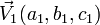
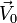 et
et 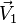 sont indépendants, le volume du solide construit sur
sont indépendants, le volume du solide construit sur  est égal à | k | . Ce réel se calcule grâce au produit mixte :
est égal à | k | . Ce réel se calcule grâce au produit mixte :
 tel que
tel que 

Le plan dans l'espace euclidien [modifier]
Vecteur orthogonal à un plan [modifier]
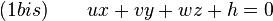

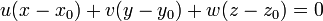
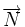 , le vecteur de coordonnées (u,, v , w), on exprime (1bis) comme suit :
, le vecteur de coordonnées (u,, v , w), on exprime (1bis) comme suit :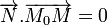
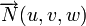 et ce vecteur est appelé un vecteur normal au plan P.
et ce vecteur est appelé un vecteur normal au plan P.Plan passant par un point et orthogonal à un vecteur non nul donné [modifier]
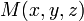 et un vecteur
et un vecteur 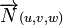 non nul. Le point M appartient au plan P, passant par
non nul. Le point M appartient au plan P, passant par  et orthogonal à
et orthogonal à 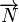 , si et seulement si :
, si et seulement si :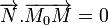
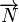 , a donc pour équation : :
, a donc pour équation : :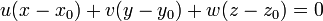
Distance algébrique d'un point M(x,y,z) à un plan P d'équation ux + vy + wz + h = 0 [modifier]
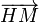 orthogonal à P.
orthogonal à P. , on montre que la distance algébrique entre M et P est donnée par :
, on montre que la distance algébrique entre M et P est donnée par :

Angles de deux plans [modifier]
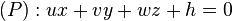

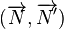
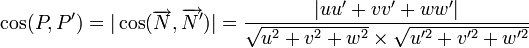
Cas particulier : Angle de plus grande pente [modifier]

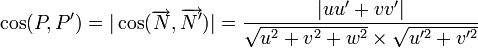
Plans perpendiculaires [modifier]
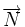 et
et  sont orthogonaux. Ce qui implique
sont orthogonaux. Ce qui implique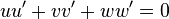
Équation de plan et déterminant [modifier]
Plan défini par un point et deux vecteurs non colinéaires [modifier]
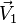 et
et  non colinéaires. Un point M (x, y, z) appartient au plan P passant par M0(x0,y0,z0) et de directions
non colinéaires. Un point M (x, y, z) appartient au plan P passant par M0(x0,y0,z0) et de directions 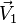 et
et  si et seulement si il existe deux réels λ et μ tels que
si et seulement si il existe deux réels λ et μ tels que 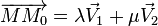 . Cette égalité exprime que
. Cette égalité exprime que 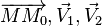 sont coplanaires.
sont coplanaires.

Plan défini par deux points et un vecteur [modifier]
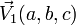 non colinéaire à
non colinéaire à  .
.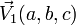 si et seulement si les trois vecteurs :
si et seulement si les trois vecteurs : sont coplanaires, donc :
sont coplanaires, donc :

Plan défini par trois points non alignés [modifier]

Annexes [modifier]
Liens internes [modifier]
08:37 Publié dans Propriétés métriques des droites et plans | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook








































Les commentaires sont fermés.