06/12/2010
Dossiers Scientifiques: classement thématique
Cette page contient une présentation thématique des articles et dossiers du site (sommaire et résumés). Ces documents portent sur toutes sortes de sujets en relation avec les mathématiques d'aujourd'hui. Nous nous efforçons de signaler en introduction de chaque document quels outils sont utilisés et quel usage peut en être fait dans l'enseignement. Les dossiers historiques sont présentés dans la rubrique "Histoire des mathématiques". Les document à caractère pédagogique sont présentés dans la rubrique "Matériaux pour la classe". Les entretiens enregistrés sont présentés dans la rubrique "vidéos". Pour toute question, remarque, proposition ; pour nous signaler une coquille, un point pas assez bien détaillé, une erreur s'étant glissée dans un texte... Un sujet vous intéresse, qui n'est pas encore traité ici ? Ecrire ici.Dossiers Scientifiques: classement thématique
|
|
Ressources du site CultureMath
Sites externes
RésumésCombinatoire, dénombrement :
Les colliers de G. Polyà
Il est ici question d'un théorème peu connu de G. Polyà, résultat qui fournit une méthode systématique pour dénombrer les coloriages possibles d'un ensemble sous l'action d'un groupe. De tels problèmes peuvent être posés de façon extrêmement simple : par exemple, combien peut-on faire de colliers différents si l'on dispose de 10 perles noires et de 3 perles rouges ? (par Thomas Chomette)
Prérequis :
| Pour revenir au sommaire : |
 |
Un peu de théorie des graphes, où comment venir à bout d'un digicode plus vite que n'importe qui. Nous nous intéressons ici à la question de savoir combien de chiffres il faut taper successivement sur un digicode pour être sûr d'avoir tapé toutes les combinaisons possibles. Il s'avère que cette question se modélise de façon agréable dans le langage des graphes orientés, et que l'on peut alors résoudre notre problème initial. Nous voyons enfin quelques applications classiques du résultat de théorie des graphes utilisé. (par Thomas Chomette) Aucun, si ce n'est une idée intuitive de ce qu'est un graphe. Tous les objets nécessaires à la résolution de notre problème sont définis, mais il est bon de pouvoir s'en faire une image mentale.Un problème de digicode
Prérequis :
| Pour revenir au sommaire : |
 |
À quelle condition peut-on dessiner un graphe dans le plan, sans que ne se croisent des arêtes dudit graphe ? Le problème est assez classique : on connaît des condition nécessaires, qui dérivent de la formule d'Euler. Nous introduisons ici ces résultats, en montrant quelques applications sur des graphes particuliers. Il existe également une caractérisation exacte, dûe au mathématicien Polonais Kuratovsky, que nous présentons à la fin de ce texte. (par Thomas Chomette) Aucun.Graphes planaires
Prérequis :
| Pour revenir au sommaire : |
 |
Nous allons nous intéresser ici au nombre de manières de ranger des boules dans des boîtes. Problème classique s'il en est : nombre d'arrangements, nombre de combinaisons... Contrairement aux apparences, ce problème n'est pas toujours si simple lorsque l'on s'impose comme ici une contrainte supplémentaire : les boîtes sont indistinguables les unes des autres. Là, les choses se compliquent ! Manipulation d'expressions algébriques complexes, de suites définies de manière récurrente. Ordres de grandeur sur les suites (suites équivalentes, négligeables l'un par rapport à l'autre). Pour la partie 1.5 : développements en série, développements limités, notations exponentielles.Combien de rangements possibles ?
Dans le cas où les boules sont, elles numérotées, on arrive à dire pas mal de choses : d'abord, on peut établir une formule explicite pour le nombre de façons de ranger n boules dans k boîtes. Et l'on détermine alors le comportement asymptotique de cette suite... Le cas des boules elles-mêmes indistinguables est plus complexe, on se contentera d'une formule de récurrence et d'un équivalent. (par Arvind Singh, ENS)Prérequis :
| Pour revenir au sommaire : |
 |
Les suites de Fibonacci, le nombre de parenthésages “légaux” possibles avec 2n parenthèses, le profil des montagnes... Ces sujets on un rapport, dans le monde des mathématiques ! Il existe en effet une manière assez générale d'étudier des suites dont la définition fait apparaître (clairement ou après analyse), des phénomènes de récurrence. Il s'agit d'introduire une série formelleassociée à cette suite. Le but de ce texte est d'introduire cette notion qui généralise celle de polynôme en autorisant les degrés infinis. Nous verrons que cet objet algébrique permet d'effectuer des manipulations combinatoires sans passer par le traitement analytique de la notion de somme infinie. Nous verrons également que ces manipulations doivent être effectuées avec prudence, et uniquement dans un cadre clairement établi. Par Farouk Boucekkine, ENS.Du Triangle de Pascal aux Séries Formelles
Prérequis :
| Pour revenir au sommaire : |
 |
Voici un texte qui nous a été envoyé par un de nos jeunes lecteurs, Thibault Bourgeron, actuellement en classe de terminale S au lycée Sainte-Marie d'Antony ! Ce travail traite de deux problèmes à résoudre par récurrence. Le premier vous est peut-être familier, puisqu'il s'agit de voir combien de contours de montagnes on peut imaginer avec n montées et n descentes (Thibault, lecteur assidu de CultureMATH, a lu notre article sur les chemins de Dyck, et nous a donc envoyé son travail, avec l'accord de ses professeurs). Le second problème consiste à déterminer le nombre de manières de découper un polygone en triangles dont les sommets sont des sommets du polygone, et dont les arêtes ne se croisent pas. Ce texte a été produit pendant son année de première S dans le cadre du club Maths-en-Jeans de son lycée, jumelé avec celui du lycée Blaise Pascal d'Orsay, sous le patronage des professeurs de mathématiques Guillaume Gervet et Marie-dominique Mouton, et de deux doctorantes, Sophie Donnet et Marie Sauvé. Outre Thibault, trois élèves ont participé à sa rédaction, Michaël Beniluz, Yves Desclercs et Alice Magnaudet (à l'époque tous en première S). Manipulation d'expressions algébriques complexes, de suites définies de manière récurrente. Fractions rationnelles (définition) Cardinal d'un ensemble (combinatoire niveau terminale)
Montagnards et polygones
Prérequis :
Imparité rythmique
Par André Bouchet
Résumé - L’ethnomusicologue Simha Arom a observé une structure rythmique asymétrique utilisée entre autres par les Pygmées Aka de la vallée de la Lobaye, République centrafricaine.
La propriété caractéristique de ces formules rythmiques, l’imparité rythmique, a été étudiée par Marc Chemillier (Mathématiques de la musique d’Afrique centrale, CultureMATH, 2009).
Cet article propose une nouvelle approche de cette propriété eten donne un théorème de caractérisation.
Lire l'article
Arithmétique, théorie des nombres :
L'Algorithme de Génération des Premiers (AGP)
Utilisation en classe - Ce texte offre un exemple original d'algorithme. La description de l'algorithme AGP est accessible à un élève de seconde. Quant aux lois mathématiques de l'AGP, elles pourraient être abordées en terminale S ou en classe préparatoire. Une version courte en anglais offre une ressource pertinente pour des classes de sections européennes "maths-anglais".
Lire l'article
Lire la version anglaise - The Prime-Generating Algorithm (PGA)
Arithmétique
 |
|
Voir aussi: Points rationnels et courbes elliptiques de Jérôme Gärtner.
Points rationnels et courbes elliptiques
 |
Jérôme Gärtner, Ecole Normale Supérieure de Cachan et Institut de mathématiques de Jussieu (Université Paris 6, Pierre et Marie Curie) Résumé - Le but de cet article est d'introduire à deux notions utilisées actuellement dans la recherche en théorie des nombres : les points rationnels et les courbes elliptiques. On y trouvera en premier lieu une explication de l'intérêt porté aux points rationnels, en lien avec le théorème de Pythagore. Ensuite, après avoir expliquer la notion de loi de groupe sur les points rationnels d'une courbe elliptique, on énonce un résultat important, le théorème de Mordell- Weil. La fin de l'article est consacrée à la manière dont ces notions interviennent dans la recherche actuelle, autour de deux exemples : un problème ouvert, la conjecture de Birch et Swinnerton-Dyer, et les points de Heegner. On trouvera en conclusion un panorama des notions relatives aux courbes elliptiques en lien avec la théorie des nombres, ainsi qu'une bibliographie détaillée. Le niveau requis est le bagage classique d'un étudiant de premier cycle (un petit peu de géométrie, et la définition d'un groupe). Importer l'article (pdf - 14 pages - 225 Ko) |
Voir aussi: Arithmétique, entretien avec Marc Hindry.
Problème des bœufs du soleil
 |
|
L'article donne la traduction en français de l'énoncé d'Archimède et détaille les calculs menant à "la" solution. Celle-ci utilise toutes les finesses de l'arithmétique, de l'algèbre des corps finis, en utilisant aussi la théorie des fractions continues pour solutionner l'équation de Pell-Fermat, clef du problème. L'effectif minimal du troupeau du Soleil est un nombre de 206 545 chiffres, qui occupent 60 pages à l'impression (serrée) et qui commence à gauche par 7760 et se termine par 1800 (pour voir ce nombre cosmique, cliquer ici). Le lecteur pourra trouver la procédure, en Maple ici, ou bien sur le web, par exemple sur le site de Philippe Dumas de l'Inria qui donne également de multiples liens. Ce même lecteur trouvera d'autres liens par Google en demandant : troupeau du Soleil Archimède ou les sites anglophones par cattle of the Sun, par exemple celui-ci. Par Lazare Georges Vidiani, Professeur de Mathématiques. Importer l'article (version pdf, 6 pages, 202 Ko) Dans le numéro spécial 12-14 de la revue Confluences 1947, numéro spécial consacré à Antoine de Saint Exupéry, dans le chapitre "voyage de l'Universel", écrit par le général Chassin, qui fut le chef de Saint-Exupéry, ce problème est évoqué, annoncé situé dans les annexes où il ne figure pas ! Après une traque de trois ans et huit mois, l'auteur a réussi à retrouver son énoncé, et en donne une solution, en rappelant le problème célèbre du Pharaon. Merci à Mr Fabien Petitjean pour ses corrections. Par Lazare Georges Vidiani, Professeur de Mathématiques. Importer l'article (version pdf, 5 pages, 131 Ko)
Le problème des nombres gelés de Saint-Exupéry
Quelques résultats et conjectures de transcendance
Nous présentons ici un panorama des résultats et conjectures les plus classiques autour de la notion de transcendance. Ce n'est bien sûr pas une revue exhaustive de l'état de la recherche dans ce domaine, mais les problèmes dont il est ici question, quoique simples dans leur formulation, restent au coeur des préoccupations actuelles. (d'après Stéphane Fischler, ENS Ulm)
Prérequis :
Sur l'algorithme RSA
L'algorithme RSA, inventé en 1978, est plus que jamais d'actualité, puisqu'il reste 20 ans plus tard la cheville ouvrière de nombreux protocoles de cryptographie utilisés pour la transmission de tout type de données. Il est basé sur un principe d'inversion modulo un très gros nombre, lui-même produit de deux très gros nombres premiers.
Nous expliquons ici le protocole ainsi que les principes d'arithmétique qu'il utilise, tout en nous intéressant également aux problèmes pratiques de sa mise en oeuvre, qui nécessite de savoir manipuler rapidement de très gros entiers, et a donc besoin d'algorithmes performants. (d'après François Maurel, Paris VII)
Prérequis :
| Pour revenir au sommaire : |
 |
Une démonstration originale de l'infinité de l'ensemble des nombres premiers
Celle que nous présentons ici, sans être radicalement différente, semble plus naturelle. Il s'agit de savoir ce qui se passerait si l'ensemble des nombres premiers était fini. On arrive alors assez vite à un problème pour décomposer tous les entiers en facteurs premiers : à partir d'un certain rang, il y aura des trous ! (d'après Joël Bellaiche, ENS Ulm, avec une contribution d'Yves Mulet Marquis, ingénieur électronicien) Prérequis :
Approximation diophantienne et réseaux
La théorie de l'approximation diophantienne est l'étude des propriétés d'approximation de nombres par des rationnels. Elle intervient dans de nombreux domaines des mathématiques. Nous présentons ici quelques premiers résultats d'approximation par des rationnels, en traitant d'abord le cas d'un seul réels, puis de plusieurs ou, ce qui revient au même, d'un vecteur dans un espace vectoriel réel de dimension finie. (par Benoît Mselati, ENS)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Le "petit théorème de Fermat" est un bijou de simplicité et d'utilité. Depuis sa découverte il y a plus de 400 ans par Fermat, on l'a redémontré d'au moins 100 manières différentes ! Dans ce texte, à la limite des programmes d'arithmétique de terminale scientifique, nous vous proposons de (re)découvrir ce petit joyau sous plusieurs points de vue, ainsi que des applications (Wilson) et des réciproques partielles. Par Géry Huvent, Michel Gouy et Alain Ladureau, dans le cadre de l'IREM de Lille.
Fermat revisité
Prérequis :
| Importer l'article entier au format ps ou pdf. |
Probabilités et statistiques :
Combien de fois faut-il battre un jeu de cartes ?
Lorsque l'on bat un jeu de cartes, selon le procédé classique qui consiste à couper le paquet en deux parties puis à alterner les cartes des deux parties pour reformer un seul tas (puis à recommencer l'opération un certain nombre de fois), le but est bien sûr qu'aucun joueur ne puisse deviner l'ordre des cartes après battage. Manifestement, si l'on ne bat qu'une seule fois, un joueur attentif qui connaissait l'ordre initial des cartes dispose encore de certaines informations. D'où la question de savoir combien de fois il faut battre le paquet de cartes pour qu'il soit "bien mélangé".
Nous introduisons ici un modèle probabiliste de l'opération de battage, et nous étudions les probabilités des différents ordres possibles des cartes après un nombre de battages donné. Puis nous nous posons la question de savoir à partir de combien de battages on peut considérer que la répartition est vraiment aléatoire, c'est-à-dire quand est-ce que la répartition des probabilités est (quasi) homogène. (par Philippe Biane, ENS/CNRS)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Avant le référendum
Les sondages d'opinions sont devenus partie intégrante de notre quotidien. Tout le monde sait comment ils sont effectués, dans les grandes ligne. Mais que signifient-ils exactement ? Quel crédit leur apporter ?
En nous basant sur cet exemple fondamental, nous introduisons dans ce texte la notion d'inférence statistique, en essayant de la décortiquer au maximum. Notre but est en l'occurrence de définir ce que peut-être une marge d'erreur, un intervalle de confiance. (par Thomas Chomette, avec l'aide de Patricia Reynaud-Bouret, ENS)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Par Clément Gallo, ENS Cachan. Texte issu d'un mémoire effectué au cours de la scolarité au département de mathématiques de l'ENS Cachan. Le texte intégral du mémoire est disponible ici.
La percolation
La percolation est un phénomène physique que l'on rencontre bien sûr lorsque l'on étudie le passage de la vapeur à travers du café, mais également des situations aussi diverses que la propagation d'un incendie de forêt, la circulation automobile, la conductivité électrique d'une alliage...
Nous introduisons ici cette théorie, partant de la notion de graphe aléatoire. Nous verrons notamment qu'il existe une notion de probabilité critique, c'est-à-dire un seuil tel qu'en-dessous la probabilité d'avoir un phénomène de percolation est nulle, et égale à 1 au-delà.
Nous nous pencherons plus particulièrement sur les cas des arbres infinis et des réseaux cubiques.
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
La corde de Bertrand
Étant donné un cercle, si l'on trace une corde au hasard sur ce cercle, quelle est la probabilité pour que celle-ci soit plus longue que le rayon du cercle ?
Cette question, connue sous le nom de "paradoxe" de la corde de Bertrand, est particulièrement judicieuse pour illustrer la notion de mesure de probabilité. Nous allons voir que la réponse varie en fonction du mode de construction, chaque façon de penser étant lié à une mesure particulière. (par Thomas Chomette, avec l'aide de Patricia Reynaud-Bouret, ENS)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Processus de branchement et descendance d'un individu.
Les processus de branchement sont des modèles introduits pour étudier le développement d'une population, dans laquelle les individus se reproduisent indépendamment les uns des autres, et selon la même loi de probabilité. Introduit au 19ème siècle pour étudier la probabilité d'extinction de noms de familles illustres en Grande Bretagne, le modèle de Galton-Watson et ses variantes trouve de nombreuses applications en biologie ou en physique nucléaire. (par Thomas Chomette, avec l'aide de Vincent Beffara, ENS)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Marches aléatoires sur Z
Quelle est la probabilité, lors d'un dépouillement, pour que le candidat majoritaire le soit tout au cours du dépouillement ? Quelle est la probabilité de ruine d'un joueur ? Combien faut-il de monnaie dans un caisse pour pouvoir servir tout le monde ? Voici quelques-unes des questions qui nous amènent à étudier la notion de marche aléatoire. Nous présentons donc ici un survol de résultats, très élémentaires au début, sur les marches aléatoires dans Z, l'ensemble des entiers relatifs. C'est ensuite l'occasion d'aborder un certain nombre de résultats assez classiques de probabilités. (par Thomas Chomette, avec l'aide de Yannick Baraud, ENS/CNRS).
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Quelle est la probabilité que Pierre gagne ? Partant de ce problème concret, les auteurs développent des algorithmes permettant de simuler une longue partie de pile ou face, échaffaudent des conjectures et les démontrent par la suite. Un bon exemple à montrer à des élèves ! Ce texte a été conçu dans le cadre du groupe de Calcul Formel de l'IREM de Lille par Géry Huvent, Michel Gouy et Alain Ladureau.
Le jeu de Pile ou Face
Pierre et Paul jouent à pile ou face selon une règle simple. Pierre joue en premier, s'il tire Pile, il gagne. Sinon, c'est au tour de Paul qui tire deux fois et qui gagne s'il tire Pile au moins une fois. Si ce n'est pas le cas, Pierre joue à nouveau et tire trois fois, et ainsi de suite...
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Par Yves Martin, IUFM de la Réunion Résumé - Lors de son axiomatisation de la géométrie euclidienne, dans ses Fondements de la géométrie, Hilbert a montré l’importance de la configuration de Desargues pour obtenir une géométrie affine. On appelle depuis “non arguésienne” une géométrie plane qui ne vérifie pas le théorème de Desargues. Le modèle le plus simple est le plan de Moulton (1902). En dehors de questions sur les fondements de la géométrie projective, avec les travaux Ruth Moufang vers 1933, la géométrie non arguésienne en général, et celle du plan de Moulton en particulier, n’ont jamais fait l’objet d’une étude spécifique, le traitement algébrique ne se prêtant pas à sa singularité. Mais depuis quelques années, les possibilités de modélisation des logiciels de géométrie dynamique récents permettent d’explorer cette géométrie sans difficulté. C’est ce que propose cet article. On y verra tout d’abord en quoi l’absence de la configuration de Desargues rend inopérant le concept de milieu quand il est considéré comme affine. Ensuite, la géométrie de Moulton vérifiant tous les autres axiomes de la géométrie euclidienne, nous pouvons effectuer des investigations sur les concepts d’angle, d’orthogonalité et de distance. Contrairement à la typologie associée aux angles pour les géométries usuelles (hyperboliques, euclidienne, elliptique) pour lesquelles la somme des angles triangles sont respectivement inférieure, égale ou supérieure à deux droit, dans le plan de Moulton, les 3 configurations se rencontrent. L’orthogonalité y est, elle aussi, est bien particulière puisque d’un point il peut ne pas passer de perpendiculaire à une droite donnée ou en passer deux – et deux seulement. La distance (ou semi distance selon les auteurs) n’est pas une métrique : l’inégalité triangulaire n’y est pas vérifié ce qui induit des résultats assez surprenants non seulement sur les triangles, mais aussi sur la distance d’un point à une droite. Par Jacques Bouteloup, professeur de mathématiques à Rouen - L'énoncé E.207 du "Coin des problèmes" de la belle revue mathématique Quadrature (Magazine de mathématiques pures et épicées) numéro 48 (Avril-juin 2003) page 47, avait pour but de montrer que les six projetés orthogonaux des sommets d'un triangle sur ses bissectrices extérieures. La solution proposée dans le numéro 51 (Janvier-Mars 2004) introduisait la notion de cercle de Taylor d'un triangle. Ce cercle est un cas particulier d'une famille générale de cercles attachés à un triangle, les cercles de Tücker, dont cet article donne la définition générale et les principales propriétés. Cet article est à paraître dans la revue Quadrature, numéro 63 Janvier-Février-Mars 2006 p 28-32. Culture Math remercie l'éditeur EDP qui l'a autorisé à diffuser l'article sur le site CultureMath. Voici, en remerciement, un lien vers le site de Quadrature http://www.edpsciences.org/journal/index.cfm?edpsname=qua... Pour les amateurs de joyaux de la géométrie du triangle, signalons quelques sites: Importer l'article (version pdf, 8 pages)
La statistique comme outil d'aide à la décision
Un texte général (sans aspects techniques). Ce texte est le résumé d'un exposé fait par l'auteur devant les élèves du lycée Parc de Vilgenis (Massy) en mars 2004. Les statistiques sont une partie souvent mal connue des mathématiques, alors même qu'elle croise la réalité bien souvent, et ce texte tente d'en montrer les aspects peu connus sans entrer dans les détails. Nous proposerons un dossier mathématiquement plus complet sur le sujet au cours de l'année 2005.
Par Gilles Stoltz, chercheur à l'ENS.
Prérequis :
Voir aussi
Géométrie :
Géométrie non arguésienne dynamique
Utilisation dans l'enseignement - Cette présentation simple d’une géométrie inhabituelle présente un grand intérêt pédagogique à plusieurs niveaux de l’enseignement. La simple manipulation des figures dynamiques peut permettre de faire sentir à des élèves de terminale ou à des étudiants de première année ce qu’est un système axiomatique. Dans un contexte de formation initiale des enseignants au sein d’un module de géométrie, mais aussi pour un questionnement didactique en formation continue, les figures de cet article sont l’occasion de travailler – outre les propriétés détaillées ci-dessus – le sens des axiomes de congruence, en particulier sur le fait qu’ils ne sont pas nécessairement liés à l’existence du mouvement dans la géométrie ainsi décrite. La géométrie de Moulton vérifie tous les axiomes de Hilbert, y compris les axiomes de congruence de segments, sauf celui (de congruence sur les angles) qui aboutit au théorème de Desargues. Pourtant dans cette géométrie, aucune translation, aucun déplacement ne vient appuyer les axiomes de congruences sur les segments: ces axiomes ne sont en rien liés au mouvement.
Les cercles de Tücker
Cubiques circulaires passant par leurs foyers singuliers
 |
Par Jacques Bouteloup, professeur de mathématiques à Rouen - Ces courbes possèdent un grand nombre de propriétés remarquables. Souvent appelées "cubiques circulaires focales", elles sont notamment étudiées dans les articles, dans la splendide revue Quadrature (Magazine de mathématiques pures et épicées), de Roux et Tixier (numéro 46 automne 2002 et numéro 47 janvier 2003) sur les configurations de Reye, où elles sont qualifiées d'axées. Dans ces articles comme dans beaucoup d'autres, il n'est pas fait de distinction entre éléments réels ou complexes. L'étude ci-après se place par contre en espace euclidien, supposant donc les éléments introduits (droites, cercles, cubiques) réels. Bien entendu il est nécessaire de supposer cet espace plongé dans son complexifié projectif, ce qui permet d'introduire les points cycliques et de définir les cubiques circulaires comme cubiques les contenant. On appelle, depuis Plücker, foyer d'une courbe un point tel que les isotropes issues de ce point soient tangentes à la courbe. Il est dit singulier si les points de contact sont les points cycliques. Le titre de cette étude est ainsi justifié. Un but fondamental de cette étude est de démontrer l'équivalence de ce passage d'une cubique circulaire par son foyer singulier avec la propriété d'être "auto-isogonale de première espèce", cette notion étant explicitée au début de l'article. |
Note de LG Vidiani : comme la cubique étudiée par Monsieur Bouteloup, n'est pas répertoriée dans le catalogue des 413 cubiques liées au triangle (voir le site remarquable de Bernard Gibert http://perso.orange.fr/bernard.gibert/ctc.html), il est naturel de lui donner le nom de son découvreur. Le beau tracé de cette courbe est dû à Alain Esculier, que nous remercions. Le lecteur pourra se rendre également sur le site http://faculty.evansville.edu/ck6/encyclopedia/ETC.html(Encyclopédie Triangle Center) où il découvrira les propriétés des 3217 points "remarquables" d'un triangle, et rerchercher ceux qui étaient connus au 19ème siècle. Importer l'article (version pdf, 5 pages) S'inspirant du problème d'Agrégation de Calcul Différentiel et Intégral (Femmes) 1947 cet article donne un critère de fermeture hexagonale et l'illustre dans le cas de faisceaux de cercles à points de base et de Poncelet, ou de solutions d'équations différentielles à variables séparables. Extrait de l’introduction - Les problèmes pouvant donner lieu à des exercices simples, qu’on peut poser en classe, tout en ouvrant à des situations plus élaborées et difficiles sont plutôt rares. Les problèmes de fermeture sont de ceux-là : on peut commencer au collège, continuer au lycée et tomber sur des situations qui paraissent insolubles ou nécessitent des outils très puissants. Souvent, un problème de fermeture facile peut en cacher un autre beaucoup plus difficile : il suffit de modifier légèrement les hypothèses. De sorte que tout un chacun peut, avec un peu d’imagination, inventer ses propres problèmes de fermeture. Par Lazare Georges Vidiani, Professeur de Mathématiques. Importer l'article (version pdf, 6 pages) Cet article traite d'une condition d'alignement et de cocyclicité de trois et quatre points sur une cubique circulaire. Son but est de montrer qu’on peut avec des calculs très réduits obtenir de très belles propriétés géométriques, qu’il serait difficille d’obtenir par des arguments géométriques (alignement, cocyclicité, bitangence). Le fait de se limiter à une courbe algébrique de degré 3, une strophoïde, ne réduit pas le principe de la méthode, car on peut démontrer qu’en fait ceci est généralisable, étant une conséquence du théorème intégral d’Abel appliqué aux courbes algébriques. Utilisation : conditions d'alignement, de cocyclicité. Par Lazare Georges Vidiani, Professeur de Mathématiques. Importer l'article (version pdf, 6 pages) Une loi de groupe est définie dans un triangle par des conditions de concours et d'alignement. L'auteur montre comment trouver et construire géométriquement l'inverse d'un point, et le composé de deux points, et même les racines carrées d'un point donné. Utilisation : exemple et illustration géométrique de la théorie des groupes et théorie du calcul barycentrique. Par Lazare Georges Vidiani, Professeur de Mathématiques. Importer l'article (version pdf, 14 pages)
Fermeture Hexagonale
Le dernier bulletin de l'APMEP n°463 d’avril de mars-avril 2006, montre, sous une forme plus élémentaire, que ces problèmes constituent une mine pour l’enseignement : voir l’article de Jean-Pierre Friedelmeyer « Les problèmes de fermeture : une mine d’exercices à ouvrir en classe », p. 267-276.
Géométrie sur une Strophoïde.
Loi de groupe dans un triangle
Les épi ou hypo trochoïdes
|
|
Cet article propose un classement complet des courbes trochoïdales obtenues par roulement sans glissement. L'auteur donne un tableau à double entrée qui permet suivant les divers paramètres (rayons du cercle de base, de roulement et rapport d'élongation) de donner immédiatement la forme de la courbe. La recherche des développées de ces courbes est une application exploitée. La théorie complète du Centre Instantané de Rotation est donnée en annexe et donne donc aussi une utilisation cinématique à cet article géométrique. Ces problèmes de roulement se retrouvent dans les problèmes d'engrenages. Des simulations animées se trouvent par exemple sur le site de Robert Férréolhttp://www.mathcurve.com/courbes2d/epitrochoid/epitrochoi... et celui d'Alain Esculier : http://aesculier.chez-alice.fr/(aller à Rubrique, Maple). Par Lazare Georges Vidiani, Professeur de Mathématiques. Importer l'article (version pdf, 15 pages) |
Depuis l'antiquité grecque, l'un des problèmes les plus fameux en mathématiques est de savoir quels sont les figures, et de manière plus générale les nombres que l'on peut construire à la règle et au compas, partant de deux points du plan qui définissent l'unité de longueur. Les réponses à ces questions sont désormais assez complètes, mais il a fallu attendre plus de deux millénaire pour cela.
Sur les nombres constructibles
Nous présentons ici une réponse assez générale au problème posé, donnant des conditions nécessaires et suffisantes de constructibilité. Celles-ci nous permettent au passage de répondre à quelques questions célèbres posées par les grecs. (par Thomas Chomette) Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Construction des polygones réguliers
Parmi les problèmes les plus célèbres en mathématiques, la construction des polygones réguliers à la règle et au compas possède une place de choix puisqu'elle a tenu en haleine les mathématiciens pendant plus de vingt siècles. Il a fallut attendre les travaux du mathématicien allemand Gauss pour que la question soit entièrement résolue.
Nous introduisons dans ce texte les résultats de Gauss. Le théorème principal démontré en annexe nécessitant quelques connaissances sur les extensions de corps (pour cela, voir par exemple le texte précédent dans lequel nous avons essayé d'introduire certains outils de manière élémentaire), nous nous penchons également sur une méthode plus simple, même si elle ne permet pas d'aboutir au résultat le plus général. (par Thomas Chomette)
Prérequis :
Pour la démonstration du théorème de Gauss (en annexe) :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Courbure des surfaces triangulées
Il existe, en géométrie riemannienne, une notion très importante qui est celle de courbure, mais qui est, hélas, très difficile à définir et à utiliser. On peut cependant, dans le cas des surfaces, en donner une vision assez simple et néanmoins assez précise.
Dans cet article est définie la courbure en un point comme le "défaut de platitude" de la surface en ce point. C'est une notion qui a une signification locale, liée à une métrique. Elle est utilisée ensuite pour présenter la caractéristique d'Euler-Poincaré des surfaces, et montrer ainsi l'intérêt de la courbure globale.
Par Frédéric Bosio, université de Poitiers. Article issu du journal de maths des élèves de l'ENS Lyon (JME), Volume 1.
Prérequis :
| Importer l'article en version pdf. | Pour revenir au sommaire : |
 |
Problème des 5 cercles
Si l'on trace les cercles circonscrits aux cinq triangles correspondant aux "branches" d'une étoile à cinq branches, on s'aperçoit que les points d'intersection de chacun de ces cercles avec le suivant sont cocycliques !
Ce problème de géométrie assez classique à été remis au goût du jour par le président chinois, à l'occasion du congrès international des mathématiciens (Pékin, août 2002)...
Par Thomas Chomette, sur une suggestion de Charles Torossian, ENS/CNRS.
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Tas d'oranges, cristaux et empilement de sphères
Comment empiler efficacement des oranges (ou tout autre fruit sphérique) de façon à obtenir un tas occupant aussi peu de volume que possible ? Est-il préférable d'empiler des couches où les fruits sont disposés en carrés, ou une disposition en triangles est-elle plus efficace ? Ce problème, en apparence anodin, mais dont le champ d'application s'étend de l'étude des cristaux à la théorie des codages informatiques, aura donné du mal aux mathématiciens pendant près de quatre siècles : dès 1610, Kepler formulait une conjecture sur la question, mais il aura fallu attendre 1998 pour que les travaux de Thomas Hales en apportent la preuve de façon rigoureuse. (Par Denis Auroux, CNRS/École Polytechnique)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Reconnaître effectivement les Ensembles Algébriques Réels
La question est de savoir s'il existe une méthode qui, étant donné un objet géométrique W, permet de savoir si W peut être décrit par des équations algébriques, à des changements qui ne modifient pas sa topologie près. Ce problème fait intervenir de manière fondamentale la notion de triangulation, et plus généralement mène à l'introduction de quelques notions importantes de topologie qui peuvent souvent se comprendre à l'aide de dessins. Dans le cas de la dimension 1 ou 2, les conditions se révèlent relativement simples.
Dans la dernière partie de ce texte, d'un abord plus ardu, on donne une idée d'outils plus sophistiqués qui permettent de présenter une méthode de décision en dimension 3, et de montrer que le problème est en pratique indécidable en dimension plus grande. (par Michel Coste, CNRS/Université de Rennes 1)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Pour nouer, il faut courber
Quand on découvre les mathématiques, on étudie des formes et des nombres. Une manière usuelle d'associer des nombres à une forme est de mesurer des longueurs. Ce texte nous présente de façon intuitive les notions de courbure et de torsion des courbes et des surfaces, et présente un théorème classique sur la courbure des nœuds.
Il peut constituer une introduction à la Courbure des surfaces triangulées, ou au texte sur Gaspard Monge. Le style adopté par l'auteur est très simple et illustré par de nombreux dessins. Quelques annotations mathématiques viennent donner une idée des outils nécessaires pour aller plus loin. (par Patrick Popescu-Pampu, Maître de Conférences, Universté Paris 7)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Une solution détaillée est fournie, ainsi que des figures interactives réalisées en CabriJAVA permettant d'illustrer les notions évoquées ainsi que certaines notions connexes. Ce texte a été conçu dans le cadre du groupe de Calcul Formel de l'IREM de Lille (par Géry Huvent, Michel Gouy et Alain Ladureau).
Autour des triangles inscrits sur une hyperbole équilatère
Ce texte a une forme inhabituelle sur ce site : c'est un problème destiné à explorer certaines propriétés de l'hyperbole y = 1/x. Il mélange géométrie plane, géométrie analytique et utilisation des moyens de calcul modernes, et pourra donner des idées d'exercices aux profeseurs... tout en leur pemettant de s'exercer !
Prérequis :
| Importer l'article en version ps ou pdf. Voir les figures. |
Pour revenir au sommaire : |
 |
Par Rémi Langevin, Professeur à l'Université de Dijon. Ce texte est extrait du recueil "De la Méthode", publié aux Presses Universitaires Franc-Comtoises sous la direction de Michel Serfati.
Gaspard Monge, de la planche à dessin aux lignes de courbure
L'expérience du dessin de plans et la curiosité scientifique de Gaspard Monge ont à notre avis influencé sa manière, très visuelle, de raisonner en mathématiques. Il était aussi un enseignant remarquable. Le souci de former les futurs cadres de la nation, donc d'expliquer à la fois les notions mathématiques et leurs éventuelles applications est sans doute lié à son besoin de voir et de représenter de manière précise les objets mathématiques qu'il définit.
Prérequis :
| Importer l'article en version ps ou pdf. |
Pour revenir au sommaire : |
 |
Par Jean Gounon, professeur de mathématiques.
Principe de Fermat; applications à la réflexion et à la réfraction
Le principe de Femat s'énonce de manière simple : Pour aller d'un point-source S à un point-détecteur D après une réflexion ou une réfraction, la lumière suit un chemin pour lequel le temps de parcours est extrêmal (i.e. minimal ou maximal). A partir de ce principe, ce texte démontre les lois classiques de la réflexion et de la réfraction (en particulier la Loi de Descartes).
Prérequis :
| Importer l'article en version ps ou pdf. |
Pour revenir au sommaire : |
 |
Nous y voyons par exemple comment mettre une structure de groupe sur une courbe elliptique, entre autres tours de magie géométrique. C'est aussi l'occasion de réflexions personnelles de l'auteur sur "ce que devrait être" un bon texte de vulgarisation mathématique, dans un style direct, explosif et divertissant. Un peu plus tard, nous donnerons un versant "théorisé" avec définitions, propriétés, etc... à cette notion. Par Michèle Audin, Professeure à l'Université Louis Pasteur de Strabourg.
Arc en ciel, soucoupes volantes, toupies, courbes elliptiques, et tout ça
Ce texte nous donne quelques exemples de singularités lagrangiennes. Mais ne vous effrayez pas tout de suite ! L'auteur prend le parti de ne jamais définir cette notion, préférant tourner autour en prenant plusieurs points de vue amusants (ceux qui donnent son titre à l'exposé) pour insuffler l'intuition de ce qu'elles sont.
Prérequis :
| Importer l'article en version pdf. |
Pour revenir au sommaire : |
 |
La théorie des nœuds est l'abstraction naturelle de cette interrogation, et le texte que nous vous proposons cette semaine en survole les bases, expliquant ce qu'est un nœud pour un mathématicien, et comment exprimer en termes rigoureux la questions « est-ce qu'il est vraiment noué ou pas ? » Par Jérôme Dubois, chercheur à l'Université de Genève.
La théorie mathématique des Nœuds
Toute personne se trouvant aux prises avec un embrouillaminis de fils est amenée à se demander si les fils sont simplement emmêlés, ou si des nœuds viennent corser l'affaire et rendre le démélage plus compliqué. Auquel cas, se pose la question de la marche à suivre pour dénouer la pelote, ou au moins d'éviter d'aggraver la situation !
Ce texte a été écrit par l'auteur pour présenter ses travaux de thèse, à l'occasion de sa participation au Prix Jeune Chercheur 2004 de la ville de Clermont-Ferrand, dont il a reçu un accessit. Prérequis :
| Importer l'article en version ps ou pdf. |
Pour revenir au sommaire : |
 |
N'hésitez pas à lui écrire si vous êtes intéressé par son travail ! Par Jean-Pierre Guidoni, professeur au collège-lycée Pascal Paoli, à Corte. Importer l'article en version pdf.
La médiatrice (en BD)
Ce texte est une petite Bande Dessinée expliquant avec humour ce qu'est la médiatrice d'un segment, à un niveau collège, et est un extrait du travail de l'auteur, qui souhaiterait trouver un éditeur.
Prérequis :
|
Pour revenir
au sommaire : |
Analyse
Les mathématiques du mouvement : Introduction informelle aux systèmes dynamiques
Résumé - Ce texte a été écrit à la fin de ma thèse, pour essayer de donner aux non-mathématiciens une idée du monde dans lequel j’avais baigné pendant quelques années. C’était l’occasion de présenter rapidement, à travers quelques exemples, la théorie des systèmes dynamiques.
Utilisation en classe - Cet article introduit de façon très accessible les mathématiques du mouvement. Une lecture commentée de ce texte à des lycéens du cycle scientifique permettrait d'évoquer en classe certaines questions que se posent les mathématiques actuelles.
Lire l'article
| Revenir au sommaire : |  |
Les équations fonctionnelles, par leur diversité, le fait qu'il n'y ait pas de méthode standard ou universelle pour les résoudre, rivalisent aussi bien avec l'arithmétique que la géométrie, pour montrer la richesse des mathématiques. Elles obligent aussi l'étudiant ou le chercheur à appréhender la nécessité d'une argumentation rigoureuse. L'extrême variété des domaines où on les rencontre (recherche, problèmes de concours, exercices d'oraux, sujets de compétitions internationales telles que les O.I.M....) ne fait que renforcer leur attrait, d'autant plus que chaque jour amène de nouveaux exemples originaux (sites web, revues, sujets de concours, ou de compétitions,...). L'article qui suit a pour but d'essayer de dégager 6 méthodes principales qui permettent de résoudre quatre vingt dix neuf pour cent des exemples proposés au niveau Classes Préparatoires Scientifiques. Les cinq premières pages (sur 14) de cet article ont été publiées dans la revue Quadrature (Magazine de mathématiques pures et épicées http://www.edpsciences.org/journal/index.cfm?edpsname=qua...) de Juillet-Septembre 2004, numéro 53 pages 7-12; elle sont reproduites, avec l'aimable autorisation du rédacteur en chef Olivier Courcelle, que nous remercions. Les neuf pages suivantes sont un catalogue d'exemples (trente cinq) très divers, avec leur référence précise et l'indication de leur solution. Pour garder une dimension raisonnable à l'article publié dans Quadrature, elles n'avaient pas été publiées, mais la dernière note de l'article précisait que les lecteurs intéressés, pouvaient demander leur envoi, ce que beaucoup ont fait à l'époque. Les voici rendues accessibles au plus grand nombre. Pour d'autres pistes et d'autres références bibliographiques les lecteurs peuvent se reporter à l'article « Racine carrée fonctionnelle » du même auteur, sur le site de CultureMath. Importer l'article (version pdf, 14 pages) Par Lazare Georges Vidiani, Professeur de Mathématiques
Equations fonctionnelles
| Revenir au sommaire : |  |
Il s'agit d'étalonner une jauge de cuve à Mazout cylindrique bombée, horizontale, et d'utiliser du calcul intégral pour établir la formule exacte de cette jauge. Importer l'article (version pdf) et la figure correspondante Par Lazare Georges Vidiani, Professeur de Mathématiques
Jauge d'une cuve à Mazout
| Revenir au sommaire : |  |
Les motifs de pelages d'animaux sont expliqués suivant la théorie de réaction-diffusion due à Turing (qui a contribué à casser les codes secrets de la machine Enigma). Qui croirait que ceci est en fait une illustration de la théorie des équations aux dérivées partielles et d'un problème de conditions aux limites? Ces modélisations servent aussi pour gérer la lutte contre les feux de forêts. Cet article est modélisé par de très belles illustrations sur le site d'Alain Esculier et d'Yann Bouret de l'ENS de Chimie UMR 8640 (lab P9) qui les a conçues à la demande de l’auteur. Utilisation : équations au dérivées partielles et chimie, équation de réaction-diffusion. Importer l'article (version pdf, 7 pages) . Par Lazare Georges Vidiani, Professeur de Mathématiques. Voici quelques illustrations animées des modèles présentés dans l'article. Les visiteurs intéressés peuvent en demander d'autres à l'auteur.
Les motifs des pelages d’animaux
|
panthère |
zèbre |
panthère rose |
|
| Revenir au sommaire : |  |
Quel lien y a t-il entre le rayon des séries entières et celui de leur produit d'Hadamard? L'auteur donne à la façon de Cyrano dans la tirade des nez de multiples applications et illustrations dont une formule donnant la somme du produit d'Hadamard en fonction de celles des deux séries arguments. Utilisation : variation originale sur les séries entières. Par Lazare Georges Vidiani, Professeur de Mathématiques.
Le produit d'Hadamard de deux séries entières
| Importer l'article (version pdf, 4 pages) . | Revenir au sommaire : |  |
Résumé: En 1870 Vassili Petrovitch Ermakov découvre des critères très fins de convergence de séries et d'intégrales ; ces critères se retrouvent (de manière anonyme) dans beaucoup d'exercices d'oraux. L'auteur en rappelle l'énoncé en illustrant leur principe. Par Lazare Georges Vidiani, Professeur de Mathématiques.
Critères d'Ermakov
Erratum: dans le dernier théorème encadré page 2, la suite pn doit être non bornée.
Utilisation: convergence des séries numériques.
| Importer l'article (version pdf, 3 pages) . | Revenir au sommaire : |  |
Inspiré du problème d'agrégation 1949 proposant de rechercher les fonctions g inconnues telles que g(g(x))=f(x) (f donnée), cet article, abondamment illustré par des exemples concrets, montre comment trouver les solutions et donne diverses applications très récentes de cette théorie (réseaux de neuronnes (et le fameux Perceptron), géographie pour la prédiction de l'occupation des sols, recherche des périodes en théorie du chaos, prédiction boursière, technique du laminage en industrie,...). Dans l'enseignement, il montre que des problèmes abstraits peuvent avoir de nombreuses applications pratiques. Erratum (12 02 09 14h30) : 8 lignes de texte avant la fin de la page 1, remplacer (x/2)^n=(y/2)^m par x/2^n=y/2^m.
Racine carrée fonctionnelle
Par Lazare Georges Vidiani, Professeur de Mathématiques.
| Importer l'article (version pdf, 8 pages) . | Revenir au sommaire : |  |
Recherche des 27 droites sur une surface cubique non réglée, représentation paramétrique, double six de Schlaffli, lien avec la théorie des groupes et même lien avec la théorie des super-cordes. L'auteur, dans un style très personnel, ne cache rien de toutes les étapes de sa recherche, et des problèmes divers soulevés et fournit même unephoto du bijou offert à Juel le 25 janvier 1925, pour son jubilé scientifique. Utilisation dans l'enseignement : pour les classes préparatoires aux grandes écoles, en relation avec la théorie des surfaces et en illustration du groupe Psp4(F2).
Le théorème de JUEL et la surface de CLEBSCH
Par Lazare Georges Vidiani, Professeur de Mathématiques.
| Lire l'article | Revenir au sommaire : |  |
Le théorème de Sharkovskii
Ce résultat est assez connu sous une forme plus faible : période 3 implique période n pour tout entier n. C'est-à-dire qu'une fonction continue, d'un segment dans lui-même, ayant un point de période 3 a nécessairement un point de période n pour tout n.
En fait, ceci est une conséquence du théorème de Sharkovskii, qui affirme que si une fonction continue d'un segment dans lui-même a un point de période m (m entier), alors cette fonction a un point de période n pour tout n plus grand que m pour l'ordre de Sharkovskii (ordre sur les entier dont 3 est bien sûr le plus petit élément).
Par Jean-Yves Briend, université de Provence. Article issu du journal de maths des élèves de l'ENS Lyon (JME), Volume 1.
Prérequis :
| Importer l'article en version pdf. | Pour revenir au sommaire : |
 |
Propagation d'épidémie
La théorie des épidémies fournit de nombreux systèmes d'équations différentielles ou aux dérivées partielles. On a d'autre part une idée intuitive du comportement de ces phénomènes, de la propagation de ces maladies. Y interviennent des phénomènes de contamination, de diffusion... Nous allons ici prendre l'exemple de la diffusion de la rage dans une population de renards, et en présenter quelques modèles assez simples.
Ceux-ci sont accompagnés de simulations numériques. Les programmes utilisés sont disponibles, commentés, en version matlab et scilab (scilab est un logiciel libre distribué par l'INRIA, que l'on peut télé-charger ici).
Par Thomas Chomette, avec l'aide d'Emmanuel Grenier, ENS Lyon.
| Article disponible en version html, ps ou pdf. | Pour revenir au sommaire : |
 |
Texte accompagné de simulations numériques en java. Les algorithmes sont également déclinés et mis à disposition en version matlab et scilab (scilab est un logiciel libre distribué par l'INRIA, que l'on peut télé-charger ici).
Petits pièges de la simulation numérique
La simulation numérique ne pose pas toujours seulement des problèmes de capacités de calcul : même avec des ordinateurs de plus en plus puissants, l'opération laisse encore des problèmes au mathématicien ! Il s'agit en effet de mettre en place des algorithmes qui fonctionnent, or même dans des cas très simples, on ne peut pas faire n'importe quoi.
Par Emmanuel Grenier, ENS Lyon. Illustrations de Thomas Chomette. Prérequis :
| L'article seul, en version ps ou pdf. Illustrations numériques, disponibles en version html. |
Pour revenir au sommaire : |
 |
Arbres et dérivée d'une fonction composée
On connaît des formules de dérivation à un ordre quelconque pour un produit de fonction (formule de Leibnitz). Pour ce qui est d'une somme de fonctions, c'est encore plus évident : la dérivée n-ième de la somme est la somme des dérivées n-ièmes, par linéarité.
En revanche, pour ce qui est de la composée de deux fonctions, on ne sais pas faire... Nous allons voir ici que le problème se transpose en quelque chose de purement combinatoire sur les arbres. Une illustration de plus des ponts surprenants qui peuvent se créer entre des domaines a priori complètement étrangers l'un à l'autre, ici l'analyse classique et la théorie des graphes !
Par Thomas Chomette, sur une suggestion de Charles Torossian, ENS/CNRS. Pour aller (beaucoup) plus loin dans le domaine, un article intitulé "Runge-Kutta methods and renormalization", par Christian Brouder, est disponible ici.
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Homographies et suites récurrentes
On apprend à tous les étudiants en mathématiques comment étudier une suite récurrente définie par une homographie : on cherche les points fixes de l'homographie, puis on définit une autre suite à l'aide de la première, en distinguant le cas où l'homographie a un point fixe double, et cette suite se révèle miraculeusement être une suite géométrique ou arithmétique...
Partant de cette méthode, on on s'aperçoit qu'en rajoutant au plan complexe un "point à l'infini", les choses s'expliquent de manière plus simple, plus élégantes, plus convaincantes. En réalité, nous avons introduit rien moins que la droite projective complexe, un des cas le plus simples de la géométrie projective, mais qui permet d'introduire de nombreuses notions fondamentales. (par Thomas Chomette, avec l'aide de Gaëtan Chenevier, ENS)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Par Jean Gounon.
L'intégration selon Riemann et selon Lebesgue
Ce texte est une présentation systématique de deux théories de l'intégration : celle de Riemann et celle de Lebesgue. Ces deux cadres sont décrits par le menu, ainsi que les résultats les plus marquants (le plus souvent sans démonstration). L'objectif de ce texte est de servir de référence rapide pour la lecture d'autres textes, ou pour avoir une idée d'ensemble de ces théories sans devoir se plonger dans les détails les plus techniques, ou acquérir au prélable trop de connaissances abstraites.
Prérequis :
| Importer l'article, en version ps ou pdf. |
Pour revenir au sommaire : |
 |
De plus, les vendeurs n'ont de cesse de vanter les qualités des signaux numériques, tant audio que vidéo. Dans cet article, nous limiterons quelque peu cet enthousiasme et verrons qu'un signal numérique construit sans précaution peut présenter des défauts perceptuels flagrants. Fort heureusement, un examen quelque peu minutieux de la nature des signaux numériques et un passage par l'analyse de Fourier nous montrerons comment aisément éviter ces défauts. Par Frédéric Cao, Chargé de recherches IRISA/INRIA.
Signal numérique et théorie de l'échantillonnage
Du compact-disc, au DVD, en passant par l'appareil photo numérique, le scanner, et une hypothétique télévision numérique (plus en panne politique que technologique), le numérique a fait une entrée progressive mais écrasante et sans doute irréversible dans la vie quotidienne. Ce n'est évidemment pas sans raison : pour le meilleur et pour le pire, les signaux numériques sont plus simple à dupliquer (et donc à diffuser), ils peuvent être efficacement compressés et transmis, ils sont faciles à stocker, et on peut aisément les manipuler.
Prérequis :
| Importer l'article, en version ps ou pdf. |
Pour revenir au sommaire : |
 |
Cet article se propose donc de calculer ces intégrales récalcitrantes (qui interviennent dans plusieurs champs de la géométrie) en n'utilisant pas de méthodes excédant le niveau Licence. Par ailleurs, l'auteur utilise un style très personnel rendant vivantes ses pérégrinations au milieu des concepts abstraits foisonnant autour de ces intégrales, et replace les idées dans leur contexte afin de ne pas noyer le lecteur dans la technique. Par Lazare Georges Vidiani, Professeur de Mathématiques, cet article est paru dans le numéro 50 de la revue Quadrature que nous remercions vivement (en particulier Olivier Courcelle qui nous a donné l'accord de publication en quelques heures !).
Les intégrales de Coxeter
En 1926, H.S.M. Coxeter calcula certaines intégrales intervenant dans des calculs de volumes, lors de ses études du groupe cristallographique. Pour ce faire, il utilisa des méthodes géométriques avancées, et soumit la découverte d'une preuve "élémentaire" à la sagacité des lecteurs de la Mathematical Gazette. Seul le mathématicien Hardy trouva une réponse !
Prérequis :
| Importer l'article, en version ps ou pdf (15 pages). |
Pour revenir au sommaire : |
 |
Cette observation contre-intuitive amène à se poser la question des probabilités sur l'ensemble des entiers naturels, et rectifier l'intuition, trompeuse, puis définir la notion d'équirépartition d'une suite de nombre dans [0;1], c'est à dire à définir rigoureusement l'idée qu'une suite peut "tapisser" uniformément [0;1]. Développant cette petite théorie, on arrivera à lever ce paradoxe apparent. Par Thomas Chomette, professeur en classes préparatoires, et Farouk Boucekkine, ENS, d'après un texte de François Fayard, professeur en classes préparatoires.
Equirépartition d'une suite de nombres
Ce texte part d'une observation expérimentale: quand on calcule une trentaine ou plus de valeurs de 2^n , on constate que le premier chiffre est nettement plus souvent "1" que n'importe quel autre. Il arrive dans plus de 30% des cas ! Mais que signifie ce pourcentge ?
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Ce texte nous présente le lemme de Baire, ainsi que son créateur, René Baire, mathématicien maudit du début du XX° siècle. Il nous raconte, comme un récit, certaines théories qui ont révolutionné l'analyse il y a une centaine d'années, en les entremêlant d'éléments biographiques sur les principaux acteurs de ces petites révolutions, Borel, Lebesgue et Baire, moins connu du fait de son histoire plus tragique. Nous y croiserons, pêle-mêle, rivalité entre chercheurs, fonctions pathologiques (continues mais pas dérivables, etc...), remarques générales et petites digressions pour connaisseurs. L'analyse, de nos jours, nécessite un arsenal de notations qui effaye facilement les lecteurs, et il est bon de se (re)plonger dans ces notions, modernes par leur contenu (toujours enseigné dans l'enseignement supérieur) mais qui ont été crées à une époque où l'on écrivait encore les mathématiques presque sans symboles... Par ailleurs, ce texte sera une source d'inspiration et une illustration très intéressante pour ceux qui souhaitent passer l'agrégation de mathématiques, le lemme de Baire et ses applications en étant de grands classiques. Il se termine sur quelques réflexions d'ordre pédagogique à propos des difficultés qu'on peut rencontrer dans la vulgarisation des mathématiques. Nous remercions à cette occasion Paul-Louis Hennequin et Animath pour nous avoir autorisé à utiliser ce texte (et celui de Michèle Audin au paravant.)
Le lemme de Baire
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Ce petit addendum de deux pages démontre un résultat simple mais surprenant : si l'on prend n chiffres quelconques, il existe une infinité de puissances de 2 commençant par ces chiffres ! Par François Lo Jacomo, informaticien, trésorier d'Animath.
Addendum sur l'équirépartition
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Théorie des jeux :
Le Berlekamp's switching game
Le ``Berlekamp's switching game'' est un jeu inventé par Elwin R. Berlekamp et David Gale. Son support est un tableau carré de m*m ampoules, contrôlées par 2m interrupteurs frontaux, un pour chaque ligne ou colonne. Quand un interrupteur est basculé, les ampoules qui étaient allumées dans la ligne ou la colonne correspondante sont éteintes, et celles qui étaient éteintes sont allumées. Le jeu consiste à trouver, pour un état initial donné, le nombre minimal d'ampoules allumées après manipulation à volonté des interrupteurs commandant les lignes et les colonnes, puis à maximiser ce nombre par un choix judicieux de l'état initial.
Par Jonathan Le Roux, ENS. Texte adapté d'un travail réalisé dans le cadre des TIPE, sous la direction de Philippe Esperet, professeur de Maths Spé MP* au lycée Henri IV, Paris Vè.
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Jeux sur les graphes et théorème de Ramsey
Si l'on prends six personnes au hasard, alors trois d'entre elles se connaissent, ou alors on peut en trouver trois dont aucune ne se connaissent. Cette remarque, en apparence anodine, permet de déboucher sur toute une théorie combinatoire. En effet, reformulée en termes de graphe, cela signifie que, si l'on colorie les arêtes du graphe complet à six sommet en deux couleurs, alors on peut trouver un triangle dont les trois arêtes sont de la même couleur. La question se pose alors pour d'autres type de configurations, et l'on verra que le résultat reste valable à condition de colorier les arêtes d'un graphe suffisamment gros. (par Thomas Chomette)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Jeux et stratégies
Comment gagner à coup sûr au jeu de Nim ? Peut-on gagner à coup sûr aux échecs ? Ou bien est-ce qu'au contraire deux ordinateurs infiniment puissants jouant l'un contre l'autre aboutiraient nécessairement à une partie nulle ?
Toutes ces questions tournent autour de la notion de stratégie, le jeu de Nim comme le jeu d'échecs étant des jeux à deux joueurs, finis. Après avoir montré que l'étude de tous ces jeux peut se ramener à des propriétés de certains arbres, nous définissons ici la notion mathématique de stratégie. L'intérêt étant que, notamment, ce formalisme nous permet de savoir que va être l'issue de la partie, si les deux joueurs jouent parfaitement. (par Thomas Chomette)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Algèbre :
Le Rubik's cube, Groupe de poche
Résumé- Ce petit texte vise à expliquer pourquoi, si on démonte le cube de Rubik et qu'on le remonte au hasard, on a une chance sur douze de pouvoir le résoudre. La démonstration est un joli exercice de théorie des groupes utilisant, en particulier, la notion d'action de groupe opérant sur un ensemble.
Utilisation en classe- Cet article illustre de façon originale la notion d’action de groupe opérant sur un ensemble. Le lecteur qui n’aurait pas manipulé cette notion depuis un certain temps pourra trouver les prérequis nécessaires sur CultureMATH dans l'article Intoduction à la théorie des groupes de Farouk Boucekkine et Thomas Chomette.
Ce texte n’est pas utilisable dans l’enseignement secondaire ;en revanche, les enseignants du supérieur trouveront dans cet article une façon originale pour aider leurs étudiants à maîtriser le vocabulaire d'action de groupes.
Lire l'article
La transformation du Boulanger
 |
|
Le lecteur est habitué aux lois de groupe usuelles dans des ensembles algébriques, parfois géométriques plans sur une hyperbole ou une cubique (en liaison avec les critères d’alignement de trois points, succédané des conséquences du théorème d’Abel, et utilisé maintenant en codage elliptique). Voici un exemple de loi de groupe sur une surface. Cette loi a été proposée dans un problème de concours à l’école supérieure des Industries chimiques de Nancy en 1947, dont l’énoncé est partiellement reproduit dans les « Exercices de Géométrie » de E. Râmis. Ce sujet fait partie d’une dizaine de problèmes très originaux pour l’époque dont l’auteur était Jean Frédéric Auguste Delsatre, qui était alors le Doyen de la Faculté des Sciences de Nancy. Son thème est le point de départ périodiquement de nombreuses questions d’oral des concours. Utilisation : montrer que la théorie des groupes a des illustrations géométriques et ne se réduit pas à des manipulations algébriques. Par Lazare Georges Vidiani, Professeur de Mathématiques. Importer l'article en version pdf (3 pages)
Loi de groupe sur une surface.
Équations algébriques
Une équation n'est rien d'autre qu'une égalité entre deux membres. Souvent, il s'agit de déterminer une certaine quantité, connaissant simplement une égalité qui fait intervenir cette quantité inconnue. On parle d'équation algébrique lorsque l'on cherche à déterminer les racines d'un polynôme. Nous allons ici nous intéresser plus spécifiquement à ce type d'équation, et voir notamment des méthodes générales pour résoudre les équations algébriques de degré allant de 1 à 4. (d'après un article de Xavier Caruso, ENS, et un historique issu du forum fr.sci.maths, dont on peut trouver une compilation sur le site faq.maths)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Intégration de polynômes, points de Gauss
Peut-on calculer l'intégrale d'une fonction (sur l'intervalle [0,1] par exemple) si l'on ne connaît que sa valeur en 3 points ? Évidemment non, sauf si l'on sait en outre qu'il s'agit d'un polynôme de degré 2 ! Facile, me direz vous : dans ce cas, la donné des valeurs en trois points, quels qu'il soient, permet de retrouver le polynôme et donc de calculer cette intégrale. Beaucoup plus fort : si l'on choisit correctement ces trois points, on peut calculer l'intégrale de n'importe quel polynôme de degré 5, en ne connaissant que sa valeur en nos trois points. Et cette fois, plus question de trouver le polynôme... (par Thomas Chomette, sur une suggestion de Charles Torossian, ENS/CNRS.)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Par Michel Broué, Professeur, Directeur de l'Institut Henri Poincaré. Cet article a été publié dans "Le temps des savoirs", Revue de l'Institut Universitaire de France, 4 , D.Rousseau & M.Morvan eds., Odile Jacob, Paris (2002), pp. 37-78. Nous remercions vivement son auteur pour son amabilité.
Les tonalités musicales vues par un mathématicien
L'objet de cet article est, en particulier, de montrer que le choix des 7 notes de la gamme classique (do-ré-mi-fa-sol-la-si) parmi les 12 notes du système tempéré (do-do#- ré-ré#-mi-fa-fa#-sol-sol#-la-la#-si) est le seul choix possible qui satisfasse à des critères naturels liés à la transposition. L'approche utilisée, qui n'emploie que des considérations mathématiques élémentaires, fournit également des justifications purement mathématiques ou combinatoires à l'usage de la gamme mineure augmentée (la-si-do-ré-mi-fa-sol#) ou d'autres gammes utilisées dans l'histoire (telle la gamme pentatonique javanaise), ou encore à l'importance d'autres gammes et accords classiques de l'harmonie musicale.
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Ce texte en deux parties a pour but d'introduire les lecteurs à cette avancée majeure du dix-neuvième siècle qu'est la notion de groupe. Il a été écrit afin de servir d'appoint aux candidats à l'agrégation interne ou externe, mais aussi pour toute personne désireuse de se cultiver ! La notion de groupe et ses applications les plus classiques est présentée ici avec deux objectifs. Premièrement, donner une base solide permettant de lire des textes utilisant cette notion (comme Les colliers de Polya. Deuxièmement, essayer de faire sentir les idées générales qui sous-tendent les définitions et résultats présentés, que l'on retrouvera dans l'étude d'autres structures algébriques. Comme le texte est long, une version courte est disponible pour ceux qui n'auraient besoin que d'une référence rapide. Ainsi, on entre ici dans des considérations plus techniques: quelques exemples plus développés, la notion de sous-groupe distingué, souvent mal comprise, décortiquée... Mais on survole également sans entrer dans les détails des applications historiques ou des développements modernes. N'hésitez pas à nous demander de développer certains points survolés ici ! Par Farouk Boucekkine (avec l'aide de Thomas Chomette), ENS.
Introduction à la Théorie des Groupes
Première Partie :
Deuxième Partie :
Cette Deuxième Partie, plus courte, a pour but d'ouvrir les notions présentées auparavant vers les travaux les plus modernes d'une part, et les applications importantes de la théorie d'autre part.
Prérequis :
| Importer la Première Partie entière au format ps ou pdf. | ||
| Importer sa version courte au format ps ou pdf. | ||
| Importer la Deuxième Partie au format ps ou pdf. | Pour revenir au sommaire : |
 |
Eh bien tous sauf un peuvent le savoir, s'ils se mettent d'accord au préalable sur la stratégie à adopter ! Maintenant imaginons qu'il y ait plusieurs couleurs, voir une infinité, et pourquoi pas, une infinité de fêtards, que se passe-t-il ? En utilisant des mathématiques de plus en plus sophisitiquées (arithmétique élémentaire niveau collège, groupes, espaces vectoriels puis théorie des ensembles), l'auteur généralise peu à peu le résultat... Par Florent Benaych-Georges, Maître de conférences en Mathématiques, Université Paris 6 et École Polytechnique.
Des chapeaux, des couleurs et des structures algébriques
Imaginez une ronde de 100 personnes, portant tous des chapeaux de deux couleurs différentes. Chacun connait la couleur du chapeau de tous les autres, mais pas celle du sien. Maintenant, chacun son tour, les joyeux lurons peuvent dire un et un seul nom de couleur. Quand tous auront parlé, combien au maximum de personnes pourront connaître à coup sûr la couleur de leur chapeau ?
Prérequis :
| Importer le texte au format ps ou pdf. |
Logique, fondements des mathématiques :
Les axiomes de Zermelo-Fraenkel
La théorie des ensembles est entre autres choses une tentative de formalisation, dans un système d'axiomes assez simples et si possible intuitifs, de l'ensemble des connaissances mathématiques. En particulier, l'essentiel de l'arithmétique ou de l'analyse se déduirait de façon élémentaire, quoique assez longue, de cette axiomatique.(par Thomas Chomette)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Construction des entiers naturels
Nous présentons ici une définition et l'étude des propriétés élémentaires de l'ensemble des entiers naturels, définis dans le cadre axiomatique de la théorie des ensembles. Nous utilisons ces propriétés sans y penser, elles nous semblent évidentes... Mais peut-être méritent elles parfois que l'on s'y attarde quelque peu ? (par Jean Gounon, professeur au lycée Camille Sée)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Entiers relatifs
Ayant construit les entiers naturels, quoi de plus naturel que de passer aux entiers relatifs. Là aussi, la présentation choisie est la plus axiomatique et rigoureuse possible. Partant de la définition des relatifs, vus comme des classes d'équivalence pour une relation d'équivalence bien choisie sur les couples d'entiers naturels, on en arrive peu à peu jusqu'à l'arithmétique élémentaire. (par Jean Gounon, professeur au lycée Camille Sée)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Nombres rationnels
Dans la droite ligne des constructions précédentes, nous construisons ici l'ensemble des rationnels, à partir d'une relation d'équivalence sur les couples de relatifs. Nous définissons les opérations plus et multiplier sur ce nouvel ensemble, la relation d'ordre, etc, en montrant que tout ceci prolonge en réalité les opérations déjà définies pour les relatifs.(par Jean Gounon, professeur au lycée Camille Sée)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Nombres réels
Ayant construit les rationnels, voici bien sûr les réels, par la méthode des suites de Cauchy. Comme pour les rationnels, il faut vérifier que le nouvel ensemble étends celui des rationnels, et que les opérations, la relation d'ordre, la valeur absolue, se prolongent à l'ensemble des réels.
Puis, sans bien sûr épuiser le sujet, nous nous penchons sur les propriétés topologiques de l'ensemble des réels : complétude, propriété de la borne supérieure ; propriétés qui sont à la base de toute l'analyse réelle. (par Jean Gounon, professeur au lycée Camille Sée)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Nombres complexes
Reste encore un pas à franchir dans nos extensions d'ensembles de nombres. Certaines équations algébriques extrêmement simples, à coefficients réels, restent sans solution réelle (par exemple, les réels négatifs ne sont pas les carrés de réels). D'où la nécessité d'étendre encore une fois notre ensemble de nombres, en formant un sur-corps du corps des réels, dont les éléments seront appelés nombres complexes. Ce sur-corps se révélera algébriquement clos, c'est-à-dire que cette fois toute équation algébrique (à coefficients complexes) aura des solutions (complexes).
Le premier texte défini l'ensemble des complexes, et motive cette construction en montrant par des moyens élémentaires que l'on a des solutions à toute équation de degré deux. Le deuxième, assez technique, introduit la notion d'argument, nécessaire au troisième et dernier texte, dont l'objet est de montrer la clôture algébrique de C. (par Jean Gounon, professeur au lycée Camille Sée, et Thomas Chomette)
Prérequis :
| Nombres complexes (ps ou pdf), argument d'un nombre complexe (ps ou pdf), clôture algébrique de C (ps ou pdf). | Pour revenir au sommaire : |
 |
Quaternions
C'est en essayant de trouver une multiplication sur les triplets de réels (la multiplication sur les complexes correspondant à une multiplication sur les couples de réels) qu'Hamilton découvrit en 1843 les quaternions sur le "Brougham Bridge" à Dublin, gravant sa découverte sur une pierre du pont. L'obstacle majeur était que les quaternions sont en fait représentés par des quadruplets (et non des triplets) de réel, ce qui fait en réalité du corps des quaternions une extension de celui des complexes, même si on perd au passage la commutativité de la multiplication.
Après avoir construit le corps des quaternions de la façon la plus élémentaire possible, nous étudions les relations entre ceux-ci et les rotations dans l'espace à 3 dimension. (d'après Jean Gounon, professeur au lycée Camille Sée)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Ordinaux
Nous introduisons la notion d'ordinal de la façon la plus élémentaire possible, afin d'en présenter quelques propriétés, qui nous ont paru les plus importantes. Nous ne prétendons pas en faire une étude complète : par exemple, nous passons sous silence les notions d'addition, de multiplication ou d'exponentiation ordinale, qui sont des notions plus difficiles qu'il n'y paraît et mériteraient plus de travail. (d'après Jean Gounon, professeur au lycée Camille Sée)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Cardinaux
Dans ce texte, nous allons présenter la théorie des cardinaux, du moins son début : définition, cardinal d'un ensemble et théorème de Cantor-Bernstein, addition et multiplication cardinale. En revanche, nous passerons sous silence le problème de l'exponentiation cardinale, qui est autrement plus compliquée. (d'après Jean Gounon, professeur au lycée Camille Sée)
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Cette construction a l'avantage de donner très facilement la densité des rationnels dans les réels, mais est en revanche plus laborieuse en ce qui concerne les opérations algébriques. A vous de choisir (vous pouvez prendre les deux !) Par ailleurs, elle peut être utile pour les concours de recrutement. Par Jean Gounon, professeur de mathématiques.
La construction des Réels par les coupures de Dedekind
Nous avons déjà vu une construction du corps des Réels dans ce site (voir ci-dessus). Nous en donnons une autre, moins complexe et moins universelle, fondée sur la relation d'ordre naturelle des rationnels.
Prérequis :
| Importer l'article en version ps ou pdf. | Pour revenir au sommaire : |
 |
Laplace, Turing et la géométrie impossible du "jeu de l'imitation"
Dans un article de 1950, devenu justement célèbre, Alan Turing propose, en vue d'opérer une comparaison fonctionnelle entre le cerveau et la machine, un jeu qu'il appelle "jeu de l'imitation". Cet article fut un pas décisif dans le domaine de la philosophie de la connaissance.
Le texte que nous vous proposons présente un point de vue cognitif sur la question de la différence entre la pensée humaine, continue, et le fonctionnement d'une machine à états discrets. (Par Giuseppe Longo, Directeur de Recherche en informatique théorique, CNRS et ENS.)
Ce texte a été publié dans la revue Intellectica, n. 35, 2002/2, pp. 131-162, nous remercions l'auteur pour son amabilité.
Prérequis :
| Importer l'article au format ps ou pdf. | Pour revenir au sommaire : |
 |
Mais il fut également un astronome et un physicien de tout premier plan, grâce à ses va-et-vient incessants entre expérience et théorie. Scientifique complet, il n'en fut pas moins homme et eut sa part de drames personnels, dans une période fort troublée de l'histoire de l'Europe : la première moitié du XIX° siècle. Dans ce dossier, nous vous proposons la biographie d'un homme de génie, qui transcenda les frontières entre les sciences. A l'aspect biographiques nous avons ajouté des remarques mathématiques dont certaines pourraient faire l'objet d'études en classe. (Par Farouk Boucekkine, ENS) La confection de ce dossier doit beaucoup au livre de Simon Gindkin histoires de mathématiciens et de physiciens, traduit en Français par Jean-Michel Kantor aux éditionsCassini. Nous vous recommandons vivement de consulter leur catalogue ! Par ailleurs, pour la question de la construction de polygones réguliers à la règle et au compas, évoquée dans ce texte, nous vous conseillons de consulter le dossierConstruction des polygones réguliers, où elle est traitée in extenso.
Carl Friedrich Gauss, le Prince des Mathématiciens
C. F. Gauss est toujours considéré par certains comme le plus grand mathématicien de tous les temps. Sa capacité calculatoire hors du commun, couplée à son goût pour la contemplation des idées abstraites l'on amené à résoudre des problèmes (parfois vieux de millénaires !) et à envisager avec une clarté géniale (bien qu'inquiète) les idées qui feraient les mathématiques du futur.
Prérequis :
| Importer l'article au format ps ou pdf. | Pour revenir au sommaire : |
 |
Par Lazare Georges Vidiani, Professeur de Mathématiques. Résumé - Cet article a été publié dans la revue Quadrature ("Magazine de Mathématiques pures et épicées") numéro 56 AVRIL JUIN 2005 P 30-31. L'éditeur EDP nous a autorisé à le reproduire sur le site culture Math et nous l'en remercions. Voici un lien vers le site de Quadrature http://www.edpsciences.org/journal/index.cfm?edpsname=qua... Dans l'article sur les intégrales de Coxeter, nous avons évoqué, le parcours exceptionnel du mathématicien suisse autodidacte Ludwig Schläfli. Il reçut le prix Steiner en 1930, pour sa découverte -avant Juel- des 27 droites d'une surface cubique non réglée (voir sur le site culture math, un excellent et audacieux article sur ce sujet). Le but de cet article est de rendre accessible la liste exhaustive des lauréats de ce prix, qui furent tous des savants d'envergure internationale.
Le prix Steiner
| Importer l'article au format pdf | Pour revenir au sommaire : |
 |
Daniel Goffinet, Professeur de Mathématiques. Résumé - Il s'agit d'un surprenant problème de collision qui a fait l'objet du "problème du mois" d'avril 2007: se présentant comme de la mécanique, il se révèle être un moyen (peu efficace!) de calculer Pi. La solution peut être obtenue par des méthodes géométriques ou algébriques. L'article comprend: Importer l'article en version pdf [158 Ko, 14 pages]
Mécanique et cinématique
Compte de rebonds
La toupie Tippe-Top
|
Lazare Georges Vidiani, Professeur de Mathématiques. Résumé - En 1952, dans le commerce des jouets, quand celui ci proposait des objets instructifs et éveillant questions et imagination, humour et habileté manuelle (Wondergraph, père la colique, etc), -contrairement à notre période où les jeux se réduisent à des peluches ou des touches de commande életronique-, une petite toupie en plastique faisait fureur chez les enfants et les adultes d'esprit jeune. Il s'agissait d'une toupie appelée Tippe-Top, de révolution, constituée de deux parties: l'une était une calotte sphérique d'axe z'z, et l'autre un cylindre d'axe z'z emmanché perpendiculairement au plan de la calotte sphérique, l'ensemble formant un seul solide. L'originalité de la toupie ainsi formée est qu'une fois lancée, elle se retourne sur son manche, en continuant de tourner. Son mouvement fascina même les deux prix Nobel de physique Pauli et Bohr :http://www.fysikbasen.dk/TippetopENGLISH.php Une revue scientifique grand public eut le malheur et l'inconscience de prétendre que cette propriété ne pouvait se justifier scientifiquement : l'année suivante cette toupie faisait l'objet de la partie V du problème d'Agrégation de Mécanique rationnelle 1953, dont l'auteur était Luc Gauthier. Gérard Egheter, dont le site donné bas de colonne 1 de la page 9 de l'article vaut le détour, m'a communiqué le corrigé manuscrit de Jean Frédéric Auguste Delsarte, que sa fille m'a autorisé à reproduire. Ce Normalien (Ulm 1922) fut notamment quatrième à l'Agrégation 1925, membre du groupe Bourbaki, fut Doyen de la faculté des Sciences de Nancy, et dès 1947 il conçut une douzaine de problèmes de concours très originaux pour l'époque (et la nôtre....) en particulier celui des Mines de Nancy 1947 dont vous aurez l'essentiel en allant voir sur culture math, l'article (excellent) loi de groupe sur une surface. Le corrigé est dans le TAPE donné en lien (Tiré A Part Electronique aimablement autorisé par le Directeur Olivier Courcelle de la Revue Quadrature 59 (Janvier Mars 2006) "Revue des mathématiques Pures et Epicées) ; Culture Math remercie l'éditeur EDP qui l'a autorisé à diffuser l'article sur le site CultureMath. Voici, en remerciement, un lien vers le site de Quadrature http://www.edpsciences.org/journal/index.cfm?edpsname=qua... |
Importer l'article en version |
Liens Une bonne animation, valant mieux qu'un long discours rasant allez voir en http://public.planetmirror.com/pub/irtc/anims/2001-04-15/... ou encore mieux localisé sur une assiette http://www.science.unitn.it/~karwasz/toys/files/mech/bacz.... (Faire un click sur les cases d'animation, puis click droit et cocher dans le menu qui apparait "diffuser dans real Player"). Petite anecdote historique : L'inventeur (1950), le danois Werner Ostberg raconte qu'il a eu l'idée de la toupie tippe top, en observant, dans la jungle sud-américaine, que lorsqu'on coupe le fond d'une calebasse http://fr.wikipedia.org/wiki/Calebasse, il présente, si on le fait tourner, les mêmes propriétés que le tippe-top En fait c'est une re-découverte (voir l'historique page 2 de .http://www.fysikbasen.dk/TippetopENGLISH.php) car l'objet date de 1890 (John Perry) et 1891 (Helene Sperl), si l'on n'accepte pas d'anticiper dès le début des années 1800 par l'étude des anagyres par Sir William Thomson et Hugh Blackburn. Sur CultureMath Arc en ciel, soucoupes volantes, toupies, courbes elliptiques, et tout ça, par Michèle Audin (2004) Voir aussi Le cas de Kowalevski, par Michèle Audin (2006) - Ce que les mathématiciens appellent, depuis 1888, « le cas de Kowalevski », c’est une sorte de gyroscope, un genre de toupie si l’on préfère, dont la découverte a ouvert quelques portes sur des allées des mathématiques que l’on n’a pas fini d’explorer. Mon choix de Sophie, par Michèle Audin (2006) - Un article sur Sophie Kowalevski, son image, sa toupie et sa réputation scientifique. Jean Gounon, lycée Camille Sée, Paris Résumé: Ce texte a pour objectif de présenter, de la façon la plus simple possible, les fondements mathématiques de la théorie de la Relativité (surtout générale) ; ces fondements constituent les bases de la branche des mathématiques appelée Calcul Tensoriel. A l'inverse des présentations habituelles qui, centrées sur la Relativité, donnent une liste rapide de quelques définitions et résultats pratiques indispensables de calcul tensoriel, cette étude s'intéresse avant tout aux bases mathématiques de la théorie physique qu'est la Relativité. Cette dernière n'est envisagée ici que du point de vue de son articulation avec la théorie mathématique qui la précède ; elle n'est donc pas développée pour elle-même : nous renvoyons, pour son contenu et la révolution qu'elle a apporté en physique, aux nombreux livres et sites consacrés à ce sujet.
Mathématiques pour les sciences physiques et les sciences de la nature
Calcul Tensoriel. Application à la relativité.
Livres
| Importer l'article en version pdf. | Pour revenir au sommaire : |
 |
Ajoutons que ce texte est une petite expérience mathématico-informatique puisqu'il inclut des formules (sous la forme de ficiers .gif) et des liens hypertexte vers un début de glossaire. Par conséquent, n'hésitez pas à nous écrire si vous avez des problèmes techniques en le lisant (à ce propos, il est préférable de le consulter avec Internet Explorer ou Mozilla, car Netscape et Safari ont du mal à aligner les images correctement avec le texte !) Enfin, ajoutons que ce document est le point de départ d'un dossier "Maths et Bio", qui s'étoffera dans les mois à venir. N'hésitez pas à nous faire des commandes ! Par Hatem Zaag, chargé de recherche CNRS à l'Ecole Normale Supérieure.
Pourquoi les équations aux dérivées partielles interviennent-elles en biologie ?
Ce texte est une introduction rapide aux problématiques qui se posent aux mathématiciens qui s'intéressent à la biologie. Partant d'une interrogation légitime ("Les maths peuvent-elles être efficaces en biologie ?"), il se concentre ensuite sur la description d'un exemple d'application intéresante, la modélisation du chimiotactisme chez certaines amibes, montrant à la fois l'intérêt du langage mathématique, et les difficultés qu'on peut avoir pour résoudre un problème aussi complexe qu'un problème de biologie.
Prérequis :
| Cet article est disponible sous format HTML. |
Pour revenir au sommaire : |
 |
Équation de la chaleur : traitement numérique.
L'équation de la chaleur est à l'origine de nombreux problèmes, souvent difficiles, et a fait couler beaucoup d'encre. Nous nous restreignons ici à un cas particulier, avec des conditions de départs assez simple, de sorte que la solution exacte soit connue. Celle-ci va nous permettre d'apprécier l'efficacité (ou les défauts) des méthode numériques de résolution approchée. On montrera et on expliquera à travers cet exemple les différences fondamentales entre méthodes implicites et explicite. Texte accompagné de simulations numériques en java. Les algorithmes sont également déclinés et mis à disposition en version matlab et scilab (scilab est un logiciel libre distribué par l'INRIA, que l'on peut télé-charger ici).
Par Thomas Chomette, avec l'aide d'Emmanuel Grenier, ENS Lyon.
Prérequis :
| L'article seul, en version ps ou pdf. Illustrations numériques et programmes, disponibles en version html. |
Pour revenir au sommaire : |
 |
Saviez-vous que le sexe des crocodiles n'est pas déterminé génétiquement dès la conception, comme c'est le cas pour nous autres mammifères ? En fait, si l'œuf est pondu près de l'eau, dans une terre humide et donc fraiche, il donnera une femelle, s'il est pondu sur une terre sèche et donc plus chaude, il donnera un mâle ! Bien entendu, un milieu "intermédiaire" donnera des résultats intermédiaires... Cette spécificité a permis aux crocodiles de survivre quelques centaines de milions d'années aux catastrophes qui ont fait diparaître nombre d'autres espèces. Ce texte nous donne un modèle mathématique pour étudier l'évolution d'une population de crocodiles, et comparer cette évolution à celle d'une population où la détermination du sexe se fait génétiquement. Par Sylvain Arlot, élève de l'Ecole Normale Supérieure.
Détermination du sexe selon la température chez les crocodiles
Prérequis :
| Importer l'article, en version ps ou pdf. |
Pour revenir au sommaire : |
 |
Nous nous intéressons ici à un modèle d'interaction proies-prédateurs, proposé par Volterra après la première guerre mondiale. Il s'agissait alors d'expliciter la dynamique des populations de sardines et de requins en mer Adriatique ; expliquer notamment pourquoi les quantités de sardines pêchées après l'interruption due à la guerre n'étaient plus aussi importantes que précédemment et pourquoi à la reprise de la pêche la proportion observée de requins avait augmenté.
Interactions entre espèces, modèle de Lotka-Volterra
C'est l'occasion d'une étude qualitative assez complète de certains systèmes différentiels. Le texte proprement dit est accompagnés de simulations numériques (applets java). Les programmes utilisés sont également disponibles, commentés, en version matlab et scilab (scilab est un logiciel libre distribué par l'INRIA, que l'on peut télé-charger ici).
D'aprés un article de Vincent Calvez et Xavier Lafon, ENS (article intégral disponible sur le site du groupe de travail Mathématiques-Biologie). Illustrations de Thomas Chomette.Prérequis :
| L'article seul, en version ps ou pdf. Illustrations numériques et programmes, disponibles en version html. |
Pour revenir au sommaire : |
 |
Il n'y a pas d'exposé général dans ce texte, qui ne parle que du cas des dimensions 3 et 4, mais les objets et les méthodes présentés ici sont asiément généralisables à une dimension finie quelconque. Par Thierry Levy, chercheur CNRS à l'ENS.
Equations de Maxwell et formes différentielles, vers la relativité restreinte
Ce texte a pour but de présenter les formes différentielles, objet très important dans les mathématiques et la physique moderne, à travers une application classique : la reformulation des Equations de Maxwell (qui modélisent l'électromagnétisme) sous une forme plus compacte et décrivant mieux les symétries observées expérimentalement des champs électrique et magnétique.
Prérequis :
| Importer l'article en version ps ou pdf. |
Pour revenir au sommaire : |
|
Histoire et épistémologie des Mathématiques :
19:30 Publié dans Dossiers Scientifiques: classement thématique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Préface du livre L’algèbre au temps de Babylone : Quand les mathématiques s’écrivaient sur de l’argile de Jens Høyrup
Une invitation à entrer dans un monde mathématique ancien
REHSEIS—SPHERE (UMR 7219, CNRS & Université Paris Diderot) - e-mail
Article déposé le 22 septembre 2010. Toute reproduction pour publication ou à des fins commerciales, de la totalité ou d'une partie de l'article, devra impérativement faire l'objet d'un accord préalable avec l'éditeur (ENS Ulm). Toute reproduction à des fins privées, ou strictement pédagogiques dans le cadre limité d'une formation, de la totalité ou d'une partie de l'article, est autorisée sous réserve de la mention explicite des références éditoriales de l'article. CultureMATH remercie les éditions Vuibert pour avoir autorisé la réédition de ce texte .

Notre connaissance des mathématiques élaborées voici quelque quatre mille ans sur les rives du Tigre et de l’Euphrate est très récente. Ce n’est que dans la première moitié du siècle dernier que le mathématicien et historien des mathématiques Otto Neugebauer ainsi que l’assyriologue Thureau-Dangin ont fait émerger un continent insoupçonné de savoirs mathématiques, en parvenant à déchiffrer des tablettes excavées au cours des décennies antérieures lors de fouilles archéologiques en Mésopotamie — c’est-à-dire, en gros, dans l’Irak contemporain. Les deux érudits ont en particulier établi, dans les années 1930, que le b² - 4ac qui accompagne aujourd’hui le trajet scolaire de tout un chacun avait eu depuis bien longtemps une forme d’existence dans les tablettes cunéiformes. Les scribes anciens nous ont en effet laissé des tablettes qui posaient systématiquement des problèmes où l’on peut reconnaître des équations quadratiques, et ils les résolvaient non moins systématiquement en recourant à un équivalent du b² - 4ac qui nous est familier. C’est depuis lors que l’on parle d’« algèbre babylonienne ».
Pour interpréter lesdites tablettes, Neugebauer et Thureau-Dangin se sont appuyés sur les connaissances mathématiques dont ils disposaient. Il n’y a là rien que de bien normal. L’historien mobilise toujours ses savoirs propres, mathématiques entre autres, au cours d’un travail d’exégèse. C’est sur cette base que Neugebauer et Thureau-Dangin ont pu percevoir, dans les textes en question, l’énoncé d’équations et leur résolution numérique à l’aide de suites d’opérations arithmétiques portant sur les données des problèmes et correspondant aux formules bien connues.
Dire que des savoirs présents entrent toujours dans la manière dont nous comprenons les écrits du passé, c’est aussi dire que toute évolution de nos connaissances mathématiques est susceptible de provoquer une mutation dans notre interprétation des textes anciens. C’est bien ce qui se produisit dans les années 1970 à propos des tablettes babyloniennes. Avec la multiplication des ordinateurs, l’intérêt pour les algorithmes a crû de façon notable en mathématiques. Dans ce contexte, la réflexion sur cette forme de pratique des mathématiques a mûri, et l’un des acteurs majeurs du développement de l’algorithmique, Donald Knuth, a proposé de relire les tablettes mésopotamiennes comme de premiers témoins de l’écriture d’algorithmes [1]. Il a depuis fait école dans l’historiographie des mathématiques de l’Antiquité.
C’est à partir de tout autres bases que Jens Høyrup a conçu une nouvelle approche des textes cunéiformes. Sa démarche fait écho aux exigences qui se sont élaborées en histoire des sciences au cours des dernières décennies et qui ont accompagné la professionnalisation de cette discipline. L’histoire des sciences s’est constitué comme domaine d’intérêt au XIXe siècle du fait, pour l’essentiel, des travaux d’amateurs éclairés. La première période fut une période de moissons, visant à établir les textes du passé et à repérer les innovations en vue de produire une chronique des progrès. Les limites de cette approche se sont manifestées de toutes parts, ce n’est pas ici le lieu d’en proposer une analyse. Disons simplement que les historiens ont été de ce fait conduits à privilégier aujourd’hui certaines questions et méthodes spécifiques.
Je retiendrai de ce processus de maturation de l’histoire des sciences une exigence essentielle qui s’est imposée et qui permet de situer l’approche des tablettes babyloniennes que Høyrup a développée, renouvelant ainsi en profondeur notre lecture de ces textes. Les historiens des sciences ne se contentent plus, en effet, d’établir le fait qu’un collectif humain savait « que ». Ils ont saisi l’importance de comprendre « comment » ce collectif humain savait « que ». On peut interpréter ce « comment » de bien des manières. J’en illustrerai quelques-unes en dégageant les traits saillants du travail de Jens Høyrup.
Que les tablettes babyloniennes manifestent une connaissance de la résolution des équations quadratiques, c’était hier un résultat. Ce n’est plus aujourd’hui, pour un historien comme Jens Høyrup, qu’un point de départ. Il s’étonne, dans un premier temps, que les interprètes contemporains glosent des termes différents employés par les scribes comme renvoyant à une même opération arithmétique. Il s’attelle dès lors à comprendre les subtilités de la langue technique à l’aide de laquelle les algorithmes sont consignés dans les textes. Ce travail d’analyse terminologique l’amène à établir un fait majeur : les termes en question ne renvoient pas seulement à des opérations arithmétiques, comme une première lecture en avait fait l’hypothèse, mais ils indiquent dans le même temps des manipulations à pratiquer sur un support graphique.
Ce résultat est essentiel à plus d’un titre. Il nous permet de comprendre que les textes cunéiformes ne sont pas de pures prescriptions, mais qu’ils rendent compte aussi bien — et par le même énoncé — des raisons pour lesquelles les opérations sont employées. Notre perception de la nature de ces écrits comme textes techniques s’en trouve profondément modifiée tout comme l’est notre compréhension de l’activité intellectuelle qui a produit ces textes et qui permet de les employer. Par ailleurs, en nous appuyant sur cette nouvelle interprétation, nous pouvons percevoir, en creux, par delà les tablettes babyloniennes, des éléments du dispositif de travail au sein duquel les scribes pratiquaient les mathématiques. Ce sont ces éléments qui ont par suite incité Jens Høyrup à se lancer à la recherche des indices qui permettraient de préciser la nature des supports graphiques qu’utilisaient les scribes.
De tout cela, il ne ressort pas une simple description de la manière dont les praticiens travaillaient les mathématiques. Nous disposons désormais d’outils d’interprétations qui nous permettent de tirer plus amplement parti des traces écrites qui sont parvenues jusqu’à nous. Nous comprenons mieux la nature des « équations » résolues à Babylone et la forme spécifique d’algèbre cultivée voici quatre mille ans dans le croissant fertile.
Un monde ancien qui avait disparu ressurgit un peu plus du néant. Un monde qui nous aide à percevoir la bigarrure des pratiques mathématiques et dans lequel nos mathématiques trouvent l’une de leurs racines.
Nous sommes redevables à Jens Høyrup de nous avoir restitué pour partie ce monde. Il a distillé des décennies de recherches sur ces tablettes pour en nous offrir l’essence dans ce livre qu’il a voulu accessible au plus grand nombre. Saisissons cette invitation à voyager par les mathématiques. Saisissons cette opportunité de comprendre comment une mathématique peut être ni tout à fait la même que la « nôtre », ni tout à fait une autre.
Références
Knuth, Donald, 1968. The art of computer programming. Reading, Mass.: Addison-Wesley Pub. Co., 1968.———, 1972. "Ancient Babylonian Algorithms", Communications of the ACM 15, no. 7 (1972): 671-677.
———, 1976. "Ancient Babylonian Algorithms", Communications of the ACM 19, no. 2 (1976): 108.
[1] L’ouvrage phare des débuts de l’algorithmique est dû à D. Knuth : Donald Knuth, The art of computer programming (Reading, Mass., 1968). D. Knuth a analysé les particularités des textes mésopotamiens du point de vue de l’écriture d’algorithmes dans Donald Knuth, "Ancient Babylonian Algorithms", Communications of the ACM15 (1972), Donald Knuth, "Ancient Babylonian Algorithms", Communications of the ACM 19 (1976). Signalons que cette transformation de notre interprétation des textes anciens ne s’est pas limitée aux tablettes mésopotamiennes, puisque sous l’influence de D. Knuth, le mathématicien Wu Wenjun proposait une nouvelle approche des écrits mathématiques de la Chine ancienne depuis la même perspective.
19:29 Publié dans L’algèbre au temps de Babylone | Lien permanent | Commentaires (12) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Approche critique comparée des nombres aztèques et mayas
Histoire des mathématiques
|
|
Index des documents |
Pages chronologiques |
Résumés
|
Résumés
Approche critique comparée des nombres aztèques et mayas
Par André Cauty, Professeur des Universités à Bordeaux 1, équipe CELIA (CNRS) Résumé - Cette approche critique des nombres aztèques et mayas voudrait attirer l'attention des lecteurs sur les principaux systèmes d'écriture du nombre en usage dans l'antiquité mésoaméricaine. Les principaux sont les numérations écrites mayas et aztèques. La numération vigésimale de position des scribes mayas, de l'époque classique et des codex du postclassique, qui l'utilisèrent pour noter les dates dites du Compte long sous la forme d'un nombre à cinq chiffres exprimant, en nombre de jours, la durée écoulée depuis la date origine de la chronologie maya (11/08/-3113). La numération vigésimale additive des scribes aztèques, qui l'utilisèrent notamment pour noter, le plus souvent sous forme de nombres ronds à un ou deux chiffres significatifs, les quantités de tributs que chaque communauté devait remettre à la Triple Alliance. Autre différence, les Mayas écrivaient de nombreuses égalités liant dates et durées, tant de la vie politique des cités que des récits mythologiques. Les Aztèques n'ont pas écrit d'égalités, et ils n'ont même pas laissé de dates en calendrier de l'année vague solaire (l'année mésoaméricaine de 18 x 20 + 5 jours). Par contre, à l'époque coloniale, les Aztèques dévelopèrent de nouvelles formes d'écritures des cadastres, et peut-être des procédés d'approximation des surfaces. Utilisation en classe - Dans son analyse comparée des numérations mayas et aztèque, l’auteur éclaire quelques aspects fondamentaux des numérations orales et écrites, et livre ainsi un matériau très riche aux enseignants qui abordent en classe, notamment dans les séries littéraires, l’histoire de la numération.
|
Autre Ressource sur CultureMATH
Ecritures des nombres, André Cauty
Les Écritures mayas du Nombre, André Cauty et Jean-Michel Hoppan
Les numérations anciennes, Christine Proust
La divination sikidy à Madagascar
Par Marc Chemillier, Directeur d'études à l'École des Hautes Études en Sciences Sociales (EHESS) Victor Randrianary, anthropologue et vidéaste (CNRS - Musée de l'Homme) Denis Jacquet, psychologue, Maître de conférence (Université de Caen) Marc Zabalia, psychologue, Maître de conférence (Université de Caen) Résumé - La divination sikidy consiste à disposer sur le sol des graines de fano (une sorte d'acacia), sous la forme d'un tableau, dans le but de lire la destinée à travers certaines configurations de graines qui apparaissent dans ce tableau. La procédure de placement des graines comporte une partie produite au hasard (où se manifeste la destinée), et une partie construite à partir de la précédente selon des règles précises. Cette partie calculée du sikidy met en œuvre des propriétés formelles élaborées qui sont celles d'une véritable structure algébrique. Utilisation en classe – Faire lire ce texte à des élèves pourrait permettre de poser une question fondamentale de l’Ethnomathématique. Lorsque des activités ne sont pas identifiées comme étant des mathématiques par ceux qui les pratiquent, comment reconnaît-on qu’elles appartiennent au champ de cette discipline ? Par quels critères ? Poser cette question au cours d’un débat ou par un questionnaire donnerait l’occasion aux élèves de s’interroger sur leur propre vision des mathématiques.
|
Page web de Marc Chemillier Site geomance
Autre Ressource sur CultureMATH
Mathématiques de la musique en Afrique centrale, Marc Chemillier
Présentation du livre Les mathématiques naturelles par son auteur Marc Chemillier
Ressources externes
Chemillier M., « Mathématiques de tradition orale », Mathématiques et sciences humaines, 178, 2007 (2), p. 11-40 (Texte au format pdf ici).
Chemillier M., « Divination et rationalité à Madagascar », K. Chemla (éd.), Actes du colloque de synthèse Histoire des savoirs, décembre 2007, p. 241-258 (Texte au format pdf ici).
Site SIKIDI : Divination à Madagascar
Newton et le problème de Pappus
Par Massimo Galuzzi, Université de Milan Résumé - Le problème de Pappus parcourt l'entière carrière scientifique de Newton. La solution de ce problème lui fournit une occasion précieuse pour mettre à l'épreuve les résultats de géométrie projective qu'il élabore progressivement à partir des années de sa jeunesse. Mais il oppose souvent ses solutions à celle donnée par Descartes en opposant la « vraie » analyse des Anciens aux déformations générées par l'usage aveugle de l'algèbre. De plus, il est un peu étonnant que Newton ait toujours considéré ce problème comme équivalent à celui de tracer une conique par cinq points, en supposant (tacitement) qu'une région du plan soit choisie par avance. C'est une attitude bien différente de celle qui anime les discussions entre Descartes, Roberval, van Schooten et Huyghens sur l'existence de deux solutions.
Utilisation en classe - Ce texte très riche, dans lequel toutes les démonstrations sont soigneusement détaillées, permet une immersion dans les méthodes mathématiques mises en œuvre par les « Anciens », reprises et poursuivies ici par Newton, pour traiter certaines questions liées aux Sections Coniques. Certains passages de ce texte pourraient certainement être lus et commentés en classe préparatoire pour donner une perspective historique à l’étude des Coniques. Les professeurs de mathématiques du secondaire trouveront pour leurs élèves quelques situations de problèmes géométriques impliquant les rapports de longueurs, les angles, et bien sûr les triangles semblables. En particulier, le problème de Pappus dans le cas du cercle, qui fait l’objet de la Section 4, offre une configuration exploitable en classe de seconde. |
Autre Ressource sur CultureMATH
Isaac Newton mathématicien : les années de formation et les premiers écrits , entretien avec Marco Panza
D'Alembert: Mathématicien des Lumières
 |
Dossier coordonné par Pierre Crépel (CNRS)
Présentation - Pour vous, qui est D'Alembert ? - C'est l'Encyclopédie, mais moins que Diderot. C'est aussi un grand mathématicien du XVIIIe siècle, mais moins qu'Euler. Voilà, en ramassé, la réponse nue qui ressort d'un petit sondage auprès d'étudiants et d'un public divers cultivé mais non spécialisé. Elle n'est pas fausse. Sans Diderot, l'Encyclopédie n'aurait jamais possédé ce sel et ne serait pas allée jusqu'au bout; sans D'Alembert, elle n'aurait eu ni cette qualité scientifique, ni cet impact européen. Tout étudiant de mathématiques a travaillé, appliqué ou entendu évoquer le théorème de D'Alembert(-Gauss) ou théorème fondamental de l'algèbre, le principe de D'Alembert en mécanique, le paradoxe de D'Alembert en hydrodynamique, le critère de D'Alembert pour les séries, l'équation de D'Alembert pour les cordes vibrantes. Or, quand Condorcet, ami et disciple de D'Alembert, a lu successivement à l'Académie les éloges d'Euler et de D'Alembert, décédés à quelques semaines d'intervalle, les observateurs ont remarqué ceci: "On ne s'attendoit pas que Condorcet mettroit Euler si fort au dessus de d'Alembert, et le public lui en a su gré." Mais sait-on que D'Alembert a été secrétaire de l'Académie française et non de l'Académie des sciences ? sait-on que son principal correspondant est Voltaire, plus que Lagrange ? sait-on que la moitié de son oeuvre mathématique se situe après l'Encyclopédie alors qu'on dit qu'il n'en fait plus guère ? sait-on qu'il a écrit mille pages d'optique aujourd'hui oubliées ? Alors ? Grand géomètre aux dires des littérateurs et bon littérateur aux dires des géomètres? Les jugements de l'Histoire sont plus que contrastés et rarement un auteur, surtout scientifique, a suscité des avis aussi tranchés et aussi opposés. L'édition en cours de ses Oeuvres Complètes permet un regard nouveau. Plus que pour d'autres "génies de la science", ce dossier sera donc l'occasion de découvertes et d'imprévus, mais aussi de soutes, ce qui n'aurait pas déplu à ce savant des Lumières. |
Autres Ressources sur CultureMATH
Ressources externes
Le processus d’abstraction dans le développement des premières théories de la mesure
| Par Jean-Philippe Villeneuve, Cégep de Rimouski, Rimouski, Québec, Canada Résumé - Nous nous intéresserons aux premières théories de la mesure élaborées à la fin du 19e siècle et nous les utiliserons pour distinguer le processus d’abstraction du processus de généralisation. En effet, nous retrouvons des généralisations dans les versions calculatoires de la mesure proposées par Peano (1887), Jordan (1892) et Lebesgue (1902). En 1898, Borel présenta une nouvelle façon de définir la mesure : au lieu de la définir par un calcul, la notion doit satisfaire une liste de propriétés. Cette nouvelle façon de définir une notion implique un changement d’attention de la part de Borel et ce changement lui permettra de « reconstruire » la notion dans le sens où certaines propriétés des versions calculatoires deviennent constitutives de la nouvelle notion. De plus, cette reconstruction implique une réorganisation des connaissances mathématiques, comme l’intégration de connaissances jusqu’alors considérées comme distinctes. Nous obtiendrons ainsi que ce changement d’attention jumelé à la reconstruction et à la réorganisation des connaissances sont des caractéristiques du processus d’abstraction réfléchissante développé par Jean Piaget. Nous utiliserons de plus les recherches d’Aline Robert et de Jean Cavaillès pour éclairer notre analyse. Nous conclurons en remarquant que le processus d’abstraction change la compréhension de la notion, ce qui n’est pas nécessairement le cas pour une généralisation, et qu’il permet d’introduire les notions « spécialisées » que nous retrouvons dans la théorie contemporaine de la mesure. |
Autre Ressource sur CultureMATH
« Les généralisations de la notion mathématique d’intégrale au 19e siècle », Jean-Philippe Villeneuve
La preuve cartésienne de la quadrature du cercle
| Par Davide Crippa, Equipe REHSEIS (CNRS et Université Paris Diderot) Résumé -Le problème de la quadrature du cercle, à savoir, le problème de construire un carré ayant même aire que celle d'un cercle donné, restait un problème ouvert parmi les mathématiciens du début du XVIIème siècle. René Descartes (1596-1650) en donna une solution dans les années 1625-1628 dont il déclara lui-même qu'elle n'était pas acceptable. Cet article examine cette solution, en s'appuyant sur une analyse donnée un siècle plus tard par Euler ainsi que sur une solution connue depuis l'antiquité et rapportée par Pappus. On s'interrogera ensuite sur les raisons qui ont amené Descartes à exclure les deux constructions en tant que non acceptables, par rapport à l'idéal d'exactitude explicité dans La Géométrie (1637). Utilisation en classe – Une lecture commentée de certains passages de cet article peut certainement être envisagée dans une classe des cycles S ou L (option « maths »). La seconde partie offre une ressource qu’il serait possible d’utiliser comme base pour une activité faisant intervenir la somme des termes d’une suite géométrique, ceci autour d’une configuration géométrique visant à rechercher une solution au problème de la quadrature du cercle. La discussion de la troisième partie concernant la recevabilité et l’exactitude de la construction géométrique d’une courbe offre un thème qui pourrait faire l’objet d’un travail interdisciplinaire entre mathématiques et philosophie. |
Autre Ressource sur CultureMATH Ressources externes
Algorithmes et puzzles : une ultime approche de Turing
| Par Lény Oumraou, Docteur agrégé de philosophie - Lycée Charles Péguy (Orléans) et Université Paris I Résumé - Alan Turing (1912-1954) est, à juste titre, considéré comme le co-inventeur de l'ordinateur (avec J. von Neumann). La « machine de Turing universelle » est bien une préfiguration théorique du « calculateur programmable ». Dans ses travaux fondateurs de 1936, Turing se référaient directement à des questions de calculabilité (les nombres réels calculables) et de décidabilité (le problème de la décision, ou Entscheidungsproblem de Hilbert). Dans l'article de 54, c'est en partant de considérations moins « confidentielles », destinées à un plus large public, qu'il présente une (petite) partie de la théorie de la calculabilité. Les « puzzles » (casse-têtes, énigmes, etc.) forment le point de départ de la discussion. Partant de ces « récréations mathématiques », Turing expose une nouvelle formalisation des algorithmes, dans l'esprit des travaux plus récents de Post et Markov. Utilisation en classe - Parmi les « puzzles » étudiés dans le texte, une place importante est donnée au taquin. En suivant la démarche de Turing, on peut envisager un examen approfondi, et non moins ludique, de ce jeu, qui fournit une intéressante application de la théorie des groupes ; on peut même considérer des versions simplifiées (3×3 cases au lieu de 4×4), ou au contraire d'une plus grande complexité, dans une approche combinatoire (méthode de partition). Il peut également illustrer des questions d'algorithmique générale (par exemple les différentes manières d'explorer un arbre) et sensibiliser aux problèmes de la théorie élémentaire de la calculabilité (notion de procédure effective, de complexité algorithmique, etc.). |
Mathématiques de la musique en Afrique centrale
| Par Marc Chemillier, Directeur d'études à l'École des Hautes Études en Sciences Sociales (EHESS) Résumé - Dans la tradition musicale savante occidentale (et cela vaut aussi pour les traditions savantes non occidentales comme la tradition chinoise), la musique a toujours été associée aux mathématiques. Dans le contexte de sociétés sans écriture, en revanche, cette association peut paraître plus surprenante. Le but de cet article est de montrer quelques cas de répertoires musicaux de tradition orale dans lesquels on peut mettre en évidence des structures musicales complexes comparables à des constructions mathématiques. |
Les généralisations de la notion d'intégrale au 19e siècle
|
Par Jean-Philippe Villeneuve, Cégep de Rimouski, Rimouski, Québec, Canada Résumé - Nous retrouvons au 19e siècle quatre façons de définir ou de comprendre la notion mathématique d’intégrale : l’intégrale de Cauchy, l’intégrale de Riemann et les versions calculatoire et axiomatique de l’intégrale de Lebesgue. Nous proposons d’étudier les généralisations de ces façons de définir l’intégrale en introduisant deux types de généralisations : les généralisations conservatives et les généralisations innovantes. Dans le premier cas, la façon de définir l’intégrale ou de calculer l’intégrale est conservée et son extension est augmentée, c’est-à-dire qu’il y a plus de fonctions qui sont intégrables selon cette façon. Dans ce second cas, la façon de comprendre l’intégrale change et il y a une réinterprétation, voire une reconstruction de la notion. Utilisation en classe - Les enseignants de mathématiques trouveront dans cette approche historique et épistémologique de la notion d’intégrale des éléments pour enrichir l’introduction historique de cette notion faite aux élèves de terminale.
Pour les classes Post-Bac, dans lesquelles l’intégrale de Riemann est approfondie, une lecture accompagnée et commentée montrerait aux élèves que la notion d’intégrale a traversé le 19e siècle d’une façon dont on peut rendre compte grâce à quelques outils conceptuels. |
A la recherche de la génèse du dernier mémoire mathématique de Georg Cantor:
Du côté de chez Franz Goldscheider (lettre de Cantor du 18 juin 1886)
|
Par Anne-Marie Décaillot, Equipe REHSEIS (CNRS, Université Paris-Diderot) Résumé - Franz Goldscheider (1852-1926) est un « ancien élève » de Cantor, professeur de mathématiques dans un lycée de Berlin. La lettre de Cantor du 18 juin 1886, dont nous donnons ci-dessous une traduction française, est la première manifestation connue d’un échange entre les deux mathématiciens, qui se poursuivra de 1886 à 1888. Cette première lettre constitue un véritable exposé introductif des fondements de la théorie cantorienne des ensembles, présentant les notions de cardinaux et d'ordinaux et leurs premières manipulations opératoires. La lettre expose, avec de nombreux exemples imagés à l’appui, les notions d’équivalence et de puissance ensemblistes ; puis l’arithmétique des nombres cardinaux met l’accent sur les spécificités opératoires concernant les nombres transfinis. La notion d’ensemble bien ordonné est alors définie, ainsi que celle cruciale de nombre ordinal et d’ensembles conformes. De nombreux exemples permettent d’éclairer les règles de calcul régissant les nombres ordinaux transfinis. Cantor parvient ainsi à la définition du nombre ordinal ω (nombre ordinal de l’ensemble des entiers ordonnés dans l’ordre naturel) et de la puissance ω* (nombre cardinal de l’ensemble des entiers). La deuxième classe de nombres apparaît alors comme l’ensemble de tous les nombres ordinaux, qui sont des types d’ensembles bien ordonnés de puissance ω*. Il y a autant de nombres ordinaux de deuxième classe que de relations de bon ordre sur l’ensemble des entiers. La lettre que nous éditons ici en langue française prouve une fois encore l'importance des correspondances dans la formation d'une pensée mathématique et permet de reconstituer la genèse du dernier grand mémoire de théorie des ensembles, les Beiträge, publié entre 1895 et 1897 par Georg Cantor, où ces notions seront publiées et approfondies.
|
Les deux premiers journaux mathématiques français
|
Les Annales de Gergonne (1810-1832) et le Journal de Liouville (1836-1845), par Christian Gerini (Université de Toulon) & Norbert Verdier (Université Paris-Sud). Résumé : Les mathématiques ont bénéficié, dans la France et l’Europe du XIXème siècle, d’une nouvelle forme de communication : les périodiques qui leur ont été dédiés. Les Annales de Joseph-Diez Gergonne, publiées mensuellement de 1810 à 1832, constituent le premier journal de mathématiques. Joseph Liouville, en digne successeur de Gergonne, publia à partir de 1836, sous une forme héritée desAnnales, le Journal de Mathématiques Pures et Appliquées. Nous nous intéressons ici à ces deux périodiques sous un angle transdisciplinaire : histoire de la diffusion scientifique en les situant par rapport à d'autres journaux de cette première moitié du XIXème siècle, histoire des mathématiques, épistémologie. Il s’agit de porter à la connaissance de la communauté des mathématiciens et des historiens des sciences des documents originaux riches d’enseignements sur la construction des concepts et théories. Ces textes sont progressivement mis à la disposition d’un public élargi via les nouveaux modes de communication et d’archivage. L’histoire de leur genèse, de leurs contenus et de leurs auteurs est de ce fait à nouveau d’actualité. Cet article s’appuie en grande partie sur la publication suivante : « Les Annales de Gergonne (1810-1832) et le Journal de Liouville (1836-1874) : une mine de textes numérisés à exploiter dans notre enseignement. », Christian Gérini & Norbert Verdier, Repères, 67, 55-68, Topiques éditions, 2007. Nous remercions vivement Yves Ducel d’avoir autorisé cette reprise sous forme électronique.
Utilisation en classe - Les lecteurs de cet article seront frappés par l'importance de la contribution des lycéens et étudiants et de leurs professeurs aux premiers périodiques mathématiques, ainsi que par le rôle qu'y jouent l'élaboration et la résolution de problèmes. Les Annales de Gergonne et le Journal de Liouville offrent ainsi des ressources inépuisables pour l'enseignement. On trouvera en annexe de l'article les "Questions du Dimanche" de Norbert Verdier, une liste de problèmes publiés dans les périodiques et ouvrages mathématiques du XIXe siècles soumis à la sagacité des lecteurs de CultureMATH. |
Tout sur les polyèdres: des solides de Platon aux étoiles de Poinsot-Kepler
  |
|
Achille Brocot, mathématicien à ses heures
 |
|
Autres ressources sur CultureMath
Les calculs du citoyen Haros. L'apprentissage du calcul décimal
 |
|
Les géomètres de la Grèce antique
|
|
Résumé - Bien des approches de la géométrie grecque ancienne sont possibles. Les grands textes des auteurs hellénistiques, notamment certains fameux problèmes tels que la quadrature du cercle ou la duplication du cube, ont joué un rôle indéniable dans l’histoire des mathématiques jusqu’à une date récente et ont intéressé — et intéressent toujours — les historiens des sciences, les enseignants, le public cultivé … Plusieurs questions restent cependant sans réponse : les premières recherches mathématiques des Grecs nous échappent en grande partie ; nous ignorons à peu près tout de la biographie (en particulier intellectuelle) des principaux géomètres ; les modalités de l’enseignement des mathématiques dans l’Antiquité nous sont fort mal connues. Bien que lacunaires, les sources ne sont pourtant pas muettes. Des oeuvres mathématiques majeures sont parvenues jusqu'à nous au terme de processus de transmission complexes, en particulier par le biais de la tradition savante écrite en langue arabe. Dans ce dossier, Bernard Vitrac présente les oeuvres d'Hippocrate, Euclide, Archimède, Apollonius, Ptolémée, Héron, Ménélaos..., et évoque des lieux et des contextes historiques particulièrement importants pour l'histoire des mathématiques (les cités ioniennes, Athènes, Alexandrie...). Le dossier se répartit en dix articles, complétés par des outils annexes qui seront utiles aux enseignants : bibliographie, chronologie, carte, ainsi qu'une liste des oeuvres mathématiques grecques parvenues jusqu'à nous. Utilisation en classe - En insistant sur le contexte historique et intellectuel du développement des mathématiques en Grèce ancienne, ce dossier intéressera aussi bien les enseignants de mathématiques que ceux d'histoire, de lettres ou de philosophie. Par leur style clair et accessible, les textes s'adressent aussi à un public de lycéens, notamment à ceux qui voudraient s'engager dans des travaux personnels encadrés en histoire des mathématiques. Des encarts contenant des démonstrations mathématiques détaillées peuvent être exploités en classe au niveau du collège ou au niveau du lycée. Autres ressources sur CultureMath
Niels Abel (1802-1829)
 |
|
Douce perspective
|
Préface du livre, par Eric Van der Oord, Inspecteur général de l’Education nationale Denis Favennec et Emmanuel Riboulet-Deyris enseignent les mathématiques en classes préparatoires aux grandes écoles. En bons mathématiciens, ils savent bien que les théories qu’ils enseignent, les définitions, les théorèmes, ces belles routes tracées pour la pensée des hommes, sont toujours construites sur un ensemble de sentiers longuement parcourus par des chercheurs aux pas parfois incertains. Dans cet ouvrage, ils nous invitent à découvrir les chemins parcourus par l’esprit humain entre la découverte de la perspective en peinture et l’invention de la géométrie projective en mathématiques. Pour mesurer l’étendue de la période étudiée, il suffit de comparer deux séries de dates : Que s’est-il passé durant ces deux siècles ? C’est ce que se proposent de montrer les auteurs. Ils feront voyager le lecteur dans un monde où l’espace de la physique mathématique et de la géométrie, familier pour les bacheliers d’aujourd’hui, n’est pas encore inventé. Un monde où, selon les conceptions d’ Aristote , un objet ne peut être considéré que dans un certain domaine, et où ses propriétés ne relèvent pas de lois universelles mais des lois de son domaine — par exemple les corps terrestres se déplacent en ligne droite, mais les corps célestes décrivent des cercles. Un monde où, en géométrie, on admet qu’un segment puisse être prolongé autant que nécessaire, mais où la droite n’est pas conçue dans sa globalité. Un monde enfin où l’infini « actuel » étant une prérogative divine, son apparition dans un tableau pourrait être considérée comme sacrilège, et où le peintre peut être tenté de cacher les points de fuite de ses perspectives. Dans ce monde, une pléiade d’artistes ont utilisé la perspective pour construire leurs tableaux, tant pour donner au sujet représenté des proportions harmonieuses que pour orienter le regard du spectateur sur l’essentiel. En examinant les nombreux tableaux commentés dans l’ouvrage, le lecteur découvrira sans cesse, selon une expression de Daniel Arasse , « cette géométrie secrète de l’oeuvre peinte qui, en tout temps, a été pour les artistes une des composantes essentielles de la beauté » . Au terme de cet itinéraire passionnant, le lecteur aura constaté, pour reprendre une phrase de l’ouvrage, que la fin assignée à la perspective, aussi bien par la théorie que par la pratique, est la production d’un sens plutôt que d’une illusion . Utilisation en classe - Cet article, ainsi que la lecture à laquelle il convie, enrichit le dossier de CultureMath sur l'histoire de la perspective. Tout comme l'article sur le mathématicien J.-H. Lambert (1728-1777), il aborde les relations étroites de la géométrie avec l'histoire de l'art, un sujet particulièrement intéressant pour les sections littéraires. Autres ressources sur CultureMath
1415 Invention de la perspective par Brunelleschi
1435 Alberti publie son De pictura
1482 Piero della Francesca publie son De prospectiva pingendi
1543 Publication de De revolutionibus orbium caelestium de Copernic
1616 Condamnation de Copernic
1633 Condamnation de Galilée
1639 Invention de la géométrie projective par Desargues
1687 Publication des Principia mathematica de Newton
Les écritures mayas du nombre
|
Résumé - ‘Les écritures mayas du nombre’ sont une synthèse des plus récents résultats d’analyses épigraphiques et linguistiques du corpus des écritures numérales et numériques réalisées par les scribes mayas depuis l’époque préclassique jusqu’à celle de la conquête espagnole. Interprétées dans le cadre des numérations parlées (de types protractif et additif) et dans celui des mesures de temps, la grande diversité des données analysées conduit à une typologie de l’ensemble des formes (notamment des zéros) et des systèmes mayas d’écriture du nombre, tant dans la représentation des dates et des petites durées, que dans celle des translations temporelles et des grandes durées. Diverses remarques présentent et discutent des usages spécifiques (âge de la Lune, durée d’une lunaison, pas de translation dans les almanachs divinatoires), des interprétations (zéro comme signe d’achèvement, d’intronisation, etc.), des distinctions marquées par les scribes (ordinal/cardinal, prospectif/ rétrospectif), ou encore des thèses alternatives (unité principale du système des mesures de temps, hypothèse courte, zéro opérateur). Utilisation en classe - Cet article intéressera les enseignants désireux d'accéder à une réflexion approfondie sur les problèmes historiques, philologiques et linguistiques que pose la compréhension des systèmes numériques anciens. Pour trouver une documentation adaptée à l'enseignement dans les classes de collège et de lycée, ils pourront se reporter au dossier "Les numérations anciennes" et en particulier à la fiche pédagogique "Nombres mayas". Autres ressources sur CultureMath
Les 15 problèmes de géométrie de la règle
|
Consulter le dossier |
|
Utilisation en classe - Les 15 problèmes de Jean-Henri Lambert sont des constructions à la règle seule qui peuvent être exploitées à tous les niveaux de l'enseignement secondaire. Certains sont bien connus des enseignants, comme le problème V (deux droites D et D' se coupent hors de la feuille; sans les prolonger, construire une droite concourante avec D et D' et passant un point donné). Ces problèmes anciens prennent un intérêt renouvelé dans le cadre des nouveaux programmes de mathématiques des sections littéraires, qui désormais abordent la perspective centrale: La problématique de la représentation de l’espace en fonction des finalités visées, artistiques ou techniques, conduit d'une part à mettre en oeuvre les connaissances géométriques, dans l'espace mais aussi dans le plan, et d'autre part à aborder des questions de nature culturelle et artistique. (p. 1) [...] Grâce au programme de l’option de première, les élèves [de terminale] disposent désormais à la fois de résultats de géométrie dans l’espace et d’un outil de visualisation des configurations, la perspective parallèle. Il s’agit maintenant d’étudier les rudiments de la perspective centrale, mode géométrique de représentation de l’espace qui a constitué, durant plusieurs siècles, le principe de la réalisation des oeuvres d’art pictural en Occident. (p. 5) Par ses relations étroites avec l'histoire de l'art, l'histoire de la perspective est un sujet d'étude particulièrement intéressant à aborder dans les sections littéraires. Autres ressources sur CultureMath
La géométrie : histoire et épistémologie
|
|
|
Utilisation en classe – Ce diaporama a été élaboré en Terminale scientifique à la demande conjointe d’Élisabeth ARBOGAST, professeur de mathématiques et Nafissa HAIDAR, professeur de philosophie, toutes deux au lycée Ribeaupierre de Ribeauvillé (Haut-Rhin). Au départ, Mme Haidar avait souhaité un exposé sur la géométrie non euclidienne et à partir de là, aborder les questions d’épistémologie au programme de la classe de Terminale Scientifique. Très vite, nous nous sommes mis d’accord sur l’objectif suivant : mettre en mouvement une dynamique de réflexion qui rompe avec le cloisonnement disciplinaire, et qui amène les élèves à se dire lorsqu’ils font des mathématiques : quel est le sens de ce que je fais en mathématiques ? En quoi est-ce une science exacte ? Comment s’est–elle construite ? Quel lien avec ce que je fais en philosophie ? Et lorsqu’ils sont en cours de philosophie : quels exemples puis-je tirer de mes autres apprentissages, mathématiques, physique, SVT, etc. pour donner corps aux concepts philosophiques, pour illustrer des thèmes comme intuition, évidence, vérité, rigueur, imagination, réalité ? Ressources externes
Systèmes numéraux en Grèce ancienne: description et mise en perspective historique
|
Les jeux de ficelle : témoins d’une activité mathématique
|
Ressources sur CultureMath Ressources externes A lire
Pourquoi, pour qui enseigner les mathématiques?
 |
|
Cet article aborde, en l'inscrivant dans une réflexion historique, une question que se pose en permanence l'institution scolaire, et que l'actualité vient de remettre au premier plan, pour ce qui est de l'élémentaire, avec la publication de l'Avis de l'Académie des Sciences sur la place du calcul dans l'enseignement primaire (voir le point de vue d'historien de Renaud d'Enfert sur cet avis, diffusé par le site EducMath) Pour mesurer l'intérêt de ce regard vers le passé, citons la conclusion: "Ce parcours partiel et trop rapide des principes qui ont guidé les orientations de différents programmes de géométrie depuis un siècle et demi illustre bien la diversité des enjeux à l’œuvre dans l’enseignement des mathématiques. Celui-ci se trouve en effet au carrefour de contraintes d’ordre disciplinaire, épistémologique, social, idéologique, pédagogique dont la résultante a dépendu des temps et des publics concernés. Les perspectives pour l’enseignement des mathématiques pour ce siècle sont ainsi à réfléchir en fonction de l’état des mathématiques, du rôle qu’elles jouent aujourd’hui dans la société et des ambitions affichées pour l’école." Autres ressources de CultureMath sur l'histoire de l'enseignement Ressources externes Du côté de l'actualité Voir l'Avis de l'Académie des Sciences sur la place du calcul dans l'enseignement primaire, adopté le 9 janvier 2007, et les premières réactions sur EducMath (commentaires de Guy Brousseau, Catherine Houdement, Jean-Pierre Kahane, Michèle Artigue, Roland Charnay, Jean-Pierre Demailly, Renaud d'Enfert ...). A lire Dans «Les Génies de la science», N° 31 mai 2007
Les matrices : formes de représentation et pratiques opératoires (1850-1930)
|
|
|
De même que, dans les mathématiques contemporaines, les matrices sont susceptibles de représenter une diversité d’objets algébriques, leur histoire se joue sur une longue période, dans des contextes divers et s’enrichit de la rencontre entre différents champs de recherche. Dans cet article nous rentrons dans le détail de textes publiés entre 1850 et 1890 par des auteurs comme Arthur Cayley, James Joseph Sylvester et Eduard Weyr. En mettant un avant les contextes culturels dans lesquels s'inscrivent ces différents auteurs, nous observerons des pratiques différentes dont la rencontre provoquera un enrichissement du champ des significations associées à la notion de matrice. Nous verrons que poser la question de l'histoire de la notion de matrice permet d'observer des aspects culturels des mathématiques antérieurs aux théories structurelles et unificatrices comme l'algèbre linéaire des années trente du XXe siècle. Cet article s'appuie sur de nombreux extraits de textes originaux placés dans le corps du texte et sous forme d'encarts, la lecture n'en est cependant jamais obligatoire et l'ensemble de l'article peut être parcouru en laissant à une seconde lecture l'étude des citations. Plusieurs problèmes mathématiques présentés dans cet article peuvent être abordés avec des étudiants. Selon le niveau de généralité choisi (matrices symétriques, diagonalisables ou quelconques, à coefficient dans un corps algébriquement clos ou dans un anneau principal) les problèmes proposés peuvent être exploités à des niveaux très différents, des premières années d'université à la préparation de l'agrégation. Le problème des types d'intersections des coniques étudié par Sylvester entre 1850 et 1851 peut donner lieu à un travail sur les difficultés posées par la multiplicitédes valeurs propres d'une matrice. Les différents types d'intersections de coniques permettent de représenter dans un cadre géométrique les différentes décompositions du polynôme caractéristique ou minimal et les différentesformes canoniques associées. Le problème de la détermination des "racines" des fonctions homographiques posé par Cayley en 1858 fournit une situation dont l'étude peut déboucher, de manière constructive, à l'introduction des "lois" du calcul matriciel et des pratiques polynomiales associées (théorème de Cayley-Hamilton). Le problème des matrices périodiques permet d'aborder les difficultés propres au calcul matriciel (anneau non intègre et non commutatif). L'ambigüité de la notion de "single quantity" de Cayley et l'efficacité des pratiques polynomiales qui l'accompagnent peuvent donner lieu à un travail sur les quantités multiples (algèbres associatives). Les travaux menés par Sylvester entre 1880 et 1885 permettent de travailler sur le problème de la définition des fonctions de matrices. Un travail peut également être mené sur les quaternions et lesnonions afin d'introduire les méthodes élaborées pour la détermination des matrices qui commutent avec une matrice donnée (polynôme minimal, matrices dérogatoires, nullité d'une matrice). Les procédés opératoires sur la forme matricielle élaborés par Eduard Weyr entre 1885 et 1890 permettent d'introduire ou d'approfondir la principale méthode de démonstration du théorème de Jordan (décomposition de l'espace en sous espaces caractéristiques invariants pour un opérateur donné). Enfin, la présentation, dans la première partie de cet article, de la synthèse théorique élaborée dans les années trente permet de mettre en évidence les enjeux pédagogiques portés par la forme matricielle. En même temps que s'élabore une synthèse qui donne à la théorie des matrices un caractère universel, les traités des années 1930 adoptent une organisation didactique basée sur le caractère opératoire de la représentation imagée des matrices, représentation présentée comme simple, efficace et permettant d'assimiler des théorèmes généraux. Résumé
Utilisation dans l'enseignement
Textes écrits, textes dits dans la tradition mathématique de l’Inde médiévale
|
Agathe Keller, équipe REHSEIS (CNRS et Université Paris 7)
|
Résumé – La tradition savante indienne est traversée par un paradoxe : une abondance de manuscrits témoigne de textes qui privilégient une transmission orale du savoir. Il en va ainsi pour les mathématiques, comme pour d’autres disciplines savantes. Cette prééminence de l’oralité comme valeur de transmission du savoir, a-t-elle eu une influence sur la manière dont on a pratiqué les mathématiques en Inde? Pour répondre à cette question, l'auteur nous entraîne dans l'aventure des manuscrits au travers de la tradition védique et de la culture sanskrite. Utilisation en classe – Les enseignants trouveront dans cet article des énoncés de problèmes stimulants pour tous les niveaux de l'enseignement secondaire (de la proportionnalité à la théorie des nombres). Ressources sur CultureMath Ressources sur le site de l'IUFM de la Réunion
Ethnomathématique dans l’océan Indien : les lambroquins à la Réunion
 |
|
Résumé – L’architecture créole réunionnaise recourt abondamment à des motifs géométriques. Les lambroquins, ces frises de bois ou de tôle qui bordent les toitures, en constituent l’un des éléments les plus caractéristiques. Dans ce dossier, on se propose de présenter l’origine, la fonction utilitaire et la fonction décorative des lambroquins, d’étudier plus spécifiquement leur structure géométrique et de les situer par rapport à l’ensemble des dessins à motifs répétitifs employés dans l’art et l’architecture. Les cinq types de lambroquins rencontrés à la Réunion, leurs fréquences d’emploi et leurs enrichissements esthétiques constituent une véritable signature ethnomathématique de la culture créole insulaire qui s’est développée dans ce département français de l’océan Indien. Utilisation en classe – À la Réunion, les lambroquins offrent un support naturellement pertinent pour enrichir l’enseignement des mathématiques en s’appuyant sur le vécu culturel des enfants. On évoque ici plusieurs expériences pédagogiques réalisées dans des collèges et des lycées de l’île, en souhaitant que les enseignants d’ailleurs puissent également s’en inspirer. Ressources sur CultureMath Ressources externes A lire
Les manuels d’arithmétique pour les marchands dans la France du XVe siècle
 |
Maryvonne Spiesser (maître de Conférence à l'Université de Toulouse III). Cet article a été publié dans le Bulletin de l’APMEP n°444, 2003, p. 32-50. Le texte diffusé par CultureMATH est la version intégrale, avec quelques corrections mineures. Il est mis en ligne sur CultureMATH avec l'autorisation de l'APMEP, que nous remercions chaleureusement. |
Résumé - Au cours du XVe siècle, un nouveau type de traités d’arithmétique pratique se développe en France en dehors de l’Université. Ce sont des ouvrages pédagogiques, qui reflètent la nécessité d’une formation mathématique pour les futurs marchands, formation dont on connaît très peu les modalités. En dehors de l’apprentissage du calcul, l’apprenti marchand apprend à gérer mathématiquement des situations qu’il rencontrera au quotidien, toutes régies par la règle de trois ; il se mesure aussi à des exercices plus plaisants, qui complètent sa formation. Les méthodes d’apprentissage sont fondées sur l’application de règles, présentées de manière algorithmique et accompagnées de nombreux exemples d’entraînement. Cet article en présente un certain nombre, pour la plupart très répandus dans ce type d’ouvrages. Le courant des « arithmétiques commerciales » puise ses sources dans un passé souvent lointain ; et sans toutefois demeurer créateur, il va perdurer jusque dans la première partie du XXe siècle, à travers les manuels d’arithmétique de l’école élémentaire. Utilisation en classe - Cet article fournit un riche matériau pour des activités en classe. En effet, les nombreux exemples sont une source d’énoncés permettant de mettre en pratique des notions mathématiques essentielles comme la proportionnalité. Par ailleurs, la formation mathématique des marchands dans l'Europe de la Renaissance est un sujet intéressant à exploiter dans le cadre d'un travail interdisciplinaire : le thème des énoncés de problème montre une production mathématique en liaison étroite avec la vie sociale, ici le négoce. Grâce à cette documentation, les professeurs d'histoire pourront notamment montrer comment la tradition commerciale a contribué à préserver et à diffuser un patrimoine qui s’est enrichi et qui a évolué au cours des temps et au contact de différentes civilisations. Enfin, les enseignants et les formateurs trouveront dans ces problèmes pratiques matière à réflexion sur la forme de l’exposé mathématique et les modes de justification, adaptés aux objectifs et au lectorat, dépendant aussi des traditions et des outils mathématiques dont on dispose. importer l'article en version pdf Ressources sur CultureMath Ressources externes
Inventer une géométrie pour l’école primaire au XIXe siècle
|
|
|
Ressources sur CultureMath Les mathématiques et l’enseignement féminin en France, Nicole Hulin, 2006 (publié dans le Bulletin de l’Union des professeurs de Spéciales, n°197, janvier 2002, p. 12-17). De l’Association des professeurs de mathématiques (APM), Nicole Hulin, 2006. Pourquoi, pour qui enseigner les mathématiques? , Hélène Gispert, 2007 (publié dans le Bulletin de l'APMEP n° 438 en janvier 2002). Ressources externes L’enseignement mathématique à l’école primaire de la Troisième République aux années 1960: enjeux sociaux et culturels d’une scolarisation «de masse», Renaud d'Enfert, 2006. L’enseignement du travail manuel dans les écoles primaires de garçons: Travaux d’élèves de l’école Louis Vauquelin de Rouen, 1886-1887, Renaud D'Enfert, 2007 (voir aussi la magnifiqueplanche d'illustrations). L’enseignement des mathématiques dans ses liens à d’autres disciplines, une perspective historique, Hélène Gispert et Nicole Hulin, article paru dans le bulletin de l'Union des Professeurs de Spéciales, n°192, octobre 2000. Les exercices pratiques de mathématiques dans l’enseignement secondaire, Conférence faite le 3 mars 1904 au musée pédagogique par Emile Borel (avec une présentation de Hélène Gispert), Gazette de la SMF. Femmes et mathématiques dans le monde occidental, Renate Tobies, Gazette de la SMF. Avis de l'Académie des Sciences sur la place du calcul dans l'enseignement primaire de janvier 2007 et dossier sur le site EducMath (voir notamment un point de vue historique par Renaud d'Enfert). A lire Le dessin à l'école de 1800 à nos jours, Renaud D'Enfert, Daniel Lagoutte, Lyon, INRP, 2004. L’introduction du travail manuel dans les écoles primaires de garçons, 1880-1900, Renaud D'Enfert, Histoire de l’éducation, n° 113, janvier 2007, pp. 31-67. L'enseignement mathématique à l'école primaire, de la Révolution à nos jours. Textes officiels réunis et présentés par Renaud d'Enfert, avec la collaboration d'Hélène Gispert et deJosiane Hélayel. Tome 1 : 1791-1914. Paris, INRP, 2003. Dans «Les Génies de la science», N° 31 mai 2007:
Ecritures des nombres
 |
|
Introduction - Tout le monde sait distinguer premier, second et dernier, ou encore un, deux et beaucoup. Mais comment construire le nombre abstrait, c’est-à-dire développer et articuler entre elles : la capacité « ordinale » de distinguer des entités sur la seule base de leur rang dans une suite, et la capacité « cardinale » de déterminer des quantités hétéroclites par la seule propriété d’avoir le même nombre d’éléments ou d’être de même mesure ? On comprend qu’il s’agit d’une longue aventure humaine collective en observant comment s’écrivent les grands nombres dans différentes parties du monde. Utilisation en classe - Cet article apporte des matériaux pour les enseignants et les élèves des sections littéraires qui, avec les programmes de 2004, découvrent une nouvelle manière d’aborder l’arithmétique : « L’étude de différents systèmes de numération historiques et actuels se révèle fructueuse tant sur le plan de l’histoire des cultures que sur le plan mathématique. Cette étude permet de revenir sur la distinction entre un objet et sa désignation (ici, nombre et écriture chiffrée), sur la distinction entre les propriétés intrinsèques des entiers naturels et celles liées aux systèmes de numération (ici divisibilité et critères de divisibilité). Elle permet un retour réflexif sur les mécanismes sous-jacents aux techniques opératoires, dont l’aspect algorithmique doit être mis en valeur. » (Programmes des lycées, mathématiques, classe de première, série littéraire, BO hors série n°5, 9 sept. 2004). Ressources sur CultureMath Ressources externes Un article de Nicole Hulin, maître de conférences honoraire à l’Université Pierre-et-Marie-Curie - Paris VI, chercheur au Centre Alexandre Koyré. Résumé - L’APMEP (association des professeurs de mathématiques de l'enseignement public) est l’une des associations de spécialistes, constituées pour accompagner les professeurs du secondaire dans l’application de la réforme majeure de 1902. Son premier Bulletin de liaison est publié en 1911. Une dizaine d’années plus tard l’APMEP va se mobiliser pour dénoncer le caractère néfaste pour l’enseignement des sciences de la réforme dite de « l’égalité scientifique » et demander le retour aux principes de 1902. lire l'article - importer l'article en fichier pdf Ressources sur CultureMath Ressources externes A lire Dans «Les Génies de la science», N° 31 mai 2007
De l’Association des Professeurs de Mathématiques
Calculer chez les marchands Assyriens au début du II e millénaire av. J.-C.
 |
|
Utilisation en classe - Cet article intéressera tout autant les professeurs de mathématiques que les professeurs d'histoire, qui y trouveront des idées d'activités interdisciplinaires pour leurs élèves. Par exemple, les calculs des marchands assyriens (conversions de la valeur des marchandises en quantités d'or, d'argent ou de grain), peuvent apporter tout à la fois des exercices d'application de la proportionnalité au collège, et une façon originale de découvrir le commerce à longue distance il y a 4000 ans. Dans le cadre de la présentation des numérations anciennes en première littéraire, on pourra s'intéresser au curieux mélange de numération sexagésimale d'origine sumérienne et de numération décimale que pratiquaient les populations du nord de la Mésopotamie. Ressources sur CultureMath Les mathématiques et l’enseignement féminin en France. Quelques jalons pour un siècle d’histoire, Nicole Hulin (article publié dans le Bulletin de l’Union des professeurs de Spéciales, n°197, janvier 2002, p. 12-17). L'auteur est ancienne élève de l’ENS (Sèvres). Elle est aujourd’hui maître de conférences honoraire à l’Université Pierre-et-Marie-Curie - Paris VI, chercheur au Centre Alexandre Koyré. Elle est par ailleurs titulaire d’une agrégation scientifique « masculine » (par dérogation spéciale). Résumé - En un siècle l’enseignement féminin est passé d’une organisation spécifique à la fusion avec l’enseignement masculin. Nous nous proposons d’indiquer ici quelques étapes de cette évolution, en centrant notre intérêt sur la partie scientifique de l’enseignement et plus particulièrement les mathématiques, tant au niveau secondaire qu’à celui du recrutement des professeurs avec l’agrégation. Ressources sur CultureMath Ressources externes A lire Dans «Les Génies de la science», N° 31 mai 2007
"Le calcul sexagésimal en Mésopotamie: enseignement dans les écoles de scribes", Christine Proust (2005)
Les mathématiques et l'enseignement féminin en France
Le compendy de la praticque des nombres
 |
|
Résumé - Le Compendy de la practique des nombres est un traité d’arithmétique écrit à la fin du XV° siècle à Lyon par un Frère Dominicain, Barthélemy de Romans. Le manuscrit est aujourd’hui conservé à la Bibliothèque Malatestiana de Cesena en Romagne (Italie). Après un bref exposé du calcul écrit utilisant la numération indo-arabe, qui se répand à cette époque dans les milieux marchands en Europe du sud (numération positionnelle, opérations sur les entiers et les fractions, calcul approché de racines carrées ou cubiques), la majeure partie de l'ouvrage est consacrée à la résolution Utilisation en classe - Les enseignants de collège et de lycée trouveront dans cet article, et plus généralement dans le très riche corpus des arithmétiques marchandes, de nombreuses idées de problèmes linéaires qui illustrent la vie sociale dans l'Europe méditerranéenne à la Renaissance. Lire l'article en version html ou importer l'article en version pdf Ressources sur CultureMath Ressources externes Pour aller plus loin, on peut se reporter à l'édition critique du manuscrit complet par l'auteur: "Une arithmétique commerciale du XVe siècle: le Compendy de la practique des nombres de Barthélemy de Romans." Turnhout, Brepols, Coll. de Travaux de l'Académie internationale d'histoire des sciences, série De diversis artibus. 762 p.
très approfondie de quelques types de problèmes linéaires. Il témoigne d’une volonté enseignante forte de la part de son auteur, notamment en direction de la formation des marchands. Mais son style montre aussi des ambitions scientifiques inhabituelles. Le traité présente en fait peu d'intérêt pour un marchand : la première partie est trop réduite pour apporter l’essentiel et la seconde est inutile à la pratique commerciale. S’il fallait le rebaptiser, on pourrait le qualifier d’essai, un essai sur quatre problèmes, destiné à illuminer l’entendement de ceulx qui vouldroient veoir les subtilitez qui y sont contenues ».
Isaac Newton mathématicien : les années de formation et les premiers écrits
 |
|
Résumé - C’est entre 1664 et1666, alors que Newton n’a pas encore 25 ans, qu’il jette les bases du calcul des « fluxions », c’est-à-dire de ce que nous appelons aujourd’hui les dérivées. Il s’agit donc d’un acte fondateur de l’analyse comme branche des mathématiques. Les deux premières années de recherche d'Isaac Newton furent probablement les plus fructueuses de sa vie de mathématicien. Marco Panza nous présente un « très mauvais étudiant dans une très mauvaise université », peu soutenu par sa famille. Mais le jeune Isaac n’est pas un « mauvais étudiant quelconque dans une mauvaise université quelconque » : il se livre à la lecture de deux œuvres mathématiques novatrices : l’Arithmetica Infinitorum de John Wallis et la Géométrie de René Descartes. La culture mathématique du jeune Newton est donc tout à fait sélective. Son génie est d’avoir reconnu que le problème traité par Wallis, les quadratures, n’est autre que le problème réciproque de celui qui est traité par Descartes, les tangentes : « Newton se rend compte d’une chose étonnante : l’algorithme de Hudde [utilisé par Descartes pour trouver les tangentes], qui apparemment s’appliquait à un problème totalement différent de celui de Wallis pour trouver les aires, est en fait le même algorithme, mais inversé. Si je prends l’algorithme pour trouver les tangentes et je l’inverse, je trouve les aires ; si je prends l’algorithme pour trouver les aires et je l’inverse, je trouve les tangentes. Pour Newton, cela ne peut pas être un hasard, il doit y avoir quelque chose de profond. Newton veut trouver une théorie pour exprimer ce phénomène, il veut trouver un objet mathématique qui contient dans son comportement cette réciprocité. Cet objet est celui qui deviendra par la suite le calcul des fluxions, c’est-à-dire un des fondements du calcul infinitésimal et de l’analyse ». 1- Pourquoi un livre sur Newton Voir les vidéos Deux ouvrages viennent d’être publiés par Marco Panza : Isaac Newton , Les Belles Lettres, Paris (2003), et Newton et les origines de l'analyse : 1664-1666, A. Blanchard (2005). De larges extraits du premier sont proposés ici. Ces textes pourront utilement accompagner les séquences vidéo dans la perspective d’une utilisation dans l’enseignement. L’enfance et l’adolescence (p. 23-25) Rudolf Bkouche, Université des Sciences et Techniques de Lille. Texte publié en 2006 dans: Proceedings of 4th International Colloquium on the Didactics of Mathematics, volume II, édité par M. Kourkoulos, G. Troulis, C. Tzanakis, Université de Crète". Résumé - Lorsque nous disons que la géométrie élémentaire se situe au carrefour des sciences mathématiques et des sciences physiques, nous signifions d'une part que les objets de la géométrie ont une origine empirique, d'autre part que leur étude relève de la méthode déductive. En cela la géométrie élémentaire peut être considérée comme participant de la physique des corps solides. La géométrie élémentaire, sous la forme que lui a donnée Euclide, apparaît ainsi comme la première étude rationnelle de phénomènes naturels (les corps solides), devenant ainsi un modèle lorsque, avec la révolution scientifique du XVIIe siècle, la physique est devenue un chapitre des mathématiques, le développement de la physique s'inscrivant dans la continuité de l'œuvre euclidienne d'une part et d'autre part pouvant être considéré comme la réalisation du programme des Seconds Analytiques. Une telle conception implique que l'enseignement de la géométrie élémentaire participe à la fois de l'enseignement des sciences mathématiques et de l'enseignement des sciences physiques. On peut dire, en contrepoint, que les mathématiques sont un chapitre de la physique, point de vue exprimé par le mathématicien Vladimir Arnold (1998). Importer l'article en version pdf Karine Chemla, Directrice de Recherches, Equipe REHSEIS (CNRS et Université Paris 7) Résumé - Cette interview en six séquences présente le traité mathématique le plus ancien qui nous ait été transmis par la tradition des lettrés en Chine. Karine Chemla nous parle du traité lui-même, mais aussi de ses commentaires et de leur manière singulière d'aborder des questions universelles (comment obtenir les méthodes les plus générales possibles? comment assurer la correction des algorithmes?), du long travail minutieux que représente l'édition critique d'un texte qui s'est transformé de générations en générations pendant deux mille ans. Et aussi des trésors que les enseignants de mathématiques et d'histoire peuvent découvrir dans ces textes anciens: des problèmes attrayants, dont les énoncés « composent une vision de la société en Chine il y a deux mille ans ». Sommaire Voir les vidéos Autres ressources, du même auteur Anne Marie Décaillot, Université Paris 5, Equipe REHSEIS (Recherches Epistémologiques et Historiques sur les Sciences Exactes et les Institutions Scientifiques) Résumé - Quelques résultats profonds de l'arithmétique supérieure ont une interprétation simple, visuelle et particulièrement élégante dans les mathématiques textiles. Ainsi en est-il d'un théorème de C. F. Gauss concernant la suite des restes (modulo p) des multiples d'un nombre a premier avec p. Ou d'un théorème énoncé par Pierre de Fermat sur les propriétés des nombres premiers de la forme 4n+1.Cet article est consacrée aux travaux originaux d'un mathématicien français du XIXe siècle en ce domaine. Il s'agit de l'arithméticien Edouard Lucas, connu par ailleurs pour les études de très grands nombres premiers qu'il effectue grâce à des tests puissants et rapides. Utilisation en classe - Quelques uns des résultats d'Edouard Lucas présentés dans cet article pourraient donner matière à d'intéressants problèmes à proposer en terminale scientifique. On peut par exemple faire le lien avec la belle activité proposée par Jean-Pierre Kahane dans "Le nombre, cet inconnu", p. 11. Dès le collège, la disposition des points de liage sur un damier peut donner l'occasion de découvrir le calcul modulaire expérimentalement, de façon très visuelle et ludique. Lire l'article en version html ou importer l'article en version pdf
Sommaire des vidéos:
2- Le petit Isaac
3- Newton autodidacte
4- La lecture de Descartes
5- La lecture de Wallis. Le calcul des fluxions
6- La place des mathématiques dans l’œuvre de Newton
(pour un meilleur affichage, nous conseillons d'ouvrir cette page en passant par le navigateur Mozilla)Documents d'accompagnement
1- La vie et l’œuvre d’Isaac Newton : repères chronologiques
2- Extraits de livre
Les premiers cahiers : notes de lecture d’un autodidacte (p. 30 ss.)
Tangentes et aires (p. 43-44)
Vers la théorie des fluxions (p. 54-55)
Vers la théorie des fonctions (p. 71)La Géométrie entre mathématiques et sciences physiques
Les Neuf Chapitres, le classique mathématique de la Chine ancienne et ses commentaires
1- Les mathématiques de Chine ancienne: des ressources pour l’enseignement aujourd'hui.
2- La coopération franco-chinoise et le travail d’édition critique des Neuf Chapitres.
3- La contenu et l’organisation du traité et ses commentaires.
4- La place des Neuf Chapitres dans l’histoire des mathématiques : comparaison avec les Eléments d’Euclide.
5- Les auxiliaires du texte : baguettes, figures et blocs.
6- La circulation des idées entre la Chine et l’Inde.
(pour un meilleur affichage, nous conseillons d'ouvrir cette page en passant par le navigateur Mozilla)
Mathématiques textiles: la géométrie des tissus d'Edouard Lucas
Liens
Des machines pour résoudre les équations différentielles
 |
Marie-José Durand-Richard, Université Paris 8, Equipe REHSEIS (Recherches Epistémologiques et Historiques sur les Sciences Exactes et les Institutions Scientifiques). Article publié conjointement avec le site Les instruments du calcul savant. Résumé - Les ordinateurs sont souvent présentés comme la convergence entre des technologies et les avancées de la logique. Mais ils proviennent également des tentatives pour mécaniser la résolution approchée des équations différentielles, marquées par une hésitation sensible entre approximation par le discret et approximation par le continu. De la machine aux différences de Charles Babbage (1791-1871) au Meccano de Douglas R. Hartree (1897-1958), en passant par l'analyseur harmonique de Lord Kelvin (1824-1907), nous examinerons quelques-unes de ces tentatives et les problématiques qui leur sont attachées. |
Utilisation en classe - Le contenu de cet atelier ne fournit vraisemblablement pas un matériau directement utilisable dans la classe par les enseignants. Son intérêt réside plutôt dans la prise en compte de problématiques attachées à l'histoire des machines mathématiques, envisagées comme élément de la culture et de l'histoire sociale. Bien que cette dimension échappe traditionnellement à l'enseignement, j'en ai personnellement eu besoin pour réconcilier la représentation des mathématiques que je m'étais forgée au cours de mes études, avec celle que m'ont longtemps renvoyée les élèves lorsque j'enseignais au collège.Il me semble qu'elle peut notamment leur permettre de saisir là comment les interactions entre les mathématiques et les autres domaines de la connaissance interviennent dans la signification du calcul. Pour aller plus loin - On trouvera cet article ainsi qu'une très riche documentation sur le site "Les instruments du calcul savant", développé par une équipe de six chercheurs, Konstantinos Chatzis, Ahmed Djebbar, Marie-José Durand-Richard, Joachim Fischer, Dominique Tournès et Galina Zverkina: "À travers l'exploration des instruments du calcul savant (calcul dépassant le niveau des opérations arithmétiques élémentaires), il s'agit de mettre en lumière des savoirs et des pratiques mathématiques négligés par l'historiographie traditionnelle, ainsi que des interactions jusqu'ici peu étudiées entre diverses communautés professionnelles (mathématiciens, ingénieurs, fabricants d'instruments...)." Importer l'article de Marie-José Durand-Richard en version pdf Denis Lanier (Lycée Malherbe de Caen) et Didier Trotoux (IUT de Caen), IREM de Basse-Normandie Précédente édition: 1996, dans "Contribution à une approche historique de l'enseignement des mathématiques", Actes de la 6° université d'été interdisciplinaire sur l'histoire des mathématiques, Presses Universitaires de Franche-Comté, collection "Les publications de l'IREM de Besançon", p. 259-294. Résumé - Le couple fréquence-probabilité, ainsi que la théorie instituant ce rapport qu'on peut appeler schématiquement "loi des grands nombres", est un leitmotiv de la période classique de l'histoire du calcul des probabilités. Il est au coeur du développement de la théorie et des préoccupations des probabilistes, comme de ses utilisateurs. Les programmes des lycées imposent de prendre une approche fréquentiste pour définir une probabilité. Cela pose le problème du statut de ces énoncés que l'on rassemble sous le nom de "loi des grands nombres". Peu de propositions mathématiques portent ce titre de "loi". Est-ce un théorème, comme il est utilisé habituellement pour le "théorème de De Moivre-Laplace ? Est-ce un énoncé extra-mathématique, admis comme prémisse à toute théorie scientifique ? D'une certaine manière, pour pouvoir faire des probabilités (et en particulier les appliquer), tout se passe comme si on devait admettre que la nature suit (au moins localement) des lois, qui permettent l'élaboration d'une théorie, à l'intérieur de laquelle on démontre ensuite cette loi. Le rapprochement avec la situation du physicien, pour embarrassante qu'elle soit pour certains mathématiciens, est flagrante. Il nous semble, d'un point de vue historique et aussi d'un point de vue pédagogique, qu'il est un peu vain de s'en tenir aux différentes définitions du concept de probabilité, en recherchant la meilleure. En revanche l'étude historique de sa mise en oeuvre et de ses problématiques nous paraît riche d'enseignements. En ce qui concerne la "loi des grands nombres", depuis son énoncé initial par Jacques Bernoulli jusqu'à la résolution du problème limite classique par Kolmogorov, le travail des probabilistes consiste à chercher à comprendre l'énoncé, à le préciser, à en évaluer la portée, à tenter de simplifier la démonstration. Du point de vue de l'histoire interne des mathématiques, il y a là, pendant deux siècles, un travail sur le texte lui-même qui est tout à fait fascinant. On verra dans la suite que ces questions ne se posaient que si l'on voulait appliquer les probabilités à d'autres domaines que les jeux de hasard. On verra aussi qu'elles recoupaient initialement des préoccupations métaphysiques - si la nature suit la loi des grands nombres, c'est qu'il y a quelqu'un qui a fabriqué le dé, d'où l'existence de Dieu - qu'on se garde bien d'aborder maintenant dans nos classes. L'histoire de la loi des grands nombres est jalonnée par quelques grands textes sans oublier que l'histoire ne s'arrête pas là. Les trois premiers pas sont marqués par Jacques Bernoulli et l'Ars Conjectandi(1713), Abraham De Moivre et la Doctrine of Chances (1756), Pierre-Simon de Laplace et la Théorie Analytique des Probabilités (1812). Nous avons choisi de centrer le travail de l'atelier sur le texte, moins connu, de De Moivre et sa reprise par Laplace. On trouvera en annexe des extraits des ouvrages de De Moivre et Laplace. Importer l'article en version pdf Denis Lanier (Lycée Malherbe de Caen) et Didier Trotoux (IUT de Caen), IREM de Basse-Normandie Précédente édition: 1998, dans "Analyse et démarche analytique", IREM de Reims, p. 231-286. Introduction - La formule dite de Stirling, qui donne une évaluation de n! pour les grandes valeurs de n, est au centre des travaux menés au début du XVIIIe siècle sur les problèmes probabilistes de passage à la limite et d'approximations. Cet article peut se présenter comme un complément au texte sur le théorème de de Moivre-Laplace. La découverte des évaluations de n! par de Moivre et Stirling a donné lieu à des travaux concomitants de ces deux mathématiciens avec des échanges de correspondance, des corrections mutuelles d'erreurs. Ces travaux se situent à un moment que l'on peut qualifier de paradoxal dans l'histoire des mathématiques. En effet les méthodes infinitésimales se développent alors de plus en plus ; elles permettent d'aborder et de résoudre des questions nouvelles. Mais la véracité des résultats obtenus ne peut plus être légitimée par une synthèse démonstrative à la grecque. Il faut donc innover, expérimenter, confronter les résultats obtenus par différentes méthodes ou différents auteurs, avant de pouvoir être sûr de la scientificité d'un énoncé. Nous savons de plus aujourd'hui que certains outils étaient employés sans la rigueur (au sens moderne du terme) nécessaire. Ce sont donc les tours et détours des démarches analytiques du début du XVIIIe siècle que nous voudrions montrer dans ce texte. Autres ressources sur les probabilités, sites externes La loi des grands nombres, le théorème de De Moivre-Laplace
La formule de Stirling
Le calcul sexagésimal en Mésopotamie: enseignement dans les écoles de scribes
 |
|
Utilisation en classe - On peut utiliser la documentation de cet article à tous les niveaux de l'enseignement, depuis la fabrication de tables de multiplication au collège jusqu'à la présentation des propriétés arithmétiques de la numération sexagésimale et du calcul en virgule flottante au lycée. A partir des exercices de calcul mésopotamiens, une réflexion plus large peut être engagée dans le cadre de la formation des enseignants, par exemple sur le concept de nombre, le principe de position, les liens entre l'apprentissage de l'écriture et du calcul.
|
Lire l'article ou importer en version pdf. |
André Warusfel Résumé: A l’origine du calcul littéral figure notamment la résolution des équations algébriques, de Babylone à Galois. Le problème de la résolution des équations P(x)=0 où P est un polynôme donné possède plusieurs types de réponses, selon ce que l’on en attend : par exemple, développements décimaux d’ordre donné des solutions (heureusement en nombre fini), construction géométrique de segments ayant pour longueurs les valeurs des racines positives de l’équation, algorithmes basés sur des extractions de racines ou emploi de fonctions spéciales (elliptiques par exemple). Leur étude a été un facteur très important de la naissance et du développement des techniques de calcul (littéral ou géométrique). Leur histoire est jalonnée par une liste impressionnante de créateurs : les babyloniens, Euclide, Diophante, Al Khwarizmi, Cardan, Viète, Descartes, Newton, Lagrange, Abel et Galois pour ne citer que ceux-là. Enfin l’informatique est venue modifier, parfois de manière importante, les points de vue que nous avions il y a cinquante ans sur ce thème. Le but de l’intervention est de préciser, à chaque fois de manière simple et assez succincte, que fut l’apport de chacun d’entre eux. Utilisation en classe - Les enseignants de tous les niveaux trouveront des idées intéressantes à faire découvrir à leurs élèves. Par exemple, on peut dès le collège résoudre des équations du second degrè grâce à la méthode de complétion du carré, ou démontrer géométriquement les identités remarquables. Mais ce sont surtout les enseignants de première qui trouveront dans cet article une excellente introduction au cours sur les équations du second degré. Importer l'article en version pdf Ressources externes Source : http://www.math.ens.fr/culturemath/histoire%20des%20maths...Calcul et géométrie: résoudre des équations algébriques
19:26 Publié dans Approche critique comparée des nombres aztèques et | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Géométrie et Théorie des Modèles
Vendredi 17 décembre, à l'ENS, Salle W. Programme : 11h : Emmanuel Breuillard (Orsay), Les théorèmes de Hrushovski et leurs versions quantitatives. 14h : Anand Pillay (Leeds), Around Manin-Mumford and Mordell-Lang 16h : Michel Coste (Rennes I), Diamètre géodésique d'ensembles définis par un petit nombre d'équations et inégalités quadratiques Programme des séances passées : 2006-07, 2007-08, 2008-09, 2009-10, 2010-11. Géométrie et Théorie des Modèles
Organisateurs : Zoé Chatzidakis et François Loeser.
Pour recevoir le programme par e-mail, écrivez à : Francois.Loeser_at_ens.fr.
Pour les personnes ne connaissant pas du tout de théorie des modèles, des notes introduisant les notions de base (formules, ensembles définissables, théorème de compacité, etc.) sont disponibles ici. Ces personnes peuvent aussi consulter les premiers chapitres du livre Model Theory and Algebraic Geometry, E. Bouscaren ed., Springer Verlag, Lecture Notes in Mathematics 1696, Berlin 1998.
Les notes de quelques-uns des exposés sont disponibles.
PROCHAINE SEANCE
La notion de sous-groups approximatif, introduite récemment par T. Tao, permet de comprendre les parties finies A d'un groupe dont la taille de l'ensemble des produits AA est beaucoup plus petite que |A|^2. Cette notion et les méthodes combinatoires utilisées pour l'étudier ont été couronnées de succès par le rôle qu'elles jouent dans la théorie spectrale des graphes (graphes expanseurs) d'une part et pour les applications arithmétiques qui en découlent (crible de Bourgain-Gamburd-Sarnak). Récemment, en connection avec la théorie des modèles et la stabilité, Hrushovski s'est intéressé au problème de la classification des groupes approximatifs et a réussi à obtenir plusieurs résultats remarquables dans cette direction. Entre autres, une classification des sous-groupes approximatifs des groupes linéaires, ainsi qu'une version améliorée du fameux théorème de Gromov sur les groupes à croissance polynomiale. Dans cet exposé je présenterai ces travaux ainsi qu'une autre approche (travail en commun avec Ben Green et Terence Tao) qui permet de retrouver certains de ces résultats et d'en donner des bornes précises, lesquelles sont souvent cruciales pour les applications.
I will discuss relationships between Manin-Mumford and Mordell-Lang over function fields in all characteristics. Of course these are “known theorems” but the subtext is the search for a direct or transparent proof of function field Mordell-Lang in positive characteristic (or at least a proof avoiding the appeal to Zariski geometries).
Les bornes sur des invariants topologiques d'ensembles algébriques réels ou semi-algébriques (en fonction du degré des polynômes définissant ces ensembles, de leur nombre et du nombre de variables) sont habituellement exponentielles en le nombre de variables (Petrovskii, Oleinik, Thom, Milnor,...). C'est aussi le cas pour la borne sur l'invariant métrique qu'est le diamètre géodésique, obtenue par D'Acunto et Kurdyka. Le cas quadratique révèle un comportement différent : A. Barvinok a donné une borne sur la somme des nombres de Betti qui est polynomiale en le nombre de variables. L'exposé vise à établir une borne également polynomiale en le nombre de variables pour le diamètre géodésique dans le cas quadratique. On passera en revue les méthodes de Barvinok (utilisation de la linéarité du gradient) et de D'Acunto et Kurdyka (methode des vallées et crêtes). Travail commun avec Seydou Moussa (Niamey).
SEANCE SUIVANTE
Vendredi 11 février 2011, à l'ENS, Salle W. Orateurs prévus : Charles Favre (Polytechnique), Ofer Gabber (IHES), Dugald Macpherson (Leeds).
SEANCES ULTERIEURES
Autres dates déjà prévues : 18 mars et 8 avril.
Adresses des lieux de rencontre
Amphithéâtre Rataud ou Galois. Il est situé dans le nouveau bâtiment, au niveau -1 : traverser ou contourner le bâtiment principal de l'ENS ; l'entrée est à droite de l'entrée principale du nouveau bâtiment ; pour ouvrir la porte vitrée il faut appuyer sur le bouton ; descendre l'escalier, la salle est devant vous sur la gauche.
Salle Henri Cartan. Contourner le bâtiment principal sur la droite, pour entrer dans l'ancien bâtiment de la bibliothèque de mathématiques (voir photo), et descendre au niveau -2, dans le couloir Rouge.
Salle R. Contourner le bâtiment principal sur la droite, pour entrer dans l'ancien bâtiment de la bibliothèque de mathématiques (voir photo), et descendre au niveau -2, dans le couloirRouge.
Salle W. Entrer dans le bâtiment principal, suivre le couloir de droite jusqu'à l'escalier B dans le coin sud-est ; monter au 3ème (= dernier) étage par l'escalier principal, puis suivre les flèches Toits du DMA : prendre le couloir, au bout du couloir tourner à droite et monter encore un étage. La salle W se trouve sur votre gauche.
19:23 Publié dans Géométrie et Théorie des Modèles | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Les géomètres de la Grèce antique
Bernard VitracLes géomètres de la Grèce antique
4- Euclide le Stoichéiôtês
Sommaire
Encarts
Figures
|
Commentant le premier Livre des Éléments d'Euclide, Proclus de Lycie se devait de préciser l'époque où son auteur vivait. Il rapporte l'anecdote suivante : « On dit qu'un jour Ptolémée demanda à Euclide s'il n'y avait pas de voie plus courte que celle des Éléments pour apprendre la géométrie. Et Euclide lui répondit qu'en géométrie il n'y avait point de voie royale ». Certains exégètes, optimistes, en ont déduit que l'Auteur des Éléments avait présenté son ouvrage au monarque, soit pour solliciter ses faveurs, soit pour l'en remercier. Nous avons vu (chapitre 3), avec Conon et Callimaque, que cela n'était pas impossible. A partir de là, ils en ont déduit que Ptolémée avait très probablement accueilli Euclide dans son Musée … où celui-ci aurait, en quelque sorte, fondé l'école mathématique d'Alexandrie. L'histoire est séduisante, mais requiert toute notre crédulité. Les bons esprits font remarquer que l'anecdote — et sa fine allusion aux routes réservées pour les courriers royaux — était devenue proverbiale et que l'on en connaît une autre version, dans les mêmes termes, à ceci près qu'elle met en scène Alexandre le Grand et Ménechme de Proconnèse, disciple d'Eudoxe de Cnide. De plus, il suffit de relire le passage de Proclus avec un peu d'attention pour percevoir son embarras à dater Euclide. Il affirme qu'Euclide était un peu plus jeune que les disciples de Platon, mais antérieur à Archimède et Ératosthène. Comme un siècle environ sépare les naissances d'Aristote et d'Archimède, il utilise l'anecdote pour faire d'Euclide un contemporain de Ptolémée I Soter. Mais l'anecdote elle-même, qu'il a dû reprendre à une source antérieure, ne précise pas de quel Ptolémée il s'agit … D'une manière quelque peu paradoxale, l'existence d'une autre version de ladite anecdote permet d'en percevoir le sens. Il ne s'agit pas d'enregistrer le souvenir d'une mémorable rencontre entre deux personnages devenus célèbres. Elles sont conçues (et l'on ne sait pas trop bien quand) pour construire une chronologie fondée sur la contemporanéité des savants avec des hommes illustres tels que les souverains. Car il n'y a pas de doutes qu'Alexandre et Ménechme étaient contemporains. On peut donc admettre qu'Euclide le fut de Ptolémée, sans doute Soter, peut-être Philadelphe. On aimerait être plus précis, mais nous ne savons rien de la vie d'Euclide, de sa famille, de sa formation, en particulier des maîtres qui furent les siens. Nous ne connaissons même pas sa cité d'origine. Les Modernes l'appellent souvent Euclide d'Alexandrie suggérant par là que la capitale des Ptolémées fut sa patrie d'adoption. Ils se fient à l'anecdote de Proclus mais aussi à un second témoignage, transmis par le Livre VII de la Collection mathématique de Pappus, quand ce dernier présente le traité des Coniques d'Apollonius et en commente la préface. Or, dans celle-ci, plus précisément dans la préface au premier Livre, Apollonius de Perge décrit, non sans fierté, le plan de son ouvrage et, à propos du Livre III, il fait remarquer que, chez Euclide, le lieu relatif à trois et quatre droites [voir Encart 1] n'est construit ni correctement, ni complètement. C'est sans doute là la plus ancienne mention d'Euclide dans la littérature ancienne conservée et c'est une critique. Pappus trouve la critique pas très fair-play et marquée du sceau de l'ingratitude. Car si Apollonius a pu dépasser l'Auteur des Éléments, c'est, dit-il, parce qu'il avait longtemps étudié à Alexandrie avec les disciples d'Euclide. On en déduit généralement que ce dernier avait lui aussi enseigné dans la capitale des Ptolémées.
Euclide à Alexandrie
Il y a beaucoup d'homonymes chez les Grecs. Euclide n'échappe pas à la règle. Au moins trois personnes portant ce nom furent célèbres dans l'Antiquité : un archonte (haut magistrat) athénien, à la fin du Ve s. (avant J.C.), le philosophe Euclide de Mégare, disciple de Socrate et Euclide le géomètre. Au Moyen Âge on confondait fréquemment le philosophe mégarique et le géomètre. Pour distinguer celui-ci les Anciens lui accolèrent un surnom. Ils forgèrent le mot "stoicheiôtês", qui signifie «l'auteur des Éléments» (stoicheia ou stoicheiôsis), le titre du plus célèbre des écrits d'Euclide, et qui devint son sobriquet.
Figure 5 - Portrait d'Euclide par Juste de Gand (XVe s.)
|
En confrontant différents témoignages, nous pouvons dresser une liste de ses œuvres. La plus célèbre est son recueil des Éléments, en treize Livres, principalement consacrés à la géométrie, mais qui incluent aussi trois Livres d'arithmétique (au sens de la théorie des nombres) (voir Encart 2 : la structure des treize Livres d'Éléments). Nous avons déjà évoqué le recueil (perdu) des Faux raisonnements ou Pseudaria (voir chapitre 2). Toujours en géométrie, nous possédons également un court traité intitulé Données, et une portion (conservée seulement dans des traductions médiévales) d'un ouvrage Sur la division des figures. Mais Euclide n'était pas seulement un géomètre : il rédigea aussi des Optiques, des Catoptriques (étude de la vision réfléchie par les miroirs), des Éléments de musique, des Phénomènes (un court traité d'astronomie physique). Des fragments conservés dans des traductions médiévales lui attribuent une étude de la balance et une preuve (rudimentaire) de la loi du levier.
L"encyclopédie" mathématique d'Euclide
Certaines attributions sont quelque peu douteuses, notamment celles des fragments mécaniques et des Catoptriques. Quant à la Division du canon qui a été transmise sous son nom, nous ne savons pas exactement quelles relations elle entretient avec l'ouvrage musical que l'Antiquité lui reconnaissait. Cela dit, l'ensemble constitue une sorte d'"encyclopédie" mathématique, composée d'ouvrages portant sur les différentes disciplines reconnues dans les classifications des sciences. En quelques décennies, nous voyons donc des philosophes (pour l'essentiel platoniciens et aristotéliciens) élaborer différents systèmes de classification des sciences mathématiques, Eudème de Rhodes rédiger l'histoire de trois d'entre elles, et Euclide composer un ensemble de traités plus ou moins élémentaires qui réorganisent et synthétisent les connaissances antérieures dans ces mêmes domaines.
Figure 4 - Instruments à cordes
|
Pour certains historiens modernes la réputation d'Euclide est donc largement usurpée. Il s'agirait, au mieux, d'un rédacteur de manuels ou d'un éditeur scientifique, au pire, d'un simple compilateur, procédant à partir des travaux des autres. Le jugement n'est pas désintéressé : il s'agit de valider un mode de lecture de ses traités, de les dépecer pour retrouver les contributions originales de ses prédécesseurs, alors que la forme même des écrits logico-déductifs rend cette entreprise à peu près impossible. La cacophonie des études qui prétendent procéder de cette manière en témoigne. Surtout ce jugement n'est pas très objectif. Il laisse de côté les témoignages d'Apollonius et de Pappus, les indications que nous avons sur des ouvrages perdus, notamment les Porismes, en trois Livres, les Lieux à la surface, en deux Livres, et peut-être des Éléments des coniques en quatre Livres. Pappus affirme notamment que la théorie du lieu analysé a été constituée, pour l'essentiel, par trois auteurs : Aristée, Euclide et Apollonius. Il s'agit cette fois de géométrie non élémentaire, incluant, entre autres, la théorie des Coniques, domaine de recherches très important et novateur au cours du III e s et même au-delà. Qu'Euclide ait travaillé sur les coniques est confirmé par la critique d'Apollonius. Le portrait de l'auteur des Éléments doit donc être nuancé : un géomètre compétent, actif dans certains domaines "de pointe", mais aussi manifestement très intéressé par la mise en forme des exposés scientifiques et la rédaction d'ouvrages de référence. Rien là de contradictoire ni d'unique dans l'histoire des sciences mathématiques. Que la gloire d'Euclide tienne aux Éléments ne fait aucun doute. Et il y a au moins deux bonnes raisons à cela ou plutôt, une bonne raison et une moins bonne. La première est que son traité est une incontestable réussite dans ce qui va devenir un genre littéraire que désigne le titre : « éléments (de) … ». Ce genre tente d'articuler deux objectifs. Car le recueil d'éléments n'est pas la simple et sèche compilation d'un fascicule de résultats; il fournit une représentation architectonique de la discipline. La seconde raison du succès d'Euclide, notamment éditorial, c'est le plan plutôt singulier qu'il a suivi et qui sera jugé sévèrement au Moyen Âge et à la Renaissance. Il faut dire qu'à bien des égards, si l'on entreprend l'étude du traité de manière continue, dans l'ordre de succession des livres — ce à quoi nous incite la structure déductive —, la progression euclidienne paraît pédagogiquement assez désastreuse.
1. Fournir une synthèse des connaissances "élémentaires" dans un domaine donné, requises pour un "premier" apprentissage.
2. Incarner simultanément un modèle de raisonnement, dans le cas qui nous intéresse, un paradigme du raisonnement déductif et démonstratif.
Figure 5 - Papyrus trouvé à Oxyrhynque: proposition 5 du Livre II des Éléments d'Euclide
|
La famille lexicale du mot grec "stoicheïon" ("élément") renvoie d'abord à l'idée de "rang", de "file", de mise en ordre par alignement. L'expérience de l'écriture alphabétique a durablement impressionné les philosophes grecs. Des composants ultimes en nombre relativement limité (moins d'une trentaine) suffisent à constituer l'ensemble des syllabes, des mots et des discours. La langue grecque les appelle aussi "éléments" ("stoicheïa"). Elle ne distingue pas toujours clairement s'il s'agit des phonèmes du langage ou des lettres du système d'écriture. Ce mode de composition d'un Tout à partir de ses constituants élémentaires est projeté sur les êtres naturels et les productions humaines. Selon Platon, le monde est constitué de quatre éléments : feu, air, eau, terre; Empédocle avait été le premier à formuler cette théorie sans toutefois utiliser le terme "élément". De même, explique Aristote, en géométrie certaines propositions se retrouvent dans la démonstration de beaucoup d'autres; ce sont celles que l'on appelle "éléments" et leur apprentissage est donc requis. Au départ la notion paraît toute relative : tel théorème est élément de tel autre. N'est "élément" à proprement parler que ce qui intervient comme constituant dans de nombreuses preuves. Sont donc exclues certaines propositions élémentaires, simples et élégantes, mais qui ne sont pas mobilisées dans beaucoup de démonstrations. Proclus, commentant Euclide, donne comme exemple le fait que les trois hauteurs d'un triangle sont concourantes. On comprend donc que la constitution d'un recueil d'éléments est à rapporter à un certain état du domaine considéré, qu'elle suppose l'accumulation de résultats significatifs suffisamment nombreux, le repérage des propriétés ou des constructions qui interviennent le plus souvent. Leur choix présuppose donc une analyse préalable — au sens quasi chimique du terme — pour déterminer les ingrédients essentiels, non plus seulement en fonction de leur usage dans une problématique déterminée, mais pour essayer de les articuler dans une architecture déductive globale dont les qualités principales seront la concision et la clarté. Ce travail d'investigation préalable — qui a sûrement connu plusieurs étapes et différents acteurs — n'est pas présenté. L'exposition est synthétique : elle procède déductivement des hypothèses aux conclusions et, parce qu'il a bien fallu interrompre le travail de décomposition à un certain moment, il faudra poser des principes ou points de départ non démontrés. Ces derniers sont en quelque sorte les plus élémentaires des éléments. Clairement il s'agit d'un procédé d'exposition d'une portion de science déjà faite et non d'une méthode de recherche. Les mathématiciens grecs l'ont particulièrement prisé et outre les Éléments d'Euclide, y compris en musique, on connaît des Éléments des coniques, attribués à Aristée, à Euclide et c'est encore sous ce titre qu'Apollonius lui-même décrit les quatre premiers livres de ses Coniques. Archimède se réfère à des Éléments de mécanique. Ce qui a fait le succès de la démarche dans le domaine de la géométrie, et plus généralement en mathématiques, c'est la possibilité de mener à bien cette remontée vers des principes indémontrables. A cause de la simplicité de ses points de départ, la rigueur de sa démarche, l'irréfutabilité (au moins apparente) des conclusions auxquelles il aboutit, le style more geometrico a exercé une puissante fascination. Déjà dans l'Antiquité certains ont donc entrepris de rédiger des Éléments d'éthique, de physique, de théologie … Le prix à payer peut être élevé. La présentation synthétique est, par définition, historiquement et heuristiquement opaque. Celle d'Euclide est parfois artificielle. La chose n'est pas bien grave tant qu'on l'étudie sous la direction d'un maître compétent, lequel fournira les explications complémentaires nécessaires. Il est d'ailleurs possible que l'auteur des Éléments ait conçu son recueil, non pas comme un manuel d'enseignement que l'étudiant aurait dû lire de manière cursive, mais plutôt comme un ouvrage de référence à consulter intelligemment. Mais il deviendra un texte scolaire, soumis au travail des enseignants et des commentateurs. Une de leurs tâches sera d'affranchir le lecteur de la linéarité déductive, de lui permettre d'anticiper, de connaître l'origine des problèmes … Ce sera aussi l'occasion de critiquer la progression euclidienne. Le traité d'Euclide est l'un des écrits mathématiques antiques parmi les plus importants quant à la taille. Outre la structure déductive qui s'exerce localement, il fallait donc en répartir la matière selon certains critères. L'un des plus prégnants a consisté à regrouper les résultats en fonction des objets sur lesquels ils portent. On peut dès lors distinguer, à la suite des Anciens, trois grands sous-ensembles : les Livres dits plans, les Livres arithmétiques et les Livres stéréométriques (voir Encart 2). Leurs objets fondamentaux respectifs sont : la figure plane, le nombre, et la figure solide. La réduction en éléments, caractéristique de la démarche euclidienne, conduit à privilégier les plus simples des figures dont le répertoire est par conséquent plutôt limité dans les Éléments : les triangles, carrés, rectangles, parallélogrammes et trapèze dans les Livres I-II; le cercle et ses segments; dans le Livre III; le Livre IV combine les deux aspects en traitant de quelques polygones réguliers inscrits dans, ou circonscrits à, un cercle. A l'autre extrémité, le Livre XIII se propose la construction des cinq solides réguliers circonscrits par une sphère. Les autres solides pris en considération sont les parallélépipèdes et les prismes (Livre XI), les pyramides, les cônes et les cylindres (Livre XII).Les Éléments : un bon titre
Les Éléments : un plan singulier
A l'issue de ce simple survol trois ou quatre traits peuvent surprendre le lecteur, traits qui ont souvent été perçus comme des anomalies. 1. L'ouvrage commence par la géométrie, avant l'arithmétique, généralement considérée comme la première des sciences mathématiques car ses objets, dénués de position, sont plus simples. 2. L'exposé de géométrie plane est cependant interrompu par un Livre d'un autre genre, le cinquième, dont on ne peut pas vraiment rendre compte en termes d'objet. Il traite derelations entre objets, celles que l'on appelle "rapport" et "proportionnalité". De plus ce Livre est d'un niveau d'abstraction incroyablement élevé par rapport à ce qui précède. La motivation qui commande une telle sophistication (l'irrationalité) n'est aucunement explicitée au niveau du Livre V lui-même. 3. Un autre Livre singulier, et ce pour deux raisons, est le Livre X. D'abord lui non plus ne laisse pas bien décrire en termes d'objets : on y trouve des lignes, des aires et des nombres. En fait il traite également de relations, celle de commensurabilité et d'incommensurabilité, au départ considérées selon un point de vue général puis particularisées pour des droites et des aires rectilignes simples. Suit alors une classification très impressionnante de droites et d'aires dites irrationnelles — environ 90 Propositions, soit un cinquième de l'ensemble du traité ! —, mais qui a été vite perçue comme indigeste, d'autant qu'elle ne semble pas justifiée par ses emplois ultérieurs. 4. On peut ajouter que l'exposé stéréométrique s'achève par la comparaison des cinq solides réguliers et que celle-ci paraît incomplète.
Figure 7 - Le temple d'Héphaïstos sur l'agora d'Athènes
|
Voilà déjà de quoi nourrir critiques et commentaires. Mais il y a pire. Les Éléments contiennent, non pas un exposé de théorie des proportions, celui du Livre V, mais deux ! Le second se trouve dans les vingt-deux premières Propositions du Livre VII. Par conséquent certains résultats se trouvent démontrés deux fois. Ainsi la Proposition V. 16 établit que « si quatre grandeurs sont en proportion, de manière alterne, elles seront aussi en proportion », tandis que VII. 13 prouve que « si quatre nombres sont en proportion, de manière alterne, ils seront aussi en proportion ». Avec nos notations modernes nous les transcrirons de la même manière : « si A : B = C : D alors A : C = B : D », la notation A : B désignant le rapport de A : B, et le signe = signifiant « être le même que … ». Car « (A, B, C, D) sont en proportion » ne signifie rien d'autre que « (A, B) sont dans le même rapport que (C, D) ». La transcription efface les différences; dans notre écriture symbolique les lettres A, B, … peuvent désigner n'importe quel type d'objets susceptibles d'entrer dans une proportion. Mais si le lecteur reprend les énoncés anciens il constatera sans peine que la différence entre V. 16 et VII. 13 réside précisément dans le fait que la première porte sur des grandeurs("megethos" en grec), la seconde sur des nombres ("arithmos" en grec). Qui plus est, s'il lit ensuite les preuves associées à nos deux énoncés — ce que nous ne ferons pas ici — le lecteur verra qu'elles sont tout à fait différentes. Elles reposent notamment sur des définitions spécifiques de « être en proportion », pour les grandeurs (Définition V. 5-6) et pour les nombres (Définition VII. 21). La notion de "nombre" est elle-même définie : il s'agit d'une multitude déterminée d'unités, autrement dit ce qui est utilisé pour faire une énumération (et qui correspond plus ou moins à nos nombres entiers naturels : 2, 3, 4, 5, …) Ni les fractions ni, a fortiori, les nombres irrationnels n'ont de place dans l'arithmétique grecque. Ce que recouvre la notion de grandeur est un peu moins clair. Originellement il s'agit d'une des trois propriétés fondamentales de la figure : sa taille. Euclide ne la définit pas (à partir de quoi le pourrait-il ?). Mais on voit dans la suite du traité qu'il subsume, sous ce terme, des lignes, des surfaces, des volumes et des angles rectilignes. Autrement dit, il l'envisage comme un objet géométrique abstrait, indépendamment de ses dimensions. Aristote l'applique à des temps, des poids … et autres grandeurs physiques. Il explique que la différence entre "nombre" et "grandeur" est constitutive : la seconde est indéfiniment divisible, tandis que la division du premier s'arrête à l'unité. Le mystère des deux théories des proportions pourrait donc s'arrêter là : puisqu'il y a deux types d'objets parfaitement distincts, le nombre et la grandeur, il est naturel qu'il y ait deux théories des proportions. Mais il y a un rebondissement : au début de son dixième Livre, Euclide "démontre" que si deux grandeurs, A, B, ont une commune mesure, leur rapport A : B, est celui d'un certain nombre M à un nombre, N. Pour prendre un exemple métrologique, si A et B sont deux longueurs et que A mesure 3 pieds tandis que B en mesure 5, le rapport de A à B sera le rapport des nombres 3 à 5. Là où nous ferions intervenir la fraction 3/5, les géomètres anciens diront que A est à B comme 3 est à 5. Autre manière de le dire : les rapports des grandeurs commensurables s'identifient à des rapports de nombres. Il ne faut pas confondre les nombres avec les grandeurs, ou avec une certaine espèce de grandeurs, mais les relations entre nombres servent à exprimer les relations entre certains types de grandeur. Nos longueurs, dans l'exemple précédent, ont un rapport exprimable, celui de 3 à 5. En revanche le côté et la diagonale d'un même carré ont un rapport qui ne peut pas s'exprimer immédiatement à l'aide des nombres (entiers) car ces deux droites sont incommensurables. Pour nous, ce rapport correspond au nombre irrationnel √2. D'un point de vue moderne, le fait qu'une relation entre grandeurs commensurables s'identifie à une relation entre nombres correspond, très grossièrement, au fait que les nombres rationnels positifs (nos fractions) constituent un sous-ensemble des nombres réels (positifs). De là à considérer que l'une des deux théories des proportions d'Euclide, celle du Livre VII, n'est qu'un cas particulier, redondant, de la première, il n'y a qu'un pas. Il est franchi dès le XVI e s. : différents auteurs, notamment Francesco Maurolyco et Gilles-Personne de Roberval, proposeront l'unification de ces deux théories en une seule. A la fin du XIX e s., en mobilisant les quelques singularités dont nous venons de parler, les historiens vont élaborer une grille de lecture des Éléments particulièrement astucieuse. Pour ce faire, ils formulent une hypothèse qui est en quelque sorte la projection, dans le passé, de ce qu'une partie des mathématiques connaissait alors : une crise dite des fondements, liée aux paradoxes émergeant dans la formalisation de la toute récente théorie des ensembles. Ces historiens ont postulé, de manière analogique, que la découverte de grandeurs incommensurables avait entraîné le même genre de "crise". Auparavant les géomètres anciens, présupposant que toutes les grandeurs étaient commensurables, auraient utilisé une théorie des proportions simple. Nous en trouverions la trace dans l'actuel Livre VII. Après la découverte de droites incommensurables, mettant en évidence les failles de ladite théorie, il s'en serait suivi une période dans laquelle on aurait évité de recourir à la théorie des proportions. Nous en aurions la confirmation dans nos Livres I à IV. Puis une nouvelle théorie aurait été mise au point, celle du Livre V, que l'on attribue généralement à Eudoxe de Cnide, un contemporain d'Aristote, s'appliquant aussi bien aux grandeurs commensurables qu'incommensurables, quand bien même c'est seulement dans le Livre X que la distinction entre grandeurs commensurables et incommensurables est introduite. Celle-ci justifie, a posteriori, le traitement sophistiqué du Livre V. Euclide aurait appliqué la théorie eudoxienne aux figures planes dans le Livre VI et aux solides dans les Livres XI à XIII. Il aurait cependant maintenu une portion de l'ancienne théorie dans son Livre VII. Il faut donc supposer soit qu'il n'est qu'un simple compilateur reprenant, non pas seulement des résultats établis antérieurement, mais des Livres complets ou des séquences entières à ses prédécesseurs, soit qu'il avait un intérêt d'historien, soucieux de conserver la trace du passé de sa discipline. Aucune de ces deux hypothèses n'est très convaincante. Si cette lecture archéologique a stimulé les études euclidiennes pendant plus d'un siècle, elle est moins en faveur aujourd'hui. Il n'y a en effet, dans les sources des V e-IV e siècles, aucune trace d'une quelconque "crise des fondements" que les mathématiques grecques aurait connue, si tant est qu'on ait déjà tenté de les fonder avant le IV e siècle. Au contraire, cette époque est celle de leur développement rapide. Quant aux singularités du plan euclidien, on peut parfaitement les expliquer autrement. Nous avons déjà vu ce qu'il en était pour le double traitement de la proportionnalité : les Anciens, à la différence des Modernes, privilégient les objets sur les relations que ces objets entretiennent. Et puisqu'il y a deux types d'objets, il est légitime d'avoir deux théories des proportions, même si le but est ensuite de voir quand on peut les coordonner (cas des grandeurs commensurables) et quand cela ne se peut pas (cas des grandeurs incommensurables). En outre la lecture attentive du traité montre que l'insertion d'une Proposition, d'une séquence (voire d'un Livre entier) se fait, autant que faire se peut, le plus près possible de l'endroit où celles-ci sont utilisées. C'est pourquoi Euclide insère le Livre X là où il est, avant le traitement de solides, car le seul usage des irrationnelles se trouve dans le Livre XIII. Et c'est donc la raison pour laquelle l'introduction de la distinction « commensurables / incommensurables » est différée jusque-là. De même, les Livres arithmétiques n'intervenant que dans le Livre X, sont insérés juste avant. Autrement dit, bien qu'il y ait un intérêt spécifique pour l'arithmétique dans les Éléments, les Livres VII à IX existent d'abord à cause de leur usage instrumental dans l'étude de l'irrationalité. On peut bien commencer le traité par de la géométrie. Enfin Euclide se conforme à une attitude qui, selon Aristote, est propre aux mathématiciens : dans une science démonstrative les principes non démontrés que l'on utilise doivent être les moins nombreux possibles. Si donc il n'y a pas besoin de la théorie des proportions entre grandeurs et de ses difficiles Définitions pour établir certains résultats non triviaux, alors on doit s'en passer. D'où le regroupement de tels résultats dans les Livres I à IV, alors que le sixième Livre s'occupe de notions, notamment celle de similitude des figures, pour lesquelles le recours à la théorie des proportions est inévitable. Euclide pousse cette attitude assez loin puisqu'il regroupe, dans les 28 premières Propositions de son Livre I, celles qui ne dépendent pas de sa cinquième demande ou postulat des parallèles. On peut même penser que cette attitude explique en partie pourquoi la stéréométrie euclidienne est si mal fondée. Plusieurs des premières Propositions du Livre XI (1, 2, 3, 7) ont des preuves très incertaines. Apparemment Euclide était persuadé de pouvoir réduire logiquement la stéréométrie à la géométrie plane, sans introduire de nouveaux postulats. L'exposé d'Euclide est donc très loin d'être parfait. Mais les singularités de sa structure ne s'expliquent pas, ou peu, par l'histoire des mathématiques préeuclidiennes comme le croyent les partisans de la lecture archéologique; elles résultent des choix mathématiques et épistémologiques du Stoicheïotês. Source : Les deux théories des proportions
La lecture archéologique des Éléments
19:21 Publié dans Les géomètres de la Grèce antique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Euclide et GéoPlan
Neuf figures pour l'enseignement secondaire. Démonstration des théorèmes de Thalès et Pythagore par la méthode des aires.Euclide et GéoPlan
Euclide et GéoPlan Info bulle no 85 Cafoc de NantesMathématiques et sciences
Ce site, très riche et fréquemment actualisé par un enseignant en retraite, Patrice Debart, concerne les niveaux mathématiques de la 6e à la Terminale. Les thèmes et les modes opératoires étant passionnants, nous avons choisi de vous orienter sur l'article concernant Euclide, Thalès et Pythagore qui mêlent histoire et mathématiques, avec une pointe d'humour parfois… Il vous reste à intégrer ce site dans vos favoris, pour enrichir en permanence vos ressources !La géométrie euclidienne
|
Euclide avec un compas |
Les mathématiques grecques se sont développées sans règle de déduction explicite. La logique d'Aristote était trop fruste pour fonder les raisonnements. Le « si… alors… » est une conception trop pauvre du langage et jusqu'au XIXe siècle les règles de déduction resteront implicites. Les axiomes comme l'« unicité d'une parallèle » ou les « cas d'égalité des triangles » ont été explicités par Euclide et fournissent un fondement de la géométrie, imparfait certes, mais sur lesquels les autres résultats reposent solidement. Avec la méthode synthétique, Euclide a organisé la géométrie de manière déductive en donnant, à partir des propriétés géométriques établies précédemment, un raisonnement pour déduire chaque propriété cherchée. |
|
Euclide par Juste de Gand (15e siècle) |
Les Éléments d'Euclide (Alexandrie 300 avant Jésus-Christ) Le texte original des Éléments n'existe pas et nous est connu que de façon apocryphe. Dans la bibliothèque du Vatican, joint au manuscrit découvert par Peyrard, on aurait découvert un CD, encore plus apocryphe, contenant des figures GéoPlan que nous livrons en exclusivité ci-dessous. Les treize livres d'Euclide constituent une synthèse remarquable des mathématiques grecques. Toutes les constructions s'y effectuent uniquement à la « règle et au compas ». |
Proposition 31 du livre I des Éléments : par un point donné, construire une ligne parallèle à une droite donnée. L'unicité se déduit du postulat 5 : si une droite, tombant sur deux droites, fait les angles intérieurs d'un même côté plus petits que deux droits, ces droites, prolongées à l'infini, se rencontreront du côté où les angles sont plus petits que deux droits. Ce postulat est par la suite plus souvent énoncé sous la forme : « Par un point il passe une et une seule parallèle à une droite donnée ».I 31. Parallèle à une droite passant par un point donné
I 1. Triangle équilatéral
Rappels Demande 3. D'un point quelconque, et avec un intervalle quelconque, décrire une circonférence de cercle. Définition 15. Un cercle est une figure plane, comprise par une seule ligne qu'on nomme circonférence ; toutes les droites, menées à la circonférence d'un des points placés dans cette figure, étant égales entre elles. Définition 24. Parmi les figures trilatères, le triangle équilatéral est celle qui a ses trois côtés égaux. Construction avec un logiciel de géométrie : Construction à la « règle et au compas » : le triangle équilatéral Paragraphe déplacé dans l'article : cercle au collège Livre I, proposition 43 Dans tout parallélogramme, les compléments des parallélogrammes autour de la diagonale sont égaux entre eux.
Placer deux points A et B et dessiner le segment [AB],
tracer les cercles de centre A et B et de rayon AB (cercles de centre A passant par B et de centre B passant par A),
construire C, un des points d'intersection des deux cercles,
tracer les segments [BC] et [AC].![]() Télécharger la figure GéoPlan triangle_equilateral.g2w
Télécharger la figure GéoPlan triangle_equilateral.g2w![]() Télécharger la figure Cabri triangle_equilateral.fig
Télécharger la figure Cabri triangle_equilateral.fig![]() Télécharger la figure GeoLabo triangle_equilateral.glb
Télécharger la figure GeoLabo triangle_equilateral.glb
SommaireI 17 . Constructions de tangentes
I 43. Partage d'un rectangle en quatre
Classe de quatrième
|
M est un point libre sur la diagonale [AC] d'un rectangle ABCD. Démontrer que les aires des deux rectangles hachurés sont égales. |
Vérification assez facile avec GéoPlan : le logiciel ne sait pas calculer l'aire d'un rectangle, mais il sait trouver la moitié de cette aire : l'aire d'un triangle formé par deux côtés et une diagonale. Indication : (AB) étant parallèle à (CD), la propriété de Thalès dans les triangles rectangles AMI et CMJ permet d'écrire : (AD) étant parallèle à (BC), la propriété de Thalès dans les triangles ALM et CKM permet d'écrire : Par transitivité Le produit des « extrêmes » est égal au produit des « moyens » : KM × MI = LM × MJ. Cas de parallélogrammes : calcul d'aires Dans un parallélogramme, l'un quelconque des parallélogramme décrit autour du diamètre avec ses deux compléments est appelé gnomon. Pour un point I du diamètre [BC] d'un parallélogramme ABDC, le parallélogramme FBHI est dit décrit autour de ce diamètre. Ses compléments sont les parallélogrammes AFIG et IHDE (de même aire). Ces trois figures forment, dans leur ensemble, le gnomon ABDFIG. Le gnomon permet d'obtenir un nouveau parallélogramme semblable au précédent. Voir aussi : nombre d'or Si une ligne droite est coupée comme on voudra, le carré de la droite entière est égal aux carrés des segments et à deux fois le rectangle contenu sous les deux segments. Dans le carré ABDC, on a la démonstration, par les aires, de l'identité remarquable : ( a + b)2 = a2 + b2 + 2ab.![]() =
= ![]() .
.![]() =
= ![]() .
.![]() =
= ![]() .
.
Aire(IBKM) = Aire(LMJD).![]() Télécharger la figure GéoPlan hom_rect.g2w
Télécharger la figure GéoPlan hom_rect.g2wII 2. Gnomon
II 4. Carré d'une somme

![]() Télécharger la figure GéoPlan hom_rect2.g2w
Télécharger la figure GéoPlan hom_rect2.g2w
II 11. Carré et rectangle de même aire
|
Couper une ligne droite telle le rectangle de la toute et de l'une des parties, soit égal au carré de l'autre Sur un segment [AB] de longueur a, trouver un point G tel que le carré de côté AG ait même aire que le rectangle de longueur a et de largeur BG.
Construction Après avoir construit le carré ABCD de côté [AB], on note E le milieu de [AD]. On complète avec le point H le carré de côtés [AF] et [AG]. La carré AGHF a même aire que le rectangle GBCI.
Solution algébrique
Avec AB = BC = a, posons AG = x, alors GB = a - x.
|
Partage d'un segment [AB] en « moyenne et extrème raison » : étant donné deux points A et B, trouver un point D tel que B, D et A forment une section dorée ; et trouver un point M tel que A, B et M forment une section dorée. Construction On note I le milieu de [AB]. Le cercle (c2) de centre I et de rayon IC coupe (AB) en D du côté de A. Le cercle (c3) de centre A et de rayon AD coupe [AB] en M. Preuve par le calcul On vérifiera facilement, en prenant AB comme unité (AB = 1) que les résultats font intervenir le nombre d'or : MA = Remarque : le cercle (c3) coupe le segment [AC] en P qui réalise la section dorée de ce segment.VI 30. Construction de la section dorée
a. Partage d'un segment en « extrême et moyenne raison »
 On considère une droite (AB) et sur la perpendiculaire à (AB) en A un point C tel que AC = AB.
On considère une droite (AB) et sur la perpendiculaire à (AB) en A un point C tel que AC = AB.
AI = ![]() ; CA = AB = 1 ; DI = IC =
; CA = AB = 1 ; DI = IC = ![]() ;
;
AM = DA = DI - AI = ![]() -
- ![]() =
= ![]() =
= ![]() = Φ - 1 ≈ 0,618 ;
= Φ - 1 ≈ 0,618 ;
MB = AB - AM = 1 - ![]() = 2 - Φ ≈ 0,382 ;
= 2 - Φ ≈ 0,382 ;
DB = DI + IB = ![]() +
+ ![]() = Φ ≈ 1,618.
= Φ ≈ 1,618.![]() ;
; ![]() = Φ ;
= Φ ; ![]() = MB ×
= MB × ![]() = (1 -
= (1 - ![]() ) × Φ = Φ - 1 =
) × Φ = Φ - 1 = ![]() =
= ![]() .
.![]() =
= ![]() d'où
d'où ![]() = Φ : le point M réalise la section dorée du segment [AB].
= Φ : le point M réalise la section dorée du segment [AB].![]() Télécharger la figure GéoPlan section_doree.g2w
Télécharger la figure GéoPlan section_doree.g2w
c. Couper une ligne droite selon la moyenne raisonLivre VI, proposition XXX |
d. Numérisation de la géométrie
Construction avec deux carrés Pacer deux points A et B tels que AB = 1. Après avoir construit le carré ABCD de côté [AB], on note E le milieu de [AD]. On complète avec le point H le carré de côtés [AF] et [AG]. Le point G partage le segment [AB] en moyenne raison. Calculs algébriques Le carré AGHF a pour côté AG = Le rectangle GBCI a pour longueur CB = 1 Son aire est 2 - Φ. Il a été démontré dans la page suites que AB/AG = AG/GB : on a bien une section dorée du segment [AB].
|
La construction avec « corde et tangente égales » a été déplacée dans la page : le nombre d'or. Les extraits contenus dans ces pages sont ceux des 15 livres des Éléments géométriques d'Euclide, traduits par D. Henrion en 1632, publiée par la Bibliothèque Nationale de France.e. Corde et tangente égales
Les Éléments d'Euclide en ligne sur le site Gallica de la BNF

On trouve aussi la première édition de F. Peyrard, publiée en 1804, lorsqu'il était bibliothécaire de l'école polytechnique.
|
D. Henrion |
|||||||||||||
|
F.Peyrard |
|
Faire de l'histoire |
La Géométrie de Descartes |
Cercles |
Médiatrice |
Grands problèmes de la géométrie grecque |
|
SommaireI 31. Parallèle à une droite passant par un point
|
Téléchargement
« Descartes et les Mathématiques »Accueil : http://debart.pagesperso-orange.fr Suggestions, remarques, problèmes : me contacter. |
||||
Moteur de recherche - Publimath - Rétrolien |
|||||
Source : http://debart.pagesperso-orange.fr/geoplan/euclide_classi...
19:19 Publié dans Euclide et GéoPlan | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Livre I des Éléments d'Euclide
Le livre I des Éléments d'Euclide pose les fondements pour la suite de l'ouvrage. Il contient :Livre I des Éléments d'Euclide
Sommaire[masquer] |
Y sont définis le point, la droite (qui chez Euclide n'est jamais qu'un segment de droite), les angles, le cercle, le triangle, le carré, le rectangle, les parallèles. Voici quelques-unes de ces définitions : Elles supposent la possibilité de tracer une droite joignant deux points, cette droite étant unique, de prolonger une droite, de construire un cercle de centre et de rayon donnés. La demande 4 admet que tous les angles droits sont égaux entre eux. Le cinquième est le plus célèbre. Il s'agit du postulat d'Euclide sur les parallèles : Les définitions et les notions communes privilégient le cercle et la droite. La géométrie d'Euclide sera donc essentiellement attachée aux constructions à la règle et au compas. Elles énoncent la transivité de l'égalité, le fait qu'une égalité ou une inégalité est conservée si on ajouter ou si on retranche une même quantité aux deux membres de l'égalité ou de l'inégalité. La dernière notion commune énonce que le tout est plus grand que la partie. Ces propositions traitent des points suivants : Ces 26 premières propositions ne font pas appel au cinquième postulat d'Euclide sur les parallèles. Il n'en est pas de même des propositions qui suivent et qui utilisent ce postulat. Documents en ligne sur le site Gallica de la BNF Les définitions [modifier]
Les demandes [modifier]
Les notions communes [modifier]
Les propositions [modifier]
Bibliographie [modifier]
Liens externes [modifier]
|
|
| Livre I ~ Livre II ~ Livre III ~ Livre IV ~ Livre V ~ Livre VI Livre VII ~ Livre VIII ~ Livre IX ~ Livre X ~ Livre XI ~ Livre XII ~ Livre XIII |
19:15 Publié dans Livre I des Éléments d'Euclide | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Euclid's Elements Book IX
![]()
Table of contents
- Propositions (36)
Propositions
- Proposition 1.
- If two similar plane numbers multiplied by one another make some number, then the product is square.
- Proposition 2.
- If two numbers multiplied by one another make a square number, then they are similar plane numbers.
- Proposition 3.
- If a cubic number multiplied by itself makes some number, then the product is a cube.
- Proposition 4.
- If a cubic number multiplied by a cubic number makes some number, then the product is a cube.
- Proposition 5.
- If a cubic number multiplied by any number makes a cubic number, then the multiplied number is also cubic.
- Proposition 6.
- If a number multiplied by itself makes a cubic number, then it itself is also cubic.
- Proposition 7.
- If a composite number multiplied by any number makes some number, then the product is solid.
- Proposition 8.
- If as many numbers as we please beginning from a unit are in continued proportion, then the third from the unit is square as are also those which successively leave out one, the fourth is cubic as are also all those which leave out two, and the seventh is at once cubic and square are also those which leave out five.
- Proposition 9.
- If as many numbers as we please beginning from a unit are in continued proportion, and the number after the unit is square, then all the rest are also square; and if the number after the unit is cubic, then all the rest are also cubic.
- Proposition 10.
- If as many numbers as we please beginning from a unit are in continued proportion, and the number after the unit is not square, then neither is any other square except the third from the unit and all those which leave out one; and, if the number after the unit is not cubic, then neither is any other cubic except the fourth from the unit and all those which leave out two.
- Proposition 11.
- If as many numbers as we please beginning from a unit are in continued proportion, then the less measures the greater according to some one of the numbers which appear among the proportional numbers.
Corollary. Whatever place the measuring number has, reckoned from the unit, the same place also has the number according to which it measures, reckoned from the number measured, in the direction of the number before it.
- Proposition 12.
- If as many numbers as we please beginning from a unit are in continued proportion, then by whatever prime numbers the last is measured, the next to the unit is also measured by the same.
- Proposition 13.
- If as many numbers as we please beginning from a unit are in continued proportion, and the number after the unit is prime, then the greatest is not measured by any except those which have a place among the proportional numbers.
- Proposition 14.
- If a number is the least that is measured by prime numbers, then it is not measured by any other prime number except those originally measuring it.
- Proposition 15.
- If three numbers in continued proportion are the least of those which have the same ratio with them, then the sum of any two is relatively prime to the remaining number.
- Proposition 16.
- If two numbers are relatively prime, then the second is not to any other number as the first is to the second.
- Proposition 17.
- If there are as many numbers as we please in continued proportion, and the extremes of them are relatively prime, then the last is not to any other number as the first is to the second.
- Proposition 18.
- Given two numbers, to investigate whether it is possible to find a third proportional to them.
- Proposition 19.
- Given three numbers, to investigate when it is possible to find a fourth proportional to them.
- Proposition 20.
- Prime numbers are more than any assigned multitude of prime numbers.
- Proposition 21.
- If as many even numbers as we please are added together, then the sum is even.
- Proposition 22.
- If as many odd numbers as we please are added together, and their multitude is even, then the sum is even.
- Proposition 23.
- If as many odd numbers as we please are added together, and their multitude is odd, then the sum is also odd.
- Proposition 24.
- If an even number is subtracted from an even number, then the remainder is even.
- Proposition 25.
- If an odd number is subtracted from an even number, then the remainder is odd.
- Proposition 26.
- If an odd number is subtracted from an odd number, then the remainder is even.
- Proposition 27.
- If an even number is subtracted from an odd number, then the remainder is odd.
- Proposition 28.
- If an odd number is multiplied by an even number, then the product is even.
- Proposition 29.
- If an odd number is multiplied by an odd number, then the product is odd.
- Proposition 30.
- If an odd number measures an even number, then it also measures half of it.
- Proposition 31.
- If an odd number is relatively prime to any number, then it is also relatively prime to double it.
- Proposition 32.
- Each of the numbers which are continually doubled beginning from a dyad is even-times even only.
- Proposition 33.
- If a number has its half odd, then it is even-times odd only.
- Proposition 34.
- If an [even] number neither is one of those which is continually doubled from a dyad, nor has its half odd, then it is both even-times even and even-times odd.
- Proposition 35.
- If as many numbers as we please are in continued proportion, and there is subtracted from the second and the last numbers equal to the first, then the excess of the second is to the first as the excess of the last is to the sum of all those before it.
- Proposition 36.
- If as many numbers as we please beginning from a unit are set out continuously in double proportion until the sum of all becomes prime, and if the sum multiplied into the last makes some number, then the product is perfect.
| Next book: Book X
Previous: Book VIII |
|
© 1996
D.E.Joyce
Clark University
Source : http://aleph0.clarku.edu/~djoyce/java/elements/bookIX/boo...
19:14 Publié dans Euclid's Elements Book IX | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Euclid's Elements Book I
![]()
Table of contents
- Definitions (23)
- Postulates (5)
- Common Notions (5)
- Propositions (48)
- Guide to Book I
Definitions
- Definition 1.
- A point is that which has no part.
- Definition 2.
- A line is breadthless length.
- Definition 3.
- The ends of a line are points.
- Definition 4.
- A straight line is a line which lies evenly with the points on itself.
- Definition 5.
- A surface is that which has length and breadth only.
- Definition 6.
- The edges of a surface are lines.
- Definition 7.
- A plane surface is a surface which lies evenly with the straight lines on itself.
- Definition 8.
- A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line.
- Definition 9.
- And when the lines containing the angle are straight, the angle is called rectilinear.
- Definition 10.
- When a straight line standing on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands.
- Definition 11.
- An obtuse angle is an angle greater than a right angle.
- Definition 12.
- An acute angle is an angle less than a right angle.
- Definition 13.
- A boundary is that which is an extremity of anything.
- Definition 14.
- A figure is that which is contained by any boundary or boundaries.
- Definition 15.
- A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure equal one another.
- Definition 16.
- And the point is called the center of the circle.
- Definition 17.
- A diameter of the circle is any straight line drawn through the center and terminated in both directions by the circumference of the circle, and such a straight line also bisects the circle.
- Definition 18.
- A semicircle is the figure contained by the diameter and the circumference cut off by it. And the center of the semicircle is the same as that of the circle.
- Definition 19.
- Rectilinear figures are those which are contained by straight lines, trilateral figures being those contained by three, quadrilateral those contained by four, and multilateral those contained by more than four straight lines.
- Definition 20.
- Of trilateral figures, an equilateral triangle is that which has its three sides equal, an isosceles triangle that which has two of its sides alone equal, and a scalene triangle that which has its three sides unequal.
- Definition 21.
- Further, of trilateral figures, a right-angled triangle is that which has a right angle, an obtuse-angled triangle that which has an obtuse angle, and an acute-angled triangle that which has its three angles acute.
- Definition 22.
- Of quadrilateral figures, a square is that which is both equilateral and right-angled; an oblong that which is right-angled but not equilateral; a rhombus that which is equilateral but not right-angled; and arhomboid that which has its opposite sides and angles equal to one another but is neither equilateral nor right-angled. And let quadrilaterals other than these be called trapezia.
- Definition 23
- Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.
Postulates
Let the following be postulated:- Postulate 1.
- To draw a straight line from any point to any point.
- Postulate 2.
- To produce a finite straight line continuously in a straight line.
- Postulate 3.
- To describe a circle with any center and radius.
- Postulate 4.
- That all right angles equal one another.
- Postulate 5.
- That, if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.
Common Notions
- Common notion 1.
- Things which equal the same thing also equal one another.
- Common notion 2.
- If equals are added to equals, then the wholes are equal.
- Common notion 3.
- If equals are subtracted from equals, then the remainders are equal.
- Common notion 4.
- Things which coincide with one another equal one another.
- Common notion 5.
- The whole is greater than the part.
Propositions
- Proposition 1.
- To construct an equilateral triangle on a given finite straight line.
- Proposition 2.
- To place a straight line equal to a given straight line with one end at a given point.
- Proposition 3.
- To cut off from the greater of two given unequal straight lines a straight line equal to the less.
- Proposition 4.
- If two triangles have two sides equal to two sides respectively, and have the angles contained by the equal straight lines equal, then they also have the base equal to the base, the triangle equals the triangle, and the remaining angles equal the remaining angles respectively, namely those opposite the equal sides.
- Proposition 5.
- In isosceles triangles the angles at the base equal one another, and, if the equal straight lines are produced further, then the angles under the base equal one another.
- Proposition 6.
- If in a triangle two angles equal one another, then the sides opposite the equal angles also equal one another.
- Proposition 7.
- Given two straight lines constructed from the ends of a straight line and meeting in a point, there cannot be constructed from the ends of the same straight line, and on the same side of it, two other straight lines meeting in another point and equal to the former two respectively, namely each equal to that from the same end.
- Proposition 8.
- If two triangles have the two sides equal to two sides respectively, and also have the base equal to the base, then they also have the angles equal which are contained by the equal straight lines.
- Proposition 9.
- To bisect a given rectilinear angle.
- Proposition 10.
- To bisect a given finite straight line.
- Proposition 11.
- To draw a straight line at right angles to a given straight line from a given point on it.
- Proposition 12.
- To draw a straight line perpendicular to a given infinite straight line from a given point not on it.
- Proposition 13.
- If a straight line stands on a straight line, then it makes either two right angles or angles whose sum equals two right angles.
- Proposition 14.
- If with any straight line, and at a point on it, two straight lines not lying on the same side make the sum of the adjacent angles equal to two right angles, then the two straight lines are in a straight line with one another.
- Proposition 15.
- If two straight lines cut one another, then they make the vertical angles equal to one another.
Corollary. If two straight lines cut one another, then they will make the angles at the point of section equal to four right angles.
- Proposition 16.
- In any triangle, if one of the sides is produced, then the exterior angle is greater than either of the interior and opposite angles.
- Proposition 17.
- In any triangle the sum of any two angles is less than two right angles.
- Proposition 18.
- In any triangle the angle opposite the greater side is greater.
- Proposition 19.
- In any triangle the side opposite the greater angle is greater.
- Proposition 20.
- In any triangle the sum of any two sides is greater than the remaining one.
- Proposition 21.
- If from the ends of one of the sides of a triangle two straight lines are constructed meeting within the triangle, then the sum of the straight lines so constructed is less than the sum of the remaining two sides of the triangle, but the constructed straight lines contain a greater angle than the angle contained by the remaining two sides.
- Proposition 22.
- To construct a triangle out of three straight lines which equal three given straight lines: thus it is necessary that the sum of any two of the straight lines should be greater than the remaining one.
- Proposition 23.
- To construct a rectilinear angle equal to a given rectilinear angle on a given straight line and at a point on it.
- Proposition 24.
- If two triangles have two sides equal to two sides respectively, but have one of the angles contained by the equal straight lines greater than the other, then they also have the base greater than the base.
- Proposition 25.
- If two triangles have two sides equal to two sides respectively, but have the base greater than the base, then they also have the one of the angles contained by the equal straight lines greater than the other.
- Proposition 26.
- If two triangles have two angles equal to two angles respectively, and one side equal to one side, namely, either the side adjoining the equal angles, or that opposite one of the equal angles, then the remaining sides equal the remaining sides and the remaining angle equals the remaining angle.
- Proposition 27.
- If a straight line falling on two straight lines makes the alternate angles equal to one another, then the straight lines are parallel to one another.
- Proposition 28.
- If a straight line falling on two straight lines makes the exterior angle equal to the interior and opposite angle on the same side, or the sum of the interior angles on the same side equal to two right angles, then the straight lines are parallel to one another.
- Proposition 29.
- A straight line falling on parallel straight lines makes the alternate angles equal to one another, the exterior angle equal to the interior and opposite angle, and the sum of the interior angles on the same side equal to two right angles.
- Proposition 30.
- Straight lines parallel to the same straight line are also parallel to one another.
- Proposition 31.
- To draw a straight line through a given point parallel to a given straight line.
- Proposition 32.
- In any triangle, if one of the sides is produced, then the exterior angle equals the sum of the two interior and opposite angles, and the sum of the three interior angles of the triangle equals two right angles.
- Proposition 33.
- Straight lines which join the ends of equal and parallel straight lines in the same directions are themselves equal and parallel.
- Proposition 34.
- In parallelogrammic areas the opposite sides and angles equal one another, and the diameter bisects the areas.
- Proposition 35.
- Parallelograms which are on the same base and in the same parallels equal one another.
- Proposition 36.
- Parallelograms which are on equal bases and in the same parallels equal one another.
- Proposition 37.
- Triangles which are on the same base and in the same parallels equal one another.
- Proposition 38.
- Triangles which are on equal bases and in the same parallels equal one another.
- Proposition 39.
- Equal triangles which are on the same base and on the same side are also in the same parallels.
- Proposition 40.
- Equal triangles which are on equal bases and on the same side are also in the same parallels.
- Proposition 41.
- If a parallelogram has the same base with a triangle and is in the same parallels, then the parallelogram is double the triangle.
- Proposition 42.
- To construct a parallelogram equal to a given triangle in a given rectilinear angle.
- Proposition 43.
- In any parallelogram the complements of the parallelograms about the diameter equal one another.
- Proposition 44.
- To a given straight line in a given rectilinear angle, to apply a parallelogram equal to a given triangle.
- Proposition 45.
- To construct a parallelogram equal to a given rectilinear figure in a given rectilinear angle.
- Proposition 46.
- To describe a square on a given straight line.
- Proposition 47.
- In right-angled triangles the square on the side opposite the right angle equals the sum of the squares on the sides containing the right angle.
- Proposition 48.
- If in a triangle the square on one of the sides equals the sum of the squares on the remaining two sides of the triangle, then the angle contained by the remaining two sides of the triangle is right.
About the Definitions
The Elements begins with a list of definitions. Some of these indicate little more than certain concepts will be discussed, such as Def.I.1, Def.I.2, and Def.I.5, which introduce the terms point, line, and surface. (Note that for Euclid, the concept of line includes curved lines.) Others are substantial definitions which actually describe new concepts in terms of old ones. For example, Def.I.10 defines a right angle as one of two equal adjacent angles made when one straight line meets another. Other definitions look like they're substantial, but actually are not. For instance, Def.I.4 says a straight line "is a line which lies evenly with the points on itself." No where in the Elements is the defining phrase "which lies evenly with the points on itself" applicable. Thus, this definition indicates, at most, that some lines under discussion will be straight lines.It has been suggested that the definitions were added to the Elements sometime after Euclid wrote them. Another possibility is that they are actually from a different work, perhaps older. In Def.I.22 special kinds of quadrilaterals are defined including square, oblong (a rectangle that are not squares), rhombus (equilateral but not a square), and rhomboid (parallelogram but not a rhombus). Except for squares, these other shapes are not mentioned in the Elements. Euclid does use parallelograms, but they're not defined in this definition. Also, the exclusive nature of some of these terms—the part that indicates not a square—is contrary to Euclid's practice of accepting squares and rectangles as kinds of parallelograms.
About the Postulates
Following the list of definitions is a list of postulates. Each postulate is an axiom—which means a statement which is accepted without proof— specific to the subject matter, in this case, plane geometry. Most of them are constructions. For instance, Post.I.1 says a straight line can be drawn between two points, and Post.I.3 says a circle can be drawn given a specified point to be the center and another point to be on the circumference. The fourth postulate, Post.I.4, is not a constuction, but says that all right angles are equal.About magnitudes and the Common Notions
The Common Notions are also axioms, but they refer to magnitudes of various kinds. The kind of magnitude that appears most frequently is that of straight line. Other important kinds are rectilinear angles and areas (plane figures). Later books include other kinds.In proposition III.16 (but nowhere else) angles with curved sides are compared with rectilinear angles which shows that rectilinear angles are to be considered as a special kind of plane angle. That agrees with Euclid's definition of them in I.Def.9 and I.Def.8.
Also in Book III, parts of circumferences of circles, that is, arcs, appear as magnitudes. Only arcs of equal circles can be compared or added, so arcs of equal circles comprise a kind of magnitude, while arcs of unequal circles are magnitudes of different kinds. These kinds are all different from straight lines. Whereas areas of figures are comparable, different kinds of curves are not.
Book V includes the general theory of ratios. No particular kind of magnitude is specified in that book. It may come as a surprise that ratios do not themselves form a kind of magnitude since they can be compared, but they cannot be added. See the guide on Book V for more information.
Number theory is treated in Books VII through IX. It could be considered that numbers form a kind of magnitude as pointed out by Aristotle.
Beginning in Book XI, solids are considered, and they form the last kind of magnitude discussed in the Elements.
The propositions
Following the definitions, postulates, and common notions, there are 48 propositions. Each of these propositions includes a statement followed by a proof of the statement. Each statement of the proof is logically justified by a definition, postulate, common notion, or an earlier proposition that has already been proven. There are gaps in the logic of some of the proofs, and these are mentioned in the commenaries after the propositions. Also included in the proof is a diagram illustrating the proof.Some of the propositions are constructions. A construction depends, ultimately, on the constructive postulates about drawing lines and circles. The first part of a proof for a constuctive proposition is how to perform the construction. The rest of the proof (usually the longer part), shows that the proposed construction actually satisfies the goal of the proposition. In the list of propositions in each book, the constructions are displayed in red.
Most of the propositions, however, are not constructions. Their statements say that under certain conditions, certain other conditions logically follow. For example, Prop.I.5 says that if a triangle has the property that two of its sides are equal, then it follows that the angles opposite these sides (called the "base angles") are also equal. Even the propositions that are not constructions may have constructions included in their proofs since auxillary lines or circles may be needed in the explanation. But the bulk of the proof is, as for the constructive propositions, a sequence of statements that are logically justified and which culminates in the statement of the proposition.
Logical structure of Book I
The various postulates and common notions are frequently used in Book I. Only two of the propositions rely solely on the postulates and axioms, namely, I.1 and I.4. The logical chains of propositions in Book I are longer than in the other books; there are long sequences of propositions each relying on the previous.| Dependencies within Book I | ||
| 1 | 2 | 3 |
| 3, 4 | 5, 6 | |
| 5 | 7 | 8 |
| 1, 3, 8 | 9, 11 | |
| 1, 4, 9 | 10 | |
| 8, 10 | 12 | |
| 11 | 13 | 14, 15 |
| 3, 4, 10, 15 | 16 | 27 |
| 13, 16 | 17 | |
| 3, 5, 16 | 18 | |
| 5, 18 | 19 | |
| 3, 5, 19 | 20 | |
| 16, 20 | 21 | |
| 3, 20 | 22 | |
| 8, 22 | 23 | |
| 3, 4, 5, 19, 23 | 24 | |
| 4, 24 | 25 | |
| 3, 4, 16 | 26 | |
| 13, 15, 27 | 28, 29 | |
| 29 | 30 | |
| 23, 27 | 31 | |
| 13, 29, 31 | 32 | |
| 4, 27, 29 | 33 | |
| 4, 26, 29 | 34 | 43 |
| 4, 29, 34 | 35 | |
| 33, 34, 35 | 36 | |
| 31, 34, 35 | 37 | |
| 31, 34, 36 | 38 | |
| 31, 37 | 39 | |
| 31, 38 | 40 | |
| 34, 37 | 41 | |
| 10, 23, 31, 38, 41 | 42 | |
| 15, 29, 31, 42, 43 | 44 | |
| 14, 29, 30, 33, 34, 42, 44 | 45 | |
| 3, 11, 29, 31, 34 | 46 | |
| 4, 14, 31, 41, 46 | 47 | |
| 3, 8, 11, 47 | 48 | |
| Next book: Book II |
|
© 1996
D.E.Joyce
Clark University
Source : http://aleph0.clarku.edu/~djoyce/java/elements/bookI/book...
19:13 Publié dans Euclid's Elements Book I | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Euclid's Elements Book X
![]()
Table of contents
- Definitions I (4)
- Propositions 1-47
- Definitions II (6)
- Propositions 48-84
- Definitions III (6)
- Propositions 85-115
Definitions I
- Definition 1.
- Those magnitudes are said to be commensurable which are measured by the same measure, and those incommensurable which cannot have any common measure.
- Definition 2.
- Straight lines are commensurable in square when the squares on them are measured by the same area, and incommensurable in square when the squares on them cannot possibly have any area as a common measure.
- Definition 3.
- With these hypotheses, it is proved that there exist straight lines infinite in multitude which are commensurable and incommensurable respectively, some in length only, and others in square also, with an assigned straight line. Let then the assigned straight line be called rational, and those straight lines which are commensurable with it, whether in length and in square, or in square only, rational, but those that are incommensurable with it irrational.
- Definition 4.
- And the let the square on the assigned straight line be called rational, and those areas which are commensurable with it rational, but those which are incommensurable with it irrational, and the straight lines which produce them irrational, that is, in case the areas are squares, the sides themselves, but in case they are any other rectilineal figures, the straight lines on which are described squares equal to them.
Propositions 1-47
- Proposition 1.
- Two unequal magnitudes being set out, if from the greater there is subtracted a magnitude greater than its half, and from that which is left a magnitude greater than its half, and if this process is repeated continually, then there will be left some magnitude less than the lesser magnitude set out. And the theorem can similarly be proven even if the parts subtracted are halves.
- Proposition 2.
- If, when the less of two unequal magnitudes is continually subtracted in turn from the greater that which is left never measures the one before it, then the two magnitudes are incommensurable.
- Proposition 3.
- To find the greatest common measure of two given commensurable magnitudes.
Corollary. If a magnitude measures two magnitudes, then it also measures their greatest common measure.
- Proposition 4.
- To find the greatest common measure of three given commensurable magnitudes.
Corollary. If a magnitude measures three magnitudes, then it also measures their greatest common measure. The greatest common measure can be found similarly for more magnitudes, and the corollary extended.
- Proposition 5.
- Commensurable magnitudes have to one another the ratio which a number has to a number.
- Proposition 6.
- If two magnitudes have to one another the ratio which a number has to a number, then the magnitudes are commensurable.
- Proposition 7.
- Incommensurable magnitudes do not have to one another the ratio which a number has to a number.
- Proposition 8.
- If two magnitudes do not have to one another the ratio which a number has to a number, then the magnitudes are incommensurable.
- Proposition 9.
- The squares on straight lines commensurable in length have to one another the ratio which a square number has to a square number; and squares which have to one another the ratio which a square number has to a square number also have their sides commensurable in length. But the squares on straight lines incommensurable in length do not have to one another the ratio which a square number has to a square number; and squares which do not have to one another the ratio which a square number has to a square number also do not have their sides commensurable in length either.
Corollary. Straight lines commensurable in length are always commensurable in square also, but those commensurable in square are not always also commensurable in length.
Lemma. Similar plane numbers have to one another the ratio which a square number has to a square number, and if two numbers have to one another the ratio which a square number has to a square number, then they are similar plane numbers.
Corollary 2. Numbers which are not similar plane numbers, that is, those which do not have their sides proportional, do not have to one another the ratio which a square number has to a square number
- Proposition 10.
- To find two straight lines incommensurable, the one in length only, and the other in square also, with an assigned straight line.
- Proposition 11.
- If four magnitudes are proportional, and the first is commensurable with the second, then the third also is commensurable with the fourth; but, if the first is incommensurable with the second, then the third also is incommensurable with the fourth.
- Proposition 12.
- Magnitudes commensurable with the same magnitude are also commensurable with one another.
- Proposition 13.
- If two magnitudes are commensurable, and one of them is incommensurable with any magnitude, then the remaining one is also incommensurable with the same.
- Proposition 14.
- Lemma. Given two unequal straight lines, to find by what square the square on the greater is greater than the square on the less. And, given two straight lines, to find the straight line the square on which equals the sum of the squares on them.
Proposition 14. If four straight lines are proportional, and the square on the first is greater than the square on the second by the square on a straight line commensurable with the first, then the square on the third is also greater than the square on the fourth by the square on a third line commensurable with the third. And, if the square on the first is greater than the square on the second by the square on a straight line incommensurable with the first, then the square on the third is also greater than the square on the fourth by the square on a third line incommensurable with the third.
- Proposition 15.
- If two commensurable magnitudes are added together, then the whole is also commensurable with each of them; and, if the whole is commensurable with one of them, then the original magnitudes are also commensurable.
- Proposition 16.
- If two incommensurable magnitudes are added together, the sum is also incommensurable with each of them; but, if the sum is incommensurable with one of them, then the original magnitudes are also incommensurable.
- Proposition 17.
- Lemma. If to any straight line there is applied a parallelogram but falling short by a square, then the applied parallelogram equals the rectangle contained by the segments of the straight line resulting from the application.
Proposition 17. If there are two unequal straight lines, and to the greater there is applied a parallelogram equal to the fourth part of the square on the less but falling short by a square, and if it divides it into parts commensurable in length, then the square on the greater is greater than the square on the less by the square on a straight line commensurable with the greater. And if the square on the greater is greater than the square on the less by the square on a straight line commensurable with the greater, and if there is applied to the greater a parallelogram equal to the fourth part of the square on the less falling short by a square, then it divides it into parts commensurable in length.
- Proposition 18.
- If there are two unequal straight lines, and to the greater there is applied a parallelogram equal to the fourth part of the square on the less but falling short by a square, and if it divides it into incommensurable parts, then the square on the greater is greater than the square on the less by the square on a straight line incommensurable with the greater. And if the square on the greater is greater than the square on the less by the square on a straight line incommensurable with the greater, and if there is applied to the greater a parallelogram equal to the fourth part of the square on the less but falling short by a square, then it divides it into incommensurable parts.
- Proposition 19.
- Lemma.
Proposition 19. The rectangle contained by rational straight lines commensurable in length is rational.
- Proposition 20.
- If a rational area is applied to a rational straight line, then it produces as breadth a straight line rational and commensurable in length with the straight line to which it is applied.
- Proposition 21.
- The rectangle contained by rational straight lines commensurable in square only is irrational, and the side of the square equal to it is irrational. Let the latter be called medial.
- Proposition 22.
- Lemma. If there are two straight lines, then the first is to the second as the square on the first is to the rectangle contained by the two straight lines.
Proposition 22. The square on a medial straight line, if applied to a rational straight line, produces as breadth a straight line rational and incommensurable in length with that to which it is applied.
- Proposition 23.
- A straight line commensurable with a medial straight line is medial.
Corollary. An area commensurable with a medial area is medial.
- Proposition 24.
- The rectangle contained by medial straight lines commensurable in length is medial.
- Proposition 25.
- The rectangle contained by medial straight lines commensurable in square only is either rational or medial.
- Proposition 26.
- A medial area does not exceed a medial area by a rational area.
- Proposition 27.
- To find medial straight lines commensurable in square only which contain a rational rectangle.
- Proposition 28.
- To find medial straight lines commensurable in square only which contain a medial rectangle.
- Proposition 29.
- Lemma 1. To find two square numbers such that their sum is also square.
Lemma 2. To find two square numbers such that their sum is not square.
Proposition 29. To find two rational straight lines commensurable in square only such that the square on the greater is greater than the square on the less by the square on a straight line commensurable in length with the greater.
- Proposition 30.
- To find two rational straight lines commensurable in square only such that the square on the greater is greater than the square on the less by the square on a straight line incommensurable in length with the greater.
- Proposition 31.
- To find two medial straight lines commensurable in square only, containing a rational rectangle, such that the square on the greater is greater than the square on the less by the square on a straight line commensurable in length with the greater.
- Proposition 32.
- To find two medial straight lines commensurable in square only, containing a medial rectangle, such that the square on the greater is greater than the square on the less by the square on a straight line commensurable with the greater.
- Proposition 33.
- Lemma.
Proposition 33. To find two straight lines incommensurable in square which make the sum of the squares on them rational but the rectangle contained by them medial.
- Proposition 34.
- To find two straight lines incommensurable in square which make the sum of the squares on them medial but the rectangle contained by them rational.
- Proposition 35.
- To find two straight lines incommensurable in square which make the sum of the squares on them medial and the rectangle contained by them medial and moreover incommensurable with the sum of the squares on them.
- Proposition 36.
- If two rational straight lines commensurable in square only are added together, then the whole is irrational; let it be called binomial.
- Proposition 37.
- If two medial straight lines commensurable in square only and containing a rational rectangle are added together, the whole is irrational; let it be called the first bimedial straight line.
- Proposition 38.
- If two medial straight lines commensurable in square only and containing a medial rectangle are added together, then the whole is irrational; let it be called the second bimedial straight line.
- Proposition 39.
- If two straight lines incommensurable in square which make the sum of the squares on them rational but the rectangle contained by them medial are added together, then the whole straight line is irrational; let it be called major.
- Proposition 40.
- If two straight lines incommensurable in square which make the sum of the squares on them medial but the rectangle contained by them rational are added together, then the whole straight line is irrational; let it be called the side of a rational plus a medial area.
- Proposition 41.
- If two straight lines incommensurable in square which make the sum of the squares on them medial and the rectangle contained by them medial and also incommensurable with the sum of the squares on them are added together, then the whole straight line is irrational; let it be called the side of the sum of two medial areas.
- Proposition 42.
- A binomial straight line is divided into its terms at one point only.
- Proposition 43.
- A first bimedial straight line is divided at one and the same point only.
- Proposition 44.
- A second bimedial straight line is divided at one point only.
- Proposition 45.
- A major straight line is divided at one point only.
- Proposition 46.
- The side of a rational plus a medial area is divided at one point only.
- Proposition 47.
- The side of the sum of two medial areas is divided at one point only.
Definitions II
- Definition 1.
- Given a rational straight line and a binomial, divided into its terms, such that the square on the greater term is greater than the square on the lesser by the square on a straight line commensurable in length with the greater, then, if the greater term is commensurable in length with the rational straight line set out, let the whole be called a first binomial straight line;
- Definition 2.
- But if the lesser term is commensurable in length with the rational straight line set out, let the whole be called a second binomial;
- Definition 3.
- And if neither of the terms is commensurable in length with the rational straight line set out, let the whole be called a third binomial.
- Definition 4.
- Again, if the square on the greater term is greater than the square on the lesser by the square on a straight line incommensurable in length with the greater, then, if the greater term is commensurable in length with the rational straight line set out, let the whole be called a fourth binomial;
- Definition 5.
- If the lesser, a fifth binomial;
- Definition 6.
- And, if neither, a sixth binomial.
Propositions 48-84
- Proposition 48.
- To find the first binomial line.
- Proposition 49.
- To find the second binomial line.
- Proposition 50.
- To find the third binomial line.
- Proposition 51.
- To find the fourth binomial line.
- Proposition 52.
- To find the fifth binomial line.
- Proposition 53.
- To find the sixth binomial line.
- Proposition 54.
- Lemma.
Proposition 54. If an area is contained by a rational straight line and the first binomial, then the side of the area is the irrational straight line which is called binomial.
- Proposition 55.
- If an area is contained by a rational straight line and the second binomial, then the side of the area is the irrational straight line which is called a first bimedial.
- Proposition 56.
- If an area is contained by a rational straight line and the third binomial, then the side of the area is the irrational straight line called a second bimedial.
- Proposition 57.
- If an area is contained by a rational straight line and the fourth binomial, then the side of the area is the irrational straight line called major.
- Proposition 58.
- If an area is contained by a rational straight line and the fifth binomial, then the side of the area is the irrational straight line called the side of a rational plus a medial area.
- Proposition 59.
- If an area is contained by a rational straight line and the sixth binomial, then the side of the area is the irrational straight line called the side of the sum of two medial areas.
- Proposition 60.
- Lemma. If a straight line is cut into unequal parts, then the sum of the squares on the unequal parts is greater than twice the rectangle contained by the unequal parts.
Proposition 60. The square on the binomial straight line applied to a rational straight line produces as breadth the first binomial.
- Proposition 61.
- The square on the first bimedial straight line applied to a rational straight line produces as breadth the second binomial.
- Proposition 62.
- The square on the second bimedial straight line applied to a rational straight line produces as breadth the third binomial.
- Proposition 63.
- The square on the major straight line applied to a rational straight line produces as breadth the fourth binomial.
- Proposition 64.
- The square on the side of a rational plus a medial area applied to a rational straight line produces as breadth the fifth binomial.
- Proposition 65.
- The square on the side of the sum of two medial areas applied to a rational straight line produces as breadth the sixth binomial.
- Proposition 66.
- A straight line commensurable with a binomial straight line is itself also binomial and the same in order.
- Proposition 67.
- A straight line commensurable with a bimedial straight line is itself also bimedial and the same in order.
- Proposition 68.
- A straight line commensurable with a major straight line is itself also major.
- Proposition 69.
- A straight line commensurable with the side of a rational plus a medial area is itself also the side of a rational plus a medial area.
- Proposition 70.
- A straight line commensurable with the side of the sum of two medial areas is the side of the sum of two medial areas.
- Proposition 71.
- If a rational and a medial are added together, then four irrational straight lines arise, namely a binomial or a first bimedial or a major or a side of a rational plus a medial area.
- Proposition 72.
- If two medial areas incommensurable with one another are added together, then the remaining two irrational straight lines arise, namely either a second bimedial or a side of the sum of two medial areas.
Proposition. The binomial straight line and the irrational straight lines after it are neither the same with the medial nor with one another.
- Proposition 73.
- If from a rational straight line there is subtracted a rational straight line commensurable with the whole in square only, then the remainder is irrational; let it be called an apotome.
- Proposition 74.
- If from a medial straight line there is subtracted a medial straight line which is commensurable with the whole in square only, and which contains with the whole a rational rectangle, then the remainder is irrational; let it be called first apotome of a medial straight line.
- Proposition 75.
- If from a medial straight line there is subtracted a medial straight line which is commensurable with the whole in square only, and which contains with the whole a medial rectangle, then the remainder is irrational; let it be called second apotome of a medial straight line.
- Proposition 76.
- If from a straight line there is subtracted a straight line which is incommensurable in square with the whole and which with the whole makes the sum of the squares on them added together rational, but the rectangle contained by them medial, then the remainder is irrational; let it be called minor.
- Proposition 77.
- If from a straight line there is subtracted a straight line which is incommensurable in square with the whole, and which with the whole makes the sum of the squares on them medial but twice the rectangle contained by them rational, then the remainder is irrational; let it be called that which produces with a rational area a medial whole.
- Proposition 78.
- If from a straight line there is subtracted a straight line which is incommensurable in square with the whole and which with the whole makes the sum of the squares on them medial, twice the rectangle contained by them medial, and further the squares on them incommensurable with twice the rectangle contained by them, then the remainder is irrational; let it be called that which produces with a medial area a medial whole.
- Proposition 79.
- To an apotome only one rational straight line can be annexed which is commensurable with the whole in square only.
- Proposition 80.
- To a first apotome of a medial straight line only one medial straight line can be annexed which is commensurable with the whole in square only and which contains with the whole a rational rectangle.
- Proposition 81.
- To a second apotome of a medial straight line only one medial straight line can be annexed which is commensurable with the whole in square only and which contains with the whole a medial rectangle.
- Proposition 82.
- To a minor straight line only one straight line can be annexed which is incommensurable in square with the whole and which makes, with the whole, the sum of squares on them rational but twice the rectangle contained by them medial.
- Proposition 83.
- To a straight line which produces with a rational area a medial whole only one straight line can be annexed which is incommensurable in square with the whole straight line and which with the whole straight line makes the sum of squares on them medial but twice the rectangle contained by them rational.
- Proposition 84.
- To a straight line which produces with a medial area a medial whole only one straight line can be annexed which is incommensurable in square with the whole straight line and which with the whole straight line makes the sum of squares on them medial and twice the rectangle contained by them both medial and also incommensurable with the sum of the squares on them.
Definitions III
- Definition 1.
- Given a rational straight line and an apotome, if the square on the whole is greater than the square on the annex by the square on a straight line commensurable in length with the whole, and the whole is commensurable in length with the rational line set out, let the apotome be called a first apotome.
- Definition 2.
- But if the annex is commensurable with the rational straight line set out, and the square on the whole is greater than that on the annex by the square on a straight line commensurable with the whole, let the apotome be called a second apotome.
- Definition 3.
- But if neither is commensurable in length with the rational straight line set out, and the square on the whole is greater than the square on the annex by the square on a straight line commensurable with the whole, let the apotome be called a third apotome.
- Definition 4.
- Again, if the square on the whole is greater than the square on the annex by the square on a straight line incommensurable with the whole, then, if the whole is commensurable in length with the rational straight line set out, let the apotome be called a fourth apotome;
- Definition 5.
- If the annex be so commensurable, a fifth;
- Definition 6.
- And, if neither, a sixth.
Propositions 85-115
- Proposition 85.
- To find the first apotome.
- Proposition 86.
- To find the second apotome.
- Proposition 87.
- To find the third apotome.
- Proposition 88.
- To find the fourth apotome.
- Proposition 89.
- To find the fifth apotome.
- Proposition 90.
- To find the sixth apotome.
- Proposition 91.
- If an area is contained by a rational straight line and a first apotome, then the side of the area is an apotome.
- Proposition 92.
- If an area is contained by a rational straight line and a second apotome, then the side of the area is a first apotome of a medial straight line.
- Proposition 93.
- If an area is contained by a rational straight line and a third apotome, then the side of the area is a second apotome of a medial straight line.
- Proposition 94.
- If an area is contained by a rational straight line and a fourth apotome, then the side of the area is minor.
- Proposition 95.
- If an area is contained by a rational straight line and a fifth apotome, then the side of the area is a straight line which produces with a rational area a medial whole.
- Proposition 96.
- If an area is contained by a rational straight line and a sixth apotome, then the side of the area is a straight line which produces with a medial area a medial whole.
- Proposition 97.
- The square on an apotome of a medial straight line applied to a rational straight line produces as breadth a first apotome.
- Proposition 98.
- The square on a first apotome of a medial straight line applied to a rational straight line produces as breadth a second apotome.
- Proposition 99.
- The square on a second apotome of a medial straight line applied to a rational straight line produces as breadth a third apotome.
- Proposition 100.
- The square on a minor straight line applied to a rational straight line produces as breadth a fourth apotome.
- Proposition 101.
- The square on the straight line which produces with a rational area a medial whole, if applied to a rational straight line, produces as breadth a fifth apotome.
- Proposition 102.
- The square on the straight line which produces with a medial area a medial whole, if applied to a rational straight line, produces as breadth a sixth apotome.
- Proposition 103.
- A straight line commensurable in length with an apotome is an apotome and the same in order.
- Proposition 104.
- A straight line commensurable with an apotome of a medial straight line is an apotome of a medial straight line and the same in order.
- Proposition 105.
- A straight line commensurable with a minor straight line is minor.
- Proposition 106.
- A straight line commensurable with that which produces with a rational area a medial whole is a straight line which produces with a rational area a medial whole.
- Proposition 107.
- A straight line commensurable with that which produces a medial area and a medial whole is itself also a straight line which produces with a medial area a medial whole.
- Proposition 108.
- If from a rational area a medial area is subtracted, the side of the remaining area becomes one of two irrational straight lines, either an apotome or a minor straight line.
- Proposition 109.
- If from a medial area a rational area is subtracted, then there arise two other irrational straight lines, either a first apotome of a medial straight line or a straight line which produces with a rational area a medial whole.
- Proposition 110.
- If from a medial area there is subtracted a medial area incommensurable with the whole, then the two remaining irrational straight lines arise, either a second apotome of a medial straight line or a straight line which produce with a medial area a medial whole.
- Proposition 111.
- The apotome is not the same with the binomial straight line.
Proposition. The apotome and the irrational straight lines following it are neither the same with the medial straight line nor with one another. There are, in order, thirteen irrational straight lines in all:
-
Medial
Binomial
First bimedial
Second bimedial
Major
Side of a rational plus a medial area
Side of the sum of two medial areas
Apotome
First apotome of a medial straight line
Second apotome of a medial straight line
Minor
Producing with a rational area a medial whole
Producing with a medial area a medial whole - Proposition 112.
- The square on a rational straight line applied to the binomial straight line produces as breadth an apotome the terms of which are commensurable with the terms of the binomial straight line and moreover in the same ratio; and further the apotome so arising has the same order as the binomial straight line.
- Proposition 113.
- The square on a rational straight line, if applied to an apotome, produces as breadth the binomial straight line the terms of which are commensurable with the terms of the apotome and in the same ratio; and further the binomial so arising has the same order as the apotome.
- Proposition 114.
- If an area is contained by an apotome and the binomial straight line the terms of which are commensurable with the terms of the apotome and in the same ratio, then the side of the area is rational.
Corollary. It is possible for a rational area to be contained by irrational straight lines.
- Proposition 115.
- From a medial straight line there arise irrational straight lines infinite in number, and none of them is the same as any preceding.
Elements Introduction - Book IX - Book XI.
© 1996
D.E.Joyce
Clark University
Source : http://aleph0.clarku.edu/~djoyce/java/elements/bookX/book...
19:12 Publié dans Euclid's Elements Book X | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Euclid's Elements Book IX Proposition 36
Proposition 36
| If as many numbers as we please beginning from a unit are set out continuously in double proportion until the sum of all becomes prime, and if the sum multiplied into the last makes some number, then the product is perfect. | |
| Let as many numbers as we please, A, B, C, and D, beginning from a unit be set out in double proportion, until the sum of all becomes prime, let E equal the sum, and let E multiplied by D makeFG.
I say that FG is perfect. For, however many A, B, C, and D are in multitude, take so many E, HK, L, and M in double proportion beginning from E. |
|
| Therefore, ex aequali A is to D as E is to M. Therefore the product of E and D equals the product of A and M. And the product of E and D is FG, therefore the product of A and M is also FG. | VII.14 VII.19 |
| Therefore A multiplied by M makes FG. Therefore M measures FG according to the units in A. And A is a dyad, therefore FG is double of M.
But M, L, HK, and E are continuously double of each other, therefore E, HK, L, M, and FG are continuously proportional in double proportion. |
|
| Subtract from the second HK and the last FG the numbers HN and FO, each equal to the first E. Therefore the excess of the second is to the first as the excess of the last is to the sum of those before it. Therefore NK is to E as OG is to the sum of M, L, KH, and E. | IX.35 |
| And NK equals E, therefore OG also equals M, L, HK, E. But FO also equals E, and E equals the sum of A, B, C, D and the unit. Therefore the whole FG equals the sum of E, HK, L, M, A, B, C, D, and the unit, and it is measured by them.
I say also that FG is not measured by any other number except A, B, C, D, E, HK, L, M, and the unit. If possible, let some number P measure FG, and let P not be the same with any of the numbers A, B, C, D, E, HK, L, or M. And, as many times as P measures FG, so many units let there be in Q, therefore Q multiplied by P makes FG. |
|
| But, further, E multiplied by D makes FG, therefore E is to Q as P is to D. | VII.19 |
| And, since A, B, C, and D are continuously proportional beginning from a unit, therefore D is not measured by any other number except A, B, or C. | IX.13 |
| And, by hypothesis, P is not the same with any of the numbers A, B, or C, therefore P does not measure D. But P is to D as E is to Q, therefore neither does E measure Q. | VII.Def.20 |
| And E is prime, and any prime number is prime to any number which it does not measure. Therefore E and Q are relatively prime. | VII.29 |
| But primes are also least, and the least numbers measure those which have the same ratio the same number of times, the antecedent the antecedent and the consequent the consequent, and E is toQ as P is to D, therefore E measures P the same number of times that Q measures D. | VII.21 VII.20 |
| But D is not measured by any other number except A, B, or C, therefore Q is the same with one of the numbers A, B, or C. Let it be the same with B.
And, however many B, C, and D are in multitude, take so many E, HK, and L beginning from E. |
|
| Now E, HK, and L are in the same ratio with B, C, and D, therefore, ex aequali B is to D as E is to L. | VII.14 |
| Therefore the product of B and L equals the product of D and E. But the product of D and E equals the product of Q and P, therefore the product of Q and P also equals the product of B and L. | VII.19 |
| Therefore Q is to B as L is to P. And Q is the same with B, therefore L is also the same with P, which is impossible, for by hypothesis P is not the same with any of the numbers set out. | VII.19 |
| Therefore no number measures FG except A, B, C, D, E, HK, L, M, and the unit. | |
| And FG was proved equal to the sum of A, B, C, D, E, HK, L, M, and the unit, and a perfect number is that which equals its own parts, therefore FG is perfect. | VII.Def.22 |
| Therefore, if as many numbers as we please beginning from a unit are set out continuously in double proportion until the sum of all becomes prime, and if the sum multiplied into the last makes some number, then the product is perfect. | |
| Q.E.D. | |
Summary of the proof
Euclid begins by assuming that the sum of a number of powers of 2 (the sum beginning with 1) is a prime number. Let p be the number of powers of 2, and let s be their sum which is prime.s = 1 + 2 + 22 + ... + 2p-1Note that the last power of 2 is 2p-1 since the sum starts with 1, which is 20.
In Euclid's proof, A represents 2, B represents 22, C represents 23, and D is supposed to be the last power of 2, so it represents 2p-1. Also, E represents their sum s, and FG is the product of E and D, so it represents s2p-1. Let's denote that last by n.
n = s2p-1The goal is to show that n is a perfect number.
In the first part of this proof, Euclid finds some proper divisors of n that sum to n. These come in two sequences:
1, 2, 22, ..., 2p-1ands, 2s, 22s, ..., 2n-2sIn his proof, the latter are represented by E, HK, L, and finally M.
It is clear that each of these is a proper divisor of n, and later in the proof Euclid shows that they are the only proper divisors of n.
Using the previous proposition, IX.35, Euclid finds the sum of the continued proportion,
s + 2s + 22s + ... + 2n-2s,to be 2n-1s – s. But s was the sum 1 + 2 + 22 + ... + 2p-1, hence,
| n = 2n-1s | = | 1 + 2 + 22 + ... + 2p-1 |
| + s + 2s + 22s + ... + 2n-2s |
Thus, n is a sum of these proper divisors.
All that is left to do is to show that they are the only proper divisors of n, for then n will be the sum of all of its proper divisors, whence a perfect number.
The remainder of the proof is detailed and difficult to follow. It hinges on IX.13 which implies that the only factors of 2p-1 are powers of 2, so all the factors of 2p-1 have been found. Here's a not-too-faithful version of Euclid's argument. Suppose n factors as ab where a is not a proper divisor of n in the list above. In Euclid's proof, P represents a and Q represents b.
Since a divides s 2p-1, but is not a power of 2, and s is prime, therefore s divides a. Then b has to be a power of 2. But then a has to be a power of 2 times s. But all the powers of 2 times s are on the list of known proper divisors. Therefore, the list includes all the proper divisors.
Mersenne primes and perfect numbers
Note that the sum, s = 1 + 2 + 22 + ... + 2p-1, equals 2p – 1, by IX.35. As this fact is not needed in the proof, Euclid omits to mention it. Thus, we can restate the proposition as follows:-
If 2p – 1 is a prime number, then (2p – 1) 2p-1 is a perfect number.
The observation that these four exponents are all prime suggests the following two questions:
- In order for 2p – 1 to be prime, is it sufficient for p to be prime?
- In order for 2p – 1 to be prime, is it necessary for p to be prime?
In 1640 Pierre de Fermat (1601-1665) wrote to Mersenne with his investigation of these primes. Fermat found three conditions on p that were necessary for 2p – 1 to be prime. One of these conditions answers the second question above— p does have to be prime. Here's a quick argument for that. If p did factor, say as ab, then 2p – 1, which is 2ab – 1, would also factor, namely as
2ab – 1 = (2a – 1) (2a(b-1) + 2a(b-2) + ... + 2a).Many mathematicians have studied Mersenne primes since then. A fairly practical testing algorithm was constructed by Lucas in 1876. He showed that the the number 2p – 1 is prime if and only if it divides the number S(p-1), where S(p-1) is defined recursively: S(1) = 4, and S(n+1) = S(n)2 – 2.
The search for more Mersenne primes, and therefore more perfect numbers, continues. It is not known if there are infinitely many or finitely many even perfect numbers. Mersenne primes are scarce, but more continue to be found. There are at least 39 of them, the largest known (as of December 2005) is 230402457 – 1. It has 9152052 digits. For more information, see the The Great Internet Mersenne Prime Search, GIMPS.
There is a also a question about odd perfect numbers: Are there any? It has been shown that there are no small odd perfect numbers; it is known that odd numbers with fewer then 300 digits are not perfect. It may well be that there are no odd perfect numbers, but to date there is no proof.
| Next book: Book X introduction
Previous proposition: IX.35 |
|
© 1996, 2005
D.E.Joyce
Clark University
Source : http://aleph0.clarku.edu/~djoyce/java/elements/bookIX/pro...
19:11 Publié dans Euclid's Elements Book IX Proposition 36 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Simon Singh
Simon Singh
|
|
Cet article est une ébauche concernant un écrivain britannique.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
Simon Singh (1964) est un écrivain et journaliste scientifique britannique. Il s'est spécialisé dans la vulgarisation de sujets mathématiques et scientifiques. Il a notamment écrit les livres Le Dernier Théorème de Fermat et Histoire des codes secrets. De l'Égypte des pharaons à l'ordinateur quantique.
Sommaire[masquer] |
Il est détenteur d'un doctorat en physique nucléaire. En 2009, il est poursuivi pour diffamation par l'association chiropratique britannique suite à un article (écrit dans le cadre de la promotion de son ouvrage Trick or Treatment? Alternative Medicine on Trial.) dans lequel il affirme que les tenants de la chiropratique font la promotion de thérapies frauduleuses (il utilisa en anglais le terme bogus). La réaction de la blogosphèrescientifique, et du mouvement sceptique contemporain, est immédiate et importante: ils soutiennent Simon Singh dans son procès et demandent une réforme de la loi britannique sur la diffamation1. Son frère aîné est Tom Singh, fondateur de la chaine de magasins anglais New Look.Biographie [modifier]
Publications [modifier]
Notes et références [modifier]
Annexes [modifier]
Articles connexes [modifier]
Liens externes [modifier]
19:09 Publié dans Simon Singh | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Congruence
Congruence
![]() Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom.
Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom.
|
Voir « congruence » sur leWiktionnaire. |
Derrière le terme de congruence se cachent des notions semblables mais de niveaux d'abstraction différents. Historiquement, la notion de congruence sur les entiers relatifs a été introduite par Gauss vers 1801.1
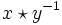 appartient à H.
appartient à H.
19:06 Publié dans Congruence | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
LIVRE Antibi math 2e livre de l'eleve 2010 - travailler en confiance
07:54 Publié dans Antibi math 2e livre de l'eleve 2010 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
LIVRE Math'x 2nde , Livre de l'élève grand format - Edition 2010
Une collection qui donne du sens au apprentissages des mathématiques. Destiné aux élèves, la manuel constitue le coeur de l'ensemble pédagogique. Math'X 2de est également disponible en petit format (18,8x25cm) et en Manuel Numérique.Math'x 2nde , Livre de l'élève grand format - Edition 2010Jean-François Chesné
07:53 Publié dans Math'x 2nde | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
05/12/2010
Bell Number
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The number of ways a set of For example, there are five ways the numbers
Bell numbers are implemented in Mathematica as BellB[n]. Though Bell numbers have traditionally been attributed to E. T. Bell as a result of the general theory he developed in his 1934 paper (Bell 1934), the first systematic study of Bell numbers was made by Ramanujan in chapter 3 of his second notebook approximately 25-30 years prior to Bell's work (B. C. Berndt, pers. comm., Jan. 4 and 13, 2010). The first few prime Bell numbers occur at indices  Bell numbers are closely related to Catalan numbers. The diagram above shows the constructions giving
where The Bell numbers are given in terms of generalized hypergeometric functions by
(K. A. Penson, pers. comm., Jan. 14, 2007). The Bell numbers can also be generated using the sum and recurrence relation
where
for
A variation of Dobiński's formula gives
where
The Bell numbers are given by the generating function
and the exponential generating function
An amazing integral representation for
(Becker and Browne 1941, Callan 2005), where The Bell number de Bruijn (1981) gave the asymptotic formula
Lovász (1993) showed that this formula gives the asymptotic limit
where
with
Touchard's congruence states
when
for
gives the minimum period of The Bell numbers also have the curious property that
(Lenard 1992), where the product is simply a superfactorial and
Becker, H. W. and Browne, D. E. "Problem E461 and Solution." Amer. Math. Monthly 48, 701-703, 1941. Bell, E. T. "Exponential Numbers." Amer. Math. Monthly 41, 411-419, 1934. Blasiak, P.; Penson, K. A.; and Solomon, A. I. "Dobiński-Type Relations and the Log-Normal Distribution." J. Phys. A: Math. Gen. 36, L273-278, 2003. Callan, D. "Cesàro's integral formula for the Bell numbers (corrected)." Oct. 3, 2005. http://www.stat.wisc.edu/~callan/papersother/cesaro/cesar.... Cesàro, M. E. "Sur une équation aux différences mêlées." Nouv. Ann. Math. 4, 36-40, 1885. Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, 1974. Conway, J. H. and Guy, R. K. In The Book of Numbers. New York: Springer-Verlag, pp. 91-94, 1996. de Bruijn, N. G. Asymptotic Methods in Analysis. New York: Dover, pp. 102-109, 1981. Dickau, R. M. "Bell Number Diagrams." http://mathforum.org/advanced/robertd/bell.html. Dickau, R. "Visualizing Combinatorial Enumeration." Mathematica in Educ. Res. 8, 11-18, 1999. Gardner, M. "The Tinkly Temple Bells." Ch. 2 in Fractal Music, Hypercards, and More Mathematical Recreations from Scientific American Magazine.New York: W. H. Freeman, pp. 24-38, 1992. Gould, H. W. Bell & Catalan Numbers: Research Bibliography of Two Special Number Sequences, 6th ed. Morgantown, WV: Math Monongliae, 1985. Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994. Lenard, A. In Fractal Music, Hypercards, and More Mathematical Recreations from Scientific American Magazine. (M. Gardner). New York: W. H. Freeman, pp. 35-36, 1992. Larrosa Canestro, I. "Bell(2841) Is Prime." Feb. 13, 2004. http://groups.yahoo.com/group/primenumbers/message/14558. Levine, J. and Dalton, R. E. "Minimum Periods, Modulo Lovász, L. Combinatorial Problems and Exercises, 2nd ed. Amsterdam, Netherlands: North-Holland, 1993. Lunnon, W. F.; Pleasants, P. A. B.; and Stephens, N. M. "Arithmetic Properties of Bell Numbers to a Composite Modulus, I." Acta Arith. 35, 1-16, 1979. Odlyzko, A. M. "Asymptotic Enumeration Methods." In Handbook of Combinatorics, Vol. 2 (Ed. R. L. Graham, M. Grötschel, and L. Lovász). Cambridge, MA: MIT Press, pp. 1063-1229, 1995. http://www.dtc.umn.edu/~odlyzko/doc/asymptotic.enum.pdf. Penson, K. A.; Blasiak, P.; Duchamp, G.; Horzela, A.; and Solomon, A. I. "Hierarchical Dobiński-Type Relations via Substitution and the Moment Problem." 26 Dec 2003. http://www.arxiv.org/abs/quant-ph/0312202/. Pitman, J. "Some Probabilistic Aspects of Set Partitions." Amer. Math. Monthly 104, 201-209, 1997. Rota, G.-C. "The Number of Partitions of a Set." Amer. Math. Monthly 71, 498-504, 1964. Sixdeniers, J.-M.; Penson, K. A.; and Solomon, A. I. "Extended Bell and Stirling Numbers from Hypergeometric Functions." J. Integer Sequences 4, No. 01.1.4, 2001. http://www.math.uwaterloo.ca/JIS/VOL4/SIXDENIERS/bell.html. Sloane, N. J. A. Sequences A000110/M1484, A000178/M2049, A051130, A051131, A054767, and A113015 in "The On-Line Encyclopedia of Integer Sequences." Stanley, R. P. Enumerative Combinatorics, Vol. 1. Cambridge, England: Cambridge University Press, pp. 33-34, 1999. Stanley, R. P. Enumerative Combinatorics, Vol. 2. Cambridge, England: Cambridge University Press, p. 13, 1999. Wilson, D. "Bell Number Question." math-fun@cs.arizona.edu mailing list. 16 Jul 2007. CITE THIS AS: Weisstein, Eric W. "Bell Number." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/BellNumber.html
|
22:16 Publié dans Bell Number | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Nombre de Bell
Nombre de Bell
En mathématiques, le n-ième nombre de Bell, qui porte le nom de Eric Temple Bell, est le nombre de partitions d'un ensemble à n éléments ou, ce qui revient au même, le nombre derelations d'équivalence sur un tel ensemble.
Sommaire[masquer] |
Premières propriétés [modifier]
- Ces nombres forment la suite A000110 de l’OEIS, dont on peut calculer à la main les premiers termes :

Pour le premier, on se convainc qu'il existe exactement une partition de l'ensemble vide : la partition vide, formée d'aucune partie. En effet ses éléments (puisqu'il n'y en a aucun) sont bien non vides et disjoints deux à deux, et de réunion vide.
- Les nombres de Bell peuvent aussi se calculer de proche en proche par la relation de récurrence suivante :
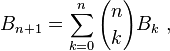
qui peut se démontrer ainsi : ayant fixé un élément x dans un ensemble à n+1 éléments, on trie les partitions suivant le nombre k d'éléments hors de la partie contenant x. Pour chaque valeur de k de 0 à n, il faut donc choisir k éléments parmi les n éléments différents de x, puis s'en donner une partition.
Série génératrice [modifier]
Pour manipuler tous les nombres de Bell, on peut s'intéresser aux séries génératrice et génératrice exponentielle associées, qui sont respectivement :

La première est par exemple1 utilisée pour étudier les classes de congruence des Bn. Quant à la seconde série formelle, elle satisfait l'équation différentielle E'(X) = eXE(X) : on le constate en écrivant la formule de récurrence sous la forme
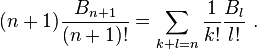
On en déduit qu'elle est égale à  à une constante multiplicative près (qu'on trouve par identification du terme constant) :
à une constante multiplicative près (qu'on trouve par identification du terme constant) :

L'identification des coefficients conduit à la formule de Dobinski :

qui est le moment d'ordre n d'une loi de Poisson de paramètre 1.
D'autres propriétés [modifier]
Ils satisfont également à la congruence de Touchard : si p est un nombre premier quelconque alors
C'est une relation de congruence modulo p.
Chaque nombre de Bell est une somme des nombres de Stirling de deuxième espèce
Plusieurs formules asymptotiques pour les nombres de Bell sont connues ; l'une d'elles est
où W est la fonction W de Lambert ; on obtient une approximation moins précise, mais plus commode d'emploi, à l'aide de l'encadrement lnx − lnlnx < W(x) < lnx ; on pourra également remarquer la similitude de l'approximation précédente avec la formule de Stirling2.
Voir Aussi [modifier]
- Partition d'un entier qui correspond au nombre de partitions d'un ensemble à n éléments indiscernables.
Notes et références [modifier]
- Daniel Barsky et Bénali Benzaghou, « Nombres de Bell et somme de factorielles », dans Journal de Théorie des Nombres de Bordeaux, vol. 16, 2004, p. 1-17 [ [pdf]texte intégral [archive] (page consultée le 1er octobre 2010) ]
- On trouvera d'autres approximations de Bn sur (en) Eric W. Weisstein, Bell Numer [archive], MathWorld..
22:11 Publié dans Nombre de Bell | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Géométrie vivante ou L'échelle de Jacob du mathématicien
13:15 Publié dans Géométrie, Géométrie vivante ou L'échelle de Jacob, Géométrie vivante ou L'échelle de Jacob du mathéma, Livres | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Math 2e 00 itiner+cdrom
13:12 Publié dans CDROM, Livres, Math 2e 00 itiner+cdrom | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
LIVRE Business math
13:10 Publié dans Business math, Livres | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook


















































































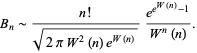

![B_n sim frac{1}{{sqrt n }}left[ {frac{n}{W(n)}} right]^{n + frac{1}{2}} e^{frac{n}{W(n)} - n - 1},](http://upload.wikimedia.org/math/c/d/d/cdd4be64077d749729e8de60d1489596.png)


