05/12/2010
Bell Number
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The number of ways a set of For example, there are five ways the numbers
Bell numbers are implemented in Mathematica as BellB[n]. Though Bell numbers have traditionally been attributed to E. T. Bell as a result of the general theory he developed in his 1934 paper (Bell 1934), the first systematic study of Bell numbers was made by Ramanujan in chapter 3 of his second notebook approximately 25-30 years prior to Bell's work (B. C. Berndt, pers. comm., Jan. 4 and 13, 2010). The first few prime Bell numbers occur at indices 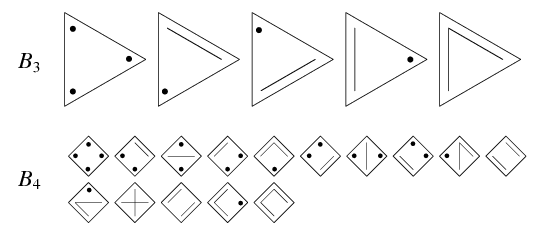 Bell numbers are closely related to Catalan numbers. The diagram above shows the constructions giving
where The Bell numbers are given in terms of generalized hypergeometric functions by
(K. A. Penson, pers. comm., Jan. 14, 2007). The Bell numbers can also be generated using the sum and recurrence relation
where
for
A variation of Dobiński's formula gives
where
The Bell numbers are given by the generating function
and the exponential generating function
An amazing integral representation for
(Becker and Browne 1941, Callan 2005), where The Bell number de Bruijn (1981) gave the asymptotic formula
Lovász (1993) showed that this formula gives the asymptotic limit
where
with
Touchard's congruence states
when
for
gives the minimum period of The Bell numbers also have the curious property that
(Lenard 1992), where the product is simply a superfactorial and
Becker, H. W. and Browne, D. E. "Problem E461 and Solution." Amer. Math. Monthly 48, 701-703, 1941. Bell, E. T. "Exponential Numbers." Amer. Math. Monthly 41, 411-419, 1934. Blasiak, P.; Penson, K. A.; and Solomon, A. I. "Dobiński-Type Relations and the Log-Normal Distribution." J. Phys. A: Math. Gen. 36, L273-278, 2003. Callan, D. "Cesàro's integral formula for the Bell numbers (corrected)." Oct. 3, 2005. http://www.stat.wisc.edu/~callan/papersother/cesaro/cesar.... Cesàro, M. E. "Sur une équation aux différences mêlées." Nouv. Ann. Math. 4, 36-40, 1885. Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, 1974. Conway, J. H. and Guy, R. K. In The Book of Numbers. New York: Springer-Verlag, pp. 91-94, 1996. de Bruijn, N. G. Asymptotic Methods in Analysis. New York: Dover, pp. 102-109, 1981. Dickau, R. M. "Bell Number Diagrams." http://mathforum.org/advanced/robertd/bell.html. Dickau, R. "Visualizing Combinatorial Enumeration." Mathematica in Educ. Res. 8, 11-18, 1999. Gardner, M. "The Tinkly Temple Bells." Ch. 2 in Fractal Music, Hypercards, and More Mathematical Recreations from Scientific American Magazine.New York: W. H. Freeman, pp. 24-38, 1992. Gould, H. W. Bell & Catalan Numbers: Research Bibliography of Two Special Number Sequences, 6th ed. Morgantown, WV: Math Monongliae, 1985. Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994. Lenard, A. In Fractal Music, Hypercards, and More Mathematical Recreations from Scientific American Magazine. (M. Gardner). New York: W. H. Freeman, pp. 35-36, 1992. Larrosa Canestro, I. "Bell(2841) Is Prime." Feb. 13, 2004. http://groups.yahoo.com/group/primenumbers/message/14558. Levine, J. and Dalton, R. E. "Minimum Periods, Modulo Lovász, L. Combinatorial Problems and Exercises, 2nd ed. Amsterdam, Netherlands: North-Holland, 1993. Lunnon, W. F.; Pleasants, P. A. B.; and Stephens, N. M. "Arithmetic Properties of Bell Numbers to a Composite Modulus, I." Acta Arith. 35, 1-16, 1979. Odlyzko, A. M. "Asymptotic Enumeration Methods." In Handbook of Combinatorics, Vol. 2 (Ed. R. L. Graham, M. Grötschel, and L. Lovász). Cambridge, MA: MIT Press, pp. 1063-1229, 1995. http://www.dtc.umn.edu/~odlyzko/doc/asymptotic.enum.pdf. Penson, K. A.; Blasiak, P.; Duchamp, G.; Horzela, A.; and Solomon, A. I. "Hierarchical Dobiński-Type Relations via Substitution and the Moment Problem." 26 Dec 2003. http://www.arxiv.org/abs/quant-ph/0312202/. Pitman, J. "Some Probabilistic Aspects of Set Partitions." Amer. Math. Monthly 104, 201-209, 1997. Rota, G.-C. "The Number of Partitions of a Set." Amer. Math. Monthly 71, 498-504, 1964. Sixdeniers, J.-M.; Penson, K. A.; and Solomon, A. I. "Extended Bell and Stirling Numbers from Hypergeometric Functions." J. Integer Sequences 4, No. 01.1.4, 2001. http://www.math.uwaterloo.ca/JIS/VOL4/SIXDENIERS/bell.html. Sloane, N. J. A. Sequences A000110/M1484, A000178/M2049, A051130, A051131, A054767, and A113015 in "The On-Line Encyclopedia of Integer Sequences." Stanley, R. P. Enumerative Combinatorics, Vol. 1. Cambridge, England: Cambridge University Press, pp. 33-34, 1999. Stanley, R. P. Enumerative Combinatorics, Vol. 2. Cambridge, England: Cambridge University Press, p. 13, 1999. Wilson, D. "Bell Number Question." math-fun@cs.arizona.edu mailing list. 16 Jul 2007. CITE THIS AS: Weisstein, Eric W. "Bell Number." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/BellNumber.html
|
22:16 Publié dans Bell Number | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook









































Les commentaires sont fermés.