L’Académie norvégienne des sciences a remis le prix Abel 2011 au mathématicien américain John Milnor pour ses découvertes pionnières dans les domaines de la topologie, de la géométrie et de l’algèbre. Une contribution très large, donc, qui est récompensée par ce prix nommé d’après le mathématicien norvégien Niels Henrik.
26/03/2011
Le mathématicien John Milnor, prix Abel 2011
Le mathématicien John Milnor, prix Abel 2011
A 80 ans, le découvreur des "sphères exotiques" à sept dimensions est récompensé pour l'ensemble de ses travaux.
- Agrandir la fonteRétrécir la fonte
- Imprimer
- Envoyer
- Partager
- Traduire
- Réagir
 Le mathématicien John Milnor, prix Abel 2011. (Abel Prize Foundation)
Le mathématicien John Milnor, prix Abel 2011. (Abel Prize Foundation)Aujourd’hui âgé de 80 ans, John Milnor, de l’Université Stony Brook de New-York, s’est notamment distingué par la découverte des «sphères exotiques» à sept dimensions en 1956. Ses travaux ont créé un champ nouveau d’investigation en mathématiques, la topologie différentielle.
John Milnor avait déjà été récompensé par la médaille Fields en 1962 –la plus haute distinction pour un mathématicien, remise avant ses 40 ans- et le prix Wolf en 1968
Le prix Abel (doté de 750.000 euros) est remis depuis 2003. Il compense l’absence des mathématiques parmi les prix Nobel.
C.D.
Sciences et Avenir.fr
25/03/11
13:15 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Algèbre de Boole
Algèbre de Boole
Source : http://www.arcanapercipio.com/lessons/algebre_de_boole/al...
Alors voilà...
"Une proposition peut être vraie OU fausse, mais ne peut pas être vraie ET fausse".
Non, non, et non, cette phrase n'est pas extraite des Mémoires du Seigneur de la Palice. Cette dépotante évidence est signée... Aristote [~384~322] !
Et oui ! Parfaitement, M'sieurs Dames ! De la Logique aristotélicienne ! De la Sagesse 100% grecque ! De la vraie Philosophie péripatéticienne et deux fois millénaire... Un minimum de respect, donc.
Comment ça, "vérité de comptoir" ? Douteriez-vous du très haut intérêt de ce genre de désarmante tautologie ? Et pourtant ! Avec sa jugeote pour seul diplôme, un certain George Boole a bâti sur ce truisme les axiomes d'une algèbre assez révolutionnaire dont les théories, lorsqu'elles se marieront aux technologies de l'électronique près d'un siècle plus tard, donneront naissance à une machine assez prometteuse appelée ordinateur.
 Truisme, axiomes, tautologie... No panic ! L'algèbre de Boole, quand on saitla prendre, est d'une logique déconcertante. Nul besoin, donc, à l'évocation de Boole, de flipper.
Truisme, axiomes, tautologie... No panic ! L'algèbre de Boole, quand on saitla prendre, est d'une logique déconcertante. Nul besoin, donc, à l'évocation de Boole, de flipper.
Arcana Percipio vous propose aujourd'hui un circuit touristique inédit, un voyage initiatique depuis les Mathématiques les plus abstraites jusqu'aux tripes électroniques de votre puce préférée.
Allez, roule Boole !
L'algèbre booléenne
Boole, qui est-ce ?

 George Boole nait en 1815 à Lincoln, Angleterre.
George Boole nait en 1815 à Lincoln, Angleterre.
A ses débuts, le petit Boole verse plutôt dans le Latin, son premier amour, et c'est plus âgé qu'il se tourne vers les Mathématiques. Totalement autodidacte, son étude sur les équations différentielles lui vaut une chaire à l'université de Cork.
En 1854, sa publication " An investigation into the Laws of Thought, on Which are founded the Mathematical Theories of Logic and Probabilities" parvient à marier de manière éclatante les mathématiques à la logique, discipline qu'il arrache de fait aux philosophes de l'époque.
An investigation into the Laws of Thought, on Which are founded the Mathematical Theories of Logic and Probabilities" parvient à marier de manière éclatante les mathématiques à la logique, discipline qu'il arrache de fait aux philosophes de l'époque.
Honoré à Oxford, Boole devient membre de la "Royal Society" la même année, mais meurt précocement, en 1864, des suites des théories de Madame Boole sur la meilleure manière de guérir une grippe.
Les lois de la pensée
Pour un non-cartésien comme l'auteur de cette page, le meilleur moyen d'approcher Boole, c'est encore de l'attaquer par derrière, l'air de rien, en faisant mine de s'amuser avec quelques dessins. Quels dessins ? Des dessins de parties, ou pour parler doctoralement, de sous-ensembles. Nous allons donc procéder de la sorte, entremêlant de façon parfaitement naïve algèbre de Boole et théorie des ensembles.
Normalement, ça ne fait pas mal.
Les parties de Boole
A la source de l'inspiration de Boole, l'intime conviction que l'algèbre traditionnelle, celle qu'il baptise lui-même "l'algèbre d'école", n'est rien d'autre que l'application aux nombres de schémas de pensée plus fondamentaux par lesquels l'esprit humain manipule, combine et redéfinit ses concepts logiques (que Boole appelle classes) selon les lois immuables de la pensée ("the laws of thought").
De manière fort simple, nous pourrions définir une classe comme l'ensemble de tous les éléments partageant un même nom ou une même caractéristique, comme par exemple "les êtres humains", "les rivières", "les cornets à piston", "les jours de grève à la SNCF", etc.
Ceci convenu, en imaginant deux classes A et B quelconques, Boole définit trois opérations fondamentales de l'esprit susceptible de s'exercer sur elles:
Bêtes deux sommes
Attention ! Bien que leur nom et leur symbole nous y poussent, ne confondons pas la somme et le produit logiques avec la somme et le produit arithmétiques, tels que nous les connaissons. Les premiers s'exercent sur des classes, les seconds sur des nombres.
Produit de première urgence
En absence de toute parenthèses explicites, le produit logique est prioritaire sur la somme logique.
Ainsi, (A.B)+C peut donc également s'écrire A.B+C.
- La SOMME LOGIQUE (logical sum), que nous noterions A + B, définissant la classe des éléments obéissant à l'une ou l'autre des définitions des classes A et B;
- La COMPLÉMENTATION (negation), que nous noterions A (ou B), définissant la classe des éléments n'obéissant pas à la définition de la classe A (ou B).
Mais ne nous emballons pas et appuyons-nous pour continuer sur l'exemple des deux classes suivantes:
- La classe A définie comme "les chasseurs",
- La classe B définie comme "les myopes".
Partant de ces deux simples définitions, nous pouvons très facilement, par le jeu de notre seule pensée, définir quatre autres classes:
- La classe A.B définie comme "les chasseurs myopes",
- La classe A+B définie comme "les chasseurs et les myopes".
- La classe A définie comme "les non-chasseurs",
- La classe B définie comme "les non-myopes".
Il existe un moyen très visuel de traduire ces concepts un peu abstraits: il consiste à considérer les classes de Boole comme des ensembles. Dès lors, les opérations fondamentales de Boole prennent des noms plus familiers à nos souvenirs scolaires:
- La somme logique de deux classes se traduit par l'union (∪) entre les deux ensembles correspondants,
- Le produit logique par l'intersection (∩),
- La complémententation par... le complément.
Survolez les différentes classes ou expressions afin de visualiser leur équivalent graphique.
Comme nous manipulons ici des ensembles plutôt que des classes, nous prendrons la précaution préalable de définir E comme l'ensemble référentiel, celui contenant tous les autres.
Les évidences booléennes
Avec un poil de curiosité mathématique, nous pourrions facilement constater que ces opérations fondamentales obéissent à quelques propriétés plus ou moins classiques mais si foncièrement évidentes qu'indémontrables.
Ce sont les axiomes de l'algèbre booléenne.
 Ainsi, en reprenant nos deux classes exemples A ("les chasseurs") et B ("les myopes") et en y ajoutant pour l'occasion une troisième classe C définie comme "les buveurs excessifs", on ne peut nier que:
Ainsi, en reprenant nos deux classes exemples A ("les chasseurs") et B ("les myopes") et en y ajoutant pour l'occasion une troisième classe C définie comme "les buveurs excessifs", on ne peut nier que:
- A + B = B + A et A . B = B . A, c'est la commutativité;
- (A + B) + C = A + (B + C) et (A . B) . C = A . (B . C) , c'est l'associativité;
- (A + B) . C = (A . C) + (B . C) mais aussi (A . B) + C = (A + C) . (B + C), c'est la distributivité;
Avec un effort de curiosité supplémentaire, nous pourrions même sans trop de problème imaginer l'existence de deux classes "remarquables", notons les "0" et "1" qui, quelle que soit la classe A, vérifieraient toujours:
- A + 0 = A
Dans l'esprit de Boole, cet élément 0 correspondait à une sorte de classe impossible, mais sur nos petits dessins à nous, on l'assimilera à l'élément vide {Ø}. - A . 1 = A
Pour Boole, cet élément 1 symbolisait la classe universelle, un espèce de grand Tout. Moins ambitieux, nous l'assimilerons sur nos dessins à E, la totalité du référentiel.
Un bon mathématicien dirait alors de 0 et 1 qu'ils sont éléments neutres: 0 à l'égard de la somme logique (+), et 1 à l'égard du produit logique (.).
Et le lascar en profiterait sans doute pour pour nous asséner un dernier axiome bien senti, tout aussi évident que les autres, qu'il appellerait axiome de la complémentation et qui dirait, de manière bien moins poétique qu'Aristote, que:
- A + A = 1, également appelé "loi du tiers exclu",
- A . A = 0, également appelé "principe de contradiction".
Comme pour nous rassurer, ces cinq axiomes fondamentaux de l'algèbre de Boole sont tous confirmés par nos modestes petits dessins. Nous verrons par la suite pourquoi ceci (nos dessins) explique si bien cela (l'algèbre de Boole).
Bon ! Maintenant, quelques minutes d'intense phosphorage neuronal...
Ça risque de secouer un brin...
Les théorèmes de l'algèbre booléenne
A partir des lois booléennes fondamentales et évidentes que nous venons de détailler, il est tout à fait possible, à l'aide de raisonnements logiques appelés démonstrations, d'établir quelques autres propositions utiles que nous appellerons théorèmes de l'algèbre de Boole:
- Théorème de l'unicité du complément: pour toute classe A, il existe une et une seule classe A telle que:
A + A = 1 et A . A = 0
- Théorèmes de l'involution: A = A
- Théorèmes d'absorption: A + A . B = A et A .(A + B) = A
- Théorème de la redondance: A . B + A . C = A . B + A . C + B . C
Ajoutons à cette liste deux théorèmes importants, dits THÉORÈMES DE MORGAN, fruits des travaux du mathématicien anglais Augustus de Morgan [1806-1871], qui annoncent que:
- le complément d'une somme logique est égal au produit logique des compléments: A + B = A . B
- le complément d'un produit logique est égal à la somme logique des compléments: A . B = A + B
Attention ! Purs littéraires s'abstenir...
Ces théorèmes de Morgan illustrent une particularité fascinante de l'algèbre booléenne: le PRINCIPE DE DUALITÉ (duality). Selon ce principe, pour toute égalité E vérifiée dans l'algèbre de Boole, il existe une égalité E*, appelée duale, qui se trouve également vérifiée. Celle-ci, qui plus est, se retrouve quasi immédiatement à partir de E puisqu'il suffit en effet:
- de permuter les opérateurs (+) et (.)
- de permuter les constantes 0 et 1
La confiance règne...
L'algèbre de Boole à facettes
Avouons-le bien volontiers: George Boole ne nous a pas légué "clef en main" cette théorie toute en formules simples et définitives. D'autres esprits illustres ont repris, approfondi et mis en ordre ces idées novatrices dont il eût néanmoins l'intuition géniale de jeter les premiers fondements. Citons, entre autres, l'anglais Augustus De Morgan [1806-1871], et les américains Charles Peirce [1839-1914] et Edward Huntington [1874-1952].
Aujourd'hui, en termes très mathématiques, on appelle algèbre de Boole (E, +, ., , 0, 1) la donnée d'un ensemble E non vide, muni de deux lois de composition interne (+ et .) commutatives et associatives, d'une application unaire ( ) et de deux éléments privilégiés (0 et 1), toutes ces données vérifiant les différents axiomes vus plus haut.
Soupir...
Pour 99% de la population, cette très jolie phrase provoquera nausées, maux de tête voire un petit raffermissement du quadriceps. Les initiés y verront au contraire le formidable canevas à une foule d'applications plus ou moins évidentes: théorie des ensembles, logique des prédicats, calcul des aléas technologiques et, ce qui nous intéressera ici plus particulièrement, technologie des composants électroniques.
Partis très loin dans des sphères très abstraites, tentons de revenir à très petits pas vers notre pécé préféré...
L'algèbre du tout ou rien
De manière rassurante, entrevoir l'immense intérêt de l'algèbre de Boole pour nos petites machines réclamera un petit effort préalable de... simplification. Et imaginer pour cela un univers booléen minimaliste, c'est-à-dire réduit à ses deux seuls éléments remarquables: "0" et "1".
Et là, miracle ! Ce cas très particulier et plutôt minimaliste de l'algèbre de Boole ouvre grand les portes sur d'inattendus horizons: à savoir, tous les domaines où règne la loi du tout ou rien, tous ces univers où toute variable ne peut prendre que deux états différents et complémentaires. Bref, les univers chamarrés de l'ALGÈBRE BINAIRE (binary algebra).
Si, pour vous aussi, la théorie est un tunnel, il semble bien que nous en voyons le bout...
Boole, au coeur de nos vies
Vrai / Faux
Dans cette algèbre booléenne que nous venons de décrire, avoir dénommé "0" et "1" nos deux éléments remarquables était pure convention d'écriture. D'ailleurs, appliqués à la théorie des ensemble, nous avons vu que ces derniers avaient pris des noms autrement plus explicites: ensemble vide (pour "0") et référentiel complet (pour "1").
Ramenés à un univers booléen minimaliste où ces deux valeurs, seules possibles, sont également complémentaires, pourquoi ne pas envisager de les rebaptiser "vrai" et "faux" ? Le "non-vrai" étant forcément "faux", et le "non-faux" obligatoirement "vrai", avouez que ces deux adjectifs colleraient plutôt bien à la "philosophie" booléenne.
Par ailleurs, l'algèbre binaire mettant en jeu des variable ne pouvant prendre que l'une ou l'autre de ces deux valeurs, il devient réalisable, pour chacun de nos trois opérateurs fondamentaux, de consigner en trois petits tableaux l'ensemble de tous les résultats possibles mettant en jeu deux variables:
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
Pas vraiment normande, notre nouvelle algèbre booléenne...
Dans ce nouveau contexte très manichéen, les résultats produits par chacun de nos opérateurs de base peuvent se résumer à trois phrases désarmantes de bon sens:
- Pour la somme logique: si A + B est "vrai", alors A est "vrai" OU B est "vrai",
- Pour le produit logique: si A . B est "vrai", alors A est "vrai" ET B est "vrai",
- Pour la complémentation: le NON "faux" est "vrai" et le NON "vrai" est "faux".
Avouez que nous avons trouvé là des noms beaucoup plus familiers pour nos trois opérateurs booléens fondamentaux. Nous les utiliserons donc dorénavant pour désigner ces derniers, mais plutôt dans leur version anglaise:
Quand et est ou
Méfions-nous quand même des subtilités de la langue; ainsi, par exemple, lorsque nous évoquons "les Hommes et les Femmes", nous ne faisons généralement pas référence aux hermaphrodites, mais bel et bien à toute personne, qu'elle soit hommeou femme. Bref, derrière nos "et" se cachent parfois de parfaits "ou".
Et maintenant, si je vous dis: "je sortirai s'il fait beau ou s'il pleut et que j'ai mon parapluie", et que j'appelle (A) la proposition "il fait beau" et (B) la proposition "j'ai mon parapluie", alors je peux très simplement exprimer mes chances de sortie par la délicieuse expression: A + A.B, digne des plus belles pages de la littérature française.
Tout cela pour vous montrer à quel point, nous, créatures pourtant si subtiles, ne cessons de jongler, sans nous en rendre compte, avec des concepts parfaitement booléens.
Sans surprise, nous appellerons VARIABLE BOOLÉENNE (boolean variables), ou encore VARIABLE LOGIQUE (logical variables), toute variable obéissant à cette algèbre binaire pour laquelle seules deux valeurs différentes et complémentaires sont possibles.
Celles-ci, comme nous l'avons vu, seront généralement notées "1" et "0", mais parfois aussi "vrai" (true) et "faux" (false).
Boole, détecteur de mensonge
On / Off
Bon, bon, bon... Nous en voyons que le précédent chapitre n'a pas du tout convaincus du très haut intérêt de l'algèbre de Boole. Pour ceux-là, nous allons donc sortir la très grosse artillerie, à savoir: une simple pile, quelques fils conducteurs et une ampoule en état de marche.
Tout va bientôt s'éclairer...
En un point donné de tout circuit électrique, deux situations très simples peuvent se produire: soit le courant "passe", soit il ne "passe pas": une simple ampoule nous l'apprendra brillamment.
Afin de symboliser ces deux états très différents, nous pourrions utiliser les termes très suggestifs de "lumière/obscurité", "on/off" ou, pourquoi pas, "1/0".
Etudions maintenant quelques montages électriques de niveau cours élémentaire:
Cliquez sur les différents interrupteurs du montage afin de voir la conséquence sur l'ampoule.
Pense-bête: contacter Varta, Duracel et toute l'industrie de la pile pour leur proposer un espace d'affichage sur le générateur de cette spectaculaire animation.
Et là, divine suprise, nous remarquons ébahis que:
- Pour le montage en parallèle: l'ampoule brille si l'interrupteur A OU l'interrupteur B est en position fermée. Ce que pourrions exprimer par: Lumière = A + B,
- Pour le montage en série: l'ampoule brille si l'interrupteur A ET l'interrupteur B sont en position fermée, soit: Lumière = A . B.
Juste le temps de nous remettre de la vive émotion causée par cette révélation et profitons encore un instant du matériel grâcieusement prêté par le club des électriciens amateurs pour constater que nos axiomes booléens se vérifient parfaitement dans ce petit monde conducteur:
Cliquez sur les différents interrupteurs du montage afin de vérifier la lumineuse pertinence des axiomes booléens.
Vous voila rassuré(e): tout ce que nous avons appris sur l'algèbre booléenne n'est donc pas complètement vain puisqu'elle semble, en effet, trouver certaines applications très lumineuses et très concrètes.
Bon, il est vrai que le rapport est encore ténu entre ces montages pour grands débutants en génie électrique et le concentré de technologie que constitue une puce savante.
Le chemin est encore long, mais il est désormais un poil éclairé !
Heu, à ce propos... Nous allons entrer dans un nouveau tunnel de théorie... Mais promis, la lumière sera encore plus vive de l'autre côté.
Fonctions booléennes
Prenez un mathématicien normalement constitué, donnez lui pour s'amuser quelques variables usagées et attendez. Tôt ou tard, la créature toute excitée viendra vous embrumer l'esprit avec des fonctions !
Et oui. Tout comme en algèbre "classique", il est tout à fait envisageable de combiner entre elles plusieurs variables booléennes à l'aide de nos opérateurs fondamentaux (OR, AND, NOT) pour former des fonctions.
Sans surprise, une telle fonction sera baptisée FONCTION BOOLÉENNE (boolean function), ou encore, FONCTION LOGIQUE (logical function).
Fonctions logiques à deux variables:
OR, NOR, XOR et consorts...
Binaire²
L'épithète "binaire" doit être ici compris comme qualifiant une opération mettant en jeu deux variables, tout comme notre opérateur NOT est un opérateur unaire.
Tous ces opérateurs sont néanmoins des opérateurs de l'algèbre binaire (dans le sens où toute variable ne peut prendre que deux valeurs), ce qui n'arrange rien à la lisibilité de cette note...
A ce stade, nous avons déjà repéré deux opérateurs binaires fondamentaux: le "OR" et le "AND", de par le fait qu'ils correspondaient à des raisonnements logiques très familiers à notre esprit humain et, cadeau bonus, qu'ils décrivaient parfaitement les montages parallèle et série d'un circuit électrique.
Mais ce ne sont pas les seuls !
Pour nous en persuader, nous allons construire un petit tableau original - comme seule l'algèbre binaire peut nous permettre d'en concevoir - afin de lister toutes les fonctions possibles pouvant mettre en jeu deux variables booléennes.
Evidemment, ça va être pénible... mais on y a mis un peu de couleur...
| Fonctions booléennes à deux variables | ||||||||||||||||||||||||||||||||
Quelles que soient les valeurs de A et B, cette fonction renvoie toujours la valeur 0. Il s'agit donc de la fonction constante: F(A, B) = 0
Intérêt discutable... |
Cette fonction, qui ne renvoie 1 que si A et B sont égaux à 1, nous la connaissons fort bien: il s'agit de notre produit logique, alias AND:
F(A, B) = A . B = A AND B |
|||||||||||||||||||||||||||||||
Fonction sans grande correspondance dans le langage parlé, mais que les spécialistes appellent inhibition:
F(A, B) = A . B |
Fonction pour laquelle la variable B ne sert pas à grand chose... Bref, la fonction unaire:
F(A, B) = A |
|||||||||||||||||||||||||||||||
Fonction inhibition comparable à la fonction ci-dessus
F(A, B) = A . B |
Fonction qui ressemble fort à la fonction ci-dessus, A endossant cette fois le rôle de la variable croupion.
F(A, B) = B |
|||||||||||||||||||||||||||||||
Fonction très intéressante, qui ne donne 1 que si les variables A et B sont de valeur différente. Nous l'appellerons fonction d'anticoïncidence, ou XOR:
F(A, B) = A . B + A . B = A XOR B |
Cette fonction là aussi, nous la connaissons déjà fort bien; c'est notre fonction OR, alias somme logique:
F(A, B) = A + B = A OR B |
|||||||||||||||||||||||||||||||
Autre fonction intéressante,complémentaire de notre fonction OR et que nous appellerons donc pour la peine fonction NOR (Not-OR):
F(A, B) = A + B = A . B = A NOR B |
Fonction ô combien remarquable, qui ne prend la valeur 1 que si A et B sont de même valeur. Bref, une fonction de coïncidence, également appelée XNOR:
F(A, B) = A . B + A . B = A XNOR B |
|||||||||||||||||||||||||||||||
Fonction pour laquelle A ne sert pas à grand chose puisque ne renvoie de fait que le complément de B. Il s'agit donc de notre fonction NOT, appliquée à B:
F(A, B) = B |
|
|||||||||||||||||||||||||||||||
Ici aussi, c'est notre fonction NOT qui se cache derrière une façade binaire, la variable B ne servant strictement à rien:
F(A, B) = A |
|
|||||||||||||||||||||||||||||||
Fonction complémentaire de notre opérateur AND, et qu'il serait donc logique d'appeler NAND:
F(A, B) = A . B = A + B = A NAND B |
Fonction somme toute optimiste, donnant 1 quels que soient les valeurs de A et B. Bref, la fonction constante:
F(A, B) = 1 |
|||||||||||||||||||||||||||||||
Parfait ! Nous n'allons pas revenir sur la beauté parfaite de notre "OR" et de notre "AND", mais attardons-nous quelques instants sur certains de ces autres opérateurs aux noms étranges...
XOR (eXclusive OR)

Le XOR, alias "ou exclusif", qui correspond à la fonction booléenne F(A, B) =A.B + A.B est un peu un "ou" version "fromage ou dessert", dans le sens où A XOR B sera "vrai" si A est "vrai" ou B est "vrai", mais pas les deux ! Cela lui vaut ses noms, sans doute plus parlants, d'opérateur d'anticoïncidence, voire, également, de comparateur de différence.
Son symbole est ⊕ et ses caractéristiques principales sont:
- Commutativité: A ⊕ B = B ⊕ A,
- Associativité: (A ⊕ B) ⊕ C = A ⊕ (B ⊕ C),
- Comportement vis-à-vis des éléments neutres: A ⊕ 0 = A et A ⊕ 1 = A,
- A ⊕ A = 0 (pas d'idempotence) et A ⊕ A = 1.
NOR (Not OR)
Comme son nom l'indique assez bien, l'opérateur NOR, noté ↓, est le complément de l'opérateur OR, c'est-à-dire A + B.
Même si cet opérateur n'a pas d'équivalent simple dans le langage parlé, son intérêt en électronique est un tout petit peu essentiel et nous allons donc expliciter quelques unes de ses propriétés:
- Commutativité: A ↓ B = B ↓ A,
- Pas d'associativité: (A ↓ B) ↓ C ≠ A ↓ (B ↓ C),
- Inversion: A ↓ 0 = A.
XNOR (eXclusive Not OR)
Booléennement parlant, XNOR est le complément de l'opérateur XOR que nous venons de voir. Vous ne serez donc pas étonné(e) d'apprendre que son petit nom soit opérateur de coïncidence, ou encore,comparateur d'identité puisque A XNOR B ne sera "vrai" que si A et B ont même valeur.
Ses principales propriétés sont:
- Commutativité: A XNOR B = B XNOR A,
- Associativité: (A XNOR B) XNOR C = A XNOR (B XNOR C),
- Comportement vis-à-vis des éléments neutres: A XNOR 0 = A et A XNOR 1 = A,
- A XNOR A = 1 (pas d'idempotence) et A XNOR A = 0.
NAND (Not AND)
L'opérateur NAND ("ET-NON"), noté ↑, est simple à assimiler puisqu'il agit comme le complément de l'opérateur AND. En clair, A ↑ B ne donnera "faux" que si A et B sont simultanément "vrai".
A l'image du NOR, le NAND n'a pas d'équivalent direct dans le langage parlé, mais son importance est tout aussi fondamentale en électronique et voici pourquoi nous allons nous intéresser à ses passionnantes propriétés:
- Commutativité: A ↑ B = B ↑ A,
- Pas d'associativité: (A ↑ B) ↑ C ≠ A ↑ (B ↑ C),
- Inversion: A ↑ 1 = A.
Fonctions booléennes à N variables
Nous venons d'étudier le cas très particulier et très simple des fonctions booléennes à deux variables. Bien évidemment, vous vous doutez qu'une fonction logique peut mettre en jeu un nombre quelconque de variables booléennes.
Ainsi, la fonction F(A, B, C) = A.B + A.C est un exemple pris tout à fait au hasard de fonction logique à trois variables.
Cartes sur table
Comme nous l'avons déjà mis en pratique, la grande particularité des fonctions booléennes est qu'elles peuvent être explorées de manière exhaustive. En effet, chaque variable de ces fonctions ne pouvant prendre que deux valeurs différentes, il devient tout à fait faisable de récapituler tous les cas possibles dans un tableau que l'on appelle alors TABLE DE VÉRITÉ (truth table).
Ainsi, si nous reprenons notre fonction booléenne définie par F(A, B, C) = A.B + A.C, nous pouvons sans trop de problème mettre au point sa table de vérité:
| A | B | C | F(A, B, C) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | ? |
Cette table comporte une colonne par variable mise en jeu par la fonction, plus une colonne terminale où l'on consigne, pour chaque combinaison des variables, la valeur prise alors par la fonction.
Canon Boole
Supposons un instant que nous ayons sous les yeux une table de vérité toute faite, sans aucune définition algébrique de la fonction associée:
| A | B | C | F(A, B, C) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Et bien cette table de vérité peut nous permettre de retrouver une définition polynômiale de la fonction F.
En effet, nous savons qu'en algèbre binaire, si nous avons une expression:
X + Y + Z + .... = 1, alors on peut dire que
X = 1 OU Y = 1 OU Z = 1...
Il est par conséquent tout à fait envisageable de définir notre fonction F comme la somme logique des différentes lignes pour lesquelles F = 1.
Conséquence toute naturelle de tout cela: deux fonctions logiques F et F' seront égales si et seulement si leur table de vérité sont identiques.
Ainsi, dans notre exemple, on peut écrire: F(A, B, C) = A.B.C + A.B.C + A.B.C + A.B.C + A.B.C
Aucune absence tolérée
Pour qu'un produit logique de N variables mérite le qualificatif de minterme, chacune de ses N variables ou son complément doit apparaître dans le produit.
Ainsi, A.C ou B.C ne sont pas des mintermes des variables A, B, C.
En groscursussien, les différents monômes de la fonction (c'est-à-dire les produits logiques A.B.C, A.B.C, A.B.C, A.B.C et A.B.C) sont appelés des MINTERMES (minterms), et la fonction F, qui se trouve alors exprimée sous la forme d'unesomme logique de mintermes est dite se trouver sous sa FORME CANONIQUE DISJONCTIVE (disjunctive canonical form), ou également première forme canonique.
Par ailleurs, dans notre univers booléen, nous pouvons également définir le complément de F comme la somme des mintermes égaux à 0. Nous avons donc aussi:
F(A, B, C) = A.B.C + A.B.C + A.B.C
Et puisque nous savons parfaitement que A = A et aussi que, grâce à ce qu'a fait Morgan, A+B = A.B, nous pouvons donc également écrire F sous la forme:
| F(A, B, C) = | A.B.C + A.B.C + A.B.C | = (A + B + C) . (A + B + C) . (A + B + C) |
De la même manière que pour le minterme, pour qu'une somme logique de N variables mérite le qualificatif de maxterme, chacune de ces N variables ou son complément doit apparaître dans la somme.
Les termes A+B+C, A+B+C et A+B+C, sommes logiques de toutes les variables de F (ou de leur complément) sont appelés MAXTERMES (maxterms) de la fonction, et cette écriture de F sous la forme de produits de maxtermes est appelée FORME CANONIQUE CONJONCTIVE (conjunctive canonical form), ou aussi parfois deuxième forme canonique.
Que vous ayez ou non compris cette histoire de canon, vous aurez de toute façon noté qu'une fonction logique peut être exprimée algébriquement de différentes façons.
Et ceci n'est pas une bonne nouvelle pour nos neurones...
Vocaboolaire de base
L'art de faire simple
La plupart du temps, une fonction logique nous sera proposée sous une forme développée plus ou moins alambiquée qu'il sera très souvent possible de fortement simplifier.
Pour ce faire, trois pistes à explorer:
Méthode algébrique
Génération spontanée
En algèbre booléenne, rien de plus simple que de faire apparaître le terme C dans le produit A.B puisque, sachant que C+C=1, on peut écrire:
A.B = A.B.(C+C) = A.B.C + A.B.C
Ceci est une règle de l'algèbre binaire: Il faut parfois savoir complexifier une expression pour mieux la simplifier ensuite.
Nous l'avons vu ensemble, l'algèbre booléenne dispose d'un véritable arsenal d'axiomes et théorèmes bien définitifs qui peuvent nous permettre de simplifier une fonction logique.
Bien souvent, la solution passe par de judicieux développements afin de faire apparaître des termes qui, par factorisations non moins habiles, vont s'annuler sur le principe que A + 1 = A ou A . 0 = 0.
Attention toutefois: la simplification algébrique demande un minimum de rigueur et de zénitude. Si vous êtes du genre à facilement oublier un A en route ou prêt(e) à tout abandonner quand retentit le jingle annonçant l'arrivée d'un pote sur MSN, envisagez peut-être directement le plan B...
Comment simplifiez-vous la fonction logique F(A, B) = (A + B) . (A + B) ?
Formes canoniques
L'annonce ne vous surprendra pas deux fois: la table de vérité d'une fonction logique à N variables comportera 2N lignes.
Dès lors, trois scénarii possibles:
Ce n'est pas parce que vous aurez exprimé votre fonction sous une forme canonique plutôt simple que celle-ci sera obligatoirement l'expression la plus simplifiée de la fonction. Très souvent, une phase de simplification algébrique permettra d'achever complètement la simplification.
- Ou la table de vérité révèle un petit nombre de cas pour lesquels la fonction est égale à 1. Dans ce cas, il sera sensé d'exprimer la fonction dans sa forme canonique disjonctive;
- Ou la table de vérité révèle un petit nombre de cas pour lesquels la fonction est égale à 0, et il sera alors pertinent d'exprimer la fonction dans sa forme canonique conjonctive, en complémentant la somme des mintermes égaux à 0;
- Ou la table de vérité ne révèle aucune prépondérance nette de résultats égaux à 0 ou 1, et on devra se résoudre à faire appel à Maurice...
Diagramme de Karnaugh
Le DIAGRAMME DE KARNAUGH (Karnaugh map) est une méthode simple et ingénieuse afin de trouver à coup sûr la forme la plus simple d'une fonction logique donnée, à partir de sa table de vérité.
A vrai dire, le diagramme de Karnaugh d'une fonction n'est ni plus ni moins que la table de vérité de celle-ci, mais mise en forme de telle manière que soient géographiquement proches les mintermes logiquement proches.
Comme le fait d'expliquer textuellement le principe de ce diagramme conduirait à une somme faramineuse de lignes totalement imbitables, nous allons plutôt illustrer nos dires par un exemple bien senti.
Soit l'anodine fonction logique F telle que F(A, B, C, D) = A + A.B + A.B.C + A.B.C.D.
Amusons-nous à développer sa table de vérité.
| A | B | C | D | F(A, B, C, D) |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Voilà ! On s'est bien poilé et nous avons, conformément à nos attentes, obtenu une table de vérité à 16 lignes.
Nous allons maintenant transformer ce tableau à seize lignes en un tableau à seize cases. Pour ce faire, nous allons répartir tous les mintermes de nos variables groupées deux à deux, mais en prenant soin de scrupuleusement respecter cette règle: il faut impérativement que le passage d'une case à une case adjacente ne traduise le changement d'état que d'une seule variable.
Normalement, nous devrions obtenir quelque chose qui ressemble à ça:
| C.D | C.D | C.D | C.D | |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 0 | 0 | 1 |
A chaque case de notre nouveau tableau correspond un minterme de la table de vérité; il est donc normal de retrouver dans notre table de Karnaugh tous les résultats possibles pour la fonction F, et donc, le même nombre de "1" et de "0".
Nous allons dès lors pouvoir procéder aux simplifications.
Pour ce faire, nous allons localiser les cases adjacentes marquées à "1" en nombre égal à une puissance de deux, c'est-à-dire les groupes de 1, 2, 4, 8, 16.... cases "1" adjacentes, en recherchant bien sûr les regroupements les plus importants. On ne garde ensuite, parmi les mintermes concernés par le regroupement, que la ou les variable(s) logique(s) commune(s) à toutes les cases.
| C.D | C.D | C.D | C.D | |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 0 | 0 | 1 |
Premier regroupement: parmi les huit cases formées par les deux premières lignes, seule la variable B est commune aux mintermes.
Notez qu'on ne peut inclure la troisième ligne dans notre premier regroupement, car nous aurions alors douze cases, douze n'étant pas une puissance de deux.
| C.D | C.D | C.D | C.D | |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 0 | 0 | 1 |
Deuxième regroupement: parmi les huit cases formées par les deuxième et troisième lignes, seule la variable A est commune aux mintermes.
Comme vous le constatez pour notre deuxième ligne, une ou plusieurs case(s) peut(vent) tout à fait servir à plusieurs regroupements.
| C.D | C.D | C.D | C.D | |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 1 | 1 | 1 |
| A.B | 1 | 0 | 0 | 1 |
Troisième regroupement: parmi les huit cases formées par la première et la dernière colonne, seule la variable C est commune aux mintermes.
Remarquez que les lignes / colonnes situées aux extrémités doivent être considérées comme adjacentes. Et cela est après tout fort logique, puisqu'une seule variable change d'état de l'une à l'autre.
Parfait ! Aucun autre regroupement n'étant possible, on recopie les mintermes n'ayant servi à aucun regroupement - ici, aucun - et on récupère les fruits de nos regroupements successifs, pour finalement obtenir:
F = B + A + C
...ce qui constitue quand même, vous êtes maintenant connaisseur(se), une fort belle simplification !
Bien évidemment, nous aurions pu parvenir au même résultat avec beaucoup moins d'efforts et un zeste de réflexion, en remarquant que la table de vérité ne recensait que deux cas où la fonction s'annulait, cas correspondant au monôme A.B.C.
Dès lors, on pouvait se remémorer le théorème de l'involution puis avoir une pensée pour Morgan pour noter que:
| F(A, B, C) = | A.B.C |
= A + B + C
|
Evidemment, vous vous doutez que la méthode de Karnaugh devient franchement hostile dès lors que le nombre de variables logiques excède quatre, puisqu'il faut dès lors faire appel à une table en 3D, du moins si l'on veut continuer d'obéir à l'obligation de ne changer qu'une seule variable d'état lors du passage d'une case à une autre.
Inutile également de préciser qu'au delà de six variables logiques, la méthode de Karnaugh devient inapplicable sans très très haute faculté d'abstraction. Il faut alors se replier vers d'autres méthodes de simplification, telle la méthode de Quine-Mac Cluskey, que nous n'aborderons pas ici car nous ne voudrions pas abuser de votre gentille attention.
Bon ! Autant le dire tout de suite, le "machin" ci-dessus en est encore à une béta pré-version 0.0 sûrement buggée jusqu'à la moëlle. Bref, un truc absolument pas fiable qui, à l'heure où sont écrites ces lignes, pourrit consciencieusement la vie de son auteur qui se mord les doigts de s'être réveillé un matin avec la lubie de créer un truc de ce style.
13:13 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
25/03/2011
E8 (mathématiques)
E8 (mathématiques)
En mathématiques,  est le plus grand groupe de Lie complexe de type exceptionnel. Son algèbre de Lie est notée
est le plus grand groupe de Lie complexe de type exceptionnel. Son algèbre de Lie est notée  .
.
E8 est de rang 8 et de dimension 248. Il est simplement connexe et son centre est trivial.
La structure E8 a été découverte en 1887 par le mathématicien norvégien Sophus Lie pour étudier la symétrie et jusqu’ici personne ne pensait que cet objet mathématique pourrait être compris, considère Jeffrey Adams, responsable de l’équipe Atlas of Lie Groups and Représentations qui réunit 18 mathématiciens et programmeurs dans le monde, dont Fokko du Cloux et Marc van Leeuwen.
Sommaire[masquer]
|
Formes réelles[modifier]
En plus du groupe de Lie complexe E8, de dimension complexe 248 (donc de dimension réelle 496), il existe trois formes réelles de ce groupe, toutes de dimension réelle 248. Les plus simples sont les formes compactes  et déployées
et déployées  (non-compacte maximale ou encore split en anglais) et il en existe une troisième, notée
(non-compacte maximale ou encore split en anglais) et il en existe une troisième, notée  .
.
Constructions[modifier]
On peut construire la forme compacte du groupe E8 comme le groupe d'automorphismes de l'algèbre de lie  correspondante. Cette algèbre possède
correspondante. Cette algèbre possède  comme sous-algèbre de dimension 120 et on peut se servir de celle-ci pour décomposer la représentation adjointe comme
comme sous-algèbre de dimension 120 et on peut se servir de celle-ci pour décomposer la représentation adjointe comme
où  est l'une des deux représentations spinorielles, de type Majorana-Weyl du groupe
est l'une des deux représentations spinorielles, de type Majorana-Weyl du groupe  dont
dont 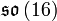 est l'algèbre de Lie.
est l'algèbre de Lie.
Si on appelle  un jeu de générateurs pour
un jeu de générateurs pour 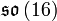 et
et  les 128 composantes de
les 128 composantes de  alors on peut écrire explicitement les relations définissant
alors on peut écrire explicitement les relations définissant  comme
comme
ainsi que
![left[J_{ij}, Q_aright] = frac14 left(gamma_igamma_j - gamma_jgamma_iright)_{ab}Q_b,](http://upload.wikimedia.org/math/b/f/1/bf123d341c9502ae0e5452733a8004ea.png) ,
,
qui correspond à l'action naturelle de  sur le spineur
sur le spineur 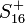 . Le commutateur restant (qui est bien un commutateur et non pas un anticommutateur) est défini entre les composantes du spineur comme
. Le commutateur restant (qui est bien un commutateur et non pas un anticommutateur) est défini entre les composantes du spineur comme
![left[Q_a, Q_bright] = gamma^{[i}_{ac}gamma^{j]}_{cb}J_{ij},](http://upload.wikimedia.org/math/5/1/6/51632689c8006bf6f240719672da191c.png) .
.
À partir de ces définitions on peut vérifier que l'identité de Jacobi est satisfaite.
Géométrie[modifier]
La forme réelle compacte de E8 peut être vue comme le groupe d'isométrie d'une variété riemannienne de dimension 128 appelée plan projectif octooctonionique. Ce nom vient de ce qu'il peut être construit en utilisant une algèbre qui est construite comme produit tensoriel des octonions avec eux-mêmes. Ce type de construction est analysé en détail par Hans Freudenthal et Jacques Tits dans leur construction du carré magique.
En physique[modifier]
Dans le cadre des théories de grande unification en physique des particules, le groupe E8 est parfois considéré comme groupe de jauge candidat dans la mesure où il contient d'une façon naturelle une série d'autres groupes de grande unifications souvent considérés. On peut le voir sous la succession d'inclusions
Par ailleurs, le groupe E8 apparait fréquemment en théorie des cordes et en supergravité. Dans la théorie des cordes hétérotiques une formulation fait apparaître  (sous forme compacte) comme groupe de jauge. Par ailleurs, lorsque la supergravité maximale est compactifiée sur un tore de dimension 8 alors la théorie résultante en dimension trois possède unesymétrie globale E8 (c'est-à-dire la forme déployée, ou maximalement non-compacte). Il a été par la suite suggéré[réf. nécessaire] qu'une version discrète, notée
(sous forme compacte) comme groupe de jauge. Par ailleurs, lorsque la supergravité maximale est compactifiée sur un tore de dimension 8 alors la théorie résultante en dimension trois possède unesymétrie globale E8 (c'est-à-dire la forme déployée, ou maximalement non-compacte). Il a été par la suite suggéré[réf. nécessaire] qu'une version discrète, notée 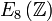 , de ce groupe serait une symétrie, appelée dans ce contexte U-dualité, de la théorie M.
, de ce groupe serait une symétrie, appelée dans ce contexte U-dualité, de la théorie M.
En novembre 2007, un physicien américain, Antony Garrett Lisi, dépose sur le site de publications scientifiques ArXiv un article très discuté sur une théorie unificatrice des forces basé sur le groupe E8.
Algèbre[modifier]
Diagramme de Dynkin[modifier]

Système de racines[modifier]
Dans la base formée par les racines simples  , le système de racines de E8 est formé d'une part de toutes les permutations de
, le système de racines de E8 est formé d'une part de toutes les permutations de
qui constitue le système de racines de  et possède
et possède  éléments (il faut rajouter les 8 générateurs du Cartan pour obtenir 120 qui est la dimension de
éléments (il faut rajouter les 8 générateurs du Cartan pour obtenir 120 qui est la dimension de  ).
).
Par ailleurs on doit ajouter à cela les 128 poids de la représentation spinorielle  de
de 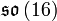 . Toujours dans la même base, ceux-ci sont représentés par les vecteurs
. Toujours dans la même base, ceux-ci sont représentés par les vecteurs
tels que la somme de toutes les coordonnées soit paire. Ils sont au nombre de 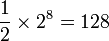 .
.
On obtient donc  racines, toutes de multiplicité 1. Par abus de langage on considère aussi parfois le vecteur nul comme une racine associée à la sous-algèbre de Cartan. Comme E8 est de rang 8, la racine nulle est alors de multiplicité 8. Ainsi au final on a bien décrit les 248 générateurs de l'algèbre
racines, toutes de multiplicité 1. Par abus de langage on considère aussi parfois le vecteur nul comme une racine associée à la sous-algèbre de Cartan. Comme E8 est de rang 8, la racine nulle est alors de multiplicité 8. Ainsi au final on a bien décrit les 248 générateurs de l'algèbre  .
.
Matrice de Cartan[modifier]
Représentations[modifier]
 se distingue des autres algèbres de Lie de dimension finie par le fait que sa plus petite représentation non-triviale est la représentation adjointe.
se distingue des autres algèbres de Lie de dimension finie par le fait que sa plus petite représentation non-triviale est la représentation adjointe.
La représentation fondamentale de E8 est de dimension 248.
Décodage du groupe  [modifier]
[modifier]
Le 19 mars 2007, l'Institut américain des mathématiques (AIM) a annoncé que des chercheurs américains et européens et après quatre ans d'efforts et plus d'un siècle après sa découverte sont parvenus à décoder l'E8, l'une des structures mathématiques les plus complexes et les plus grandes. Le noyau dur du groupe de chercheurs est formé de sept mathématiciens, cinq Américains et deux Français : Jeffrey Adams de l'Université du Maryland, Dan Barbasch de Université Cornell, John Stembridge de l'Université du Michigan, Peter Trapa de l'Université de l'Utah, Marc van Leeuwen de l'Université de Poitiers, David Vogan du Massachusetts Institute of Technology et Fokko du Cloux de l'Université de Lyon1.
Selon Peter Sarnak, professeur de mathématiques à l'Université Princeton et président du comité scientifique de AIM, le décodage de ce groupe pourrait ouvrir la porte à d'autres innovations dans le domaine de la programmation informatique.
« Cette percée est importante non seulement pour faire avancer les connaissances mathématiques de base mais aussi pour faciliter les calculs par ordinateur permettant de résoudre des problèmes complexes, [...]. Le décodage de cette structure appelée E8 pourrait aussi très bien avoir des applications en mathématiques et physique qu'on ne découvrira pas avant plusieurs années. »
— Peter Sarnak, Le Monde, 19 mars 2007
Parmi les objets sous-jacents aux groupes de Lie, on trouve toutes sortes de figures géométriques telles que les sphères, les cônes, les cylindres dans l’espace à trois dimensions. Mais les choses se corsent lorsque l’on étudie ces objets dans des espaces de dimensions supérieures. « Comprendre et classer les structures  a été critique pour comprendre des phénomènes dans de nombreux domaines des mathématiques incluant l’algèbre, la géométrie, la théorie des nombres ainsi que la physique et la chimie », commente Peter Sarnak, professeur de mathématique à l’université de Princeton et président du comité scientifique de l’AIM.
a été critique pour comprendre des phénomènes dans de nombreux domaines des mathématiques incluant l’algèbre, la géométrie, la théorie des nombres ainsi que la physique et la chimie », commente Peter Sarnak, professeur de mathématique à l’université de Princeton et président du comité scientifique de l’AIM.
Ces calculs ont nécessité de nouvelles techniques mathématiques et des capacités de calcul des ordinateurs qui n'existaient pas il y a encore peu d'années, précisent les chercheurs. L’opération a pris 77 heures et a nécessité un supercalculateur doté de 200 Go de mémoire vive, et a produit un résultat de l’ordre de 60 Go dont la taille peut être comparée à 60 fois celle du génome humain. L’équipe attendait donc de trouver un supercalculateur capable d’effectuer les calculs lorsque Noam Elkies, un mathématicien de l’université Harvard a mis en évidence un moyen de découper le projet en éléments plus simples. Chaque élément produit un sous-ensemble du résultat et leur réunion permet de donner la solution complète au problème. À l’été 2006, trois membres de l’équipe, dont Fokko du Cloux, ont décomposé le programme en plusieurs éléments. Les calculs ont été réalisés sur une machine de l’université de Washington.
L’ordre de grandeur et la nature du calcul est à rapprocher du projet de séquençage du génome humain, indique le communiqué de presse diffusé par AIM. Alors que l’ensemble des informations du génome représente un volume de 1 Go, le résultat de l’E8 est environ 60 fois plus important avec des données hautement compressées. Écrit sur un papier, ce résultat couvrirait un espace équivalent à la taille de Manhattan.
Quelques chiffres sur le calcul de  [modifier]
[modifier]
Quelques idées sur la taille du résultat final1 :
- Le résultat du calcul E8 est une matrice de 453 060 lignes et colonnes.
- La matrice comporte 205 263 363 600 éléments,
- Si chaque élément de cette matrice était écrit sur une surface de 2,5 cm2, la matrice aurait une dimension d’un carré de plus de 10 km de côté.
- Nombre de polynômes distincts : 1 181 642 979,
- nombre de coefficients dans les polynômes distincts : 13 721 641 221,
- plus grand coefficient : 11 808 808,
- polynôme ayant le plus grand coefficient : 152 q22 + 3472 q21 + 38 791 q20 + 293 021 q19 + 1 370 892 q18 + 4 067 059 q17 + 7 964 012 q16 + 11 159 003 q15 + 11 808 808 q14 + 9 859 915 q13 + 6 778 956 q12 + 3 964 369 q11 + 2 015 441 q10 + 906 567 q9 + 363 611 q8 + 129 820 q7 + 41 239 q6 + 11 426 q5 + 2 677 q4 + 492 q3 + 61 q2 + 3 q,
- valeur de ce polynôme pour q=1 : 60 779 787,
- polynôme ayant la plus grande valeur (lorsque q=1) découvert jusqu'à présent (mai 2007) : 1 583 q22 + 18 668 q21 + 127 878 q20 + 604 872 q19 + 2 040 844 q18 + 4 880 797 q17 + 8 470 080 q16 + 11 143 777 q15 + 11 467 297 q14 + 9 503 114 q13 + 6 554 446 q12 + 3 862 269 q11 + 1 979 443 q10 + 896 537 q9 + 361 489 q8 + 129 510 q7 + 41 211 q6 + 11 425 q5 + 2 677 q4 + 492 q3 + 61 q2 + 3 q,
- valeur pour ce polynôme pour q=1 : 62 098 473.
Notes et références[modifier]
- AIM math: Representations of E8 [archive]
Voir aussi[modifier]
Articles connexes[modifier]
- Groupe de Lie
- Algèbre de Lie
- Système de racines
- Diagramme de Dynkin
Liens externes[modifier]
- [pdf] Théorie de A. Garrett Lisi sur l'utilisation de E8 pour réunifier les différentes forces physiques et la physique quantique
- (fr) Groupe de Lie E8 : une clé pour la théorie des supercordes ?
- (en) Taille de certaines lignes de calcul du groupe E8
- (fr) Une solution mathématique aux dimensions démesurées Article de Techno-science.net
- [pdf] Représentation graphique de E8
- (fr) Garrett Lisi sur la théorie du Tout Conférence TED 2008 (VOST FR) www.ted.com
- Portail des mathématiques
11:34 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Algèbre enveloppante
Algèbre enveloppante
|
|
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
En mathématiques, on peut construire l'algèbre enveloppante  d'une algèbre de Lie
d'une algèbre de Lie  . Il s'agit une algèbre unitaire qui permet de rendre compte de la plupart des propriétés de
. Il s'agit une algèbre unitaire qui permet de rendre compte de la plupart des propriétés de  .
.
Sommaire[masquer] |
Algèbres de Lie[modifier]
Soit K un corps commutatif de caractéristique différente de 2. Une algèbre de Lie  sur K est un espace vectoriel muni d'une apllication bilinéaire
sur K est un espace vectoriel muni d'une apllication bilinéaire ![(x,y) mapsto [x,y]](http://upload.wikimedia.org/math/7/5/e/75e87350f83275e11f126171780fd7ca.png) de
de 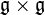 dans
dans  qui vérifie les propriétés suivantes :
qui vérifie les propriétés suivantes :
![forall x in mathfrak{g}, [x,x]=0](http://upload.wikimedia.org/math/f/3/2/f3223a3fe063412bb2f5033ba34850f5.png) ;
;![forall x,y,z in mathfrak{g}, [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0](http://upload.wikimedia.org/math/6/7/d/67d115952cf9c1c691b6053868febb0d.png)
Tout espace vectoriel V peut être muni d'une structure d'algèbre de Lie, en posant ![forall x,y in V, [x,y]=0](http://upload.wikimedia.org/math/8/6/9/8697bab9adc96fe793676eb0843e4edc.png) . Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne. Un autre exemple, fondamental pour ce qui suit, est le suivant. Soit V un espace vectoriel sur K. L'espace vectoriel End(V) des endomorphismes de V peut être muni d'une structure d'algèbre de Lie, en posant :
. Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne. Un autre exemple, fondamental pour ce qui suit, est le suivant. Soit V un espace vectoriel sur K. L'espace vectoriel End(V) des endomorphismes de V peut être muni d'une structure d'algèbre de Lie, en posant : ![[u,v]=ucirc v-vcirc u](http://upload.wikimedia.org/math/e/c/e/ecea3c23938418479a1064ef02f67bb2.png) . On note également
. On note également  l'algèbre de Lie ainsi obtenue. Lorsque V est de dimension finie n,
l'algèbre de Lie ainsi obtenue. Lorsque V est de dimension finie n,  s'identifie aux matrices de taille
s'identifie aux matrices de taille  à coefficient dans K. On la note alors
à coefficient dans K. On la note alors 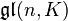 .
.
La construction d'une algèbre enveloppante répond au problème réciproque : à partir d'une algèbre de Lie  , peut-on construire une algèbre associative dont le commutateur correspond au crochet de Lie de
, peut-on construire une algèbre associative dont le commutateur correspond au crochet de Lie de  ?
?
L'algèbre enveloppante[modifier]
Construction[modifier]
A partir de l'algèbre de Lie  , on peut construire le produit tensoriel
, on peut construire le produit tensoriel  et plus généralement
et plus généralement  . On note par convention
. On note par convention  . On considère alors l'algèbre tensorielle de
. On considère alors l'algèbre tensorielle de  , définie par
, définie par  . On note σ l'application canonique de
. On note σ l'application canonique de  dans
dans  . L'algèbre tensorielle satisfait une propriété universelle : pour toute application linéaire τ de
. L'algèbre tensorielle satisfait une propriété universelle : pour toute application linéaire τ de  dans une algèbre avec unité A, il existe un unique morphisme d'algèbre
dans une algèbre avec unité A, il existe un unique morphisme d'algèbre  tel que
tel que 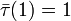 et
et  .
.
Pour construire l'algèbre enveloppante, il faut encore tenir compte de la structure d'algèbre de Lie de  . On veut donc forcer
. On veut donc forcer  à être égal à [X,Y]. Plus formellement, soit J l'idéal bilatère engendré par les
à être égal à [X,Y]. Plus formellement, soit J l'idéal bilatère engendré par les ![Xotimes Y-Yotimes X-[X,Y]](http://upload.wikimedia.org/math/e/f/a/efa058d8548e9c2c9d27cf84332bdfff.png) , pour
, pour  . L'algèbre enveloppante
. L'algèbre enveloppante  est alors le quotient de
est alors le quotient de  par l'idéalJ. L'injection canonique de
par l'idéalJ. L'injection canonique de  dans
dans  passe au quotient et fournit alors un morphisme
passe au quotient et fournit alors un morphisme 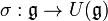 .
.
Notons  l'image de
l'image de 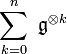 dans
dans  . Lorsque l'algèbre de Lie
. Lorsque l'algèbre de Lie  est de dimension finie,
est de dimension finie,  est un sous-espace vectoriel de dimension finie de
est un sous-espace vectoriel de dimension finie de  . Dans tous les cas, on a la filtration suivante :
. Dans tous les cas, on a la filtration suivante :  .
.
Exemple Considérons l'algèbre de Lie abélienne K, de dimension 1. Dans ce cas, le crochet de Lie est identiquement nul. L'idéal J est alors engendré par les vecteurs  , pour
, pour  . On vérifie alors dans ce cas que
. On vérifie alors dans ce cas que ![U(K) cong K[T]](http://upload.wikimedia.org/math/0/c/9/0c96d59ae426e695ac9de9520e7472a9.png) (l'algèbre des polynômes en une indéterminée).
(l'algèbre des polynômes en une indéterminée).
Propriété universelle[modifier]
Comme pour l'algèbre tensorielle, on peut caractériser l'algèbre enveloppante de  par une propriété universelle :
par une propriété universelle :
Propriété universelle de l'algèbre enveloppante — Soit  une application linéaire de
une application linéaire de  dans une algèbre associative avec unité A telle que
dans une algèbre associative avec unité A telle que
![varphi([X,Y])=varphi(X)varphi(Y)-varphi(Y)varphi(X)](http://upload.wikimedia.org/math/3/e/9/3e97049ebe943b16508bcef76c30c203.png) , pour tout
, pour tout  . Alors il existe un unique morphisme d'algèbre
. Alors il existe un unique morphisme d'algèbre  tel que
tel que  et
et  .
.
Remarque L'unicité provient du fait que  est engendrée par 1 et
est engendrée par 1 et  . L'existence s'obtient à partir de la propriété universelle de l'algèbre tensorielle.
. L'existence s'obtient à partir de la propriété universelle de l'algèbre tensorielle.
Cette propriété universelle a une conséquence importante en théorie des représentations, à savoir toute représentation de  dans un espace vectoriel V s'étend de manière unique en un morphisme d'algèbre entre
dans un espace vectoriel V s'étend de manière unique en un morphisme d'algèbre entre  et End(V).
et End(V).
Théorème de Poincaré-Birkhoff-Witt et ses conséquences[modifier]
Le théorème de Poincaré-Birkhoff-Witt(PBW) donne une base de l'algèbre enveloppante et ainsi permet de mieux en comprendre la structure. Pour en simplifier un peu l'énoncé, nous le donnons pour une algèbre de Lie de dimension finie.
Théorème de Poincaré-Birkhoff-Witt — L'application  est injective. Soit
est injective. Soit  une base de
une base de  . Alors les monômes
. Alors les monômes  ,
,  , forment une base de
, forment une base de  .
.
Voici quelques conséquences importantes de PBW :
- Soit
 une sous-algèbre de Lie de
une sous-algèbre de Lie de  . Alors
. Alors 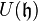 s'identifie à une sous-algèbre associative de
s'identifie à une sous-algèbre associative de  .
. - Supposons que
 soit la somme directe de deux sous-algèbres :
soit la somme directe de deux sous-algèbres :  . Alors l'algèbre
. Alors l'algèbre  est isomorphe au produit tensoriel
est isomorphe au produit tensoriel  .
. - Soit Kn l'algèbre de Lie abélienne de dimension n. Alors U(Kn) est isomorphe à l'algèbre de polynômes
![K[T_1,ldots,T_n]](http://upload.wikimedia.org/math/2/0/4/20496667b52257abfbda4b3696b1f9c5.png) .
. - Soit V un espace vectoriel. Tout morphisme d'algèbre de
 dans End(V) donne par restriction une représentation de
dans End(V) donne par restriction une représentation de  dans V. En tenant compte de la remarque de la partie précédente, cela fournit une équivalence de catégories entre la catégorie des représentations de
dans V. En tenant compte de la remarque de la partie précédente, cela fournit une équivalence de catégories entre la catégorie des représentations de  et celle des représentations de l'algèbre
et celle des représentations de l'algèbre  .
.
Dans certains cas, il est possible de décrire explicitement l'algèbre enveloppante. Soit G un groupe de Lie réel, d'algèbre de Lie  . Notons
. Notons  le complexifié de
le complexifié de  . Soit
. Soit  . On construit alors l'opérateur différentiel
. On construit alors l'opérateur différentiel 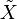 sur
sur  par :
par :
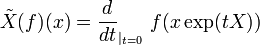 , pour
, pour  et
et  . L'opérateur
. L'opérateur 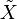 est un exemple d'opérateur différentiel invariant à gauche (i.e. commutant avec les translations à gauche par des vecteurs de G). Notons D(G) l'ensemble des opérateurs différentiels invariants à gauche. On a donc une application
est un exemple d'opérateur différentiel invariant à gauche (i.e. commutant avec les translations à gauche par des vecteurs de G). Notons D(G) l'ensemble des opérateurs différentiels invariants à gauche. On a donc une application  . Cette application s'étend en une application de
. Cette application s'étend en une application de  dans D(G). Cette application définit par propriété universelle un morphisme d'algèbre de
dans D(G). Cette application définit par propriété universelle un morphisme d'algèbre de  dans D(G). Ce morphisme est un fait unisomorphisme. Ainsi l'algèbre enveloppante de
dans D(G). Ce morphisme est un fait unisomorphisme. Ainsi l'algèbre enveloppante de  s'identifie avec l'algèbre des opérateurs différentiels invariants à gauche sur G.
s'identifie avec l'algèbre des opérateurs différentiels invariants à gauche sur G.
Exemple Regardons le cas simple de l'algèbre de Lie  . Le groupe de Lie
. Le groupe de Lie  a pour algèbre de Lie
a pour algèbre de Lie  , qui a pour complexifié
, qui a pour complexifié  . Ici
. Ici  est l'espace usuel des fonctions
est l'espace usuel des fonctions  à valeurs dans
à valeurs dans  . Ainsi, pour
. Ainsi, pour  , l'opérateur
, l'opérateur 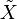 est donné par
est donné par  . Autrement dit, l'opérateur est donné par
. Autrement dit, l'opérateur est donné par 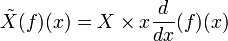 . D'autre part, un opérateur différentiel
. D'autre part, un opérateur différentiel 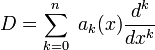 sur G est invariant à gauche si et seulement si
sur G est invariant à gauche si et seulement si  . Ainsi, on a
. Ainsi, on a 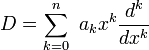 , ce qui identifie
, ce qui identifie  avec
avec ![mathbb{C}[T]](http://upload.wikimedia.org/math/5/d/a/5da3c864653f85dd225b9b00e48bd866.png) , qui est isomorphe à
, qui est isomorphe à  comme nous l'avons déjà remarqué.
comme nous l'avons déjà remarqué.
Représentation adjointe[modifier]
L'algèbre de Lie  agit sur elle-même via la représentation adjointe
agit sur elle-même via la représentation adjointe  définie par ad(X)(Y) = [X,Y], pour
définie par ad(X)(Y) = [X,Y], pour  . Cette représentation s'étend en une représentation de
. Cette représentation s'étend en une représentation de  sur son algèbre enveloppante, via la formule
sur son algèbre enveloppante, via la formule  , pour
, pour  et
et  . Cette représentation laisse stable les sous-espaces
. Cette représentation laisse stable les sous-espaces  et donc aussi les quotients
et donc aussi les quotients  . Lorsque
. Lorsque  est de dimension finie,
est de dimension finie,  est aussi de dimension finie. Cela fournit donc toute une famille de représentations de dimension finie de
est aussi de dimension finie. Cela fournit donc toute une famille de représentations de dimension finie de  .
.
L'algèbre symétrique[modifier]
Un autre quotient de l'algèbre tensorielle joue un rôle important : l'algèbre symétrique. Soit I l'idéal bilatère de  engendré par les vecteurs
engendré par les vecteurs  . L'algèbre symétrique
. L'algèbre symétrique  est l'algèbre quotient
est l'algèbre quotient  . C'est une algèbre associative et commutative. On note toujours σ l'application canonique de
. C'est une algèbre associative et commutative. On note toujours σ l'application canonique de  dans
dans  . Comme pour l'algèbre enveloppante, l'algèbre symétrique satisfait une propriété universelle :
. Comme pour l'algèbre enveloppante, l'algèbre symétrique satisfait une propriété universelle :
Propriété universelle de l'algèbre symétrique — Soit C une algèbre associative et commutative, avec unité. Pour toute application linéaire 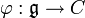 , il existe un unique morphisme d'algèbre
, il existe un unique morphisme d'algèbre  tel que
tel que  et
et  .
.
Les deux algèbres symétrique et enveloppante sont reliées par une application de symétrisation. En effet, on construit une application  comme suit :
comme suit :
 où
où  désigne le groupe des permutations de n éléments. En fait, l'application Sym est un isomorphisme linéaire de
désigne le groupe des permutations de n éléments. En fait, l'application Sym est un isomorphisme linéaire de  sur
sur  (la structure d'algèbre n'est pas conservée en général car
(la structure d'algèbre n'est pas conservée en général car  n'est pas commutative lorsque l'algèbre de Lie
n'est pas commutative lorsque l'algèbre de Lie  n'est pas abélienne).
n'est pas abélienne).
Structure d'anneau de l'algèbre enveloppante[modifier]
On suppode dans cette partie que le corps de base K est de caractéristique nulle.
Généralités[modifier]
L'algèbre enveloppante  est en particulier un anneau. L'étude de cette structure d'anneau est fondamentale en théorie des représentations. L'anneau U est sans diviseur de zéro (autrement dit le produit de deux éléments non nuls de U est également non nul). L'anneau U est noethérien : toute suite croissante d'idéaux est stationnaire. Cependant U n'est pasartinien : par exemple, l'idéal bilatère engendré par
est en particulier un anneau. L'étude de cette structure d'anneau est fondamentale en théorie des représentations. L'anneau U est sans diviseur de zéro (autrement dit le produit de deux éléments non nuls de U est également non nul). L'anneau U est noethérien : toute suite croissante d'idéaux est stationnaire. Cependant U n'est pasartinien : par exemple, l'idéal bilatère engendré par  contient l'idéal engendré par
contient l'idéal engendré par  , qui contient l'idéal engendré par
, qui contient l'idéal engendré par  , etc.
, etc.
Centre de l'algèbre enveloppante[modifier]
Le centre de l'algèbre enveloppante est  . En fait, comme
. En fait, comme  engendre
engendre  , on a aussi
, on a aussi  . Même lorsque l'algèbre de Lie
. Même lorsque l'algèbre de Lie  a un centre trivial, l'algèbre enveloppante peut avoir un centre non trivial (voire gros).
a un centre trivial, l'algèbre enveloppante peut avoir un centre non trivial (voire gros).
Exemple Soit  l'algèbre de Lie des marices complexes de taille
l'algèbre de Lie des marices complexes de taille 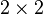 , de trace nulle. Une base de
, de trace nulle. Une base de  est donnée par les matrices suivantes :
est donnée par les matrices suivantes :

Le vecteur suivant est un élément du centre  :
:  . Plus précisement, on peut démontrer que
. Plus précisement, on peut démontrer que ![Z(U(mathfrak{g}))=mathbb{C}[Omega]](http://upload.wikimedia.org/math/b/c/e/bce008597faaac0cedbfe906b9608620.png) . Autrement dit, le vecteur Ω engendre l'algèbre
. Autrement dit, le vecteur Ω engendre l'algèbre  . Ceci est un cas particulier d'un résultat de Harish-Chandra et d'un résultat de Chevalley sur le centre des algèbres enveloppantes desalgèbres de Lie semi-simples.
. Ceci est un cas particulier d'un résultat de Harish-Chandra et d'un résultat de Chevalley sur le centre des algèbres enveloppantes desalgèbres de Lie semi-simples.
L'algèbre  joue un rôle fondamental en théorie des représentations. En effet, le lemme de Schur affirme que tout opérateur qui commute à une représentation irréductible d'une algèbre de Lie complexe est une homothétie. D'après ce qui précède, si (π,V) est une représentation irréductible de l'algèbre de Lie complexe
joue un rôle fondamental en théorie des représentations. En effet, le lemme de Schur affirme que tout opérateur qui commute à une représentation irréductible d'une algèbre de Lie complexe est une homothétie. D'après ce qui précède, si (π,V) est une représentation irréductible de l'algèbre de Lie complexe  , alors l'opérateur π(Z) associé à n'importe quel vecteur Z de
, alors l'opérateur π(Z) associé à n'importe quel vecteur Z de  commute à tous les π(X),
commute à tous les π(X),  . Donc π(Z) est une homothétie. Ceci est vrai pour tout Z dans le centre de l'algèbre enveloppante. On obtient ainsi un caractère du centre, c'est-à-dire un morphisme d'algèbre de
. Donc π(Z) est une homothétie. Ceci est vrai pour tout Z dans le centre de l'algèbre enveloppante. On obtient ainsi un caractère du centre, c'est-à-dire un morphisme d'algèbre de  dans
dans  , que l'on appelle le caractère infinitésimal de la représentation π. Ainsi l'étude des caractères du centre de l'algèbre enveloppante fournit des informations importantes pour l'étude des représentations irréductibles de
, que l'on appelle le caractère infinitésimal de la représentation π. Ainsi l'étude des caractères du centre de l'algèbre enveloppante fournit des informations importantes pour l'étude des représentations irréductibles de  .
.
Idéaux de l'algèbre enveloppante[modifier]
Toute représentation de  s'étend canoniquement en une représentation de
s'étend canoniquement en une représentation de  , c'est-à-dire un morphisme d'algèbre
, c'est-à-dire un morphisme d'algèbre  . Le noyau de π est un idéal de
. Le noyau de π est un idéal de  . D'autre part, si la représentation (π,V) est irréductible (ou même seulement cyclique), il existe un vecteur v de V tel que l'application
. D'autre part, si la représentation (π,V) est irréductible (ou même seulement cyclique), il existe un vecteur v de V tel que l'application  , soit surjective. La représentation V s'identifie alors avec le quotient de
, soit surjective. La représentation V s'identifie alors avec le quotient de  par le noyau de cette application. Ces deux faits montrent l'importance de comprendre les idéaux de
par le noyau de cette application. Ces deux faits montrent l'importance de comprendre les idéaux de  .
.
Références[modifier]
- N. Bourbaki, Groupes et algèbres de Lie
- Jacques Dixmier, Algèbres enveloppantes Éditions Jacques Gabay, Paris, 1996. ISBN 2-87647-014-4
- James E. Humphreys, Introduction to Lie Algebras and Representation Theory, Second printing, revised. Graduate Texts in Mathematics, 9. Springer-Verlag, New York, 1978. ISBN 0-387-90053-5
- Nathan Jacobson, Lie algebras, Republication of the 1962 original. Dover Publications, Inc., New York, 1979. ISBN 0-486-63832-4
- Anthony Knapp, Representation theory of semisimple groups: an overview based on examples, Princeton University Press, 2001. Reprint of the 1986 original. ISBN 0-691-09089-0
Voir aussi[modifier]
11:32 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Représentation d'algèbre de Lie
Représentation d'algèbre de Lie
|
|
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
Source : http://fr.wikipedia.org/wiki/Repr%C3%A9sentation_d'alg%C3...
Livres : Représentation d'algèbre de Lie
En mathématiques, une représentation d'une algèbre de Lie est une façon d'écrire cette algèbre comme une algèbre de matrices, ou plus généralement d'endomorphismes d'un espace vectoriel, avec le crochet de Lie donné par le commutateur.
Sommaire[masquer] |
Algèbres de Lie[modifier]
Soit K un corps commutatif de caractéristique différente de 2. Une algèbre de Lie  sur K est un espace vectoriel muni d'une apllication bilinéaire
sur K est un espace vectoriel muni d'une apllication bilinéaire ![(x,y) mapsto [x,y]](http://upload.wikimedia.org/math/7/5/e/75e87350f83275e11f126171780fd7ca.png) de
de 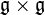 dans
dans  qui vérifie les propriétés suivantes :
qui vérifie les propriétés suivantes :
![forall x in mathfrak{g}, [x,x]=0](http://upload.wikimedia.org/math/f/3/2/f3223a3fe063412bb2f5033ba34850f5.png) ;
;![forall x,y,z in mathfrak{g}, [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0](http://upload.wikimedia.org/math/6/7/d/67d115952cf9c1c691b6053868febb0d.png)
Tout espace vectoriel V peut être muni d'une structure d'algèbre de Lie, en posant ![forall x,y in V, [x,y]=0](http://upload.wikimedia.org/math/8/6/9/8697bab9adc96fe793676eb0843e4edc.png) . Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne. Un autre exemple, fondamental pour ce qui suit, est le suivant. Soit V un espace vectoriel sur K. L'espace vectoriel End(V) des endomorphismes de V peut être muni d'une structure d'algèbre de Lie, en posant :
. Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne. Un autre exemple, fondamental pour ce qui suit, est le suivant. Soit V un espace vectoriel sur K. L'espace vectoriel End(V) des endomorphismes de V peut être muni d'une structure d'algèbre de Lie, en posant : ![[u,v]=ucirc v-vcirc u](http://upload.wikimedia.org/math/e/c/e/ecea3c23938418479a1064ef02f67bb2.png) . On note également
. On note également  l'algèbre de Lie ainsi obtenue. Lorsque V est de dimension finie n,
l'algèbre de Lie ainsi obtenue. Lorsque V est de dimension finie n,  s'identifie aux matrices de taille
s'identifie aux matrices de taille  à coefficient dans K. On la note alors
à coefficient dans K. On la note alors 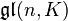 .
.
Une sous-algèbre de Lie de  est un sous-espace vectoriel
est un sous-espace vectoriel  de
de  stable par le crochet de Lie, i.e. tel que
stable par le crochet de Lie, i.e. tel que ![forall x,y in mathfrak{h}, [x,y] in mathfrak{h}](http://upload.wikimedia.org/math/f/4/3/f43e3feae72d881ec0c5811b4c166016.png) .
.
Exemples
- Si
 est une algèbre de Lie abélienne alors tout sous-espace vectoriel de
est une algèbre de Lie abélienne alors tout sous-espace vectoriel de  est automatiquement une sous-algèbre de Lie.
est automatiquement une sous-algèbre de Lie. - Le sous-espace vectoriel de
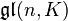 formé des matrices de trace nulle est une sous-algèbre de Lie de
formé des matrices de trace nulle est une sous-algèbre de Lie de 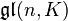 car tr(AB) = tr(BA) pour toutes matrices A et B. Cette sous-algèbre est notée
car tr(AB) = tr(BA) pour toutes matrices A et B. Cette sous-algèbre est notée  .
.
Un idéal d'une algèbre de Lie  est un sous-espace vectoriel
est un sous-espace vectoriel  de
de  tel que
tel que ![forall xin mathfrak{g}, yin mathfrak{h}, [x,y] in mathfrak{h}](http://upload.wikimedia.org/math/7/4/c/74c078f25ba2a4b38726a906c20aac88.png) . Tout idéal d'une algèbre de Lie est en particulier une sous-algèbre de Lie (mais la réciproque est fausse).
. Tout idéal d'une algèbre de Lie est en particulier une sous-algèbre de Lie (mais la réciproque est fausse).
Exemples
- Si
 est une algèbre de Lie abélienne alors tout sous-espace vectoriel de
est une algèbre de Lie abélienne alors tout sous-espace vectoriel de  est automatiquement un idéal.
est automatiquement un idéal. - La sous-algèbre de Lie
 de
de 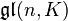 est un idéal.
est un idéal.
Un morphisme entre deux algèbres de Lie  et
et  est une application linéaire
est une application linéaire 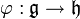 telle que
telle que ![forall x,y in mathfrak{g}, varphi([x,y])=[varphi(x),varphi(y)]](http://upload.wikimedia.org/math/3/b/e/3be01a86f4f2f1c4d2431f784e4347f4.png) . Le noyau d'un morphisme d'algèbres de Lie est alors un idéal de l'algèbre de Lie source et l'image une sous-algèbre de Lie de l'algèbre de Lie but. Un isomorphisme entre deux algèbres de Lie est morphisme d'algèbre de Lie qui est un isomorphisme d'espace vectoriel.
. Le noyau d'un morphisme d'algèbres de Lie est alors un idéal de l'algèbre de Lie source et l'image une sous-algèbre de Lie de l'algèbre de Lie but. Un isomorphisme entre deux algèbres de Lie est morphisme d'algèbre de Lie qui est un isomorphisme d'espace vectoriel.
Exemples
- Si
 est une sous-algèbre de Lie de
est une sous-algèbre de Lie de  alors l'inclusion de
alors l'inclusion de  dans
dans  est un morphisme d'algèbre de Lie, de noyau nul et d'image
est un morphisme d'algèbre de Lie, de noyau nul et d'image  .
. - Si
 est un idéal de
est un idéal de  alors il existe une unique structure d'algèbre de Lie sur l'espace vectoriel quotient
alors il existe une unique structure d'algèbre de Lie sur l'espace vectoriel quotient 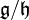 telle que la projection canonique
telle que la projection canonique  soit un morphisme d'algèbre de Lie. Le noyau de p est alors
soit un morphisme d'algèbre de Lie. Le noyau de p est alors  et son image
et son image 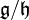 . L'algèbre de Lie
. L'algèbre de Lie 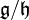 ainsi définie s'appelle l'algèbre de Lie quotient de
ainsi définie s'appelle l'algèbre de Lie quotient de  sur
sur  . Par exemple l'algèbre de Lie quotient
. Par exemple l'algèbre de Lie quotient  est isomorphe à l'algèbre de Lie abélienne K.
est isomorphe à l'algèbre de Lie abélienne K.
Représentations[modifier]
Définitions[modifier]
Une représentation de l'algèbre de Lie  dans un espace vectoriel V est la donnée d'un morphisme
dans un espace vectoriel V est la donnée d'un morphisme  . Autrement dit, π est une application linéaire qui vérifie également
. Autrement dit, π est une application linéaire qui vérifie également ![forall x,y in mathfrak{g}, pi([x,y])=pi(x)circpi(y)-pi(y)circpi(x)](http://upload.wikimedia.org/math/0/0/8/0080e112135e13fa673bfb501e2b8780.png) . On note (π,V) cette représentation ou simplement V lorsqu'il n'y a pas d'ambiguité possible sur π. On dit aussi que V est un
. On note (π,V) cette représentation ou simplement V lorsqu'il n'y a pas d'ambiguité possible sur π. On dit aussi que V est un  -module ou simplement un module. On note parfois
-module ou simplement un module. On note parfois  au lieu de π(x)(v) l'action de l'élément
au lieu de π(x)(v) l'action de l'élément  sur le vecteur
sur le vecteur  .
.
Une représentation (π,V) est dite fidèle si le morphisme π est injectif. Dans ce cas, l'algèbre de Lie  peut être vue comme une sous-algèbre de Lie de
peut être vue comme une sous-algèbre de Lie de  .
.
Une sous-représentation d'une représentation (π,V) de  est la donnée d'un sous-espace vectoriel W de V stable par l'action de
est la donnée d'un sous-espace vectoriel W de V stable par l'action de  , i.e. tel que
, i.e. tel que  . En particulier, pour qu'une droite vectorielle D engendrée par un vecteur v soit stable il faut et il suffit que v soit un vecteur propre commun à tous les endomorphismes π(x). Une représentation (π,V) est irréductible si elle n'admet aucune sous-représentation propre, c'est-à-dire autre que les sous-espaces {0} et V. En particulier toute représentation (π,V) de dimension 1 est irréductible, car dans ce cas les seuls sous-espaces vectoriels de V sont précisement {0} et V. Soit V' une sous-représentation de (π,V). La représentation quotientest la représentation
. En particulier, pour qu'une droite vectorielle D engendrée par un vecteur v soit stable il faut et il suffit que v soit un vecteur propre commun à tous les endomorphismes π(x). Une représentation (π,V) est irréductible si elle n'admet aucune sous-représentation propre, c'est-à-dire autre que les sous-espaces {0} et V. En particulier toute représentation (π,V) de dimension 1 est irréductible, car dans ce cas les seuls sous-espaces vectoriels de V sont précisement {0} et V. Soit V' une sous-représentation de (π,V). La représentation quotientest la représentation  de
de  dans l'espace quotient V / V' définie par
dans l'espace quotient V / V' définie par  .
.
Un morphisme entre deux représentations (π,V) et (π',V') d'une même algèbre de Lie  est la donnée d'une application linéaire
est la donnée d'une application linéaire  qui commute à l'action de
qui commute à l'action de  , c'est-à-dire telle que
, c'est-à-dire telle que  . Lorque
. Lorque  est un isomorphisme d'espace vectoriel, on dit que les deux représentations sont isomorphes. L'ensemble de tous les morphismes entre les représentations (π,V) et (π',V') forme un espace vectoriel, noté
est un isomorphisme d'espace vectoriel, on dit que les deux représentations sont isomorphes. L'ensemble de tous les morphismes entre les représentations (π,V) et (π',V') forme un espace vectoriel, noté  .
.
Le lemme de Schur est un résultat important pour la compréhension de cet espace  . En voici l'énoncé :
. En voici l'énoncé :
Lemme de Schur —
- Soient V et V' deux représentations irréductibles d'une algèbre de Lie
 . Soit
. Soit  . Alors
. Alors  est soit l'application nulle soit un isomorphisme. En particulier, si V et V' ne sont pas isomorphes,
est soit l'application nulle soit un isomorphisme. En particulier, si V et V' ne sont pas isomorphes,  .
. - Supposons ici que le corps K soit algébriquement clos. Soit V une représentation irréductible de dimension finie de
 . Alors tout morphisme
. Alors tout morphisme  est un multiple de l'identité. En d'autres termes,
est un multiple de l'identité. En d'autres termes,  .
.
Remarques
- Le premier point du lemme de Schur résulte du fait que
 est une sous-représentation de V et
est une sous-représentation de V et  une sous-représentation de V'.
une sous-représentation de V'. - Le deuxième point du lemme de Schur résulte du fait que tout endomorphisme d'un espace vectoriel de dimension finie admet au moins une valeur propre λ sur un corps algébriquement clos. Par conséquent
 est un morphisme de V dans V qui n'est pas un isomorphisme. D'après le premier point, il s'agit donc de l'application nulle, i.e.
est un morphisme de V dans V qui n'est pas un isomorphisme. D'après le premier point, il s'agit donc de l'application nulle, i.e.  . Ce résultat est encore valable en dimension infinie mais nécessite la puissance du théorème spectral.
. Ce résultat est encore valable en dimension infinie mais nécessite la puissance du théorème spectral. - Le deuxième point du lemme de Schur est faux pour un corps non algébriquement clos. Supposons par exemple
 . Considérons la représentation (π,V) donnée par la formule
. Considérons la représentation (π,V) donnée par la formule 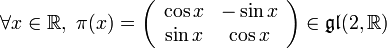 . On vérifie que (π,V) est une représentation irréductible de l'algèbre de Lie abélienne
. On vérifie que (π,V) est une représentation irréductible de l'algèbre de Lie abélienne  . Considérons y = 45o et posons
. Considérons y = 45o et posons  . Comme l'algèbre de Lie
. Comme l'algèbre de Lie  est abélienne,
est abélienne,  est un morphisme de V dans V. On peut d'ailleurs vérifier que
est un morphisme de V dans V. On peut d'ailleurs vérifier que  est bien un isomorphisme. Cependant
est bien un isomorphisme. Cependant  n'est pas un multiple de l'identité. Remarquons à ce propos que
n'est pas un multiple de l'identité. Remarquons à ce propos que  n'a pas de valeurs propres réelles (ce qui explique pourquoi la preuve du deuxième point du lemme n'est pas valable dans ce cas).
n'a pas de valeurs propres réelles (ce qui explique pourquoi la preuve du deuxième point du lemme n'est pas valable dans ce cas).
Exemples[modifier]
- Une représentation d'une algèbre de Lie abélienne
 est une application linéaire à valeurs dans un sous-espace commutatif de l'espace des endomorphismes d'un espace vectoriel V. Par exemple, si V est de dimension fini, on peut représenter
est une application linéaire à valeurs dans un sous-espace commutatif de l'espace des endomorphismes d'un espace vectoriel V. Par exemple, si V est de dimension fini, on peut représenter  par des matrices diagonales (qui commutent entre elles).
par des matrices diagonales (qui commutent entre elles). - La représentation triviale de
 dans un espace vectoriel V est la représentation π définie par
dans un espace vectoriel V est la représentation π définie par  .
. - Si
 , on définit la représentation naturelle de
, on définit la représentation naturelle de  comme la représentation
comme la représentation  définie par
définie par 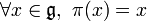 . Plus généralement la représentation naturelle d'une sous-algèbre de Lie
. Plus généralement la représentation naturelle d'une sous-algèbre de Lie  de
de 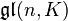 est définie comme l'inclusion de
est définie comme l'inclusion de  dans
dans 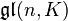 . Elle est donc à valeurs dans Kn.
. Elle est donc à valeurs dans Kn. - La représentation adjointe d'une algèbre de Lie
 est la représentation
est la représentation  définie par
définie par ![forall x in mathfrak{g}, ad(x): y in mathfrak{g} mapsto [x,y] in mathfrak{g}](http://upload.wikimedia.org/math/8/8/f/88ff3fa6e010a55f36d8b87327a5fd4f.png) .
. - Soit
 l'algèbre de Lie abélienne de dimension 1, définie sur
l'algèbre de Lie abélienne de dimension 1, définie sur  . Considérons l'espace
. Considérons l'espace  . On définit une représentation de
. On définit une représentation de  dans V par la formule
dans V par la formule  , où
, où  .
.
Constructions de représentations[modifier]
- Somme directe : soient (π,V) et (π',V') deux représentations de
 . On définit la représentation somme directe
. On définit la représentation somme directe  dans l'espace vectoriel
dans l'espace vectoriel 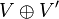 par la formule
par la formule  . Dans ce cas,
. Dans ce cas,  et
et  sont des sous-représentations de
sont des sous-représentations de 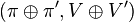 .
. - Produit tensoriel : soient (π,V) et (π',V') deux représentations de
 . On définit la représentation produit tensoriel
. On définit la représentation produit tensoriel  dans l'espace vectoriel
dans l'espace vectoriel 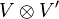 par la formule
par la formule 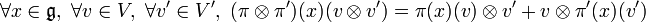 .
. - Contragrédiente : soit (π,V) une représentation de
 . On définit la représentation contragrédiente π * dans l'espace vectoriel dual V * par la formule
. On définit la représentation contragrédiente π * dans l'espace vectoriel dual V * par la formule  .
. - Espace des morphismes : soient (π,V) et (π',V') deux représentations de
 . Nous avons vu comment définir l'espace vectoriel
. Nous avons vu comment définir l'espace vectoriel  des morphimes de V dans V'. On définit une représentation encore notée π de
des morphimes de V dans V'. On définit une représentation encore notée π de  sur cet espace par la formule
sur cet espace par la formule  .
. - Restriction à une sous-algèbre de Lie : soit (π,V) une représentation de
 . Soit
. Soit  une sous-algèbre de Lie de
une sous-algèbre de Lie de  . Alors
. Alors  est une représentation de
est une représentation de  , appelée la restriction de (π,V) à
, appelée la restriction de (π,V) à  . On la note parfois
. On la note parfois 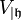 par abus de notations.
par abus de notations.
Une représentation de  est indécomposable si elle n'est pas isomorphe à la somme directe de deux sous-représentations propres. En particulier, toute représentation irréductible est indécomposable, mais la réciproque est fausse. Une représentation est semi-simple (ou complétement réductible) si elle est isomorphe à une somme directe de sous-représentations irréductibles (éventuellement en nombre infini). Une représentation indécomposable et semi-simple est nécessairement irréductible.
est indécomposable si elle n'est pas isomorphe à la somme directe de deux sous-représentations propres. En particulier, toute représentation irréductible est indécomposable, mais la réciproque est fausse. Une représentation est semi-simple (ou complétement réductible) si elle est isomorphe à une somme directe de sous-représentations irréductibles (éventuellement en nombre infini). Une représentation indécomposable et semi-simple est nécessairement irréductible.
Exemples:
- Soit
 l'algèbre de Lie abélienne de dimension 1 sur le corps
l'algèbre de Lie abélienne de dimension 1 sur le corps  . On définit une représentation π de
. On définit une représentation π de  dans
dans  par la formule
par la formule  . Cette représentation n'est pas irréductible. Par exemple la droite D1 engendrée par le vecteur
. Cette représentation n'est pas irréductible. Par exemple la droite D1 engendrée par le vecteur 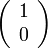 est stable, tout comme la droiteD2 engendrée par le vecteur
est stable, tout comme la droiteD2 engendrée par le vecteur  . Il s'agit donc de deux sous-représentations de π, irréductibles car de dimension 1. Or on a
. Il s'agit donc de deux sous-représentations de π, irréductibles car de dimension 1. Or on a  . Donc la représentation π est semisimple.
. Donc la représentation π est semisimple. - Avec les notations de l'exemple précédent, on peut aussi considérer la représentation π' dans
 définie par la formule
définie par la formule  . A nouveau la droiteD1 est un sous-espace stable. Donc la représentation π' n'est pas irréductible. Plus généralement, on peut vérifier que D1 est la seule droite stable et donc la seule sous-représentation de π'. Ainsi π' est indécomposable.
. A nouveau la droiteD1 est un sous-espace stable. Donc la représentation π' n'est pas irréductible. Plus généralement, on peut vérifier que D1 est la seule droite stable et donc la seule sous-représentation de π'. Ainsi π' est indécomposable. - Gardons toujours les mêmes notations. On définit la représentation π'' de
 dans
dans  par la formule
par la formule  . On peut vérifier qu'il n'y a pas de droites stables par la représentation π''. En d'autres termes, π'' est irréductible.
. On peut vérifier qu'il n'y a pas de droites stables par la représentation π''. En d'autres termes, π'' est irréductible.
Ces trois exemples traduisent le fait qu'une matrice réelle peut être soit diagonalisable, soit trigonalisable mais pas diagonalisble, ou ne possède pas de valeurs propres réelles. On voit ainsi que la notion de représentation d'une algèbre de Lie généralise la notion classique de réduction des endomorphismes.
Lien avec les représentations de l'algèbre enveloppante[modifier]
L'algèbre enveloppante d'une algèbre de Lie[modifier]
Soit A une algèbre associative avec unité. Alors il existe sur A une structure d'algèbre de Lie pour laquelle le crochet de Lie est donné par la formule ![forall a,b in A, [a,b]=ab-ba](http://upload.wikimedia.org/math/3/6/e/36ed7366f61db225948e1e425e1a1074.png) . On note parfois AL cette algèbre de Lie. Ainsi toute algèbre associative fournit une algèbre de Lie. Nous avons vu que
. On note parfois AL cette algèbre de Lie. Ainsi toute algèbre associative fournit une algèbre de Lie. Nous avons vu que  est un exemple de cette construction. Peut-on donner une réciproque à ce résultat ? Peut-on construire une algèbre associative à partir d'une algèbre de Lie. Cette idée conduit à la notion d'algèbre enveloppante d'une algèbre de Lie.
est un exemple de cette construction. Peut-on donner une réciproque à ce résultat ? Peut-on construire une algèbre associative à partir d'une algèbre de Lie. Cette idée conduit à la notion d'algèbre enveloppante d'une algèbre de Lie.
Soit  une algèbre de Lie sur K. Soit
une algèbre de Lie sur K. Soit  l'algèbre tensorielle de
l'algèbre tensorielle de  . Soit J l'idéal bilatère de
. Soit J l'idéal bilatère de  engendré par les tenseurs
engendré par les tenseurs ![x otimes y - y otimes x - [x,y] in T(mathfrak{g})](http://upload.wikimedia.org/math/2/5/7/25730dde99f61e92ddf418741d424129.png) pour tous x ety de
pour tous x ety de  . L'algèbre enveloppante de
. L'algèbre enveloppante de  est l'algèbre associative unitaire définie comme le quotient
est l'algèbre associative unitaire définie comme le quotient  . On la note
. On la note  . La composition
. La composition 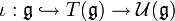 s'appelle l'application canonique de
s'appelle l'application canonique de  dans son algèbre enveloppante. En tant qu'algèbre,
dans son algèbre enveloppante. En tant qu'algèbre,  est engendrée par 1 et l'image
est engendrée par 1 et l'image  . De plus, ι est un morphisme d'algèbre de Lie de
. De plus, ι est un morphisme d'algèbre de Lie de  dans
dans  . L'algèbre enveloppante d'une algèbre de Lie satisfait la propriété universelle suivante :
. L'algèbre enveloppante d'une algèbre de Lie satisfait la propriété universelle suivante :
Propriété universelle de l'algèbre enveloppante — Soit A une algèbre associative avec une unité. Soit  un morphisme d'algèbres de Lie de
un morphisme d'algèbres de Lie de  dans AL. Alors il existe un unique morphisme d'algèbres associatives Φ de
dans AL. Alors il existe un unique morphisme d'algèbres associatives Φ de  dans A tel que Φ(1) = 1 et
dans A tel que Φ(1) = 1 et 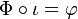 .
.
Exemple:
- Si
 est une algèbre de Lie abélienne, alors son algèbre enveloppante s'identifie à son algèbre symétrique
est une algèbre de Lie abélienne, alors son algèbre enveloppante s'identifie à son algèbre symétrique  , qui elle même s'identifie (après choix d'une base) à une algèbre de polyômes. En particulier,
, qui elle même s'identifie (après choix d'une base) à une algèbre de polyômes. En particulier,  est isomorphe à l'algèbre des polynômes à une indeterminée K[X].
est isomorphe à l'algèbre des polynômes à une indeterminée K[X].
Représentations d'une algèbre de Lie vs Représentations de son algèbre enveloppante[modifier]
Soit (π,V) une représentation de  . Comme
. Comme  est une algèbre associative avec unité, la propiété universelle de
est une algèbre associative avec unité, la propiété universelle de  implique qu'il existe un unique morphisme d'algèbres
implique qu'il existe un unique morphisme d'algèbres  telle que
telle que 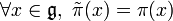 . Cette opération permet donc de passer d'une représentation d'une algèbre de Lie à un morphisme d'algèbres associatives. Réciproquement, tout morphisme d'algèbres associatives
. Cette opération permet donc de passer d'une représentation d'une algèbre de Lie à un morphisme d'algèbres associatives. Réciproquement, tout morphisme d'algèbres associatives  donne par restriction à
donne par restriction à  un morphisme d'algèbres de Lie, c'est-à-dire à une représentation de
un morphisme d'algèbres de Lie, c'est-à-dire à une représentation de  . Ce principe s'interprète comme une équivalence de catégories entre la catégorie des représentations d'une algèbre de Lie donnée et la catégorie des représentations de son algèbre enveloppante.
. Ce principe s'interprète comme une équivalence de catégories entre la catégorie des représentations d'une algèbre de Lie donnée et la catégorie des représentations de son algèbre enveloppante.
Ce nouveau point de vue est important car il permet de considérer de nouveaux objets fondamentaux. Le premier d'entre eux est l'annulateur d'une représentation. Soit (π,V) une représentation de  . Notons encore par la lettre π la représentation de
. Notons encore par la lettre π la représentation de  qu'il s'en déduit. Alors l'annulteur de V est l'ensemble
qu'il s'en déduit. Alors l'annulteur de V est l'ensemble  . C'est un idéal bilatère de
. C'est un idéal bilatère de  car π est un morphisme d'algèbre. Tout idéal qui est l'annulateur d'une représentation irréductible de
car π est un morphisme d'algèbre. Tout idéal qui est l'annulateur d'une représentation irréductible de  s'appelle un idéal primitif.
s'appelle un idéal primitif.
Soit (π,V) une représentation de  . Notons encore par la lettre π la représentation de
. Notons encore par la lettre π la représentation de  qu'il s'en déduit. Pour tout v dans V, l'ensemble
qu'il s'en déduit. Pour tout v dans V, l'ensemble  définit une sous-représentation non nulle de V. Lorsque V est irréductible, on a donc
définit une sous-représentation non nulle de V. Lorsque V est irréductible, on a donc  . Plus généralement, une représentation V est dite cyclique s'il existe
. Plus généralement, une représentation V est dite cyclique s'il existe  tel que
tel que  . Le vecteur v est appelé un vecteur cyclique. Une représentation V est irréductible si et seulement si tout vecteur non nul de V est cyclique. Une représentation Vest dite de type fini s'il existe un nombre fini de vecteurs
. Le vecteur v est appelé un vecteur cyclique. Une représentation V est irréductible si et seulement si tout vecteur non nul de V est cyclique. Une représentation Vest dite de type fini s'il existe un nombre fini de vecteurs  de V tels que
de V tels que  . Une représentation irréductible est donc de type finie. Soit V une représentation cyclique et soit v un vecteur cyclique. On définit alors une application
. Une représentation irréductible est donc de type finie. Soit V une représentation cyclique et soit v un vecteur cyclique. On définit alors une application  par la formule
par la formule  . Le noyau de
. Le noyau de  est l'annulateur de v, noté Ann(v). Il s'agit d'un idéal à gauche de
est l'annulateur de v, noté Ann(v). Il s'agit d'un idéal à gauche de  . Comme V est cyclique, l'image de
. Comme V est cyclique, l'image de  est égale à tout V. On en déduit donc que
est égale à tout V. On en déduit donc que  . Ainsi toute représentation cyclique (et en particulier toute représentation irréductible) apparaît comme un quotient de l'algèbre enveloppante de
. Ainsi toute représentation cyclique (et en particulier toute représentation irréductible) apparaît comme un quotient de l'algèbre enveloppante de  . De plus, lorsque V est irréductible l'idéal Ann(v)est maximal. Ainsi la classification des représentations irréductibles de
. De plus, lorsque V est irréductible l'idéal Ann(v)est maximal. Ainsi la classification des représentations irréductibles de  est équivalente à la classification des idéaux à gauche maximaux de son algèbre enveloppante.
est équivalente à la classification des idéaux à gauche maximaux de son algèbre enveloppante.
Exemple Considérons l'algèbre de Lie commutative  . Identifions son algèbre enveloppante avec l'anneau de polynômes
. Identifions son algèbre enveloppante avec l'anneau de polynômes ![mathbb{C}[X]](http://upload.wikimedia.org/math/6/d/d/6ddcc166f3aa1cea808fa816f33ec673.png) . Cet anneau est principal et donc ses idéaux sont engendrés par un unique polynôme. De plus, si un polynôme P(X) peut se décomposer sous la forme P(X) = Q(X)(X − a), alors l'idéal (P) engendré par P est contenu dans l'idéal (X −a) engendré par X − a. Le théorème de d'Alembert-Gauss implique alors que les idéaux maximaux de
. Cet anneau est principal et donc ses idéaux sont engendrés par un unique polynôme. De plus, si un polynôme P(X) peut se décomposer sous la forme P(X) = Q(X)(X − a), alors l'idéal (P) engendré par P est contenu dans l'idéal (X −a) engendré par X − a. Le théorème de d'Alembert-Gauss implique alors que les idéaux maximaux de ![mathbb{C}[X]](http://upload.wikimedia.org/math/6/d/d/6ddcc166f3aa1cea808fa816f33ec673.png) sont les idéaux de la forme (X − a), pour a décrivant tout
sont les idéaux de la forme (X − a), pour a décrivant tout  . Le quotient
. Le quotient ![mathbb{C}[X]/(X-a)](http://upload.wikimedia.org/math/1/5/5/155462b2e946c4c988602a2a27055577.png) correspondant est alors isomorphe à
correspondant est alors isomorphe à  et l'action de
et l'action de ![mathbb{C}[X]](http://upload.wikimedia.org/math/6/d/d/6ddcc166f3aa1cea808fa816f33ec673.png) est donnée par
est donnée par  et
et 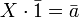 . Regardons à présent le quotient
. Regardons à présent le quotient ![mathbb{C}[X]/(P)](http://upload.wikimedia.org/math/7/6/1/761213716fa77688fbb80916637c12d6.png) où P(X) = (X − a)(X − b). Si
où P(X) = (X − a)(X − b). Si 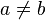 , le quotient est une représentation semi-simple, somme directe des deux représentations irréductibles
, le quotient est une représentation semi-simple, somme directe des deux représentations irréductibles ![mathbb{C}[X]/(X-a)](http://upload.wikimedia.org/math/1/5/5/155462b2e946c4c988602a2a27055577.png) et
et ![mathbb{C}[X]/(X-b)](http://upload.wikimedia.org/math/6/0/2/602a28d49033d8f2b7f339929ae9489a.png) . La situation est fondamentalement différente lorsque a = b. Dans ce cas, le quotient est un espace vectoriel de dimension 2 sur lequel l'opérateur donné par la multiplication par X − a est nilpotent d'indice 2. En termes de représentation de l'algèbre de Lie
. La situation est fondamentalement différente lorsque a = b. Dans ce cas, le quotient est un espace vectoriel de dimension 2 sur lequel l'opérateur donné par la multiplication par X − a est nilpotent d'indice 2. En termes de représentation de l'algèbre de Lie  , ce quotient correspond à la représentation donnée par la formule
, ce quotient correspond à la représentation donnée par la formule  , qui est indécomposable mais pas irréductible.
, qui est indécomposable mais pas irréductible.
Induction[modifier]
Soit  une algèbre de Lie. Soit
une algèbre de Lie. Soit  une sous-algèbre de Lie de
une sous-algèbre de Lie de  . Soit (π,V) une représentation de
. Soit (π,V) une représentation de  . Nous avons vu que nous pouvons obtenir une représentation de
. Nous avons vu que nous pouvons obtenir une représentation de  par restriction. La notion d'algèbre enveloppante va donner un moyen simple de considérer le problème réciproque. Soit donc (π',V') une représentation de
par restriction. La notion d'algèbre enveloppante va donner un moyen simple de considérer le problème réciproque. Soit donc (π',V') une représentation de  , que l'on voit comme une représentation de son algèbre enveloppante
, que l'on voit comme une représentation de son algèbre enveloppante 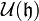 . Une conséquence du théorème de Poincaré-Birkhoff-Witt est que
. Une conséquence du théorème de Poincaré-Birkhoff-Witt est que 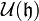 apparaît comme une sous-algèbre de
apparaît comme une sous-algèbre de  . D'autre part,
. D'autre part,  fournit une représentation de
fournit une représentation de  en faisant agir
en faisant agir  par multiplication à gauche sur les tenseurs. On construit alors la représentation
par multiplication à gauche sur les tenseurs. On construit alors la représentation  . On l'appelle la représentation induite de
. On l'appelle la représentation induite de  à
à  par (π',V').
par (π',V').
Lien avec les représentations des groupes de Lie[modifier]
Dans cette partie, le corps K est  (ou
(ou  ). Un groupe de Lie G est une variété différentielle réelle (ou complexe) munie de deux applications
). Un groupe de Lie G est une variété différentielle réelle (ou complexe) munie de deux applications  et
et  lisses (ou holomorphes) telles que
lisses (ou holomorphes) telles que 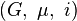 soit un groupe. Le corps K lui-même est un groupe de Lie commutatif. Le groupe GL(n,K) des matrices inversibles de taille n est un autre exemple de groupes de Lie. Un morphisme de groupes de Lie est un morphisme de groupes différentiable (ou holomorphe). Une représentation de dimension finie du groupe de LieG est un morphsime de G dans GL(n,K).
soit un groupe. Le corps K lui-même est un groupe de Lie commutatif. Le groupe GL(n,K) des matrices inversibles de taille n est un autre exemple de groupes de Lie. Un morphisme de groupes de Lie est un morphisme de groupes différentiable (ou holomorphe). Une représentation de dimension finie du groupe de LieG est un morphsime de G dans GL(n,K).
Les groupes de Lie sont reliés aux algèbres de Lie. En effet, l'espace tangent à un groupe de Lie G en l'identité est une algèbre de Lie de dimension finie, appelée algèbre de Lie du groupe G et notée  . Par exemple, l'algèbre de Lie de K est K lui-même ; l'algèbre de Lie de GL(n,K) est
. Par exemple, l'algèbre de Lie de K est K lui-même ; l'algèbre de Lie de GL(n,K) est 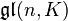 . Comme l'algèbre de Lie du groupe de Lie G est l'espace tangent en l'identité, elle ne dépend en fait que de la composante connexe de l'identité. Ainsi par exemple, le groupe
. Comme l'algèbre de Lie du groupe de Lie G est l'espace tangent en l'identité, elle ne dépend en fait que de la composante connexe de l'identité. Ainsi par exemple, le groupe  des matrices réelles de déterminant strictement positif a la même algèbre de Lie que
des matrices réelles de déterminant strictement positif a la même algèbre de Lie que  . Par contre, à isomorphisme près, il existe un unique groupe de Lie connexe et simplement connexe ayant une algèbre de Lie (de dimension finie) donnée.
. Par contre, à isomorphisme près, il existe un unique groupe de Lie connexe et simplement connexe ayant une algèbre de Lie (de dimension finie) donnée.
Comme tout morphisme 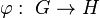 entre groupes de Lie est par hypothèse différentiable, il induit une application entre les algèbres de Lie sous-jacentes
entre groupes de Lie est par hypothèse différentiable, il induit une application entre les algèbres de Lie sous-jacentes 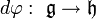 . Cette application
. Cette application  est en fait un morphisme d'algèbres de Lie. En particulier, pour H = GL(n,K), toute représentation d'un groupe de Lie G donne naissance à une représentation de dimension finie de son algèbre de Lie
est en fait un morphisme d'algèbres de Lie. En particulier, pour H = GL(n,K), toute représentation d'un groupe de Lie G donne naissance à une représentation de dimension finie de son algèbre de Lie  . Réciproquement, toute représentation de dimension finie d'une algèbre de Lie
. Réciproquement, toute représentation de dimension finie d'une algèbre de Lie  provient d'une représentation de l'unique groupe de Lie simplement connexe ayant pour algèbre de Lie
provient d'une représentation de l'unique groupe de Lie simplement connexe ayant pour algèbre de Lie  .
.
Remarque Il existe des notions plus fortes de représentations de groupes de Lie permettant d'étendre la théorie à la dimension infinie, tout en conservant un analogue de ce dernier résultat. Il s'agit par exemple de représentations admissibles et de la notion de 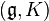 -modules.
-modules.
Catégorie de modules[modifier]
Soit  une algèbre de Lie. L'ensemble de tous les
une algèbre de Lie. L'ensemble de tous les  -modules (ou de manière équivalente de toutes les représentations de
-modules (ou de manière équivalente de toutes les représentations de  ) forme une catégorie, notée
) forme une catégorie, notée  . Cette catégorie estabélienne. En particulier, on peut considérer des suites exactes de modules. Une suite exacte dans
. Cette catégorie estabélienne. En particulier, on peut considérer des suites exactes de modules. Une suite exacte dans  est la donnée de trois modules M, N, P et de deux morphismes
est la donnée de trois modules M, N, P et de deux morphismes 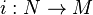 injectif et
injectif et  surjectif. On note
surjectif. On note 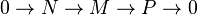 une telle suite. Un module P est projectif si toute suite exacte
une telle suite. Un module P est projectif si toute suite exacte 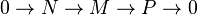 est scindée, c'est-à-dire s'il existe un morphisme
est scindée, c'est-à-dire s'il existe un morphisme  tel que
tel que  . Une définition équivalente est la suivante : le module P est projectif si pour tout morphisme surjectif
. Une définition équivalente est la suivante : le module P est projectif si pour tout morphisme surjectif 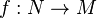 et tout morphisme
et tout morphisme  il existe un unique morphisme
il existe un unique morphisme  tel que
tel que  . De manière duale, un module I est injectif si toute suite exacte
. De manière duale, un module I est injectif si toute suite exacte  est scindée. Une définition équivalente est la suivante : le module I est injectif si pour tout morphisme injectif
est scindée. Une définition équivalente est la suivante : le module I est injectif si pour tout morphisme injectif 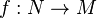 et tout morphisme
et tout morphisme  il existe un unique morphisme
il existe un unique morphisme  tel que
tel que 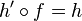 .
.
Comme tout module est aussi un module sur l'anneau  , on peut reprendre les notions générales de modules sur un anneau. Un module M est de longueur fini s'il existe une suite finie de sous-modules
, on peut reprendre les notions générales de modules sur un anneau. Un module M est de longueur fini s'il existe une suite finie de sous-modules  telle que les quotients successifs Mi + 1 / Mi soient des modules irréductibles. Une telle suite s'appelle unesuite de Jordan-Hölder de M. Pour un module de longueur finie, la classe d'isomorphismes des quotients ne dépend que du module M. En particulier, l'entier n ne dépend que du module M et est appelé la longueur du module M. Par exemple, tout module irréductible est de longueur 1, toute somme directe de deux modules irréductibles est de longueur 2.
telle que les quotients successifs Mi + 1 / Mi soient des modules irréductibles. Une telle suite s'appelle unesuite de Jordan-Hölder de M. Pour un module de longueur finie, la classe d'isomorphismes des quotients ne dépend que du module M. En particulier, l'entier n ne dépend que du module M et est appelé la longueur du module M. Par exemple, tout module irréductible est de longueur 1, toute somme directe de deux modules irréductibles est de longueur 2.
Un module M est artinien si toute suite décroissante de sous-modules  est stationnaire. Par exemple, tout module de dimension finie est artinien. Un module M est noethérien si toute suite croissante de sous-modules
est stationnaire. Par exemple, tout module de dimension finie est artinien. Un module M est noethérien si toute suite croissante de sous-modules  est stationnaire. Comme l'algèbre enveloppante
est stationnaire. Comme l'algèbre enveloppante  est un anneau noethérien, un module M est noethérien si et seulement s'il est de type fini. Un module est de longueur fini si et seulement s'il est noethérien et artinien.
est un anneau noethérien, un module M est noethérien si et seulement s'il est de type fini. Un module est de longueur fini si et seulement s'il est noethérien et artinien.
Exemple: Un module de dimension finie est toujours noethérien et artinien, et est donc toujours de longueur fini. Ceci n'est plus valable en dimension infinie, même pour une algèbre de Lie abélienne. Supposons par exemple que  . Considérons le module
. Considérons le module ![L=mathbb{C}[X]](http://upload.wikimedia.org/math/6/0/2/602bd4aa8a8bd385bddbcbb0c0ab6e71.png) où l'action de
où l'action de  est donnée par la multiplication par le scalaire z. L'action de
est donnée par la multiplication par le scalaire z. L'action de ![mathcal{U}(mathbb{C})=mathbb{C}[X]](http://upload.wikimedia.org/math/a/5/7/a57221d1077e5e9e886a8d7f281ef765.png) est donc donnée par la multiplication à gauche. Ainsi tout idéal à gauche est un sous-module de L. Notons (P) l'idéal engendré par le polynôme P. Soit
est donc donnée par la multiplication à gauche. Ainsi tout idéal à gauche est un sous-module de L. Notons (P) l'idéal engendré par le polynôme P. Soit  une suite infinie de nombre complexes. On a alors la suite décroissante suivante :
une suite infinie de nombre complexes. On a alors la suite décroissante suivante :  . C'est une suite non stationnaire de sous-modules, dont les quotients successifs sont des modules irréductibles (car de dimension 1). Ainsi L n'est pas artinien et n'est pas de longueur finie. Notons que L est noethérien car c'est un module de type fini (en fait cyclique, engendré par le polynôme constant 1).
. C'est une suite non stationnaire de sous-modules, dont les quotients successifs sont des modules irréductibles (car de dimension 1). Ainsi L n'est pas artinien et n'est pas de longueur finie. Notons que L est noethérien car c'est un module de type fini (en fait cyclique, engendré par le polynôme constant 1).
Une sous-catégorie pleine de  est artinienne (respectivement noethérienne) si tous ses objets sont des modules artiniens (respectivement noethériens). Dans une sous-catégorie pleine de
est artinienne (respectivement noethérienne) si tous ses objets sont des modules artiniens (respectivement noethériens). Dans une sous-catégorie pleine de  artinienne et noethérienne tout objet est de longueur finie. Une sous-catégorie pleine de
artinienne et noethérienne tout objet est de longueur finie. Une sous-catégorie pleine de  a assez de projectifs si pour tout objet M de la sous-catégorie il existe un module projectif P dans la sous-catégorie et un morphisme surjectif de P sur M. Elle a assez d'injectifs si pour tout objet M de la sous-catégorie il existe unmodule injectif I dans la sous-catégorie et un morphisme injectif de M dans I.
a assez de projectifs si pour tout objet M de la sous-catégorie il existe un module projectif P dans la sous-catégorie et un morphisme surjectif de P sur M. Elle a assez d'injectifs si pour tout objet M de la sous-catégorie il existe unmodule injectif I dans la sous-catégorie et un morphisme injectif de M dans I.
Références[modifier]
- N. Bourbaki, Éléments de mathématique, Groupes et algèbres de Lie, Chapitre 1, Springer, 2007 (ISBN 978-3-540-35335-5)
- Jacques Dixmier, Algèbres enveloppantes, Jacques Gabay, 1996 (ISBN 2-87647-014-4)
- Brian Hall, Lie Groups, Lie Algebras, and Representations, Springer, 2003 (ISBN 978-0-387-40122-5)
- James Humphreys, Introduction to Lie Algebras and Representation Theory, Second printing, revised. Graduate Texts in Mathematics, 9. Springer, 1978 (ISBN 0-387-90053-5)
- Nathan Jacobson, Lie algebras, Republication of the 1962 original, Dover, 1979 (ISBN 0-486-63832-4)
Voir aussi[modifier]
11:30 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Groupe de Lie
Groupe de Lie
|
|
Cet article ne cite pas suffisamment ses sources (septembre 2009).
Si vous connaissez le thème traité, merci d'indiquer les passages à sourcer avec {{Référence souhaitée}} ou, mieux, incluez les références utiles en les liant aux notes de bas de page. (Modifier l'article)
|
Source : http://fr.wikipedia.org/wiki/Groupe_de_Lie
En mathématiques, un groupe de Lie est un groupe qui est continu, c'est-à-dire que chaque élément du groupe peut être approché d'aussi près que l'on veut par une suite d'autres éléments du groupe. Un groupe de Lie est en fait un peu plus qu'un groupe continu : il est en plus lisse[pas clair], et on peut faire du calcul différentiel dessus. Ces groupes sont nommés ainsi en l'honneur du mathématicien norvégien Sophus Lie, qui les introduisit afin d'étudier certaines propriétés des équations différentielles.
Sommaire[masquer] |
Histoire[modifier]
Sophus Lie lui-même considérait que la théorie des groupes continus était née lors de l'hiver 1873-1874, mais le biographe Hawkins suggère que la théorie est née des recherches effectuées par Lie durant les quatre années précédentes (de 1869 à 1873).
Une partie des idées initiales de Lie furent développées en collaboration avec Felix Klein, qu'il rencontrait quotidiennement durant les jours d'octobre des années 1869 à 1872, à Berlin d'abord, puis Paris, Gőttingen et Erlangen.
Les résultats de Lie furent publiés dans des journaux norvégiens lors de la décennie 1870, et son œuvre gagna rapidement le reste de l'Europe. En 1884, un jeune mathématicien allemand, Friedrich Engel travailla avec Lie à la création d'un exposé systématique de la théorie des groupes continus, lequel fut publié en trois volumes sous le titre Theorie der Transformationsgruppen, en 1888, 1890 et 1893.
Un développement important de la théorie fut ensuite réalisé par Wilhelm Killing. La généralisation par Elie Cartan, mena à la classification des algèbres de Lie semi-simples et aux travaux d'Hermann Weyl sur les représentations des groupes de Lie compacts.
La théorie des groupes de Lie fut exposée méthodiquement dans le langage mathématique moderne par Claude Chevalley.
Définitions[modifier]
Une structure algébrique G est un groupe de Lie réel ou complexe lorsque :
- G est une variété différentiable réelle ou complexe ;
- G, munie de deux fonctions G×G
 G (multiplication) et G
G (multiplication) et G G (inversion), est un groupe (c'est-à-dire possède une loi associative — pas forcément commutative — avec un élément neutre, chaque élément ayant un symétrique) ;
G (inversion), est un groupe (c'est-à-dire possède une loi associative — pas forcément commutative — avec un élément neutre, chaque élément ayant un symétrique) ; - les applications de multiplication et d'inversion sont différentiables ou holomorphes.
Il est également possible de définir un groupe de Lie comme une variété différentielle munie d'opérations de groupe seulement continues. Cette définition est équivalente à la précédente et est une interprétation du 5e problème de Hilbert.
La dimension d'un groupe de Lie est définie comme sa dimension en tant que variété.
Il existe également une notion analogue de Groupe de Lie p-adique lorsque la variété différentielle sous-jacente est remplacée par un ensemble analytique p-adique. Ce sera le cas, par exemple, du groupe des points p-adiques d'un groupe algébrique.
Premiers exemples simples[modifier]
Un exemple simple est le groupe des matrices de rotation 2×2, noté SO(2, ) :
) : 
Il est paramétré par un seul angle λ : sa variété est donc unidimensionnelle (un cercle). C'est bien un groupe car l'inverse d'un élément de paramètre λ est donné par l'élément de paramètre −λ et le produit des éléments de paramètres λ et μ est donné par l'élément de paramètre λ+μ.
À l'inverse,  n'est pas un groupe continu, car il n'y a aucun élément entre 1 et 2.
n'est pas un groupe continu, car il n'y a aucun élément entre 1 et 2.
Propriétés[modifier]
Types de groupes de Lie[modifier]
Les groupes de Lie sont classables selon leur propriétés algébriques (abélien, simple, semisimple, résoluble, nilpotent), ou bien topologiques (connexe, simplement connexe, compact).
Ils sont également usuellement classés en quatre types, représentés dans le tableau d'exemples plus bas :
- Groupes de Lie réels, basés sur le groupe
 .
. - Groupes de Lie complexes, basés sur le groupe
 .
. - Groupes de Lie quaternioniques, basés sur le groupe des quaternions
 .
. - Groupes de Lie exceptionnels.
Homomorphismes et isomorphismes[modifier]
Si G et H sont deux groupes de Lie (tous deux réels ou complexes), alors un homomorphisme de groupes de Lie f : G H est un homomorphisme de groupe qui est également unefonction différentiable ou holomorphe (il suffit en fait que f soit continue).
H est un homomorphisme de groupe qui est également unefonction différentiable ou holomorphe (il suffit en fait que f soit continue).
La composition de deux homomorphismes de groupes de Lie est un homomorphisme de groupes de Lie et la classe de tous les groupes de Lie est une catégorie dont les flèches sont les homomorphismes de groupes de Lie. Deux groupes de Lie sont dits isomorphes s'il existe entre eux un homomorphisme bijectif dont la réciproque est également un homomorphisme.
La classe des groupes de Lie réels ou complexes de dimension n identifiés à isomorphisme près est un ensemble.
Algèbre de Lie associée à un groupe de Lie[modifier]
Il est possible d'associer naturellement à tout groupe de Lie G une algèbre de Lie. Il existe deux manières équivalentes d'introduire cette algèbre de Lie. L'une consiste à introduire un espace de champs de vecteurs sur G, la seconde consiste à munir l'espace tangent en l'élément neutre d'un crochet de Lie, dérivant de l'expression locale de la loi interne de G.
Comme algèbre de champs de vecteurs[modifier]
G désigne un groupe de Lie réel ou complexe de dimension n. Pour g un élément de G, l'application Lg : G G définie par Lg(f) = gf est un difféomorphisme de la variété réelle ou complexe sous-jacente à G. Un champ de vecteurs X sur G est dit invariant à gauche lorsque pour tout couple d'élément g et h de G, on a : dLg(Xh) = Xgh (où on note Xa la valeur du champ de vecteurs X au point a).
G définie par Lg(f) = gf est un difféomorphisme de la variété réelle ou complexe sous-jacente à G. Un champ de vecteurs X sur G est dit invariant à gauche lorsque pour tout couple d'élément g et h de G, on a : dLg(Xh) = Xgh (où on note Xa la valeur du champ de vecteurs X au point a).
Pour toute variété différentielle réelle ou complexe M, l'espace vectoriel réel ou complexe des champs de vecteurs sur M, noté I(M), est muni d'une structure naturelle d'algèbre de Lie réelle ou complexe, dont le crochet est le crochet de champs de vecteurs. La naturalité signifie exactement que tout morphisme f:M N entre variétés induit un morphisme d'algèbres de Lie f* : I(N)
N entre variétés induit un morphisme d'algèbres de Lie f* : I(N) I(M). En particulier, pour M = N = G, on dispose d'automorphismes (Lg)* de l'algèbre de Lie I(G). L'ensemble des points fixes communs à tous ces automorphismes (Lg)* est une sous-algèbre de Lie de I(G), notée g. Ses éléments sont les champs de vecteurs invariants à gauche sur G.
I(M). En particulier, pour M = N = G, on dispose d'automorphismes (Lg)* de l'algèbre de Lie I(G). L'ensemble des points fixes communs à tous ces automorphismes (Lg)* est une sous-algèbre de Lie de I(G), notée g. Ses éléments sont les champs de vecteurs invariants à gauche sur G.
Comme espace tangent[modifier]
Soit TeG l'espace tangent en e à G, e désignant l'élément neutre de G. L'application 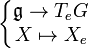 (où Xe est la valeur de X en l'élément neutre) est un isomorphisme linéaire. La structure d'algèbre de Lie de g se transporte donc, via cet isomorphisme, en une structure d'algèbre de Lie sur l'espace vectoriel TeG
(où Xe est la valeur de X en l'élément neutre) est un isomorphisme linéaire. La structure d'algèbre de Lie de g se transporte donc, via cet isomorphisme, en une structure d'algèbre de Lie sur l'espace vectoriel TeG
Cette structure peut se définir directement. Supposons donnée f une carte locale de G en l'élément neutre e avec f(e)=0, alors, l'application produit lue dans la carte locale f est au second ordre près :
f(f-1(a).f-1(b))=a+b+B(a,b)+...
où B est une forme bilinéaire antisymétrique. La structure d'algèbre de Lie sur TeG est donnée par :
- [X,Y] = B(X,Y).
Application exponentielle[modifier]
Dans la première présentation, tout vecteur X de g est par définition un champ de vecteurs invariant à gauche sur G. L'invariance à gauche implique que son flot est globalement défini. L'exponentielle de X est définie comme l'image au temps 1 de l'élément neutre e de G. Plus précisément, il existe une unique fonction  dont la dérivée est donnée par :
dont la dérivée est donnée par :
et telle que c(0) = e.
Elle possède la propriété remarquable suivante :
pour tous s et t.
Si l'on note, pour v = Xe, ev = c(1), une reparamétrisation incluant la variable t montre que :
![c(t) = e^{tv}qquad [eq.3]](http://upload.wikimedia.org/math/f/9/6/f960208fb71afe952ce33fea615c5a97.png) .
.
On peut alors vérifier :
 .
.
Cette fonction est également appelée fonction exponentielle et relie l'algèbre de Lie g au groupe de Lie G. Elle définit un difféomorphisme entre un voisinage de 0 dans g et un voisinage de e dans G. Toutefois, en général, l'application exponentielle n'est pas surjective, ni injective.
Un sous-groupe à un paramètre de G est une application différentiable c  G vérifiant l'identité eq.2 ci-dessus. À tout sous-groupe à un paramètre c est associé un unique élément Xde g vérifiant : c(t) = etv.
G vérifiant l'identité eq.2 ci-dessus. À tout sous-groupe à un paramètre c est associé un unique élément Xde g vérifiant : c(t) = etv.
Classification algébrique des groupes de Lie[modifier]
Plusieurs groupes de Lie peuvent partager la même algèbre de Lie associée. Cependant, à toute algèbre de Lie g correspond un groupe de Lie simplement connexe G, unique à isomorphisme près. De plus cet isomorphisme est uniquement déterminé par l'isomorphisme d'algèbre de Lie associé. Tout groupe de Lie connexe dont l'algèbre de Lie est isomorphe àg se réalise comme quotient de G par un sous-groupe normal discret.
Un groupe de Lie connexe est simple, semisimple, résoluble, nilpotent ou abélien si et seulement si son algèbre de Lie associée possède la propriété de même nom. En particulier, la classification des algèbres de Lie semi-simples donne une classification des groupes de Lie simplement connexes et semi-simples.
Exemples[modifier]
Groupes de Lie réels (groupes de Lie classiques)[modifier]
| Groupe de Lie | Description | Propriétés | Algèbre de Lie | Description | Dimension |
|---|---|---|---|---|---|
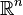 |
Espace euclidien muni de l'addition | Abélien ; Simplement connexe, non compact | 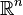 |
Le crochet de Lie est nul | n |
 |
Nombres réels non nuls munis de la multiplication | Abélien ; Non connexe, non compact |  |
Le crochet de Lie est nul | 1 |
 |
Nombres réels strictement positifs munis de la multiplication | Abélien ; Simplement connexe, non compact |  |
Le crochet de Lie est nul | 1 |
 |
Nombres complexes de module 1 munis de la multiplication | Abélien ; Connexe, non simplement connexe, compact |  |
Le crochet de Lie est nul | 1 |
 |
Groupe général linéaire :matrices réelles n×ninversibles | Non connexe, non compact |  |
Matrices n×n, le crochet de Lie étant le commutateur | n² |
 |
matrices réelles n×n à déterminant positif | Simplement connexe, non compact |  |
Matrices n×n, le crochet de Lie étant le commutateur | n² |
 |
Groupe spécial linéaire : matrices réelles de déterminant 1 | Simplement connexe, non compact si n > 1 |  |
Matrices carrées de trace nulle, le crochet de Lie étant le commutateur | n²-1 |
 |
Groupe orthogonal : matrices orthogonales réelles | Non connexe, compact | 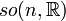 |
Matrices antisymétriques carrées réelles, le crochet de Lie étant le commutateur ;  est isomorphe à est isomorphe à  et et  muni du produit vectoriel muni du produit vectoriel |
n(n - 1)/2 |
 |
Groupe spécial orthogonal : matrices orthogonales réelles de déterminant 1 | Simple et semisimple pour n=3 et n≥5 ; Connexe, compact, non simplement connexe pour n≥2 | 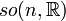 |
Matrices antisymétriques carrées réelles, le crochet de Lie étant le commutateur | n(n - 1)/2 |
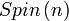 |
Groupe Spin | Simple et semisimple pour n=3 et n≥5 ; Simplement connexe, compact | 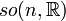 |
Matrices antisymétriques carrées réelles, le crochet de Lie étant le commutateur | n(n - 1)/2 |
 |
Groupe symplectique :matrices symplectiquesréelles | Simple, semisimple ; Non compact |  |
Matrices réelles satisfaisant JA + ATJ = 0 où J est la matrice antisymétrique standard | n(2n + 1) |
 |
Groupe unitaire : matrices unitaires n×n complexes | Non simplement connexe, compact ; Isomorphe à S1 pour n=1 |  |
Matrices carrées complexes A vérifiant A=-A*, le crochet de Lie étant le commutateur | n² |
 |
Groupe spécial unitaire : matrices unitaires complexesn×n de déterminant 1 | Simple et semisimple pour n≥2 ; Simplement connexe, compact |  |
Matrices carrées complexes de traces nulles A vérifiantA=-A*, le crochet de Lie étant le commutateur | n²-1 |
 |
Quaternions de module 1 munis de la multiplication, également noté  |
Simple, semisimple ; Simplement connexe, compact ; Topologiquement une sphère, isomorphe à  et et  |
 |
Quaternions de partie réelle nulle, le crochet de Lie étant leproduit vectoriel ; Isomorphe aux vecteurs réels de dimension 3, également isomorphe à  et et  |
3 |
 |
Groupe compact symplectique : matrices unitaires n×n quaternioniques | Simple, semisimple ; Compact, simplement connexe |  |
Matrices quaternioniques carrées A vérifiant A=-A*, le crochet de Lie étant le commutateur | n(2n + 1) |
Groupes de Lie complexes[modifier]
Les dimensions sont données sur  . (Tout groupe ou algèbre de Lie complexe peut être vu comme un groupe ou une algèbre de Lie réel de dimension double.)
. (Tout groupe ou algèbre de Lie complexe peut être vu comme un groupe ou une algèbre de Lie réel de dimension double.)
| Groupe de Lie | Description | Propriétés | Algèbre de Lie | Description | Dimension |
|---|---|---|---|---|---|
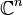 |
Espace euclidien muni de l'addition | Abélien ; Simplement connexe, non compact | 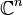 |
Le crochet de Lie est nul | n |
 |
Nombres complexes non nuls munis de la multiplication | Abélien ; Non simplement connexe, non compact |  |
Le crochet de Lie est nul | 1 |
 |
Groupe général linéaire : matricescomplexes n×n inversibles | Simplement connexe, non compact ; Isomorphe à pour n=1 pour n=1 |
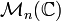 |
Matrices n×n, le crochet de Lie étant le commutateur | n² |
 |
Groupe spécial linéaire : matrices complexes de déterminant 1 | Simple, semisimple ; Simplement connexe, non compact pour n≥2 |  |
Matrices carrées de trace nulle, le crochet de Lie étant le commutateur | (n²-1) |
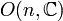 |
Groupe orthogonal : Matrices orthogonalescomplexes | Non connexe, non compact pour n≥2 |  |
matrices antisymétriques carrées complexes, le crochet de Lie étant le commutateur | n(n-1) |
 |
Groupe spécial orthogonal : matrices orthogonales complexes de déterminant 1 | Simple et semisimple pour n=3 et n≥5 ; Non simplement connexe, non compact pour n≥2 |  |
Matrices antisymétriques carrées complexes, le crochet de Lie étant le commutateur | n(n-1) |
 |
Groupe symplectique : matrices symplectiques complexes | Simple et semisimple ; Non compact |  |
Matrices complexes satisfaisant JA+ATJ=0 où J est la matrice antisymétrique standard | 2n(2n+1) |
Groupes de Lie quaternioniens[modifier]
Les dimensions sont données sur 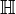 .
.
| Groupe de Lie | Description | Propriétés | Algèbre de Lie | Description | Dimension |
|---|---|---|---|---|---|
 |
Quaternions non nuls munis de la multiplication | Simplement connexe, non compact |  |
Quaternions, le crochet de Lie étant le commutateur | 1 |
Groupes de Lie exceptionnels[modifier]
On répertorie cinq groupes de Lie dits exceptionnels, notés respectivement E6, E7, E8, F4 et G2.
Voir aussi[modifier]
Articles connexes[modifier]
- Espace homogène
- Action de groupe de Lie
- Action hamiltonienne
- Représentation
- Représentation coadjointe
- Application moment
- E8 (mathématiques)
- Groupe algébrique (l'analogue algébrique des groupes de Lie, ce sont des variétés algébriques munies d'une structure de groupe).
- Groupe classique
Sites externes[modifier]
- Site du Projet Atlas de résolution des représentations des groupes de Lie (National Science Foundation, American Institute of Mathematics)
Bibliographie[modifier]
- Rached Mneimné et Frédéric Testard, Introduction à la théorie des groupes de Lie classiques [détail des éditions]
- Roger Godement, Introduction à la théorie des groupes de Lie, Springer, 2004 (ISBN 978-3-540-20034-5)
- (en) John M. Lee, Introduction to smooth manifolds, Springer, 2002
- (en) Ivan Kolář, Peter Michor (de) et Jan Slovák, Natural operations in differential geometry, Springer, 1993
- Bourbaki, Éléments de mathématique, Groupes et algèbres de Lie, Springer, 2006-2007
- (en) Sigurdur Helgason (de), Differential geometry, Lie groups and symmetric spaces, Academic Press, 1978
11:29 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Algèbre de Lie
Algèbre de Lie
Source : http://fr.wikipedia.org/wiki/Alg%C3%A8bre_de_Lie
En mathématiques, une algèbre de Lie, nommée en l'honneur du mathématicien Sophus Lie, est un espace vectoriel qui est muni d'un crochet de Lie, c'est-à-dire d'une loi de composition interne bilinéaire, antisymétrique et qui vérifie l'identité de Jacobi. Une algèbre de Lie est un cas particulier d'algèbre sur un corps.
Sommaire[masquer] |
Définitions, exemples et premières propriétés[modifier]
Définition[modifier]
Soit  un corps commutatif.
un corps commutatif.
Une algèbre de Lie sur  est un espace vectoriel
est un espace vectoriel  sur
sur  muni d'une application bilinéaire
muni d'une application bilinéaire ![(x,y) mapsto [x,y]](http://upload.wikimedia.org/math/7/5/e/75e87350f83275e11f126171780fd7ca.png) de
de 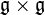 dans
dans  qui vérifie les propriétés suivantes:
qui vérifie les propriétés suivantes:
![forall x in mathfrak{g}, [x,x]=0](http://upload.wikimedia.org/math/f/3/2/f3223a3fe063412bb2f5033ba34850f5.png) ;
;![forall x,y,z in mathfrak{g}, [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0](http://upload.wikimedia.org/math/6/7/d/67d115952cf9c1c691b6053868febb0d.png)
Le produit [x,y] est appelé crochet de Lie (ou simplement crochet) de x et y. Puisque le crochet est une fonction bilinéaire alternée de x,y, on a aussi l'identité [x,y] = − [y,x] pour tousx,y dans  . L'identité (2) ci-dessus est appelée l'identité de Jacobi.
. L'identité (2) ci-dessus est appelée l'identité de Jacobi.
Une sous-algèbre de Lie de  est un sous-espace vectoriel de
est un sous-espace vectoriel de  stable pour le crochet de Lie. Toute sous-algèbre de Lie de
stable pour le crochet de Lie. Toute sous-algèbre de Lie de  est munie de manière évidente d'une structure d'algèbre de Lie sur
est munie de manière évidente d'une structure d'algèbre de Lie sur  .
.
Remarque : contrairement aux algèbres tensorielles (et aux algèbres de Clifford, dont les algèbres extérieures), les algèbres de Lie ne sont pas unitaires, ni associatives.
Quelques exemples classiques d'algèbres de Lie[modifier]
- Tout espace vectoriel E peut être muni d'une structure d'algèbre de Lie, en posant
![forall x,y in E, [x,y]=0](http://upload.wikimedia.org/math/4/7/b/47b2e0b6393e77c2e6376834f8c87276.png) . Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne.
. Une telle algèbre de Lie, où le crochet de Lie est identiquement nul, est appelée abélienne. - On peut, à partir de (A, * ), une algèbre associative sur un corps, construire une algèbre de Lie, de la façon suivante : on pose
![forall x,y in A, [x,y]=x*y-y*x](http://upload.wikimedia.org/math/5/9/7/59711ef28af13f749a361b567295a858.png) (c'est lecommutateur des deux éléments x et y). Il est facile de vérifier que l'on définit ainsi sur A une structure d'algèbre de Lie.
(c'est lecommutateur des deux éléments x et y). Il est facile de vérifier que l'on définit ainsi sur A une structure d'algèbre de Lie.- Inversement, toute algèbre de Lie
 est contenue dans une algèbre associative, appelée algèbre enveloppante, dans laquelle le crochet de Lie coïncide avec le crochet défini ci-dessus. L'algèbre enveloppante est beaucoup plus grande que l'algèbre de départ.
est contenue dans une algèbre associative, appelée algèbre enveloppante, dans laquelle le crochet de Lie coïncide avec le crochet défini ci-dessus. L'algèbre enveloppante est beaucoup plus grande que l'algèbre de départ.
- Inversement, toute algèbre de Lie
- Comme exemple concret de la situation ci-dessus, considérons
 , l'espace des matrices
, l'espace des matrices  à coefficients dans
à coefficients dans  . C'est une algèbre associative pour le produit matriciel usuel. On peut donc également lui donner une structure d'algèbre de Lie, avec le crochet [A,B] = AB − BA. On note
. C'est une algèbre associative pour le produit matriciel usuel. On peut donc également lui donner une structure d'algèbre de Lie, avec le crochet [A,B] = AB − BA. On note  cette algèbre, lorsque l'on considère sa structure d'algèbre de Lie.
cette algèbre, lorsque l'on considère sa structure d'algèbre de Lie. - Bien évidemment, tout sous-espace vectoriel de
 stable par le crochet est une algèbre de Lie. Ainsi, on peut vérifier que l'ensemble des matrices de trace nulle est une algèbre de Lie, que l'on note
stable par le crochet est une algèbre de Lie. Ainsi, on peut vérifier que l'ensemble des matrices de trace nulle est une algèbre de Lie, que l'on note  .
.- En fait, le théorème d'Ado montre que toute algèbre de Lie de dimension finie peut être vue comme une sous-algèbre de
 .
.
- En fait, le théorème d'Ado montre que toute algèbre de Lie de dimension finie peut être vue comme une sous-algèbre de
- Un autre exemple fondamental, plus géométrique, est le suivant. Soit M une variété différentielle. Alors l'espace vectoriel formé par les champs de vecteurs sur M possède une structure naturelle d'algèbre de Lie, sans être une algèbre.
- En particulier, l'ensemble des vecteurs de Killing d'une variété forme une algèbre de Lie, qui correspond au groupe d'isométries de la variété considérée.
- L'espace euclidien tri-dimensionnel
 avec le produit vectoriel comme crochet de Lie est une algèbre de Lie.
avec le produit vectoriel comme crochet de Lie est une algèbre de Lie.
Morphismes et idéaux[modifier]
Un morphisme d'algèbre de Lie  est une application linéaire φ qui respecte le crochet de Lie, c'est-à-dire telle que
est une application linéaire φ qui respecte le crochet de Lie, c'est-à-dire telle que
![forall a,b in mathfrak{g}, phi([a,b])=[phi(a),phi(b)]](http://upload.wikimedia.org/math/7/9/f/79fe9d02198bb8da7ba2c3fe5df52add.png) .
.
Un idéal de  est un sous-espace vectoriel
est un sous-espace vectoriel  tel que
tel que ![forall ginmathfrak{g}, forall hin mathfrak{h}, [g,h]inmathfrak{h}](http://upload.wikimedia.org/math/9/f/e/9fe5cc6e32f7a61a988f42d549cb43b3.png) . C'est en particulier une sous-algèbre de Lie. Si une algèbre de Lie n'admet pas d'idéal non trivial, elle est dite simple.
. C'est en particulier une sous-algèbre de Lie. Si une algèbre de Lie n'admet pas d'idéal non trivial, elle est dite simple.
Si  est un idéal de
est un idéal de  , on peut former le quotient de
, on peut former le quotient de  par
par  : c'est l'espace vectoriel quotient
: c'est l'espace vectoriel quotient 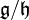 , muni du crochet défini par
, muni du crochet défini par ![[g+mathfrak{h},g'+mathfrak{h}] = [g,g']](http://upload.wikimedia.org/math/8/2/d/82d29f5c4eb7af6feb2661af74a7bd29.png) . La projection
. La projection 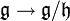 est alors un morphisme d'algèbres de Lie.
est alors un morphisme d'algèbres de Lie.
Une représentation d'une algèbre de Lie  est un morphisme
est un morphisme 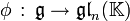 . Autrement dit, c'est une application linéaire telle que φ([g,h]) = φ(g)φ(h) − φ(h)φ(g).
. Autrement dit, c'est une application linéaire telle que φ([g,h]) = φ(g)φ(h) − φ(h)φ(g).
Le morphisme  défini par ad(g)(h) = [g,h] définit une représentation de
défini par ad(g)(h) = [g,h] définit une représentation de  , appelée représentation adjointe. L'identité de Jacobi exprime précisément le fait que ad respecte le crochet. Le noyau de cette représentation est le centre
, appelée représentation adjointe. L'identité de Jacobi exprime précisément le fait que ad respecte le crochet. Le noyau de cette représentation est le centre ![Z(mathfrak{g})={ginmathfrak{g}forall hinmathfrak{g} [g,h]=0}](http://upload.wikimedia.org/math/a/f/e/afe7160b530a847134d5f4291027ee9c.png) de l'algèbre de Lie
de l'algèbre de Lie 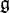 .
.
Relation avec les groupes de Lie et les groupes algébriques[modifier]
Les algèbres de Lie sont naturellement associées aux groupes de Lie. Si G est un groupe de Lie et 1 son élément neutre, alors l'espace tangent en 1 à G est une algèbre de Lie ; la construction exacte de cette algèbre est détaillée dans la section correspondante de l'article Groupe de Lie. La même construction est valable pour les groupes algébriques. On note en général en petites lettres gothiques l'algèbre de Lie associée à un groupe de Lie, ou à un groupe algébrique. Ainsi, comme on l'a déjà vu,  désigne l'ensemble des matrices carrées de taille n et
désigne l'ensemble des matrices carrées de taille n et 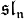 désigne l'ensemble des matrices carrées de taille n de trace nulle. De la même façon,
désigne l'ensemble des matrices carrées de taille n de trace nulle. De la même façon,  désigne l'ensemble des matrices carrées A de taille n antisymétriques, etc. Dans tous ces exemples, le crochet de Lie n'est rien d'autre que le commutateur : [A,B]=AB-BA.
désigne l'ensemble des matrices carrées A de taille n antisymétriques, etc. Dans tous ces exemples, le crochet de Lie n'est rien d'autre que le commutateur : [A,B]=AB-BA.
Si φ est un morphisme de groupes entre deux groupes de Lie G et H, et si l'on suppose φ différentiable, alors sa différentielle en l'identité sera un morphisme entre les algèbres de Lie  et
et  de G et H. En particulier, à une représentation de G différentiable, on associe une représentation de
de G et H. En particulier, à une représentation de G différentiable, on associe une représentation de  .
.
La classification des algèbres de Lie est utilisée de façon cruciale pour l'étude des groupes de Lie, des groupes algébriques et de leurs représentations.
Classification[modifier]
Si 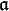 et
et 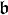 sont deux sous-algèbres de Lie d'une algèbre de Lie
sont deux sous-algèbres de Lie d'une algèbre de Lie  , notons
, notons ![[mathfrak{a},mathfrak{b}]](http://upload.wikimedia.org/math/c/5/2/c528d5c197e3f72db0a9bbc760333ee4.png) le sous-espace vectoriel engendré par les éléments de la forme [a,b] pour
le sous-espace vectoriel engendré par les éléments de la forme [a,b] pour  et
et 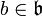 .
.
Algèbres de Lie nilpotentes[modifier]
Une algèbre de Lie est dite nilpotente lorsque toute suite de commutateurs ![[[[g_1,g_2],g_3],dots,g_n]](http://upload.wikimedia.org/math/4/8/a/48ab7757f1f2f8ed370a0f9d8acecd13.png) finit par être nulle, lorsque n devient suffisamment grand.
finit par être nulle, lorsque n devient suffisamment grand.
Plus précisément, définissons Ci par  et
et ![C_{i+1}=[C_i,mathfrak{g}]](http://upload.wikimedia.org/math/3/b/2/3b21f80fad4a73cdcc2c55569abfd0d0.png) .
.
S'il existe un i tel que Ci=0, on dit que  est nilpotente. Cette notion est à mettre en parallèle avec celle de groupe nilpotent. Il est facile de voir que toute algèbre de Lie abélienne est nilpotente.
est nilpotente. Cette notion est à mettre en parallèle avec celle de groupe nilpotent. Il est facile de voir que toute algèbre de Lie abélienne est nilpotente.
L'algèbre  des matrices triangulaires strictes, c'est-à-dire de la forme
des matrices triangulaires strictes, c'est-à-dire de la forme  fournit un exemple d'algèbre de Lie nilpotente.
fournit un exemple d'algèbre de Lie nilpotente.
Le théorème d'Engel affirme que toute sous-algèbre nilpotente de  est en fait simultanément trigonalisable et donc conjuguée à une sous-algèbre de
est en fait simultanément trigonalisable et donc conjuguée à une sous-algèbre de  .
.
Algèbres de Lie résolubles[modifier]
Définissons par récurrence Di par 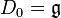 et Di + 1 = [Di,Di]
et Di + 1 = [Di,Di]
S'il existe un i tel que Di=0, on dit que  est résoluble. Comme dans le cas des algèbres nilpotentes, cette notion correspond à celle de groupe résoluble. Il est facile de voir que toute algèbre de Lie nilpotente est résoluble.
est résoluble. Comme dans le cas des algèbres nilpotentes, cette notion correspond à celle de groupe résoluble. Il est facile de voir que toute algèbre de Lie nilpotente est résoluble.
Un exemple d'algèbre de Lie résoluble est donné par l'algèbre 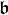 des matrices triangulaires supérieures dans
des matrices triangulaires supérieures dans  .
.
Le théorème de Lie montre que, si 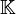 est algébriquement clos et de caractéristique nulle, alors toute sous-algèbre de Lie résoluble de
est algébriquement clos et de caractéristique nulle, alors toute sous-algèbre de Lie résoluble de  est conjuguée à une sous-algèbre de
est conjuguée à une sous-algèbre de 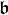
Algèbres de Lie semi-simples et réductives[modifier]
On dit qu'une algèbre de Lie  est semi-simple lorsqu'elle ne contient pas d'idéal résoluble non trivial.
est semi-simple lorsqu'elle ne contient pas d'idéal résoluble non trivial.  est dite réductive lorsque sa représentation adjointe est semi-simple.
est dite réductive lorsque sa représentation adjointe est semi-simple.
Lorsque 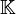 est de caractéristique nulle, et que
est de caractéristique nulle, et que  est de dimension finie, la semi-simplicité de
est de dimension finie, la semi-simplicité de  est équivalente à la non-dégénerescence de la forme de Killing K(x,y) définie par K(x,y) = tr(ad(x)ad(y)), où tr désigne la trace. Par ailleurs,
est équivalente à la non-dégénerescence de la forme de Killing K(x,y) définie par K(x,y) = tr(ad(x)ad(y)), où tr désigne la trace. Par ailleurs,  est réductive si et seulement si
est réductive si et seulement si ![[mathfrak{g},mathfrak{g}]](http://upload.wikimedia.org/math/3/f/1/3f1683bcf0fa96e29329efca70a1d284.png) est semi-simple.
est semi-simple.
On peut montrer que, sous les mêmes hypothèses, toute algèbre de Lie semi-simple est en fait une somme directe d'algèbres de Lie simples.
Les algèbres de Lie simples de dimension finie sur le corps  des nombres complexes sont classifiées par les diagrammes de Dynkin. Il y a donc 4 familles d'algèbres de Lie simples (ou 3 si on considère Bn et Dn comme une même famille) et 5 algèbres de Lie exceptionnelles, correspondant chacune à un diagramme de Dynkin différent.
des nombres complexes sont classifiées par les diagrammes de Dynkin. Il y a donc 4 familles d'algèbres de Lie simples (ou 3 si on considère Bn et Dn comme une même famille) et 5 algèbres de Lie exceptionnelles, correspondant chacune à un diagramme de Dynkin différent.
- À un diagramme de Dynkin de type
 correspond l'algèbre de Lie
correspond l'algèbre de Lie 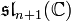 .
.
- À un diagramme de Dynkin de type
 correspond l'algèbre de Lie
correspond l'algèbre de Lie 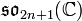 .
.
- À un diagramme de Dynkin de type
 correspond l'algèbre de Lie
correspond l'algèbre de Lie  .
.
- À un diagramme de Dynkin de type
 correspond l'algèbre de Lie
correspond l'algèbre de Lie  .
.
- Les algèbres de Lie exceptionnelles, correspondant aux diagrammes de Dynkin restants (de type E6, E7, E8, F4 et G2) n'ont pas d'interprétation aussi simple.
L'algèbre de Lie  est, elle, réductive et son algèbre de Lie dérivée est
est, elle, réductive et son algèbre de Lie dérivée est  .
.
Les algèbres de Lie semi-simples de dimension finie sur le corps  des nombres réels sont classifiées par les involutions d'algèbres de Lie complexe ou, de façon équivalente, par lesinvolutions de systèmes de racines. Ceci correspond à la notion d'algèbre de Lie symétrique. Comme classe d'algèbre de Lie simple réelle, on peut citer:
des nombres réels sont classifiées par les involutions d'algèbres de Lie complexe ou, de façon équivalente, par lesinvolutions de systèmes de racines. Ceci correspond à la notion d'algèbre de Lie symétrique. Comme classe d'algèbre de Lie simple réelle, on peut citer:
- Les algèbres de Lie compactes. Ce sont les algèbres de Lie de groupes compacts. Il y en a exactement une qui correspond à chaque algèbre de Lie complexe.
- Les algèbres de Lie complexes vues comme algèbres de Lie réelles.
- Les autres peuvent être classées en familles AI, AII, AIII, BI, CI, CII, DI, DIII et en algèbres exeptionelles
EI, EII, EIII, EIV (de type E6) EV, EVI, EVII (de type E7) EVIII, EIX (de type E8) FI, FII (de type F4) et GI (de type G2) suivant la notation d'Helgason1)
Dimension infinie[modifier]
Il n'y a pas de classification générale des algèbres de Lie de dimension infinie mais plusieurs classes de telles algèbres ont été étudiées.
- Une algèbre de Kac-Moody est une algèbre de Lie définie abstraitement en termes de générateurs et relations codés par une matrice de Cartan généralisée non nécessairement définie positive. Elles peuvent donc être de dimension infinie. Leur classification générale est encore hors de portée mais plusieurs sous-types sont connus
- Une algèbre de Kac-Moody affine possède la propriété que tous les sous-diagrammes de Dynkin de son diagramme de Dynkin correspondent à des sous-algèbres de Lie de dimension finie. Sa matrice de Cartan généralisée est alors de corang 1. Les algèbres de Kac-Moody affines ont été classifiées par Victor G. Kac. Elles sont très utilisées enphysique théorique dans l'étude des théories conformes des champs et en particulier dans l'étude des modèles WZW.
- Une algèbre de Kac-Moody hyperbolique possède un diagramme de Dynkin connexe avec la propriété que si on lui retire une racine, on obtient une algèbre de Lie semi-simple de dimension finie ou bien une algèbre de Kac-Moody affine. Elles ont été également classifiées et sont de rang 10 au maximum. Leur matrice de Cartan généralisée est non dégénérée et de signature Lorentzienne (c’est-à-dire avec exactement une direction négative).
- algèbre de Kac-Moody généralisée ou algèbre de Borcherds: c'est un type d'algèbre de Lie généralisant le concept d'algèbre de Kac-Moody dont la matrice de Cartan généralisée peut posséder des racines simples nommées imaginaires pour lesquelles l'élément diagonal de la matrice de Cartan généralisée est négatif. Elles ont été introduite par Richard Ewen Borcherds dans le cadre de l'étude de la conjecture monstrous moonshine.
Généralisation[modifier]
Il existe différentes sortes de généralisations des algèbres de Lie, on citera les superalgèbres de Lie, les groupes quantiques, les algèbres de Leibniz, les algèbres pré-Lie.
Références[modifier]
- Bourbaki, Groupes et algèbres de Lie
- Dixmier, Jacques Algèbres enveloppantes Éditions Jacques Gabay, Paris, 1996. ISBN 2-87647-014-4
- Humphreys, James E. Introduction to Lie Algebras and Representation Theory, Second printing, revised. Graduate Texts in Mathematics, 9. Springer-Verlag, New York, 1978. ISBN 0-387-90053-5
- Jacobson, Nathan, Lie algebras, Republication of the 1962 original. Dover Publications, Inc., New York, 1979. ISBN 0-486-63832-4
- S. Helgason, Differential Geometry and Symmetric Spaces [archive]
Voir aussi[modifier]
11:28 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
10/03/2011
La figure et le monde, archéologie de la géométrie, Peuples paysans sans écriture et premières civilisations Olivier Keller Etude (broché). Paru en 08/2006
20:08 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Le dossier Pythagore , Du chamanisme à la mécanique quantique Pierre Brémaud Essai (broché). Paru en 09/2010
20:07 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Byrne , Six books of Euclid Werner Oechslin Guide en anglais (broché). Paru en 05/2010
20:06 | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook











































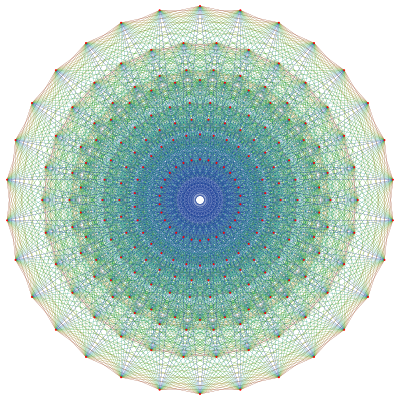

![left[J_{ij}, J_{kell}right] = delta_{jk}J_{iell} - delta_{jell}J_{ik} - delta_{ik}J_{jell} + delta_{iell}J_{jk},](http://upload.wikimedia.org/math/f/8/d/f8ddba45c26b81da3205c690d5648aeb.png)




![c'(t) = X[c(t)]qquad [eq.1]](http://upload.wikimedia.org/math/2/2/1/221d26faae62a0bbd5bd41a335944438.png)
![c(s + t) = c(s).c(t)qquad [eq.2]](http://upload.wikimedia.org/math/b/c/e/bce93f16e470559e54834d2b3f18bf49.png)



