30/01/2010
Le triangle de Reuleaux
Le triangle de Reuleaux
Le 4 janvier 2010, par Serge Cantat
Chargé de Recherche à l'Université Rennes 1 (page web)
Le triangle de Reuleaux est une figure de géométrie plane élémentaire, mais intrigante, qui peut être présentée à des élèves de collège. Elle jouit de propriétés remarquables, qui sont parfois difficiles à établir et à généraliser.
Le triangle de Reuleaux
L’objet de ce mois-ci concerne la géométrie de certaines parties du plan. Commençons par la plus simple, le disque, représenté ci-dessous en jaune. Le diamètre du disque n’a pas d’importance dans ce qui suit, et nous choisirons nos unités de mesure pour qu’il soit égal à 1 Ce disque jaune est donc l’ensemble des points du plan situés à une distance du centre inférieure à 1
Ce disque jaune est donc l’ensemble des points du plan situés à une distance du centre inférieure à 1 2 ; la courbe qui borde ce disque est un cercle de diamètre 1
2 ; la courbe qui borde ce disque est un cercle de diamètre 1

La position exacte du centre n’a pas non plus d’importance pour la propriété suivante. Prenons deux droites parallèles qui ne coupent pas le disque et qui sont situées de part et d’autre du disque ; rapprochons-les de celui-ci, en les gardant toujours parallèles à la direction qu’elles avaient initialement, jusqu’à ce qu’elles viennent chacune toucher le disque en un point. L’écart entre les deux droites est alors égal au diamètre du disque, ceci quelques soient les droites initialement choisies. On dit que le disque et le cercle sont de largeur constante. Ce que nous allons voir, c’est qu’il existe beaucoup d’autres parties du plan de largeur constante.
Le premier exemple est le triangle de Reuleaux. Pour le définir, le plus simple est de partir d’un triangle équilatéral dont nous noterons A B etC les trois sommets. L’équilatéralité signifie que les distances AB
B etC les trois sommets. L’équilatéralité signifie que les distances AB BC et CA entre les sommets sont égales, et nous supposerons que cette distance entre sommets vaut 1
BC et CA entre les sommets sont égales, et nous supposerons que cette distance entre sommets vaut 1 Ainsi, le cercle de centre A et de rayon 1 passe par les sommets B et C
Ainsi, le cercle de centre A et de rayon 1 passe par les sommets B et C De même, le cercle de centre B et de rayon 1 passe par C et A
De même, le cercle de centre B et de rayon 1 passe par C et A et le cercle de centre C et de rayon 1 passe par A et B
et le cercle de centre C et de rayon 1 passe par A et B Traçons ces trois cercles. Ils bordent trois disques de rayon1
Traçons ces trois cercles. Ils bordent trois disques de rayon1 Le triangle de Reuleaux est l’intersection de ces trois disques ; ce n’est donc pas un triangle au sens usuel. Comme on le voit sur la figure présentée ci-dessous, le triangle de Reuleaux s’obtient en ajoutant trois lunules au triangle équilatéral ABC dont nous sommes partis.
Le triangle de Reuleaux est l’intersection de ces trois disques ; ce n’est donc pas un triangle au sens usuel. Comme on le voit sur la figure présentée ci-dessous, le triangle de Reuleaux s’obtient en ajoutant trois lunules au triangle équilatéral ABC dont nous sommes partis.

Pour tracer un triangle de Reuleaux avec un compas, il n’est pas utile de suivre pas à pas la construction précédente. Écartez votre compas d’une unité, puis choisissez un point A dans le plan où vous plantez votre compas. Tracez un grand arc de cercle C1 Plantez alors votre compas en un point B situé sur cet arc C1
Plantez alors votre compas en un point B situé sur cet arc C1 près de l’une des extrémités de celui-ci, et tracez maintenant un deuxième arc de cercle C2 en sorte que C2passe par A et vienne couper l’arc C1 en un point C
près de l’une des extrémités de celui-ci, et tracez maintenant un deuxième arc de cercle C2 en sorte que C2passe par A et vienne couper l’arc C1 en un point C Plantez maintenant votre compas au point C et tracer l’arc de cercle passant par A et B
Plantez maintenant votre compas au point C et tracer l’arc de cercle passant par A et B Vous voyez surgir le triangle de Reuleaux. Si vous désirez faire apparaître le triangle équilatéral évoqué ci-dessus, il suffit de relier les sommetsA
Vous voyez surgir le triangle de Reuleaux. Si vous désirez faire apparaître le triangle équilatéral évoqué ci-dessus, il suffit de relier les sommetsA B et C avec une règle.
B et C avec une règle.
Les figures présentées ici ont été réalisées en suivant ce canevas à l’aide du matériel de CM1 de ma fille ainée.

Comme annoncé plus haut, la propriété remarquable du triangle de Reuleaux s’énonce ainsi : le triangle de Reuleaux est de largeur constante. En effet, lorsque deux droites parallèles viennent toucher le triangle de Reuleaux en se rapprochant de part et d’autre, l’une d’entre elles le touche en l’un des sommets A B ou C
B ou C et la seconde le touche en un point de l’arc de cercle opposé ; ainsi, l’écart entre les deux droites est égal à 1
et la seconde le touche en un point de l’arc de cercle opposé ; ainsi, l’écart entre les deux droites est égal à 1 le rayon du cercle. Reformulons cette propriété : si l’on découpe un triangle de Reuleaux dans une plaque de granit et qu’on vient le serrer avec une clé anglaise, l’écart de la clé anglaise ne dépend pas de la position du triangle de Reuleaux. Autrement dit, une fois serrée, on peut tourner la pièce de granit sans changer l’écart de la clé et, ce faisant, la pièce reste en permanence en contact avec les bords de l’ustensile. Ou encore, si vous faites rouler le triangle de granit entre deux règles parallèles situées à une distance unité l’une de l’autre, le triangle de Reuleaux touchera en permanence le bord des deux règles.
le rayon du cercle. Reformulons cette propriété : si l’on découpe un triangle de Reuleaux dans une plaque de granit et qu’on vient le serrer avec une clé anglaise, l’écart de la clé anglaise ne dépend pas de la position du triangle de Reuleaux. Autrement dit, une fois serrée, on peut tourner la pièce de granit sans changer l’écart de la clé et, ce faisant, la pièce reste en permanence en contact avec les bords de l’ustensile. Ou encore, si vous faites rouler le triangle de granit entre deux règles parallèles situées à une distance unité l’une de l’autre, le triangle de Reuleaux touchera en permanence le bord des deux règles.
Convexes de largeur constante
Nous voyons donc qu’il y a au moins deux parties du plan qui sont de largeur constante, le disque et le triangle de Reuleaux. Peut-on en construire d’autres ? La réponse est oui, mais avant de continuer il convient d’exclure certaines constructions sans intérêt. Si l’on évide un petit trou dans un triangle de Reuleaux ou dans un disque, on crée une nouvelle partie du plan dont la largeur est constante, mais pour la raison idiote qu’aucune modification n’a été effectuée au bord, là où la clé anglaise vient serrer la pièce de granit étudiée.
Avant de continuer nous allons donc introduire une définition utile. Nous dirons qu’une partie D du plan est convexe si elle satisfait la propriété suivante : quelque soit la paire de points A et B situés dans D la totalité du segment joignant A à B est contenue dans D
la totalité du segment joignant A à B est contenue dans D

Le triangle de Reuleaux est convexe ; si on le perce, il ne l’est plus. D’autres exemples sont fournis sur la figure ci-contre. La partie jaune à gauche est convexe, tandis que la partie orange H en forme de haricot, ne l’est pas. La plus petite partie convexe qui contient H s’obtient en ajoutant la portion jaune bordée par H d’un côté et par un segment de l’autre ; la droite contenant ce segment vient toucher le bord de H en deux points distincts. Ce fait, à lui seul, montre que H ne peut pas être de largeur constante car si l’on serre H avec une clé anglaise dont un côté touche le bord de H en deux points, alors on ne peut plus tourner H sans agrandir l’écart de la clé.
en forme de haricot, ne l’est pas. La plus petite partie convexe qui contient H s’obtient en ajoutant la portion jaune bordée par H d’un côté et par un segment de l’autre ; la droite contenant ce segment vient toucher le bord de H en deux points distincts. Ce fait, à lui seul, montre que H ne peut pas être de largeur constante car si l’on serre H avec une clé anglaise dont un côté touche le bord de H en deux points, alors on ne peut plus tourner H sans agrandir l’écart de la clé.
Ainsi, lorsque D est une partie du plan de largeur constante alors, après avoir boucher les trous éventuels de D on obtient une partie convexe qui reste de largeur constante. De plus, le bord de cette partie ne contient aucun segment ; autrement dit, les droites parallèles qui viennent enserrer D de part et d’autre touchent chacune D en exactement un point.
on obtient une partie convexe qui reste de largeur constante. De plus, le bord de cette partie ne contient aucun segment ; autrement dit, les droites parallèles qui viennent enserrer D de part et d’autre touchent chacune D en exactement un point.
L’étude des parties du plan de largeur constante se ramène donc à l’étude de celles qui sont convexes.
Pour les parties convexes du plan, on dispose d’une caractérisation moins poétique de de la propriété largeur constante à l’aide de plaques d’égouts. La forme d’une plaque d’égouts doit être telle qu’elle ne peut jamais tomber dans le trou qu’elle vient boucher. Si le trou a la forme d’un triangle de Reuleaux, d’un disque, ou de toute autre courbe de largeur constante, alors la plaque qui vient l’obstruer ne peut tomber : quel que soit l’orientation de la plaque, elle touchera les bords du trou sans pouvoir chuter sur la tête de l’ouvrier travaillant au fond. A l’inverse, la plaque verte ci-dessous n’est pas de largeur constante et, de fait, en tournant d’un quart de tour et en basculant, elle tomberait dans les égouts, son grand côté à la verticale et son petit côté à l’horizontal .

Il s’agit maintenant de construire de nouvelles parties convexes du plan qui sont de largeur constante, égale à 1 pour fixer les idées. Construire la partie ou la courbe qui l’encercle constituent le même problème. Nous chercherons donc à construire de telles courbes, et parlerons decourbes de largeur constante.

C’est encore le mécanicien Franz Reuleaux [1] qui nous apporte des exemples. On peut tout d’abord répéter une construction similaire en remplaçant le triangle équilatéral ABC utilisé ci-dessus par un polygone régulier ayant un nombre impair de côtés. Plutôt que de se livrer à un cours sur la construction de polygones réguliers, contentons nous de contempler un film délicieusement vintage.
On peut aussi reprendre la construction au compas que nous avons décrite en la généralisant au p’tit bonheur la chance. Pour cela on part d’un point A0 et l’on trace un petit arc de cercle C1 centré en A0 dont l’on note A1 et A2 les extrémités. On trace ensuite un arc de cercle centré en A1 partant de A0
partant de A0 et s’approchant de A2
et s’approchant de A2 et un arc de cercle centré en A2
et un arc de cercle centré en A2 partant de A0
partant de A0 et s’approchant de A1
et s’approchant de A1 Deux nouvelles extrémités apparaissent et l’on répète le procédé à partir de celles-ci. En traçant un nombre impair d’arcs de cercles on peut ainsi tracer une courbe qui est la frontière d’une partie convexe de largeur constante. La figure ci-dessous illustre ce procédé. [2]
Deux nouvelles extrémités apparaissent et l’on répète le procédé à partir de celles-ci. En traçant un nombre impair d’arcs de cercles on peut ainsi tracer une courbe qui est la frontière d’une partie convexe de largeur constante. La figure ci-dessous illustre ce procédé. [2]

Nous disposons donc maintenant de nombreuses parties du plan qui sont de largeur constante. On peut déjà se féliciter : l’architecture en a profité, les pièces de monnaie, et les moteurs aussi. Le lecteur en verra apparaître au fil des illustrations de ce texte. Mon but maintenant est de mener le lecteur à un joli problème de mathématique encore ouvert de nos jours, et pour cela mieux vaut passer directement à la suite.
Buffon et Didon
Les courbes de largeur constante donnée ont un périmètre fixé ! Ainsi, le triangle de Reuleaux, comme toute courbe de largeur constante égale à 1, a le même périmètre que le disque de diamètre unité, il vaut 
 Le film vintage mentionné ci-dessus illustre ceci aux alentours d’une minute et vingt seconde. Cette propriété remarquable peut être démontrée en faisant appel à un autre objet mathématique célèbre, l’aiguille de Buffon. Le problème de l’aiguille de Buffon est le suivant. Traçons des droites parallèles sur le sol en les espaçant régulièrement de sorte que la distance entre deux droites consécutives est constamment égale à une distance L fixée. Prenons maintenant une aiguille de longueur l plus petite que L ; ainsi, lorsque l’aiguille repose sur le plan, elle coupe au plus une des droites que nous avons tracées. Le problème proposé par Buffon en 1733 est le suivant : quelle est la probabilité que l’aiguille, lancée au hasard sur le plan, coupe l’une des droites tracées ? La réponse est
Le film vintage mentionné ci-dessus illustre ceci aux alentours d’une minute et vingt seconde. Cette propriété remarquable peut être démontrée en faisant appel à un autre objet mathématique célèbre, l’aiguille de Buffon. Le problème de l’aiguille de Buffon est le suivant. Traçons des droites parallèles sur le sol en les espaçant régulièrement de sorte que la distance entre deux droites consécutives est constamment égale à une distance L fixée. Prenons maintenant une aiguille de longueur l plus petite que L ; ainsi, lorsque l’aiguille repose sur le plan, elle coupe au plus une des droites que nous avons tracées. Le problème proposé par Buffon en 1733 est le suivant : quelle est la probabilité que l’aiguille, lancée au hasard sur le plan, coupe l’une des droites tracées ? La réponse est
 lL
lL

Ainsi, lorsque l’espace entre les droites parallèles est fixé à L=1 cette probabilité vaut (2
cette probabilité vaut (2
 )l
)l Si l’on fait un grand nombre de lancers de l’aiguille sur le plan, le nombre des lancers pour lesquels l’aiguille intersecte l’une des droites du quadrillage sera donc approximativement égal à
Si l’on fait un grand nombre de lancers de l’aiguille sur le plan, le nombre des lancers pour lesquels l’aiguille intersecte l’une des droites du quadrillage sera donc approximativement égal à

 (longueur de l'aiguille)
(longueur de l'aiguille) (nombre de lancers)
(nombre de lancers)
Ou encore, si l’on lance notre aiguille N fois et que l’on note I le nombre total d’intersections observées, alors
 2
2 IN
IN
l’égalité devenant exacte dans la limite d’un nombre infini de lancers. Ceci vaut en fait pour n’importe quelle courbe Z Supposons en effet qu’on veuille calculer la longueur d’une courbe Z tracée dans un plan. Prenons du fil de fer et tordons-le pour qu’il épouse la forme de la courbe Z
Supposons en effet qu’on veuille calculer la longueur d’une courbe Z tracée dans un plan. Prenons du fil de fer et tordons-le pour qu’il épouse la forme de la courbe Z Allons ensuite nous placer au-dessus d’un parquet dont les lattes sont toutes de largeur 1
Allons ensuite nous placer au-dessus d’un parquet dont les lattes sont toutes de largeur 1 Lançons le fil de fer sur le parquet et considérons le nombre de points d’intersection total entre la courbe en fil de fer et les droites qui bordent les lattes. Si la courbe Z est un segment de longueur inférieure à 1
Lançons le fil de fer sur le parquet et considérons le nombre de points d’intersection total entre la courbe en fil de fer et les droites qui bordent les lattes. Si la courbe Z est un segment de longueur inférieure à 1 nous observons à chaque fois 0 ou 1 intersection. Mais pour une courbe Z plus longue ou plus tordue, plusieurs points d’intersection peuvent être obtenus. Maintenant, effectuons N lancers et faisons la somme I de toutes les intersections observées. Alors, lorsque N tend vers l’infini, le rapport (
nous observons à chaque fois 0 ou 1 intersection. Mais pour une courbe Z plus longue ou plus tordue, plusieurs points d’intersection peuvent être obtenus. Maintenant, effectuons N lancers et faisons la somme I de toutes les intersections observées. Alors, lorsque N tend vers l’infini, le rapport (
 2)(I
2)(I N) tend vers la longueur de la courbe Z
N) tend vers la longueur de la courbe Z
Avec un peu d’imagination, nous pouvons maintenant inverser le lancer. La courbe Z est maintenant tracée au sol, immobile. C’est le plancher qu’on va lancer. Si cela vous inquiète, pensez à une grande feuille de papier calque rayée de droites parallèles faisant des bandes de largeur unité. Nous pouvons lancer le calque sur la courbe Z aléatoirement un grand nombre N de fois. Notons encore I le nombre total d’intersections observées entre les droites tracées sur le calque et la courbe Z Quand le nombre de lancers devient très grand, le rapport I
Quand le nombre de lancers devient très grand, le rapport I N s’approche de(2
N s’approche de(2
 )
) (Longueur de Z). [3]
(Longueur de Z). [3]
Nous pouvons maintenant démontrer la propriété des courbes de largeur constante annoncée. Prenons une courbe de largeur constante égale à1 Lançons la sur un plan qui a été rayé de droites parallèles espacées d’une unité. Une fois sur le plan, la courbe ne peut être située dans une bande entre deux des droites sans toucher aucune de ces droites, car sinon sa largeur serait inférieure à la largeur de la bande, donc inférieure (strictement) à 1
Lançons la sur un plan qui a été rayé de droites parallèles espacées d’une unité. Une fois sur le plan, la courbe ne peut être située dans une bande entre deux des droites sans toucher aucune de ces droites, car sinon sa largeur serait inférieure à la largeur de la bande, donc inférieure (strictement) à 1 Seuls deux cas peuvent donc se produire. Ou bien la courbe coupe une droite en deux points : elle est à cheval entre les deux bandes situées de part et d’autre de la droite. Ou bien la courbe est contenue dans une bande, mais touche les deux droites qui la délimitent. Ainsi, dans tous les cas, le nombre de points d’intersection de la courbe avec les droites tracées dans le plan est égal à 2 ; ceci quelque soit le lancer effectué. Si l’on effectue N lancers, le nombre total d’intersections est donc égal à 2N
Seuls deux cas peuvent donc se produire. Ou bien la courbe coupe une droite en deux points : elle est à cheval entre les deux bandes situées de part et d’autre de la droite. Ou bien la courbe est contenue dans une bande, mais touche les deux droites qui la délimitent. Ainsi, dans tous les cas, le nombre de points d’intersection de la courbe avec les droites tracées dans le plan est égal à 2 ; ceci quelque soit le lancer effectué. Si l’on effectue N lancers, le nombre total d’intersections est donc égal à 2N La formule de Buffon fournit alors
La formule de Buffon fournit alors
 longueur d'une courbe de largeur constante 1
longueur d'une courbe de largeur constante 1  =2
=2
 2=
2=

On retrouve le périmètre du disque de diamètre 1 (donc de rayon 1 2) : toutes les courbes de largeur constante égale à 1 partagent le même périmètre
2) : toutes les courbes de largeur constante égale à 1 partagent le même périmètre 
 De même, le périmètre des courbes de largeur constante L est égal à
De même, le périmètre des courbes de largeur constante L est égal à  L
L
Ceci, plus la solution du problème de Didon [4] nous apprend que le cercle est la courbe de largeur constante donnée qui enclôt l’aire la plus grande. Les triangles de Reuleaux admettent une caractérisation opposée :
Les courbes de largeur constante donnée qui entourent une aire minimale sont les triangles de Reuleaux.
Cette caractérisation des triangles de Reuleaux est dûe à Wilhelm Blaschke et Henri Lebesgue, elle date des années 1910, et est difficile à établir.
Nous pouvons maintenant contempler un joli film issu du site russe déjà cité par Étienne Ghys dans son article sur la machine à marcher. Il illustre élégamment les remarques précédentes et décrit
- une autre construction de courbes de largeur constante ;
- un moteur d’automobile utilisant le triangle de Reuleaux ;
- un mécanisme utilisé pour les projecteurs cinématographiques.
Hexagones de Julius Pál
Si je n’ose présenter ici une preuve de la caractérisation des triangles de Reuleaux dûe à Blaschke et Lebesgue, je ne peux m’empêcher d’expliquer une jolie construction qui permet de comparer toute courbe de largeur constante à des triangles de Reuleaux qui lui sont proches et qui peut donc être utilisée pour démontrer le théorème de Blaschke et Lebesgue. Cette construction est dûe à un mathématicien hongrois, Julius Pál.
Pour la comprendre, commençons par un problème de nature différente qui tracasse pas mal de familles les dimanches d’été : pendant que grand-père se fait roussir la barbe au-dessus du barbecue, papa essaie de placer au milieu de la pelouse la table de jardin qu’il vient d’acheter. Au bout d’un quart d’heure de jurons, il rentre se servir un pastis en hurlant qu’à cause de cette satanée pelouse sa table ne sera jamais stable. Et pourtant. Pourtant, il suffit d’opérer comme suit. Plaçons la table au hasard sur la pelouse ; si elle est bancale, c’est que deux pieds de la table situés en diagonale sont sur le sol, tandis que chacun des deux autres pieds est soit sur le sol, soit décolé, suivant qu’on appuie ici ou là ; il y a donc deux diagonales distinctes, la diagonale d’appui et la diagonale bancale. Tournons maintenant la table progressivement d’un quart de tour. La position finale des diagonales a été inversée, la diagonale d’appui est devenue bancale et la diagonale bancale a maintenant les deux pieds sur terre. Ainsi, au cours de la rotation de la table d’un quart de tour, il y a au moins une position où les deux diagonales échangent leur rôle ; à ce moment là, les quatre pieds de la table touchent le sol simultanément et la table n’est plus bancale (en revanche, elle peut être légèrement penchée suivant l’inclinaison de la pelouse).
Appliquons ce principe de démonstration pour nos courbes de largueur constante. Nous allons montrer que toute courbe de largeur constante est inscrite dans un hexagone régulier dont les côtés sont tous tangents à la courbe. Chaque côté de l’hexagone touche donc la courbe en un unique point. Les hexagones réguliers sont ceux pour lesquels tous les côtés ont même longueur et tous les angles aux sommets sont égaux ; ces deniers valent 120 (soit un tiers de tour). Voici un tel hexagone, avec un triangle de Reuleaux inscrit à l’intérieur pour décorer.
(soit un tiers de tour). Voici un tel hexagone, avec un triangle de Reuleaux inscrit à l’intérieur pour décorer.

Voici maintenant un hexagone régulier, à gauche et, à droite, un hexagone obtenu en faisant coulisser deux côtés parallèles de l’hexagone précédent. De la sorte, nous n’avons changé ni les angles aux sommets ni l’écart entre les côtés opposés ; pourtant, le nouvel hexagone n’est pas régulier.

Donnons nous une courbe P de largeur constante égale à 1 Choisissons deux droites parallèles L et L
Choisissons deux droites parallèles L et L venant toucher la courbe en deux points opposés ; elles sont donc séparées l’une de l’autre d’une unité. Ce choix étant fait, il existe deux paires de droites qui font un angle de120
venant toucher la courbe en deux points opposés ; elles sont donc séparées l’une de l’autre d’une unité. Ce choix étant fait, il existe deux paires de droites qui font un angle de120 avec les deux premières et viennent enserrer la courbe P en des points opposés ; la distance entre ces droites est encore égale à 1 carP est de largeur constante. A priori, l’hexagone formé par ces 6 droites n’est pas régulier car, pour qu’il le soit, il faut que ses 6 côtés aient même longueur, ce qui n’est pas automatique. C’est toutefois un hexagone très spécial : les angles aux sommets valent bien 120
avec les deux premières et viennent enserrer la courbe P en des points opposés ; la distance entre ces droites est encore égale à 1 carP est de largeur constante. A priori, l’hexagone formé par ces 6 droites n’est pas régulier car, pour qu’il le soit, il faut que ses 6 côtés aient même longueur, ce qui n’est pas automatique. C’est toutefois un hexagone très spécial : les angles aux sommets valent bien 120
 et l’écart entre deux côtés parallèles quelconques est égal à 1
et l’écart entre deux côtés parallèles quelconques est égal à 1 Notons A
Notons A B
B C
C D
D E et F les sommets successifs de cet hexagone (voir la figure ci-dessous).
E et F les sommets successifs de cet hexagone (voir la figure ci-dessous).

On remarque alors que cet hexagone est régulier dès que la longueur AB est égale à la longueur DE Si ce n’est pas le cas, on peut donc supposer que AB est strictement plus grand (ou plus petit) que DE
Si ce n’est pas le cas, on peut donc supposer que AB est strictement plus grand (ou plus petit) que DE Faisons maintenant tourner progressivement cette construction en conservant l’appellation des sommets : la courbe P est fixe, mais les deux droites parallèles L et L
Faisons maintenant tourner progressivement cette construction en conservant l’appellation des sommets : la courbe P est fixe, mais les deux droites parallèles L et L font un demi tour, si bien que les six sommets tournent autour de P
font un demi tour, si bien que les six sommets tournent autour de P Une fois le demi tour complètement effectué, les sommets A et B ont été échangés avec les sommets D et E
Une fois le demi tour complètement effectué, les sommets A et B ont été échangés avec les sommets D et E Si la longueur initiale AB est plus grande (ou plus petite) que DE
Si la longueur initiale AB est plus grande (ou plus petite) que DE c’est le contraire qui se produit après ce demi tour ; il y a donc bien un instant au cours de la rotation pour lequel AB=DE
c’est le contraire qui se produit après ce demi tour ; il y a donc bien un instant au cours de la rotation pour lequel AB=DE et pour cet instant l’hexagone ABCDEF est régulier, ce qu’il fallait démontrer.
et pour cet instant l’hexagone ABCDEF est régulier, ce qu’il fallait démontrer.
La figure suivante représente une courbe de largeur constante (elle borde l’union des zones oranges et jaune), un hexagone régulier dans lequel elle est inscrite, et un triangle de Reuleaux qui lui est proche (il entoure la partie jaune et les trois portions vertes). Le lecteur curieux pourra consulter le chapitre 7 du livre [5] pour voir comment cette figure montre que les triangles de Reuleaux entourent une aire minimale.

Solides de Meissner
Quel est l’analogue du triangle de Reuleaux pour les solides convexes, c’est-à-dire pour les parties convexes de l’espace de dimension 3 ? Il s’agit d’abord de savoir comment transposer la propriété « de largeur constante » en dimension 3 Nous dirons donc qu’un solide S est de largeur constante si la largeur entre deux plans parallèles quelconques qui viennent serrer le solide est constante. Pour visualiser cette définition, il suffit de penser à une presse constituée de deux plaques reliées par un pas de vis : posons le solide S sur la plaque inférieure et manœuvrons la presse pour que la plaque supérieure vienne serrer le solide ; S est de largeur constante si la hauteur de la plaque supérieure ne doit pas dépendre de la position du solide S
Nous dirons donc qu’un solide S est de largeur constante si la largeur entre deux plans parallèles quelconques qui viennent serrer le solide est constante. Pour visualiser cette définition, il suffit de penser à une presse constituée de deux plaques reliées par un pas de vis : posons le solide S sur la plaque inférieure et manœuvrons la presse pour que la plaque supérieure vienne serrer le solide ; S est de largeur constante si la hauteur de la plaque supérieure ne doit pas dépendre de la position du solide S
Prenons une courbe de largeur constante qui possède un axe de symétrie, par exemple le triangle de Reuleaux, ou la pièce de fifty pence représentée ci-dessous, puis faisons tourner la courbe dans l’espace autour de son axe. Le solide entouré par cette surface est de largeur constante.

Une autre construction consiste à généraliser celle du triangle de Reuleaux. Prenons donc un tétraèdre régulier. C’est une pyramide dont toutes les faces sont des triangles équilatéraux. Les quatre sommets A B
B C et D sont donc tous à la même distance (disons d’une unité) les uns des autres. La sphère de centre A et de rayon 1 passe ainsi par B
C et D sont donc tous à la même distance (disons d’une unité) les uns des autres. La sphère de centre A et de rayon 1 passe ainsi par B C et D
C et D L’intersection des quatre sphères de centre 1 centrées aux sommets forme un solide parfois appelé tétraèdre de Reuleaux. Le malheur, c’est qu’il n’est pas de largeur constante. Le bonheur, c’est qu’on peut modifier légèrement la construction pour qu’il le devienne. L’idée est dûe à Ernst Meissner et Friedrich Schilling : prenons l’un des côtés T du tétraèdre initial et prolongeons un peu les deux faces contenant ce côté. Elles viennent alors intersecter le tétraèdre de Reuleaux sur deux arcs de cercles C1 et C2
L’intersection des quatre sphères de centre 1 centrées aux sommets forme un solide parfois appelé tétraèdre de Reuleaux. Le malheur, c’est qu’il n’est pas de largeur constante. Le bonheur, c’est qu’on peut modifier légèrement la construction pour qu’il le devienne. L’idée est dûe à Ernst Meissner et Friedrich Schilling : prenons l’un des côtés T du tétraèdre initial et prolongeons un peu les deux faces contenant ce côté. Elles viennent alors intersecter le tétraèdre de Reuleaux sur deux arcs de cercles C1 et C2 Retirons la partie située entre C1 et C2 et remplaçons-la par le nouveau morceau obtenu en faisant tourner l’arc de cercleC1 jusqu’à l’arc de cercle C2 autour de l’axe T
Retirons la partie située entre C1 et C2 et remplaçons-la par le nouveau morceau obtenu en faisant tourner l’arc de cercleC1 jusqu’à l’arc de cercle C2 autour de l’axe T On répète alors cette opération trois fois, soit avec trois côtés T
On répète alors cette opération trois fois, soit avec trois côtés T T
T et T" qui bordent une face du tétraèdre soit avec trois côtés partant d’un même sommet. Nous obtenons deux solides différents, les deux solides de Meissner, qui sont de largeur constante. Pour contempler l’un de ces solides, le mieux est de se rendre sur la page créée par Cristof Weber, de l’université de Zurich.
et T" qui bordent une face du tétraèdre soit avec trois côtés partant d’un même sommet. Nous obtenons deux solides différents, les deux solides de Meissner, qui sont de largeur constante. Pour contempler l’un de ces solides, le mieux est de se rendre sur la page créée par Cristof Weber, de l’université de Zurich.
Le problème ouvert que j’ai mentionné plus haut s’énonce ainsi :
Les solides de largeur constante donnée dont le volume est minimum sont-ils exactement les solides de Meissner ?
Apparemment, la réponse n’est pas connue.
Notes
[1] Franz Reuleaux (1829-1905) est un mécanicien allemand du dix-neuvième siècle réputé qui a contribué à de nombreuses avancées en mécanique, cinématique, et ingénierie. Il fût parfois critiqué, paraît-il, pour avoir une approche un peu trop mathématique de la mécanique... L’ université Cornell, aux Etats-Unis, a créé un bâtiment en son honneur et lui dédie plusieurs sites web : site de la bibliothèque ; site du laboratoire de mathématique .
[2] Cette construction est un progrès véritable, puisqu’on peut
- passer à la limite en utilisant une infinité d’arcs de cercles pour construire de nouvelles courbes de largeur constante ;
- démontrer que toute courbe de largeur constante (égale à 1) peut être approchée par des courbes ainsi formées par des morceaux de cercles de rayon 1

[3] La formule de Cauchy et Crofton dit essentiellement la même chose : la somme (ou plutôt l’intégrale), sur l’ensemble des droites affines du plan, du nombre de points d’intersection entre les droites et une courbe Z fixée est égale à (une constante fixe fois) la longueur de la courbe. Il faut intégrer par rapport à une mesure sur l’espace des droites qui est invariante par rotations et translations ; le choix de la mesure détermine la constante.
[4] Voir le billet de Benoît Kloeckner sur l’inégalité isopérimétrique
[5] H. G. Eggleston : Convexity, Cambridge Tracts in Mathematics and Mathematical Physics, No. 47, (1958), Cambridge University Press
Source : http://images.math.cnrs.fr/Le-triangle-de-Reuleaux.html
17:44 Publié dans Le triangle de Reuleaux | Lien permanent | Commentaires (0) | Tags : le triangle de reuleaux |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Louis Bachelier
Louis Bachelier
11 mars 1870 - 28 avril 1946
Le 15 octobre 2006, par Laurent Carraro et Pierre Crépel
(Cet article, écrit en 2006, est issu de la version papier d’Images des mathématiques.)
Incroyable destinée, pour un mathématicien contemporain, que celle de Bachelier, qui fut d’abord déconsidéré, qui obtint son premier poste fixe à l’université (de Besançon) à 57 ans, et ne devint célèbre que 20 ans après sa mort.
LOUIS Bachelier naquit au Havre, dans une famille habituée aux affaires bancaires et commerciales. Il fit des études sans éclat, puis soutint son doctorat sous la direction de Poincaré le 29 mars 1900, avec seulement la mention “honorable”, sous le titre “Théorie de la spéculation”. Ce travail, qui a pour objet l’application du calcul des probabilités aux opérations de la Bourse, est suivi de nombreux autres notes, mémoires et ouvrages originaux sur les probabilités, rédigés malgré la situation très précaire de leur auteur.

La thèse de Bachelier contient, et cela de trois façons différentes, la première théorie mathématique du mouvement brownien (cinq ans avant Einstein). Ainsi, en utilisant une terminologie moderne, le mouvement brownien est vu tour à tour comme le processus à accroissements indépendants et homogènes dont les trajectoires sont continues, comme le processus à temps continu limite de marches au hasard symétriques, et enfin comme le processus de Markov dont l’équation “forward” de Kolmogorov est l’équation de la chaleur. Bachelier procède à une étude “fine” des trajectoires du mouvement brownien trente ans avant Paul Lévy, à l’aide du principe de réflexion, de la propriété de Markov forte.
On peut interpréter cette thèse comme le confluent de deux traditions apparemment très éloignées :
- La première, qui sert de ligne directrice mathématique à son auteur, est celle de la physique mathématique française de J. Fourier, de G. Lamé et évidemment de H. Poincaré. Bachelier tire d’ailleurs explicitement ses analogies (tel le rayonnement de la probabilité) de ces idées.
- La seconde, ce sont les modèles de raisonnement tacites des spéculateurs en Bourse qu’on trouve, sous des expressions certes moins formalisées, dans la seconde moitié du XIXe siècle. Ainsi un ouvrage de Jules Regnault de 1863 renferme-t-il déjà, en termes plus “littéraires”, le cadre conceptuel de l’application du calcul des probabilités aux opérations de Bourse, notamment le fait que “l’écart pris sur un grand nombre d’opérations est en raison directe de la racine carrée du temps”.
Bachelier a été méprisé, fort peu lu et encore moins compris, et il en a beaucoup souffert : Gevrey et P. Lévy ont cru (à tort) qu’il s’était grossièrement trompé ; seul Kolmogorov a reconnu la profondeur de ses travaux, dans les années trente. Or, non seulement, sa thèse était remarquable, mais ses recherches ultérieures l’étaient quelquefois encore davantage et passèrent à peu près inaperçues, malgré un certain soutien de Poincaré.
Par exemple, son mémoire de 1906 donne-t-il les définitions de grandes classes de processus aléatoires apparus par la suite : processus à accroissements indépendants, processus de Markov, processus d’Ornstein-Uhlenbeck. Ces définitions apparaissent comme conséquences d’une théorie plus générale : celle des équations différentielles stochastiques que Bachelier développe ici, sans toute la rigueur à laquelle nous sommes habitués maintenant, à l’aide d’un vocabulaire issu des jeux de hasard. Deux fonctions jouent un rôle central dans son mémoire, la première, appelée espérance relative à une partie est le terme de “drift” de l’équation différentielle stochastique, alors que la seconde, appelée fonction d’instabilité relative à une partie, est évidemment le coefficient de diffusion de cette même équation. Bachelier raisonne plutôt en trajectoire : ses équations définissent bien un mouvement, en cela il fait penser à Langevin (1908), puis à Itō et Lévy, plus tard. L. Bachelier a en outre introduit une théorie intéressante de la “probabilité inverse” et de la “probabilité des causes”, c’est-à-dire de l’estimation statistique, qu’il a d’ailleurs reprise dans un traité de calcul des probabilités, aussi clair que remarquable, publié en 1912.
N.B. Pour toutes précisions, voir Courtault Jean-Michel & Kabanov Youri (dir.), Louis Bachelier. Aux origines de la finance mathématiqueBesançon, Presses de l’Université de Franc-Comtoises, 2002.
Références
Bachelier, L. (1900), Théorie de la spéculation, Annales de l’Ecole Normale Supérieure, 17, p. 21-86
Bachelier, L. (1906), Théorie des probabilités continues, Journal de mathématiques pures et appliquées, 2, p. 259-327
Bachelier, L. (1912), Calcul des probabilités, Gauthier-Villars, Paris
Gobet, E. (2004), Les mathématiques appliquées au coeur de la finance, Images des mathématiques.
Regnault, J. (1863), Calcul des chances et philosophie de la Bourse, Mallet-Bachelier, Paris
17:42 Publié dans Louis Bachelier | Lien permanent | Commentaires (0) | Tags : louis bachelier |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Mandelbulb
Mandelbulb
Le 16 janvier 2010, par Jos Leys
Mathematical Imagery (page web)
... ou la quête de l’ensemble Mandelbrot en trois dimensions.
IL y a un mois, on voyait apparaître un peu partout sur internet des images d’une nouvelle famille d’ensembles fractals. C’est un groupe d’amateurs, enthousiastes d’images fractales, qui en ont fait la découverte en collaborant dans un forum. Une discussion en ligne sur le sujet du « vrai Mandelbrot 3D » a démarré en septembre et avait plus de 500 contributions vers la fin de novembre. Des dizaines de personnes ont participé en faisant des suggestions de modifications sur les formules et sur les techniques de visualisations, mais on doit attribuer l’idée pour le Mandelbulb, le « bulbe Mandelbrot » à Daniel White etPaul Nylander.
De quoi s’agit-il ?
 De nombreux lecteurs connaissent probablement l’image de gauche qui est l’ensemble Mandelbrot en 2D. Pour chaque nombre complexe
De nombreux lecteurs connaissent probablement l’image de gauche qui est l’ensemble Mandelbrot en 2D. Pour chaque nombre complexe 
 z2+c
z2+c
Prendre le carré du nombre complexe
La figure est fractale : même élargie à l’extrême on voit des détails époustouflants (voir par exemple ce film, extrait de Dimensions, où on peut aussi voir l’effet de prendre le carré d’un nombre complexe sur une photo).
Il ne faut pas se limiter au carré d’un nombre complexe. Si on itère 
 zp+c
zp+c
Depuis sa découverte en 1979 par Benoît Mandelbrot, de très nombreux amateurs ont créé des images fractales basées sur la simple formule d’itération que nous avons vue. Voilà donc une chose dont on a des millions de peintures, mais aucune sculpture !
Une question est devenue comme le Graal des amateurs de fractales : existe-t-il un équivalent en trois dimensions de l’ensemble Mandelbrot ?
L’ensemble Mandelbrot consiste d’une cardioïde entourée de cercles de toutes tailles, qui à leur tour sont entourés de différentes formes, comme des spirales, qui deviennent de plus en plus petites. Il y a des vrilles où poussent des copies minuscules de l’ensemble.
En trois dimensions, on imagine donc un corps principal muni de quelques sphères, et sur les sphères des sphères plus petites, etc. Il va de soi qu’on aimerait voir des vrilles où poussent des copies minuscules de l’ensemble qui à leur tour ont des vrilles microscopiques, etc.
Il faut dire tout de suite que personne n’a encore trouvé un tel objet mais, d’autre part, on n’a pas encore démontré qu’un tel objet n’existe pas. Cela donne la motivation aux amateurs de fractales de continuer leur quête !
Le « Bristorbrot »
Comment pourrait-on essayer de trouver un tel objet ? Voici un premier effort :
Pour l’ensemble de Mandelbrot, on a besoin de nombres complexes

On met la partie réelle  y
y z
z
Définissons ces nombres à trois composantes. On impose que



Si on a 
 w2+c
w2+c
C’est Doug Bristor, un programmeur anglais qui a proposé ce système en 1995 : voici ce que ça donne.

Voici les coupes à travers les plans

Ici non plus, il ne faut pas se limiter à prendre le carré de ces nombres « triplex », on peut aussi dessiner des « Bristorbrot » de plus haut degré.
Si, dans 
 z2+c
z2+c

Le système de Bristor est un bel effort mais on ne peut pas dire qu’on ait trouvé le Saint Graal !
Dessiner des objets fractals en 3D
Avant de revenir au Mandelbulb, parlons un peu des méthodes pour visualiser de tels objets 3D. Pour les fractales 2D il suffit de faire une itération pour chaque pixel de l’image. Si le point s’éloigne de l’origine il sera en dehors de l’ensemble et il reste à décider quelle couleur on donnera à ce pixel. On pourrait simplement colorer tous les pixels « en dehors » en blanc et les pixels « dedans » en noir, mais il y a beaucoup d’autres méthodes. On déclare un pixel comme « en dehors » si son module devient plus grand qu’un nombre qu’on a choisi à l’avance. Les méthodes pour colorer les pixels sont souvent basées sur le nombre d’itérations avant que le module ne devienne assez grand pour être déclaré « en dehors ».
Pour représenter un objet 3D, on doit penser à l’image comme un plan de projection. On choisit un point de vue virtuel et on tire des rayons de ce point de vue vers chaque point du plan de projection, donc vers chaque pixel de l’image. Pour chaque rayon, il faut maintenant découvrir si le rayon rencontre l’objet fractal et, si oui, à quel endroit sur le rayon.
Le plus simple serait de bouger un point sur un rayon vers le plan de projection à petits pas, faire l’itération à chaque pas, et s’arrêter quand l’itération du point sur le rayon nous dit qu’on est « dedans ». Le problème, évidemment, c’est qu’on ne sait pas a priori où se trouve l’objet fractal et on devrait prendre des pas infinitésimaux pour ne rien manquer (rappelez-vous que notre objet pourrait avoir des vrilles très fines) et on risque de prendre un grand nombre de pas inutiles si le rayon ne coupe même pas l’objet. Cela « coûte très cher » en temps de calcul.

Si par contre on connaît une estimation de la distance entre un point sur un rayon et l’objet fractal, on peut d’abord avancer avec un pas plus grand et ajuster les pas lorsqu’on s’approche de l’objet. Heureusement, on peut calculer une telle estimation, ce qui permet de dessiner les objets très rapidement. Vous trouverez les principes de deux méthodes en dépliant : la méthode « analytique » et une méthode développée parDavid Makin.
 Quand on a trouvé le point d’intersection d’un rayon avec l’objet, on doit encore colorer le pixel qui correspond à ce rayon. Heureusement, les fractales n’ont pas de couleur préférée, on peut donc choisir, mais ce sont bien des objets 3D dont la couleur va varier selon la lumière qui tombe sur ce point. Il faut aussi décider si le point est dans l’ombre ou pas. C’est pourquoi il faut savoir à quel endroit sur le rayon se trouve l’intersection, car cela va permettre de mettre en rapport la position du point et la position d’une source de lumière virtuelle. Pour faire tout cela correctement, il nous faut aussi la normale sur la surface fractale. Problème ! Les surfaces fractales n’ont pas de normale car elles sont a prioritrès irrégulières. On résout cela en trouvant quelques autres points d’intersection très près du point principal et en considérant la surface comme étant lisse localement. Avec les coordonnées de ces points on peut calculer un produit vectorielpour approximer une normale.
Quand on a trouvé le point d’intersection d’un rayon avec l’objet, on doit encore colorer le pixel qui correspond à ce rayon. Heureusement, les fractales n’ont pas de couleur préférée, on peut donc choisir, mais ce sont bien des objets 3D dont la couleur va varier selon la lumière qui tombe sur ce point. Il faut aussi décider si le point est dans l’ombre ou pas. C’est pourquoi il faut savoir à quel endroit sur le rayon se trouve l’intersection, car cela va permettre de mettre en rapport la position du point et la position d’une source de lumière virtuelle. Pour faire tout cela correctement, il nous faut aussi la normale sur la surface fractale. Problème ! Les surfaces fractales n’ont pas de normale car elles sont a prioritrès irrégulières. On résout cela en trouvant quelques autres points d’intersection très près du point principal et en considérant la surface comme étant lisse localement. Avec les coordonnées de ces points on peut calculer un produit vectorielpour approximer une normale.
Cette technique de « raytracing » est assez rapide. Les images ci-dessous prennent environ une minute à calculer (taille 1000*1000 pixels) [2]. À noter qu’il est possible de programmer de tels algorithmes sur les processeurs de la carte graphique de l’ordinateur, ce qui permet de calculer ces images en une fraction d’une seconde !
Le « Mandelbulb »

Revenons sur la quête du Mandelbrot 3D.
Un point dans l’espace à trois dimensions est décrit par trois coordonnées  y
y z
z
On obtient les angles par  x2+y2
x2+y2
Voici l’idée de Daniel White : comme le passage au carré consiste de doubler l’angle et à prendre le carré du module, on définit le « carré » d’un point en coordonnées sphériques comme
 =R2sin(2p)cos(2t)
=R2sin(2p)cos(2t) =R2sin(2p)sin(2t)
=R2sin(2p)sin(2t) =R2cos(2p)
=R2cos(2p)
ou plus généralement :  =Rqsin(qp)cos(qt)
=Rqsin(qp)cos(qt) =Rqsin(qp)sin(qt)
=Rqsin(qp)sin(qt) =Rqcos(qp)
=Rqcos(qp)
 wq+c
wq+c
Voici ce qu’on obtient avec

Une déception ! L’objet ne ressemble même pas l’ensemble de Mandelbrot. Il est vrai qu’on repère quelques éléments fractals sur l’objet, comme les petits « arbres » sur le côté gauche mais si on veut trouver le fameux Graal, il va falloir chercher ailleurs, semble-t-il.
Mais pourquoi ne pas essayer ce que ça donne avec d’autres valeurs de

Cela va dans la bonne direction, c’est-à-dire que l’objet devient plus régulier. Alors on essaie

En augmentant le degré il semble que de plus en plus de « bulbes » poussent sur l’objet. Prenons

... et sautons vers

C’est ce Mandelbulb de degré 8 qui est devenu le plus populaire mais rien ne nous empêche de dessiner le Mandelbulb de degré 16 :

Pour mieux apprécier les détails de l’objet, voici encore quelques vues de plus près :

L’animation en bas prouve que l’objet est bien fractal : c’est un zoom d’ordre
Regardez aussi quelques autres images sur le site de l’auteur. On peut aussi admirer une image géante par Daniel White ici.
On n’a donc pas encore trouvé ce Saint Graal et la quête continue ; mais on a fait cette belle découverte du Mandelbulb en route. Si vous voulez participer et suivre quelles autres choses concoctent tous ces amateurs, il suffit de s’inscrire sur Fractalforums.com. Vous y serez le bienvenu !
Notes
[1] Jussi HARKONEN. On smooth fractal coloring techniques. (Master’s thesis)
[2] Les images de cet article ont été calculées avec le logiciel Ultrafractal sur un ordinateur à double cœur.
[3] Dans les algorithmes des logiciels, on utilise la fonction atan2(x,y) qui est équivalente à
17:36 Publié dans Mandelbulb | Lien permanent | Commentaires (0) | Tags : mandelbulb |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Images mathématiques




































17:25 Publié dans Images mathématiques | Lien permanent | Commentaires (0) | Tags : images mathématiques |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
21/01/2010
Liens vers des sites de mathématiques
- Academy of Sciences of the Czech Republic
- American Institute of Mathematics
- Argonne National Lab, Mathematics and Computer Science
- AT&T Bell Laboratories Research
- Australian CSIRO Math/Stat
- Australian Mathematical Sciences Institute (AMSI)
- Basic Research Institute in the Mathematical Sciences
- Budapest Semesters in Mathematics Program
- CMU Center for Nonlinear Analysis
- Center for Advanced Studies, Research and Development in Sardinia Applied Math Group
- Center for Applied Mathematics and Theoretical Physics (U Maribor)
- CCM, The Center for Coputational Mathematics, University of Colorado, Denver
- Center for Dynamical Systems and Nonlinear Studies
- Centre for Engineering and Industrial Mathematics (U Wollongong)
- Centre for Experimental & Constructive Mathematics
- Center for Gravitational Physics and Geometry
- Centre Emile Borel
- Centre for Industrial and Applied Mathematics (U South Australia)
- Centre for Innovation in Mathematics Teaching
- Centro Internazionale Matematico Estivo
- Centre International de Mathématiques Pures et Appliquées
- Centre International de Recontres Mathématiques (CIRM)
- Centro de Investigación en Matemáticas A.C (Mexico)
- Centre de Mathématiques (École Polytechnique)
- Centre de Mathematiques Appliquees (École des Mines de Paris)
- Center for Mathematical Analysis, Geometry, and Dynamical Systems
- Center for the Mathematical Sciences (UWisconsin)
- Centre de Recerca Matemàtica (Barcelona)
- Centre de recherches mathématiques (UMontréal)
- Center for Research in Scientific Computation (at NCSU)
- Center for Statistical and Mathematical Computing
- Centrum voor Wiskunde en Informatica (CWI)
- Claremont Research Institute of Applied Mathematical Sciences (CRIAMS)
- The Clay Mathematics Institute (CMI)
- Collège de France, Sciences Mathématiques, Physiques et Naturelles
- Computer Algebra Information Network
- Cornell Center for Applied Mathematics
- Courant Institute of NYU
- CTI Centre for Mathematics and Statistics
- Diffiety Instute of the Russian Academy of Natural Sciences
- DIMACS
- Euler Institute fot Discrete Mathematics and its Applications
- The Euler International Mathematical Institute
- Erwin Schrodinger Institute of Mathematical Physics
- Euromath Center
- EURHomogenization
- The Fields Institute for Research in Mathematical Sciences
- Fuzzy Logic Laboratory Linz
- Geometry Center (UMinn)
- Groupe Fractales (INRIA)
- Indian Statistical Institute
- Industrial Mathematics Institute (Linz)
- Institut de Mathématiques de Bordeaux
- Institut des Hautes Etudes Scientifiques IHES
- Institute for Advanced Study
- Institute of Applied and Computational Mathematics
- Institute for Computational Fluid Dynamics
- Institute for Computer Applications in Science and Engineering
- Institute of Cybernetics, Applied Math. Dept. (Estonia)
- Institute of Mathematics and Geometry (Faculty of Civil Engineering and Architecture) University of Innsbruck, Austria
- Institut für Dynamische Systeme (Bremen)
- Institute for Experimental Mathematics (Essen)
- Institute for Mathematical Research (FIM, ETH-Zuerich)
- Institute for Studies in Theoretical Physics and Mathematics (IPM)
- Institut Fourier, Université Joseph Fourier
- Institut Henri Poincare
- Institute of Information Theory and Automation (Czech Academy of Sciences)
- Institute of Mathematical Sciences (India)
- Institut of Mathematics, University of Liege
- Institut d'Informatique et de Mathématiques Appliquées de Grenoble
- Institute for Mathematics and its Applications
- Institut de Mathématiques Appliquées
- Institute of Mathematics and Computer Science in Medicine (IMDM)
- Institut de Mathématique de Jussieu (Paris VI et Paris VII)
- Institute of Mathematics and Informatics (Bulgarian Academy of Sciences)
- Institute of Mathematics and Informatics Lithuania
- Institute of Mathematics, Physics and Mechanics (Ljubljana)
- Institute of Mathematics of the Polish Academy of Sciences
- Instituto de Matemática Pura e Aplicada (Brazil)
- Instituto de Matematicas y Estadistica (Uruguay)
- Institute of Mathematical Sciences Hong Kong
- Instituto Nacional de Pesquisas Espaciais Brazil (applied math)
- Institute of Numerical Mathematics (RAS)
- Institute for Pure and Applied Mathematics at UCLA
- Institut de Recherche Mathématique Avancée (IRMA)
- Institut de Recherche Mathematique de Rennes (IRMAR)
- Institut des sciences mathematiques (ISM)
- Institute of Statistical Mathematics (Japan)
- International Centre of Excellence for Education in Mathematics (ICE-EM)
- International Centre for Mathematical Sciences, Edinburgh
- International Centre for Theoretical Physics
- Isaac Newton Institute for Mathematical Sciences
- Konrad-Zuse-Zentrum (Berlin)
- Laboratory for Computer Aided Mathematics (U Helsinki)
- Manchester Centre for Computational Mathematics
- Mathematical Analysis Research Group
- Mathematical Sciences Research Institute
- Mathematics Institute of the Romanian Academy (IMAR)
- Mathematisches Forschungsinstitut Oberwolfach
- Max-Planck Institut f"ur Mathematik, Bonn
- Max-Planck Institut f"ur Mathematik in den Naturwissenschaften, Leipzig
- Mittag-Leffler Institute
- Pacific Institute for the mathematical sciences
- pLab Project (Salzburg)
- Programme de Recherches Coordonnées, Mathématiques et Informatique
- Research Centre of Applied Mathematics CIRAM (Bologna)
- Research Institute for Mathematical Sciences RIMS (Kyoto)
- Research Institute for Symbolic Computation (RISC-Linz)
- Steklov Institute of Mathematics, Russian Academy of Sciences
- Steklov Mathematical Institute
- Systems Analysis Laboratory (Helsinki UT)
- Tata Institute of Fundamental Research (India)
- University of Graz Institute of Mathematics
- Unión Matemática Argentina
- UMass Center for Geometry Analysis Numerics and Graphics
- University of Minnesota Geometry Center
- University of Nevada, Reno Mathematics Center
- Virtual Institute of Mathematical Sciences
- Visual Math Institute
- Weierstraß-Institute for Applied Analysis and Stochastics (WIAS)
- Magnet High Schools in Mathematics
- Bronx High School of Science
- Central Virginia Governor's School for Science and Technology
- Illinois Mathematics and Science Academy
- Massachusetts Academy of Mathematics and Science
- Mississippi School for Mathematics and Science
- Montgomery Blair High School
- New Horizons Governor's School (VA)
- North Carolina School of Science and Mathematics
- Oklahoma School of Science and Mathematics
- Roanoke Valley Governor's School for Science and Technology (VA)
- Thomas Jefferson High School for Science and Technology
11:27 Publié dans Liens vers des sites de mathématiques | Lien permanent | Commentaires (0) | Tags : liens vers des sites de mathématiques |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Les flottants au format double
![]()
![]()
![]()
![]()
suivant: Opérations sur les flottants monter: Les réels précédent: Virgule fixe et flottante. Index
Les flottants au format double
Cette section développe les notions de la section précédente pour les flottants machine, utilisables dans les langage de programmation usuels, elle peut être omise. La représentation d'un double en mémoire se compose de 3 parties : le bit de signe s = ±1 sur 1 bit, la mantisse M
Pour écrire un nombre sous cette forme, il faut d'abord chercher par quel multiple de 2 il faut le diviser pour obtenir un réel r dans [1, 2[, ce qui permet de déterminer l'exposant e. Ensuite on écrit la représentation en base 2 de r - 1
- -2
Signe négatif. Il faut diviser sa valeur absolue 2 par 21 pour être entre 1 et 2 dont e + 1 - 210 = 1, l'exposant est e = 210. On a alors r = 1, r - 1 = 0. Représentation
1 10000000000 00000000...0000 - 1.5=3/2
Signe positif, compris entre 1 et 2 dont l'exposant vérifie e + 1 - 210 = 0 soit e = 210 -1 = 29 +28 +27 +26 +25 +24 +23 +22 +21 +20. On a r - 1 = 1/2 = 2-1. D'où la représentation
0 01111111111 10000000...0000 - 6.4=32/5
Positif. Il faut le diviser par 22 pour avoir 8/5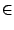 [1, 2[ donc e + 1 - 210 = 2 soit e = 210 + 1. Ensuite r = 3/5 qu'il faut écrire en base 2 (cf. section précédente), on écrit donc les 52 premiers éléments du développement avec une règle d'arrondi du dernier bit au nombre le plus proche. Ici le bit suivant le dernier
[1, 2[ donc e + 1 - 210 = 2 soit e = 210 + 1. Ensuite r = 3/5 qu'il faut écrire en base 2 (cf. section précédente), on écrit donc les 52 premiers éléments du développement avec une règle d'arrondi du dernier bit au nombre le plus proche. Ici le bit suivant le dernier 1001est un1, on arrondit donc à1010. D'où la représentation
0 1000000001 100110011001...10011010
0.3 - 3*0.1 n'est pas nul. Des représentations spéciales (avec e = 0 ou e = 211 - 1) ont été introduites pour représenter ±![]() (pour les flottants plus grands en valeur absolue que le plus grand flottant représentable), et pour représenter les nombres non nuls plus petits que le plus petit flottant représentable de la manière exposée ci-dessus (on parle de flottants dénormalisés), ainsi que le nombre NaN (Not a Number) lorsqu'une opération a un résultat indéfini (par exemple 0/0).
(pour les flottants plus grands en valeur absolue que le plus grand flottant représentable), et pour représenter les nombres non nuls plus petits que le plus petit flottant représentable de la manière exposée ci-dessus (on parle de flottants dénormalisés), ainsi que le nombre NaN (Not a Number) lorsqu'une opération a un résultat indéfini (par exemple 0/0).
suivant: Opérations sur les flottants monter: Les réels précédent: Virgule fixe et flottante. Index Retour à la page principale de mat249 Source : http://www-fourier.ujf-grenoble.fr/~parisse/mat249/mat249... Source :
11:23 Publié dans Les flottants au format double | Lien permanent | Commentaires (0) | Tags : les flottants au format double |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Séries entières
![]()
![]()
![]()
![]()
suivant: Série alternée monter: Développement de Taylor, séries précédent: La fonction exponentielle Index
Séries entières.
Les séries de type prendre la limite lorsque n tend vers l'infini du développement de Taylor en x=0 sont de la forme
![$displaystyle {frac{{f^{[n]}(0)}}{{n!}}}$](http://www-fourier.ujf-grenoble.fr/~parisse/mat249/mat249/img83.png)
On peut s'intéresser plus générallement à
S'il existe un point x0 tel que | anx0n| est borné (ce sera le cas en particulier si la série converge en x0), alors
la série converge donc en x si | x| < | x0| et on peut majorer le reste de la série au rang n par
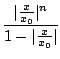
la vitesse de convergence est donc du même type que pour le théorème du point fixe (le nombre de termes à calculer pour trouver une valeur approchée avec k décimales dépend linéairement k, les constantes sont d'autant plus grandes que | x| est grand).
alors la série converge pour | x| < | x0| et pour n
On en déduit qu'il existe un réel positif R ![]() 0 éventuellement égal à +
0 éventuellement égal à + ![]() tel que la série converge (la limite de la somme jusqu'à l'infini existe) lorsque | x| < R et n'existe pas lorsque | x| > R, ce réel est appelérayon de convergence de la série. Par exemple ce rayon vaut +
tel que la série converge (la limite de la somme jusqu'à l'infini existe) lorsque | x| < R et n'existe pas lorsque | x| > R, ce réel est appelérayon de convergence de la série. Par exemple ce rayon vaut + ![]() pour l'exponentielle, le sinus ou le cosinus. Il est égal à 1 pour la série géométrique
pour l'exponentielle, le sinus ou le cosinus. Il est égal à 1 pour la série géométrique ![]() xn (car elle diverge si | x| > 1 et converge si | x| < 1). On ne peut pas dire ce qui se passe génériquement lorsqu'on est à la limite, c'est-à-dire lorsque | x| = R (si R
xn (car elle diverge si | x| > 1 et converge si | x| < 1). On ne peut pas dire ce qui se passe génériquement lorsqu'on est à la limite, c'est-à-dire lorsque | x| = R (si R ![]() +
+ ![]() ). Mais cela n'a en fait pas trop d'importance en pratique car même si la série converge, elle converge souvent trop lentement pour donner de bonnes approximations. En fait, la vitesse de convergence d'une série entière de rayon R
). Mais cela n'a en fait pas trop d'importance en pratique car même si la série converge, elle converge souvent trop lentement pour donner de bonnes approximations. En fait, la vitesse de convergence d'une série entière de rayon R ![]() +
+ ![]() est en gros la même que celle d'une série géométrique de raison | x|/R.
est en gros la même que celle d'une série géométrique de raison | x|/R.
Lorsque 2 séries ont un rayon de convergence non nul, alors on peut effectuer leur somme, leur produit comme des polynômes et la série somme/produit a un rayon de convergence au moins égal au plus petit des 2 rayons de convergence des arguments. On peut inverser une série entière non nulle en 0 en appliquant
et on obtient une série entière de rayon de convergence non nul. On peut aussi composer deux séries entières g et f en gof (avec les règles de calcul de composition des polynômes) si f (0) = 0. On peut enfin dériver et intégrer une série entière terme à terme dans son rayon de convergence.
On dit qu'une fonction est développable en série entière en 0 si elle est égale à son développement de Taylor en 0 sommé jusqu'en l'infini dans un disque de centre 0 et de rayon non nul. Les fonctions exponentielle, sinus, cosinus sont donc développables en série entière en 0. La fonction tangente également car le dénominateur cosinus est non nul en 0, mais son rayon de convergence n'est pas l'infini et le calcul des an est assez complexe. La fonction (1 + x)![]() est développable en séries entières pour tout
est développable en séries entières pour tout ![]()
![]()
![]() avec un rayon de convergence 1 (ou l'infini pour
avec un rayon de convergence 1 (ou l'infini pour ![]() entier positif).
entier positif).
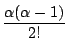 x2 + ... +
x2 + ... + 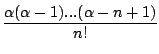 xn + ...
xn + ...Pour
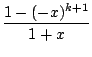
En intégrant par rapport à x, on obtient que ln(1 + x) est développable en série entière en 0 de rayon de convergence 1 et
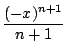
On peut calculer de manière analogue le développement en série entière de arctan(x) en iintégrant celui de 1/(1 + x2), de même pour arccos(x) et arcsin(x) en intégrant celui de (1 - x2)-1/2.
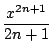 ,
,On peut donc calculer ln, arctan, ... par ces formules, mais il faut répondre à la question où arrête-t-on la somme pour obtenir une précision donnée? Dans le cas de ln(1 + x), on pourrait répondre comme avec l'exponentielle en majorant la dérivée n + 1-ième, mais ce n'est plus faisable pour arctan, arcsin, arccos. On va donner un autre critère qui ne nécessite pas de calculer cette dérivée mais utilise l'alternance des signes dans la somme.
suivant: Série alternée monter: Développement de Taylor, séries précédent: La fonction exponentielle Index Retour à la page principale de mat249 Source : http://www-fourier.ujf-grenoble.fr/~parisse/mat249/mat249...
11:10 Publié dans Séries entières | Lien permanent | Commentaires (0) | Tags : séries entières |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Index - fourier.ujf-grenoble.fr
![]()
![]()
![]()
suivant: À propos de ce monter: Mat 249 précédent: Quelques références
Index
- atan
- Séries entières.
- Bezout
- Arithmétique des polynomes: Bézout
- bit
- Les flottants au format
- complexe
- Types composés.
- contractante
- Le point fixe
- convexe
- La méthode de Newton.
- cos
- La fonction exponentielle
- determinant
- Déterminant
- diagonalisation
- Réduction exacte des endomorphismes
- division euclidienne
- Entiers courts et longs
- double
- Les flottants au format
- erreur
- Erreur absolue, relative et | Erreurs d'arrondis du pivot
- exp
- La fonction exponentielle
- exposant
- Les flottants au format
- expression
- Types composés.
- factorisation
- Multiplicité des racines. | Factorisation dans
 . | Calcul approché des racines | Factorisation dans
. | Calcul approché des racines | Factorisation dans  | Factorisation exacte
| Factorisation exacte - flottant
- Les flottants au format
- fonction
- Types composés.
- Gauss
- Le pivot de Gauss
- integration
- Intégration numérique
- interpolation
- Approximation polynomiale
- inverse
- Inverse
- iterations inverses
- Itérations inverses
- ker
- Noyau
- lagrange
- Approximation polynomiale | Approximation polynomiale
- liste
- Types composés.
- ln
- La fonction logarithme
- LU
- La méthode de factorisation
- mantisse
- Les flottants au format
- matrice
- Types composés.
- multiplicite
- Multiplicité des racines.
- Newton
- La méthode de Newton. | La méthode de Newton.
- Newton-Cotes
- Newton-Cotes
- noyau
- Noyau
- ordre
- Ordre d'une méthode
- pivot
- Le pivot de Gauss
- point fixe
- Le point fixe
- point milieu
- Les rectangles et les
- polynome
- Types composés.
- polynome caracteristique
- Polynome caractéristique
- polynome minimal
- Polynome minimal
- puissance
- Méthode de la puissance
- quadrature
- Intégration numérique
- racine
- Multiplicité des racines. | Calcul approché des racines
- racines rationnelles
- Factorisation exacte
- rationnel
- Entiers courts et longs
- rectangle
- Les rectangles et les
- reduction
- Réduction sous forme échelonnée
- rref
- Réduction sous forme échelonnée
- sequence
- Types composés.
- serie alternee
- Série alternée
- serie entiere
- Séries entières.
- Simpson
- Simpson
- sin
- La fonction exponentielle
- squarefree
- Multiplicité des racines.
- Sturm
- Factorisation dans
- symbole
- Types composés.
- Taylor
- Développement de Taylor, séries
- trapeze
- Les rectangles et les
- vecteur
- Types composés.
- Source :
- http://www-fourier.ujf-grenoble.fr/~parisse/mat249/mat249...
11:09 Publié dans Index - fourier.ujf-grenoble.fr | Lien permanent | Commentaires (0) | Tags : index - fourier.ujf-grenoble.fr |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Erreur absolue, relative et propagation des erreurs
![]()
![]()
![]()
![]()
suivant: Types composés. monter: Les réels précédent: Erreurs Index
Erreur absolue, relative et propagation des erreurs.
On a vu précédemment que pour représenter un réel, on devait l'arrondir, ce qui introduit une erreur même si le réel est connu exactement (par exemple 1/10). Voyons comment se propagent les erreurs dans les opérations arithmétiques de base : on distingue l'addition, la multiplication et l'inversion. La soustraction se ramène à l'addition car le calcul de l'opposé n'introduit aucune erreur nouvelle. Pour l'addition, si |x - x0|
on dit que les erreurs absolues s'additionnent.
Mais comme il faut représenter x0 + y0 en machine, on doit ajouter une erreur d'arrondi, qui est proportionnelle à la valeur absolue de x0 + y0 d'où la notion d'erreur relative :
Remarquons au passage que les erreurs de mesure expérimentales sont pratiquement toujours des erreurs relatives.
Donc lorsqu'on effectue une addition (ou une soustraction) de deux réels sur machine, on doit additionner les deux erreurs absolues sur les opérandes et ajouter une erreur d'arrondi (relative de 2-53, à titre d'exercice, on pourra vérifier que cette erreur d'arrondi est majorée par l'erreur absolue de la somme x + y dès l'instant où x et y ont eux-même une erreur d'arrondi).
Lorsqu'on effectue une multiplication de deux nombres x, y dont les représentants x0, y0 sont non nuls, on a
l'erreur relative est donc la somme des erreurs relatives et du produit des erreurs relatives (on peut souvent négliger le produit devant la somme). Il faut aussi y ajouter une erreur relative d'arrondi de 2-53 surx0y0.
On observe que la multiplication est une opération posant moins de problèmes que l'addition, car on manipule toujours des erreurs relatives, par exemple si l'erreur relative sur deux doubles x et y non nuls est de 2-53, alors l'erreur relative sur xy sera de
Lorsque l'erreur relative sur les données est grande devant 2-53, l'erreur relative d'arrondi final est négligeable, on peut alors dire que les erreurs relatives s'additionnent pour un produit (c'est aussi vrai pour un quotient: exercice!). Par contre, si on additionne deux nombres dont le représentant de la somme est proche de 0, la somme des erreurs absolues peut devenir non négligeable par rapport à la somme des représentants, entrainant une erreur relative très grande. Par exemple si x est représenté par x0 = 1 + 2-52 avec une erreur d'arrondi de 2-53 et y par y0 = - 1 avec la même erreur d'arrondi, l'addition de x et yrenvoie 2-52 avec une erreur absolue de 2*2-53 (ici il n'y a pas d'arrondi lorsqu'on fait la somme). C'est une erreur relative de 1 (qui domine largement l'erreur d'arrondi) ce qui signifie que dans la mantisse, seul le premier bit sur les 52 a un sens, la perte de précision est très grande.
Une autre conséquence importante est que l'addition de réels sur machine n'est pas une opération associative, par exemple
alors que
Si on a plusieurs termes à additionner, il faut commencer par additionner entre eux les termes les plus petits, pour que les petits termes ne soient pas absorbés un à un dans les erreurs d'arrondi (les petits ruisseaux font les grands fleuves).
Exercice : pour calculer la valeur numérique d'une dérivée de fonction, il vaut mieux calculer (f (x + h) - f (x - h))/(2h) que (f (x + h) - f (x))/h. Attention à ne pas prendre h trop petit, sinon x + h = x.
Remarquons néanmoins que les erreurs calculées ici sont des majorations des erreurs réelles (ou si on préfère l'erreur obtenue dans le pire des cas), statistiquement les erreurs sur les résultats sont moindres. Il est d'ailleurs souvent trop difficile de calculer la majoration rigoureuse de l'erreur pour des calculs complexes. Lorsqu'on doute de la précision d'un calcul, un test peu couteux consiste à refaire ce calcul en utilisant des flottants en précision plus grande et tester si le résultat varie en fonction du nombre de chiffres significatifs utilisés. On peut aussi faire varier légèrement les données et observer la sensibilité du résultat. Si on veut travailler en toute rigueur sans pour autant calculer les erreurs à priori, il faut utiliser un logiciel utilisant des intervalles pour représenter les réels (par exemple la bibliothèque C MPFI).
suivant: Types composés. monter: Les réels précédent: Erreurs Index Retour à la page principale de mat249 Source : http://www-fourier.ujf-grenoble.fr/~parisse/mat249/mat249...
11:08 Publié dans Erreur absolue, relative et propagation des erreur | Lien permanent | Commentaires (0) | Tags : erreur absolue, relative et propagation des erreurshttp:www-fourier.ujf-grenoble |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
Arithmétique des polynomes: Bézout et applications
On considère les polynômes à une variable à coefficients dans ![]() ou
ou ![]() ou
ou ![]() . Les algorithmes de base déjà évoqués sont l'évaluation en un point (méthode de Horner), l'addition, la soustraction, la multiplication et la division euclidienne de A par B
. Les algorithmes de base déjà évoqués sont l'évaluation en un point (méthode de Horner), l'addition, la soustraction, la multiplication et la division euclidienne de A par B ![]() 0 :
0 :
A l'aide de la division euclidienne, on peut calculer le PGCD de deux polynômes par l'algorithme d'Euclide. Nous allons présenter l'algorithme d'Euclide étendu (ou de Bézout)
Algorithme :
On construit en fait 3 suites (Un), (Vn) et (Rn) telles que :
- on initialise U0 = 1, V0 = 0, R0 = A et U1 = 0, V1 = 1, R1 = B
- on calcule les indices n + 2 en fonction de n et n + 1 en effectuant la division euclidienne de Rn par Rn+1 Rn = QnRn+1 + Rn+2, Un+2 = Un - QnUn+1, Vn+2 = Vn - QnVn+1
- on s'arrête au dernier reste non nul
Exemple :
A = x3 -1, B = x2 + 1, les rangs 0 et 1 sont donnés ci-dessus. Au rang 2, Q0 est le quotient euclidien de A par B (fonction quo) donc x, d'où
Puis on divise x2 + 1 par - x - 1, quotient - x + 1, donc
Preuve de l'algorithme :
On montre facilement par récurrence que la relation AUn + BVn = Rn est conservée. Comme Rn est la suite des restes, le dernier reste non nul est bien le pgcd de A et B. D'autre part, examinons les degrés des Vk. Supposons que deg(A) ![]() deg(B) (sinon on échange A et B). Au rang n = 0, V0 = 0 donc V2 = - Q0V1, aux rangs suivants le degré de Qn est non nul (car le degré de Rn+1 est strictement inférieur au degré de Rn) On montre donc par récurrence que la suite des degrés de Vn est croissante et que :
deg(B) (sinon on échange A et B). Au rang n = 0, V0 = 0 donc V2 = - Q0V1, aux rangs suivants le degré de Qn est non nul (car le degré de Rn+1 est strictement inférieur au degré de Rn) On montre donc par récurrence que la suite des degrés de Vn est croissante et que :
Comme deg(Qn)=deg(Rn)-deg(Rn+1), on en déduit que
Donc si n + 2 est le rang du dernier reste non nul, Vn+2 = V et degV=degA-degRn+1 est donc strictement inférieur au degré de A (car Rn+1, l'avant-dernier reste non nul, est de degré plus grand ou égal à 1). On en déduit enfin que le degré de U est strictement inférieur au degré de B, car AU = R - BV, le degré de BV est strictement inférieur à celui de B plus celui de A.
L'identité de Bézout permet de résoudre plus générallement une équation du type
où A, B, C sont trois polynômes donnés, à condition que C soit divisible par le pgcd de A et B. L'ensemble des solutions s'obtient à partir d'une solution particulière U, V de Bézout, notons c = C/gcd(A, B), on a alors
et l'ensemble des solutions est donné par u = cU - PB, v = cV + PA où P est un polynôme quelconque. Si le degré de C est plus petit que le degré de A plus le degré de B, il existe une solution ``priviligiée'', on prend pour u le reste de la division euclidienne de cU par B, v est alors le reste de la division euclidienne de cV par A pour des raisons de degré.
Exemple : si on veut résoudre
on multiplie U = x - 1 et V = 1 + x - x2 par x2 ce qui donne une solution
l'ensemble des solutions est de la forme
et la solution priviligiée (de degrés minimaux) est
L'identité de Bézout intervient dans de nombreux problèmes en particulier la décomposition en éléments simples d'une fraction rationnelle. Si le dénominateur D d'une fraction se factorise en produit de 2 facteurs D = AB premiers entre eux, alors il existe deux polynômes u et v tels que N = Au + Bv, donc
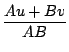 =
=
Si de plus N/D est une fraction propre (degré de N plus petit que celui de D), alors u/B et v/A sont encore des fractions propres (en calculant le reste de la division euclidienne pour u et v comme expliqué ci-dessus).
Par exemple :
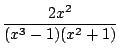 =
= 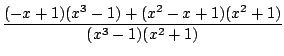 =
= 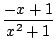 +
+ 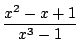
Les applications sont diverses, citons
- le calcul de primitive de fraction rationnelles (et tout ce qui s'y ramène), par exemple
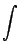
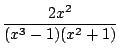 = =
= = 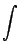
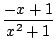 +
+ 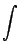
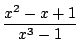
Puis on fait apparaitre la dérivée du dénominateur au numérateur pour éliminer les x, 2x = (x2 + 1)'
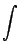
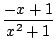
= - 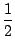
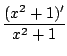 +
+ 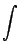
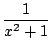 +
+ 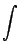
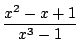
= - 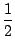 ln(x2 +1) + arctan(x) +
ln(x2 +1) + arctan(x) + 
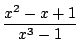
pour faire le calcul complet, il faut aussi décomposer la fraction restante (exercice!) - le calcul de transformée de Laplace inverse de fractions rationnelles, l'idée est la même, sauf qu'on remplace l'intégrale par la transformée de Laplace inverse (et les formules donnant la transformée inverse de 1/(x - p), 1/(x2 + p2), p/(x2 + p2) respectivement exp(px), sin(xp)/p, cos(px)) (calcul non exigible à l'examen)
- le calcul du terme d'ordre n du développement de Taylor en 0 d'une fraction rationnelle. On décompose, et on se ramène à des séries dont le terme général est connu, comme (a + x)-n. Par exemple pour connaitre le développement de 1/(x2 - 3x + 2), on factorise le dénominateur 1/((x - 1)(x - 2)), on décompose
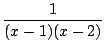 =
= 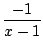 +
+ 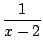 =
= 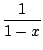 -
- 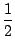
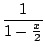
et on développe, le terme d'ordre n est donc 1 - (1/2)n+1.
Il faut néanmoins savoir factoriser un polynôme, ce dont nous parlerons dans la section suivante.
Exercice : Calculer l'intégrale
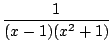
en utilisant l'identité de Bézout pour décomposer la fraction rationnelle. Trouver à l'aide de cette décomposition le terme d'ordre n du développement de Taylor de la fraction à intégrer, vérifier avec un logiciel de calcul formel que les termes d'ordre 0 à 3 sont corrects.
Una autre application est l'élimination dans les systèmes polynomiaux, par exemple considérons le système de 2 équations à 2 inconnues (intersection d'une ellipse et d'un cercle) :
En calculant les coefficients de Bézout des 2 polynômes en x x2 + y2 - 9 et x2 +2y2 - 2xy - 7 et en multipliant au besoin par le PPCM (plus grand commun multiple) des dénominateurs, on obtient à droite de l'équation de Bézout un polynôme ne dépendant que de y et qui s'annule aussi aux solutions du système, on peut alors résoudre en y (en factorisant) puis en x. Ici par exemple ce polynome est 5y4 -32y2 + 4. Cette méthode se systématise, le polynome obtenu par élimination d'une variable est appelé résultant.
Retour à la page principale de mat249 Source : http://www-fourier.ujf-grenoble.fr/~parisse/mat249/mat249...
06:50 Publié dans Arithmétique des polynomes: Bézout et applications | Lien permanent | Commentaires (0) | Tags : arithmétique des polynomes: bézout et applications |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook



