20/11/2010
Suite d'entiers
Suite d'entiers
En mathématiques, une suite d'entiers peut être précisée explicitement en donnant une formule pour ses n-ièmes termes, ou implicitement en donnant une relation entre ses termes. Par exemple, la suite 0, 1, 1, 2, 3, 5, 8, 13, ... (la suite de Fibonacci) est formée en commençant avec 0 et 1, puis en additionnant deux termes consécutifs pour obtenir le suivant : c'est une définition implicite. La suite 0, 3, 8, 15, ... est formée en se fondant sur la formule 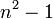 pour le n-ième terme : c'est une définition explicite.
pour le n-ième terme : c'est une définition explicite.
Des suites d'entiers qui ont leurs propres noms sont :
- Les nombres de Catalan
- Les nombres d'Euler
- Les nombres de Fibonacci
- Les nombres figurés
- Les nombres de Lucas
- Les nombres pratiques
- Les nombres premiers de Mersenne
Une suite d'entiers est une suite calculable, s'il existe un algorithme qui, pour un n donné, calcule an, pour tout n > 0. Une suite d'entiers est une suite définissable, s'il existe un certain énoncé P(x) qui est vrai pour cette suite d'entiers x et faux pour toutes les autres suites d'entiers. L'ensemble des suites d'entiers calculables et définissables est dénombrable, avec les suites calculables d'un sous-ensemble propre des suites définissables. L'ensemble de toutes les suites d'entiers est non-dénombrable ; ainsi, la plupart des suites d'entiers ne sont pas dénombrables et ne peuvent pas être définies.
Voir aussi [modifier]
Liens internes [modifier]
Lien externe [modifier]
- Journal des suites d'entiers (en anglais). Les articles sont disponibles librement en ligne.
13:53 Publié dans Suite d'entiers | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
















































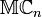
Les commentaires sont fermés.