20/11/2010
Nombre de Liouville
En mathématiques, et plus précisément en théorie des nombres, un nombre de Liouville est un nombre réel x avec la propriété suivante : pour tout nombre entier positif n, il existe des entiers p et q avec Un nombre de Liouville peut ainsi être approché « de manière très fine » par une suite de nombres rationnels. En 1844, Joseph Liouville montra que tous les nombres vérifiant l'inégalité ci-dessus sont transcendants, établissant ainsi pour la première fois l'existence de tels nombres.Nombre de Liouville
 et tels que
et tels que .
.
Sommaire[masquer] |
Remarquons d'abord que si x est un nombre de Liouville, pour tout nombre entier positif n, il existe alors un nombre infini de paires d'entiers (p,q) obéissant à l'inégalité ci-dessus : il suffit en effet de prendre des couples (p,q) associés à des entiers m égaux à kn , ils fournissent k couples La première partie de l'inégalité prouve que ce qui contredit la définition . La constante de Liouville est le réel défini par alors, pour tous les entiers positifs n, nous avons La constante de Liouville est le premier exemple de nombre réel dont on a prouvé la transcendance. La fraction continue est l'outil auquel pense Liouville pour construire des nombres de Liouville et donc transcendants. L'article associé présente un autre exemple de cette nature, illustrant la méthode préconisée par le mathématicien. La mesure irrationnelle d'un nombre réel x mesure la manière d'approcher un nombre par des rationnels. À la place de n'importe quel n permis pour la puissance de q, nous trouvons la borne supérieure de l'ensemble de nombres réels soit satisfaite par un nombre infini de paires d'entiers (p, q) avec q > 0. Pour toute valeur Les nombres de Liouville sont précisément les nombres ayant une mesure irrationnelle infinie. En 1844, Joseph Liouville montra que les nombres avec cette propriété ne sont pas seulement irrationnels, mais sont toujours transcendants (voir la démonstration ci-dessous). Il utilisa ce résultat pour fournir le premier exemple explicite de nombre transcendant : la constante de Liouville définie plus haut. En revanche, bien que chaque nombre de Liouville soit transcendant, tout nombre transcendant n'est pas un nombre de Liouville. Il a été démontré que La démonstration procède en établissant premièrement la propriété des nombres algébriques irrationnels. Cette propriété dit essentiellement que les nombres algébriques irrationnels ne peuvent pas être approchés correctement par les nombres rationnels. Un nombre de Liouville est irrationnel mais n'a pas cette propriété, donc il ne peut pas être algébrique et doit être transcendant. Le lemme suivant est connu habituellement comme le théorème de Liouville sur l'approximation diophantienne, car il existe plusieurs autres résultats connus comme théorèmes de Liouville. Lemme : Si Comme conséquence de ce lemme, soit x un nombre de Liouville ; comme noté dans le texte de l'article, x est alors irrationnel. Si x est algébrique, alors par le lemme, il existe un certain entier n et un certain réel positif A tel que pour tous les p, q Soit r un entier positif tel que ce qui contredit le lemme ; par conséquent x n'est pas algébrique, et est ainsi transcendant. Paul Erdös a démontré1 en 1962 que tout nombre réel pouvait s'écrire comme somme et comme produit de deux nombres de Liouville.Irrationalité des nombres de Liouville [modifier]
 associés à n car
associés à n car .
.
Il est relativement facile de démontrer que si x est un nombre de Liouville, alors x est un nombre irrationnel. Supposons le contraire ; alors il existe des entiers c, d avec 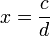 . Soit nun entier positif tel que
. Soit nun entier positif tel que 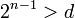 . Alors, il existerait deux entiers p et q tels que
. Alors, il existerait deux entiers p et q tels que .
.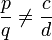 , donc
, donc
Constante de Liouville [modifier]

La constante de Liouville est un nombre de Liouville ; si nous définissons  et
et 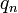 comme suit :
comme suit :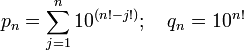
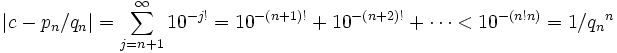
Mesure irrationnelle d'un réel [modifier]
 tels que la propriété
tels que la propriété
 inférieure à cette borne supérieure, l'ensemble de tous les rationnels
inférieure à cette borne supérieure, l'ensemble de tous les rationnels  satisfaisant l'inégalité ci-dessus est une approximation fine de x; réciproquement, si
satisfaisant l'inégalité ci-dessus est une approximation fine de x; réciproquement, si  est plus grand que la borne supérieure, alors il n'existe pas de telles suites qui convergent finement vers x.
est plus grand que la borne supérieure, alors il n'existe pas de telles suites qui convergent finement vers x.Transcendance des nombres de Liouville [modifier]
 est transcendant, mais pas un nombre de Liouville.
est transcendant, mais pas un nombre de Liouville. est un nombre irrationnel qui est la racine d'un polynôme f de degré n > 1 à coefficients entiers, alors il existe un nombre réel A > 0 tel que, pour tous les entiers p, q, avec q > 0,
est un nombre irrationnel qui est la racine d'un polynôme f de degré n > 1 à coefficients entiers, alors il existe un nombre réel A > 0 tel que, pour tous les entiers p, q, avec q > 0, .
.Démonstration de l'assertion [modifier]
 .
. . Soit m = r + n, alors, puisque x est un nombre de Liouville, il existe des entiers a, b > 1 tel que
. Soit m = r + n, alors, puisque x est un nombre de Liouville, il existe des entiers a, b > 1 tel que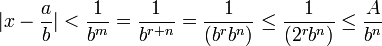
Théorème d'Erdös [modifier]
Annexes [modifier]
Notes et références [modifier]
Voir aussi [modifier]
Lien externe [modifier]
13:57 Publié dans Nombre de Liouville | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
















































Les commentaires sont fermés.