19/11/2010
Troncature
²Troncature
|
|
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
En mathématiques, la troncature est un terme utilisé pour couper le développement décimal d'un nombre à un certain nombre de chiffres après la virgule, ou le développement limitéd'une fonction à un certain ordre.
Sommaire[masquer] |
Par exemple, considérons les nombres réels: Pour tronquer ces nombres à quatre décimales, seuls sont gardés les quatre chiffres après la virgule. Le résultat serait: Remarquons que dans certains cas, la troncature donne le même résultat qu'un arrondi, mais ne correspond pas à un arrondissage par excès; elle découpe simplement les décimales à une position précise (du moins pour les nombres positifs). L'erreur de troncature ne peut excéder deux fois l'erreur maximale d'un arrondi. On peut s'interroger sur l'existence de la troncature d'un nombre négatif a, car alors la disparition des chiffres de a à partir d'un certain rang ne se fait pas grâce à la partie entière de a, mais grâce à la partie entière de -a. La troncature peut être effectuée en utilisant la fonction partie entière. Soit où [a] désigne la partie entière de a. La troncature peut être généralisée à d'autres systèmes que le système de base dix. Par exemple, on peut vouloir tronquer une longueur exprimée en centimètres au pouce près (c'est du pouce du système impérial anglo-saxon dont il s'agit ici). Le résultat sera un nombre de centimètres qui sera un multiple de l'équivalent en centimètre du pouce. Il sera inférieure à la valeur non tronquée et l'erreur de troncature devra être inférieure strictement à la valeur du pouce en centimètres. Pour cela, il existe une formule qui généralise la formule de troncature décimale : où [x] désigne la partie entière de x. Et où a désigne l'unité de troncature. Dans l'exemple de la troncature au pouce près, a vaut 2,54 (un pouce vaut 2,54 centimètres). Avec cette formule, tronquer un nombre à deux décimales (ou à 10 − 2 près) reviendra à prendre 10 − 2 pour valeur de a. Et l'on peut constater facilement, si l'on pose a = 1, que la troncature à l'unité près correspond bien à la partie entière.Troncature d'un nombre [modifier]
Troncature et fonction partie entière [modifier]
 un nombre à tronquer et
un nombre à tronquer et 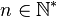 , le nombre de chiffres à garder après la virgule, la troncature dex à n décimales est égale à:
, le nombre de chiffres à garder après la virgule, la troncature dex à n décimales est égale à:![frac{left[ 10^n cdot x right]}{10^n},](http://upload.wikimedia.org/math/2/6/f/26f7520ee495adaae5d771798033e3e7.png)
Généralisation de la troncature [modifier]
![left[frac{x}{a}right] cdot a](http://upload.wikimedia.org/math/0/3/f/03f51a9e8ae0e7400fa385e6b84c5fa4.png)
Voir aussi [modifier]
Troncature d'un développement limité [modifier]
Lien externe [modifier]
07:39 Publié dans Troncature | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook








































Les commentaires sont fermés.