Théorème de Lagrange sur les polynômes : Mathématique

D	L	M	M	J	V	S
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28

« Théorème de Lagrange sur les groupes | Page d'accueil | Multiplicateur de Lagrange »

19/11/2010

Théorème de Lagrange sur les polynômes

Cet article est une ébauche concernant les mathématiques.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Pour les articles homonymes, voir Théorème de Lagrange.

Il s'agit d'un résultat trouvé par le mathématicien Joseph-Louis Lagrange^{[réf. souhaitée]} concernant les polynômes. Soit P un polynôme tel que:

$P(x) = x^n+sum_{i=0}^{n-1}{a_i x^i}$

où les $a i$ sont réels.

Alors si a est une racine de P, a vérifie

$|a| leq 1+max(|a_0|,ldots,|a_{n-1}|).$

Ce théorème reste vrai si les $a i$ et $a$ sont complexes et l'inégalité est même stricte. Mieux : par le théorème de Rouché, le polynôme P admet n racines (comptées avec leurs multiplicités) dans le disque complexe ouvert de centre 0 et de rayon 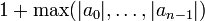$1+max(|a_0|,ldots,|a_{n-1}|)$ , ce qui fournit une preuve du théorème de d'Alembert-Gauss en plus de la majoration annoncée.