19/11/2010
Anneau Z/nZ
En mathématiques, et plus particulièrement en algèbre, Z/nZ est un cas particulier d'anneau, correspondant au calcul modulaire sur les restes des entiers dans la division par n. Tout anneau unitaire contient soit un sous-anneau isomorphe à Z/nZ soit à Z l'anneau des entiers. Cet anneau joue un rôle particulier en arithmétique, il est en effet l'outil de base de l'arithmétique modulaire. L'article Congruence sur les entiers traite le même sujet avec une approche plus didactique et moins exhaustive, tandis que l'article Arithmétique modulaire traite de l'histoire de ce concept, des outils utilisés ainsi que de ses applications.Anneau Z/nZ
Sommaire[masquer] |
La division euclidienne dans Z montre que cet ensemble est un anneau euclidien, en conséquence Z est un anneau principal. Cela signifie que pour tout idéal I de Z, il existe un entier ntel que I est égal à nZ. Comme les idéaux nZ et -nZ sont confondus, il est toujours possible de choisir n positif. Dans toute la suite de l'article n désigne un entier positif. La construction de Z/nZ correspond à la construction générale des anneaux quotients. Ici la relation d'équivalence correspond à la classique congruence sur les entiers. Un élément deZ/nZ est la classe des éléments ayant tous le même reste par la division euclidienne par n. Un élément est identifié par un membre de sa classe, souvent l'entier compris entre 0 et n - 1. Il est parfois noté La théorie des anneaux permet directement de démontrer certaines propriétés de l'anneau. C'est une conséquence directe du fait que Z l'est. Un anneau est principal si et seulement si tous ses ideaux sont principaux. Si un anneau est principal, son quotient par un idéal est aussi principal, or Z est un anneau principal. En pratique et comme pour Z, tous les sous-groupes additifs et tous les sous-anneaux sont aussi des idéaux principaux. Si m est un diviseur de n alors il existe un unique ideal de Z/nZisomorphe à Z/mZ, ce résultat est une conséquence directe de la troisième proposition du paragraphe Théorème fondamental de l'article groupe cyclique. Un anneau est dit de Bézout si et seulement si pour tout élément a et b n'ayant comme diviseurs communs que les éléments inversibles, il existe deux éléments α et β tel que α.a + β.b= 1. Z/nZ est un anneau de Bézout car tout anneau principal l'est. Si n n'est pas premier, alors l'anneau Z/nZ n'est pas intègre, il n'est donc ni euclidien ni factoriel. La structure du groupe (Z/nZ) est celle d'un groupe monogène, c'est-à-dire engendré par un unique élément. Si n est égal à 0 on obtient un groupe isomorphe à Z et à n'importe quel groupe monogène d'ordre infini. Si n est différent de 0, alors le groupe est cyclique, sa structure est explicitée dans l'article détaillé. La logique du théorème chinois s'applique encore, ainsi les propriétés du paragraphe Théorème chinois de l'article Groupe cyclique s'appliquent encore. Il suffit pour les vérifier de valider que le morphisme de groupe utilisé est aussi un morphisme d'anneau. Note : Si u et v ne sont pas premiers entre eux, alors l'anneau produit ne contient pas d'élément d'ordre supérieur au ppcm de u et de v. Cet anneau n'est donc pas isomorphe à l'anneauZ/u.vZ. Cette proposition entraîne une décomposition unique de Z/nZ en facteurs premiers. Le théorème fondamental de l'arithmétique montre que n se décompose de la manière unique suivante: Ou (pi) est une famille de k nombres premiers tous distincts et αi des entiers supérieurs ou égaux à un. Les puissances des nombres premiers du produit sont tous premiers entre eux. Une simple récurrence montre : En effet, cette proposition est une conséquence directe de l'identité de Bézout. Supposons n premier, alors si a est un entier premier avec n, c'est-à-dire non multiple de n, il existe deux entiers b et c tel que : Ce qui signifie que la classe de a est inversible d'inverse la classe de b. Réciproquement si n n'est pas premier, il existe deux entiers a et b différents de n et de 1 tel que leur produit est égal à n. La classe de a ainsi que la classe de b sont des diviseurs de zéro, ce qui n'existe pas dans un corps. Soit A un anneau unitaire, il existe un unique morphisme d'anneau φ de Z dans A qui à 1Z associe 1A. Soit n l'entier positif tel que le noyau de φ soit égal à nZ. La décomposition canonique de φ (cf le paragraphe Morphisme d'anneau de l'article Idéal) montre qu'il existe un sous-anneau de A isomorphe à Z/nZ. Ainsi, tout anneau unitaire contient un sous-anneau isomorphe soit à Z dans le cas où n est égal à 0, soit à Z/nZ. C'est une des raisons qui rend cette famille d'anneau intéressante. Le groupe des unités d'un anneau correspond au groupe multiplicatif formé des éléments inversibles. De tels éléments sont appelés unité. Si m est premier avec n alors il est inversible, sinon soit d un diviseur commun différent de un, soit k l'entier tel que d.k = n, le fait que m.k soit un multiple de n montre que m est un diviseur de zéro et donc est non inversible. Un élément du groupe additif Z/nZ est générateur si et seulement s'il est premier avec n, car son ordre est alors égal à n. Or le paragraphe Indicatrice d'Euler de l'article Groupe cycliquemontre que le nombre d'éléments générateurs est égal à φ(n). Dans le cas où n est premier c'est-à-dire si l'anneau est un corps, la structure est la suivante : En effet, tout élément autre que celui nul est inversible, l'ordre du groupe multiplicatif est donc n - 1. Le groupe multiplicatif est naturellement fini, il admet un exposant e, l'exposant est leplus petit commun multiple des ordres des différents éléments du groupe multiplicatif. Considérons le polynôme de Z/nZ[X] suivant : Xe - 1. Il admet pour racines tous les éléments du groupe multiplicatif donc n - 1 racines différentes. Or tout polynôme à coefficients dans un corps possède un degré supérieur ou égal à son nombre de racines. On en déduit que e est supérieur ou égal à n - 1. Le théorème de Lagrange, qui a pour corollaire le fait que l'ordre d'un élément est un diviseur de l'ordre du groupe, montre que e est égal à n - 1. Pour conclure il suffit de constater que tout groupe abélien fini possède un élément d'ordre l'exposant, cette propriété est démontrée dans l'article détaillé. Le groupe multiplicatif possède un élément d'ordre le cardinal du groupe et qui est donc primitif, ce qui montre que le groupe est cyclique et termine la démonstration. Remarque : un raisonnement de cette nature montre que tout groupe multiplicatif fini d'un corps commutatif est aussi cyclique. Dans le cas où n n'est pas premier, la structure est naturellement celle d'un groupe abélien fini elle correspond donc à un produit de groupes cycliques d'après le théorème de Kronecker. La structure est plus complexe que celle du cas précédent, plusieurs propositions sont nécessaires pour l'expliciter. C'est une conséquence du théorème chinois. Le théorème fondamental de l'arithmétique limite alors l'étude au cas ou n est égal à pr avec p un nombre premier et r un entier strictement positif. Deux configurations se présentent : Tous les cas ne sont pas traités, il reste celui ou p est égal à deux et r est égal à un ou deux. Cependant ces cas sont triviaux, le groupe contient un ou deux éléments et par conséquent est cyclique. Serge Lang, Algèbre [détail des éditions]Construction de Z/nZ [modifier]
Idéaux de Z [modifier]
Anneau quotient [modifier]
 ou
ou  , ainsi dans Z/6Z,
, ainsi dans Z/6Z, 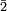 désigne la classe contenant les éléments 2, 8, 14 etc... Quand il n'existe pas d'ambigüité, on utilise simplement la lettre a.
désigne la classe contenant les éléments 2, 8, 14 etc... Quand il n'existe pas d'ambigüité, on utilise simplement la lettre a.
Propriétés [modifier]
Propriétés élémentaires [modifier]
Structure additive [modifier]
Théorème chinois [modifier]

Cas où Z/nZ est un corps [modifier]

Caractéristique d'un anneau [modifier]
Groupe des unités [modifier]
Cas où n est premier [modifier]
Cas où n n'est pas premier [modifier]
Voir aussi [modifier]
Liens externes [modifier]
Références [modifier]
19:06 Publié dans Anneau Z/nZ | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook








































Les commentaires sont fermés.