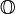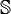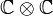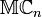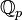20/11/2010
Tessarine
En mathématiques, les tessarines sont une idée introduite par James Cockle en 1848. La notion inclut à la fois les nombres complexes ordinaires et les nombres complexes fendus. Une tessarine t peut être décrite comme une matrice 2 x 2 où w et z peuvent être des quaternions quelconques. Si w et z sont des nombres complexes, on obtient les nombres bicomplexes.Tessarine
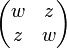 ,
,
Sommaire[masquer] |
Lorsque z = 0, alors t correspond à un nombre complexe ordinaire, qui est w lui-même. Lorsque w et z sont tous deux des nombres réels, alors t correspond à un nombre complexe fendu, w + j z. La tessarine particulière possède la propriété suivante : Son produit matriciel au carré est la matrice identité. Cette propriété a conduit Cockle à appeler la tessarine j un "nouvel imaginaire en algèbre". L'importance de l'anneau commutatif et associative de toutes les tessarines semble avoir eu moins d'importance que cette tessarine particulière ainsi que le plan qu'elle crée au-delà de la ligne réelle. Lorsque w et z sont à la fois des nombres complexes (a, b, c, d réels) alors l'algèbre t est isomorphe aux quaternions coniques Ils sont aussi isomorphes aux nombres bicomplexes (à partir des nombres multicomplexes) de base À noter que j dans les nombres bicomplexes est identifié avec le signe opposé de j à partir de ci-dessus. Lorsque w et z sont à la fois des quaternions (de base Les tessarines, lorsque w et z sont des nombres complexes, forment un anneau commutatif et associatif (différent des quaternions qui ne constituent pas un anneau commutatif). Ils permettent aussi les puissances, les racines et les logarithmes de qui ont leur déterminant / module égale à 0 et par conséquent ne peuvent pas être inversés multiplicativement. De plus, l'arithmétique contient des diviseurs de zéro Les quaternions forment un anneau inversible sans diviseurs de zéro, et peut aussi être représenté par des matrices de forme 2 x 2.Isomorphismes avec les autres systèmes de nombres [modifier]
Nombres complexes [modifier]
Nombres complexes fendus [modifier]

Quaternions coniques, nombres bicomplexes [modifier]


 , de base
, de base  , avec les identités suivantes :
, avec les identités suivantes :
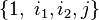 si une identité :
si une identité :
Octonions coniques / sédénions coniques [modifier]
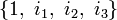 ), alors l'algèbre t est isomorphe aux octonions coniques ; permettant les octonions pour w et z (de base
), alors l'algèbre t est isomorphe aux octonions coniques ; permettant les octonions pour w et z (de base 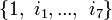 ), l'algèbre résultante est identique aux sédénions coniques.[réf. nécessaire]
), l'algèbre résultante est identique aux sédénions coniques.[réf. nécessaire]Propriétés algébriques [modifier]
 , qui est une racine non réelle de 1. Ils ne forment pas un corps à cause des éléments idempotents
, qui est une racine non réelle de 1. Ils ne forment pas un corps à cause des éléments idempotents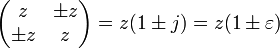
 .
.Références [modifier]
13:52 Publié dans Tessarine | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook