20/11/2010
Nombre multicomplexe
En mathématiques, les nombres multicomplexes, dont l'ensemble est noté Un nombre multicomplexe x peut être écrit de manière unique sous la forme avec Si n= 2, on retrouve les nombres complexes. L'algèbre obtenue est isomorphe à l'algèbre quotient Il est possible d'écrire tout nombre multicomplexe x non nul sous la forme d'une représentation exponentielle Un cas particulier des nombres multicomplexes (pour n = 4) sont les nombres bicomplexes.Nombre multicomplexe
 , forment une algèbre commutative de dimension n sur le corps des nombres réels, engendrée par un élément e qui satisfait
, forment une algèbre commutative de dimension n sur le corps des nombres réels, engendrée par un élément e qui satisfait  (avec n > 1).
(avec n > 1).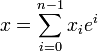
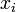 réels.
réels.![frac{mathbf{R}[X]}{(X^n+1)}](http://upload.wikimedia.org/math/f/a/4/fa43dbe4650e2fcf835b5ac16f7e3ab8.png) .
. .
.Références [modifier]
12:18 Publié dans Nombre multicomplexe | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
















































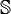
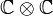
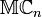 Nombre multicomplexe •
Nombre multicomplexe •