05/12/2010
Nombre de Bell
Nombre de Bell
En mathématiques, le n-ième nombre de Bell, qui porte le nom de Eric Temple Bell, est le nombre de partitions d'un ensemble à n éléments ou, ce qui revient au même, le nombre derelations d'équivalence sur un tel ensemble.
Sommaire[masquer] |
Premières propriétés [modifier]
- Ces nombres forment la suite A000110 de l’OEIS, dont on peut calculer à la main les premiers termes :

Pour le premier, on se convainc qu'il existe exactement une partition de l'ensemble vide : la partition vide, formée d'aucune partie. En effet ses éléments (puisqu'il n'y en a aucun) sont bien non vides et disjoints deux à deux, et de réunion vide.
- Les nombres de Bell peuvent aussi se calculer de proche en proche par la relation de récurrence suivante :
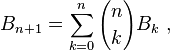
qui peut se démontrer ainsi : ayant fixé un élément x dans un ensemble à n+1 éléments, on trie les partitions suivant le nombre k d'éléments hors de la partie contenant x. Pour chaque valeur de k de 0 à n, il faut donc choisir k éléments parmi les n éléments différents de x, puis s'en donner une partition.
Série génératrice [modifier]
Pour manipuler tous les nombres de Bell, on peut s'intéresser aux séries génératrice et génératrice exponentielle associées, qui sont respectivement :

La première est par exemple1 utilisée pour étudier les classes de congruence des Bn. Quant à la seconde série formelle, elle satisfait l'équation différentielle E'(X) = eXE(X) : on le constate en écrivant la formule de récurrence sous la forme
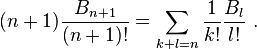
On en déduit qu'elle est égale à  à une constante multiplicative près (qu'on trouve par identification du terme constant) :
à une constante multiplicative près (qu'on trouve par identification du terme constant) :

L'identification des coefficients conduit à la formule de Dobinski :

qui est le moment d'ordre n d'une loi de Poisson de paramètre 1.
D'autres propriétés [modifier]
Ils satisfont également à la congruence de Touchard : si p est un nombre premier quelconque alors
C'est une relation de congruence modulo p.
Chaque nombre de Bell est une somme des nombres de Stirling de deuxième espèce
Plusieurs formules asymptotiques pour les nombres de Bell sont connues ; l'une d'elles est
où W est la fonction W de Lambert ; on obtient une approximation moins précise, mais plus commode d'emploi, à l'aide de l'encadrement lnx − lnlnx < W(x) < lnx ; on pourra également remarquer la similitude de l'approximation précédente avec la formule de Stirling2.
Voir Aussi [modifier]
- Partition d'un entier qui correspond au nombre de partitions d'un ensemble à n éléments indiscernables.
Notes et références [modifier]
- Daniel Barsky et Bénali Benzaghou, « Nombres de Bell et somme de factorielles », dans Journal de Théorie des Nombres de Bordeaux, vol. 16, 2004, p. 1-17 [ [pdf]texte intégral [archive] (page consultée le 1er octobre 2010) ]
- On trouvera d'autres approximations de Bn sur (en) Eric W. Weisstein, Bell Numer [archive], MathWorld..
22:11 Publié dans Nombre de Bell | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook








































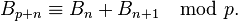

![B_n sim frac{1}{{sqrt n }}left[ {frac{n}{W(n)}} right]^{n + frac{1}{2}} e^{frac{n}{W(n)} - n - 1},](http://upload.wikimedia.org/math/c/d/d/cdd4be64077d749729e8de60d1489596.png)